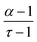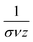Open Access Article
Open Access ArticleBrain-like critical dynamics and long-range temporal correlations in percolating networks of silver nanoparticles and functionality preservation after integration of insulating matrix†
Niko
Carstens
 a,
Blessing
Adejube
a,
Thomas
Strunskus
a,
Franz
Faupel
a,
Blessing
Adejube
a,
Thomas
Strunskus
a,
Franz
Faupel
 a,
Simon
Brown
a,
Simon
Brown
 b and
Alexander
Vahl
b and
Alexander
Vahl
 *a
*a
aInstitute for Materials Science, Chair for Multicomponent Materials, Faculty of Engineering, Kiel University, Kaiserstraße 2, D-24143 Kiel, Germany. E-mail: alva@tf.uni-kiel.de
bThe MacDiarmid Institute for Advanced Materials and Nanotechnology, School of Physical and Chemical Sciences, Te Kura Matū, University of Canterbury, Private Bag 4800, Christchurch 8140, New Zealand
First published on 10th May 2022
Abstract
Random networks of nanoparticle-based memristive switches enable pathways for emulating highly complex and self-organized synaptic connectivity together with their emergent functional behavior known from biological neuronal networks. They therefore embody a distinct class of neuromorphic hardware architectures and provide an alternative to highly regular arrays of memristors. Especially, networks of memristive nanoparticles (NPs) poised at the percolation threshold are promising due to their capabilities of showing brain-like activity such as critical dynamics or long-range temporal correlation (LRTC), which are closely connected to the computational capabilities in biological neuronal networks. Here, we adapt this concept to networks of Ag-NPs poised at the electrical percolation threshold, where the memristive properties are governed by electro-chemical metallization. We show that critical dynamics and LRTC are preserved although the nature of individual memristive gaps throughout the network is fundamentally changed by filling the gaps with an insulating matrix. The results in this work generate important contributions towards the practical applicability of critical dynamics and LRTC in percolating NP networks by elucidating the consequences of NP network encapsulation, which is considered as an important step towards device integration.
Introduction
Conventional computer technology is facing fundamental limitations, which are related to hardware architecture (von-Neumann bottleneck), the integration density of transistors (envisioned end of Moore's law) and a tremendous increase in estimated power consumption. These limitations have greatly stimulated the research into novel and unconventional computation concepts.1 The field of neuromorphic engineering aims to solve these challenges by designing novel types of computational hardware, which draw inspiration from biological principles like signal thresholding, synaptic plasticity, parallelism and hierarchy or in-memory computing.2 In the past decade, memristive devices played a key role as fundamental building units in the design of neuromorphic hardware and significant effort was focused on mass integration of memristive devices on wafer scales.3–6 The key characteristic of a memristive device is its reconfigurable resistance state. Among different types of memristive devices, filamentary switching devices based on electrochemical metallization (ECM) principles7 are of special interest. The major working principle of this type of memristive devices is the reconfiguration of metallic filaments in nanoscale switching gaps in response to the application of external voltage or current stimuli. Accordingly, the conductance of the nanogaps is determined by the state of the metallic filament. Diverse switching dynamics such as non-volatile filamentary switching,7 diffusive switching8 or highly dynamic spiking behavior9,10 have been reported. However, the creation of networks of memristive devices approaching brain-like complexity via traditional top-down fabrication technologies poses several challenges as the performance of each memristive device and the enormous degree of connectivity within the network has to be under precise control.1 In view of these challenges, fabrication of neuromorphic devices based on self-assembly approaches appears to be a promising and feasible alternative route.11,12 Such devices are typically implemented via the formation of a complex network of memristive gaps with a stochastic distribution. In these networks, the emerging collective dynamical is exploited. Following such approaches neuromorphic functionalities can be implemented, circumventing the necessity of a precise wiring, spatial assembly, and tailoring of switching characteristics of individual memristive units. Such approaches turned out to be feasible for reservoir computing, where complex dynamical systems showing short-term memory and spatio-temporal correlations are required.13–16 Recently several reports have shown the existence of different potential building units from which complex emergent networks can be formed. Networks assembled from Au-NPs above the percolation threshold exhibit complex memristive switching patterns, which are caused by atomic rearrangements between adjacent Au-NPs induced by electrical currents.17 Networks of polymer-coated Ag-nanowires formed by random self-assembly also show emergent dynamics applicable for the design of neuromorphic systems.18,19Recently, the technical implementation of critical dynamics in neuromorphic systems via self-assembled networks of memristive switches gained considerable interest. This is motivated by findings from neuroscience indicating that biological neuronal networks operate in a regime of critical dynamics, which is seen as beneficial for solving computational tasks efficiently.20 The presence of critical dynamics in biological neuronal systems was supported by the fact that spontaneous neural activity in cortical tissues takes place via brief bursts separated by periods of highly reduced activity, so-called “neural avalanches”.20,21 Experimental observations of this avalanche activity in cortical neuron tissues from rats suggest that avalanches exhibit scale-invariant dynamics where the occurrence of different avalanche sizes can be described by a probability distribution in the form of a power law.21 The origin of such behavior is frequently related to self-organized criticality. Self-organized criticality can be seen as a generating mechanism for avalanches and associated scale-invariant dynamics.22
In general, critical dynamics universally occur in systems which are poised at the transition between two phases, which are composed of a multitude of dynamical units that influence each other.20 There, a macroscopically observed avalanche may be triggered by a microscopic local change in the system that is collectively passed along the system due to the mutual interaction between single units. Several computational benefits have been described for this state, including the maximization of dynamic range, signal transmission and information capacity.23 Based on this, it was hypothesized that the brain also operates at the edge of the transition between complete ordering and disordering.24 With regard to memristive systems, hints on critical dynamics were found in networks of metal-insulator-metal switches (Ag–Ag2S–Ag). This network showed spatially distributed switching throughout the network and power-law scaling of persistent metastable network states.25 Recently, networks of Sn-NPs poised at the electrical percolation threshold (a second order phase transition) were shown to exhibit critical dynamics with corresponding avalanche patterns similar to those observed in neural tissues.26 Critical dynamics in random networks of memristive switches are expressed by scale-invariance in dynamic features of the network. These dynamic features include the fluctuations in magnitude and temporal structure of network conductance that originate from the underlying memristive activity. Moreover, fluctuations of the network conductance are organized in avalanche patterns, which indicates that the memristive activity in the network is correlated. Characteristic for critical dynamics are scale-invariant distributions of avalanche sizes and durations.26 Further, those networks implement long-range temporal correlations (LRTC), which is commonly a concomitant feature of critical dynamics. LRTC is a dynamical feature of a system, describing that the past activity of the system determines the future activity at any given time, which indicates capabilities to implement a dynamical memory. Such a dynamical memory is beneficial for mapping of temporal information into a system, a property that is important in the context of reservoir computing.15,16 One common procedure for proving the presence of LRTC in a system is to demonstrate a power-law decay of the autocorrelation functions in the time domain.27 Another indication for LRTC can be found by scale-invariant fluctuations in the network activity, also in the time domain. In this connection, detrended fluctuation analysis (DFA) is a frequently used method to characterize such scale-free fluctuation and to demonstrate LRTC.28 Because of the dynamical memory properties, LRTC is seen as beneficial for neuromorphic computation approaches.16 To implement critical dynamics and LRTC, both features that suggest brain-like degree of complexity, into neuromorphic systems tailoring the connectivity (by poising at the percolation threshold) within networks of NP-based memristive switches appear to be a feasible strategy. However, the practical applicability of this approach can be still debated and also the understanding of the origin of the emergent phenomena has to be improved. Particularly, an elaboration of this concept towards composite systems is still missing so far and would be beneficial to support practical applicability.
In this work, we extend the concept of implementing critical dynamics and LRTC for neuromorphic systems via Ag-NPs networks poised at the electrical percolation threshold (in the following named as “percolating NP networks”) and address the question how filling the memristive gaps in the network with an insulating matrix influences the network dynamics and applicability. The use of Ag-NPs in this work is motivated by the fact, that the nanoscale behavior of Ag-NP-based memristive gaps is already well-understood,8,29 which provides suitable complementary knowledge for future development, aiming to understand the emergence of collective phenomena in random memristive networks. A Haberland-type gas aggregation source (GAS)30 was used for the vapor phase synthesis of Ag-NPs. Generally, a GAS offers a broad choice between elemental and alloy NPs and good control on the properties,31 which allows to extend the engineering of memristive gaps towards Ag-based alloy NP systems with enhanced stability and degree of freedom.29 For the practical application of percolating NP networks in neuromorphic systems maintaining their functionality within a composite system is highly relevant. This is because encapsulation of the network into an insulating medium is in most cases an inevitable step of electronic device integration. However, there is only insufficient knowledge about the consequences on the overall network dynamics, when the character of the underlying memristive units are fundamentally altered by filling the gaps with an insulating material. This is because critical dynamics of percolating NP networks reported so far were in an exposed scenario, i.e. without encapsulation of the network. Although several reports on the electronic properties of composite systems comprising percolating NP networks exists,32,33 a connection between the brain-like dynamics (i.e. critical dynamics and LRTC) and integration of percolating NP networks into insulating matrices has not yet been made. In particular, this poses questions regarding to the consequences for the network functionality (and therefore practical applicability), when the nature of the memristive gaps throughout the network is fundamentally altered by filling the gaps with an insulating matrix. Therefore, we fabricated exposed percolating NP networks and compared them with similar networks, which were covered with ceramic layers of SiOxNy. Comparing both network types, the nature of the memristive gaps is changed from air-type (for exposed NPs) to solid-state-type (for embedded NPs). Characterization of percolating NP networks is done by evaluating their temporal patterns of memristive switching activity in response to a constant stimulus (voltage input) towards hallmarks of brain-like behavior, such as critical dynamics21 and LRTC.27 For the quantification of LRTC, autocorrelation functions34 and detrended fluctuation analysis28 were applied. Critical dynamics in the network activity is demonstrated by the emergence of scale-invariance and the according power laws in dynamical network features. Particularly, this requires an avalanche analysis analogous to approaches used in neuroscience.21 The main focus of this work is to demonstrate, that the network behavior applicable for neuromorphic systems (i.e. critical dynamics and LRTC) is preserved when an insulating matrix is added to the percolating NP network.
Results
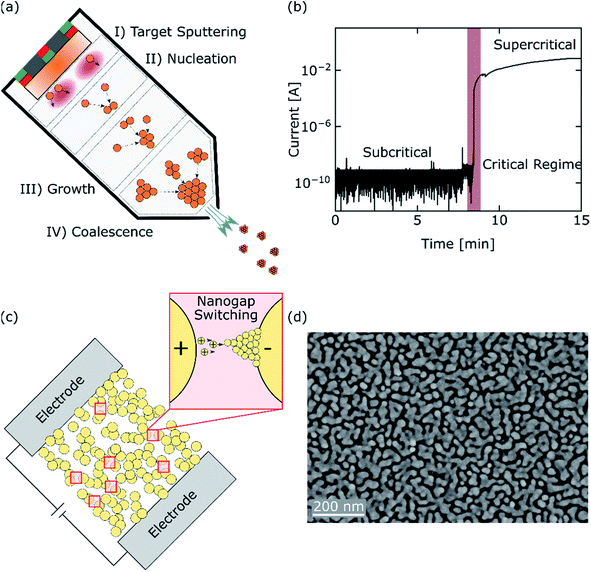
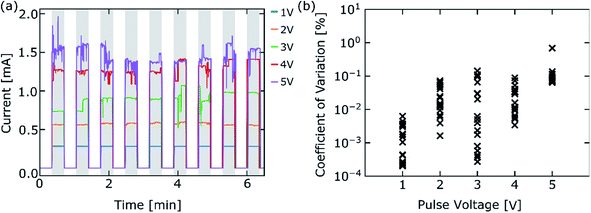
Fig. 1 summarizes the fabrication route and illustrates morphological properties of percolating NP networks, as investigated in this work. Ag-NPs are synthesized following the GAS technique, as illustrated in Fig. 1a. Ag atoms are sputtered by a DC magnetron from a metallic target into a high-pressure sub-chamber leading to a vapor phase aggregation of NPs and transport along the pressure gradient from the GAS into a deposition chamber. High-resolution TEM images of individual Ag-NPs can be found in the ESI S1.† Networks of Ag-NPs were deposited onto lithographically structured Si wafer pieces with multiple electrode. The lateral filling fraction of the Ag-NPs corresponds to the electrical percolation threshold. To achieve this, the network conductance was monitored in situ during the deposition of Ag-NPs and the deposition was stopped after the onset of conduction, aiming for the critical dynamical regime.26 This is elucidated in Fig. 1b, which shows the measured current flowing through the network during the deposition process with increasing Ag-NP filling fraction. The deposition of Ag-NPs was stopped at the steep slope of current increase (i.e. at the electrical percolation transition). For those samples in this work, where the dynamics were studied under the presence of an insulating matrix, networks were subsequently covered by a SiOxNy layer (from reactive magnetron sputter deposition) in the same vacuum system.A schematic illustration of percolating NP networks is shown in Fig. 1c. In the critical regime around the percolation threshold, there is no conducting path of the size of the whole system scale, but a multitude of memristive gaps is randomly distributed through the whole network. It has been previously reported that NP networks poised at the percolation threshold have scale-free morphological properties, meaning that the number of potential memristive gaps per group of electrically connected NPs follows a power law distribution.16 This means the conductance of percolating NP networks is not determined by a persistent conductive path, but by the states of all memristive gaps throughout the network. The state of memristive gaps are prone to be resistively switched by electrochemical metallization (ECM) upon application of external voltage stimuli. A SEM image showing the real morphology of a percolating NP network without matrix is given in Fig. 1d. An outline of the electrical behavior of percolating NP networks is given in Fig. 2a. There, a percolating NP network without matrix was tested under application of voltage pulses with varying amplitude. The current levels in response to external stimulation of 1 V can be interpreted by a persistent network state with stable conductance. This is reasoned by the fact, that fluctuations of the current level are too low to discriminate them against noise. In contrast to the response from 1 V pulses, the current levels exhibit distinct jumps between different levels at higher voltage amplitudes. These jumps originate from resistive switching activity of the memristive gaps, distributed through the whole network. Electrical fields across the memristive gaps are able to induce the formation or disintegration of filaments, switching the gaps to a conducting or insulating state, respectively.35 Accordingly, resistive switching events, which are occurring in individual gaps, are changing the overall state of the network (in terms of conductance). We denote a distinct change of network conductance (which can be clearly discriminated against noise) as a network transition event. The exact definition of a network transition event used in this work is given in the methods part. While comparing the network responses at different voltages, it can be seen that the richness of network transition events appears to increase with the applied voltage, meaning that the frequency and magnitude of network transition events becomes larger with increasing the voltage amplitude. We quantified this observation by the coefficient of variations CV (ratio of standard deviation to the mean) calculated for the current responses from each individual pulse (see methods). By this, CV characterizes the fluctuation of network conductance observed within one applied voltage pulse. A scatter plot of the CV for nine pulses plotted against pulse voltage is given in Fig. 2b, which indicates that the fluctuation of the network conductance levels increase with voltage amplitude. This can be related to the typical threshold behavior of filament-type memristive gaps. It is commonly reported for Ag-based NP memristive switching8,29 and individual Ag-filaments in a nanogap10 that they exhibit a threshold behavior in their switching dynamics. The origin of such a threshold behavior mainly comes from the underlying cation mobility and redox processes.7 Presumably, the threshold behavior of the macroscopic percolating NP network is a reflection of the underlying threshold mechanisms of individual memristive gaps. The presence of a threshold behavior for switching activity was similarly observed in networks with insulating matrix, as illustrated in the ESI S2.†
Long-term sequence of network transition events
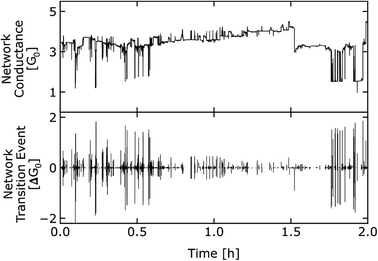
The percolating NP networks are investigated towards the emergence of brain-like dynamics (critical dynamics and LRTC) in their electrical response. A particular focus lies on the question whether the existence of an insulating matrix (filling the memristive gaps) changes the network functionality. For this purpose, in total six percolating NP networks were fabricated and an SiOxNy matrix was added to three of them. The other three samples remained exposed. To acquire the network dynamics (i.e. the temporal sequence of network transition events), long-term current measurements over similar measurement times of ≈11.5 h were conducted (see methods). All samples were stressed with the same external bias level of 5 V. A representative time window of 2 h of the current response for a network without matrix is plotted in Fig. 3 (top). It illustrates the complex memristive switching pattern with a multitude of transitions between different conductance states. For the sake of convenience, values related to the network conductance are given in units of conductance quantum G0 = 7.748 × 10−5 S. Values in the order of G0 are typical for percolating NP networks and emerges in the limit where the conductance is limited by nanoscale gaps and corresponding atomic scale filaments.36 Microscopically the observed pattern results from the complex and recurrent interconnectivity of a large number of memristive gaps in the network. A memristive switching event locally at a certain gap leads to a redistribution of the electrical fields within the network, which in turn could trigger switching at other gaps. By this, disturbance of one memristive gap could lead to a prolonged cascade of transitions between multiple metastable conductance states of the whole network. This mechanism leads to the characteristic avalanche behavior of percolating NP networks. A thresholding routine (see methods) was applied to the temporal sequence of conductance changes to extract the network transition events and to discriminate them against noise. In particular, all transition events below 0.01 G0 were omitted, which is above the noise level of the measurement setup. By this, all network transition events contributing to the evaluation are real effects from the samples and noise effects from the measurement setup are excluded. Illustrations of the thresholding procedure are further given in the ESI S3 and S4.† The temporal sequence of network transition events resulting from the 2 h window displayed in Fig. 3 is shown in the bottom panel. A first glance suggests that the network transition events appear to be more clustered than it would be expected by chance. This is a first indication on temporal correlations and avalanche-like dynamics in the temporal sequence of transition events.Long-range temporal correlations
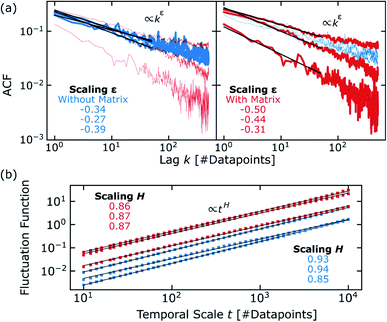
In biological neuronal networks, information is present in collective activity patterns showing self-affine properties and presence of LRTC.27 Furthermore, LRTC is a phenomenon that frequently coexists with critical dynamics of biological neuronal networks.27 To identify self-affine properties and LRTC in the temporal sequence of network transition events, temporal correlations were quantified by two different methods: autocorrelation functions (ACFs) and detrended fluctuation analysis (DFA). The ACFs shown in Fig. 4a suggests a slow correlation decay in the form of a power law, which implies that network transition events in the past have a significant influence on current events. Such a behavior is considered as a long-term memory in temporal processes.28 In addition, calculating the ACFs of shuffled temporal sequences of network transition events results in complete destruction of any correlation (see ESI S5†). Decay slopes ε of the ACFs were determined via linear regression in a shorter range until a lag k of 50 data points and showed that the slopes for percolating NP networks with insulating matrix tend to be only slightly higher than for networks without. More importantly, the presence of autocorrelation remains, even after addition of an insulating matrix. We note that the comparison in ACFs between networks with and without matrix is elaborated here based on a representation until a maximum lag of 500 data points, however, we emphasize that autocorrelation is still existent in all samples up to higher lags too (see ESI S6†).The second method, DFA, is an already well-established tool in neurobiology to detect LRTC in neural oscillations and to find estimations for the Hurst exponent.28 In this context, Hurst exponents are used to determine whether neuronal activity is positively or negatively correlated and to quantify the extent of temporal correlations.28 The major advantage of DFA is that it can be applied to non-stationary temporal sequences. Since it is expected that critical dynamics imposes a considerable non-stationarity (due to the characteristically occurring avalanches, as described in the next sections), we applied DFA to the temporal sequence of network transition events to gain insights that are complementary to the ACFs. The results of the DFA, which are log-log plots of the fluctuation function (quantifies the temporal fluctuation of network transition events, see methods or ref. 28) versus temporal scale t (window size as number of data points showing the degree of fluctuation, see methods or ref. 28) where the linear scaling H is an estimation of the Hurst exponent. The DFA results are given in Fig. 4b. Here, the Hurst exponent describes correlations in the activity (i.e. temporal sequence of network transition events) of the percolating NP networks, analogously to approaches from neuroscience. Power law scaling is observed for the whole observed range indicating strong LRTC. Moreover, the magnitudes of Hurst exponents confirm positive correlations for all samples, as already observed from the ACFs.28,34 Conducting the DFA with shuffled temporal sequences also leads to destruction of any temporal correlation, which is expressed by a strongly decreased Hurst exponent (see ESI S7†). The DFA supports the most important observation from the ACF analysis regarding the impact of adding an insulating matrix for the network functionality. Only minor variations on the qualitative level (networks with matrix exhibit slightly higher fluctuation functions and lower Hurst exponents) can be supposed, however, the presence of strong positive correlations does not considerably change after addition of an insulating matrix.
Scale-invariant dynamics
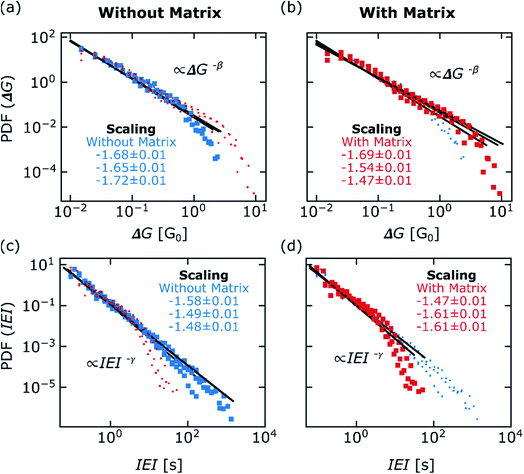
Further evaluation with respect to brain-like dynamics in percolating NP networks with and without matrix is dedicated to power-law behavior and occurrences of avalanches. For this purpose, the statistical features of thresholded network transition events (see Fig. 3 bottom for representative illustration) were investigated. This includes the magnitude of a network transition event ΔG, given as absolute change of network conductance. Further, the temporal structure of the network transition events was quantified by interevent intervals IEI, which is the time between two consecutive events. Probability density functions (PDFs) of the extracted magnitudes of network transition events are plotted together with the according power law fits (by maximum-likelihood method) in Fig. 5a and b. The power law fits show good agreement to the observed PDFs over the whole experimental range. To confirm the existence of heavy-tails in the distributions, likelihood-ratio tests37 including the whole observed range were applied to test the power law fitting against a potentially better description by exponential PDFs. For all samples, power law fits were statistically more significant than exponential fits, which underlines the scale-invariance of the ΔG distribution over the observed range. A scale-invariant distribution of network transition events ΔG indicate, that numerous gaps distributed all over the network are involved in the observed dynamics. The calculated power law exponents β are describing the scaling of ΔG for the six samples and show close similarities. They were determined as 1.68, 1.65 and 1.72 for networks without and 1.69, 1.54 and 1.47 for networks with insulating matrix.Furthermore, PDFs of the extracted IEIs together with the according power law fits involving the whole observed range are given in the panels of Fig. 5c and d. Again, likelihood-test confirmed that power laws are more significant representations of the data than exponential PDFs. The occurrence of scale-invariant IEI distributions is, besides the results from ACFs and DFA, another characteristic for a temporally correlated structure. We note that the observed range of IEIs for percolating NP networks without insulating matrix extends over 4 orders of magnitude, as given in Fig. 5c, whereas the observed range in case of existence of an insulating matrix is narrower, with a stronger truncation at higher IEI values. However, this is likely to be an effect of slightly higher event rates observed for networks with insulating matrix, as discussed in the ESI S8.† The power law exponent γ describes the scaling of IEIs. γ ranged from 1.48 to 1.58 for networks without insulating matrix and from 1.47 to 1.61 for networks with insulating matrix. Taking into account that the power law exponents β and γ, describing the magnitudes and temporal structures of network transition events, respectively, are closely similar, the results indicate that all samples behaved in a similar way.
Avalanche analysis
Fig. 6 depicts the evaluation of the temporal sequence of network transition events with respect to avalanches. The evaluation scheme for avalanche was adapted from approaches in neuroscience.21 For avalanche analysis, the temporal sequence is cut into time bins, which have the size of the mean value of all IEIs. An avalanche is defined by a sequence of time bins where each bin shows at least one network transition event. Then, avalanche sizes S and durations T are defined as number of network transition events and number of time bins within one avalanche, respectively. The observed PDFs of avalanche sizes S together with the according power law fits over the whole observed range are shown in Fig. 6a and b. Plots of the observed PDFs for avalanche durations T are shown in Fig. 6c and d, again with power law fits over the whole observed range. In these plots, τ and α denote the power law exponents of avalanche sizes and durations, respectively. The representation scheme and color codes are the same as in Fig. 5. Likelihood-ratio tests including the whole observed range again showed that power laws are better descriptions for avalanche size and duration PDFs than the exponential form. To extract the power law exponents from avalanche size and duration PDFs, lower bounds xmin (see methods) were estimated to account for the apparent deviations from power law behavior at small scales. To estimate suitable bounds in the low value regime, we followed the guidelines developed in ref. 37 and 38. The power law exponents together with standard errors as uncertainties, which were calculated under application of a xmin value, are given as insets in the plots of Fig. 6. The corresponding fits of values above xmin are provided in the ESI S9.†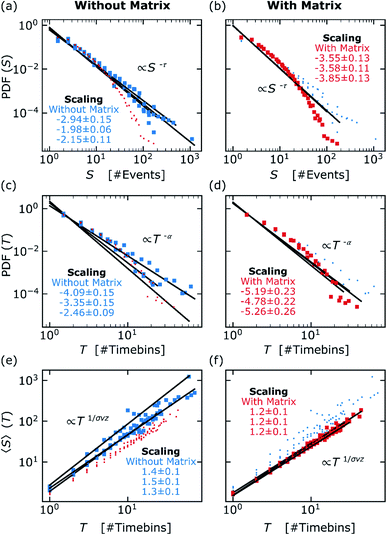 | ||
Fig. 6 Analysis of the temporal sequence of network transition events towards avalanches. Color code for samples without/with insulating matrix is blue/red. (a) and (b) show the PDFs of avalanche sizes S together with a maximum-likelihood power law fit over the whole observed range for samples without and with insulating matrix, respectively. The power law exponents τ noted within the plots were not calculated based on (the shown) fits over the whole range, but under application of a xmin value. Reduced plots showing the fits above xmin, which were decisive for extracting the exponents τ, are given in the ESI S9.† The uncertainties given for the power law exponents equals the standard error. (c) and (d) show the PDFs of avalanche durations T following the same evaluation scheme, as for avalanche sizes. (e) and (f) show the dependence between mean avalanche size S(T) and avalanche duration T. From these slopes, the characteristic power law exponents 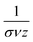 were extracted by linear regression for each sample. were extracted by linear regression for each sample. | ||
Differences in the avalanche statistics between percolating NP networks with and without insulating matrix are becoming apparent. Firstly, the probability for larger scale avalanche sizes and durations is higher for networks without insulating matrix. Secondly, different tendencies in the calculated power law exponents were observed. The power law scaling τ for networks without insulating matrix were 2.94, 1.98 and 2.15 whereas the scaling was steeper for networks with insulating matrix (3.55, 3.58 and 3.85). The same tendency was observed for avalanche durations where values for α were estimated as 4.09, 3.35 and 2.46 for networks without and 5.19, 4.78 and 5.26 for networks with insulating matrix.
In order to characterize another property of critical dynamics,39,40 the dependence between the mean avalanche size S(T) for given durations T is plotted, as shown in Fig. 6e and f. From this, the characteristic power law exponent 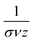 can be extracted via the slope of S(T). For percolating networks without insulating matrix, the mean avalanche size for a given duration scales with 1.4, 1.5 and 1.3, whereas the scaling was 1.2, 1.2 and 1.2 for networks with insulating matrix. According to theory, the power law exponent for avalanche size τ and durations α are connected to
can be extracted via the slope of S(T). For percolating networks without insulating matrix, the mean avalanche size for a given duration scales with 1.4, 1.5 and 1.3, whereas the scaling was 1.2, 1.2 and 1.2 for networks with insulating matrix. According to theory, the power law exponent for avalanche size τ and durations α are connected to 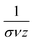 via the crackling noise relationship:39,40
via the crackling noise relationship:39,40
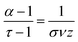 | (1) |
An overview of the evaluation of this relationship for all samples is given in Table 1. Although the theoretical crackling noise relationship is not perfectly met by most of the samples, the experimentally determined values are in reasonable agreement, with only one sample without insulating matrix (sample 2) as exception. However, we note that this does not change the representative character of sample 2, because it exhibits all more significant hallmarks on critical dynamics (LRTC, scale-invariant network dynamics and avalanches) in line with all other samples. Generally, the evaluation of the crackling noise relationship crucially requires accurate estimations of the exponents α and τ, which could not have been the case for sample 2. Nonetheless, the crackling noise relationship provides additional support, that critical dynamics are observed in percolating NP networks without matrix, as well as for networks where an insulating matrix was added.
Discussion
The results in this work demonstrate that the implementation of brain-like behavior, such as critical dynamics or LRTC, via NP networks poised at the percolation threshold is feasible for a broader range of material systems. In contrast to similar NP-based memristive networks in the literature,26,41 the memristive activity Ag-NP based networks presented here is expected to be significantly dominated by electrochemical metallization (ECM).8,35,42 More importantly, the comparison between percolating Ag-NP networks with and without a SiOxNy matrix shows, that the switching dynamics is preserved after the addition of an insulating matrix. Similar network behavior, in terms of temporal correlations in the sequence of network transition events, scale-invariance of dynamical features like magnitudes of network transition events and interevent intervals and presence of scale-invariant avalanches, was observed in both systems. This indicates that the collective behavior of memristive gaps is preserved upon addition of SiOxNy. These observations lead to important implications regarding the practical application of percolating NP networks. The results imply that tailoring the network connectivity (which is done here by the electrical percolation threshold) and insulating matrix integration (through addition of a ceramic layer) can be treated as independent from each other in the fabrication procedure. This is highly beneficial, because the establishment of network functionality (i.e. critical dynamics and LRTC) still solely requires tailoring of the NP filling factor and a deliberate insulating matrix integration does not considerably affect these functionalities.From a general point of view, the dynamics in a system of highly interconnected dynamical units crucially depends on the underlying network connectivity23,43 and dynamical properties of the individual units,44,45 which makes both features important for the engineering of critical dynamics and LRTC in memristive material systems. Regarding the properties of individual memristive gaps, it can be expected that their dynamics are governed by a volatile character. This can be argued from the fact that rather low currents are flowing through individual gaps during formation of filamentary structures, which commonly leads to formation of thin (and therefore volatile) filaments.10,29 Comparable volatile dynamics were, for instance, also observed for Ag/PVP/Ag cross-points in Ag-nanowire networks.46 Moreover, it is expected that the memristive gaps do not behave uniformly, but that the degree of volatility underlies a certain variance. This is reasoned by the fact, that the time for spontaneous decay of a filament strongly depends on parameters like the filament thickness or curvature on the filamentary structures, which was comprehensively described for the dynamics in Ag-nanowire/silk/Ag-nanowire cross-point structures.47 The observed similarity in the critical dynamics and LRTC of both systems is to a certain degree surprising, because the underlying ECM-based physical mechanisms, by which filaments within the memristive gaps are formed and disintegrated,8,29,48 are presumably altered upon addition of an insulating layer like SiOxNy. Consequently, the dynamical properties of individual memristive gaps are also expected to be altered. Major consequences of adding a matrix would include for instance, that the migration of Ag+-species is now enabled within a volume instead of migration on a surface (when a matrix is missing). Furthermore, the interfacial energies of filaments and diffusivity of Ag-species, which affects filament morphology, are altered.8,47 Although the conditions, that are responsible for the memristive gap dynamics, are different for percolating NP networks with and without matrix, our results suggests that the underlying dynamics behave similarly. A possible explanation for this can be provided from a kinetic point of view, under the assumption that a common rate determining mechanism influences the dynamics of both systems similarly. According to literature,35,42 the ECM-based memristive dynamics of filamentary Ag-structures can be kinetically limited by one of three different mechanisms, which contribute to the formation of filaments: Nucleation at cathodic sites (which initiates filamentary growth), migration of Ag+-species across the gap or electron-transfer at the Ag-gap interface during electrochemical oxidation. If one of these three mechanisms is rate limiting for the percolating NP networks with and without matrix, from a kinetic viewpoint, this mechanism could determine the dynamics equally in both systems. We expect that rate limitation by nucleation does not play a role for percolating Ag-NP networks, because a growing filament and a cathodic site will be the same metal, which consequently excludes any significant nucleation barrier. Further, the migration of Ag+-species across the gaps is not considered as a common rate-determining step, because surface migration (networks without matrix) and volume migration (with matrix) are expected to behave kinetically different. Only the electron-transfer rate at the Ag-gap interface, mainly depending on the kind of active metal, could contribute similar kinetics to both systems. Reasoning from a kinetic point of view, a common rate determining mechanism will most likely result in a similar behaviour of both systems. We thus propose that a similarity in the electron-transfer rate of both systems (with and without insulating matrix) could be an explanation for the similarity in the observed dynamics.
Conclusion and outlook
In conclusion, we expand the concept of implementing brain-like critical dynamics and LRTCs via percolating NP networks for neuromorphic applications26 towards Ag-NP based systems, where the memristive gap dynamics is governed by electrochemical metallization. The network dynamics were characterized via ACFs and DFA (indicating the existence of LRTCs) and analysis of scale-invariant dynamical features and avalanches (indicating critical dynamics). More importantly, it was shown that these functionalities are preserved, when insulating SiOxNy matrices were added onto the percolating NP networks, which fundamentally changes the nature of memristive gaps from air-type to solid-state type. This was supported by the absence of qualitative differences in the critical dynamics and LRTCs of networks with and without matrix. Both systems exhibited long-range temporal correlations in the sequence of network transition events, scale-invariance of dynamical features like magnitudes of network transition events and interevent intervals and presence of scale-invariant avalanches. These findings strengthen the prospects regarding to practical applicability of percolating NP networks in neuromorphic systems, because embedding the system (which must be carefully poised at the percolation transition) without functionality loss is inevitable for a potential device integration procedure. For future progress in this field, we suggest to combine the understanding of nanoscale Ag-based electrochemical memristive switching dynamics (which has been extensively studies in a broad range of materials systems) with network science approaches, to model the collective network behavior. This may allow for understanding of the emergent features observed here for the percolating Ag-NP networks, and especially may elucidate further details on the impact of an insulating matrix.Materials and methods
Preparation of percolating NP networks
Conventional UV lithography processes (application of image reversal photoresist and a lift-off process) were used to fabricate electrode structures on commercial Si-wafers with 1 μm thick thermal oxide (Siegert Wafer), as illustrated in the ESI S10.† Either Au or Pt in combination with an adhesion promoter were used as electrode materials (thickness varied between 50 nm and 80 nm) due to their electrochemical passivity. A custom-built Haberland-type GAS30 attached to an in-house high vacuum deposition setup was used for the deposition of the Ag-NPs to build up the network in the spacing (∼10 μm) between the electrodes. During the deposition of the Ag-NPs a potential of 3 V was applied across the electrodes and the current was monitored continuously using a Keithley 2450 source measure unit and an electrical feedthrough system. The deposition of Ag-NPs was stopped by a shutter system after detection of the electrical percolation transition (see Fig. 1b where the electrical percolation transition becomes apparent at around 8.5 min). When required, the insulating matrix was deposited from another DC magnetron in same deposition chamber without breaking the vacuum by reactive sputtering from a Si target and under a gas mixture of 50 sccm Ar and 0.44 sccm N2. Qualitative XPS analysis (see ESI S11†) indicates that the resulting matrix material is silicon oxynitride, formed by oxidation subsequent to the deposition. The effective thickness of the covering matrix was 22 nm. The SEM micrograph that was taken from a percolating NP network without matrix deposited on an electrode structure as described above, conducted on a Zeiss Ultra Plus microscope.Measurement of network dynamics
For the present study, the dynamics of 6 percolating Ag-NP networks was probed with 3 samples having no matrix and 3 samples having a silicon oxynitride matrix. To probe the network dynamics, the samples were measured by continuous detection of the current response (with 84 ms temporal resolution) to the application of a constant DC bias using a Keithley 2400 source measure unit. For each of the 6 samples, a continuous long-term measurement of ≈11.5 h under a DC potential of 5 V was performed. The data in Fig. 2a was acquired under pulsed stimulation (with high levels at different amplitudes ranging from 1 V and 5 V and a low level of always zero) with a pulse width of approximately 20 s.Coefficient of variation
The coefficient of variation (CV) was applied to characterize the fluctuations of current levels observed during the pulse stimulation measurement, as shown in Fig. 2a. The CV was calculated for the current data acquired at each pulse and is given as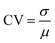 | (2) |
Autocorrelation function
The autocorrelation function (ACF) ρk of a discrete temporal for a given lag k can be estimated as34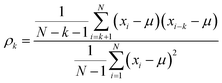 | (3) |
Detrended fluctuation analysis
Detrended fluctuation analysis (DFA) was used as a second method to characterize temporal correlations and self-affinity in the temporal sequence of (non-thresholded) absolute conductance changes. The major advantage of DFA is that influences from non-stationaries (which are expected for the present data due to alternating periods with avalanche activity and absent activity) are reduced in the quantification. The following DFA algorithm according to ref. 28 was applied, which can be used to extract the Hurst coefficient H of a discrete time series:Firstly, the mean subtracted cumulative sum series yt of the time series xi can be calculated
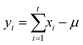 | (4) |
| F(W) = σiW | (5) |
Finally, the fluctuation function F(W) can be plotted versus window size W on a double logarithmic scale. The slope of F(W) calculated via linear regression delivers an estimation of the Hurst exponent H.
Power law statistics and avalanche analysis
Prior to power law and avalanche analysis, a thresholding procedure (see ESI S3 and S4†) was applied to discriminate network transition events in the network state against noise. A network transition event in the context of this work means a measurable change in conductance of a percolated NP network, which in addition satisfies the following thresholding procedure. As a first thresholding condition, all changes in conductance smaller than 0.01 G0 were discarded to account for the noise level of the electrical measurement instrumentation. As a second condition, only switching events were taken into the evaluation, which exceed fluctuations of 3 standard deviations (defined by the past 30 values in the temporal sequence). Only above-threshold transition events were subject to the power law and avalanche analysis. All probability density function (PDF) fittings in this work were done using the Python package “Powerlaw”.37 This Python package follows the principles developed in ref. 38. These fittings have the general power law form (where x is the distributed quantity and b is the power law scaling exponent)| f(x) ∝ x−b | (6) |
PDF fittings of network transition event magnitudes ΔG and interevent intervals IEIs were done by maximum likelihood estimation of the power law exponents β and γ, respectively. Fitting of ΔG and IEIs PDFs was done over the whole observed range.
Avalanches were defined analogously to the common evaluation scheme as in neurobiology.21 The temporal sequence of network transition events is separated into time bins having the width of the mean IEI value. An avalanche is defined as a sequence of bins, where each bin shows at least one transition event. Avalanches are separated by periods with absent activity (i.e. sequential bins having zero transition events). The avalanche size S is determined as number of transition events in one avalanche and the avalanche duration T is the number of time bins. The fitted PDFs for avalanche sizes and distributions as shown in Fig. 6 are done via maximum likelihood estimation without a lower bound xmin, to show the good agreement of power laws with the whole observed range. The maximum likelihood estimations of the exponents τ and α, instead, were performed by constraining the PDF fitting to a lower bound xmin, to account for slight deviation at small scale occurrences. The value for xmin was determined by minimization of the Kolmogorov–Smirnov distance (as proposed by ref. 38) and under the additional constraint that σ/b < 0.05 (σ is the standard error of the estimated power law exponent) to exclude that xmin is chosen too high and valid data will be discarded. All fits above xmin, that were decisive for estimating the power law exponents τ and α as mentioned in Fig. 6 are given in the ESI S9.†
All fitted power law PDFs in this work were tested against exponential PDF (which could be indicative of non-correlated temporal sequences) with respect to the whole observed range via likelihood-ratios, as proposed in ref. 38. Each test suggested, that the power law form is the better description than the exponential form under confirmation of statistical significance (we observed p-values ≪0.1). Furthermore, the whole power law and avalanche analysis was representatively done for a shuffled temporal sequence of network transition events from a sample without insulating matrix, as shown in the ESI S12.† There, it can be seen that power law statistics become destroyed upon shuffling the sequence of network transition events, which indicates loss of correlated activity.
Data availability
The data generated and analyzed in this study are available from the corresponding author on reasonable request.Author contributions
Conceptualization: N. C., A. V., F. F.; Formal analysis: N. C., A. V.; Funding acquisition: A. V., F. F.; Investigation: N. C., B. A.; Methodology: N. C., S. B.; Supervision: A. V., S. B., F. F., T. S.; Visualization: N. C.; Writing – original draft: N. C.; Writing – review and editing: A. V., B. A., F. F., S. B., T. S.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors would like to thank Ole Gronenberg and Lorenz Kienle for performing the TEM investigations and providing TEM images. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 434434223 – SFB1461.References
- M. A. Zidan, J. P. Strachan and W. D. Lu, Nat. Electron., 2018, 1, 22–29 CrossRef.
- J. D. Kendall and S. Kumar, Appl. Phys. Rev., 2020, 7(1) DOI:10.1063/1.5129306.
- T. Zhang, K. Yang, X. Xu, Y. Cai, Y. Yang and R. Huang, Phys. Status Solidi Rapid Res. Lett., 2019, 13, 1–21 Search PubMed.
- Y. Van De Burgt, A. Melianas, S. T. Keene, G. Malliaras and A. Salleo, Nat. Electron., 2018, 1, 386–397 CrossRef.
- S. Saïghi, C. G. Mayr, T. Serrano-Gotarredona, H. Schmidt, G. Lecerf, J. Tomas, J. Grollier, S. Boyn, A. F. Vincent, D. Querlioz, S. La Barbera, F. Alibart, D. Vuillaume, O. Bichler, C. Gamrat and B. Linares-Barranco, Front. Neurosci., 2015, 9, 1–16 Search PubMed.
- J. Q. Yang, R. Wang, Y. Ren, J. Y. Mao, Z. P. Wang, Y. Zhou and S. T. Han, Adv. Mater., 2020, 32, 1–32 Search PubMed.
- J. H. Cha, S. Y. Yang, J. Oh, S. Choi, S. Park, B. C. Jang, W. Ahn and S. Y. Choi, Nanoscale, 2020, 12, 14339–14368 RSC.
- Z. Wang, S. Joshi, S. E. Savel’ev, H. Jiang, R. Midya, P. Lin, M. Hu, N. Ge, J. P. Strachan, Z. Li, Q. Wu, M. Barnell, G. L. Li, H. L. Xin, R. S. Williams, Q. Xia and J. J. Yang, Nat. Mater., 2017, 16, 101–108 CrossRef CAS PubMed.
- R. Midya, Z. Wang, S. Asapu, S. Joshi, Y. Li, Y. Zhuo, W. Song, H. Jiang, N. Upadhay, M. Rao, P. Lin, C. Li, Q. Xia and J. J. Yang, Adv. Electron. Mater., 2019, 5, 1–7 Search PubMed.
- N. Carstens, A. Vahl, O. Gronenberg, T. Strunskus, L. Kienle, F. Faupel and A. Hassanien, Nanomaterials, 2021, 11, 1–16 CrossRef PubMed.
- Z. Kuncic and T. Nakayama, Adv. Phys. X, 2021, 6(1) DOI:10.1080/23746149.2021.1894234.
- S. K. Bose, J. B. Mallinson, R. M. Gazoni and S. A. Brown, IEEE Trans. Electron Devices., 2017, 64, 5194–5201 CAS.
- H. O. Sillin, R. Aguilera, H. H. Shieh, A. V. Avizienis, M. Aono, A. Z. Stieg and J. K. Gimzewski, Nanotechnology, 2013, 24(38) DOI:10.1088/0957-4484/24/38/384004.
- C. Du, F. Cai, M. A. Zidan, W. Ma, S. H. Lee and W. D. Lu, Nat. Commun., 2017, 8, 1–10 CrossRef CAS PubMed.
- G. Milano, G. Pedretti, K. Montano, S. Ricci, S. Hashemkhani, L. Boarino, D. Ielmini and C. Ricciardi, Nat. Mater., 2022, 21, 195–202 CrossRef CAS PubMed.
- S. Shirai, S. K. Acharya, S. K. Bose, J. B. Mallinson, E. Galli, M. D. Pike, M. D. Arnold and S. A. Brown, Netw. Neurosci., 2019, 4, 432–447 CrossRef PubMed.
- C. Minnai, A. Bellacicca, S. A. Brown and P. Milani, Sci. Rep., 2017, 7, 1–8 CrossRef CAS.
- A. Diaz-Alvarez, R. Higuchi, P. Sanz-Leon, I. Marcus, Y. Shingaya, A. Z. Stieg, J. K. Gimzewski, Z. Kuncic and T. Nakayama, Sci. Rep., 2019, 9, 1–13 CAS.
- J. Hochstetter, R. Zhu, A. Loeffler, A. Diaz-Alvarez, T. Nakayama and Z. Kuncic, Nat. Commun., 2021, 12 DOI:10.1038/s41467-021-24260-z.
- D. R. Chialvo, Nat. Phys., 2010, 6, 744–750 Search PubMed.
- J. M. Beggs and D. Plenz, J. Neurosci., 2003, 23, 11167–11177 CrossRef CAS PubMed.
- P. Bak, C. Tang and K. Wiesenfeld, Phys. Rev. A, 1988, 38, 364–374 CrossRef PubMed.
- W. L. Shew and D. Plenz, Neuroscientist, 2013, 19, 88–100 CrossRef PubMed.
- J. Hesse and T. Gross, Front. Syst. Neurosci., 2014, 8, 1–14 Search PubMed.
- A. Z. Stieg, A. V. Avizienis, H. O. Sillin, C. Martin-Olmos, M. Aono and J. K. Gimzewski, Adv. Mater., 2012, 24, 286–293 CrossRef CAS PubMed.
- J. B. Mallinson, S. Shirai, S. K. Acharya, S. K. Bose, E. Galli and S. A. Brown, Sci. Adv., 2019, 5, eaaw8438 CrossRef CAS PubMed.
- K. Linkenkaer-Hansen, V. V. Nikouline, J. M. Palva and R. J. Ilmoniemi, J. Neurosci., 2001, 21, 1370–1377 CrossRef CAS PubMed.
- R. Hardstone, S. S. Poil, G. Schiavone, R. Jansen, V. V. Nikulin, H. D. Mansvelder and K. Linkenkaer-Hansen, Front. Physiol., 2012, 1–13 Search PubMed.
- A. Vahl, N. Carstens, T. Strunskus, F. Faupel and A. Hassanien, Sci. Rep., 2019, 9, 1–10 Search PubMed.
- H. Haberland, M. Karrais, M. Mall and Y. Thurner, J. Vac. Sci. Technol., A, 1992, 10, 3266–3271 CrossRef CAS.
- A. Vahl, J. Strobel, W. Reichstein, O. Polonskyi, T. Strunskus, L. Kienle and F. Faupel, Nanotechnology, 2017, 28(17) DOI:10.1088/1361-6528/aa66ef.
- H. Takele, S. Jebril, T. Strunskus, V. Zaporojchenko, R. Adelung and F. Faupel, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 345–350 CrossRef CAS.
- U. Schürmann, W. Hartung, H. Takele, V. Zaporojtchenko and F. Faupel, Nanotechnology, 2005, 16, 1078–1082 CrossRef.
- A. Eke, P. Herman, L. Kocsis and L. R. Kozak, Physiol. Meas., 2002, 23(1) DOI:10.1088/0967-3334/23/1/201.
- S. A. Chekol, S. Menzel, R. W. Ahmad, R. Waser and S. Hoffmann-Eifert, Adv. Funct. Mater., 2021, 2111242 Search PubMed.
- A. Sattar, S. Fostner and S. A. Brown, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef PubMed.
- J. Alstott, E. Bullmore and D. Plenz, PLoS One, 2014, 9(1) DOI:10.1371/journal.pone.0085777.
- A. Clauset, C. R. Shalizi and M. E. J. Newman, SIAM Rev., 2009, 51, 661–703 CrossRef.
- J. P. Sethna, K. A. Dahmen and C. R. Myers, Nature, 2001, 410, 242–250 CrossRef CAS PubMed.
- N. Friedman, S. Ito, B. A. W. Brinkman, M. Shimono, R. E. L. Deville, K. A. Dahmen, J. M. Beggs and T. C. Butler, Phys. Rev. Lett., 2012, 108, 1–5 CrossRef PubMed.
- M. Mirigliano, D. Decastri, A. Pullia, D. Dellasega, A. Casu, A. Falqui and P. Milani, Nanotechnology, 2020, 31(23) DOI:10.1088/1361-6528/ab76ec.
- S. Menzel, S. Tappertzhofen, R. Waser and I. Valov, Phys. Chem. Chem. Phys., 2013, 15, 6945–6952 RSC.
- D. B. Larremore, W. L. Shew and J. G. Restrepo, Phys. Rev. Lett., 2011, 106, 1–4 CrossRef PubMed.
- R. Zeraati, V. Priesemann and A. Levina, Front. Phys., 2021, 9, 1–17 Search PubMed.
- M. D. Pike, S. K. Bose, J. B. Mallinson, S. K. Acharya, S. Shirai, E. Galli, S. J. Weddell, P. J. Bones, M. D. Arnold and S. A. Brown, Nano Lett., 2020, 20, 3935–3942 CrossRef CAS PubMed.
- G. Milano, G. Pedretti, M. Fretto, L. Boarino, F. Benfenati, D. Ielmini, I. Valov and C. Ricciardi, Adv. Intell. Syst., 2020, 2, 2000096 CrossRef.
- W. Wang, M. Wang, E. Ambrosi, A. Bricalli, M. Laudato, Z. Sun, X. Chen and D. Ielmini, Nat. Commun., 2019, 10, 1–9 CrossRef PubMed.
- S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00121g |
| This journal is © The Royal Society of Chemistry 2022 |