 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Treatment of spin–orbit coupling with internally contracted multireference coupled cluster theory†
Andreas
Köhn
 * and
Julia
Netz
* and
Julia
Netz

Institute for Theoretical Chemistry, University of Stuttgart, Pfaffenwaldring 55, DE-70569 Stuttgart, Germany. E-mail: koehn@theochem.uni-stuttgart.de
First published on 10th June 2025
Abstract
We present the formalism for computing state-interaction matrix elements within the multistate extension of internally contracted multireference coupled-cluster theory. In particular, we focus on the determination of spin–orbit coupling matrix elements. A pilot implementation is presented and tested for the zero-field splitting of atomic 2P and 3P terms as well as for molecular 2Π terms. We also investigate the impact of the non-Hermiticity of the underlying coupled-cluster theory on spin–orbit couplings between non-equivalent states. For this, we consider the coupling between the 3Σ− ground state and the 1Π excited state of NH for several interatomic distances. Only a very small asymmetry is found for this case, but it is also seen that the present theory has to be carefully revisited with respect to the treatment of the response of the reference coefficients in order to avoid artefacts.
1 Introduction
Spin–orbit interactions1 are at the heart of many important phenomena, such as intersystem crossing,1,2 being important for the photophysics of organic dyes, or zero-field splitting of the ground state of transition metal or rare earth ions, giving rise to their unique magnetic properties3,4 and making them interesting candidates for molecular magnetism, spintronics and quantum technology.5 The computational modelling of spin–orbit interactions was pursued early on in quantum chemistry, starting with perturbation approaches within configuration interaction (CI) theory.6–9 There also exist implementations that include the spin–orbit effects directly into the self-consistent solutions10,11 and full relativistic treatments based on the Dirac equation.12For light and medium-sized nuclei, spin–orbit coupling matrix elements do not exceed 2000 cm−1 (0.25 eV) and the perturbative approach is usually sufficient. While the size of spin–orbit coupling effects are qualitatively well recovered by small CI expansions, a more quantitative treatment calls for the inclusion of dynamic correlation effects. This can of course be accomplished by larger multireference CI expansions,7,8 or by (multiconfiguration) perturbation theory.13–17 For large molecules, density functional theory is an alternative option.18,19
In terms of accurate wavefunction theory, coupled-cluster theory is the most desirable target due to its high accuracy and size-consistency.20 However, appropriate extensions of the theory have to be developed in order to make it applicable to near-degenerate states,21,22 for which spin–orbit coupling is often most important. Pioneering work has been carried out at the level of equation-of-motion ionisation potential coupled-cluster (EOMIP-CC) theory by Klein and Gauss.23 This approach was later generalised to further EOM approaches (like electron-attachment or spin–flip) by Epifanovsky et al.,24 which significantly widens the scope of spin-cases that can be treated. Spin–orbit effects for multireference coupled-cluster theory have for the first time been explored by of Mück and Gauss25 who focused on Mukherjee's state-specific multireference coupled-cluster (Mk-MRCC) theory.26,27
In the present work, we seek to integrate spin–orbit effects into internally contracted multireference coupled-cluster (icMRCC) theory.28–35 While some works exist that combine icMRCC energies and spin–orbit interaction matrix elements from small CI expansions to arrive at spin–orbit coupled states of small molecules,36,37 the aim of the present work is to also include dynamic correlation effects on the matrix elements. To this end, we exploit that the solutions of the icMRCC equations, despite obtained in a state-specific fashion, can also be viewed as the solutions of a multistate framework33,35 such that they can be directly used as zeroth-order function for the evaluation of spin–orbit coupling matrix elements.
The present work is organised as follows: in Sections 2.1–2.3, we review the icMRCC theory for state specific energies and first-order properties, as well as the multistate extension of the theory. In Section 2.4 we introduce the new equations for treating state interactions within the multistate framework and its application to spin–orbit coupling (Section 2.5). In Section 3.1, we shortly describe the implementation and show thereafter the first exploratory results obtained by the new approach. These consist of the zero-field splittings of atoms, Section 3.2, and molecules with degenerate ground state, Section 3.3. In addition we will investigate the impact of the non-Hermiticity of the coupled-cluster approach, Section 3.4.
2 Theory
2.1 Internally contracted multireference coupled-cluster theory
The internally contracted multireference coupled-cluster (icMRCC) wavefunction30,31 is defined as | (1) |
Dynamical electron correlation is introduced by the cluster operator
 | (2) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) ρ and corresponding cluster amplitudes tρ. The index ρ runs over all included excitations, e.g. one- and two-body excitations in case of the icMRCC singles and doubles (icMRCCSD) approximation. For the present work, we keep the notation rather abstract, for a more detailed definition of the excitation manifold see for example ref. 34. For the purposes of the present work it suffices to say that the excitation manifold includes excitations that promote electrons from doubly occupied orbitals into partially occupied or unoccupied orbitals in either the active space or the secondary space (virtual orbitals), but they also promote electrons within the active space or from the active space into the secondary space. Purely active excitations that only reshuffle electrons inside the active space are omitted, instead the expansion coefficients cμ will be reoptimised. As the excitation spaces overlap, the excitation operators do not commute in general, at variance to the single-reference case. The specific choice of the excitation manifold requires special considerations in order to avoid linear dependencies and to achieve size-consistency, as discussed previously.31,34,38
ρ and corresponding cluster amplitudes tρ. The index ρ runs over all included excitations, e.g. one- and two-body excitations in case of the icMRCC singles and doubles (icMRCCSD) approximation. For the present work, we keep the notation rather abstract, for a more detailed definition of the excitation manifold see for example ref. 34. For the purposes of the present work it suffices to say that the excitation manifold includes excitations that promote electrons from doubly occupied orbitals into partially occupied or unoccupied orbitals in either the active space or the secondary space (virtual orbitals), but they also promote electrons within the active space or from the active space into the secondary space. Purely active excitations that only reshuffle electrons inside the active space are omitted, instead the expansion coefficients cμ will be reoptimised. As the excitation spaces overlap, the excitation operators do not commute in general, at variance to the single-reference case. The specific choice of the excitation manifold requires special considerations in order to avoid linear dependencies and to achieve size-consistency, as discussed previously.31,34,38
By inserting the icMRCC wavefunction, eqn (1), into the electronic Schrödinger equation with the (non-relativistic) clamped-nuclei electronic Hamiltonian Ĥ, the equations to determine the cluster amplitudes tρ and coefficients cμ can be derived. We use the linked form of the projection approach, where we first premultiply both sides of the Schrödinger equation by e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) before projecting to excited configurations. We obtain the amplitude equations
before projecting to excited configurations. We obtain the amplitude equations
 | (3) |
by projecting to the non-redundant internally contracted manifold  .
.
Projection onto the reference space determinants leads to an eigenvalue problem
 | (4) |
Heffμν = 〈Φμ|e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φν〉. |Φν〉. | (5) |
The equations, eqn (3) and (4) are solved simultaneously, the lowest eigenvalue of the effective Hamiltonian gives the icMRCC energy.
2.2 Expectation values
In analogy to single-reference coupled-cluster theory, molecular properties can be computed within the icMRCC framework by introducing a stationary energy functional.31,39 For a more compact notation, we define the similarity transformed Hamiltonian![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = e− = e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) | (6) |
and write the desired energy functional as:
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = 〈 = 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 0| 0|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |ψ0〉 + 〈ψ0| |ψ0〉 + 〈ψ0|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |ψ0〉 − E(〈 |ψ0〉 − E(〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 0|ψ0〉 − 1). 0|ψ0〉 − 1). | (7) |
This expression contains additional coefficients, which are contained in the left-hand reference function
 | (8) |
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) operator
operator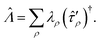 | (9) |
The energy E appears here as Lagrange multiplier for the normalization condition 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 0|ψ0〉 = 1.
0|ψ0〉 = 1.
Taking the derivatives with respect to λρ and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) μ recovers, by construction, the amplitude and coefficient equations, eqn (3) and (4). Requiring stationarity with respect to the cluster amplitudes and the reference coefficients leads to two additional equations. The condition ∂cμ
μ recovers, by construction, the amplitude and coefficient equations, eqn (3) and (4). Requiring stationarity with respect to the cluster amplitudes and the reference coefficients leads to two additional equations. The condition ∂cμ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = 0 leads to39
= 0 leads to39
〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 0|( 0|(![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) − E)|Φμ〉 + 〈ψ0| − E)|Φμ〉 + 〈ψ0|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φμ〉 + 〈Φμ| |Φμ〉 + 〈Φμ|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |ψ0〉 = 0, |ψ0〉 = 0, | (10) |
and the condition ∂tρ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = 0 gives
= 0 gives
〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 0|(∂tρ 0|(∂tρ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) )|ψ0〉 + 〈ψ0| )|ψ0〉 + 〈ψ0|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) (∂tρ (∂tρ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) )|ψ0〉 = 0. )|ψ0〉 = 0. | (11) |
The last term on the left-hand side of eqn (10) results from the derivative of the internally contracted projection manifold. As this term vanishes in the limit of a complete cluster operator, it has been argued to neglect this term (neglect of internal projection response, NIPR).39Eqn (10) and (11) can be summarized as a homogenous linear set of equations
 | (12) |
For any perturbation
Ĥ(ε) = Ĥ + ε![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) | (13) |
the first-order response of the system can now be computed as
∂ε![[script L]](https://www.rsc.org/images/entities/char_e144.gif) |ε=0 = 〈 |ε=0 = 〈![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) 0| 0|![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) |ψ0〉 + 〈ψ0| |ψ0〉 + 〈ψ0|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) |ψ0〉 |ψ0〉 | (14) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) = e−
= e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) e
e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . Note that the orbital response was neglected in this approximation.
. Note that the orbital response was neglected in this approximation.
2.3 Multistate extension
The icMRCC theory can be extended to a multistate framework.33 The reference function |ψ0〉 is generalized to a model space M0 = {|ψi〉} of multiconfigurational wavefunctions. These are normalized, 〈ψi|ψi〉 = 1, but not necessarily orthogonal. We therefore introduce the biorthogonal complements | (15) |
 | (16) |
The correlated states are then generated by the wave operator
 | (17) |
| ÛÛ = Û | (18) |
After inserting the operators into the Bloch equations ĤÛ = ÛĤÛ, one arrives at an expression for the amplitudes:33
 | (19) |
Here,  are excitation operators in the non-redundant manifold for the respective reference state. The effective Hamiltonian is given as
are excitation operators in the non-redundant manifold for the respective reference state. The effective Hamiltonian is given as
Heffji = 〈![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) j|e− j|e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (i)Ĥe (i)Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (i)|ψi〉 (i)|ψi〉 | (20) |
The equations are invariant under orbital rotations within the orbital subspaces, but depend on the choice of the model space expansion. As discussed in ref. 33, solving the state specific icMRCC equations, eqn (3) and (4) leads to solutions that give vanishing coupling matrix elements via the effective Hamiltonian and thus effectively decouple the multistate equations, ref. 19. As a consequence, the state-specific solutions of the icMRCC equations can also be viewed as the solutions of the multistate icMRCC (MS-icMRCC) theory.
2.4 Transition moments in multistate theory
We consider individually optimised icMRCC wavefunctions of two states|Ψa〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) a|ψa〉, a|ψa〉, | (21) |
|Ψb〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b|ψb〉 b|ψb〉 | (22) |
and assume, for the course of the present work, that they have different spatial symmetry. We introduce the shortcuts
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) a = e− a = e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) aĤe aĤe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) a, a, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) b = e− b = e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) bĤe bĤe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b b | (23) |
Heffab = 〈![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) a| a|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) b|ψb〉 = 0, b|ψb〉 = 0, | (24) |
Heffba = 〈![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) b| b|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) a|ψa〉 = 0. a|ψa〉 = 0. | (25) |
Due to the assumption of different symmetry for the wavefunctions, these elements are zero and guarantee that the icMRCC equations for obtaining the two states, |Ψa〉 and |Ψb〉, were decoupled, irrespective of the actual nature of the biorthogonal states 〈![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i|. In fact there is a slight complication that the states 〈
i|. In fact there is a slight complication that the states 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) i| entering the left-hand wavefunction in the expression for the expectation value, eqn (8), and the biorthogonal states that were introduced in the multistate theory, eqn (15), are not the same. In the present work, we will focus on the response of the cluster amplitudes and neglect those of the reference coefficients (vide infra).
i| entering the left-hand wavefunction in the expression for the expectation value, eqn (8), and the biorthogonal states that were introduced in the multistate theory, eqn (15), are not the same. In the present work, we will focus on the response of the cluster amplitudes and neglect those of the reference coefficients (vide infra).
In order to arrive at an expression for the transition moments, we introduce a perturbation to the Hamiltonian
Ĥ(ε) = Ĥ + ε![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) . . | (26) |
The perturbed amplitudes and wave functions are
| tbρ(ε) = tbρ + εtb,(1)ρ + … | (27) |
| |ψb(ε)〉 = |ψb〉 + ε|ψb(1)〉 + … | (28) |
and the effective first-order Hamiltonian becomes
 | (29) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) b = e−
b = e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b
b![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) e
e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b. In order to cut down the complexity, we will neglect the reference state response in the following and therefore ignore the last two terms of (29). Still, the equations include perturbed amplitudes tb,(1)ρ. In order to avoid amplitudes that explicitly depend on the perturbing operator, we employ the Lagrange formalism of coupled-cluster response theory and set up the following functional:
b. In order to cut down the complexity, we will neglect the reference state response in the following and therefore ignore the last two terms of (29). Still, the equations include perturbed amplitudes tb,(1)ρ. In order to avoid amplitudes that explicitly depend on the perturbing operator, we employ the Lagrange formalism of coupled-cluster response theory and set up the following functional: | (30) |
It contains the objective quantity as the first term, the second and third term involve the operator
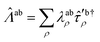 | (31) |
 | (32) |
This functional is required to be stationary with respect to variations of the amplitudes, and for vanishing perturbations we get
 | (33) |
The second term on the right-hand side vanishes due to eqn (24). This leaves us with the following linear set of equations, from which ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ab can be determined:
ab can be determined:
 | (34) |
Note that these equations are independent of the specific perturbing operator. The desired coupling matrix elements for any perturbing operator ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) are given by
are given by
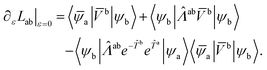 | (35) |
2.5 Spin–orbit coupling matrix elements
As specific perturbation, we consider here the spin–orbit operator. A simple, yet accurate approximation is the mean-field spin–orbit operator8,41,42 | (36) |
 | (37) |
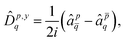 | (38) |
 | (39) |
The operator has triplet spin symmetry, which implies that the required multipliers ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ab are also triplet operators.
ab are also triplet operators.
The 〈![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) a| states in eqn (35) are formally the left-hand solutions of the effective Hamiltonian, which is a bit inconvenient in general as the left-hand side eigenvalue problem involves similarity transformed matrix elements e−
a| states in eqn (35) are formally the left-hand solutions of the effective Hamiltonian, which is a bit inconvenient in general as the left-hand side eigenvalue problem involves similarity transformed matrix elements e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) iĤe
iĤe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) i of all model space states. Within the present work, we have chosen the ad hoc provision to use the coefficients
i of all model space states. Within the present work, we have chosen the ad hoc provision to use the coefficients ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) μ from the state-specific Λ equations, eqn (12). The expression for the spin–orbit interaction matrix elements reads therefore
μ from the state-specific Λ equations, eqn (12). The expression for the spin–orbit interaction matrix elements reads therefore
HSOab = 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) a| a|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) bSOMF|ψb〉 + 〈ψb| bSOMF|ψb〉 + 〈ψb|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) ab ab![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) bSOMF|ψb〉 bSOMF|ψb〉 | (40) |
−〈ψb|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) abe− abe−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) be be![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) a|ψa〉 〈 a|ψa〉 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) a| a|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) bSOMF|ψb〉 = HSO,effab + HSO,Λab − SΛabHSO,effab bSOMF|ψb〉 = HSO,effab + HSO,Λab − SΛabHSO,effab | (41) |
The matrix elements can be partitioned into contributions that are very similar to those found by Mück and Gauss for the Mk-MRCC theory.25
3 Results and discussion
3.1 Implementation and computational setup
Integrals and CASSCF orbitals were imported from the Molpro program package.43–47 CASSCF optimizations always included state-averaging over all relevant orbitals, in particular avoiding symmetry breaking in atomic P or molecular Π states. The spin–orbit mean-field integrals were based on the Breit–Pauli operator,8 where the two-electron contributions were contracted with the state-averaged CASSCF density.Based on these integrals, the GeCCo code48 was employed to carry out state-specific icMRCCSD computations for the relevant states, including reference relaxation. The resulting coefficients cμ and amplitudes tρ were stored for the subsequent computations. For each state, also the state-specific Λ equations were solved39 and the ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) μ coefficients were stored, too. All coefficients and amplitudes are spin-adapted, but are stored in their explicit spin-orbital representation for one specific MS state. Usually the smallest MS (0 or 1/2) is used. For the computation of the coupling between triplet states the MS = 1 components had to be used, as the SO coupling matrix element between the MS = 0 components is vanishing.
μ coefficients were stored, too. All coefficients and amplitudes are spin-adapted, but are stored in their explicit spin-orbital representation for one specific MS state. Usually the smallest MS (0 or 1/2) is used. For the computation of the coupling between triplet states the MS = 1 components had to be used, as the SO coupling matrix element between the MS = 0 components is vanishing.
The spin–orbit computations were implemented by a plug-in code for GeCCo, which sets up the relevant equations in symbolic form. Details of this are given in the ESI,† which also contains sample inputs and program outputs that illustrate the procedure.
The code in particular autogenerates all the required equations. It starts by generating the contributions to the Lagrange expression, eqn (30). In accordance with the general truncation rules employed for icMRCCSD,31 the energy terms retain the cluster operator terms up to quartic terms and the amplitude equation terms up to quadratic order. The generated terms are then further processed symbolically: by symbolic derivation, the linear set of equations to determine Λab is generated, see eqn (34), and by replacing the (unperturbed) Hamiltonian by the spin–orbit operator, the final expressions for the transition matrix elements are obtained, see eqn (35) and (40), respectively. These equations are then translated into a sequence of binary tensor contractions, which are evaluated numerically.
The computational complexity of icMRCCSD formally scales as that of comparable multireference CI methods, that is, O(N6) with system size N for fixed active space size (O(M4) with basis set size M), and factorially with the number of active orbitals. In comparison to multireference CI computations, the prefactor for icMRCCSD is large for the present non-optimal implementation.49 The non-linear amplitude and reference coefficient equations, eqn (3) and (4), can sometimes be hard to converge. For the computation of spin–orbit matrix elements, in addition the Λ equations, eqn (12) for each state and the Lagrange multiplier equations, eqn (34), need to be solved. The computational complexity of these equations is the same as for the amplitude equations, but they are usually easier to converge due to their linear nature.
The test computations employed the cc-pCVXZ (X = D, T, Q) basis sets.50,51 Both calculations correlating only valence electrons and calculations including the next-lower electronic shell were run. For comparison, additional computations were carried out at the CASCI and MRCI level, using the Molpro code.8,43,52
3.2 Atomic zero-field splitting
As a first set of test cases, we consider the spin–orbit coupling in the lowest term of the atoms Al, Si, S, and Cl. The results are summarized in Table 1. As reference, the table reports the effective spin–orbit coupling constant computed from the experimental fine structure splittings given in ref. 53. In Table 1, we particularly list the different contributions that add up to the final MS-icMRCCSD coupling matrix element, see also eqn (41). These results show that the main contribution comes from the effective Hamiltonian term but that the effects of the Λ and overlap terms are significant and improve the result towards the experimental reference value. The improvement of correlated calculations like icMRCCSD and MRCI with respect to CASCI is particularly obvious for the core-correlation effects, which naturally require an extended correlation space. For the icMRCCSD computations, core-correlation effects particularly enter through the effective Hamiltonian term and the Λ term, whereas the overlap term does not change much. Within the very similar expression derived for the Mk-MRCCSD theory, the overlap term was also interpreted as a dimensionless screening factor for the effective Hamiltonian matrix element:25| HSO,effab − SΛabHSO,effab = ξHSO,effab | (42) |
| System/settingsb | MS-icMRCC | CASCI | MRCI | Exp.a | |||
|---|---|---|---|---|---|---|---|
| H SO,effab | H SO,Λab | −SΛabHSO,effab | Total | ||||
| a Computed from energy splittings given in ref. 53. b System: atom and term as indicated; settings: ‘fc’ = frozen core, ‘cc’ = core-correlation, and basis sets used. | |||||||
| Al 2P | |||||||
| fc cc-pCVDZ | −31.8 | 1.2 | 1.4 | −29.1 | −34.0 | −29.7 | |
| fc cc-pCVTZ | −32.3 | 1.1 | 1.6 | −29.6 | −34.5 | −30.2 | |
| fc cc-pCVQZ | −32.5 | 1.1 | 1.7 | −29.7 | −34.7 | −30.4 | |
| cc cc-pCVDZ | −34.5 | −1.4 | 1.5 | −34.4 | −34.0 | −37.9 | |
| cc cc-pCVTZ | −35.8 | −2.1 | 1.7 | −36.2 | −34.5 | −39.8 | |
| cc cc-pCVQZ | −35.9 | −2.3 | 1.7 | −36.5 | −34.7 | −40.4 | −37.35 |
| Si 3P | |||||||
| fc cc-pCVDZ | −62.5 | 0.6 | 1.4 | −60.5 | −63.7 | −61.4 | |
| fc cc-pCVTZ | −63.7 | 0.5 | 1.6 | −61.5 | −64.6 | −62.5 | |
| fc cc-pCVQZ | −63.8 | 0.5 | 1.6 | −61.7 | −64.7 | −62.6 | |
| cc cc-pCVDZ | −67.1 | −4.0 | 1.4 | −69.7 | −63.7 | −73.6 | |
| cc cc-pCVTZ | −69.0 | −5.1 | 1.6 | −72.5 | −64.6 | −76.2 | |
| cc cc-pCVQZ | −69.4 | −5.3 | 1.6 | −73.2 | −64.7 | −76.8 | −73.7 |
| S 3P | |||||||
| fc cc-pCVDZ | 178.3 | −3.6 | −4.1 | 170.7 | 181.5 | 173.0 | |
| fc cc-pCVTZ | 180.4 | −3.6 | −5.8 | 170.9 | 182.9 | 173.9 | |
| fc cc-pCVQZ | 180.7 | −3.7 | −6.1 | 171.0 | 183.3 | 174.2 | |
| cc cc-pCVDZ | 186.8 | 5.0 | −4.2 | 187.7 | 181.5 | 198.2 | |
| cc cc-pCVTZ | 189.9 | 6.9 | −6.0 | 190.8 | 182.9 | 202.7 | |
| cc cc-pCVQZ | 190.8 | 7.4 | −6.2 | 192.0 | 183.3 | 204.3 | 194.61 |
| Cl 2P | |||||||
| fc cc-pCVDZ | 272.3 | −2.6 | −5.3 | 264.3 | 272.4 | 265.4 | |
| fc cc-pCVTZ | 274.5 | −2.9 | −7.7 | 263.8 | 273.7 | 265.9 | |
| fc cc-pCVQZ | 275.2 | −2.9 | −8.1 | 264.3 | 274.4 | 266.6 | |
| cc cc-pCVDZ | 283.5 | 9.0 | −5.5 | 287.1 | 272.4 | 288.6 | |
| cc cc-pCVTZ | 287.0 | 11.0 | −7.9 | 290.1 | 273.7 | 292.7 | |
| cc cc-pCVQZ | 288.3 | 11.8 | −8.2 | 291.8 | 274.4 | 294.5 | 294.12 |
The values for ξ = (1 − SΛab) are all in the range of 0.95–0.98 for the atomic examples.
Basis set effects are not strongly pronounced for the considered cases, the differences between the cc-pVCDZ and cc-pVCQZ results are at most 5 per cent (for silicon). Concerning a comparison of the MRCI and the MS-icMRCCSD results, the two methods appear to be en par for the considered cases. There is a slight tendency for MRCI to overshoot the experimental references for Al, Si, and S by 3 to 10 cm−1 but this is partially an effect of using the mean-field approach for the spin–orbit operator. In fact, using the full two-electron operator improves the MRCI results8 (see ESI† for detailed results). Effects of similar size have previously been observed for spin–orbit coupling matrix elements in transition metal compounds.54 Our present MS-icMRCCSD implementation, however, is restricted to effective one-electron operators, therefore we could not investigate this effect further for the coupled-cluster case.
3.3 Spin–orbit splitting in molecular 2Π states
The spin–orbit splittings of 2Π radicals have been investigated in a number of previous works8,23,25 as test cases with well-established reference values. In Table 2 we report results using large cc-pCVQZ basis sets and correlated core electrons. We consider both runs with minimal CAS and full-valence CAS. More detailed results on the different contributions to the MS-icMRCCSD values can be found in the ESI.† The MS-icMRCCSD results are compared to values obtained from CASCI and MRCI calculations, and literature results for Mk-MRCCSD25 (minimal CAS) and EOMIP-CCSD.24| Method | CASb | OH | SH | SeH | ClO | SN |
|---|---|---|---|---|---|---|
| a All computations employ the cc-pCVQZ basis set, core electrons were correlated (except CASCI), 1s cores of S and Cl and 1s2s2p core of Se was kept frozen. Used equilibrium distances – OH: 0.9697 Å, SH: 1.3409 Å, SeH: 1.5811 Å, ClO: 1.5696 Å, SN: 1.4940 Å; the same structures were used in ref. 8 and 25. b Minimal active space: (3,2) for OH, SH, SeH, and ClO; (1,2) for SN. c Full valence active space: (7,5) for OH, SH, SeH; (13,8) for ClO; (11,8) for SN. d Extending the active space by a 4π orbital improves CASCI to −301.7 cm−1 and MRCI to −317.4 cm−1, see ref. 8. e Values taken from ref. 25. f Values taken from ref. 24. g A better value is obtained by EOMEA-CCSD: 226.8 cm−1. h Values taken from ref. 55 (OH, SH, SN), ref. 56 (SeH), and ref. 57 (ClO). | ||||||
| MS-icMRCCSD | Min.b | −135.8 | −375.7 | −1672.3 | −308.1 | 230.1 |
| Full val.c | −135.5 | −374.9 | n/a | n/a | 221.5 | |
| CASCI | Min.b | −138.8 | −351.6 | −1617.7 | −202.2 | 195.0 |
| Full val.c | −138.8 | −350.5 | −1612.0 | −252.0d | 213.1 | |
| MRCI | Min.b | −136.8 | −380.9 | −1709.0 | −225.8 | 218.0 |
| Full val.c | −136.7 | −380.3 | −1704.3 | −276.2d | 226.2 | |
| Mk-MRCCSDe | Min.b | −135.1 | −375.2 | −1707.9 | −312.3 | n/a |
| EOMIP-CCSDf | −136.7 | −371.6 | −1680.4 | −308.3 | 242.9g | |
| Exp.h | −139.2 | −377.0 | −1764.4 | −320.3 | 222.9 | |
For the homologous series OH, SH, and SeH, the spin–orbit splitting increases strongly, as expected, where SeH is certainly a borderline case for the application of the Breit–Pauli operator. For the lightest case, OH, all methods and choices of active space agree within 3 cm−1 and are also close to the experimental reference. For SH, core-correlation effects become more important and CASCI clearly underestimates the coupling. As for the case of OH, the spin–orbit couplings of SH computed by MS-icMRCCSD and Mk-MRCCSD are very similar, and rather close to the experimental reference result (deviation of approximately 2 cm−1). Larger deviations from experiment (up to 90 cm−1) are found for SeH. Part of the deviations may come from the use of the Breit–Pauli operator, EOMIP-CCSD computations reported by Cheng et al.58 also report a value of −1673 cm−1 for the Breit–Pauli operator, while employing the spin–orbit operator from exact two-component theory (X2C) gives −1717 cm−1. In addition, there is also an impact of the correlation of additional inner core shells.58 In the present work, we only considered the correlation of the 3s3p3d semi-core of Se. For instance, the Mk-MRCCSD computations of ref. 25 correlate all electrons, leading to the slightly larger value of −1708 cm−1 quoted in Table 2.
For the three hydrides, so far no significant differences between employing a minimal CAS and a full valence CAS was found. This is clearly different for the case of ClO. Here, the CASCI and MRCI results are clearly different for the two choices of active space, and yet both are not sufficient for a quantitative description. The MRCI value for the full-valence CAS is −276 cm−1, which is still more than 40 cm−1 off the experimental result of −320 cm−1. As shown by Berning et al.,8 the MRCI description can be improved by adding a set of 4π orbitals to the active space, resulting in nearly quantitative agreement with experiment.
In coupled-cluster theory, already the minimal active space gives a comparatively good result. The values for MS-icMRCCSD, Mk-MRCCSD and EOMIP-CCSD range between −308 and −312 cm−1. Unfortunately, the MS-icMRCCSD computation with a large active space failed due to memory problems and we cannot report a value here.
The results for the last case, SN, however, appear promising for MS-icMRCCSD theory. Here, we also find significant effects of going beyond the minimal active space and the MS-icMRCCSD result is very close to the experimental reference.
3.4 Non-Hermiticity of coupled-cluster theory
All the previous examples have in common that they concern spin–orbit coupling between equivalent, degenerate states. Therefore, the pair of adjoint matrix elements fulfils the required symmetry condition . However, the non-Hermiticity of coupled-cluster theory does not guarantee this in general.
. However, the non-Hermiticity of coupled-cluster theory does not guarantee this in general.
Here, we investigate the spin–orbit coupling matrix elements between two non-equivalent states of the NH radical, its X3Σ− ground state and the c1Π excited state. The molecule has been recently studied in detail due to its relevance for astrochemistry, particularly its photodissociation cross sections in the UV range were investigated, with special focus on the c1Π state.59
With this example, we also want to demonstrate the performance of MS-icMRCCSD in the bond-breaking regime, where multireference effects become strong. We therefore have covered distances between 0.5 Å (repulsive tail) and 3.2 Å (dissociative tail). Of course, the full treatment of the system requires much more states to be investigated (ref. 59 considers 12 low-lying electronic states), which is beyond our present scope; we will focus on the coupling of this single pair of states.
Table 3 summarizes the results, further details are given in the ESI.† The two states couple rather strongly at short distances and also at their equilibrium distances at approximately 1.0 to 1.1 Å. The excited 1Π state has a broad avoided crossing at around 1.8 to 2.0 Å (see ESI† for the energy curves), and for longer distances, the spin–orbit coupling drops rapidly towards zero.
| R | CASCI | MRCI | MS-icMRCC using 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) | | |
MS-icMRCC using 〈ψ| | |||
|---|---|---|---|---|---|---|---|
| H SOab = HSOba | H SOab = HSOba | H SOab | H SOba | H SOab | H SOba | ||
| a All calculations use the cc-pCVDZ basis set, the 1s core of nitrogen was kept frozen. | |||||||
| 0.5 | 24.18 | 23.52 | 21.72 | 21.82 | 21.71 | 21.84 | 21.78 |
| 0.8 | 20.91 | 20.70 | 19.05 | 19.14 | 19.02 | 19.10 | 19.06 |
| 1.0 | 19.75 | 19.53 | 18.00 | 18.03 | 17.92 | 18.01 | 17.96 |
| 1.2 | 19.34 | 18.48 | 16.81 | 16.68 | 16.72 | 16.90 | 16.81 |
| 1.4 | 18.90 | 16.74 | 14.69 | 14.63 | 14.65 | 14.89 | 14.77 |
| 1.5 | 18.09 | 15.17 | 13.06 | 12.98 | 13.03 | 13.25 | 13.14 |
| 1.6 | 16.60 | 13.12 | 11.12 | 11.07 | 11.11 | 11.29 | 11.20 |
| 1.8 | 11.96 | 8.65 | 7.30 | 7.37 | 7.29 | 7.40 | 7.35 |
| 2.0 | 7.43 | 5.27 | 4.51 | 4.75 | 4.51 | 4.59 | 4.55 |
| 2.2 | 4.25 | 3.10 | 2.71 | 3.17 | 2.70 | 2.76 | 2.73 |
| 2.5 | 1.53 | 1.25 | 1.14 | 2.36 | 1.14 | 1.19 | 1.17 |
| 2.8 | 0.30 | 0.38 | 0.45 | 2.66 | 0.45 | 0.50 | 0.47 |
| 3.2 | 0.26 | 0.02 | 0.09 | 0.01 | 0.08 | 0.11 | 0.09 |
The run of the coupling is also shown in Fig. 1. MRCI and icMRCCSD are in good agreement, the CASCI curves behaves slightly differently at intermediate distances, most likely due to a different position of the avoided crossing in the absence of dynamical correlation. This again demonstrates the utility of spin–orbit coupling matrix elements from correlated computations that include state interactions (which is ensured for icMRCCSD with reference relaxation33).
With respect to the matrix elements from MS-icMRCCSD we make one observation that is documented in Table 3 and which calls for further development of the theory concerning the proper Lagrange multipliers for the reference coefficients. In eqn (40) we have proposed to use the ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) μ coefficient from the Λ equations from the individual states. Using this definition, we get the matrix elements listed in Table 3 under ‘MS-icMRCC using 〈
μ coefficient from the Λ equations from the individual states. Using this definition, we get the matrix elements listed in Table 3 under ‘MS-icMRCC using 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) |’. For R < 1.8 Å this leads to very similar matrix elements HSOab and HSOba with deviations of less than 0.3 cm−1. For larger distances, however, a problem appears; while the HSOab matrix elements (which use the cluster amplitudes from the 1Π state and the
|’. For R < 1.8 Å this leads to very similar matrix elements HSOab and HSOba with deviations of less than 0.3 cm−1. For larger distances, however, a problem appears; while the HSOab matrix elements (which use the cluster amplitudes from the 1Π state and the ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) μ coefficients from the 3Σ− state) still follow the trend of the MRCI computations, the HSOba matrix elements do not. The latter are computed from the cluster amplitudes of the 3Σ− state and the
μ coefficients from the 3Σ− state) still follow the trend of the MRCI computations, the HSOba matrix elements do not. The latter are computed from the cluster amplitudes of the 3Σ− state and the ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) μ coefficients of the 1Π state. A close analysis of the contributions (see also ESI†) shows that the latter are the main cause of the deviations. Possibly, this effect is connected to the avoided state crossing, which also leads to slow convergence of the icMRCCSD amplitude and coefficient equations. The convergence of the (linear) Λ equations is less problematic and inspection of the amplitudes does not indicate a major numerical problem. Nevertheless, the 〈
μ coefficients of the 1Π state. A close analysis of the contributions (see also ESI†) shows that the latter are the main cause of the deviations. Possibly, this effect is connected to the avoided state crossing, which also leads to slow convergence of the icMRCCSD amplitude and coefficient equations. The convergence of the (linear) Λ equations is less problematic and inspection of the amplitudes does not indicate a major numerical problem. Nevertheless, the 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) b|ĤSOMF|ψa〉 CASCI-like contribution is clearly the main term that is responsible for the non-physical result.
b|ĤSOMF|ψa〉 CASCI-like contribution is clearly the main term that is responsible for the non-physical result.
If we replace the ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) μ amplitudes by the icMRCC reference state amplitudes cμ, we get the results listed in Table 3 under ‘MS-icMRCC using 〈ψ|’. In fact, the alternative HSOab matrix elements deviate only marginally from the initial formulation and so do the HSOba for short distances. In the critical region beyond 1.8 Å, however, the alternative formulation avoids the artefacts described above, and the HSOab and HSOba matrix elements agree within 0.3 cm−1 for all tested bond distances. In case of a pure two-state interaction, the resulting energy splitting is proportional to
μ amplitudes by the icMRCC reference state amplitudes cμ, we get the results listed in Table 3 under ‘MS-icMRCC using 〈ψ|’. In fact, the alternative HSOab matrix elements deviate only marginally from the initial formulation and so do the HSOba for short distances. In the critical region beyond 1.8 Å, however, the alternative formulation avoids the artefacts described above, and the HSOab and HSOba matrix elements agree within 0.3 cm−1 for all tested bond distances. In case of a pure two-state interaction, the resulting energy splitting is proportional to 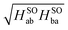 and we use this procedure to compute an ‘averaged’ coupling matrix element. These are also the values used for Fig. 1.
and we use this procedure to compute an ‘averaged’ coupling matrix element. These are also the values used for Fig. 1.
Conclusions
We have presented the theory of interstate coupling matrix elements within a multistate framework for internally contracted multireference coupled-cluster (MS-icMRCC) theory. The equations were implemented in a pilot code based on our specialised symbolic algebra program GeCCo and tested for the computation of spin–orbit coupling matrix elements, using a mean-field Breit–Pauli operator. Apart from computing the state-specific icMRCC wavefunctions for the individual states, the formalism requires solving an additional linear system of equations for each coupled pair. The theory is very similar to that presented by Mück and Gauss25 for state-specific Mk-MRCCSD theory, but can be more easily applied to larger active spaces.Demonstrative results were obtained for the zero-field splitting of the lowest terms (2P or 3P) of the atoms Al, Si, S, and Cl, as well as for the 2Π terms of OH, SH, SeH, ClO, and SN. Active spaces of different sizes (minimal and full valence) were used, and the impact of core-correlation contributions was investigated; these are particularly significant for the heavier atoms. The MS-icMRCCSD results are very accurate and match those of multireference configuration interaction (MRCI). The advantage of the MS-icMRCCSD approach with respect to MRCI is the extensivity of the theory, which holds the promise to keep the same accuracy also for large systems. The currently investigated systems, however, are clearly too small to demonstrate this.
We have also investigated the impact of the non-Hermiticity of coupled-cluster theory on the spin–orbit coupling matrix elements between non-equivalent states. To this end, we investigated the coupling between the 3Σ− ground state and the 1Π excited state of NH for several interatomic distances. The impact of non-Hermiticity was not very large for this case, the differences between the adjoint matrix elements are less than 0.3 cm−1 for matrix elements of an average size of 10 cm−1. It was found, however, that the treatment of the response of the reference coefficient has to be carefully reviewed in order to avoid artefacts.
Author contributions
The research reported in this work was conceived and carried out by A. K., based on an initial investigation carried out by J. N. under the supervision of A. K.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
The authors dedicate this work to Professor Christel Marian on the happy occasion of her 70th birthday and in recognition of her pioneering contributions to the quantum chemical treatment of spin–orbit interactions. A. K. also acknowledges the support by the Stuttgart Center for Simulation Science (SimTech).Notes and references
- C. M. Marian, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2011, 2, 187–203 Search PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- M. Feng and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574–7594 CrossRef CAS PubMed.
- S. T. Liddle and J. V. Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- B. A. Hess, R. J. Buenker, C. M. Marian and S. D. Peyerimhoff, Chem. Phys., 1982, 71, 79–85 CrossRef CAS.
- D. R. Yarkony, Int. Rev. Phys. Chem., 1992, 11, 195–242 Search PubMed.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833 CrossRef CAS.
- P. k Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2013, 138, 104113 CrossRef PubMed.
- T. Bodenstein, A. Heimermann, K. Fink and C. Wüllen, ChemPhysChem, 2022, 23, e202100648 CrossRef CAS PubMed.
- A. Almoukhalalati, S. Knecht, H. J. A. Jensen, K. G. Dyall and T. Saue, J. Chem. Phys., 2016, 145, 074104 CrossRef PubMed.
- V. Jovanović, I. Lyskov, M. Kleinschmidt and C. M. Marian, Mol. Phys., 2017, 115, 109–137 CrossRef.
- L. Lang and F. Neese, J. Chem. Phys., 2019, 150, 104104 CrossRef PubMed.
- R. Majumder and A. Y. Sokolov, J. Phys. Chem. A, 2023, 127, 546–559 CrossRef CAS PubMed.
- R. Majumder and A. Y. Sokolov, J. Chem. Theory Comput., 2024, 20, 4676–4688 CrossRef CAS PubMed.
- Z. Zhao and F. A. Evangelista, J. Phys. Chem. Lett., 2024, 15, 7103–7110 CrossRef CAS PubMed.
- S. Schmitt, P. Jost and C. V. Wüllen, J. Chem. Phys., 2011, 134, 194113 CrossRef PubMed.
- F. Dinkelbach, M. Kleinschmidt and C. M. Marian, J. Chem. Theory Comput., 2017, 13, 749–766 CrossRef CAS PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef CAS PubMed.
- A. Köhn, M. Hanauer, L. A. Mück, T.-C. Jagau and J. Gauss, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2013, 3, 176–197 Search PubMed.
- K. Klein and J. Gauss, J. Chem. Phys., 2008, 129, 194106 CrossRef PubMed.
- E. Epifanovsky, K. Klein, S. Stopkowicz, J. Gauss and A. I. Krylov, J. Chem. Phys., 2015, 143, 064102 CrossRef PubMed.
- L. A. Mück and J. Gauss, J. Chem. Phys., 2012, 136, 111103 CrossRef PubMed.
- U. S. Mahapatra, B. Datta and D. Mukherjee, J. Chem. Phys., 1999, 110, 6171–6188 CrossRef CAS.
- F. A. Evangelista, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2006, 125, 154113 CrossRef PubMed.
- A. Banerjee and J. Simons, Int. J. Quantum Chem., 1981, 19, 207–216 CrossRef CAS.
- A. Banerjee and J. Simons, J. Chem. Phys., 1982, 76, 4548–4559 CrossRef CAS.
- F. A. Evangelista and J. Gauss, J. Chem. Phys., 2011, 134, 114102 CrossRef PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2011, 134, 204111 CrossRef PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2012, 136, 204107 CrossRef PubMed.
- Y. A. Aoto and A. Köhn, J. Chem. Phys., 2016, 144, 074103 CrossRef PubMed.
- A. Köhn, J. A. Black, Y. A. Aoto and M. Hanauer, Mol. Phys., 2020, 118, e1743889 CrossRef.
- R. G. Adam, A. Waigum and A. Köhn, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e70023 Search PubMed.
- M. M. F. de Moraes and Y. A. Aoto, Theor. Chem. Acc., 2020, 139, 71 Search PubMed.
- M. M. F. de Moraes and Y. A. Aoto, J. Mol. Spectrosc., 2022, 385, 111611 CrossRef CAS.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2012, 137, 131103 CrossRef PubMed.
- P. K. Samanta and A. Köhn, J. Chem. Phys., 2018, 149, 064101 CrossRef PubMed.
- B. Jeziorski and H. J. Monkhorst, Phys. Rev. A:At., Mol., Opt. Phys., 1981, 24, 1668–1681 CrossRef CAS.
- B. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2024.1, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- A. Köhn, R. G. Adam, Y. A. Aoto, A. Bargholz, J. Black, M. Hanauer, P. Samantaet al. GitHub, see https://github.com/ak-ustutt/GeCCo-public.
- J. A. Black, A. Waigum, R. G. Adam, K. R. Shamasundar and A. Köhn, J. Chem. Phys., 2023, 158, 134801 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- A. Kramida, Yu. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.12), [Online]. Available: https://physics.nist.gov/asd [2025, April 29]. National Institute of Standards and Technology, Gaithersburg, MD., 2024.
- J. Netz, A. O. Mitrushchenkov and A. Köhn, J. Chem. Theory Comput., 2021, 17, 5530–5537 CrossRef CAS PubMed.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of diatomic molecules, Van Nostrand Reinhold Company, 1979 Search PubMed.
- P. Bollmark, B. Lindgren, B. Rydh and U. Sassenberg, Phys. Scr., 1978, 17, 561–564 CrossRef CAS.
- J. A. Coxon, Can. J. Phys., 1979, 57, 1538–1552 CrossRef CAS.
- L. Cheng, F. Wang, J. F. Stanton and J. Gauss, J. Chem. Phys., 2018, 148, 044108 CrossRef PubMed.
- T. Uhlíková, S. N. Yurchenko, A. N. Perri, J. Tennyson and G.-S. Kim, J. Chem. Phys., 2025, 162, 144108 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01698c |
| This journal is © the Owner Societies 2025 |


