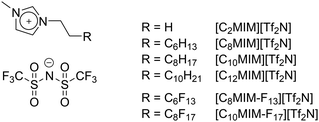To mix or not to mix: charge and polarity effects on alkyl/fluoroalkyl compound miscibility

Abstract

The (im)miscibility of hydrocarbons and perfluorocarbons is well known, depends on the chain lengths involved and has been exploited widely in many different areas of chemistry. One area where mixing hydrocarbon- and fluorocarbon-containing moieties is of current interest is in ionic liquids (ILs), where physicochemical properties may be tuned via the preparation of mixtures. Recent work has shown that mixtures of the methylimidazolium ILs [C_nMIM][Tf₂N] and [C_nMIM-F_2m+1][Tf₂N] (m = n–2) are miscible when a perfluorooctyl chain is used (n = 10), which is unexpected at this chain length. In order to explore the influence of electrostatic attraction between ions in this observed miscibility, related, neutral N-substituted imidazoles C_nIm and C_nIm-F_2m+1 employing hydrocarbon and semiperfluorocarbon chains, and their mixtures, were prepared. The mixtures were miscible at room temperature for n = 8 and immiscible for n = 10. The miscible mixtures were investigated by surface tension, small-angle X-ray and neutron scattering methods and by atomistic molecular dynamics simulations. The data show that while the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x are continuously miscible, some preferential aggregation of alkyl and fluoroalkyl chains is nonetheless present, mirroring the behaviour observed for the IL mixtures [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N], yet in contrast to the shorter-chain mixtures [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] where no aggregates are seen. As such, it has been possible to draw some conclusions concerning the ability of electrostatic interactions between the ions to suppress the otherwise expected immiscibility of the alkyl and fluoroalkyl chains.

---

Introduction

It has been known for some time that hydrocarbons and fluorocarbons tend to be immiscible and that the critical temperature (T_c) of mixing increases with increasing chain length.¹ For example, T_c for hexane/perfluorohexane mixtures has been determined to be 22.8 °C, while for octane/perfluorooctane it is 75.4 °C,² which has likely led to the idea that so-called ‘fluorous behaviour’ (i.e. phase separation of hydrocarbons and fluorocarbons) begins with a perfluorooctyl fragment. The fact that the two chain types can support different solubilities and can be immiscible has been used to advantage in many fields of chemistry,^3,4 including, but not limited to, liquid crystals,^5–7 surfactants and emulsions,^8–10 gas solubility,^11,12 supercritical CO₂,¹³ self-assembly,^14–17 refrigerants¹⁸ and catalysis.¹⁹ The use of fluorinated chains has also been a topic of interest in ionic liquids (ILs), with examples based on heavily fluorinated organic anions,^20–22 as well as cations with semiperfluoroalkyl chains.^23–27

We have recently reported on the preparation and properties of binary IL mixtures, as the ability to tune the properties of ILs through the composition of mixtures is more efficient than realising similar properties through successive preparations of bespoke, individual components.^28–34 Initial investigations considered imidazolium ILs in which short- and long-chain components were mixed (Fig. 1).³¹ Here, evidence emerged for preferential surface enrichment of long-chain components ([C₁₂MIM][Tf₂N]) dissolved in short-chain homologues ([C₂MIM][Tf₂N]), as well as for the influence of the chain lengths of the individual components on the formation of percolated liquids (i.e. where there are continuous, but separated, polar and apolar domains).

Fig. 1 Components of the IL mixtures studied previously.

In addition, we have prepared and studied mixtures where one component has a hydrocarbon chain and the other a semiperfluorocarbon chain.^32–34 The potential for immiscibility between the different chain types may well express itself in the bulk organisation of these fluid mixtures and it is also of interest to understand the surface structure given that some gases are preferentially soluble in fluorous media compared to their hydrocarbon equivalents.³⁵ Such understanding becomes of value if the mixtures were deployed as solvents for gaseous reactions, for example in the context of supported ionic liquid phases (SILPs).³⁶ Therefore, being able to understand, and by implication control, the mixing of hydrocarbon- and fluorocarbon-containing elements in a mixture is of real value.

In these previous studies,^30,32–34 the four two-component mixtures below (structures in Fig. 1) were studied using a combination of reactive-atom scattering coupled with laser-induced fluorescence (RAS-LIF), surface tension, viscometry, small-angle X-ray (SAXS) and neutron (SANS) scattering, all complemented by molecular dynamics (MD) simulations.

[C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N]

[C₁₀MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] [C₈MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N]

An observation from this work that is perhaps remarkable is that, while fluorous behaviour is often observed on the introduction of a perfluorooctyl chain, it is interesting that the mixtures [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N] are continuously miscible ([C₁₀MIM-F₁₇]⁺ has a C₈F₁₇-chain). In considering why this might be, one factor of potential significance is the electrostatic cation⋯anion attractions that could act to overcome the perceived tendency of the different chain types to de-mix. To try to understand this better, we undertook the synthesis of related neutral N-alkylimidazoles to probe this further.

Results

Synthesis

The syntheses of the target compounds are shown in Fig. 2 and four materials were prepared – C₈Im, C₈Im-F₁₃, C₁₀Im and C₁₀Im-F₁₇. The N-alkylimidazoles were obtained in good yields (80–87%) via reaction of Na⁺ Im⁻ (either pre-prepared or generated in situ) with C_nH_2n+1Br (n = 8 or 10) and were purified by short-path, vacuum distillation following work-up. The precursor for the semiperfluorinated analogues was C_mF_2m+1–CH₂CH₂–I, which could not be reacted under the same conditions, as the imidazolate anion induced Hoffmann elimination generating C_mF_2m+1–CH=CH₂. Therefore, the semiperfluoroalkyl iodide was reacted with two molar equivalents of imidazole over several days leading to low-to-moderate yields of the target compounds; details of both syntheses are found in the ESI.‡ Following work-up, these products were also purified by short-path, vacuum distillation and were isolated in yields of around 35%. The products were characterised using ¹H and ¹⁹F NMR spectroscopy and combustion analysis.

Fig. 2 Synthetic routes to the N-alkylimidazole materials.

X-ray crystal structure of C₈Im-F and C₁₀Im-F

Single crystals of C₈Im-F₁₃ and C₁₀Im-F₁₇ were obtained from diethyl ether/pentane, both crystallising in the P₂₁/c space group (CCDC deposition numbers 2417550 and 2417551, respectively‡). Note that while it was possible to refine the structure of C₈Im-F₁₃ to a final R-factor of <4%, the crystals available for the diffraction experiment with C₁₀Im-F₁₇ were layered and gave broad, streaky diffraction patterns. As such, the final R-factor for C₁₀Im-F₁₇ was ca. 8%, which is good enough for the level of characterisation required and the discussion that follows.

The two materials are, within the constraints of the different chains lengths, very close to being isostructural and isomorphous. Thus, the cell dimensions for C₈Im-F₁₃ and C₁₀Im-F₁₇ are: a = 23.8130(4) Å and 30.1835(5) Å, b = 5.42950(10) Å and 5.56120(10) Å, c = 11.1728(2) Å and 10.3336(2) Å, respectively, with unit cell angles of α = γ = 90° (by definition), β = 94.196(2)° and 93.232(2)°, again respectively. As such, the molecular structure and packing of the two compounds can be discussed in terms of one homologue as shown in Fig. 3.

Fig. 3 Aspects of the crystal and molecular structure of C₈Im-F₁₃: (a) lamellar packing viewed down the b-axis; (b) view along the (fluoro)carbon chain showing the helicity; (c) face-to-face organisation of imidazole rings.

The methylene groups bound to the imidazole ring orient the chain close to perpendicular to the plane of the ring and the first four (difluoro)methylene carbons (2 × CH₂ and 2 × CF₂) adopt an essentially antiperiplanar disposition as can be seen in Fig. 3. Beyond this, the steric requirements of the F atoms determine that the chains begin to adopt a helical arrangement (Fig. 3b), which common in perfluoroalkyl chains. The molecules behave essentially as amphiphilic materials inasmuch as the packing resembles a simple bilayer structure with the more polar imidazole rings adopting a face-to-face arrangement in the middle and the non-polar semiperfluoroalkyl chains emanating out (Fig. 3a and c). Analysis of the closest approaches of atoms in adjacent molecules shows a limited inter-chain F⋯F separation of 2.658(2) Å, a (methylene)C–H⋯N separation of 2.644(2) Å and a F⋯H–C_ring separation of 2.418(2) Å.

Mixture studies

C₈Im and C₁₀Im are colourless liquids at room temperature, but their melting points may be detected by cooling the materials to low temperature in a DSC, holding and then re-heating. Done this way, the melting point of C₈Im was determined as 20 °C, while that for C₁₀Im is −20 °C, although neither reliably appears on every cool-hold-heat cycle. By comparison, C₈Im-F₁₃ and C₁₀Im-F₁₇ are colourless solids that melt at 55 °C and 93 °C, respectively.

C₈Im and C₈Im-F₁₃

A 50 : 50 mol% mixture of C₈Im and C₈Im-F₁₃ was prepared and held between two microscope slides, which were then placed on a hot stage mounted on an optical microscope. On heating, C₈Im-F₁₃ was seen to dissolve in C₈Im and, insofar as could be seen optically, the two were continuously miscible and remained as a single phase on cooling back to room temperature.

Following this initial observation, mixtures were prepared at 10 mol% compositional intervals. They were heated to a temperature at which the mixture was liquid, sonicated and then further equilibrated for three days at 60 °C to ensure good mixing, after which their melting points were determined by DSC. The curves are found in the ESI‡ (Fig. S3) and the data extracted therefrom (Fig. 4) show that there is a eutectic composition at 50 : 50 mol% and that for all the measured compositions that have >50 mol% C₈Im-F₁₃, the melting point is above room temperature, while for those with <50 mol% C₈Im-F₁₃ the melting points are below room temperature. Interestingly, extrapolating the experimental curve from 90% to 100% C₈Im does not match the observed melting point. For mixtures with >50 mol% C₈Im-F₁₃, when undisturbed they remain as supercooled liquids at ambient temperature but solidify immediately if subjected to mechanical shock.

Fig. 4 Plot of the onset temperature of melting for mixtures of C₈Im and C₈Im-F₁₇.

After preparation, some samples were further equilibrated at 60 °C for a period of a month and, as an additional check for miscibility, a small aliquot was taken both from the very top and very bottom of the vial; the ¹H NMR spectrum was recorded for each. Given the significantly greater density of C₈Im-F compared to C₈Im (see below), if the two materials were immiscible then different proportions of the two components would be expected in the different aliquots. This was probed by integration of the N–CH₂– hydrogens, which are found at 3.98 and 4.28 ppm for C₈Im and C₈Im–F₁₃, respectively. The NMR spectra (Fig. S4, ESI‡) show identical integrations in both, thus providing no evidence for phase separation. This procedure was then repeated for mixtures that had been allowed to stand for a period of several months at room temperature with identical results.

C₁₀Im and C₁₀Im-F₁₇

Mixtures of C₁₀Im and C₁₀Im-F₁₇ could not be formed at room temperature, even with prolonged sonication and mixing. The two components did mix on heating above 70 °C, but then phase separated on cooling.

Surface tension

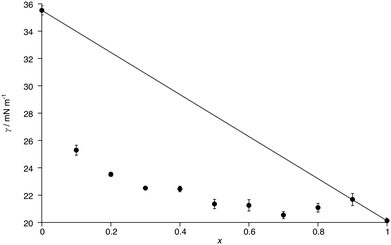
The surface tension (γ) of C₈Im and of mixtures of C₈Im and C₈Im-F₁₃ was evaluated at 55 °C using the pendant drop method. The exception was the measurement made for pure C₈Im-F₁₃ which was carried out at 58.5 °C. The density of C₈Im was measured to be 0.91 g cm⁻³ at 20 °C, while the density (also at 20 °C) for C₈Im-F₁₃ was determined as 1.75 g cm⁻³, as described in the ESI.‡

The plot in Fig. 5 shows the measured surface tension as a function of composition as well as an idealised line that represents a simple linear dependency on composition. It is immediately evident that the surface tension of C₈Im drops very substantially on the addition of only 10 mol% C₈Im-F₁₃ and that from 50 mol% C₈Im-F₁₃ where γ = 18.6 mN m⁻¹, it drops only a further 1.3 mN m⁻¹ to pure C₈Im-F₁₃. This is entirely consistent with preferential concentration of C₈Im-F₁₃ at the surface of C₈Im and is discussed in more detail below, where the magnitude of the excess surface tension is also considered.

Fig. 5 Plot of surface tension vs. composition for the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x; some error bars are smaller than the symbols. The line represents the linear evolution of surface tension with composition.

Small-angle scattering

SAXS

It is well-known that ILs possess short-range order that is observed in scattering experiments using X-rays and neutrons.^37–40 The ordering arises in one part from the separation of the (charged) polar and (uncharged) apolar parts of the ILs where one (or both) of the ions possess a long chain, and in another part from the organisation of the component ions. Curious to see what, if any, ordering might be present in these related, neutral imidazoles where there is no charge ordering due to the presence of ions, preliminary SAXS experiments were first obtained using pure C₈Im and pure C₈Im-F₁₃. Both showed scattering that is similar to related ionic materials and so a systematic study was undertaken of a series of mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x, with data recorded over the range 0.15 < q < 1.5 Å⁻¹ (equivalent to ≈42 to 4.2 Å) and plotted in Fig. 6.

Fig. 6 SAXS data for the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x offset for clarity (scale of the y-axes is normalised counts and varies in the different plots): (a) data for all compositions; (b) data for compositions showing a clear PNPP; (c) data for compositions not showing a clear PNPP.

Fig. 6a shows the data for all compositions and reveals the presence of a reflection at ca. 1.4 > q > 1.2 Å⁻¹ whose position varies with composition, representing an increased spacing as x increases.

This reflection represents the separation between nearest-neighbour molecules and is observed widely, from isotropic liquids to much more ordered liquid-crystalline materials.^41,42

Fig. 6a shows that the position of this reflection varies very little for 0.4 ≤ x ≤ 1, while outside of this range it moves to larger q (smaller separation). In the compositional range 0.4 ≤ x ≤ 1, the reflection is found at q ≈ 1.2 Å⁻¹, which corresponds to a spacing of 5.3 Å that is indicative of separation between fluorocarbon chains. At smaller values of x where the proportion of C₈Im is much higher, q increases to 1.47 Å⁻¹ (4.3 Å) at x = 0 representing the spacing between adjacent alkyl chains. The evolution with composition of the spacing corresponding to this reflection is shown in Fig. S6a (ESI‡). In the literature of ILs, a reflection at these values of q is also known as the Contact Peak (CP), where it is held to represent the spacing between adjacent cations and anions.³⁷ This is addressed in the Discussion below.

The scattering data also show a broader peak at smaller values of q, whose dimensions are consistent with local bilayer organisation correlated over short distances. This demonstrates that there is a separation of the polar (imidazole) and non-polar (chains) parts of the molecules in these neutral materials, for example as seen in the solid-state organisation in the single-crystal X-ray diffraction studies above. This reflection is analogous to the polar non-polar peak (PNPP) observed in many ILs and its evolution as a function of composition is not straightforward and so it is helpful to consider Fig. 6b and c, which compartmentalise the data according to composition. Thus, Fig. 6b shows four compositions (x = 0 and 0.7 to 1) where there is a distinct PNPP, while Fig. 6c shows the other compositions where there is no clear PNPP. The PNPP is at q = 0.35 Å⁻¹ for pure C₈Im and q = 0.32 Å⁻¹ for pure C₈Im-F₁₃, corresponding to spacings of 18.1 Å and 19.6 Å, respectively. Given that the length of C₈Im-F₁₃ from its crystal structure is ca. 13.7 Å in its all-trans arrangement, the observed spacings are consistent with a local bilayer structure, albeit with some chain interdigitation and/or folding as the bilayer dimensions are less than twice the molecular length.

Fig. 6c, however, shows a very different picture and, as exemplified where x = 0.3, there is a strong contribution from scattering at appreciably lower values of q. Thus, the data in Fig. 6c show a superposition of this low-q scattering and the PNPP, which have been deconvoluted through fitting (Fig. S6c, ESI‡) and will be discussed in conjunction with the SANS data below. The form and position of the low-q scattering suggest the presence of small scattering objects that could arise from the preferential aggregation of fluoroalkyl or alkyl chains in the mixtures. In order to clearly fit the dimensions of these scattering objects, it was necessary to collect data to much smaller values of q and, as this was not possible with the X-ray instrumentation employed, a complementary series of small-angle neutron scattering experiments were carried out on beamline D16 at the ILL in Grenoble.

SANS

The data, collected in the range 0.05 ≤ q ≤ 1 Å⁻¹ (= 126 to 6.3 Å), are again shown across three plots noting that the q-range in these experiments does not fully capture reflection found for q > 1 Å⁻¹. Fig. 7a shows the data for all compositions, Fig. 7b shows data for compositions with a clear PNPP, while Fig. 7c shows data for the remaining compositions. With data available to lower values of q, the scattering from aggregates is more readily visible and is again convoluted with the PNPP at most compositions. Where the PNPP is clearly visible in Fig. 7b its dimensions can be seen to differ slightly from those obtained from SAXS, being 17.2 Å for pure C₈Im (18.1 Å from SAXS) and 20.6 Å (19.6 Å from SAXS) for pure C₈Im-F₁₃. These differences are small and likely arise as a result of the different contrasts for the two different techniques.

Fig. 7 SANS data for the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x: (a) data for all compositions; (b) data for compositions showing a clear PNPP; (c) data for compositions not showing a clear PNPP. The y-axis is normalised counts although the scale is different in the different plots and data are offset vertically for clarity.

The SAXS and SANS data were fitted using SasView⁴³ using a combination of Lorentzian functions to describe peaks and a spherical form factor to describe the low-q scattering from small scattering objects (see ESI,‡ for details).

Two main conclusions can be drawn from the fitting. First is that it is possible to account for the low-q scattering using a model based on spherical aggregates. These can be imagined as aggregates of fluorocarbon chains against a hydrogenous ‘background’ for smaller values of x, while at larger values of x it is an inverse picture of hydrogenous units in the fluorous ‘background’. The sphere radius is not clearly defined for many of the compositions and so a value of around 10 Å, chosen by fits to the SANS data where x = 0.2–0.4 in which the sphere radius can be seen and allowed to vary a little to get the best fits, was used across the series of data (Fig. S6e, ESI‡).

What both the SAXS and SANS data show is that the PNPP spacing is not a simple linear function of composition with respect to the values for the pure materials, rather it increases significantly from ca. 18 Å at x = 0 to a maximum of ca. 24 Å at x = 0.5 (Fig. S6c, ESI‡) before decreasing again to ca. 20 Å at x = 1. This behaviour may reflect the necessity for the mutual accommodation of chains of different volumes into the local bilayer organisation when there are similar numbers of alkyl and fluroalkyl chains. It is also noteworthy that the value for the PNPP is greater for C₈Im-F₁₃ compared to C₈Im. As the PNPP reflects bilayer organisation, then the origin of the difference is not necessarily straightforward. However, in common with data obtained previously for [C₈MIM][Tf₂N] and [C₈MIM-F₁₃][Tf₂N], MD calculations performed for the neutral materials shows that there is a greater population of molecules in the all-trans configuration for C₈Im-F₁₃ compared to C₈Im (Fig. S8, ESI‡). This reflects the rather rigid nature of fluorocarbon chains and so the larger dimensions for the PNPP of C₈Im-F₁₃ likely reflects both this rigidity and the availability of chains with gauche linkages in C₈Im, which will act to compress the PNPP distance.

Molecular dynamics

Details of the MD calculations for the two pairs of mixtures, [C₈Im]_1−x[C₈Im-F₁₃]_x and [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x, are found in the ESI;‡ structure factors, S(q) were determined across the phase diagram for both.

S(q) data for [C₈Im]_1−x[C₈Im-F₁₃]_x at 10 mol% intervals and for [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x at selected compositional intervals are shown in Fig. 8a and b (fewer data were evaluated for the C₁₀ mixtures as the evolution of the data with composition was similar). In the case of [C₈Im]_1−x[C₈Im-F₁₃]_x a PNPP is evident at low q which varies around q ≈ 0.3 Å⁻¹, while there is a higher-q feature that would correspond to a CP and which moves to lower q (greater spacing) as x increases. The same broad features are also seen in the data for [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x, the only appreciable difference being the q-value for the bilayer reflection, which is slightly smaller reflecting the longer chain lengths involved.

Fig. 8 Calculated S(q) for: (a) [C₈Im]_1−x[C₈Im-F₁₃]_x evaluated at 10 mol% intervals and (b) selected compositions of [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x.

The evolution of the spacing corresponding to the two reflections as a function of composition for the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x is shown in Fig. S6b and d (ESI‡). The data show a rather monotonic increase with increasing x for the higher-q reflection (Fig. S6b, ESI‡), which differs from the slightly more nuanced picture obtained from the scattering experiments, which shows quite a steep increase from a spacing of ca. 4.3 Å for pure C₈Im up to ca. 5.3 Å at a mole fraction of C₈Im-F₁₃ of 0.4 after which the spacing is essentially constant (Fig. S6a, ESI‡). There is, however, scatter in the lower-q data (Fig. 8) and the peak at x = 0.1 is rather broad, largely on account of the finite size of the simulation box and indeed the error for these data is estimated to be ≈±1 Å. While this makes it difficult to draw hard conclusions, they do mirror the experimental data (Fig. S6d, ESI‡) inasmuch as there is an overall positive deviation from a simple linear correlation of distance with composition, particularly at higher values of x.

While the size of the simulation box possible with these calculations means that features arising from small aggregates are not seen in the S(q) plots, it is nonetheless possible to interrogate the MD trajectories to look for aggregation patterns. This has been done for all compositions studied and full results are included in the ESI,‡ while selected plots of probability distribution functions are included here in order to develop appropriate arguments. In these plots, the y-axis represents the probability (Pn_a) of finding a chain belonging to an aggregate of a particular size n_a (x-axis) normalised by the total number of corresponding molecules in the MD simulation box, which illustrates the distribution of aggregates in the mixtures.

The probability distribution functions for the chains of pure C₈Im and pure C₈Im-F₁₃ (Fig. 9a – the distribution function for C₈Im appears identical – Fig. S9a, ESI‡) are located at n_a = 1 which, as expected, shows percolation in each case. Then, on introduction of 0.1 mol fraction of C₈Im-F₁₃ to C₈Im, while C₈Im remains percolated (which it effectively does to x = 0.3, Fig. S9b, ESI‡), small aggregates of C₈Im-F₁₃ are observed up to around n_a ≈ 0.05 (Fig. 9b). The size of the C₈Im-F₁₃ aggregates increases for x = 0.2 (Fig. 9c) and then at x = 0.3, there is a step change with the observation of much larger aggregates in addition to smaller ones, the latter appearing with higher probability (Fig. 9d).

Fig. 9 Discrete probability distribution function, P(n_a), for the fluorous chains of C₈Im-F₁₃ belonging to a non-polar aggregate in the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x for: (a) x = 1.0; (b) x = 0.1; (c) x = 0.2; (d) x = 0.3 and (e) x = 0.4, and similarly for the hydrocarbon chains of C₈Im in the same mixtures for (f) x = 0.4.

Increasing the proportion of C₈Im-F₁₃ still further to x = 0.4 shows that while small aggregates remain, C₈Im-F₁₃ is approaching percolation (Fig. 9e), while the percolation in C₈Im is starting to break down with small aggregates starting to appear (Fig. 9f). Then for mixtures of composition 0.5 ≤ x ≤ 0.9, the behaviour in effect reverses as C₈Im-F₁₃ becomes percolated while aggregates of C₈Im appear with increasing probability. Thus, the picture that emerges is one that would seem to show miscible, percolated domains of the two components at the intermediate compositions with aggregates in evidence at all mixture compositions studied. As such, this provides a very good parallel with the SANS data in particular, where aggregates are most evident.

Discussion

In considering (im)miscibility between hydrocarbons and fluorocarbons, there is widespread use of the idea of a 'fluorous effect', whereby fluorous chains are held to prefer to be with other fluorous chains rather than with hydrocarbon chains, leading to localised phase separation and the potential for both hydrocarbon and fluorous domains.^1–4 An elegant computational study by Pollice and Chen proposed the origin of the effect as the preference for an intermolecular HH and an intermolecular FF interaction over two intermolecular HF interactions.⁴⁴ This being the case, then judicious use of hydrocarbon and fluorocarbon chains can lead to important effects in self-organisation, which can be seen quite effectively in, for example, the literature of liquid crystals.⁴¹

It is generally held that fluorous behaviour tends to start when the fluorocarbon chain contains eight carbon atoms or more. It is not easy to find a definitive origin of these ideas, but perhaps a clue comes from the critical temperatures for the mixtures of hexane/perfluorohexane and of octane/perfluorooctane, which are 296 K and 349 K, respectively.² Thus, the former is around room temperature, while the latter is appreciably higher and so it is perhaps apparent how 'fluorous' and perfluorooctyl may have evolved to be, in effect, somewhat synonymous. However, the fact that the mixtures exhibit a critical point means that, above that given temperature, they become miscible (akin to an upper consolute temperature),^45,46 so that the immiscibility can be overcome – in this case thermally. Indeed, such arguments have been deployed to account for an unexpected liquid crystal phase sequence in some planar complexes of gold(III) which contained both hydrocarbon and fluorocarbon chains.⁴⁷

Returning to the materials studied in this work, if, to a first approximation, the mixtures being studied are regarded simply as R-C₆H₁₃/R-C₆F₁₃ (C₈Im/C₈Im-F₁₃) and R-C₈H₁₇/R-C₈F₁₇ (C₁₀Im/C₁₀Im-F₁₇) where R = Im-CH₂CH₂–, then based on the discussion in the previous paragraphs it is perhaps not entirely surprising that C₁₀Im and C₁₀Im-F₁₇ are immiscible at room temperature, as the latter contains a perfluorooctyl chain, although they are found to mix at temperatures above around 70 °C. The same approach is also consistent with the observed miscibility of C₈Im and C₈Im-F₁₃. However, if C₁₀Im and C₁₀Im-F₁₇ are modified chemically via methylation to introduce charge by preparation of [C₁₀MIM][Tf₂N] and [C₁₀MIM-F₁₇][Tf₂N], then the two components now become miscible at room temperature.³⁴ As such, not only can temperature overcome the immiscibility of hydrocarbon and fluorocarbon chains, but electrostatic charge within ionic liquids is able to do so, too. However, from the data collected as part of this study, there is a great deal else that can be learned and other parallels that can be drawn with the ionic analogues.

The scattering experiments of the [C₈Im]_1−x[C₈Im-F₁₃]_x mixtures probed the local organisation of the materials, revealing three main features: a reflection at small spacings (q ≈ 1.3 Å⁻¹), one at larger spacings (q ≈ 0.3 Å⁻¹) and then low-angle scattering starting below q ≈ 0.5 Å⁻¹. The position of the first of these varied with composition and moved to smaller q as the proportion of C₈Im-F₁₃ increased, simply reflecting the fact the fluorocarbons chains are more voluminous than their hydrocarbon equivalents and so the intermolecular separation naturally increases. Indeed, the same effect was reported in the IL mixtures [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] and [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N].³⁴ In the IL literature, this reflection is referred to as the contact peak (CP) and is held to represent nearest-neighbour cation⋯anion separation. However, the materials under study here are neutral and yet the evolution of this reflection as a function of composition is the same as in their ionic equivalents. As noted recently by Emerson et al.,⁴² this reflection is in fact generic for all liquids and represents the separation between adjacent moieties (for example, it is a ubiquitous feature in the scattering patterns of calamitic liquid crystals).⁴¹ The scattering from adjacent moieties may indeed then reflect cations and anions, but equally it is evident that they can reflect any (fluoro)alkyl chains that are present, be they found in charged or neutral species. As such, both commonly used terms, namely adjacency peak and contact peak are evidently fit for purpose, although perhaps the former better represents its universality. It is then entirely expected that the mid-q charge-ordering peak (COP), often seen in ILs at q ≈ 0.8 Å⁻¹, is not observed in the current study.

In ILs, the reflection often seen in the approximate range 0.2 ≤ q ≤ 0.4 Å⁻¹ (representing spacings of around 15–30 Å) is the PNPP, which represents local bilayer organisation of the molecules (with a short correlation length) arising from the separation of the (charged) polar regions from the (uncharged) apolar regions. The PNPP observed for C₈Im represents a spacing of 18 Å, while for C₈Im-F₁₃ it is 20 Å. The length of a C₈ chain is ≈10 Å (be it hydrogenous or fluorous), while the imidazole unit is ca. 4.5 Å in diameter and its disposition with respect to the chain is flexible in the liquid, owing to rotation at the methylene groups adjacent to it. As such, the observed spacings are consistent with local bilayer organisation with some chain interdigitation and/or, for the more flexible C₈Im, chain folding.

Thus, while neutral, the fact that these materials order in this way implies a degree of amphiphilicity and, as the electrostatic potential surfaces for C₈Im and C₈Im-F₁₃ show (Fig. 10), this is quite consistent with a concentration of negative potential at the unfunctionalised imidazole nitrogen. The equivalent surfaces calculated for the equivalent ILs (Fig. S10, ESI‡) show a much greater difference in electrostatic potential between headgroup and chains.

Fig. 10 Calculated surface electrostatic potential (the functional employed is CAM-B3LYP with the 6-311G(3df,3pd) basis set) for (a) C₈Im and (b) C₈Im-F₁₃ at an isosurface of 64.15 e ų.

Curious to explore this amphiphilicity further, the surface tension was determined as noted above and the first point of interest is its magnitude for C₈Im which, at γ = 35.5 mN m⁻¹, is broadly comparable with that of 1-octanol (27.5 mN m⁻¹).⁴⁸ Introduction of the perfluorohexyl unit reduces the surface tension significantly and so for C₈Im-F₁₃ it was evaluated as γ = 20.1 mN m⁻¹, consistent with the generally lower surface tension of fluoro-substituted amphiphiles compared to their hydrocarbon analogues (the surface tension of 1H,1H-perfluorooctan-1-ol is 17.5 mN m⁻¹).⁴⁹ These values can be compared with data determined for the N-methylated, cationic equivalents as their bistriflimide salts [C₈MIM][Tf₂N] and [C₈MIM-F₁₃][Tf₂N] (Table 1), revealing that the addition of charge reduces γ appreciably where there is a hydrocarbon chain. However, the values of γ for C₈Im-F₁₃ and [C₈MIM-F₁₃][Tf₂N] are much closer to one another, suggesting a much greater influence of the perfluorinated chain fragment in determining the surface tension. This is also seen in considering the normalised excess surface tension (i.e. the difference between the surface tension calculated for a linear relationship with composition and the actual surface tension normalised for the total change in surface tension) for both series of mixtures as well as data for the mixtures [C₂MIM]_1−x[C₁₂MIM]_x[Tf₂N] and [C₁₀MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] (Fig. 11). The curve for each data set has the same basic form showing the greatest excess at x ≈ 0.2 to 0.4, but the difference for the [C₈Im]_1−x[C₈Im-F₁₃]_x mixtures is greater than for the [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] mixtures, which in turn are slightly greater than for the [C₂MIM]_1−x[C₁₂MIM]_x[Tf₂N] and [C₁₀MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] mixtures. The similarity of the data sets for the IL pairs perhaps points to some damping of the effect of the perfluoroalkyl chain by some combination of the charged headgroup or the anion.

Table 1 Surface tension data for pairs of hydrocarbon/fluorocarbon imidazole derivatives

Compound	γ/mN m^−1
a Measured at 296 K. b Measured at 331.5 K. c Measured at 328 K. d Value at 296 K (see ESI).
[C8MIM][Tf2N]	30.4^a
[C8MIM-F13][Tf2N]	21.9^a
C8Im	35.5^c (39.8^d)
C8Im-F13	20.1^b (25.9^d)

---

Fig. 11 Excess surface tension (%) for the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x, [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N], [C₁₀MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] and [C₂MIM]_1−x[C₁₂MIM]_x[Tf₂N].^28,30,34

Returning now to the scattering data and as outlined above, low-q scattering in the SAXS data became a dominant feature for 0.1 < x < 0.7 suggesting the presence of aggregates, which is more clearly evident in the SANS data collected to even smaller values of q. The low-q scattering could be fitted using a model containing spherical scattering objects, for which the sphere radius was relatively well defined in the SANS data for x = 0.2–0.5, where it decreased slightly with increasing x, from 10.2 to 9.8 Å. This is around the length of one fluoroalkyl or alkyl chain. However, the sphere radius was partially or totally obscured by the PNPP for other compositions. The MD data (Fig. 9 and Fig. S9, ESI‡) show the formation of fluorocarbon chain aggregates for 0.1 ≤ x ≤ 0.3, after which C₈Im-F₁₃ starts to approach percolation, noting that while C₈Im-F₁₃ percolates at x = 0.4, C₈Im does not percolate until x = 0.5.

It is then of interest to compare the behaviour of the mixtures discussed here with those of the related ILs reported recently. Thus, the two components of the mixtures [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N], which have the same chain lengths as the materials just discussed, are co-miscible at all compositions and there is very little to no low-q scattering in the SANS data. This is mirrored in the MD simulations (Fig. 12) where, on addition of [C₈MIM-F₁₃][Tf₂N] to [C₈MIM][Tf₂N], the percolation of [C₈MIM][Tf₂N] is lost and [C₈MIM-F₁₃][Tf₂N] appears over a very wide range of aggregate sizes, effectively representing a continuum of the fluorinated component in the hydrocarbon medium. This situation gradually reverses as the proportion of [C₈MIM-F₁₃][Tf₂N] increases. Thus, the aggregates observed in mixtures of the neutral materials C₈Im and C₈Im-F₁₃ are not observed in the related ILs with the same chain length.

Fig. 12 Discrete probability distribution function, P(n_a), for [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N]: [C₈MIM]⁺ chains at (a) x = 0.35; (c) x = 0.5; [C₈MIM-F₁₃]⁺ chains at (b) x = 0.35; (d) x = 0.5. Reproduced from ref. 34.

Considering now the mixtures [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N], here the two components are co-miscible at all compositions, but on addition of [C₁₀MIM-F₁₇][Tf₂N] to [C₁₀MIM][Tf₂N] (Fig. 13), the latter remains effectively percolated while small aggregates form of [C₁₀MIM-F₁₇][Tf₂N] with a much tighter size distribution than seen in the mixtures [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] (Fig. 12). As the proportion of [C₁₀MIM-F₁₇][Tf₂N] increases, its effective aggregate size increases to the extent that it is moving towards percolation and now it is [C₁₀MIM][Tf₂N] showing formation of aggregates in the medium of [C₁₀MIM-F₁₇][Tf₂N].

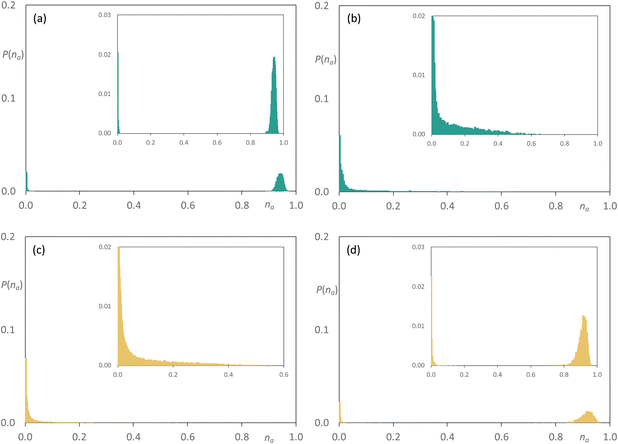Fig. 13 Discrete probability distribution function, P(n_a), for [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N]: [C₁₀MIM]⁺ chains at (a) x = 0.35; (c) x = 0.5; [C₁₀MIM-F₁₇]⁺ chains at (b) x = 0.35; (d) x = 0.5. Reproduced from ref. 34.

The behaviour is also reflected in the radial distribution functions as shown in Fig. 14, which reflect the distance (r) and probability of interaction g(r) between the terminal carbon atoms of the hydrogenous chain (CT) and fluorous chain (CTF). The data for [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] (Fig. 14a) reveal that g(r) for CT-CTF is halfway between that values for CT-CT and CTF-CTF showing that the two components are well mixed, whereas for [C₁₀MIM]_1−x[C₁₀MIM-F₁₃]_x[Tf₂N] in Fig. 14b, g(r) (CT-CTF) is lower than the halfway mark between g(r) (CT-CT) and g(r) (CTF-CTF), implying that chains that are alike (alkyl or fluoroalkyl) have a higher probability of being found together than is the case in [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N], consistent with both miscibility and aggregate formation in [C₁₀MIM]_1−x[C₁₀MIM-F₁₃]_x[Tf₂N].

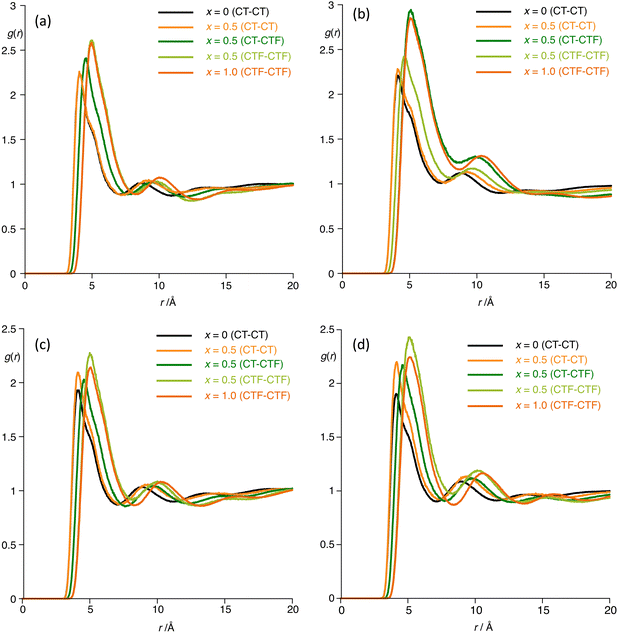Fig. 14 Radial distribution functions g(r) for the mixtures (a) [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N]; (b) [C₁₀MIM]_1−x[C₁₀MIM-F₁₃]_x[Tf₂N]; (c) [C₈Im]_1−x[C₈Im-F₁₃]_x, and (d) [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x.

Then, in the neutral systems (Fig. 14c), in both cases g(r) (CT–CTF) is actually less than g(r) (CT–CT), but interestingly both g(r) (CT–CT) and g(r) (CTF–CTF) are greater in the 50 : 50 mixture than in the pure components, with the difference being greater in the C₁₀ system. Therefore, while removal of electrostatic charge has modified the observed g(r) profiles, they are nonetheless consistent with formation of aggregates in the mixture series [C₈Im]_1−x[C₈Im-F₁₃]_x and similarly indicate non-ideal mixing for [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x, noting that given the timescales and length scales over which the MD simulations are carried out, they are themselves unable to capture immiscibility of the components.

As noted earlier, the longer chain neutral imidazoles C₁₀Im and C₁₀Im-F₂₁ are not miscible at room temperature and, in this context, it is interesting to note that on extending the length of the chains in the related ILs to C₁₂, then mixtures between [C₁₂MIM][Tf₂N] and [C₁₂MIM-F₂₁][Tf₂N] are also immiscible.⁵⁰ Thus, two mixtures of [C₁₂MIM]_1−x[C₁₂MIM-F₂₁]_x[Tf₂N] were prepared for x = 0.05 and 0.2. At x = 0.05 and 60 °C, we were able to see some scattering in SANS experiments (Fig. S12, ESI‡), but for x = 0.2 only a reasonably sharp reflection was observed in the scattering data in addition to visible crystals of [C₁₂MIM-F₂₁][Tf₂N] suggesting that, at this temperature, the two components were not miscible. Indeed, even the mixture with x = 0.05 crystallised during transportation to the Grenoble beamline, effectively confirming the immiscibility of the two components at ambient temperature.

The behaviour of the new materials reported here and their related ILs can then be summarised diagrammatically as shown in Fig. 15. Thus, the components of [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] are miscible at all compositions and no aggregates are observed. However, if both carbon chain lengths are increased by two units, then the mixtures [C₁₀MIM]_1−x[C₁₀MIM-F₁₃]_x[Tf₂N], while also miscible at all concentrations, also show the formation of aggregates, allowing some expression of the latent tendency for C₈H₁₇- and C₈F₁₇- units to associate with alike chains with a slightly higher probability than with unlike chains. However, maintaining the overall C₈ chain length in the related neutral imidazoles C₈Im and C₈Im-F₁₃ shows a parallel with the behaviour of [C₁₀MIM]_1−x[C₁₀MIM-F₁₃]_x[Tf₂N] as the components are miscible while aggregates are observed.

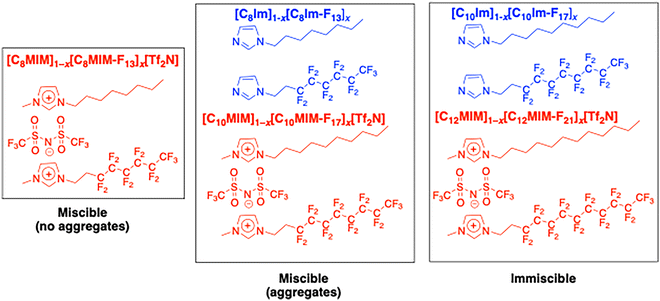Fig. 15 A summary of (im)miscibility and aggregate formation in related neutral (blue) and ionic (red) imidazole derivatives.

Extending the chains still further to charged materials [C₁₂MIM][Tf₂N] and [C₁₂MIM-F₂₁][Tf₂N] and the neutral materials C₁₀Im and C₁₀Im-F₁₇, leads, in both cases, to immiscibility. Thus, it seems that the effect of adding two CF₂ groups to the chain of a N-semiperfluoroalkylimidazole in mixtures with its hydrogenous analogue with the same overall carbon chain length is suppressed if the two components are 'converted' into the related, charged 1-methyl-3-semiperfluoroalkylimidazolium bistriflimide salts.

Summary and conclusions

Study of the series of mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x shows that the two components are miscible at all compositions at 20 °C. The X-ray single crystal structure of C₈Im-F₁₃ (and indeed of its longer homologue C₁₀Im-F₁₇) shows an amphiphilic, bilayer organisation, and a study of the surface tension across the compositional range presents clear evidence for preferential concentration of the more surface-active fluorinated component at the surface. Interestingly, comparison of the excess surface tension for these mixtures with data for the mixtures [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] and [C₂MIM]_1−x[C₁₂MIM]_x[Tf₂N] shows a rather universal form for the curve when the excesses are normalised for the difference in the surface tension of the two components.

Small-angle X-ray and neutron scattering data [C₈Im]_1−x[C₈Im-F₁₃]_x shows an adjacency (contact) peak between ca. 1.4 > q > 1.2 Å⁻¹ in SAXS whose position reflects composition, so that there is a greater side-to-side separation consequent on the presence of the more voluminous fluorocarbon chains. A reflection (PNPP) at lower values of q (ca. 0.3 Å⁻¹ and seen in both SAXS and SANS) arises from the organisation of the components into a bilayer that percolates the medium, albeit with short correlation lengths. Comparison of the observed spacing with the dimensions of the components as derived from the single-crystal structure determination suggests some sort of interdigitated arrangement. However, at most compositions, the PNPP is not easily visible in either SAXS or SANS data owing to the superposition of scattering from small aggregates, which is particularly evident in the neutron experiments where data were collected at much smaller values of q (to 0.05 Å⁻¹).

An analogous study of the longer-chain mixtures [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x was, however, precluded by the observation that at room temperature, the two materials were immiscible.

Scattering data and the results of atomistic MD calculations for [C₈Im]_1−x[C₈Im-F₁₃]_x were compared with analogous data obtained from the related mixtures of ionic materials, namely [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N] and [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N]. Thus, while small aggregates were observed in the mixtures [C₈Im]_1−x[C₈Im-F₁₃]_x, this was not the case for the related salts [C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N], where both scattering and MD data showed homogeneous mixing of the fluoroalkyl and alkyl chains. However, in the longer-chain [C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N] mixtures, the data were much closer to those for the neutral C₈ mixtures, with evidence of aggregate formation.

Thus, and as represented in Fig. 15, there is an evolution from mixtures ([C₈MIM]_1−x[C₈MIM-F₁₃]_x[Tf₂N]) that are miscible and mix without aggregation, to those that are miscible but where aggregates form ([C₁₀MIM]_1−x[C₁₀MIM-F₁₇]_x[Tf₂N] and [C₈Im]_1−x[C₈Im-F₁₃]_x) and ultimately to those that are immiscible, at least at room temperature ([C₁₂MIM]_1−x[C₁₂MIM-F₂₁]_x[Tf₂N] and [C₁₀Im]_1−x[C₁₀Im-F₁₇]_x). Each ‘step’ along the way corresponds to the addition of two difluoromethylene groups, whose effect is mitigated by the introduction of charge via methylation of the imidazole ring and concomitant incorporation of a bistriflimide counter-anion. This reveals an interesting and ‘opposing’ pairs of changes – such knowledge adds beneficially to the ability to control aspects of self-organisation predictively through molecular design.

Experimental

All experimental details are found in the ESI.‡

Author contributions

The project was conceptualised by DWB and JMS. Experimental investigation was undertaken by JL, EG-B and NSE. MD calculations were performed by KS. Experimental data were processed and analysed by EG-B, JL, BD, NSE, SS, DWB and JMS. Supervision was provided by DWB, JMS, NSE, BD and JNCL. The original draft was written by DWB and then reviewed and edited by all authors. Funding and beamtime were secured by DWB, JMS and NSE. Data were curated by DWB and JL. TFNT and ACW collected the crystallographic data and solved and refined the structures.

Conflicts of interest

The authors declare no conflicts of interest.

Data availability

The data supporting this article have been included as part of the ESI,‡ or are found at https://doi.org/10.15124/16830606-74f1-42b0-b747-90ca0e61414d (NMR, MS, SAXS & surface tension data) and https://doi.org/10.5291/ILL-DATA.9-12-720 (D16 SANS data).

Acknowledgements

We thank the Wild Fund of the Department of Chemistry (JL), University of York (TFNT) and the EPSRC (NSE; EP/T031174/1) for funding, the ILL for the allocation of beamtime (Grant No. 9-12-720) and STFC for funding the access, FCT (Portugal) for support to KS from project 2023.09286.CEECIND and Professor Karen Edler (Lund University) for many stimulating discussions. The authors take great pleasure in dedicating this paper to Giuseppe Resnati on the occasion of his 70th birthday. JMS and DWB have been grateful recipients of his hospitality and that of his colleagues in Milano – in particolare, formaggio e passito all’aperitivo. Grazie Giuseppe e tante congratulazioni.

References

1. J. D. Dunitz, ChemBioChem, 2004, 5, 614–621.
2. J. B. Gilmour, J. O. Zwicker, J. Katz and R. L. Scott, J. Phys. Chem., 1967, 71, 3259–3270.
3. D. M. Lemal, J. Org. Chem., 2004, 69, 1–11.
4. I. T. Horváth, Fluorous Chemistry, Springer-Verlag, Berlin, Heidelberg, 2012.
5. F. Guittard, E. T. de Givenchy, S. Geribaldi and A. Cambon, J. Fluorine Chem., 1999, 100, 85–96.
6. C. J. Wilson, D. A. Wilson, A. E. Feiring and V. Percec, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 2498–2508.
7. C. Tschierske, Liq. Cryst., 2012, 318, 1–108.
8. S. W. Wang and R. E. Marchant, Macromolecules, 2004, 37, 3353–3359.
9. C. Holtze, A. C. Rowat, J. J. Agresti, J. B. Hutchison, F. E. Angilè, C. H. J. Schmitz, S. Köster, H. Duan, K. J. Humphry, R. A. Scanga, J. S. Johnson, D. Pisignano and D. A. Weitz, Lab Chip, 2008, 8, 1632–1639.
10. N. M. Kovalchuk, A. Trybala, V. Starov, O. Matar and N. Ivanova, Adv. Colloid Interface Sci., 2014, 210, 65–71.
11. M. F. C. Gomes and A. A. H. Pádua, J. Phys. Chem. B, 2003, 107, 14020–14024.
12. D. Almantariotis, A. S. Pensado, H. Q. N. Gunaratne, C. Hardacre, A. A. H. Pádua, J. Y. Coxam and M. F. C. Gomes, J. Phys. Chem. B, 2017, 121, 426–436.
13. J. Eastoe, A. Dupont and D. C. Steytler, Curr. Opin. Colloid Interface Sci., 2003, 8, 267–273.
14. M. Monduzzi, Curr. Opin. Colloid Interface Sci., 1998, 3, 467–477.
15. M. P. Krafft and J. G. Riess, Chem. Rev., 2009, 109, 1714–1792.
16. J. G. Riess, Curr. Opin. Colloid Interface Sci., 2009, 14, 294–304.
17. M. Cametti, B. Crousse, P. Metrangolo, R. Milani and G. Resnati, Chem. Soc. Rev., 2012, 41, 31–42.
18. A. J. Sicard and R. T. Baker, Chem. Rev., 2020, 120, 9164–9303.
19. E. de Wolf, G. van Koten and B. J. Deelman, Chem. Soc. Rev., 1999, 28, 37–41.
20. K. Shimizu, A. A. Freitas and J. N. C. Lopes, J. Mol. Liq., 2017, 226, 28–34.
21. O. Russina, F. Lo Celso, M. Di Michiel, S. Passerini, G. B. Appetecchi, F. Castiglione, A. Mele, R. Caminiti and A. Triolo, Faraday Discuss., 2013, 167, 499–513.
22. A. B. Pereiro, M. J. Pastoriza-Gallego, K. Shimizu, I. M. Marrucho, J. N. C. Lopes, M. M. Piñeiro and L. P. N. Rebelo, J. Phys. Chem. B, 2013, 117, 10826–10833.
23. L. F. Lepre, L. Pison, I. Otero, A. Gautier, J. Dévemy, P. Husson, A. A. H. Pádua and M. C. Gomes, Phys. Chem. Chem. Phys., 2019, 21, 8865–8873.
24. A. S. M. C. Rodrigues, A. M. Fernandes, J. Dévemy, M. C. Gomes and L. M. N. B. F. Santos, J. Mol. Liq., 2019, 282, 385–391.
25. G. D. Smith, O. Borodin, J. J. Magda, R. H. Boyd, Y. S. Wang, J. E. Bara, S. Miller, D. L. Gin and R. D. Noble, Phys. Chem. Chem. Phys., 2010, 12, 7064–7076.
26. T. L. Merrigan, E. D. Bates, S. C. Dorman and J. H. Davis, Chem. Commun., 2000, 2051–2052.
27. O. T. D. Abafe, M. M. Azim, B. S. Martincigh and A. Stark, J. Mol. Liq., 2022, 349, 118104.
28. D. W. Bruce, C. P. Cabry, J. N. C. Lopes, M. L. Costen, L. D'Andrea, I. Grillo, B. C. Marshall, K. G. McKendrick, T. K. Minton, S. M. Purcell, S. Rogers, J. M. Slattery, K. Shimizu, E. Smoll and M. A. Tesa-Serrate, J. Phys. Chem. B, 2017, 121, 6002–6020.
29. C. P. Cabry, L. D'Andrea, K. Shimizu, I. Grillo, P. X. Li, S. Rogers, D. W. Bruce, J. N. C. Lopes and J. M. Slattery, Faraday Discuss., 2018, 206, 265–289.
30. E. J. Smoll, M. A. Tesa-Serrate, S. M. Purcell, L. D’Andrea, D. W. Bruce, J. M. Slattery, M. L. Costen, T. K. Minton and K. G. McKendrick, Faraday Discuss., 2018, 206, 497–522.
31. C. P. Cabry, L. D'Andrea, N. S. Elstone, S. Kirchhecker, A. Riccobono, I. Khazal, P. X. Li, S. E. Rogers, D. W. Bruce and J. M. Slattery, Phys. Chem. Chem. Phys., 2022, 24, 15811–15823.
32. N. S. Elstone, K. Shimizu, E. V. Shaw, P. D. Lane, L. D'Andrea, B. Demé, N. Mahmoudi, S. E. Rogers, S. Youngs, M. L. Costen, K. G. McKendrick, J. C. Lopes, D. W. Bruce and J. M. Slattery, J. Phys. Chem. B, 2023, 127, 7394–7407.
33. S. M. Purcell, P. D. Lane, L. D’Andrea, N. S. Elstone, D. W. Bruce, J. M. Slattery, E. J. Smoll, S. J. Greaves, M. L. Costen, T. K. Minton and K. G. McKendrick, J. Phys. Chem. B, 2022, 126, 1962–1979.
34. N. S. Elstone, E. V. Shaw, K. Shimizu, J. S. Lai, B. Demé, P. D. Lane, M. L. Costen, K. G. McKendrick, S. Youngs, S. E. Rogers, J. N. C. Lopes, D. W. Bruce and J. M. Slattery, Faraday Discuss., 2024, 253, 55–78.
35. K. Li, Y. L. Wang, C. L. Wang, F. Huo, S. J. Zhang and H. Y. He, J. Am. Chem. Soc., 2024, 146, 25569–25577.
36. R. Fehrmann, A. Riisager and M. Haumann, Supported Ionic Liquids: Fundamentals and Applications, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014.
37. K. Shimizu, C. E. S. Bernardes and J. N. C. Lopes, J. Phys. Chem. B, 2014, 118, 567–576.
38. J. N. A. C. Lopes and A. A. H. Padua, J. Phys. Chem. B, 2006, 110, 3330–3335.
39. A. Triolo, O. Russina, H. J. Bleif and E. Di Cola, J. Phys. Chem. B, 2007, 111, 4641–4644.
40. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426.
41. D. M. Agra-Kooijman and S. Kumar, Handbook of Liquid Crystals, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014, pp. 1–38.
42. M. S. Emerson, R. Ogbodo and C. J. Margulis, Faraday Discuss., 2024, 253, 11–25.
43. https://www.sasview.org, (accessed 05/06/2025).
44. R. Pollice and P. Chen, J. Am. Chem. Soc., 2019, 141, 3489–3506.
45. P. J. Clements, S. Zafar, A. Galindo, G. Jackson and I. A. McLure, J. Chem. Soc., Faraday Trans., 1997, 93, 1331–1339.
46. A. L. Archer, M. D. Amos, G. Jackson and I. A. McLure, Int. J. Thermophys., 1996, 17, 201–211.
47. R. R. Parker, A. J. McEllin, X. B. Zeng, J. M. Lynam and D. W. Bruce, Liq. Cryst., 2022, 49, 1162–1173.
48. https://www.surface-tension.de, (accessed 05/06/2025).
49. M. K. Bernett, N. L. Jarvis and W. A. Zisman, J. Phys. Chem., 1962, 66, 328–336.
50. A. P. Abbott, R. Atkin, M. D. Bala, S. J. Brown, D. W. Bruce, P. Carbone, F. Castiglione, M. C. Gomes, J. F. Dufrêche, K. J. Edler, A. Feeney, K. Goloviznina, J. L. Gómez-Estévez, T. S. Groves, B. Hansen, R. Hendrikse, C. Holm, P. Illien, R. Kjellander, A. Kornyshev, C. J. Margulis, J. Maurer, S. R. Miao, S. Perkin, E. Rezabal, B. R. de Moraes, B. Roling, B. Rotenberg, J. Sangoro, N. Schaeffer, M. Schönhoff, K. Shimizu, J. M. Slattery, N. Taylor, Y. Umebayashi, A. van den Bruinhorst, M. Watanabe and F. Zills, Faraday Discuss., 2024, 253, 146–180.

---

Footnotes

† Dedicated to Professor Giuseppe Resnati on the occasion of his 70th birthday, celebrating a career in fluorine and non-covalent chemistry.

‡ Electronic supplementary information (ESI) available. CCDC 2417550 and 2417551. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5cp01737h

---