Unveiling sodium storage mechanisms in hard carbon via machine learning-driven simulations integrated with accurate site occupation identification

Abstract

Hard carbon (HC) has attracted considerable interest as a promising anode material for sodium-ion batteries (SIBs) due to its high specific capacity, excellent cycling stability, and cost-effectiveness. Nevertheless, the sodium storage mechanism in HC remains poorly understood owing to challenges in precisely characterizing its structural disorder, complexity, and intricate interatomic interactions. In this work, we investigate the sodium storage behavior in HC anodes using a machine learning potential (MLP) integrated with a random forest-based sodium insertion site identification framework. The trained MLP accurately captures both the structural features of HC and the sodium insertion behavior. HC comprises an amorphous network of defects, edges, graphitic domains, and nanopores, primarily interconnected through sp/sp²/sp³-hybridized carbon bonds. For the first time, we simulate the continuous voltage profile associated with the stepwise sodium insertion during both the charging and overcharging states. This voltage profile reproduces experimental observations and disentangles the contributions of adsorption, intercalation, and pore filling, offering a pathway to elucidate the storage mechanisms across different systems and rationalize the discrepancies observed in experiments. During the overcharging stage, excessively short Na–Na distances enhance repulsion, leading to negative voltages. Besides, the formation of sodium clusters was observed, which pose a safety risk to the battery. Our findings demonstrate that machine learning-based simulations constitute a powerful and emerging approach for investigating sodium storage mechanisms and offer valuable guidance for the experimental optimization of HC anodes. Moreover, this strategy can be extended to other electrodes, electrolytes in SIBs, and even alternative battery systems.

---

Introduction

Sodium-ion batteries (SIBs) have emerged as a promising rechargeable battery technology for large-scale energy storage, owing to sodium's natural abundance and cost-effectiveness.^1–10 Among the anode candidates for SIBs, hard carbon (HC) demonstrates compelling advantages including low cost, environmental benignity, and tunable microstructures, establishing its viability for commercial deployment.^11–19 Nevertheless, the atomic-scale sodium storage mechanism in HC remains incompletely resolved, stemming from its intricate yet disordered architecture featuring abundant defects, edges, curved graphene domains, and hierarchical porosity.^2,4 These structural characteristics induce complex C–C and Na–C interactions that collectively govern ion adsorption, intercalation, and pore-filling processes.^20–25

The sodium storage mechanism in HC has been debated for decades, with competing models proposed to rationalize the characteristic voltage profile featuring a sloping region (>0.1 V) and a plateau region (<0.1 V).^4,6,26–29 The “intercalation–filling” model proposed by Stevens and Dahn posits that sodium storage occurs via interlayer intercalation and nanopore filling.³ Interlayer intercalation provides a stable contribution to capacity but is constrained by the intrinsic layer spacing of HC; excessive intercalation may damage the layered structure and compromise the cycling stability. In contrast, nanopore filling is the primary source of high capacity in HC, with the pore size and distribution directly determining the upper limit of filling capacity. If the pore size is too small, the transport of sodium ions is hindered, ultimately reducing the rate capability of the material. Cyclic voltammetry profiles reported by Cao et al. revealed an additional pair of redox peaks distinct from those in lithium-based systems, suggesting an “adsorption–intercalation” mechanism.³⁰ Mitlin et al. observed voltage-dependent interlayer expansion via X-ray diffraction (XRD), further corroborating the intercalation process.³¹ Furthermore, Li et al. correlated sodium capacity with tunable interlayer spacing achieved via heteroatom doping, reinforcing the role of intercalation in sodium storage.³² The adsorption process primarily occurs at defect sites and edges on the HC surface, which can rapidly accommodate sodium ions and significantly enhance the rate performance. However, the adsorption capacity is limited by the specific surface area, and excessive defects may reduce the electrical conductivity. Interlayer intercalation contributes to maintaining the structural stability, and the synergy between the two processes enables a balanced performance between high rate capability and long cycle life. Nevertheless, this mechanism does not account for the capacity contribution of pore structures and could hardly explain the origin of capacity in the low-potential region. Li et al. detected no interlayer spacing change during sodiation via high-resolution transmission electron microscopy (HRTEM) while identifying metallic sodium signatures in the plateau region through X-ray photoelectron spectroscopy (XPS), supporting an “adsorption–filling” mechanism.³³ The high activity of adsorption sites enhances the adsorption kinetics of sodium ions, while pore filling compensates for the limited adsorption capacity. However, because interlayer intercalation is not involved, structural stability depends on the rigidity of the pore framework; pore collapse during long-term cycling can lead to rapid capacity decay. Recently, small- and wide-angle X-ray scattering (SAXS/WAXS) analyses by Yamada et al. revealed concurrent interlayer expansion and pore filling, proposing a unified “adsorption–intercalation–filling” mechanism.³⁴ In this mechanism, adsorption ensures high-rate performance, intercalation maintains structural stability, and filling increases the total capacity. However, this mechanism previously lacked direct atomic-scale evidence, and the dynamic evolution of the three processes during sodium insertion remained unclear, making it difficult to accurately guide structural optimization of HC materials. Despite these advances, the persistence of these controversies stems from the lack of effective atomic-scale methods to capture sodium storage processes. A comprehensive atomic-scale framework linking voltage profile characteristics, sodium storage mechanisms, and microstructure engineering remains elusive, hindering the rational design of advanced HC anodes.^35–40

Atomic-scale investigations of the sodium storage mechanism in HC primarily rely on experimental characterization and theoretical simulations, both of which have made significant progress. Experimentally, Grey et al. employed operando ²³Na solid-state nuclear magnetic resonance (ssNMR) combined with pair distribution function (PDF) analysis to reveal the formation of sodium clusters within closed pores during the low-voltage plateau region.⁴¹ Chisholm et al. utilized aberration-corrected transmission electron microscopy (TEM) to identify pentagonal and heptagonal ring defects in curved graphene sheets and elucidated their role in inducing nanopore formation. Fujiwara et al. further confirmed, via ex situ XRD and Raman spectroscopy, the reversible expansion and contraction of graphene interlayer spacing induced by Na intercalation and deintercalation. However, current experimental characterization techniques generally can hardly achieve atomic-level resolution, and most methods are challenging to implement under operando conditions, limiting the ability to capture the dynamic sodium storage process under realistic conditions.⁴² On the theoretical side, Youn et al. employed density functional theory (DFT) calculations to evaluate the energetic favorability of AA-stacked graphite domains for Na intercalation and the stability of Na₄ clusters on defective graphene.⁴³ Hoster et al. applied entropy profiling and molecular dynamics (MD) simulations, concluding that sodium deposition on pore walls is thermodynamically more favorable than pore interior filling, with the Na binding energy being dependent on the pore size.⁴⁴ Liu et al. further demonstrated through DFT calculations that the energy barrier for Na intercalation decreases significantly when the graphene interlayer spacing exceeds 3.7 Å.^30,45 While first-principles calculations provide high accuracy, they are inherently limited by system size, making large-scale simulations computationally challenging. Classical MD simulations can achieve large-scale modeling, but their accuracy is relatively lower, and the results often deviate from experimental observations. Consequently, theoretical simulations remain constrained by the difficulty in simultaneously achieving high accuracy and large spatiotemporal scales.

Recently, machine learning (ML) methods have been increasingly applied across various research fields and hold great potential for investigating the sodium storage mechanisms in HC.^46–48 On one hand, ML models can rapidly establish quantitative relationships between structural features and the electrochemical performance in HC, thereby uncovering intrinsic correlations.^48–51 On the other hand, ML potentials (MLPs), trained on first-principles calculation data as reference, enable high-accuracy simulations, and MLP-based MD simulations facilitate large-scale modeling.^52–54 Such simulations can more comprehensively account for experimental factors, offering a promising approach for in-depth elucidation of the microscopic mechanisms underlying sodium storage.

Herein, we developed an MLP integrated with a random forest (RF)-based site identification algorithm as a robust platform for investigating the intrinsic sodium storage mechanism in HC.^55–59 A curated dataset encompassing diverse atomic configurations of sodium, carbon, and sodium–carbon systems was constructed. Leveraging this dataset, we trained an MLP capable of accurately capturing the complex interatomic interactions within the Na–HC systems. Implementation of an RF classifier enabled accurate identification and categorization of sodium storage sites into adsorption, intercalation, and pore-filling types. By synergistically combining the MLP with site identification, we investigated the sodium storage process in HC and simulated the voltage profile in stepwise, atom-by-atom sodium insertion. The simulation results distinctly resolve the contributions of different site types to voltage and capacity at each stage. This study provides a powerful methodological framework for probing microscopic sodium storage mechanisms and links atomic-scale sodium behavior with macroscopic electrochemical performance, contributing to resolving long-standing mechanistic controversies surrounding the HC anode in SIBs and laying a theoretical foundation for understanding sodium storage, diffusion processes and the rational design of high-performance HC anodes.

Methods

MLP training

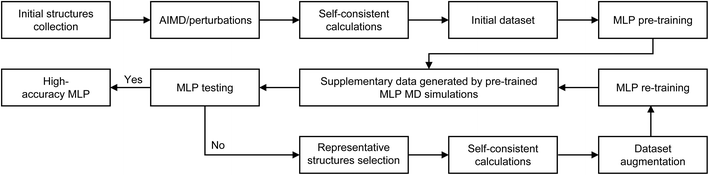
The workflow for MLP training is illustrated in Fig. 1. The main training process will be explained in detail below.

Fig. 1 The workflow for MLP training.

Initial structure collection. To develop a high-accuracy MLP, a high-quality dataset with structural diversity and completeness is required. Existing bulk and surface structures were first collected, and simple models including sodium, carbon, and sodium–carbon systems were constructed to serve as initial structures.

Ab initio MD (AIMD) simulations and structural perturbations. AIMD simulations and structural perturbations are the main methods to enrich the initial structures. AIMD was performed on the initial structures, with intentional lattice distortions introduced to enhance structural diversity. Temperature was controlled with a Nosé–Hoover thermostat.⁶⁰ Comprehensive sampling of sodium insertion configurations, including adsorption, intercalation, and pore filling, was conducted across a wide range of temperatures (200–5000 K) and pressures (0–5 GPa).⁵²

Initial dataset. First-principles self-consistent (SC) calculations were carried out using the Projector Augmented Wave (PAW) method within the Vienna Ab initio Simulation Package (VASP) for all initial structures.⁶¹ The Perdew–Burke–Ernzerhof (PBE) functional was employed for electronic exchange-correlation,⁶² with long-range van der Waals interactions corrected using the DFT-D3 method.⁶³ A plane-wave energy cutoff of 500 eV and a k-point spacing of 0.03 Å⁻¹ were adopted.⁶⁴ The above methods, functionals, and parameters ensure the accuracy of the SC results and the subsequent MLP training. Structures, energies and forces from SC calculations comprise the initial datasets.

MLP pre-training. The initial dataset was first subjected to principal component analysis (PCA) and then split into training and test sets at a ratio of 9 : 1. The neuroevolution potential (NEP) framework, a type of MLP optimized via neuroevolution algorithms, was employed. Its key advantage lies in dynamically refining the neural network architecture, enabling accurate representation of complex interatomic interactions while maintaining the computational efficiency.⁵⁹ NEP training was performed using the Graphics Processing Units Molecular Dynamics (GPUMD) package,⁵⁹ with four models trained concurrently using identical hyperparameters which are the framework parameters set prior to training, including the number of neural network layers set as 3, training steps set as 4 × 10⁵, the number of neurons set as 100 and the cutoff radius set as 7.0 Å, which were tuned to prevent underfitting or overfitting.

MLP testing. The loss function measures the deviation between MLP-predicted and DFT reference values and serves as a core metric to test the accuracy of trained MLP. The objective of training is to minimize the loss function. In this work, root-mean-square error (RMSE) was used as the loss function, with weights for energy, force, and virial set to λ_e = 1.0, λ_f = 1.0, and λ_v = 0.1, respectively. A smaller RMSE indicates a higher accuracy of the trained MLP. The performance of the MLP model was further evaluated via RMSEs in its predictions of energy, force, and virial.

Supplementary data by pre-trained MLP MD simulations. Typically pre-trained MLP or MLP trained once cannot achieve the required accuracy. Therefore, it is necessary to supplement the initial dataset by generating extended structures. In this work, the extended structures were generated using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS),⁶⁵ a high-efficiency classical MD simulation package based on the pre-trained MLP, to reduce the computational cost of AIMD simulations. Supplementary datasets were processed using an active learning workflow implemented in the GPUMD package,⁵⁸ which efficiently explores previously uncharted configuration spaces. To avoid redundant data and ensure structural diversity, structures exhibiting significant force deviations were filtered, and representative configurations were selected via principal component analysis (PCA)—a common method to determine the correlation between the newly generated structures and those in the initial dataset.⁶⁶ For all the selected structures, DFT SC calculations were performed following the above methods and parameters to obtain energies, atomic forces and virial, constituting fundamental data components to supplement the initial dataset.

MLP re-training. After enriching the dataset, the MLP was re-trained, and its accuracy was evaluated through testing. If the accuracy converged, the MLP training was considered complete; otherwise, the workflow returned to “MD simulations via the trained MLP” step, incorporating representative data into the dataset, and re-training the MLP. This process was repeated until the desired level of accuracy was achieved.

Initial construction of the HC model

The initial HC structures were generated using the trained NEP model. In particular, 5000 carbon atoms were randomly distributed within a 41.4 × 41.4 × 41.4 ų simulation box, followed by high-temperature NVT MD simulations at 4000 K for 4 ps. To capture the structural evolution of HC during the annealing process and to obtain representative models for subsequent studies, the configurations corresponding to 1 ps, 2 ps, and 4 ps of the annealing process were selected.

HC model construction with sodium insertion

Having established the stable HC models, we next investigated sodium insertion behavior within this structural framework. A three-step screening procedure was then employed to identify optimal sodium insertion sites: (i) spatial screening: potential sites were identified under spatial constraints (minimum Na–Na distance: 3.0 Å; minimum Na–C distance: 2.0 Å) to mitigate strong coulombic repulsion, generating an initial candidate list; (ii) SC calculation screening: SC calculations using the trained MLP were performed on candidates by traversing the sodium insertion list, selecting the 50 configurations with the lowest energies; (iii) geometry optimization screening: the selected configurations underwent minimization via the conjugate gradient (CG) algorithm to determine global energy minima. This procedure was iterated until all candidate sites in the list were evaluated. To simulate the overcharging behavior, 1000 sodium atoms were inserted into the HC model (Na/C ratio = 1 : 5), corresponding to a theoretical capacity of 446.7 mA h g⁻¹.

Sodium site identification

Following the determination of optimal sodium insertion sites via the aforementioned screening procedure, we performed a systematic classification of these sites to elucidate their structural characteristics and the corresponding sodium storage mechanisms. Sodium insertion site identification can be accomplished through a two-step protocol: potential intercalation sites were first identified via geometric analysis of sodium and carbon atomic arrangements. Adsorption and pore-filling sites were subsequently distinguished using an ML classifier.⁴⁴ For each target sodium atom, the local carbon environment within a 5.0 Å radius was analyzed. Intercalation site identification requires (i) the presence of at least two carbon networks, each comprising a minimum of eight carbon atoms around the sodium atom; (ii) sufficient planarity of fitted carbon planes (the root mean square deviation of the carbon atomic position from the fitted plane is less than 0.35 Å in this study); (iii) dihedral angle between the fitted planes within defined ranges (<35° or >145°); (iv) location of the sodium atom within the projection area of each carbon network onto its fitted plane.

ML algorithms chosen for site identification

To achieve accurate and comprehensive identification of sodium insertion sites in HC, we employed several ML algorithms commonly used for classification, including RF, support vector machine (SVM), and clustering, as detailed below:

RF. A supervised learning model composed of multiple decision trees, offering strong resistance to overfitting and exhibiting high classification accuracy when capturing complex correlations between structural features and site types.

SVM. A supervised learning method that constructs an optimal classification hyperplane in high-dimensional feature space. By maximizing the margin, it enables accurate discrimination among different categories of sodium insertion sites.

Clustering. An unsupervised learning approach that automatically partitions sodium sites into distinct groups based on structural feature similarity, without the need for labeled samples.

ML model training for site identification

The algorithms were subsequently applied to discriminate adsorption sites from pore-filling sites. To construct the dataset, the HC models corresponding to 1 ps and 4 ps were selected, and sodium atoms were incrementally inserted into these models following the procedure described above. Thus, we obtained a total of 2000 data points by inserting 1000 sodium atoms into each of the two HC models. For each inserted sodium atom, the local atomic environment (within 5.0 Å of each sodium atom) and the corresponding binding energies (referenced to bulk sodium) were extracted. 0.1 eV is a commonly used threshold in experiments to distinguish the sloping region from the plateau region.^4,6,26–29 The sloping region indicates stronger interactions between sodium and the HC anode, mainly contributed by adsorption and intercalation sites, whereas the plateau region reflects weaker interactions, primarily due to intercalation and pore-filling sites. Since we have already screened intercalation sites using geometric criteria, 0.1 eV can serve as a cutoff to further distinguish adsorption sites from pore-filling sites, i.e., sites with binding energy >0.1 eV were designated as adsorption sites, while those <0.1 eV were classified as pore-filling sites.^4,6,26–29 Fourteen structural features were extracted, including the number of sodium and carbon atoms. PCA was used to evaluate the effectiveness of these features. The ML classifier was trained to establish feature-site correlations, with the optimized model ultimately categorizing sodium sites as adsorption or pore-filling types. The dataset was split into training and test sets at a ratio of 4 : 1, followed by model training and evaluation based on aforementioned RF, SVM and clustering algorithms.

Analyses of ML models

To quantitatively evaluate the classification performance of the ML models, we performed the following analyses:

Feature importance evaluation. Features were ranked according to their importance derived from the RF model. Top-ranked features are considered the most influential for predictions, whereas lower-ranked features contribute less. Feature importance is a core metric for measuring the degree of influence of each structural feature on the model's classification results. A higher value indicates that the feature plays a more critical role in distinguishing between different types of sodium storage sites. It helps us quickly identify the key structural parameters that determine sodium storage behavior.

Pearson correlation. A measure that quantifies the strength and direction of the linear relationship between two variables. Its correlation coefficient ranges from −1 to 1. The closer the coefficient is to 1 or −1, the stronger the linear correlation between the two variables; a coefficient close to 0 indicates that there is almost no linear correlation between them. In this study, it is mainly used to quantify the strength of the correlation between the 14 selected structural features and the types of sodium storage sites.

Receiver operating characteristic (ROC). A widely adopted metric for evaluating the performance of binary classification models. In this study, the binary classification task corresponds to distinguishing absorption sites from pore-filling sites. The area under the ROC curve (AUC) obtained was employed as a key quantitative measure to assess the discriminative power of the model in differentiating these two types of sodium storage sites.

Shapley Additive exPlanations (SHAP) summary plot. In the SHAP summary plot, the horizontal axis represents the SHAP value, indicating both the direction and magnitude of a feature's contribution to the prediction. A positive SHAP value (SHAP > 0) denotes a positive contribution of the feature to the prediction, whereas a negative value (SHAP < 0) indicates a negative contribution. The absolute value reflects the strength of the impact. The color of each point corresponds to the feature value for the given sample, with red indicating high values and blue indicating low values. We employed SHAP to interpret the RF model, thereby quantitatively analyzing the direction and magnitude of each structural feature's contribution to site classification, while providing a visual representation of feature importance and the potential correlation with sodium storage behavior.

Results and discussion

Construction of the MLP model

The dataset comprises three structural categories: pure sodium, pure carbon, and Na_xC structures, totaling 6183 configurations. Pure sodium systems include sodium atoms, clusters and bulk phases. Pure carbon systems encompass four subtypes: amorphous carbon, layered carbon (e.g. graphite and graphene), spherical carbon (e.g. fullerene) and tubular carbon (e.g. carbon nanotube). The Na_xC system covers sodium concentrations from x = 0 to 0.25, including overcharging states. Fig. S1 illustrates the dataset composition (Table S1). After training the MLP (Fig. 1), we validated the NEP against DFT calculations. The RMSEs for energy and force are 21.6 meV per atom and 427.8 meV Å⁻¹,⁶⁷ respectively, demonstrating close agreement with DFT values (Fig. S2a and b). Energy calculations of various Na–C structures using the developed MLP reveal minimal deviations (<41.8 meV per atom) from DFT references, validating the force field's accuracy and applicability for modeling sodium storage behavior of HC anodes (Fig. S2c and d).

Analysis of HC models

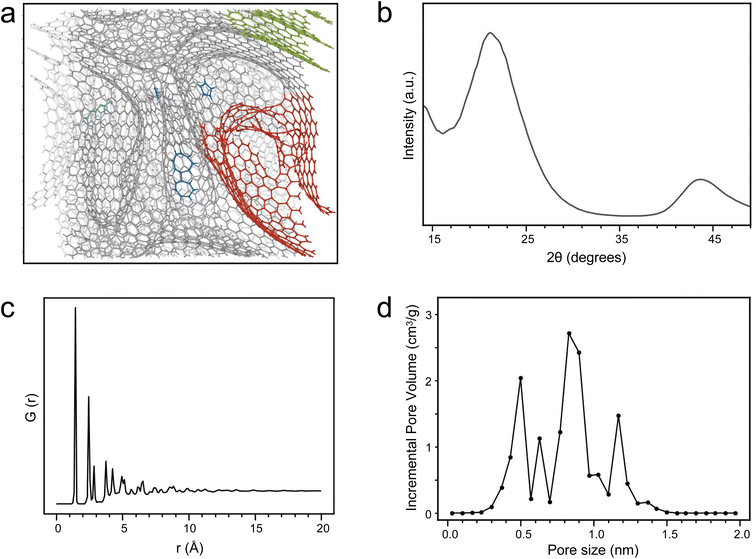
Following the development of the well-trained MLP, we constructed HC models (Fig. S3). As shown in Fig. 2a, the HC model exhibits a highly disordered carbon network with a density of 1.4 g cm⁻³, well within the characteristic range of experimental HC materials (1.2–2.0 g cm⁻³).^9,68–74 This relatively low density facilitates larger interlayer spacing and porous structures, beneficial for sodium ion insertion and transport.^54–56 Our HC model exhibits distinct defects, edge configurations, graphitic domains, and porous architectures (Fig. 2a and S4),⁷⁵ The fractions of sp-, sp²-, and sp³-hybridized carbon atoms are 1.1%, 98.7%, and 0.2%, respectively. Collectively, these features define the intrinsic structural characteristics of HC materials. The sp-hybridized carbon concentrates at edges or defect sites, while the sp³-hybridized carbon predominates in interlayer cross-linking regions. The simulated XRD patterns exhibit characteristic graphitic peaks at 21.22° and 43.68°, which are ascribed to the (002) and (101) planes in graphitic carbon (Fig. 2b). The interlayer spacing estimated from the (002) peak from XRD is 4.18 Å, in agreement with experimental measurements (3.7–4.2 Å).^9,28,76,77 As illustrated in Fig. 2c, the radial distribution function (RDF) exhibits a sharp primary peak at 1.42 Å^78,79 and a secondary peak at 2.42 Å, corresponding to the sp² C–C bond length and the distance between carbon atoms and their second-nearest neighbors in graphite, respectively, indicating the predominance of the sp²-hybridized layered graphitic structures with short-range order. We extracted five-, six-, and seven-membered rings from the HC structure and computed the corresponding RDF profiles (Fig. S5). The RDF peaks of six-membered rings well aligned with those of the overall HC structure, demonstrating that six-membered rings constitute the dominant structural motif. The RDF peaks of five-membered rings appear at 1.42 Å and 2.31 Å, generally consistent with previous reports.^79–81 Compared to six-membered rings, the next-nearest neighbor C–C distances in five-membered rings are shorter, primarily due to compressive strain and reduced bond angles. The RDF peaks of seven-membered rings appear at 1.44 Å, 2.55 Å, and 3.25 Å, in good agreement with previous studies.^81–83 Relative to six-membered rings, the next-nearest and third-nearest neighbor distances in seven-membered rings are larger, largely owing to the larger bond angles. At increasing radial distances, the RDF exhibits damped oscillations, with amplitudes decaying rapidly, confirming the amorphous nature and long-range disorder of the HC structure.

Fig. 2 Structure and characterization of the HC model. (a) Atomic structure of the HC model, with representative local features of defects, edges, graphitic domains and nanopores colored in dark blue, light blue, green and red, respectively. (b) XRD pattern. (c) RDF. (d) Pore size distribution of the HC model.

Pores constitute critical domains for sodium-ion storage and transport within the HC architecture, wherein micropores primarily contribute to high sodium storage capacity.^84–86 In particular, micropores with size below 2 nm serve as the primary region for sodium cluster filling and contribute most significantly to the overall sodium storage capacity.⁸⁶ As presented in Fig. 2d, the pore size distribution of the constructed HC model demonstrates that all the pores are micropores (<2 nm).⁸⁴ A distinct series of peaks are observed in the 0.3–1.5 nm range, with a dominant peak at 0.8 nm accounting for 41.3% of the total pore volume. This micropore-dominated configuration significantly enhances the specific surface area, increases available sites for sodium-ion adsorption and pore filling, and improves rate capability.⁸⁴

Collectively, the constructed HC model replicates key structural attributes of experimentally characterized HCs, including local atomic configurations, bonding environments, interlayer distances and pore size distribution. Subsequent studies will utilize this model to identify sodium storage sites and simulate voltage profiles.

Sodium storage site identification

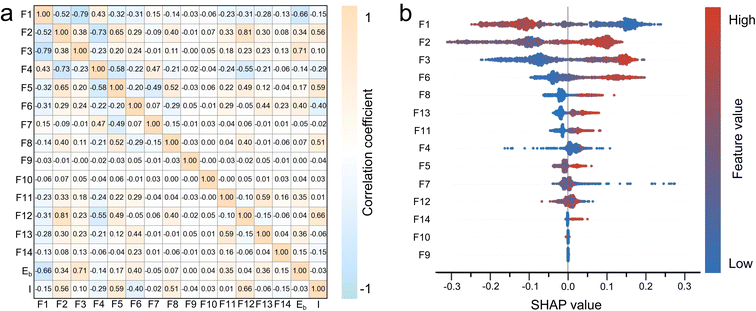
Given that intercalation exhibits more distinct geometric features, we employed structural information to preliminarily identify intercalation sites. Subsequently, the RF algorithm was applied to distinguish adsorption and pore-filling sites. Before training the model, 14 structural descriptors were selected, including the coordination environment (F1/F2: coordination number of sodium ions/carbon atoms and F3/F4: distance to the nearest sodium ion/carbon atom), fitted carbon plane (F5: number of fitted carbon planes, F6: maximum flatness of fitted carbon planes, F7: distance to the structure formed by projecting the carbon network onto fitted planes, and F8: dihedral angle between fitted carbon planes), and polygon information (F9–F14: numbers of 3–8-membered carbon rings). Subsequently, PCA was applied to the 14 structural feature descriptors to reduce the high-dimensional feature space to a three-dimensional representation (detailed contribution of each feature to the three principal components are provided in Table S2), thereby validating their discriminative completeness for the three types of sodium sites and facilitating effective separation among the site categories (Fig. S6). The results revealed that the three types of storage sites form distinct clusters in the feature space, demonstrating the discriminative capability of the selected descriptors for classifying different site categories. A screening model was then developed based on the RF algorithm. The ROC curve presented in Fig. S7 yielded an AUC value of 0.94 (close to 1), further confirming the robust screening performance of the 14 structural descriptors within the RF framework.

We first constructed the Pearson correlation matrix encompassing 14 features along with the binding energy E_b (relative to the energy of bulk Na). As shown in Fig. 3a, features F7 (−0.05), F9 (0.00), and F10 (0.04) exhibit an extremely weak correlation with the binding energy. Features F1 (−0.66) and F4 (−0.14) show a negative correlation with binding energy, suggesting that an increased coordination number and a decreased distance of the surrounding sodium atoms favor the weakening of the binding energy. The remaining features exhibit varying degrees of positive correlation with the binding energy. Additionally, few features exhibit strong correlations (value > 0.70), indicating the mutual independence of the selected features. F1 exhibits a positive correlation with F4 while showing varying degrees of negative correlation with the remaining features. Notably, its negative correlations with F2 and F3 are particularly strong. Generally, considering the spatial effect, a higher number of sodium ions surrounding a central sodium ion correlates with a relatively lower number of surrounding carbon atoms. This will cause a relative negative correlation with the fitted plane parameters (F5–F8) and the polygon features (F9–F14), albeit with a weak correlation strength. The remaining correlations can be analogously explained based on spatial effects. Further analysis reveals that F2 exhibits a greater number of strong associations with other features, primarily because F3 through F14 all pertain to carbon-related characteristics. It is noteworthy that the number of 5-membered rings (F11) and the number of 7-membered rings (F13) display a significant positive correlation (0.51). This implies that, in our simulated structures, topological defects in the form of 5|7 pairs are energetically more stable than the isolated 5-membered or 7-membered rings.⁸⁷

Fig. 3 Feature extraction for sodium site identification. (a) Pearson correlation matrix of 14 features, the intercalation site and the binding energy, with orange and blue indicating positive and negative correlations, respectively. (b) SHAP summary plot of feature importance. F1/F2: coordination number of sodium ions/carbon atoms, F3/F4: distance to the nearest sodium ion/carbon atom, F5: number of fitted carbon planes, F6: maximum flatness of fitted carbon planes, F7: distance to the structure formed by projecting the carbon network onto fitted planes, F8: dihedral angle between fitted carbon planes, and F9–F14: numbers of 3–8-membered carbon rings. E_b denotes the binding energy. I represents the intercalation sites.

Subsequently, we evaluated the feature importance. As can be seen from Fig. S8, the coordination environment features (F1–F4) have the most significant impact, accounting for 67.3%. Specifically, the importance values are F1 (0.248), F3 (0.210), and F2 (0.152). This indicates that the coordination environment, including the number of atoms and their distances, has the most prominent effect. It also validates the higher correlation among F1, F2, and F3 mentioned in the previous correlation analysis. The next most important feature is F6 (0.101), which suggests that the irregularity of the carbon surface may lead to energy-unstable structures, thereby facilitating adsorption. The importance of F4 (0.063) is significantly reduced, consistent with its weak correlation with the highly important F1 and F3. The importance of other features related to the fitting planes and polygons is even lower, which is in line with their insensitivity in distinguishing adsorption and pore filling.

The correlation between the 14 selected structural features and the intercalation site was analyzed further. As shown in Fig. 3a, features F2, F5, F6, F8, and F12 exhibit pronounced correlations with intercalation sites. Among them, F2, F5, F8, and F12 show positive correlations. A higher carbon coordination number (F2) indicates a dense arrangement of the surrounding carbon atoms, suggesting an increased likelihood of forming honeycomb-like motifs and a higher degree of graphitization. A larger number of fitted carbon planes (F5) and a smaller dihedral angle between carbon layers (F8) imply a higher probability of forming interlayer spaces composed of multiple carbon planes. Similarly, an increased count of six-membered rings (F12) indicates enhanced graphitization, thereby promoting the formation of intercalation sites. In contrast, feature F6 is negatively correlated with intercalation sites, primarily because a larger flatness value indicates reduced planarity, which is unfavorable for intercalation.

The SHAP summary plot was generated to illustrate the association of each feature with adsorption/filling identification. As shown in Fig. 3b, features F1, F3, F2, and F6 rank the highest, indicating the greater importance of the coordination environment in distinguishing adsorption and pore-filling sites. This finding aligns with the conclusions drawn from our earlier importance assessments. Moreover, features F2, F3, F5, F6, F8, F11, F13, and F14 exhibit positive correlations with adsorption. Increases in these feature values could enhance the probability of sodium ions encountering defective or edge carbon atoms. Conversely, F1 shows a positive correlation with pore-filling. This is primarily because higher values of F1 either increase the likelihood of being surrounded by sodium ions or reduce the probability of encountering nearby defective carbon atoms. Notably, the SHAP dependence of features F4, F7, F10, and F12 displays weak sensitivity to its feature values, reflecting their limited relevance in adsorption/filling identification. This observation is consistent with both our aforementioned feature importance evaluation and correlation matrix analysis. Regarding feature F9, SHAP values are predominantly distributed near zero, suggesting an extremely weak correlation with adsorption/filling behavior. We speculate this might be related to the scarcity of triangular rings in the samples due to their high energy states.

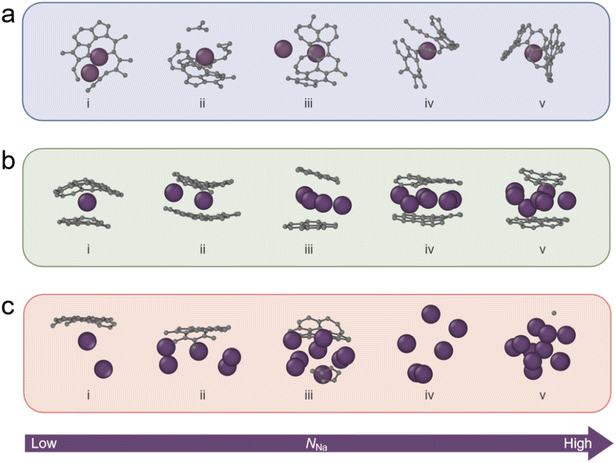
Fig. 4 presents our identification results for sodium sites at different sodiation stages, encompassing adsorption, intercalation, and filling sites. The results demonstrate that nearly all sites are accurately identified, achieving an identification accuracy of 86.1% (Fig. S9). Compared to other models, this RF model outperformed both SVM (84.2%) and clustering (78.2%), demonstrating its superior prediction accuracy in identifying adsorption and pore-filling sites (Fig. S10 and S11). Furthermore, the dominant insertion sites evolve as sodiation progresses. Taking adsorption as an example, initial adsorption preferentially occurs at defect sites (Fig. 4a-i), while later in the adsorption process, it shifts towards edge sites (Fig. 4a-v). This is consistent with the generally higher binding energy associated with defect sites. Similarly, during intercalation and pore filling (Fig. 4b and c), we observe that as the number of inserted sodium ions increases, clustering of sodium ions tends to occur between the graphite layers and within the filled regions. This clustering phenomenon also contributes to a reduction in the sodium–carbon binding energy as sodiation progresses.

Fig. 4 Site identification of the inserted sodium ion. Illustration of the local environments of sodium atoms within a cutoff radius of 5.0 Å in our HC structure: (a) adsorption sites, (b) Intercalation sites, and (c) Pore-filling sites.

Voltage profile simulation

Subsequently, we simulated the voltage profile during the stepwise insertion of sodium ions. The calculation formula is as follows:⁸⁸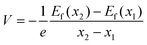where e is the elementary charge; x₁ and x₂ represent the number of inserted sodium ions before and after insertion, respectively. E_f(x₂) and E_f(x₁), respectively, denote the formation energies corresponding to the inserted x₁ and x₂ sodium ions, defined as

E_f(x) = E_HC−Na − E_HC − xE_Na(bulk) (2)

where E_HC−Na, E_HC, and E_Na(bulk) correspond to the total energy of the HC structure with x inserted sodium ions, the energy of the HC structure and the energy of a sodium atom in the bulk phase, respectively. In our simulation, we chose x₂ − x₁ = 1.

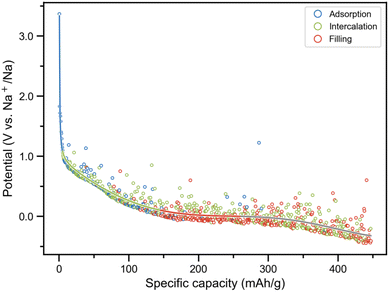
Fig. 5 presents the simulated voltage profile. By integrating the RF-based site identification model, the insertion sites were classified, and the voltage contribution from each site type were quantitatively determined via fitting analysis. During the initial sodiation stage (N ≤ 11), sodium ions exclusively occupied adsorption sites (blue curve in Fig. 5 and S12a). The sodium atoms were predominantly located at surface topological defects, such as five- and seven-membered rings and edge sites, forming 4–6 coordination bonds with neighboring carbon atoms (bond length: 2.3–2.6 Å) and exhibiting a high binding energy (>1.08 eV). The corresponding XRD simulation demonstrates an invariant interlayer spacing of 4.18 Å (Fig. S13), which unequivocally confirms the absence of intercalated sodium. At this adsorption only stage, the voltage precipitously drops from 3.37 eV to 1.08 eV (dV/dN = −0.20 V per Na). As sodiation progressed (12 < N ≤ 327), sodium ions progressively populated intercalation sites while initiating pore-filling occupation (green curve in Fig. 5 and S12b). XRD analysis reveals a pronounced shift of the (002) peak toward larger angles, indicating interlayer expansion from 4.18 Å to 4.23 Å (Fig. S13), which directly confirms the contribution of intercalation. Each sodium atom is coordinated by 10–15 nearest-neighbor carbon atoms, with Na–C distances ranging from 2.4 Å to 3.5 Å. The number of neighboring sodium atoms continues to increase from 0.27 to 1.57. The voltage declined from 1.08 eV to 0.10 eV with a moderate slope (dV/dN = −0.03 V per Na). Site population showed an intercalation and adsorption stage (57.6%), supplemented by adsorption (32.6%) and pore filling (9.81%), characteristic of the intercalation-governed regime. Upon deeper sodiation (328 < N ≤ 585), the system enters a characteristic plateau region with negligible voltage decay (dV/dN = −0.004 V per Na). At this stage, sodium atoms predominantly aggregate to form clusters within the pores. Initially, the coordination number of neighboring sodium atoms is 1.57, which increases markedly to 3.30 as the filling progresses, indicative of sodium clustering. Further analysis shows that the spatial distribution of sodium atoms within nanopores is strongly influenced by the pore size and pore wall structure: in micropores with smooth, graphite-like walls, sodium atoms tend to form small clusters comprising 3–5 atoms; whereas in mesopores with diameters of 1–2 nm and defective pore walls, the cluster sizes are larger, typically consisting of 5–8 sodium atoms. Despite progressive interlayer expansion (4.35 Å at N = 585) (Fig. S13), pore filling emerges as the dominant contributor to sodium storage capacity (60.1%), surpassing intercalation (33.9%) and adsorption (6.1%) (red line in Fig. 5 and S12c). Our analysis explicitly resolves three distinct regimes: adsorption only (steep slope), intercalation and adsorption (moderate slope), and pore-filling dominated (plateau), reproducing the experimentally reported “adsorption–intercalation–filling” mechanism.³⁴ At full sodiation (N = 585), the specific capacity reached 261.3 mA h g⁻¹ at 0 V, with intercalation contributing the largest fraction (46.2%), exceeding the contributions from pore filling (31.4%) and adsorption (22.4%), indicative of a relatively high degree of graphitization in the HC model. Unlike most experimentally synthesized HCs, which are prepared via targeted design strategies such as activation to generate abundant micropores, heteroatom doping, or controlling the degree of graphitization to balance interlayer spacing and defect density, our model utilizes a pristine, impurity-free carbon framework with relatively ordered layer stacking. This structural characteristic facilitates sodium intercalation but limits contributions from surface adsorption and pore filling, resulting in a lower total capacity compared to structurally engineered, high-capacity HCs. The capacity may be further enhanced by future tuning the HC microstructure. Through such microstructural optimization, a deeper understanding of alternative sodium storage mechanisms might be achieved, enabling the elucidation of correlations between HC structural features and performance such as sodium diffusion and cycling stability.

Fig. 5 The voltage profile during the gradual sodiation of our HC model. The fitted curves for the adsorption only, intercalation and adsorption and pore-filling dominated stages are colored in blue, green and red, respectively.

It should be noted that a stage in which a particular type of site is dominant merely indicates that the proportion of that site type is the highest among the three site categories within that specific stage (Table S3); it does not imply that the proportion of this site type reaches its overall maximum in that stage across the entire sodiation process. For instance, among adsorption sites, only 8.5% are present in the adsorption only stage, 79.2% in the intercalation and adsorption stage, and 12.3% in the pore-filling dominated stage.; for intercalation sites, 67.4% are in the intercalation and adsorption stage, while 32.6% are in the filling-dominated stage.

Finally, the overcharging process was explicitly considered. Upon voltage descent to 0 V (N > 588), overcharging behavior occurs on the HC anode. During this stage (grey line in Fig. 5), inserted sodium ions predominantly populate pore-filling (51.0%) and intercalation (47.8%) sites (Fig. S12d and S13). XRD simulations reveal a further increased average interlayer spacing (4.56 Å), confirming partial sodium retention in intercalated configurations (Fig. S13). In the overcharging stage, the HC structure does not induce slippage or delamination of the graphitic layers, and the nanopore structure is largely preserved (Fig. S14a and b), with pore sizes predominantly ranging from 0.3 to 1.5 nm (Fig. S14c). Notably, the mean shortest Na–Na distance is 3.65 Å, markedly smaller than that observed during the charging stage (4.59 Å) and even shorter than the Na–Na bond length in bulk sodium (Fig. S14d). This observation suggests that, on one hand, the intercalation process intensifies the electrostatic repulsion among inserted sodium ions, thereby introducing an energy penalty that manifests as negative voltage;⁸⁹ on the other hand, Na aggregation occurs under overcharging, forming sodium clusters coordinated with 5.67 sodium atoms, indicative of the initial nucleation of sodium dendrites. Further investigation by tuning the structural features of HC could provide deeper insight into the overcharge behavior, offering theoretical guidance for the rational design of safer HC anodes.

Conclusion

This study provides an in-depth investigation of the sodium storage mechanism in HC for SIBs by synergistically integrating MLP with RF-based site identification methodologies. Leveraging the well-trained MLP, we have successfully constructed an atomistically accurate HC model that faithfully reproduces the structural features observed experimentally. Utilizing our site identification approach, we simulated the atom-by-atom voltage profile during sodiation and deconvoluted the respective contributions of adsorption, intercalation, and pore-filling sites to sodium storage. Furthermore, overcharging simulations reveal that the formation of sodium clusters constitutes a critical factor driving dendrite growth and associated safety concerns. Our studies verify that MLP is a powerful and versatile tool for building HC structures and studying the surface/interface evolution and the sodium storage mechanism not only in HC but also extendable to other SIB electrode materials, opening new avenues for the rational design of high-performance SIB components.

Author contributions

X. W., F. D. and Z. W. conceived the idea and designed the simulations. X. W. and F. D. supervised the work. Z. W. performed MLP and model training, structure construction, site identification, and voltage simulation. G. S., G. W. and M. W. helped in data analysis and discussion. X. W. and Z. W. wrote the manuscript. All authors contributed to the discussion and commenting on the paper.

Conflicts of interest

There are no conflicts to declare.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and its supplementary information (SI). The code and input parameters of this simulation work are available on request from the authors.

Supplementary information: dataset composition, training and validation of the MLP; the formation process and the local features of the HC model; the PCA, ROC, and feature importance evaluation of the features; site identification accuracy of the RF, SVM, and clustering model; visualization of the site identification and the interlayer spacing evolution and atomic distance during the sodiation; structural evolution of HC before and after the overcharging stage; and the distribution of each insertion site in different stages. See DOI: https://doi.org/10.1039/d5sc07068f.

Acknowledgements

The authors acknowledge the National Natural Science Foundation of China (52372054, 22333005, and 22461160283), National Key R&D Program of China (2024YFA1409600), the Youth Innovation Promotion Association CAS (2022366), Guangdong Talents Program (2024TQ08A381), Guangdong Provincial Department of Education Innovation Team Program (2023KCXTD056), Shenzhen Science and Technology Program (JCYJ20240813154813018), the research program from Suzhou Laboratory (SK-1502-2024-055), High Talent Support from Shenzhen Institute of Advanced Technology (SE3G0991010) and the startup grant from Shenzhen University of Advance Technology.

References

1. J. Y. Hwang, S. T. Myung and Y. K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614.
2. J. M. Stratford, A. K. Kleppe, D. S. Keeble, P. A. Chater, S. S. Meysami, C. J. Wright, J. Barker, M.-M. Titirici, P. K. Allan and C. P. Grey, J. Am. Chem. Soc., 2021, 143, 14274–14286.
3. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 1271.
4. N. Sun, Z. Guan, Z. Liu, Y. Cao, Q. Zhu, H. Liu, Z. Wang, P. Zhang and B. Xu, Adv. Energy Mater., 2019, 9, 1901351.
5. C. Bommier and X. Ji, Isr. J. Chem., 2015, 55, 486–507.
6. X. Dou, I. Hasa, D. Saurel, C. Vaalma, L. Wu, D. Buchholz, D. Bresser, S. Komaba and S. Passerini, Mater. Today, 2019, 23, 87–104.
7. F. Sun, H. Wang, Z. Qu, K. Wang, L. Wang, J. Gao, J. Gao, S. Liu and Y. Lu, Adv. Energy Mater., 2021, 11, 2002981.
8. Y. Jin, P. M. L. Le, P. Gao, Y. Xu, B. Xiao, M. H. Engelhard, X. Cao, T. D. Vo, J. Hu, L. Zhong, B. E. Matthews, R. Yi, C. Wang, X. Li, J. Liu and J.-G. Zhang, Nat. Energy, 2022, 7, 718–725.
9. J. Liu, L. Huang, H. Wang, L. Sha, M. Liu, Z. Sun, J. Gu, H. Liu, J. Zhao, Q. Zhang and L. Zhang, Electrochem. Energy Rev., 2024, 7, 34.
10. S. J. R. Prabakar, J. Jeong and M. Pyo, Electrochim. Acta, 2015, 161, 23–31.
11. X. Chen, C. Liu, Y. Fang, X. Ai, F. Zhong, H. Yang and Y. Cao, Carbon Energy, 2022, 4, 1133–1150.
12. H. Hou, X. Qiu, W. Wei, Y. Zhang and X. Ji, Adv. Energy Mater., 2017, 7, 1602898.
13. V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5, 5884–5901.
14. M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958.
15. H. Kim, J. Hong, Y.-U. Park, J. Kim, I. Hwang and K. Kang, Adv. Funct. Mater., 2015, 25, 534–541.
16. Y. Fang, L. Xiao, Z. Chen, X. Ai, Y. Cao and H. Yang, Electrochem. Energy Rev., 2018, 1, 294–323.
17. D. Wu, F. Sun, Z. Qu, H. Wang, Z. Lou, B. Wu and G. Zhao, J. Mater. Chem. A, 2022, 10, 17225–17236.
18. H. Yang, R. Xu and Y. Yu, Energy Storage Mater., 2019, 22, 105–112.
19. L.-F. Zhao, Z. Hu, W.-H. Lai, Y. Tao, J. Peng, Z.-C. Miao, Y.-X. Wang, S.-L. Chou, H.-K. Liu and S.-X. Dou, Adv. Energy Mater., 2021, 11, 2002704.
20. K. Tang, L. Fu, R. J. White, L. Yu, M.-M. Titirici, M. Antonietti and J. Maier, Adv. Energy Mater., 2012, 2, 873–877.
21. L. Li, W. Liu, H. Dong, Q. Gui, Z. Hu, Y. Li and J. Liu, Adv. Mater., 2021, 33, 2004959.
22. X. Zhang, J. Hu, Y. Cheng, H. Y. Yang, Y. Yao and S. A. Yang, Nanoscale, 2016, 8, 15340–15347.
23. S. Komaba, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Adv. Funct. Mater., 2011, 21, 3859–3867.
24. H. Alptekin, H. Au, E. Olsson, J. Cottom, A. C. S. Jensen, T. F. Headen, Q. Cai, A. J. Drew, M. C. Ribadeneyra and M.-M. Titirici, Adv. Mater. Interfaces, 2022, 9, 2101267.
25. C. Bommier, D. Mitlin and X. Ji, Prog. Mater. Sci., 2018, 97, 170–203.
26. F. Xie, Z. Xu, Z. Guo and M.-M. Titirici, Prog. Energy, 2020, 2, 042002.
27. T. Zhang, L. Yang, X. Yan and X. Ding, Small, 2018, 14, 1802444.
28. W. Shao, H. Shi, X. Jian, Z.-S. Wu and F. Hu, Adv. Energy Sustainability Res., 2022, 3, 2200009.
29. Y. Fujii, H. Yoshimo, R. Tatara, Z. T. Gossage, A. Koizumi and S. Komaba, ACS Appl. Energy Mater., 2025, 8, 6577–6585.
30. Y. Cao, L. Xiao, M. L. Sushko, W. Wang, B. Schwenzer, J. Xiao, Z. Nie, L. V. Saraf, Z. Yang and J. Liu, Nano Lett., 2012, 12, 3783–3787.
31. J. Ding, H. Wang, Z. Li, A. Kohandehghan, K. Cui, Z. Xu, B. Zahiri, X. Tan, E. M. L. Lotfabad, B. C. Olsen and D. Mitlin, ACS Nano, 2013, 7, 11004–11015.
32. Z. Li, C. Bommier, Z. S. Chong, Z. Jian, T. W. Surta, X. Wang, Z. Xing, J. C. Neuefeind, W. F. Stickle, M. Dolgos, P. A. Greaney and X. Ji, Adv. Energy Mater., 2017, 7, 1602894.
33. Y. Li, Y.-S. Hu, M.-M. Titirici, L. Chen and X. Huang, Adv. Energy Mater., 2016, 6, 1600659.
34. Y. Morikawa, S. Nishimura, R. Hashimoto, M. Ohnuma and A. Yamada, Adv. Energy Mater., 2020, 10, 1903176.
35. D.-S. Bin, Y. Li, Y.-G. Sun, S.-Y. Duan, Y. Lu, J. Ma, A.-M. Cao, Y.-S. Hu and L.-J. Wan, Adv. Energy Mater., 2018, 8, 1800855.
36. Y. Wang, M. Li, Y. Zhang and N. Zhang, Nano Res., 2024, 17, 6038–6057.
37. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 4428.
38. T. Perveen, M. Siddiq, N. Shahzad, R. Ihsan, A. Ahmad and M. I. Shahzad, Renewable Sustainable Energy Rev., 2020, 119, 109549.
39. A. Gomez-Martin, J. Martinez-Fernandez, M. Ruttert, M. Winter, T. Placke and J. Ramirez-Rico, Chem. Mater., 2019, 31, 7288–7299.
40. K. C. Wasalathilake, H. Li, L. Xu and C. Yan, J. Energy Chem., 2020, 42, 91–107.
41. J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Chem. Commun., 2016, 52, 12430–12433.
42. S. Komab, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Adv. Funct. Mater., 2011, 21, 3859–3867.
43. Y. Youn, B. Gao, A. Kamiyama, K. Kubota, S. Komaba and Y. Tateyama, npj Comput. Mater., 2021, 7, 48.
44. M. P. Mercer, M. Nagarathinam, E. M. Gavilán-Arriazu, A. Binjrajka, S. Panda, H. Au, M. Crespo-Ribadeneyra, M.-M. Titirici, E. P. M. Leiva and H. E. Hoster, J. Mater. Chem. A, 2023, 11, 6543–6555.
45. D. Billaud, F. X. Henry and P. Willmann, Mater. Res. Bull., 1993, 28, 477–483.
46. M. Liu, J. Li, Y. Wang, S. Guo, L. Zhao and Z. Wang, Green Energy and Intelligent Transportation, 2026, 5, 100299.
47. Y. Zhang, H. Huang, J. Tian, C. Li, Y. Jiang, Z. Fan and L. Pan, Energy Storage Mater., 2023, 63, 103069.
48. T. Ji, X. Liu, D. Sheng, Y. Li, H. Ruan, H. Guo, Z. X. Shen and L. Lai, Energy Storage Mater., 2024, 71, 103563.
49. T. Qi, X. Zhang, K. Xiong, H. Yang, S. Zhang and H. Chen, J. Mater. Chem. A, 2025, 13, 17748–17771.
50. J. Liao, Y. Jin, K. Sun, A. Wang, G. Zhang, L. Zhou, W. H. Yang, M. Fan, J. Jiang, Y. Wen and S. Wang, J. Power Sources, 2025, 631, 236323.
51. S. Y. Owusu, RSC Sustainability, 2025, 3, 3133–3134.
52. C. Qian, D. Qian, D. Hedman, P. Li, S. Y. Kim and F. Ding, Small, 2024, 20, 2404274.
53. Y. Liu, T. Gao, Q. Xiao, Y. Ruan, Q. Chen, B. Wang and J. Huang, npj Comput. Mater., 2025, 11, 285.
54. D. Hedman, B. McLean, C. Bichara, S. Maruyama, J. A. Larsson and F. Ding, Nat. Commun., 2024, 15, 4076.
55. K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722.
56. V. Botu, R. Batra, J. Chapman and R. Ramprasad, J. Phys. Chem. C, 2017, 121, 511–522.
57. M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301.
58. C. Zheng, C. Chen, Y. Chen and S. P. Ong, Patterns, 2020, 1, 100013.
59. Z. Fan, Y. Wang, P. Ying, K. Song, J. Wang, Y. Wang, Z. Zeng, K. Xu, E. Lindgren, J. M. Rahm, A. J. Gabourie, J. Liu, H. Dong, J. Wu, Y. Chen, Z. Zhong, J. Sun, P. Erhart, Y. Su and T. Ala-Nissila, J. Chem. Phys., 2022, 157, 114801.
60. S. Nosé, Mol. Phys., 2002, 100, 191–198.
61. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
62. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
63. J. C. Sancho-García, J. L. Brédas and J. Cornil, Chem. Phys. Lett., 2003, 377, 63–68.
64. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
65. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
66. A. Maćkiewicz and W. Ratajczak, Comput. Geosci., 1993, 19, 303–342.
67. V. L. Deringer and G. Csányi, Phys. Rev. B, 2017, 95, 094203.
68. Z. Tang, R. Zhang, H. Wang, S. Zhou, Z. Pan, Y. Huang, D. Sun, Y. Tang, X. Ji, K. Amine and M. Shao, Nat. Commun., 2023, 14, 6024.
69. M. Thompson, Q. Xia, Z. Hu and X. S. Zhao, Mater. Adv., 2021, 2, 5881–5905.
70. A. Beda, F. Rabuel, M. Morcrette, S. Knopf, P.-L. Taberna, P. Simon and C. M. Ghimbeu, J. Mater. Chem. A, 2021, 9, 1743–1758.
71. X. Yu, S. Chen, B. Tang, X.-L. Li, J. Zhou, Y. Ren, J. Wei, C. Yang, Y. Guo, Z. Zhou and S.-H. Bo, ACS Energy Lett., 2024, 9, 4441–4449.
72. L. Xie, C. Tang, Z. Bi, M. Song, Y. Fan, C. Yan, X. Li, F. Su, Q. Zhang and C. Chen, Adv. Energy Mater., 2021, 11, 2101650.
73. Y. Li, Y. Lu, Q. Meng, A. C. S. Jensen, Q. Zhang, Q. Zhang, Y. Tong, Y. Qi, L. Gu, M.-M. Titirici and Y.-S. Hu, Adv. Energy Mater., 2019, 9, 1902852.
74. Y. Liu, H. Dai, L. Wu, W. Zhou, L. He, W. Wang, W. Yan, Q. Huang, L. Fu and Y. Wu, Adv. Energy Mater., 2019, 9, 1901379.
75. T. W. Surta, E. Koh, Z. Li, D. B. Fast, X. Ji, P. A. Greaney and M. R. Dolgos, Adv. Energy Mater., 2022, 12, 2200647.
76. W. Shao, H. Shi, X. Jian, Z.-S. Wu and F. Hu, Advanced Energy Storage Research, 2022, 3, 2200009.
77. W. Zhao, S. Zhang, H. Lai, W. He, B. K. Yap, U. Feleni, X. Peng, J. Cui and L. Zhong, Carbon Energy, 2025, 7, e70047.
78. J. Li, C. Peng, J. Li, J. Wang and H. Zhang, Energy Fuels, 2022, 36, 5937–5952.
79. K. Hedberg, L. Hedberg, D. S. Bethune, C. A. Brown, H. C. Dorn, R. D. Johnson and M. De Vries, Science, 1991, 254, 410–412.
80. C. T. Toh, H. Zhang, J. Lin, A. S. Mayorov, Y.-P. Wang, C. M. Orofeo, D. B. Ferry, H. Andersen, N. Kakenov, Z. Guo, I. H. Abidi, H. Sims, K. Suenaga, S. T. Pantelides and B. Özyilmaz, Nature, 2020, 577, 199–203.
81. Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186.
82. H. Daniels, R. Brydson, B. Rand and A. Brown, Philos. Mag., 2007, 87, 4073–4092.
83. M. Maruyama and S. Okada, Jpn. J. Appl. Phys., 2014, 53, 06JD02.
84. W. Zhang, Y. Du, Y. Qiu, C. Li, I. Razanau, A. Kaisha, F. Xu and H. Wang, Adv. Energy Mater., 2025, 15, e03884.
85. L. K. Iglesias, E. N. Antonio, T. D. Martinez, L. Zhang, Z. Zhuo, S. J. Weigand, J. Guo and M. F. Toney, Adv. Energy Mater., 2023, 13, 2302171.
86. W. Jian, X. Qiu, H. Chen, J. Yin, W. Yin, H. N. Alshareef and W. Zhang, ACS Nano, 2025, 19, 22201–22216.
87. Q. Yuan, Z. Xu, B. I. Yakobson and F. Ding, Phys. Rev. Lett., 2012, 108, 245505.
88. F. Fu, X. Wang, L. Zhang, Y. Yang, J. Chen, B. Xu, C. Ouyang, S. Xu, F.-Z. Dai and W. E, Adv. Funct. Mater., 2023, 33, 2303936.
89. Y. Jin, S. Sun, M. Ou, Y. Liu, C. Fan, X. Sun, J. Peng, Y. Li, Y. Qiu, P. Wei, Z. Deng, Y. Xu, J. Han and Y. Huang, ACS Appl. Energy Mater., 2018, 1, 2295–2305.

---