Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
MWCNT-driven modulation of thermal and flow properties in PTT/PP polymer systems
Ajitha A.
Ramachandran
*a,
Arunima
Reghunadhan
 b,
P. S.
Sari
a,
Miroslav
Huskić
c and
Sabu
Thomas
b,
P. S.
Sari
a,
Miroslav
Huskić
c and
Sabu
Thomas
 *de
*de
aDepartment of Polymer Science and Rubber Technology, Cochin University of Science and Technology, Kochi, Kerala, India. E-mail: ajithaar1988@gmail.com
bBernal Institute & School of Engineering, University of Limerick, Castletroy, V94 T9PX, Ireland
cPomurje Science and Innovation Centre, Lendavska ulica 5a, 9000 Murska Sobota, Slovenia
dSchool of Energy Materials, Mahatma Gandhi University, Kottayam, Kerala 686 560, India. E-mail: sabuthomas@mgu.ac.in
eTrivandrum Engineering Science & Technology (TrEST) Research Park, Thiruvananthapuram, Kerala, India
First published on 16th December 2025
Abstract
The thermal and viscoelastic performance of polymer blends is decisive for their deployment in advanced engineering and electronic applications. Here, we report a systematic investigation of immiscible poly(trimethylene terephthalate) (PTT)/polypropylene (PP) blends reinforced with multiwalled carbon nanotubes (MWCNTs). While the incorporation of MWCNTs did not markedly alter the thermal degradation profiles, it significantly modified the viscoelastic behavior by inducing a constrained polymer region within the PTT phase. Quantitative analysis of filler dispersion effectiveness, entanglement density, reinforcing efficiency, and constrained volume provides new insights into nanotube–matrix interactions. Rheological results revealed a terminal-to-nonterminal transition with increasing nanotube content, confirming percolated network formation at low filler loadings. These findings establish clear structure–property correlations that extend beyond qualitative descriptions, offering a predictive framework for tailoring immiscible blends through nanofiller engineering. Such insights highlight the potential of PTT/PP/MWCNT systems in functional applications, including lightweight structural components and conductive composites for electronics.
1. Introduction
The development of polymer blends with enhanced thermal and viscoelastic performance is central to meeting the demands of modern engineering and electronic applications. A solid understanding of thermal stability, melting, and crystallization temperatures is crucial when creating polymer blends for a range of industrial applications. In particular, the ability to control thermal stability, crystallization, and relaxation behavior directly governs processability and service reliability. However, when two immiscible polymers are combined, their weak interfacial adhesion often compromises performance. To overcome this, compatibilizers and nanoscale fillers have been widely explored to stabilize morphology and introduce synergistic properties.1 The melting and crystallization temperatures of polymer components in various blend systems are significantly impacted by the addition of nanofillers.2 The dynamic mechanical properties of blends are influenced by interfacial properties, morphology, intermolecular interactions, and composition of polymers. In addition, the viscoelastic properties of prepared blends and composites greatly depend on the processing conditions, morphology, dispersion, and structural properties of fillers.3 The morphology and rheology of multiphase polymer systems are interrelated and influence the final performance of materials. Rheological analysis can be considered the main route to study the structure (micro) of the prepared polymer structures as the melt rheological properties are very sensitive to the morphology and dispersion of nanofillers.4,5 Moreover, these techniques are useful to identify the existence of internal structures in the composites.6–8 Rheological studies are important for the fabrication of composites to understand the viscoelastic properties, microstructure, and dynamics. The critical loading of a filler at which a liquid-to-solid-like transition occurs can be designated as rheological percolation. Filler–filler interactions and filler–polymer interactions have great significance in determining the reinforcement effect. Generally, the filler network formation and filler–matrix interactions reduce the polymer chain mobility.Carbon nanotubes (CNTs) are among the most effective nanofillers due to their exceptional aspect ratio, electrical conductivity, and reinforcing potential. Numerous studies have shown that CNTs can alter crystallization kinetics, improve dynamic mechanical performance, and even act as compatibilizing agents in many immiscible blends.9–11 Several studies have reported on the thermal and viscoelastic studies of multi-walled carbon nanotube (MWCNT) incorporated polymer blend nanocomposites. Zare et al.12 reported that morphology and phase separation have a large effect on the properties of polymer blends and their nanocomposites. They confirmed this by correlating the results of morphological and rheological studies of poly(lactic acid) (PLA)/poly(ethylene oxide) (PEO) blends and PLA/PEO/CNT nanocomposites. Zhao et al. reported that CNTs can act as effective compatibilizing agents and simultaneously enhance the mechanical, thermal, and electrical properties of an immiscible blend of polyvinylidene fluoride (PVDF)/poly-L-lactic acid (PLLA).13 Zheng et al. investigated that the incorporation of carboxylated CNTs (CNT-COOHs) into an epoxy (EP)/polysulfone (PSF) blend could enhance the fracture toughness and thermal properties of the blend due to the action of CNT-COOHs.14 The electrical and melt rheological properties of polycarbonate (PC)/poly(styrene-acrylonitrile) (SAN) blends were investigated by Liebscher et al.,15 and the melt rheological studies of the composites showed higher reinforcing effects for composites with worse dispersion. Taraghi et al. observed that with the addition of MWCNTs, the storage modulus of the PC/ethylene propylene copolymer (EPC) blends was increased. They explained it with the strong interfacial interactions between the matrix and MWCNTs.16 Despite these advances, the underlying mechanisms by which nanofillers influence viscoelastic behavior, particularly the formation of constrained polymer regions and the transition from liquid-like to solid-like rheology, remain insufficiently understood.
Poly(trimethylene terephthalate) (PTT), an engineering thermoplastic with favorable stiffness and crystallinity, suffers from limited thermal stability, while polypropylene (PP) offers processability and cost-effectiveness but lacks dimensional stability. Blending PTT with PP presents a pathway to balance these properties, though immiscibility is a major challenge. Only a few reports have addressed PTT/PP systems, typically using fibers or grafted compatibilizers, and almost none have systematically examined the role of CNTs in tuning their viscoelastic performance.17,18 As evidenced by our previous reports, we projected that PTT/PP blends will offer robust engineering materials with good properties.19,20 Considering the difficulty in miscibility and fabrication, MWCNTs were incorporated into the blends to offer compatibilization and to result in a high-performance material with striking properties of both PTT and PP. One of the proven applications of the highly conductive MWCNT-incorporated PTT/PP composites was the EMI shielding.19,21
Our earlier studies did not investigate how CNTs influence the flow behavior, relaxation dynamics, or chain confinement in this immiscible system. The present study addresses the gaps by investigating the influence of multiwalled carbon nanotubes (MWCNTs) on the thermal, morphological, and viscoelastic properties of immiscible PTT/PP blends. Emphasis is placed on quantifying filler dispersion effectiveness, entanglement density, reinforcing efficiency, and the formation of constrained regions within the PTT phase, the parameters rarely reported in blend nanocomposites. By correlating rheological transitions with morphological evidence, this work provides new insight into nanotube–polymer interactions and offers a predictive framework for engineering immiscible blends toward high-performance applications.
2. Materials and methods
2.1. Materials
The polymers used in this study, poly(trimethylene terephthalate) (PTT) with a number average molecular weight (Mn) of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 g mol−1, was obtained from DuPont Industries (USA), while polypropylene (PP, grade H350 FG) was sourced from Reliance India Ltd. The MWCNTs (NANOCYL NC7000, purchased from Nanocyl, Belgium), with an average diameter of 9.5 nm, an average length of 1.5 μm, and a carbon purity of 90%, were used as fillers for composite preparation.22
500 g mol−1, was obtained from DuPont Industries (USA), while polypropylene (PP, grade H350 FG) was sourced from Reliance India Ltd. The MWCNTs (NANOCYL NC7000, purchased from Nanocyl, Belgium), with an average diameter of 9.5 nm, an average length of 1.5 μm, and a carbon purity of 90%, were used as fillers for composite preparation.22
2.2. Methods
Poly(trimethylene terephthalate)/polypropylene blends and their composites with MWCNTs were prepared by melt mixing using a Brabender melt mixer. Blending was carried out at 230 °C and 90 rpm for 10 minutes. The mixed compounds were compression molded and taken for analysis. Fig. 1 shows the schematic representation of the sample preparation. PTT/PP blends and MWCNT-based nanocomposites of varying compositions were examined to assess the impact of MWCNTs on their thermal and viscoelastic behavior.22,23 | ||
| Fig. 1 Schematic representation of PTT/PP blend and nanocomposite preparation. The figure illustrates the melt-mixing process in the mixer, followed by compression molding. | ||
2.3. Characterization techniques
The surface characteristics of the compounds were analyzed using a scanning electron microscope (SEM; JEOL model-JSM-6390) and a transmission electron microscope (JEOL JEM-2100 HRTEM). Samples from cryofracture after tensile testing were used for SEM with gold coating for making it conductive, and ultramicrotome cut samples were used in TEM. A microscopic investigation was carried out to understand the dispersion and localization of MWCNTs in the polymer matrix. The melting characteristics of the samples were recorded on a PerkinElmer DSC, and thermal stability was studied using a PerkinElmer Diamond TG/DTA instrument. About 10 mg of the sample was weighed and placed in the TGA pan. Both DSC and TGA measurements were performed at a heating rate of 10 °C min−1. Dynamic mechanical analysis (DMA) of the compounds was performed on a TA Instruments (USA) DMA Q800 dynamic thermal analyzer in the temperature range between −50 and 200 °C at a heating rate of 2 °C min−1, at a frequency of 1 Hz and an amplitude of 10 micrometers, using a single cantilever. The samples had the dimensions 10 mm (L) × 15 mm (W) × 5 mm (T). Parallel-plate rheological measurements were performed with a 25 mm setup (MCR 102, Anton Paar, USA) at 240 °C in the frequency-sweep method at a constant strain of 5% within the range 0.1–100 rad s−1 with samples of 1 mm thickness.22,233. Results and discussion
3.1. Morphological studies
A better understanding of the miscibility and the interfacial adhesion between the two polymer components can be obtained from the morphological investigation conducted using electron microscopy. The blends exhibited immiscibility, primarily due to insufficient adhesion between the PTT and PP phases. The optimum property composition was fixed at 90PTT and 10PP.19–21SEM and TEM analyses confirmed the immiscibility of PTT/PP blends, as evidenced by distinct phase-separated domains of PP within the PTT matrix (Fig. 2a). The incorporation of MWCNTs reduced the PP domain size and enhanced interfacial adhesion, indicating a compatibilization effect. TEM revealed preferential localization of MWCNTs within the PTT phase, consistent with π–π interactions between the aromatic rings of PTT and the nanotube surface (Fig. 2c). This selective partitioning is critical, as it governs the extent of chain confinement and viscoelastic reinforcement. Compared with similar immiscible blends, the observed morphological stabilization in PTT/PP is more pronounced, underscoring the strong affinity of MWCNTs for PTT.12
3.2. Thermogravimetric analysis (TGA)
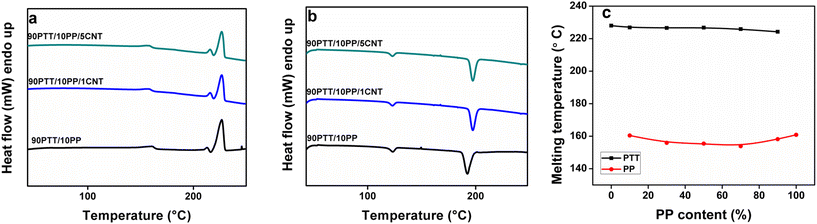
Thermogravimetric analysis revealed a two-step degradation for PTT/PP blends, corresponding to individual polymer decomposition (Fig. 3). Blending shifted the onset degradation temperature above that of neat PTT, confirming stabilization via the PP phase. The CNTs show their inclusion in the blend system by altering the thermal profile, even though the effect is not very notable (Fig. 4). From Fig. 3d, most of the curves show slightly higher degradation than their blend counterparts in Fig. 3b. In addition, the change in peak intensity indicates that CNTs slow down the degradation of the blend system. DSC thermograms (Fig. 5 and 6) showed double melting peaks for both PTT and PP, reflecting immiscibility and multiple crystalline populations. MWCNTs did not significantly alter melting points but slightly increased crystallization temperatures, consistent with their nucleating role. The inclusion of 1 wt% MWCNT showed only a very negligible increase in the horizontal region in the initial stages and also at the degradation step of the thermogram.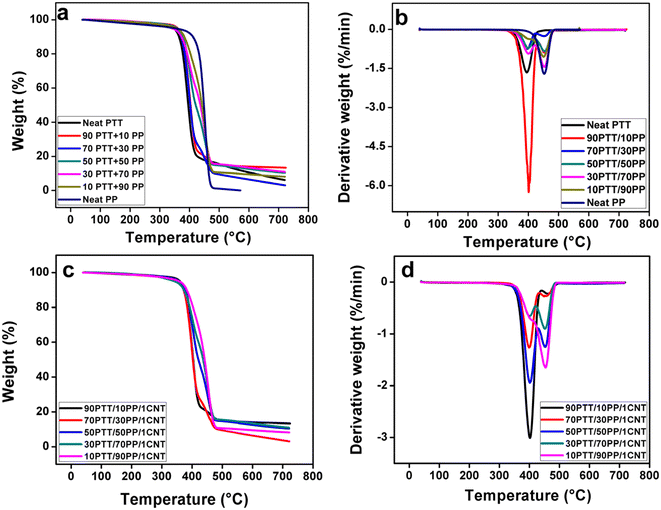 | ||
| Fig. 3 TGA (a and c) and DTGA (b and d) graphs of neat polymer components, PTT/PP blends, and corresponding nanocomposites with 1 wt% MWCNTs. | ||
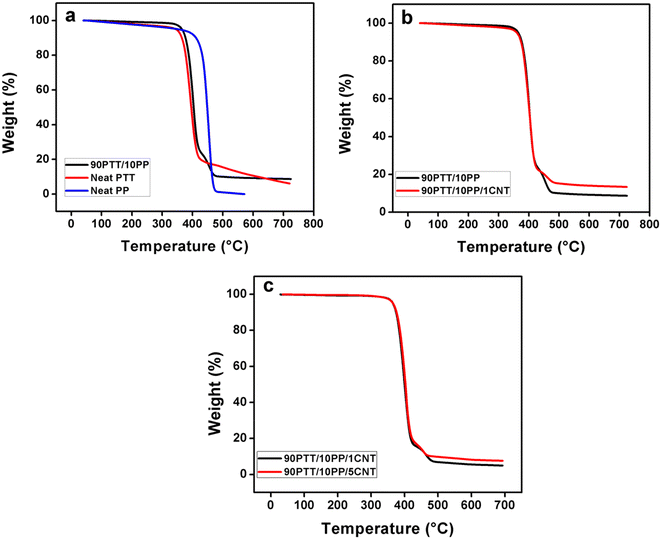 | ||
| Fig. 4 Comparison of TGA curves: (a) neat polymers PTT, PP and 90PTT/10PP blend, (b) blend and composites and (c) composites with 1 wt% and 5 wt% CNTs. | ||
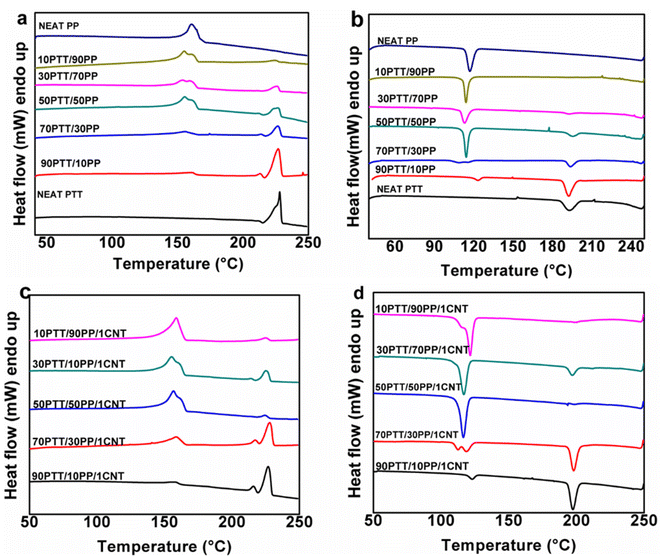 | ||
| Fig. 5 (a) & (c) Melting thermograms of blends with different wt% of PTT and PP and their composites, respectively, and (b) & (d) cooling endotherms of blends and composites, respectively. | ||
3.3. Differential scanning calorimetry (DSC)
Studies on the melting parameters of blends and their composites have great importance in fundamental research and for the finalization of their end-use applications. Fig. 5 shows the thermograms corresponding to all prepared blends and their composites with 1 wt% MWCNTs. In the case of the blends, two separate melting endotherms were observed that revealed the characteristics of an immiscible blend. On blending PTT and PP, the Tm of both components displayed a slight drop, which is owing to the immiscibility of the system (Fig. 6) but not much variation with MWCNTs (Fig. 5c).The melting thermograms of the blends and composites with 1 wt% MWCNTs showed double melting peaks for both PP and PTT. Depending on the thermal conditions applied, polymer crystals formed can show different morphologies. As a result, multiple melting behaviors can be observed.24 Hence, it can be suggested that multiple melting behaviors of different polymers occur mainly owing to their difference in structure, the coexistence of their different crystalline forms, the formation of crystals with different stabilities, or the recrystallization taking place during the DSC scan. The recrystallization occurs mainly due to the melting–remelting process, and hence, the double melting peak arises due to the melting of primary crystallites and the melting of the recrystallized crystallites with different stabilities. The double melting behavior exhibited by PTT has already been reported.25,26 The Tg of PTT was increased by blending with PP, and it was further increased with MWCNTs, which is attributable to the hindered motion of polymer chains.
Cooling thermograms (Fig. 5b and d) of PTT/PP blends and their composites with 1 wt% MWCNTs showed the same trend as that of the melting thermograms. Neat PTT observed a crystallization temperature (Tc) of 192.67 °C, while that of 100PP was observed at 116.98 °C. The two crystallization temperatures observed in the blends and composites revealed the immiscibility of the system. The addition of different MWCNT loadings resulted in minimal changes in the melting temperature (Tm), while Tc of PTT and PP were increased, and this is due to the nucleation effect of MWCNTs (Fig. 6a and b).
The melting temperatures of the polymers varied slightly in the blend system. The melting temperature of pure PTT was 128 °C and that of PP was 160.86 °C, while upon blending the polymers at different compositions, for PTT, the melting temperature decreased slightly, but the average decrease was very negligible. In the case of the PP phase, the temperature decreased gradually up to 70 percent of PP but showed an increase when the amount of PP was 90 wt% in the blend, approaching the actual melting temperature. The changes are shown graphically in Fig. 6. This implies that the blending process influences the miscibility of the polymers. As the composition varies, the melting behavior is changed which initiates a smooth mixing of PTT in PP and vice versa.
The percentage crystallinity of PTT and PP was calculated according to eqn (1)
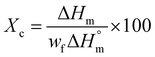 | (1) |
 is the melting enthalpy of the 100% crystalline sample and wf denotes the weight fraction.27 For neat PTT,
is the melting enthalpy of the 100% crystalline sample and wf denotes the weight fraction.27 For neat PTT,  is 145.5 J g−1, and for neat PP, it is 207 J g−1.28 The calculated crystallinity of PTT and PP in the case of blends and composites (with 1 wt% MWCNTs) is shown in the graph as a function of PTT content (Fig. 7). With the incorporation of MWCNTs, the crystallinity of PTT and PP slightly increased owing to the nucleation effect of MWCNTs.
is 145.5 J g−1, and for neat PP, it is 207 J g−1.28 The calculated crystallinity of PTT and PP in the case of blends and composites (with 1 wt% MWCNTs) is shown in the graph as a function of PTT content (Fig. 7). With the incorporation of MWCNTs, the crystallinity of PTT and PP slightly increased owing to the nucleation effect of MWCNTs.
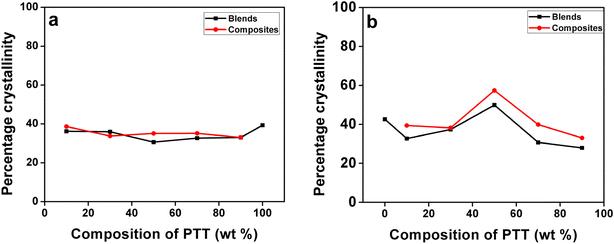 | ||
| Fig. 7 Crystallinity of (a) PTT and (b) PP in blends and composites (values calculated using standard enthalpy from DSC data). | ||
3.4. Dynamic mechanical analysis (DMA)
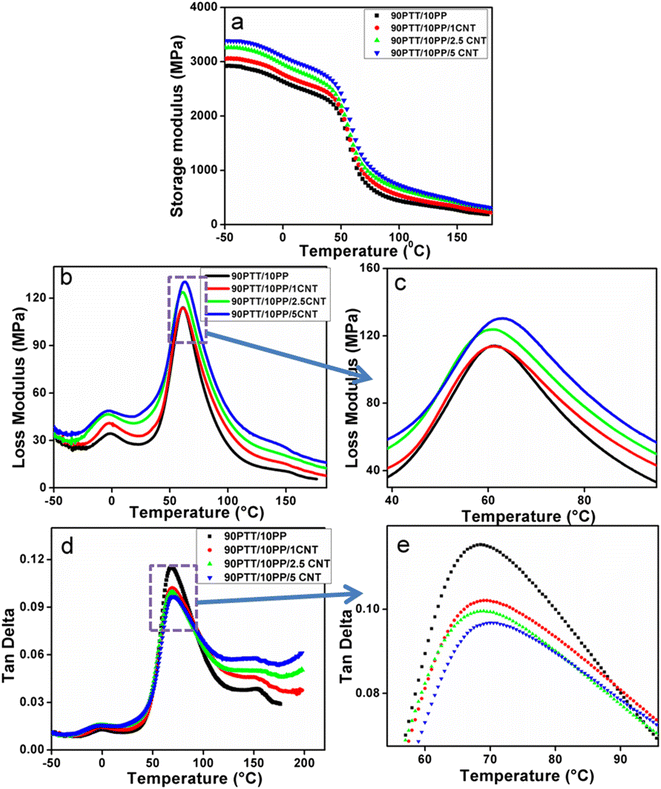
Dynamic mechanical analysis is an excellent technique to follow the relaxation of polymer chains and to assess the stiffness and damping properties of prepared composite materials.5,29–31 The storage modulus (E′) values of the PTT/PP blends lie between those of the neat polymeric components, which confirmed the immiscibility of the PTT/PP blends (Fig. 8(a)). It was also observed that the storage modulus lowered with a rise in temperature due to the upsurge in molecular mobility of the polymer chains. Fig. 8(b) shows the variation of the loss modulus (E″) as a function of temperature for neat PP, neat PTT, and the 90PTT/10PP blend.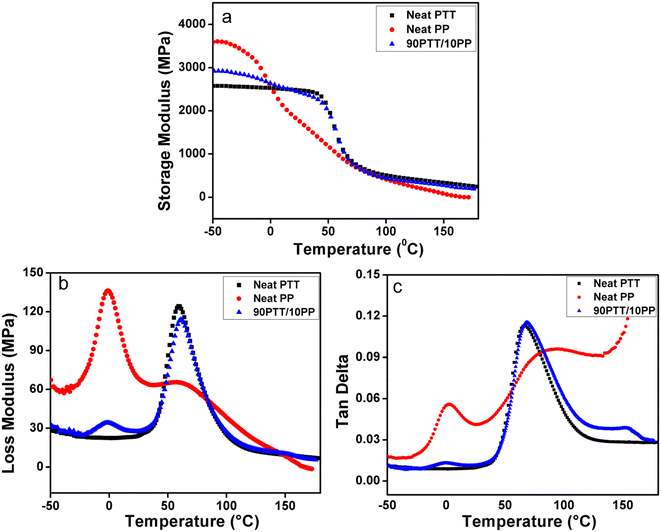 | ||
Fig. 8 Dynamic mechanical properties of neat PTT, neat PP, and the 90PTT/10PP blend: (a) storage modulus (E′) as a function of temperature, (b) loss modulus (E″) and (c) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. δ. | ||
The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ versus temperature curve provides information regarding the damping properties of the material, reflecting the balance between the viscous and elastic stages of the analyzed material. As the temperature rises, the damping values reach an extreme, which corresponds to the transition region (glassy to rubbery transition). The peak temperature implies the glass transition temperature (Tg). In the glassy region, the mobility of polymer chains is restricted (elastic), while with increasing temperature, the transition occurs from the glassy to the rubbery stage which results in the viscous flow of the material due to the freer movement of polymer segments.30
δ versus temperature curve provides information regarding the damping properties of the material, reflecting the balance between the viscous and elastic stages of the analyzed material. As the temperature rises, the damping values reach an extreme, which corresponds to the transition region (glassy to rubbery transition). The peak temperature implies the glass transition temperature (Tg). In the glassy region, the mobility of polymer chains is restricted (elastic), while with increasing temperature, the transition occurs from the glassy to the rubbery stage which results in the viscous flow of the material due to the freer movement of polymer segments.30
Fig. 8(c) shows the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ versus temperature graph, and it provided information regarding the transitions taking place in the neat polymer components and blends. In the tangent
δ versus temperature graph, and it provided information regarding the transitions taking place in the neat polymer components and blends. In the tangent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve of neat PP, two peaks are observed: the temperature range between −8 and 20 °C corresponds to the glassy to rubbery transition (β-transition of PP). The peak maximum denotes the Tg, and the observed Tg of PP is 2.4 °C; the range between 60 °C and 120 °C corresponds to the α-relaxation of PP due to the movement of intracrystalline amorphous segments.32–34 In the case of PTT, the maximum at 66.2 °C corresponds to its Tg. The temperature range from 45 to 120 °C represents the glassy to rubbery transition region of PTT. The tan
δ curve of neat PP, two peaks are observed: the temperature range between −8 and 20 °C corresponds to the glassy to rubbery transition (β-transition of PP). The peak maximum denotes the Tg, and the observed Tg of PP is 2.4 °C; the range between 60 °C and 120 °C corresponds to the α-relaxation of PP due to the movement of intracrystalline amorphous segments.32–34 In the case of PTT, the maximum at 66.2 °C corresponds to its Tg. The temperature range from 45 to 120 °C represents the glassy to rubbery transition region of PTT. The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve of the 90PTT/10PP blend showed two more maxima, and this sheds light on the immiscibility of the blend since the two tan
δ curve of the 90PTT/10PP blend showed two more maxima, and this sheds light on the immiscibility of the blend since the two tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peaks correspond to the transition peaks of PTT and PP. The peak around 68.3 °C corresponds to the Tg of PTT and that around −1.8 °C corresponds to the Tg of PP.
δ peaks correspond to the transition peaks of PTT and PP. The peak around 68.3 °C corresponds to the Tg of PTT and that around −1.8 °C corresponds to the Tg of PP.
In the case of the 90PTT/10PP blend, E′ increased with MWCNT loading especially below Tg, due to the stiffening effect of the MWCNTs. As the temperature increased, the storage modulus showed a sudden decrease at a particular temperature which represents Tg. Similar to the neat 90PTT/10PP blend, its composites with MWCNTs also showed two glass transition regions: the first one corresponds to the PP phase, and the second one corresponds to that of PTT; this confirmed the immiscibility of the composites. The improved storage modulus of the composites of the PTT/PP blend with MWCNTs sheds light on the enhanced load-bearing capacity of the composites compared to the neat PTT/PP blend.
Thus, the enhanced storage modulus of the blend system with MWCNTs indicates the effective reinforcement effect of MWCNTs and the interactions between MWCNTs and the polymer matrix. The network of dispersed MWCNTs in the PTT phase limits the mobility of polymer chains, resulting in a higher modulus.
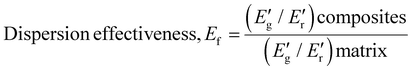 | (2) |
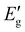 and
and 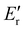 are the storage modulus values of the blend nanocomposite of 90PTT/10PP with MWCNTs and the neat 90PTT/10PP blend at glassy (−50 °C) and rubbery regions (110 °C).
are the storage modulus values of the blend nanocomposite of 90PTT/10PP with MWCNTs and the neat 90PTT/10PP blend at glassy (−50 °C) and rubbery regions (110 °C).
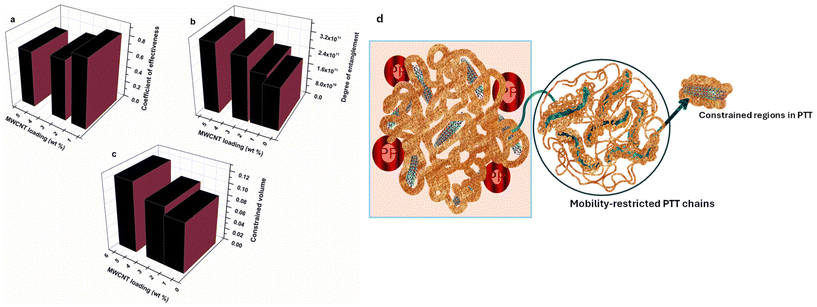
The calculated values of Ef for combinations with varying nanotube loadings are given in Table 2 and Fig. 10(a). A low value of Ef indicates a higher effectiveness of filler dispersion in the polymer matrix.
The MWCNTs in the PTT/PP blend system were calculated using eqn (3):
| Degree of entanglement, φ = E′/6 RT | (3) |
| Amount of PTT (in wt%) | Amount of PP (in wt%) | Amount of CNT (in wt%) | Designation given |
|---|---|---|---|
| 90 | 10 | 0 | 90PTT/10PP |
| 90 | 10 | 0.25 | 90PTT/10PP/0.25 |
| 90 | 10 | 0.5 | 90PTT/10PP/0.5CNT |
| 90 | 10 | 1 | 90PTT/10PP/1CNT |
| 90 | 10 | 2.5 | 90PTT/10PP/2.5CNT |
| 90 | 10 | 5 | 90PTT/10PP/5CNT |
| Ec = Em (1 + rVf) | (4) |
| Reinforcing efficiency, r = [(Ec/Em) − 1]/Vf | (5) |
The calculated reinforcing effectiveness of MWCNTs in the PTT/PP blend is given in Table 2. The high value of reinforcing efficacy for composites with 1 wt% MWCNTs indicates strong interactions between PTT and MWCNTs. It was noticed that the value of the reinforcing efficiency factor slightly decreased for the 90PTT/10PP/2.5CNT composites and followed a decreasing trend with higher loadings. As the quantity of MWCNTs increases, there is a potential for the increased filler–filler interactions, thereby agglomeration of MWCNTs takes place with the result that reinforcing efficiency decreases.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curves
δ curves
| MWCNT loading (wt%) | Effectiveness of dispersion (Ef) | Degree of entanglement (φ) | Reinforcing efficiency (R) | Volume of the constrained region (C) |
|---|---|---|---|---|
| 1 | 0.874 | 2.57 × 1011 | 23.68 | 0.085 |
| 2.5 | 0.760 | 3.16 × 1011 | 22.28 | 0.099 |
| 5 | 0.714 | 3.48 × 1011 | 14.82 | 0.120 |
Fig. 9(b and c) depicts the E″ versus temperature curves of the optimum concentration blends with MWCNTs. The assimilation of MWCNTs into the blends caused a broadening of the corresponding peaks of PTT and PP, which is due to the restriction of the relaxation process caused by the network formation of MWCNTs in the composites. The high E″ with MWCNT loading is attributed to the rise in the internal friction and enhanced energy dissipation.30
The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve of composites of the PTT/PP blend with various MWCNT loading showed three peaks. The first one represents the Tg of PP (β-relaxation), the second one corresponds to the Tg of PTT, while the third broad peak corresponds to the α-relaxation of PP (Fig. 9(d)). From the graph, it was also noticed that the incorporation of MWCNTs has more influence on the peak of PTT than on that of PP. This behavior is ascribed to the preferential distribution of carbon nanotubes in the PTT phase and their interactions with the polymer chains. From the graph, it was pointed out that the peak height (peak area) of PTT decreases with MWCNT loading, which again confirmed the better interaction between PTT and MWCNTs. Hence, it was noted that additional energy dissipation occurred with the incorporation of MWCNTs into the PTT/PP blend. Thus, a decrease in the tan
δ curve of composites of the PTT/PP blend with various MWCNT loading showed three peaks. The first one represents the Tg of PP (β-relaxation), the second one corresponds to the Tg of PTT, while the third broad peak corresponds to the α-relaxation of PP (Fig. 9(d)). From the graph, it was also noticed that the incorporation of MWCNTs has more influence on the peak of PTT than on that of PP. This behavior is ascribed to the preferential distribution of carbon nanotubes in the PTT phase and their interactions with the polymer chains. From the graph, it was pointed out that the peak height (peak area) of PTT decreases with MWCNT loading, which again confirmed the better interaction between PTT and MWCNTs. Hence, it was noted that additional energy dissipation occurred with the incorporation of MWCNTs into the PTT/PP blend. Thus, a decrease in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak of the composites of PTT/PP with MWCNTs confirmed minimal heat build-up due to the reduced damping characteristics.5
δ peak of the composites of PTT/PP with MWCNTs confirmed minimal heat build-up due to the reduced damping characteristics.5
From the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve, it was very clear that there was a shift in the tan
δ curve, it was very clear that there was a shift in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak of PTT to a higher temperature. This reveals the increase in Tg of PTT (Fig. 9(e)). The reduction in the tan
δ peak of PTT to a higher temperature. This reveals the increase in Tg of PTT (Fig. 9(e)). The reduction in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak height and the shift of Tg to higher temperatures in PTT indicate restricted polymer chain mobility, attributed to physical interactions between MWCNTs and the PTT matrix. The interactions between MWCNTs and PTT lead to the formation of a constrained polymer region around the MWCNTs. This is an effective nanophase (effective constrained length around the MWCNTs) formation in the blend system, and as an outcome, the segmental mobility of adjacent polymer chains is arrested. This limited movement of polymer chains will create a constrained region (schematically represented in Fig. 10(d)), and it can be estimated using the tan
δ peak height and the shift of Tg to higher temperatures in PTT indicate restricted polymer chain mobility, attributed to physical interactions between MWCNTs and the PTT matrix. The interactions between MWCNTs and PTT lead to the formation of a constrained polymer region around the MWCNTs. This is an effective nanophase (effective constrained length around the MWCNTs) formation in the blend system, and as an outcome, the segmental mobility of adjacent polymer chains is arrested. This limited movement of polymer chains will create a constrained region (schematically represented in Fig. 10(d)), and it can be estimated using the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak (Table 2, Fig. 10(c)).
δ peak (Table 2, Fig. 10(c)).
By analyzing the decrease in peak intensity or peak area of the PTT phase in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ plot (Fig. 10(e)), it is possible to calculate the volume of the constrained area (C) (eqn (6)):
δ plot (Fig. 10(e)), it is possible to calculate the volume of the constrained area (C) (eqn (6)):
| Volume of the constrained area, C = 1 − [(1 − C0) W/W0] | (6) |
The volume of the constrained region in the PTT phase was estimated by considering the selective localization of MWCNTs in the PTT phase, and the values are presented in Table 2 and Fig. 10(c). It was observed that the volume of the limited mobility region in the PTT phase was increased with MWCNT loadings. This indicates a strong interaction between PTT and MWCNTs, thereby forming a constrained region around MWCNTs by the restriction of mobility of PTT chains. Fig. 10(d) represents a schematic depiction of the constrained region in 90PTT/10PP/MWCNT composites having the constrained region due to the restricted PTT polymer chains and the mobile PP phase.
3.5. Rheological studies
Fig. 11 shows the rheological properties in which Fig. 11(a) shows the storage modulus (E′) as a function of frequency. Detailed analysis of the graph indicated that the neat polymers displayed terminal behavior with a clear dependence on frequency. The storage modulus of 90PTT/10PP blend increased with MWCNT loading, and a terminal to non-terminal transition was observed (liquid to solid viscoelastic behavior). This confirmed the interconnected network formation of MWCNTs in the matrix and the restricted motion of polymer chains because of this network formation.32,37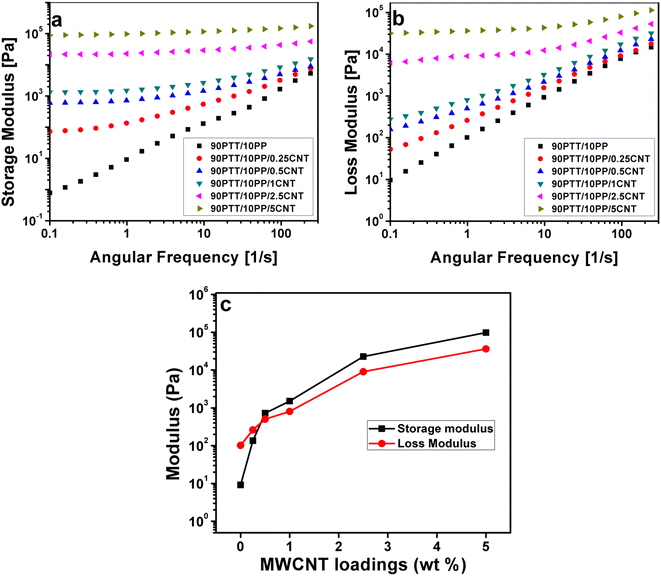 | ||
| Fig. 11 Variation of (a) E′, (b) E″ and (c) comparison between E′ and E″ as a function of MWCNT loading at 0.1 rad s−1. | ||
The increase in nanotube loading will promote the mutual interactions between the nanotubes, thereby enhancing the establishment of a network. At a critical amount of MWCNT, rheological percolation occurs, and the storage modulus increases effectively due to the significant network creation of MWCNTs throughout the arrangement. The rise in the storage modulus is attributed to the polymer–filler and filler–filler interactions, finer distribution of particles, and particle size distribution.
When the frequency of shear is high, the polymer chains will not get enough time to relax. This means that at those higher frequencies, the storage modulus shows an increase because of a lower relaxation time, which in turn can lead to the disentanglement of MWCNT networks. At very low frequencies, ample time is available for the relaxation process to occur, making the system highly responsive to interfacial phenomena. Elevated storage modulus values at depleted frequencies correspond to a more elastic structure, where polymer chain mobility is inhibited by the filler network formation in the composites. Fig. 11(b) shows the loss modulus (E″) values as a function of frequency, which also showed a similar trend to that of the storage modulus with frequency. At elevated frequencies, differences in the modulus among the composites were negligible, supporting the conclusion that MWCNTs do not significantly impact the short-range dynamic motions of polymer chains. Fig. 11(c) shows a comparison between the storage and loss moduli as a function of MWCNT loading.
The inconsistency of storage modulus, E′ and loss modulus E″ of the 90PTT/10PP blend and related composites at three different angular frequencies is shown in Fig. 12. At all frequencies, the composites show the same gradual increase in the behavior of samples from 90PTT/10PP to the 90PTT/10PP/5CNT composite.
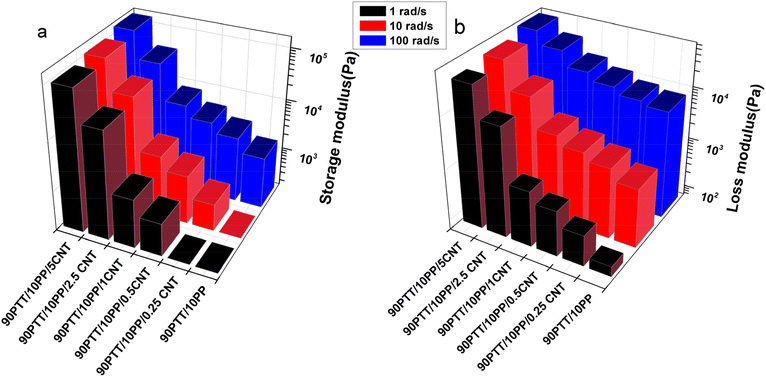 | ||
| Fig. 12 (a) E′ and (b) E″ of 90PTT/10PP blends and composites at three different angular frequencies. | ||
As already noted, at low frequencies, the polymer chains attain a fully relaxed state, demonstrating terminal flow behavior and adhering to scaling laws, E′ α ω2 and E″ α ω, which means that the slope of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E′ versus log
E′ versus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω plot approaching 2 and the slope of log
ω plot approaching 2 and the slope of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E″ versus log
E″ versus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω approaching 1 describe the terminal behavior. The observed decrease in slope and the disappearance of terminal behavior are indicative of non-terminal behavior, arising from the network structure formed by the fillers. In the case of PTT/PP blends and composites, the scaling laws for E′ and E″ are shown in Table 3. The slope of the plots decreased with MWCNT loadings. This confirmed the terminal to non-terminal transition behavior of composites (liquid to pseudo-solid rheological behavior).32,38,39
ω approaching 1 describe the terminal behavior. The observed decrease in slope and the disappearance of terminal behavior are indicative of non-terminal behavior, arising from the network structure formed by the fillers. In the case of PTT/PP blends and composites, the scaling laws for E′ and E″ are shown in Table 3. The slope of the plots decreased with MWCNT loadings. This confirmed the terminal to non-terminal transition behavior of composites (liquid to pseudo-solid rheological behavior).32,38,39
| Samples | Slope of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E′ vs. log E′ vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω ω |
Slope of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E″ vs. log E″ vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω ω |
|---|---|---|
| 90PTT/10PP | 1.12 | 1.03 |
| 90PTT/10PP/0.25CNT | 0.26 | 0.70 |
| 90PTT/10PP/0.5CNT | 0.07 | 0.50 |
| 90PTT/10PP/1CNT | 0.05 | 0.47 |
| 90PTT/10PP/2.5CNT | 0.01 | 0.17 |
| 90PTT/10PP/5CNT | 0.02 | 0.05 |
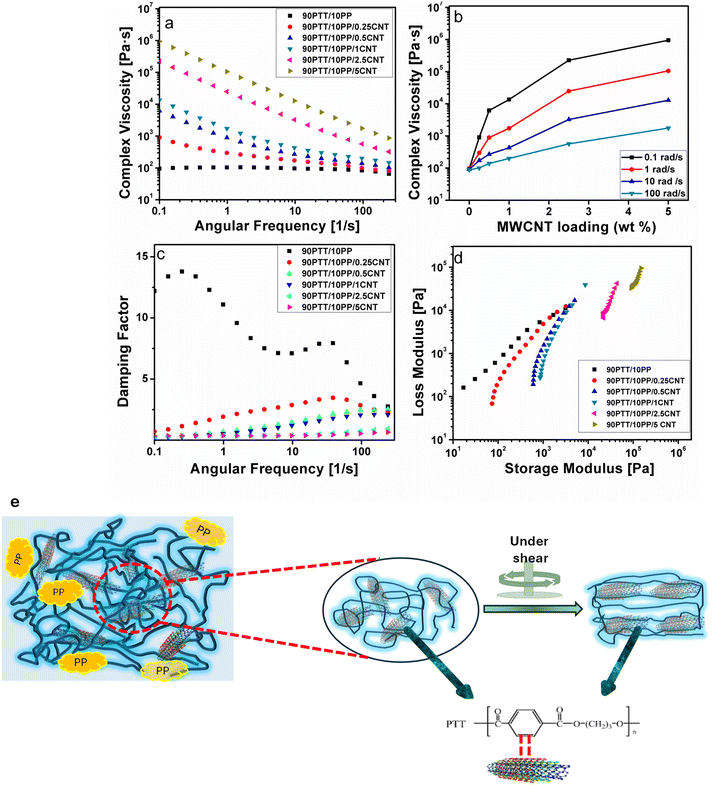
As illustrated in Fig. 13(a), the complex viscosity of the neat polymer remains nearly constant across different angular frequencies. This suggests that, under applied shear, the disentanglement and re-entanglement of polymer chains occur simultaneously, maintaining a steady viscosity characteristic of Newtonian fluids. In contrast, when multi-walled carbon nanotubes (MWCNTs) are introduced, their alignment under shear disrupts the reformation of polymer entanglements. This interference leads to a reduction in melt viscosity, indicating shear-thinning behaviour. Fig. 13(e) presents a schematic depiction of how MWCNTs align and interact with polymer chains during shear.
In this study, the 90PTT/10PP blend exhibited a Newtonian plateau at low angular frequencies and transitioned to shear-thinning behaviour at higher frequencies. The addition of multi-walled carbon nanotubes (MWCNTs) to the PTT/PP blend led to an overall increase in complex viscosity, with a nearly linear rise observed as the MWCNT loading increased, particularly evident at lower frequencies. Fig. 13(a) presents the complex viscosity of different composites as a function of angular frequency. The influence of MWCNTs on viscosity was more pronounced at low frequencies; however, this effect diminished at higher frequencies due to the onset of shear-thinning behaviour, where the applied shear likely disrupts the MWCNT network. The absence of a Newtonian plateau in the composites suggests that the increased viscosity results from strong filler–polymer and filler–filler interactions. These interactions form a physical network among MWCNTs that significantly contributes to the rheological behaviour of the composites. Fig. 13(b) further illustrates how complex viscosity varies with MWCNT content and angular frequency, showing a consistent increase in viscosity with higher MWCNT loading and a decrease in viscosity with increasing frequency.
The degree of non-Newtonian behavior can be understood from the shear-thinning exponent value. According to the Power law,
| Viscosity, η = Aωn | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η versus log
η versus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω plot, and it has the significance that the pseudoplastic, dilatant and Newtonian behavior of polymers can be predicted from the obtained ‘n’ values. Polymers that have ‘n’ values such as n < 1, n > 1, and n = 1 represent the pseudoplastic, dilatant, and Newtonian behavior of polymers, respectively.37,40 In the present study, the shear-thinning exponent values for the 90PTT/10PP blend and its composites are given in Table 4.
ω plot, and it has the significance that the pseudoplastic, dilatant and Newtonian behavior of polymers can be predicted from the obtained ‘n’ values. Polymers that have ‘n’ values such as n < 1, n > 1, and n = 1 represent the pseudoplastic, dilatant, and Newtonian behavior of polymers, respectively.37,40 In the present study, the shear-thinning exponent values for the 90PTT/10PP blend and its composites are given in Table 4.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η vs. log
η vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω plots
ω plots
| Samples | Slopes of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η vs. log η vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω ω |
|---|---|
| 90PTT/10PP | 0.031 |
| 90PTT/10PP/0.25CNT | −0.48 |
| 90PTT/10PP/0.5CNT | −0.85 |
| 90PTT/10PP/1CNT | −0.90 |
| 90PTT/10PP/2.5CNT | −0.96 |
| 90PTT/10PP/5CNT | −0.96 |
From Fig. 13(c), it is clear that the blend nanocomposites exhibited a lower damping factor than the neat blend, which is related to solid-like behavior. That is, the liquid-like viscoelastic behavior of the neat blend decreased with MWCNT loading. A more solid-like behavior was attained for the blend with 5 wt% MWCNT.5 The rheological analysis also threw light on the dispersion of MWCNTs in the blend. It can be suggested that MWCNTs were homogeneously dispersed in the blend and were evident from the higher complex viscosity and storage modulus.7
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E′ versus log
E′ versus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E″ should coincide in the Cole–Cole plot. But in the case of a heterogeneous system, the Cole–Cole plot will not form a semicircle, and with the addition of fillers, the slope of the plot should change.40,41Fig. 13(d) shows the Cole–Cole plot for the neat PTT/PP blend and PTT/PP/MWCNT composites. The changes in the slope of the plot with MWCNT loading were very clear. This can be linked to the variation in morphology of blends with the addition of MWCNTs due to the dispersion of MWCNTs in the PTT matrix and the improved polymer–MWCNT interactions. The large slope difference at higher MWCNT loadings indicates the aggregation of MWCNTs in the polymer system. Moreover, the deviation from a linear relationship between E′ and E″ with MWCNTs indicates the formation of a network of MWCNTs in the PTT matrix.42 Hence, the Cole–Cole plot confirmed that the rheological behavior of PTT/PP blends can be affected by MWCNTs. There are many studies reported with similar behavior of composites with the addition of nanofillers.22
E″ should coincide in the Cole–Cole plot. But in the case of a heterogeneous system, the Cole–Cole plot will not form a semicircle, and with the addition of fillers, the slope of the plot should change.40,41Fig. 13(d) shows the Cole–Cole plot for the neat PTT/PP blend and PTT/PP/MWCNT composites. The changes in the slope of the plot with MWCNT loading were very clear. This can be linked to the variation in morphology of blends with the addition of MWCNTs due to the dispersion of MWCNTs in the PTT matrix and the improved polymer–MWCNT interactions. The large slope difference at higher MWCNT loadings indicates the aggregation of MWCNTs in the polymer system. Moreover, the deviation from a linear relationship between E′ and E″ with MWCNTs indicates the formation of a network of MWCNTs in the PTT matrix.42 Hence, the Cole–Cole plot confirmed that the rheological behavior of PTT/PP blends can be affected by MWCNTs. There are many studies reported with similar behavior of composites with the addition of nanofillers.22
The combined evidence from morphology, DMA, and rheology points to a twofold role of MWCNTs: (i) selective localization in PTT, creating constrained regions that suppress segmental mobility, and (ii) network formation above a percolation threshold, imparting pseudo-solid-like behavior. The balance between these mechanisms explains the contrasting trends of reinforcing efficiency (peaking at 1 wt%) and the increased constrained volume at higher loadings (Table 4). Such quantification advances the understanding of filler-induced confinement in immiscible blends and provides a framework extendable to other thermoplastic systems.
4. Conclusions
The present study filled the gap in research on immiscible PTT/PP blend nanocomposites by quantifying dispersion effectiveness, entanglement density, reinforcing efficiency, and constrained polymer volume, parameters that have never been reported for this immiscible blend. By correlating selective CNT localization with thermal, mechanical, and rheological transitions, this work provides the first predictive structure–property framework for engineering CNT-modified PTT/PP blends. DMA results highlighted the significant influence of MWCNTs on the dynamic mechanical behavior of the blend. The estimated volume of the constrained region provided insights into the interaction between the PTT phase and the incorporated MWCNTs.Rheological studies demonstrated that MWCNTs had a notable impact on the flow and viscoelastic properties of the blends. At low frequencies, an upturn in complex viscosity was observed, accompanied by non-terminal behavior in the storage modulus versus frequency curve. The storage modulus increased with MWCNT content, reaching its peak at 5 wt%, which exceeded that of the unfilled blend. The rise in the storage modulus (E′) with higher MWCNT loadings also contributed to improved elastic characteristics. Overall, the MWCNT-reinforced PTT/PP blends exhibit superior properties, suggesting their strong potential for use in advanced engineering applications. Also, as an extension of the work, the effects of CNT functionalization, in situ compatibilizer formation, long-term thermo-oxidative stability, percolation under dynamic shear and detailed crystallization kinetics will be studied.
Conflicts of interest
The authors have no conflicts to present.Author contributions
Conceptualization, methodology, formal analysis, validation, data curation, and writing – original draft: Ajitha A. R.; writing – review & editing and visualization: Arunima Reghunadhan; methodology and writing – review & editing: Sari. P.S. and Miroslav Huskic; and conceptualization and supervision: Sabu Thomas.Data availability
All the data associated with the article will be made available from the corresponding authors upon request.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5lp00324e.
Acknowledgements
The authors would like to thank UGC, New Delhi, India, for the financial support (JRF scheme, ref no. 17-06/2012(i) EU-V).References
- Y. Xu, X. Yao, Z. Zhang, D. Zhu, H. Na, J. Zhu and C. Fang, Mater. Today Commun., 2025, 42, 111500 CrossRef.
- B. Özsarıkaya, S. H. Yetgin, A. Durmuş and F. Çalışkan, Mater. Sci. Eng., B, 2025, 314, 118016 CrossRef.
- B. Kryszak, A. Ujčić, V. Gajdošová, M. Šlouf and K. Szustakiewicz, J. Mater. Res. Technol., 2025, 37, 2919–2934 CrossRef.
- K. Jayanarayanan, N. Rasana and R. K. Mishra, in Thermal and Rheological Measurement Techniques for Nanomaterials Characterization, ed. S. Thomas, R. Thomas, A. K. Zachariah and R. K. Mishra, Elsevier, 2017, pp. 123–157 Search PubMed.
- A. Rostami, M. Masoomi, M. J. Fayazi and M. Vahdati, RSC Adv., 2015, 5, 32880–32890 RSC.
- S. E. Zeltmann, K. A. Prakash, M. Doddamani and N. Gupta, Composites, Part B, 2017, 120, 27–34 CrossRef CAS.
- Q. Zhang, F. Fang, X. Zhao, Y. Li, M. Zhu and D. Chen, J. Phys. Chem. B, 2008, 112, 12606–12611 CrossRef CAS.
- M. Liebscher, L. Tzounis, P. Pötschke and G. Heinrich, Polymer, 2013, 54, 6801–6808 CrossRef CAS.
- G. Mittal, V. Dhand, K. Y. Rhee, S. J. Park and W. R. Lee, Korean Society of Industrial Engineering Chemistry, 2015, preprint, DOI:10.1016/j.jiec.2014.03.022.
- F. H. Gojny, M. H. G. Wichmann, B. Fiedler and K. Schulte, Compos. Sci. Technol., 2005, 65, 2300–2313 CrossRef CAS.
- A. M. Kunjappan, M. A. Poothanari, A. A. Ramachandran, M. Padmanabhan, L. Mathew and S. Thomas, Polym. Int., 2019, 68, 637–647 CrossRef CAS.
- Y. Zare, H. Garmabi and K. Y. Rhee, Composites, Part B, 2018, 144, 1–10 CrossRef CAS.
- X. Zhao, H. Wang, Z. Fu and Y. Li, ACS Appl. Mater. Interfaces, 2018, 10, 8411–8416 CrossRef.
- N. Zheng, W. Sun, H. Y. Liu, Y. Huang, J. Gao and Y. W. Mai, Compos. Sci. Technol., 2018, 159, 180–188 CrossRef.
- M. Liebscher, J. Domurath, B. Krause, M. Saphiannikova, G. Heinrich and P. Pötschke, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 79–88 CrossRef.
- I. Taraghi, F. Abdolhossein, P. Sandra and Z. Roslaniec, Compos. Interfaces, 2018, 25, 275–286 CrossRef.
- M. R. H. Zargar, A. Ghaffarian, A. Ebrahimzade and A. M. Shoushtari, Fibers Polym., 2020, 21, 2753–2768 CrossRef.
- M. R. H. Zargar and A. M. Shoushtari, J. Macromol. Sci., Part B: Phys., 2019, 58, 723–748 CrossRef.
- A. R. Ajitha, P. Mohammed Arif, M. K. Aswathi, L. P. Mathew, V. G. Geethamma, N. Kalarikkal, S. Thomas and T. Volova, New J. Chem., 2018, 42, 13915–13926 RSC.
- A. R. Ajitha, V. G. Geethamma, L. Mathew, P. Saha, N. Kalarikkal, S. Thomas and M. Strankowski, Polym. Test., 2018, 68, 395–404 CrossRef.
- A. A. Ramachandran, L. P. Mathew and S. Thomas, Eur. Polym. J., 2019, 118, 595–605 CrossRef.
- A. A. Ramachandran, A. Reghunadhan, A. M. Kunjappan, L. P. Mathew, S. Thomas, D. Laroze and M. Strankowski, New J. Chem., 2020, 44, 16557–16568 RSC.
- A. R. Ajitha, P. M. Arif, M. K. Aswathi, L. P. Mathew, V. G. Geethamma, N. Kalarikkal, S. Thomas and T. Volova, New J. Chem., 2018, 42, 13915–13926 RSC.
- S. H. Jafari, A. Kalati-vahid, H. A. Khonakdar, A. Asadinezhad, U. Wagenknecht and D. Jehnichen, eXPRESS Polym. Lett., 2012, 6, 148–158 CrossRef.
- M. Run, H. Yanping, S. Hongzan and X. Hu, J. Macromol. Sci., Part B: Phys., 2009, 48, 13–24 CrossRef.
- W. Zeng, H. Li, T. Liu and S. Yan, Chin. Sci. Bull., 2008, 53, 2145–2155 CrossRef.
- S. Jose, J. Parameswaranpillai, B. Francis, A. S. Aprem and S. Thomas, AIMS Mater. Sci., 2016, 3, 1177–1198 Search PubMed.
- S. H. Jafari, A. Kalati-vahid, H. A. Khonakdar, A. Asadinezhad, U. Wagenknecht and D. Jehnichen, eXPRESS Polym. Lett., 2012, 6, 148–158 CrossRef.
- P. Balakrishnan, M. S. Sreekala, M. Kunaver, M. Huskić and S. Thomas, Carbohydr. Polym., 2017, 169, 176–188 CrossRef PubMed.
- J. Jyoti, B. P. Singh, A. K. Arya and S. R. Dhakate, RSC Adv., 2016, 6, 3997–4006 RSC.
- N. Wang, N. Gao, Q. Fang and E. Chen, Mater. Des., 2011, 32, 1222–1228 CrossRef.
- C. I. Ferreira, O. Bianchi, M. A. S. Oviedo, R. V. B. Oliveira, R. S. Mauler, C. I. Ferreira, O. Bianchi, M. A. S. Oviedo, R. V. B. de Oliveira and R. S. Mauler, Polim.: Cienc. Tecnol., 2013, 23, 456–461 CrossRef.
- J. P. Mofokeng, A. S. Luyt, T. Tábi and J. Kovács, J. Thermoplast. Compos. Mater., 2011, 25, 927–948 CrossRef.
- M. M. Mazidi, M. K. Razavi Aghjeh, H. A. Khonakdar and U. Reuter, RSC Adv., 2016, 6, 1508–1526 RSC.
- R. Banerjee and S. S. Ray, ACS Omega, 2023, 8, 27969–28001 CrossRef PubMed.
- M. K. Aswathi, M. Padmanabhan, L. Mathew, P. Saha, R. Terzano, N. Kalarikkal, T. Volova and S. Thomas, Polym. Eng. Sci., 2019, 59, E435–E445 CrossRef.
- A. Gupta and V. Choudhary, J. Mater. Sci., 2014, 49, 3839–3846 CrossRef.
- X. Gao, A. I. Isayev, X. Zhang and J. Zhong, Compos. Sci. Technol., 2017, 144, 125–138 CrossRef.
- X. Wang, Z. He, J. Yang, N. Zhang, T. Huang, Y. Wang and Z. Zhou, Composites, Part A, 2016, 91, 105–116 CrossRef.
- E. Elias, S. Chandran, A. K. Zachariah, V. Kumar V, S. M. A, S. Bose, F. G. Souza, Jr. and S. Thomas, RSC Adv., 2016, 6, 85107–85116 RSC.
- P. Pötschke, T. D. Fornes and D. R. Paul, Polymer, 2002, 43, 3247–3255 CrossRef.
- Y. Xiao, W. Wang, X. Chen, T. Lin, Y. Zhang, J. Yang, Y. Wang and Z. Zhou, Composites, Part A, 2016, 90, 614–625 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |