Open Access Article
Open Access ArticleDeep learning-driven microfluidic chip architecture design for intelligent particle motion control
Hongxia
Li†
 *a,
Xuhui
Chen†
*a,
Xuhui
Chen†
 a,
Du
Qiao†
a,
Xue
Zhang
a,
Jiang
Zhang
a,
Jianan
Zou
a,
Danyang
Zhao
a,
Xuhong
Qian
b and
Honglin
Li
*b
a,
Du
Qiao†
a,
Xue
Zhang
a,
Jiang
Zhang
a,
Jianan
Zou
a,
Danyang
Zhao
a,
Xuhong
Qian
b and
Honglin
Li
*b
aState Key Laboratory of High-Performance Precision Manufacturing, Dalian University of Technology, Dalian 116023, China
bInnovation Center for AI and Drug Discovery, School of Pharmacy, East China Normal University, Shanghai 200062, China. E-mail: hlli@hsc.ecnu.edu.cn
First published on 14th January 2026
Abstract
Precise spatiotemporal manipulation of particles in complex microfluidic channel networks (MCNs) underlies numerous advanced applications, but remains constrained by the difficulty of rapidly translating prescribed trajectories into manufacturable device designs. In this work, we introduce a modular deep learning framework that overcomes these limitations by decomposing MCNs into standardized, reusable functional modules with well-characterized fluidic and structural properties. For each module, a dedicated neural network predicts the full spatiotemporal particle state—including position, velocity, and transit time—under diverse flow conditions. A multi-module reconfiguration algorithm (MMRA) assembles these local predictions into continuous, device-scale trajectories while rigorously preserving physical state continuity. This approach enables deterministic port routing and precise spatiotemporal scheduling on “DUT” and “grid” chips, with a mean absolute timing error below 0.031 s. Integrated into PathChip, our user-friendly end-to-end design platform, the proposed approach enables users to specify target particle behaviors and automatically generate optimized module sequences, geometries, and control parameters, producing fabrication-ready device blueprints. Using this reverse design workflow, the integration of 5000 modules can be completed in as little as 18 s. This work establishes a structurally scalable pathway toward programmable, device-level spatiotemporal particle manipulation in microfluidics, with broad implications for lab-on-a-chip automation, high-throughput screening, and adaptive microfluidic systems.
1 Introduction
Precise spatiotemporal manipulation of particles in microfluidic systems underlies transformative advances in biomedicine and chemical synthesis.1–3 By exploiting microscale flow phenomena within microchannels, precise spatial control over the motion of diverse particles, including polymer monolayers,4 colloidal particles,5 vesicles,6 single cells,7 and even bacteria,8 has been successfully achieved. However, in complex microfluidic channel networks (MCNs), particle trajectories encode not only spatial routing but also timing information that directly determines downstream functionality. From steering drug carriers through vascular-like networks,9,10 orchestrating single-cell sequencing workflows,11,12 to executing time-resolved reactions in droplet microreactors,13,14 the ability to predict the position, velocity, and arrival time of micro/nanoparticles with high fidelity promises unprecedented control over biological and chemical processes at the microscale.15 Yet, implementing complex, user-defined control of particle spatiotemporal trajectories in MCNs and translating them into channel geometries remains a formidable challenge.Conventional design utilizes numerical simulations, demonstrating its advantages in nonlinear flow analysis and facilitating iterative optimization of the equipment. However, when dealing with complex, large-scale channel networks and particle trajectories, traditional approaches are usually computationally intensive, as they rely on computationally intensive multiphysics simulations and empirical iterative tuning.16–20 These approaches suffer from two limitations when targeting complex global behaviors. Firstly, the complex topological connections and coupling of local flow fields in MCNs lead to the highly nonlinear behavior of particle flow, which leads to expensive time cost and increased risk of non-convergence.21–23 Additionally, translating a desired spatiotemporal particle behavior (e.g., a specific sequence of movements at defined times and locations24,25) into an optimal device geometry and operational protocol is an ill-posed, non-intuitive inverse problem. Consequently, the design of microfluidic systems for sophisticated particle choreography is often slow, empirical, and limited in scope.
Deep learning (DL) has emerged as an emerging tool that provides efficient methods for fast prediction, and assisting in automated design exploration.26,27 Recent works demonstrate capability of DL in predicting the mapping relationship between complex flow fields and particle behavior,28–30 or optimizing simple device components.31,32 However, these approaches are typically confined to forward prediction, and struggle when confronted with the historical state-dependence and long-range correlations inherent to particle transport in complex MCNs.33,34 On the other hand, the inability to explicitly embed the physical connection between paths makes it difficult to predict and control the movement of particles over long distances and long periods of time.35 Therefore, there is currently a lack of a scalable framework for holistically prediction and control of complex, device-scale spatiotemporal particle trajectories. Furthermore, while certain DL models facilitate inverse design for rudimentary components36 or discrete outputs e.g. droplet size,37,38 prevailing methodologies typically lack the granularity and flexibility requisite for translating intricate spatiotemporal path requirements into actionable device specifications and operational protocols.39
Here, we introduce a novel modular modeling and trajectory prediction strategy as shown in Fig. 1. We decouple MCNs into a series of standardized, reusable single modules with different fluidic or structural driving characteristics. The specific flow paths of the particles within the channel obtained using sheath flow focusing are shown in Fig. 1a. A dedicated DL model predicts instantaneous spatiotemporal particle motion information within each module under varying actuation conditions. On this basis, a multi-module reconfiguration algorithm (MMRA) then assembles these module-level predictions into continuous, device-scale trajectories, ensuring physical state continuity across transitions (Fig. 1b). We experimentally validate the framework on a “DUT” chip, demonstrating deterministic routing to prescribed outlets and active spatiotemporal planning enabled by precise delay control. In a grid-based chip architecture, the framework achieves a mean absolute timing error below 0.031 s. These capabilities are integrated into PathChip, a user-friendly end-to-end platform, that enables users to specify desired behaviors and automatically generates optimized module sequences, geometries, and operating parameters, producing fabrication-ready blueprints (Fig. 1c). Using this reverse design workflow, the integration of 5000 modules can be completed in as little as 18 s. This work establishes a scalable and generalizable route toward programmable, high-fidelity spatiotemporal particle control across complex microfluidic architectures.
2 Results
2.1 Dataset generation
To enhance the generalization and predictive performance of the neural network, we constructed a well-annotated and feature-diverse dataset. A total of 20 input parameters were selected to form a high-dimensional feature space, encompassing microchannel geometry, flow conditions, and particle properties (Fig. 2a). Detailed parameter definitions and constraints are provided in Fig. S1, Table S1 and Methods 4.4. The selected 20 parameters capture dominant behaviors under low-Reynolds-number microchannel transport. Particle diameter and density are treated as explicit input parameters, allowing the learned mapping to capture size-dependent migration and routing behavior within each module. Factors such as flow regime transitions, fluid rheology, and interfacial interactions were excluded in this initial study due to their negligible impact within our experimental domain. Using Latin hypercube sampling (LHS), we generated 500 uniformly distributed samples across the input space. The uniformity of the sample distribution was evaluated by computing the normalized minimum Euclidean distance between sample points40 (eqn (1)), as shown in Fig. 2bi. | (1) |
where Dij denotes the Euclidean distance between the i-th and j-th samples, dmini is the minimum distance from the i-th sample to all others, xi represents the i-th sample, and d is the feature dimensionality. As shown in Fig. 2bi, the normalized minimum distances are centered around 0.5, indicating a uniformly distributed sampling across the parameter space. We further assessed the distribution of geometric and flow configurations. As shown in Fig. 2bii and iii, the three representative channel types occur in approximately equal proportions, and the inlet (1), none (0), and outlet (−1) flow states across the three branches are evenly represented. This balanced sampling ensures comprehensive coverage of particle dynamics across diverse structural and flow conditions.
A complete dataset was constructed using both numerical simulations and particle-tracking experiments (Fig. 2c). We developed a coupled laminar flow-particle transport numerical model to simulate particle motion under 500 distinct parameter configurations. The validity of the numerical model is detailed in Note S1. A subset of the simulation cases, matching the physical properties of polystyrene (PS) microparticles, was selected and perturbed to generate 100 additional configurations for experimental data collection. This 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between simulated and experimental samples ensured a balanced design between model-driven inference and empirical observation. In total, we obtained 6000 independent particle trajectory samples, each with a unique combination of channel geometry, flow conditions, and particle properties. For each case, four output features were extracted: outlet label OL, particle position ratio OR at the outlet cross-section, particle instantaneous velocity
1 ratio between simulated and experimental samples ensured a balanced design between model-driven inference and empirical observation. In total, we obtained 6000 independent particle trajectory samples, each with a unique combination of channel geometry, flow conditions, and particle properties. For each case, four output features were extracted: outlet label OL, particle position ratio OR at the outlet cross-section, particle instantaneous velocity 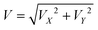 at the outlet, and particle migration time T from inlet to outlet. Detailed definitions of these four features are provided in Note S2. This dataset forms the foundation for neural network training, supporting robust spatiotemporal trajectory prediction of particles in complex microchannel environments.
at the outlet, and particle migration time T from inlet to outlet. Detailed definitions of these four features are provided in Note S2. This dataset forms the foundation for neural network training, supporting robust spatiotemporal trajectory prediction of particles in complex microchannel environments.
2.2 Single-module for particle motion prediction
In branched networks, the local flow distribution, hydrodynamic resistances, and geometric variations collectively determine how particles migrate across the device.41 Accurate, module-level trajectory prediction thus allows designers to rationally position reaction chambers,42 sorting units,43 or outlet collectors44 based on the expected particle pathway. For biological or chemical workflows that require controlled routing, such as size-based cell enrichment,45 vesicle separation,46 and sequential reagent exposure,47 trajectory prediction can achieve precise control.To accurately predict particle motion within single module, we designed, trained, and optimized four deep neural network models. These models map local flow field conditions, channel geometry, and particle properties into four outputs related to spatiotemporal control of particle trajectories (see Note S3 for model specifications). They contain: (i) the downstream branch selected by the particle, defined as outlet label OL, (ii) its lateral position at the module exit, defined as the position of the particle at the outlet OR, (iii) its instantaneous velocity V, and (iv) the transit time through the module, defined as migration time T. These four neural networks are collectively referred to as the particle motion prediction model (PMPM), as illustrated in Fig. 3a. Leverage these deep learning models, we can obtain the exit descriptor of a single module to represent the movement state of particles in each module, while ignoring the movement information of particle trajectories inside the module. This simplification greatly reduces the global data volume requirements and prediction time, thus enabling the need for accurate prediction of complex, long-distance particle trajectories to be met. In addition, the flexibility of module assembly also makes it possible to automate the inverse design of complex, large-scale microchannel networks.
80% of the dataset was used for model training, and the remaining 20% was reserved for testing. The coincidence degree between the particle outlet OL prediction and the experimental data of the trained model on the test set was 96.9 ± 0.5%, with standard deviation calculated over five independent train–test splits. The confusion matrix (Fig. 3bi) shows strong agreement between predicted particle outlet choice and the experimental data, indicating high fidelity in outlet selection for particles. For OR, V and T prediction tasks, the parity plots exhibit a near-diagonal trend (Fig. 3bii–iv), indicating that the OR, V and T of the particles at the outlet coincide well with the experimental data. To further evaluate the accuracy of particle motion state prediction, we visualized the classification probability, that is the probability of which downstream branch the particle chooses, distribution on the test set and marked the point at which the particle enters the wrong branching channel (Fig. 3c). For OR, V and T prediction tasks, we computed the coefficient of determination (R2), root-mean-square error (RMSE), and mean absolute error (MAE) (Fig. 3d; detailed values in Table S3). The predicted probabilities exhibit clear separation among different outlets, with stable performance and no evident outlet bias. Misclassifications is often near adjacent channel boundaries or close to branching inlets where subtle flow variations can influence particle routing. In practice, the proximity of particles to these areas should be avoided as much as possible (misclassification examples show in Fig. S4). For regression tasks, prediction errors of OR and T appear more scattered. The OR shows relatively high RMSE (0.114), reflecting higher variability, but had no significant effect on the prediction.
To evaluate the accuracy of model predictions, we performed particle focusing experiments, the experimental platform and method are shown in Fig. 3e, Video S1 and Methods 4.3. Within the parameters of the experiment, the particles were successfully focused at the specified position. Particles located at the center of the cross section of the particle flow were selected as targets, and the corresponding position, velocity, and time measurements were extracted. Based on the configured experimental parameters, the PMPM model was employed to predict the corresponding OR, V, and T values, and the predictions were compared with the experimental results. The corresponding absolute errors (AE) are shown in Fig. 3f. In comparison, the prediction accuracy of V, and T is higher than OR, but overall it remains below 0.2, show the prediction effect is better. The MAEs for OR, V, and T were 0.098, 0.006 m s−1, and 0.008 s, respectively. The largest AE was observed in OR, reaching up to 0.16, and exhibiting sensitivity to both flow rate and channel type. Under low flow conditions and in type-1 channels (straight type channel), particle paths were more deterministic due to more accurate predictions. In contrast, type-3 channels (double curved type channel) showed frequent nonlinear deviations, reducing spatial prediction precision. Specifically, the MAE of OR was 0.065 for type-1 channels and 0.134 for type-3 channels, highlighting a significant performance gap. In practice, type-1 channels are recommended as primary structural templates or optimization targets for inverse design tasks requiring high trajectory fidelity.
Discrepancies in the predictions likely arise from nonlinear couplings among input features, such as channel asymmetry, local shear gradients, or particle–fluid interactions.48 These nonlinear interactions are inherent to inertial microfluidics,41 and hold well in the range of laminar flow (Re < 10) considered in this work. The regions where errors arise are consistent with known to be prone to perturbations in inertial microfluidics, such as cross-sectional expansions, turning junctions, or sharp geometric perturbations. These errors belong to the inherent errors of model prediction, and should be minimized in the practical application of these vulnerable regions of prediction, or additional targeted modeling of these regions to narrow the error.
Finally, we investigated the effect of dataset size on model accuracy. Models were trained on incrementally larger subsets ranging from 100 to 6000 samples, with each configuration repeated five times. For evaluation the accuracy of model training, 20% of the original dataset was randomly selected as a consistent test set. The resulting performance curves are shown in Fig. 4. For OL, T, and V, model accuracy plateaued once the training set exceeded 1000 samples, reaching performance comparable to that of the full dataset. In contrast, prediction of OR exhibited a stronger dependence on dataset size, indicating that high-resolution spatial descriptors require a larger sample pool to enable precise trajectory reconstruction.
2.3 Multi-module reconstruction of particle trajectory
To extend trajectory inference to global microchannel networks and module-level prediction to device level microfluidic networks, we developed a multi-module reconfiguration algorithm (MMRA). The MCNs were decomposed into standardized functional discrete single-module with well-defined geometric and hydrodynamic characteristics, each enabling accurate local prediction of particle motion. By concatenating each modular particle motion data predicted with high accuracy, the modular particle motion data can be reassembly into long trajectories in a complex MCNs. MMRA was implemented within the PathChip framework and applied to multi-branch channel networks, as illustrated in Fig. 5a. By abstracting and modularizing the network, MMRA enables efficient global trajectory inference across complex channel topologies.In order to realize efficient transmission of particle motion data, we use mathematical language to transplant MCNs to a computer for processing. The unified digital structure and equivalent circuit model of the MCNs architecture is constructed for global inference, as shown in Fig. 5b. Flow distribution across branches is estimated using a fluid–circuit analogy. Each module in the MCNs is assigned a unique identifier, and the entire network is encoded as an undirected, unweighted adjacency matrix. Leveraging the fluid–electrical analogy,49 Hagen–Poiseuille's law (eqn (2)) is approximated by Ohm's law (eqn (3)) to rapidly estimate pressure-driven flow across the network (see Methods 2.8 for implementation details). Based on the adjacency matrix, an equivalent electrical circuit of MCN is established, where resistors and wires represent fluidic connections; resistance corresponds to hydrodynamic resistance, and circuit nodes represent fluidic junctions. The fluid inlet node is connected to the positive terminal of a voltage source, while outlets are grounded, emulating a boundary condition of zero pressure (0 MPa).
| Δp = p+ − p− = QRH | (2) |
| V = V+ − V− = IRE | (3) |
MMRA achieves progressive expansion of particle trajectories by iteratively propagating particle state predictions between connected modules. At each step, the predicted particle motion results outputs from the current module—including the outlet label OL, particle position OR at the outlet, instantaneous velocity V, and transit time T—are passed as the particle entry conditions for the downstream module. Among these, OL and OR are critical in determining the subsequent path selection, ensuring continuity of particle state across the MCN. As illustrated in Fig. 5ci, MMRA initiates from a specified inlet module, infers the next module index based on the adjacency matrix, the digital connection map of the modules, and OL, and maps the current OR to the inlet position IR of the subsequent module. This process iterates until the particle reaches a designated outlet, completing the cross-module spatiotemporal trajectory construction (Fig. 5cii). The reconstructed module sequence is then reassembled into the original network layout and rendered via PathChip for global trajectory visualization (Fig. 5ciii). MMRA does not interfere with intra-module predictions but functions as a coordination framework for information propagation and path logging, which are assembled into a continuous trajectory that ultimately outputs a particle state sequence across modules. By preserving both spatial and temporal information, the method enables efficient evaluation of particle routing, cumulative transit time, and arrival location across complex microfluidic circuits. Experimental results indicate that a five-module trajectory prediction takes 0.631 ± 0.051 s on average (n = 10), demonstrating the framework's efficiency and scalability for rapid trajectory inference in MCNs.
To validate the effectiveness of multi-module trajectory inference, we fabricated a microfluidic chip based on the abstracted MCNs show in Fig. 5a, and conducted particle tracking experiments. Using sheath flow focusing, we focused a suspension of 1 μm PS particles at the center position IR = 0.4 and injected them through a straight channel into MCNs. As shown in Fig. 5d and Video S2, the trajectory of a representative particle followed the path node 1 → 2 → 6 → 7 → 5, eventually flows out through outlet 2. This trajectory is consistent with the MMRA-based prediction in Fig. 5ciii, confirming the accuracy of MMRA. To further demonstrate trajectory controllability, we designed and fabricated a channel shaped as the letters “DUT”, composed of multiple non-standard modules. The inter-module connections were abstracted via geometric similarity and mapped to approximate canonical module types. Under the MMRA framework, iterative adjustment of inlet parameters enabled directional guidance of particle motion. As shown in Fig. 5e, particles were focused at IR = 0.5 and successfully guided through the letters “D”, “U”, and “T” under the prescribed flow conditions, exiting from the tail of the “T.” The experimental trajectory aligns with the MMRA prediction (see Video S2), demonstrating the predictive capability of PMPM in non-standard structures and the effectiveness of MMRA in controlling particle motion within physical microfluidic chips.
2.4 Particle trajectory and delay control
In chemical and biological assays, precise temporal coordination and spatial sequencing are critical, such as coordinating multi-step reactions,50 staged reagent exposure,51 or timed delivery,52 requiring tight control over the delivery path and transmission delay of reagents or stimuli.53–55 To explore this potential, we leveraged the developed neural network model PMPM to simulate delay-based control strategies for intrachannel particles transport. PMPM predicts the transit time of particles in the module, and is extended to the complete long trajectory time in the overall channel by MMRA. Different particle trajectories correspond to different flow times. Therefore, by controlling the particle trajectory, it is possible to control the transit time of particles in the channel. As a proof of concept, a 5 × 5 microfluidic grid chip as shown in Fig. 6a was designed to achieve time-delay control of particles.Ensuring that the predicted time of particles in the module is consistent with the transit time of particle in the actual experiment module is the basis for achieving accurate prediction of the complete trajectory time. Due to structural discrepancies between module junctions in the grid microchannel and standard configurations in the training dataset, directly applying the original time-prediction model will introduce systematic errors. Thus, we performed residual correction on the module transit time prior to global trajectory prediction.56 The true transit time Tt and the model-prediction time Tp under 50 uniform sampling flow conditions were used to train a lightweight neural network to model the nonlinear residual relationship between Tt and Tp. The sampling module in the actual experiment is shown in Fig. 6b, and the prediction time and real-time sampling are shown in Fig. 6c. This network takes the original prediction Tp as input and outputs the residual R = Tt − Tp, refine time prediction.
To evaluate time-delay control accuracy based on trajectory prediction, we predicted both the particle paths and transit times in grid microchannel (Fig. 6d). The model first estimated the uncorrected transit time Ti for each module (where i denotes the module index), and computed the total uncorrected trajectory time 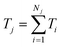 , where j indexes the trajectory and Nj is the number of modules in the j-th path. A trained neural network was then applied to correct each module-level time prediction, yielding corrected transit times Ticorr. and total corrected trajectory times
, where j indexes the trajectory and Nj is the number of modules in the j-th path. A trained neural network was then applied to correct each module-level time prediction, yielding corrected transit times Ticorr. and total corrected trajectory times 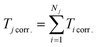 . As shown in Fig. 6e, we experimentally replicated the predicted flow settings, recording the actual particle trajectories and their corresponding total transit times Tjtrue. Video documentation is provided in Video S3. Comparison between Tjtrue and Tjcorr. yielded absolute residuals RAcorr. = |Tjtrue − Tjcorr.|, shown in Fig. 6f. The MAE between predicted and the actual data decreased significantly from 0.932 s (uncorrected) to 0.031 s after correction, with the maximum RAcorr. limited to 0.0965 s. These results confirm the robustness of accurate delay control using residual correction and demonstrate the ability of the developed model to achieve high-precision delay control. By linking spatiotemporal trajectory prediction with physical execution, this framework opens new opportunities for precise temporal coordination in microfluidic systems.
. As shown in Fig. 6e, we experimentally replicated the predicted flow settings, recording the actual particle trajectories and their corresponding total transit times Tjtrue. Video documentation is provided in Video S3. Comparison between Tjtrue and Tjcorr. yielded absolute residuals RAcorr. = |Tjtrue − Tjcorr.|, shown in Fig. 6f. The MAE between predicted and the actual data decreased significantly from 0.932 s (uncorrected) to 0.031 s after correction, with the maximum RAcorr. limited to 0.0965 s. These results confirm the robustness of accurate delay control using residual correction and demonstrate the ability of the developed model to achieve high-precision delay control. By linking spatiotemporal trajectory prediction with physical execution, this framework opens new opportunities for precise temporal coordination in microfluidic systems.
2.5 Inverse design automation
Finally, we propose the automated inverse design (AID) approach (see Fig. S5 for workflows) rapidly produces initial structural layouts, offering a scalable and efficient solution particularly suited for early-stage development or applications lacking design priors. We extended the PathChip framework by incorporating an AID module with optimization capability. The assumptions underlying this inverse design process are detailed in Note S4. Given a predefined flow condition and a target trajectory, the system autonomously generates a channel configuration that satisfies the design objectives. Two key components are required to support this functionality: an adjacency matrix module (Fig. 7a) and an equivalent circuit analysis module (see Fig. S6 for circuit model configuration). The adjacency matrix ensures consistency in module indexing during trajectory propagation. The circuit module, based on fluid–circuit analogy, reformulates the microfluidic network as a solvable Kirchhoff current–voltage system. This allows the program to directly ingest flow-related parameters and compute global flow rates across branches internally. The Kirchhoff current and voltage formulations corresponding to the adjacency matrix in Fig. 7a are provided in Table S4.To enable automated path planning towards a target particle trajectory or specified outlet condition, we implemented a particle swarm optimization (PSO) algorithm to iteratively tune microchannel structural parameters. As illustrated in Fig. 7b, the optimization objective is defined by the discrepancy between the predicted path and the target trajectory, quantified as the difference between the total path length and the number of sequentially matched nodes (eqn (4)). This objective reflects the alignment accuracy between the generated and desired trajectories.
| Objective Function = NT − NM | (4) |
To demonstrate the design efficiency of AID, we integrated 10 to 5000 modules on the chip without prior knowledge, and for each condition, the AID algorithm was run 10 times. The design time of the AID algorithm and the corresponding number of modules are shown in Fig. 7e. The design time of the AID algorithm increases roughly linearly with the increase of the number of modules. Detailed data are provided in Table S5. In the case of running 5000 modules, the average computation time of AID algorithm is 18.821 s, which indicates that the algorithm has high design efficiency in the face of complex large-scale module integration.
3 Discussion
This study presents an integrated framework that combines DL with modular modeling to enable high-precision spatiotemporal prediction, control, and automated structural optimization of particle transport in MCNs. By decomposing complex channels into functional modules, and PMPM is constructed to accurately predict particle routing, outlet position, velocity, and transit time within MCNs. Subsequently, MMRA then assembles global trajectories from local predictions, supporting dynamic control across scales. Residual correction further improves time prediction accuracy, making the framework suitable for multi-step reactions and delivery scheduling. Finally, by integrating the trajectory prediction with optimization, we achieved automated inverse design of complex microchannel structures under target trajectory constraints. Using this reverse design workflow, the integration of 5000 modules can be completed in as little as 18 s.The DL framework developed in this study demonstrates architectural scalability and device-level adaptability within the microfluidic regimes evaluated. The scalability claimed in this work refers to structural scalability achieved through modular assembly rather than generalizability across all possible microfluidic conditions. While its current predictive scope is limited to laminar flow regimes, canonical module geometries, passive particle transport, and rigid particles, the modular framework is inherently extensible. Specifically, additional physical effects—including viscosity variations, surface interactions, multiparticle coupling, and complex channel geometries—can be systematically incorporated as new training data and corresponding module models become available. Moreover, the framework naturally supports extension to deformable objects through the integration of deformation-related descriptors. Built upon particle-like dynamics, the framework extends beyond synthetic microparticles (e.g., drug carriers57) to other point-like entities such as droplets,58 bioactive particles such as cells,59 exosomes,60 vesicles61 and bacteria,8 and even micro/nanorobots.39,62,63 The system's modular design also facilitates integration with broader automation platforms, such as droplet generation systems for trajectory prediction under varying conditions37 or cell-sorting devices for automated routing and precise allocation.64 These diverse applications demonstrate the approach's adaptability and translational potential across microfluidic domains.
4 Methods
4.1 Materials
Microfluidic channels were fabricated using polydimethylsiloxane (PDMS) due to its high optical transparency, making it suitable for real-time imaging. Quartz substrates were used as the chip base, and SU-8 2075 was employed as the negative photoresist. Polystyrene (PS) microspheres with diameters of 1 μm, 5 μm, and 10 μm and a density of 1.05 g cm−3 were used as model particles for both dataset generation and validation experiments. Anhydrous ethanol (density: 0.79 g cm−3) served as the carrier fluid. PS particles were prepared at a concentration of 50 mg mL−1 in ultrapure water, with a coefficient of variation (CV) below 3%. Prior to introduction into the chip, the PS suspension was diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (v/v) with ethanol. To minimize aggregation and prevent channel blockage, 10% (v/v) Tween-20 was added to the diluted solution and sonicated to ensure uniform dispersion. All microchannels were rendered hydrophobic to prevent particle adhesion to PDMS surfaces.
10 (v/v) with ethanol. To minimize aggregation and prevent channel blockage, 10% (v/v) Tween-20 was added to the diluted solution and sonicated to ensure uniform dispersion. All microchannels were rendered hydrophobic to prevent particle adhesion to PDMS surfaces.
4.2 Mcirofluidic chips fabrication
Microdevices were fabricated using standard soft lithography techniques. A negative photoresist SU-8 mold was first patterned onto a quartz substrate via photolithography. PDMS prepolymer and curing agent were mixed at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio, thoroughly degassed under vacuum, and cast onto the SU-8 mold. The mixture was cured at 110 °C for 90 minutes to form an elastic PDMS layer with embedded rectangular microchannel structures. Inlet and outlet ports were punched into the cured PDMS at designated locations. The PDMS layer and a glass substrate were then surface-activated using an oxygen plasma treatment system (Plutovac, PLUTO-F) and irreversibly bonded to form sealed microchannels. The assembled chip was further cured at 85 °C for 90 minutes to enhance bonding strength and structural stability.
1 mass ratio, thoroughly degassed under vacuum, and cast onto the SU-8 mold. The mixture was cured at 110 °C for 90 minutes to form an elastic PDMS layer with embedded rectangular microchannel structures. Inlet and outlet ports were punched into the cured PDMS at designated locations. The PDMS layer and a glass substrate were then surface-activated using an oxygen plasma treatment system (Plutovac, PLUTO-F) and irreversibly bonded to form sealed microchannels. The assembled chip was further cured at 85 °C for 90 minutes to enhance bonding strength and structural stability.
4.3 Particle trajectory experiment
A syringe pump (LongerPump, LSP02-1B) was used to inject the diluted PS microsphere suspension and anhydrous ethanol into designated inlets of the microfluidic chip to establish a stable flow field. A high-speed camera (Revealer, AE120M, 2000 fps) mounted on an inverted biological microscope (Murzider, MSD351) was employed to capture particle motion. Video recordings were acquired using the camera's dedicated image acquisition software for image processing and particle trajectory extraction. A schematic of the experimental setup is provided in Fig. S7.4.4 Input feature limitation
To account for external factors influencing particle trajectories and accommodate the geometric variability in conventional microfluidic chips, a total of 20 parameters were selected across three domains: flow conditions, channel geometry, and particle properties. These parameters include inlet velocity, inflow/outflow configurations, channel width, inter-channel angles, particle diameter, and particle density. The parameter space considered in this study corresponds to single-phase Newtonian microflows operating in the low-Reynolds-number laminar regime (Re < 10). Under these conditions, fluid viscosity and flow type remain fixed and thus do not introduce independent variability in particle dynamics. The current PathChip framework is validated within a well-defined domain of laminar microflows, consistent with the operating range of the experimental platform. Certain parameter combinations may result in physical interference between channels or generate inconsistent flow states due to randomness of sampling. Therefore, we introduce constraint formulations to avoid infeasible configurations during randomized parameter sampling. | (5) |
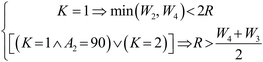 | (6) |
4.5 Numerical simulation
Numerical simulations were employed to emulate structural variations in microfluidic channels and to investigate how changes in channel parameters influence particle trajectories. COMSOL Multiphysics was selected as the simulation platform. The numerical model integrates two coupled modules—laminar flow and particle tracing for fluid flow—to simulate particle trajectories within microchannels. The laminar flow module is governed by the incompressible Navier–Stokes equations (eqn (7)):| ρ(u·∇)u = ∇·[−pI + K] + Fρ∇·u = 0K = μ(∇u + (∇u)T) | (7) |
The particle tracing module follows the Newtonian equations of motion (eqn (8)):
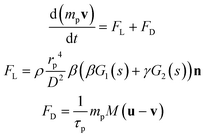 | (8) |
 | (9) |
The default fluid properties from the COMSOL materials library were used to define the flow domain. Channel geometries were constructed in external CAD software and directly imported into the simulation environment. Within the laminar flow module, inlet and outlet boundaries were specified; inlet flow velocities were assigned based on sampled flow parameters, while a pressure point constraint of 0 MPa was applied at the outlet. In the particle tracing for fluid flow module, inlet 1 was defined as the particle injection boundary, with ten particles uniformly introduced per inlet. All simulations were performed under dilute particle conditions, where particle–particle interactions and particle-induced flow perturbations are negligible. The model is therefore applicable to passive, single-particle transport in laminar microfluidic flows. Particle–wall interactions were configured as adhesive, and particle properties—including size and density—were assigned based on sampled values. Drag and lift forces were included in the force model. A steady-state solution was first obtained for the flow field, followed by a transient simulation of particle trajectories. The resulting outputs included particle paths, velocities, and transit times within the microfluidic domain.
4.6 Fluid–circuit analogy
In drawing an analogy between microfluidic channels and electrical circuits, the correspondence between hydraulic resistance and electrical resistance must be clarified with respect to their governing factors. The hydraulic resistance RH of a rectangular microchannel is given by eqn (10): | (10) |
To simplify eqn (10), a geometric coefficient Cg can be introduced, yielding eqn (11):
 | (11) |
Analogously, the electrical resistance RE of a circuit element is defined as in eqn (12):
 | (12) |
4.7 Design aids
We developed a MATLAB-based application, PathChip, which integrates both particle trajectory prediction and reconstruction algorithms into a unified platform. The application provides a visual interface to explore predicted trajectories alongside their corresponding structural parameter sets, and enables interactive module reconfiguration by adjusting design parameters of individual channel units. A demonstration of the user interface is provided in Fig. S10.PathChip comprises the following core functionalities: initialization, parameter configuration, parameter generation, visualization window, trajectory output, visualization utilities, and data export. The initialization module includes network retraining, transfer learning, data import, save path selection, and training execution, enabling either full retraining or fine-tuning of the embedded neural network models with additional data. The parameter configuration module provides schematic illustrations and configurable ranges for each structural parameter to support user comprehension and control. The parameter generation module allows both manual and automated parameter design, including batch generation, user-defined constraints, and channel shape customization for automated design, as well as control of inlets and outlets. The visualization window renders the predicted particle trajectories within the corresponding channel geometries. The trajectory output module displays numerical results of the predictions and includes functionality for animation generation to support post-analysis. Visualization utilities facilitate the overlay and comparison of experimental and simulated trajectories, as well as integration of trajectories generated through manual or automated design, allowing for external data import and dynamic animation rendering. Finally, the export module supports exporting parameter tables and visualization snapshots for downstream reporting or analysis.
Author contributions
Hongxia Lia: supervision, funding acquisition, Xuhui Chen: writing – original draft, writing – review & editing, conceptualization, data curation, formal analysis, methodology, software, project administration, validation, visualization, investigation, Du Qiao: writing – original draft, writing – review & editing, validation, visualization, investigation, Xue Zhang: visualization, investigation, Jiang Zhang: visualization, investigation, Jianan Zou: visualization, investigation, Danyang Zhao: supervision, Xuhong Qian: supervision, funding acquisition, resources, Honglin Li: supervision, funding acquisition, resources.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relations hips that could have appeared to influence the work reported in this paper.Data availability
All data supporting the findings of this study are available within the paper and supplementary information (SI) or upon reasonable request from the corresponding author.Supplementary information: the SI includes detailed descriptions of the input features, the neural network construction, and the modeling assumptions used for the automated inverse design framework, etc. See DOI: https://doi.org/10.1039/d5lc01185j.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (82425104), the National Natural Science Foundation of China (11502044), Fundamental Research Funds for the Central Universities (DUT22JC08), the National Key R&D Program of China (2022YFC3400501 and 2022YFC3400504). We acknowledge Penghe Yin, Xi Zhang and Pan Sun from Key Laboratory for Micro/Nano Technology and System of Liaoning Province for the firm support and kind help.References
- J. M. Ayuso, M. Virumbrales-Munoz, J. M. Lang and D. J. Beebe, A role for microfluidic systems in precision medicine, Nat. Commun., 2022, 13, 3068, DOI:10.1038/s41467-022-30384-7.
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, The present and future role of microfluidics in biomedical research, Nature, 2014, 507, 181–189, DOI:10.1038/nature13118.
- Y. T. Zeng, et al., Miniaturizing chemistry and biology using droplets in open systems, Nat. Rev. Chem., 2023, 7, 439–455, DOI:10.1038/s41570-023-00483-0.
- D. J. Mai, A. Saadat, B. Khomami and C. M. Schroeder, Stretching Dynamics of Single Comb Polymers in Extensional Flow, Macromolecules, 2018, 51, 1507–1517, DOI:10.1021/acs.macromol.7b02759.
- D. Kumar, A. Shenoy, S. S. Li and C. M. Schroeder, Orientation control and nonlinear trajectory tracking of colloidal particles using microfluidics, Phys. Rev. Fluids, 2019, 4, 114203, DOI:10.1103/PhysRevFluids.4.114203.
- C. Lin, et al., Vesicle dynamics in large amplitude oscillatory extensional flow, J. Fluid Mech., 2021, 929, A43, DOI:10.1017/jfm.2021.885.
- E. M. Johnson-Chavarria, U. Agrawal, M. Tanyeri, T. E. Kuhlman and C. M. Schroeder, Automated single cell microbioreactor for monitoring intracellular dynamics and cell growth in free solution, Lab Chip, 2014, 14, 2688–2697, 10.1039/c4lc00057a.
- D. L. Englert, M. D. Manson and A. Jayaraman, Investigation of bacterial chemotaxis in flow-based microfluidic devices, Nat. Protoc., 2010, 5, 864–872, DOI:10.1038/nprot.2010.18.
- S. T. Sanjay, et al., Recent advances of controlled drug delivery using microfluidic platforms, Adv. Drug Delivery Rev., 2018, 128, 3–28, DOI:10.1016/j.addr.2017.09.013.
- M. Maeki, N. Kimura, Y. Sato, H. Harashima and M. Tokeshi, Advances in microfluidics for lipid nanoparticles and extracellular vesicles and applications in drug delivery systems, Adv. Drug Delivery Rev., 2018, 128, 84–100, DOI:10.1016/j.addr.2018.03.008.
- F. Lan, B. Demaree, N. Ahmed and A. R. Abate, Single-cell genome sequencing at ultra-high-throughput with microfluidic droplet barcoding, Nat. Biotechnol., 2017, 35, 640–646, DOI:10.1038/nbt.3880.
- B. B. Yellen, et al., Massively parallel quantification of phenotypic heterogeneity in single-cell drug responses, Sci. Adv., 2021, 7, eabf9840, DOI:10.1126/sciadv.abf9840.
- K. J. Li and J. Wu, Recent advances in microfluidic platforms for single particle analysis, TrAC, Trends Anal. Chem., 2023, 165, 117139, DOI:10.1016/j.trac.2023.117139.
- S. Mashaghi, A. Abbaspourrad, D. A. Weitz and A. M. van Oijen, Droplet microfluidics: A tool for biology, chemistry and nanotechnology, TrAC, Trends Anal. Chem., 2016, 82, 118–125, DOI:10.1016/j.trac.2016.05.019.
- X. Hou, et al., Interplay between materials and microfluidics, Nat. Rev. Mater., 2017, 2, 17016, DOI:10.1038/natrevmats.2017.16.
- D. Qiao, et al., Microfluidic separation of particles by synergistic effect of geometry-induced hydrodynamics and magnetic field, Chin. Chem. Lett., 2024, 35, 108646, DOI:10.1016/j.cclet.2023.108646.
- H. X. Li, et al., Mechanism of nanoparticle aggregation in gas-liquid microfluidic mixing, Chin. Chem. Lett., 2024, 35, 108747, DOI:10.1016/j.cclet.2023.108747.
- H. X. Li, et al., Computational fluid dynamics analysis of droplet generation in microfluidic multi-cell coupled systems, Phys. Fluids, 2021, 33, 103313, DOI:10.1063/5.0065885.
- H. Li, et al., Mixing in a co-flow-focusing structured droplet-based micromixer, Chem. Eng. Sci., 2024, 288, 119854 CrossRef CAS.
- L. Li, et al., Multi-field coupling particle flow dynamic behaviors of the microreactor and ultrasonic control method, Powder Technol., 2025, 454, 120731, DOI:10.1016/j.powtec.2025.120731.
- N. Rousset, et al., Controlling bead and cell mobility in a recirculating hanging-drop network, Lab Chip, 2023, 23, 4834–4847, 10.1039/d3lc00103b.
- G. Kelly, N. Bizmark, B. Chakraborty, S. S. Datt and T. G. Fai, Modeling the Transition between Localized and Extended Deposition in Flow Networks through Packings of Glass Beads, Phys. Rev. Lett., 2023, 130, 128204, DOI:10.1103/PhysRevLett.130.128204.
- Q. M. Qi and E. S. G. Shaqfeh, Time-dependent particle migration and margination in the pressure-driven channel flow of blood, Phys. Rev. Fluids, 2018, 3, 034302, DOI:10.1103/PhysRevFluids.3.034302.
- M. T. Chung, D. Núñez, D. W. Cai and K. Kurabayashi, Deterministic droplet-based co-encapsulation and pairing of microparticles via active sorting and downstream merging, Lab Chip, 2017, 17, 3664–3671, 10.1039/c7lc00745k.
- L. Nan, T. J. Mao and H. C. Shum, Self-synchronization of reinjected droplets for high-efficiency droplet pairing and merging, Microsyst. Nanoeng., 2023, 9, 24, DOI:10.1038/s41378-023-00502-6.
- H. Liu, L. Nan, F. Chen, Y. Zhao and Y. Zhao, Functions and applications of artificial intelligence in droplet microfluidics, Lab Chip, 2023, 23, 2497–2513, 10.1039/d3lc00224a.
- D. McIntyre, A. Lashkaripour, P. Fordyce and D. Densmore, Machine learning for microfluidic design and control, Lab Chip, 2022, 22, 2925–2937, 10.1039/d2lc00254j.
- Y. D. Zhang, et al., Machine Learning-Enhanced Predictive Modeling for Arbitrary Deterministic Lateral Displacement Design and Test, IEEE Trans. NanoBiosci., 2025, 24, 46–62, DOI:10.1109/tnb.2024.3415365.
- K. Yiannacou and V. Sariola, Acoustic Manipulation of Particles in Microfluidic Chips with an Adaptive Controller that Models Acoustic Fields, Adv. Intell. Syst., 2023, 5, 2300058, DOI:10.1002/aisy.202300058.
- D. B. Brückner and C. P. Broedersz, Learning dynamical models of single and collective cell migration: a review, Rep. Prog. Phys., 2024, 87, 056601, DOI:10.1088/1361-6633/ad36d2.
- A. A. Volk, et al., AlphaFlow: autonomous discovery and optimization of multi-step chemistry using a self-driven fluidic lab guided by reinforcement learning, Nat. Commun., 2023, 14, 1403, DOI:10.1038/s41467-023-37139-y.
- A. M. Schweidtmann, et al., Machine learning meets continuous flow chemistry: Automated optimization towards the Pareto front of multiple objectives, Chem. Eng. J., 2018, 352, 277–282, DOI:10.1016/j.cej.2018.07.031.
- X. C. Liu, P. K. Das and S. Hilgenfeldt, Principles of hydrodynamic particle manipulation in internal Stokes flow, J. Fluid Mech., 2025, 1007, A33, DOI:10.1017/jfm.2025.64.
- R. E. Migacz, G. Durey and J. T. Ault, Convection rolls and three-dimensional particle dynamics in merging solute streams, Phys. Rev. Fluids, 2023, 8, 114201, DOI:10.1103/PhysRevFluids.8.114201.
- T. T. Zhou, et al., AI-aided geometric design of anti-infection catheters, Sci. Adv., 2024, 10, eadj1741, DOI:10.1126/sciadv.adj1741.
- X. Huang, et al., Control-Logic Synthesis of Fully Programmable Valve Array Using Reinforcement Learning, IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst., 2024, 43, 277–290, DOI:10.1109/tcad.2023.3309740.
- A. Lashkaripour, et al., Machine learning enables design automation of microfluidic flow-focusing droplet generation, Nat. Commun., 2021, 12, 25, DOI:10.1038/s41467-020-20284-z.
- A. Lashkaripour, et al., Design automation of microfluidic single and double emulsion droplets with machine learning, Nat. Commun., 2024, 15, 83, DOI:10.1038/s41467-023-44068-3.
- H. Dong, et al., AI-enhanced biomedical micro/nanorobots in microfluidics, Lab Chip, 2024, 24, 1419–1440, 10.1039/d3lc00909b.
- J. H. Lee, Minimum Euclidean distance evaluation using deep neural networks, AEU-Int. J. Electron. Commun., 2019, 112, 152964, DOI:10.1016/j.aeue.2019.152964.
- J. Zhang, et al., Fundamentals and applications of inertial microfluidics: a review, Lab Chip, 2016, 16, 10–34, 10.1039/c5lc01159k.
- L. Chen, J. J. Kim and P. S. Doyle, Microfluidic platform for selective microparticle parking and paired particle isolation in droplet arrays, Biomicrofluidics, 2018, 12, 024102, DOI:10.1063/1.5011342.
- P. Sajeesh and A. K. Sen, Particle separation and sorting in microfluidic devices: a review, Microfluid. Nanofluid., 2014, 17, 1–52, DOI:10.1007/s10404-013-1291-9.
- D. Huh, et al., Gravity-driven microfluidic particle sorting device with hydrodynamic separation amplification, Anal. Chem., 2007, 79, 1369–1376, DOI:10.1021/ac061542n.
- S. C. Hur, A. J. Mach and D. Di Carlo, High-throughput size-based rare cell enrichment using microscale vortices, Biomicrofluidics, 2011, 5, 022206, DOI:10.1063/1.3576780.
- H. Y. Zhang and D. Lyden, Asymmetric-flow field-flow fractionation technology for exomere and small extracellular vesicle separation and characterization, Nat. Protoc., 2019, 14, 1027–1053, DOI:10.1038/s41596-019-0126-x.
- M. Hitzbleck and E. Delamarche, Reagents in microfluidics: an 'in' and 'out' challenge, Chem. Soc. Rev., 2013, 42, 8494–8516, 10.1039/c3cs60118h.
- G. Lauricella, M. M. Naderi, J. Zhou, I. Papautsky and Z. L. Peng, Bifurcation of equilibrium positions for ellipsoidal particles in inertial shear flows between two walls, J. Fluid Mech., 2024, 984, A47, DOI:10.1017/jfm.2024.152.
- K. W. Oh, K. Lee, B. Ahn and E. P. Furlani, Design of pressure-driven microfluidic networks using electric circuit analogy, Lab Chip, 2012, 12, 515–545 Search PubMed.
- J. Wang, P. H. Chao, S. Hanet and R. M. van Dam, Performing multi-step chemical reactions in microliter-sized droplets by leveraging a simple passive transport mechanism, Lab Chip, 2017, 17, 4342–4355, 10.1039/c7lc01009e.
- G. Pascali, G. Mazzone, G. Saccomanni, C. Manera and P. A. Salvadori, Microfluidic approach for fast labeling optimization and dose-on-demand implementation, Nucl. Med. Biol., 2010, 37, 547–555, DOI:10.1016/j.nucmedbio.2010.03.006.
- X. Li, P. Zwanenburg and X. Y. Liu, Magnetic timing valves for fluid control in paper-based microfluidics, Lab Chip, 2013, 13, 2609–2614, 10.1039/c3lc00006k.
- X. B. Cao, et al., Towards an active droplet-based microfluidic platform for programmable fluid handling, Lab Chip, 2023, 23, 2029–2038, 10.1039/d3lc00015j.
- M. Yafia, Microfluidic chain reaction of structurally programmed capillary flow events, Nature, 2022, 605, 464–469, DOI:10.1038/s41586-022-04683-4.
- D. Lee, et al., Capillary flow control in lateral flow assays via delaminating timers, Sci. Adv., 2021, 7, eabf9833, DOI:10.1126/sciadv.abf9833.
- C. Briat, E. A. Yavuz, G. Karlsson and Ieee, IEEE INFOCOM Conference, 2012, pp. 2050–2058 Search PubMed.
- S. Mehraji and D. L. DeVoe, Microfluidic synthesis of lipid-based nanoparticles for drug delivery: recent advances and opportunities, Lab Chip, 2024, 24, 1154–1174, 10.1039/d3lc00821e.
- T. Moragues, et al., Droplet-based microfluidics, Nat. Rev. Methods Primers, 2023, 3, 32, DOI:10.1038/s43586-023-00212-3.
- C. Y. Liu, et al., Harnessing the Manipulation of Single Cells to Construct Biological Structures: Tools and Applications, Adv. Funct. Mater., 2024, 34, 2316357, DOI:10.1002/adfm.202316357.
- J. C. Contreras-Naranjo, H. J. Wu and V. M. Ugaz, Microfluidics for exosome isolation and analysis: enabling liquid biopsy for personalized medicine, Lab Chip, 2017, 17, 3558–3577, 10.1039/c7lc00592j.
- I. K. Herrmann, M. J. A. Wood and G. Fuhrmann, Extracellular vesicles as a next-generation drug delivery platform, Nat. Nanotechnol., 2021, 16, 748–759, DOI:10.1038/s41565-021-00931-2.
- L. D. Yang, et al., Autonomous environment-adaptive microrobot swarm navigation enabled by deep learning-based real-time distribution planning, Nat. Mach. Intell., 2022, 4, 480–493, DOI:10.1038/s42256-022-00482-8.
- M. Medany, L. Piglia, L. Achenbach, S. K. Mukkavilli and D. Ahmed, Model-based reinforcement learning for ultrasound-driven autonomous microrobots, Nat. Mach. Intell., 2025, 7, 1076–1090, DOI:10.1038/s42256-025-01054-2.
- Y. Wang, et al., Time-resolved microfluidic flow cytometer for decoding luminescence lifetimes in the microsecond region, Lab Chip, 2020, 20, 655–664, 10.1039/c9lc00895k.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |