Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An applied machine learning framework for waste lithium-ion battery leaching with integrated preliminary environmental and economic assessment
André
Nogueira
 a,
Filipe H. B.
Sosa
a,
Filipe H. B.
Sosa
 a,
Ana C.
Dias
b,
João A. P.
Coutinho
a,
Ana C.
Dias
b,
João A. P.
Coutinho
 a and
Nicolas
Schaeffer
a and
Nicolas
Schaeffer
 *a
*a
aCICECO – Aveiro Institute of Materials, Department of Chemistry, University of Aveiro, 3810-193 Aveiro, Portugal. E-mail: nicolas.schaeffer@ua.pt
bCentre for Environmental and Marine Studies (CESAM), Department of Environment and Planning, University of Aveiro, 3810-193 Aveiro, Portugal
First published on 20th November 2025
Abstract
Technological innovation has led to the widespread adoption of lithium-ion batteries (LIBs) for portable energy storage. Correspondingly, sustainable solutions to end-of-life battery disposal are crucial to manage their growing volume. Beyond their potentially hazardous nature, waste LIBs contain several economically relevant critical raw materials such as lithium, manganese and cobalt. However, their recovery by hydrometallurgical approaches often relies on the excessive use of corrosive solutions during the leaching steps, negatively impacting the atomic efficiency, effluent treatment, and cost of the process. Despite numerous studies on the topic, identifying optimal leaching conditions is challenging given the variety of available battery chemistries and leaching agents, compounded by economic and environmental concerns. This work presents a methodical, data-driven approach to model the leaching of key metals from oxide-based LIB cathode active materials using machine learning algorithms, implementing pairwise difference algorithms for data augmentation. The developed model underwent thorough evaluation and screening, and its output is integrated to compute a simplified economic and environmental assessment, accounting for key performance indicators such as heating requirements, solvent cost, and environmental impact, thereby enabling an agile screening of potential preliminary leaching conditions. The methodology described herein is an important step in integrating emerging computational tools in the development of novel, greener metal recycling processes.
Green foundation1. This work introduces a machine learning (ML) framework to optimize the recycling of lithium-ion batteries (LIBs). This data-driven approach aims to reduce the excessive use of harmful chemicals in the leaching step of hydrometallurgical battery recycling. The key advance is an integrated toolkit that combines leaching yield prediction with preliminary economic and environmental assessment tools, enabling more agile screening and development of greener and more efficient metal recycling processes.2. The contribution to green chemistry takes the form of the “LIB Leaching Toolkit”, a software tool that integrates ML-powered leaching yield prediction with a qualitative economic and environmental assessment tools for a more holistic approach to process design. The underlying model showed strong predictive performance, with a coefficient of determination of 0.933 on unseen test data. 3. This work can be advanced by expanding the dataset to include more varied cathode chemistry data and, crucially, data on the contaminants present in real waste battery streams. This would improve the applicability of the toolkit to real-world scenarios, highlighting its potential for use in a digital twin setting for more informed process design and control. |
1. Introduction
The proliferation of lithium-ion batteries (LIB) across industries and applications, from portable electronics to electric vehicles and grid storage, implies the need to develop efficient and sustainable end-of-life solutions. However, LIB cathode chemistry is highly varied: ternary battery cathodes, containing lithium, nickel, manganese and cobalt oxide, represent around 58% of the entire market; lithium iron phosphate-based cathodes have another 32%. The remaining around 10% are composed of lithium manganese oxide, lithium manganese nickel oxide and nickel cobalt aluminum battery cathodes.1 Additionally, each of those chemistries multiply into several variations as the battery cathode materials are developed and tuned for specific purposes. This inherent variability is often compounded during collection and initial processing, where different battery types are processed together, often without adequate sorting. Legislation was proposed to the European Parliament and the Council of the European Union to improve battery labelling, including the use of QR codes to provide consumers and operators with better information. However, with some of these measures not taking full effect until 2027, there is a pressing need to improve the recycling of batteries already in circulation.2The recycling of valuable and critical materials like lithium, nickel, manganese, cobalt and graphite present in LIB is a key step in reducing the environmental footprint of battery production by introducing a circular economy for these materials. Different possible avenues for LIB recycling, including pyrometallurgy, hydrometallurgy, biometallurgy, direct recycling, or a combination of options, are reported for LIB recycling.3 Hydrometallurgy is projected to remain the most common battery cathode recycling process, accounting for 90% of global capacity in 2030, due to its high yields, favorable economics and flexibility in handling different cathode chemistries and waste streams.4 Hydrometallurgy hinges on using leaching agents, usually aqueous solutions containing strong chemical oxidizers, to leach metals from the active material. Metals are then recovered from the pregnant solution through precipitation, deposition, solvent extraction or other separation methods. Hydrometallurgical processes can offer high efficiency and purity in metal recovery, from battery waste.5 However, careful process optimization is essential to minimize the drawbacks of this approach. The leaching step directly affects any downstream separation processes and is typically associated with the largest chemical consumption, incurring significant environmental impact. Leaching inherently leads to large wastewater and carbon dioxide emissions, as much as 6.6 kg of wastewater and 42 kg of carbon dioxide per electric vehicle cell.6 Generated wastewater may contain heavy metals, sodium, phosphate, and sulphates, all of which carry significant environmental impact.6 From an economic perspective, hydrometallurgical processes typically involve the use of excess quantities of reagents, implying potentially high operating costs. Furthermore, high purity recovery of critical materials from waste remains a challenge due to the costly separation processes needed to separate the transition metals after leaching. These aspects make careful consideration of the leaching step even more important to facilitate downstream recovery.7 The combined heterogeneity in feedstock and processing pathways requires the need for flexible recycling operations in which optimal leaching conditions can be quickly screened and adapted as new needs arise, bypassing experimental re-optimization and excessive chemical requirements.
Machine-learning (ML) techniques offer a way to overcome the limitations of first-principles chemical models, leveraging data-driven approaches to model complex patterns and predict leaching performance of real-world waste streams. This transition from first principles to a data-driven philosophy is especially relevant for application to variable real-world waste, where a complete mechanistic understanding of the chemical processes at play is often impractical. Additionally, flexible and robust computational modeling of leaching processes enables real-time tuning and optimization, maximizing yield while minimizing environmental impact and cost. ML is a useful tool for the optimization of processes, covering the LIB value-chain from manufacturing to recycling.8,9 The manufacture of LIB is highly sensitive to variations in process parameters, which will directly influence cell performance. Duquesnoy et al.10,11 used physics-based and ML models to predict ideal manufacturing parameters to produce electrodes for specific battery applications. ML approaches were also utilized to improve the performance and longevity of LIB.12 Additionally, significant efforts were directed towards the development of ML-based battery life models to optimize battery charging and use.13
More recently, ML techniques were identified to improve e-waste recycling processes, extending beyond the manufacture to the disposal of LIB. Zhou14 developed a ML model that pairs machine vision with convolutional neural networks to achieve high accuracy classification of mixed e-waste into different categories, helping to overcome one of the major challenges of e-waste recycling. Continuing the recycling process, works by Ebrahimzade et al.15 and Niu et al.16 used different ML approaches to successfully model the leaching of LIB, addressing another aspect of the battery recycling problem by being able to predict leaching efficiency from experimental conditions. However, both approaches have limitations in how they model the chemical systems. The first is highly specific, supporting exclusively sulfuric acid and hydrogen peroxide. This narrow focus means its predictions are not applicable to other leaching agents. While the model developed by Niu et al.16 is broader, its chemical descriptors for the acids are limited to the first dissociation constant of each one. This simplification tries to represent a complex chemical system using a single value, which cannot fully capture acid structure, multiple deprotonations, and others. Recent work by Zhou et al.17 showcases the thorough development of a methodology for the efficient development of deep eutectic solvents (DES) for LIB cathode leaching. Their approach allows for the rapid identification of new solvents using ML models, enabling significantly more targeted screening of leaching agents thank traditional trial-and-error methods.
Looking beyond LIB leaching to other hydrometallurgical leaching applications, ML models were successfully applied to capture the leaching performance of copper from various minerals.
Table 1 summarizes previous studies that have used ML algorithms for leaching modelling, highlighting their specific applications. However, existing research focuses on predictive accuracy for the metal leaching step in isolation, neglecting to showcase its potential when integrated into broader operational frameworks. Embedded within systems that enable simulation, optimization and technical-economic-environmental analysis, ML models can act as predictive engines, simulating process outcomes under different feedstock and operating conditions therefore enabling more informed process design and control.
| Ref. | Models | Use | Leaching agent | Best | # Points |
|---|---|---|---|---|---|
| Ebrahimzade et al.15 | ANN | Leaching from waste LIBs | H2SO4 + H2O2 | ANN | 685 |
| Niu et al.16 | XGB, RF, SVM, AdaBoost | Leaching from waste LIBs | 25 different acids | XGB | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
| Zhou et al.17 | CGAN | DES discovery for LIB leaching | DES | CGAN | 791 |
| Zhang et al.18 | MLR, SVM, DT, RF, ANN, GBR | Pyrolusite leaching | H2SO4 + FeSO4 | SVM | 304 |
| Mathaba and Banza19 | ANN | Co and Cu leaching | H2SO4 | ANN | 32 |
| Flores and Leiva20 | RF, SVM, ANN | Cu leaching | H2SO4 | ANN | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 581 |
| Daware et al.21 | RF, GBR, SVM, XGB, AdaBoost | Cu leaching from PCBs | Acids with pKa between 6 and 3 | GBR | 1320 |
A significant hurdle to the broader integration of ML tools is the scarcity of readily available, high-quality data. A smaller dataset limits the kinds of models that can be used, support vector machines, gradient boosting algorithms and random forests being reported as particularly well suited to data-restricted datasets.22 However, the use of more data-hungry methods may still be possible by using data augmentation techniques. One example of this approach is the pairwise difference (PD) algorithm described by Tynes et al.23 to improve prediction and uncertainty quantification in chemical search. This meta-algorithm operates on pairs of data points. During training, the model learns to predict differences between all possible pairs of input points. For prediction, test points are paired with all training set points, generating a set of predictions that can be treated as a distribution where the mean is the final prediction, and the dispersion serves as an uncertainty measure. This approach has been shown to reliably improve the performance of the random forest algorithm across various chemical ML tasks.23
In this work, ML approaches were used to model the leaching of Li, Mn, Ni and Co from oxide-based LIB cathode material using a range of organic and inorganic acids. Data was collected by surveying published articles on LIB recycling and/or available data from our laboratory. Experimental conditions and yields were compiled and formatted for consistency. Previously reported approaches were compared with models that exploit pairwise differences (PD) algorithms for data augmentation. Then, we demonstrate how these models can be integrated into a simplified techno-economic and environmental impact assessment tool, thus allowing for rapid screening and optimization of leaching conditions. The best-performing model was integrated into a Python application, the “LIB Leaching Toolkit” and performance was assessed using two case studies. This framework enables not only predicting leaching efficiency, but also considering economic and environmental implications, showcasing more flexible, data-driven models potentially deployable within a digital twin or process development context.
2. Methodology
2.1. Data collection and formatting
A total of 718 data points were manually extracted from 22 different articles published between 1998 and 2023 on the leaching of oxide-based black mass material as detailed in Table S1.24–45 Tabulated data was copied directly when available, whereas plots were processed to extract relevant data: reaction conditions (cathode composition, temperature, acid kind, acid and hydrogen peroxide concentration, solid to liquid ratio and reaction time) and leaching yields (Li, Ni, Mn and Co yield, standard). Literature data was supplemented with unpublished work from the REVITALISE project consortium (https://revitalise-project.eu/), making a total set of 913 leaching data points, each containing a set of reaction conditions and the leaching yields for Li, Ni, Mn and Co. The selected features correspond to the most common leaching parameters across the surveyed literature, and all represent easily controllable factors at a laboratory scale.The composition of the LIB cathodes was standardized using the Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn
Mn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co molar ratio as it is defined in the common general formula for ternary LIB cathodes—LiNixMnyCo1−x−yO2. These values were normalized such that the sum of the Ni, Mn and Co content was equal to 1. Hence, the LIB composition may be characterized by three variables, inputNi, inputMn, and inputCo. For example, NMC111, containing equimolar amounts of all three metals, is represented as inputNi = inputMn = inputCo = 0.33. The reaction conditions themselves were described using five parameters: leaching temperature in °C, acid concentration in mol L−1, hydrogen peroxide concentration in wt%, solid-to-liquid ratio in g L−1 and sampling time in minutes.
Co molar ratio as it is defined in the common general formula for ternary LIB cathodes—LiNixMnyCo1−x−yO2. These values were normalized such that the sum of the Ni, Mn and Co content was equal to 1. Hence, the LIB composition may be characterized by three variables, inputNi, inputMn, and inputCo. For example, NMC111, containing equimolar amounts of all three metals, is represented as inputNi = inputMn = inputCo = 0.33. The reaction conditions themselves were described using five parameters: leaching temperature in °C, acid concentration in mol L−1, hydrogen peroxide concentration in wt%, solid-to-liquid ratio in g L−1 and sampling time in minutes.
A comprehensive set of molecular descriptors was employed to represent the different acids in the dataset. These included properties such as the acid dissociation constants (pKa) and the number of available protons. Whenever available, the solubility product (KSP) of the corresponding lithium, nickel, manganese and cobalt salts in water at 20 °C were also included as direct inputs. Additionally, other molecular descriptors were dynamically retrieved from the SMILES string of each acid using the RDKit package.46 A complete overview of the features is available in Table S2 of the SI. This expanded representation, although increasing complexity, provides a more comprehensive description of each acid's behavior compared to previous approaches, which have primarily only used the acid concentration and first dissociation constant.16 This improved representation aims to improve the modelling performance of lesser-represented acids and the overall generalizability of the models.
The compiled leaching data contains 12 different organic and inorganic acids. To allow for appropriate modelling, it was necessary to encode the acid type into a numeric value. The first dissociation constant was chosen for its availability for all the acids of interest. However, picking a single number to differentiate between acids is a simplified approach, limiting the generalization potential of the models, particularly as it fails to differentiate between mono-, di- and tri-protic acids. This limitation was overcome by using the three first dissociation constants, when available, as well as through using other molecular descriptors. Fig. S1 displays the distribution of acids in the working dataset, revealing a pronounced bias towards hydrochloric and sulfuric acids, which collectively account for over 65% of the data points.
2.2. Batch leaching
Batch experiments were set up in 3 mL glass vials, into which 1 mL of preheated acid was added to an appropriate amount of LiNixMnyCo1−x−yO2 cathode powder. Stirring was maintained at 500 RPM throughout. Temperature was controlled using a preheated metal block into which the vials are inserted. After the leaching time elapsed, the vial was removed from heating and its contents centrifuged at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 2 minutes. The leachate was decanted, and the solid residue washed with deionized water several times before drying in a 50 °C oven overnight.
000 rpm for 2 minutes. The leachate was decanted, and the solid residue washed with deionized water several times before drying in a 50 °C oven overnight.
A complete digestion of the cathode active material was done using 4 M HCl to enable yield computation. The concentration of lithium was measured using a Mettler Toledo DX207-Li ISE half-cell electrode. Quantification of Ni, Mn and Co in solution was performed using a Bruker S2 Picofox Total Reflection X-ray Fluorescence (TXRF) spectrometer, equipped with a molybdenum X-ray source. The analysis was performed at a voltage of 50 kV and a current of 600 μA. Quartz sample carriers were pre-coated with 10 μL of a solution of silicon in isopropanol (SERVA) and dried at 323 K. Samples were diluted in a 1 wt% polyvinyl alcohol solution and spiked with a known concentration of yttrium standard, adjusted to the metal content of the samples. 10 μL of the diluted and spiked samples were transferred to the preheated carriers and dried at 353 K. TXRF measurement was carried out for 300 s.
2.3. Model training and implementation
The simplified data flow chart in Fig. 1 outlines the systematic approach to data partitioning and model training. The data was randomly split into a test set, containing 15% (or 137 points), and a training set, containing the remaining 85% (776 points). The test set was only used to assess and compare the models against each other, ensuring the assessment was made with data that are not embedded in the models. Each of the models were fitted onto the training data using 5-fold cross-validation. Hyperparameter optimization for each of the models was done using the optuna package as described below. The trained models were then used to predict leaching yields of the test data set and compute fit and error statistics.Random forest (RF), gradient boosting regression (GBR) and multilayer perceptron (ANN) models were implemented in Python 3.12.3 using the scikit-learn package version 1.5.1.47 The optuna package was used to perform Bayesian optimization of the model hyperparameters instead of a conventional grid search methodology. By sampling within the ranges available in Table S3 of the SI, the optimization algorithm is able to estimate the impact of varying each of the hyperparameters to enable a more targeted and efficient optimization.48 A detailed description of the hyperparameter optimization is described in the “Hyperparameter optimization” section of the SI. Model selection was performed using the entire set of features under consideration, detailed in Table S2. The models were first compared using performance metrics such as the coefficient of determination (R2), mean absolute error (MAE), median absolute error (MedAE), mean squared error (MSE) and root mean squared error (RMSE). Equations for these metrics are available in Table S4 of the SI.
Further analysis and selection of the models involved performing several statistical tests. An independent-samples Kruskal–Wallis test was used to identify significant differences in the mean absolute error (MAE) between groups (different acids, cathode chemistries, yield ranges). When significant differences were found, pairwise Dunn's tests were then performed to identify the source of these differences. Additionally, Wilcoxon signed-rank tests were conducted to assess if more complete feature sets were significantly better performing than a base set of features.
The optimized scikit-learn models were compressed into .gz files using joblib 1.4.2 for easier distribution and deployment. The code for this project is archived on Zenodo at https://doi.org/10.5281/zenodo.16096943.
2.4. LIB leaching toolkit
The optimized model was integrated into a simple application, coined LIB Leaching Toolkit, developed using Python 3.12.3. A graphical user interface was implemented using tkinter. The environmental impact metrics are based on those available on the Ecoinvent 3.9.1 database, as listed in Table S5 of the SI.49 To utilize these metrics, users must supply their own licensed Ecoinvent data, as it is not distributed with the toolkit. A complete list of packages is available on this project's Zenodo.The general flow of data within the LIB Leaching Toolkit application is depicted in Fig. 2.
The first step of the LIB Leaching Toolkit is loading the pre-trained PD-GBR model, the training data (required for applying the PD method) and the ‘sample data’, containing the leaching scenarios for which yields will be calculated. The sample data can be generated using the toolkit's built-in tool (as illustrated in Fig. 3), which allows for varying a single parameter across a range of custom, evenly spaced values while holding others constant. Alternatively, users can create sample data by editing a provided template spreadsheet.
The feature set is then expanded by applying the PD algorithm to generate all pairwise feature combinations between the training and sample data. The toolkit then computes predictions for the average and standard deviation of extraction yields for Li, Ni, Mn and Co. The results are stored as a Pandas DataFrame object and exported as a spreadsheet.
Having estimated the extraction yields, the toolkit computes a mass balance to determine the required reagents for the leaching process. All calculations are based on 1000 kg of LIB cathode material. The process begins by calculating the total volume of the diluted acid solution required for a given solid-to-liquid ratio. From this volume and the specified acid concentration (mol L−1), the total moles of acid are determined. The mass of pure acid is then calculated using its molar mass, which is subsequently adjusted to find the required mass of the concentrated stock solution by accounting for its purity. Finally, the volume of water needed for dilution is calculated by subtracting the volume of the concentrated acid from the total volume of the prepared leaching solution. The results are stored in a Pandas DataFrame for further analysis and manipulation.
Following mass balance calculations, the toolkit performs a simplified economic assessment to estimate the costs associated with each leaching scenario. This includes estimates of the reagent costs as well as the energy needs for heating and mixing, detailed in Tables S6 and S7 of the SI. Other factors like equipment sizing and cost, solvent recovery, and wastewater treatment were omitted to enable a more flexible yet simplified approach that can be more broadly applicable. The reagent cost is calculated directly from the mass of concentrated acid determined in the mass balance, multiplied by its bulk price. The heating cost is estimated by calculating the energy (in kWh) required to raise the temperature of the calculated volume of water from an assumed ambient temperature of 25 °C to the specified reaction temperature, using the specific heat capacity of water. The mixing energy is calculated based on the total slurry volume (liquid + solids), a defined mixing power requirement (in kW m−3), and the total reaction time. Both heating and mixing energy requirements are converted to a monetary cost using a fixed price per kWh. To enable a comparison between different leaching strategies, the costs are normalized by the total mass of Li, Ni, Mn, and Co recovered (calculated using the predicted yields), providing a final metric in euros per kg of metal leached. Economic assessment is essential for evaluating the financial viability of different approaches. Even a simplified analysis allows for preliminary comparison and selection of leaching conditions.
Using the yields and mass balance results, the toolkit can perform a simplified environmental impact assessment. The amount of acid used in each scenario is multiplied by a set of environmental impact assessment parameters, commonly available in life-cycle assessment (LCA) databases such as Ecoinvent. These parameters quantify the potential environmental impacts associated with the production of acids considered in this study: acetic acid, ascorbic acid, citric acid, formic acid, hydrochloric acid, lactic acid, nitric acid, oxalic acid, and sulfuric acid. The impact metrics aim to capture the impacts on climate change, broader ecosystem and human health effects, and resource use. It is important to note that the parameters provided are only illustrative examples and should be updated by the user with relevant LCA data for their specific context. Environmental impact assessment provides valuable insights into the sustainability of leaching processes. By integrating this assessment, the toolkit places environmental considerations at the core of process development.
Finally, the toolkit facilitates a comparative analysis of leaching scenarios. This is achieved by performing pairwise t-tests to determine statistical differences between leaching conditions. These enable the user to identify which variations in process parameters lead to significant changes in leaching performance. Paired with environmental and cost data, this becomes an invaluable tool to minimize cost and environmental impact. The toolkit also calculates selectivities and enrichment factors to aid process tuning and selection. The toolkit provides visualization tools in the form of scatter and bar plots and heatmaps and allows exporting results as spreadsheets and image files, exemplified in Fig. 4. These visualizations allow intuitive interpretation of the data in formats that researchers and engineers are familiar with, once again bridging the gap between computer and chemical engineering and process development.
2.5. Case studies
To illustrate the robustness and use of the integrated framework, three case studies were conducted. The first assesses the performance of the PD-GBR model, using predicted yields at different temperatures to estimate the activation energy for each metal and compare it with literature values. The second presents the techno-economic and environmental impact analysis capabilities of the toolkit. The LIB Leaching Toolkit was utilized to predict leaching yields and estimate economic and environmental impacts. All tests in this scenario were performed with fixed experimental conditions: NMC111 cathode, 40 °C, 50 g L−1, 60 minutes and an acid concentration of 1 mol L−1. Environmental and economic impacts were calculated based on the processing of 1000 kg of cathode. The final case study investigates the model's ability to extrapolate metal leaching to leaching agents not in the original dataset and compare them with experimental data. Experimental conditions were set at NMC111 cathode, 65 °C, 50 g L−1, 60 minutes leaching and 2 mol L−1. Acid solutions were prepared by diluting the appropriate amount of acid using deionized water. The acids used were hydrochloric acid (37%) and phosphoric acid (≥85%) from Honeywell, methanesulfonic acid (≥99.5%) and glycine (≥98.5%) from Sigma-Aldrich, glutaric acid (99%) from Aldrich, and oxalic acid (98%) from Alfa Aesar.3. Discussion
3.1. Input data analysis
Prior to modelling the leaching data, initial analysis focused on examining the distribution of the input features and leaching targets and identifying potential biases and limitations in the dataset. Basic descriptive statistics of the features are available in Table S8. The mode is especially informative for understanding feature distribution. Notably, the modal values for inputNi, inputMn and inputCo align with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, characteristic of NMC111, and the modal acid type corresponds to a pKa1 of −8.0 – hydrochloric acid (HCl). This suggests a strong bias towards NMC111 leaching with HCl within the dataset. Additionally, the close agreement between the average and mode of inputNi, inputMn and inputCo reinforces the potential overrepresentation of NMC111 compared to other NMC types. The overrepresentation could lead to models biased towards NMC111 leaching behavior and limit the potential generalizability to other cathode chemistries. This hypothetical limitation is compounded by the simplified representation of the chemical system within the data. While these parameters are the conditions one would expect to control in a leaching experiment, they offer a simplistic view of the chemical environment and of the solid substrate. It means that the leaching model might not be able to effectively differentiate the performance of different acids, namely the di- and tri-protic acids included in the data set. These potential issues were addressed by using RDKit to retrieve a comprehensive set of chemical descriptors, expanding the number of features used to characterize each leaching environment, as detailed in section 3.2. Additionally, it would be possible to employ selective resampling techniques such as SMOTE to combine oversampling of less represented leaching conditions and under-sampling of NMC111/HCl data points to build a more evenly distributed data set.50
1 ratio, characteristic of NMC111, and the modal acid type corresponds to a pKa1 of −8.0 – hydrochloric acid (HCl). This suggests a strong bias towards NMC111 leaching with HCl within the dataset. Additionally, the close agreement between the average and mode of inputNi, inputMn and inputCo reinforces the potential overrepresentation of NMC111 compared to other NMC types. The overrepresentation could lead to models biased towards NMC111 leaching behavior and limit the potential generalizability to other cathode chemistries. This hypothetical limitation is compounded by the simplified representation of the chemical system within the data. While these parameters are the conditions one would expect to control in a leaching experiment, they offer a simplistic view of the chemical environment and of the solid substrate. It means that the leaching model might not be able to effectively differentiate the performance of different acids, namely the di- and tri-protic acids included in the data set. These potential issues were addressed by using RDKit to retrieve a comprehensive set of chemical descriptors, expanding the number of features used to characterize each leaching environment, as detailed in section 3.2. Additionally, it would be possible to employ selective resampling techniques such as SMOTE to combine oversampling of less represented leaching conditions and under-sampling of NMC111/HCl data points to build a more evenly distributed data set.50
Analyzing the leaching yield statistics, presented in Table S9, reveals that while complete extraction is possible for all metals of interest (mode and maximum yields of 1.00), the average extraction within the dataset varies significantly. Lithium exhibits the highest average extraction (xLi = 0.78), suggesting it leaches more readily under the acidic test conditions in the set than the transition metals (xNi = 0.64, xMn = 0.58, xCo = 0.57). The disparity in the average leaching efficiencies highlights the need to optimize recycling methodologies, particularly to maximize manganese and cobalt extraction.
The potential of linear relationships between the selected features and metal leaching yields was assessed by computing the Pearson correlation coefficients. The coefficients, ranging from −1 to +1, quantify the strength and direction of the linear relation between each feature and target. Values near the extremes indicate strong linear correlation, while values close to zero suggest a lack of linear relationship. As depicted in Fig. 5, the coefficients reveal predominantly weak linear correlations between the features and targets. The absence of strong correlations showcases the necessity of employing more sophisticated, non-linear modeling techniques to accurately capture the complex interplay of factors governing the leaching process.
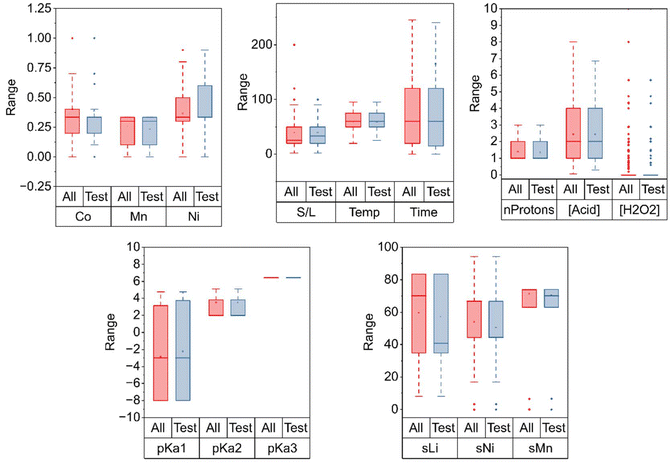
Having analyzed the input data, the subsequent phase focused on the preparation of the dataset for the machine learning modeling process. Fig. 6 displays a comparison between the entire dataset and the data that was set aside for testing, confirming that the latter is indeed representative of the dataset. The distributions of the features in both the full dataset and the test set exhibit similar medians, interquartile ranges and overall spread. The test split preserves the underlying data characteristics, ensuring that the model evaluation is conducted on a sample that reflects the original data distribution.
3.2. Model and feature selection
Several authors applied data science approaches to model chemical leaching reactions, including leaching from waste LIBs. Based on the study comparison presented in Table 1, three models were selected for further investigation: random forests (RF) showed consistent success across various leaching applications; gradient boosting methods, particularly Gradient Boosting Regression (GBR) and Extreme Gradient Boosting (XGB), proved effective in capturing the complex relationships involved in leaching processes; Artificial Neural Networks (ANN) offer flexibility and adaptability, making them capable of modelling non-linear and intricate patterns in leaching data. To potentially improve model performance and calculate a prediction error estimation, a pairwise difference regression technique was also employed. This approach, adapted from the work of Tynes et al.,23 denoted as PD-RF, PD-GBR and PD-ANN, involves transforming the original dataset into pairwise differences. Instead of training the models on individual data points, they are trained on the differences between pairs of data points. This simple transformation squares the number of training samples available, potentially improving model accuracy – especially useful when a relatively small dataset is used. Additionally, by pairing new data points with all the points in the training set, this method generates a distribution of predictions, effectively anchoring the predictions to the known data. The standard deviation of this distribution of predictions provides an estimate of the prediction uncertainty.Model performance was assessed using the coefficient of determination (R2), mean squared error (MSE) and mean absolute error (MAE). The training statistics, available in Table S10 of the SI, show an adequate fit of the RF and GBR models, with R2 values of 0.888 and 0.958, respectively. The ANN model was less effectively trained, with an R2 of 0.711. While ANN are powerful, versatile models, they typically require a large amount of data to be trained effectively. With a limited dataset of 776 points, the model likely did not have enough information to reliably learn these parameters and identify the underlying patterns in the data. However, these results highlight the advantages of data augmentation using the PD approach: the PD-ANN models were more effectively trained than their more basic counterparts (training R2 increased from 0.711 to over 0.946). The PD-GBR model achieved the best fit to the training data, with an R2 of 0.997. It was not possible to assess the performance of the PD-RF model, as the model training exhausted the resources of the machines available for training, illustrating the potential inadequacy of RF to work with large datasets (7762 points). It is noteworthy that applying the PD algorithm to augment the dataset allowed a better fit of both the ANN and GBR models.
Analyzing the test statistics in Table 2 to compare the models, it is clear that the GBR and PD-GBR models are the best suited to the modelling task, with a testing R2 of 0.914 and 0.933 respectively and comparatively low error statistics. The RF and PD-ANN models perform similarly, with R2 of around 0.803 in both cases. The poorly trained ANN model falls behind in testing, with an R2 of 0.684. Considering the similar performance of the GBR and PD-GBR models, the PD version was chosen to continue this work. The increased complexity and model size are outweighed by the slightly increased training and testing performance and the ability to provide error estimates. A comparison of experimental and PD-GBR predicted results in Fig. 7, confirms the goodness of fit with points evenly distributed around the diagonal line, indicating a lack of systematic bias in the predictions across the range of leaching yields and elements. The experimental vs. predicted plots for the remaining models are available in Fig. S2 of the SI.
 | ||
| Fig. 7 Plot comparing the experimental and predicted leaching yields of the various LiNixMnyCo1−x−yO2 materials using the PD-GBR model for all tested acids. | ||
| Model | R 2 | MAE | MedAE | MSE | RMSE |
|---|---|---|---|---|---|
| RF_full | 0.803 | 0.096 | 0.074 | 0.018 | 0.134 |
| GBR_full | 0.914 | 0.062 | 0.041 | 0.008 | 0.090 |
| ANN_full | 0.684 | 0.132 | 0.104 | 0.031 | 0.174 |
| PD-GBR_full | 0.933 | 0.051 | 0.028 | 0.006 | 0.079 |
| PD-ANN_full | 0.804 | 0.093 | 0.064 | 0.018 | 0.134 |
In addition to the features that were explicitly included in the dataset, several properties were retrieved based on the acid SMILES string using the RDKit package version 2024.09.06 for Python.51 The goal was to improve the description of the leaching environment and potentially extend the predictive capabilities of the models to acids beyond those in the original dataset. Due to the substantial number of potential features available through this package, a descriptor selection and grouping were performed:
• Basic molecular properties, including the reaction conditions and number of atoms.
• Properties related to Lipinski's rule of five for drug discovery: octanol–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P), topological polar surface area (TPSA), the number of hydrogen bond donors and acceptors and the molar mass.
P), topological polar surface area (TPSA), the number of hydrogen bond donors and acceptors and the molar mass.
• Charge properties, represented by the maximum and minimum partial charge on any atom of the molecule.
• Polarizability of the molecule, represented by its molar refractivity.
• Molecular structure, quantifying the presence of specific groups such as carboxylic acid, C–O bonds, primary amine, tertiary amine, halogen atoms, aliphatic hydroxyl groups, and the number of sulfur atoms.
A series of tests were performed, training PD-GBR models with different feature sets to assess the impact of different features on model performance. Table S11 provides an overview of the model-feature pairs evaluated, starting with the inclusion of all available features and progressively dropping groups. Model training was performed as described above.
The training statistics, detailed in Table S12, demonstrate a consistently strong fit for the PD-GBR models to the training data. All models achieved R2 values exceeding 0.97 and low error metrics, indicating their ability to capture the underlying patterns in the data. The PD-GBR models maintain good performance on the unseen test data (Table S13). The PD-GBR-full model, containing all features, yielded the best test metrics with an R2 of 0.9332 and MAE of 0.0513, showing a very good predictive performance. Notably, the other feature sets closely follow this model performance-wise. Highlights include feature sets that exclude log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA, number of hydrogen bond donors and acceptors and molecular weight, as well as the set that excludes the maximum and minimum partial charge and molar refractivity of the acid molecules. These two sets achieve a R2 of 0.9296 and 0.9297, respectively. Interestingly, comparing the simplest set, containing only basic experimental parameters, with the full set, revealed only a moderate penalty in model performance. The simpler set yielded an R2 of 0.9222 and MAE of 0.0566, compared to the full set's R2 of 0.9332 and MAE of 0.0513.
P, TPSA, number of hydrogen bond donors and acceptors and molecular weight, as well as the set that excludes the maximum and minimum partial charge and molar refractivity of the acid molecules. These two sets achieve a R2 of 0.9296 and 0.9297, respectively. Interestingly, comparing the simplest set, containing only basic experimental parameters, with the full set, revealed only a moderate penalty in model performance. The simpler set yielded an R2 of 0.9222 and MAE of 0.0566, compared to the full set's R2 of 0.9332 and MAE of 0.0513.
While the remarkably similar performance between sets suggests that a simpler feature set performs equally well on the current dataset, a strategic choice was made to use the full feature set. This more comprehensive description of the chemical environment is aimed at enhancing the model's potential generalizability to acid chemistries outside of the training set, at the cost of additional model complexity and training time. Consequently, the remainder of this work employs the PD-GBR-full model, using the features listed in Table S2.
3.3. Model analysis
To compare the fit of the PD-GBR model between the different acids, the data was divided into four groups, considering the three most well-represented acids in the dataset: hydrochloric acid (HCl), sulfuric acid, nitric acid and “other” acids, primarily organic acids. Initial analysis of the MAE of each group revealed differences in the MAE of prediction for each acid. Nitric acid exhibited the highest MAE at 0.0772, followed by HCl at 0.0563, sulfuric acid at 0.5232 and the lowest for the other acids group at 0.0390. An independent-samples Kruskal–Wallis test, performed on the absolute error of each estimation, indicated a significant difference between groups (p < 0.001) with 95% certainty, leading to the investigation of this divergence. A pairwise Dunn's test, detailed in Table S14 of the SI, confirmed a statistically significant lower MAE of the “other acids” group when compared with HCl (p = 0.016), sulfuric acid (p = 0.010) and nitric acid (p = 0.002). Conversely, no statistically significant differences were found between the other three acid groups – the predictive performance for HCl, sulfuric and nitric acid systems is statistically similar. This analysis demonstrates that, despite HCl and sulfuric acid representing approximately 66% of the dataset, the developed model performs well, or even better, on the less well-represented acids in the dataset, as visually depicted in Fig. 8.Beyond acid type, the influence of the feature set on the predictive accuracy was also examined. Wilcoxon signed-rank tests were performed to assess if the observed performance variations could be attributed to the more comprehensive feature set. These tests compared the MAE of prediction for each acid group using the full feature set against a base set, which included only basic experimental parameters and acid descriptors. Crucially, Fig. 8 and the test statistics presented in Table S15 show that the only group where the base set exhibited a significantly higher MAE was the “other” acids category (p = 0.016). No significant differences were found for the other acid groups. While the expanded feature set does not offer an advantage for the most common inorganic acids in the dataset, its inclusion proves helpful in describing less represented acids (primarily more complex organic acids).
To better assess the model's robustness, its predictive capability was evaluated across different experimental yield ranges. The data was divided into three groups according to the experimental yields: the first one for yields under 0.3 (MAE = 0.043), the second one for yields between 0.3 and 0.7 (MAE = 0.058), the third one for yields above 0.7 (MAE = 0.050). A Kruskal–Wallis test, performed on the absolute error of each estimation, indicated very significant differences between groups (p < 0.001). An ad-hoc pairwise Dunn's test was performed, whose results are available in Table S16, demonstrating that there are significant differences between the group with low yields (y < 0.3) and the other two. Surprisingly, the PD-GBR model appears to estimate lower yields slightly more accurately than higher yields. Another aspect of the model's generalizability is its performance across different target metals. An independent-samples Kruskal–Wallis test was performed to assess if the predictive performance is different for the target metals (Li, Mn, Co, and Ni) under consideration. A p-value of 0.668 was obtained, indicating no significant differences exist between the MAE for the target metals.
To complete the analysis, the model's performance was examined across different cathode chemistries. The predictions for NMC333 (MAE = 0.046), NMC622 (MAE = 0.102), NMC811 (MAE = 0.028) and remaining chemistries (MAE = 0.051) were compared. A p-value of under 0.001 in the independent-samples Kruskal–Wallis indicates there are differences between cathode chemistries, which were probed using pairwise Dunn's tests. The pairwise comparisons, detailed in Table S17, reveal several significant differences. NMC811, which exhibited the lowest MAE, showed significantly better predictions compared to the “other” chemistries (p-value = 0.044) and NMC622 (p-value < 0.001), which had the highest MAE. The difference between NMC811 and NMC333 was not found to be significant. Similarly, the predictions for NMC333 were significantly better than NMC622 (p-value < 0.001) but not significantly different from the “other” chemistries. The “other” chemistries also showed better predictions than NMC622 (p-value < 0.001). Collectively, these results indicate that the model's predictive performance varies significantly across cathode chemistries. NMC811 and NMC333, representing over 55% of the testing data, generally perform better or similarly to each other and the “other” group, while NMC622, around 11% of the testing data, consistently obtains significantly higher prediction errors compared to the remaining categories.
3.4. Application
Developing accurate and versatile models for LIB leaching is crucial for developing and optimizing recycling processes. However, the true value of these models lies in their application to real-world scenarios. To this end, a Python application was developed, named “LIB Leaching Toolkit”, incorporating the PD-GBR work developed above with environmental and economic impact assessment strategies to obtain a more holistic approach to the study of LIB recycling. The goal of this work was to provide a user-friendly platform to enable rapid evaluation of leaching yields, selectivity, environmental impacts and economic viability, allowing for rapid evaluation of leaching strategies by developing a user-friendly graphical user interface. This integrated approach bridges the gap between data science and chemical engineering, streamlining the development of LIB recycling strategies. The capabilities and limitations of this approach are better illustrated using three case studies.The leaching kinetics were fitted to four different kinetic models using a least squares methodology: linear model (x = kt), shrinking core model (SCM) with chemical reaction control (1 − (1 − x)1/3 = kt), SCM with product layer diffusion control (1–3(1 − x)2/3 + 2(1 − x) = kt) and SCM with a combination of film diffusion and chemical reaction control 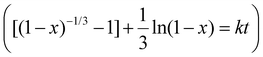 .52 A comparative study, detailed in Table S18, revealed that the mixed model provided the best fit for the data. This model was used to determine the rate constant (k) for each metal at each temperature from the slope of the linearized plot. The Arrhenius plot in Fig. 9 was constructed by plotting the natural logarithm of the rate constant against the reciprocal of the absolute temperature. From the slope of this plot, equal to −Ea/R, the activation energies were calculated, as presented in Table 3. The calculated activation energies are consistent with reported values for similar leaching systems, further validating the predictive capabilities of the PD-GBR model that was developed.53,54 A direct comparison with literature values is provided in Table 3.
.52 A comparative study, detailed in Table S18, revealed that the mixed model provided the best fit for the data. This model was used to determine the rate constant (k) for each metal at each temperature from the slope of the linearized plot. The Arrhenius plot in Fig. 9 was constructed by plotting the natural logarithm of the rate constant against the reciprocal of the absolute temperature. From the slope of this plot, equal to −Ea/R, the activation energies were calculated, as presented in Table 3. The calculated activation energies are consistent with reported values for similar leaching systems, further validating the predictive capabilities of the PD-GBR model that was developed.53,54 A direct comparison with literature values is provided in Table 3.
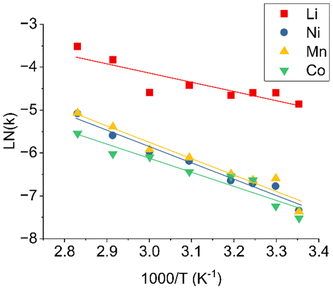 | ||
| Fig. 9 Arrhenius plot for the leaching of Li, Ni, Mn, and Co from NMC111 cathodes between 25–80 °C. The slopes of the linear regression are used to calculate the activation energies (Ea) presented in Table 3. The simulated kinetics data used to compute the kinetic parameters are available in Fig. S3 of the SI. | ||
However, reported activation energies can vary significantly between studies. This variation may stem from differences in the methodologies used to determine the rate constant and whether and how distinct dissolution stages are considered. Furthermore, the morphology of the cathode material plays a key role in determining if the process is limited by diffusion or chemical reaction constraints.38,55 It is also crucial to consider that the dataset at the basis of the model contains data from pristine cathode material, battery cathode, and isolated oxides without binders. Consequently, the model's prediction of activation energy likely represents a generalized kinetic behavior, rather than the kinetics of a single, idealized material, reflecting the mixed nature of the source data.
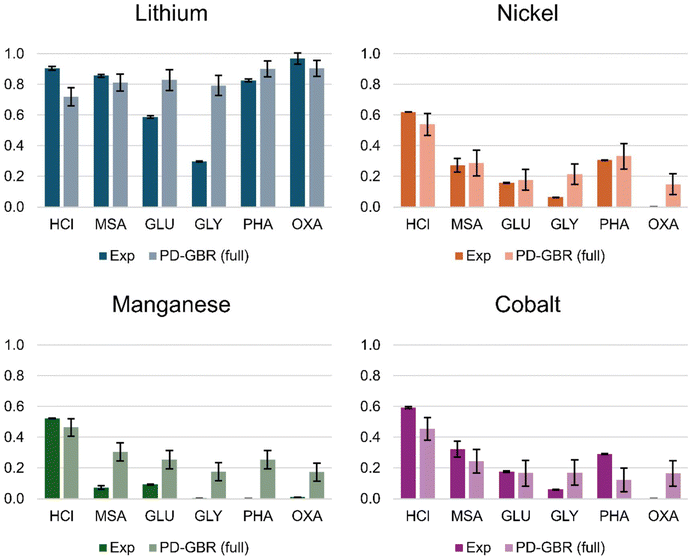
The Toolkit was used to predict yields and calculate impact metrics for a set of six different acids. The tests were conducted on fixed conditions: NMC111, 40 °C, 50 g L−1, 60 min leaching, 1 mol L−1 of acid. Environmental impacts and costs were calculated for 1000 kg of cathode material. Keeping the experimental conditions fixed allows to isolate the effect of the different acids on leaching and environmental and economic impact. Fig. 10 displays the predicted yields and standard deviation for the leaching scenarios outlined. The results indicate that hydrochloric acid and ascorbic acids are predicted to be the most effective leaching agents under these conditions. Despite the common greener perceptions of organic acids compared to inorganic ones, it is crucial to also take economic and environmental considerations into account. Fig. 11 ranks each acid according to the environmental impacts of its production, including upstream impacts, calculated for the quantity needed in each leaching scenario using the Environmental Footprint 3.1 impact assessment method.56 Taking this into account, the organic acids perform worse than hydrochloric and sulfuric acid across all impact categories for the leaching scenarios considered. This can be attributed to the production of organic acids often relying on inorganic acids. Citric and lactic acid, for example, are produced first as calcium citrate and calcium lactate through fermentation processes. A pathway to recover the acids is the addition of sulfuric acid to precipitate calcium sulfate, leaving the organic acid solution.57,58
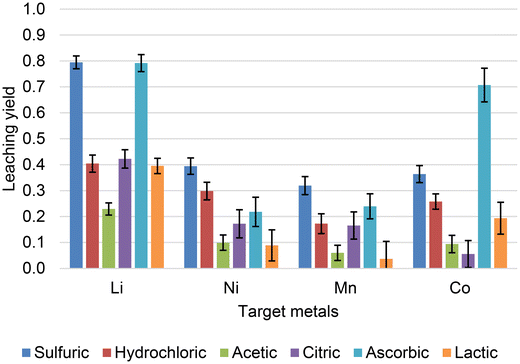 | ||
| Fig. 10 Metal leaching yields from NMC111 predicted by the developed PD-GBR model for fixed conditions: 40 °C, 50 g L−1, 60 min leaching, 1 mol L−1 of acid. | ||
The estimated reagent, mixing and heating costs, available in Fig. 12, are consistent with the results of Fig. 11, showing that inorganic hydrochloric and sulfuric acids have significantly lower costs when compared to the selected organic acids. This allows to conclude that for the purposes of NMC leaching, inorganic acids like hydrochloric and sulfuric acid might be advantageous both from an economical and environmental perspective, in apparent contradiction with the greener perception of organic leaching agents. Despite the limitations of this simplified comparative approach, the relative economic and environmental impact assessment is strongly supported by recent LCA studies, revealing that inorganic acids can remain more environmentally viable options for LIB cathode recycling compared to organic acids, primarily due to lower quantity of reagents needed.59,60 These works also identified sulfuric acid as having a lower environmental impact than lactic, ascorbic, or citric acid, whilst acetic acid was also evaluated as a better alternative to these within organic acids.
 | ||
| Fig. 12 Costs per kg of metal leached from NMC in thousands of euros (all price inputs are summarized in Tables S6 and S7 of the SI). | ||
However, it is important to stress that the results of the “LIB Leaching Toolkit” should only serve as a preliminary screening tool and does not substitute a comprehensive LCA or detailed economic analysis. The environmental impact estimates are calculated based on quite narrow process boundaries, considering only the production of the acid needed for each leaching scenario. Additional environmental impacts during leaching, such as gaseous emissions of Cl2 when using HCl, and the recovery and/or neutralization of the acids downstream of the leaching step are not considered in the calculations. Finally, the conclusions may not extrapolate when considering an overall hydrometallurgical process as the choice of lixiviant and process integration influences subsequent separation units and the effluent volumes generated.
3.5. Case study 3 – beyond the training set
A final case study explores the toolkit's ability to handle leaching agents not included in the training data. Acids from different families were selected: methanesulfonic acid (MSA), glutaric acid (GLU), glycine (GLY) and phosphoric acid (PHA), not included in the original set; hydrochloric (HCl) and oxalic acid (OXA), the most and one of the least abundant acids in the dataset, were included for comparison. These acids were selected purposefully due to their large structural difference in functional groups or leaching mechanisms to the most represented acids in the training set, providing a test of the model's robustness and highlighting its current limitations. This case study probes the toolkit's versatility in evaluating diverse leaching scenarios and its potential for extrapolation to novel conditions. Conditions were arbitrarily fixed for the leaching of NMC111: 65 °C, 60 min, 50 g L−1, 2 mol L−1 of acid. The following leaching agents were tested experimentally and the experimental yields compared with the yields predicted by the PD-GBR model.As shown in Fig. 13, the model generally presents good agreement with experimental results for lithium across most acid systems. Predictions for MSA and PHA – two acids with functional groups not included in the training set, and OXA – a poorly represented acid in the training set whose corresponding metal transition complexes are poorly soluble, are remarkably close to experimental. Leaching results for the HCl system are underestimated but within the error margin, whilst the GLU system is overestimated. The zwitterionic GLY system was notably poorly characterized by the model, being significantly different in nature to the acids included in the training set. This is somewhat expectable due to the more complex pH-dependent speciation of amino acids and self-buffering effect. For example, whilst the first dissociation constant input of GLY in the model was pKa = 2.3, the experimentally measured pH of the leach solution was significantly higher at 6.2. Such a discrepancy suggests that additional parameters might be required to properly capture leaching using zwitterions. Importantly, the experimental results for GLY are in accordance with previous works that report poor leaching yields in the absence of an additional reducing agent.61
The prediction of lithium, nickel, and cobalt yield for almost all acids is in reasonable to excellent agreement with experimental results. The two notable exceptions are GLY and OXA, which are both problematically overestimated. As discussed in the case of OXA, the poorly soluble nature of the corresponding transition metal oxalate complexes is likely contributing to the observed overestimation. Whilst the solubility products of the respective acid salts were included as model inputs when available, pondering its importance is required to better dissociate “leaching performance” from the final metal concentration in solution for acids likely to exhibit leaching and provoke subsequent precipitation.
Unfortunately, manganese leaching yield predictions were considerably overestimated for all acids except those included in the training set (HCl). This consistent overestimation could indicate systematic bias in the model. These results appear to contradict the analysis discussed prior, which showed that the PD-GBR was not significantly worse at predicting manganese yields than any of the others for acids in the training set. In fact, those results show a lower MAE in lower yield systems, which should lead to improved manganese predictions, considering that Mn leaching yields are on average lower than the other metals. In addition to the unique redox behavior of manganese (discussed below) which complicates the prediction, a further contribution to the systematic overestimation of the leaching yield may be due to the available data used during training. For Mn, 40% of the data pertains to a leaching yield of 0.75 or higher, whereas 80% of the data shows a yield of over 0.25. As the model developed herein is entirely data-driven, this bias in the data could explain the difficulty of predicting low manganese yield, especially in completely untested systems such as the ones selected for this case study. This problem is exacerbated for less manganese-rich cathode chemistries, as data points with 0.2 lithium equivalent amounts of manganese or less show a statistically significantly higher (p < 0.001) average manganese yield (0.71) than the general population of data points (0.58). Future work on the model refinement will seek to address this gap in the data.
Another possible explanation lies in the distinctive behavior of manganese during the leaching of battery cathodes. After an initial “self-regulating” step where the transition metals in the LIB cathode exhibit similar leaching behavior, the dissolution enters a second stage where manganese in solution decreases, resulting in an atypical leaching behavior when compared with the other transition metals. The underlying cause is the occurrence of side reactions, such as the disproportionation or oxidation of Mn2+ ions and the precipitation of higher-valence MnxOy species. These reactions lead to surface reorganization and the formation of new manganese phases, including metastable birnessite and subsequently γ-type manganese oxide. As a result, a manganese-rich core–shell structure forms, driven by the presence of divalent manganese in the solution.55 A possible approach to capture the irregular solubility of Mn with leaching time is to include more chemical descriptors, such as the oxidation reduction potential of the solutions, to help establish more extrapolation points for the machine learning model. Unfortunately, there is currently a lack of such data that precludes its inclusion.
Results from Fig. 13 suggest that while the model and feature set offer some generalizability to acids outside the training data (as demonstrated by the MSA and PHA results), care must be taken to validate the predictions, especially for manganese rich chemistries. However, the PD-GBR model developed herein proved a worthwhile tool for preliminary studies of acids outside the training set, if not for a definite, accurate prediction of leaching experiments.
4. Conclusion
The development of ML algorithms for modelling metal leaching is an important step in improving battery recycling technology. However, poor data availability challenges the implementation of conventional ML approaches. This work presents the first application of PD to LIB recycling, demonstrating its capability to improve model accuracy when working with a limited dataset. The developed PD-GBR model proved the most effective among those tested, exhibiting strong predictive performance and the ability to offer error estimations.Beyond modeling and prediction, this work bridges the gap between data science and chemical engineering, by integrating the ML models into a user-friendly toolkit. This allows for evaluation and optimization of reaction conditions, by offering both yield predictions and preliminary economic and environmental impact assessments. For these assessments, the cost metrics focused on reagent, mixing and heating expenses. Similarly, the environmental impact assessment is limited to the impact of acid production and does not extend to downstream wastewater treatment, which would be crucial in a full LCA. Albeit simplified, an integrated approach such as this one is invaluable for streamlining the development of sustainable LIB processes. Additionally, the ability to quickly simulate process outcomes under varying conditions, as demonstrated in the case studies, highlights the potential of this kind of approach for faster iteration and process optimization, enabling more informed process design and control for recycling plants.
While the models presented herein generally exhibit good agreement with experimental data, limitations in the generalization of novel conditions were observed and highlight the need to validate all modelling tools for a specific purpose. For example, for acids not included in the training set, a good predictive performance was observed for MSA and PHA, but the model struggled with other more diverse leaching agents like zwitterionic glycine. These findings underscore the need for more comprehensive and diverse datasets to improve model performance, robustness and generalizability prior to its broader application in process development and digital twin settings. Future efforts will focus in addressing these biases as well as capturing more relevant industrial conditions. This includes the influence of copper and aluminum ion impurities, known to impact the redox leaching of black mass, as well as leaching yields in mixed acid solutions.62
Although preliminary, this work emphasizes the importance of integrating emerging computational tools into the development of greener, better metal recycling processes. The LIB Leaching Toolkit serves as an important preliminary study tool for agile screening and optimization of leaching conditions, paving the way for more efficient and environmentally conscious battery recycling. The natural continuation of this work would be to expand the dataset to include a greater range of cathode materials and acids, particularly focusing on real waste streams and possible contaminants, which were disregarded for this work.
Author contributions
André Nogueira: methodology, data curation, software, investigation, writing – original draft, writing – review & editing. Filipe H. B. Sosa: methodology, investigation, writing – review & editing. Ana C. Dias: resources, writing – review & editing. João A. P. Coutinho: funding acquisition, writing – review & editing. Nicolas Schaeffer: writing – original draft, writing – review & editing, supervision, conceptualization, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
Data will be made available on request. The code for this project is archived on Zenodo at https://doi.org/10.5281/zenodo.16096943.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5gc04752h.
Acknowledgements
This work was developed within the scope of the project CICECO Aveiro Institute of Materials, https://doi.org/10.54499/UIDB/50011/2020, https://doi.org/10.54499/UIDP/50011/2020, https://doi.org/10.54499/LA/P/0006/2020 UID/50011/2025 (https://doi.org/10.54499/UID/50011/2025) & LA/P/0006/2020 (https://doi.org/10.54499/LA/P/0006/2020), financed by national funds through the FCT/MCTES (PIDDAC). Filipe H. B. Sosa acknowledges FCT – Fundação para a Ciência e a Tecnologia, I.P. for the researcher contract CEECIND/07209/2022 (https://doi.org/10.54499/2022.07209.CEECIND/CP1720/CT0019) under the Scientific Employment Stimulus Individual Call 2022. André Nogueira acknowledges FCT – Fundação para a Ciência e a Tecnologia, I.P for project/grant 2023.01418.BD (https://doi.org/10.54499/2023.01418.BD). Ana C. Dias also acknowledges funding by national funds through FCT – Fundação para a Ciência e a Tecnologia I.P, under the project/grant UID/50006 + LA/P/0094/2020 (https://doi.org/10.54499/LA/P/0094/2020). The authors thank the EU's Horizon Europe programme Revitalise (Grant agreement ID: 101137585) (https://doi.org/10.3030/101137585) for funding. N. Schaeffer acknowledges the European Union for the European Research Council (ERC) for the starting grant DESignSX (Grant agreement ID: 101116461) (https://doi.org/10.3030/101116461). The authors acknowledge the researchers whose publicly available data on lithium-ion battery leaching were essential for the construction of the dataset used in this work. The authors also gratefully acknowledge Flávia N. Braga for her expertise and availability in performing some of the analytical work required for this project.References
- E. Silva and A. Chen, Batteries: Emerging chemistries create trade-offs in cost, performance [Internet]. S&P Global Market Intelligence; 2023 June [cited 2024 Apr 11]. Available from: https://www.spglobal.com/marketintelligence/en/news-insights/latest-news-headlines/batteries-emerging-chemistries-create-trade-offs-in-cost-performance-75866899.
- Proposal for a REGULATION OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL concerning batteries and waste batteries, repealing Directive 2006/66/EC and amending Regulation (EU) No 2019/1020 [Internet]. 2020. Available from: https://eur-lex.Europa.eu/legal-content/EN/TXT/?uri=celex:52020PC0798.
- Z. J. Baum, R. E. Bird, X. Yu and J. Ma, Lithium-Ion Battery Recycling–Overview of Techniques and Trends, ACS Energy Lett., 2022, 7(2), 712–719 CrossRef
.
-
IEA, Recycling of Critical Minerals [Internet], Paris, 2024. Available from: https://www.iea.org/reports/recycling-of-critical-minerals Search PubMed
.
- Y. Wang, N. An, L. Wen, L. Wang, X. Jiang and F. Hou,
et al., Recent progress on the recycling technology of Li-ion batteries, J. Energy Chem., 2021, 55, 391–419 CrossRef
.
- F. Duarte Castro, E. Mehner, L. Cutaia and M. Vaccari, Life cycle assessment of an innovative lithium-ion battery recycling route: A feasibility study, J. Cleaner Prod., 2022, 368, 133130 CrossRef
.
- K. Davis and G. P. Demopoulos, Hydrometallurgical recycling technologies for NMC Li-ion battery cathodes: current industrial practice and new R&D trends, RSC Sustainability, 2023, 1(8), 1932–1951 RSC
.
- S. Shilpa, G. Kashyap and R. B. Sunoj, Recent Applications of Machine Learning in Molecular Property and Chemical Reaction Outcome Predictions, J. Phys. Chem. A, 2023, 127(40), 8253–8271 CrossRef PubMed
.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger and K. R. Müller,
et al., Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems, Chem. Rev., 2021, 121(16), 9816–9872 CrossRef PubMed
.
- M. Duquesnoy, C. Liu, D. Z. Dominguez, V. Kumar, E. Ayerbe and A. A. Franco, Machine learning-assisted multi-objective optimization of battery manufacturing from synthetic data generated by physics-based simulations, Energy Storage Mater., 2023, 56, 50–61 CrossRef
.
- M. Duquesnoy, C. Liu, V. Kumar, E. Ayerbe and A. A. Franco, Toward high-performance energy and power battery cells with machine learning-based optimization of electrode manufacturing, J. Power Sources, 2024, 590, 233674 CrossRef
.
- Y. Chen, K. S. S. Alamin, D. Jahier Pagliari, S. Vinco, E. Macii and M. Poncino, Electric Vehicles Plug-In Duration Forecasting Using Machine Learning for Battery Optimization, Energies, 2020, 13(16), 4208 CrossRef
.
- J. Dong, Z. Yu, X. Zhang, J. Luo, Q. Zou and C. Feng,
et al., Data-driven predictive prognostic model for power batteries based on machine learning, Process Saf. Environ. Prot., 2023, 172, 894–907 CrossRef
.
- E. P. Zhou, Machine Learning For The Classification And Separation Of E-Waste. In: 2022 IEEE MIT Undergraduate Research Technology Conference (URTC) [Internet]. 2022 [cited 2025 Apr 1]. pp. 1–5. Available from: https://ieeexplore.ieee.org/document/10002242.
- H. Ebrahimzade, G. R. Khayati and M. Schaffie, Leaching kinetics of valuable metals from waste Li-ion batteries using neural network approach, J. Mater. Cycles Waste Manage., 2018, 20(4), 2117–2129 CrossRef
.
- B. Niu, X. Wang and Z. Xu, Application of machine learning to guide efficient metal leaching from spent lithium-ion batteries and comprehensively reveal the process parameter influences, J. Cleaner Prod., 2023, 410, 137188 CrossRef
.
- F. Zhou, D. Shi, W. Mu, S. Wang, Z. Wang and C. Wei,
et al., Machine learning models accelerate deep eutectic solvent discovery for the recycling of lithium-ion battery cathodes, Green Chem., 2024, 26(13), 7857–7868 RSC
.
- Z. Zhang, X. Zhang, D. Zhang, X. Zhang, F. Qiu and W. Li,
et al., Application of Machine Learning in a Mineral Leaching Process–Taking Pyrolusite Leaching as an Example, ACS Omega, 2022, 7(51), 48130–48138 CrossRef PubMed
.
- M. Mathaba and J. Banza, Application of machine learning approach (artificial neural network) and shrinking core model in cobalt(II) and copper(II) leaching process, J. Environ. Sci. Health, Part A, 2024, 59(1), 25–32 CrossRef PubMed
.
- V. Flores and C. Leiva, A Comparative Study on Supervised Machine Learning Algorithms for Copper Recovery Quality Prediction in a Leaching Process, Sensors, 2021, 21(6), 2119 CrossRef PubMed
.
- S. Daware, S. Chandel and B. Rai, A machine learning framework for urban mining: A case study on recovery of copper from printed circuit boards, Miner. Eng., 2022, 180, 107479 CrossRef
.
- B. Dou, Z. Zhu, E. Merkurjev, L. Ke, L. Chen and J. Jiang,
et al., Machine Learning Methods for Small Data Challenges in Molecular Science, Chem. Rev., 2023, 123(13), 8736–8780 CrossRef PubMed
.
- M. Tynes, W. Gao, D. J. Burrill, E. R. Batista, D. Perez and P. Yang,
et al., Pairwise Difference Regression: A Machine Learning Meta-algorithm for Improved Prediction and Uncertainty Quantification in Chemical Search, J. Chem. Inf. Model., 2021, 61(8), 3846–3857 CrossRef PubMed
.
- P. Zhang, T. Yokoyama, O. Itabashi, T. M. Suzuki and K. Inoue, Hydrometallurgical process for recovery of metal values from spent lithium-ion secondary batteries, Hydrometallurgy, 1998, 47(2), 259–271 CrossRef
.
- C. K. Lee and K. I. Rhee, Preparation of LiCoO2 from spent lithium-ion batteries, J. Power Sources, 2002, 109(1), 17–21 CrossRef
.
- R. C. Wang, Y. C. Lin and S. H. Wu, A novel recovery process of metal values from the cathode active materials of the lithium-ion secondary batteries, Hydrometallurgy, 2009, 99(3), 194–201 CrossRef
.
- L. Li, J. Ge, F. Wu, R. Chen, S. Chen and B. Wu, Recovery of cobalt and lithium from spent lithium ion batteries using organic citric acid as leachant, J. Hazard. Mater., 2010, 176(1), 288–293 CrossRef PubMed
.
- L. Li, J. Lu, Y. Ren, X. X. Zhang, R. J. Chen and F. Wu,
et al., Ascorbic-acid-assisted recovery of cobalt and lithium from spent Li-ion batteries, J. Power Sources, 2012, 218, 21–27 CrossRef
.
- P. Meshram, B. D. Pandey and T. R. Mankhand, Recovery of valuable metals from cathodic active material of spent lithium ion batteries: Leaching and kinetic aspects, Waste Manage., 2015, 45, 306–313 CrossRef PubMed
.
- L. P. He, S. Y. Sun, X. F. Song and J. G. Yu, Leaching process for recovering valuable metals from the LiNi 1/3 Co 1/3 Mn 1/3 O 2 cathode of lithium-ion batteries, Waste Manage., 2017, 64, 171–181 CrossRef PubMed
.
- W. Gao, X. Zhang, X. Zheng, X. Lin, H. Cao and Y. Zhang,
et al., Lithium Carbonate Recovery from Cathode Scrap of Spent Lithium-Ion Battery: A Closed-Loop Process, Environ. Sci. Technol., 2017, 51(3), 1662–1669 CrossRef PubMed
.
- R. Golmohammadzadeh, F. Rashchi and E. Vahidi, Recovery of lithium and cobalt from spent lithium-ion batteries using organic acids: Process optimization and kinetic aspects, Waste Manage., 2017, 64, 244–254 CrossRef PubMed
.
- L. Li, E. Fan, Y. Guan, X. Zhang, Q. Xue and L. Wei,
et al., Sustainable Recovery of Cathode Materials from Spent Lithium-Ion Batteries Using Lactic Acid Leaching System, ACS Sustainable Chem. Eng., 2017, 5(6), 5224–5233 CrossRef
.
- W. S. Chen and H. J. Ho, Recovery of Valuable Metals from Lithium-Ion Batteries NMC Cathode Waste Materials by Hydrometallurgical Methods, Metals, 2018, 8(5), 321 CrossRef
.
- W. Gao, J. Song, H. Cao, X. Lin, X. Zhang and X. Zheng,
et al., Selective recovery of
valuable metals from spent lithium-ion batteries – Process development and kinetics evaluation, J. Cleaner Prod., 2018, 178, 833–845 CrossRef
.
- W. Xuan, A. Otsuki and A. Chagnes, Investigation of the leaching mechanism of NMC 811 (LiNi0.8Mn0.1Co0.1O2) by hydrochloric acid for recycling lithium ion battery cathodes, RSC Adv., 2019, 9(66), 38612–38618 RSC
.
- K. H. Chan, J. Anawati, M. Malik and G. Azimi, Closed-Loop Recycling of Lithium, Cobalt, Nickel, and Manganese from Waste Lithium-Ion Batteries of Electric Vehicles, ACS Sustainable Chem. Eng., 2021, 9(12), 4398–4410 CrossRef
.
- W. Xuan, A. de Souza Braga, C. Korbel and A. Chagnes, New insights in the leaching kinetics of cathodic materials in acidic chloride media for lithium-ion battery recycling, Hydrometallurgy, 2021, 204, 105705 CrossRef
.
- E. Kim, T. Ahn and T. Y. Kim, New method for selective recovery of manganese from NCM-based cathode material of spent Li-ion batteries, Geosyst. Eng., 2022, 25(3–4), 143–149 CrossRef
.
- L. F. Guimarães, A. B. Botelho Junior and D. C. R. Espinosa, Sulfuric acid leaching of metals from waste Li-ion batteries without using reducing agent, Miner. Eng., 2022, 183, 107597 CrossRef
.
- L. M. J. Rouquette, M. Petranikova and N. Vieceli, Complete and selective recovery of lithium from EV lithium-ion batteries: Modeling and optimization using oxalic acid as a leaching agent, Sep. Purif. Technol., 2023, 320, 124143 CrossRef
.
- T. Jiang, Q. Shi, Z. Wei, K. Shah, H. Efstathiadis and X. Meng,
et al., Leaching of valuable metals from cathode active materials in spent lithium-ion batteries by levulinic acid and biological approaches, Heliyon, 2023, 9(5), e15788 CrossRef PubMed
.
- N. Vieceli, P. Benjamasutin, R. Promphan, P. Hellström, M. Paulsson and M. Petranikova, Recycling of Lithium-Ion Batteries: Effect of Hydrogen Peroxide and a Dosing Method on the Leaching of LCO, NMC Oxides, and Industrial Black Mass, ACS Sustainable Chem. Eng., 2023, 11(26), 9662–9673 CrossRef
.
- J. Partinen, P. Halli, B. P. Wilson and M. Lundström, The impact of chlorides on NMC leaching in hydrometallurgical battery recycling, Miner. Eng., 2023, 202, 108244 CrossRef
.
- S. Sahu and N. Devi, Two-step leaching of spent lithium-ion batteries and effective regeneration of critical metals and graphitic carbon employing hexuronic acid, RSC Adv., 2023, 13(11), 7193–7205 RSC
.
- G. Landrum, P. Tosco, B. Kelley, R. Rodriguez, D. Cosgrove, R. Vianello, et al., rdkit/rdkit: 2024_09_6 (Q3 2024) Release [Internet]. Zenodo; 2025 [cited 2025 May 7]. Available from: https://zenodo.org/doi/10.5281/zenodo.14943932.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel,
et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12(85), 2825–2830 Search PubMed
.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Optuna: A Next-generation Hyperparameter Optimization Framework. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining [Internet]. New York, NY, USA: Association for Computing Machinery; 2019 [cited 2025 Mar 26]. p. 2623–2631. (KDD ‘19). Available from: https://dl.acm.org/doi/10.1145/3292500.3330701.
- G. Wernet, C. Bauer, B. Steubing, J. Reinhard, E. Moreno-Ruiz and B. Weidema, The ecoinvent database version 3 (part I): overview and methodology, Int. J. Life Cycle Assess., 2016, 21(9), 1218–1230 CrossRef
.
- N. V. Chawla, K. W. Bowyer, L. O. Hall and W. P. Kegelmeyer, SMOTE: Synthetic Minority Over-sampling Technique, J. Artif. Intell. Res., 2002, 16, 321–357 CrossRef
.
- G. Landrum, P. Tosco, B. Kelley, R. Rodriguez, D. Cosgrove, R. Vianello, et al., rdkit/rdkit: 2024_09_6 (Q3 2024) Release [Internet]. Zenodo; 2025 [cited 2025 May 7]. Available from: https://zenodo.org/records/14943932.
- M. C. Apua and M. S. Madiba, Leaching kinetics and predictive models for elements extraction from copper oxide ore in sulphuric acid, J. Taiwan Inst. Chem. Eng., 2021, 121, 313–320 CrossRef
.
- M. A. H. Shuva and A. S. W. Kurny, Dissolution Kinetics of Cathode of Spent Lithium Ion Battery in Hydrochloric Acid Solutions, J. Inst. Eng. (India): Ser. D, 2013, 94(1), 13–16 Search PubMed
.
- Z. Takacova, T. Havlik, F. Kukurugya and D. Orac, Cobalt and lithium recovery from active mass of spent Li-ion batteries: Theoretical and experimental approach, Hydrometallurgy, 2016, 163, 9–17 CrossRef
.
- E. Billy, M. Joulié, R. Laucournet, A. Boulineau, E. De Vito and D. Meyer, Dissolution Mechanisms of LiNi1/3Mn1/3Co1/3O2 Positive Electrode Material from Lithium-Ion Batteries in Acid Solution, ACS Appl. Mater. Interfaces, 2018, 10(19), 16424–16435 CrossRef PubMed
.
-
S. Andreasi Bassi, F. Biganzoli, N. Ferrara, A. Amadei, A. Valente and S. Sala, et al., Updated characterisation and normalisation factors for the environmental footprint 3.1 method [Internet], Publications Office of the European Union, 2023 [cited 2025 July 29]. Available from: https://data.Europa.eu/doi/10.2760/798894 Search PubMed
.
- J. Kim, Y. M. Kim, V. R. Lebaka and Y. J. Wee, Lactic Acid for Green Chemical Industry: Recent Advances in and Future Prospects for Production Technology, Recovery, and Applications, Fermentation, 2022, 8(11), 609 CrossRef
.
-
S. Kulprathipanja, Separation of citric acid from fermentation broth [Internet], EP0324210A1, 1989 [cited 2025 July 17]. Available from: https://patents.google.com/patent/EP0324210A1/en Search PubMed
.
- M. Iturrondobeitia, C. Vallejo, M. Berroci, O. Akizu-Gardoki, R. Minguez and E. Lizundia, Environmental Impact Assessment of LiNi1/3Mn1/3Co1/3O2 Hydrometallurgical Cathode Recycling from Spent Lithium-Ion Batteries, ACS Sustainable Chem. Eng., 2022, 10(30), 9798–9810 CrossRef
.
- S. Mousavinezhad, S. Kadivar and E. Vahidi, Comparative life cycle analysis of critical materials recovery from spent Li-ion batteries, J. Environ. Manage., 2023, 339, 117887 CrossRef PubMed
.
- Z. Xu, L. Ye, Y. Yu, H. Gong, Z. Xiao and L. Ming,
et al., A Green and Efficient Recycling Strategy for Spent Lithium-Ion Batteries in Neutral Solution Environment, Angew. Chem., Int. Ed., 2025, 64(17), e202414899 CrossRef PubMed
.
- J. Partinen, P. Halli, S. Helin, B. P. Wilson and M. Lundström, Utilizing Cu+ as catalyst in reductive leaching of lithium-ion battery cathode materials in H2SO4–NaCl solutions, Hydrometallurgy, 2022, 208, 105808 CrossRef
.
| This journal is © The Royal Society of Chemistry 2026 |