 Open Access Article
Open Access ArticleDFT meets Bayesian inference: creating a framework for the assignment of calculated vibrational frequencies
Michael Nicolaou ,
Hans M. Senn
,
Hans M. Senn ,
Emma Gibson
,
Emma Gibson *,
Mario González-Jiménez
*,
Mario González-Jiménez and
Laia Vilà-Nadal
and
Laia Vilà-Nadal *
*
The School of Chemistry University of Glasgow Joseph Black Building, University Avenue, Glasgow G12 8QQ, UK. E-mail: Emma.Gibson@glasgow.ac.uk; laia.vila-nadal@glasgow.ac.uk
First published on 20th January 2026
Abstract
Volatile Organic Compounds (VOCs) are abundant in nature and play vital roles in industries such as food, fragrance, and pharmaceuticals. Aromatic VOCs like vanillin are especially valuable, driving research into sustainable chemical processes, including the conversion of biomass into high-value chemicals. Understanding the molecular structure and vibrational behavior of these compounds is essential for designing and optimising such processes. In this work, we explore how computational modelling can be used to predict and interpret vibrational spectra of VOCs. We also introduce a statistical approach using Bayesian inference to improve how theoretical predictions are matched to experimental observations. This combined strategy enhances the reliability and clarity of spectral interpretation, offering a more consistent framework for studying complex organic molecules.
Introduction
Aromatic Volatile Organic Compounds (VOCs), such as vanillin, have wide-ranging applications in food, cosmetics, and pharmaceuticals.1 They play an important role in petrochemical transition strategies,2 acting as a critical link between renewable biomass sources,3 and fine chemicals.4 Phenylpropanoid VOCs in particular act as a driving force for recent advances in lignin conversion to value-added chemicals,5–8 a highly promising scientific frontier that aims for the depolymerisation of lignin, an abundant, yet complex biopolymer that constitutes a large fraction of plant matter.2,9,10 Aromatic VOCs are highly sought after in the food, cosmetics, and fragrance industries due to their strong organoleptic characteristics.11–14In parallel, the structural complexity of lignin—a heterogeneous biopolymer found in plant cell walls—continues to pose a major challenge in sustainable chemical conversion. Its irregular monomer composition and variable linkages, which differ across plant species and extraction methods, complicate both structural identification and the assessment of chemical treatments.2,10 As a result, analytical tools such as GC-MS,6,7 NMR,10,15,16 and IR/Raman spectroscopy17,18 are essential for characterising lignin and its depolymerisation products.
Computational Density Functional Theory (DFT) methods provide an invaluable tool for innumerable applications, such as mechanistic studies of catalytical environments,19–21 aiding in the understanding of catalytical processes and identification of catalytical products. DFT modelling is, however, fundamentally approximate, and needs experimental benchmarking when choosing a system to model and caution when interpreting the findings. This is further compounded by a notoriously expansive catalogue of available methodology parameters,22,23 (choice of functional, basis set or other factors such as dispersion) and even strategies enhancing DFT with other approaches, such as QM/MM methods24 and machine learning.25 This can be especially daunting when studying convoluted systems, such as vibrational fingerprints, where intensities are approximate and frequencies are off-set.26 These challenges are especially evident in vibrational spectroscopy, where the harmonic approximation27 is commonly used to reduce computational cost. While practical, this simplification introduces frequency errors, as it neglects anharmonicity. Calculation of vibrational frequencies also ignores phenomena like combination bands and Fermi resonance. This becomes exacerbated when studying systems in the solid or liquid state, where environmental effects are involved, such as hydrogen bonding and π-stacking of aromatic rings. While solid state calculations are possible using periodic DFT, it escalates the complexity and thus computational cost of a calculation, and is limited by the requirement of having prior knowledge of the system's structure. Static scaling factors are typically applied to correct frequency offsets, but interpretation still requires manual assignment—often a tedious and uncertain process. Recently, the integration of statistical models and machine learning has propelled the rise of digital chemistry—a data-driven paradigm that enhances the design, analysis, and interpretation of chemical systems.28,29 In this context, IR spectral prediction is becoming increasingly automated, accurate, and scalable, offering powerful tools for materials discovery, reaction monitoring, and structural elucidation.30 To overcome these issues, we introduce a Bayesian framework that enhances vibrational mode assignment from single molecule DFT calculations to non-gas phase IR spectra by statistically linking theoretical frequencies with experimental bands. Bayes' theorem allows us to quantify the likelihood of each potential match, offering a structured and reproducible alternative to subjective interpretation.
In this work, we have combined experimental results with our calculated vibrational data to benchmark a range of DFT methods for modelling aromatic VOCs and identify the most time-efficient and accurate approach. Following the protocol established by Alecu et al.,26 we report universal scaling factors for these methods. Furthermore, we create a framework and demonstrate how Bayesian inference can be used as a tool to enhance and strengthen spectral interpretation. The following ten aromatic compounds were used to test our proposed method: vanillin, 4-hydroxybenzaldehyde, syringaldehyde, cinnamaldehyde, cuminaldehyde, eugenol, estragole, coumarin, dihydrocoumarin, and umbelliferone, resulting in facilitated spectral interpretation and vibrational mode identification (Fig. 1).
Methodology
Computational method
All computational calculations were performed using the Gaussian 16 software31 on the University of Glasgow School of Chemistry High-Performance Computing (HPC) cluster. Molecule visualisations were performed using the GaussView-5 software.32Molecular geometry optimisation and vibrational frequency calculations of vanillin molecules were performed at different exchange–correlation (XC) functional levels of theory (S1) across the GGA (Generalised-Gradient Approximation), mGGA (meta-GGA), hybrid (HF exchange energy contribution), meta-hybrid, range-separated hybrid and double-hybrid (HF and post-HF XC contribution) “rungs” (BP86,33,34 PBE,35 OPBE,35–37 M06-L38, B3LYP,33,38,39 ωB97X-D,40,41 PBE0,35,42 M06,43 M06-2X43 and PBE0-DH44), as well as using ab initio post-HF second-order Møller–Plesset perturbation theory (MP2),45–49 using the 6-311++G(2d,2p) triple-ζ split-valence polarised Pople Gaussian-type orbital (GTO) basis set for H, C and O50,51 with diffuse orbitals for all atoms.
To determine the point of basis set convergence and study the effects of basis set parameters, such as polarisation and diffuse functions, the same calculations were also performed at the M06-2X XC functional level of theory using different basis sets (3-21G, 6-31G, 6-31G(d,p), 6-311G, 6-311G(d,p), 6-311+G, cc-pVDZ, cc-pVTZ, cc-pVQZ, aug-cc-pVTZ, aug-cc-pVQZ,52 def2-TZVP, def2-QZVP53), as M06-2X has been extensively used in studies on similar molecules and suggested to be suitable for small-medium molecules54 and main-group thermochemistry.43,55
All calculations were performed using spin-restricted (“closed shell”) orbitals and structures pre-optimised using Universal Force-Field (UFF)56 Molecular Mechanics (MM).
Vibrational frequency calculations (IR and Raman), were performed using the harmonic approximation model (S3).27
DFT-calculated vibrational frequencies were convolved and plotted using Python.57–60 Gaussian broadening was applied (S8) around the calculated frequencies with a standard deviation of 8, representing a full width at half maximum (FWHM) of approximately 19 cm−1. All spectra were normalised when plotted.
Experimental details
Vanillin (4-hydroxy-3-methoxybenzaldehyde) (8.18718), 4-hydroxybenzaldehyde (54590-F), syringaldehyde (4-hydroxy-3,5-dimethoxybenzaldehyde) (S7602), cinnamaldehyde (2E-3-phenylprop-2-enal) (W228613), cuminaldehyde (4-isopropylbenzaldehyde) (135178), eugenol (2-methoxy-4-(prop-2-en-1-yl)phenol) (E51791), estragole (4-allylanisole) (A29208), coumarin (C4261), dihydrocoumarin (D104809) and umbelliferone (7-hydroxycoumarin) (H24003) were obtained from Sigma-Aldrich.Experimental IR spectra were measured using a dry-air purged Bruker Vertex 70 spectrometer equipped with a Globar lamp, a Deuterated L-alanine doped Tri-Glycine Sulphate (DLaTGS) detector, a potassium bromide (KBr) beamsplitter, and a diamond ATR accessory (Bruker Platinum ATR Unit A225), at a resolution of 1 cm−1, averaging over 16 scans at a range of 350–4000 cm−1. The gas phase IR spectrum of vanillin was taken from the NIST Chemistry WebBook.61
Computational benchmark
To determine the most efficient method to model the selected VOCs, a benchmark of the studied methodologies has been carried out. The calculated bond lengths (excluding bonds with H-atoms) of vanillin have been compared to single-crystal X-ray crystallographic data (S10) found through the CCDC database62 (CID: 13006628) from Velavan et al.63Fig. 2 shows the geometry of vanillin as found in the crystallographic file. The average bond length for each of the 11 bonds was taken as the average bond length of 4 vanillin molecules present in the periodic crystal unit.
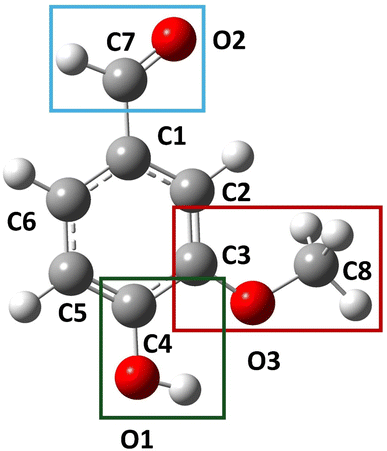 | ||
| Fig. 2 Structure of vanillin in single crystal (CCDC62 CID 1306628 (ref. 63)). The coloured boxes highlight characteristic functional groups of vanillin. | ||
To gauge the efficiency of each method, the Mean Absolute Deviation (MAD) (S4) between calculated and reference bond lengths was compared with the job CPU time for the geometry optimisation of a pre-optimised input structure.
The calculation of vibrational modes and frequencies employs harmonic approximation,27 in which normal modes and frequencies are calculated based on the second derivatives of the energy with respect to atomic displacements. This is done to avoid the calculation of higher-order terms and simplify the calculation. Additionally, DFT calculations were performed on a single molecule, which is different from the experimental IR spectrum of a crystal or liquid.
As a result, computed vibrational frequencies differ from those observed experimentally via IR spectroscopy. It is thus important to gauge the expected magnitude of this deviation when attempting to make such a comparison. For errors due to anharmonicity, a scaling factor, which depends on the method used, is conventionally applied.
In their study, Alecu et al.26 showed that fundamental frequency scaling factors, which can be universally applied to frequency calculations to reduce the error by that method, can be obtained from the comparison of calculated frequency values to the experimentally observed frequencies of a suggested database containing 38 modes of vibration across 15 molecules, referred to in their study as “F38/10”.26 The scaling factor (λF) can then be calculated as:
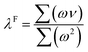 | (1) |
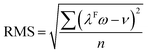 | (2) |
The scaling factor for M06-2X/def2-TZVP was calculated for validation. A scaling factor of 0.945 was obtained which is in close agreement to the 0.946 reported by the authors, exhibiting a scaled RMS deviation of the dataset of 48 cm−1, showing a clear improvement from the 147 cm−1 unscaled deviation. A clear improvement in the accuracy of the methods when calculating the frequencies of the F38/10 database (S13) can be seen with the application of the reported scaling factors.
The RMS was optimised with respect to λF (S13) and the scaled RMS deviations present similar values to those of scaling factors reported, with the significant exception of cases using basis sets lacking polarisation (3-21G, 6-31G, 6-311G, 6-311++G), which still exhibit large RMS deviations after being scaled. We selected 17 bands in the solid state IR spectrum of vanillin for comparison with theoretical values. These can be seen as the labelled bands in Table 2.
Frequency calculations on the optimised vanillin structures were performed using the selected methods. The frequencies for the fundamental modes of vibration were scaled using the scaling factors obtained from literature where available (M06-2X/: 6-31G(d,p), 6-311G(d,p), aug-cc-pVTZ, def2-TZVP and def2-QZVP)26,64,65 and using the scaling factors calculated in the present work for the other methods (Table 1). The internal coordinates and contributions of involved bonds, angles and dihedral angles for each normal mode were also recorded.
| Methodology | λF | RMS deviationa (cm−1) | |
|---|---|---|---|
| Scaled | Unscaled | ||
| a Calculated from the F38/10 database26 (S13).b Reproduced and compared with literature. | |||
| Functionals using 6-311++G(2d,2p) | |||
| MP2-FC | 0.955 | 77 | 136 |
| BP86 | 0.989 | 34 | 43 |
| PBE | 0.986 | 33 | 47 |
| OPBE | 0.969 | 42 | 88 |
| M06-L | 0.959 | 32 | 107 |
| B3LYP | 0.963 | 28 | 103 |
| ωB97X-D | 0.948 | 41 | 137 |
| PBE0 | 0.950 | 34 | 130 |
| M06 | 0.956 | 45 | 118 |
| M06-2X | 0.944 | 44 | 148 |
| PBE0-DH | 0.935 | 42 | 170 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Basis sets used with M06-2X | |||
| 3-21G | 0.969 | 139 | 158 |
| 6-31G | 0.954 | 136 | 178 |
| 6-311G | 0.960 | 109 | 147 |
| 6-311++G | 0.962 | 126 | 158 |
| cc-pVDZ | 0.947 | 54 | 144 |
| cc-pVTZ | 0.945 | 47 | 147 |
| cc-pVQZ | 0.944 | 49 | 149 |
| aug-cc-pVQZ | 0.945 | 49 | 148 |
| def2-TZVPb | 0.945 | 48 | 147 |
The calculated frequencies, after applying the optimised scaling factor for the respective method, were matched against the experimental bands and the difference in wavenumbers was used to calculate the Mean Signed Deviation (MSD), Mean Absolute Deviation (MAD) and Standard Deviation (STD) (S12).
Fig. 3 shows the plot of frequency MAD (cm−1) across the characteristic bands against CPU time.
The lowest MADs (10–15 cm−1) are obtained when using mGGA or higher-rung functionals and with a polarised double/triple-ζ or higher basis sets.
The hybrid functionals M06, M06-2X, PBE0 and ωB97X-D, as well as the mGGA functional M06-L, have the fastest job completion times (2–5 hours) while yielding low MADs. The fastest job completions at basis set convergence are observed using the 6-311++G(2d,2,p), def2-TZVP or cc-pVDZ basis sets (1–5 hours). PBE0 in particular shows the overall lowest error and fastest calculation time of all hybrid functionals.
Bayesian inference
Frequency calculations can identify and illustrate a vibrational mode, but assigning this mode to the correct experimental band is not always straightforward. To identify the most probable theoretical-to-experimental band assignments, we employed a Bayesian inference method, calibrated using the model's performance on vanillin. Bayes' theorem provides a tool for iterative updating of a “hypothesis” (H) through the introduction of new “evidence” (E) (S7).
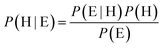 | (3) |
Fig. 4 illustrates the workflow of Bayesian inference in this study. In the context of this paper, a hypothesis was taken to be a unique set of assignments of all theoretical bands to experimentally observed bands within the spectrum range of 680–1800 cm−1, within a range of ±40 cm−1 (45 cm−1 in the case of p-hydroxy benzaldehyde) of the theoretical band (S19). In each iteration, the evidence was treated as the probability of a theoretical band being observed at its predicted frequency, given the experimental assignment specified by the hypothesis. This probability was then modelled using a Gaussian distribution centered on the expected calculated value, with the mean and standard deviation determined from the benchmarking of the computational method.
Results and discussion
Spectral analysis
Matching the scaled calculated frequencies of the studied molecules using PBE0/6-311++G(2d,2p) with the equivalent experimentally observed bands allows for the elucidation of the vibrational modes responsible for the transmittance bands in the experimental spectra. Additionally, deviation metrics obtained are needed for the probability modelling of band assignments used in the Bayesian framework. To facilitate the assignment of characteristic DFT-calculated frequencies of vanillin to the solid state IR spectrum, an experimental gas phase IR spectrum (NIST61) was also compared. Fig. 5 shows the solid state and gas phase experimental spectra of vanillin, as well as a visualised DFT-calculated spectrum. This visualisation enables the comparison between the computational and experimental spectra. The calculated spectra have been visualised using a custom Python57–60 script (S8). Computational normal mode analysis extracted from the calculations and vibrational mode animations have been used to determine the nature of the highlighted bands. Individual atomic changes in distance (R), angle (A) and dihedral angle (D) were used to assist in elucidating the nature of the vibrational modes. The vibrational frequencies were cross-referenced with expected values for the type of vibration and were found to be in good agreement.66–68 | ||
| Fig. 5 Aligned experimental solid state (black), gas phase61 (blue) and DFT (red) IR spectra of vanillin. DFT calculation performed using PBE0/6-311++G(2d,2p) with a scaling factor of 0.950. Highlighted regions indicate assigned bands used in evaluating deviation statistics from DFT calculated frequencies to solid state bands. | ||
Table 2 shows the assigned vibrational modes to the absorption bands observed in the experimental solid state, gas phase and DFT calculated IR spectra of vanillin.
| Band | Wavenumber (cm−1) | Band assignmenta | Solid state intensity | |||
|---|---|---|---|---|---|---|
| Solid state | Gas phase | DFT | Transmittance (%) | Relative | ||
| a ν refers to stretching, δ refers to in-plane bending, γ refers to out-of-plane bending. “symm.” and “asymm.” indicate symmetrical or asymmetrical vibration between the atoms of the same group. “i. ph.” and “o. ph.” indicate in and out out-of phase vibrations between different groups.b Experimentally not clearly observable or combined into larger band (e.g. band shoulder). | ||||||
| 1 | 812 | 818 | 794 | γ(C–H) 2 adjacent aromatic symm. (wagging) | 68 | m |
| 2 | 859 | 874 | 854 | γ(C–H) lone aromatic | 62 | s |
| 3 | 1025 | 1034 | 1024 | ν(O–CH3), δ(C–C–C) aromatic ring bend | 60 | s |
| — | N/Ab | N/Ab | 1087 | δ(C–H) o.ph. adjacent aromatic (Scissoring) | — | — |
| 4 | 1121 | 1118 | 1123 | δ(C–H) aromatic, δ(O–C–H) aldehyde, ν(C–OCH3) | 53 | vs |
| 5 | 1151 | 1150 | 1151 | δ(CH3), δ(C–O–H) | 49 | vs |
| 6 | 1170 | 1182 | 1173 | δ(C–H) aromatic, δ(O–C–H) aldehyde, ν(C–OCH3) | 61 | s |
| — | N/Ab | N/Ab | 1225 | o. ph. (ν(C–OCH3), ν(C–OH)), δ(C–H) aromatic | — | — |
| 7 | 1264 | N/Ab | 1241 | ν(C–OH), δ(C–O–H), δ(C–H) aromatic | 57 | s |
| 8 | 1298 | 1274 | 1274 | i. ph. (ν(C–OCH3), ν(C–OH)), ν(C–C) aromatic, δ(C–H) aromatic | 62 | s |
| — | N/Ab | N/Ab | 1341 | δ(C–H) aldehyde, δ(C–H) aromatic, δ(C–O–H) | — | — |
| 9 | 1371 | N/Ab | 1378 | ν(C–C–C) aromatic (“Kekulé’s”), δ(O–C–H) ether, δ(C–O–H), δ(C–H) aldehyde | 78 | m |
| 10 | 1397 | 1390 | 1402 | δ(CH3) symm. (“Umbrella”), δ(C–O–H), δ(C–H) aldehyde | 76 | m |
| 11 | 1428 | 1438 | 1433 | δ(CH3) asymm., ν(C–C–C) aromatic (“semi-circular”) | 61 | s |
| 12 | 1509 | 1510 | 1485 | ν(C–C–C) aromatic (“semi-circular”) | 64 | s |
| 13 | 1586 | 1598 | 1579 | ν(C–C–C) aromatic (“quadrant”) | 60 | s |
| 14 | 1662 | 1718 | 1696 | ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) aldehyde O) aldehyde |
54 | vs |
| 15 | 2861 | 2722 | 2769 | ν(C–H) aldehyde | 84 | w |
| — | N/Ab | 2810 | 2892 | ν(C–H) methyl symm. | — | — |
| 16 | 2945 | 2962 | 2957 | ν(C–H) methyl asymm. | 83 | w |
| 17 | 3020 | 3014 | 3013 | ν(C–H) methyl asymm. | 82 | w |
| — | N/Ab | 3074 | 3065 | ν(C–H) lone aromatic | — | — |
| — | 3146 | 3578 | 3621 | ν(O–H) alcohol | 79 | w |
In regards to the solid state noticeable medium bands can be found at 812 and 859 cm−1, which correspond to the out-of-plane aromatic C–H bending fingerprint of the 1,3,4-tri substituted ring, involving the in-phase wagging mode of the adjacent 5,6-position and the bending mode of the 2-position C–H bonds respectively.66 A strong band at 1025 cm−1 is attributed to the C–OCH3 ether stretching vibration and ring deformation mode. Very strong bands observed at 1121, 1151 and 1170 cm−1 respectively are assigned to modes caused primarily by in-plane bending modes of the aromatic C–H bonds, but also alcohol and ether bending and ether stretching modes. It should be noted that the gas phase and DFT bands corresponding to these bands show lower intensity. Strong bands at 1264 and 1298 cm−1 are assigned to alcohol C–O stretching, and in-phase ether and alcohol C–O stretching modes. A medium band observed at 1371 cm−1 is assigned to the specific “Kekulé” ring stretching mode, as well as related bends. The medium and strong bands observed at 1397 and 1428 cm−1 respectively are attributed to methyl CH3 (ether) in and out-of-phase bends. Strong bands at 1509 and 1586 cm−1 correspond to characteristic ring “Semi-circular” and “Quadrant” vibrations. The strong band 1662 is caused by the aldehyde C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode. A weak doublet at 2861 cm−1 corresponds to the aldehyde C–H stretching vibration. Weak bands can be observed at 2945 and 3020, which are loosely assigned stretching vibrations of the methyl and aromatic C–H bonds. The gas phase and DFT spectra provide clearer profiles of these vibrations, allowing clearer distinction between the symmetric and asymmetric methyl C–H, and a ring lone C–H stretching mode. A characteristic broad band at 3146 cm−1 corresponds to the O–H stretching mode, seen as sharp stronger bands at higher frequencies in the gas phase and DFT-calculated spectra.
O stretching mode. A weak doublet at 2861 cm−1 corresponds to the aldehyde C–H stretching vibration. Weak bands can be observed at 2945 and 3020, which are loosely assigned stretching vibrations of the methyl and aromatic C–H bonds. The gas phase and DFT spectra provide clearer profiles of these vibrations, allowing clearer distinction between the symmetric and asymmetric methyl C–H, and a ring lone C–H stretching mode. A characteristic broad band at 3146 cm−1 corresponds to the O–H stretching mode, seen as sharp stronger bands at higher frequencies in the gas phase and DFT-calculated spectra.
Computation and band assignment of VOCs
The same computational approach was then applied to optimise and calculate the vibrational frequencies of a selection of important volatile organic compounds (VOCs). A conformational search was performed to determine the global minimum conformer for all compounds (S15). Frequency calculations were performed on the lowest-energy conformer for each compound using PBE0/6-311++G(2d,2p). Compound key vibrations in the theoretical spectra were selected, and their vibrational modes were identified (S18). A Python57–60 script was used to process the theoretical frequencies and experimental bands within 680–1800 cm−1, generate all acceptable hypotheses and iteratively apply Bayes' theorem to determine the feasibility (S19) of each hypothesis.In the context of this paper, a hypothesis was taken to be an assignment of all represented theoretical vibrations to experimental bands. The evidence presented in each iteration was calculated as the likelihood that a theoretical vibration would have the observed frequency it has, given that it represented the experimental band assigned in the specific hypothesis. This probability was modelled as a Gaussian probability density distribution around an expected value (experimental band shifted by the MSD) and the STD calculated during the benchmark. The result of this procedure is a relative probability value for each hypothesis, which quantifies the likelihood of that hypothesis to be correct, given the expected accuracy of the DFT calculation, thus identifying band assignments that are more plausible than others (S19). Those hypotheses were then examined, and the most reasonable hypothesis was considered based on IR intensity and chemical sense. Fig. 6 shows the experimental-to-theoretical comparison of the chosen modes for all studied molecules. The x-axis corresponds to the experimentally obtained band frequencies for the assigned bands, and the y-axis corresponds to the scaled calculated frequencies for the vibrational modes (scaling factor of 0.950 for PBE0/6-311++G(2d,2p)).
A systematic underestimation of the frequencies was observed, as most assigned frequencies predict a lower value than the experimental band. While some of the vibrations show great agreement between theory and experiment, aromatic C–H wagging modes and C–O stretching modes are calculated within 10–30 cm−1 of the experiment, leading to a deviation of 1–4% for C–H wagging and 2% for C–O stretching modes. CH3 deformations show excellent agreement for vanillin, whereas a consistently negative deviation of around 30 cm−1 (2–3%) is observed for syringaldehyde, cuminaldehyde, eugenol, estragole and dihydrocoumarin (CH2 deformations). Aromatic ring “semi-circular” and “quadrant” modes show good agreement across all the molecules with most calculations falling within 40 cm−1 below the experimental bands (∼2.5%). The MSD for all molecules, except umbelliferone, is negative, indicating that for the chosen set of molecules and vibrations, the mean error metrics could also be improved by applying a higher scaling factor. This is expected when considering the comparison between single molecule calculations to solid or liquid state systems, in which the bond vibrations and affected by intermolecular interactions.
The calculated values across all identified modes exhibit MADs ranging from 10 cm−1 to 20 cm−1 (0.9–1.8%) (Fig. 7), showing good agreement between the experimental spectra and assigned theoretical frequencies.
 | ||
| Fig. 7 DFT-calculated (PBE0/6-311++G(2d,2p)) MAD (%) (opaque) and MSD (%) (transparent) across all studied vibrational modes for all compounds compared to experimental IR bands. | ||
Using this approach to assign theoretical frequencies to experimental bands allows for more coherent identification of recurring key vibrations for the studied molecules. These vibrations include the fingerprint aromatic C–H out-of-plane bending modes (650–900 cm−1), phenyl and aryl ether C–O stretching modes (1000–1300 cm−1), CH3 and CH2 deformation (1300–1500 cm−1) and ring C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching (“semi-circular” and “quadrant”; 1400–1650 cm−1) modes.
C stretching (“semi-circular” and “quadrant”; 1400–1650 cm−1) modes.
Conclusions
The computational benchmarking for the geometry optimisation and vibrational frequency calculations of vanillin across a selection of computational methods, including an ab initio method and different DFT XC-functionals, as well as basis sets, has been completed and the most efficient method for calculations of vanillin in terms of accuracy and time determined to be PBE0/6-311++G(2d,2p). Hybrid functionals using a polarised triple-ζ basis set have shown to be sufficient for convergence to the lowest error values.Optimised scaling factors, following the method proposed by Alecu26 et al. are reported in this paper for method/basis set combinations for which scaling factors were not previously available in the literature, to the best of our knowledge.
A spectral analysis of vanillin has been performed, in which the characteristic DFT-calculated vibrational modes are assigned to experimentally observed solid state IR bands. This was enabled by comparing between DFT, gas phase61 and solid state, allowing for better association between experiment and theory, and for gauging of the expected deviations when comparing single molecule DFT to non-gas phase experimental IR spectra. Using the normal modes obtained by the frequency calculation, the nature of each vibrational mode is thus explained, allowing for better understanding of the characteristic groups of vanillin responsible for each vibration.
A Bayesian approach was then applied to identify important vibrational modes in a selection of crucial volatile aromatic compounds (p-hydroxy benzaldehyde, syringaldehyde, cinnamaldehyde, cuminaldehyde, eugenol, estragole, coumarin, dihydrocoumarin and umbelliferone). The theoretical frequencies were assigned to experimental bands based on the calculated deviation statistics, using Bayes' theorem (S7) (S19). The performance of our approach was assessed by comparing the theoretical frequencies with their matched experimental bands, showing good performance with MAD (%) values between 1 and 2% for all compounds.
Key vibrations found in aromatic systems (aromatic C–H bending and ring C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes) were identified (where observable) in all molecules (S18) and compared with the experimental spectra.
C stretching modes) were identified (where observable) in all molecules (S18) and compared with the experimental spectra.
A negative MSD across all molecules, except umbelliferone, in the studied spectral range suggests that a higher scaling factor for the method would improve the fit of these frequencies to their experimental spectra.
In summary, an efficient computational method and a universal scaling factor (PBE0/6-311++G(2d,2p) with a scaling factor of 0.950) are reported and used to analyse the solid state experimental IR spectrum of vanillin. Bayesian inference is used to provide a framework for matching single molecule theoretical to experimental solid and liquid state IR vibrational frequencies of a selection of important volatile organic chemicals and the consistency of the method is tested by comparing indicative vibrational mode frequencies to experimentally assigned IR bands. Key vibrational modes of all compounds are identified and matched on the experimental IR spectrum.
Author contributions
M. N. performed the DFT calculations, developed the Bayesian inference model, carried out data analysis and visualisation, and wrote the original draft. H. M. S. supervised the computational methodology and contributed to data interpretation and manuscript review. M. G.-J. acquired and processed the experimental IR spectra and contributed to vibrational mode interpretation. L. V.-N. and E. G. co-supervised the project; L. V.-N. led the theoretical aspects, including DFT benchmarking and modelling strategy, while E. G. provided guidance on experimental design and chemical relevance. Both contributed to project conception and funding acquisition. L. V.-N. also oversaw project administration and manuscript preparation. All authors discussed the results and contributed to the final version of the manuscript. ChatGPT (OpenAI) was used under author supervision to improve grammar and clarity in sections of the manuscript; all scientific content was written and verified by the authors.Conflicts of interest
There are no conflicts to declare.Data availability
Data supporting the findings of this study, including IR and Raman spectra, are available from the Enlighten: Research Data Repository, University of Glasgow, at DOI: http://dx.doi.org/10.5525/gla.researchdata.2064. Custom Python57–59 scripts60 used for Bayesian inference, data analysis, DFT spectra visualisation and figure generation of this study are archived on Zenodo at DOI: https://doi.org/10.5281/zenodo.17513057. The source code is also available from the GitHub repositories https://github.com/MichaelNicolaou/Bayesian_IR_peak_assignments. The DFT calculations performed are openly available in the ioChem-BD (https://iochem-bd.bsc.es/browse/)69 database. The benchmark, scaling factor, conformer and frequency calculations performed throughout the current study can be found under the ioChem-BD handle: DOI: https://doi.org/10.19061/iochem-bd-6-283. All datasets and code are released under a CC-BY-4.0 licence.Supplementary information (SI): the methods used, data collected and processed and information used in the current study. See DOI: https://doi.org/10.1039/d5dd00453e.
Acknowledgements
The authors acknowledge past and present members of the University of Glasgow (UofG) LVN-group for helpful comments during the preparation of the manuscript. Financial support for this work was provided by University of Glasgow and the Engineering and Physical Sciences Research Council Grants (EP/T517896/1, EP/W524359/1, Project reference: 2749007), Royal Society of Chemistry RSC-Hardship Grant (COVID-19). We also thank the University of Glasgow (UofG) Early Career Development Programme (ECDP) 2021, the UofG Reinvigorating Research Scheme 2022, and the School of Chemistry for long-lasting support. Computations were performed on the UofG School of Chemistry's “Topcat” High-Performance Computer (HPC) cluster, we thank Mr Stuart Mackay for helping with the submission and management of the calculations on the HPC. We thank Mr Marcox Pun from the UofG School of Chemistry's teaching staff and Dr Diana Castro from the Cronin Group for assistance with IR vibrational measurements. Finally, we thank Dr Clare Rumsey, Mr Mohaned Hassan and Mrs Hannah Nevill from Omanos Analytics Ltd (https://www.omanosanalytics.org/) for providing a training opportunity in data analysis with Bayesian statistics through an industrial placement PhD opportunity. Images of leaf and computer used in TOC graphical abstract taken from flaticon.com (http://flaticon.com) (credit to Freepik (https://www.freepik.com/)).Notes and references
- F. Liaqat, et al., Extraction, purification, and applications of vanillin: A review of recent advances and challenges, Ind. Crops Prod., 2023, 204, 117372 CrossRef CAS.
- A. Rahimi, A. Ulbrich, J. J. Coon and S. S. Stahl, Formic-acid-induced depolymerization of oxidized lignin to aromatics, Nature, 2014, 515, 249–252 CrossRef CAS.
- J. G. Linger, D. R. Vardon, M. T. Guarnieri, E. A. Karp, M. T. Hunsinger, M. A. Franden, C. W. Johnson, G. Chupka, T. J. Strathmann, P. T. Pienkos, G. T. Beckham and G. W. Herring, Lignin valorization through integrated biological funneling, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12013–12018 CrossRef CAS.
- C. T. Palumbo, J. Xu, H. Zhang, M. Yan, Y. Li, P. Zhou, K. C. Swanson, H. Guo, D. Mei, A. R. Motagamwala, J. A. Dumesic and G. W. Huber, Catalytic carbon-carbon bond cleavage in lignin via manganese-zirconium-mediated autoxidation, Nat. Commun., 2024, 15, 862 CrossRef CAS PubMed.
- M. Fache, et al., Vanillin Production from Lignin and Its Use as a Renewable Chemical, ACS Sustain. Chem. Eng., 2016, 4, 35–46 CrossRef CAS.
- T. Voitl and P. R. von Rohr, Oxidation of lignin using aqueous polyoxometalates in the presence of alcohols, ChemSusChem, 2008, 1, 763–769 CrossRef CAS PubMed.
- H. Werhan, et al., Acidic oxidation of kraft lignin into aromatic monomers catalyzed by transition metal salts, Holzforschung, 2011, 65, 703–709 CAS.
- M. B. Hocking, Vanillin: Synthetic Flavoring from Spent Sulfite Liquor, J. Chem. Educ., 1997, 74, 1055–1059 CrossRef CAS.
- N. G. Lewis, A 20th century roller coaster ride: a short account of lignification, Curr. Opin. Plant Biol., 1999, 2, 153–162 CrossRef CAS.
- C. Crestini, et al., On the structure of softwood kraft lignin, Green Chem., 2017, 19, 4104–4121 RSC.
- Natural Flavours, Fragrances, and Perfumes: Chemistry, Production, and Sensory Approach, ed. G. Sreeraj, N. Pulikkal Sukumaran, J. Jacob, S. Thomas and S. Soni, Wiley-VCH, Weinheim, 2023 Search PubMed.
- A. K. Sinha, et al., A comprehensive review on vanilla flavor: Extraction, isolation and quantification of vanillin and others constituents, Int. J. Food Sci. Nutr., 2008, 59, 299–326 CrossRef CAS PubMed.
- R. Sellamuthu, in Encyclopedia of Toxicology, Elsevier, 3rd edn, 2014, pp. 539–541 Search PubMed.
- A. Jenkins and N. K. Erraguntla, in Encyclopedia of Toxicology, Elsevier, 3rd edn, 2014, pp. 912–914 Search PubMed.
- L. Zhang, G. Henriksson and G. Gellerstedt, The formation of β-β structures in lignin biosynthesis - are there two different pathways?, Org. Biomol. Chem., 2003, 1, 3621–3624 RSC.
- R. W. Houston and N. H. Abdoulmoumine, Investigation of the thermal deconstruction of β-β′ and 4-O-5 linkages in lignin model oligomers by density functional theory (DFT), RSC Adv., 2023, 13, 6181–6190 Search PubMed.
- C. G. Boeriu, et al., Characterisation of structure-dependent functional properties of lignin with infrared spectroscopy, Ind. Crops Prod., 2004, 20, 205–218 CrossRef CAS.
- I. W. Cordova, et al., Using Molecular Conformers in COSMO-RS to Predict Drug Solubility in Mixed Solvents, Ind. Eng. Chem. Res., 2024, 63, 9565–9575 CrossRef CAS.
- S. M. Rogers, A. Thetford, N. Dimitratos, A. Villa and P. P. Wells, et al., Tandem Site- and Size-Controlled Pd Nanoparticles for the Directed Hydrogenation of Furfural, ACS Catal., 2017, 7, 2266–2274 CrossRef CAS.
- W. Zhang, et al., A DFT study of the aldol condensation reaction in the processing of ethanol to 1,3-butadiene on a MgO/SiO2 surface, New J. Chem., 2022, 46, 559–571 Search PubMed.
- L. Kabalan, I. Kowalec, R. C. A. Catlow and A. J. Logsdail, A computational study of the properties of low- and high-index Pd, Cu and Zn surfaces, Phys. Chem. Chem. Phys., 2021, 23, 14649–14661 Search PubMed.
- M. Bursch, et al., Best Practice DFT Protocols for Basic Molecular Computational Chemistry, Angew. Chem., Int. Ed., 2022, e202205735 CAS.
- H. Kruse, et al., Why the standard B3LYP/6-31G* model chemistry should not be used in DFT calculations of molecular thermochemistry: Understanding and correcting the problem, J. Org. Chem., 2012, 77, 10824–10834 Search PubMed.
- J. Guan and Y. Lu, et al., Computational infrared and Raman spectra by hybrid QM/MM techniques: A study on molecular and catalytic material systems, Philos. Trans. R. Soc., A, 2023, 381, 20220234 CrossRef CAS.
- J. M. Parrilla-Gutiérrez, et al., Electron density-based GPT for optimization and suggestion of host–guest binders, Nat. Comput. Sci., 2024, 4, 200–209 CrossRef.
- I. M. Alecu, et al., Computational thermochemistry: Scale factor databases and scale factors for vibrational frequencies obtained from electronic model chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- J. W. Ochterski, Vibrational Analysis in Gaussian, 1999 Search PubMed.
- S. H. M. Mehr, Digital discovery and the new experimental frontier, Digital Discovery, 2025, 4, 892–895 RSC.
- F. Teixeira and M. N. D. S. Cordeiro, Improving Vibrational Mode Interpretation Using Bayesian Regression, J. Chem. Theory Comput., 2019, 15, 456–470 Search PubMed.
- I. Pupeza, et al., Field-resolved infrared spectroscopy of biological systems, Nature, 2020, 577, 52–59 CrossRef CAS PubMed.
- M. Frisch, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. Dennington et al., Gaussview 05 Search PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A:At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 8822–8824 Search PubMed.
- J. P. Perdew, et al., Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- W. Hoe, et al., Assessment of a new local exchange functional OPTX, Chem. Phys. Lett., 2001, 341, 319–328 CrossRef CAS.
- N. C. Handy and A. J. Cohen, Left-right correlation energy, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- P. J. Stephens, et al., Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11624–11627 CrossRef.
- C. Lee, et al., Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. Da Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Phys. Chem., 2008, 128, 084106 Search PubMed.
- J. Da Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- E. Brémond and C. Adamo, Seeking for parameter-free double-hybrid functionals: The PBE0-DH model, J. Chem. Phys., 2011, 135, 24106 CrossRef PubMed.
- M. J. Frisch, et al., A direct MP2 gradient method, Chem. Phys. Lett., 1990, 166, 275–280 Search PubMed.
- M. J. Frisch, et al., Semi-direct algorithms for the MP2 energy and gradient, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- M. Head-Gordon, et al., MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- S. Saebo and J. Almlof, Avoiding the integral storage bottleneck in LCAO calculations of electron correlation, Chem. Phys. Lett., 1989, 154, 83–89 Search PubMed.
- M. Head-Gordon and T. Head-Gordon, Analytic MP2 frequencies without fifth-order storage. Theory and application to bifurcated hydrogen bonds in the water hexamer, Chem. Phys. Lett., 1994, 220, 122–128 Search PubMed.
- R. Krishnan, et al., Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, et al., Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301 Search PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- É. Brémond, et al., Benchmarking Density Functionals on Structural Parameters of Small-/Medium-Sized Organic Molecules, J. Chem. Theory Comput., 2016, 12, 459–465 Search PubMed.
- Y. Zhao and D. G. Truhlar, Density functionals with broad applicability in chemistry, Acc. Chem. Res., 2008, 41, 157–167 Search PubMed.
- A. K. Rappé, et al., UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 Search PubMed.
- G. Van Rossum, Python 3 Reference Manual, 2009, preprint, 3.9.13 Search PubMed.
- C. R. Harris, et al., Array programming with NumPy, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- The pandas development team, Pandas, 2020, Zenodo, version 1.4.4 Search PubMed.
- M. Nicolaou, https://github.com/MichaelNicolaou/Vanillin-Data-Analysis.
- W. E. Wallace, Infrared Spectra, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom, and W. G. Mallard, National Institute of Standards and Technology, 20899, Gaithersburg, MD, 2005 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge structural database, Acta Crystallogr., 2016, B72, 171–179 Search PubMed.
- R. Velavan, et al., Organic compounds: Vanillin-I, Acta Crystallogr., 1995, C51, 1131–1133 CAS.
- S. Kanchanakungwankul et al., Database of Frequency Scale Factors for Electronic Model Chemistries – Version 5, 2021 Search PubMed.
- K. Biernacki, et al., Physicochemical Properties of Choline Chloride-Based Deep Eutectic Solvents with Polyols: An Experimental and Theoretical Investigation, ACS Sustain. Chem. Eng., 2020, 8, 18712–18728 CrossRef CAS.
- P. Larkin, Infrared and Raman Spectroscopy: Principles and Spectral Interpretation, Elsevier, 2011 Search PubMed.
- C. J. Pouchert Pouchert and Aldrich chemical company, The Aldrich library of FT-IR spectra, 1985 Search PubMed.
- L. J. Bellamy, The Infrared Spectra of Complex Molecules, 3rd edn, Chapman and Hall, London, 1980 Search PubMed.
- M. Álvarez-Moreno, et al., Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform, J. Chem. Inf. Model., 2015, 55, 95–103 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |




