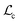Open Access Article
Open Access ArticleHierarchical attention graph learning with LLM enhancement for molecular solubility prediction
Yangxin
Fan
 a,
Yinghui
Wu
a,
Yinghui
Wu
 a,
Roger H.
French
a,
Roger H.
French
 b,
Danny
Perez
b,
Danny
Perez
 c,
Michael G.
Taylor
c,
Michael G.
Taylor
 c and
Ping
Yang
c and
Ping
Yang
 *c
*c
aDepartment of Computer Science, Case Western Reserve University, Cleveland, OH, USA. E-mail: yxf451@case.edu; yxw1650@case.edu
bDepartment of Material Science, Case Western Reserve University, Cleveland, OH, USA. E-mail: rxf131@case.edu
cTheoretical Division, Los Alamos National Laboratory, Los Alamos, NM, USA. E-mail: danny_perez@lanl.gov; mgt16@lanl.gov; pyang@lanl.gov
First published on 15th December 2025
Abstract
Solubility quantifies the concentration of a molecule that can dissolve in a given solvent. Accurate prediction of solubility is essential for optimizing drug efficacy, improving chemical and separation processes, and waste management, among many other industrial and research applications. Predicting solubility from first principles remains a complex and computationally intensive physicochemical challenge. Recent successes of graph neural networks for molecular learning tasks inspire us to develop HASolGNN, a hierarchical–attention graph neural network for solubility prediction. (1) HASolGNN adopts a three-level hierarchical attention framework to leverage atom-bond, molecular, and interaction-graph level features. This allows a more comprehensive modeling of both intra-molecular and inter-molecular interactions for solute–solvent dissolution as a complex system. (2) To mitigate the impact of small amounts of annotated data, we also investigate the role of Large Language Models (LLMs), and introduce HASolGNN-LLMs, an LLM-enhanced predictive framework that leverages LLMs to infer annotated features and embeddings to improve representation learning. Our experiments verified that (1) HASolGNN outperforms the state-of-the-art methods in solubility prediction; and (2) HASolGNN-LLMs effectively exploits LLMs to enhance sparsely annotated data and further improves overall accuracy.
1 Introduction
Solubility is broadly relevant to many applications, including nuclear waste separation,1,2 environmental pollution control,3 development of advanced materials in the semi-conductor industry,4,5 autonomous robotics synthesis,6,7 crystallization,8 and protein ligand bonding in the biomedical field.9,10 In particular, aqueous solubility refers to the solubility of a solute in water. It plays an essential role in pharmaceutical science,11–13 since (1) accurate prediction of solubility is critical for selecting promising drug candidates during the screening process, and (2) all drugs in the body exert their therapeutic effects in the form of aqueous solutions, which means lower solubility diminishes both their efficacy and bioavailability. Therefore, high-precision computational methods for solubility prediction can substantially decrease the experimental costs and time associated with drug development14 while enabling chemists to develop formulations that maximize drug efficacy and improve patient outcomes.
Fig. 1 shows a solubility prediction pipeline, involving four components: solubility dataset curation, description generation, model training, and solubility prediction. Solubility data typically refer to the SMILES15 of solute and solvent pairs, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S (log-scale solubility), as well as the molecular features such as melting point (MP), molecular weight (MW), and volume. The pipeline then converts the SMILES into (1) molecular graphs and (2) molecular fingerprints (physiochemical features). Molecular graphs will be used to train graph neural networks (GNNs) and their variants (e.g., ref. 16–19), while molecular fingerprints are typically used by traditional machine learning and domain methods (e.g., ref. 20–23). Next, the models predict solubility for critical applications in areas such as drug discovery.
S (log-scale solubility), as well as the molecular features such as melting point (MP), molecular weight (MW), and volume. The pipeline then converts the SMILES into (1) molecular graphs and (2) molecular fingerprints (physiochemical features). Molecular graphs will be used to train graph neural networks (GNNs) and their variants (e.g., ref. 16–19), while molecular fingerprints are typically used by traditional machine learning and domain methods (e.g., ref. 20–23). Next, the models predict solubility for critical applications in areas such as drug discovery.
 | ||
| Fig. 1 Solubility prediction pipeline. Solubility prediction models are categorized into three major types, with critical applications spanning fields such as material separation and drug discovery. | ||
1.1 State-of-the-art
Solubility prediction has been a long-standing challenge. A host of methods have been developed to predict the solubility of molecular systems. Recent approaches fall into three categories: (1) domain-specific methods, rooted in principles of quantum mechanics and thermodynamics; (2) traditional ML-based methods, which leverage established regression models and ensemble learning to predict solubility; and more recently, (3) graph neural network (GNN)-based methods, which utilize molecular graphs to model atoms and bonds and train GNNs as regression or classifiers.(1) Domain-specific methods adhere to the quantitative structure–property relationship (QSPR) framework.24 They regress solubility against a selected set of molecular descriptors, capturing the structural and physicochemical properties of compounds. Depending on the underlying theoretical foundation, such methods employ a range of mathematical models, including differential and partial differential equations, to predict solubility.22,23,25
(2) Among ML-based methods, boosting methods such as XGBoost20 and random forest21 have been widely applied. Other ML models include multi-layer perceptron (MLP)26 and artificial neural networks (ANNs).27,28 These methods take molecular fingerprints as input features, leveraging the encoded molecular-level structural information to predict solubility.
(3) Several GNN-based methods were developed, which exploit graph convolutional networks (GCNs),16,17 gated graph neural networks (GGNNs),29,30 node-level attention-based graph attention networks (GATs),31,32 and molecular representation learning integrating both node- and graph-level attention mechanisms (AttentiveFP).18,33 Among these methods, AttentiveFP has demonstrated superior performance, establishing itself as the current leading approach in GNN-based solubility prediction.18
Apart from the methods specifically developed for solubility prediction, recent studies have extended graph neural networks to related molecular property prediction tasks. Leenhouts et al.34 introduced SolProp-mix, a GNN-based framework for predicting solvation free energy and enthalpy in solvent mixtures. Building on previous D-MPNN models for pure solvents, they proposed a permutation-invariant pooling function (MolPool) that enables learning across mixtures of arbitrary composition. Similarly, Jung et al.35 developed a GNN framework to predict solubility in multicomponent solvent systems. They compared two GNN architectures: a concatenation model versus a subgraph model, with the latter showing higher accuracy by better capturing solute–solvent interactions. They incorporated a teacher–student semi-supervised distillation (SSD) approach to expand chemical coverage and improve prediction robustness.
1.2 Challenges & opportunities
While the aforementioned approaches have been applied for solubility prediction, several data challenges, and hence opportunities for improvement, remain.(1) Rich features, “small” annotated data. Most methods fit models on molecular fingerprints alone. Sequential encoding often overlooks high-value features at the atom and bond (“edges” between atoms), and topological features at the molecular level. On the other hand, such features may be scarce in small and heterogeneous sources, among which few are annotated or labeled.
(2) Inter-molecular interaction: solubility is determined by a dynamic interaction process involving solute and solvent pairs. Existing GNN-based methods often model the solubility with atom- and bond-level representations of the solute alone, but lack the necessary expressiveness to explicitly and holistically characterize the dynamic interactions of solute–solvent pairs, and hence often hardly generalize for accurate solubility analysis.
(3) Existing domain-specific methods are often constrained by domain hypotheses and models, mostly leading to case-by-case analysis. Most methods are specialized for aqueous solubility or limited to fixed groups of solvents. Hence existing methods are often hard to be generalized for solubility prediction.
In response, we advocate the development of a solubility predictive framework as a “general recipe” to be broadly applied across diverse solute–solvent systems. Such a framework should be able to (a) best harvest a “hierarchy” of features from atom-, bond-, and molecular-level features, as well as environmental and other external features; (b) characterize inter-molecular interaction for more comprehensive and accurate modeling of solubility; and (c) easily integrate, annotate and align heterogeneous features with few or no annotated data.
1.3 Contribution
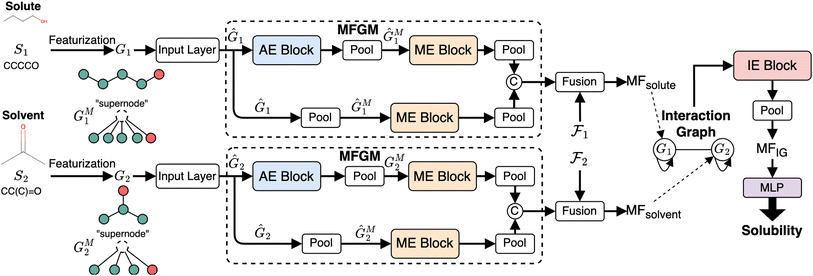
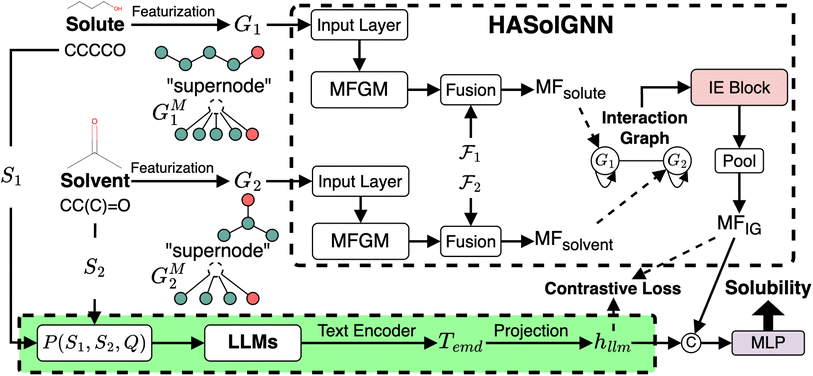
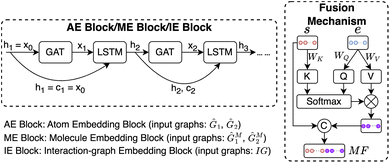
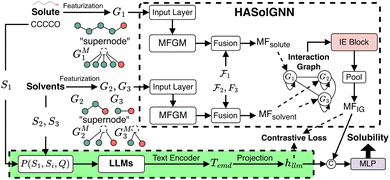
To address these challenges, we propose HASolGNN, a physics-informed graph model for solvent analysis.(1) We propose HASolGNN, an expressive framework that can capture hierarchical, multi-level interactions and patterns among atom, bond, and (inter- and intra-) molecular features. HASolGNN enables solubility prediction across a wide range of solute–solvent pairs, irrespective of solvent types. HASolGNN achieves this through the integration of hierarchical attention mechanisms across three key components: the atom embedding (AE) block, the molecular embedding (ME) block, and the interaction-graph embedding (IE) block. Experimental results demonstrate that HASolGNN significantly outperforms the state-of-the-art graph neural network methods, establishing new benchmarks in performance.
(2) We further propose HASolGNN-LLMs that integrates large-language models (LLMs) as a modular component, leveraging contrastive learning for fusion with HASolGNN to address the “small dataset” challenges frequently encountered by the scientific community. Our experiments show that HASolGNN-LLMs yields substantial improvements in solubility prediction under such data-scarce conditions, offering a potential solution to this common limitation.
(3) We conduct a new comprehensive evaluation of the performance of diverse graph neural network variants on three extensive and representative public solubility datasets, benchmarking our method's performance against the state-of-the-art methods. Our efforts offer valuable insights into the use of GNNs for solubility prediction that benefit both the chemistry and computer science communities.
We summarize other related work below.
1.4 Graph learning for system-level regression
Graph Neural Networks (GNNs)36 have been extensively studied for general graph analysis tasks. A GNN may exploit spectral-based, attention-based, and spatial-based convolutions to manipulate node features, edge features, and graph-level representations. Notable variants include graph convolutional networks (GCNs),37 GraphSAGE,38 graph attention networks (GATs),39 and graph isomorphic networks (GINs).40 While GNNs are widely adopted for node classification or link prediction, the use of GNNs for system modeling with multiple participating molecules has been much less explored. As aforementioned, existing GNN-based methods, while being adaptable for graph-based molecular property prediction, rely on graph-level pooling strategies to produce numeric predictions for solubility. Therefore, these approaches overlook the potentially complex interactions among molecules, as they remain constrained to explicitly model the interactions among molecules in a dynamic system.1.5 Graph learning for molecular property prediction
Recent effort has applied graph learning for molecular property prediction. Recurrent graph neural networks (RGNNs)41–45 were among the first GNNs utilized for molecular property prediction. RGNNs iteratively apply shared weight matrices, enabling the model to capture dependencies over multiple iterations. Conv-GNNs46–50 introduce iteration-specific weights, enhancing flexibility and expressiveness. Specifically, spectral Conv-GNNs operate in the spectral domain using graph Laplacian transformations, while spatial Conv-GNNs directly aggregate features from neighboring nodes. Architectural innovations such as advance pooling strategies,51,52 skip-connections,53,54 and architecturally distinct GNNs55,56 can be integrated into GNNs in general to improve feature aggregation for molecular system modeling. We consider these as potential opportunities to improve our methods in the future.2 Methods
2.1 Preliminary
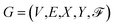 , where V is a node set, in which each node represents an atom; and E refers to the set of edges (bonds) between atoms. X is a node feature matrix, where each entry xu represents the node feature vector of node v ∈ V. The node feature vector includes atomic number, degree (number of bonds connected to the atom), formal charge, number of unpaired electrons (radical electrons), hybridization state (e.g., sp3, sp2, and sp), aromaticity, number of implicit hydrogen atoms, chirality and chirality type.19
, where V is a node set, in which each node represents an atom; and E refers to the set of edges (bonds) between atoms. X is a node feature matrix, where each entry xu represents the node feature vector of node v ∈ V. The node feature vector includes atomic number, degree (number of bonds connected to the atom), formal charge, number of unpaired electrons (radical electrons), hybridization state (e.g., sp3, sp2, and sp), aromaticity, number of implicit hydrogen atoms, chirality and chirality type.19
Similarly, Y is a bond feature matrix, where for each edge (bond) e ∈ E, Ye is a feature vector that contains bond type (single, double, triple, or aromatic), conjugation (binary, 1 if the bond is conjugated, 0 otherwise), ring (1 if the bond is part of a ring, 0 otherwise), and stereo (a one-hot encoded vector of length 4 to represent the stereochemistry of the bond).57
In addition, 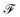 contains graph-level features, encompassing structural and functional characteristics (e.g. molecular weight and total charge), along with environmental factors such as temperature and pH, which influence the molecule's behavior.
contains graph-level features, encompassing structural and functional characteristics (e.g. molecular weight and total charge), along with environmental factors such as temperature and pH, which influence the molecule's behavior.
Solubility prediction is a special case of the above system-level regression problem when p = 2, specifying two interacting classes of molecules: the solute (G1) and the solvent (G2). Our goal is to train a GNN model M, which takes G1 and G2 as input to minimize solubility prediction errors 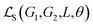 , where L and θ refer to ground-truths and the set of parameters in M, respectively.
, where L and θ refer to ground-truths and the set of parameters in M, respectively.
Conventional GNNs fall short of directly serving as a desired model M due to limited expressiveness. Ideally, (1) M should be able to exploit the rich features from different levels in G1 and G2, ranging from atom-level to molecule-level; (2) M should be expressive enough to describe the physical nature of solubility as an interactive system, which not only capture molecule-level embeddings, but also capture complex atomic and bond interactions, as well as the “non-local” interactions among the molecules. This allows explicit modeling of the molecular interactions between the solute and the solvent pairs, beyond what a straightforward application of GNNs can express.
2.2 HASolGNN framework
We next introduce the HASolGNN architecture and its key components including the input layer, atom embedding block, molecular embedding block, and interaction-graph embedding block.2.2.1.1 Featurization and input layer. HASolGNN converts the SMILES representations of solute S1 and solvent S2 into the featurized solute graph
 and solvent graph
and solvent graph 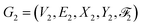 . The input layer standardizes them into Ĝ1 and Ĝ2 by combining their node and bond features;
. The input layer standardizes them into Ĝ1 and Ĝ2 by combining their node and bond features;
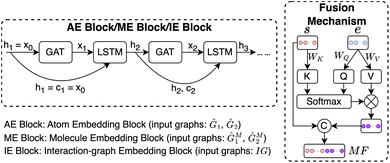
2.2.1.2 Molecular fingerprint generation module (MFGM). HASolGNN fits Ĝ1 and Ĝ2 into MFGMs. Each MFGM is composed of one Atom Embedding (AE) block and two Molecule Embedding (ME) blocks. The AE block processes G1 or G2, while the ME blocks take G1M or G2M as input. Here, G1M (resp. G2M) refines its original counterpart G1 (resp. G2) with a simple “star-structure”, each containing a centering “supernode” connected to all the atoms in G1 or G2. The embeddings produced by the AE block are fed into the first ME block. In contrast, the second ME block directly utilizes the initial node and bond features of the molecular graphs;
2.2.1.3 Embedding fusion. HASolGNN leverages a novel fusion mechanism to combine the embeddings representing molecule level representations of the solute and solvent from the two MFGMs with graph-level features
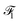 and
and 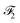 to generate the molecular fingerprints MFsolute for the solute and MFsolvent for the solvent;
to generate the molecular fingerprints MFsolute for the solute and MFsolvent for the solvent;
2.2.1.4 Interaction graph. HASolGNN constructs the interaction graph comprising two nodes: G1, representing the solute with MFsolute as its node features, and G2, representing the solvent with MFsolvent as its node features. The integration-graph embedding (IE) block processes the interaction graph to produce the system-level fingerprint MFIG, which is passed to the output layer to predict solubility (Fig. 3).
We next detail the key components of HASolGNN.
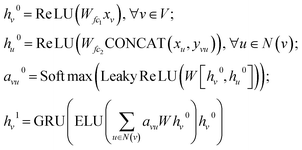 | (1) |
| (ht+1,ct+1) = LSTM(GAT(ht,AG),(ht,ct)), t∈[1,k] | (2) |
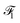 and
and 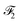 that capture contextual information such as environmental factors (EFs) with the embeddings from the output of the MFGM, which convey structural relationships. Our fusion mechanism, illustrated in Fig. 5, comprises two steps: (1) cross-attention and (2) concatenation.
that capture contextual information such as environmental factors (EFs) with the embeddings from the output of the MFGM, which convey structural relationships. Our fusion mechanism, illustrated in Fig. 5, comprises two steps: (1) cross-attention and (2) concatenation.
The cross-attention module consists of learnable parameters: query WQ, key WK, and value WV. These are used to compute the cross-attention scores between the structural GNN embeddings and the EFs. Specifically, it calculates the cross-attention score between the molecule-level structural representation s obtained from the MFGM and the environmental factors vector e defined in Sec. 2, where s serves as the key, representing the referenced information. The resulting attention weight α transforms e into e′, which will be then concatenated with s to derive the molecular fingerpints MFsolute for the solute and MFsolvent for the solvent. Formally, we represent the fusion mechanism as follows:
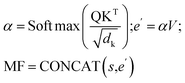 | (3) |
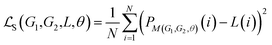 | (4) |
2.3 LLM-enhanced HASolGNN
To mitigate the challenge posed by small datasets, we present HASolGNN-LLMs, an LLM-enhanced variant of HASolGNN. It leverages LLMs as (1) a feature enricher: expanding the feature space and enhancing molecular representations to maximize the utility of available context for solubility prediction from unstructured textual input such as lab, instrument or literature; and (2) a pseudo-annotator: providing estimations of solubility that are guided by proper prompting and conform to the context.2.3.1.1 Generating textual descriptions. HASolGNN-LLMs incorporates a customizable library of LLMs, including, for example, GPT-4 (ref. 58) and Llama 3 (ref. 59), to generate textual descriptions of solubility estimations based on their structural and chemical properties of both solute and solvent molecules. Specifically, given a solute–solvent pair, we incorporate the SMILES strings of the solute S1 and solvent S2 to query LLMs with the following template P(S1, S2, Q)†:
Here Q refers to user-specified, task-specific domain knowledge such as knowledge about the chemical structure.10,61 In practice, Q consists of curated documents that outline key factors influencing solubility, include illustrative examples and contain answers from relevant literature. This ensures that the generated descriptions are grounded in established chemical knowledge.
2.3.1.2 Deriving the embedding hllm. Upon the generation of textual descriptions by LLMs, HASolGNN-LLMs utilizes a text encoder such as SciBERT62 and PubmedBERT63 to transform chemical textual descriptions into global-level text embeddings Temd by extracting the [CLS]62 token embedding. Given the high dimensionality of Temd, HASolGNN-LLMs employs a multi-layer perceptron (MLP) to project Temd into a low-dimensionality latent space, hllm, aligning its dimensionality with that of the MFIG to ensure compatibility. In the case of SciBERT, we specify the process as follows:
| hllm = MLP(SciBERT(LLMs(P(S1,S2,Q)))) | (5) |
2.3.1.3 Embedding enhancement. To integrate the embeddings from HASolGNN with the LLM module effectively, HASolGNN-LLMs learns a joint representation by combining the system-level HASolGNN embeddings MFIG with the textual embeddings hllm derived from the LLM module. We employ an unsupervised contrastive loss, Lc (please refer to Eqn. (6)), to minimize the distance between MFIG and hllm for the same solute–solvent pair. Besides, we incorporate a negative sampling strategy64 to construct negative solute–solvent pairs (τ, τ′), where τ = (S1, S2) and
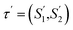 such that τ ≠ τ′. For these negative pairs, Lc maximizes the distance (minimizes the similarity) between MFIG of τ and hllm of τ′, ensuring proper separation between positive and negative pairs. This allows HASolGNN-LLMs to differentiate between positive and negative pairs, improving its predictive and representational capabilities.
such that τ ≠ τ′. For these negative pairs, Lc maximizes the distance (minimizes the similarity) between MFIG of τ and hllm of τ′, ensuring proper separation between positive and negative pairs. This allows HASolGNN-LLMs to differentiate between positive and negative pairs, improving its predictive and representational capabilities.
2.3.1.4 Loss Function. The loss function of HASolGNN-LLMs
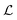 comprises (1) a supervised
comprises (1) a supervised 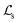 that captures the solubility prediction errors from HASolGNN and (2) an unsupervised contrastive loss
that captures the solubility prediction errors from HASolGNN and (2) an unsupervised contrastive loss 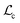 to ensure the proper enhancement by combing the system-level MFIG from HASolGNN and the projected hllm derived from the LLM module. We formulate
to ensure the proper enhancement by combing the system-level MFIG from HASolGNN and the projected hllm derived from the LLM module. We formulate 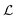 as follows:
as follows: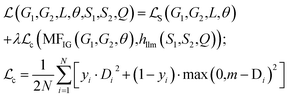 | (6) |
Here, Di is the distance equal to one minus the similarity between the i-th MFIG and i-th hllm, m is a margin value, λ denotes the balancing factor between 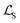 and
and 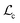 , and yi indicates whether the pair is positive (yi = 1) or negative (yi = 0).
, and yi indicates whether the pair is positive (yi = 1) or negative (yi = 0).
 in solvent
in solvent  . Fig. 8 provides the corresponding response from GPT -4 for the above prompt. We highlight the key words in different colors and their corresponding responses in same color.
. Fig. 8 provides the corresponding response from GPT -4 for the above prompt. We highlight the key words in different colors and their corresponding responses in same color.
How LLMs help the small-data challenge? The LLM component in HASolGNN-LLMs is designed to address the small-data limitation by infusing domain knowledge and generating complementary representations that go beyond what can be learned from limited labeled samples. Specifically, LLMs act as both a feature enricher and a pseudo-annotator. (1) As a feature enricher, the LLM leverages its pretrained knowledge of chemical language and concepts to produce detailed, structure-aware textual descriptions of solute–solvent pairs, which are then encoded into dense embeddings. These embeddings enrich the molecular feature space with contextual chemical information that may not be directly observable from graph structures alone. (2) As a pseudo-annotator, the LLM provides approximate solubility estimations through guided prompting, effectively augmenting supervision in low-data regimes. By aligning these LLM-derived embeddings with the graph-based representations using a contrastive loss, HASolGNN-LLMs learns to transfer chemically relevant patterns from the LLM's large-scale pretraining to the solubility prediction task, thereby improving generalization and robustness despite the small dataset size.
 | ||
| Fig. 8 Response from GPT-4 for the prompt in Fig. 6. | ||
3 Results and discussion
We experimentally evaluate the performance of HASolGNN, comparing it with ten GNN baseline models. Moreover, we evaluate the performance of HASolGNN-LLMs to understand whether or how LLMs may be exploited. Our source code, datasets, and a full version of the paper are made available ‡.3.1 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S units on average across the three datasets, reflecting the experimental uncertainty inherent in solubility measurements. HASolGNN's test error (MAE ≈ 0.73 log
S units on average across the three datasets, reflecting the experimental uncertainty inherent in solubility measurements. HASolGNN's test error (MAE ≈ 0.73 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S for Exp-DB and ≈ 0.75 log
S for Exp-DB and ≈ 0.75 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S for BigSolDB) is consistent with statistical limit, suggesting that the performance is noise-limited rather than model-limited, indicating that further improvements are constrained by data noise rather than by the expressiveness or capacity of HASolGNN.
S for BigSolDB) is consistent with statistical limit, suggesting that the performance is noise-limited rather than model-limited, indicating that further improvements are constrained by data noise rather than by the expressiveness or capacity of HASolGNN.
(1) Exp-DB:65 this dataset contains 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 experimentally measured solubility values at temperatures of 298 K (±2 K). Each value corresponds to a unique solute–solvent pair. It is the largest dataset in terms of unique pair counts. (2) MolMerger:66 it comprises 6975 unique solute–solvent pairs, each with a measured solubility value at temperatures near 273 K. The MolMerger dataset integrates data from three distinct sources: 4964 values from BigSolDB,15 1093 values from BNNLabs Solubility,67 and 972 values from ESOL.68 (3) BigSolDB:15 the largest solubility dataset in terms of sample sizes. It includes 54
637 experimentally measured solubility values at temperatures of 298 K (±2 K). Each value corresponds to a unique solute–solvent pair. It is the largest dataset in terms of unique pair counts. (2) MolMerger:66 it comprises 6975 unique solute–solvent pairs, each with a measured solubility value at temperatures near 273 K. The MolMerger dataset integrates data from three distinct sources: 4964 values from BigSolDB,15 1093 values from BNNLabs Solubility,67 and 972 values from ESOL.68 (3) BigSolDB:15 the largest solubility dataset in terms of sample sizes. It includes 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 273 individual solubility values for 830 unique molecules and 138 distinct solvents, measured over a temperature range of 243.15 to 403.15 K at atmospheric pressure. Despite its size, BigSolDB contains fewer unique solute–solvent pairs compared to the other two datasets, with only 4964 unique pairs.
273 individual solubility values for 830 unique molecules and 138 distinct solvents, measured over a temperature range of 243.15 to 403.15 K at atmospheric pressure. Despite its size, BigSolDB contains fewer unique solute–solvent pairs compared to the other two datasets, with only 4964 unique pairs.
For Exp-DB and MolMerger, no environmental features are reported. For BigSolDB, the only reported environmental feature is temperature.
We ensure that data splitting for all datasets is performed strictly based on unique solute–solvent pairs. In particular, BigSolDB contains multiple solubility measurements for identical solute–solvent pairs across varying temperatures. To prevent data leakage, we group all entries sharing the same solute–solvent pair as a single unit before performing the split. This guarantees that all temperature-dependent measurements of a given pair remain entirely within one subset (training, validation, or testing). For Exp-DB and MolMerger, we partitioned each dataset based on unique solute–solvent pairs, assigning 60% for training, 20% for validation, and 20% for testing to ensure fair and consistent performance evaluation. For BigSolDB, because solute–solvent pairs exhibit distinct temperature ranges, we adopted a slightly adjusted split of 62.2% for training, 18.5% for validation, and 19.3% for testing to maintain balanced coverage across temperature conditions.
We trained all baselines with consistent settings (data splits, hyperparameter tuning, etc.) for fair comparisons. Only AttentiveFP adopted a two-level (atom and molecular) representation. For the rest, we adopted, as a routine, the node-level features (SMILES).
3.2 Results and discussion
| Methods | Exp-DB | MolMerger | BigSolDB |
|---|---|---|---|
| GCN16 | 0.9911 | 0.9450 | 1.2926 |
| GAT31 | 0.9538 | 0.8856 | 1.3035 |
| GraphSAGE69 | 0.9971 | 0.9446 | 1.2851 |
| GIN18 | 0.9519 | 0.9520 | 1.2691 |
| GatedGNN29 | 0.9191 | 0.8518 | 1.2592 |
| ResGatedGNN29 | 0.9606 | 0.8754 | 1.2830 |
| CGCN70 | 1.0184 | 0.9758 | 1.3534 |
| GraphTransformer71 | 0.9452 | 0.9006 | 1.2737 |
| MFGNN30 | 0.9542 | 0.8425 | 1.2695 |
| AttentiveFP33 | 0.8688 | 0.8036 | 1.0521 |
| XGBoost72 | 1.0293 | 0.9847 | 1.3858 |
| MPFP73 | 0.9635 | 0.8702 | 1.2781 |
| HASolGNN (ours) | 0.7315 | 0.7124 | 0.7408 |
| Improvements over AttentiveFP | 15.81% | 11.35% | 29.59% |
 | ||
| Fig. 9 Visualization of solubility prediction errors of HASolGNN vs. AttentiveFP on Exp-DB (MAE & R-squared). | ||
How LLMs improve performance on “small” datasets? To study how the LLM module potentially improves the performance over the small dataset, we randomly sample subsets with sample size ranging from 116 to 1160, corresponding to 1% to 10% the size of the Exp-DB dataset. For each sample size, we randomly sample 50 different sample sets and calculate the average and standard deviation from them, as shown in Fig. 10. We follow the same training, validation, and test split proportions described in Sec. 3.1. We observe the followings from Fig. 10: (1) HASolGNN-LLMs consistently achieves lower test MAE (higher test R-squared) compared to HASolGNN as the sample size grows from 1% to 10% of Exp-DB; (2) the error reduction (improvements in R-squared) achieved by HASolGNN-LLMs gradually reduces as the sample size increases; and (3) for both HASolGNN and HASolGNN-LLMs, the errors decrease (R-squared increases) as the sample size grows. The shrinking reduction of errors and improvements of R-squared by HASolGNN-LLMs can be attributed to the higher data availability and quality as more samples are included, which enhances the effectiveness of supervised graph learning. Notably, at the 10% sampling rate, the performance gain (reduction in MAE) achieved by HASolGNN-LLMs is only 0.0114, suggesting that the benefit of the LLM module gradually diminishes. Nonetheless, performance at small data sizes is extremely valuable given the significant cost of obtaining effective experimental data for new classes of systems (Fig. 11).
 | ||
| Fig. 11 Visualization of solubility prediction errors of HASolGNN vs. HASolGNN-LLMs on a small dataset (test set size = 62). | ||
We next investigate how incorporating the LLM module may help under the inductive learning setting on BigSolDB. This scenario presents challenges due to dataset sparsity, which arises from the limited amount of unique solute–solvent pairs in BigSolDB. Fig. 12 illustrates the performance of HASolGNN-LLMs and Attentive-LLM in predicting solubility of an out-of-sample test solute–solvent pair across varying temperatures. We observe that incorporating the LLM module to both AttentiveFP and HASolGNN can significantly improve the solubility prediction in the inductive setting.
As illustrated in Table 2, we observe the followings: (1) incorporating the IE Block into HASolGNN reduces the test MAE by an average of 17.16% across all three datasets compared to HASolGNN w/o. IE and an average of 8.34% compared to HASolGNN w/o. IE w. CA; (2) adding the ME block improves test MAE by an average of 10.24% across all datasets; (3) incorporating the AE block into HASolGNN has less impacts on prediction errors compared to IE and ME blocks, reducing the test MAE by 4.72%; and (4) replacing the sum pooling with average pooling increases the test MAE by 23.93% while substituting it with maximal pooling results in an 11.02% increase in test MAE. Our experiments have confirmed the effectiveness of the key components and justify the design choices including the IE block, ME block, AE block, and sum pooling. Together, these components contribute significantly to the improved solubility prediction achieved by HASolGNN.
| I: Interaction embedding (IE) | Exp-DB | MolMerger | BigSolDB |
|---|---|---|---|
| HASolGNN w. IE | 0.7315 | 0.7124 | 0.7408 |
| HASolGNN w/o. IE1 | 0.8394 | 0.8014 | 1.0219 |
| HASolGNN w/o. IE w. CA2 | 0.7928 | 0.7657 | 0.8263 |
| Improvements over1 | 12.86% | 11.11% | 27.51% |
| Improvements over2 | 7.73% | 6.96% | 10.34% |
| II: Molecular embedding (ME) | Exp-DB | MolMerger | BigSolDB |
|---|---|---|---|
| HASolGNN w. ME | 0.7315 | 0.7124 | 0.7408 |
| HASolGNN w/o. ME | 0.7560 | 0.8354 | 0.8491 |
| Improvements | 3.24% | 14.73% | 12.75% |
| III: Atom embedding (AE) | Exp-DB | MolMerger | BigSolDB |
|---|---|---|---|
| HASolGNN w. AE | 0.7315 | 0.7124 | 0.7408 |
| HASolGNN w/o. AE | 0.7610 | 0.7720 | 0.7601 |
| Improvements | 3.89% | 7.72% | 2.54% |
| IV: Different pooling | Exp-DB | MolMerger | BigSolDB |
|---|---|---|---|
| HASolGNN w. Average pooling | 0.9033 | 0.7865 | 1.0214 |
| HASolGNN w. Maximal pooling | 0.8570 | 0.7643 | 0.8045 |
| Improvements | 17.17% | 7.29% | 8.60% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, as detailed in Sec. 3.1. Fig. 14 visualizes the solubility prediction errors of HASolGNN compared to AttentiveFP on the completely unseen test dataset of MolMerger. This test presents the most challenging solubility prediction scenario where both solute and solvent graphs are unseen during the model training. The results demonstrate that HASolGNN predictions align more closely with the ideal fit (where predicted values exactly match actual values) in the most challenging case. Specifically, compared to AttentiveFP, HASolGNN (1) achieves a 9.93% lower test MAE and (2) reduces the number of predictions with absolute errors over two (outside the two green lines) by 35.32%.
2 ratio, as detailed in Sec. 3.1. Fig. 14 visualizes the solubility prediction errors of HASolGNN compared to AttentiveFP on the completely unseen test dataset of MolMerger. This test presents the most challenging solubility prediction scenario where both solute and solvent graphs are unseen during the model training. The results demonstrate that HASolGNN predictions align more closely with the ideal fit (where predicted values exactly match actual values) in the most challenging case. Specifically, compared to AttentiveFP, HASolGNN (1) achieves a 9.93% lower test MAE and (2) reduces the number of predictions with absolute errors over two (outside the two green lines) by 35.32%.
 | ||
| Fig. 14 Visualization of solubility prediction errors of HASolGNN vs. AttentiveFP on MolMerger (completely unseen setting, where both solute and solvent in the test set are unseen during training). | ||
We observe the larger prediction spread under the “new chemical classes” setting, as shown in Fig. 14, compared to the “pair-unseen” scenario illustrated in Fig. 9. This arises because (1) both solutes and solvents in the test set are unseen during training, forcing the model to extrapolate beyond its learned chemical domain; (2) unlike the “pair-unseen” scenario, where individual solute and solvent embeddings have been learned previously—this case lacks familiar structural or interaction patterns, leading to greater epistemic uncertainty and wider residual variance; (3) the unseen molecules also introduce distribution shifts in molecular features and interaction behaviors, further increasing prediction dispersion. Despite this challenge, HASolGNN maintains lower bias and error than AttentiveFP by leveraging its hierarchical solute–solvent encoding and interaction fusion, which transfer generalizable chemical relations across classes (Table 3).
| Dataset | Sample size | Unique solutes | Unique solvents | Test MAE (trained on1) | Test MAE (trained on2) |
|---|---|---|---|---|---|
| BigSolDB1 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 273 273 |
830 | 138 | 0.7408 | 0.8521 |
| BigSolDB v22 | 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944 944 |
1448 | 213 | 1.0932 | 0.9275 |
Case study: trained on BigSolDB and tested on BigSolDB v2. To evaluate the generalizability of HASolGNN, we conduct a case study by applying the HASolGNN model M, originally trained on BigSolDB,15 to BigSolDB v2,75 the most extensive and up-to-date solubility dataset for organic compounds. Compared to BigSolDB, BigSolDB v2 contains 91.52% more solubility measurements and 74.45% more unique compounds. On this substantially larger dataset, the pre-trained M attains a MAE of 1.10 on BigSolDB v2. This is slightly higher than the test MAE of 0.93 achieved by a HASolGNN model newly trained on BigSolDB v2, which is expected given the sheer size and diversity of BigSolDB v2, as well as broader temperature range that is outside the trained model.
4 Conclusion
We have proposed HASolGNN, a novel graph learning framework optimized to effectively exploit multi-level features, and both intra- and inter-molecular interactions for solubility analysis. HASolGNN outperforms all the baseline models, establishing a new benchmark in solubility prediction performance. Notably, HASolGNN outperforms the state-of-the-art AttentiveFP by further reducing MAE by 15.81%, 11.35%, and 29.59% on the Exp-DB, MolMerger, and BigSolDB dataset, respectively. The superior performance of HASolGNN benefits from its novel and more intricate design compared to previous methods, as verified by our ablation studies. Unlike previous GNN methods for solubility prediction that focus only on atom- and molecule-level interactions and often fail to capture the complex dynamics of solute–solvent interplay, HASolGNN introduces a novel hierarchical encoding framework that models the dissolution process across multiple scales. Attention mechanisms are integrated at each level, atom and bond level (AE block), molecular (ME block), and system-level interaction (IE block), enabling HASolGNN to jointly learn fine-grained structural details and higher order solute–solvent dynamics. Besides, our experiments also demonstrate the robustness of HASolGNN, showing that it generalizes well to new chemical classes and unseen solute–solvent pairs. On the MolMerger split with mutually exclusive solutes and solvents, HASolGNN reduces the amount of large-error (absolute error over two) predictions by 35.52% compared to AttentiveFP. When directly applied to BigSolDB v2 without retraining, the pre-trained model trained by BigSolDB maintains strong performance with a MAE of 1.10, close to 0.93 MAE achieved by retraining. Critically, we have shown that HASolGNN (MAE ≈ 0.75 in BigSolDB) approaches the same aleatoric data limit (MAE = 0.5–1 in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S) as identified in previous work, indicating that a further improvement in the accuracy of our models likely requires improved datasets.28
S) as identified in previous work, indicating that a further improvement in the accuracy of our models likely requires improved datasets.28
We have also introduced a new variant of HASolGNN with the enhancement of LLMs, HASolGNN-LLMs, which integrates a pluggable and fine-tunable LLM module to tackle small-dataset challenges such as data scarcity and biased sampling. To evaluate the effectiveness of HASolGNN-LLMs, we conducted controlled experiments on Exp-DB by randomly sampling subsets ranging from 1% to 10% the size of the Exp-DB dataset. Across all sample sizes, HASolGNN-LLMs consistently achieved lower prediction errors than HASolGNN, confirming the advantage of leveraging LLM-enriched feature space in data-limited regimes. We observe that the smaller the dataset, the larger the performance gains achieved by HASolGNN-LLMs. At the 5% sampling level, the reduction narrows to about 0.03 while at the 1% sampling rate, HASolGNN-LLMs reduces the average MAE by more than 0.08 compared to HASolGNN. In conclusion, our experimental studies have verified that HASolGNN-LLMs yields substantial improvements in solubility prediction and remains robust for out-of-sample test pairs.
Author contributions
Y. F., Y. W., R. F., and M. G. T. designed the experiments and methodologies. M. G. T. supervised the development of the GNN framework and helped perform data curation and analysis. Y. F. conducted the experiments, performed the analysis, and prepared the figures. P. Y. and D. P. conceived the idea and supervised the project. All authors contributed to discussions and jointly authored the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
All datasets, source codes of model and training, running examples, and pre-trained models presented in this paper are available in the HASolGNN GitHub repository (https://github.com/Yangxin666/HASolGNN) and are also publicly available on Zenodo under the DOI https://doi.org/10.5281/zenodo.17848849.Supplementary information: we provide a proof of the computational complexity of HASolGNN and introduce Para-HASolGNN, a three-level parallel training algorithm to accelerate the training process of HASolGNN. See DOI: https://doi.org/10.1039/d5dd00407a.
Acknowledgements
Y. F., Y. W., and R. F. are supported by the Department of Energy's National Nuclear Security Administration under Award Number(s) DE-NA0004104. D. P., M. G. T., and P. Y. acknowledge the support by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Element Chemistry Program under contract KC0302031 E3M2 at Los Alamos National Laboratory (LANL), which is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (contract no. 89233218CNA000001). This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award BES-ERCAP0023367 and BES-ERCAP0033948.Notes and references
- X. Xu, T. Han, J. Huang, A. A. Kruger, A. Kumar and A. Goel, ACS Appl. Mater. Interfaces, 2021, 13, 53375–53387 CrossRef PubMed.
- K. De Jesus, R. Rodriguez, D. Baek, R. Fox, S. Pashikanti and K. Sharma, J. Mol. Liq., 2021, 336, 116006 CrossRef.
- C. Long, Z. Jiang, J. Shangguan, T. Qing, P. Zhang and B. Feng, Chem. Eng. J., 2021, 406, 126848 CrossRef.
- M. Bouzidi, F. Yahia, S. Ouni, N. B. H. Mohamed, A. S. Alshammari, Z. R. Khan, M. Mohamed, O. A. Alshammari, A. Abdelwahab and A. Bonilla-Petriciolet, et al. , Opt. Mater., 2024, 116575 Search PubMed.
- B. Liu, J. Li, W. Yang, X. Zhang, X. Jiang and Y. Bando, Small, 2017, 13, 1701998 CrossRef PubMed.
- P. Shiri, V. Lai, T. Zepel, D. Griffin, J. Reifman, S. Clark, S. Grunert, L. P. Yunker, S. Steiner and H. Situ, et al. , Iscience, 2021, 24, xx–yy Search PubMed.
- N. J. Szymanski, Y. Zeng, H. Huo, C. J. Bartel, H. Kim and G. Ceder, Mater. Horiz., 2021, 8, 2169–2198 RSC.
- Y. J. Li, K. Wu, Y. Li, Y. Zhang, J. J. Liu and X. Z. Wang, J. Chem. Eng. Data, 2018, 63, 27–38 CrossRef.
- X. Du, Y. Li, Y.-L. Xia, S.-M. Ai, J. Liang, P. Sang, X.-L. Ji and S.-Q. Liu, Int. J. Mol. Sci., 2016, 17, 144 CrossRef PubMed.
- R. Qing, S. Hao, E. Smorodina, D. Jin, A. Zalevsky and S. Zhang, Chem. Rev., 2022, 122, 14085–14179 CrossRef PubMed.
- B. Das, A. T. Baidya, A. T. Mathew, A. K. Yadav and R. Kumar, Bioorg. Med. Chem., 2022, 56, 116614 CrossRef PubMed.
- A. Jouyban, E. Rahimpour and Z. Karimzadeh, J. Mol. Liq., 2021, 343, 117587 CrossRef.
- D. V. Bhalani, B. Nutan, A. Kumar and A. K. Singh Chandel, Biomedicines, 2022, 10, 2055 Search PubMed.
- J. Liu, X. Lei, C. Ji and Y. Pan, Front. Pharmacol, 2023, 14, 1255181 CrossRef PubMed.
- L. Krasnov, S. Mikhaylov, M. Fedorov and S. Sosnin, 2023.
- J. Chen, S. Zheng, H. Zhao and Y. Yang, J. Cheminf., 2021, 13, 1–10 Search PubMed.
- S. Lee, M. Lee, K.-W. Gyak, S. D. Kim, M.-J. Kim and K. Min, ACS Omega, 2022, 7, 12268–12277 Search PubMed.
- W. Ahmad, H. Tayara and K. T. Chong, ACS Omega, 2023, 8, 3236–3244 Search PubMed.
- Z. Xiong, D. Wang, X. Liu, F. Zhong, X. Wan, X. Li, Z. Li, X. Luo, K. Chen and H. Jiang, et al. , J. Med. Chem., 2019, 63, 8749–8760 CrossRef PubMed.
- O. Jovic and R. Mouras, Molecules, 2023, 29, 19 CrossRef PubMed.
- D. S. Palmer, N. M. O'Boyle, R. C. Glen and J. B. Mitchell, J. Chem. Inf. Model., 2007, 47, 150–158 CrossRef PubMed.
- J. McDonagh, T. van Mourik and J. B. Mitchell, Mol. Inf., 2015, 34, 715–724 Search PubMed.
- A. Jouyban, A. Shayanfar, V. Panahi-Azar, J. Soleymani, B. Yousefi, W. Acree Jr and P. York, J. Pharm. Sci., 2011, 100, 4368–4382 CrossRef PubMed.
- P. Llompart, C. Minoletti, S. Baybekov, D. Horvath, G. Marcou and A. Varnek, Sci. Data, 2024, 11, 303 CrossRef PubMed.
- P. Ruelle, C. Rey-Mermet, M. Buchmann, H. Nam-Tran, U. W. Kesselring and P. Huyskens, Pharm. Res., 1991, 8, 840–850 Search PubMed.
- H. R. Amedi, A. Baghban and M. A. Ahmadi, J. Mol. Liq., 2016, 216, 411–422 Search PubMed.
- E. M. Tosca, R. Bartolucci and P. Magni, Pharmaceutics, 2021, 13, 1101 CrossRef PubMed.
- L. Attia, J. W. Burns, P. S. Doyle and W. H. Green, Nat. Commun., 2025, 16, 7497 Search PubMed.
- W. Ahmad, H. Tayara, H. Shim and K. T. Chong, Int. J. Mol. Sci., 2024, 25, 715 CrossRef PubMed.
- G. Panapitiya, M. Girard, A. Hollas, J. Sepulveda, V. Murugesan, W. Wang and E. Saldanha, ACS Omega, 2022, 7, 15695–15710 CrossRef PubMed.
- S. Lee, H. Park, C. Choi, W. Kim, K. K. Kim, Y.-K. Han, J. Kang, C.-J. Kang and Y. Son, Sci. Rep., 2023, 13, 957 CrossRef PubMed.
- T. Zheng, J. B. Mitchell and S. Dobson, ACS Omega, 2024, 9, 35209–35222 CrossRef.
- N. Saquer, R. Iqbal, J. D. Ellis and K. Yoshimatsu, Digital Discovery, 2024, 3, 602–609 Search PubMed.
- R. J. Leenhouts, N. Morgan, E. Al Ibrahim, W. H. Green and F. H. Vermeire, Chem. Eng. J., 2025, 513, 162232 CrossRef.
- H. Jung, C. D. Stubbs, S. Kumar, R. Pérez-Soto, S.-m. Song, Y. Kim and S. Kim, Digital Discovery, 2025, 4, 1492–1504 RSC.
- Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and S. Y. Philip, IEEE Transact. Neural Networks Learn. Syst., 2020, 32, 4–24 Search PubMed.
- T. N. Kipf and M. Welling, arXiv, 2016, preprint, arXiv:1609.02907, DOI:10.48550/arXiv.1609.02907.
- W. Hamilton, Z. Ying and J. Leskovec, Adv. Neural Inf. Process. Syst., 2017, 30, xx–yy Search PubMed.
- P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, et al. , stat, 2017, 1050, 10–48550 Search PubMed.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, arXiv, 2018, preprint, arXiv:1810.00826, DOI:10.48550/arXiv.1810.00826.
- A. Lusci, G. Pollastri and P. Baldi, J. Chem. Inf. Model., 2013, 53, 1563–1575 Search PubMed.
- C. Merkwirth and T. Lengauer, J. Chem. Inf. Model., 2005, 45, 1159–1168 CrossRef.
- M. Withnall, E. Lindelöf, O. Engkvist and H. Chen, J. Cheminf., 2020, 12, 1 Search PubMed.
- F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner and G. Monfardini, IEEE Trans. Neural Network., 2008, 20, 61–80 Search PubMed.
- E. N. Feinberg, D. Sur, Z. Wu, B. E. Husic, H. Mai, Y. Li, S. Sun, J. Yang, B. Ramsundar and V. S. Pande, ACS Cent. Sci., 2018, 4, 1520–1530 CrossRef PubMed.
- D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Adv. Neural Inf. Process. Syst., 2015, 28, xx–yy Search PubMed.
- C. W. Coley, R. Barzilay, W. H. Green, T. S. Jaakkola and K. F. Jensen, J. Chem. Inf. Model., 2017, 57, 1757–1772 CrossRef PubMed.
- X. Wang, Z. Li, M. Jiang, S. Wang, S. Zhang and Z. Wei, J. Chem. Inf. Model., 2019, 59, 3817–3828 Search PubMed.
- S. Ryu, J. Lim, S. H. Hong and W. Y. Kim, arXiv, 2018, preprint, arXiv:1805.10988, DOI:10.48550/arXiv.1805.10988.
- Z. Hao, C. Lu, Z. Huang, H. Wang, Z. Hu, Q. Liu, E. Chen and C. Lee, Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining, 2020, pp. 731–752 Search PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea, et al. , J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef.
- Z. Chen, L. Chen, S. Villar and J. Bruna, Adv. Neural Inf. Process. Syst., 2020, 33, 10383–10395 Search PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner, M. Steijaert, J. K. Wegner, H. Ceulemans, D.-A. Clevert and S. Hochreiter, Chem. Sci., 2018, 9, 5441–5451 Search PubMed.
- M. Meng, Z. Wei, Z. Li, M. Jiang and Y. Bian, IEEE 10th International Conference on Software Engineering and Service Science (ICSESS), 2019, pp. 263–266 Search PubMed.
- N. Sukumar and J. Pask, Int. J. Numer. Methods Eng., 2009, 77, 1121–1138 CrossRef.
- K. Zhou, Y. Dong, K. Wang, W. S. Lee, B. Hooi, H. Xu and J. Feng, Proceedings of the 30th ACM International Conference on Information & Knowledge Management, 2021, pp. 2728–2737 Search PubMed.
- J. Wu, J. Wang, Z. Wu, S. Zhang, Y. Deng, Y. Kang, D. Cao, C.-Y. Hsieh and T. Hou, J. Chem. Inf. Model., 2022, 62, 5975–5987 CrossRef.
- J. Achiam, S. Adler, S. Agarwal, L. Ahmad, I. Akkaya, F. L. Aleman, D. Almeida, J. Altenschmidt, S. Altman, S. Anadkatet al., arXiv, 2023, preprint, arXiv:2303.08774, DOI:10.48550/arXiv.2303.08774.
- A. Grattafiori, A. Dubey, A. Jauhri, A. Pandey, A. Kadian, A. Al-Dahle, A. Letman, A. Mathur, A. Schelten, A. Vaughanet al., arXiv, 2024, preprint, arXiv:2407.21783, DOI:10.48550/arXiv.2407.21783.
- Full, 2025, https://github.com/Yangxin666/HASolGNN/blob/main/HASolGNN_full.pdf.
- W. L. Jorgensen and E. M. Duffy, Adv. Drug Deliv. Rev., 2002, 54, 355–366 CrossRef PubMed.
- I. Beltagy, K. Lo and A. Cohan, arXiv, 2019, preprint, arXiv:1903.10676, DOI:10.48550/arXiv.1903.10676.
- Y. Gu, R. Tinn, H. Cheng, M. Lucas, N. Usuyama, X. Liu, T. Naumann, J. Gao and H. Poon, ACM Trans. Comput. Healthc., 2021, 3, 1–23 Search PubMed.
- R. Miao, Y. Yang, Y. Ma, X. Juan, H. Xue, J. Tang, Y. Wang and X. Wang, Inf. Sci., 2022, 613, 667–681 Search PubMed.
- Y. Kim, H. Jung, S. Kumar, R. S. Paton and S. Kim, Chem. Sci., 2024, 15, 923–939 Search PubMed.
- V. Ramani and T. Karmakar, J. Chem. Theory Comput., 2024, 20, 6549–6558 CrossRef.
- S. Boobier, D. R. Hose, A. J. Blacker and B. N. Nguyen, Nat. Commun., 2020, 11, 5753 CrossRef PubMed.
- J. S. Delaney, J. Chem. Inf. Comput. Sci., 2004, 44, 1000–1005 CrossRef PubMed.
- Q. Chen, Y. Zhang, P. Gao and J. Zhang, Artif. Intell. Chem., 2023, 1, 100010 CrossRef.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef PubMed.
- Y. Qiu, J. Chen, K. Xie, R. Gu, Z. Qi and Z. Song, Chem. Eng. Sci., 2024, 300, 120559 CrossRef.
- A. Yang, S. Sun, H. Mi, W. Wang, J. Liu and Z. Y. Kong, Ind. Eng. Chem. Res., 2024, 63, 8293–8305 CrossRef.
- H.-C. Liao, Y.-H. Lin, C.-H. Peng and Y.-P. Li, ACS Eng. Au, 2025, 5, 530–539 CrossRef.
- F. J. Pontes, G. Amorim, P. P. Balestrassi, A. Paiva and J. R. Ferreira, Neurocomputing, 2016, 186, 22–34 CrossRef.
- L. Krasnov, D. Malikov, M. Kiseleva, S. Tatarin, S. Sosnin and S. Bezzubov, Sci. Data, 2025, 12, 1236 CrossRef PubMed.
Footnotes |
| † We showcase example prompts and LLM responses in the full version.60 |
| ‡ https://github.com/Yangxin666/HASolGNN |
| This journal is © The Royal Society of Chemistry 2026 |