 Open Access Article
Open Access ArticleEfficient quantum simulation of non-adiabatic molecular dynamics with precise electronic structure
Tianyi
Li
 ab,
Yumeng
Zeng
a,
Qiming
Ding
ab,
Yumeng
Zeng
a,
Qiming
Ding
 a,
Zixuan
Huo
a,
Xiaosi
Xu
c,
Jiajun
Ren
d,
Diandong
Tang
a,
Zixuan
Huo
a,
Xiaosi
Xu
c,
Jiajun
Ren
d,
Diandong
Tang
 *e,
Xiaoxia
Cai
*f and
Xiao
Yuan
*a
*e,
Xiaoxia
Cai
*f and
Xiao
Yuan
*a
aCenter on Frontiers of Computing Studies, School of Computer Science, Peking University, Beijing 100871, China. E-mail: xiaoyuan@pku.edu.cn
bÉcole Normale Supérieure Paris-Saclay, Université Paris-Saclay, 91190 Gif-sur-Yvette, France
cGraduate School of China Academy of Engineering Physics, Beijing 100193, China
dKey Laboratory of Theoretical and Computational Photochemistry, Ministry of Education, College of Chemistry, Beijing Normal University, Beijing 100875, China
eDepartment of Chemistry, University of Washington, Seattle, WA 98195-1700, USA. E-mail: tangdd@uw.edu
fInstitute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China. E-mail: xxcai@ihep.ac.cn
First published on 14th January 2026
Abstract
In the study of non-adiabatic chemical processes such as photocatalysis and photosynthesis, non-adiabatic molecular dynamics (NAMD) is an indispensable theoretical tool, which requires precise potential energy surfaces (PESs) of ground and excited states. Quantum computing offers promising potential for calculating PESs that are intractable for classical computers. However, its realistic application poses significant challenges to the development of quantum algorithms that are sufficiently general to enable efficient and precise PES calculations across chemical systems with diverse properties and to seamlessly adapt existing NAMD theories to quantum computing. In this work, we introduce a quantum-adapted extension to the Landau–Zener-Surface-Hopping (LZSH) NAMD. This extension incorporates curvature-driven hopping corrections that protect the population evolution while maintaining the efficiency gained from avoiding the computation of non-adiabatic couplings (NACs) and preserving the trajectory independence that enables parallelization. Furthermore, to ensure the high-precision PESs required for surface hopping dynamics, we develop a sub-microhartree-accurate PES calculation protocol. This protocol supports active space selection, enables parallel acceleration either on quantum or classical clusters, and demonstrates adaptability to diverse chemical systems—including the charged H3+ ion and the C2H4 molecule, a prototypical multi-reference benchmark. This work paves the way for practical application of quantum computing in NAMD, showcasing the potential of parallel simulation on quantum-classical heterogeneous clusters for ab initio computational chemistry.
Introduction
Ab initio molecular dynamics (AIMD) simulations are indispensable for elucidating mechanisms underlying chemical and biological processes, providing atomistic insights into phenomena ranging from charge carrier dynamics in materials,1 excited-state dynamics of transition metal complexes,2 and proton transfer in solvation processes3 to photochemical reactions.4,5 A foundational early approach of AIMD is the Born–Oppenheimer molecular dynamics framework, which leverages the Born–Oppenheimer approximation to decouple electronic and nuclear degrees of freedom. This approach has been proven valuable for simulating equilibrium properties and slow dynamic processes in systems where the Born–Oppenheimer approximation holds.6–9However, the Born–Oppenheimer approximation breaks down when the energy gap between electronic states becomes close, leading to strong non-adiabatic effects, which is crucial for understanding a broad spectrum of chemical phenomena. This occurs in scenarios involving conical intersections, avoided crossings, or ultra-fast electronic transitions, such as in photochemistry,10–12 charge transfer,13–15 or vibronic relaxation processes.16–23 Under these conditions, Born–Oppenheimer molecular dynamics fails to capture the traveling of nuclear wavepackets across multiple potential energy surfaces (PESs) and is not able to describe excited-state dynamics and simulate photophysics and photochemistry reactions.
To fully simulate those processes, non-adiabatic molecular dynamics (NAMD) is necessary. Full quantum dynamics treats both electronic and nuclear degrees of freedom quantum mechanically, with the multi-configurational time-dependent Hartree24 method being a prominent example; however, its computational cost escalates rapidly with system size. In contrast, mixed quantum-classical dynamics approximates nuclear motion classically while retaining quantum-mechanical treatment of electrons, enabling efficient simulations of larger systems over relevant timescales. Several schemes fall under this category, including mean-field approaches, ab initio multiple spawning, and trajectory surface hopping.25–28 Among surface hopping methods, the widely adopted fewest switches surface hopping (FSSH)29 propagates nuclear trajectories classically on a single active PES while allowing stochastic hops between states based on transition probabilities. These probabilities are computed equally from three key quantities: non-adiabatic coupling (NAC), which represents the interaction between electronic states induced by nuclear motion; the nuclear time step, which scales the probability to ensure proper integration over the trajectory; and electronic coefficients, which encode the quantum amplitudes and coherences among states—though the update of these electronic coefficients itself relies on NAC to capture non-adiabatic effects during propagation. In addition to NAC, energy gaps between PESs and their derivatives offer more accessible electronic properties for driving state transitions, leading to efficient variants such as Landau–Zener-Surface-Hopping (LZSH),30 Zhu–Nakamura surface hopping (ZNSH),31–33 and curvature-driven surface hopping (κSH).34–36 These protocols construct hopping events without explicit computation of NAC, making them well-suited for interfacing with electronic structure methods that may not readily provide such quantities.37
Despite these advances, solving the multi-state electronic structure remains a major challenge for NAMD on classical computers. Accurate treatment of conical intersections and strongly correlated systems often requires full configuration interaction (FCI), which scales exponentially with the number of orbitals and electrons, necessitating an exponential number of Slater determinants,38 which is intractable for classical computers. While density functional theory (DFT) provides a computationally efficient alternative with O(N3) or O(N4) scaling, it faces challenges in accurately describing multi-configurational wavefunctions and excitation energies in non-adiabatic regimes.39,40 These challenges motivate the exploration of quantum algorithms, which inherently exploit superposition and entanglement to efficiently solve the electronic Schrödinger equation for correlated systems, promising exponential speedups for NAMD in regimes inaccessible to classical-computing methods.41–43
Quantum algorithms for chemistry simulation are exemplified by the quantum phase estimation (QPE) method in the fault-tolerant quantum computing (FTQC) regime, which can theoretically achieve accuracy comparable to FCI, provided a suitable initial state is prepared (e.g., via adiabatic state preparation).44,45 Nevertheless, current quantum devices fall short in supporting QPE circuits of practical width, depth, qubit fidelity, and gate fidelity, compounded by the immaturity of quantum error correction. Near-term quantum algorithms, represented by Variational Quantum Eigensolver (VQE), offer a compromise by adopting a heuristic time complexity and tolerating moderate noise levels.46,47 Grounded in the variational principle, VQE optimizes parametrized quantum circuits to approximate molecular energy spectra and corresponding electronic states. For larger-scale systems, the second-quantization on which the VQE framework is based enables the selection of chemically significant molecular orbitals (MOs), forming an active space that captures essential chemical properties within constrained circuit sizes.45,48 This complete active space (CAS) method is particularly vital for extending quantum-computing simulations to realistic molecular systems without exceeding resources of noisy intermediate-scale quantum (NISQ).49
Advancements in NISQ algorithms have significantly enhanced the computation of molecular excited states. Among these, the variational quantum deflation (VQD) method extends the VQE by incorporating overlap penalties to enforce approximate orthogonality with previously computed states, enabling sequential search of higher-energy eigenstates.50,51 However, its iterative framework escalates computational demands, limits parallelization, and propagates errors in noisy settings. In contrast, subspace-based approaches enhance efficiency by restricting calculations to predefined excitation sectors. For instance, the subspace-search VQE (SSVQE) simultaneously optimizes a set of orthogonal initial states, reducing optimization iterations compared to serial search.52 Complementing subspace concepts with a sampling strategy, sample-based quantum diagonalization (SQD) constructs and diagonalizes effective Hamiltonian matrices via quantum sampling, claimed to support large qubit systems and mitigate noise effects, yet it relies heavily on ample sampling for achieving high precision.53,54 Building on similar foundations, Quantum Subspace Expansion (QSE) employs explicit projections onto Fermionic subspaces, yielding physically guaranteed variational upper bounds for excited-state energies.55–58 Another prominent approach, the quantum equation-of-motion (QEOM), leverages subspace concepts while incorporating equation-of-motion (EOM) formalisms in classical-computing quantum chemistry, could ensure size-intensity and inherently introduce the contribution of de-excitation.59–61 However, for QSE and QEOM, the choice and number of operators used in subspace construction determine the algorithm's ability to capture physical properties62 and efficiency and robustness. The exquisite design of subspaces tailored to specific systems remains an on-going topic. Furthermore, to meet the NISQ constraints, optimization strategies at the implementation level leave a valuable area for exploration.
In this work, we introduce a practical quantum-computing NAMD framework, seamlessly integrated with our sub-microhartree-accuracy calculations of PESs across diverse chemical systems, including H3+ and C2H4, and compatible with parallel acceleration on both real quantum computers and quantum algorithm simulators on classical computers. While recent explorations62,63 have advanced quantum-computing electronic structure solvers by comparing methods such as QEOM, QSE, and de-excited QSE, or employing VQD for sequential orthogonal excited-state searches, our approach pursues a distinct goal of achieving sub-microhartree precision through a hybrid subspace-based quantum-computing electronic structure solver that adapts operator selections to different chemicals, enhancing accuracy via problem-adapted subspace operator selection and integration of SSVQE for parallel optimization of multiple reference states prior to QSE application. We also rigorously assess the numerical stability of quantum-computed PESs and incorporate an efficient curvature-driven correction scheme for state transitions tailored to quantum-computing electronic structure solvers. In the NAMD evolution, whereas prior studies focused on FSSH requiring NAC computations, we focus on adapting LZSH for quantum algorithms, introducing an improved LZSH scheme that stabilizes dynamics more efficiently. These innovations, combined with a two-level parallelization framework and task-specific algorithmic extensions, yield substantial speedups without compromising PES precision, collectively elevating the robustness, efficiency, and practical viability of quantum-enhanced LZSH-NAMD simulations for broader chemical research (Fig. 1).
 | ||
| Fig. 1 Work flow of on-the-fly quantum solver for electronic-structure observables, with parallelization of QSE. | ||
Methods
Capturing molecular properties on a quantum computer
The electronic molecular Hamiltonian in second quantization is expressed as65
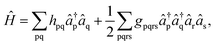 | (1) |
In the CAS framework,66 we partition the orbitals into core (inactive), active, and virtual (inactive) sets. The core orbitals are doubly occupied, and their contributions are incorporated into an effective one-electron potential. The active space consists of m orbitals and n electrons, where strong correlations are expected, such as in bond-breaking regions or excited states. Selecting the active orbitals is crucial for accuracy and efficiency. General strategies include identifying orbitals based on chemical intuition, such as valence orbitals involved in bonding or antibonding interactions, or using orbital energies and occupancies from preliminary calculations. For smaller active spaces (e.g., CAS(2,2) or CAS(4,4)), manual selection is common, visualizing molecular orbitals from Hartree–Fock calculations to choose frontier orbitals such as the highest occupied molecular orbital, the lowest unoccupied molecular orbital, or those directly participating in the chemical process of interest, ensuring that the space captures the dominant static correlation with minimal computational cost. For larger active spaces (e.g., CAS(10,10) or beyond), automated strategies are preferred to handle complexity, such as the ranked-orbital approach,67 entropy-based selection from uncorrelated natural orbitals combined with the density matrix renormalization group,68 or machine learning selection,69 which systematically expand the space while maintaining convergence. In this work, we use a selection strategy based on orbital energies and occupancies from preliminary calculations, where the active space comprises contiguous frontier orbitals around the Fermi level to efficiently capture dominant static correlations.
The Hamiltonian is then restricted to excitations within this active space, yielding
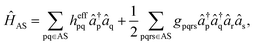 | (2) |
Since quantum computers operate on qubits rather than fermions, the fermionic Hamiltonian must be mapped to a qubit Hamiltonian to enable simulation via quantum circuits. To achieve this, we apply the Jordan–Wigner (JW) transformation.70 The JW mapping encodes fermionic operators into an O(1) number of Pauli strings as
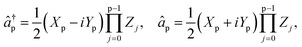 | (3) |
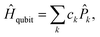 | (4) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) k are Pauli strings mapped from effective one-electron integral terms and two-electron integral terms and ck are coefficients obtained by summing the coefficients of the same Pauli strings.
k are Pauli strings mapped from effective one-electron integral terms and two-electron integral terms and ck are coefficients obtained by summing the coefficients of the same Pauli strings.
| |ψ(θ)〉QC = Û(θ)|Φ0〉. | (5) |
Common ansatzes include the unitary coupled-cluster (UCC) form, such as UCCSD, which approximates the exponential cluster operator:71
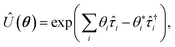 | (6) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) i are excitation operators mapped to qubits. The energy expectation value is
i are excitation operators mapped to qubits. The energy expectation value is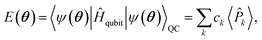 | (7) |
Beyond the canonical single-reference VQE in selected active spaces, multi-reference features can be incorporated to enhance the ground-state search in systems exhibiting strong static correlation. One such extension is the SSVQE, which expands the variational search into a larger subspace spanned by multiple orthogonal reference states52 in selected active spaces.
In SSVQE, a set of k mutually orthogonal initial reference states {|ϕj〉}j=1k is selected, often including the Hartree–Fock state and additional configurations to introduce multi-reference features. The same parametrized unitary operator Û(θ) is applied to each reference, producing trial states |ψj(θ)〉 = Û(θ)|ϕj〉. The variational cost function is defined as a weighted sum of the energy expectation values:
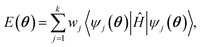 | (8) |
In the Tamm-Dancoff Approximation for QSE (TDA-QSE),76 the subspace is constructed by applying low-rank excitation operators ʵ to a reference state |ψk〉QC, generating basis vectors; the excitations only include single excitations â†pâq and double excitations â†pâ†qârâs:
| |ϕµ〉 = ʵ|ψk〉QC. | (9) |
| Hµν = 〈ϕµ|Ĥqubit|ϕν〉, Sµν = 〈ϕµ|ϕν〉, | (10) |
| Hc = ESc. | (11) |
The Fermion operators ʵ and Êν could be transformed and decomposed into the O(1) number of Pauli operators by the Jordan–Wigner transformation just like how ĤAS transformed into Ĥqubit in eqn (3). Excited-state energies and eigenvectors are obtained by solving the generalized eigenvalue problem:
The number of matrix elements scales as 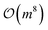 , where m is the number of selected orbitals. This results in an overall operator complexity of
, where m is the number of selected orbitals. This results in an overall operator complexity of 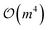 .
.
Beyond TDA-QSE, the general QSE framework supports a versatile set of fermionic operators in second quantization, enabling flexible subspace construction for systems with specific electron structures, such as those near conical intersections or avoided crossings. Each operator has an inverse (its Hermitian adjoint, e.g., de-excitations for excitations), which can enhance the description of physical properties.62 Below, we list extensible operator classes, their second quantization forms, and their computational complexities, assuming a spin-orbital basis with m active spatial orbitals. Summations (e.g., p > q) ensure proper antisymmetrization, and spin-adapted forms77 are used where applicable to target singlet states (S2 = 0).
• Higher-order excitations: these extend single and double excitations to triples, quadruples, and beyond, capturing higher-order electron correlations critical for multi-reference systems. For a triple excitation (from occupied orbitals i, j, and k to virtual orbitals a, b, and c):
| Êabcijk = aâ†aâ†bâ†câkâjâi. | (12) |
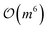 , quadruples as
, quadruples as  , and general k-th order excitations as
, and general k-th order excitations as 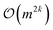 , with de-excitations sharing the same complexity. Spin-adapted forms, constructed analogously to single and double excitations, commute with Ŝ2, reducing the constant factor in the subspace dimension.
, with de-excitations sharing the same complexity. Spin-adapted forms, constructed analogously to single and double excitations, commute with Ŝ2, reducing the constant factor in the subspace dimension.
• Spin-flip operators: these alter spin multiplicity by flipping electron spins while conserving orbital occupancy, useful for describing open-shell configurations. A single spin-flip (e.g., α to β in orbitals p and q):
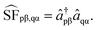 | (13) |
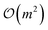 and double spin-flips as
and double spin-flips as  . These operators are not naturally restricted to singlet states, as they couple different spin sectors, increasing the subspace dimension unless filtered by Ŝ2 commutation.
. These operators are not naturally restricted to singlet states, as they couple different spin sectors, increasing the subspace dimension unless filtered by Ŝ2 commutation.
• Spin-mixing operators: these couple different spin sectors without flipping spins, enabling transitions between states of differing spin multiplicities while preserving total spin projection. A representative operator:
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) pqrs = â†pαâ†qβâsβârα. pqrs = â†pαâ†qβâsβârα. | (14) |
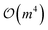 and, like spin-flip operators, are not inherently restricted to singlets, requiring Ŝ2 filtering to target singlet states.
and, like spin-flip operators, are not inherently restricted to singlets, requiring Ŝ2 filtering to target singlet states.
• Orbital rotations: these unitary transformations mix orbitals within the active space, optimizing orbital bases for response properties or strong correlation. The generator is anti-Hermitian:
 | (15) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) , as (
, as (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) )† = −
)† = −![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) . Orbital rotations scale as
. Orbital rotations scale as 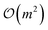 and are naturally spin-adapted, commuting with Ŝ2, making them efficient for singlet subspaces.
and are naturally spin-adapted, commuting with Ŝ2, making them efficient for singlet subspaces.
• Non-diagonal couplings: these couple configurations across the orbital space without strict occupancy constraints, enhancing subspace flexibility. A general non-diagonal double coupling:
| Ĉpqrs = â†pâ†qâsâr. | (16) |
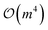 , and the inverse form would be in the form of â†râ†sâqâp. Spin adaptation could be achieved by symmetrically (or antisymmetrically) combining α–β pairs, yielding operators that commute with Ŝ2 and reduce the effective dimensionality of the excitation subspace.
, and the inverse form would be in the form of â†râ†sâqâp. Spin adaptation could be achieved by symmetrically (or antisymmetrically) combining α–β pairs, yielding operators that commute with Ŝ2 and reduce the effective dimensionality of the excitation subspace.
• Electron–electron interaction operators: these directly incorporate two-body interaction terms from the molecular Hamiltonian, capturing dynamic and static electron correlations. These are derived from the Hamiltonian's two-electron integrals Vpqrs. Including these operators enhances the subspace's ability to describe correlation effects, but requires careful selection of significant integrals (e.g., |Vpqrs| > ε) to manage computational cost. A representative operator is
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) pqrs = gpqsrâ†pâ†qâsâr. pqrs = gpqsrâ†pâ†qâsâr. | (17) |
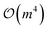 , matching double excitations. Spin-adapted forms are constructed similarly by ensuring commutation with Ŝ2.
, matching double excitations. Spin-adapted forms are constructed similarly by ensuring commutation with Ŝ2.
Implementation-level adaptations and optimizations could ameliorate the constant-factor overhead. When the number of selected expansion operators is large, the S matrix may become ill-conditioned.78 We could adopt regularization methods to maintain numerical stability at the implementation level.79
Beyond its role in accessing excited states, QSE also serves as a powerful quantum error mitigation technique by projecting noisy or non-optimal reference states into a carefully constructed subspace that isolates and corrects errors inherent to near-term quantum hardware.80–82 In this context, QSE leverages excitation operators to expand the reference state, enabling the identification and suppression of noise-induced artifacts through the diagonalization of the projected Hamiltonian and overlap matrices, effectively restoring physical fidelity without requiring full error correction protocols. This application of QSE for error mitigation represents a distinct research branch, complementary to its excited-state computations, with ongoing developments focusing on adaptive operator selection and regularization to enhance robustness against quantum errors.
In our approach, the reference state |Ψ0〉 is obtained using VQE or SSVQE. Excited states could be constructed using the result of QSE, where the excited state wavefunctions |Ψk〉 (for k ≥ 1) could be written as linear combinations of the reference state and applications of excitation operators Ei:57
 | (18) |
Nuclear forces are the negative gradients of the electronic energy with respect to nuclear coordinates R:
| Fk(R) = −∇REk(R), | (19) |
Two primary methods exist for computing these gradients: the finite difference method (FDM) and Hellmann–Feynman method (HFM).
The FDM provides a numerical gradient. It could approximate the gradient via central differences85
 | (20) |
The HFM provides analytical gradients. The Hellmann–Feynman theorem states that for an exact or variationally optimized wavefunction |Ψ〉 of a Hamiltonian Ĥ(λ) depending on a parameter λ, the derivative of the energy E(λ) = 〈Ψ|Ĥ|Ψ〉 (assuming normalization 〈Ψ|Ψ〉 = 1) with respect to λ is given by86,87
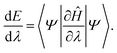 | (21) |
This result follows from differentiating the energy expression:
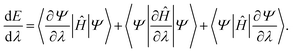 | (22) |
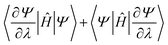 vanishes, as required by the eigenvalue equation (Ĥ − E)|Ψ〉 = 0 and the normalization condition 〈Ψ|Ψ〉 = 1. Furthermore, upon adopting a gauge where the global phase of |Ψ(λ)〉 is chosen such that
vanishes, as required by the eigenvalue equation (Ĥ − E)|Ψ〉 = 0 and the normalization condition 〈Ψ|Ψ〉 = 1. Furthermore, upon adopting a gauge where the global phase of |Ψ(λ)〉 is chosen such that 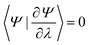 , each term vanishes individually. For a variationally prepared wavefunction, if it is optimal with respect to its parameters, the response term will be zero by the variational principle, making the theorem applicable to states given by VQE or QSE.87
, each term vanishes individually. For a variationally prepared wavefunction, if it is optimal with respect to its parameters, the response term will be zero by the variational principle, making the theorem applicable to states given by VQE or QSE.87
In implementation, we would use the finite basis set to construct the wave function. When using atom-centered basis sets (e.g., Gaussian orbitals), the basis functions will depend implicitly on nuclear positions, and since λ corresponds to nuclear coordinates Rα, the force will be −〈Ψ|∂Ĥ/∂Rα|Ψ〉. This would introduce additional contributions known as Pulay terms or Pulay forces. These arise because the derivative must account for the basis set's coordinate dependence:88
 | (23) |
The derivative Hamiltonian ∂Ĥ/∂Rα is thus computed in the MO basis, incorporating electron integrals transformed via the MO coefficients from a preceding Hartree–Fock calculation. Specifically, the force operators are derived as89
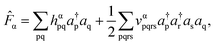 | (24) |
Finally, on a quantum computer, these Fermionic operators are mapped to qubit operators using the Jordan–Wigner transformation, and expectation values are evaluated via
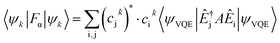 | (25) |
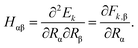 | (26) |
Direct analytical computation of the Hessian on a quantum computer is challenging due to the need for higher-order responses. Instead, we could compute the Hessian via finite differences of the Hellmann–Feynman gradients:
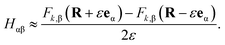 | (27) |
For each displacement, the molecular geometry is updated, and a new Hartree–Fock calculation provides updated MO coefficients. The calculation of electronic-structure observables is then repeated to obtain the ground-state energy and gradient at the perturbed geometry. The full Hessian is assembled as a (3N × 3N) matrix (N: the number of atoms).
Time evolution as a surface hopping dynamics
Wigner sampling provides a phase-space distribution that approximates the quantum mechanical density for the initial vibrational state, typically the ground state at zero temperature.93 For a molecule treated as a set of harmonic oscillators derived from the Hessian matrix, the Wigner distribution in normal coordinates Q and conjugate momenta P is given by
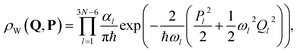 | (28) |
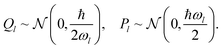 | (29) |
On the classical computer, these normal-mode samples are transformed back into Cartesian coordinates and velocities using the eigenvectors from the Hessian diagonalization, ensuring that the initial ensemble captures zero-point energy and quantum-mechanical delocalization effects.93 The sampled trajectories are then propagated on the adiabatic PESs computed via VQE and QSE.72,95 Non-adiabatic transitions are handled via the LZSH algorithm, a computationally efficient variant of Tully's FSSH that approximates hopping probabilities using the Landau–Zener formula without needing time-dependent electronic coefficients or NAC.29 In LZSH, at each time step Δt, for the current active state k and each other state l ≠ k, the energy gap Δkl = |Ek − El| is monitored. A hop is considered only if the gap reaches a local minimum (i.e., Δkl(t) > Δkl(t − Δt) and Δkl(t) < Δkl(t + Δt) in a retrospective check), indicating passage through an avoided crossing.96 The hopping probability from k to l is then given by the Landau–Zener formula for the transition probability:97,98
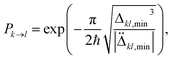 | (30) |
A challenge of LZSH NAMD is its sensitivity to the choice of the nuclear time step, and it could be less reliable for systems involving more than two electronic states due to oversimplified multi-state interactions. Another critical challenge in LZSH NAMD is the presence of discontinuities in the PESs, which can manifest as artificial local minima in the energy gap when the dynamics reach the far end of the dissociation region where PESs are closely spaced. These artifacts, arising from numerical instabilities in electronic structure solvers (despite high accuracy), lead to erroneous transition probabilities and non-physical dynamics. Hard-coded filtering risks losing valuable information, so, inspired by Jíra et al.,100 we implement a curvature-induced transition protection algorithm tailored for quantum-computing electronic solvers. This approach suppresses spurious transitions from PES fractures over small displacement intervals, relying solely on energy gap information already available in the LZSH procedure (thus requiring no additional electronic-structure calculations) and efficiently refines the dynamics for more physically consistent system evolution (Fig. 2).
 | ||
| Fig. 2 Work flow of parallel LZSH dynamics (represented by eqn (30)) that co-operates with an on-the-fly quantum-computing electronic-structure property solver. | ||
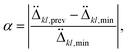
Specifically, the algorithm computes a coefficient α that measures the relative change in the second derivative (curvature) of the energy gap Δkl between the step immediately preceding the detected minimum and the minimum itself:
 | (31) |
![[greek Delta with two dots above]](https://www.rsc.org/images/entities/i_char_e1b1.gif) kl,prev and
kl,prev and ![[greek Delta with two dots above]](https://www.rsc.org/images/entities/i_char_e1b1.gif) kl,min are the curvatures at those respective steps. The purpose of α is to detect whether the minimum is likely an unphysical artifact (e.g., from a discontinuity-induced fracture) rather than a genuine physical feature: a large α indicates an abrupt, suspicious change in the curvature. If α > cblock, the hop is blocked as the minimum is deemed discontinuity-induced (i.e., a trivial crossing); if calert ≤ α ≤ cblock, a warning is issued (potentially flagging a sharp but physical conical intersection, akin to a nontrivial crossing); otherwise, the hop proceeds normally. The thresholds calert and cblock are empirical values, summarized as 0.3 and 1.3.100 This safeguard promotes smooth curvature changes to eliminate spurious crossings arising from numerical artifacts, while preserving physically meaningful ones, thereby improving stability without resorting to hard-coded filters or additional quantum evaluations.
kl,min are the curvatures at those respective steps. The purpose of α is to detect whether the minimum is likely an unphysical artifact (e.g., from a discontinuity-induced fracture) rather than a genuine physical feature: a large α indicates an abrupt, suspicious change in the curvature. If α > cblock, the hop is blocked as the minimum is deemed discontinuity-induced (i.e., a trivial crossing); if calert ≤ α ≤ cblock, a warning is issued (potentially flagging a sharp but physical conical intersection, akin to a nontrivial crossing); otherwise, the hop proceeds normally. The thresholds calert and cblock are empirical values, summarized as 0.3 and 1.3.100 This safeguard promotes smooth curvature changes to eliminate spurious crossings arising from numerical artifacts, while preserving physically meaningful ones, thereby improving stability without resorting to hard-coded filters or additional quantum evaluations.
Implementations
Surface-hopping NAMD simulations require repeated execution of electronic structure solvers. In subspace quantum electronic structure solvers, QSE incurs a significant cost, requiring the estimation of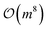 matrix elements, inspired by the serial prototype,101 noting that the computation of QSE matrix elements in eqn (10) can be parallelized. Each expectation value 〈
matrix elements, inspired by the serial prototype,101 noting that the computation of QSE matrix elements in eqn (10) can be parallelized. Each expectation value 〈![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) k〉 for Pauli strings in decomposed operators can be estimated independently. We leverage this by performing parallel computations across multiple processors for classical-computing quantum algorithm simulation or real-device quantum computing. On the theoretical level, we exploit the Hermitian feature of QSE matrices to halve the matrix estimation overhead, which is a general strategy. Another optimization applies to systems where dynamics simulations involve only singlet excited-state energies: by selecting operators that commute with Ŝ2, we achieve a fourfold reduction in the operator count. Furthermore, for specific target states in particular systems, operators with negligible contributions could also be eliminated based on their respective physical nature, enabling problem-specific operator savings.
k〉 for Pauli strings in decomposed operators can be estimated independently. We leverage this by performing parallel computations across multiple processors for classical-computing quantum algorithm simulation or real-device quantum computing. On the theoretical level, we exploit the Hermitian feature of QSE matrices to halve the matrix estimation overhead, which is a general strategy. Another optimization applies to systems where dynamics simulations involve only singlet excited-state energies: by selecting operators that commute with Ŝ2, we achieve a fourfold reduction in the operator count. Furthermore, for specific target states in particular systems, operators with negligible contributions could also be eliminated based on their respective physical nature, enabling problem-specific operator savings.
The surface hopping framework requires a sufficiently large ensemble of trajectories to mitigate statistical noise and accurately capture the underlying physical behavior. Given the resource-intensive nature of quantum algorithm simulators, we leverage the inherent independence of trajectories within the ensemble to enhance computational efficiency at the engineering level. Each trajectory, initialized from the Wigner distribution by calling the program immigrated from Newton-X-2.4-B06,102 evolves autonomously under the surface hopping dynamics, allowing for parallelization across multiple processors or computational nodes. In implementation, the initial phase-space points Ql, and Pl are assigned to parallel workers. Each worker propagates its assigned subset of trajectories forward in time using the classical-computing integrator on the active surface, interspersed with hop evaluations at each step. The quantum computations for energies Ek and forces Fk are invoked on-demand for each trajectory's current geometry. On the other hand, the curvature-induced hopping correction could maintain computational efficiency. The parameter α in eqn (31) can be obtained using a backward difference of the energy-gap curvatures between the current and previous time steps, eliminating the need for additional wavefunction calculations beyond those already performed in the standard LZSH propagation. The curvature at each time step is computed via the central difference of the energy gaps at neighboring steps:
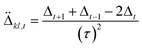 | (32) |
where τ is the time step size. Note that the energy gap at the trial step t + 1 is already calculated in the standard LZSH algorithm to locate the local minimum that triggers surface hopping according to eqn (30). By estimating α using a backward difference of curvatures (relying only on information up to step t + 1), we avoid any additional propagation to a hypothetical t + 2 step that would otherwise be required for a forward or central difference.
The simulator programs for subspace quantum algorithms are implemented using MindSpore Quantum 0.11.0,103 Quri-parts 0.19.0,104 and Qulacs 0.5.6.105 To construct our hybrid quantum-classical (both in the physical sense and computational sense) program, we referred to a canonical implementation of the classical AIMD framework in MLatom 3.10 (ref. 106–109) as an initial baseline.
We use PySCF 2.8.0 (ref. 110) to perform the classical-computing reference calculation at the same level corresponding to the quantum-computing solver as the exact solution. All electronic-structure property calculations employ the STO-3G basis set. We pick the UCCSD ansatz111 for the C2H4 use case and k-UpUCCGSD ansatz112 for the H3+ use case respectively. For the VQE parameter optimizer, we use LBFGS.113,114 In the LZSH program, we pick the time step to be 0.2 fs. On the Wigner sampling for the initial condition preparation, we assume a simple 0 K temperature and δ impulse for excitation, without the filtering using the excitation window. During the NAMD propagation, velocities are rescaled uniformly along their current direction upon a successful hop to compensate for the energy difference between the target and initial electronic states, with the kinetic energy adjusted by the negative of this gap to maintain total energy conservation. A frustrated hop will leave the trajectory at the current electronic state. At the step of curvature-induced hopping correction, given that the instability only occurs at the final stage of dissociation where PESs are very close (see 5d), we set calert = 0.3 and cblock = 0.9.
Results
In the first subsection, we focus on the 3-orbital-2-electron (CAS(3,2)) space with the charged H3+ ion. For this system, we compare PESs along dissociation geometries using the TDA-QSE (as introduced in eqn (9), we denote as “QSE” in the following discussions for simplicity) and operator extended QSE methods (e.g. for electron–electron interaction in eqn (17) or other operators introduced, we denote as “QSE*“), highlighting the systematic accuracy improvement of the QSE* approach. We then evaluate two gradient computation methods (FDM and HFM) under QSE and QSE*, including a comparison of different FDM step lengths. Additionally, we present LZSH-NAMD simulation results using QSE and QSE* as electronic structure solvers, augmented with the curvature-induced hopping correction.In the second subsection, we would demonstrate adaptability by focusing on a larger molecule C2H4. Using hybrid subspace quantum-computing electronic structure solvers, we capture key chemical properties within a selected 2-orbital-2-electron active space (CAS(2,2)): the conical intersection during the ‘pyramidalization’ process of C2H4. We validate high-accuracy quantum-computed PESs along the model path on the quantum simulator, followed by nuclear forces computed via the FDM. Finally, we validate our method along a NAMD trajectory.
We compute all the PESs and forces of both H3+ and C2H4 without the geometric symmetry assumption, which validates the practicality of the electronic structure solvers in NAMD. We selected small basis sets and active spaces to balance computational resources, which necessitate numerous repeated quantum algorithm executions on classical-computing simulators. A larger basis set or active spaces would increase qubit requirements, substantially prolonging VQE and QSE times, escalating overall computation demands despite our parallel optimizations. We opt Hartree as the energy unit which is related to the electronvolt (eV) by the conversion factor of 1 hartree ≈ 27.211 eV.
In the remaining subsections, to further evaluate the near-term practical potential, we calculated these observables with a noisy quantum algorithm simulator on a classical computer. As a complement to the long-term potential, we validated some PES calculations for triplet states of H3+ and CH2O, preliminarily exploring quantum simulations of open-shell systems. Finally, we validate the speedup of our two-level parallelization framework by comparing it to the serial versions.
Use case I: H3+ results in CAS(3,2)
The PESs for the H3+ cation in its CAS(3,2) space were computed along a dissociation coordinate, where one hydrogen atom is displaced from the equilateral triangular equilibrium geometry. This path encompasses regions of conical intersection between the S1 and S2 excited states near r ≈ 0.85 Å. The singlet adapted VQE (single reference version, as introduced in eqn (7), with the k-UpUCCGSD ansatz) was employed for the S0 state, while the singlet adaptation, in both QSE and QSE* variants, was utilized for the S1 and S2 states. The QSE* approach, incorporating additional electron–electron interaction operators, thus provides a more accurate description of electron correlation energy for the ion system.Fig. 3(a) illustrates the PESs over an extended dissociation range (0–3 Å) with an interval of 0.05 Å between adjacent points, comparing the computed energies against exact FCI references (note that for H3+, CAS(3,2) already takes all the electrons and orbitals, so here in this case, UCCSD equals FCI). The VQE S0 curve closely tracks the exact ground-state PES, exhibiting a deep potential well at equilibrium bond length, followed by a smooth rise to the dissociation limit. For the excited states, the QSE method yields noticeable deviations, which fail to accurately capture the critical behavior, resulting in oscillations and energy offsets. In contrast, the QSE* method demonstrates good fidelity, with both S1 and S2 curves overlaying the exact references across the entire coordinate, including the flat dissociation plateau beyond r ≈ 2.0 Å.
 | ||
| Fig. 3 PES result along demonstrative disassociation geometries of H3+ in CAS(3,2). Gray lines represent the reference results, purple markers denote the singlet-adapted QSE results, and green markers denote the singlet-adapted QSE* results (augmented with the electron–electron interaction operators that preserve singlet spin multiplicity, as introduced in eqn (17)). (a) PES results compare two methods, with an interval of 0.05 Å between adjacent points. (b) PES results around the intersection region comparing two methods, with an interval of 0.0005 Å. | ||
A magnified view around the conical intersection region (0.852–0.86 Å) is provided in Fig. 3(b), highlighting the PES accuracy even with an interval of 0.0005 Å between adjacent points. The QSE* results reproduce the conical intersection with high precision, whereas the QSE introduces erratic fluctuations indicative of subspace incompleteness due to inadequate selection of operators.
Quantitative energy errors, summarized in Table 1, further underscore these observations. For the PES with an interval of 0.5 Å, VQE achieves root-mean-square error (RMSE) and mean absolute error (MAE) values on the order of 10−14 hartree, affirming its robustness for ground-state simulations. The extended method attains comparable sub-microhartree accuracy for S1 (RMSE = 2.02 × 10−13 hartree) and S2 (RMSE = 1.49 × 10−14 hartree), with maximum errors below 10−11 hartree-orders of magnitude better than the QSE, which incurs RMSEs of 9.23 × 10−3 hartree and 5.40 × 10−3 hartree for S1 and S2, respectively. Similar trends persist in the regime with an interval of 0.0005 Å, where QSE* errors remain at the 10−14 hartree level, while QSE errors escalate to the millihartree scale (e.g., RMSE = 4.37 × 10−3 hartree for S2), reflecting its numerical instability near the intersection.
| ΔE (Hartree) | VQE S0 | QSE* S1 | QSE* S2 | QSE S1 | QSE S2 |
|---|---|---|---|---|---|
| 0.05 Å interval | |||||
| RMSE | 9.59 × 10−14 | 2.02 × 10−13 | 1.49 × 10−14 | 9.23 × 10−3 | 5.40 × 10−3 |
| Max error | 4.49 × 10−13 | 1.34 × 10−12 | 8.56 × 10−14 | 4.88 × 10−2 | 3.14 × 10−2 |
| MAE | 3.87 × 10−14 | 6.62 × 10−14 | 5.73 × 10−15 | 3.35 × 10−3 | 2.02 × 10−3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| 0.0005 Å interval | |||||
| RMSE | 6.97 × 10−14 | 1.48 × 10−14 | 1.50 × 10−14 | 1.20 × 10−3 | 4.37 × 10−3 |
| Max error | 1.39 × 10−13 | 3.31 × 10−14 | 4.56 × 10−14 | 2.65 × 10−3 | 6.77 × 10−3 |
| MAE | 5.12 × 10−14 | 8.87 × 10−15 | 6.29 × 10−15 | 7.22 × 10−4 | 3.49 × 10−3 |
The results presented in Fig. 4, Tables 2 and 3 provide evaluations of the accuracy and robustness of the quantum-computing electronic structure solver for computing nuclear forces. Specifically, we compare the HFM (as in eqn (21)) and FDM (as in eqn (20)) applied within VQE and QSE frameworks, including a QSE* variant. These approaches are assessed against exact analytical forces of reference. Since the calculation of H3+ is naturally located on a plane, here on the model trajectory (freezing the positions of the first and third hydrogen atoms), we define the left and right hydrogen atoms as being on the x-axis, and the middle hydrogen atom as starting from the midpoint and moving to one side along the y-axis. We focus on the y-component of the force on the central hydrogen atom as a function of separation distance r.
 | ||
| Fig. 4 HFM force results and FDM force results with different step lengths. (a) QSE*-HFM force of each excited state. (b)–(d) FDM force comparison between QSE and QSE* of different FDM step lengths. | ||
| ΔF (Ha Å−1) | VQE-HFM S0 | QSE-HFM S1 | QSE*-HFM S1 | QSE-HFM S2 | QSE*-HFM S2 |
|---|---|---|---|---|---|
| RMSE | 9.53 × 10−8 | 1.96 × 10−2 | 2.00 × 10−10 | 6.59 × 10−3 | 0.00 |
| Max error | 9.60 × 10−7 | 7.97 × 10−2 | 2.10 × 10−9 | 3.80 × 10−2 | 0.00 |
| MAE | 2.37 × 10−8 | 1.05 × 10−2 | 0.00 | 1.94 × 10−3 | 0.00 |
| ΔF (Ha Å−1) | VQE-FDM S0 | QSE-FDM S1 | QSE*-FDM S1 | QSE-FDM S2 | QSE*-FDM S2 |
|---|---|---|---|---|---|
| δ = 0.001 | |||||
| RMSE | 1.23 × 10−6 | 4.74 | 4.28 × 10−6 | 2.81 × 10−1 | 4.32 × 10−6 |
| Max error | 9.32 × 10−6 | 2.56 × 101 | 3.44 × 10−5 | 1.78 | 3.51 × 10−5 |
| MAE | 3.62 × 10−7 | 1.47 | 1.13 × 10−6 | 8.90 × 10−2 | 1.24 × 10−6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| δ = 0.010 | |||||
| RMSE | 1.23 × 10−4 | 6.09 × 10−1 | 4.27 × 10−4 | 2.37 × 10−1 | 4.31 × 10−4 |
| Max error | 9.33 × 10−4 | 2.55 | 3.41 × 10−3 | 1.36 | 3.47 × 10−3 |
| MAE | 3.62 × 10−5 | 2.64 × 10−1 | 1.13 × 10−4 | 8.04 × 10−2 | 1.24 × 10−4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| δ = 0.100 | |||||
| RMSE | 1.27 × 10−2 | 2.41 × 10−1 | 3.15 × 10−2 | 2.32 × 10−1 | 3.21 × 10−2 |
| Max error | 9.73 × 10−2 | 1.31 | 2.02 × 10−1 | 1.37 | 2.13 × 10−1 |
| MAE | 3.66 × 10−3 | 9.40 × 10−2 | 9.95 × 10−3 | 8.15 × 10−2 | 1.11 × 10−2 |
The HFM results, as illustrated in the noiseless simulations shown in Fig. 4(a), demonstrate that the QSE*-HFM approach yields forces that closely track the exact curve across all examined states (S0, S1, and S2), with minimal deviations even in regions of steep potential gradients or of conical intersection. Quantitative errors of forces in Table 2 underscore this fidelity: for the QSE*-HFM method, RMSEs are on the order of 10−10 Ha Å−1 or lower for S1 and S2, with max error not exceeding 2.1 × 10−9 Ha Å−1 and MAE effectively zero within numerical precision. In contrast, QSE-HFM exhibits significantly higher errors for excited states, with RMSE values of 1.96 × 10−2 Ha Å−1 for S1 and 6.59 × 10−3 Ha Å−1 for S2, reflecting challenges in capturing subspace instabilities. For the ground state (S0), VQE-HFM achieves sub-microhartree accuracy (max error 9.60 × 10−7 Ha Å−1). These findings highlight the applicability of the QSE*, which incorporates additional operators to replenish the subspace, thereby enabling the HFM to deliver accurate forces for multi-state dynamics without empirical corrections.
Turning to the FDM in Fig. 4(b)–(d), the force profiles reveal a strong dependence on the finite-difference step size δ. For small δ (e.g., 0.001 Å), both QSE-FDM and QSE*-FDM approximate the exact forces well. Table 3 quantifies this trend: at δ = 0.001 Å, RMSE for VQE-FDM S0 is 1.23 × 10−6 Ha Å−1, while QSE-FDM S1 balloons to 4.74 Ha Å−1, indicative of amplified errors. Increasing δ to 0.01 Å and 0.1 Å systematically degrades accuracy across all methods, with RMSE rising by 2 orders of magnitude. Notably, QSE* consistently outperforms QSE in FDM contexts, suggesting that the extended subspace better stabilizes finite differences.
Fig. 5 demonstrates the population evolution during the NAMD simulations of the H3+ dissociation process, comparing the performance of the reference classical-computing exact solver with that of quantum computing approaches, including the VQE, QSE and QSE* methods. Fig. 5(a) and (b) illustrates the state populations as a function of time for the reference FCI (left, on the classical computer) and VQE-QSE (right, simulated on the classical computer via a quantum algorithm simulator) methods. In the FCI-driven simulation, which serves as a reference, the state S1 (blue) depopulates gradually over the initial 4 fs, transferring population primarily to S1 (orange), which peaks around 5 fs before decaying. After 5 fs, S0 (blue) receives a smaller but steady population increase. This behavior is indicative of efficient non-adiabatic transfer driven by conical intersections in the H3+ PESs, which are well-known to facilitate ultra-fast relaxation in this system.115 In contrast, the VQE-QSE based simulation exhibits more oscillatory population transfers, with S1 showing pronounced fluctuations between 2 and 6 fs and S2 displaying erratic rises and falls, indicative of PES fractures and instability.
The population evolution by the VQE-QSE* with canonical LZSH (Fig. 5(c)) and VQE-QSE* with curvature-induce-corrected LZSH (Fig. 5(d)) is presented. Fig. 5(c) exhibits a smooth transition but instantly turns to oscillations after 6 fs, suggesting sudden emergence of hopping events at the late stage of dissociation, which we ascribe to the discontinuity of PESs with a small displacement interval at the far dissociation plateau, where PESs tend to be close and parallel. In Fig. 5(d), the application of the curvature-driven hopping correction technique (as introduced in eqn (31)) significantly stabilizes the dynamics and makes populations evolve more smoothly, without losing the essential physical picture of the evolution, with S2 smoothly depopulating and S1 & S0 stabilizing, closely mimicking the reference population behavior.
In addition, the sharp oscillations observed in Fig. 5(b) and (c) arise not only from the numerical instability of the quantum-computing PES solver but also from an insufficient number of trajectories. In surface-hopping NAMD simulations, a sufficiently large number of trajectories is essential for mitigating statistical noise and achieving reliable ensemble averaging. However, emulating quantum algorithms on classical computers is computationally demanding; thus, to accommodate limited resources, all simulations presented in Fig. 5 employ only 50 trajectories. The erratic fluctuations in panel (b) persist throughout the dynamics, highlighting the inherent instability of the VQE-QSE solver and the inadequacy of the trajectory count. Panel (c), which employs the improved VQE-QSE* method without curvature-induced hopping correction, exhibits smooth initial behavior but deviates from the exact reference. A similar trend is observed in panel (d) upon application of the curvature correction, where the population evolution does not precisely match the reference. These artifacts primarily originate from the insufficient number of trajectories in the LZSH ensemble.
To quantify the accuracy of the quantum electronic structure solver and to reveal the underlying cause of the late-6 fs oscillation, Fig. 6(a) compares the PESs at late dissociation times from 4 fs onward, where the surfaces S0, S1, and S2 of both reference and VQE-QSE* converge smoothly and closely. Dotted lines depict the absolute energy errors relative to the exact solution, revealing that VQE-QSE* errors remain below 10−7 hartree but spike intermittently. Note that the initial guess heritage of VQE during the PES calculation could not fully smoothen such microscopic spikes. These artifacts, though small, can induce unphysical hops in regions of near-degeneracy.
The geometric trajectories of the molecular ensemble, visualized in Fig. 6(b), demonstrate the realistic dissociation trajectories in the x–y plane, given by the hopping corrected LZSH-NAMD with the VQE-QSE* solver. The trajectories fan out symmetrically from the central equilibrium geometry, with clusters branching toward positive and negative y-directions. The multi-colored lines indicate temporal evolution, with earlier times near the origin and later dispersion. Atoms in the same trajectory share the same color, whose initial positions and momentum are determined by Wigner sampling.
Use case II: C2H4 results in CAS(2,2)
To assess the adaptability of the subspace-based quantum electronic structure solvers in capturing the PESs, we examine the pyramidalization pathway of C2H4 within the complete active space (CAS(2,2)) framework, which encompasses the π and π* orbitals. Fig. 7(a) illustrates the PES with a large displacement interval along the pyramidalization angle ϕ, comparing the exact diagonalization results (gray lines) with SSVQE[0]-QSE and SSVQE[0]-QSE*.Quantitative energy errors for these solvers are summarized in Table 4. Among PESs with an interval degree of 3 and 0.3 between data points, all the hybrid subspace-based solvers reached sub-microhartree accuracy. Compared to the CAS(3,2) ionic system examined in the preceding section, the current system features a smaller active space, enabling QSE to exhibit high accuracy in the exemplified regime as well. This underscores the utility of QSE in certain scenarios. However, the QSE* demonstrates slightly lower fidelity because expanding subspaces with extra operators would introduce more linear independence, which leads to a larger condition number of overlapping matrix S, affecting numerical stability.
| ΔE (Hartree) | SSVQE[0] | SSVQE[0]-QSE | SSVQE[0]-QSE* | SSVQE[1] |
|---|---|---|---|---|
| 3-Degree interval angle | ||||
| RMSE | 1.033 × 10−13 | 7.666 × 10−14 | 7.415 × 10−13 | — |
| Max error | 2.416 × 10−13 | 1.847 × 10−13 | 9.948 × 10−13 | — |
| MAE | 8.266 × 10−14 | 5.921 × 10−14 | 7.375 × 10−13 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 0.3-Degree interval angle | ||||
| RMSE | 1.033 × 10−13 | 7.666 × 10−14 | 7.415 × 10−13 | 8.67 × 10−3 |
| Max error | 2.416 × 10−13 | 1.847 × 10−13 | 9.948 × 10−13 | 9.03 × 10−3 |
| MAE | 8.266 × 10−14 | 5.921 × 10−14 | 7.375 × 10−13 | 8.60 × 10−3 |
Here, we present the results prior to energy ordering of the states. Unlike the conventional scenario, where VQE is used to search the ground state followed by QSE to obtain excited states, here, SSVQE (as introduced in eqn (8)) yields the higher-energy V state116 in the region before the conical intersection. In contrast, QSE, by expanding the subspace, expands the lower-energy N state in this region. Furthermore, SSVQE demonstrates robust state-tracking capabilities. After the conical intersection, SSVQE continues to track the V state (which now becomes the ground state), while QSE, leveraging the reference state from this region, accurately extends to the higher-energy excited state.
A more detailed examination of the region of PESs with an interval of 0.3° around the conical intersection is provided in Fig. 7(b), where we compare the energy of the N-state and V-state directly from SSVQE. The hybrid subspace-based solvers maintain high fidelity to the exact curves, with correct transitions through the conical intersection region. In contrast, the SSVQE-solo results deviate noticeably. This behavior indicates that where the weighted sum of energies from orthogonal references (eqn (8)) is insufficient to resolve all subspaces without additional constraints, it requires a more advanced SSVQE extension or other methods.
The force calculations along the pyramidalization coordinate of the first carbon atom in C2H4 within the CAS(2,2) active space reveal the efficacy of the FDM integrated with quantum electronic structure solvers for excited-state properties. As illustrated in Fig. 8 and Table 5 taking the x-axis for demonstration, the reference exact forces (gray lines) are closely reproduced by both the hybrid subspace-based solvers, with deviations becoming more pronounced at larger FDM step lengths (δ). For δ = 0.001, the computed forces overlay nearly identically with the exact profile across the full range of dihedral angles, capturing changes around the conical intersection. In contrast, larger steps (δ = 0.01 and 0.1) introduce systematic errors, manifesting as offsets.
| ΔF (Hartree Angstrom−1) | S0 | S1 |
|---|---|---|
| δ = 0.001hartree | ||
| RMSE | 3.740 × 10−7 | 2.187 × 10−7 |
| Max error | 6.312 × 10−7 | 4.209 × 10−7 |
| Mean absolute error | 3.238 × 10−7 | 1.946 × 10−7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| δ = 0.010hartree | ||
| RMSE | 3.29165 × 10−5 | 1.78885 × 10−5 |
| Max error | 5.12144 × 10−5 | 2.91406 × 10−5 |
| Mean absolute error | 2.94293 × 10−5 | 1.48558 × 10−5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| δ = 0.100hartree | ||
| RMSE | 3.2648329 × 10−3 | 1.7893454 × 10−3 |
| Max error | 5.0488511 × 10−3 | 2.9237422 × 10−3 |
| Mean absolute error | 2.9277802 × 10−3 | 1.4836350 × 10−3 |
Complementing the static analysis, Fig. 8(b) and Table 6 present the SSVQE-QSE* PESs along the geometry of a LZSH-NAMD reference trajectory, capturing the temporal evolution of S0 and S1 energies in 30 fs. However, along this realistic trajectory, QSE fails largely at many geometries; thus only QSE* results are presented. The SSVQE-QSE* energies for S0 and S1 faithfully reproduce the result using the exact reference electronic solver.
| ΔE (Hartree) | S0 | S1 |
|---|---|---|
| RMSE | 1.57 × 10−13 | 2.5747180 × 10−8 |
| Max error | 7.53 × 10−13 | 1.06571761 × 10−7 |
| Mean absolute error | 1.12 × 10−13 | 1.1482544 × 10−8 |
Noisy results
In Fig. 9 and Table 7 we demonstrate the PES and nuclear forces of two chemical systems C2H4 and H3+, under noisy quantum simulation conditions. For C2H4, in the range before the conical intersection, the noisy QSE fails to expand the N-state based on the V-state searched by noisy SSVQE. This revealed that quantum noise significantly impacts the cooperation of the hybrid subspace-based quantum solver, preventing it from reaching the target states.| ΔE (Hartree) | S0 | S1 | S2 |
|---|---|---|---|
| RMSE | 3.556 × 10−2 | 2.240 × 10−2 | 1.409 × 10−2 |
| Max error | 7.966 × 10−2 | 5.650 × 10−2 | 3.961 × 10−2 |
| MAE | 3.092 × 10−2 | 1.917 × 10−2 | 9.822 × 10−3 |
In contrast, the H3+ system exhibits a smoother response to noise, manifesting as a consistent offset in the PES and nuclear forces. Notably, QSE calculations based on noisy ground states yielded excited-state deviations smaller than those of the corresponding noisy ground states. This behavior is attributed to the error mitigation capabilities inherent in the QSE framework (as introduced in the previous section), showing its robustness in noisy environments.
Triplet results
To further explore the utility of the subspace quantum-computing electronic structure solver, we evaluated its performance in computing triplet state energies, as shown in Fig. 10 and Table 8. For CH2O, the CAS(3,2) active space consisted of the three Hartree–Fock canonical orbitals straddling the Fermi level. Here, the QSE consistently yields three degenerate or near-degenerate energy values for triplet states. We explored two strategies for processing these values: averaging the three energies or selecting the median value, with the latter often proving more accurate. These findings demonstrate QSE's potential for investigating more sophisticated excited-state dynamics in future studies.| ΔE (Hartree) | T1 average | T2 average | T1 middle | T2 middle |
|---|---|---|---|---|
| H 3 + | ||||
| RMSE | 1.14 × 10−3 | 1.83 × 10−4 | 0.0 | 0.0 |
| Max error | 5.65 × 10−3 | 9.99 × 10−4 | 0.0 | 0.0 |
| MAE | 4.19 × 10−4 | 3.75 × 10−5 | 0.0 | 0.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| CH 2 O | ||||
| RMSE | 6.80 × 10−8 | — | 0.0 | — |
| Max error | 3.40 × 10−7 | — | 0.0 | — |
| MAE | 1.36 × 10−8 | — | 0.0 | — |
Computational resource analysis
To quantify the impact of our parallelization strategies on computational efficiency, we present benchmark results from executing the QSE algorithm via a quantum algorithm simulator on a classical computer, focusing on wall-clock times for key components of the excited-state dynamics simulation. Fig. 11(a) illustrates the CPU times required for ground-state energy evaluations using VQE with UCCSD (1a: 4.86 s) and its noisy variant (1b: 72.42 s), excited-state subspace diagonalizations via various QSE implementations (2a–2g), and force computations employing FDM or HFM approaches (3a–3d). Notably, the parallelized QSE implementations demonstrate substantial speedups over their serial counterparts. For the spin-adapted singlet variant, the parallel QSE (2a: 8.93 s) achieves approximately a 12-fold reduction compared to the serial QSE (2c: 104.91 s), attributable to the concurrent evaluation of expectation values for the independent Pauli strings in the H and S matrices (eqn. (10)). Similarly, for the triplet QSE, parallelization (2b: 84.35 s) yields a comparable 12× speedup relative to the serial case (2d: 990.99 s). The CAS(4,2) (4o2e) QSE-triplet (2e: 1617.02 s), which incorporates excitation operators, incurs additional overhead due to the increased subspace dimension, highlighting the trade-off between accuracy and efficiency in a larger subspace. Under noisy conditions, emulating realistic quantum hardware errors, the parallel singlet QSE (2f: 131.35 s) remains efficient. For QSE*, since we have expanded more operators and conducted parallel estimation on these operators, the acceleration effect will be more significant if there is sufficient hardware.At the force computation level, the HFM approach (3b: 6.09 s) outperforms the FDM (3a: 248.90 s) by 41× in the noiseless regime, reflecting the lower measurement demands of direct derivative evaluations compared to the FDM. Noise channel simulation amplifies this disparity, with the noisy FDM (3c: 2553.15 s) being 21× slower than the noisy HFM (3d: 119.31 s).
Extending to full trajectory propagation, Fig. 11(c) depicts the cumulative computation time as a function of time steps for a representative non-adiabatic dynamics simulation under LZSH, comparing noiseless and noisy scenarios with parallel versus serial QSE integrated into VQE for ground-state preparation, alongside HFM or FDM for forces. The parallel QSE configurations consistently exhibit shallower slopes, indicating reduced per-step overhead. For instance, the noiseless VQE with parallel-QSE and HFM (blue line) accumulates 105 s by 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, whereas the serial-QSE equivalent (green line) approaches 106 s, a 10× difference arising from the distributed measurement strategy. This gap widens in noisy emulations, where parallel-QSE with the FDM (purple line) remains below 107 s, while serial-QSE with the FDM (magenta line) exceeds it, emphasizing the robustness of parallelization to noise channel computation. The HFM variants are generally preferred over their FDM counterparts within each category, aligning with the single-point benchmarks, though the asymptotic scaling remains dominated by the QSE matrix construction.
000 steps, whereas the serial-QSE equivalent (green line) approaches 106 s, a 10× difference arising from the distributed measurement strategy. This gap widens in noisy emulations, where parallel-QSE with the FDM (purple line) remains below 107 s, while serial-QSE with the FDM (magenta line) exceeds it, emphasizing the robustness of parallelization to noise channel computation. The HFM variants are generally preferred over their FDM counterparts within each category, aligning with the single-point benchmarks, though the asymptotic scaling remains dominated by the QSE matrix construction.
Beyond the per-trajectory level, our trajectory-level parallelization exploits the parallel nature of the ensemble, distributing independent Wigner-sampled trajectories across computational nodes. While not explicitly benchmarked here due to hardware constraints, scaling analyses suggest near-linear speedups with the number of processors, limited only by load balancing in asynchronous hop events. Collectively, these optimizations reduce overall simulation wall times by 1–2 orders of magnitude for typical photochemistry applications with 10–100 trajectories and active spaces of 4–8 orbitals, paving the way for efficient quantum-classical hybrid simulations.
While our benchmarks focus on validating the efficiency gains from parallelization (via classical-computing emulations of quantum algorithms), it is important to contextualize these results against traditional classical computational chemistry software. At present, simulations of quantum algorithms on a classical computer are substantially slower than well-optimized classical programs (e.g., those implemented in C++/Fortran with extensive algorithmic refinements), stemming from the emulation's need to mimic quantum operations through matrix-vector computations (or matrix–matrix computation for a noisy quantum circuit) with limited optimizations to preserve universality. Moreover, current quantum hardware lacks the necessary fidelity for high-precision electronic structure calculations, precluding direct comparisons of real quantum runtimes.
In terms of user experience, classical software programs (e.g. Pyscf,110 Molpro,117 Psi4,118etc.) offer seamless access to a broad array of properties beyond energies, such as spin expectation values (S2) and configuration interaction coefficients facilitated by storing the full wavefunction in classical memory for efficient post-processing. Quantum approaches, by contrast, require explicit measurements for each desired observable—e.g., additional shots for S2via spin operators—and accessing configuration interaction coefficients demands quantum state tomography to retrieve all 2n amplitudes (n being the number of spin orbitals), which is exponentially challenging and resource-intensive. Thus, while quantum methods hold promise for scaling to larger systems, classical quantum chemistry software currently provides a more convenient and comprehensive workflow.
Conclusion
In this work, we have developed an efficient quantum computational framework for NAMD, in which parallelization is supported for both high-precision PES calculation and quantum-algorithm adapted LZSH trajectory simulation. Our approach integrates the CAS framework with VQE and its subspace variant SSVQE, to adaptably prepare reference states. Additionally, we incorporate QSE and its extended variant QSE* for accurate excited-state calculations. Beyond energy spectrum computation, our method enables the calculation of nuclear forces by interfacing quantum-computing PES solvers with the HFM and FDM. Another advancement is the seamless integration of quantum algorithms with the LZSH framework, augmented by curvature-induced hopping corrections to mitigate PES fluctuations at dissociation limits.Numerical benchmarks on H3+, C2H4, and CH2O demonstrate sub-microhartree accuracy on PESs by our hybrid subspace quantum-computing electronic structure solvers. By validating the problem-tailored QSE operator extension, we enhance the adaptability of our approach across those diverse chemical systems. The incorporation of quantum-computing electronic structure solvers and curvature-driven hopping correction in LZSH significantly improves the robustness of NAMD simulations while preserving efficiency, as evidenced by comparisons with exact reference results. Furthermore, computational resource analysis shows that our two-level parallelization framework delivers substantial computational speedups, fully transferable to a real quantum computer, without compromising precision.
This work advances quantum computational NAMD by addressing critical bottlenecks in efficiency and robustness at both the trajectory level and electronic structure levels, while enhancing the adaptability and precision of PES calculation. These advancements pave the way for exploring non-adiabatic effects in polyatomic molecules beyond classical computational limits while facilitating the practical utility of quantum computing. However, challenges persist, including the systematic handling of S matrix ill-conditioning in QSE, ansatz expressivity in VQE, and integration with advanced infrastructures to handle quantum noise. Future efforts will focus on integrating orbital optimization techniques, such as the complete active space self-consistent field (CASSCF) method, developing systematic QSE extension strategies, and exploring the embedding of quantum computing in other NAMD frameworks.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI) of this article. Data and scripts for this paper, including the PES, forces and NAMD initial conditions, are available at Zenodo at: https://doi.org/10.5281/zenodo.17865112. The code utilized in this study is available in the project Gitee repository: https://gitee.com/mindspore/mindquantum/new/research/paper_with_code/Efficient_Quantum_Simulation_of_Non-Adiabatic_Molecular_Dynamics_with_Precise_Electronic_Structure. Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00433k.Acknowledgements
This work was supported by the NSAF (Grant No. U2330201), the National Natural Science Foundation of China (Grant No. 22303005), the Innovation Program for Quantum Science and Technology (Grant No. 2023ZD0300200), the CPS-Yangtze Delta Region Industrial Innovation Center of Quantum and Information Technology-MindSpore Quantum Open Fund, and the High-performance Computing Platform of Peking University.References
- O. V. Prezhdo, others Efficient Modeling of Quantum Dynamics of Charge Carriers in Materials Using Short Nonequilibrium Molecular Dynamics, J. Phys. Chem. Lett., 2023, 14, 8289–8295 CrossRef PubMed.
- L. González and P. Marquetand, The Quest to Simulate Excited-State Dynamics of Transition Metal Complexes, JACS Au, 2021, 1, 1130–1150 Search PubMed.
- C. Li and G. A. Voth, Using Constrained Density Functional Theory to Track Proton Transfers and to Sample Their Associated Free Energy Surface, J. Chem. Theory Comput., 2021, 17, 5759–5765 CrossRef CAS PubMed.
- B. F. E. Curchod and T. J. Mart'inez, Ab Initio Nonadiabatic Quantum Molecular Dynamics, Chem. Rev., 2018, 118, 3305–3336 Search PubMed.
- S. Mai and L. Gonz'alez, Molecular Photochemistry: Recent Developments in Theory, Angew. Chem., Int. Ed., 2020, 59, 16832–16846 CrossRef CAS PubMed.
- M. Born and J. R. Oppenheimer, Zur Quantentheorie der Molekeln, Ann. Phys., 1927, 389, 457–484 Search PubMed.
- R. N. Barnett and U. Landman, Born-Oppenheimer molecular-dynamics simulations of finite systems: Structure and dynamics of (H2O)2, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2081–2097 Search PubMed.
- T. D. Kühne, M. Krack, F. R. Mohamed and M. Parrinello, Efficient and Accurate Car-Parrinello-like Approach to Born-Oppenheimer Molecular Dynamics, Phys. Rev. Lett., 2007, 98, 066401 CrossRef PubMed.
- A. M. N. Niklasson, Extended Born-Oppenheimer Molecular Dynamics, Phys. Rev. Lett., 2008, 100, 123004 CrossRef PubMed.
- L. X. Chen, Probing Transient Molecular Structures in Photochemical Processes Using Laser-Initiated Time-Resolved X-Ray Absorption Spectroscopy, Chem. Rev., 2004, 104, 2665–2692 Search PubMed.
- B. F. E. Curchod and I. Tavernelli, Ultrafast Spectroscopy of Photoactive Molecular Systems from First Principles: Where We Stand Today and Where We Are Going, J. Phys. Chem. Lett., 2020, 11, 6271–6281 Search PubMed.
- E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. van Grondelle, Quantum Coherence in Photosynthesis for Efficient Solar-Energy Conversion, Nat. Phys., 2014, 10, 676–682 Search PubMed.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, J. Rosenthal, G. W. Coates and T. J. Meyer, Proton-Coupled Electron Transfer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS PubMed.
- M. H. V. Huynh and T. J. Meyer, Proton-Coupled Electron Transfer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Proton-Coupled Electron Flow in Protein Redox Machines, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed.
- W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Electronic Structure, Dynamics & Spectroscopy, World Scientific, Singapore, 2004, vol. 15 Search PubMed.
- G. A. Worth and L. S. Cederbaum, Beyond Born-Oppenheimer: Molecular Dynamics Through a Conical Intersection, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- B. G. Levine and T. J. Martínez, Isomerization Through Conical Intersections, Annu. Rev. Phys. Chem., 2007, 58, 613–634 CrossRef CAS PubMed.
- S. Matsika, Reviews in Computational Chemistry, John Wiley & Sons, Ltd, Hoboken, NJ, 2007, pp. 83–124 Search PubMed.
- S. Matsika and P. Krause, Nonadiabatic Events and Conical Intersections, Annu. Rev. Phys. Chem., 2011, 62, 621–643 CrossRef CAS PubMed.
- B. G. Levine, M. P. Esch, B. S. Fales, D. T. Hardwick, W.-T. Peng and Y. Shu, Conical Intersections at the Nanoscale: Molecular Ideas for Materials, Annu. Rev. Phys. Chem., 2019, 70, 21–43 CrossRef PubMed.
- L. Shen, B. Xie, Z. Li, L. Liu, G. Cui and W.-H. Fang, Role of Multistate Intersections in Photochemistry, J. Phys. Chem. Lett., 2020, 11, 8490–8501 CrossRef CAS PubMed.
- S. Matsika, Electronic Structure Methods for the Description of Nonadiabatic Effects and Conical Intersections, Chem. Rev., 2021, 121, 9407–9449 CrossRef CAS PubMed.
- M. Beck, A. Jäckle, G. Worth and H.-D. Meyer, The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- L. L. E. Cigrang, et al., Roadmap for Molecular Benchmarks in Nonadiabatic Dynamics, J. Phys. Chem. A, 2025, 129, 7023–7050 CrossRef CAS PubMed.
- X. Li, J. C. Tully, H. B. Schlegel and M. J. Frisch, Ab initio Ehrenfest dynamics, J. Chem. Phys., 2005, 123, 084106 CrossRef.
- M. Ben-Nun, J. Quenneville and T. J. Martínez, Ab Initio Multiple Spawning: Photochemistry from First Principles Quantum Molecular Dynamics, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef CAS.
- R. K. Preston and J. C. Tully, Trajectory Surface Hopping Approach to Nonadiabatic Molecular Collisions: The Reaction of H+ with D2, J. Chem. Phys., 1971, 55, 562–572 CrossRef.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS , introduces the fewest switches surface hopping (FSSH) algorithm, which LZSH builds upon, providing a framework for nonadiabatic dynamics..
- A. K. Belyaev, C. Lasser and G. Trigila, Landau–Zener type surface hopping algorithms, J. Chem. Phys., 2014, 140, 224108 CrossRef PubMed.
- C. Zhu and H. Nakamura, Theory of nonadiabatic transition for general two-state curve crossing problems. I. Nonadiabatic tunneling case, J. Chem. Phys., 1994, 101, 10630–10647 CrossRef CAS.
- C. Zhu, H. Kamisaka and H. Nakamura, New implementation of the trajectory surface hopping method with use of the Zhu–Nakamura theory, J. Chem. Phys., 2001, 115, 3031–3044 CrossRef CAS.
- C. Zhu, H. Kamisaka and H. Nakamura, New implementation of the trajectory surface hopping method with use of the Zhu–Nakamura theory. II. Application to the charge transfer processes in the 3D DH2+ system, J. Chem. Phys., 2002, 116, 3234–3243 CrossRef CAS.
- Y. Shu, L. Zhang, X. Chen, S. Sun, Y. Huang and D. G. Truhlar, Nonadiabatic Dynamics Algorithms with Only Potential Energies and Gradients: Curvature-Driven Coherent Switching with Decay of Mixing and Curvature-Driven Trajectory Surface Hopping, J. Chem. Theory Comput., 2022, 18, 1320–1328 CrossRef CAS PubMed.
- X. Zhao, Y. Shu, L. Zhang, X. Xu and D. G. Truhlar, Direct Nonadiabatic Dynamics of Ammonia with Curvature-Driven Coherent Switching with Decay of Mixing and with Fewest Switches with Time Uncertainty: An Illustration of Population Leaking in Trajectory Surface Hopping Due to Frustrated Hops, J. Chem. Theory Comput., 2023, 19, 1672–1685 CrossRef CAS PubMed.
- X. Zhao, I. C. D. Merritt, R. Lei, Y. Shu, D. Jacquemin, L. Zhang, X. Xu, M. Vacher and D. G. Truhlar, Nonadiabatic Coupling in Trajectory Surface Hopping: Accurate Time Derivative Couplings by the Curvature-Driven Approximation, J. Chem. Theory Comput., 2023, 19, 6577–6588 CrossRef CAS PubMed.
- J. Suchan, J. Janoš and P. Slavíček, Pragmatic Approach to Photodynamics: Mixed Landau–Zener Surface Hopping with Intersystem Crossing, J. Chem. Theory Comput., 2021, 17, 3444–3457 Search PubMed.
- J. J. Eriksen and J. Gauss, The Shape of Full Configuration Interaction to Come, J. Phys. Chem. Lett., 2021, 12, 418–427 CrossRef CAS PubMed , for FCI exponential scaling..
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for Density Functional Theory, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed , for DFT limitations in strong correlation..
- L. Lacombe and N. T. Maitra, Non-adiabatic approximations in time-dependent density functional theory: progress and prospects, npj Comput. Mater., 2023, 9, 111 CrossRef , for DFT limitations in nonadiabatic regimes..
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS , for quantum computing in the electronic structure..
- K. Head-Marsden, J. Flick, C. J. Ciccarino and P. Narang, Quantum Information and Algorithms for Correlated Quantum Matter, Chem. Rev., 2021, 121, 3061–3120 CrossRef CAS PubMed , for quantum algorithms for correlated systems..
- S. Lee, et al., Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry, Nat. Commun., 2023, 14, 1952 CrossRef CAS PubMed , for exponential speedup in quantum chemistry..
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated Quantum Computation of Molecular Energies, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- M. Reiher, N. Wiebe, K. M. Svore, D. Wecker and M. Troyer, Elucidating Reaction Mechanisms on Quantum Computers, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7555–7560 CrossRef CAS.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New J. Phys., 2016, 18, 023023 CrossRef.
- S. Zhao, D. Tang, X. Xiao, R. Wang, Q. Sun, Z. Chen, X. Cai, Z. Li, H. Yu and W.-H. Fang, Quantum Computation of Conical Intersections on a Programmable Superconducting Quantum Processor, J. Phys. Chem. Lett., 2024, 15, 7244–7253 CrossRef CAS PubMed.
- J. Preskill, Quantum Computing in the NISQ era and beyond, Quantum, 2018, 2, 79 CrossRef.
- O. Higgott, D. Wang and S. Brierley, Variational Quantum Computation of Excited States, Quantum, 2019, 3, 156 CrossRef.
- S. Belaloui, N. E. Belaloui and A. Benslama, On the Simulation of Conical Intersections in Water and Methanimine Molecules Via Variational Quantum Algorithms, arXiv, 2025, preprint, arXiv:2507.22670, DOI:10.48550/arXiv.2507.22670.
- K. M. Nakanishi, K. Mitarai and K. Fujii, Subspace-search variational quantum eigensolver for excited states, Phys. Rev. Res., 2019, 1, 033062 CrossRef CAS.
- J. Robledo-Moreno, et al., Chemistry beyond the scale of exact diagonalization on a quantum-centric supercomputer, Sci. Adv., 2025, 11(25), eadu9991 CrossRef CAS.
- S. Barison, J. Robledo Moreno and M. Motta, Quantum-centric computation of molecular excited states with extended sample-based quantum diagonalization, Quantum Sci. Technol., 2025, 10, 025034 CrossRef.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- Y. Tong, V. V. Albert, J. Preskill and Y. Su, Generalized Quantum Subspace Expansion, Phys. Rev. Lett., 2022, 129, 020502 CrossRef PubMed.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Increasing the Representation Accuracy of Quantum Simulations of Chemistry without Extra Quantum Resources, Phys. Rev. X, 2020, 10, 011004 CAS.
- M. Urbanek, D. Camps, R. Van Beeumen and W. A. de Jong, Chemistry on Quantum Computers with Virtual Quantum Subspace Expansion, J. Chem. Theory Comput., 2020, 16, 5425–5431 CrossRef CAS PubMed.
- D. Alfonso, Y.-L. Lee, H. P. Paudel and Y. Duan, Chemical applications of variational quantum eigenvalue-based quantum algorithms: Perspective and survey, Appl. Phys. Rev., 2025, 12, 031304 CAS.
- P. J. Ollitrault, A. Kandala, C.-F. Chen, M. Pistoia, A. Mezzacapo, K. Temme, M. Takita, J. Rice and A. J.-A. Martin, others Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor, Phys. Rev. Res., 2020, 2, 043140 CrossRef CAS.
- H. R. Grimsley, N. I. Mayhall, D. Claudino, N. M. Tubman, C. A. Morrison, M. Metcalf, S. E. Economou and E. Barnes, Challenging excited states from adaptive quantum eigensolvers: subspace expansions vs. state-averaged strategies, Quantum Sci. Technol., 2025, 10, 025003 CrossRef.
- A. Gandon, A. Baiardi, P. Ollitrault and I. Tavernelli, Nonadiabatic Molecular Dynamics with Fermionic Subspace-Expansion Algorithms on Quantum Computers, J. Chem. Theory Comput., 2024, 20, 5951–5963 CrossRef CAS PubMed.
- E. Sangiogo Gil, M. Oppel, J. S. Kottmann and L. González, SHARC meets TEQUILA: mixed quantum-classical dynamics on a quantum computer using a hybrid quantum-classical algorithm, Chem. Sci., 2025, 16, 596–609 RSC.
- C. Hempel, C. Maier, J. Romero, J. McClean, T. Monz, H. Shen, P. Jurcevic, B. P. Lanyon, P. Love, R. Babbush, A. Aspuru-Guzik, R. Blatt and C. F. Roos, Quantum Chemistry Calculations on a Trapped-Ion Quantum Simulator, Phys. Rev. X, 2018, 8, 031022 CAS.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Publications, New York, 1989, Originally published by McGraw-Hill in 1982 Search PubMed.
- J. Tilly, P. Sriluckshmy, A. Patel, E. Fontana, I. Rungger, E. Grant, R. Anderson, J. Tennyson and G. H. Booth, Reduced density matrix sampling: Self-consistent embedding and multiscale electronic structure on current generation quantum computers, Phys. Rev. Res., 2021, 3, 033230 CrossRef CAS.
- D. S. King and L. Gagliardi, A Ranked-Orbital Approach to Select Active Spaces for High-Throughput Multireference Computation, J. Chem. Theory Comput., 2021, 17, 2817–2831 Search PubMed.
- Z. Luo, Y. Ma, C. Liu and H. Ma, Efficient Reconstruction of CAS-CI-Type Wave Functions for a DMRG State Using Quantum Information Theory and a Genetic Algorithm, J. Chem. Theory Comput., 2017, 13, 4699–4710 Search PubMed.
- W. Jeong, S. J. Stoneburner, D. King, R. Li, A. Walker, R. Lindh and L. Gagliardi, Automation of Active Space Selection for Multireference Methods via Machine Learning on Chemical Bond Dissociation, J. Chem. Theory Comput., 2020, 16, 2389–2399 Search PubMed.
- P. Jordan and E. Wigner, Über das Paulische Äquivalenzverbot, Z. Phys., 1928, 47, 631–651 Search PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 Search PubMed.
- J. Tilly, others The Variational Quantum Eigensolver: A review of methods and best practices, Phys. Rep., 2022, 986, 1–45 Search PubMed , reviews the CASCI-VQE method, detailing its application in quantum chemistry for computing adiabatic potential energy surfaces..
- A. Asthana, A. Kumar, V. S. A. Abraham, P. A. Bhobe, A. K. Pal and T. S. Mahesh, Contextual subspace variational quantum eigensolver calculation of the dissociation curve of fermion-boson system on a superconducting quantum processor, npj Quantum Inf., 2024, 10, 25 Search PubMed.
- M. Matoušek, K. Pernal, F. Pavošević and L. Veis, Variational Quantum Eigensolver Boosted by Adiabatic Connection, J. Phys. Chem. A, 2024, 128, 687–698 CrossRef PubMed.
- W. Mizukami, K. Mitarai, Y. O. Nakagawa, Y. Ibe, Y. Koh and N. Koizumi, Orbital optimized unitary coupled cluster theory for quantum computer, Phys. Rev. Res., 2020, 2, 033421 Search PubMed.
- P. J. Ollitrault, A. Kandala, C.-F. Chen, M. Pistoia, A. Mezzacapo, K. Temme, M. Takita, J. Rice and A. J.-A. Martin, others Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor, Phys. Rev. Res., 2020, 2, 043140 CrossRef CAS.
- A. Gandon, A. Baiardi, M. Rossmannek, W. Dobrautz and I. Tavernelli, Quantum computing in spin-adapted representations for efficient simulations of spin systems, PRX Quantum, 2025, 6, 030306 CrossRef.
- E. N. Epperly, L. Lin and Y. Nakatsukasa, A Theory of Quantum Subspace Diagonalization, SIAM J. Matrix Anal. Appl., 2022, 43, 1263–1290 CrossRef.
- C. Umeano, F. M. C. Jamet, L. P. Lindoy, I. Rungger and O. Kyriienko, Quantum subspace expansion approach for simulating dynamical response functions of Kitaev spin liquids, Phys. Rev. Mater., 2025, 9, 034401 Search PubMed.
- N. Yoshioka, H. Hakoshima, Y. Matsuzaki, Y. Tokunaga, Y. Suzuki and S. Endo, Generalized Quantum Subspace Expansion, Phys. Rev. Lett., 2022, 129, 020502 CrossRef CAS PubMed.
- Z. Cai, Quantum Error Mitigation using Symmetry Expansion, Quantum, 2021, 5, 548 CrossRef.
- J. R. McClean, Z. Jiang, N. C. Rubin, R. Babbush and H. Neven, Decoding quantum errors with subspace expansions, Nat. Commun., 2020, 11, 636 CrossRef CAS PubMed.
- I. O. Sokolov, P. K. Barkoutsos, L. Moeller, P. Suchsland, G. Mazzola and I. Tavernelli, Microcanonical and finite-temperature ab initio molecular dynamics simulations on quantum computers, Phys. Rev. Res., 2021, 3, 013125 Search PubMed.
- T. E. O'Brien, M. Streif, N. C. Rubin, R. Santagati, Y. Su, W. J. Huggins, J. J. Goings, N. Moll, E. Kyoseva, M. Degroote, C. S. Tautermann, J. Lee, D. W. Berry, N. Wiebe and R. Babbush, Efficient quantum computation of molecular forces and other energy gradients, Phys. Rev. Res., 2022, 4, 043210 CrossRef.
- P. Pulay, Analytical derivatives, forces, force constants, molecular geometries, and related response properties in electronic structure theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 169–181 Search PubMed , for finite differences and Pulay forces in MO-based methods..
- I. N. Levine, Quantum Chemistry, Pearson, 6th edn, 2009, For the Hellmann–Feynman theorem derivation and its application to variational wavefunctions Search PubMed.
- J. Lai, Y. Fan, Q. Fu, Z. Li and J. Yang, Accurate and efficient calculations of Hellmann–Feynman forces for quantum computation, J. Chem. Phys., 2023, 159, 114113 Search PubMed , for the Hellmann–Feynman theorem in the context of VQE and analytical gradients..
- S. Pathak, I. E. López, A. J. Lee, W. P. Bricker, R. L. Fernández, S. Lehtola and J. A. Rackers, Accurate Hellmann–Feynman forces from density functional calculations with augmented Gaussian basis sets, J. Chem. Phys., 2023, 158, 014104 CrossRef CAS PubMed , for Pulay forces and basis set dependence in Hellmann-Feynman calculations..
- T. E. O'Brien, B. Senjean, R. Sagastizabal, X. Bonet-Monroig, A. Dutkiewicz, F. Buda, L. DiCarlo and L. Visscher, Calculating energy derivatives for quantum chemistry on a quantum computer, npj Quantum Inf., 2019, 5, 113 CrossRef , for derivative Hamiltonian and force operators in VQE, including MO-based force calculations..
- J. Jiří, S. Petr and B. F. E. Curchod, Selecting Initial Conditions for Trajectory-Based Nonadiabatic Simulations, Acc. Chem. Res., 2025, 58(2) DOI:10.1021/acs.accounts.4c00687.
- M. Barbatti, S. Mai, M. Richter, M. Ruckenbauer, B. P. Fingerhut, F. Plasser, T. Schnappinger, M. Oppel, P. Marquetand, K. Sen and H. Lischka, Newton-X Platform: New Software Developments for Surface Hopping and Nuclear Ensembles, J. Chem. Theory Comput., 2022, 18, 6851–6865 CrossRef CAS PubMed.
- J. Suchan, D. Hollas, B. F. E. Curchod and P. Slav'iček, On the importance of initial conditions for excited-state dynamics, Faraday Discuss., 2018, 212, 307–330 RSC.
- D. A. McQuarrie and J. D. Simon, Physical Chemistry: A Molecular Approach, 2000, Provides a detailed explanation of Wigner sampling and the Wigner distribution for harmonic oscillators in phase space, suitable for initializing quantum nuclear effects Search PubMed.
- C. F. Kammerer and P. Gérard, Wigner Measures and Molecular Propagation Through Generic Energy Level Crossings, Prépublication de l'Université de Cergy-Pontoise, 2002, Discusses Wigner measures in the context of molecular propagation, relevant for understanding Wigner sampling in nonadiabatic dynamics Search PubMed.
- X. Bian, et al., Quantum Solver of Contracted Eigenvalue Equations (QSE) for Quantum Chemistry, J. Chem. Theory Comput., 2021, 17, 2854–2866 Search PubMed , describes the quantum solver of contracted eigenvalue equations (QSE) for computing potential energy surfaces in quantum chemistry..
- M. Barbatti, Nonadiabatic dynamics with trajectory surface hopping in the adiabatic representation, J. Chem. Phys., 2011, 135, 174102 Search PubMed , details the detection of local minima in energy gaps for surface hopping and handling of nonadiabatic transitions without explicit coupling vectors..
- G. A. Hagedorn, Proof of the Landau–Zener formula in an adiabatic limit with small eigenvalue gaps, Commun. Math. Phys., 1991, 136, 433–449 CrossRef , provides a rigorous mathematical analysis of the Landau–Zener formula, foundational for nonadiabatic transition probabilities in LZSH..
- L. Wang, et al., A class of Landau-Zener type surface hopping algorithms, J. Chem. Phys., 2014, 140, 124106 CrossRef PubMed , compares Landau–Zener formulae for nonadiabatic transition probabilities, including their application in surface hopping algorithms..
- N. Sisourat, et al., Ultrafast dynamics of H2O+ following photoionization in the 20-35 eV energy range, J. Chem. Phys., 2015, 142, 104307 CrossRef PubMed , describes a practical implementation of Landau–Zener surface hopping for water molecule photodynamics, including input file specifications and velocity rescaling..
- T. Jíra, J. Janoš and P. Slavíček, Critical Assessment of Curvature-Driven Surface Hopping Algorithms, J. Chem. Theory Comput., 2025, 21, 9784–9798 CrossRef.
- W. Mizukami, Chemqulacs: Quantum chemistry code for quantum circuit simulators and quantum computers, GitHub repository, 2025, https://github.com/wmizukami/chemqulacs, accessed on August 16, 2025.
- M. Barbatti, et al., Newton-X Platform: New Software Developments for Surface Hopping and Nuclear Ensembles, J. Chem. Theory Comput., 2022, 18, 6851–6865 CrossRef CAS PubMed.
- X. Xu, et al., MindSpore Quantum: A User-Friendly, High-Performance, and AI-Compatible Quantum Computing Framework, arXiv, 2024, preprint, arXiv:2406.17248, DOI:10.48550/arXiv.2406.17248.
- Inc., Q, Contributors QURI Parts: An open source library suite for creating and executing quantum algorithms on various quantum computers and simulators, https://github.com/QunaSys/quri-parts, 2022.
- Y. Suzuki, et al., Qulacs: a fast and versatile quantum circuit simulator for research purpose, Quantum, 2021, 5, 559 CrossRef.
- P. O. Dral, MLatom: A Program Package for Quantum Chemical Research Assisted by Machine Learning, J. Comput. Chem., 2019, 40, 2339–2347 Search PubMed.
- P. O. Dral, F. Ge, B.-X. Xue, Y.-F. Hou, M. Pinheiro Jr, J. Huang and M. Barbatti, MLatom 2: An Integrative Platform for Atomistic Machine Learning, Top. Curr. Chem., 2021, 379, 27 CrossRef CAS PubMed.
- P. O. Dral, et al., MLatom 3: A Platform for Machine Learning-Enhanced Computational Chemistry Simulations and Workflows, J. Chem. Theory Comput., 2024, 20, 1193–1213 CrossRef CAS PubMed.
- P. O. Dral, et al., MLatom: A Package for Atomistic Simulations with Machine Learning, 2013–2024 Search PubMed.
- Q. Sun, et al., Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, A quantum computing view on unitary coupled cluster theory, Chem. Soc. Rev., 2022, 51, 1659–1684 RSC.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, Generalized Unitary Coupled Cluster Wave functions for Quantum Computation, J. Chem. Theory Comput., 2018, 15, 311–324 CrossRef PubMed.
- D. C. Liu and J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Program., 1989, 45, 503–528 CrossRef.
- X.-H. Zha, C. Zhang, D. Fan, P. Xu, S. Du, R.-Q. Zhang and C. Fu, The impacts of optimization algorithm and basis size on the accuracy and efficiency of variational quantum eigensolver, arXiv, 2021, preprint, arXiv:2006.15852, DOI:10.48550/arXiv.2006.15852.
- S. Mukherjee, D. Mukhopadhyay and S. Adhikari, Conical intersections and diabatic potential energy surfaces for the three lowest electronic singlet states of H_3+, J. Chem. Phys., 2014, 141, 204306 CrossRef PubMed.
- S. Saade and H. G. A. Burton, Excited State-Specific CASSCF Theory for the Torsion of Ethylene, J. Chem. Theory Comput., 2024, 20, 3466–3477 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- D. G. A. Smith, et al., PSI4 1.4: Open-source software for high-throughput quantum chemistry, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |







