 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
When machine learning models learn chemistry I: quantifying explainability with matched molecular pairs
Kerrin Janssena,
Jan M. Wollschläger b,
Jonny Proppe*a and
Andreas H. Göller
b,
Jonny Proppe*a and
Andreas H. Göller *c
*c
aTU Braunschweig Institute of Physical and Theoretical Chemistry, Gauss Str 17, 38106 Braunschweig, Germany. E-mail: j.proppe@tu-braunschweig.de
bBayer AG Pharmaceuticals, R&D, Machine Learning Research, 13353 Berlin, Germany
cBayer AG Pharmaceuticals, R&D, Computational Molecular Design, 42096 Wuppertal, Germany. E-mail: andreas.goeller@bayer.com
First published on 9th February 2026
Abstract
Explainability methods in machine learning-driven research are increasingly being used, but it remains challenging to assess their reliability without deeply investigating the specific problem at hand. In this work, we present a Python-based Workflow for Interpretability Scoring using matched molecular Pairs (WISP). This workflow can be applied to assess the performance of explainability methods on any given dataset containing SMILES and is model-agnostic, making it compatible with any machine learning model. Evaluation on two physics-based datasets demonstrates that the explanations reliably capture the predictions of the respective machine learning models. Furthermore, our workflow reveals that explainability methods can only meaningfully reflect the property of interest when the underlying models achieve high predictive accuracy. Therefore, the explainability performance on a test set can function as a quality measure of the underlying model. To ensure compatibility with any model type, we developed an atom attributor, which generates atom-level attributions for any model using any descriptor that can be obtained using SMILES representations. This method can also be applied as a standalone explainability tool, independently of WISP. WISP enables users to interpret a wide range of machine learning models in the chemical domain and gain valuable insights into how these models operate and the extent to which they capture underlying chemical principles.
1 Introduction
Machine learning is a powerful tool to support decision-making across many areas of the life sciences.1–3 It can save time and resources for laboratory scientists, for example in the development of new bioactive compounds through quantitative structure–activity relationship (QSAR) models, the optimization of drug properties such as absorption, distribution, metabolism, excretion, and toxicity (ADMET), or in computer-aided synthesis planning (CASP).4–10 By incorporating model explanations11–13 into the workflow, the ‘black-box’ nature of these models can be reduced, trust in the predictions can be increased, and molecular design can be enhanced when combined with chemical intuition.14,15Visualization techniques, such as heatmaps of model explanations, can help clarify model behavior and inspire new research directions.4–6,9,16–19 In this context, the model explanations refer to attributions assigned to each atom by the respective explainability method, indicating the contribution of each atom to the predicted property of interest. Such visual tools can be valuable for both machine learning experts and non-experts.6 Machine learning experts can use the heatmaps as a sanity check to visually verify what their models have learned.20 For non-experts, these heatmaps provide an accessible tool to guide molecular design decisions without requiring detailed knowledge of the underlying machine learning model.
Various approaches for interpretability have already been described in the literature.21–23 For example, the XSMILES approach by Heberle et al. assigns attributions to each character in the input SMILES and presents them in an interactive format.15 Besides understanding the behavior of ML models, Humer et al. highlighted the challenge of comparing different explainable AI (XAI) methods as an important open research question.6 Being able to compare different XAI methods and their performance gives users the opportunity to choose the most suitable explainability approach for the problem at hand. Humer et al. addressed these tasks through an interactive two-dimensional visualization of molecules with their respective heatmaps, as well as a table view summarizing model performances.6 Building on this work, we introduce a workflow for interpretability scoring using matched molecular pairs (WISP) and a descriptor- and model-agnostic chemical explainability method — the atom attributor. Humer et al. also highlighted the lack of a connection between performance metrics and explainability in interactive tools, which is precisely one of the key aspects WISP is designed to address.6
To assess the performance of different explainability methods, we made use of matched molecular pairs (MMPs). MMPs are pairs of chemically similar molecules that differ by only a small, well-defined structural change, such as the substitution of a functional group.24 The portion of the molecule that changes is referred to as the variable part, while the unchanged portion is called the constant part. Because only a single structural modification separates the pair, changes in molecular properties can often be directly linked to this specific difference.25 This connection between structural differences and the resulting property change in the MMP can be used to quantify explainability methods, since an effective explainability method should be able to link the predicted property change to the relevant chemical motif.26 This concept is similar to the approach used by Wellawatte et al., who employed counterfactuals to explain the influence of functional group changes on model outcomes.22 Counterfactuals describe the minimal modification required to change an outcome, a concept rooted in both philosophical reasoning and mathematical analysis.13,14,27–29 Likewise, Vangala et al. used MMPs to evaluate their explainability method pBRICS, which determines fragment importances.30 With WISP, we are now able to quantitatively assess the performance of explainability methods, providing broader and more robust insights than relying solely on the analysis of specific MMPs within a dataset. By providing a quantitative evaluation, these performance measures indicate how well the explainability methods account for both the predicted outcomes and the property of interest, i.e., the extent to which the model has learned the underlying chemistry of the experimental data.
WISP enables us to assess whether a machine learning model genuinely captures underlying chemical relationships, or whether it merely learns numerical patterns without reflecting meaningful chemistry. We aim to quantify the chemical understanding of the method's performance and use it to assess the explainability performance for any given dataset (Fig. 1). WISP allows users to either evaluate the explainability of an existing model on a dataset or train a new model within its workflow, making it accessible to both experts and non-experts. After preprocessing and model evaluation, WISP computes attributions using model- and descriptor-agnostic methods, allowing users to apply different explainers (e.g., the atom attributor, RDKit or SHAP). This aligns with the findings of Li et al., who recommend employing multiple explainability methods for comparative evaluation.31 Matched molecular pairs (MMPs) are generated to quantitatively assess attribution accuracy through parity plots and metrics, providing a measure of how well explanations generalize to new data.
This workflow (Fig. 1) enables users to gain valuable insights into chemical data and model behavior, and to select models that align more closely with chemical intuition. Reflecting on negative results can further help identify patterns or factors that may contribute to inaccurate explanations—and, by extension, to unreliable predictions. We also aim to evaluate how accurate models need to be in order to reliably reflect underlying chemical relationships, providing valuable guidance for future model development and application.
In this work, we describe the design and functionality of WISP, detailing how each component of the code contributes to quantifying different explainability methods (Sec. 2). We then evaluate the model performances (Sec. 3.1) and apply WISP to the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (Sec. 3.2), experimental log
P (Sec. 3.2), experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (Sec. 3.3), and solubility datasets (Sec. 3.4) to demonstrate the workflow's outcomes and illustrate how these results can be interpreted and used. Whether you are facing challenges for structural changes in molecular design, want to evaluate the quality of your machine learning model, or seek systematic ways to improve it, WISP provides the necessary insights and tools to support these tasks.
P (Sec. 3.3), and solubility datasets (Sec. 3.4) to demonstrate the workflow's outcomes and illustrate how these results can be interpreted and used. Whether you are facing challenges for structural changes in molecular design, want to evaluate the quality of your machine learning model, or seek systematic ways to improve it, WISP provides the necessary insights and tools to support these tasks.
2 Methods
2.1 WISP workflow
To quantify the performance of the explainability methods, we examined the attributions in the context of matched molecular pairs (MMPs). To achieve this, we summed the attributions of each atom (attri) of the variable part (N1 and N2) for each molecule and calculated the difference between these sums for each matched molecular pair. Details on how the attributions were calculated can be found in Section 2.4.
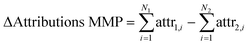 | (1) |
This difference is then compared with the difference in the model predictions (pred1;2) for the pair,
| ΔPredictions MMP = pred1 − pred2 | (2) |
Next, the squared Pearson correlation coefficient (eqn (3)) and the accuracy (eqn (4)) can be calculated for both differences.
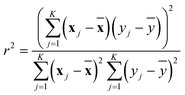 | (3) |
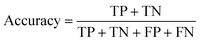 | (4) |
For the squared Pearson correlation coefficient, the sums iterate over the dataset with K datapoints. The index j refers to a single datapoint, while ȳ and x denote the respective means. The accuracy indicates the percentage of molecules for which the attributions are correctly assigned in terms of sign. In this context, true positives (TP) and true negatives (TN) represent molecules where the sign of the attribution matches the sign of the prediction. Conversely, false positives (FP) and false negatives (FN) correspond to molecules where this sign agreement is not present. This allows the quantification of how well the explainability methods capture the changes in the model's predictions.
Additionally, we created a histogram of the ΔAttributions MMP for the constant part of each pair. Here, each data point represents the change in the attributions within the constant part of a single MMP.
For (mostly) group-additive tasks like Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, a robust explainability method should yield a Δ of zero for the constant part. By analyzing this histogram, one can assess how much variability the constant part introduces and to what extent this affects the reliability of the explainability method. In cases where no intermolecular interactions between the molecules of the dataset play a role, this metric should correlate with the variability in the constant part and thus with the quality of the machine learning model.
P, a robust explainability method should yield a Δ of zero for the constant part. By analyzing this histogram, one can assess how much variability the constant part introduces and to what extent this affects the reliability of the explainability method. In cases where no intermolecular interactions between the molecules of the dataset play a role, this metric should correlate with the variability in the constant part and thus with the quality of the machine learning model.
In WISP, users can choose whether they want to evaluate the explainability performance of an existing model on a given dataset (Fig. 1, top row) or whether they wish to provide only a dataset and have WISP train a model within the workflow (Fig. 1, bottom row). This flexibility also makes WISP accessible to users who may not be familiar with machine learning. After preprocessing, the attributions for the input dataset are computed (Sec. 2.4) and, if no machine learning model is supplied, one will be trained and evaluated (Fig. 1, right). Because the atom attributor is model- and descriptor-agnostic, it is always applied within the WISP framework. If the trained model uses RDKit fingerprints or Morgan fingerprints, the RDKit attributions are also generated. SHAP attributions are calculated only if the input features are Morgan fingerprints and the model is compatible with the SHAP explainer. This aspect is not discussed in detail here but can be found in part II of this paper series. Subsequently, MMPs are generated from the input data, and the atom indices of variable and constant parts of the molecules are determined to enable quantitative evaluation of the attributors, including parity plots and accuracy scores (eqn (4)).
If the model is trained within the workflow, WISP also computes the explanations on the training and test sets separately. This provides insights into how well the explanations generalize to unseen data.
2.2 Datasets and preprocessing
We evaluated WISP and the atom attributor by applying them to two different datasets covering three endpoints (i.e., properties of interest). These endpoints represent a broad range of prediction tasks and varying levels of difficulty. Additional endpoints such as yield prediction, pKi values for the inhibition of coagulation Factor Xa, and AMES mutagenicity can be found in part II of this series.We tested the validity of the workflow using the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P as a property of interest.32 Crippen log
P as a property of interest.32 Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is defined as a purely additive property, which is why we considered it the simplest evaluation task. Since the Crippen log
P is defined as a purely additive property, which is why we considered it the simplest evaluation task. Since the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P model assigns contributions to hydrogen atoms within molecules, these must be taken into account in the present investigation.33 However, the inclusion and evaluation of hydrogen atoms is not part of the standard WISP workflow in order to reduce the computing times and was therefore only used to evaluate the calculated Crippen log
P model assigns contributions to hydrogen atoms within molecules, these must be taken into account in the present investigation.33 However, the inclusion and evaluation of hydrogen atoms is not part of the standard WISP workflow in order to reduce the computing times and was therefore only used to evaluate the calculated Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values. The next prediction task is the experimental log
P values. The next prediction task is the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, which is inherently noisier due to systematic and random measurement effects and thus more challenging to learn and explain than the Crippen log
P, which is inherently noisier due to systematic and random measurement effects and thus more challenging to learn and explain than the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P.32 The solubility dataset (solubility in water) should also be well-suited for explanation by the interpretability methods, since the underlying interactions are comparatively simple.32 This stands in contrast to more challenging tasks such as binding to a biological receptor, where complex protein–ligand interactions must be considered rather than only solvent–solute interactions.
P.32 The solubility dataset (solubility in water) should also be well-suited for explanation by the interpretability methods, since the underlying interactions are comparatively simple.32 This stands in contrast to more challenging tasks such as binding to a biological receptor, where complex protein–ligand interactions must be considered rather than only solvent–solute interactions.
The preprocessing of the datasets was performed using a module based on RDKit's (version 2024.09.6)  .34 The settings were configured to process molecules with up to 1000 atoms, consider a maximum of 10 tautomers during tautomer canonicalization, retain only the largest fragment when one SMILES contained multiple fragments, and apply normalization and sanitization. This step ensures that molecules represented differently are treated equally throughout the workflow. Duplicate SMILES with different property-of-interest entries due to one of the previous steps were removed, and in cases of duplicates with identical property-of-interest entries, only one entry was retained.
.34 The settings were configured to process molecules with up to 1000 atoms, consider a maximum of 10 tautomers during tautomer canonicalization, retain only the largest fragment when one SMILES contained multiple fragments, and apply normalization and sanitization. This step ensures that molecules represented differently are treated equally throughout the workflow. Duplicate SMILES with different property-of-interest entries due to one of the previous steps were removed, and in cases of duplicates with identical property-of-interest entries, only one entry was retained.
2.3 Model training
To enable robust evaluation of the explainability methods, WISP includes a model training routine when no pre-trained model is provided by the user. By default, an 80/20 train/test split is applied to the data. For model training, we integrated both algorithms and the
algorithms and the  framework to ensure that the best-performing model can be selected for each prediction task based on the training MAE.
framework to ensure that the best-performing model can be selected for each prediction task based on the training MAE.  offers access to deep learning models, which are widely recognized as state-of-the-art for molecular property prediction.35,36 For instance, the portfolio of
offers access to deep learning models, which are widely recognized as state-of-the-art for molecular property prediction.35,36 For instance, the portfolio of  includes an implementation of directed message-passing neural networks (D-MPNNs), making cutting-edge deep learning approaches accessible to users of any level of expertise.36 D-MPNNs have been shown to outperform baseline models like random forests trained on Morgan fingerprints in 9 out of 15 benchmark datasets.36,37 However, since they do not consistently outperform simpler models in every case and bear the risk of overfitting, we ensured that WISP supports a diverse range of model types to cover various use cases and data characteristics.
includes an implementation of directed message-passing neural networks (D-MPNNs), making cutting-edge deep learning approaches accessible to users of any level of expertise.36 D-MPNNs have been shown to outperform baseline models like random forests trained on Morgan fingerprints in 9 out of 15 benchmark datasets.36,37 However, since they do not consistently outperform simpler models in every case and bear the risk of overfitting, we ensured that WISP supports a diverse range of model types to cover various use cases and data characteristics.
 ); LASSO Regression (
); LASSO Regression (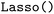 ); Bayesian Ridge Regression (
); Bayesian Ridge Regression (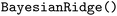 ); Random Forest Regression (
); Random Forest Regression (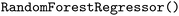 ); Gradient Boosting Regression (
); Gradient Boosting Regression (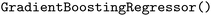 ); Support Vector Regression (
); Support Vector Regression (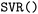 ); Gaussian Process Regression (
); Gaussian Process Regression (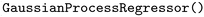 ) with the
) with the 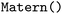 kernel and Multi-layer Perceptron Regression (
kernel and Multi-layer Perceptron Regression (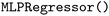 ), all implemented in
), all implemented in 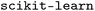 (version 1.6.1).38 For each model and feature combination, a
(version 1.6.1).38 For each model and feature combination, a 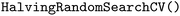 hyperparameter search was conducted using five-fold cross-validation on the training data. The parameter grid comprised a total of 82 hyperparameter combinations, while random seeds were kept constant. The results of the grid search can be found in Table SI-2. The mean absolute error (MAE, eqn (5)) was calculated for each fold, and the average MAE across all folds was used to compare model–feature combinations. The combination with the lowest average MAE was selected as the best model. The optimized model was then retrained on the entire training set and subsequently evaluated on the test set. Evaluation metrics included the squared Pearson correlation coefficient (r2, eqn (3)), the mean absolute error (MAE, eqn (5)), the root mean squared error (RMSE, eqn (6)), and the maximum absolute error (AEmax, eqn (7)). Here, x refers to the target property, and y refers to its predicted value. The summation is carried out over all K datapoints, with j indexing each datapoint individually. The term ȳ stands for the average of the predictions.
hyperparameter search was conducted using five-fold cross-validation on the training data. The parameter grid comprised a total of 82 hyperparameter combinations, while random seeds were kept constant. The results of the grid search can be found in Table SI-2. The mean absolute error (MAE, eqn (5)) was calculated for each fold, and the average MAE across all folds was used to compare model–feature combinations. The combination with the lowest average MAE was selected as the best model. The optimized model was then retrained on the entire training set and subsequently evaluated on the test set. Evaluation metrics included the squared Pearson correlation coefficient (r2, eqn (3)), the mean absolute error (MAE, eqn (5)), the root mean squared error (RMSE, eqn (6)), and the maximum absolute error (AEmax, eqn (7)). Here, x refers to the target property, and y refers to its predicted value. The summation is carried out over all K datapoints, with j indexing each datapoint individually. The term ȳ stands for the average of the predictions.
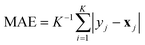 | (5) |
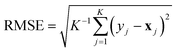 | (6) |
| AEmax = max{|yj − xj|}j=1K | (7) |
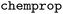 package (version 2.2.0) into the WISP workflow to enable the training and evaluation of deep learning models.36 For model training, we implemented a workflow where the predefined training set is split internally, using an 80/20 split to create a validation set during fitting. We employed the
package (version 2.2.0) into the WISP workflow to enable the training and evaluation of deep learning models.36 For model training, we implemented a workflow where the predefined training set is split internally, using an 80/20 split to create a validation set during fitting. We employed the 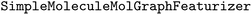 with
with 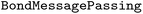 and
and 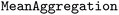 . For the feed-forward component, we used the
. For the feed-forward component, we used the 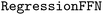 module. After training for 50 epochs (default), the MAE on the entire training set was determined and compared to the
module. After training for 50 epochs (default), the MAE on the entire training set was determined and compared to the 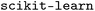 models to select the best-performing model type.
models to select the best-performing model type.2.4 Explainability methods
To enable comparison of all attribution methods across different datasets, we normalize the attributions by dividing each atom's attribution by the standard deviation of all attributions within the respective dataset. WISP supports the inclusion of any attribution method applicable to molecules. By default, it integrates the atom attributor, the RDKit attributor, and a SHAP-based attributor. Since the atom attributor is the only model— and descriptor—agnostic method among these, it is the primary focus in this work. The RDKit and SHAP attributors are described in detail in part II of this series.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P dataset, this amounts to approximately 324 mutant predictions in order to attribute each molecule. The number of valid mutations per atom is denoted by G. Valid mutated SMILES are then featurized and passed to the model to predict the property of interest (predmutated,h). The attribution for each atom is calculated as the average difference between the model's prediction on all mutated SMILES and the original SMILES prediction,
P dataset, this amounts to approximately 324 mutant predictions in order to attribute each molecule. The number of valid mutations per atom is denoted by G. Valid mutated SMILES are then featurized and passed to the model to predict the property of interest (predmutated,h). The attribution for each atom is calculated as the average difference between the model's prediction on all mutated SMILES and the original SMILES prediction,
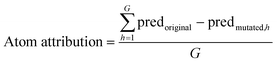 | (8) |
Building on Zhao et al.‘s work, we adapted our atom attributor to be descriptor-independent, enabling its use beyond models trained on CDDD embeddings as in the original implementation.39 Additionally, we introduced a validity check for mutated SMILES, which was not present in the original code, and focused on attributing atoms rather than every character of a SMILES string.
2.5 MMP generation
The matched molecular pairs (MMPs) were generated using the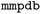 tool version 3.1.1.40 The process involved fragmenting and subsequently indexing the molecules to create a database of MMPs. The fragmentation followed these rules: a maximum of 100 heavy atoms per molecule (
tool version 3.1.1.40 The process involved fragmenting and subsequently indexing the molecules to create a database of MMPs. The fragmentation followed these rules: a maximum of 100 heavy atoms per molecule (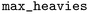 ), up to 10 rotatable bonds (
), up to 10 rotatable bonds (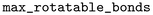 ), and exactly one cut in the variable fragment part (
), and exactly one cut in the variable fragment part ( ). Chirality was preserved during fragmentation (
). Chirality was preserved during fragmentation (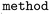 ), the RDKit standard salt remover was applied (
), the RDKit standard salt remover was applied (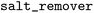 ), and the maximum number of “up” enumerations was set to 1000 (
), and the maximum number of “up” enumerations was set to 1000 (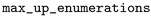 ), which controls stereochemistry enumeration. For indexing, default settings were used with some parameters explicitly set: a maximum of 10 heavy atoms in the variable fragment (
), which controls stereochemistry enumeration. For indexing, default settings were used with some parameters explicitly set: a maximum of 10 heavy atoms in the variable fragment (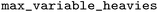 ), an environment radius between 0 and 5 (
), an environment radius between 0 and 5 (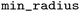 and
and 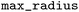 ), a maximum ratio of 0.2 for the variable part heavy atoms (non-hydrogen atoms) relative to the whole molecule heavy atoms (
), a maximum ratio of 0.2 for the variable part heavy atoms (non-hydrogen atoms) relative to the whole molecule heavy atoms (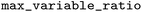 ), and all transformations were retained (
), and all transformations were retained (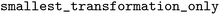 set to
set to  ). In this work, we primarily used the default settings of the
). In this work, we primarily used the default settings of the 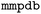 tool, except for setting the number of cuts to 1 and limiting the maximum ratio of the variable part to 0.2.40 These modifications were introduced to align with the definition of a matched molecular pair (small, well-defined structural change). To illustrate the impact of these settings, we performed an additional WISP run with the maximum variable ratio constraint disabled. The corresponding results are provided in the SI (Table SI-1). After creating the MMP database, the property of interest was loaded into the database using the
tool, except for setting the number of cuts to 1 and limiting the maximum ratio of the variable part to 0.2.40 These modifications were introduced to align with the definition of a matched molecular pair (small, well-defined structural change). To illustrate the impact of these settings, we performed an additional WISP run with the maximum variable ratio constraint disabled. The corresponding results are provided in the SI (Table SI-1). After creating the MMP database, the property of interest was loaded into the database using the 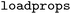 function. Finally, duplicate MMP entries were removed, retaining only the pair with the largest number of atoms in the constant part. This results in 920 to 2544 MMPs for the databases considered in this study (Table 1).
function. Finally, duplicate MMP entries were removed, retaining only the pair with the largest number of atoms in the constant part. This results in 920 to 2544 MMPs for the databases considered in this study (Table 1).
2.6 Creation of heatmaps
Heatmaps were created to visualize the atom attributions directly on the molecular structures. This was done using the function in RDKit. To ensure comparability between different heatmaps in one dataset, they were scaled so that the maximum color intensity reflects the 70th percentile of the absolute atom attributions in the entire dataset. This approach, inspired by Harren et al., ensures that the atom coloring maintains a sufficiently high visual intensity for meaningful interpretation.5
function in RDKit. To ensure comparability between different heatmaps in one dataset, they were scaled so that the maximum color intensity reflects the 70th percentile of the absolute atom attributions in the entire dataset. This approach, inspired by Harren et al., ensures that the atom coloring maintains a sufficiently high visual intensity for meaningful interpretation.5
3 Results and discussion
3.1 Model performances
The chemprop model trained on the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is the best-performing model in this study (Table 2) and is therefore most suited to quantify the error introduced by the machine learning model compared to the exact, rule-based reference. To further investigate the impact of model performance on explanation quality, we trained two models on the experimental log
P is the best-performing model in this study (Table 2) and is therefore most suited to quantify the error introduced by the machine learning model compared to the exact, rule-based reference. To further investigate the impact of model performance on explanation quality, we trained two models on the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P dataset. First, by disabling the GNN functionality, we derived the best possible model architecture available within the
P dataset. First, by disabling the GNN functionality, we derived the best possible model architecture available within the  library (Section 2.3.1), which in this case was a linear, an SVR and a GBR model (Table 2). In parallel, we trained the best-performing model for this task, i.e., a
library (Section 2.3.1), which in this case was a linear, an SVR and a GBR model (Table 2). In parallel, we trained the best-performing model for this task, i.e., a  graph neural network. The performance difference between these two models is substantial: The SVR model achieves an r2 of 0.49, while the
graph neural network. The performance difference between these two models is substantial: The SVR model achieves an r2 of 0.49, while the  model reaches an r2 of 0.74 (Table 2). A t test evaluating the significance of the model performances is provided in Table SI-3. Overall, across all regression tasks in this work, where the training was done by WISP, models based on the
model reaches an r2 of 0.74 (Table 2). A t test evaluating the significance of the model performances is provided in Table SI-3. Overall, across all regression tasks in this work, where the training was done by WISP, models based on the  architecture consistently outperform the models trained with
architecture consistently outperform the models trained with  .
.
| Property of interest | Model type | r2 | R2 | MAE | RMSE | AEmax | Model source |
|---|---|---|---|---|---|---|---|
Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
MolGraph; chemprop | 0.93 | 0.93 | 0.24 | 0.38 | 2.84 | WISP |
Exp log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
MolGraph; chemprop | 0.74 | 0.74 | 0.47 | 0.63 | 3.12 | WISP |
| Solubility | MolGraph; chemprop | 0.89 | 0.89 | 0.52 | 0.72 | 3.78 | WISP |
Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
Morgan fingerprint; Bayesian Ridge | 0.72 | 0.72 | 0.52 | 0.73 | 5.06 | WISP (no GNN) |
Exp log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
MACCS fingerprint; SVR | 0.49 | 0.49 | 0.66 | 0.88 | 4.19 | WISP (no GNN) |
| Solubility | MACCS fingerprint; Gradient Boosting | 0.77 | 0.77 | 0.73 | 1.06 | 5.39 | WISP (no GNN) |
3.2 Proof of concept: Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) P
P
In this work, we specifically compare the exact, rule-based Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P—which is perfectly explainable—to a machine-learned log
P—which is perfectly explainable—to a machine-learned log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P prediction. This comparison allows us to estimate the error introduced by the machine learning model in the explanations.
P prediction. This comparison allows us to estimate the error introduced by the machine learning model in the explanations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) P. As demonstrated by Rasmussen et al., the Crippen log
P. As demonstrated by Rasmussen et al., the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P serves as an effective benchmark for heatmap-based interpretability approaches.19 The Crippen log
P serves as an effective benchmark for heatmap-based interpretability approaches.19 The Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is an estimated log
P is an estimated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value calculated by summing fixed contributions from different atom types, yielding the calculated value Pcalc (eqn (9)).33
P value calculated by summing fixed contributions from different atom types, yielding the calculated value Pcalc (eqn (9)).33
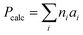 | (9) |
Here, the number of atoms of one specific type i is denoted by n, while a represents the contribution of the atom type.33 This makes the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P an excellent proof of concept for the WISP workflow, as the Δ values from eqn (1) ideally correspond exactly to the Δ in the calculated Crippen log
P an excellent proof of concept for the WISP workflow, as the Δ values from eqn (1) ideally correspond exactly to the Δ in the calculated Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P.
P.
As expected, the Δ in contributions from the entire molecule is in perfect agreement (r2 = 1.00) with the Δ in the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (Fig. 2a). However, when considering only the variable part of the molecule, the squared Pearson correlation coefficient between its contribution Δ and the Crippen log
P (Fig. 2a). However, when considering only the variable part of the molecule, the squared Pearson correlation coefficient between its contribution Δ and the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P Δ decreases to 0.93 (Fig. 2b). This reduction is attributable to the fact that Crippen atom contributions are dependent on the local chemical environment. For example, a carbonyl group adjacent to an aromatic system contributes +0.11, whereas the same group in an aliphatic environment contributes −0.15 to the Crippen log
P Δ decreases to 0.93 (Fig. 2b). This reduction is attributable to the fact that Crippen atom contributions are dependent on the local chemical environment. For example, a carbonyl group adjacent to an aromatic system contributes +0.11, whereas the same group in an aliphatic environment contributes −0.15 to the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P.33 This neighborhood dependency also explains the outliers observed in the difference of the constant part (Fig. 2d), where ideally the contribution difference should be zero, as the constant part should remain unchanged between matched molecular pairs (MMPs). To further investigate this issue, we included in the analysis a neighboring atom of the variable part that originally belonged to the constant part (Fig. 2c), resulting in a significantly improved correlation. This finding confirms that the reduced correlation in the variable part arises from the dependency of atom contributions on their immediate chemical surroundings. Still remaining deviations from the ideal correlation can be resolved by including a second neighboring atom, further supporting this conclusion.
P.33 This neighborhood dependency also explains the outliers observed in the difference of the constant part (Fig. 2d), where ideally the contribution difference should be zero, as the constant part should remain unchanged between matched molecular pairs (MMPs). To further investigate this issue, we included in the analysis a neighboring atom of the variable part that originally belonged to the constant part (Fig. 2c), resulting in a significantly improved correlation. This finding confirms that the reduced correlation in the variable part arises from the dependency of atom contributions on their immediate chemical surroundings. Still remaining deviations from the ideal correlation can be resolved by including a second neighboring atom, further supporting this conclusion.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) P. To quantify the influence of the machine learning model and the attribution method on explainability performance, a machine learning model was trained to predict the Crippen log
P. To quantify the influence of the machine learning model and the attribution method on explainability performance, a machine learning model was trained to predict the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (Table 2). The resulting model explainability demonstrates a significantly higher squared Pearson correlation coefficient (r2 = 0.77) (Fig. 4b), than the second-best SVR model (r2 = 0.45) (Fig. 7b) on the test set. Since the model operates on molecular graphs, only the atom attributor from the attributors used in this work is applicable for generating explanations in this case.
P (Table 2). The resulting model explainability demonstrates a significantly higher squared Pearson correlation coefficient (r2 = 0.77) (Fig. 4b), than the second-best SVR model (r2 = 0.45) (Fig. 7b) on the test set. Since the model operates on molecular graphs, only the atom attributor from the attributors used in this work is applicable for generating explanations in this case.The explainability performance on the test set closely mirrors that of the training set (Fig. 3). This consistency is expected, given the model's high predictive performance (Table 2), which suggests it is equally capable of providing meaningful explanations for both training and test data. This finding underscores that accurate predictions are a prerequisite for generating meaningful explanations on unseen data.
When comparing the explainability performance of the machine learning-based approach (Fig. 3) with the direct Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P calculation (Fig. 2), the former scores significantly worse in terms of the r2 value across all cases. This demonstrates how essential the influence of the
P calculation (Fig. 2), the former scores significantly worse in terms of the r2 value across all cases. This demonstrates how essential the influence of the  machine learning model as well as the attribution method is on the final explanations, and suggests that an r2 of 0.79 on the MMPs may represent the practical upper limit for this setup (Fig. 3b).
machine learning model as well as the attribution method is on the final explanations, and suggests that an r2 of 0.79 on the MMPs may represent the practical upper limit for this setup (Fig. 3b).
Examining individual example structures from the training and test sets (Fig. 5, left) shows that the machine-learned Crippen model correctly captures the overall trend and correctly attributes the amino group and fluorine, which is the variable part of the matched molecular pair. However, when comparing the ground-truth Crippen heatmap (Fig. 5, top left) to the heatmap produced by the machine-learned model (Fig. 5, bottom left), it becomes clear that the latter attributes the aromatic atoms with higher values than the ground truth but still with near constant attributions of the constant part.
 | ||
| Fig. 5 Comparison of heatmaps for the matched molecular pair consisting of CHEMBL247366 (test set) and CHEMBL594707 (training set), generated using WISP. | ||
To qualitatively assess how well the explanations reflect the model predictions, we calculated the accuracy of the ΔAttributions MMP (eqn (1)) in relation to the differences in predicted values, i.e., if the directions of the machine predictions and the attributions for the pairs are consistent (Table 3). Interestingly, the accuracy appears to improve when only the variable part of the molecule is considered. However, this observation is not consistent with the quantitative analysis presented in Fig. 3. One possible explanation lies in the presence of small variations around zero, which can increase the likelihood of false positives or negatives. In this example, the overall heatmap coloring—i.e., the reliability of the attributions—can be trusted with an accuracy of 80% on the training set and 84% on the test set.
| Property of interest (POI) | Training set | Test set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r2 whole molecule to pred. | r2 variable part to pred. | r2 whole molecule to POI | Std constant part | Accuracy variable part to pred. | r2 whole molecule to pred. | r2 variable part to pred. | r2 whole molecule to POI | Std constant part | Accuracy variable part to pred. | |
Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
0.73 | 0.79 | 0.66 | 2.85 | 0.90 | 0.73 | 0.77 | 0.64 | 3.10 | 0.93 |
Exp log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P GNN P GNN |
0.61 | 0.61 | 0.49 | 4.95 | 0.83 | 0.61 | 0.63 | 0.41 | 3.71 | 0.79 |
| Solubility | 0.85 | 0.90 | 0.78 | 4.32 | 0.94 | 0.91 | 0.96 | 0.77 | 5.59 | 0.95 |
Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P linear P linear |
0.63 | 0.49 | 0.30 | 4.39 | 0.79 | 0.74 | 0.55 | 0.05 | 5.30 | 0.80 |
Exp log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P SVR P SVR |
0.96 | 0.50 | 0.87 | 20.99 | 0.76 | 0.96 | 0.45 | 0.17 | 16.03 | 0.70 |
| Solubility GBR | 0.57 | 0.86 | 0.39 | 5.19 | 0.87 | 0.65 | 0.96 | 0.60 | 3.44 | 0.93 |
3.3 Experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) P
P
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P model training set (Fig. 6c), despite the model's relatively low performance (Table 2). The squared Pearson correlation coefficient for the explainability of the entire molecule is 0.96 on both the training and test sets (Fig. 6a and 7a). However, the explainability performance for the variable part of the MMP is considerably lower, with squared Pearson correlation coefficients of 0.50 for the training set and 0.47 for the test sets (Fig. 6b and 7b). The variation in the constant part is substantial, with standard deviations of 20.99 and 16.03 for the training and test set, respectively, indicating that the constant part introduces significant variability to the attributions. The largest discrepancy between the explainability of the training and test sets lies in the model's ability to explain the experimental values. For the training set, the model demonstrates reasonable explanatory power, with an r2 of 0.87 for the whole molecule. In contrast, on the test set, the r2 drops sharply to 0.17. These results suggest that the model fails to learn the underlying chemistry and, consequently, heatmaps generated from the test data should not be used to guide experimental decisions. Therefore, a drop in explainability performance on the test set can be regarded as a quality measure for the underlying model, which can be used systematically to improve the model or the training data, ultimately enabling the development of models that truly capture chemical relationships.
P model training set (Fig. 6c), despite the model's relatively low performance (Table 2). The squared Pearson correlation coefficient for the explainability of the entire molecule is 0.96 on both the training and test sets (Fig. 6a and 7a). However, the explainability performance for the variable part of the MMP is considerably lower, with squared Pearson correlation coefficients of 0.50 for the training set and 0.47 for the test sets (Fig. 6b and 7b). The variation in the constant part is substantial, with standard deviations of 20.99 and 16.03 for the training and test set, respectively, indicating that the constant part introduces significant variability to the attributions. The largest discrepancy between the explainability of the training and test sets lies in the model's ability to explain the experimental values. For the training set, the model demonstrates reasonable explanatory power, with an r2 of 0.87 for the whole molecule. In contrast, on the test set, the r2 drops sharply to 0.17. These results suggest that the model fails to learn the underlying chemistry and, consequently, heatmaps generated from the test data should not be used to guide experimental decisions. Therefore, a drop in explainability performance on the test set can be regarded as a quality measure for the underlying model, which can be used systematically to improve the model or the training data, ultimately enabling the development of models that truly capture chemical relationships.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P model, explainability on the training set does not improve for either the whole molecule or the variable part (Fig. 8) compared to the SVR model. However, the variability in the constant part is significantly reduced (Fig. 8d), with the standard deviation decreasing from 20.99 in the SVR model (Fig. 6d) to 4.95 in the GNN model (Fig. 8d). Additionally, the explainability performance for both the variable part and the property of interest on the test set increases substantially. Consequently, this model (Fig. 9) is considerably better suited to explain future data compared to the SVR model.
P model, explainability on the training set does not improve for either the whole molecule or the variable part (Fig. 8) compared to the SVR model. However, the variability in the constant part is significantly reduced (Fig. 8d), with the standard deviation decreasing from 20.99 in the SVR model (Fig. 6d) to 4.95 in the GNN model (Fig. 8d). Additionally, the explainability performance for both the variable part and the property of interest on the test set increases substantially. Consequently, this model (Fig. 9) is considerably better suited to explain future data compared to the SVR model.
Examining the accuracy of the variable part reveals a similar trend (Table 3). The explainability of the GNN model appears superior in capturing the trends of the variable part, whereas the SVR model demonstrates strong explainability for the whole molecule, consistent with the observations described above.
This difference between the SVR and GNN models also becomes evident when examining an example MMP (Fig. 5, right). For the SVR model (Fig. 5, top right), both molecules are almost uniformly colored, indicating that the model does not capture any meaningful structure–property relationships. In contrast, the heatmap derived from the GNN model is more detailed and shows that the nitrogen atoms in the right molecule are generally assigned a slightly negative contribution (Fig. 5, bottom right), reflecting the expected effect of heteroatoms decreasing lipophilicity. This more nuanced attribution is absent in the left molecule. A likely reason for this difference is that the left molecule is part of the test set, whereas the right molecule was included in the training set.
Different MMPs from this dataset are also discussed in the work of Humer et al.6 Here, Class Attribution Maps (CAMs) were used for atom-level attribution.6,41 In comparison, our heatmaps resemble their “base model” explanations, which are similarly more uniform than those from their more complex “XAI model”.6 Notably, their heatmaps show considerable variability in the constant parts of the molecules, whereas the results of this work fluctuate less—a marker of reliability (Fig. 5, right).
3.4 Solubility
The solubility model is the second-best performing model after the Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P model (Table 2). This is also reflected in the performance of its explanations: The correlation for the variable part partly forms a near–perfect correlation line (Fig. 10 and 11b panels). The MMPs contributing to this near–perfect correlation mostly involve relatively small variable regions, often consisting of the exchange of a single substituent on an aromatic ring. Moreover, it appears feasible to explain not only the predictions but also the solubility itself, as indicated by the high squared Pearson correlation coefficient of up to 0.77 on the test set (Fig. 11c). This represents the best test-set performance among all experiments conducted in this study and highlights the high quality of this model. Importantly, no significant drop in explainability performance between the training and test sets was observed, further supporting this conclusion, as discussed in Section 3.3.1. The slight improvements observed in the performance on the test set may be due to its small size: while the training set contains 574 MMPs, the test set includes only 44 MMPs. In the histogram of the constant part of the molecule (Fig. 10 and 11, panel d), ‘shoulders’ appear around a Δ of −10 and 10. These features arise from MMPs where, for example, a methyl group or halogen is exchanged for another small group, or a hydroxy group is replaced by a hydrogen atom.
P model (Table 2). This is also reflected in the performance of its explanations: The correlation for the variable part partly forms a near–perfect correlation line (Fig. 10 and 11b panels). The MMPs contributing to this near–perfect correlation mostly involve relatively small variable regions, often consisting of the exchange of a single substituent on an aromatic ring. Moreover, it appears feasible to explain not only the predictions but also the solubility itself, as indicated by the high squared Pearson correlation coefficient of up to 0.77 on the test set (Fig. 11c). This represents the best test-set performance among all experiments conducted in this study and highlights the high quality of this model. Importantly, no significant drop in explainability performance between the training and test sets was observed, further supporting this conclusion, as discussed in Section 3.3.1. The slight improvements observed in the performance on the test set may be due to its small size: while the training set contains 574 MMPs, the test set includes only 44 MMPs. In the histogram of the constant part of the molecule (Fig. 10 and 11, panel d), ‘shoulders’ appear around a Δ of −10 and 10. These features arise from MMPs where, for example, a methyl group or halogen is exchanged for another small group, or a hydroxy group is replaced by a hydrogen atom.
Qualitatively, the accuracy for the variable part is the highest across all experiments performed in this work. Accordingly, the user can rely on the attribution coloring of the variable part for 94% of the MMPs in the training set and 95% in the test set (Table 3).
4 Conclusion
In this work, we present WISP, a framework designed to qualitatively and quantitatively assess molecular model explainability, along with a novel, model- and descriptor-agnostic atom attributor. The matched molecular pair (MMP) analysis proved invaluable in assessing whether local structural changes are correctly reflected in the heatmaps, providing an objective sanity check alongside global correlation metrics. Our results show that the performance of explainability methods depends strongly on the underlying model quality.Our findings demonstrate that when a machine learning model achieves high predictive performance, it is usually capable of providing meaningful and reliable explanations for previously unseen data. The Crippen log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P served as a benchmark to define the upper bound for explainability when the true atom contributions to the property of interest are known, highlighting how model imperfections inevitably introduce systematic attribution errors (Table 3). Our results for the experimental log
P served as a benchmark to define the upper bound for explainability when the true atom contributions to the property of interest are known, highlighting how model imperfections inevitably introduce systematic attribution errors (Table 3). Our results for the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P dataset highlight how strongly model performance influences explainability performance. Here, the impact of model quality on the r2 of the variable part, the standard deviation of the constant part, and the r2 for the explanations on the test set becomes clear. On the test set, the r2 for the variable part is improved by 0.18 units with the better-performing model, while the standard deviation of the constant part decreases by 12.32 units. Since the explanation of unseen data is a key goal, having a well-performing model is essential to achieve this. While not an implication—see, e.g., the SVR log
P dataset highlight how strongly model performance influences explainability performance. Here, the impact of model quality on the r2 of the variable part, the standard deviation of the constant part, and the r2 for the explanations on the test set becomes clear. On the test set, the r2 for the variable part is improved by 0.18 units with the better-performing model, while the standard deviation of the constant part decreases by 12.32 units. Since the explanation of unseen data is a key goal, having a well-performing model is essential to achieve this. While not an implication—see, e.g., the SVR log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P model with high variability in the constant parts of the MMPs—we find evidence for a strong potential of high explainability on well-performing models. Consequently, there is a clear need to continue developing and validating robust, high-performing models to enable explanations that truly reflect underlying chemical relationships. A drop in explainability performance on the test set can serve as a valuable quality measure for the model's lacking ability to generalize and capture real chemical effects, guiding targeted improvements to both the model architecture and the training data.
P model with high variability in the constant parts of the MMPs—we find evidence for a strong potential of high explainability on well-performing models. Consequently, there is a clear need to continue developing and validating robust, high-performing models to enable explanations that truly reflect underlying chemical relationships. A drop in explainability performance on the test set can serve as a valuable quality measure for the model's lacking ability to generalize and capture real chemical effects, guiding targeted improvements to both the model architecture and the training data.
In summary, WISP provides an accessible, systematic way to scrutinize and compare model explanations, helping to identify where models succeed, where they fail, and how they can be improved. Our atom attributor extends explainability beyond specific embeddings or descriptors, offering a flexible approach for diverse molecular modeling tasks. Together, these contributions move us closer to the goal of truly interpretable and reliable AI-driven predictions in chemistry and drug discovery.
Author contributions
JMW + AHG: conceptualization, KJ + JMW: data curation, KJ: formal analysis, JP + AHG: funding acquisition, KJ: investigation, KJ + JMW: methodology, JP + AHG: project administration, JP + AHG: resources, KJ + JMW: software, JMW + JP + AHG: supervision, KJ: validation, KJ: visualization, KJ: writing – original draft, KJ + JMW + JP + AHG: writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
All the code for the presented work, as well as the URL to the public web app, are available on GitHub at https://github.com/kerjans/ml-XAI. An archived version of the whole code is provided at zenodo at https://doi.org/10.5281/zenodo.17055142.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5dd00398a.
Acknowledgements
JP acknowledges funding by Germany's joint federal and state program supporting early-career researchers (WISNA) established by the Federal Ministry of Education and Research (BMBF). The authors acknowledge Philipp Held (TU Braunschweig) for providing explanatory Jupyter notebooks on WISP. During the preparation of this work, the authors employed ChatGPT/OpenAI to improve phrasing and assist with coding. All generated content was carefully reviewed and edited by the authors, who take full responsibility for the accuracy and content of the publication.References
- E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg, O. Isayev, S. Curtalolo, D. Fourches, Y. Cohen, A. Aspuru-Guzik, D. A. Winkler, D. Agrafiotis, A. Cherkasov and A. Tropsha, Chem. Soc. Rev., 2020, 49, 3525–3564 Search PubMed.
- L. Zhang, J. Tan, D. Han and H. Zhu, Drug Discovery Today, 2017, 22, 1680–1685 CrossRef PubMed.
- K. Jorner, A. Tomberg, C. Bauer, C. Sköld and P.-O. Norrby, Nat. Rev. Chem., 2021, 5, 240–255 Search PubMed.
- P. Polishchuk, J. Chem. Inf. Model., 2017, 57, 2618–2639 CrossRef CAS PubMed.
- T. Harren, H. Matter, G. Hessler, M. Rarey and C. Grebner, J. Chem. Inf. Model., 2022, 62, 447–462 CrossRef CAS PubMed.
- C. Humer, H. Heberle, F. Montanari, T. Wolf, F. Huber, R. Henderson, J. Heinrich and M. Streit, J. Cheminf., 2022, 14, 21 Search PubMed.
- A. H. Göller, L. Kuhnke, F. Montanari, A. Bonin, S. Schneckener, A. ter Laak, J. Wichard, M. Lobell and A. Hillisch, Drug Discovery Today, 2020, 25, 1702–1709 Search PubMed.
- K. Janssen and J. Proppe, J. Chem. Inf. Model., 2025, 65, 1862–1872 CrossRef CAS PubMed.
- Y. Sushko, S. Novotarskyi, R. Körner, J. Vogt, A. Abdelaziz and I. V. Tetko, J. Cheminf., 2014, 6, 48 Search PubMed.
- M. Eckhoff, J. V. Diedrich, M. Mücke and J. Proppe, J. Phys. Chem. A, 2024, 128, 343–354 Search PubMed.
- D. Gunning, M. Stefik, J. Choi, T. Miller, S. Stumpf and G.-Z. Yang, Sci. Robot., 2019, 4, eaay7120 Search PubMed.
- J. D. Lee and K. A. See, Hum. Factors, 2004, 46, 50–80 Search PubMed.
- T. Miller, AI, 2019, 267, 1–38 Search PubMed.
- J. Jiménez-Luna, F. Grisoni and G. Schneider, Nat. Mach. Intell, 2020, 2, 573–584 Search PubMed.
- H. Heberle, L. Zhao, S. Schmidt, T. Wolf and J. Heinrich, J. Cheminf., 2023, 15, 2 Search PubMed.
- J. Jiménez-Luna, M. Skalic, N. Weskamp and G. Schneider, J. Chem. Inf. Model., 2021, 61, 1083–1094 CrossRef PubMed.
- A. Chatzimparmpas, R. M. Martins, I. Jusufi and A. Kerren, IV, 2020, 19, 207–233 Search PubMed.
- G. Marcou, D. Horvath, V. Solov’ev, A. Arrault, P. Vayer and A. Varnek, Mol. Inform., 2012, 31, 639–642 CrossRef CAS PubMed.
- M. H. Rasmussen, D. S. Christensen and J. H. Jensen, SciPost Che, 2023, 2, 002 CrossRef.
- M. Matveieva and P. Polishchuk, J. Cheminf., 2021, 13, 41 CAS.
- T. Janela and J. Bajorath, J. Chem. Inf. Model., 2023, 63, 7032–7044 CrossRef CAS PubMed.
- G. P. Wellawatte, H. A. Gandhi, A. Seshadri and A. D. White, J. Chem. Theory Comput., 2023, 19, 2149–2160 Search PubMed.
- D. Luo, W. Cheng, D. Xu, W. Yu, B. Zong, H. Chen and X. Zhang in Proceedings of the 34th International Conference on Neural Information Processing Systems, Curran Associates Inc., Red Hook, NY, USA, 2020, pp. 19620–19631 Search PubMed.
- J. Hussain and C. Rea, J. Chem. Inf. Model., 2010, 50, 339–348 Search PubMed.
- D. Stumpfe, H. Hu and J. Bajorath, ACS Omega, 2019, 4, 14360–14368 Search PubMed.
- J. Jiménez-Luna, M. Skalic and N. Weskamp, J. Chem. Inf. Model., 2022, 62, 274–283 Search PubMed.
- J. Woodward and C. Hitchcock, Nos, 2003, 37, 1–24 Search PubMed.
- A. Reutlinger, Philos. Sci, 2016, 83, 733–745 Search PubMed.
- D. Kahneman and D. T. Miller, Psychol. Rev, 1986, 93, 136–153 Search PubMed.
- S. R. Vangala, S. R. Krishnan, N. Bung, R. Srinivasan and A. Roy, J. Chem. Inf. Model., 2023, 63, 5066–5076 Search PubMed.
- S. Li, X. Wang and A. Barnard, Mach. Learn.: Sci. Technol, 2025, 6, 013002 Search PubMed.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530 Search PubMed.
- S. A. Wildman and G. M. Crippen, J. Chem. Inf. Comput. Sci., 1999, 39, 868–873 CrossRef CAS.
- G. Landrum, P. Tosco, B. Kelley, R. Rodriguez, D. Cosgrove, R. Vianello, P. sriniker, P. Gedeck, G. Jones, N. Schneider, E. Kawashima, D. Nealschneider, A. Dalke, M. Swain, B. Cole, S. Turk, A. Savelev, C. Tadhurst, A. Vaucher, M. Wójcikowski, I. Take, V. F. Scalfani, R. Walker, K. Ujihara, D. Probst, J. Lehtivarjo, H. Faara, G. Godin, A. Pahl and J. Monat, rdkit/rdkit: 2024_09_5 (Q3 2024) Release, 2025 Search PubMed.
- H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, Drug Discovery Today, 2018, 23, 1241–1250 CrossRef PubMed.
- E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green and C. J. McGill, J. Chem. Inf. Model., 2024, 64, 9–17 Search PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 5304–5305 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn Res., 2011, 12, 2825–2830 Search PubMed.
- L. Zhao, F. Montanari, H. Heberle and S. Schmidt, Artif. Intell. Life Sci., 2022, 2, 100047 Search PubMed.
- A. Dalke, J. Hert and C. Kramer, J. Chem. Inf. Model., 2018, 58, 902–910 Search PubMed.
- P. E. Pope, S. Kolouri, M. Rostami, C. E. Martin and H. Hoffmann in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, Long Beach, CA, USA, 2019, pp. 10764–10773 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |










