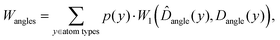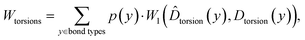Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Applications of modular co-design for de novo 3D molecule generation
Danny
Reidenbach†
 *a,
Filipp
Nikitin†‡
*a,
Filipp
Nikitin†‡
 *bc,
Olexandr
Isayev
*bc,
Olexandr
Isayev
 bc and
Saee Gopal
Paliwal
bc and
Saee Gopal
Paliwal
 a
a
aNVIDIA, Santa Clara, CA, USA. E-mail: dreidenbach@nvidia.com
bRay and Stephanie Lane Computational Biology Department, Carnegie Mellon University, Pittsburgh, PA, USA. E-mail: fnikitin@andrew.cmu.edu
cDepartment of Chemistry, Carnegie Mellon University, Pittsburgh, PA, USA
First published on 9th January 2026
Abstract
De novo 3D molecule generation is a pivotal task in drug discovery. However, many recent geometric generative models struggle to produce high-quality geometries, even if they able to generate valid molecular graphs. To tackle this issue and enhance the learning of effective molecular generation dynamics, we present Megalodon – a family of scalable transformer models. These models are enhanced with basic equivariant layers and trained using a joint continuous and discrete denoising co-design objective. We assess Megalodon's performance on established molecule generation benchmarks and introduce new 3D structure benchmarks that evaluate a model's capability to generate realistic molecular structures, particularly focusing on geometry precision. We show that Megalodon achieves state-of-the-art results in 3D molecule generation, conditional structure generation, and structure energy benchmarks using diffusion and flow matching. Furthermore, we demonstrate that scaling Megalodon produces up to 49× more valid molecules at large sizes and 2–10× lower energy compared to the prior best generative models. The code and the model are available at https://github.com/NVIDIA-Digital-Bio/megalodon.
1 Introduction
Molecular Generative models have been heavily explored due to the allure of enabling efficient virtual screening and targeted drug design.1 Similar to the rise in their application to computer vision (CV),2,3 Diffusion and Flow Matching models have been applied for tasks including molecule design, molecular docking, and protein folding.4–6 Across CV and chemical design, the scaling of model architectures and training data have seen significant accuracy improvements but questions surrounding how to scale effectively still persist.7Specifically for 3D molecule generation (3DMG), where the task is to unconditionally generate valid and diverse 3D molecules, diffusion models have shown great promise in enabling accurate generation starting from pure noise.8 The iterative nature of diffusion models allows them to explore a diverse range of molecular configurations, ideally providing valuable insights into potential drug candidates and facilitating the discovery of novel compounds. However, unlike in CV, which has seen systematic evaluations of training data and scaling, with tangible benchmark results,9 measuring success in de novo molecule generation is quite difficult. As a result, there is a nonlinear path to determining what truly is making an impact if, in each model, the data, architecture, training objective, and benchmarks differ. Furthermore, the commonly shared 3DMG benchmarks that do exist only evaluate molecular topologies, ignoring geometry, conformational energy, and model generalization to large molecule sizes – all quantities that are imperative for real-world use. In this work, we explore the above in the context of 3DMG and its interpretable benchmarks to directly target larger molecules.
Our main contributions are as follows:
• We present Megalodon, a scalable transformer-based architecture for multi-modal molecule diffusion and flow matching. This is the first 3DMG model to be tested with both objectives, with both obtaining state-of-the-art results. We show that our diffusion model excels at structure and energy benchmarks, whereas our flow matching model yields better 2D stability and the ability to use 25× fewer inference steps than its diffusion counterpart.
• Megalodon is the first model capable of unconditional molecule generation and conditional structure generation without retraining or finetuning.
2 Background
2.1 3D molecule generation
In de novo 3D molecule generation (3DMG), a molecule's 3D structure and 2D topology are simultaneously generated. We define a molecule M = (X, H, E, C) with N atoms where X ∈ RN×3, H ∈ {0, 1}N×A, E ∈ {0, 1}N×N×B, and C ∈ {0,1}N×D represents the atom coordinates, element types, bond types adjacency matrix, and formal charges respectively. Here, A denotes the number of atom types, B the number of bond types, and D the number of formal charge states. X is modeled as a continuous variable, whereas H, E, and C are discrete one-hot variables. X is modeled as a continuous variable whereas H, E, and C are discrete one-hot variables.2.2 Important qualities of 3D molecules
The GEOM dataset10 is widely used for 3D molecular structure (conformer) generation tasks, containing 3D conformations from both the QM9 and drug-like molecule (DRUGS) databases, with the latter presenting more complex and realistic molecules. Conformers in the dataset were generated using CREST,11 which performs extensive conformational sampling based on the semi-empirical extended tight-binding method (GFN2-xTB).12 This ensures that each conformation represents a local minimum in the GFN2-xTB potential energy surface (PES).A key requirement for generative models is their ability to implicitly learn PES of the training data and produce molecules that are local minima of the PES. However, since GFN2-xTB is itself a model rather than a universal energy function, comparing energies across different potentials (e.g., using GFN2-xTB optimized structures but computing energies with MMFF13) can introduce systematic errors. Differences in potential models, such as optimal bond lengths, may lead to unreliable results. Overall, the goal of 3DMG is to generate valid molecules mimicking the energy landscape of the GEOM dataset.
2.3 Related work
Hoogeboom et al.8 first introduced continuous diffusion modeling for coordinates and atom types using a standard equivariant graph neural network (EGNN) architecture.14 Following this, many models have been produced that make slight changes to the architecture and diffusion interpolant schedule to generate atom coordinates and types.15 While initially effective, they rely on OpenBabel16 software to infer chemical bonds, which is a standalone hard problem and introduces additional sources of error into the pipeline. So, methods began to generate the bond locations and types in the generative process.17 Vignac et al.18 was the first to use continuous diffusion for coordinates and discrete diffusion for the atom and bond types, removing the OpenBabel requirement. Le et al.19 used the same training objective but introduced a more effective equivariant architecture. Recently Irwin et al.20 uses continuous and discrete flow matching with a latent equivariant graph message passing architecture to show improved performance.Xu et al.21 introduces GeoLDM a geometric latent diffusion model for 3DMG. GeoLDM applies its diffusion process over a learned latent representation. So rather than updating the atom position and types in euclidean space everything is done inside the model. Similar to EDM, GeoLDM uses OpenBabel for bond prediction. Pinheiro et al.22 takes a different approach than majority of prior work in representing molecules as 3D voxels rather than graphs. This is akin to 3D image processing rather than point cloud processing. This however requires a recovery process as the voxels are not a natural molecule representation. Voxels however provide a better link to the applications of vision models which majority of the diffusion framework was created for. Lastly, Song et al.23 introduces GeoBFN a Geometric Bayesian Flow Network, that unlike diffusion models operate in the parameter space rather then product space. While the integration of 3D voxels would not work for Megalodon, latent diffusion and BFN extensions are something relevant to future work.
2.4 Stochastic interpolants
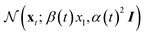 , this is,
, this is,| xt = α(t)ε + β(t)x1, | (1a) |
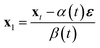 | (1b) |
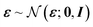 and x1 ∼ pdata(x1). Common choices for the interpolation include (assuming t ∈ [0, 1]), with t = 1 corresponding to data and t = 0 to noise:
and x1 ∼ pdata(x1). Common choices for the interpolation include (assuming t ∈ [0, 1]), with t = 1 corresponding to data and t = 0 to noise:
• Variance-preserving SDE-like from the diffusion model literature:26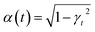 and
and 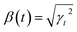 with some specific “noise schedule” γt which is commonly written as
with some specific “noise schedule” γt which is commonly written as 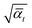 from Ho et al.27
from Ho et al.27
• Conditional linear vector field:24α(t) = 1 – (1 – σmin)t and β(t) = t with some smoothening of the data distribution σmin.
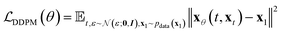 | (2) |
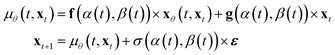 | (3) |
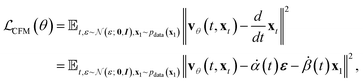 | (4) |
In practice, many methods use a “data prediction” objective to simplify training, which gives rise to the following loss function and inference Euler ODE update step following the conditional linear vector field.20,24
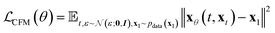 | (5) |
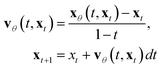 | (6) |
For scalar discrete random variables with K categories at, at−1 ∈ 1, …, K the forward transition probabilities can be represented by matrices: [Qt]ij = q(at = j|at+1 = i). Starting from our data a1 or aT (where T is the total number of discrete time steps),§ we obtain the following T – t + 1 step marginal and posterior at time t:
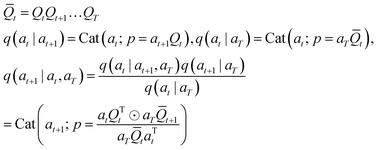 | (7) |
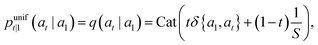 | (8) |
Diffusion models inherently rely on simulating Gaussian stochastic processes. In the forward process, data points are progressively noised, converging towards a Gaussian distribution. This process, derived from score-based generative models, aims to learn the score function (the gradient of the data distribution's log density) to reverse the diffusion process. The generative model effectively solves a Stochastic Differential Equation (SDE) that describes how data diffuses towards noise and how it can be denoised in reverse. The reverse process requires SDE simulation at every step, which involves sampling from a learned probabilistic model that estimates how to remove noise. This involves simulating random variables at each time step, making diffusion models highly dependent on repeated stochastic simulation.
Flow Matching, on the other hand, learns a continuous vector field that deterministically “flows” one distribution to another. The model learns this flow by matching the velocity field that pushes samples from a source distribution to a target distribution. Once the vector field is learned, generating samples involves solving an ODE that defines a continuous and deterministic trajectory from the source to the target distribution. Unlike diffusion models, which require simulating a series of stochastic transitions (noising and denoising) over many steps, flow matching learns a single, continuous flow. Sampling involves solving an ODE (or, in some cases, a deterministic SDE with noise) to move from the base distribution to the target in a smooth, deterministic fashion.
For DDPM, the equations only hold for the Gaussian path with access to a well-formed score function. This is why techniques like mini-batch Optimal Transport (OT) can be applied to FM but not diffusion to align pdata and pref.30 In FM, the vector field is learned, which, in the absence of OT, can be derived as a function of the score function, but having access to the score function is not a requirement to sample deterministically (simulation-free).
3 Methods
3.1 Megalodon Architecture
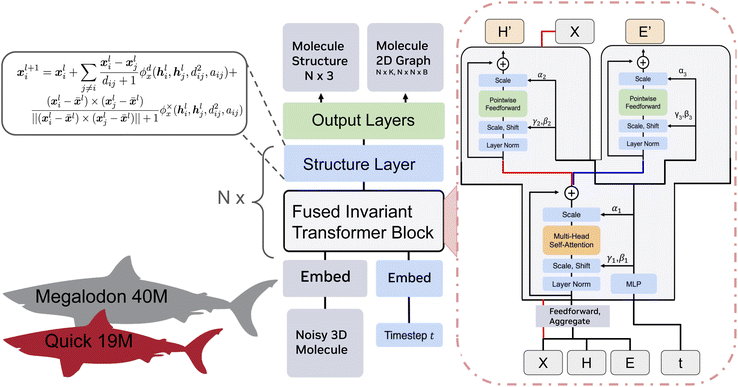
Since 3DMG allows for the simultaneous generation of a discrete 2D molecular graph and its 3D structure, we intentionally designed our architecture with a core transformer trunk to better model discrete data.31,32Fig. 1 illustrates the model architecture, which is comprised of N blocks made up of fused invariant transformer blocks and simple structure update layers, followed by linear layers for discrete data projection. | ||
| Fig. 2 Time and interpolation comparison between Megalodon and Megalodon-flow. (a) Time distributions used for molecule generation. (b) FM linear vs. diffusion cosine interpolant. | ||
In the fused invariant transformer block, the embedded structure, atom types, and bond types are fused and aggregated to create a single molecule feature. This is passed into a standard multi-head attention module with adaptive layernorm. The scaled output is then passed into separate adaptive layernorm feedforward blocks for the atom types and bond types. The transformer also produces an unchanged molecule structure via a residual connection to the input. The updated atom and bond types are then passed into a simple structure layer. The structure layer only updates the predicted structure via a standard distance-based EGNN update with a cross-product term.4,14 At a high level, the transformer block updates our discrete invariant data, and our equivariant layer updates our structure. For more details, please see Appendix B.
We introduce a generative scaling benchmark, and as we show, the performance of 3DMG models is correlated with the size of the generated molecules. We note that our large model is, in fact, not that large compared to recent biological models33,34 and can be further scaled beyond 40 M params if further benchmarks are developed.
3.2 Training objective
We explore Megalodon in the context of diffusion and flow matching. For our diffusion flavored model, following Vignac et al.,18 Le et al.19 we use the same weighted cosine noise schedules, DDPM, and discrete D3PM objective. When using conditional flow matching, we apply the same training objective and hyperparameters as Irwin et al.,20 including equivariant optimal transport. In this way, for diffusion and flow matching, we train and evaluate our model in an identical way including hyperparameters to prior models of same types.In our experiments with EQGAT-diff, we found that the diffusion objective with data-like priors possesses an interesting but potentially harmful behavior. Although the noise sample from the data-prior and the true data sample have bonds, the model consistently generates no bonds for all time ≤0.5, which corresponds to an interpolation with ≤70% of the data as seen in Fig. 2(b). Therefore there is no useful information for the edge features in half the training and inference samples. As a result, only when the structure error is low, as the model starts with 70% data in the interpolation, does the bond prediction accuracy jump to near-perfect accuracy. Thus, only when the structure is accurate was the 2D graph accurate, which is counterintuitive to the independent and simultaneous objective. In other words, the 2D graph does not inform the 3D structure as one would expect to happen, and we would want equal importance on the 2D topology and 3D structure.
To address this inefficiency, as the structure, atom type, and bond type prediction inform each other to improve molecule generation, we introduce a subtle change to the training procedure similar to Campbell et al.29 Keeping each data type having its own independent noise schedule, we enable a concrete connection between the discrete and continuous data that it is modeling. Explicitly, rather than sampling a single time variable, we introduce a second noise variable to create tcontinuous and tdiscrete, both sampled from the same time distribution. Now discrete and continuous data are interpolated with their respective time variable and maintain the independent weighted noise schedules. We note that the MiDi weighted cosine schedules were already adding different levels of noise for the same time value. Now, we take that one step further and allow the model to fill in the structure given the 2D graph and learn to handle more diverse data interpolations.
3.3 Self conditioning
Following Chen et al.,35 we train Megalodon with self-conditioning similar to prior biological generative models.20,36,37 We found that constructing self-conditioning as an outer model wrapper with a residual connection led to faster training convergence: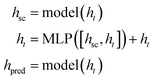 | (9) |
Specifically for 3DMG, self-conditioning is applied independently to each molecule component M = (X, H, E, C), where the structure component uses linear layers without bias and all discrete components operate over the raw logits rather than the one-hot predictions.
4 Experiments
4.1 Data
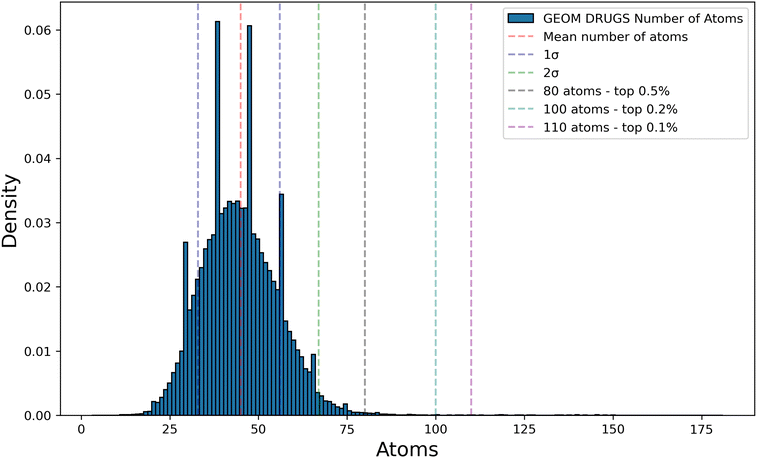
GEOM drugs is a dataset of drug-like molecules with an average size of around 44 atoms.10 Following standard practice in prior work,18–20 we train on the five lowest-energy conformers per molecule, using the same splits as these baselines. We emphasize that traditional metrics are calculated by first sampling molecule sizes from the dataset (Fig. 4) and then generating molecules with the sampled number of atoms, including explicit hydrogens. We show in Section 4.1 that this does not illustrate the full generative capacity, as in many real-world instances, people want to generate molecules with greater than 100 atoms.384.2 Unconditional de novo generation
| Model | Steps | 2D topological (↑) | 3D distributional (↓) | |||
|---|---|---|---|---|---|---|
| Atom stab. | Mol stab. | Validity | Bond angle | Dihedral | ||
| a Denotes taken from EQGAT-diff. | ||||||
| EDM + OpenBabela | 1000 | 0.978 | 0.403 | 0.363 | — | — |
| MiDia | 500 | 0.997 | 0.897 | 0.705 | — | — |
| EQGAT-diffx0disc | 500 | 0.998 | 0.935 | 0.830 | 0.858 | 2.860 |
| EGNN + cross product | 500 | 0.982 | 0.713 | 0.223 | 14.778 | 17.003 |
| Megalodon-quick | 500 | 0.998 | 0.961 | 0.900 | 0.689 | 2.383 |
| Megalodon | 500 | 0.999 | 0.977 | 0.927 | 0.461 | 1.231 |
| SemlaFlow | 100 | 0.998 | 0.979 | 0.920 | 1.274 | 1.934 |
| Megalodon-flow | 100 | 0.999 | 0.988 | 0.944 | 1.286 | 2.379 |
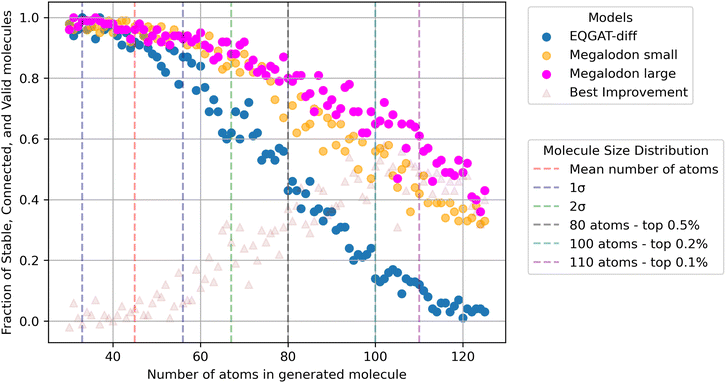 | ||
| Fig. 3 Diffusion model performance as a function of molecule size. Note the ability for Megalodon to generate valid and stable molecules with little training data support. | ||
We emphasize that Table 1 illustrates only a slice of the performance via the average of 5 K molecules sampled from the train set size distribution. We note that although molecules with greater than 72 atoms make up ≤1% of the train set, Megalodon demonstrates roughly 2–49× better performance than EQGAT-diff for the larger half of the generated molecule sizes. We hypothesize that since molecule stability is a discrete 2D measurement, the transformer blocks in Megalodon allow it to better generalize even if seeing similar molecules in less than 0.1% of the training data. In other words, the ability of transformers to excel at modeling discrete sequential data improves our generative performance. We want to point out that all tested models are trained with identical datasets, hyperparameters, diffusion schedules, and training objectives. The only difference is the architecture. We also see that the ability to scale our simple architecture allows the model to even better generate molecules outside the region of data support. Lastly, we chose to focus on only the diffusion models here as they exhibit the best structure benchmark performance.
4.3 Conditional structure generation
Similar to the 3D molecule generation task, we use the GEOM-drugs dataset to evaluate the conditional structure generation capabilities of our model. Given all unconditional 3DMG models are trained with independent noising of coordinates, atoms, and, in some cases, bonds, we want to evaluate how accurate the structural component is. We note this is something that is lacking from the existing prior benchmarks, as when generating de novo molecules, there is no ground truth structure to compare against. In the task of conditional structure generation, all models are given the molecule 2D graph (atom types, bonds) and asked to generate the 3D structure in which ground truth data exists. Given Vignac et al.18 and Jing et al.39 use different train/test splits, we evaluate all methods on the overlap of 200 held-out molecules, with all methods generating 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 structures in total. Due to the similarities with the baselines and its superior unconditional structure accuracy, we compare Megalodon trained with diffusion against recent methods with public reproducible code.
634 structures in total. Due to the similarities with the baselines and its superior unconditional structure accuracy, we compare Megalodon trained with diffusion against recent methods with public reproducible code.
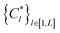 and {Ck}k∈[1,K] respectively be the sets of ground truth and generated structures:
and {Ck}k∈[1,K] respectively be the sets of ground truth and generated structures: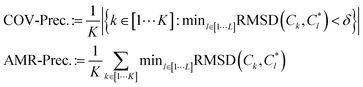 | (10) |
In comparison, Megalodon generates structures with competitive precision and recall by building a relationship between the discrete and continuous data directly in the training process described in Section 3. Half the time all data types are independently noised as normal with their respective time variables and schedules, the other half we only add noise to the structure. Therefore, our model learns to build a relationship between true 2D graphs and their 3D structure, as well as any interpolation between the three data tracks that are interpolated independently with different schedulers (Table 2).
| Method | Recall | Precision | ||||||
|---|---|---|---|---|---|---|---|---|
| Coverage ↑ | AMR ↓ | Coverage ↑ | AMR ↓ | |||||
| Mean | Med | Mean | Med | Mean | Med | Mean | Med | |
| a Bolded best, italicized second best | ||||||||
| GeoDiff | 42.1 | 37.8 | 0.835 | 0.809 | 24.9 | 14.5 | 1.136 | 1.090 |
| Tor. diff. | 75.3 | 82.3 | 0.569 | 0.532 | 56.5 | 57.9 | 0.778 | 0.731 |
| EQGAT | 0.8 | 0.0 | 2.790 | 2.847 | 0.1 | 0.0 | 3.754 | 3.771 |
| Megalodon | 71.4 | 75.0 | 0.573 | 0.557 | 61.2 | 63.1 | 0.719 | 0.696 |
Megalodon demonstrates that its unconditional discrete diffusion objective is crucial for its conditional performance. In other words, the discrete diffusion training objective improves the conditional continuous generative performance. This is evident in the comparison between GeoDiff and Megalodon. GeoDiff is trained on the same conditional Euclidean structure objective as Megalodon (with similar EGNN-based architecture) with 10× more diffusion steps, with both models taking in identical inputs. We see that since Megalodon is able to generate molecules from pure noise, it better learns structure and as a result can be prompted to generate accurate structures.
Interestingly, compared to Torsional diffusion, which initializes the 3D structure with an RDKit approximation to establish all bond lengths and angles and then only modifies the dihedral angles, we see quite competitive performance. Before, it was understood that by restricting the degrees of freedom with good RDKit structures, the performance jump from GeoDiff to Torsional diffusion was observed. Now we see that with the same euclidean diffusion process, similar accuracy improvements can be gained by learning how to generate accurate discrete molecule topology via discrete diffusion. We want to note that there have been recent advances on top of Torsional diffusion41 and other conformer-focused models that are not public.42 We use this benchmark more to analyze the underlying multi-modal diffusion objective and focus on the underlying model comparisons. Megalodon is not a conformer generation model but a molecule generation model capable of de novo and conditional design. Overall, Megalodon shows how independent time interpolation and discrete diffusion create the ability for the model to be prompted or guided with a desired 2D topology to generate accurate 3D structures.
4.4 Unconditional structure-based energy benchmarks
| Model | Bond length | Bond angles | Dihedral | Median ΔErelax | Mean ΔErelax |
|---|---|---|---|---|---|
| a 100-step evaluation (SemlaFlow-compatible). b 500-step evaluation (diffusion-aligned). | |||||
| GEOM-drugs | 0.0000 | 0.00 | 7.2 × 10−3 | 0.00 | 1.0 × 10−3 |
| EQGAT-diff | 0.0076 | 0.95 | 7.98 | 6.36 | 11.06 |
| Megalodon-quick | 0.0085 | 0.88 | 7.28 | 5.78 | 9.74 |
| Megalodon | 0.0061 | 0.66 | 5.42 | 3.17 | 5.71 |
| SemlaFlow | 0.0309 | 2.03 | 6.01 | 32.96 | 93.13 |
| Megalodon-flowa | 0.0112 | 0.930 | 5.63 | 5.90 | 8.61 |
| Megalodon-flowb | 0.0101 | 0.79 | 4.07 | 4.60 | 6.10 |
We note that while the loss function between FM and diffusion is identical in this instance, we see both flow models have an considerably larger bond length error, which translates to a similar energy performance gap. The xTB energy function is highly sensitive to bond lengths; small deviations in bond lengths can lead to significant increases in energy due to the steepness of the PES in these dimensions. A precise representation of bond lengths is crucial because inaccuracies directly impact the calculated energy, making bond length errors a primary contributor to higher relaxation energies in flow models.
When increasing the number of integration steps to 500, the gap between diffusion and flow matching narrows substantially, although flow matching still yields slightly higher relaxation energies. This behavior is fully aligned with prior analyses in SiT paper,3 which attribute the remaining gap to the inherent advantages of stochastic interpolants in capturing fine-grained geometric structure. Importantly, because a flow-matching model is trained only once and can be evaluated at arbitrary numbers of integration steps, practitioners can directly trade off computation for geometric precision, making FM particularly flexible for downstream applications that demand tunable accuracy.
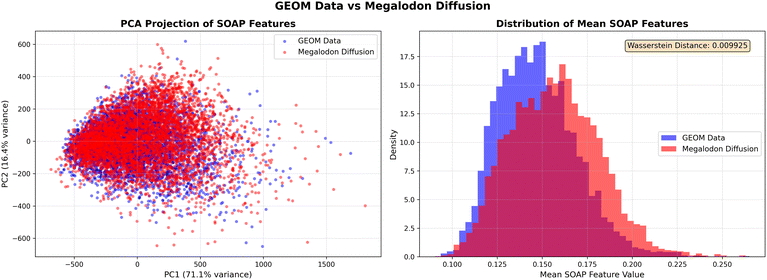
We also include a SOAP-based44 comparison in the Appendix Section C.4, which shows that Megalodon's generated structures closely track the geometric manifold of GEOM. Appendix Fig. 6 provides several examples of generated molecules, and we additionally include two SDF files containing structures produced by the Megalodon and Megalodon-flow models.
5 Conclusions
Megalodon enables the accurate generation of de novo 3D molecules with both diffusion and flow matching. We show with a scalable augmented transformer architecture that significant improvements are gained, especially when generating outside the region of support for the training distribution as it pertains to molecule sizes. Megalodon demonstrates the ability to achieve great accuracy in conditional structure generation due to being trained to generate complete molecules from scratch. We also introduce more interpretable quantum mechanical energy benchmarks that are grounded in the original creation of the GEOM drugs dataset.While unconditional generation alone is rarely directly actionable in drug discovery, the proposed framework provides a strong foundation for a wide range of structure-based tasks. The architectural components introduced in Megalodon, together with its ability to generate full 3D geometries from scratch, can be leveraged for structure-based drug design (SBDD), conformer generation, fragment or pharmacophore–guided molecule construction, and other spatially conditioned design problems. In addition, the flexibility of our implementation allows the codebase to be rapidly adapted to any of these settings, enabling systematic comparisons of diffusion and flow-matching approaches on task-specific objectives. In this sense, Megalodon functions not only as an unconditional generator but as a practical foundation model whose learned spatial priors can be transferred across downstream molecular design workflows.
While we show that Megalodon performs well across a variety of 3D de novo molecules tasks there are still some limitations that are worthy of discussion.
Megalodon like Le et al.19 and the prior edge prediction generative models before it relies on maintaining N2 edge features, which is quite expensive. Recently20 was able to avoid this issue for a majority of the model architecture by fusing the edge and atom features, but this creates a trade-off between model speed and accuracy. Our ablations show that the larger edge features are critical for strong energy performance, so it is still an open question for how to best deal with discrete edge types as each atom can have a maximum of 6 bonds at a time, so is needing to model all N potential pairings at all times really necessary? We leave future work to explore this in greater depth.
As discussed herein, the existing 3D molecule generation benchmarks are quite limited. A common theme that has been discussed in prior work.19,20 While we make strides in expanding the field of view of de novo design and energy-based benchmarks. More work needs to be done to measure important qualities, as even for common conditional design benchmarks, metrics such as QED are not meaningful in practice, and even more complex properties like protein-ligand binding affinity can be directly optimized for with non-3D structure-based methods.45 For these reasons, we looked to explore conditional structure generation, but across the board, small molecule benchmarking is a current field-wide limitation when compared to the current drug discovery practices.
A general limitation of current 3D molecular generative models, including Megalodon, is that they inherit both the representational constraints of their architectures and the chemical coverage of the training data. Because our model uses a one-hot atom-type representation, it cannot generalize to elements not present in the training set, and this interacts with the limitations of GEOM-drugs, a gas-phase semiempirical dataset with a relatively narrow medicinal-chemistry bias. Unlike 2D or SMILES-based language models, which benefit from vast and chemically diverse datasets spanning a wide range of elements, the amount of available high-quality optimized 3D conformer data is far more limited. As a result, 3D generators tend to remain close to the GEOM-drugs distribution. To improve downstream applicability, future work may involve training on more chemically diverse 3D datasets with broader element coverage and developing larger, more representative 3D molecular datasets that extend beyond the chemical space currently available.
Overall, we explore the similarities and differences between flow matching and diffusion while improving 3D molecule design.
Conflicts of interest
There are no conflicts to declare.Data availability
The implementation of the Megalodon model, along with pre-trained weights and data processing scripts, is available at the GitHub repository: https://github.com/NVIDIA-Digital-Bio/megalodon. A persistent, citable snapshot of the codebase is archived on Zenodo under the DOI: https://github.com/NVIDIA-Digital-Bio/megalodon. The provided scripts enable both reproducible model training from scratch and sampling from existing models.Appendix
A Equating continuous Gaussian diffusion and flow matching
A part of our work was to explore when to use diffusion versus flow matching and what the empirical differences are. We show below that from a training perspective in the continuous domain, they can be made equivalent.It can be shown that this objective under the Gaussian setting is a time-dependent scalar multiple of the standard denoising objective explored in Ho et al.27 Let's insert eqn (1b) into the flow matching objective
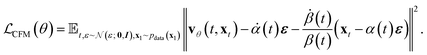 | (11) |
Now we see that we can construct an objective that is similar to the “noise prediction” objective that is used in diffusion models:
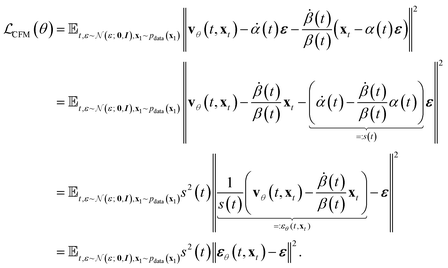 | (12) |
We see that the resulting mean squared error of noise prediction is the original core loss derived in Ho et al.27 This allows us to choose time-dependent scalars via the time distribution itself or the noise or variance schedule to equate the CFM and Diffusion objectives.
In the generative modeling case, we interpolate between a data distribution and a Gaussian density, meaning all data-conditional paths are Gaussian. In that special case, we can, in fact, easily extract the score function from the regular flow matching objective, and we get stochastic sampling for free. We know that xt ∼ p(xt|x1) follows Gaussian probability paths. Based on eqn (1), we know that
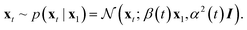 | (13) |
Let's calculate the score:
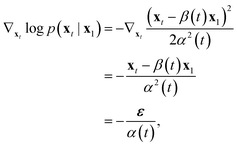 | (14) |
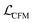 in eqn (12) and see that we obtain denoising score matching,46 which implies that εθ(t, xt), or analogously vθ(t, xt) via their connection, learn a model of the marginal score ∇xt
in eqn (12) and see that we obtain denoising score matching,46 which implies that εθ(t, xt), or analogously vθ(t, xt) via their connection, learn a model of the marginal score ∇xt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(xt).
p(xt).
Specifically, we have alternatively
εθ(t, xt) = −α(t)∇xt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(xt), p(xt), | (15) |
 | (16) |
We note that these equations only hold for a Gaussian prior without optimal transport.
B Megalodon architecture
| Parameter | Megalodon quick | Megalodon |
|---|---|---|
| Invariant edge feature dimension | 64 | 256 |
| Invariant node feature dimension | 256 | 256 |
| Number of vector features | 64 | 128 |
| Number of layers | 10 | 10 |
| Number of FiT attention heads | 4 | 4 |
| Distance feature size | 16 | 128 |
B.1.1 Input/output layers. Megalodon takes the input molecules structures and projects them into a N × D tensor where D is the number of vector features. After all augmented transformer blocks, the predicted structure is projected back down to N × 3.
Similarly, the input discrete components are projected from their one hot variable to a hidden dimension size. The bonds leverage the edge feature size, and the atom types and charges use the node feature size. After all augmented transformer blocks, final prediction heads are applied to project the values back into their respective vocabulary size for discrete prediction.
B.1.2 Fused invariant transformer block. Our Fused Invariant Transformer (FiT) block has several key differences compared to other diffusion transformers.2
• Rather than just operating over the discrete atom type features H, we operate over a fused feature 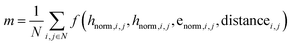 where hnorm and enorm are the outputs of the time conditioned adaptive layer norm for the atom type and edge type features. The distance features are the concatenation of scalar distances and dot products. We note that this fusing step is important to ground the simple equivariant structure update layer to the transformer trunk.
where hnorm and enorm are the outputs of the time conditioned adaptive layer norm for the atom type and edge type features. The distance features are the concatenation of scalar distances and dot products. We note that this fusing step is important to ground the simple equivariant structure update layer to the transformer trunk.
• We employ query key normalization.34,47
• The multi-head attention is applied to m to produce mha_out and then used directly in the standard feed-forward to produce Hout. To create Eout we mimic the same steps but use f(mha_outi + mha_outj) for all edges between nodes i and j. Our feed-forward is the standard SWiGLU layer with a feature projection of 4. We note that this feed-forward for edge features is the most expensive component of the model, which is why Megalodon-quick is designed the way it is.
B.1.3 Structure layer. Following Schneuing et al.,4 the structure layer of Megalodon consists of a single EGNN layer with a positional and cross-product update component. Before this operation, all inputs are normalized to prevent value and gradient explosion, a common problem faced when using EGNNs.14 The invariant features use standard layer norm, whereas the equivariant features use an E3Norm.18
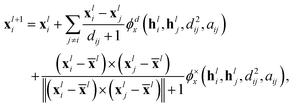 | (17) |
Megalodon-flow was trained using the data splits and adaptive data loader from Irwin et al.,20 which does not discard molecules though was prefiltered to only include molecules with ≤72 atoms. It was trained for 200 epochs on 8 A100 NVIDIA GPUs.
C Extended unconditional generation
| Model | 2D topological (↑) | 3D distributional (↓) | ||||
|---|---|---|---|---|---|---|
| Steps | Atom stab. | Mol stab. | Validity | Bond angle | Dihedral | |
| a Denotes taken from MiDi. | ||||||
| MiDia | 500 | 0.998 | 0.975 | 0.979 | 0.670 | — |
| EQGAT-diffx0disc | 500 | 0.998 | 0.977 | 0.979 | 0.365 | 0.815 |
| Megalodon-quick | 500 | 0.999 | 0.986 | 0.988 | 0.241 | 0.662 |
| Megalodon | 500 | 0.999 | 0.986 | 0.987 | 0.422 | 0.637 |
| SemlaFlow | 100 | 0.999 | 0.986 | 0.986 | 0.775 | 1.194 |
| Megalodon-flow | 100 | 0.998 | 0.973 | 0.976 | 0.804 | 0.970 |
We trained SemlaFlow and EQGAT-diff from scratch while using MiDi results from the original paper. In their original codebases, both MiDi and EQGAT-Diff were trained on molecular representations with three bond types: single, double, and triple, whereas Semla included aromatic bonds. We found that the inclusion of aromatic bonds negatively impacted molecular stability metrics, even though any molecule can be represented without them in a molecular graph using the Kekulized form. To ensure comparability, we trained all models using only single, double, and triple bonds.
In Table 5 we observe that Megalodon-quick achieves the best overall performance on QM9 in terms of both 2D (topological) and 3D (distributional) metrics. This outcome makes intuitive sense because Megalodon-quick is a more lightweight variant, and smaller models often suit datasets of reduced scale, such as QM9, more effectively. In contrast, Megalodon-flow appears to be too large for this dataset, leading to slightly weaker performance; however, we include it here for completeness and consistency with results on GEOM drugs.
While flow matching benefits from fewer integration steps (here 100 steps), the diffusion-based objective with more denoising steps (in our case, 500) ultimately achieves stronger 3D quality metrics. Thus, the trade-off between computational efficiency (fewer steps) and generative fidelity (more steps) is highlighted once again in this smaller-scale setting.
| Model | 2D topological (↑) | 3D distributional (↓) | ||||
|---|---|---|---|---|---|---|
| Steps | Atom stab. | Mol stab. | Connected validity | Bond angle | Dihedral | |
| a Uses the original Semla-Flow preprocessing (variance-1 scaling; >72-atom molecules removed). b Denotes taken from EQGAT-diff. | ||||||
| EDM + OpenBabelb | 1000 | 0.978 | 0.403 | 0.363 | — | — |
| MolDiff taken from Peng et al.48 | 1000 | — | — | 0.739 | — | — |
| GeoBFN taken from Song et al.23 | 2000 | 0.862 | 0.917 | — | — | — |
| MiDib | 500 | 0.997 | 0.897 | 0.705 | — | — |
| EQGAT-diffx0disc | 100 | 0.996 | 0.891 | 0.768 | 1.772 | 3.514 |
| EQGAT-diffx0disc | 500 | 0.998 | 0.935 | 0.830 | 0.858 | 2.860 |
| EGNN + cross product | 500 | 0.982 | 0.713 | 0.223 | 14.778 | 17.003 |
| Megalodon-quick | 500 | 0.998 | 0.961 | 0.900 | 0.689 | 2.383 |
| Megalodon | 100 | 0.998 | 0.939 | 0.817 | 0.871 | 3.367 |
| Megalodon | 500 | 0.999 | 0.977 | 0.927 | 0.461 | 1.231 |
| SemlaFlow | 20 | 0.997 | 0.962 | 0.875 | 2.188 | 3.173 |
| SemlaFlow | 100 | 0.998 | 0.979 | 0.920 | 1.274 | 1.934 |
| Megalodon-flow | 20 | 0.998 | 0.937 | 0.852 | 2.695 | 3.892 |
| Megalodon-flow | 100 | 0.999 | 0.98 | 0.944 | 1.286 | 2.379 |
| Megalodon-flowa | 100 | 0.997 | 0.990 | 0.948 | 0.976 | 2.085 |
| Megalodon-flow | 500 | 0.999 | 0.991 | 0.965 | 0.438 | 1.646 |
We also include EGNN + cross product which is similar to Megalodon except the transformer layers were replaced by the standard invariant and edge feature updates in Satorras et al.14 Prior methods exist that improve upon EDM + Open Babel and maintain that bonds are generated external to the model via Open Babel.15 We do not include such methods in our comparison as, for the most part, public code with weights is not available, and Open Babel introduces significant bias and errors, which make evaluating the model difficult.15,17
Open Babel, while a powerful tool for molecular manipulation and conversion, can introduce several potential errors, particularly in the context of bond assignment and 3D structure generation. Some common errors include:
• Incorrect bond orders: Open Babel often assigns bond orders based on geometric heuristics or atom types, which can lead to inaccuracies, especially in complex or exotic molecules where bond orders are not trivial.
• Geometric distortions: when converting between different formats or generating 3D coordinates, Open Babel may generate suboptimal or distorted geometries, especially if the input structure is incomplete or poorly defined.
• Protonation state assumptions: Open Babel may incorrectly infer or standardize protonation states, which can lead to chemical inaccuracies, especially in sensitive systems such as drug-like molecules or biologically active compounds.
• Ambiguous aromaticity: Open Babel can sometimes misinterpret or incorrectly assign aromaticity, which can lead to an incorrect representation of the molecular structure.
• Missing stereochemistry: while converting or generating structures, stereochemistry can be incorrectly assigned or lost altogether, affecting the overall molecular properties.
where p(y) is the probability of atom type y, W1 denotes the Wasserstein-1 distance,
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) angle(y) is the bond angle distribution for atom type y in the generated data, and Dangle(y) is the corresponding distribution in of test set.
angle(y) is the bond angle distribution for atom type y in the generated data, and Dangle(y) is the corresponding distribution in of test set.
Similarly, for torsion angles, the metric is calculated as:
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) torsion(y) is the torsion angle distribution for bond type y in the generated data, and Dtorsion(y) is the corresponding distribution in the test set. Since we utilized RDKit to identify torsions, the torsional distribution difference was computed only for valid molecules.
torsion(y) is the torsion angle distribution for bond type y in the generated data, and Dtorsion(y) is the corresponding distribution in the test set. Since we utilized RDKit to identify torsions, the torsional distribution difference was computed only for valid molecules.
D Megalodon molecule visualization
Acknowledgements
O. I. acknowledges support by the NSF grant CHE-2154447. This work used Expanse at SDSC and Delta at NCSA through allocation CHE200122 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by NSF grants #2138259, #2138286, #2138307, #2137603, and #2138296.References
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules, ACS Cent. Sci., 2018, 4, 268–276 Search PubMed.
- W. Peebles and S. Xie, Scalable Diffusion Models with Transformers, arXiv, 2022, preprint, arXiv:2212.09748, DOI:10.48550/arXiv.2212.09748.
- N. Ma, M. Goldstein, M. S. Albergo, N. M. Boffi, E. Vanden-Eijnden, and S. Xie, SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers, arXiv, 2024, preprint, arXiv:2401.08740, DOI:10.48550/arXiv.2401.08740.
- A. Schneuing, Y. Du, C. Harris, A. Jamasb, I. Igashov, W. Du, T. Blundell, P. Lió, C. Gomes, M. Welling, M. Bronstein, and B. CorreiaStructure-based Drug Design with Equivariant Diffusion Models, arXiv, 2022, preprint, arXiv:2210.13695, DOI:10.48550/arXiv.2210.13695.
- G. Corso, H. Stärk, B. Jing, R. Barzilay, and T. Jaakkola, DiffDock: Diffusion Steps, Twists, and Turns for Molecular Docking, in International Conference on Learning Representations (ICLR), 2023 Search PubMed.
- J. Abramson, et al., Accurate structure prediction of biomolecular interactions with AlphaFold 3, Nature, 2024, 630, 493–500 Search PubMed.
- J. Durairaj, Y. Adeshina, Z. Cao, X. Zhang, V. Oleinikovas, T. Duignan, Z. McClure, X. Robin, G. Studer, D. Kovtun and E. Rossi, PLINDER: The protein-ligand interactions dataset and evaluation resource, bioRxiv, 2024 DOI:10.1101/2024.07.17.603955.
- E. Hoogeboom, V. G. Satorras, C. Vignac, and M. Welling, Equivariant diffusion for molecule generation in 3d, in International conference on machine learning, 2022, pp. 8867–8887 Search PubMed.
- P. Esser, S. Kulal, A. Blattmann, R. Entezari, J. Müller, H. Saini, Y. Levi, D. Lorenz, A. Sauer, F. Boesel, D. Podell, T. Dockhorn, Z. English, and R. Rombach, Scaling Rectified Flow Transformers for High-Resolution Image Synthesis, Forty-first International Conference on Machine Learning, 2024 Search PubMed.
- S. Axelrod and R. Gómez-Bombarelli, GEOM, energy-annotated molecular conformations for property prediction and molecular generation, Sci. Data, 2022, 9, 185 CrossRef CAS PubMed.
- P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker and C. Plett, et al., CREST—A program for the exploration of low-energy molecular chemical space, J. Chem. Phys., 2024, 160(11) DOI:10.1063/5.0197592.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 Search PubMed.
- T. A. Halgren, Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- V. G. Satorras, E. Hoogeboom, and M. Welling, E (n) equivariant graph neural networks, International conference on machine learning, 2021, pp. 9323–9332 Search PubMed.
- Y. Song, J. Gong, M. Xu, Z. Cao, Y. Lan, S. Ermon, H. Zhou, and W.-Y. Ma, Equivariant Flow Matching with Hybrid Probability Transport for 3D Molecule Generation, in Thirty-seventh Conference on Neural Information Processing Systems, 2023 Search PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An open chemical toolbox, J. Cheminf., 2011, 3, 33 Search PubMed.
- P. Walters, Generative Molecular Design Isn't As Easy As People Make It Look, 2024, https://practicalcheminformatics.blogspot.com/2024/05/generative-molecular-design-isnt-as.html.
- C. Vignac, N. Osman, L. Toni, and P. Frossard, MiDi: Mixed Graph and 3D Denoising Diffusion for Molecule Generation, arXiv, 2023, preprint, arXiv:2302.09048, DOI:10.48550/arXiv.2302.09048.
- T. Le, J. Cremer, F. Noe, D.-A. Clevert, and K. T. Schütt, Navigating the Design Space of Equivariant Diffusion-Based Generative Models for De Novo 3D Molecule Generation, in The Twelfth International Conference on Learning Representations, 2024 Search PubMed.
- R. Irwin, A. Tibo, J. P. Janet and S. Olsson, SemlaFlow--Efficient 3D Molecular Generation with Latent Attention and Equivariant Flow Matching, arXiv, 2024, preprint, arXiv:2406.07266, DOI:10.48550/arXiv.2406.07266.
- M. Xu, A. Powers, R. Dror, S. Ermon, and J. Leskovec, Geometric Latent Diffusion Models for 3D Molecule Generation, arXiv, 2023, preprint, arXiv:2305.01140, DOI:10.48550/arXiv.2305.01140.
- P. O. Pinheiro, J. Rackers, J. Kleinhenz, M. Maser, O. Mahmood, A. M. Watkins, S. Ra, V. Sresht, and S. Saremi, 3D molecule generation by denoising voxel grids, arXiv, 2024, preprint, arXiv:2306.07473, DOI:10.48550/arXiv.2306.07473.
- Y. Song, J. Gong, Y. Qu, H. Zhou, M. Zheng, J. Liu, and W.-Y. Ma, Unified Generative Modeling of 3D Molecules via Bayesian Flow Networks, arXiv, 2024, preprint, arXiv:2403.15441, DOI:10.48550/arXiv.2403.15441.
- Y. Lipman, R. T. Q. Chen, H. Ben-Hamu, M. Nickel, and M. Le, Flow Matching for Generative Modeling, The Eleventh International Conference on Learning Representations, 2023 Search PubMed.
- M. S. Albergo, N. M. Boffi, and E. Vanden-Eijnden, Stochastic Interpolants: A Unifying Framework for Flows and Diffusions, arXiv, 2023, preprint, arXiv:2303.08797, DOI:10.48550/arXiv.2303.08797.
- Y. Song, J. Sohl-Dickstein, D. P. Kingma, A. Kumar, S. Ermon, and B. Poole, Score-Based Generative Modeling through Stochastic Differential Equations, International Conference on Learning Representations (ICLR), 2021 Search PubMed.
- J. Ho, A. Jain, and P. Abbeel, Denoising Diffusion Probabilistic Models, arXiv, 2020, preprint, arXiv:2006.11239, DOI:10.48550/arXiv.2006.11239.
- J. Austin, D. D. Johnson, J. Ho, D. Tarlow and R. Van Den Berg, Structured denoising diffusion models in discrete state-spaces, Adv. Neural Inf. Process., 2021, 34, 17981–17993 Search PubMed.
- A. Campbell, J. Yim, R. Barzilay, T. Rainforth, and T. Jaakkola, Generative Flows on Discrete State-Spaces: Enabling Multimodal Flows with Applications to Protein Co-Design, arXiv, 2024, preprint, arXiv:2402.04997, DOI:10.48550/arXiv.2402.04997.
- A. Tong, N. Malkin, G. Huguet, Y. Zhang, J. Rector-Brooks, K. Fatras, G. Wolf, and Y. Bengio, Improving and generalizing flow-based generative models with minibatch optimal transport, arXiv, 2023, preprint, arXiv:2302.00482, DOI:10.48550/arXiv.2302.00482.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Attention is all you need, Adv. Neural Inf. Process., 2017, vol. 30 Search PubMed.
- T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell and S. Agarwal, Language models are few-shot learners, Advances in neural information processing systems, 2020, 33, 1877–1901 Search PubMed.
- Z. Lin, H. Akin, R. Rao, B. Hie, Z. Zhu, W. Lu, N. Smetanin, R. Verkuil, O. Kabeli and Y. Shmueli, others Evolutionary-scale prediction of atomic-level protein structure with a language model, Science, 2023, 379, 1123–1130 CrossRef CAS PubMed.
- T. Hayes, R. Rao, H. Akin, N. J. Sofroniew, D. Oktay, Z. Lin, R. Verkuil, V. Q. Tran, J. Deaton, M. Wiggert and R. Badkundri, Simulating 500 million years of evolution with a language model, Science, 2025, 387(6736), 850–858 CrossRef CAS PubMed.
- T. Chen, R. Zhang, and G. Hinton, Analog bits: Generating discrete data using diffusion models with self-conditioning, arXiv, 2022, preprint, arXiv:2208.04202, DOI:10.48550/arXiv.2208.04202.
- J. Yim, B. L. Trippe, V. De Bortoli, E. Mathieu, A. Doucet, R. Barzilay, and T. Jaakkola, SE (3) diffusion model with application to protein backbone generation, arXiv, 2023, preprint, arXiv:2302.02277, DOI:10.48550/arXiv.2302.02277.
- H. Stärk, B. Jing, R. Barzilay, and T. Jaakkola, Harmonic Self-Conditioned Flow Matching for Multi-Ligand Docking and Binding Site Design, arXiv, 2024, preprint, arXiv:2310.05764, DOI:10.48550/arXiv.2310.05764.
- M. Békés, D. R. Langley and C. M. Crews, PROTAC targeted protein degraders: the past is prologue, Nat. Rev. Drug Discovery, 2022, 21, 181–200 CrossRef PubMed.
- B. Jing, G. Corso, J. Chang, R. Barzilay, and T. Jaakkola, Torsional Diffusion for Molecular Conformer Generation, arXiv, 2022, preprint, arXiv:2206.01729, DOI:10.48550/arXiv.2206.01729.
- M. Xu, L. Yu, Y. Song, C. Shi, S. Ermon, and J. Tang, GeoDiff: A Geometric Diffusion Model for Molecular Conformation Generation, in International Conference on Learning Representations, 2022 Search PubMed.
- G. Corso, Y. Xu, V. De Bortoli, R. Barzilay, and T. Jaakkola, Particle guidance: non-iid diverse sampling with diffusion models, arXiv, 2023, preprint, arXiv:2310.13102, DOI:10.48550/arXiv.2310.13102.
- Y. Wang, A. A. Elhag, N. Jaitly, J. M. Susskind and M. A. Bautista, Swallowing the Bitter Pill: Simplified Scalable Conformer Generation, arXiv, 2023, preprint, arXiv:2311.17932, DOI:10.48550/arXiv.2311.17932.
- F. Nikitin, I. Dunn, D. R. Koes and O. Isayev, GEOM-drugs revisited: toward more chemically accurate benchmarks for 3D molecule generation, Digital Discovery, 2025, 4, 3282–3291 Search PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 184115 Search PubMed.
- D. Reidenbach, EvoSBDD: Latent Evolution for Accurate and Efficient Structure-Based Drug Design, in ICLR 2024 Workshop on Machine Learning for Genomics Explorations, 2024 Search PubMed.
- P. Vincent, A Connection Between Score Matching and Denoising Autoencoders, Neural Comput., 2011, 23, 1661–1674 CrossRef PubMed.
- A. Henry, P. R. Dachapally, S. S. Pawar, and Y. Chen, Query-Key Normalization for Transformers, in Findings of the Association for Computational Linguistics: EMNLP 2020, 2020, pp. 4246–4253 Search PubMed.
- X. Peng, J. Guan, Q. Liu, and J. Ma, MolDiff: Addressing the Atom-Bond Inconsistency Problem in 3D Molecule Diffusion Generation, in Proceedings of the 40th International Conference on Machine Learning, 2023, pp. 27611–27629 Search PubMed.
Footnotes |
| † These authors contributed equally. |
| ‡ Work performed during internship at NVIDIA. |
| § We adjust the direction of time for diffusion to match the FM equations such that T = 1 is data. |
| ¶ Checkpoint from public code has 2 sets of 23.2 M params, one for the last gradient step and EMA weights. |
| This journal is © The Royal Society of Chemistry 2026 |