 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic predictions for SN2 reactions using the BERT architecture: comparison and interpretation
Chloe
Wilson†
 *a,
María
Calvo
*a,
María
Calvo
 a,
Stamatia
Zavitsanou
a,
Stamatia
Zavitsanou
 a,
James D.
Somper
a,
James D.
Somper
 a,
Ewa
Wieczorek
a,
Ewa
Wieczorek
 a,
Tom
Watts
a,
Tom
Watts
 a,
Jason
Crain
a,
Jason
Crain
 b and
Fernanda
Duarte
b and
Fernanda
Duarte
 *a
*a
aPhysical and Theoretical Chemistry Laboratory, University of Oxford, 12 Mansfield Road, Oxford OX1 3TA, UK. E-mail: fernanda.duartegonzalez@chem.ox.ac.uk; chloe12345wilson@hotmail.com
bIBM Research, The Hartree Centre STFC Laboratory, Sci-Tech Daresbury, Warrington WA4 4AD, UK
First published on 26th December 2025
Abstract
The accurate prediction of reaction rates is an integral step in elucidating reaction mechanisms and designing synthetic pathways. Traditionally, kinetic parameters have been derived from activation energies obtained from quantum mechanical (QM) methods and, more recently, machine learning (ML) approaches. Among ML methods, Bidirectional Encoder Representations from Transformers (BERT), a type of transformer-based model, is the state-of-the-art method for both reaction classification and yield prediction. Despite its success, it has yet to be applied to kinetic prediction. In this work, we developed a BERT model to predict experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values of bimolecular nucleophilic substitution (SN2) reactions and compared its performance to the top-performing Random Forest (RF) literature model in terms of accuracy, training time, and interpretability. Both BERT and RF models exhibit near-experimental accuracy (RMSE ≈ 1.1
k values of bimolecular nucleophilic substitution (SN2) reactions and compared its performance to the top-performing Random Forest (RF) literature model in terms of accuracy, training time, and interpretability. Both BERT and RF models exhibit near-experimental accuracy (RMSE ≈ 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) on similarity-split test data. Interpretation of the predictions from both models reveals that they successfully identify key reaction centres and reproduce known electronic and steric trends. This analysis also highlights the distinct limitations of each; RF outperformed BERT in identifying aromatic allylic effects, while BERT showed stronger extrapolation capabilities.
k) on similarity-split test data. Interpretation of the predictions from both models reveals that they successfully identify key reaction centres and reproduce known electronic and steric trends. This analysis also highlights the distinct limitations of each; RF outperformed BERT in identifying aromatic allylic effects, while BERT showed stronger extrapolation capabilities.
Introduction
Reaction rate prediction is crucial for understanding reaction mechanisms and optimising synthetic pathways towards desired target compounds. Transition state theory (TST) connects the experimental rate constant (k) to the Gibbs free energy of activation (ΔG‡) through the Eyring equation, | (1) |
While quantum mechanical (QM) methods, such as Density Functional Theory (DFT), are commonly used to estimate ΔG‡, they often fail to provide the required chemical accuracy of 1 kcal mol−1, which roughly corresponds to a change in k of one order of magnitude.1–3 This failure has been associated with the use of low-level electronic structure methods,4,5 inaccurate description of entropic contributions,4–6 and poor description of solvent effects by implicit solvent models.4,5,7 Reactive Force Fields, such as ReaxFF8 and the empirical valence bond (EVB)9 method, can, in principle, address the challenge of describing reactivity in explicit solvent; however, their parameterisation remains time-consuming.
In recent years, machine learning (ML) has emerged as a promising alternative for efficiently computing reaction kinetics. This includes the use of machine-learned interatomic potentials (MLIPs) that reduce the cost of modelling solvent explicitly,10 as well as ML models that predict QM-computed activation barriers or experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values.1–3 Given the limited availability of experimental kinetic data, DFT has often been used for training these models despite its inherent limitations. Prominent QM-based ML models developed for activation energy predictions include the work of Green et al.,11 who developed a graph-based deep learning model (directed message passing neural network: D-MPNN) to predict gas-phase activation energies for various reaction types. Grayson et al. employed transfer learning (TL) to adapt a pre-trained NN initially trained on Diels–Alder reactions to predict barriers for other pericyclic reactions, thus reducing the need for extensive datasets.12 Recently, Li et al. systematically explored the use of TL, delta learning (aligning low-level QM data with CCSD(T)-F12a targets), and feature engineering (incorporating computed molecular properties) to improve activation energy predictions using the D-MPNN model, finding delta learning to be the most effective approach.13
k values.1–3 Given the limited availability of experimental kinetic data, DFT has often been used for training these models despite its inherent limitations. Prominent QM-based ML models developed for activation energy predictions include the work of Green et al.,11 who developed a graph-based deep learning model (directed message passing neural network: D-MPNN) to predict gas-phase activation energies for various reaction types. Grayson et al. employed transfer learning (TL) to adapt a pre-trained NN initially trained on Diels–Alder reactions to predict barriers for other pericyclic reactions, thus reducing the need for extensive datasets.12 Recently, Li et al. systematically explored the use of TL, delta learning (aligning low-level QM data with CCSD(T)-F12a targets), and feature engineering (incorporating computed molecular properties) to improve activation energy predictions using the D-MPNN model, finding delta learning to be the most effective approach.13
Models trained on experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values have been pioneered by Madzhidov et al.14 However, due to the scarcity of experimental data, they have been limited to a handful of reaction types, including SN2,14–17 E2,14,18 and cycloadditions.14,19–22 To predict the reaction rates for these types, the authors developed Random Forest (RF) models that use in silico Design and Data Analysis (ISIDA) fragments,23 along with information about reaction conditions, including the solvent dielectric constant and temperature. The models achieved an RMSE ≤ 1.0
k values have been pioneered by Madzhidov et al.14 However, due to the scarcity of experimental data, they have been limited to a handful of reaction types, including SN2,14–17 E2,14,18 and cycloadditions.14,19–22 To predict the reaction rates for these types, the authors developed Random Forest (RF) models that use in silico Design and Data Analysis (ISIDA) fragments,23 along with information about reaction conditions, including the solvent dielectric constant and temperature. The models achieved an RMSE ≤ 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k on validation data, with the SN2 model further evaluated on an external test set.14 For cycloaddition reactions, they demonstrated that conjugated quantitative structure–property relationships (conjugated QSPR), which embed the Arrhenius equation into the ML architecture (in this case, a Ridge Regressor and a Neural Network), accurately predicted experimental values of log
k on validation data, with the SN2 model further evaluated on an external test set.14 For cycloaddition reactions, they demonstrated that conjugated quantitative structure–property relationships (conjugated QSPR), which embed the Arrhenius equation into the ML architecture (in this case, a Ridge Regressor and a Neural Network), accurately predicted experimental values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, pre-exponential factor log
k, pre-exponential factor log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, and activation energy (Ea). On the validation data, R2 values of 0.75, 0.57, and 0.90 for log
A, and activation energy (Ea). On the validation data, R2 values of 0.75, 0.57, and 0.90 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, log
k, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, and Ea, respectively, were achieved (RMSE not provided).22
A, and Ea, respectively, were achieved (RMSE not provided).22
In addition to reaching high accuracy, interpretability in ML models has become increasingly important.24 Interpretability can help identify sources of prediction error,14,25 identify influential features,12,26,27 and verify whether predictions are chemically meaningful.11,22,28–30 For example, in kinetics predictions, Green et al.11 demonstrated how learned reaction representations from their D-MPNN model clustered in terms of reaction type and reactivity. Similarly, von Lilienfeld et al.28 interpreted their Reactant-To-Barrier (R2B) model by plotting the difference between the predicted E2 and SN2 barriers based on LG, nucleophile, and R groups, demonstrating its predictions aligned with heuristic reactivity rules. Furthermore, Persson et al.30 developed an equivariant graph neural network (GNN) that uses frontier molecular orbital coefficients of reactants and products as node features to predict QM activation barriers of SN2 reactions, as well as molecular orbital coefficients of the transition state, allowing for chemically intuitive interpretations. Madzhidov et al.14 also analysed the importance of solvent descriptors in predicting reaction rates and showed that their conjugated QSPR model successfully replicated the Arrhenius relationship between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k and temperature.22 Here, we interpret Madzhidov's RF in the context of known reactivity rules and compare its performance to a Bidirectional Encoder Representations from Transformers (BERT) model.
k and temperature.22 Here, we interpret Madzhidov's RF in the context of known reactivity rules and compare its performance to a Bidirectional Encoder Representations from Transformers (BERT) model.
Transformer-based models, particularly BERT, have gained popularity in chemistry as an alternative to shallow ML models, treating chemistry as a language task. These models have been applied to a range of (bio)chemical applications, including molecular discovery,31,32 reaction classification,33 and yield prediction.34 We refer the reader to relevant reviews illustrating the use and extension of transformer models for chemical applications.35–37 In kinetic prediction, learned reaction representations from a pretrained BERT model have been used as a descriptor for predicting activation free energies of SNAr reactions using Gaussian Process Regression (GPR), achieving an RMSE of 1.4 ± 0.2 kcal mol−1 (1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) on validation data.26,38 However, to our knowledge, no transformer-based models have been trained directly for kinetic prediction.
k) on validation data.26,38 However, to our knowledge, no transformer-based models have been trained directly for kinetic prediction.
Here, we train a BERT model to predict rates for SN2 reactions and compare its performance against the RF model originally reported by Madzhidov et al.14 To evaluate the ability of the models to learn the underlying reactivity rules, we conducted a feature importance analysis using Kuz'min prediction contributions39 for RF and Integrated Gradients (IGs)40,41 for BERT (Fig. 1). Our results show that both models achieve near-experimental accuracy on similarity-split test data (RMSE ≈ 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) and identify key reaction centres, as well as known electronic and steric effects. However, limitations were also identified: RF struggled with log
k) and identify key reaction centres, as well as known electronic and steric effects. However, limitations were also identified: RF struggled with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k extrapolation, while the BERT model had difficulty recognising aromatic effects.
k extrapolation, while the BERT model had difficulty recognising aromatic effects.
 | ||
Fig. 1 Overview of the reaction under study and feature representation. (a) Pictorial representation of an SN2 reaction, highlighting the nucleophile (red), leaving group (LG, orange), electrophilic C (purple), and substituting R groups (grey). (b) In the RF model, features are represented using ISIDA fragments, reciprocal temperature, and solvent properties. In the BERT model, features are encoded from SMILES strings. Although not shown, ionic strength and mole fractions of each solvent component were appended to the SMILES, as shown here for reciprocal temperature. (c) The influence of a given feature on the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k is computed using Kuz'min prediction contributions56 for RF and IGs54,55 for BERT; Q, K, V, and df denote queries, keys, values, and feature dimension respectively, used to calculate self-attention scores in the BERT model, E denotes BERT token embeddings, and H[CLS] denotes the hidden representation of the [CLS] token prepended to the SMILES input. k is computed using Kuz'min prediction contributions56 for RF and IGs54,55 for BERT; Q, K, V, and df denote queries, keys, values, and feature dimension respectively, used to calculate self-attention scores in the BERT model, E denotes BERT token embeddings, and H[CLS] denotes the hidden representation of the [CLS] token prepended to the SMILES input. | ||
Results and discussion
Dataset analysis
Before training the BERT model on the SN2 data compiled by Madzhidov et al.,17 which was used to train their rate prediction RF model,14 we performed a detailed analysis of this data set. This dataset initially comprised 4830 SN2 reactions and their corresponding experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values. After removing unbalanced reactions and duplicates, we reduced the dataset to 4666 entries. We then added 196 new SN2 reactions with experimental log
k values. After removing unbalanced reactions and duplicates, we reduced the dataset to 4666 entries. We then added 196 new SN2 reactions with experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values, bringing the total to 4862 reactions (Fig. 2). These additional reactions included phosphine nucleophiles (36 reactions), azide leaving groups (4 reactions), and electrolyte solutions (16 reactions), thus increasing chemical diversity. Reinforcing this idea, 83% of the new reactions had a Tanimoto similarity (ST) < 0.4 to the initial 4666 reactions (Fig. S2b). The range of log
k values, bringing the total to 4862 reactions (Fig. 2). These additional reactions included phosphine nucleophiles (36 reactions), azide leaving groups (4 reactions), and electrolyte solutions (16 reactions), thus increasing chemical diversity. Reinforcing this idea, 83% of the new reactions had a Tanimoto similarity (ST) < 0.4 to the initial 4666 reactions (Fig. S2b). The range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k also expanded from 1.6 to −7.7 (ΔG‡ = 16.1–29.5) to 1.6 to −12.3 (ΔG‡ = 16.1–36.1). Throughout this work, log
k also expanded from 1.6 to −7.7 (ΔG‡ = 16.1–29.5) to 1.6 to −12.3 (ΔG‡ = 16.1–36.1). Throughout this work, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp refers to the experimental log
kexp refers to the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k and log
k and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred refers to the values predicted by the RF and BERT models.
kpred refers to the values predicted by the RF and BERT models.
 | ||
| Fig. 2 TMAP of the total training set of 4862 SN2 reactions. 4666 of these were compiled by ref. 26 (shown in grey), and 196 were added in the current work to increase the chemical diversity of the training data (shown in black). | ||
Despite diversifying the training data, the model's Root Mean Square Error (RMSE) on the test data from ref. 14 (referred to here as Test 1 ≡ 73 reactions), remained at 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. However, for out-of-domain reactions (Test 2 ≡ 56 reactions, including phosphine nucleophiles (4 reactions), azide leaving groups (5 reactions), and electrolyte solutions (12 reactions), see Methods), the test RMSE improved from 2.0 ± 0.0
k. However, for out-of-domain reactions (Test 2 ≡ 56 reactions, including phosphine nucleophiles (4 reactions), azide leaving groups (5 reactions), and electrolyte solutions (12 reactions), see Methods), the test RMSE improved from 2.0 ± 0.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (the baseline RMSE predicting the mean log
k (the baseline RMSE predicting the mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp of the training data) to 1.4 ± 0.2
kexp of the training data) to 1.4 ± 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (Fig. 3a). The greatest contribution to this improved RMSE came from the electrolyte-containing reactions, with a complete breakdown provided in Fig. S3. Consequently, this revised RF model was employed in this study. To ensure generalisability, reactions with ST > 0.4 to the diversified data set were excluded from all test sets (Fig. S2a).
k (Fig. 3a). The greatest contribution to this improved RMSE came from the electrolyte-containing reactions, with a complete breakdown provided in Fig. S3. Consequently, this revised RF model was employed in this study. To ensure generalisability, reactions with ST > 0.4 to the diversified data set were excluded from all test sets (Fig. S2a).
 | ||
| Fig. 3 Evaluation of prediction accuracy and interpretability in RF and BERT models. (a) Learning curve showing the change in RMSE of the RF model from ref. 14 upon increasing the chemical diversity of the training data (evaluated using 56 out-of-domain reactions). (b) RMSE comparison between the RF and BERT models (evaluated using 129 external test reactions) and 30 DFT calculations carried out at the CPCM(solvent)CCSD(T)/def2-TZVP//PBE0-D3BJ/def2-SVP level of theory. (c) Percentage of accurate predictions where the nucleophilic (Nu), leaving group (LG) and electrophilic carbon (C) atoms were high impact features in the RF and BERT models. (d) Percentage of accurate predictions where temperature and solvent were high impact features in the RF and BERT models. A detailed breakdown of solvent property impact in RF is provided in Fig. S9a. | ||
Comparison of RF and BERT
We evaluated the performance of the RF and BERT models based on accuracy and training time using a test set of 129 reactions, which included 41 unique nucleophiles, 43 unique substrates, 10 unique solvents, and a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k range of −8.2–1.2 (see Methods). Importantly, all test data had ST < 0.4 to the training data, so prediction accuracy reflects model performance on novel reactions (Fig. S2a).
k range of −8.2–1.2 (see Methods). Importantly, all test data had ST < 0.4 to the training data, so prediction accuracy reflects model performance on novel reactions (Fig. S2a).
Both models showed comparable accuracy (RMSE/log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k: 1.2 ± 0.1 for RF and 1.1 ± 0.1 for BERT) on the combined test data (129 reactions, Fig. S1b, with learning curves in Fig. S4a). However, the RF model significantly outperformed BERT in training speed, taking 256 seconds compared to BERT's 52.9 hours on CPUs. Although BERT's training time could be accelerated on GPUs, which are better suited for deep learning tasks (see Methods for details).
k: 1.2 ± 0.1 for RF and 1.1 ± 0.1 for BERT) on the combined test data (129 reactions, Fig. S1b, with learning curves in Fig. S4a). However, the RF model significantly outperformed BERT in training speed, taking 256 seconds compared to BERT's 52.9 hours on CPUs. Although BERT's training time could be accelerated on GPUs, which are better suited for deep learning tasks (see Methods for details).
We also compared both models to a dummy model that always predicted the mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp of the training data, which resulted in an RMSE of 2.0 ± 0.0
kexp of the training data, which resulted in an RMSE of 2.0 ± 0.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. Additionally, we benchmarked both models against log
k. Additionally, we benchmarked both models against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values calculated using DFT at the CPCM(solvent)CCSD(T)/def2-TZVP//PBE0-D3BJ/def2-SVP level of theory. The DFT predictions yielded an RMSE of 2.5 kcal mol−1 ≡ 1.9
k values calculated using DFT at the CPCM(solvent)CCSD(T)/def2-TZVP//PBE0-D3BJ/def2-SVP level of theory. The DFT predictions yielded an RMSE of 2.5 kcal mol−1 ≡ 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (Fig. 3b) and required 6.8 hours (using 4 CPU cores and allocated up to 4 GB each) for 30 reactant complexes and TS geometry optimisation and frequency calculations, contrasting with the prediction time of less than 1 second for both RF and BERT models.
k (Fig. 3b) and required 6.8 hours (using 4 CPU cores and allocated up to 4 GB each) for 30 reactant complexes and TS geometry optimisation and frequency calculations, contrasting with the prediction time of less than 1 second for both RF and BERT models.
In our analysis of test reactions, we categorised predictions into accurate (upper quartile ≡ 32 reactions) and inaccurate (lower quartile ≡ 32 reactions, Fig. 4a and S5). Of the accurate predictions made by RF, 44% were also accurately predicted by BERT. Conversely, 56% of RF's inaccurate predictions overlap with those from BERT.
This analysis highlights that while both models achieved similar overall accuracy, they differed in the specific reactions they accurately or inaccurately predicted, suggesting they have learned different underlying relationships. RF offers a more practical solution for rapid deployment and retraining, while BERT may be better suited for large datasets, where its richer representations and interpretability tools can be fully leveraged. Further improvements in predictive performance are likely to depend more on data quality than on the choice of the model architectures.
Interpreting the models
We then examined the ability of RF and BERT models to identify key features influencing reactivity. Our analysis included evaluating the contributions from each reaction centre: nucleophilic (Nu) atom, leaving group (LG) atom, and electrophilic carbon (C) atoms (Fig. 1a), as well as temperature (represented as T−1), solvent polarity and proticity. To quantify feature importances, values were calculated relative to a dummy model that predicts the mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp of the training data for each test reaction, where the feature importance is thus set to zero. Features considered high impact were defined as those falling within the upper quartile of importance in the test data (Fig. 4b).
kexp of the training data for each test reaction, where the feature importance is thus set to zero. Features considered high impact were defined as those falling within the upper quartile of importance in the test data (Fig. 4b).
Both the RF and BERT models agreed on the importance of reaction centres and conditions. For example, in accurate predictions, the LG atom emerged as a high impact feature in over 90% of cases, while the Nu atom was significant in 75% of accurate predictions for both RF and BERT (Fig. 3c); however, BERT occasionally underestimated the importance of the Nu atom for inaccurate predictions (SI 5.3). In contrast, the electrophilic C atom was consistently identified as high impact in all of RF's accurate predictions, but only in 38% of those made by BERT. This discrepancy arises from the differences in how features are represented. RF considers the electrophilic carbon as part of a larger molecular fragment that includes its surrounding environment, allowing it to directly capture steric effects. In contrast, BERT represents the electrophilic carbon as a single token representation, which may overlook these environmental influences.
Temperature also emerged as a high-impact feature in 97% of accurate predictions for both models, demonstrating their ability to recognise key physical features (Fig. 3d). In the RF model, the solvent is represented by 13 distinct properties,17 with each property being high impact in 90–100% of accurate predictions (full breakdown provided in Fig. S9a), in line with the original analysis using RF in ref. 14 Conversely, in BERT, where solvent is represented by SMILES strings, its importance as a high impact feature was found in 72% of accurate predictions; however, its importance was not observed for inaccurate predictions (SI 5.3). These results show that both models identify chemically meaningful features as relevant for the prediction task, particularly RF.
To further assess whether RF and BERT effectively learned key structural and physical effects, we evaluate the feature importance of high impact features, including LG, steric, allylic, temperature, and solvent effects, on either increasing (positive sign) or decreasing (negative sign) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred (Fig. 5).
kpred (Fig. 5).
Both models show a positive correlation between halide size and reactivity (rates: Cl < Br < I). In the RF model, where LG atoms were represented by C–I, C–Br, C–Cl and C–F fragments, C–I increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred across all examples. The presence of Br showed mixed effects on log
kpred across all examples. The presence of Br showed mixed effects on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred, while Cl had no significant effect in two reactions and decreased log
kpred, while Cl had no significant effect in two reactions and decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in one reaction. In the BERT model, where LG was represented by I, Br, Cl and F tokens, I and Br increased log
kpred in one reaction. In the BERT model, where LG was represented by I, Br, Cl and F tokens, I and Br increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in all cases where they were high impact (12 and 5 reactions, respectively), while Cl decreased log
kpred in all cases where they were high impact (12 and 5 reactions, respectively), while Cl decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in the two examples involving this LG. These results show that both models recognise the importance of LG size in determining reactivity, with iodide demonstrating the most pronounced positive effect across both models.
kpred in the two examples involving this LG. These results show that both models recognise the importance of LG size in determining reactivity, with iodide demonstrating the most pronounced positive effect across both models.
Our analysis shows that both models recognised that steric hindrance decreases SN2 reactivity. In the RF model, substituted centres consistently decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in the four reactions where they were high impact, while these features increased log
kpred in the four reactions where they were high impact, while these features increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in 10 reactions with unsubstituted centres. For the two reactions where C–C and C–C–C fragments decreased log
kpred in 10 reactions with unsubstituted centres. For the two reactions where C–C and C–C–C fragments decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred, this was attributed to a spurious correlation (see discussion in SI. 5.2.1). Similarly, a spurious correlation was observed in three reactions with unsubstituted centres where the C–C–C–C fragment decreased log
kpred, this was attributed to a spurious correlation (see discussion in SI. 5.2.1). Similarly, a spurious correlation was observed in three reactions with unsubstituted centres where the C–C–C–C fragment decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred (see discussion in SI. 5.2.1). In the BERT model, we found that substituted centres decreased log
kpred (see discussion in SI. 5.2.1). In the BERT model, we found that substituted centres decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in all reactions where they were high impact (6 reactions), while unsubstituted centres increased it.
kpred in all reactions where they were high impact (6 reactions), while unsubstituted centres increased it.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C–C
C, C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C, and C–C:C fragments, respectively (where ‘:’ is an aromatic bond), while in the BERT model, these groups were described using tokens ‘
C, and C–C:C fragments, respectively (where ‘:’ is an aromatic bond), while in the BERT model, these groups were described using tokens ‘![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ’, ‘
’, ‘![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ’, and ‘c’, with ‘c’ representing an aromatic carbon bonded to the centre.
’, and ‘c’, with ‘c’ representing an aromatic carbon bonded to the centre.
Overall, both models recognised that allylic groups increase SN2 reactivity. However, BERT was limited in identifying this effect on reactivity with aromatic groups. In the RF model, alkyne bonds increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in both instances where they appeared in the accurate predictions subset. Furthermore, aromatic groups also increased log
kpred in both instances where they appeared in the accurate predictions subset. Furthermore, aromatic groups also increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in 4 out of 6 reactions; the two reactions where aromatic groups decreased log
kpred in 4 out of 6 reactions; the two reactions where aromatic groups decreased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred were attributed to their presence in the nucleophile (see Fig. S8). In the BERT model, alkenes increased log
kpred were attributed to their presence in the nucleophile (see Fig. S8). In the BERT model, alkenes increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in one reaction and were low impact in the other, while alkynes increased log
kpred in one reaction and were low impact in the other, while alkynes increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred in the 4 reactions considered. Aromatic groups, however, had a negligible effect in the BERT model. Feature engineering by adding physical descriptors may improve the learning of these effects.26
kpred in the 4 reactions considered. Aromatic groups, however, had a negligible effect in the BERT model. Feature engineering by adding physical descriptors may improve the learning of these effects.26
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k with increasing T−1 (Pearson's correlation coefficient rp ≥ −0.97 for both models). The correlation was seen for both the predicted log
k with increasing T−1 (Pearson's correlation coefficient rp ≥ −0.97 for both models). The correlation was seen for both the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values and feature importances of T−1 (Fig. S6, predictions shown for one representative example in Fig. 5d). Hence, both models successfully captured the mathematical relationship between log
k values and feature importances of T−1 (Fig. S6, predictions shown for one representative example in Fig. 5d). Hence, both models successfully captured the mathematical relationship between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k and temperature.
k and temperature.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, solvent effects were not analysed for the RF model (Fig. S10). In the BERT model, solvent effects were evaluated by analysing the contribution of polar (ε > 15) protic and aprotic solvent SMILES in accurate predictions with anionic and neutral nucleophiles. The distribution of solvents was as follows: 3 polar protic and 6 polar aprotic for anionic nucleophiles, and 15 polar protic and 8 polar aprotic for neutral nucleophiles (Fig. 5e). No accurate predictions with non-polar solvent (ε < 15) were obtained.
k, solvent effects were not analysed for the RF model (Fig. S10). In the BERT model, solvent effects were evaluated by analysing the contribution of polar (ε > 15) protic and aprotic solvent SMILES in accurate predictions with anionic and neutral nucleophiles. The distribution of solvents was as follows: 3 polar protic and 6 polar aprotic for anionic nucleophiles, and 15 polar protic and 8 polar aprotic for neutral nucleophiles (Fig. 5e). No accurate predictions with non-polar solvent (ε < 15) were obtained.
The BERT model consistently predicted that polar protic solvents decrease log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, while polar aprotic solvents increase log
k, while polar aprotic solvents increase log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k with anionic nucleophiles (two reactions for protic and six reactions for aprotic solvent). For neutral nucleophiles, polar solvents generally increased log
k with anionic nucleophiles (two reactions for protic and six reactions for aprotic solvent). For neutral nucleophiles, polar solvents generally increased log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred where solvent was high impact (five reactions for protic, four for aprotic). An exception was 2-amino-1-methylbenzimidazole reacting with ethyl iodide in methanol (5 reactions), which displayed a spurious correlation.
kpred where solvent was high impact (five reactions for protic, four for aprotic). An exception was 2-amino-1-methylbenzimidazole reacting with ethyl iodide in methanol (5 reactions), which displayed a spurious correlation.
In summary, both BERT and RF models recognised LG, temperature, steric, and allylic effects to varying extents. Analysis of inaccurate predictions showed similar trends to accurate ones, reinforcing the reliability of these assessments. This consistency indicates that inaccurate predictions were not due to the inability of the models to capture key effects.
Exploring model limitations (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) k extrapolation)
k extrapolation)
To evaluate the ability of each model to extrapolate to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values outside the range of the training data, we analysed the relationship between distance in log
k values outside the range of the training data, we analysed the relationship between distance in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp from the training median (training median = −3.4
kexp from the training median (training median = −3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k), and prediction error for each reaction in the test data (Fig. 6). Here, the x-axes were divided into positive and negative distance to capture extrapolation to log
k), and prediction error for each reaction in the test data (Fig. 6). Here, the x-axes were divided into positive and negative distance to capture extrapolation to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values greater than the training median and those less than the training median. For the BERT model, a low correlation between distance from the training median and prediction error was observed (Spearman's correlation coefficient rs = 0.29). This result suggests that BERT extrapolates well to log
k values greater than the training median and those less than the training median. For the BERT model, a low correlation between distance from the training median and prediction error was observed (Spearman's correlation coefficient rs = 0.29). This result suggests that BERT extrapolates well to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values far from the training median. Contrarily, the RF model exhibited a modest correlation (rs = 0.40) between distance from the training median and prediction error for log
k values far from the training median. Contrarily, the RF model exhibited a modest correlation (rs = 0.40) between distance from the training median and prediction error for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k > the training median and a strong positive correlation (rs = 0.65) for log
k > the training median and a strong positive correlation (rs = 0.65) for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k < the training median. This implies that RF is limited in its ability to extrapolate to log
k < the training median. This implies that RF is limited in its ability to extrapolate to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k below the training median.
k below the training median.
 | ||
Fig. 6 Prediction error vs. distance in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp from the training median (Δlog kexp from the training median (Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp) for each reaction in the test data, for the RF and BERT models. kexp) for each reaction in the test data, for the RF and BERT models. | ||
In conclusion, both models can extrapolate to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k > the training median but BERT proved more reliable in extrapolating to log
k > the training median but BERT proved more reliable in extrapolating to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k < the training median. However, this is to be expected given that BERT has a linear prediction layer, while RF bases its predictions on training averages.
k < the training median. However, this is to be expected given that BERT has a linear prediction layer, while RF bases its predictions on training averages.
Conclusions
In this work, we trained a BERT model to predict the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values of SN2 reactions and compared its performance to the RF literature model14 in terms of accuracy, training time, and ability to capture known reactivity rules.
k values of SN2 reactions and compared its performance to the RF literature model14 in terms of accuracy, training time, and ability to capture known reactivity rules.
In addition, we diversified the dataset of SN2 reactions curated by Madzhidov et al.17 used to train their RF,14 by introducing 196 new reactions curated from literature. We show that increasing the chemical diversity of the training data broadens the applicability of the model to new areas of chemical space, in particular for reactions in electrolyte solutions.
When comparing both the RF and BERT models trained on this diversified data, we observed that while both models achieved similar prediction accuracy (RMSE ≈ 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k), the RF model showed a clear advantage in training speed. Additionally, both models identified key reaction centres as important for accurate predictions, along with known factors that influence the reaction rate, such as the nature of the LG, sterics, allylic groups, temperature, and solvent (BERT only). However, each model exhibited specific limitations: RF had difficulties with extrapolating log
k), the RF model showed a clear advantage in training speed. Additionally, both models identified key reaction centres as important for accurate predictions, along with known factors that influence the reaction rate, such as the nature of the LG, sterics, allylic groups, temperature, and solvent (BERT only). However, each model exhibited specific limitations: RF had difficulties with extrapolating log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values, and BERT failed to recognise aromatic effects. Despite these limitations, each model compensates for the other's weaknesses, confirming that both RF and BERT are effective models for rate prediction and capable of capturing fundamental chemical principles in their predictions.
k values, and BERT failed to recognise aromatic effects. Despite these limitations, each model compensates for the other's weaknesses, confirming that both RF and BERT are effective models for rate prediction and capable of capturing fundamental chemical principles in their predictions.
Future work should focus on expanding the applicability of these models to a wider range of chemical reactions via fine-tuning. We recognise that a key challenge will be the availability of experimental kinetic data beyond E2, SN2, cycloadditions, and SNAr reactions. Although promising initiatives such as the Open Reaction Database44 and data mining strategies offer potential solutions to improve the generalisation of available models, these could be used alongside QM-generated data through multi-fidelity approaches. For success, diversity rather than quantity alone will be essential to enhance model generalisation.
Methodology
Data
The training and test data used in this work can be visualised in the TMAPs shown in Fig. 2 and S1b, respectively (interactive versions provided on Github, see Data availability). The training data contained 4862 reactions with 449 unique nucleophiles, 298 unique substrates, 155 unique solvent systems, had a temperature range of 232.15–425.15 K, and a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k range of −12.3–1.6. The test data contained 129 reactions with 41 unique nucleophiles, 43 unique substrates, 10 unique solvent systems, had a temperature range of 252.15–461.00 K, and log
k range of −12.3–1.6. The test data contained 129 reactions with 41 unique nucleophiles, 43 unique substrates, 10 unique solvent systems, had a temperature range of 252.15–461.00 K, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k range of −8.2–1.2. All test data had a Tanimoto similarity (ST) < 0.4 to the training data, so prediction accuracy reflects model performance on novel reactions (Fig. S2a). Here, reaction A was said to have an ST > X to reaction B if the nucleophile and substrate of A respectively had an ST > X to the nucleophile and substrate of B, otherwise, reaction A is said to have an ST < X to reaction B. Note that 0.4 is a standard ST threshold41 and imposed a similarity constraint effectively without a significant reduction in test set size.
k range of −8.2–1.2. All test data had a Tanimoto similarity (ST) < 0.4 to the training data, so prediction accuracy reflects model performance on novel reactions (Fig. S2a). Here, reaction A was said to have an ST > X to reaction B if the nucleophile and substrate of A respectively had an ST > X to the nucleophile and substrate of B, otherwise, reaction A is said to have an ST < X to reaction B. Note that 0.4 is a standard ST threshold41 and imposed a similarity constraint effectively without a significant reduction in test set size.
The training data utilised for this study builds upon the SN2 data compiled by Madzhidov et al.,17 which they used to train their rate prediction RF model.14 The original dataset consists of 4830 SN2 reactions and their experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values, which were cleaned in the current work to remove unbalanced reactions (109 reactions), duplicates (46 reactions), and known CV outliers17 (9 reactions), resulting in 4666 reactions from ref. 14. The SMILES used to generate the ISIDA fragments were also canonicalised in the current work to improve interpretability (i.e., so each molecular fragment is only represented by 1 ISIDA fragment). The chemical diversity in the training data was increased by including 196 SN2 reactions manually curated in the current work.45–56 Specifically, 83% of the reactions curated in this work have an ST < 0.4 to the reactions from ref. 14, and therefore add structural diversity (Fig. S2b). Furthermore, the reactions curated in this work introduce an additional nucleophile type into the data: phosphines (36 reactions), as well as an additional LG: azide (4 reactions), and an additional solvent type: electrolyte solutions (16 reactions). The log
k values, which were cleaned in the current work to remove unbalanced reactions (109 reactions), duplicates (46 reactions), and known CV outliers17 (9 reactions), resulting in 4666 reactions from ref. 14. The SMILES used to generate the ISIDA fragments were also canonicalised in the current work to improve interpretability (i.e., so each molecular fragment is only represented by 1 ISIDA fragment). The chemical diversity in the training data was increased by including 196 SN2 reactions manually curated in the current work.45–56 Specifically, 83% of the reactions curated in this work have an ST < 0.4 to the reactions from ref. 14, and therefore add structural diversity (Fig. S2b). Furthermore, the reactions curated in this work introduce an additional nucleophile type into the data: phosphines (36 reactions), as well as an additional LG: azide (4 reactions), and an additional solvent type: electrolyte solutions (16 reactions). The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k range was also increased from −7.7–1.6 to −12.3–1.6.
k range was also increased from −7.7–1.6 to −12.3–1.6.
The test data is comprised of 73 test reactions compiled by Madzhidov et al.17 used to evaluate their rate prediction RF model14 (those with ST < 0.4 to the training data, Test 1), and 56 reactions manually curated in the current work (Test 2).45,47–55 The latter represent an area of chemical space outside the applicability domain of ref. 14's training data. Firstly, Test 2 has a low chemical similarity to ref. 14's training data, in comparison to Test 1. This was quantified by the percentage of reactions with ST < 0.2 to ref. 14's training data: 46% and 12% for Test 2 and Test 1, respectively (Fig. S2c and d). ST < 0.2 is used here as all test data have an ST < 0.4 to the training data. Secondly, Test 2 contains species not included in ref. 14's training data: 12 reactions in electrolyte, 5 reactions with azide LGs, and 4 reactions with phosphine nucleophiles.
Machine-learning & DFT
| GCCSD(T) ≈ ECCSD(T) + GPBE0 − EPBE0 | (2) |
To obtain the DFT RMSE in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, the DFT ΔG‡ values (in kcal mol−1) were converted to log
k, the DFT ΔG‡ values (in kcal mol−1) were converted to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k using the Eyring equation (eqn (1)). Further DFT details are provided in SI 3.
k using the Eyring equation (eqn (1)). Further DFT details are provided in SI 3.
Calculation times
BERT and RF training times were estimated as the time taken for RMSE convergence over five CV folds (optimisation curves provided in Fig. S4). This corresponds to 256 s for RF and 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 s (52.9 h) for BERT on 8 vCPUs of Intel® x86-64 CPU (64 GiB RAM). The BERT training time was 13
305 s (52.9 h) for BERT on 8 vCPUs of Intel® x86-64 CPU (64 GiB RAM). The BERT training time was 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 s (3.7 h) on GPU (1 NVIDIA V100 PCIe 16 GB GPU), which is incompatible with the Scikit-learn implementation of RF. Even on GPU, BERT is significantly slower than RF.
311 s (3.7 h) on GPU (1 NVIDIA V100 PCIe 16 GB GPU), which is incompatible with the Scikit-learn implementation of RF. Even on GPU, BERT is significantly slower than RF.
BERT and RF prediction times were calculated for five random samples of 30 test reactions (one sample per CV fold) and averaged. DFT times correspond to 30 reactant complexes and TS geometry optimisation and frequency calculations. The averaging over samples for the ML prediction time is to account for the fact that different samples were used to calculate the ML and DFT prediction times, due to some of the lower-molecular weight reactions required for DFT calculations failing to meet the ST < 0.4 requirement for the ML test data.
Accurate and inaccurate predictions
Accurate and inaccurate predictions are defined as those with the 25% smallest and 25% largest prediction errors (averaged over the five CV folds), respectively.Uncertainty estimation
Predictions and feature importances in this work are quoted as the mean over the five CV folds, with the standard error of the mean (σM) providing an uncertainty estimate. When summing over feature importances, the uncertainties were propagated using eqn (3). Here, σM,prop is the propagated uncertainty and N is the total number of uncertainties being propagated over.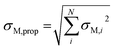 | (3) |
Calculating feature importances
Feature importances were calculated using the state-of-the-art method for each model: Kuz'min prediction contributions39 for RF and Integrated Gradients (IGs)40,41 for BERT. Prediction contributions were calculated using Treeinterpreter v.0.2.3,61 and IGs using LayerIntegratedGradients from Captum v.0.4.0.62 The magnitude of a feature's importance corresponds to the feature's influence on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred, while the sign corresponds to whether the feature increased (positive) or decreased (negative) log
kpred, while the sign corresponds to whether the feature increased (positive) or decreased (negative) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred.
kpred.
High impact features
Features were defined as “high impact” for a prediction if their mean feature importance over the five CV folds was >75% of mean importances assigned to the test data, corresponding to a prediction contribution with magnitude ≥0.001 in RF, and IG with magnitude ≥0.03 in BERT. Features that were not high impact are referred to as “low impact”. In RF, reaction centre atoms (Nu, LG, electrophilic C) were considered important if any ISIDA fragment with a substructure match to the atom was high impact, while temperature and solvent properties were said to be important if their numerical value was high impact. Meanwhile in the BERT model, reaction centre atoms were said to be important if the SMILES token representing the atom (or any one of the tokens representing the atom for symmetrical molecules with equivalent Nu, LG, or C atoms) was high impact, while temperature was considered important if the [RecipTemp] token or any token corresponding to significant figures of the reciprocal temperature was high impact. Regarding solvent, this was considered a high impact feature of the BERT model if ≥50% of solvent tokens on the reactants side were high impact. A threshold of ≥50% was employed (as opposed to 100%) to account for the fact that some solvent moieties (such as hydrogen bond donors) are expected to be more relevant to reactivity prediction than others.It is noted that each reaction centre atom also has a mapped atom in the products. The importance of these mappings is discussed in SI 5.4.
Analysing structural and physical effects
To assess whether RF and BERT effectively learned key structural and physical effects, we evaluated whether high impact features align with known reactivity rules including LG, steric, allylic, temperature, and solvent effects. To analyse structural and physical effects, the feature importances (positive sign ≡ increase log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred, or negative sign ≡ decrease log
kpred, or negative sign ≡ decrease log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred) of key reaction centre atoms (and bonds) were evaluated. Here, features with an importance of zero within the associated error were categorised as low impact. The importance of each feature is relative to that of a dummy model that predicts the mean log
kpred) of key reaction centre atoms (and bonds) were evaluated. Here, features with an importance of zero within the associated error were categorised as low impact. The importance of each feature is relative to that of a dummy model that predicts the mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp of the training data for each test reaction. By definition, all features of the dummy model have an importance of zero.
kexp of the training data for each test reaction. By definition, all features of the dummy model have an importance of zero.
To analyse LG effects, reactions with I, Br, Cl, and F LGs were considered, represented by C–I, C–Br, C–Cl and C–F fragments in RF and I, Br, Cl, and F tokens in BERT. Steric effects were analysed using reactions with alkyl-substituted centres are modelled by C–C, C–C–C, and C–C–C–C fragments in the RF model, and tokens of electrophilic and substituting C atoms in BERT. Here, the importance of these features in reactions with unsubstituted centres was used as a control. Meanwhile, allylic effects were assessed using reactions with alkene, alkyne, and aromatic groups bound to the electrophilic centre, which were represented by C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C–C
C, C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C, and C–C:C fragments in RF (where ‘:’ is an aromatic bond), and
C, and C–C:C fragments in RF (where ‘:’ is an aromatic bond), and ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ,
, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) and c tokens in BERT (where c is an aromatic carbon bonded to the centre). For centres with multiple substituents, the feature importances were summed over the corresponding high impact C,
and c tokens in BERT (where c is an aromatic carbon bonded to the centre). For centres with multiple substituents, the feature importances were summed over the corresponding high impact C, ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ,
, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) or c tokens in the BERT model (this is not relevant to RF where features are represented by counts of molecular fragments).
or c tokens in the BERT model (this is not relevant to RF where features are represented by counts of molecular fragments).
When evaluating temperature effects, feature importances correspond to the importance of the reciprocal temperature feature in RF, and the sum over importances of SMILES tokens representing temperature (the “[RecipTemp]” token or any token of the numerical value) in BERT. Regarding solvent effects in the BERT model (solvent effects were not evaluated for RF, see discussion in SI 5.2.3), the standard threshold of ε = 15 was used to define polar (>15), and non-polar (<15) solvents,63 while protic and aprotic solvents were defined as those with (protic) or without (aprotic) a proton bonded to a heteroatom. The importance of the solvent was taken as the sum over importances of high impact solvent tokens. Here, the solvent was said to be low impact if none of its tokens were high impact. Note that feature importances were summed over all temperature tokens, but only high impact solvent tokens. This is because solvent effects were analysed by categorising the feature importances into positive (increase log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred), negative (decrease log
kpred), negative (decrease log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred), or low impact (negligible effect on log
kpred), or low impact (negligible effect on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kpred), while temperature effects were evaluated by observing the correlation between feature importance and temperature.
kpred), while temperature effects were evaluated by observing the correlation between feature importance and temperature.
In RF, fragments containing I, Br, Cl or F LGs, or alkene, alkyne, or aromatic groups that aren't mentioned above were excluded from analysis to avoid confounding effects from other atoms and bonds. Additionally, reactions where C–C, C–C–C, or C–C–C–C fragments contain the product atom mapping of a nucleophilic C− atom were omitted from the analysis of steric effects in RF, to avoid confounding nucleophilic effects, as were reactions where the solvent acted as a nucleophile in the analysis of solvent effects in the BERT model. Similarly, reactions containing substituent groups other than alkyl were excluded from the analysis of steric effects in both models, as were reactions containing substituent groups other than alkene/alkyne/aromatic and alkyl in the analysis of allylic effects.
Author contributions
Study conception and design: Chloe Wilson and Fernanda Duarte; data collection: Chloe Wilson and María Calvo; analysis and interpretation of results: Chloe Wilson, Fernanda Duarte, Stamatia Zavitsanou, James D. Somper, Ewa Wieczorek, and Tom Watts; draft manuscript preparation: all authors; supervision: Fernanda Duarte and Jason Crain.Conflicts of interest
There are no conflicts to declare.Data availability
All custom code and associated datasets referenced in the manuscript are available at the following GitHub repository: https://github.com/duartegroup/InterpretingMLKinetics (initial release v1.0.0, DOI: https://doi.org/10.5281/zenodo.17980697).Supplementary information (SI): detailed settings for model training, data sets used, and DFT calculations. It also provides further analyses on the interpretation of the model and inaccurate predictions. See DOI: https://doi.org/10.1039/d5dd00192g.
Acknowledgements
CW is supported by the University of Oxford Medical Science Division and IBM/EPSRC. EW acknowledges funding from the EPSRC CDT in Sustainable Approaches to Biomedical Science: Responsible and Reproducible Research – SABS:R3 (EP/S024093/1). TW acknowledges funding from the EPSRC CDT in Synthesis for Biology and Medicine (EP/L015838/1). JDS thanks New College for the Yeotown Scholarship. This work utilised the IBM Cloud platform and local facilities at Oxford.References
- E. Komp, N. Janulaitis and S. Valleau, Progress towards machine learning reaction rate constants, Phys. Chem. Chem. Phys., 2021, 24, 2692–2705 RSC.
- K. Jorner, A. Tomberg, C. Bauer, C. Sköld and P.-O. Norrby, Organic reactivity from mechanism to machine learning, Nat. Rev. Chem., 2021, 5, 240–255 CrossRef CAS PubMed.
- T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Machine learning activation energies of chemical reactions, WIREs Comput. Mol. Sci., 2021, 12(4), e1593 CrossRef.
- R. E. Plata and D. A. Singleton, A case study of the mechanism of alcohol-mediated Morita Baylis-Hillman reactions. The importance of experimental observations, J. Am. Chem. Soc., 2015, 137, 3811–3826 CrossRef CAS PubMed.
- Z. Liu, C. Patel, J. N. Harvey and R. B. Sunoj, Mechanism and reactivity in the Morita-Baylis-Hillman reaction: the challenge of accurate computations, Phys. Chem. Chem. Phys., 2017, 19, 30647–30657 RSC.
- L. Chan, G. M. Morris and G. R. Hutchison, Understanding Conformational Entropy in Small Molecules, J. Chem. Theory Comput., 2021, 17, 2099–2106 CrossRef CAS PubMed.
- M. H. Dehabadi, H. Saidi, F. Zafari and M. Irani, Computational Insights into Mechanism and Kinetics of Organic Reactions: Multiscale Modeling of SN2 and Claisen Rearrangements, Sci. Rep., 2024, 14, 16791 CrossRef PubMed.
- A. C. T. v. Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef.
- A. Warshel and R. M. Weiss, An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes, J. Am. Chem. Soc., 1980, 102, 6218–6226 CrossRef CAS.
- H. Zhang, V. Juraskova and F. Duarte, Modelling chemical processes in explicit solvents with machine learning potentials, Nat. Commun., 2024, 15, 6114 CrossRef CAS PubMed.
- C. A. Grambow, L. Pattanaik and W. H. Green, Deep Learning of Activation Energies, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef CAS PubMed.
- S. G. Espley, E. H. E. Farrar, D. Buttar, S. Tomasi and M. N. Grayson, Machine learning reaction barriers in low data regimes: a horizontal and diagonal transfer learning approach, Digital Discovery, 2023, 2, 941–951 RSC.
- H.-C. Chang, M.-H. Tsai and Y.-P. Li, Enhancing Activation Energy Predictions under Data Constraints Using Graph Neural Networks, J. Chem. Inf. Model., 2025, 65, 1367–1377 CrossRef CAS PubMed.
- A. Rakhimbekova, T. N. Akhmetshin, G. I. Minibaeva, R. I. Nugmanov, T. R. Gimadiev, T. I. Madzhidov, I. I. Baskin and A. Varnek, Cross-validation strategies in QSPR modelling of chemical reactions, SAR QSAR Environ. Res., 2021, 32, 207–219 CrossRef CAS PubMed.
- A. A. Kravtsov, P. V. Karpov, I. I. Baskin, V. A. Palyulin and N. S. Zefirov, Prediction of rate constants of S N 2 reactions by the multicomponent QSPR method, Dokl. Chem., 2011, 440, 299–301 CrossRef CAS.
- T. I. Madzhidov, P. G. Polishchuk, R. I. Nugmanov, A. V. Bodrov, A. I. Lin, I. I. Baskin, A. A. Varnek and I. S. Antipin, Structure-reactivity relationships in terms of the condensed graphs of reactions, Russ. J. Org. Chem., 2014, 50, 459–463 CrossRef CAS.
- T. Gimadiev, T. Madzhidov, I. Tetko, R. Nugmanov, I. Casciuc, O. Klimchuk, A. Bodrov, P. Polishchuk, I. Antipin and A. Varnek, Bimolecular Nucleophilic Substitution Reactions: Predictive Models for Rate Constants and Molecular Reaction Pairs Analysis, Mol. Inf., 2019, 38, e1800104 CrossRef PubMed.
- T. I. Madzhidov, A. V. Bodrov, T. R. Gimadiev, R. I. Nugmanov, I. S. Antipin and A. A. Varnek, Structure–reactivity relationship in bimolecular elimination reactions based on the condensed graph of a reaction, J. Struct. Chem., 2016, 56, 1227–1234 CrossRef.
- T. I. Madzhidov, T. R. Gimadiev, D. A. Malakhova, R. I. Nugmanov, I. I. Baskin, I. S. Antipin and A. A. Varnek, Structure–reactivity relationship in Diels–Alder reactions obtained using the condensed reaction graph approach, J. Struct. Chem., 2017, 58, 650–656 CrossRef CAS.
- M. Glavatskikh, T. Madzhidov, D. Horvath, R. Nugmanov, T. Gimadiev, D. Malakhova, G. Marcou and A. Varnek, Predictive Models for Kinetic Parameters of Cycloaddition Reactions, Mol. Inf., 2019, 38, e1800077 CrossRef PubMed.
- J. Ravasco and J. A. S. Coelho, Predictive Multivariate Models for Bioorthogonal Inverse-Electron Demand Diels-Alder Reactions, J. Am. Chem. Soc., 2020, 142, 4235–4241 CrossRef CAS PubMed.
- D. Zankov, T. Madzhidov, I. Baskin and A. Varnek, Conjugated quantitative structure-property relationship models: Prediction of kinetic characteristics linked by the Arrhenius equation, Mol. Inf., 2023, e2200275, DOI:10.1002/minf.202200275.
- F. Ruggiu, G. Marcou, A. Varnek and D. Horvath, ISIDA Property-Labelled Fragment Descriptors, Mol. Inf., 2010, 29, 855–868 CrossRef CAS PubMed.
- C. Molnar, Interpretable Machine Learning, Leanpub, 2020 Search PubMed.
- P. van Gerwen, K. R. Briling, C. Bunne, V. Ram Somnath, R. Laplaza, A. Krause and C. Corminboeuf, EquiReact: An equivariant neural network for chemical reactions, arXiv, 2023, preprint, DOI:10.1038/s42256-020-00284-w.
- K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Machine learning meets mechanistic modelling for accurate prediction of experimental activation energies, Chem. Sci., 2021, 12, 1163–1175 RSC.
- T. Lewis-Atwell, D. Beechey, Ö. Şimşek and M. N. Grayson, Reformulating Reactivity Design for Data-Efficient Machine Learning, ACS Catal., 2023, 13506–13515, DOI:10.1021/acscatal.3c02513.
- S. Heinen, G. F. von Rudorff and O. A. von Lilienfeld, Toward the design of chemical reactions: Machine learning barriers of competing mechanisms in reactant space, J. Chem. Phys., 2021, 155, 064105 CrossRef CAS PubMed.
- E. H. E. Farrar and M. N. Grayson, Machine learning and semi-empirical calculations: a synergistic approach to rapid, accurate, and mechanism-based reaction barrier prediction, Chem. Sci., 2022, 13, 7594–7603 RSC.
- S. Vijay, M. C. Venetos, E. W. C. Spotte-Smith, A. D. Kaplan, M. Wen and K. A. Persson, CoeffNet: predicting activation barriers through a chemically-interpretable, equivariant and physically constrained graph neural network, Chem. Sci., 2024, 15, 2923–2936 RSC.
- A. M. Bran and P. Schwaller, Transformers and Large Language Models for Chemistry and Drug Discovery, arXiv, 2023, preprint, arXiv:2310.06083v1, DOI:10.48550/arXiv.2310.06083.
- N. Janakarajan, T. Erdmann, S. Swaminathan, T. Laino and J. Born, Language models in molecular discovery, arXiv, 2023, preprint, arXiv:2309.16235v1, DOI:10.48550/arXiv.2309.16235.
- P. Schwaller, D. Probst, A. C. Vaucher, V. H. Nair, D. Kreutter, T. Laino and J.-L. Reymond, Mapping the space of chemical reactions using attention-based neural networks, Nat. Mach. Intell., 2021, 3, 144–152 CrossRef.
- P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, Prediction of chemical reaction yields using deep learning, Mach. Learn.: Sci. Technol., 2021, 2, 015016–015023 Search PubMed.
- S. Madan, M. Lentzen, J. Brandt, D. Rueckert, M. Hofmann-Apitius and H. Fröhlich, Transformer models in biomedicine, BMC Med. Inf. Decis. Making, 2024, 24, 214 CrossRef PubMed.
- J. Jiang, L. Chen, L. Ke, B. Dou, C. Zhang, H. Feng, Y. Zhu, H. Qiu, B. Zhang and G.-W. Wei, A review of transformer models in drug discovery and beyond, J. Pharm. Anal., 2025, 15, 101081 CrossRef PubMed.
- M. C. Ramos, C. J. Collison and A. D. White, A review of large language models and autonomous agents in chemistry, Chem. Sci., 2025, 16, 2514–2572 RSC.
- E. Heid and W. H. Green, Machine Learning of Reaction Properties via Learned Representations of the Condensed Graph of Reaction, J. Chem. Inf. Model., 2022, 62, 2101–2110 CrossRef CAS PubMed.
- V. E. Kuz'min, P. G. Polishchuk, A. G. Artemenko and S. A. Andronati, Interpretation of QSAR Models Based on Random Forest Methods, Mol. Inf., 2011, 30, 593–603 CrossRef PubMed.
- M. Sundararajan, A. Taly and Q. Yan, presented in part at the Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 2017 Search PubMed.
- D. P. Kovacs, W. McCorkindale and A. A. Lee, Quantitative interpretation explains machine learning models for chemical reaction prediction and uncovers bias, Nat. Commun., 2021, 12, 1695–1703 CrossRef CAS PubMed.
- C.-H. Wu, B. Galabov, J. I. C. Wu, S. Ilieva, P. v. R. Schleyer and W. D. Allen, Do π-Conjugative Effects Facilitate SN2 Reactions?, J. Am. Chem. Soc., 2014, 136, 3118–3126 CrossRef CAS PubMed.
- B. Galabov, G. Koleva, H. F. Schaefer Iii and W. D. Allen, Nucleophilic Influences and Origin of the SN2 Allylic Effect, Chem.–Eur. J., 2018, 24, 11637–11648 CrossRef CAS PubMed.
- S. M. Kearnes, M. R. Maser, M. Wleklinski, A. Kast, A. G. Doyle, S. D. Dreher, J. M. Hawkins, K. F. Jensen and C. W. Coley, The Open Reaction Database, J. Am. Chem. Soc., 2021, 143, 18820–18826 CrossRef CAS PubMed.
- W. A. Henderson and S. A. Buckler, The Nucleophilicity of Phosphines, J. Am. Chem. Soc., 1960, 82, 5794–5800 CrossRef CAS.
- K. Okamoto, H. Matsuda, H. Kawaski and H. Shingu, Kinetic Studies of Bimolecular Nucleophilic Substitution. V. Rates of SN2 and E2 Reactions of 1,2-Dichloroethane with Various Nucleophiles in Aqueous Solutions, Bull. Chem. Soc. Jpn., 1967, 40, 1917–1920 CrossRef CAS.
- D. F. DeTar, D. F. McMullen and N. P. Luthra, Steric Effects in SN2 Reactions, J. Am. Chem. Soc., 1978, 100(8), 2484–2493 CrossRef CAS.
- F. G. Bordwell and S. R. Mrozack, SN2 Reactions of Carbanions with Primary and Secondary Alkyl Bromides in Dimethyl Sulfoxide Solution, J. Org. Chem., 1982, 47, 3802–3803 CrossRef CAS.
- F. G. Bordwell and D. L. Hughes, SN2 Reactions of Nitranions with Benzyl Chlorides, J. Am. Chem. Soc., 1984, 106, 3234–3240 CrossRef CAS.
- T. J. Rao, G. Punnaiah and E. V. Sundaram, Kinetics of the Reaction of Alkyl Bromides with Nucleophiles Containing Nitrogen Atoms, Proc. Indian Acad. Sci., 1986, 97, 55–61 CrossRef CAS.
- T. L. Amyes and W. P. Jencks, Concerted Bimolecular Substitution Reactions of Acetal Derivatives of Propionaldehyde nd Benzaldehyde, J. Am. Chem. Soc., 1989, 111, 7900–7909 CrossRef CAS.
- N. S. Banait and W. P. Jencks, Reactions of Anionic Nucleophiles with a-D-Glucopyranosyl Fluoride in Aqueous Solution Through a Concerted ANDN (SN2) mechanism, J. Am. Chem. Soc., 1991, 113, 7951–7958 CrossRef CAS.
- Y. Kondo, M. Urade, Y. Yamanishi and X. Chen, Relative reactivity of methyl iodide to ethyl iodide in nucleophilic substitution reactions in acetonitrile and partial desolvation accompanying activation, J. Chem. Soc., Perkin Trans. 2, 2002, 1449–1454 RSC.
- F. Ruff, Reaction Constants Derived from Activation Parameters for the Evaluation of Substituent and Solvent Effects, Internet Electron. J. Mol. Des., 2004, 3, 474–498 CAS.
- V. M. Vlasov, Energetics of bimolecular nucleophilic reactions in solution, Russ. Chem. Rev., 2006, 75, 765–796 CrossRef CAS.
- F. Ruff and O. Farkas, Effect of Substituents on Activation Parameters in Aliphatic SN2 Reactions. A DFT Study, J. Org. Chem., 2006, 71, 3409–3416 CrossRef CAS PubMed.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson, E. Bakshy, BOTORCH: A Framework for Efficient Monte-Carlo Bayesian Optimization, arXiv, 2020, preprint, arXiv:1910.06403, DOI:10.48550/arXiv.1910.06403.
- E. Bakshy, L. Dworkin, B. Karrer, K. Kashin, B. Letham, A. Murthy and S. Singh, presented in part at the NIPS, Montréal, Canada, 2018 Search PubMed.
- F. Neese, The ORCA program system, WIREs Comput. Mol. Sci., 2011, 2, 73–78 CrossRef.
- T. A. Young, J. J. Silcock, A. J. Sterling and F. Duarte, autodE: Automated Calculation of Reaction Energy Profiles- Application to Organic and Organometallic Reactions, Angew. Chem., Int. Ed., 2021, 60, 4266–4274 CrossRef CAS PubMed.
- A. Saabas, treeinterpreter, https://pypi.org/project/treeinterpreter/, accessed 28/02/2023.
- N. Kokhlikyan, V. Miglani, M. Martin, E. Wang, B. Alsallakh, J. Reynolds, A. Melnikov, N. Kliushkina, C. Araya, S. Yan, O. Reblitz-Richardson, Captum: A unified and generic model interpretability library for PyTorch, arXiv, 2020, preprint, arXiv:2009.07896, DOI:10.48550/arXiv.2009.07896.
- T. H. Lowry and K. S. Richardson, Mechanism And Theory In Organic Chemistry, Harper & Row, New York, 1976 Search PubMed.
Footnote |
| † Current address: Xyme Ltd, Inventa, Botley Road, Oxford, England, OX2 0HA. E-mail: E-mail: cwilson@xyme.ai |
| This journal is © The Royal Society of Chemistry 2026 |


