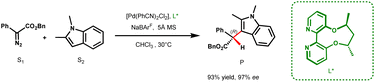A combined experimental and computational study reveals a crossover between conventional cross-coupling and carbene insertion pathways in a Pd catalyzed C(sp²)–H insertion

Abstract

Computational (DFT and DLPNO-CCSD(T)) calculations along with experimental tools (deuterium labelling, kinetic studies using VTNA, ESI-HRMS and UV) are used to probe the mechanism of a Pd(II)-catalyzed enantioselective carbene insertion into C(sp²)–H of indole. Using deuterium labelling studies, we demonstrate the intermediacy of a metal-hydride species, which contrasts with mechanistic routes for other transition metals (Rh, Fe, Au, Cu, etc.). Our VTNA study reveals the order to be one in both diazo and indole, which along with microkinetic modelling aligns well with the computationally predicted mechanism. The mechanism is further supported by the detection of the most stable intermediate in the catalytic cycle using ESI-HRMS. An investigation into the origin of stereoselectivity using DLPNO-CCSD(T) presents a new paradigm, wherein stereocontrol arises during the formation of the Pd carbene itself as opposed to proton transfer steps found for all other metal catalysts.

---

Introduction

The indole scaffold has found widespread utility in the pharmaceutical and agrochemical industries, with over 200 potential drug candidates introduced to the market for the treatment of cancer, type 2 diabetes, and HIV, containing this key structural motif.¹ One of the most effective methods for functionalizing indole is via carbenes generated from diazo precursors. Traditionally, these reactions are catalyzed by transition metals such as Rh, Cu, Pd, and Fe.^2–8 When using α-aryl-α-diazoacetates as the carbene precursor, Fe catalysts typically afford only modest enantioselectivity, while Rh catalysts generally require a chiral Brønsted acid as a cocatalyst for achieving high enantioselectivities.^5,9 On the other hand, Cu and Pd catalysts have been shown to yield high enantioselectivity solely through the use of chiral ligands.^3,7 However, the underlying mechanism remains largely unexplored, thereby posing a significant challenge in developing a general catalyst for carbene insertion reactions. Earlier DFT studies have primarily focused on Rh, Cu, Au, and Ag catalyzed reactions where ylides/enols act as intermediates in the catalytic cycle.^2,10–14 Despite these repertoires of mechanistic investigations, the origin of stereoinduction for many carbene insertion reactions, especially those employing chiral ligands, remains unclear.

Pd based systems are quintessential catalysts for various cross-coupling reactions. However, their use in X–H (X = O, N, S, C(sp²)) insertion reactions utilizing diazo precursors is more recent and currently underutilized. In 2015, Zhou and co-workers reported a base-free Brønsted acid-free protocol for a highly enantioselective Pd-catalyzed carbene insertion into the C3–H bond of electron rich indole derivatives, using aryl diazo esters as carbene precursors, through the use of ACBP (axially chiral bipyridine) ligands (Scheme 1).⁷ Their report demonstrates the ability of Pd to efficiently catalyze the enantioselective C(sp²)–H insertion of carbenes. There are a few other reports where Pd works efficiently in catalyzing enantioselective carbene insertion into the O–H bond of phenol and the N–H bond of aromatic heterocycles with high ee values using spirobox, biimidazole and ACBP ligands.¹⁴

Scheme 1 Pd-catalyzed C3–H functionalization of indole using the ACBP (L*) ligand.

While excellent stereoselectivity has been obtained in all these reactions, the general mechanistic framework remains fuzzy. The use of diazo precursors in cross-coupling reactions that proceed via a migratory insertion pathway is well-established (vide infra).¹⁵ In X–H insertion reactions, the preferred pathway remains ambiguous, whether it follows a conventional Pd-catalyzed cross-coupling route or the typical carbene insertion reaction pathway seen for Rh, Fe, Au and Cu catalyzed transformations. A major consequence of an incomplete understanding at the molecular level has been the slow development of Pd catalyzed carbene insertion reactions.

In the Rh(II)-catalyzed functionalization of indole at C3, Fox and co-workers postulated a mechanism involving a Rh-ylide with oxocarbenium characteristics.² Recently, our group, through a detailed mechanistic study, studied the origin of enantioselectivity in the case of Fe and Rh catalyzed indole alkylation reactions by invoking Fe and Rh bound enol pathways, respectively.^16,46,47 Hu and coworkers reported a computational investigation of a Pd/chiral guanidine catalyzed N–H insertion reaction.¹³ The authors postulated the formation of a Pd–H intermediate and the nucleophilic attack of the amine onto the metallocarbene intermediate to be the stereodetermining step. However, the authors considered neither the conventional cross-coupling pathway typically adopted in Pd-catalyzed carbene migratory insertion reactions nor the enol pathway of transition metal catalyzed carbene insertion reactions. Furthermore, in another Rh/guanidine-based O–H insertion, the reaction was shown to proceed via a guanidine assisted enol pathway.¹⁷ It remains unclear whether guanidine acts as a ligand or as a co-catalyst in Rh and Pd catalysis. Malkov and coworkers recently studied the mechanism of Pd catalyzed indole alkylation with chiral bipyridine-N,N′-dioxides as ligands.¹⁸ The authors proposed a conventional cross coupling pathway involving CMD (concerted metalation deprotonation). The main finding of the work was the role of Pd nanoparticles. However, the mechanism based on ESI-HRMS and computational studies is ambiguous and so is the formation of active catalytic Pd–OH species. The different mechanisms with different ligands further highlight the complexity of metal catalyzed carbene insertion reactions.

The general catalytic cycle of Pd catalyzed cross-coupling reactions involves the formation of a Wheland intermediate R–Pd (2) via S_EAr (electrophilic aromatic substitution). Other commonly accepted mechanisms for the formation of organometallic species are oxidative addition, C–H activation, transmetalation, CMD, or S_EAr (electrophilic aromatic substitution).^19,20 It is followed by the reaction of 2 with the carbene precursor to form a metallocarbene intermediate 3 and subsequently a zwitterion 4 is rapidly generated via migratory insertion (Scheme 2). This zwitterion species 4 is also formed in carbene insertion reactions catalyzed by Rh, Cu, Fe, Au, etc.^2,9–13,16 The formation of this zwitterion may also take place via an alternative pathway, where the first step involves the formation of a metallocarbene species 6via N₂ extrusion. Owing to the high electrophilicity of the carbene carbon in 6, it undergoes a nucleophilic attack, forming the common zwitterionic species, 4. This is followed by β-hydride elimination leading to intermediate 5 and then a hydride transfer to generate the final product, 8. In other metal catalyzed carbene insertion reactions, either a direct 1,2-proton transfer yields the product or an enol 7 is formed via a 1,4-proton transfer. This enol subsequently tautomerizes, generating the final product, 8 (Scheme 2).

Scheme 2 The conventional carbene insertion and cross coupling catalytic cycles.

At present, it is unclear which mechanistic route is adopted in Pd catalyzed reactions and whether a crossover between the two catalytic cycles occurs or not. This in turn has not allowed for an unambiguous assignment of the stereodetermining step. This contrasts with other metal catalyzed carbene insertion reactions, where generally the final tautomerization takes place in a stereoselective manner.

In the present report, we resolve the mechanistic conundrum and delineate the stereocontrol in the Pd catalyzed indole alkylation reaction through a detailed computational and experimental study. Our study reveals an interesting mechanistic paradigm in Pd catalysis and an unprecedented stereodetermining step. The mechanistic understanding obtained from the current study will be important in other X–H insertions that are likely to adopt a similar route, and more importantly, in three component reactions, which have been unsuccessful in yielding high enantioselectivities.²¹ The discussions in the subsequent text are based on the relative free energies (taking active species A as the reference) at the SMD_(DCM)/B3LYP-D3/6-311+G(d,p),LANL2DZ(Pd)//B3LYP-D3/6-31G(d,p),LANL2DZ(Pd) level of theory unless otherwise specified. For crucial TSs and stationary points, free energies are also reported at the SMD_(DCM)/DLPNO-CCSD(T)/def2-TZVP//B3LYP-D3/6-31G(d,p),LANL2DZ(Pd) level of theory.²² For all calculations, we have employed the substrates shown in Scheme 1. Additional calculations with α-methyl-α-diazoester are also carried out, the details of which are given in the ESI.†²³

Results and discussion

Active catalytic species

We first investigate the nature of the active species. Previous reports suggest that the primary function of NaBAr^F is the abstraction of chloride from [Pd(PhCN)₂Cl₂], resulting in the active catalytic species A, which is a dicationic complex with Pd in the II oxidation state (Fig. 1).^14a,b,24,25 This is supported by PXRD (powder X-ray diffraction) analysis, where a small amount of an insoluble white solid assumed to be sodium chloride is formed after the completion of the reaction.^24a,25 To further understand the nature of active catalytic species, we recorded the UV-Vis spectra of the [Pd(bpy)Cl₂] (where bpy is 2,2′-bipyridine, an achiral ligand that mimics the axially chiral bipyridine ligand employed by Zhou⁷ and co-workers) complex, the [Pd(PhCN)₂Cl₂] complex, and a mixture comprising [Pd(PhCN)₂Cl₂], bpy, and NaBAr^F. The spectrum of the mixture indicated the coordination of bpy to Pd(II). Additionally, the spectrum for this mixture was distinct from those of both [Pd(PhCN)₂Cl₂] and [Pd(bpy)Cl₂], providing further evidence that NaBAr^F acts as a chloride scavenger to form A (Fig. 1).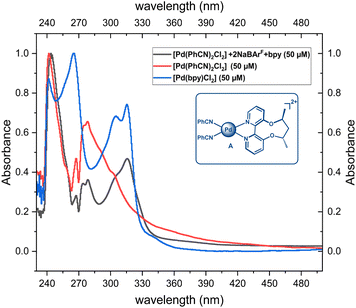

Fig. 1 Plausible active catalytic species, A, and UV-Vis spectra for the [Pd(PhCN)₂Cl₂] + bpy + NaBAr^F mixture, [Pd(bpy)Cl₂] and [Pd(PhCN)₂Cl₂].

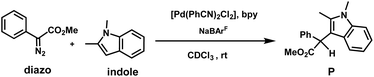
We also carried out the full reaction, i.e., C3–H insertion of 1,2-dimethyl-1H-indole using methyl-α-diazo-α-phenylacetate as the carbene precursor using the [Pd(bpy)Cl₂] catalyst under similar reaction conditions as shown in Scheme 1, which resulted in a much lower yield (53%), ruling out the substitution of the PhCN ligand with the bpy ligand in the actual reaction with the [Pd(PhCN)₂Cl₂] catalyst. Apart from A, we also considered alternative active species with a partial abstraction of chloride ions, resulting in a cationic Pd complex (vide infra). However, the activation free energy barriers were found to be higher in energy than those of catalytic species, A.²⁶ Based on our studies and previous reports, an active species, A, is the most plausible one, and further discussions are based on it.

Formation of intermediate Dvia the conventional cross coupling pathway and carbene

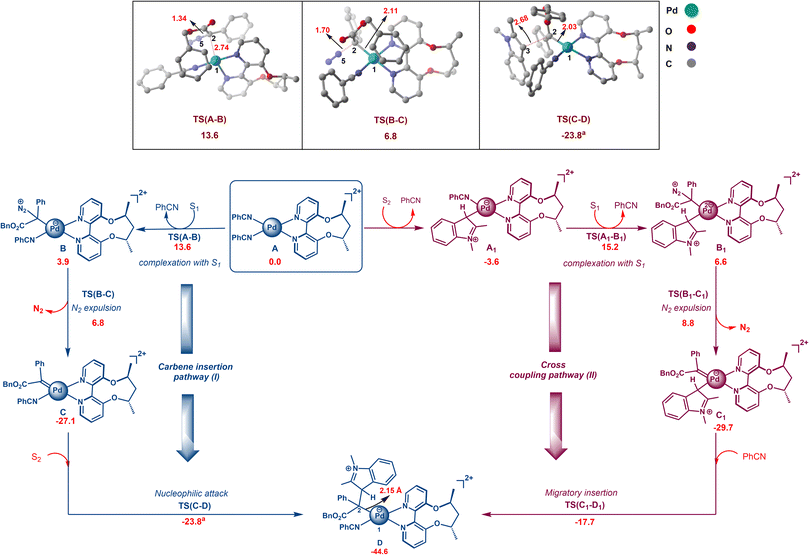
We now discuss the mechanism using DFT calculations involving the carbene insertion pathway and cross coupling route, starting with active species A (Scheme 3). All calculations are performed with the chiral ACBP ligand. In the carbene insertion pathway, I, the first step involves the formation of a tetrahedral intermediate BviaTS(A–B) with an activation free-energy barrier of 13.6 kcal mol⁻¹, followed by metallocarbene (C) formation viaTS(B–C). The C2–Pd1 distance in TS(A–B) is 2.74 Å, whereas in TS(B–C), leading to the metallocarbene C, the distance between C2 and Pd1 is 2.11 Å (Scheme 3). The formation of the tetrahedral intermediate, B, is generally not observed for other metal catalyzed reactions, except for Fe.²⁷ The next step involves the nucleophilic attack of indole via its C3 position on the metallocarbene CviaTS(C–D) and has an activation free energy barrier of 3.3 kcal mol⁻¹ with an elongated C2–C3 bond distance (2.68 Å). In the ensuing metal ylide D, Pd is connected to the carbene carbon with a Pd1–C2 distance of 2.15 Å. We also considered an alternative conventional cross-coupling pathway to intermediate D. Here, indole S₂ instead of directly attacking the carbene carbon first coordinates to Pd to generate intermediate A₁. Alternative mechanistic pathways involving a CMD type mechanism were also investigated but were found to be higher in energy.²⁸

Scheme 3 Formation of zwitterion Dvia nucleophilic attack and migratory insertion pathways. Optimized geometries for TSs with distances in Å. Relative free energies (kcal mol⁻¹) are at the SMD_(DCM)/B3LYP-D3/6-311+G(d,p),LANL2DZ(Pd)//B3LYP-D3/6-31G(d,p),LANL2DZ(Pd) level of theory. Hydrogens are removed for clarity. ^aRelative free energy (kcal mol⁻¹) is at the SMD_(DCM)/B3LYP-D3/6-311+G(d,p),LANL2DZ(Pd)//B3LYP/6-31G(d,p),LANL2DZ(Pd) level of theory.

Additional support for discarding the C–H activation route in the absence of an added base comes from a control experiment with a diazo substrate with a stoichiometric amount of Pd. Even after 4 hours, 73% indole remains unreacted, as seen from ¹H-NMR. We were not able to characterize the remaining 27%. However, crystal structures resembling intermediate A₁ have been reported earlier, where the complex shows a σ–π continuum for the indole–metal interaction in indole–palladium(II) complexes, where the C3–H proton of indole remains unaffected.²⁹ The next step is the formation of the tetrahedral complex B₁ with carbene precursor S₁ through TS(A₁–B₁) with a relative free energy of 15.2 kcal mol⁻¹. In the next step, Pd–indolium (3H-indol-3-yl palladium) carbene species C₁ is formed by N₂ expulsion from B₁viaTS(B₁–C₁) with an activation free energy barrier of 8.8 kcal mol⁻¹ (Scheme 3). Subsequently, migratory insertion takes place viaTS(C₁–D) to generate metal ylide D with an activation free energy barrier of 12.0 kcal mol⁻¹ (Scheme 3). A comparison between the two pathways, viz. nucleophilic attack and migratory insertion steps, reveals that TS(A–B) has a lower energy than TS(A₁–B₁), thus favoring the nucleophilic attack mechanism (Scheme 3). Since this presents a critical juncture for the mechanism, we carried out single point calculations at the DLPNO-CCSD(T) level and found the energy difference between TS(A–B) and TS(A₁–B₁) to be 7.1 kcal mol⁻¹, further supporting our mechanistic hypothesis of the nucleophilic pathway being the favored route.

Pathways originating from zwitterion D

Following the formation of the zwitterion D, there exist several mechanistic possibilities as shown in Scheme 4 leading to the product.³⁰ A comparison amongst different pathways reveals the enol pathway to be the most favorable, which is observed for other metal catalyzed reactions as well. The formation of an enol viaTS(D–E_a) is a feasible process at room temperature requiring an activation free energy barrier of 19.1 kcal mol⁻¹. Once the enol is formed, it can dissociate from the metal centre and undergo a 1,3-proton transfer, leading to the final product. This tautomerization has been studied quite extensively and forms the basis of cooperative catalytic systems employing chiral Brønsted acids.^9,10c,31

Scheme 4 Formation of alkylated indole products via 1,2-proton transfer, metal–enol and metal–enolate pathways. The relative free energies (kcal mol⁻¹) are given in parentheses at the SMD_(DCM)/B3LYP-D3/6-311+G(d,p),LANL2DZ(Pd)//B3LYP-D3/6-31G(d,p),LANL2DZ(Pd) level of theory for the formation of alkylated product P from zwitterion Dvia the enol pathway.

However, in the absence of an added co-catalyst, the 1,3-proton transfer via a strained four-membered TS would possess a high energetic barrier. This can be clearly seen from the high activation free energy barrier of 60.8 kcal mol⁻¹ in forming PviaTS(E_free–P) (ESI, Fig. S7†). However, recently we have shown that the enol does not necessarily have to dissociate from the metal centre, and adventitious water molecules can participate in the tautomerization step.^16,31 This also forms the basis of stereoinduction, where only ligands on the metal are employed as the chiral source. Thus, in this case as well, we studied the Pd-associated enol pathway, where the enol is bound to Pd and water molecules help in the proton transfer.³² All other TSs without the assistance of water molecules were found to be higher in energy (ESI, Fig. S7†). Our calculated activation free energy barrier of water assisted tautomerization is 31.5 kcal mol⁻¹ with respect to D (Scheme 4).³³

In our previous study with a Rh catalyst, we performed an indole alkylation reaction with D-indole under standard reaction conditions using the procedure reported by Fox and co-workers.^2,16b The incorporation of H suggested the participation of external water molecules. To test whether external solvent molecules also participate under the given conditions, we performed similar experiments. We carried out the C3–H insertion of 1,2-dimethyl-1H-indole using methyl-α-diazo-α-phenylacetate as the carbene precursor with the catalyst combination of [Pd(PhCN)₂Cl₂], 2,2′-bipyridine (an achiral ligand that mimics the axially chiral bipyridine ligand employed by Zhou and co-workers),⁷ and NaBAr^F in freshly distilled dry toluene following the procedure reported by Zhou. We intentionally added 25 equivalents of D₂O to specifically monitor the proton transfer step for 16 hours (reaction (1), Scheme 5).

Scheme 5 Deuterium exchange studies to delineate the participation of water.

Deuterium incorporation was observed in the C3-alkylated product, with a D : H ratio of 66 : 34. However, a control experiment (reaction (2), Scheme 5) without the carbene precursor in the presence of D₂O showed a similar D : H ratio (62 : 38) for the indole substrate, indicating deuterium exchange of the substrate itself under the reaction conditions. If D₂O were indeed participating in a 1,3-proton transfer in the course of the reaction, the D : H ratio of the product in reaction 1 would be significantly higher than 62 : 38. We also performed the reaction using 1,2-dimethyl-1H-indole-3-d without any added H₂O or D₂O in the presence of 5 Å MS as an additive and observed proton incorporation in the C3-alkylated product with a D : H ratio of nearly 08 : 92 (reaction (3), Scheme 5). Again, the corresponding control experiment showed a similar D : H ratio starting from 1,2-dimethyl-1H-indole-3-d (reaction (4), Scheme 5). While the reactions in Scheme 5 indicate that solvent molecules are not participating in the product formation, we wanted to further understand the origin of the deuterium scrambling in the reactant, i.e., 1,2-dimethyl-1H-indole-3-d. It should be noted that the alkylated product does not undergo any D scrambling (ESI, Section 12.6†). To get a better understanding of the reaction mechanism, it is also imperative to understand the kinetics of deuterium scrambling in the reactant relative to the product formation.

The reaction (Scheme 6) gives a yield of 58% in one hour without adding any MS; therefore, all subsequent reactions are carried out without MS for one hour. To understand the origin of D scrambling, we conducted several control experiments in toluene and concluded that various components—[Pd(PhCN)₂Cl₂], 2,2′-bipyridine, and NaBAr^F—contribute to the exchange. However, NaBAr^F is the primary contributor, likely due to the presence of acidic impurities in the reaction mixture originating from these components, although the exact nature of these impurities is uncertain (Scheme 6). Since the exchange occurs even in the absence of the Pd catalyst, its participation can be ruled out. While it is clear that acidic impurities participate in the exchange in the reactant, we wanted to check whether the final enol tautomerization step can be catalyzed by an acid. Since the nature of the impurity is unclear, we performed calculations with a Brønsted acid (chiral phosphoric acid) and found TS(E_free–P)_CPA to be lower in energy (19.6 kcal mol⁻¹) than the earlier TS(E_a–P)_2wat (31.5 kcal mol⁻¹).³⁴ However, in TS(E_free–P)_CPA, the enol is metal-free, and thus such a model with an achiral acid impurity cannot explain the high stereoselectivity (98% ee) in the current reaction (the corresponding Pd-associated TS was found to be 6.1 kcal mol⁻¹ higher in energy).³⁴ Additional control experiments in the presence of an added acid and base were also carried out, where both these added species contribute to an exchange.^35,36

Scheme 6 Reaction (1) showing product yield in the absence of molecular sieves in 1 h in dry toluene. Reactions (2–9) showing the D : H exchange ratio in 1,2-dimethyl-1H-indole-3-d (D : H = 95 : 5) under various conditions.

We also carried out the reaction with D-indole in CHCl₃ to understand the role of the solvent. Here, after one hour, the D : H ratio changes from 75 : 25 to 33 : 67 (Fig. 2). We performed additional experiments at different time intervals. The yield of the product in the first 10 minutes is only 14%, whereas the D : H ratio of the unreacted indole changes from 75 : 25 to 49 : 51. Thus, the exchange reaction is faster than the product formation. Gratifyingly, we notice that the D : H ratio in the unreacted indole remains constant after 10 minutes and so does the D : H ratio in the product (Fig. 2). Similar experiments were also carried out in toluene, where we see a similar trend.³⁷ This clearly indicates that no external water molecules participate in the course of the reaction. Since the D : H ratio in the reactant and product remains similar, it can be further concluded that C–H/Pd–H bond cleavage is not involved in the rate determining step (RDS).

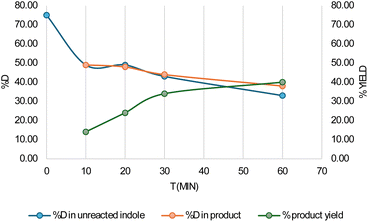Fig. 2 %D in unreacted indole and alkylated product and yield of the indole alkylated product with time in chloroform solvent.

Based on these experiments and computationally calculated activation free energy barriers (the lowest barrier was 31.5 kcal mol⁻¹ for a Pd-associated water assisted enol pathway, which is very high for a room temperature reaction), we rule out any water assisted 1,3-proton transfer, and therefore the proton transfer to yield the final product must necessarily proceed through a different pathway.

Inspired by Pd-catalyzed cross-coupling reactions involving carbenes as shown in Scheme 2, we conceptualized a Pd–H species (F/F₁) as a possible intermediate (Scheme 7). The β-hydride elimination from the C3 of indole to the Pd centre in the metal ylide Dvia a late TS(D–F) with an activation free energy barrier of 21.4 kcal mol⁻¹ leads to the formation of the Pd–H species, F. Here the methylene indolium coordinates to Pd in an η²-fashion (Scheme 7). The formation of an ene-bound Pd complex after β-hydride elimination is a typical behavior of Pd-catalyzed cross-coupling reactions.^19,20 Pd–C2 and Pd–C3 distances are 2.16 Å and 2.28 Å, respectively, in TS(D–F). Initially, we anticipated that the transfer of a proton from the indolium species to Pd(II) would lead to its oxidation to Pd(IV). However, the process unfolds differently: there is a simultaneous transfer of a proton from the indolium C3–H to Pd along with the breaking of the C–Pd bond, leading to a formal hydride transfer. This results in the generation of a Pd(II)-coordinated methylene indolium species F, thus avoiding Pd(II)/Pd(IV) oxidation due to the latter's instability. Such an iminium type complex is also found in the literature, where it is highly electrophilic in nature and susceptible to being attacked by a nucleophile.³⁸ Here, the hydride at Pd–H behaves similar to a nucleophile to rearomatize the indolium ring.

Scheme 7 Formation of alkylated indole via the Pd–H pathway starting from metal ylide D. Optimized geometries are given for TSs with distances in Å. Relative free energies are given in kcal mol⁻¹. For the TS geometries, hydrogens are removed for clarity.

In TS(D–F), the methylene indolium and Pd–H are coplanar as can be observed from the dihedral angle, φ_{C3–C2–Pd1–H4}, which is −2.1°. This dihedral angle changes to −12.8° in intermediate F. Subsequently, intermediate F isomerizes to a related geometry F₁viaTS(F–F₁), where the transferring hydride is closer to C2 and the φ_{C3–C2–Pd1–H4} dihedral is −128.1° (Scheme 7). The interconversion barrier between F and F₁viaTS(F–F₁) is 1.5 kcal mol⁻¹ (Scheme 7). The Gibbs free energy barrier of dissociation of the methylene indolium group from [L*Pd–H4] viaTS(F–F₂) is 9.7 kcal mol⁻¹, indicating that interconversion of F to F₁ is favorable over dissociation of the methylene indolium group from the [L*Pd–H4] moiety. The nature of the stereodetermining step is governed by the lower interconversion barrier (vide infra).

To understand the nature of interaction between [L*Pd–H] and methylene indolium species in F₁, we performed EDA-NOCV (Energy Decomposition Analysis-Natural Orbitals for Chemical Valence) calculations.³⁹ The major contribution toward orbital interaction may be attributed to the NOCV pairs Δρ1 and Δρ2, as shown in Fig. 3.

Fig. 3 Major contributing NOCV pairs to the deformation density Δρ associated with the formation of the F₁ complex between [L*Pd–H] and methylene indolium by ETS-NOCV analysis. The contour value is |Δρ| = 0.004 a.u. The blue/red contours show the accumulation/depletion of electron density. The part not involved in the given interactions is omitted for clarity.

The first interaction shows the outflow of electrons from the d_xy orbital of Pd and the σ orbital of Pd–H toward π* of the C2–C3 double bond. The corresponding energy contribution toward orbital interaction is −31.5 kcal mol⁻¹. The next dominant contribution toward orbital interaction shows the outflow of electrons from the π orbital of the C2–C3 double bond toward an empty d_x²−y² orbital of Pd and the σ* orbital of Pd–H with the corresponding interaction energy equal to −18.9 kcal mol⁻¹. It is clear from the NOCV pairs that there is an interaction between Pd–H and C2–C3 bonds.

Electron transfer from the C2–C3 double bond toward σ* of Pd–H facilitates weakening of the Pd–H bond and thus, an extremely facile stereospecific migratory insertion viaTS(F₁–P₁) is observed, which leads to the Pd-bound product P₁, which is subsequently released with the concomitant regeneration of the catalyst (Scheme 7).

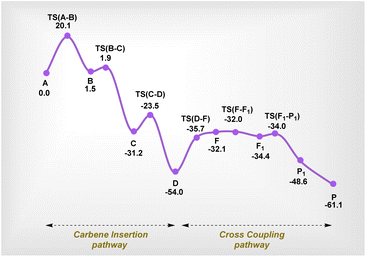
The overall free energy profile at the DLPNO-CCSD(T) level is given in Scheme 8. The mechanism proceeds via a catalytic cycle comprising two halves, where isomerization viaTS(F–F₁) is the most likely RDS. This also aligns well with our deuterium labelling experiments discussed above. It can be clearly seen that intermediate D is the most stable species, and therefore we made attempts to detect it using experimental methods. The detection of this intermediate via NMR proved to be very complex; therefore, we resorted to ESI-HRMS. Gratifyingly, we detected a species that supports the existence of intermediate D (Scheme 7).⁴⁰

Scheme 8 Free energy profile (kcal mol⁻¹) for the lowest energy pathway of carbene insertion into the C3–H bond of indole via the Pd–H intermediate at the SMD_(DCM)/DLPNO-CCSD(T)/def2-TZVP//B3LYP-D3/6-31G(d,p),LANL2DZ(Pd) level of theory.

Kinetic studies using VTNA

To further support our proposed mechanism, we conducted kinetic studies using the VTNA (Variable Time Normalization Analysis) approach developed by Burés⁴¹ and coworkers for the model reaction shown in Scheme 9, which was slightly modified from the procedure given by Zhou and coworkers.^7,41 The reactions were monitored using in situ¹H-NMR.

Scheme 9 Standard reaction used for kinetic studies.

As a first step, to check the robustness of the catalytic system, we carried out the “same excess” experiment. A complete overlay of the plots indicates no catalyst deactivation or product inhibition (Fig. 4(a)). Subsequently, we conducted “different excess” experiments to determine the order with respect to diazo, indole and the Pd catalyst. It should be noted that to determine the order with respect to the catalyst, the concentration of both bpy and NaBAr^F was unchanged from the standard conditions (Table 1). We observed a first order behaviour for Pd, diazo and indole (Fig. 4(b)–(d)).

Fig. 4 (a) “Same excess” experiments for probing the deactivation or product inhibition in the catalyst, (b) “different excess” study for order in the Pd catalyst, (c) “different excess” study for order in indole, (d) “different excess” study for order in diazo, (e) monitoring of reaction progress with respect to the product in different pathways using COPASI. It should be noted that for all experiments ((a)–(d)), the concentration of bpy and NaBAr^F was kept fixed at 5 mol% and 12 mol%, respectively.

Table 1 VTNA experiments

Experiment	[Diazo]	[Indole]	[Pd]
Standard	0.042 M	0.072 M	5 mol%
Same excess	0.026 M	0.056 M	5 mol%
Diazo excess	0.024 M	0.072 M	5 mol%
Indole excess	0.042 M	0.040 M	5 mol%
Pd excess	0.042 M	0.072 M	6 mol%

---

First order dependence on both diazo (1.0) and indole (1.0) fits well with our computational model of the isomerization step being rate determining in nature. We further turned to kinetic modelling using COPASI software.⁴² The kinetic constants for different mechanisms were estimated based on the parameter estimation tool in COPASI. It can be seen from Fig. 4(e) that the computationally calculated lowest energy pathway, i.e., the crossover pathway (Scheme 8), fits best with the experimental profile. Other mechanisms show a poor fit.⁴³

Stereochemical model

We now turn our attention to the nature of the stereodetermining step and the origin of high stereoselectivity. A careful analysis of different TSs involved in the minimum energy pathway reveals an unprecedented stereodetermining step that is different from other metal catalyzed reactions, where the final enol–keto tautomerization step generally controls the stereoselectivity.

We begin our discussion with the formation of the tetrahedral intermediate, B. As shown in Scheme 10, a chiral centre is generated at C2, resulting in diastereomeric intermediates, B_R and B_S. It remains to be seen if the stereochemical information generated at this junction can be carried forward in the subsequent intermediates along the catalytic cycle. From intermediate B, N₂ expulsion takes place preferentially near the site of the PhCN ligand, resulting in an axially chiral metallocarbene C, termed point to axial chirality transfer.

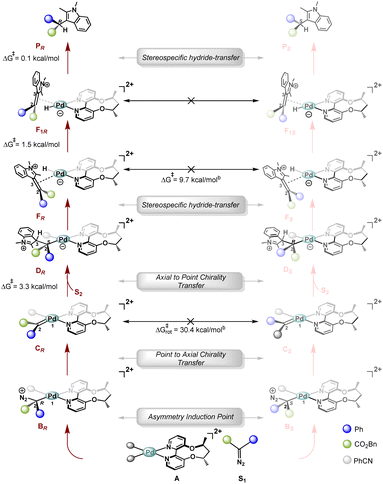Scheme 10 Plausible stereochemical model from theoretical calculations.^{a a}Subscripts R/S refer to the stereochemistry of the final product being formed in that pathway and not the stereochemistry of the intermediates being considered. The activation free energy barriers are with respect to the preceding intermediates. ^bCorresponding TSs are given in Fig. S9 of the ESI.†

The nucleophilic attack of indole on the C2 of this axially chiral metallocarbene C can happen at the re face or the si face, leading to the formation of zwitterion D. For instance, in the case of intermediate C_R, the approach of indole from the si face to form D_R is facilitated by minimal steric crowding (PhCN is present and the free volume is calculated to be 35.6%), while on the re face, the presence of the bidentate ligand (ACBP, L*) hinders this attack (the corresponding free volume is 19.1%), thereby preventing the formation of D_S (Fig. 5).

Fig. 5 Steric map showing percentage free volume (%V_f) available in metallocarbene C_R calculated using SambVca 2.1.⁴⁴

Analogously, in the case of C_S, D_S is preferentially formed due to the facile attack of indole from the re face. Further, it must be noted that the two diastereomeric metallocarbenes, C_R and C_S, cannot interconvert, as rotation about the Pd1–C2 double bond possesses an activation free energy barrier of 30.0 kcal mol⁻¹, while the subsequent nucleophilic attack has a barrier of only 3.3 kcal mol⁻¹. This is again unlike a Curtin–Hammett situation, and precluding any interconversion, one of them will preferentially lead to the formation of the corresponding zwitterion D. Hence, in this step, the stereochemical information is relayed over to the zwitterion D through an axial to point chirality transfer.

The formation of the Pd–H intermediate, F, via a hydride transfer from C3 of 2,3-dimethylindole to Pd is stereospecific as it only occurs from one face, and therefore, the two diastereomeric zwitterions D_R and D_S result in the formation of diastereomeric intermediates: F_R and F_S, respectively. The intermediate F isomerizes to F₁viaTS(F–F₁) with a Gibbs free energy barrier of 1.5 kcal mol⁻¹. The dissociation of the ene from the Pd centre that will allow interconversion between F_R and F_S, however, has a barrier of 9.7 kcal mol⁻¹, thereby again ruling out a Curtin–Hammett situation. Since F and F₁ are merely isomers, the interconversion between F_1R and F_1S will also possess an equivalent barrier of 9.7 kcal mol⁻¹. Furthermore, the final hydride transfer viaTS(F₁–P₁) presents a Gibbs free energy barrier of only 0.1 kcal mol⁻¹, resulting in this step being stereospecific in nature (Scheme 10). Since the final hydride transfer to yield the product is stereospecific as well, the stereochemical information generated in the very first step involving the diazoester complexation by the chiral catalyst is carried forward across all subsequent steps in the catalytic cycle. Hence, the stereopreference of the chiral catalyst in the formation of tetrahedral intermediate B necessarily guides the stereochemical outcome of the entire reaction. We performed a thorough conformational sampling to find TSs leading to the formation of diastereomeric tetrahedral intermediates (B_R and B_S) and the gap between the most stable TSs was found to be 1.6 kcal mol⁻¹ (DLPNO-CCSD(T)/def2tzvp calculations), corresponding to 87% ee (experimental ee is 97%) with R being the major enantiomer.

Conclusions

We have studied Pd(II)-catalyzed enantioselective carbene insertion into the C3–H bond of indole through computational methods along with experimental tools. Herein, we demonstrate that the generation of a metal ylide via nucleophilic attack of indole on metallocarbene following the typical carbene insertion pathway is favoured over the migratory insertion pathway, which is generally observed as the RDS in Pd-catalyzed cross-coupling reactions involving carbenes. Subsequently, the reaction goes through the route involving a Pd–H species, which contrasts with other metal catalyzed carbene insertion pathways, viz. enol and metal–enolate pathways. We have further carried out kinetic studies to determine the order with respect to both indole and diazo and find the experimentally determined orders of 1.0 to match well with the predicted mechanism. Using deuterium labeling studies, we show that external solvent molecules do not participate in the mechanism, which indirectly supports the Pd-hydride pathway. Gratifyingly, using ESI-HRMS we were able to detect the lowest lying intermediate, D (metal ylide), of the catalytic cycle. The hydride transfer in this palladium-hydride intermediate takes place stereospecifically to give the alkylated indole product, implying that stereoinduction is invoked during the formation of the tetrahedral intermediate, B. Such a reaction mechanism that merges two well-established catalytic cycles is fundamentally interesting and can potentially have wider implications in the field of Pd catalysis. Additionally, the novel stereodetermining step can open new avenues in carbene insertion pathways and can avoid the typical issues of metal-free species seen in other metal-catalyzed reactions.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

G. J. conceived and designed the project. A. T. carried out all the calculations. A. T., K. G., A. G. and A. S. performed the experiments. A. T. and G. J. wrote the manuscript with inputs from A. G.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

G. J. acknowledges the research grant (SPG/2021/003445) from the Science and Engineering Research Board (SERB). We thank SERC, IISc, for computing facilities. A. T. thanks IISc for the fellowship. We are grateful to Prof. Santanu Mukherjee, IISc, for allowing us to use his lab facilities. We would also like to thank Prof. Uday Maitra and Mr Gaurav Sharma, IISc, for helping us with the UV measurements. We would also like to thank Prof. Jordi Burés (ICIQ, Spain) for his helpful suggestions on VTNA.

Notes and references

1. (a) R. J. Sundberg, Indoles, Academic Press, New York, 1996;; (b) A. F. Pozharskii, A. R. Katritzky and A. T. Soldatenkov, Heterocycles in Life and Society: An Introduction to Heterocyclic Chemistry, Biochemistry and Applications, Wiley, Chichester, 2011;; (c) S. Cacchi and G. Fabrizi, Chem. Rev., 2005, 105, 2873–2920.
2. A. DeAngelis, V. W. Shurtleff, O. Dmitrenko and J. M. Fox, J. Am. Chem. Soc., 2011, 133, 1650–1653.
3. (a) X. Gao, B. Wu, Z. Yan and Y.-G. Zhou, Org. Biomol. Chem., 2016, 14, 8237–8240; (b) M. Delgado-Rebollo, A. Prieto and P. J. Pérez, ChemCatChem, 2014, 6, 2047–2052.
4. T.-Y. Wang, X.-X. Chen, D.-X. Zhu, L. W. Chung and M.-H. Xu, Angew. Chem., Int. Ed., 2022, 61, e202207008.
5. (a) D. A. Vargas, A. Tinoco, V. Tyagi and R. Fasan, Angew. Chem., Int. Ed., 2018, 57, 9911–9915; (b) Y. Cai, S.-F. Zhu, G.-P. Wang and Q.-L. Zhou, Adv. Synth. Catal., 2011, 353, 2939–2944.
6. J.-B. Chen and Y.-X. Jia, Org. Biomol. Chem., 2017, 15, 3550–3567.
7. X. Gao, B. Wu, W.-X. Huang, M.-W. Chen and Y.-G. Zhou, Angew. Chem., Int. Ed., 2015, 54, 11956–11960.
8. (a) T. Goto, Y. Natori, K. Takeda, H. Nambu and S. Hashimoto, Tetrahedron: Asymmetry, 2011, 22, 907–915; (b) H. M. L. Davies and S. J. Hedley, Chem. Soc. Rev., 2007, 36, 1109–1119.
9. (a) H. Qiu, D. Zhang, S. Liu, L. Qiu, J. Zhou, Y. Qian, C. Zhai and W. Hu, Acta Chim. Sinica, 2012, 70, 2484–2488; (b) Y.-Y. Ren, S.-F. Zhu and Q.-L. Zhou, Org. Biomol. Chem., 2018, 16, 3087–3094.
10. (a) Y. Liu, Z. Yu, J. Z. Zhang, L. Liu, F. Xia and J. Zhang, Chem. Sci., 2016, 7, 1988–1995; (b) Y. Liu, Z. Luo, J. Z. Zhang and F. Xia, J. Phys. Chem. A, 2016, 120, 6485–6492; (c) Y. Liu, Z. Yu, Z. Luo, J. Z. Zhang, L. Liu and F. Xia, J. Phys. Chem. A, 2016, 120, 1925–1932.
11. (a) S. Harada, K. Tanikawa, H. Homma, C. Sakai, T. Ito and T. Nemoto, Chem.–Eur. J., 2019, 25, 12058–12062; (b) B. Xu, S.-F. Zhu, Z.-C. Zhang, Z.-X. Yu, Y. Ma and Q.-L. Zhou, Chem. Sci., 2014, 5, 1442–1448.
12. Y. Liang, H. Zhou and Z.-X. Yu, J. Am. Chem. Soc., 2009, 131, 17783–17785.
13. (a) J. Li, Z. Su, J. Wang and C. Hu, J. Catal., 2018, 364, 426–436; (b) Q. Xie, X.-S. Song, D. Qu, L.-P. Guo and Z.-Z. Xie, Organometallics, 2015, 34, 3112–3119.
14. (a) H.-Q. Shen, H.-P. Xie, L. Sun and Y.-G. Zhou, Organometallics, 2019, 38, 3902–3905; (b) X.-L. Xie, S.-F. Zhu, J.-X. Guo, Y. Cai and Q.-L. Zhou, Angew. Chem., Int. Ed., 2014, 53, 2978–2981; (c) V. Arredondo, S. C. Hiew, E. S. Gutman, I. D. U. A. Premachandra and D. L. Van Vranken, Angew. Chem., Int. Ed., 2017, 56, 4156–4159; (d) Y. Zhu, X. Liu, S. Dong, Y. Zhou, W. Li, L. Lin and X. Feng, Angew. Chem., Int. Ed., 2014, 53, 1636–1640.
15. (a) W.-Y. Yu, Y.-T. Tsoi, Z. Zhou and A. S. C. Chan, Org. Lett., 2009, 11, 469–472; (b) C. Peng, G. Yan, Y. Wang, Y. Jiang, Y. Zhang and J. Wang, Synthesis, 2010, 24, 4154–4168; (c) G. T. Thomas, K. Ronda and J. S. McIndoe, Dalton Trans., 2021, 43, 15533–15537; (d) R. J. Sullivan, G. P. R. Freure and S. G. Newman, ACS Catal., 2019, 9, 5623–5630; (e) G. Lennon, C. O'Boyle, A. I. Carrik and P. Dingwall, Catal. Sci. Technol., 2023, 13, 372–380.
16. (a) R. Balhara and G. Jindal, J. Org. Chem., 2022, 87, 7919–7933; (b) M. S. Harariya, R. Gogoi, A. Goswami, A. K. Sharma and G. Jindal, Chem.–Eur. J., 2023, 29, e202301910.
17. J. Li, X. Meng, C. Hu and Z. Su, J. Org. Chem., 2019, 84, 15020–15031.
18. Y. Fukazawa, V. Y. Vaganov, J. V. Burykina, A. N. Fakhrutdinov, R. I. Safiullin, F. Plasser, A. E. Rubtsov, V. P. Ananikov and A. V. Malkov, Adv. Synth. Catal., 2024, 366, 121.
19. (a) Q. Xiao, Y. Zhang and J. Wang, Acc. Chem. Res., 2013, 46, 236–247; (b) Y. Xia, D. Qiu and J. Wang, Chem. Rev., 2017, 117, 13810–13889; (c) N. Jha, N. P. Khot and M. Kapur, Chem. Rec., 2021, 21, 4088–4122.
20. (a) D. Solé, F. Mariani, M. L. Bennasar and I. Fernández, Angew. Chem., Int. Ed., 2016, 55, 6467–6470; (b) D. Solé, A. Amenta, F. Mariani, M. L. Bennasar and I. Fernández, Adv. Synth. Catal., 2017, 359, 3654–3664; (c) W. Li, H. Zhang, K. Chen, H. Jiang, J. Sun and S. Zhu, Chem. Sci., 2022, 13, 12396–12402; (d) D. Solé, F. Pérez-Janer, M. L. Bennasar and I. Fernández, Eur. J. Org Chem., 2018, 4446–4455; (e) J. Huo, K. Zhong, Y. Xue, M. Lyu, Y. Ping, Z. Liu, Y. Lan and J. Wang, J. Am. Chem. Soc., 2021, 143, 12968–12973.
21. (a) K. Gupta, M. S. Harariya, A. Tyagi and G. Jindal, ChemCatChem, 2024, 16, e202301215; (b) Z. S. Chen, X. Y. Huang, Q. Liu, D. X. Song, F. Yang and K. Ji, J. Catal., 2023, 417, 52–59; (c) Q. Chen, T. Huang, Y. Shao, S. Tang and J. Sun, J. Org. Chem., 2023, 88, 3308–3312; (d) P. Ou, L. Zhu, Y. Yu, L. Ma and X. Huang, Org. Lett., 2022, 24, 4160–4164; (e) B. Lu, X. Liang, J. Zhang, Z. Wang, Q. Peng and X. Wang, J. Am. Chem. Soc., 2021, 143, 11799–11810.
22. Full computational and experimental details are given in the ESI†.
23. Full details on calculation with the α-methyl-α-diazoester (benzyl 2-diazopropanoate) substrate are given in ESI, Section 10†.
24. (a) C. N. Slattery, L.-A. Clarke, A. Ford and A. R. Maguire, Tetrahedron, 2013, 69, 1297–1301; (b) L. A. Evans, N. Fey, J. N. Harvey, D. Hose, G. C. Lloyd-Jones, P. Murray, A. G. Orpen, R. Osborne, G. J. J. Owen-Smith and M. Purdie, J. Am. Chem. Soc., 2008, 130, 14471–14473; (c) H.-Q. Shen, C. Liu, J. Zhou and Y.-G. Zhou, Org. Chem. Front., 2018, 5, 611–614.
25. (a) V. Postils, M. Rodríguez, G. Sabenya, A. Conde, M. M. Díaz-Requejo, P. J. Pérez, M. Costas, M. Solà and J. M. Luis, ACS Catal., 2018, 8, 4313–4322; (b) Y.-Z. Zhang, S.-F. Zhu, Y. Cai, H.-X. Mao and Q.-L. Zhou, Chem. Commun., 2009, 5362–5364; (c) B. Wang, I. G. Howard, J. W. Pope, E. D. Conte and Y. Deng, Chem. Sci., 2019, 10, 7958–7963; (d) C. N. Slattery, L.-A. Clarke, S. O'Neill, A. Ring, A. Ford and A. R. Maguire, Synlett, 2012, 23, 765–767.
26. Detailed information is given in ESI, Fig. S11†.
27. D. A. Sharon, D. Mallick, B. Wang and S. Shaik, J. Am. Chem. Soc., 2016, 138, 9597–9610.
28. Alternative mechanisms involving either oxidative addition or CMD were also considered; however, both were found to be higher in energy. Details are given in Sections 4.1 and 8.2 of the ESI,† respectively.
29. K. Yamamoto, S. Kimura and T. Murahashi, Angew. Chem., Int. Ed., 2016, 55, 5322–5326.
30. Further details on the higher energy pathways are given in Fig. S3–S7 of the ESI†.
31. Y. Li, Y.-T. Zhao, T. Zhou, M.-Q. Chen, Y.-P. Li, M.-Y. Huang, Z.-C. Xu, S.-F. Zhu and Q.-L. Zhou, J. Am. Chem. Soc., 2020, 142, 10557–10566.
32. (a) S. Jana, C. Empel, C. Pei, P. Aseeva, T. V. Nguyen and R. M. Koenigs, ACS Catal., 2020, 10, 9925–9931; (b) Y. Xia, Y. Liang, Y. Chen, M. Wang, L. Jiao, F. Huang, S. Liu, Y. Li and Z.-X. Yu, J. Am. Chem. Soc., 2007, 129, 3470–3471.
33. Further details are given in Fig. S7 in the ESI†.
34. Detailed information is given in ESI, Section 6†.
35. Detailed information is given in ESI, Section 12.3†.
36. (a) This contrasts with the case where cooperative participation of the Rh catalyst and CPA is noticed in the stereo-controlling transition state in asymmetric amination of diazo-acetate by tert-butyl carbamate catalyzed by dirhodium tetra(trifluoro)acetate and chiral SPINOL-phosphoric acid; ; (b) H. K. Kisan and R. B. Sunoj, Chem. Commun., 2014, 50, 14639–14642.
37. Detailed information is given in ESI, Section 12.5†.
38. M. Mortén, M. Hennum and T. Bonge-Hansen, Beilstein J. Org. Chem., 2015, 11, 1944–1949.
39. (a) ADF2020.102, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands; (b) M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681–687; (c) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580; (d) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
40. Full information is given in Section 13 of ESI†.
41. (a) J. Burés, Angew. Chem., Int. Ed., 2016, 55, 2028–2031; (b) A. Martínez-Carrión, M. G. Howlett, C. Alamillo-Ferrer, A. D. Clayton, R. A. Bourne, A. Codina, A. Vidal-Ferran, R. W. Adams and J. Burés, Angew. Chem., Int. Ed., 2019, 58, 10189–10193; (c) D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302–4320.
42. S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Bioinformatics, 2006, 22, 3067–3074.
43. More information on VTNA and microkinetic modelling is given in Sections 14 and 15, respectively, of the ESI†.
44. L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872–879.
45. R. Balhara, R. Chatterjee and G. Jindal, Chem. Soc. Rev., 2024, 53, 11004–11044.
46. D. Dodiya, M. S. Harariya and G. Jindal, Synlett, 2025, 36, A–I.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00777a

---