Open Access Article
Open Access ArticleFlipping out: role of arginine in hydrophobic interactions and biological formulation design†
Jonathan W. P.
Zajac
 ae,
Praveen
Muralikrishnan
be,
Idris
Tohidian
c,
Xianci
Zeng
d,
Caryn L.
Heldt
ae,
Praveen
Muralikrishnan
be,
Idris
Tohidian
c,
Xianci
Zeng
d,
Caryn L.
Heldt
 c,
Sarah L.
Perry
c,
Sarah L.
Perry
 d and
Sapna
Sarupria
d and
Sapna
Sarupria
 *ae
*ae
aDepartment of Chemistry, University of Minnesota, Minneapolis, MN 55455, USA. E-mail: sarupria@umn.edu
bDepartment of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
cDepartment of Chemical Engineering, Michigan Technological University, Houghton, MI 49931, USA
dDepartment of Chemical Engineering, University of Massachusetts Amherst, MA 01003, USA
eChemical Theory Center, University of Minnesota, Minneapolis, MN 55455, USA
First published on 11th March 2025
Abstract
Arginine has been a mainstay in biological formulation development for decades. To date, the way arginine modulates protein stability has been widely studied and debated. Here, we employed a hydrophobic polymer to decouple hydrophobic effects from other interactions relevant to protein folding. While existing hypotheses for the effects of arginine can generally be categorized as either direct or indirect, our results indicate that direct and indirect mechanisms of arginine co-exist and oppose each other. At low concentrations, arginine was observed to stabilize hydrophobic polymer folding via a sidechain-dominated direct mechanism, while at high concentrations, arginine stabilized polymer folding via a backbone-dominated indirect mechanism. Upon introducing partially charged polymer sites, arginine destabilized polymer folding. Further, we found arginine-induced destabilization of a model virus similar to direct-mechanism destabilization of the charged polymer and concentration-dependent stabilization of a model protein similar to the indirect mechanism of hydrophobic polymer stabilization. These findings highlight the modular nature of the widely used additive arginine, with relevance in the information-driven design of stable biological formulations.
1 Introduction
Maintaining native protein structures in biological formulations poses a challenge, and is commonly addressed by strategic additive incorporation.1–3 Arginine stands out as a frequently employed additive in such formulations, spanning both therapeutic proteins4 and vaccines.5,6 Arginine has been widely used as an aggregation suppressor, an agent for protein refolding, a cryoprotectant during lyophilization, and in protein purification.7–9 Once hailed as a universal stabilizer, emerging studies paint a foggier picture of the effects of arginine. In some settings, the presence of arginine has accelerated the aggregation,10–12 denaturation,13–15 and inactivation16,17 of certain proteins and viruses. Additional studies have found that arginine mechanisms are dependent on concentration.18–21 Hence, the existing literature on arginine reveals a lack of a cohesive understanding of its multi-faceted effects on protein stability.In general, additive effects on protein stability are thought to be either direct or indirect. Direct mechanisms involve direct protein–additive interactions, while indirect mechanisms influence protein stability by modulating the surrounding solvent structure. It remains debated whether arginine acts primarily via a direct or indirect mechanism. Several studies called attention to direct interactions between arginine and aromatic residues,7,22,23 acidic residues,12,20,24 and hydrophobic moieties.25,26 Other studies have proposed clusters of free arginine molecules in solution enable the crowding out of protein–protein interactions,20,23,27,28 or alteration of hydration shell water dynamics.29,30 The wide range of observations related to the role of arginine on protein stability suggests that arginine harbors diverse, context-dependent mechanisms.
To elucidate the mechanisms through which arginine influences protein stability, this study focuses on its effects on hydrophobic interactions. Hydrophobic interactions are key in several biologically relevant phenomena, including protein folding and stability.31–39 Additives in solutions are known to modulate the strength of hydrophobic interactions, and in turn, the stability of proteins.40–46 For example, simulation studies have shown trimethylamine N-oxide (TMAO) has a negligible effect on or strengthens hydrophobic interactions,42,47–51 while these interactions are weakened in urea solutions.41,43,44,52–56 Indeed, the effects of TMAO and urea on hydrophobic interactions are consistent with their experimentally-observed roles as a protein stabilizer and denaturant, respectively.45,57–60
Molecular dynamics (MD) simulations have provided valuable insights towards understanding these mechanisms as they relate to hydrophobicity. Several studies have used a hydrophobic polymer model for describing the role of solvent and additives on protein-like folding.43,44,61–64 The use of a hydrophobic polymer model enables the decoupling of additive effects on hydrophobic vs. other interactions, which is challenging to do in experiments. Additionally, comparing trends for purely hydrophobic interactions with experimental observations allows for inferences about the underlying physics. In the present study, we utilize MD simulations of a hydrophobic polymer to characterize the effects of arginine on many-body hydrophobic interactions pertinent to protein stability and contextualize these findings within larger-scale models for biological formulations.
Overall, we found arginine stabilizes hydrophobic polymer folding at all concentrations under study. We discovered that arginine sits on the edge of a mechanistic flip, balancing between direct- and indirect-dominated effects. As a consequence of this balance, we found subtle modulation of the polymer chemistry (via partial charge incorporation) changes arginine from a stabilizing additive to a destabilizer of polymer folding. Consequently, in practical examples of formulation design, we observed arginine has variable effects on a model virus and protein.
2 Methods
2.1 Hydrophobic polymer system setup and molecular dynamics simulations
We simulated a hydrophobic polymer in arginine solutions at different concentrations (Table S1†). All simulations were performed using GROMACS 2021.4 (ref. 65 and 66) with the PLUMED 2.8.0 (ref. 67 and 68) patch applied. The hydrophobic polymer was modeled as a linear coarse-grained chain with 26 monomers, where each monomer represents a CH2 unit with Lennard-Jones parameters σ = 0.373 nm and ε = 0.5856 kJ mol−1.42 Box dimensions were defined such that 1.5 nm of space separated the fully elongated polymer from the nearest box edge. For simulations with no polymer, the same box dimensions were used. Arginine was modeled in accordance with a pH of 7, resulting in a protonated sidechain (Fig. S1†). An equal number of arginine molecules and Cl− atoms were added to the box until the desired concentration was reached. The TIP4P/2005 (ref. 69) model was used to describe water, and the CHARM22 force field was used for arginine and Cl−.70All simulations were initially subject to energy minimization using the steepest descent algorithm. NVT equilibration was carried out for 1 ns at 300 K, followed by a 1 ns NPT equilibration at 300 K and 1 atm. During equilibration, temperature was controlled according to the V-rescale thermostat,71 while pressure was controlled via the Berendsen barostat.72 Following equilibration, NPT production runs were completed using the Nosé–Hoover thermostat73 and Parrinello–Rahman barostat.74 Production runs were completed for 20 ns for arginine/water systems, and between 50–250 ns per window for arginine/polymer/water replica exchange umbrella sampling (REUS) runs. This represents total simulation time of 1.8–9 μs for each system studied depending on the convergence time (see Table S2† for further details). In all simulations, the Particle Mesh Ewald (PME) algorithm was used for electrostatic interactions with a cut-off of 1 nm. A reciprocal grid of 42 × 42 × 42 cells was used with 4th order B-spline interpolation. A single cut-off of 1 nm was used for van der Waals interactions. The neighbor search was performed every 10 steps. Lorentz–Berthelot mixing rules75,76 were used to calculate non-bonded interactions between different atom types, except for polymer–water oxygen interactions (Fig. S2 and Table S2†).
2.2 Replica exchange umbrella sampling
REUS77 simulations were completed to sample the hydrophobic polymer conformational landscape in arginine solutions. The radius of gyration (Rg) of the hydrophobic polymer was used as the reaction coordinate to describe polymer folding/unfolding. 12 umbrella potential windows were centered between Rg = 0.3 and Rg = 0.9 nm, with a spacing of 0.05 nm. A force constant of K = 5000 kJ mol−1 nm−2 was used in all windows, with the exception of the window centered at Rg = 0.45, which used K = 1000 kJ mol−1 nm−2 (Fig. S3†).The potential of mean force (PMF) along the radius of gyration of the polymer was calculated as W(Rg) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P(Rg)). Biased probability distributions were reweighted according to the Weighted Histogram Analysis Method (WHAM).78 The free energy of polymer unfolding (ΔGu) was calculated according to:
ln(P(Rg)). Biased probability distributions were reweighted according to the Weighted Histogram Analysis Method (WHAM).78 The free energy of polymer unfolding (ΔGu) was calculated according to:
 | (1) |
 . The convergence of our REUS runs was assessed by examining the evolution of PMFs from three replicate simulations (Fig. S4†).
. The convergence of our REUS runs was assessed by examining the evolution of PMFs from three replicate simulations (Fig. S4†).
We decomposed the PMF into individual components to further investigate the role of arginine in polymer folding. Following the methods outlined by several others,46,79–81 the PMF was separated into intrapolymer degrees of freedom in vacuum, Wvac, and a solvent contribution, Wsolv as:
| W(Rg) = Wvac(Rg) + Wsolv(Rg) | (2) |
In accordance with perturbation theory approaches applied to solvation phenomena,37,39,82–87 the solvent contribution can be described as involving two steps: (i) creating a polymer-sized cavity in solution (Wcav(Rg)), and (ii) turning on attractive polymer–solvent interactions (Eps(Rg)). Wsolv(Rg) can then be written as:
| Wsolv(Rg) = Wcav(Rg) + Eps(Rg) | (3) |
| Eps(Rg) = Epw(Rg) + Epa(Rg) + Epc(Rg) | (4) |
2.3 Preferential interaction coefficients
Distribution of arginine with respect to the polymer can be described via the preferential interaction coefficient (ΓPA),88–90 | (5) |
 | (6) |
2.4 Hydrogen bond analysis
Hydrogen bonds were calculated according to geometric criteria of a donor–acceptor distance of r ≤ 0.35 nm and donor–hydrogen–acceptor angle of 150° < θ < 180°.94 Hydrogen bond existence correlation functions for water–water and arginine–water interactions were estimated according to:95–97 | (7) |
2.5 Contact coefficients
Contact coefficients (CC) give a measure of excipient preference for interacting with specific residues. Here, we computed CCs as described by Stumpe and Grubmüller:98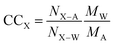 | (8) |
2.6 Protein and virus simulation setup
Porcine parvovirus (PPV) and hen egg white lysozyme (HEWL) were used as large-scale models for formulation design. To model PPV, we constructed a surface model using 15 monomers from the published crystal structure (PDB: 1K3V).99 This was achieved by selecting three reference Cα atoms from the 5-fold pore of the viral surface, and aligning the vector normal to these points with the z-axis of the simulation box. Box dimensions were 24 × 24 × 12 nm, with the capsid surface model extending approximately 9 nm in the z-direction.During equilibration, a position restraint with a force constant of 1000 kJ mol−1 nm−2 was applied to all capsid atoms within 1.5 nm from the wall. Capsid atoms between 1.5 nm and 3.0 nm from the wall were restrained with a force constant between 1–1000 kJ mol−1 nm−2, with atoms further from the wall scaled to a lesser extent. Capsid atoms further than 3.0 nm from the wall were left fully flexible. PPV simulations were carried out in the NVT ensemble – first for 1 ns to reach the target temperature, followed by 50 ns to allow the solvent to relax. 100 ns production runs, with positional restraints on the capsid removed, were then completed and used for further analysis. Equilibration of the PPV surface systems was measured according to Cα RMSD and was observed to reach a steady state within 50 ns (Fig. S6†).
To prevent diffusion of excipient molecules into the capsid interior, a wall was placed at z = 0 nm, and the capsid surface was positioned on top of this wall (Fig. S6†). The validity of the surface model for PPV was assessed by measuring residue–residue correlations within capsid proteins relative to a fully assembled capsid (Fig. S7†). We find that the residue–residue correlations are well-conserved in the surface model. Because this surface model lacks the full context of a fully assembled capsid, our approach is understandably limited in reproducing protein–protein fluctuations relative to a fully-assembled capsid (Fig. S8†). We surmise that because the surface model retains its assembled structure and conserves the residue–residue correlations it is a sufficient model for assessing virus–excipient interactions at a fraction of the computational cost required for fully-assembled capsid simulations.
Arginine molecules were added to the exterior of the capsid surface model to reach a target concentration of 0.1 M, and Na+ and Cl− atoms were distributed throughout the box to both neutralize the system and reach a concentration of 0.15 mM. Analysis was carried out on the converged portion of the trajectory, which constituted an aggregate sampling time of 750 ns across monomers.
HEWL was modeled from an available crystal structure (PDB: 1LYZ),100 and simulated in solution with 0.1, 0.2, 1.0, and 2.0 M arginine. HEWL simulations were carried out in the NVT ensemble for 1 ns to equilibrate to the target temperature, followed by 1 ns NPT simulations to reach the target density. HEWL production runs were completed for 100 ns in the NPT ensemble, reaching conformational equilibration within 20 ns (Fig. S5†). For both HEWL and PPV, the force field, thermostats, and barostats matched those used for the hydrophobic polymer systems.
2.7 Experimental temperature stability studies
Liquid samples of PPV in arginine solutions were prepared in triplicates and were put in either a heat block at 60 °C101 or in a fridge at 4 °C for 72 hours. The titer of PPV was determined by 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT) colorimetric cell viability assay.101 Differential scanning fluorimetry (DSF) was performed to compute the hydrophobic exposure temperature (HET) of HEWL in arginine solutions.102,103 More details for both experimental methods are included in the ESI.†3 Results and discussion
3.1 Arginine favors hydrophobic polymer folding
Fig. 1a shows the PMF along the Rg reaction coordinate. In all solutions, free energy minima were observed at approximately 0.4 and 0.8 nm (configurations labeled I and III in Fig. 1g), along with a prominent free energy barrier at ∼0.6 nm representing the transition between folded and unfolded states (Fig. 1a). In pure water, hydrophobic polymer folding is unfavorable, with the unfolded state favored by ∼0.3 kT. In contrast, at all arginine concentrations, the folded state of the polymer is favored relative to pure water, and a monotonic increase in ΔGu is observed. An additional barrier at ∼0.45 nm was identified separating two folded states, labeled as I and II in Fig. 1a. Representative polymer configurations were identified using the HDBSCAN104 algorithm (Fig. S9†). | ||
| Fig. 1 PMF decomposition in 0.0 M, 0.25 M, 0.5 M, and 1.0 M arginine solutions. (a) The PMF obtained along the Rg reaction coordinate, W(Rg), (b) vacuum component, Wvac, (c) cavitation component, Wcav, (d) polymer–water interactions, Epw, (e) polymer–arginine interactions, Epa, and (f) polymer–Cl− interactions, Epc. (g) Representative configurations along the reaction coordinate as denoted in (a) as I, II, and III. (h) Changes in overall free energy of unfolding (ΔΔGu), cavitation contribution (ΔΔGcav), polymer–water interactions (ΔΔEpw), and polymer–arginine interactions (ΔΔEpa). Increasing arginine concentration is denoted by increased shading (light to dark) and is indicated by arrows in (a–f). The polymer in water alone is shown in black, where appropriate. Mean values were estimated from three replicate REUS simulations. Error bars are reported as described in the ESI.† All plots are normalized to 0 at Rg = 0.4 nm, where appropriate. | ||
The folded polymer ensemble in arginine solutions exhibits free energy minima corresponding to globular (∼0.4 nm) and hairpin-like (∼0.5 nm) configurations (labeled I and II in Fig. 1g). Arginine clusters encapsulating the hydrophobic polymer are observed in each state (Fig. S10†). We propose that the free energy barrier separating these two states arises from an energetic penalty associated with breaking these encapsulating clusters. Such a mechanism is similar to that observed by Li et al.,26 who observed arginine-mediated suppression of hydrophobic association.
3.2 Decomposition of arginine effects on polymer folding
Fig. 1b–f shows the decomposition of the PMF into various components. The vacuum component, Wvac, favors the folded state of the polymer, associated with favorable intrapolymer interactions and configurational entropy upon folding (Fig. 1b). Because this component does not depend on the presence of arginine, a balance of the remaining components dictates the effect of arginine on hydrophobic polymer folding.Cavity formation is a crucial step in hydrophobic hydration phenomena, and has been shown to play an important role in governing the folding behavior of the hydrophobic polymer.43,44,61–64Wcav is calculated as Wsolv(Rg) − Eps(Rg), as described in the Methods section. The cavitation component favors the folded state (Fig. 1c), reflecting a strong hydrophobic driving force for polymer folding.61,79
Attractive polymer–water interactions become more favorable with increasing Rg (Fig. 1d), indicating polymer–water interactions oppose polymer folding. It is worth noting that the free energy minima at ∼0.8 nm in the unfolded ensemble is observed in an aqueous environment (Fig. 1a), but not in vacuum (Fig. 1b). This minima arises due to favorable polymer–water interactions, consistent with prior MD simulations that showed water-mediated interactions drive large hydrophobic solutes apart.62,87,105 Additionally, sufficient dewetting of the hydrophobic polymer is a hypothesized bottleneck to folding,61,79,106 resulting in the free energy barrier at ∼0.6 nm separating the folded and unfolded states.
Attractive polymer–arginine interactions approach an energetic minima at ∼0.5 nm (Fig. 1e), giving rise to the global minimum observed in the overall PMF. Polymer–Cl− interactions were observed on the order of thermal fluctuations, consistent with previous observations that Cl− ions are depleted from the local domain of hydrophobic solutes.41,107
Fig. 1h shows the change in each component upon unfolding in arginine solution relative to that observed in water. In Fig. 1h, the first Δ arises from the difference between folded and unfolded states (e.g., ΔE = 〈Eu〉 − 〈Ef〉), and represents the free energy associated with a state change from folded to unfolded. The second Δ arises from the free energy difference between arginine solution (ΔEarg) and water (ΔEwat) (e.g., ΔΔE = ΔEarg − ΔEwat).
With increasing arginine concentration, we observed an increasingly favorable cavitation component for folding (Fig. 1h). Specifically, we observe a change in sign in the cavitation component from negative (unfavorable) to positive (favorable) with increasing arginine concentration. In other words, formation of a smaller cavity becomes more favorable at high arginine concentration. Concurrently, preferential polymer–arginine interactions are observed to increase with increasing arginine concentration. Thus, we hypothesize that arginine may strengthen hydrophobic interactions associated with hydrophobic polymer folding via a surfactant-like mechanism. Such a mechanism has been described in detail for alcohol cosolvents and TMAO, where preferential cosolvent adsorption to the polymer–solvent interface drives hydrophobic polymer folding.51,108 Our findings strengthen the notion that the effective attraction between hydrophobic solutes in the presence of amphiphilic cosolvents (such as arginine, alcohols, and TMAO) may be a generalizable phenomenon.
Looking at the trends in ΔΔEpw, we found that in 0.25 M arginine solutions, the polymer–water component favors polymer unfolding relative to in pure water (Fig. 1h). This is consistent with prior work that reported the key role of water–solute interactions in hydrophobic behavior.46,80,85,109–115 At 0.5 M and 1.0 M arginine concentrations, this component favors polymer folding. With arginine present, the local domain of the polymer exhibits a reduction in the average number of water molecules (Fig. S11†), indicating an effective expulsion of water. This, in turn, diminishes polymer–water interactions that resist polymer folding.
The polymer–arginine contribution favors the folded polymer state at 0.25 M and 0.5 M arginine concentrations relative to in pure water (Fig. 1h). However, at 1.0 M arginine concentrations, polymer–arginine interactions promote polymer unfolding. Together, these results indicate that neither direct nor indirect mechanistic hypotheses alone can describe the effects of arginine on hydrophobic polymer folding.
3.3 Mechanistic flip with increasing arginine concentration
To investigate potential competing effects of direct and indirect mechanisms, we combined the components of our PMF decomposition, delineating between those linked to direct effects (polymer–arginine and polymer–Cl−; ΔΔGdir) and indirect effects (cavitation and polymer–water; ΔΔGind) of arginine (Fig. 2a). | ||
| Fig. 2 Components of the free energy of hydrophobic polymer unfolding in 0.25 M, 0.50 M, and 1.0 M (a) arginine, (b) guanidinium, and (c) glycine solutions. Changes in overall free energy of unfolding (ΔΔGu), direct interactions (ΔΔGdir), and indirect effects (ΔΔGind) are shown. Increasing additive concentration is denoted by increased shading (light to dark; left to right). Mean values are reported from three replicate REUS simulations. Error bars were estimated via error propagation (see ESI for details†). | ||
We discovered that, with increasing concentration, the mechanism underlying the effects of arginine transitions from direct to indirect dominance. At 0.25 M, cavity formation and polymer–water interactions oppose polymer folding, while arginine–polymer interactions favor folding. The balance of these components gives rise to ΔΔGdir > ΔΔGind, resulting in the net stabilization of folded conformations and supporting the direct mechanism hypothesis (Fig. 2a).
In contrast, for the high-concentration regime (0.5 M and 1.0 M), cavity formation and polymer–water attractive interactions favor polymer folding, while attractive arginine–polymer interactions favor unfolding of the hydrophobic polymer. In this case, indirect components dominate the free energy difference (ΔΔGdir < ΔΔGind), stabilizing polymer folding and supporting the indirect hypothesis (Fig. 2a).
Thus, within the range of concentrations studied, we have uncovered that arginine exists at the edge of a mechanistic flip between direct- and indirect-dominated stabilization of many-body hydrophobic interactions. The identification of this mechanistic switch may explain the variety of hypotheses in the existing arginine literature. Because arginine is situated on this razor's edge, small changes associated with the chemistry of a protein surface, the addition of cosolvents to solution, or differences in sample preparation may cause significant changes in the modulation of hydrophobic interactions due to arginine.
3.4 Distinct roles of arginine's sidechain and backbone
Arginine is comprised of a polar backbone and an aliphatic sidechain characterized by a guanidinium group. To investigate the roles of these components on hydrophobic polymer folding, we completed an additional PMF decomposition in guanidinium and glycine solutions (see ESI for simulation details†). At all concentrations under study, we observed that guanidinium favors the hydrophobic polymer folding primarily via a direct mechanism, while glycine stabilizes polymer folding primarily via an indirect mechanism (Fig. 2b and c).In the case of guanidinium, stabilization is driven entirely by attractive polymer–guanidinium interactions that favor folding, while polymer–water interactions and cavity formation oppose polymer folding (Fig. 2b). In glycine solutions, however, stability is driven by the inverse mechanism; polymer–water interactions and the cavitation component favor folding, while folding is opposed by attractive polymer–glycine interactions (Fig. 2c). Based on these findings, we characterize arginine as exhibiting a guanidinium-like mechanism at low concentrations and a glycine-like mechanism at high concentrations.
While glycine is known to be an effective stabilizer of proteins,21,116,117 our observations obtained for guanidinium are somewhat surprising due to its common role as a protein denaturant.118–120 Several studies have stressed the importance of direct interactions in guanidinium-induced denaturation, primarily via breaking salt bridges, competing for intra-protein hydrogen bonds, and interacting with aromatic moieties via cation–pi stacking.119,121,122 Usually, this occurs at high concentrations of guanidinium salts. Our findings suggest that while guanidinium may stabilize hydrophobic interactions at low concentrations, this is outweighed by denaturing mechanisms at high concentrations.
3.5 Resolving polymer–arginine–water interactions
Thermodynamic analyses of arginine effects on polymer folding discussed above indicate that direct and indirect mechanisms co-exist and compete at all concentrations under study. To probe this further, we characterize the molecular interactions between arginine, water, and the polymer. Specifically, we look at hydrogen bonding between arginine and water to describe hydration patterns of the arginine sidechain and backbone groups. Preferential interactions are used to elucidate the balance of polymer–arginine–water interactions.To describe how arginine interacts with water, we considered hydrogen bonding interactions between water and backbone (COO−, NH3+) or sidechain (Gdm+) atoms of arginine. Overall, the number of backbone-water hydrogen bonds is greater than sidechain-water hydrogen bonds (Fig. 3a). We further observe the fraction of occupied hydrogen bonding sites to be higher for backbone groups than the sidechain (Fig. S12†). The hydrogen bond existence autocorrelation function for the 0.25 M arginine solution revealed hydrogen bonds formed between backbone-water atoms are, on average, longer-lived than sidechain-water hydrogen bonds (Fig. 3b). As arginine concentration increases, hydrogen bond lifetimes also increase for both arginine–water and water–water interactions (Fig. S13†). In principle, this may be considered a stabilizing property of arginine, as a growing body of literature has supported the role of stabilizing osmolytes in increasing hydrogen bond lifetimes and reducing water dynamics.123–129
Pairwise radial distribution functions (RDFs) were computed between the water oxygen (OW) and either the alpha carbon (CA) or guanidinium carbon (CZ) of arginine to quantify the local structure of water around arginine molecules (Fig. 3c). The first peak in the OW–CA RDF was observed to increase slightly with concentration. This indicates preferential hydration of the backbone group as more arginine molecules are introduced to the solution. There is, however, no such change observed in the OW–CZ RDF with concentration. A representative snapshot of water interactions with a single arginine molecule is shown in Fig. 3d (2D representation is shown in Fig. S14†). Together, these results indicate that the backbone of arginine is the primary site for interaction with water.
While we found arginine preferentially interacts with water via its backbone, we hypothesized arginine interacts with the polymer via its sidechain. It has been reported elsewhere that dehydration of the planar guanidinium face is important in forming face–face stacking interactions in aqueous guanidinium solutions.130 In our case, the dehydrated face of guanidinium is expected to play a key role in direct arginine–polymer interactions, similar to interactions observed between guanidinium and hydrophobic/aromatic protein residues.7,22,23,131
Wyman–Tanford theory relates the dependence of any equilibrium process (such as protein folding) and preferential interaction as:132–134
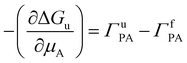 | (9) |
Preferential interaction coefficients for guanidinium and glycine solutions are shown in Fig. 4b and c, respectively. We observed that at all concentrations, guanidinium preferentially interacts with the hydrophobic polymer (Fig. 4b). This is consistent with experimental evidence, as well as a prior simulation study that observed attractive guanidinium–polymer interactions with a model hydrophobic polymer.43,80 Glycine, meanwhile, was found to be preferentially excluded from the local domain of the hydrophobic polymer (Fig. 4c). This finding is consistent with the observed preference for the backbone of arginine to hydrogen bond with water, relative to the sidechain. Elsewhere, glycine has been observed to deplete from the surface of several model miniproteins, consistent with our findings.136
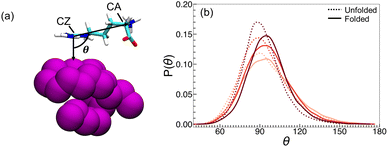
To explore whether the preferential interactions of arginine with polymer and water are accompanied by preferential orientations, we computed an orientation parameter inspired by Shukla and Trout.137 This parameter was computed as the angle formed in three-dimensional space between polymer–CZ and CZ–CA vectors (Fig. 5a). The monomer closest to CZ is taken for the polymer–CZ vector. Angles where θ > 90° indicate the arginine backbone orients towards the bulk solvent, while θ < 90° indicates the arginine backbone orients towards the polymer. We observed that for all concentrations, the probability P(θ) is skewed towards angles greater than 90° (Fig. 5b).
Further, for all arginine concentrations, the mean value of θ for the folded state is greater than that observed for unfolded configurations (Fig. 5b). This preferential orientation of arginine enables the hydrophobic face of the guanidinium sidechain to interact with the hydrophobic polymer, while extension of the backbone towards the bulk enables additional interactions with either water or other free arginine molecules. The greater ability for arginine to adopt preferred orientations in the folded state, particularly at 0.25 M, may partially explain the favorable ΓPA values described previously.
4 Contextualizing the mechanistic flip of arginine
4.1 Arginine destabilizes a charged polymer
To explore whether we could shift arginine further towards a direct-dominated mechanism, we modified our hydrophobic polymer to include four beads with opposing partial charges (Fig. 6a). In pure water, charged polymer folding was observed to be favorable, resulting in a prominent free energy minimum at Rg ∼0.5 nm (Fig. 6b). Relative to the hydrophobic polymer, this is indicative of a conformational preference of the polymer to adopt hairpin-like, rather than globule-like, configurations (II and I in Fig. 6a, respectively).Upon addition of either 0.25 M or 1.0 M arginine, folding of the charged polymer becomes less favorable (Fig. 6c). We attribute this to a preference for arginine to interact with the charged sites, which are more accessible to arginine in the unfolded state. Indeed, at both concentrations, attractive polymer–arginine interactions dominate (Fig. 6d), driving polymer unfolding. This model demonstrates that even subtle changes to the chemistry of a macromolecule can re-balance arginine mechanisms.
4.2 Implications for formulation design
Arginine-induced destabilization of a charged polymer illustrates that, when hydrophobic interactions compete with other effects, the effectiveness of arginine as a stabilizer can be altered. To better understand this feature of arginine, we explored the temperature stability of two models for formulation design: PPV and HEWL.PPV is a non-enveloped virus with a single stranded DNA genome.138 The PPV capsid is a spherical shell comprised of 60 copies of viral proteins (VP) VP1, VP2, and VP3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, arranged in an icosahedral symmetry.99 Due to the relatively small size and structural simplicity of PPV, recent studies have employed the virus as a model for investigating virus purification and thermostabilization techniques.101,139–141
1 ratio, arranged in an icosahedral symmetry.99 Due to the relatively small size and structural simplicity of PPV, recent studies have employed the virus as a model for investigating virus purification and thermostabilization techniques.101,139–141
HEWL, meanwhile, is a relatively small protein with a well-defined fold (PDB: 1LYZ) and high stability.100,142 Due to these features, it has been widely used as a model for protein folding143–145 and exploring osmolyte effects.116,146,147 HEWL has also been used to investigate aggregation-suppressing effects of arginine. Several studies have proposed that arginine interacts favorably with aromatic and acidic residues of HEWL, which limits solvent exposure of aggregation-prone patches.7,20,22,23,148 Arginine has also been observed to enhance the heat-induced aggregation of bovine serum albumin and β-lactoglobulin, but not HEWL – highlighting its context-dependent effects.11
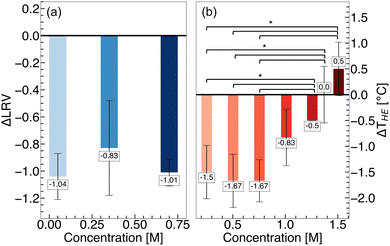
To understand the effect of arginine on these biomolecules, temperature stability assays were carried out at different concentrations of arginine. For PPV, we completed an infectivity assay (see ESI for Experimental details†) following virus incubation at 60 °C for 3 days – sufficiently long to observe a significant decrease in the infectious titer.139 Log reduction values (LRV) describe the decrease in the infectious titer of heat-treated virus, relative to the initial virus solution. We found, at all investigated arginine concentrations, more infectious PPV is lost relative to in buffer alone, resulting in negative ΔLRV values (Fig. 7a). Such a finding indicates reduced temperature stability of the virus in arginine solutions.
For HEWL, we completed a thermal shift assay (see ESI for details†) to quantify the hydrophobic exposure temperature (THE) of the protein.102,103 At low concentrations (0.2–1.0 M) of arginine, a decrease in THE is observed relative to buffer alone, indicating destabilization of HEWL (Fig. 7b). With increasing arginine concentration (1.5 M), the temperature stability of HEWL improves. Such a finding closely resembles the temperature stability of ovalbumin and lysozyme in arginine solutions reported by Vagenende et al.20 The findings at low concentrations of arginine are in contrast to the stabilization of hydrophobic polymer folding observed in the MD simulations. Thus, we infer that at these concentrations, the destabilizing effects of arginine on HEWL arise from interactions beyond hydrophobic interactions. We surmise that with increasing arginine concentrations, the strengthening of hydrophobic interactions dominates over the destabilizing effects, resulting in the stabilization of HEWL.
4.3 Molecular-level investigation of formulation models
The lack of consensus regarding the effects of arginine – further accentuated by our investigation of PPV and HEWL temperature stability – may be rationalized by the positioning of arginine at the edge of the mechanistic flip described in the present work. Additionally, we have shown that when charged beads are added to a hydrophobic polymer, this subtle change results in complete arginine-induced destabilization. To better understand the connection between the mechanistic flip of arginine and the relevance of differing molecular contexts, we completed straightforward MD simulations of HEWL and PPV systems in arginine solution.The PPV major capsid protein, VP2, is known to self-assemble into virus-like particles that are non-pathogenic, but are morphologically similar to native PPV virions.149 Experimental identification of this structure99 enables PPV for molecular-level investigations via molecular simulations. On the capsid surface, prominent structural features include a canyon surrounding a pore at the 5-fold axis of symmetry, protruding spikes located at the 3-fold axis of symmetry, and a dimple on the 2-fold axis of symmetry.99 We found that the use of 15 VP2 proteins is the minimum system size required to capture these structural features, reducing the system size from ∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to ∼750
000 to ∼750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. With this truncation, we were able to reach conformational equilibrium in a computationally-feasible amount of time, which was not possible for a fully-assembled capsid system (Fig. S5†). This surface model also accurately reproduced residue–residue cross-correlations of a fully-assembled capsid (Fig. S7†), reflecting accurate local protein dynamics. We note, however, that global protein–protein dynamics are not perfectly captured (Fig. S8†). Together, this approach enables simulations of virus–excipient interactions at timescales accessible to MD without sacrificing atomistic resolution.
000 atoms. With this truncation, we were able to reach conformational equilibrium in a computationally-feasible amount of time, which was not possible for a fully-assembled capsid system (Fig. S5†). This surface model also accurately reproduced residue–residue cross-correlations of a fully-assembled capsid (Fig. S7†), reflecting accurate local protein dynamics. We note, however, that global protein–protein dynamics are not perfectly captured (Fig. S8†). Together, this approach enables simulations of virus–excipient interactions at timescales accessible to MD without sacrificing atomistic resolution.
At the PPV surface in 0.25 M arginine solution, we observed preferential arginine accumulation at various sites across the surface (Fig. 8a and c). Specifically, via calculation of contact coefficients of different residue types distributed across the PPV capsid surface, we identified significant accumulation of arginine near negatively charged glutamate and aspartate residues. From these findings, we hypothesize that direct interactions between arginine and charged residues at the PPV surface drive the instability observed from experiments. In this case, the dominating mechanism may be similar to that observed for arginine-induced unfolding of a charged polymer.
For HEWL, we completed simulations of 0.1 M, 0.2 M, 1.0 M, and 2.0 M arginine solutions. With increasing concentration, we observed an increase in preferential exclusion of arginine and reduction of arginine density local to the protein (Fig. 8b and d). This trend matches the concentration-dependent exclusion of arginine from various proteins reported elsewhere.20,27,93,134,150 This finding, along with the increase in HEWL melting temperature observed at high arginine concentration, suggests that arginine imparts stabilization of HEWL via indirect effects. On the other hand, direct arginine–HEWL interactions may be destabilizing, which explains the decreased melting temperature of HEWL while arginine is less excluded from the local domain of the protein.
5 Conclusions
Overall, our findings illuminate the intricate mechanisms underlying the multi-faceted effects of arginine on hydrophobic polymer folding. Arginine was observed to increase the favorability of many-body hydrophobic interactions, a key factor in protein stabilization. Our observations reveal a nuanced interplay in the impact of arginine on hydrophobic interactions, teetering on the edge of a mechanistic flip. At low concentrations, direct sidechain-driven interactions dominate, shifting to indirect backbone-driven effects at high concentrations.The simultaneous presence of competing direct and indirect effects implies that changes in the chemistry of a protein surface, the addition of co-additives to solution, or differences in sample preparation, may cause significant changes in the mechanism of action of arginine. A shift towards the direct mechanism risks guanidinium-like denaturation of native proteins by disrupting electrostatic and hydrogen-bonding interactions. Conversely, a shift towards the indirect mechanism may yield glycine-like stabilization of native proteins through preferential hydration.
We illustrated examples of the context-dependent effects of arginine through models of protein (HEWL) and virus (PPV) stability. We observed that arginine destabilizes PPV across a wide concentration range, which we attribute to destabilizing direct arginine–PPV interactions. This mechanism resembles the effects of arginine on a charged polymer model, suggesting that in both cases, arginine-induced destabilization via charge–charge interactions outweighs arginine-induced stabilization of hydrophobic interactions. We further found that arginine destabilizes HEWL at low concentrations and stabilizes HEWL at high concentrations, which we found is associated with an increased exclusion of arginine from the HEWL surface. This mechanism closely resembles the concentration-dependence of the indirect mechanism of arginine in a hydrophobic polymer model. Hence, at high concentrations, HEWL destabilization due to arginine charge–charge interactions may be opposed by an overall stabilization of hydrophobic interactions.
Classical models may underestimate weak hydrogen-bonding interactions, such as CH–O hydrogen bonds, that have been found to be important in some protein-solvent systems such as in relative temperature-dependent stability of hydrogen bonds in an α-helix versus in a 310-helix.151–154 While osmolyte–protein and osmolyte–water interactions are generally consistent between classical and quantum mechanics,155–157 some discrepancies have also been reported.158 Thus, it will be interesting to further probe the effects reported here using ab initio simulations that explicitly account for the impact of electronic structure on stability. However, the computational cost of such simulations remains prohibitive in terms of high-throughput investigations of excipient effects. For this reason, the acceleration of ab initio simulations through methods such as multiple time-stepping159 or machine learning frameworks160 is critical for the application of such methods towards biological formulation design.
Our results suggest overall that arginine is uniquely situated for use in formulations due to the tunable, context-dependent properties of its effects. Hence, while arginine may not be considered the universal stabilizer it once was, its balance between direct- and indirect-driven stabilization of hydrophobic interactions solidifies its significance in formulation design.
Data availability
Data for this article, including simulation parameter files and analysis scripts, are available at https://github.com/SAMPEL-Group/Arginine-Hydrophobic-Polymer.Author contributions
JWPZ: investigation – computational, validation, formal analysis, visualization, writing – original draft, writing – review and editing; PM: investigation – computational, validation, writing – review and editing; IT: conceptualization, investigation – experimental, writing – review and editing; XZ: investigation – experimental, writing – review and editing; CLH: conceptualization, funding acquisition, resources, writing – review and editing; SLP: conceptualization, funding acquisition, resources, writing – review and editing; SS: conceptualization, methodology, validation, supervision, project administration, funding acquisition, resources, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the National Science Foundation under DMREF Grant No. 2118788, 2118693, and 2118638. Computational resources were provided by the Minnesota Supercomputing Institute at the University of Minnesota – Twin Cities. We thank computing resources through the ACCESS program for providing additional resources at the San Diego Supercomputing Cluster at the University of California – San Diego.Notes and references
- S. H. Jeong, Arch. Pharmacal Res., 2012, 35, 1871–1886 CrossRef CAS PubMed.
- W. Wang, Int. J. Pharm., 2005, 289, 1–30 CrossRef CAS.
- S. Y. Patro, E. Freund and B. S. Chang, Biotechnol. Annu. Rev., 2002, 8, 55–84 CAS.
- T. Arakawa, K. Tsumoto, Y. Kita, B. Chang and D. Ejima, Amino Acids, 2007, 33, 587–605 CrossRef CAS PubMed.
- J. Hamborsky, A. Kroger and C. Wolfe, Epidemiology and prevention of vaccine-preventable diseases, Centers for Disease Control and Prevention, Atlanta, GA, 13th edn, 2015 Search PubMed.
- M. J. Mistilis, J. C. Joyce, E. S. Esser, I. Skountzou, R. W. Compans, A. S. Bommarius and M. R. Prausnitz, Drug Delivery Transl. Res., 2017, 7, 195–205 CrossRef CAS.
- K. Tsumoto, M. Umetsu, I. Kumagai, D. Ejima, J. Philo and T. Arakawa, Biotechnol. Prog., 2004, 20, 1301–1308 CrossRef CAS PubMed.
- K. Tsumoto, D. Ejima, Y. Kita and T. Arakawa, Protein Pept. Lett., 2005, 12, 613–619 CrossRef CAS.
- P. Stärtzel, J. Pharm. Sci., 2018, 107, 960–967 CrossRef.
- E. Smirnova, I. Safenkova, B. Stein-Margolina, V. Shubin and B. Gurvits, Amino Acids, 2013, 45, 845–855 CrossRef CAS PubMed.
- D. Shah, A. R. Shaikh, X. Peng and R. Rajagopalan, Biotechnol. Prog., 2011, 27, 513–520 CrossRef CAS PubMed.
- T. B. Eronina, N. A. Chebotareva, N. N. Sluchanko, V. V. Mikhaylova, V. F. Makeeva, S. G. Roman, S. Y. Kleymenov and B. I. Kurganov, Int. J. Biol. Macromol., 2014, 68, 225–232 CrossRef CAS.
- Q. Xie, T. Guo, J. Lu and H.-M. Zhou, Int. J. Biochem. Cell Biol., 2004, 36, 296–306 CrossRef CAS PubMed.
- B. Anumalla and N. P. Prabhu, Appl. Biochem. Biotechnol., 2019, 189, 541–555 CrossRef CAS.
- T. Arakawa and N. K. Maluf, Int. J. Biol. Macromol., 2018, 107, 1692–1696 Search PubMed.
- C. Meingast and C. L. Heldt, Biotechnol. Prog., 2020, 36, e2931 CrossRef CAS PubMed.
- C. L. Meingast, P. U. Joshi, D. G. Turpeinen, X. Xu, M. Holstein, H. Feroz, S. Ranjan, S. Ghose, Z. J. Li and C. L. Heldt, Biotechnol. J., 2021, 16, 2000342 CrossRef CAS PubMed.
- R. J. Falconer, C. Chan, K. Hughes and T. P. Munro, J. Chem. Technol. Biotechnol., 2011, 86, 942–948 CrossRef CAS.
- S. V. Thakkar, S. B. Joshi, M. E. Jones, H. A. Sathish, S. M. Bishop, D. B. Volkin and C. Russell Middaugh, J. Pharm. Sci., 2012, 101, 3062–3077 CrossRef CAS PubMed.
- V. Vagenende, A. X. Han, M. Mueller and B. L. Trout, ACS Chem. Biol., 2013, 8, 416–422 CrossRef CAS.
- L. Platts and R. J. Falconer, Int. J. Pharm., 2015, 486, 131–135 CrossRef CAS.
- T. Arakawa, D. Ejima, K. Tsumoto, N. Obeyama, Y. Tanaka, Y. Kita and S. N. Timasheff, Biophys. Chem., 2007, 127, 1–8 CrossRef CAS PubMed.
- D. Shukla and B. L. Trout, J. Phys. Chem. B, 2010, 114, 13426–13438 CrossRef CAS.
- Y. K. Ng and L. Konermann, J. Am. Chem. Soc., 2024, 146, 8394–8406 CrossRef CAS PubMed.
- U. Das, G. Hariprasad, A. S. Ethayathulla, P. Manral, T. K. Das, S. Pasha, A. Mann, M. Ganguli, A. K. Verma, R. Bhat, S. K. Chandrayan, S. Ahmed, S. Sharma, P. Kaur, T. P. Singh and A. Srinivasan, PLoS One, 2007, 2, e1176 CrossRef.
- J. Li, M. Garg, D. Shah and R. Rajagopalan, J. Chem. Phys., 2010, 133, 054902 CrossRef.
- C. P. Schneider and B. L. Trout, J. Phys. Chem. B, 2009, 113, 2050–2058 CrossRef CAS PubMed.
- C. P. Schneider, D. Shukla and B. L. Trout, J. Phys. Chem. B, 2011, 115, 7447–7458 CrossRef CAS PubMed.
- S. Santra, S. Dhurua and M. Jana, J. Chem. Phys., 2021, 154, 084901 CrossRef CAS.
- S. Santra and M. Jana, J. Phys. Chem. B, 2022, 126, 1462–1476 CrossRef CAS.
- W. Kauzmann, Adv. Protein Chem., 1959, 14, 1–63 CrossRef CAS PubMed.
- C. Tanford, J. Am. Chem. Soc., 1962, 84, 4240–4247 CrossRef CAS.
- C. Tanford, Science, 1978, 200, 1012–1018 CrossRef CAS.
- K. A. Dill, Biochemistry, 1990, 29, 7133–7155 CrossRef CAS.
- H. J. Savage, C. J. Elliott, C. M. Freeman and J. L. Finney, Farad. Trans., 1993, 89, 2609–2617 RSC.
- G. Hummer, S. Garde, A. Garcıa and L. Pratt, Chem. Phys., 2000, 258, 349–370 CrossRef CAS.
- L. R. Pratt and A. Pohorille, Chem. Rev., 2002, 102, 2671–2692 CrossRef CAS.
- A. Ben-Naim, Hydrophobic interactions, Plenum Press, New York, 2005 Search PubMed.
- D. Chandler, Nature, 2005, 437, 640–647 CrossRef CAS PubMed.
- S. N. Timasheff, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 67–97 CrossRef CAS.
- T. Ghosh, A. Kalra and S. Garde, J. Phys. Chem. B, 2005, 109, 642–651 CrossRef CAS.
- M. V. Athawale, J. S. Dordick and S. Garde, Biophys. J., 2005, 89, 858–866 CrossRef CAS.
- M. V. Athawale, S. Sarupria and S. Garde, J. Phys. Chem. B, 2008, 112, 5661–5670 CrossRef CAS.
- R. Zangi, R. Zhou and B. J. Berne, J. Am. Chem. Soc., 2009, 131, 1535–1541 CrossRef CAS PubMed.
- D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- N. F. A. van der Vegt and D. Nayar, J. Phys. Chem. B, 2017, 121, 9986–9998 CrossRef CAS.
- S. Paul and G. N. Patey, J. Phys. Chem. B, 2008, 112, 11106–11111 CrossRef CAS.
- R. D. Macdonald and M. Khajehpour, Biophys. Chem., 2013, 184, 101–107 CrossRef CAS.
- P. Ganguly, N. F. A. Van Der Vegt and J.-E. Shea, J. Phys. Chem. Lett., 2016, 7, 3052–3059 CrossRef CAS.
- Z. Su, G. Ravindhran and C. L. Dias, J. Phys. Chem. B, 2018, 122, 5557–5566 CrossRef CAS PubMed.
- A. Folberth, S. Bharadwaj and N. F. A. Van Der Vegt, Phys. Chem. Chem. Phys., 2022, 24, 2080–2087 RSC.
- A. Wallqvist, D. G. Covell and D. Thirumalai, J. Am. Chem. Soc., 1998, 120, 427–428 CrossRef CAS.
- M. Ikeguchi, S. Nakamura and K. Shimizu, J. Am. Chem. Soc., 2001, 123, 677–682 CrossRef CAS.
- N. F. A. Van Der Vegt, M.-E. Lee, D. Trzesniak and W. F. Van Gunsteren, J. Phys. Chem. B, 2006, 110, 12852–12855 CrossRef CAS.
- M.-E. Lee and N. F. A. Van Der Vegt, J. Am. Chem. Soc., 2006, 128, 4948–4949 CrossRef CAS PubMed.
- T. A. Shpiruk and M. Khajehpour, Phys. Chem. Chem. Phys., 2013, 15, 213–222 RSC.
- A. Wang and D. W. Bolen, Biochemistry, 1997, 36, 9101–9108 CrossRef CAS.
- Q. Zou, B. J. Bennion, V. Daggett and K. P. Murphy, J. Am. Chem. Soc., 2002, 124, 1192–1202 CrossRef CAS.
- B. J. Bennion and V. Daggett, Proc. Natl. Acad. Sci. U.S.A., 2003, 100, 5142–5147 CrossRef CAS PubMed.
- P. Ganguly, D. Bubák, J. Polák, P. Fagan, M. Draćínský, N. F. A. Van Der Vegt, J. Heyda and J.-E. Shea, J. Phys. Chem. Lett., 2022, 13, 7980–7986 CrossRef CAS.
- P. R. ten Wolde and D. Chandler, Proc. Natl. Acad. Sci. U.S.A., 2002, 99, 6539–6543 CrossRef CAS PubMed.
- D. Nayar and N. F. A. van der Vegt, J. Phys. Chem. B, 2018, 122, 3587–3595 CrossRef CAS.
- J. Mondal, G. Stirnemann and B. J. Berne, J. Phys. Chem. B, 2013, 117, 8723–8732 CrossRef CAS.
- S. N. Jamadagni, R. Godawat and S. Garde, Langmuir, 2009, 25, 13092–13099 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127–136 CrossRef.
- D. Berthelot, C. R. Acad. Sci., 1898, 126, 1703–1855 Search PubMed.
- Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6051 CrossRef CAS.
- F. Zhu and G. Hummer, J. Comput. Chem., 2012, 33, 453–465 CrossRef CAS.
- M. V. Athawale, G. Goel, T. Ghosh, T. M. Truskett and S. Garde, Proc. Natl. Acad. Sci. U.S.A., 2007, 104, 733–738 CrossRef CAS.
- R. Godawat, S. N. Jamadagni and S. Garde, J. Phys. Chem. B, 2010, 114, 2246–2254 CrossRef CAS PubMed.
- S. Dasetty and S. Sarupria, J. Phys. Chem. B, 2021, 125, 2644–2657 CrossRef CAS.
- L. R. Pratt and D. Chandler, J. Chem. Phys., 1977, 67, 3683–3704 CrossRef CAS.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- P. R. T. Wolde, J. Phys.: Condens. Matter, 2002, 14, 9445–9460 CrossRef.
- D. M. Huang and D. Chandler, J. Phys. Chem. B, 2002, 106, 2047–2053 CrossRef CAS.
- S. Garde, A. E. Garcıa, L. R. Pratt and G. Hummer, Biophys. Chem., 1999, 78, 21–32 CrossRef CAS.
- D. Ben-Amotz, Annu. Rev. Phys. Chem., 2016, 67, 617–638 CrossRef CAS.
- G. Scatchard, J. Am. Chem. Soc., 1946, 68, 2315–2319 CrossRef CAS.
- E. F. Casassa and H. Eisenberg, Adv. Prot. Chem., Elsevier, 1964, vol. 19, pp. 287–395 Search PubMed.
- J. A. Schellman, Biopolymers, 1987, 26, 549–559 CrossRef CAS PubMed.
- H. Inoue and S. N. Timasheff, Biopolymers, 1972, 11, 737–743 CrossRef CAS.
- M. Record and C. Anderson, Biophys. J., 1995, 68, 786–794 CrossRef CAS PubMed.
- D. Shukla, C. Shinde and B. L. Trout, J. Phys. Chem. B, 2009, 113, 12546–12554 CrossRef CAS.
- M. Ferrario, M. Haughney, I. R. McDonald and M. L. Klein, J. Chem. Phys., 1990, 93, 5156–5166 CrossRef CAS.
- A. Luzar and D. Chandler, J. Chem. Phys., 1993, 98, 8160–8173 CrossRef CAS.
- A. Luzar and D. Chandler, Nature, 1996, 379, 55–57 CrossRef CAS.
- A. Luzar, J. Chem. Phys., 2000, 113, 10663–10675 CrossRef CAS.
- M. C. Stumpe and H. Grubmüller, J. Am. Chem. Soc., 2007, 129, 16126–16131 CrossRef CAS.
- A. A. Simpson, B. Hébert, G. M. Sullivan, C. R. Parrish, Z. Zádori, P. Tijssen and M. G. Rossmann, J. Mol. Biol., 2002, 315, 1189–1198 CrossRef CAS.
- R. Diamond, J. Mol. Biol., 1974, 82, 371–391 CrossRef CAS.
- P. U. Joshi, C. Decker, X. Zeng, A. Sathyavageeswaran, S. L. Perry and C. L. Heldt, Biomacromolecules, 2024, 25, 741–753 CrossRef CAS PubMed.
- S. A. Seabrook and J. Newman, ACS Comb. Sci., 2013, 15, 387–392 CrossRef CAS.
- S. Shi, A. Semple, J. Cheung and M. Shameem, J. Pharm. Sci., 2013, 102, 2471–2483 CrossRef CAS.
- L. McInnes, J. Healy and S. Astels, J. Open Source Softw., 2017, 2, 205 Search PubMed.
- M. Makowski, C. Czaplewski, A. Liwo and H. A. Scheraga, J. Phys. Chem. B, 2010, 114, 993–1003 CrossRef CAS.
- D. Dhabal, Z. Jiang, A. Pallath and A. J. Patel, J. Phys. Chem. B, 2021, 125, 5434–5442 CrossRef CAS PubMed.
- A. Kalra, N. Tugcu, S. M. Cramer and S. Garde, J. Phys. Chem. B, 2001, 105, 6380–6386 CrossRef CAS.
- S. Bharadwaj, D. Nayar, C. Dalgicdir and N. F. A. Van Der Vegt, Commun. Chem., 2020, 3, 165 CrossRef CAS PubMed.
- S. Gómez, N. Rojas-Valencia, S. A. Gómez, C. Cappelli, G. Merino and A. Restrepo, Chem. Sci., 2021, 12, 9233–9245 RSC.
- C. A. Cerdeiriña and P. G. Debenedetti, J. Chem. Phys., 2016, 144, 164501 CrossRef.
- H. S. Ashbaugh, T. M. Truskett and P. G. Debenedetti, J. Chem. Phys., 2002, 116, 2907–2921 CrossRef CAS.
- N. Choudhury and B. M. Pettitt, J. Am. Chem. Soc., 2005, 127, 3556–3567 CrossRef CAS PubMed.
- M. V. Athawale, S. N. Jamadagni and S. Garde, J. Chem. Phys., 2009, 131, 115102 CrossRef.
- N. Choudhury and B. M. Pettitt, J. Phys. Chem. B, 2005, 109, 6422–6429 Search PubMed.
- H. S. Ashbaugh and M. E. Paulaitis, J. Am. Chem. Soc., 2001, 123, 10721–10728 CrossRef CAS.
- T. Arakawa and S. Timasheff, Biophys. J., 1985, 47, 411–414 Search PubMed.
- K. C. Bauer, S. Suhm, A. K. Wöll and J. Hubbuch, Int. J. Pharm., 2017, 516, 82–90 CrossRef CAS PubMed.
- D. B. Watlaufer, S. K. Malik, L. Stoller and R. L. Coffin, J. Am. Chem. Soc., 1964, 86, 508–514 CrossRef.
- H. Meuzelaar, M. R. Panman and S. Woutersen, Angew. Chem., 2015, 127, 15470–15474 CrossRef.
- S. K. Jha and S. Marqusee, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 4856–4861 CrossRef CAS PubMed.
- C. E. Dempsey, P. E. Mason, J. W. Brady and G. W. Neilson, J. Am. Chem. Soc., 2007, 129, 15895–15902 CrossRef CAS PubMed.
- J. Heyda, H. I. Okur, J. Hladílková, K. B. Rembert, W. Hunn, T. Yang, J. Dzubiella, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2017, 139, 863–870 CrossRef CAS.
- M. Hishida, R. Anjum, T. Anada, D. Murakami and M. Tanaka, J. Phys. Chem. B, 2022, 126, 2466–2475 CrossRef CAS.
- G. S. Jas, E. C. Rentchler, A. M. Słowicka, J. R. Hermansen, C. K. Johnson, C. R. Middaugh and K. Kuczera, J. Phys. Chem. B, 2016, 120, 3089–3099 CrossRef CAS.
- A. Diaz and V. Ramakrishnan, Comput. Biol. Chem., 2023, 105, 107883 CrossRef CAS PubMed.
- G. Saladino, M. Marenchino, S. Pieraccini, R. Campos-Olivas, M. Sironi and F. L. Gervasio, J. Chem. Theory Comput., 2011, 7, 3846–3852 CrossRef CAS PubMed.
- I. Jahan and S. M. Nayeem, RSC Adv., 2020, 10, 27598–27614 RSC.
- J. Zeman, C. Holm and J. Smiatek, J. Chem. Eng. Data, 2020, 65, 1197–1210 CrossRef CAS.
- R. Gazi, S. Maity and M. Jana, ACS Omega, 2023, 8, 2832–2843 CrossRef CAS.
- M. Vazdar, J. Heyda, P. E. Mason, G. Tesei, C. Allolio, M. Lund and P. Jungwirth, Acc. Chem. Res., 2018, 51, 1455–1464 CrossRef CAS.
- P. Gund, J. Chem. Educ., 1972, 49, 100 Search PubMed.
- J. Wyman, Adv. Protein Chem., Elsevier, 1964, vol. 19, pp. 223–286 Search PubMed.
- S. N. Timasheff, Proc. Natl. Acad. Sci. U.S.A., 2002, 99, 9721–9726 Search PubMed.
- D. Shukla, C. P. Schneider and B. L. Trout, Adv. Drug Delivery Rev., 2011, 63, 1074–1085 Search PubMed.
- J. Mondal, D. Halverson, I. T. S. Li, G. Stirnemann, G. C. Walker and B. J. Berne, Proc. Natl. Acad. Sci. U.S.A., 2015, 112, 9270–9275 CrossRef CAS.
- M. Mukherjee and J. Mondal, J. Phys. Chem. B, 2020, 124, 6565–6574 Search PubMed.
- D. Shukla and B. L. Trout, J. Phys. Chem. B, 2011, 115, 1243–1253 CrossRef CAS.
- A. F. Streck and U. Truyen, Curr. Issues Mol. Biol., 2020, 33–46 CrossRef PubMed.
- X. Mi, W. C. Blocher McTigue, P. U. Joshi, M. K. Bunker, C. L. Heldt and S. L. Perry, Biomater. Sci., 2020, 8, 7082–7092 RSC.
- M. F. Gencoglu, E. Pearson and C. L. Heldt, J. Biotechnol., 2014, 186, 83–90 Search PubMed.
- M. F. Tafur, K. S. Vijayaragavan and C. L. Heldt, Antiviral Res., 2013, 99, 27–33 CrossRef CAS.
- B. Matthews, Advances in Protein Chemistry, Elsevier, 1995, vol. 46, pp. 249–278 Search PubMed.
- C. M. Dobson, P. A. Evans and S. E. Radford, Trends Biochem. Sci., 1994, 19, 31–37 CrossRef CAS.
- T. Yoshimura, H. Noguchi, T. Inoue and N. Saitô, Biophys. Chem., 1991, 40, 277–291 CrossRef CAS.
- G. Merlini and V. Bellotti, Clin. Chim. Acta, 2005, 357, 168–172 CrossRef CAS PubMed.
- M. M. Santoro, Y. Liu, S. M. A. Khan, L. X. Hou and D. W. Bolen, Biochemistry, 1992, 31, 5278–5283 CrossRef CAS PubMed.
- B. Adamczak, M. Wieczór, M. Kogut, J. Stangret and J. Czub, Biochem. J., 2016, 473, 3705–3724 CrossRef CAS.
- S. Brudar and B. Hribar-Lee, Int. J. Mater. Sci., 2023, 24, 1197 CAS.
- P. Rueda, J. Fominaya, J. P. Langeveld, C. Bruschke, C. Vela and J. Casal, Vaccine, 2000, 19, 726–734 CrossRef CAS PubMed.
- T. K. Cloutier, C. Sudrik, N. Mody, S. A. Hasige and B. L. Trout, mAbs, 2020, 12, 1816312 CrossRef.
- S. Horowitz and R. C. Trievel, J. Biol. Chem., 2012, 287, 41576–41582 CrossRef CAS.
- S. Scheiner, Phys. Chem. Chem. Phys., 2011, 13, 13860 RSC.
- A. Tkatchenko, M. Rossi, V. Blum, J. Ireta and M. Scheffler, Phys. Rev. Lett., 2011, 106, 118102 CrossRef.
- O. T. Unke, M. Stöhr, S. Ganscha, T. Unterthiner, H. Maennel, S. Kashubin, D. Ahlin, M. Gastegger, L. Medrano Sandonas, J. T. Berryman, A. Tkatchenko and K.-R. Müller, Sci. Adv., 2024, 10, eadn4397 CrossRef CAS.
- V. Spiwok, Molecules, 2017, 22, 1038 CrossRef PubMed.
- V. Spiwok, P. Lipovová, T. Skálová, E. Vondráčková, J. Dohnálek, J. Hašek and B. Králová, J. Comput.-Aided Mol. Des., 2006, 19, 887–901 CrossRef.
- C. J. Sahle, M. A. Schroer, J. Niskanen, M. Elbers, C. M. Jeffries and C. Sternemann, Phys. Chem. Chem. Phys., 2020, 22, 11614–11624 RSC.
- M. K. Tiwari and R. K. Murarka, Phys. Chem. Chem. Phys., 2021, 23, 5527–5539 RSC.
- R. Kar, S. Mandal, V. Thakkur, B. Meyer and N. N. Nair, J. Chem. Theory Comput., 2023, 19, 8351–8364 CrossRef CAS.
- V. Botu and R. Ramprasad, Int. J. Quantum Chem., 2015, 115, 1074–1083 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation details, error estimations, and additional analysis. See DOI: https://doi.org/10.1039/d4sc08672d |
| This journal is © The Royal Society of Chemistry 2025 |