Implementing magnetic properties on demand with a dynamic lanthanoid–organic framework

Abstract

We present the synthesis of a lanthanoid–organic framework (LOF) featuring a dynamic structure that exhibits tunable magnetic properties. The LOF undergoes breathing and gate-opening phenomena in response to changes in DMF content and N₂ sorption, leading to the emergence of new crystal phases with distinct characteristics. Notably, the desolvated form of the LOF excels as a single-ion magnet, while the fully activated structure demonstrates impressive qubit properties, exhibiting Rabi oscillations up to 60 K. Our work enables precise control over the LOF's geometry, allowing us to selectively tailor its magnetic behavior to achieve either of these two intriguing functionalities.

---

Introduction

Flexible Metal–Organic Frameworks (MOFs) differ from regular rigid MOFs by their ability to undergo reversible structural changes with external stimuli, such as temperature, pressure, or the addition/removal of guest molecules.^1–7 Different types of flexibility have been reported,^8,9 including breathing,^10,11 swelling,¹² and gate opening mechanisms,^13–16 which imply variations in the pore size of the MOF, the shape of the pore, and, in some cases, even in the connectivity.¹⁶ Interestingly, these structural modifications may have a direct influence on the inherent physical properties of the MOF, particularly those that rely directly on the structure and topology of the material and open up the possibility of finely tuning such properties at will. For instance, we have recently reported that the breathing phenomenon of MUV-2, which occurs upon exposure to different solvents, yields a change in the ligand planarity that is directly associated with a change of up to 1.1 V in the redox potential of the different forms.¹⁷ The tuning of magnetic properties has also been reported in dynamic magnetic MOFs, thus allowing the magnetisation of the compound to be modulated or switched on–off,¹⁸ although typically this is caused by a change in the connection between the different metal nodes.^19,20

The implementation of slow magnetic relaxation in MOFs can be easily achieved by using lanthanoid centres as metal nodes, yielding lanthanoid–organic frameworks, or LOFs.^21–23 Lanthanoids are attractive not only for the design of Single-Ion Magnets (SIMs²⁴), but their large magnetic anisotropy and long relaxation times make them suitable candidates for quantum computing and spin-based electronics,²⁵ which has also been reported in LOFs.²⁶ The effect of the structural changes of a responsive MOF and other coordination complexes on their slow magnetic relaxation has been extensively studied in the existing literature.^27–30 However, the potential impact of such flexibility on the quantum properties still remains a relatively unexplored area.

Herein, we present a dynamic magnetic LOF that exhibits two different types of flexibility. On one hand, different crystal transitions take place by varying the DMF lattice molecules (as-synthesised, desolvated, and fully activated forms). Moreover, the fully activated phase exhibits an abrupt gate-opening phenomenon upon the sorption of N₂. This multiflexibility, a rather unusual phenomenon,³¹ is an ideal platform that can then be exploited to tailor the magnetic properties upon selection of suitable lanthanoid ions. Thus, the desolvated form that incorporates Dy results in the best candidate as a single-ion magnet (SIM), whereas the activated form incorporating Gd shows the best quantum coherence and spin-lattice relaxation and is sensible to the adsorption of N₂.

Results and discussion

Structural study and characterisation

The solvothermal reaction of LnCl₃ with 1,3,5-tri(4-carboxyphenyl)benzene (H₃BTB) in N,N-dimethylformamide (DMF) produces single crystals with all the lanthanoid centres (Ln = La, Ce, Pr, Sm, Eu, Gd, Tb, Dy, Ho, Er, and Y) (see Section S1 in the ESI for details‡). Single crystal X-ray diffraction (SCXRD) reveals two different families of compounds, hereafter called LOF1 and LOF2. LOF1 group, with molecular formula [Ln(BTB)(DMF)]·xDMF, comprises Ln = La (x = 0.62), Ce (x = 0.63), and Pr (x = 0.75) and crystallizes in the P2₁/c space group, whereas LOF2, with molecular formula [Ln(BTB)(DMF)]·2DMF, comprises Sm–Er and Y, and crystallizes in the P2₁ space group (see Section S3 in the ESI for crystallographic details‡). Both structures consist of Ln-carboxylate chains which are further connected by BTB³⁻ ligands. Each BTB³⁻ ligand connects to 3 different chains, and each chain is connected to 6 other chains via 6 BTB³⁻ ligands, giving rise to a pseudohexagonal topology (Fig. 1 and S1‡). The two structures differ in terms of the coordination number of their Ln centres and the conformation of the BTB ligand. In the case of LOF1, two crystallographically independent Ln centres (Ln01 and Ln02) are found in the structure but presenting similar coordination environments, with both centres coordinated by six carboxylic groups and one DMF molecule. However, in the case of Ln01 there are three chelating carboxylates (with 6 coordinated oxygen atoms) and three monodentate carboxylate ligands (with 3 coordinated oxygen atoms), whereas in Ln02 there are two chelating carboxylates (with 4 coordinated oxygen atoms) and four monodentate carboxylates (with 4 coordinated oxygen atoms). This leaves a total coordination number of 10 for Ln01 and 9 for Ln02 (see Section S3 for more details‡). In the case of LOF2, the structure comprises two crystallographically independent lanthanoid atoms which are each linked to eight oxygen atoms. Four of these oxygens are chelating carboxylates from the BTB ligands, three others belong to bridging carboxylate units shared with the neighbouring lanthanoid, and the last one belongs to a coordinated DMF molecule.

Fig. 1 (Left) Crystal structure of LOF1. Hydrogen atoms and solvent molecules have been omitted for clarity. (Top right) Rodlike chains that run parallel to the c-axis. The two crystallographically different lanthanoid atoms are depicted in dark and light purple. (Bottom right) Coordination environment of the lanthanoid centres. More details can be found in Fig. S2 and S3.‡

A close inspection of the thermogravimetric analysis (TGA) profile reveals two distinct behaviours between LOF1 and LOF2 (Fig. 2 and S11‡). Whereas LOF1 displays two clearly differentiated mass losses at 120 °C and 225 °C, these occur almost simultaneously before reaching 150 °C in LOF2. Powder X-ray diffraction (PXRD) measured after heating the samples at 150 and 300 °C show two phase transitions in LOF1, while the pattern of LOF2 experiences a broadening of the peaks most likely attributed to a loss of crystallinity due to the loss of solvent molecules (Fig. S5‡). Further SCXRD studies reveal that heating the as-synthesised LOF1 (from now on called LOF1_as form) at 150 °C under vacuum removes a significant portion of the DMF molecules from the pores, causing a phase transition resulting in the desolvated form (LOF1_des) (Fig. 2a). Although the rodlike chains and their connectivity by the BTB³⁻ ligands are maintained, a change in the orientation of the ligands has been found with the removal of the major part of the solvated DMF molecules (Fig. 2b). This rotation leads to the loss of one Ln–O bond from the carboxylic group to its adjacent Ln neighbour in the chain, as it is highlighted in pink, blue, orange, and green in Fig. 2b. All these deformations result in an increment of the asymmetric unit compared to the as-synthesised structure, resulting in four crystallographically independent Ln atoms (depicted in different colours in Fig. 2b). In addition, two out of four of the Ln centres are coordinated to DMF molecules. If the heating is increased up to 300 °C, SCXRD shows that the remaining coordinated DMF molecules are also removed and a new phase transition provides the activated form (LOF1_act) (Fig. 2a). In this phase, the Ln–O bonds that had changed are restored, and all BTB ligands and Ln centres are crystallographically equivalent (Fig. 2b). Each carboxylate is fully coordinated to one Ln atom and one of the oxygens is shared with the next Ln neighbour, acting as a bridge. Each Ln atom presents a total coordination number of 9, consisting of 3 chelating carboxylates and 3 shared oxygens. The resulting structure is more symmetrical than LOF1_as and LOF1_des forms, as illustrated in Fig. S4.‡ Moreover, as Fig. 2a shows, the overall structure of the activated form resembles to the as-synthesised form (LOF1_as) rather than the desolvated form (LOF1_des). Thus, LOF1_des can be considered as a snapshot of the transient phase upon complete evacuation of the MOF, and reveals important structural changes required for the removal of guest molecules despite the similarities of the initial and final phases.

Fig. 2 (a) Structures of LOF1_as, LOF1_des, and LOF1_act, respectively. (b) Side view of LOF1_as (bottom), LOF1_des (middle), and LOF1_act (top) chains. Crystallographically independent Ln atoms are depicted in different colours in each form. The carboxylates that change their coordination in each phase transition have been highlighted in pink, blue, orange, and green (see the text for details‡). (c) Comparison of the experimental PXRD patterns upon heating at different temperatures (as indicated in the figure) and the simulated diffractograms (in different shades of purple) for each phase. (d) Thermogravimetric profiles of La-LOF1 (blue), Ce-LOF1 (yellow), Pr-LOF1 (green), and Dy-LOF2 (red). (e) Experimental PXRD after exposure to DMF vapours and reactivation.

Interestingly, PXRD upon heating at different temperatures reveals that there are no other intermediate phases (Fig. 2c) and that the transition to LOF1_des is fully complete at 100 °C. To study the reversibility of the system, the crystals of LOF1_des and LOF1_act were exposed under DMF vapours. The PXRD patterns showed that the transition between LOF1_as and LOF1_des is reversible, but once LOF1_act is formed, the system cannot revert to the original phase. Instead, a new one is obtained, LOF1_reDMF (Fig. 2e, S9, and S10‡). The total content of DMF molecules for each phase was determined through TGA and NMR (see Sections S6 and S7 in the ESI‡).

The N₂ adsorption capacity was measured for the flexible (LOF1) and the rigid (LOF2) structures. In the case of the flexible group, both LOF1_des and LOF1_act forms were measured (Fig. 3), observing that the activated structure outperforms the desolvated one. This is not surprising considering that LOF1_des still presents coordinated DMF molecules occupying part of the space of the pores. More interestingly, LOF1_act undergoes a single-step transformation (typical of a gate opening phenomenon^13–16) with a threshold pressure of 0.1 atm for Pr-LOF1, 0.15 atm for Ce-LOF1, and 0.2 atm for La-LOF1. This phenomenon where the sorption capacity increases abruptly is also present in the high-pressure N₂ isotherms at room temperature (Fig. S17‡), although it is not observed with CO₂ (Fig. S18 and S19‡). In contrast, no sorption step was observed in the case of Dy-LOF2, confirming the lack of flexibility in the structure (Fig. 3).

Fig. 3 N₂ adsorption isotherms of La-LOF1 (blue), Ce-LOF1 (yellow), Pr-LOF1 (green), and Dy-LOF2 (red) at 77 K. For La, Ce, and Pr-LOF1, activated and desolvated forms were measured and are depicted in darker and lighter colours, respectively.

Static and dynamic magnetic properties

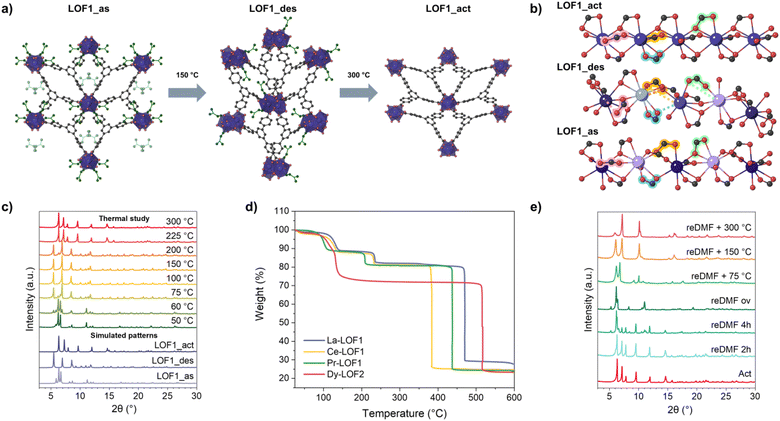
The study of the magnetic properties of LOFs was explored by creating hybrids of the diamagnetic La-LOF1 structure with small amounts of paramagnetic metal nodes (i.e. Dy and Gd) (see Section S1 in the ESI for experimental details‡). Importantly, it should be noted that the pure Dy- and Gd-LOFs are rigid structures, whereas doping La-LOF1 results in flexible structures. Different doping ratios were explored and the preservation of the dynamic LOF structure was examined by PXRD. The maximum amount of Ln-doping that the structure can admit was found to be 20%. Above this, the separate formation of the rigid structure (characteristic of the smaller lanthanoids) takes place, giving rise to a physical mixture of the two different frameworks (Fig. S7‡). The doping percentage was determined by Inductively Coupled Plasma spectroscopy (ICP-MS) (Table S1‡). The variable-temperature static magnetic susceptibilities, χ_M, of La-Dy-LOF1 (20%) were determined for the three different phases, as-synthesised, desolvated and activated (Fig. S21‡). In all cases, the obtained χ_MT values coincide at room temperature and are close to the expected value (14.1 emu mol_Dy⁻¹ K) for a Dy^III ion with a ⁶H_15/2 ground state. This is in full agreement with the fact that the isolated Dy^III magnetic centres are diluted in diamagnetic La^III matrices.

Considering a g-factor of 1.33 for S = 5/2 Dy^III, the magnetic data were fitted using a simplified model that accounts only for the second-order zero-field splitting (ZFS) parameters D and E. The results obtained are as follows: D = 12 cm⁻¹ and E = 2 cm⁻¹ for La-Dy-LOF1_as, D = 7 cm⁻¹ and E = 1 cm⁻¹ for La-Dy-LOF1_des, and D = 3.5 cm⁻¹ and E = 0.5 cm⁻¹ for La-Dy-LOF1_act. Alternating current (AC) magnetic susceptibility measurements were conducted to probe the slow magnetic relaxation of the dynamic LOFs. The measurements were performed as a function of the static magnetic field, being 2000 Oe the optimal field to induce frequency-dependent in-phase (χ′) and out-of-phase (χ′′) susceptibility signals (Fig. S22–S25‡). Under this field, all three samples exhibit slow magnetic relaxation, evidencing the SIM behaviours of the anisotropic Dy^III in the 3D extended LOF structures (Fig. 4). The relaxation times (τ) at different temperatures were extracted by fitting the frequency dependence of χ′ and χ′′ using a generalised Debye model (see Section 9 in the ESI‡). The obtained values were used to evaluate the temperature dependence of τ, which can be described with the following expression:

τ⁻¹ = τ_QTM⁻¹ + CTⁿ + τ₀⁻¹ exp(−U_eff/k_BT)

where the first and the second terms denote the quantum tunneling of magnetisation (QTM and Raman mechanisms), U_eff is the effective relaxation barrier in the Orbach process and τ₀ is a pre-exponential factor. The resulting fitting is depicted in Fig. 4d, observing that among the three different structures, La-Dy-LOF1_des exhibits the best SIM behaviour with the longest relaxation times below 10 K and the largest U_eff (= 31.3(8) cm⁻¹).

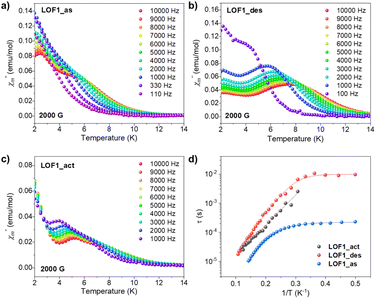Fig. 4 Temperature dependence of the out-of-phase signal χ′′ of La-Dy-LOF1_as (a), La-Dy-LOF1_des (b) and La-Dy-LOF1_act (c) at different frequencies, under 2000 G DC magnetic fields. (d) Comparison of the temperature dependence of relaxation times of the three samples at 2000 G applied DC field. Solid lines represent the fitting including Orbach, Raman and quantum tunnelling of magnetisation (see the text‡).

Analysis of the qubit properties

The feasibility of MOFs as quantum units for quantum information processing has been explored in order to achieve a two/three-dimensional organisation of qubits.^26,32–36 In this line, our group has previously reported a Gd^III-based MOF with quantum coherence results similar to discrete Gd^III complexes,^37,38 with T₂ = 612 ns at 3.5 K, and Rabi oscillations detected up to 40 K.²⁶ With the aim of testing the potential quantum properties of our flexible LOFs, we synthesised the La-Gd-LOF1 hybrid by introducing a 0.1% of Gd^III ions with quenched spin–orbit coupling (see ESI for detailed synthesis and characterisation‡). The energy spectra of the three La-Gd-LOF1 samples (as, des, and act) were first studied by echo-detected field-swept (EDFS) EPR spectroscopy (Fig. 5a). Extracted from these analyses, La-Gd-LOF1_des and La-Gd-LOF1_act show larger magnetic anisotropies (larger D and E values) for the S = 7/2 spin of the Gd^III ion (Table S11‡), and their spin echo signals span over the whole range of the measured magnetic fields (0–7000 G). All the spin sublevels of La-Gd-LOF1_des and La-Gd-LOF1_act can be distinguished and accessed within the S = 7/2 multiplet (Fig. S35‡). Among the detected peaks at different magnetic fields, some were chosen as observer points (OPs) to perform time-dependent pulsed EPR measurements (OP1-13 for La-Gd-LOF1_act, OP1-8 for La-Gd-LOF1_des and OP1 for La-Gd-LOF1_as) (Fig. S36–S40‡). Among these three samples, La-Gd-LOF1_act shows the best values for quantum coherence (T₂) and spin–lattice relaxation times (T₁). The longest T₂ (2.2 μs) is recorded for OP5-6 at 3.5 K, which is much longer than our previously reported Gd^III-MOF. The spin echo signal is observable up to 70 K (Fig. S36, S37, and S41‡), a record temperature in Gd^III-complexes. It is noteworthy that this robust coherence is achieved even in a compound in which the decoherence is favoured by the presence of hydrogen atoms in high concentration. The temperature dependence of T₁ and T₂ show a similar trend for different OPs, except for the T₂ values of OP1 (80 G). In this case, the magnetic field might not be strong enough to suppress the flip-flop spin relaxation caused by adjacent magnetic centres.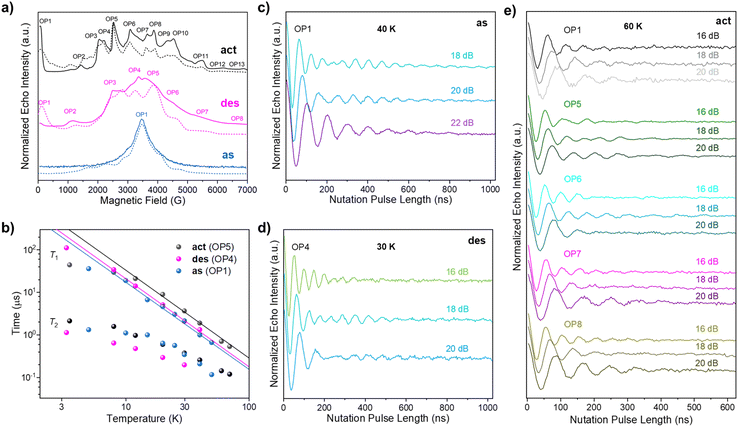

Fig. 5 (a) X-band EDFS spectra recorded at 4 K for La-Gd-LOF1_as, La-Gd-LOF1_des and La-Gd-LOF1_act. The dashed lines represent the best fits (see the text‡). The observer positions (OPs) indicate the magnetic fields where time-dependent pulsed EPR measurements were performed. (b) Temperature dependence of T₁ and T₂ at the most intense OPs for the three LOF samples. The solid lines represent the best fits of T₁vs. T (see the text‡). (c) Rabi oscillations of La-Gd-LOF1_as at 40 K at OP1 using different microwave powers. (d) Rabi oscillations of La-Gd-LOF1_des at 30 K at OP4 using different microwave powers. (e) Rabi oscillations of La-Gd-LOF1_act at 60 K using different microwave powers.

To analyze the potential structural dependence of the spin dynamics in these three samples, the temperature dependence of T₁ at the most intense OPs was fitted by a Raman-like relaxation process as T₁ = C⁻¹T⁻ⁿ (Fig. 5b). The values obtained for La-Gd-LOF1_act are C = 2.6(7) × 10⁻⁴ μs⁻¹ K⁻ⁿ and n = 2.06(8). While the n values obtained for La-Gd-LOF1_des and La-Gd-LOF1_as are essentially identical (2.07(5) and 2.04(7), respectively), their larger C values indicate faster Raman processes (4.1(6) × 10⁻⁴ and 5.2(11) × 10⁻⁴ μs⁻¹ K⁻ⁿ, respectively). This slower spin-lattice relaxation for LOF1_act is in line with the absence of DMF molecules coordinated to Gd^III. Nutation experiments were then conducted to test the coherence manipulation of the spin superposition states, a prerequisite for quantum information processing in these LOFs. Taking La-Gd-LOF1_act as an example, different attenuations (16, 18 and 20 dB) of the microwave power were used to distinguish the coherent Rabi oscillation and the Larmor precession of the H nuclei (Fig. S42‡). The frequency of the former (Ω_R) varies with the microwave power while the frequency of the latter is a linear function of the applied magnetic field. The slope of the observed Larmor precession versus the magnetic field is determined as 42.84 MHz/T, which is very close to the gyro ratio of H (γ_H = 42.58 MHz/T). As illustrated in Fig. S42,‡ OP1-8 exhibit different Ω_R, corresponding to different transitions within the S = 7/2 multiplet. Based on the ZFS parameters extracted from CW and EDFS EPR spectra, the Rabi frequencies at different magnetic fields were further calculated using a rotation-wave approximation method, which agrees well with the experimental results obtained after Fourier transforms. The detection of multiple frequencies for a given OP is due to the excitation of nearby transitions. This phenomenon can be suppressed by using a stronger attenuation power (20 dB) with a higher pulse selectivity (Fig. S42a‡). Remarkably, Rabi oscillations can be detected up to 60 K (Fig. 5e), which is, to the best of our knowledge, the highest temperature reported so far for any Gd^III-based system with a high-spin (S = 7/2) ground state. These Rabi oscillations are also observable for La-Gd-LOF1_as and La-Gd-LOF1_des (Fig. 5c, d, and S43‡), where the highest temperatures studied have been 40 K and 30 K, respectively. Due to the gate-opening phenomenon observed in N₂ sorption measurements, we further investigated the magnetic properties of La-Gd-LOF upon adsorbing N₂. Fig. 6a shows the temperature-variable continuous-wave (CW) EPR spectra of the activated and the N₂-containing LOFs, which reveals differences in the spectra even at room temperature. As can be observed, this difference becomes more prominent at lower temperatures, which can be better appreciated in the second-derivative EPR spectra (Fig. 6b). The slight variation in the metal coordination environment after N₂ sorption within the pores of the LOF structure is likely the cause. Therefore, these porous materials could be useful as a sensor to detect N₂ even at room temperature. Variable-temperature CW EPR spectra of both systems (activated and N₂-containing) were nicely reproduced using ZFS parameters, which vary depending on the temperature and N₂ adsorption (Fig. S44 and S45‡). This analysis leads to the conclusion that the magnetic anisotropy is reduced upon warming up, and the ability to detect the presence of N₂ becomes weaker. The temperature dependence of ZFS parameters was also analysed for La-Gd-LOF1_as, indicating a similar thermally-assisted reduction of the magnetic anisotropy (Fig. S46‡). There have been some examples reporting qubit-MOFs hybrids as spin-sensors relying on the change in the motion of the encapsulated qubit with the adsorption of the analyte by the MOF.^39,40 However, to the best of our knowledge there is no example of a sensor where the spin response originates from the MOF itself and its inherent flexibility.

Fig. 6 (a) CW EPR spectra of La-Gd-LOF1_act and La-Gd-LOF1_act-N₂ at different temperatures. The green and grey areas highlight the differences between both spectra. (b) Second derivatives of the EPR signals at the green region previously selected. Dashed lines represent simulated spectra.

Conclusions

In this work, we have synthesised a new family of dynamic LOFs with the possibility of creating hybrid structures with magnetic metal nodes that provide interesting magnetic properties on demand. The dynamism of the material relies on the observation of different flexible modes triggered by the variation of the DMF content of the lattice or the interaction with N₂. The LOF exhibits a breathing behaviour in the first reversible transition between LOF1_as and LOF1_des forms, followed by a non-reversible phase transition from LOF1_des to LOF1_act. Finally, a gate-opening phenomenon has been observed in the LOF1_act form. Moreover, the introduction of different metal ions in these structures allows for the creation of magnetically-doped LOFs. Depending on the doping magnetic metal and the crystal phase that the material adopts, the LOF can act as a SIM or a spin qubit. For a SIM behaviour, the doping candidate is Dy (20%) and the desolvated form shows the longest relaxation times below 10 K and the largest U_eff of 31.3(8) cm⁻¹. On the other hand, when doping with Gd (0.1%), the fully activated form performs as an excellent qubit system, leading to the slowest relaxation times (T₂ = 2.2 μs) among the three different phases. Remarkably, the detection of Rabi oscillations at 60 K represents the highest temperature ever reported for any Gd^III-based system. The responsive behavior of the fully activated structure, which was first observed in the gas sorption isotherms, was later confirmed in the EPR measurements upon adsorbing N₂. The noticeable differences in the spectra of the sample in the presence and absence of N₂ highlight the potential application of the material as a sensor to detect this gas even at room temperature.

Data availability

The data supporting this article have been included as part of the ESI.‡ The characterization data files are available on Zenodo open repository (DOI: 10.5281/zenodo.14537129).

Author contributions

I. G.-M. and Z. H. equally contributed to this work.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

This work has been supported by the European Union (ERC-2016-CoG 724681-S-CAGE), grants PID2023-152920NB-I00, and María de Maeztu Centre of Excellence Programmes CEX2019-000919-M, funded by MCIN/AEI/10.13039/501100011033 and cofinanced by FEDER, and the Generalitat Valenciana (CIPROM/2022/48, and IDIFEDER2021/075). I. G.-M. thanks MICIU for a pre-doctoral fellowship (FPU19/00474). This study forms part of the Advanced Materials and Quantum Communication programmes, supported by MCIN with funding from European Union NextGenera-tionEU (PRTR-C17.I1) and by Generalitat Valenciana (projects MFA/2022/31 and COMCUANTICA/010). We also thank the University of Valencia for research facilities (SCSIE).

Notes and references

1. R. E. Morris and L. Brammer, Chem. Soc. Rev., 2017, 46, 5444–5462.
2. G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399.
3. S. K. Elsaidi, M. H. Mohamed, D. Banerjee and P. K. Thallapally, Coord. Chem. Rev., 2018, 358, 125–152.
4. J. H. Lee, S. Jeoung, Y. G. Chung and H. R. Moon, Coord. Chem. Rev., 2019, 389, 161–188.
5. N. Li, J. Pang, F. Lang and X. H. Bu, Acc. Chem. Res., 2024, 57, 2279–2292.
6. S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F. X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352.
7. S. Ehrling, E. M. Reynolds, V. Bon, I. Senkovska, T. E. Gorelik, J. D. Evans, M. Rauche, M. Mendt, M. S. Weiss, A. Pöppl, E. Brunner, U. Kaiser, A. L. Goodwin and S. Kaskel, Nat. Chem., 2021, 13, 568–574.
8. I. Senkovska, V. Bon, L. Abylgazina, M. Mendt, J. Berger, G. Kieslich, P. Petkov, J. L. Fiorio, J.-O. Joswig, T. Heine, L. Schaper, C. Bachetzky, R. Schmid, R. A. Fischer, A. Pöppl, E. Brunner and S. Kaskel, Angew. Chem., Int. Ed., 2023, 62, e202218076.
9. Z. Liu, L. Zhang and D. Sun, Chem. Commun., 2020, 56, 9416–9432.
10. C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526.
11. E. J. Carrington, C. A. McAnally, A. J. Fletcher, S. P. Thompson, M. Warren and L. Brammer, Nat. Chem., 2017, 9, 882–889.
12. C. Mellot-Draznieks, C. Serre, S. Surblé, N. Audebrand and G. Férey, J. Am. Chem. Soc., 2005, 127, 16273–16278.
13. D. Fairen-Jimenez, S. A. Moggach, M. T. Wharmby, P. A. Wright, S. Parsons and T. Düren, J. Am. Chem. Soc., 2011, 133, 8900–8902.
14. M. E. Casco, Y. Q. Cheng, L. L. Daemen, D. Fairen-Jimenez, E. V. Ramos-Fernández, A. J. Ramirez-Cuesta and J. Silvestre-Albero, Chem. Commun., 2016, 52, 3639–3642.
15. J. Seo, R. Matsuda, H. Sakamoto, C. Bonneau and S. Kitagawa, J. Am. Chem. Soc., 2009, 131, 12792–12800.
16. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
17. M. Souto, J. Romero, J. Calbo, I. J. Vitórica-Yrezábal, J. L. Zafra, J. Casado, E. Ortí, A. Walsh and G. Mínguez Espallargas, J. Am. Chem. Soc., 2018, 140, 10562–10569.
18. N. Monni, J. J. Baldoví, V. García-López, M. Oggianu, E. Cadoni, F. Quochi, M. Clemente-León, M. L. Mercuri and E. Coronado, Chem. Sci., 2022, 13, 7419.
19. J. Zhang, W. Kosaka, Y. Kitagawa and H. Miyasaka, Nat. Chem., 2021, 13, 191–199.
20. H. Miyasaka, N. Motokawa, S. Matsunaga, M. Yamashita, K. Sugimoto, T. Mori, N. Toyota and K. R. Dunbar, J. Am. Chem. Soc., 2010, 132, 1532–1544.
21. J. J. Baldoví, E. Coronado, A. Gaita-Ariño, C. Gamer, M. Giménez-Marqués and G. Mínguez Espallargas, Chem.–Eur. J., 2014, 20, 10695–10702.
22. J. Castells-Gil, J. J. Baldoví, C. Martí-Gastaldo and G. Mínguez Espallargas, Dalton Trans., 2018, 47, 14734–14740.
23. M. L. Mortensen, S. Bisht, M. Abbas, H. Firouzi, G. T. McCandless, M. Shatruk and K. J. Balkus, Inorg. Chem., 2024, 63, 219–228.
24. J. M. Van Raden, D. I. Alexandropoulos, M. Slota, S. Sopp, T. Matsuno, A. L. Thompson, H. Isobe, H. L. Anderson and L. Bogani, J. Am. Chem. Soc., 2022, 144, 8693–8706.
25. A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309.
26. J. López-Cabrelles, L. Escalera-Moreno, Z. Hu, H. Prima-García, G. Mínguez Espallargas, A. Gaita-Ariño and E. Coronado, Inorg. Chem., 2021, 60, 8575–8580.
27. E. Coronado and G. Mínguez Espallargas, Chem. Soc. Rev., 2013, 42, 1525–1539.
28. G. Mínguez Espallargas and E. Coronado, Chem. Soc. Rev., 2018, 47, 533–557.
29. E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104.
30. A. E. Thorarinsdottir and T. D. Harris, Chem. Rev., 2020, 120, 8716–8789.
31. S. M. Hyun, J. H. Lee, G. Y. Jung, Y. K. Kim, T. K. Kim, S. Jeoung, S. K. Kwak, D. Moon and H. R. Moon, Inorg. Chem., 2016, 55, 1920–1925.
32. T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M. E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 12090–12101.
33. M. Wakizaka, S. Gupta, Q. Wan, S. Takaishi, H. Noro, K. Sato and M. Yamashita, Chem.–Eur. J., 2024, 30, e202304202.
34. C. J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, Chem. Sci., 2019, 10, 1702–1708.
35. L. Vujević, B. Karadeniz, N. Cindro, A. Krajnc, G. Mali, M. Mazaj, S. M. Avdoshenko, A. A. Popov, D. Žilić, K. Užarević and M. Kveder, Chem. Sci., 2023, 14, 9389–9399.
36. A. Urtizberea, E. Natividad, P. J. Alonso, M. A. Andrés, I. Gascón, M. Goldmann and O. Roubeau, Adv. Funct. Mater., 2018, 28, 1801695.
37. G. Handzlik, M. Magott, M. Arczyński, A. M. Sheveleva, F. Tuna, M. Sarewicz, A. Osyczka, M. Rams, V. Vieru, L. F. Chibotaru and D. Pinkowicz, J. Phys. Chem. Lett., 2020, 11, 1508–1515.
38. M. J. Martínez-Pérez, S. Cardona-Serra, C. Schlegel, F. Moro, P. J. Alonso, H. Prima-García, J. M. Clemente-Juan, M. Evangelisti, A. Gaita-Ariño, J. Sesé, J. Van Slageren, E. Coronado and F. Luis, Phys. Rev. Lett., 2012, 108, 247213.
39. J. Zhang, L. Liu, C. Zheng, W. Li, C. Wang and T. Wang, Nat. Commun., 2023, 14, 4922.
40. A. Yamauchi and N. Yanai, Acc. Chem. Res., 2024, 57, 2963–2972.

---

Footnotes

† Dedicated to Professor Marius Andruh on the occasion of his 70th birthday.

‡ Electronic supplementary information (ESI) available: Experimental methods, detailed crystallographic data and supporting characterisation. CCDC 2384447–2384455. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc07042a

§ These authors contributed equally.

---