Electrostatically tuning radical addition and atom abstraction reactions with distonic radical ions

Abstract

Although electrostatic catalysis can enhance the kinetics and selectivity of reactions to produce greener synthetic processes, the highly directional nature of electrostatic interactions has limited widespread application. In this study, the influence of oriented electric fields (OEF) on radical addition and atom abstraction reactions are systematically explored with ion-trap mass spectrometry using structurally diverse distonic radical ions that maintain spatially separated charge and radical moieties. When installed on rigid molecular scaffolds, charged functional groups lock the magnitude and orientation of the internal electric field with respect to the radical site, creating an OEF which tunes the reactivity across the set of gas-phase carbon-centred radical reactions. In the first case, OEFs predictably accelerate and decelerate the rate of molecular oxygen addition to substituted phenyl, adamantyl, and cubyl radicals, depending on the polarity of the charged functional group and dipole orientation. In the second case, OEFs modulate competition between chlorine and hydrogen atom abstraction from chloroform based on interactions between charge polarity, dipole orientation, and radical polarizability. Importantly, this means the same charge polarity can induce different changes to reaction selectivity. Quantum chemical calculations of these reactions with DSD-PBEP86-D3(BJ)/aug-cc-pVTZ show correlations between the barrier heights and the experimentally determined reaction kinetics. Field effects are consistent between phenyl and cubyl scaffolds, pointing to through-space rather than through-bond field effects, congruent with computations showing that the same effects can be mimicked by point charges. These results experimentally demonstrate how internal OEFs generated by carefully placed charged functional groups can systematically control radical reactions.

---

Introduction

Electrostatic reaction catalysis is a relatively new, but rapidly growing, field in molecular chemistry.^1–9 Early investigations in this field were inspired by nature, where charged residues in the non-polar pockets of enzyme active sites induce oriented electric fields (OEF) to activate complexes for catalytic activity.^10–14 In one such example, Boxer and co-workers used Stark spectroscopy to show that an extended hydrogen-bonding network in the ketosteroid isomerase active site composed of a tyrosine triad and aspartic acid residue exert an electric field strength of 14.4(6) V nm⁻¹ onto the carbonyl moiety of the sterol substrate.^15,16 This OEF opposes the larger dipole moment along the C–O bond axis during enolization and thus selectively stabilises the rate-determining transition state (TS). Viewed though valence bond theory,^2,3,17 the OEF enhances the stability of an ionic resonance structure of the TS during enolate formation, increasing its polarity and hence electrostatic stabilization. The presence of the OEF was estimated to account for 72% of the total catalytic effect of the enzyme during enolization of 5-androstene-3,17-dione.^11,15 OEFs are also implicated in water droplets,^18–20 where increased proton concentrations at the surface of micron sized droplets are suspected to instigate spontaneous oxidation of organic molecules and catalyse reactions.^21–24

Recent landmark theoretical and experimental studies show that OEFs can alter product selectivity and control reactivity under single molecule conditions, which could ultimately lead to greener, more atom-economic reactions.^25–28 Aragonés et al. demonstrated electrostatic catalysis of a Diels–Alder reaction by tethering dienes to a scanning tunnelling microscopy tip and dienophiles to a gold surface to orient the electric field with respect to the reactants,²⁵ validating earlier theoretical predictions by Shaik and co-workers.²⁸ However, their highly directional nature makes electrostatic effects difficult to reliably harness in bulk conditions, where molecules are typically unaligned, and remains a major obstacle for large-scale industrial adoption. Additionally, the strength of the electric field diminishes rapidly from the external source due to ionic and/or solvent screening,¹⁰ whilst also being susceptible to dielectric breakdown of solvents when externally applied fields have strengths of 0.01–0.1 V nm⁻¹.⁵ Although research is underway to overcome this limitation by controlling the orientation of molecules in bulk conditions,^29–31 or through interfacial electric fields,^32–34 alternative strategies have emerged. Species with charged functional groups or noncovalently bound metal ions sidestep these experimental challenges by locking the position of charge on a molecule, which maintains the same internal OEF in close proximity to the reaction centre.^35,36 For example, a cationic ammonium substituent at the ortho-position of the phenyl rings in an iron tetraphenylporphyrin complex decreased catalytic overpotential and increased turnover frequencies for carbon dioxide reduction, whilst the opposite was observed for anionic groups or when the substituent was at the para-position.³⁷ OEFs can also have unexpected consequences on reactivity, such as with SOMO–HOMO conversion, where covalent bond energies have been shown to significantly decrease when a remote negatively-charged functional group is introduced.^38–41 Though previous studies have attempted to quantify the effects of OEFs on chemical reactions using theoretical methods,^42–44 further advances in the field of electrostatic catalysis require the careful benchmarking of computational methods against a broader suite of experimental measurements.

Distonic radical ions – species with spatially separated charge and radical moieties on the same molecule – contain an internal OEF which influences the reactivity of the radical site.^45–48 Since the first experimental detection of distonic radical ions,^49–51 studies have attempted to unravel the interplay between the charge and radical sites of these molecules, although it was not until the first synthesis of a rigid distonic radical ion in the 1990s that these effects could be systematically examined.^52,53 Growing evidence, using such rigid scaffolds, suggests that the charged moiety primarily modulates the reactivity of distonic radical ions via through-space (electrostatic) interactions.^27,54–56 Distonic radical ions are often highly reactive and so are difficult to study using typical solution-phase methodologies. Fortunately, however, the charged moiety on these species allows for their preparation, isolation, storage, and characterisation in the gas phase using mass spectrometers.^57–59 Various methods for generating distonic radical ions have been developed, including collision-induced dissociation and photodissociation from halogenated precursors,^{45,52,60–66} which allow for the systematic synthesis of rigid distonic radical ions with carefully controlled internal OEFs. Moreover, precise kinetics can be readily measured for a range of distonic radical ion–molecule reactions by synthesising and isolating these species within the controlled chemical environment of the high-vacuum region of a mass spectrometer, providing a readout of the effect of the internal OEF on radical reactivity in the absence of solvent.

Here we utilise this distonic radical ion approach with an ion-trap mass spectrometer in conjunction with high-level double-hybrid quantum chemical calculations to measure the impact of OEFs on two radical reactions: (1) radical addition to dioxygen and (2) hydrogen- and chlorine-atom abstraction from chloroform. These results demonstrate how charged functional groups can control gas-phase radical reactions in a predictable and tuneable manner by creating an internal OEF that alters the rate-limiting TS. The rigid separation and well-defined orientation between charge and radical sites is enforced with novel precursors based on substituted benzene and the rigid three-dimensional cage structures of adamantane and cubane. The isosteric relationship between 1,4-substituted benzenes and saturated cubanes validates the through-space (electrostatic) nature of these charge interactions.

Methods

Computational methods

Electronic structure calculations were performed using Gaussian 16, revision C.01.⁶⁷ For oxygen reactions, relaxed potential energy scans were performed along the dissociating C–O bond lengths using the DSD-PBEP86-D3(BJ)/aug-cc-pVDZ functional and basis set.^68–71 Geometry optimisations for the pre-reactive complex, O₂ adduct, and the key TS were calculated at the DSD-PBEP86-D3(BJ)/aug-cc-pVDZ level of theory and, unless otherwise stated, single point energy calculations using a triple zeta basis set (i.e., DSD-PBEP86-D3(BJ)/aug-cc-pVTZ) obtained the electronic energies for these structures. For the chloroform reactions, geometry optimisations and single-point energy calculations utilised the DSD-PBEP86-D3(BJ)/aug-cc-pVDZ functional and basis set. The DSD-PBEP86-D3(BJ) double-hybrid functional has been designed to account for long-range interactions, such as those present in pre-reactive complexes, to provide accurate energies for these structures by including both an empirical dispersion correction and SCS-MP2 correlation.⁷² Similar methods (DSD-PBEPBE-D3/aug-cc-pVTZ) have been shown to be robust for accurate geometries and energies in electric fields.⁷³ Minima were assigned as stationary points with no imaginary frequencies, while transition states were assigned as stationary points with exactly one imaginary frequency. All energies include the unscaled zero-point energy correction and are reported in kJ mol⁻¹. Electrostatic field strength calculations were performed with the QUANT package from the TITAN python code.⁷⁴ Optimised geometries and electron densities for these calculations were obtained from the electronic structure calculations described above.

Materials and synthesis of radical precursors

Radical precursors 4-iodoaniline (Sigma-Aldrich, 98%), 2-fluoro-4-iodoaniline (Sigma-Aldrich, 98%), 4-iodo-2-methylaniline (Sigma-Aldrich, 97%), 4-iodo-2-methoxyaniline (Sigma-Aldrich, 97%), 2-amino-5-iodophenol (AK Scientific, 98%), 1,3-adamantane dicarboxylic acid (Sigma-Aldrich, 98%), and 1,4-benzene dicarboxylic acid (terephthalic acid, Sigma-Aldrich, 98%) were commercially available. We have previously reported the synthesis of 3-iodoadamantanecarboxylic acid by treatment of 3-hydroxyadamantane-carboxylic acid with aqueous HI,⁵⁵ and the same procedure was adapted for the synthesis of 4-iodoadamantane-1-amino hydroiodide, which was used without further purification ([M − I]⁺ calc. m/z 278.0400, found m/z 278.0405). Precursors 4-iodocubane-1-carboxylic acid (S4) and 4-iodocubane-1-amino hydrochloride (S6) were synthesised and characterised as detailed in the ESI.†

Ion–molecule reactions

Gas-phase distonic radical ion–molecule reactions were performed on a modified linear quadrupole ion-trap mass spectrometer (LTQ XL, Thermo Scientific, San Jose, CA) operating Xcalibur version 3.0 software and equipped with a heated electrospray ionisation (HESI) source described in detail elsewhere.^75,76 Methanol solutions containing 5–10 μM of radical precursors were directly infused at a rate of 5–10 μL min⁻¹ into the source. Target radical ions were then generated by photodissociation of precursors through homolytic C–I bond cleavage. Photodissociation (PD) experiments were performed on the same instrument that had been previously modified to allow optical access to the ion-trapping region.⁷⁷ Precursor ions were mass-selected using an isolation width of 1.0–2.0 Da and irradiated with a single pulse of 266 nm light from a Nd:YAG laser (Continuum Minilite II; ca. 4.5 mJ per pulse at 266 nm). The laser timing was triggered by the rising edge of a TTL pulse that coincided with the beginning of the activation stage of a MS² experiment. Normalised collision energy (NCE) was set to zero for PD experiments. Background air within the instrument provided a sufficient concentration of dioxygen to observe O₂ reactions. Although not explicitly controlled, the [O₂] remains constant over hour-long timescales which allows accurate reaction rates to be measured using a calibration reaction (vide infra).^61,63,76,78 For reactions with chloroform, a continuous flow of chloroform seeded in the helium buffer gas was supplied to the mass spectrometer using a custom-built gas-mixing manifold as previously described (Scheme S2†) and the [CHCl₃] determined using a calibration reaction (vide infra). The flow of helium was controlled by a chemically inert PEEKsil tube (50 μm I.D. × 100 mm; Trajan Scientific P/N 0624252), providing a pressure reading of 0.8–1.0 × 10⁻⁵ Torr on the instrument ion gauge, which indicates an ion-trap pressure of ∼2.5 mTorr,⁷⁷ previously experimentally determined to be 2.58 ± 0.13 mTorr.⁶³ The flow of chloroform gas, supplied from a liquid reservoir, was controlled by passing this gas through a separate, chemically inert PEEKsil tube (25 μm I.D. × 100 mm; Trajan Scientific P/N 0624226) before mixing with the helium gas supply prior to the mass spectrometer.

Further experiments to examine the pressure dependence of rate constant measurements of distonic radical ions with dioxygen were conducted in the low- (<1 mTorr) and high-pressure (5 mTorr) regions of a hybrid dual linear ion-trap mass spectrometer (LTQ Velos Orbitrap Elite, Thermo Scientific, San Jose, CA, USA). Methanol solutions containing 5–10 μM of dicarboxylate radical precursors, adjusted to pH 10 using aqueous ammonia,⁷⁹ were directly infused at a rate of 5–10 μL min⁻¹ into the HESI source. Precursor dianions were mass-selected and subjected to collision-induced dissociation in a MS² experiment to generate the singly charged radical anion via oxidative decarboxylation using a NCE of 25%.^63,64,80

Pseudo-first-order rate constants were obtained by recording a series of mass spectra as a function of storage time for each reaction between the radical ion and neutral reagent. The reaction time was defined as the interval between the isolation of the selected radical ion and ejection of all ions from the trap for detection. Reaction times of 5–10 000 ms were set using the activation time parameter within the instrument control software. For the reactions with both dioxygen and chloroform, there was significant charge-loss for the precursor adamantyl, cubyl and phenyl anions, likely due to electron transfer to dioxygen, and so the pseudo-first-order rate constants were determined in MS² experiments that were benchmarked against the relative abundance of iodide (m/z 127) formed during photoactivation as this was constant (Fig. S10, S11, S13, S14 and S15†). For the chloroform reactions, the product branching ratios, determined by the asymptote of a single exponential function fitted to the kinetic profile of the reaction, were also benchmarked against the relative abundance of iodide formed during photoactivation. In contrast, the cationic distonic radicals did not exhibit competing charge-loss chemistries and so kinetics were monitored following re-isolation of the reactant radical ions by conventional MS³ experiments.

Fitting the plot of the mean radical ion abundance against reaction time yielded the pseudo-first-order rate constant k₁ (Fig. S2–S6, S8–S11, S13–S18†). Second-order rate constants k₂ were obtained from k₁ and the concentration of dioxygen ([O₂]) or chloroform ([CHCl₃]) present in the ion-trap region of the mass spectrometer. The neutral reagent concentrations under each set of reaction conditions were determined from the calibration reactions of 3-dehydroadamantylcarboxylate radical anion⁶³ to be for [O₂] ca. 2–6 × 10¹⁰ molecules cm⁻³ (Fig. S11†) and for [CHCl₃] ca. 1–3 × 10¹² molecules cm⁻³ (Fig. S13†). Under these conditions, the concentration of neutral reagents is at least 10⁶ greater than the trapped ions, ensuring pseudo-first order conditions with respect to the radical ions.⁶³ The temperature of ions stored within a linear quadrupole ion-trap has been measured as 318 ± 23 K,⁸¹ in agreement with an earlier estimate of 307 ± 1 K,⁶³ which can be taken as the effective temperature for ion-molecule reactions observed herein. Reaction efficiencies, Φ (i.e., the percentage of ion–molecule collisions that resulted in product formation), were determined by dividing the second-order rate constant by the parameterised trajectory theory capture value for dioxygen (α = 1.562 ų, μ = 0 D) and chloroform (α = 8.129 ų, μ = 1.040 D) at 307 K.^82,83 The accuracy of the rate constants are estimated to be ±50% due to uncertainty in the neutral reactant number density in the ion trap. The precision of rate measurements recorded under identical experimental conditions is on the order of ±10% and thus enables confident comparison between reaction rates (vide infra).

Results and discussion

Electrostatic influence on radical addition to molecular oxygen

The neutral phenyl radical reaction with dioxygen has been used to explore the agreement between experimental rate constants and those predicted by theoretical modelling across various temperature and pressure regimes. Using a 4-point microcanonical Rice–Ramsperger–Kassel–Marcus master equation (RRKM-ME) model incorporating a pre-reactive complex (PRC), transition state (TS) and the phenylperoxyl radical intermediate, calculations using the double hybrid DSD-PBE86-D3(BJ) functional are able to replicate the lack of pressure dependence of this reaction in experiments (Fig. 1A).^84,85 This was attributed to the short lifetime of the PRC and the high exothermicity of the extensive RO₂˙ covalent surface that likely inhibits recrossing back to the PRC. Indeed, as demonstrated in previous studies for aromatic distonic radicals, the bimolecular kinetics are predominantly controlled by the transition state connecting the PRC to the covalent intermediate and there is a negligible effect on the modelled rate constant whether recrossing from the covalent intermediate to the PRC is operating or not.^27,45,46 Since the reaction coordinates of these systems are similar and the substrates generally rigid, the kinetics have been shown to correlate with the height of the forward TS relative to the energy of the separated reactants. Thus, the effect of an internal OEF on the relative height of the key TS in the neutral phenyl radical reaction with dioxygen, which involve the formation of the covalent carbon–oxygen bond, was initially explored.

Fig. 1 (A) Potential energy scheme showing the energies (in kJ mol⁻¹) of the rate-limiting TS for the neutral phenyl radical + O₂ addition (black),⁸⁴ and with a +1 e point charge (red) or −1 e point charge (blue) applied 4 Å away from the radical site relative to the neutral, separated reactants calculated at the DSD-PBEP86-D3(BJ)/aug-cc-pVTZ level of theory. (B) TS stationary point structures and TS dipole moments of phenyl radical + O₂ when (i) a +1 e point charge (indicated by a red dot) is applied 4 Å away from the radical site along the axis of the dipole moment, (ii) no point charge is applied, i.e. the neutral archetype, or (iii) a −1 e point charge (indicated by a blue dot) is applied at the same point. This is equivalent to an electric field strength of −9.9 V nm⁻¹ at the radical site. (C) The change in TS energy relative to the neutral TS induced by a fixed negative (blue) and positive (red) point charge placed 4 Å away from the radical site at different angles from the dipole moment. (D) The change in the TS energy relative to the neutral TS induced by a 0, 0.25, 0.5, 0.75, and 1 e negative (blue) and positive (red) electric field applied at different angles from the dipole moment axis. Note that the neutral TS was not re-optimized for any of the point charge (A–C) or electric field (D) calculations.

Fig. 1B shows the optimised geometry and dipole moment for the key transition state (TS) of the phenyl radical + O₂ reaction calculated using DSD-PBEP86-D3(BJ). The TS dipole for this reaction is aligned from the radical site to the para-position of the phenyl ring, which suggests that a charged functional group at this position will create an OEF with the maximum electrostatic impact on the energy of this TS. A favourable internal OEF aligned along this dipole (i.e., introducing a negatively charged functional group) should stabilise this TS by reducing the TS dipole moment which would, in turn, increase the reaction rate.⁵⁴ Placing a positively-charged functional group would instead be expected to increase this barrier and consequently decrease the reaction rate. Computationally this can be modelled by placing a point charge near the optimised, neutral TS structure along the axis of the dipole moment. In our case we have achieved this by placing a (i) +1 e, (ii) zero, and (iii) −1 e point charge at the para-position of the optimised TS for the phenyl + O₂ reaction (Fig. 1B). The charge was positioned 4 Å away from the radical site; a distance similar to the charge-radical distance in 4-dehydroanilinium (4.17 Å). So positioned, the point charge generates an internal electric field strength of −9.9 V nm⁻¹ at the radical site, nearly ten times larger than the external electric field strength modelled in prior solution-phase electrostatic catalysis studies due to the closer proximity of the radical and charged moiety.²⁵ Comparing these three structures, the TS dipole moment increases in magnitude with a positive charge leading to a relatively higher TS (+2.2 kJ mol⁻¹) and decreases in magnitude with a negative charge leading to a relatively lower TS (−8.8 kJ mol⁻¹) compared to the neutral system (−1.6 kJ mol⁻¹) as expected (Fig. 1A and B). Although (de)stabilisation will be greatest along the dipole, changing the angle of the OEF with respect to the dipole moment will also induce a smaller (de)stabilisation effect.

The change in energy of this TS relative to the TS of the neutral reaction as a function of angle for a +1 e and a −1 e point charge is included in Fig. 1C. In this plot, 0° corresponds to a point charged aligned with the axis of the dipole moment, i.e., at the para-position of the phenyl radical. This shows that the effect of the OEF is maximised along the axis of the dipole moment and changes as a function of angle. This plot is symmetric for the positive and negative point charge which indicates that the effect of a negatively charged OEF can be replicated by an equal magnitude positively charged OEF placed at the same distance from the radical centre in the opposite direction within the molecule. Additionally, due to the polarizability of this TS, the destabilisation of this barrier is smaller in magnitude than stabilisation. This asymmetric effect has been observed in previous studies.^54,86–88 This suggests that when the polarizability of the TS is larger than the reactants it is more challenging to electrostatically reduce reactivity rather than enhance it. Fig. 1D shows the relative change in TS energy as a function of the angle of the OEF with different electrostatic field strengths. In this plot the change in TS energy decreases as the field strength decreases. Thus, by introducing a more (or less) localised charged functional group the magnitude of stabilisation or destabilisation will increase (or decrease). These results suggest that the kinetics of radical addition to dioxygen could be systematically tuned by modifying the orientation and functionality of charged functional groups placed around the radical site.

Three experimental constructs were deployed to investigate the influence of electric field strength and orientation on radical addition to dioxygen. Namely: (i) variation of the charge carrying group; (ii) incorporation of electron-withdrawing and -donating moieties; and (iii) comparison with distonic radical ions generated from rigid adamantane and cubane cages. The structural space explored across these constructs is summarised in Scheme 1, where TS structures were optimised for the radical addition to oxygen to compare with experimentally determined reaction kinetics. These comparisons include five previously published distonic radical ion oxidation reaction rates^63,76,79 and eight additional reactions measured here for the first time (Table 1). Representative mass spectra (Fig. S1 and S7†) and kinetic profiles (Fig. S2–S6 and S8–S11†) for these newly reported reactions between O₂ and the conjugated radical cations (4-dehydroanilinium 3, 2-fluoro-4-dehydroanilinium 4, 2-methyl-4-dehydroanilinium 5, 2-hydroxy-4-dehydroanilinium 6, and 2-methoxy-4-dehydroanilinium 7 ions), and the non-conjugated radical ions (4-dehydrocubylammonium 1, 3-dehydroadamantylammonium 2, 4-dehydrocubylcarboxylate 9 ions) can be found in the ESI† (as well as the titration reaction between O₂ and 3-dehydroadamantylcarboxylate anion 10). These reactions include both dioxygen addition to give the peroxyl radical as the major product ion (e.g., reactions 2–6 and 10) and addition–elimination reactions that include products such as phenoxyl radicals formed via the peroxyl radical intermediate (e.g., reactions 1, 7, 8, and 11–13).^76,79

Scheme 1 Structures of the distonic radical ions and neutral radicals used in this study. Distonic radical + O₂ reactions are numbered while labels refer to distonic radical + CHCl₃ reactions.

Table 1 Second-order rate constants, reaction efficiencies and relative transition state energies for reaction of neutral phenyl radical and distonic radical ions with dioxygen

Radical	Rate constant k2^a (cm^3 molecule^−1 s^−1)	Reaction efficiency^b (%)	TS energy (kJ mol^−1)	Reaction number
a Errors represent 2σ of the fitted kinetic profile for newly reported rate constants. b For ion-molecule reactions, literature reaction efficiencies were recalculated for consistency. c Consumption of the precursor ion (5.7 ± 2.0) × 10^−11 cm^3 molecule−1 s^−1 multiplied by a branching fraction of 0.35 obtained from the asymptote of peroxyl product formation to remove contributions from side reactions (see Fig. S9). d The electronic energy for this reaction is calculated at the DSD-PBEP86-D3(BJ)/aug-cc-pVDZ level of theory, though this is expected to have minimal impact on the accuracy of the relative TS energies (see Table S3).
Phenyl radical^85,93,94	(1.2–1.8) × 10^−11	5 ± 1	−1.7	a
4-Dehydrocubylammonium cation	(2.0 ± 0.2) × 10^−11	3.6 ± 0.4	+5.8	1
3-Dehydroadamantylammonium cation	(2.0 ± 0.7) × 10^−11^c	3.5 ± 1.2	+4.8^d	2
4-Dehydroanilinium cation	(2.4 ± 0.1) × 10 ^−11	4.0 ± 0.2	+1.4	3
2-Fluoro-4-dehydroanilinium cation	(2.7 ± 0.1) × 10 ^−11	4.6 ± 0.2	+1.0	4
2-Methyl-4-dehydroanilinium cation	(2.9 ± 0.2) × 10 ^−11	4.9 ± 0.3	−0.1	5
2-Hydroxy-4-dehydroanilinium cation	(2.5 ± 0.1) × 10^−11	4.3 ± 0.2	+1.2	6
2-Methoxy-4-dehydroanilinium cation	(5.8 ± 0.3) × 10 ^−11	10.0 ± 0.5	−5.5	7
4-Dehydro-N,N,N-trimethylanilinium cation^76	(3.6 ± 0.6) × 10 ^−11	6.3 ± 1.0	+1.4	8
4-Dehydrocubylcarboxylate anion	(11.3 ± 1.1) × 10^−11	19.8 ± 1.9	−8.3	9
3-Dehydroadamantylcarboxylate anion^63	(8.5 ± 0.4) × 10^−11	15.1 ± 0.7	−15.9^d	10
4-Dehydrophenylcarboxylate anion^79	(5.4 ± 0.2) × 10^−11	9.3 ± 0.3	−6.7	11
4-Dehydrotrifluoroboratophenyl anion^76	(5.6 ± 0.6) × 10 ^−11	9.8 ± 1.0	−9.4	12
4-Dehydrosulfonatophenyl anion^79	(4.2 ± 0.4) × 10^−11	7.4 ± 0.7	−5.6	13

---

At these trap pressures (ca. 2.5 mTorr), collisions with the helium buffer gas occur on the order of every 10 μs and the species on the covalent-addition surface can have sufficiently long lifetimes to be stabilised by buffer gas collisions and detected, as observed during prior investigations of similar reaction systems using ion-trap mass spectrometry.^45,89–91 However, the experimentally determined second-order rate constants measured and subsequent reaction efficiencies are reflective of the intrinsic reactivity of these radicals –through a common pre-reactive complex– not collisional cooling efficiency. This has been demonstrated by some of us in a recent paper on the rates for addition reactions of distonic radical ions measured in ion-trap mass spectrometers being well-predicted using statistical rate theory (RRKM) within the low pressure regime, which would not hold were the measurements a reflection of collisional cooling efficiency.⁴⁵ Indeed, this supports the model that the lifetime of the PRC is considerably shorter than the buffer gas collision rate and thus the rate constant is dependent on the height of the covalent bond-forming TS following the PRC (vide supra). Further, prior work has shown that lifetimes of covalent reaction intermediates following this rate-limiting TS can be significantly longer than the buffer gas collision rate, particularly for large systems and/or those with significant resonance stabilization, allowing for their effective detection by ion-trap mass spectrometry.⁹² To provide further support for the reliability of the relative rate constants across different pressure regimes, we repeated measurements of a representative addition (reaction 10, O₂C-Ad˙ + O₂) and addition–elimination (reaction 11, O₂C-Ph˙ + O₂) reaction on a different mass spectrometer operating linear ion-traps at two different helium gas pressure regimes and obtained the same relative pseudo-first order reaction rate constants as provided in Table 1 within error (see Table S1†). The relative electronic energy of the TS for each distonic radical ion + O₂ reaction 1–13 is calculated at the DSD-PBEP86-D3(BJ)/aug-cc-pVTZ level of theory (Table 1) to compare with the relative TS energies of the six neutral phenyl radicals (a–f) with O₂ (Table S2†).

Charge carrier variations

Fig. 2A plots the calculated TS barrier energy against the experimental reaction efficiency for the thirteen distonic radical ion oxidation reactions 1–13, where blue diamonds represent anionic radicals and red diamonds represent cationic radicals. The single black data point is the neutral phenyl radical + O₂ reaction and the error bar for this reaction represents the difference in the room-temperature second-order rate constant determined by the three available experimental datasets at 300 K, noting that this reaction was determined to be pressure independent over a pressure range of 30–760 Torr.^85,93,94 Thirteen of these fourteen data points demonstrate a linear increase in reaction efficiency with a lowering of the computed TS energy for peroxyl radical formation, including for both stabilized addition and addition–elimination reactions (vide supra). Interestingly, the 4-dehydrocubylcarboxylate anion 9 appears as an outlier to this linear trend and is discussed further below. Linear regression analysis of the remaining thirteen data points returns a strong correlation between the computed peroxyl-radical forming TS and the reaction kinetics (R² = 0.91). This trend is consistent with previous systematic studies on distonic radical ion-molecule addition reactions with other, non-polar neutral reagents, namely, acetylene and ethylene.^46,47 In Fig. 2A, all anionic radical reactions are faster than the neutral phenyl + O₂ reaction, and all cationic reactions – except for one outlier (2-methoxy-4-dehydroanilinium 7) – are within error or slower than neutral phenyl, in agreement with the calculations from Fig. 1. The rationale for the position of 7 on the trend line was explored by examining the transition state dipole moments of these reactions and is discussed in the next section.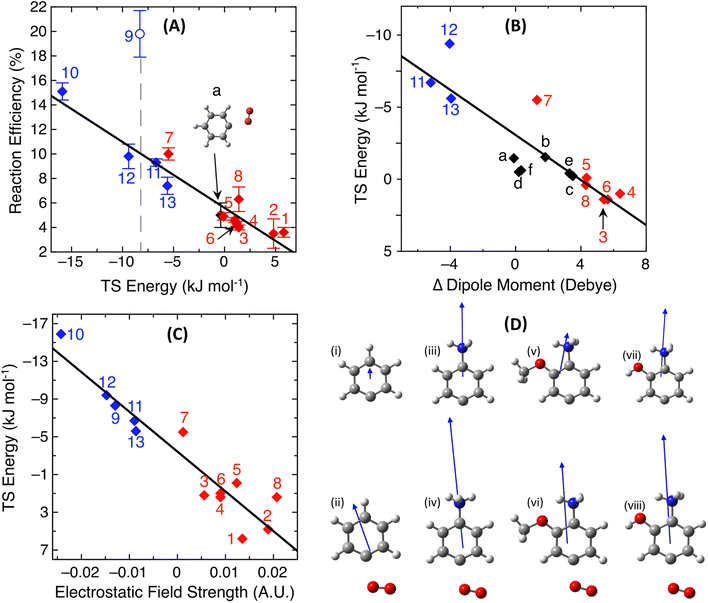

Fig. 2 (A) Correlation plot showing the experimental reaction efficiency against the energy of the key TS for a range of room temperature reactions of oxygen with distonic radical anions (blue diamonds), distonic radical cations (red diamonds) and the neutral phenyl radical (black diamond), R² = 0.91. The outlier 4-dehydrocubylcarboxylate radical anion 9 (blue circle) has been excluded from the linear fit. (B) Correlation plot between the energy of the TS and the magnitude of change between the ground state and the transition state dipole moment for a range of phenyl-type distonic radical and neutral oxidation reactions, R² = 0.76. Black diamonds represent a range of calculated substituted neutral phenyl radical + O₂ reactions as seen in Scheme 1. Data points for the reactions d and f are on top of one another. (C) Correlation plot between the TS energy against the electrostatic field strength at the radical site for each distonic radical ion calculated using the TITAN code, R² = 0.89. (D) The optimised structure and dipole moment of (i) phenyl, (ii) TS of phenyl a, (iii) 4-dehydroanilinium, (iv) TS of 4-dehydroanilinium 3, (v) 2-methoxy-4-dehydroanilinium, (vi) TS of 2-methoxy-4-dehydroanilinium 7, (vii) 2-hydroxy-4-dehydroanilinium, and (viii) TS of 2-hydroxy-4-dehydroanilinium 6.

The 4-dehydrocubylcarboxylate anion 9 (blue circle) had a measured reaction efficiency of +19.7%, which is much larger than the ∼10% efficiency predicted based on the computed −8.3 kJ mol⁻¹ TS energy and correlation with the other thirteen peroxyl-forming reactions in the set (Fig. 2A). Close examination of the experimental reaction kinetics for the 4-dehydrocubylcarboxylate radical anion with O₂ reveal that, in contrast to the other distonic radical anions,^63,76,79 no ionic products consistent with oxidation via a peroxyl radical intermediate were observed (Fig. S7†). Instead, the predominant reaction channel leading to the decay of the reactant is either direct charge loss by electron transfer or fragmentation to low m/z product ions below the low mass cut-off of the ion-trap mass spectrometer. The high efficiency of this reaction and its deviation from the correlation in Fig. 2A supports the hypothesis that the reaction likely does not proceed via a peroxyl-radical intermediate –or at least not via the transition state located– but rather an alternative pathway (see Scheme S1†). While the precise reaction pathway undertaken by 4-dehydrocubylcarboxylate anion 9 in the presence of oxygen is beyond the scope of the current work, the semi-empirical trend established herein was able to clearly identify a deviation from the reaction pathway that would have been assumed based on experiment or theory alone.

Substitution effects

Fig. 2B shows the correlation plot between the calculated TS energy and the difference in dipole moment between the ground state and TS structures for the phenyl-type distonic radical oxidation reactions 3–8 and 11–13 (red and blue diamonds) and a range of neutral aromatic radical oxidation reactions a–f (black diamonds, Table S2†) outlined in Scheme 1. Inserting a functional group adjacent to the para-position shifts the angle of the transition state dipole which reduces the magnitude of (de)stabilising interactions. This explains why the substituted anilinium radical cations 3–8 are situated on or above the trendline in Fig. 2B as these dipole moments are aligned off-axis from the destabilising positive ammonium moiety. The reactivity of the 2-methoxy-4-dehydroanilinium radical cation 7 can also be explained by these substitution effects. As seen in Fig. 2D, the methoxy functional group shifts the dipole moment of the distonic radical ion significantly more off axis compared to 4-dehydroanilinium 3 and 2-hydroxy-4-dehydroaniliminium 6, which subsequently reduces the magnitude of the change in the dipole moment at the TS compared to the neutral phenyl radical. Thus, the methoxy substituent induces a stabilising effect rather than a destabilising effect from the internal positive charge.

Despite maintaining close to the same distance between the radical site and charged functional group with no subsequent change to the angle of the dipole moment, the rate of oxidation fluctuates between the three phenyl-type distonic radical anions (11–13). For these reactions, the variation in the rate of oxidation is attributed to changes in charge density, which consequently alters the electrostatic field strength at the radical site for each reaction. To probe this further, the magnitude of the electrostatic field strength induced by each charged functional group has been calculated using the TITAN code.⁷⁴Fig. 2C shows the correlation plot between the barrier height and the calculated OEF strength calculated along the axis of the dipole 0.1 Å away from the radical site for each distonic radical ion using TITAN. A general correlation is observed between the TS energy and the electrostatic field strength calculated at the radical site (R² = 0.89). This is expected as this calculation only includes electrostatic interactions and thus is a more simplistic model of this interaction compared to the TS energies. Nevertheless, across the three substituted phenyl radical anions, the induced field strength ranges from 12 > 11 > 13 in agreement with the experimentally measured rates of reaction (Table 1). These calculations indicate changes in charge localisation control the reactivity of these radical anions.

Comparisons of conjugated and nonconjugated systems

The reactions of O₂ with the conjugated phenyl radical cation 3 and anion 11 are compared here to the non-conjugated cubyl radical cation 1 and anion 9. Although the experiments reveal that oxygen addition is not observed for the cubyl radical anion 9 (see Fig. S7†), inspection of the computed pathway via the peroxyl-radical forming TS is instructive for comparison to the phenyl radical anion isosteres. The calculated charged moiety-radical distance of 4-dehydroanilinium 3 is 4.17 Å, which is close to the charged moiety-radical distance of 4-dehydrocubylammonium 1 (4.11 Å) (Fig. 3A). The same is true for the analogous separations in anionic 4-dehydrophenylcarboxylate 11 (4.19 Å) and 4-dehydrocubylcarboxylate 9 (4.30 Å). Thus, although the cubyl radicals are saturated and cannot exhibit significant through-bond stabilisation, the electrostatic field induced at the radical sites will be relatively similar between the two sets of phenyl and cubyl type radicals. As such, if (de)stabilisation of the TS occurs primarily via a through-space effect for these systems, rather than through-bond, the TS will be similar across both phenyl and cubyl radicals. If on the other hand (de)stabilisation occurs primarily via through-bond effects, the TS of the cubyl radicals will approach the TS energy of the neutral phenyl radical. As summarised in Fig. 3B, the calculated TS of 4-dehydrophenylcarboxylate 11 (−6.7 kJ mol⁻¹) is close to the calculated TS of 4-dehydrocubylcarboxylate 9 (−8.3 kJ mol⁻¹). The TS of 4-dehydroanilinium 3 and 4-dehydrocubylammonium 1 lie further apart (+1.4 kJ mol⁻¹, +5.8 kJ mol⁻¹). Crucially, however, the cubyl type radical is more destabilised compared to the phenyl type radical in this case. This difference can be explained in part based on the significantly higher dipole moment of 4-dehydrocubylammonium compared to 4-dehydroanilinium (9.1 D vs. 7.8 D) which suggests that the charge density, and thus the electrostatic destabilisation, is larger for the cubyl type radical.

Fig. 3 (A) Optimised structures and dipole moments of (i) phenyl, (ii) TS of phenyl a, (iii) 4-dehydroanilinium, (iv) TS of 4-dehydroanilinium 3, (v) 4-dehydrocubylammonium, (vi) TS of 4-dehydrocubylammonium 1, (vii) 3-dehydroadamantylammonium, (viii) 3-dehydroadamantylammonium 2, (ix) 4-dehydrophenylcarboxylate, (x) TS of 4-dehydrophenylcarboxylate 11, (xi) 4-dehydrocubylcarboxylate, (xii) TS 4-dehydrocubylcarboxylate 9, (xiii) 3-dehydroadamantylcarboxylate, and (xiv) 3-dehydroadamantylcarboxylate 10. Charged moiety–radical and C–O distances are provided for each separated radical and TS, respectively. (B) Changes to the TS for oxygen addition to phenyl (solid lines), cubyl (dashed lines) and adamantyl (dotted lines) radicals caused by cationic (red) and anionic (blue) charged functional groups. All energies are in kJ mol⁻¹.

While 3-dehydroadamantylcarboxylate anion 10 reacts with O₂ to give a dioxygen adduct (Fig. S7†), the analogous 4-dehydrocubylcarboxylate anion 9 is found experimentally to undergo more efficient competing chemistries leading to undetected neutral products (vide supra). The difference between the two bridgehead systems is likely a result of (i) increased ring-strain of the cubyl radical compared to the adamantyl radical and (ii) the co-linearity of the charge and radical in the cube facilitating orbital overlap that is minimised in the adamantane scaffold.⁹⁵ Nevertheless, the calculations predict a larger stabilisation of the TS for 3-dehydroadamantylcarboxylate 10 (−15.9 kJ mol⁻¹) compared to 4-dehydrocubylcarboxylate 9 (−8.3 kJ mol⁻¹). Like the cubyl radical, the adamantyl radical is saturated so this difference in the TS energies must originate from changes to through-space stabilisation. However, the dipole moment points off axis for the adamantyl radical, which makes it difficult to compare directly with the phenyl and cubyl radical systems which are symmetric. Additionally, though this comparison is further hampered by the slightly smaller aug-cc-pVDZ basis set used to calculate the adamantyl radical, this is expected to have minimal impact on the accuracy of the relative TS energies (see Table S3†). Nevertheless, this lower TS for oxidation of the adamantyl anion 10 is likely caused by a combination of the reduced charged functional group–radical distance (3.7 Å in the 3-dehydroadamantylcarboxylate anion 10vs. 4.3 Å in the 4-dehydrocubylcarboxylate 9) and the increased polarizability of the adamantyl radical (Fig. 3A). In contrast, this increased polarizability helps negate the impact of the closer cationic charged functional group, reducing the destabilisation of the TS for 3-dehydroadamantylammonium 2 compared to 4-dehydrocubylammonium 1 (+4.8 kJ mol⁻¹ and +5.8 kJ mol⁻¹), such that the reaction efficiencies are similar for these two cationic reactions within experimental uncertainty (Table 1).

Electrostatic influence on radical atom abstraction reactions

In contrast to molecular oxygen, chloroform has a permanent dipole moment (1.040 D)⁹⁶ which suggests that electrostatic interactions will be more significant, since there is a second dipole which can now interact with the OEF. Scheme 1 depicts the nine radicals for which the H-atom transfer (HAT) and Cl-atom transfer (CAT) reactions were examined. The anionic and cationic radical ions correspond to replacing a hydrogen of the phenyl, adamantyl, and cubyl radical with either a carboxylate or ammonium charged functional group. One key difference between these three radicals is polarization which increases from phenyl (70.4 a.u.) to cubyl (78.2 a.u.) to adamantyl (125.5 a.u.) at the DSD-PBEP86-D3(BJ)/aug-cc-pVDZ level of theory. The optimised structure and TS dipole for the neutral cubyl HAT and CAT reactions with chloroform are included in Fig. 3. For the HAT reaction the dipole points directly away from the radical site whereas the dipole for the CAT reaction points off axis due to the orientation of the chloroform molecule. Like the oxidation reactions above, a charged functional group introduced along the axis of the TS dipole will have the greatest effect on the TS energy. As such, since the charged functional group is placed directly in the path of the dipole moment for the phenyl and cubyl distonic radical ions a larger change in TS energy for HAT is expected compared to the adamantyl radical. An asymmetric response is instead expected for the CAT reaction depending on the alignment of the chloroform molecule at the TS. For the adamantyl radical this is important as the dipole can either point towards the charged functional group if the interaction is favourable, or away from the charged function group if the interaction is unfavourable (Fig. S19, ESI†). This means that across the three radicals a larger stabilisation of CAT is expected for adamantyl when a favourable electrostatic field is introduced, while an unfavourable electrostatic field will induce a smaller CAT destabilisation for adamantyl.

The orientation of these dipoles indicates that an anionic charged functional group will stabilise the TS and enhance the radical reactivity as the dipole moment points away from the radical site towards the incoming neutral (Fig. 4), while a cationic charged functional group will destabilise the TS and thus decelerate these reactions. This is the same trend as the oxidation reactions from the previous section. Differences in polarizability between the TS for HAT and CAT, however, also impacts the magnitude of (de)stabilisation from the internal OEF which alters the selectivity of these competing reactions. The resonance contributors from valence bond theory^97,98 for both HAT and CAT that rationalise how these electrostatic interactions arise are included in Fig. 4.⁹⁹ Using valence bond theory, the key TS for HAT and CAT are represented as three resonance contributors, but since the trichloromethyl radical (produced during HAT) is a better electron acceptor than the dichloromethyl radical (produced during CAT), the carbanion resonance contributor for this reaction will have a larger interaction with the internal electrostatic field. This is sometimes referred to as a polar effect and suggests that the TS for HAT will have the largest change in energy induced by the OEF. Additionally, since polarizability increases sizably from phenyl/cubyl to adamantyl (70.4/78.2 to 125.5), the carbanion resonance contributors will be disproportionately stabilised for adamantyl reactions.

Fig. 4 Optimised structures and resonance contributors for the TS of HAT and CAT of the neutral cubyl radical from chloroform (estimates of the weighting of these valence structures based on natural spin densities are provided in Table S5†).

Fig. 5 shows the calculated DSD-PBEP86-D3(BJ)/aug-cc-pVDZ potential energy schemes for the HAT and CAT reactions between chloroform and (a) cubyl, adamantyl, and phenyl, (b) cubyl–CO₂⁻, adamantyl–CO₂⁻, and phenyl–CO₂⁻, and (c) cubyl–NH₃⁺, adamantyl–NH₃⁺, and phenyl–NH₃⁺ radicals. All energies are in kJ mol⁻¹ relative to the corresponding separated reactants. The predicted kinetics of these reactions follow the expected trend, where a positive charge increases the TS energy, while the negative charge lowers the corresponding TS energy (d). The only exception was phenyl–NH₃⁺ which showed a small (4 kJ mol⁻¹) stabilisation in the CAT barrier, although this is within the error of the calculations.¹⁰⁰ However, even when recalculated with a larger basis set (aug-cc-pVTZ) this unexpected small stabilisation persists for phenyl–NH₃⁺ compared to phenyl (4 kJ mol⁻¹, Fig. S20†). Further, this same trend is induced by point charges, where both a negative and positive point charge decreased the barrier for CAT from phenyl–NH₃⁺ (Fig. S20†), suggesting that this is not an artifact of the method. Although the precise cause of this stabilisation remains unclear, it may originate from the significant off axis orientation of the TS dipole for the neutral phenyl CAT reaction which is supressed with the introduction of these charged functional groups (Fig. 6). A similar off axis dipole component also occurs for the CAT of neutral cubyl, but this angle is less extreme (6D) due to the increased electron density of the cubyl radical which likely suppresses this stabilisation effect for cubyl–NH₃⁺.

Fig. 5 Potential energy schemes showcasing the transition state and adduct energies for the competing HAT and CAT reactions from chloroform for all nine radical reactions. (A) Neutral radical reactions are in black, (B) anionic radical reactions are in blue, and (C) cationic radical reactions are in red. All energies are in kJ mol⁻¹ relative to the separated reactants. (D) Comparison of the effect of cationic and anionic substitution on the TS of CAT and HAT. These energies are in kJ mol⁻¹ relative to the neutral TS barrier.

Fig. 6 Optimised structures and dipole moments for the CAT TS of (A) phenyl–NH₃⁺, (B) phenyl, (C) phenyl–CO₂⁻, and (D) cubyl. Both cationic and anionic substitution reduce the magnitude of the off-axis component of the phenyl dipole moment.

Compared to the neutral radical reactions, the anionic charged functional group stabilises the TS for HAT but destabilises the H-atom addition product, whilst stabilising both the TS for CAT and the Cl-atom addition product (Fig. 5B). The cationic charged functional group has the inverse, although not equal, effect (Fig. 5C). Differences in polarizability between these radical species means that the magnitude of (de)stabilisation is not symmetric between the radical reactions. For example, with adamantyl–CO₂⁻ the barrier for HAT undergoes a small stabilisation (4 kJ mol⁻¹ lower than neutral adamantane), while the CAT barrier undergoes a larger stabilisation (6 kJ mol⁻¹ lower than neutral adamantane), which suggests that the ratio of H/Cl abstraction will decrease (Fig. 5D). For the cubyl–CO₂⁻ barrier heights, although the HAT barrier is more exothermic at −36 kJ mol⁻¹ compared to −20 kJ mol⁻¹ in the neutral system, the CAT barrier changes from endothermic in the neutral system (+10 kJ mol⁻¹) to exothermic in the anionic reaction (−5 kJ mol⁻¹). This makes the CAT pathway more competitive as the barrier is now below the entrance channel, thus lowering the H/Cl ratio. In contrast, for phenyl–CO₂⁻ the barrier for CAT still lies above thermoneutral (+5 kJ mol⁻¹) suggesting that only HAT will proceed efficiently which would manifest as a large increase in the H/Cl abstraction ratio. Thus, the same electrostatic charge is expected to induce a different effect on the rates of competing reaction channels, changing the overall kinetics and the selectivity of this radical reaction. Furthermore, the cationic charged functional group is predicted to raise the barrier for CAT and HAT above thermoneutral for the adamantyl reaction, suggesting that this OEF will inhibit both reactions. However, for the cubyl–NH₃⁺ and phenyl–NH₃⁺ radical reactions, the cationic functional group inhibits the CAT reaction, but the barrier for HAT is still below thermoneutral which suggests only HAT will occur efficiently and thus increase the H/Cl ratio. The CAT barrier is more destabilised for cubyl–NH₃⁺ compared to phenyl–NH₃⁺ and this can be rationalised based on differences in the 3D structure of the electron density between these two radicals (Fig. S21†).

To evaluate these computational predictions, we compared these calculated trends to experimental observations from these reactions. Experimental branching ratios for the nine radical reactions with chloroform are presented in Table 2. The branching ratios for the three neutral radicals are taken from previous publications,^99,101 which were calculated using the yield of isolated products from solution-phase reactions. Since the kinetics of these solution-phase reactions were not monitored directly, it is possible that secondary reactions could affect these values. Branching ratios for the six distonic radical ions are determined from direct gas-phase ion-trap kinetics measurements and are thus more reliable. Representative mass spectra (Fig. S12†) and kinetic profiles (Fig. S13 to S18†) along with experimental second-order rate constants (Table S4†) for each distonic radical ion reaction are provided in the ESI,† which show significantly slower rates of reaction for the radical cations with chloroform compared to the radical anions. As expected from the calculations above, the anionic charged functional group reduces the H/Cl ratio for the adamantyl–CO₂⁻ reaction compared to the neutral adamantyl radical (0.92 vs. 2) while the cationic charged functional group inhibits both adamantyl–NH₃⁺ HAT and CAT reactions completely. The cubyl–NH₃⁺ reaction, although slower than the anionic reactions, exclusively produced the HAT product within the limit of detection of the instrument (k_H/k_Cl > 10), while the H/Cl ratio was higher for the cubyl–CO₂⁻ radical anion compared to the adamantyl–CO₂⁻ radical (78.1 vs. 0.92). This stands in contrast with the phenyl radical reactions where both the cationic and anionic charged functional groups enhanced the H/Cl ratio compared to the neutral radical (3.8 vs. 3.4 and 289 vs. 3.4, respectively).

Table 2 Relative H/Cl branching ratios for the nine radical reactions with chloroform. Experimental second order rate constants for each distonic radical ion reaction are provided in Table S4 of the ESI

Radical	k H/kCl^b	Radical	k H/kCl^b	Radical	k H/kCl^b
a Data taken from isolated product yields of previously published solution-phase reactions.^99,101 b Errors are one standard deviation (n = 3). c Only HAT was observed. No reaction observed (NRobs).
Phenyl^a	3.4	Adamantyl^a	2	4-Carbomethoxycubyl^a	>82
Phenyl-NH3^+	3.8 ± 0.1	Adamantyl-NH3^+	NRobs	Cubyl-NH3^+	>10^c
Phenyl-CO2^−	289 ± 19.2	Adamantyl-CO2^−	0.92 ± 0.05	Cubyl-CO2^−	78.1 ± 15.1

---

The H/Cl ratio increase of phenyl–CO₂⁻ agrees with the calculations above which predict that HAT can proceed efficiently, whilst CAT is inhibited by a barrier above the entrance channel energy, ultimately leading to a large k_H/k_Cl. The increased H/Cl abstraction ratio of 3.8 for phenyl–NH₃⁺ was surprising given that the large endothermic barrier of +17 kJ mol⁻¹ for CAT was expected to render this pathway unfeasible at room temperature. However, ion–molecule reactions with endothermic transition states up to +10 kJ mol⁻¹ have been observed previously in ion-trap mass spectrometers due to the Boltzmann distribution of ion energies,^102,103 whilst the error in the branching ratios for slow ion–molecule reactions that approach the lower limit of detection of the experiment is larger. Together with maximum potential errors in the theoretical method of around 7–8 kJ mol⁻¹ for barrier heights based on benchmarking studies,¹⁰⁰ and the possibility of tunnelling in slow chlorine reactions,^104,105 it is reasonable that the slow experimentally observed CAT reaction from phenyl–NH₃⁺ is still viable despite the calculated barrier in Fig. 5C.

Conclusion

In this paper, systematically modified internal OEFs are used to control the rate of radical oxidation and the selectivity of radical H-atom vs. Cl-atom transfer from chloroform. In the first set of reactions, an anionic charged functional group introduced in the para position of the phenyl radical accelerated the rate of oxidation, while a positive functional group decelerated the same reaction. This change in reaction rate was correlated to the energy of the key rate-limiting TS of these reactions. Introducing neutral substitution groups altered the angle of the TS dipole which modulated the (de)stabilisation of this TS. Single point energy calculations replicated these trends by introducing a point charge or an OEF around the neutral phenyl radical, suggesting that these effects are primarily electrostatic in nature. Further evidence against significant through-bond effects was provided by the inclusion of cubyl and adamantyl radicals, which showed the same trend in reactivity when substituted with a positive or negatively charged functional group, reinforcing the through-space nature of these interactions.

Radical oxidation reactions are crucial chemical processes that initiate combustion. In both atmospheric and combustion environments, oxidation competes with polycyclic hydrocarbon formation to produce smaller propagating radicals while also providing the thermal energy for further molecular weight growth reactions.¹⁰⁶ However, questions remain about these fundamental reactions. Recent high-level calculations at the DSD-PBEP86 level of theory have located a TS for the neutral phenyl + O₂ reaction, in contrast to the previously accepted models of an energetically barrierless reaction.⁸⁴ However, insufficient available experimental data prevented the validation of these calculations. Here, we have used the distonic radical ion approach with an ion-trap mass spectrometer to provide precise (±10%) rate measurements of oxygen addition to benchmark the computational predictions. The high precision enables confident systematic comparison between reaction rates, independent of the potentially larger absolute uncertainties associated with measurements of ion molecular reactions in the gas phase (>± 50%). The correlation between the cationic, anionic and neutral phenyl radical reaction rates provides experimental evidence that the phenyl radical oxidation reaction indeed proceeds through a barrier on the potential energy surface and that the experimental trend is adequately captured by the chosen theoretical method. Notably, for these reactions the gradient of this correlation is relatively flat with a change of 20 kJ mol⁻¹ in the TS energy only increasing the efficiency by a factor of 5. This suggests that the reactivity effects observed for these reactions are also due to changes in the shape of the attractive reaction profile of a variational TS which must consequently also control the reaction rate. Furthermore, the reaction of 4-dehydrocubylcubylcarboxylate 9 with dioxygen was identified as an outlier; a critical insight that was only gained by a robust comparison between gas-phase experiment and theory. This highlights the limitation of using only one of these approaches in the absence of the other as the mechanism of this reaction would have otherwise been misinterpreted.

Chloroform is an important solvent used in a range of organic and industrial reactions. Investigations have also examined chloroform as a reactive reagent, such as hydrogen atom donation in Barton reductive decarboxylation reactions¹⁰⁷ as explored by Ko et al.^99,108 These studies showed a facile direct hydrogen atom transfer from chloroform to alkyl radicals generating the Barton reduction product along with new products arising from chlorine atom transfer. These experiments indicate that these reactions occur under kinetic control and are aided by polar effects and quantum mechanical tunnelling at the key rate limiting TS, which favours the thermodynamically unfavoured hydrogen atom transfer products. Thus, across all reactions only a small portion of chlorine atom donation occurred, despite these products being more thermodynamically favoured. The calculations and experimental results described herein indicate that introducing charged functional groups can preferentially promote either HAT or CAT for these radical reactions. Specifically, an anionic functional group increased the H/Cl abstraction ratio for the cubyl radical, while the same charged functional group decreased the H/Cl abstraction ratio for the adamantyl radical, relative to the respective unsubstituted neutral radicals. In contrast, a cationic functional group produced only the H-atom abstraction product for the cubyl radical and quenched the reaction completely for the adamantyl radical, while both a cationic and anionic functional group increased the H/Cl abstraction ratio of the phenyl radical. These results demonstrate that the same charged functional group can induce different effects on competing reactions, rationalised by alterations in the polarizability of the competing transition states using valence bond theory. Furthermore, for both abstraction reactions, the anionic functional group enhanced the rate of reaction while the cationic functional group decreased the reactivity of the radicals. These experimental trends corresponded to changes in the key rate-limiting TS for these reactions and highlight that although charged functional groups can control the selectivity and reaction rate of radical reactions primarily via electrostatic interactions, this technique requires careful consideration of both substitution and polar effects, particularly when competing reactions are involved. Previous studies investigating the catalysis of reactions with external OEFs in the solution-phase show that polar solvents diminish catalytic interactions by shielding reactants. It remains to be seen if this shielding effect will occur for these chloroform atom abstraction reactions when internal OEFs induced by charged functional groups are present. However, we would predict that the strength of the internal OEF would be less impacted by solvation than external OEFs given the fixed proximity of the charge to the reaction centre. The magnitude of the relative reaction rates would likely be suppressed in the solution-phase compared to the gas-phase,^109,110 but the trends should be translatable once tunnelling is accounted for in the former. As such, extending these results to the solution-phase, particularly with polar solvents which may both attenuate the net transition dipole but also stabilize the charge-induced polarization,⁶ is a critical future target. Though these polar effects may inhibit desired reactions if unaccounted for, carefully controlling and understanding these interactions through a combination of theoretical and experimental approaches (both in gas- and solution-phases) can enhance the practitioner's growing toolbox of methods used to synthetically control electrostatic catalysis reactions.

Data availability

The data presented here are available for download from the Queensland University of Technology Research Data Finder archive at https://doi.org/10.25912/RDF_1718945540597.

Author contributions

C. M. W., G. d. S., S. J. B. and A. J. T. conceptualised, acquired funding and supervised this project. S. J. B. and A. J. T. provided project administration. O. J. S., S. C. B., B. L. J. P., D. L. M., S. D. H., H. X., P. V. B., G. P. S., D. G. H., B. B. K. developed the methodologies, undertook the investigation including data analysis and visualisation. O. J. S. and S. C. B. prepared the original draft of the manuscript and all authors contributed to review and editing of the submitted version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge access and training on advanced instrumentation through the Central Analytical Research Facility (CARF) at the Queensland University of Technology. A. J. T., G. d. S. and S. J. B. acknowledge financial support for this research from the Australian Research Council (ARC) through the Discovery Project scheme (DP170101596 and DP240100612). The authors also acknowledge the generous allocation of computing resources by the NCI National Facility (Canberra, Australia) under Merit Allocation Scheme. In addition, the authors thank The University of Queensland (UQ) and the Commonwealth Scientific and Industrial Research Organisation (CSIRO, Melbourne) for financial support. The Australian Research Council for a Future Fellowship award (FT110100851) to C. M. W. is also gratefully acknowledged. S. D. H. gratefully acknowledges the Northcote Trust and Britain–Australia Society for their award of the Northcote Graduate Scholarship.

References

1. S. Shaik, D. Mandal and R. Ramanan, Oriented electric fields as future smart reagents in chemistry, Nat. Chem., 2016, 8(12), 1091–1098.
2. S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Pérez and M. L. Coote, Harnessing electrostatic catalysis in single molecule, electrochemical and chemical systems: a rapidly growing experimental tool box, Chem. Soc. Rev., 2018, 47(14), 5146–5164.
3. T. Stuyver, D. Danovich, J. Joy and S. Shaik, External electric field effects on chemical structure and reactivity, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2020, 10(2), e1438.
4. S. Shaik, D. Danovich, J. Joy, Z. Wang and T. Stuyver, Electric-field mediated chemistry: uncovering and exploiting the potential of (oriented) electric fields to exert chemical catalysis and reaction control, J. Am. Chem. Soc., 2020, 142(29), 12551–12562.
5. A. B. Weberg, R. P. Murphy and N. C. Tomson, Oriented internal electrostatic fields: an emerging design element in coordination chemistry and catalysis, Chem. Sci., 2022, 13(19), 5432–5446.
6. M. T. Blyth, B. B. Noble, I. C. Russell and M. L. Coote, Oriented internal electrostatic fields cooperatively promote ground-and excited-state reactivity: A case study in photochemical CO₂ capture, J. Am. Chem. Soc., 2019, 142(1), 606–613.
7. L. R. Dalton, P. A. Sullivan and D. H. Bale, Electric field poled organic electro-optic materials: state of the art and future prospects, Chem. Rev., 2010, 110(1), 25–55.
8. P. Saura, D. Riepl, D. M. Frey, M. Wikström and V. R. Kaila, Electric fields control water-gated proton transfer in cytochrome c oxidase, Proc. Natl. Acad. Sci. U.S.A., 2022, 119(38), e2207761119.
9. K. Bhattacharyya, S. Karmakar and A. Datta, External electric field control: driving the reactivity of metal-free azide–alkyne click reactions, Phys. Chem. Chem. Phys., 2017, 19(33), 22482–22486.
10. N. G. Léonard, R. Dhaoui, T. Chantarojsiri and J. Y. Yang, Electric fields in catalysis: From enzymes to molecular catalysts, ACS Catal., 2021, 11(17), 10923–10932.
11. S. D. Fried and S. G. Boxer, Electric fields and enzyme catalysis, Annu. Rev. Biochem., 2017, 86, 387–415.
12. S. Shaik, S. P. De Visser and D. Kumar, External electric field will control the selectivity of enzymatic-like bond activations, J. Am. Chem. Soc., 2004, 126(37), 11746–11749.
13. I. T. Suydam, C. D. Snow, V. S. Pande and S. G. Boxer, Electric fields at the active site of an enzyme: Direct comparison of experiment with theory, Science, 2006, 313(5784), 200–204.
14. P. Hanoian, C. T. Liu, S. Hammes-Schiffer and S. Benkovic, Perspectives on electrostatics and conformational motions in enzyme catalysis, Acc. Chem. Res., 2015, 48(2), 482–489.
15. S. D. Fried, S. Bagchi and S. G. Boxer, Extreme electric fields power catalysis in the active site of ketosteroid isomerase, Science, 2014, 346(6216), 1510–1514.
16. Y. Wu and S. G. Boxer, A Critical Test of the Electrostatic Contribution to Catalysis with Noncanonical Amino Acids in Ketosteroid Isomerase, J. Am. Chem. Soc., 2016, 138(36), 11890–11895.
17. L. Rincón, J. R. Mora, F. J. Torres and R. Almeida, On the activation of σ-bonds by electric fields: A Valence Bond perspective, Chem. Phys., 2016, 477, 1–7.
18. H. Hao, I. Leven and T. Head-Gordon, Can electric fields drive chemistry for an aqueous microdroplet?, Nat. Commun., 2022, 13(1), 280.
19. H. Xiong, J. K. Lee, R. N. Zare and W. Min, Strong electric field observed at the interface of aqueous microdroplets, J. Phys. Chem. Lett., 2020, 11(17), 7423–7428.
20. J. K. Lee, S. Banerjee, H. G. Nam and R. N. Zare, Acceleration of reaction in charged microdroplets, Q. Rev. Biophys., 2015, 48(4), 437–444.
21. X. Yan, R. M. Bain and R. G. Cooks, Organic reactions in microdroplets: Reaction acceleration revealed by mass spectrometry, Angew. Chem., Int. Ed., 2016, 55(42), 12960–12972.
22. J. K. Lee, S. Kim, H. G. Nam and R. N. Zare, Microdroplet fusion mass spectrometry for fast reaction kinetics, Proc. Natl. Acad. Sci. U.S.A., 2015, 112(13), 3898–3903.
23. Z. Wei, Y. Li, R. G. Cooks and X. Yan, Accelerated reaction kinetics in microdroplets: Overview and recent developments, Annu. Rev. Phys. Chem., 2020, 71, 31–51.
24. M. F. Ruiz-Lopez, J. S. Francisco, M. T. Martins-Costa and J. M. Anglada, Molecular reactions at aqueous interfaces, Nat. Rev. Chem, 2020, 4(9), 459–475.
25. A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic catalysis of a Diels–Alder reaction, Nature, 2016, 531(7592), 88–91.
26. X. Huang, C. Tang, J. Li, L.-C. Chen, J. Zheng, P. Zhang, J. Le, R. Li, X. Li and J. Liu, Electric field–induced selective catalysis of single-molecule reaction, Sci. Adv., 2019, 5(6), eaaw3072.
27. O. J. Shiels, S. J. Marlton and A. J. Trevitt, Protonation Isomer Specific Ion–Molecule Radical Reactions, J. Am. Chem. Soc., 2023, 145(28), 15024–15029.
28. R. Meir, H. Chen, W. Lai and S. Shaik, Oriented electric fields accelerate Diels–Alder reactions and control the endo/exo selectivity, ChemPhysChem, 2010, 11(1), 301–310.
29. S. Fleischer, Y. Zhou, R. W. Field and K. A. Nelson, Molecular orientation and alignment by intense single-cycle THz pulses, Phys. Rev. Lett., 2011, 107(16), 163603.
30. C. P. Koch, M. Lemeshko and D. Sugny, Quantum control of molecular rotation, Rev. Mod. Phys., 2019, 91(3), 035005.
31. D. Yokoyama, Molecular orientation in small-molecule organic light-emitting diodes, J. Mater. Chem., 2011, 21(48), 19187–19202.
32. C. F. Gorin, E. S. Beh, Q. M. Bui, G. R. Dick and M. W. Kanan, Interfacial Electric Field Effects on a Carbene Reaction Catalyzed by Rh Porphyrins, J. Am. Chem. Soc., 2013, 135(30), 11257–11265.
33. C. F. Gorin, E. S. Beh and M. W. Kanan, An Electric Field–Induced Change in the Selectivity of a Metal Oxide–Catalyzed Epoxide Rearrangement, J. Am. Chem. Soc., 2012, 134(1), 186–189,  DOI:10.1021/ja210365j.
34. L. Zhang, R. B. D. Espíndola, B. B. Noble, V. R. Gonçales, G. G. Wallace, N. Darwish, M. L. Coote and S. Ciampi, Switchable Interfaces: Redox Monolayers on Si(100) by Electrochemical Trapping of Alcohol Nucleophiles, Surfaces, 2018, 1(1), 3–11.
35. L. Li, P. A. Salvador and G. S. Rohrer, Photocatalysts with internal electric fields, Nanoscale, 2014, 6(1), 24–42.
36. Y. Guo, W. Shi and Y. Zhu, Internal electric field engineering for steering photogenerated charge separation and enhancing photoactivity, EcoMat, 2019, 1(1), e12007.
37. I. Azcarate, C. Costentin, M. Robert and J.-M. Savéant, Through-space charge interaction substituent effects in molecular catalysis leading to the design of the most efficient catalyst of CO2-to-CO electrochemical conversion, J. Am. Chem. Soc., 2016, 138(51), 16639–16644.
38. S. So, B. B. Kirk, U. Wille, A. J. Trevitt, S. J. Blanksby and G. Da Silva, Reactions of a distonic peroxyl radical anion influenced by SOMO–HOMO conversion: an example of anion-directed channel switching, Phys. Chem. Chem. Phys., 2020, 22(4), 2130–2141.
39. A. Kumar and M. D. Sevilla, SOMO–HOMO level inversion in biologically important radicals, J. Phys. Chem. B, 2018, 122(1), 98–105.
40. G. Gryn’ova and M. L. Coote, Origin and scope of long-range stabilizing interactions and associated SOMO–HOMO conversion in distonic radical anions, J. Am. Chem. Soc., 2013, 135(41), 15392–15403.
41. P. Franchi, E. Mezzina and M. Lucarini, SOMO–HOMO conversion in distonic radical anions: an experimental test in solution by EPR radical equilibration technique, J. Am. Chem. Soc., 2014, 136(4), 1250–1252.
42. A. A. Arabi and C. F. Matta, Effects of external electric fields on double proton transfer kinetics in the formic acid dimer, Phys. Chem. Chem. Phys., 2011, 13(30), 13738–13748.
43. E. M. Kempfer-Robertson and L. M. Thompson, Effect of oriented external electric fields on the photo and thermal isomerization of azobenzene, J. Phys. Chem. A, 2020, 124(18), 3520–3529.
44. G. E. Amer, F. I. A. Razak, S. Sapari, H. Nur and S. A. Setu, Elucidating the alkene hydrogenation reaction based on cotton textile reduced graphene oxide under the influence of external electric field: Illustration of new noble method, Heliyon, 2023, 9(4), e14888.
45. O. J. Shiels, J. A. Turner, P. Kelly, S. J. Blanksby, G. da Silva and A. J. Trevitt, Modelling reaction kinetics of distonic radical ions: a systematic investigation of phenyl-type radical addition to unsaturated hydrocarbons, Faraday Discuss., 2022, 238, 475–490.
46. O. J. Shiels, P. Kelly, C. C. Bright, B. L. Poad, S. J. Blanksby, G. Da Silva and A. J. Trevitt, Reactivity Trends in the Gas-Phase Addition of Acetylene to the N-Protonated Aryl Radical Cations of Pyridine, Aniline, and Benzonitrile, J. Am. Soc. Mass Spectrom., 2021, 32(2), 537–547.
47. O. J. Shiels, P. Kelly, S. J. Blanksby, G. Da Silva and A. J. Trevitt, Barrierless Reactions of Three Benzonitrile Radical Cations with Ethylene, Aust. J. Chem., 2020, 73(8), 705–713.
48. P. E. Williams, B. J. Jankiewicz, L. Yang and H. I. Kenttamaa, Properties and reactivity of gaseous distonic radical ions with aryl radical sites, Chem. Rev., 2013, 113(9), 6949–6985.
49. B. F. Yates, W. J. Bouma and L. Radom, Distonic radical cations: Guidelines for the assessment of their stability, Tetrahedron, 1986, 42(22), 6225–6234.
50. L. Radom, W. J. Bouma, R. H. Nobes and B. F. Yates, A theoretical approach to gas-phase ion chemistry, Pure Appl. Chem., 1984, 56(12), 1831–1842.
51. B. F. Yates, W. J. Bouma and L. Radom, Detection of the prototype phosphonium (CH₂PH₃), sulfonium (CH₂SH₂) and chloronium (CH₂ClH) ylides by neutralization-reionization mass spectrometry: a theoretical prediction, J. Am. Chem. Soc., 1984, 106(20), 5805–5808.
52. L. J. Chyall and H. I. Kenttamaa, The 4-dehydroanilinium ion: a stable distonic isomer of ionized aniline, J. Am. Chem. Soc., 1994, 116(7), 3135–3136.
53. K. M. Stirk, L. M. Kiminkinen and H. I. Kenttamaa, Ion-molecule reactions of distonic radical cations, Chem. Rev., 1992, 92(7), 1649–1665.
54. T. Mondal, S. Shaik, H. Kenttämaa and T. Stuyver, Modulating the radical reactivity of phenyl radicals with the help of distonic charges: it is all about electrostatic catalysis, Chem. Sci., 2021, 12(13), 4800–4809.
55. D. L. Marshall, G. Gryn’ova, B. L. Poad, S. E. Bottle, A. J. Trevitt, M. L. Coote and S. J. Blanksby, Experimental evidence for long-range stabilizing and destabilizing interactions between charge and radical sites in distonic ions, Int. J. Mass Spectrom., 2019, 435, 195–203.
56. C. J. Petzold, E. D. Nelson, H. A. Lardin and H. I. Kenttämaa, Charge-site effects on the radical reactivity of distonic ions, J. Phys. Chem. A, 2002, 106(42), 9767–9775.
57. S. Billets, H. Jaffe and F. Kaplan, Gas phase studies of N-nitrosamines by ion cyclotron resonance spectroscopy, Org. Mass Spectrom., 1973, 7(4), 431–440.
58. M. B. Prendergast, B. B. Kirk, J. D. Savee, D. L. Osborn, C. A. Taatjes, P. Hemberger, S. J. Blanksby, G. Da Silva and A. J. Trevitt, Product detection study of the gas-phase oxidation of methylphenyl radicals using synchrotron photoionisation mass spectrometry, Phys. Chem. Chem. Phys., 2019, 21(32), 17939–17949.
59. S. Hammerum, Distonic radical cations in gaseous and condensed phase, Mass Spectrom. Rev., 1988, 7(2), 123–202.
60. C. C. Bright, M. B. Prendergast, P. D. Kelly, J. P. Bezzina, S. J. Blanksby, G. da Silva and A. J. Trevitt, Highly efficient gas-phase reactivity of protonated pyridine radicals with propene, Phys. Chem. Chem. Phys., 2017, 19(46), 31072–31084.
61. M. B. Prendergast, B. B. Kirk, J. D. Savee, D. L. Osborn, C. A. Taatjes, K.-S. Masters, S. J. Blanksby, G. Da Silva and A. J. Trevitt, Formation and stability of gas-phase o-benzoquinone from oxidation of ortho-hydroxyphenyl: a combined neutral and distonic radical study, Phys. Chem. Chem. Phys., 2016, 18(6), 4320–4332.
62. M. B. Prendergast, P. A. Cooper, B. B. Kirk, G. da Silva, S. J. Blanksby and A. J. Trevitt, Hydroxyl radical formation in the gas phase oxidation of distonic 2-methylphenyl radical cations, Phys. Chem. Chem. Phys., 2013, 15(47), 20577–20584.
63. D. G. Harman and S. J. Blanksby, Investigation of the gas phase reactivity of the 1-adamantyl radical using a distonic radical anion approach, Org. Biomol. Chem., 2007, 5(21), 3495–3503.
64. D. G. Harman and S. J. Blanksby, Trapping of a tert-adamantyl peroxyl radical in the gas phase, Chem. Commun., 2006,(8), 859–861.
65. A. K. Y. Lam, C. Li, G. Khairallah, B. B. Kirk, S. J. Blanksby, A. J. Trevitt, U. Wille, R. A. J. O’Hair and G. da Silva, Gas-phase reactions of aryl radicals with 2-butyne: experimental and theoretical investigation employing the N-methyl-pyridinium-4-yl radical cation, Phys. Chem. Chem. Phys., 2012, 14(7), 2417–2426.
66. C. H. Li, G. N. Khairallah, A. K. Y. Lam, R. A. J. O’Hair, B. B. Kirk, S. J. Blanksby, G. da Silva and U. Wille, Reaction of Aromatic Peroxyl Radicals with Alkynes: A Mass Spectrometric and Computational Study Using the Distonic Radical Ion Approach, Chem.–An Asian J., 2013, 8(2), 450–464.
67. M. Frisch; G. Trucks; H. Schlegel; G. Scuseria; M. Robb; J. Cheeseman; G. Scalmani; V. Barone; G. Petersson and H. Nakatsuji, Gaussian 16, revision C. 01, Gaussian, Inc., Wallingford CT, 2016.
68. G. Santra, N. Sylvetsky and J. M. Martin, Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4, J. Phys. Chem. A, 2019, 123(24), 5129–5143.
69. F. Yu, L. X. Fu and Y. Yang, DSD-PBEP86-NL and DOD-PBEP86-NL functionals for noncovalent interactions: Basis set effects and tentative applications to large noncovalent systems, Int. J. Quantum Chem., 2017, 117(19), e25417.
70. S. Kozuch and J. M. Martin, DSD-PBEP86: in search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections, Phys. Chem. Chem. Phys., 2011, 13(45), 20104–20107.
71. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, Perspectives on basis sets beautiful: Seasonal plantings of diffuse basis functions, J. Chem. Theory Comput., 2011, 7(10), 3027–3034.
72. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19(48), 32184–32215.
73. T. Scheele and T. Neudecker, Investigating the accuracy of density functional methods for molecules in electric fields, J. Chem. Phys., 2023, 159(12), 124111.
74. T. Stuyver, J. Huang, D. Mallick, D. Danovich and S. Shaik, TITAN: A code for modeling and generating electric fields—features and applications to enzymatic reactivity, J. Comput. Chem., 2020, 41(1), 74–82.
75. C. S. Hansen, B. B. Kirk, S. J. Blanksby, R. A. O'Hair and A. J. Trevitt, UV photodissociation action spectroscopy of haloanilinium ions in a linear quadrupole ion trap mass spectrometer, J. Am. Soc. Mass Spectrom., 2013, 24(6), 932–940.
76. P. E. Williams, D. L. Marshall, B. L. Poad, V. R. Narreddula, B. B. Kirk, A. J. Trevitt and S. J. Blanksby, Comparing positively and negatively charged distonic radical ions in phenylperoxyl forming reactions, J. Am. Soc. Mass Spectrom., 2018, 29(9), 1848–1860.
77. T. Ly, B. B. Kirk, P. I. Hettiarachchi, B. L. Poad, A. J. Trevitt, G. da Silva and S. J. Blanksby, Reactions of simple and peptidic alpha-carboxylate radical anions with dioxygen in the gas phase, Phys. Chem. Chem. Phys., 2011, 13(36), 16314–16323.
78. B. B. Kirk, D. G. Harman and S. J. Blanksby, Direct Observation of the Gas Phase Reaction of the Cyclohexyl Radical with Dioxygen Using a Distonic Radical Ion Approach, J. Phys. Chem. A, 2010, 114(3), 1446–1456.
79. B. B. Kirk, D. G. Harman, H. I. Kenttämaa, A. J. Trevitt and S. J. Blanksby, Isolation and characterization of charge-tagged phenylperoxyl radicals in the gas phase: direct evidence for products and pathways in low temperature benzene oxidation, Phys. Chem. Chem. Phys., 2012, 14(48), 16719–16730.
80. D. R. Reed, M. Hare and S. R. Kass, Formation of gas-phase dianions and distonic ions as a general method for the synthesis of protected reactive intermediates. Energetics of 2, 3-and 2, 6-dehydronaphthalene, J. Am. Chem. Soc., 2000, 122(43), 10689–10696.
81. W. A. Donald, G. N. Khairallah and R. A. J. O’Hair, The Effective Temperature of Ions Stored in a Linear Quadrupole Ion Trap Mass Spectrometer, J. Am. Soc. Mass Spectrom., 2013, 24(6), 811–815.
82. T. Su and M. T. Bowers, Ion-polar molecule collisions: the effect of ion size on ion-polar molecule rate constants; the parameterization of the average-dipole-orientation theory, Int. J. Mass Spectrom. Ion Phys., 1973, 12(4), 347–356.
83. T. Su and W. J. Chesnavich, Parametrization of the ion–polar molecule collision rate constant by trajectory calculations, J. Chem. Phys., 1982, 76(10), 5183–5185.
84. O. J. Shiels, S. J. Marlton, B. L. Poad, S. J. Blanksby, G. da Silva and A. J. Trevitt, Gas-Phase Phenyl Radical+ O₂ Reacts via a Submerged Transition State, J. Phys. Chem. A, 2024, 128(2), 413–419.
85. K. Tanaka, M. Ando, Y. Sakamoto and K. Tonokura, Pressure dependence of phenylperoxy radical formation in the reaction of phenyl radical with molecular oxygen, Int. J. Chem. Kinet., 2012, 44(1), 41–50.
86. D. Chen, Y. Li, X. Li, X. Hong, X. Fan and T. Savidge, Key difference between transition state stabilization and ground state destabilization: increasing atomic charge densities before or during enzyme–substrate binding, Chem. Sci., 2022, 13(27), 8193–8202.
87. L. Chen, J. Dang, J. Du, C. Wang and Y. Mo, Hydrogen and halogen bonding in homogeneous external electric fields: modulating the bond strengths, Chem.–Eur. J., 2021, 27(56), 14042–14050.
88. R. Van Lommel, R. H. Verschueren, W. M. De Borggraeve, F. De Vleeschouwer and T. Stuyver, Can the Philicity of Radicals Be Influenced by Oriented External Electric Fields?, Org. Lett., 2021, 24(1), 1–5.
89. S. Gronert, Mass spectrometric studies of organic ion/molecule reactions, Chem. Rev., 2001, 101(2), 329–360.
90. P. Liere, V. Steiner, K. Jennings, R. March and J. Tabet, Influence of ion activation and thermalization effects on reaction rate constants in a quadrupole ion trap mass spectrometer, Int. J. Mass Spectrom. Ion Processes, 1997, 167, 735–751.
91. D. J. Douglas, A. J. Frank and D. Mao, Linear ion traps in mass spectrometry, Mass Spectrom. Rev., 2005, 24(1), 1–29.
92. P. D. Kelly, C. C. Bright, S. J. Blanksby, G. da Silva and A. J. Trevitt, Molecular Weight Growth in the Gas-Phase Reactions of Dehydroanilinium Radical Cations with Propene, J. Phys. Chem. A, 2019, 123(41), 8881–8892.
93. T. Yu and M.-C. Lin, Kinetics of the C₆H₅ + O₂ reaction at low temperatures, J. Am. Chem. Soc., 1994, 116(21), 9571–9576.
94. K. Tonokura, Y. Norikane, M. Koshi, Y. Nakano, S. Nakamichi, M. Goto, S. Hashimoto, M. Kawasaki, M. Sulbaek Andersen and M. Hurley, Cavity ring-down study of the visible absorption spectrum of the phenyl radical and kinetics of its reactions with Cl, Br, Cl₂, and O₂, J. Phys. Chem. A, 2002, 106(24), 5908–5917.
95. J. C. Walton, Bridgehead radicals, Chem. Soc. Rev., 1992, 21(2), 105–112.
96. P. Reinhart, Q. Williams and T. Weatherly, Microwave Measurements of the Dipole Moments of CFCl₃ and CHCl₃ and Their Pressure-Broadened Spectra, J. Chem. Phys., 1970, 53(4), 1418–1421.
97. D. Cooper; J. Gerratt and M. Raimondi, Modern valence bond theory, Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, 1987, vol. 69, pp. 319–397.
98. S. S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, John Wiley & Sons, 2007.
99. J. Ho, J. Zheng, R. n. Meana-Pañeda, D. G. Truhlar, E. J. Ko, G. P. Savage, C. M. Williams, M. L. Coote and J. Tsanaktsidis, Chloroform as a hydrogen atom donor in Barton reductive decarboxylation reactions, J. Org. Chem., 2013, 78(13), 6677–6687.
100. A. Najibi and L. Goerigk, A comprehensive assessment of the effectiveness of orbital optimization in double-hybrid density functionals in the treatment of thermochemistry, kinetics, and noncovalent interactions, J. Phys. Chem. A, 2018, 122(25), 5610–5624.
101. R. F. Bridger and G. A. Russell, Directive effects in the attack of phenyl radicals on carbon-hydrogen bonds, J. Am. Chem. Soc., 1963, 85(23), 3754–3765.
102. M. N. Glukhovtsev, b. A. Pross and L. Radom, Gas-phase identity S_N2 reactions of halide anions with methyl halides: a high-level computational study, J. Am. Chem. Soc., 1995, 117(7), 2024–2032.
103. S. C. Brydon, C. Thomson, R. A. O’Hair and J. M. White, Electronic and Steric Effects on the Reactivity of Seleniranium Ions with Alkenes in the Gas Phase, J. Org. Chem., 2023, 88(14), 9629–9644.
104. C. Castro and W. L. Karney, Heavy-Atom Tunneling in Organic Reactions, Angew. Chem., 2020, 132(22), 8431–8442.
105. W. H. Saunders Jr, Calculations of isotope effects in elimination reactions. New experimental criteria for tunneling in slow proton transfers, J. Am. Chem. Soc., 1985, 107(1), 164–169.
106. D. S. Parker, R. I. Kaiser, T. P. Troy, O. Kostko, M. Ahmed and A. M. Mebel, Toward the oxidation of the phenyl radical and prevention of PAH formation in combustion systems, J. Phys. Chem. A, 2015, 119(28), 7145–7154.
107. D. H. Barton and D. Crich, A new method for the radical deoxygenation of tertiary alcohols, J. Chem. Soc., Chem. Commun., 1984,(12), 774–775.
108. E. J. Ko, G. P. Savage, C. M. Williams and J. Tsanaktsidis, Reducing the cost, smell, and toxicity of the Barton reductive decarboxylation: Chloroform as the hydrogen atom source, Org. Lett., 2011, 13(8), 1944–1947.
109. D. K. Bohme and G. I. Mackay, Bridging the gap between the gas phase and solution: transition in the kinetics of nucleophilic displacement reactions, J. Am. Chem. Soc., 1981, 103(4), 978–979.
110. J. M. Garver, Y.-r. Fang, N. Eyet, S. M. Villano, V. M. Bierbaum and K. C. Westaway, A Direct Comparison of Reactivity and Mechanism in the Gas Phase and in Solution, J. Am. Chem. Soc., 2010, 132(11), 3808–3814.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2336194. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc06333c

‡ These authors have contributed equally.

---