The inductive effect does not explain electron density in haloacetates: are our textbooks wrong?

Abstract

The inductive effect is a central concept in chemistry and is often exemplified by the pK_a values of acetic acid derivatives. The reduction in pK_a is canonically attributed to the reduction in the electron density of the carboxylate group through the inductive effect. However, wave functional theory calculations presented herein reveal that the charge density of the carboxylate group is not explained by the inductive effect. For a series of trihaloacetates (trichloro–, chlorodifluoro– and trifluoro–) we find that the trichloro group has the greatest reduction on the charge density of the carboxylate oxygen atoms; change in charge density is inversely related to substituent electronegativity. These puzzling results are experimentally supported by investigating three independent systems: literature gas phase acidities, specific ion effects in a model thermoresponsive polymer system, and nuclear magnetic resonance (NMR) spectroscopy of haloalkanes. Changes in the solubility of poly(N-isopropylacrylamide), PNIPAM, due to the presence of different (substituted) acetates allow ionic charge densities to be examined. These studies confirmed the unexpected charge density and substituent–electronegativity relationship. Further analysis of the literature showed anomalous charge densities for haloalkanes with ¹³C NMR spectroscopy and gas phase acidity of polyatomic acids. In summary, these independent results show that the induction effect does not explain pK_a trends across the haloacetic acids.

---

1 Introduction

In many university-level chemistry textbooks, we are taught that the inductive effect is responsible for the formation of partial charges and permanent dipole moments within molecules due to the polarisation of σ-bonds.^1–6 This polarisation arises as a result of electronegativity differences between the atoms across the bond, generating partial charges within molecules, which, in conjunction with the molecule's shape and size, govern their inter-molecular interactions. These interactions in turn dictate physical properties such as boiling point, viscosity, and reactivity.

In reality, however, substitution effects in organic molecules are far more complicated than simple σ-bond inductive effects. In addition to σ-bond induction, Taft and Topsom identified three distinct substituent effects, resonance, polarisability and field effects.⁷ Resonance and polarisability effects are, respectively, the delocalisation of electrons across multiple bonds and the susceptibility of an atom's or molecule's electron density to shift in the presence of an external electric field. Field effects refer to the intramolecular polarisation of an atom/molecule through space, resulting from a localised charge or dipole,^5,7–9 and can influence a molecule's geometry and physical properties.¹⁰ Whilst not typically particularly strong, the range over which field effects occur is generally much greater than inductive effects.¹⁰ As field effects are electrostatic in origin, they are influenced by the dielectric functions of the system, therefore the solvent has a considerable impact on the magnitude of the effect.^10,11 Though the inductive effect is strongest across a single bond,⁷ its effect is reportedly experienced up to 3–4 single bonds from the site of polarisation,^5,12–14 with the strength of the inductive effect correlated to the strength of the dipole established at the substituent site.⁷

Despite the complexity of such substituent effects, it is frequently only σ-bond induction that is cited as the cause for changes in molecular properties. The effect of alpha substitution on the pK_a of acetic acid is commonly used to demonstrate the importance of the inductive effect.^1,2,6,12 Substitution of hydrogen on the alpha carbon with highly electronegative halogens significantly decreases the pK_a of the resultant haloacetic acids, with more electronegative groups having a greater impact.^1,2,12 Beyond exemplar molecules in textbooks, haloacetates have real-world importance, in particular, they are used in peptide synthesis,¹⁵ but also present significant adverse health effects.^16,17 Induction in these halogenated acetates is considered in Fig. 1a, where the pK_a decreases monotonically with the increasing electronegativity of the alpha substituent(s). The electron-withdrawing capabilities of alpha substituents for four halogenated acetates are shown in Fig. 1b. Supposedly, the electron-withdrawing substituent(s) redistribute the charge density away from the carboxylate group, stabilising the anionic conjugate base. This is in contrast to the un-substituted acetate which is destabilised by the electron donating methyl group. The stabilisation of the haloacetates, and thus the shift in their pK_a values, is attributed to entropic differences between deprotonated substituted acetate systems; lower charge densities caused by the inductive effect¹ result in weaker solvation requirements and hence a more favourable charged state. This mechanism is not only described in common undergraduate textbooks but also appears in educational journals,^6,12 and is ubiquitous amongst widely subscribed, open-source online resources and tutorials.^20–25

Fig. 1 Ion properties of substituted acetic acids and acetates and their relationship to pK_a values. (a) The effect of the mean Pauling electronegativity¹⁸ of the alpha substituent(s) on the pK_a of several substituted acetic acids; (b) The traditional story: structures of four substituted acetates with electron-withdrawing and donating capabilities indicated; (c) the pK_a of conjugated acids of substituted acetates as a function of DDEC6 calculated partial charge on the conjugate base O⁻ charge; (d–g) atomic DDEC6 (ref. 19) partial charges in the deprotonated substituted acetates as a function of mean Pauling electronegativity of the alpha substituents for: (d) X-group (alpha substituent); (e) alpha carbon; (f) the carboxylate carbon, and (g) oxygen. DDEC6 charges calculated using MP2/aug-cc-pVQZ.

2 Results and discussion

2.1 Induction cannot explain simulated charge densities

To the best of our knowledge, there have been no direct investigations into the relationship between the electronegativity of the substituent alpha group atoms and the charge density of the carboxylate group of haloacetates. However, if the canonical mechanism by which the pK_a of these substituted acetates is lowered is correct, then one would expect the same trends to be present when examining a plot of pK_a against the calculated partial charge of the charged oxygen of the conjugated base. Surprisingly, this is not the case, with a non-monotonic relationship between the pK_a of the conjugate acids of tri-substituted acetate anions and their O⁻ partial charges (Fig. 1c). Here, it can be seen that trifluoroacetate (CF₃COO⁻) has a more negative partial charge on its oxygen atoms compared to chlorodifluoro- and trichloroacetate (CClF₂COO⁻ and CCl₃COO⁻, respectively). This is contrary to our fundamental understanding of the inductive effect and its ability to influence pK_a values. Indeed, if just the haloacetates are considered, a reverse relationship is evident between the O⁻ partial charge and the pK_a of the conjugate acids. These results were observed across a number of computational methods (see Fig. S1†) which suggests it is not an artefact of the choice of charge decomposition scheme, functional or basis set. The reliability of the partial charges calculated using the DDEC6 method used here has been compared between M06-2X/aug-cc-pVDZ and MP2/aug-cc-PVQZ values for a large number of ions in Gregory et al.²⁶

To better understand these results, we assess the partial charges throughout the entire structure of the substituted acetates (Fig. 1d–g). Taking first the alpha substituent (X, Fig. 1d), the partial charge decreases monotonically with the mean electronegativity of the X group. In compensation for this, the partial charge of the alpha carbon (Fig. 1e) increases monotonically. Continuing along the molecule, the partial charge of the carbon in the carboxylate group (Fig. 1f) is inversely proportional to the mean electronegativity of the alpha substituent. All of these changes are consistent with our current understanding of the inductive effect; the more electronegative fluorine draws electron density away from the alpha carbon more effectively than the chlorine, reducing the charge on the carbon in the carboxylate group. However, when examining the partial charge of the O⁻ as a function of the electronegativity of the X group (Fig. 1g), a similar non-monotonic relationship to that in Fig. 1c is observed. We emphasise that this result is counter to the conventional explanation of pK_a reduction due to charge redistribution arising from the inductive effect. Further, these results were obtained for a single ion in a vacuum, and so this property is inherent to the ion and is not due to ion–ion or ion–solvent interactions.

To account for the delocalisation of electron density across the carboxylate group, the summation of the partial charges of the constituent atoms (i.e. C + O + O) and are presented in Fig. 2. Incredibly, the anomalous relationship between substituent electronegativity and the partial charge demonstrated in Fig. 1g is magnified when the entire carboxylate group is considered. A reduction in charge density of the carboxylate group for the trichloro substituted ion is observed which is consistent with the traditional understanding of inductive effects. For the acetates containing fluorine groups (chlorodifluoro–, trifluoro–), the charge density of the carboxylate group is larger (more negative) than the un-substituted acetate. This is a highly counter-intuitive result. Fluorine substitution has been shown to have unusual effects on chemical reactivity and molecular geometry, collectively denoted as the ‘fluorine effect’ or ‘negative fluorine effect’.^27–31 While there is still some debate over the exact mechanism underpinning these effects, there is strong evidence that hyperconjugation between electron-rich regions (σ-bonds, π-systems, and nonbonding electron pairs) with the antibonding orbitals of carbon–fluorine σ-bonds plays a critical role.³⁰ We return to this hyperconjugation discussion below.

Fig. 2 Charge densities of carboxylate groups in substituted acetates. The relationship between the mean Pauling electronegativity¹⁸ of the alpha substituent(s) on the carboxylate group. This value comes from the summation of the partial charges of the carboxylate carbon, and the two oxygen atoms as shown in Fig. 1f/g. DDEC6 charges calculated using MP2/aug-cc-pVQZ. The COO⁻ axis has been inverted to aid in understanding.

Despite the implications of these novel computational results, the elegance of the relationship between substituent electronegativity and pK_a is compelling and has resulted in (halo)acetates being an exemplar system to demonstrate the significance of substituent effects. However, there are many relatively poorly understood complexities regarding pK_a values of polyatomic acids, including solvent effects,^32–34 temperature,^32,35,36 ionic strength,^36,37 and the identity of the counterion.³⁸ As an extreme example, the pK_a of weak polybases can shift several pH units when compared to their monomer or small molecule equivalents.^39,40 Indeed, Fig. S2† demonstrates the clear lack of definitive relationships between pK_a and the charge density of conjugate bases. Why pK_a correlates with X electronegativity but not carboxylate charge density is unclear and, while charge density certainly contributes, pK_a is a solution property and so must arise from interactions between the acid, conjugate base, solvent, and counterions. For example, homoconjugation between the neutral acids and their charged conjugate bases likely also plays a role in determining pK_a.^41,42

To experimentally validate the computational results in Fig. 1 we investigate three systems in which charge density effects can be measured directly: gas phase acidities, specific ion effects on the behaviour of a thermoresponsive polymer, and nuclear magnetic resonance (NMR) spectroscopy.

2.2 Gas phase acidities match quantum chemical calculations

Proof of the influence of solvent on experimentally observed pK_a values and validation of our computational results is observed in the gas phase acidity value of difluoro- and dichloro-acetic acids.⁷ The reported gas-phase acidity, measured via the deprotonation energy relative to the value for acetic acid, for CCl₂HCOOH and CF₂HCOOH are −17.2 and −14.2 kcal mol⁻¹, respectively; i.e. the chloro-substituted acid is more acidic than the fluoro-substituted analogue. These gas phase reactions remove the influence of solvent on the pK_a and thus are simpler to interpret. Taft and Topsom attribute the difference in acidity of these two molecules to polarisability effects, as they state that the field effect (in the gas phase) is comparable between the two substituent groups.⁷ A similar phenomenon can be seen in the acidities of 4-X-bicyclo[2,2,2]octane-carboxylic acids, 4-X-bicyclo[2,2,1]heptane-1-carboxylic acids, and 4-substituted cubane-1-carboxylic acids.^5,7,8,43 In these later examples, the substituent is located at least five σ bonds from the carboxylic acid group and thus induction and polarisability effects, both of which are short-ranged, should not affect the overall acidity. Therefore any differences in acidity must result from differences in the strength of field effects. In the case of the bicyclo[2,2,2]octane carboxylic acids, the acidity increases in the order of F < Cl < Br substituents. This ordering is opposite to the electronegativity of the substituents and is consistent with our computational results in Fig. 1. The importance of field effects is also observed in dichloroethano-bridged anthracene derivatives, where the distance of the chloro substituents from the acid group has a major impact on the molecular acidity.⁴³ These gas phase acidities most directly compare to the wave functional theory (WFT) results from Fig. 1, where an isolated ion in a vacuum is considered.

2.3 Ion charge densities influence the impact of salt on the solvation of a thermoresponsive polymer

The presence of different ions can stabilise (salt-in) or destabilise (salt-out) macromolecules such as proteins or synthetic polymers.^44–47 Indeed the role of acetate ions on protein aggregation rates has previously been examined.⁴⁸ A common model system for investigating these specific ion effects is to examine changes in the thermoresponsive behaviour of poly(N-isopropylacrylamide), PNIPAM (Fig. 3a).^49,50 PNIPAM exhibits a first-order phase transition, commonly known as the lower critical solution temperature, LCST, at ≈32 °C in water. The exact temperature at which PNIPAM precipitates from solution is modified by the concentration and identity of any ions present. In aqueous electrolytes, ions with higher charge densities tend to have a salting-out effect (previously known as a kosmotropic effect), while more charge diffuse ions have a reduced salting-out effect or, at certain concentrations, act to stabilise and salt-in the polymer, modestly increasing the LCST of PNIPAM (previously known as the chaotropic effect).^26,49,50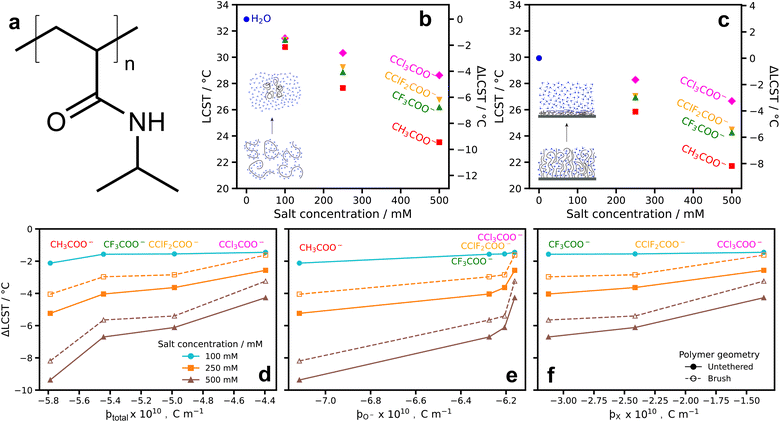

Fig. 3 Changes in LCST of poly(N-isopropylacrylamide) (PNIPAM) in the presence of substituted acetates (a) PNIPAM structure; (b) ΔLCST of untethered PNIPAM from cloud point measurements in aqueous, substituted-acetate electrolytes; (c) ΔLCST of surface-grafted PNIPAM brushes in the same electrolytes. Values from ellipsometrically determined brush thickness (Fig. S3†); (d–f) ΔLCST of untethered and surface-grafted PNIPAM as a function of each ion's ϸ_total, and partial ϸ values.

The magnitude (and nature) of effect an anion imparts on the LCST of PNIPAM is dictated by subtle, but profound, differences in the strength of ion–polymer, ion–solvent, and polymer–solvent interactions, with the counter-cation modulating the strength of the phenomena.^50–52 Our previous work has shown that the strength of these interactions is determined by the ion's radial charge density, ϸ.²⁶ This parameter, ϸ, has been shown to predict where ions fall on the classical Hofmeister series.²⁶ As ϸ is a measure of the site-specific radial charge density, it correlates directly with the partial charges of the oxygen atoms for acetate ions. This is demonstrated in Fig. S4† which shows the linear relationship between ϸ and the partial charge of oxygen in the carboxylate groups. In clear terms, for anions, ϸ is the primary parameter in determining the nature and relative magnitude of the effect of an anion on the LCST of PNIPAM.

While the charge density of the ion has been demonstrated to be the dominating factor that dictates specific ion effects, we must briefly discuss how ions influence the LCST of PNIPAM. By understanding these mechanisms, we can address the relationship between the LCST changes of PNIPAM and ion charge density, thus validating the computational results in Fig. 1. The comparatively weakly hydrated ions “salt-in” PNIPAM and have a favourable interaction with the polymer in a solvated environment.^26,49,53,54 This “ion binding” stabilises the polymer and can increase the LCST. More strongly hydrated ions, such as acetate are depleted from the polymer–solvent interface and thus do not provide this increased thermal stability. In addition, it has been proposed that these ions can dehydrate PNIPAM through polarisation of the water molecules and destabilisation of the hydrophobic hydration of the polymer through increased surface tension.⁴⁹ Salting-out effects due to ion bridging have also been observed in other systems, although that mechanism is unlikely to apply to this system.⁵⁵ The degree to which ions deplete from the polymer–solvent interface is thus determined by the balance of interactions between the ions, polymer, and solvent, which is in turn determined by the charge density of the ions.

Fig. 3b/c shows the LCST of untethered and surface-grafted PNIPAM, respectively, in aqueous electrolytes of four (substituted) acetates as a function of salt concentration. For the untethered polymer, LCST values were determined by cloud point turbidity measurements, while for the surface-grafted PNIPAM brush, layer thickness as a function of temperature was measured with spectroscopic ellipsometry and the LCST taken as the point of inflection of a sigmoid fit (Fig. S3†). Details surrounding this analysis approach are documented by Robertson et al.⁵⁶ The LCST of surface-grafted PNIPAM in pure H₂O is lower than the untethered LCST which can be attributed to differences in polymer molecular weight and the surface confinement of the polymer chains.^57,58 For both tethered and untethered PNIPAM, a monotonic decrease in the LCST with increasing concentration is observed for all electrolytes, consistent with related studies of PNIPAM and other neutral polymers.^50,59 For all concentrations, the ordering of the effect imparted by the substituted acetates on the LCST of PNIPAM is the same order as the partial charge of the oxygen atoms on the charged moieties; i.e., CH₃COO⁻ > CF₃COO⁻ > CClF₂COO⁻ > CCl₃COO⁻ (see Fig. 1c). We reiterate that these partial charge values are the inverse of what is expected for substituted ions according to classical inductive effects.

In Fig. 3d–f, we present the relationship between ϸ_total (the total charge density of the anion), as well as the site-specific ϸ_O⁻, and ϸ_X values and the change in LCST of untethered and surface-grafted PNIPAM. These results are consistent with our understanding of charge density and changes in LCST, with the largest ϸ_total (most charge dense) ion, acetate, having the greatest impact on the LCST, whilst trichloroacetate, the least charge dense (smallest ϸ_total), imparts the smallest effect. This trend also occurs for the site-specific ϸ values (ϸ_O⁻, and ϸ_X; Fig. 3e/f). ϸ_O⁻ values match the trend in the change in LCST, albeit with a more complex, non-linear relationship. The ϸ_X values are consistent with the partial charges, in Fig. 1d, with the largest charge density present on the fluorine substituents of CF₃COO⁻. Interpreting the results in Fig. 3 through the lens in which specific ion effects influence the LCST of PNIPAM, experimentally validates the unusual charge densities of the carboxylate ions in Fig. 1.

To complement these experimental studies, symmetry-adapted perturbation theory (SAPT) calculations as well as molecular dynamics (MD) simulations were performed. The SAPT-derived interaction energies between these ions and a PNIPAM fragment (or water) molecule (Fig. S5†) illustrate the same trends as in Fig. 3. In these results, the strength of ion–polymer or ion–solvent interactions is shown to vary with charge density. Further discussion of these results is provided in the ESI.† Spatial distribution functions obtained from MD simulations are also reported in Fig. S6† and demonstrate differences in the nature of the interaction between the different acetate ions and PNIPAM. Most importantly, the results from both SAPT and MD indicate that ions interact most strongly through the charged oxygen groups of the substituted acetate ions and not through hydrophobic “tail” group interactions. As such, it is the charge density of the ions that dictates the extent of ion binding to the polymer, which in turn modulates the salting-out effects imparted by the acetates.

It is clear that complex specific ion effects and their influence on the LCST of PNIPAM are related to the charge density of the ions. The order of substituted acetate charge densities correlations with LCST data according to the standard Hofmeister anion series.⁶⁰ It is worth noting that perturbations to the Hofmeister series can arise due to numerous factors,⁶¹ including ion pairing,⁵⁵ or changes of the cation identity.⁶² The strong correlation of the LCST data with charge density suggests these are not dominant factors for this system. Variations in charge density influence the net balance of ion–polymer and ion–solvent interactions, and thus allow this system to act as an experimental probe to verify the unusual charge densities of the substituted acetates.

Neutron reflectometry was also employed to examine how the temperature-dependent structure of a PNIPAM brush is influenced by the presence of 500 mM of the acetate salts. Fig. 4a shows the polymer volume fraction of a PNIPAM brush at 27 °C, with the inset showing the experimental and modelled data. Data was modelled using a Markov chain Monte Carlo sampling method,^63,64 which produced high-quality fits under all conditions. The change in brush structure in Fig. 4a is consistent with the turbidity and ellipsometry measurements in Fig. 3b/c, with the extent of brush collapse proportional to the magnitude of the anion's ϸ_total. A comprehensive suite of brush volume fraction profiles is presented in Fig. S7,† which is entirely consistent with the results in Fig. 3.

Fig. 4 Structure of PNIPAM brushes and salt distributions. (a) Polymer volume fraction profiles of a PNIPAM brush as determined by neutron reflectometry in D₂O at 27 °C. Measurements in 500 mM solutions for the sodium salt acetates. Inset shows raw and modelled data highlighting the high quality of fit; (b) raw and modelled neutron reflectometry of a PNIPAM brush in contrast matched solution (SLD = 0.8 × 10⁻⁶ Å⁻²) at 32 °C. At this contrast, the reflectivity is due to scattering from salt ions, allowing for the determination of the density of salt within the brush structures; (c) extracted interfacial volumes for the salts determined via neutron reflectometry. The inset shows a magnification at higher temperatures.

Contrast variation reflectometry experiments were also performed to reveal the distribution of salt within a PNIPAM brush. Interfacial distribution profiles of the (substituted) acetates were resolved by matching the isotopic contrast of the solvent (D₂O/H₂O) to that of the polymer. These profiles correspond to the surface excess of acetate arranged within the brush. A similar approach has been employed to determine counterion distributions around PNIPAM microgels with small angle neutron scattering (SANS),⁶⁵ but has not been demonstrated previously with neutron reflectometry. Fig. 4b shows the experimental and modelled data for the four salt solutions, again highlighting the high quality of the fit. Corresponding data for all conditions can be found in the ESI (Fig. S7 and S8).†Fig. 4c shows the interfacial volume of the ions at the interface, which is a convenient measure of salt concentration within the brush. At low temperatures when the brush is highly solvated, the reflectivity profiles of the ions are rather featureless (Fig. S8†). As such the interfacial volume values possess very large uncertainties. This combined with the variations in the brush thickness between the salts for a given temperature makes meaningful interpretation difficult. However, at higher temperatures, the brush collapses and the thickness is invariant across all conditions. While there is still a reasonable degree of uncertainty in these interfacial volume values, a trend appears in the concentrations of the salts within the collapsed brush at 32 °C, with the concentration increasing in the order CH₃COO⁻ < CF₃COO⁻ < CClF₂COO⁻ < CCl₃COO⁻. This trend is consistent with the observation that the charge density of substituted acetates in aqueous solution is inverse to that expected from induction effects, resulting in the least charge dense CCl₃COO⁻ binding most strongly with the PNIPAM brush at 27 °C and 32.5 °C.⁶⁶

2.4 ¹³C NMR confirms anomalous substituent effects

Further experimental evidence for unexpected long-range substituent effects can be seen in the previously reported ¹³C chemical shifts of haloalkanes determined by NMR.⁶⁷ In Fig. 5, the ¹³C NMR shifts of a series of 1-haloalkanes and 1-alcohols are shown. Here, a greater chemical shift indicates a more electronically de-shielded carbon nucleus. For C1 (Fig. 5a–c), the chemical shifts are proportional to our current understanding of the inductive effect, with more electronegative substituents (F, O, Cl) withdrawing more electron density than other substituents (I, Br). However, at C2 and C3 for the longer chain alkanes (Fig. 5d/e and f respectively), an inverse relationship between the electronegativity of the substituent and the chemical shift can be seen. Similar results can be seen in the corresponding ¹H NMR (Fig. S9†).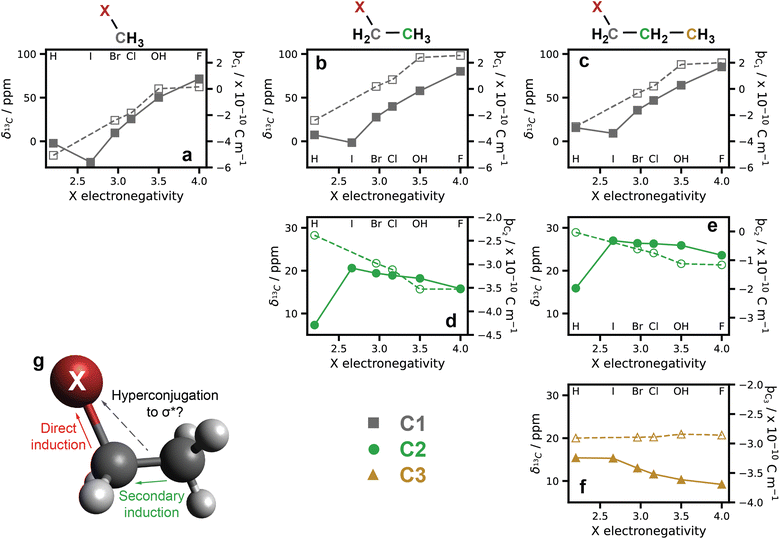

Fig. 5 Substituted alkanes ¹³C NMR wave function theory (WFT) charge densities: ¹³C NMR chemical shifts of a number of 1-halo- and 1-alcohol alkanes (C_n = 1, 2, or 3) in CDCl₃ against the substituent electronegativity. NMR values were extracted from Pretsch et al.⁶⁷ while electronegativity values were taken from Wells.⁶⁸ NMR values are indicated with solid symbols and lines. For C1 (a–c) an increased chemical shift, and therefore electronic de-shielding, is observed with increasing electronegativity in keeping with our understanding of substituent effects. For C2 (d and e) and C3 (f), an inverse relationship between substituent electronegativity and de-shielding is observed, contrary to expected results. Qualitatively the same results are observed for charge densities calculated from WFT (parameterised by ϸ_C values) denoted with open symbols and dashed lines. (g) A cartoon showing the hypothesised electron withdrawing hyperconjugation giving rise to these effects.

It is known that heavy atom effects can influence NMR spectra,^69–71 and so as verification, WFT calculations were also performed on this series of haloalkanes. Charge density is parameterised as partial ϸ_C values and are shown as open symbols in Fig. 5. Qualitatively the same trends as in the NMR results are observed with electron density of C₂ counter-intuitively decreasing with increasing electronegativity of the substituent atom. The consistency of these NMR and WFT results highlights the anomalous relationship between substituent electronegativity and charge, and also suggests that this phenomenon is not unique to a specific system.

3 Conclusions

Why then do the larger halogens withdraw more electron density from C2 and C3 carbons in 1-haloalkanes and from the charged oxygens in substituted acetates? According to Taft and Topsom, the strength of field effects of –CCl₃ and –CF₃ groups is identical in the gas phase.⁷ In non-polar solvents, the field strength around a fluoro substituent is identical to a chloro group, while in polar solvents F > Cl.^10,11 As such it is unlikely that field effects on their own are responsible for all of the anomalous behaviour discussed above. Differences in the acidity of chloro- and fluoro-substituted molecules have been previously attributed to polarisability differences. However, polarisability effects should not impact the electronic distribution of a molecule/ion in isolation. It is possible, indeed likely, that in the substituted acetates hyperconjugation occurs between the π-system of the carboxylate group and the antibonding orbitals of the CX₃ group. From the wave function theory calculations, slight differences in bond lengths between the in-plane and out-of-plane C–X bonds are observed (Table S2†). These differences are greater for the trichloro-substituted acetate suggesting a greater extent of hyperconjugation. There is also a more noticeable increase in the C–C bond length in CCl₃COO⁻ compared to CF₃COO⁻. It is known that hyperconjugation effects are typically lower for substituents with greater electronegativity.^72–74 In the haloalkanes, hyperconjugation between the σ(C₂–H) or σ(C₂–C₃) and σ*(C₁–X) could also occur giving rise to the counter-intuitive electron densities. Thus, hyperconjugation could help to explain the unexpected charge density of the carboxylate groups in substituted acetates and haloalkanes. Further computational work including geometry/bond rotation studies could help elucidate the role that hyperconjugation plays in anomalous charge densities in substituted systems.

Data availability

The data supporting this article have been included as part of the ESI:† all synthetic and characterisation protocols. Comparison of charge densities from different decomposition methods. Relationship between charge density and pK_a. In situ ellipsometry data. Oxygen partial charge and charge density relationships. Symmetry adapted perturbation theory results. Density functional tight binding molecular dynamics spatial distribution functions. In situ neutron reflectometry. ¹H NMR of 1-haloalkanes. Data files are available upon request from the authors.

Author contributions

Edwin C. Johnson: conceptualisation, project administration, methodology, investigation, formal analysis, software, data curation, writing – original draft, visualisation, writing – review & editing, funding acquisition. Kasimir P. Gregory: conceptualisation, methodology, investigation, formal analysis, software, data curation, writing – original draft, visualisation, writing – review & editing, funding acquisition. Hayden Robertson: methodology, investigation, formal analysis, software, data curation, writing – original draft, visualisation, writing – review & editing, funding acquisition. Isaac J. Gresham: methodology, investigation, formal analysis, software, data curation, writing – original draft, visualisation, writing – review & editing, funding acquisition. Andrew R. J. Nelson: methodology, software, writing – review & editing, supervision, funding acquisition. Vincent S. J. Craig: writing – review & editing, funding acquisition. Stuart W. Prescott: investigation, software, supervision, funding acquisition. Alister J. Page: resources, methodology, writing – review & editing, supervision, funding acquisition. Grant B. Webber: resources, methodology, writing – review & editing, supervision, funding acquisition. Erica J. Wanless: project administration, resources, writing – review & editing, supervision, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Australian Centre for Neutron Scattering Program Grant (PP9789) under P8583. E. C. J., K. P. G., H. R., and I. J. G. thank the Australian Government for providing research training scholarships. E. C. J., H. R. and I. J. G. also thank AINSE Ltd for providing financial assistance via PGRA Awards. This research was supported with funding from the Australian Research Council through a Discovery Grant (DP230102030). K. P. G. would like to acknowledge that this work was supported by the NCI Adapter Scheme, with computational resources provided by NCI Australia, an NCRIS-enabled capability supported by the Australian Government.

Notes and references

1. P. Sykes, A guide to Mechanisms in Organic Chemistry, 5th edn, Longman, 1961.
2. J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford University Press, 2001.
3. M. John, Fundamentals of Organic Chemistry, Cengage Learning, Inc, 2002.
4. P. S. Bailey and C. A. Bailey, Organic Chemistry: A Brief Survey of Concepts and Applications, Prentice-Hall, 1995.
5. E. V. Anslyn and D. A. Dougherty, in Experiments related to thermodynamics and kinetics, University Science Books, 2006, ch. 8, pp. 421–489.
6. V. A. Stepanova and J. K. West, J. Chem. Educ., 2024, 101(7), 2815–2822.
7. R. W. Taft and R. D. Topsom, in Progress in Physical Organic Chemistry: The Nature and Analysis of Substituent Electronic Effects, Wiley, 1987, ch. 1, pp. 1–83.
8. T. W. Cole, C. J. Mayers and L. M. Stock, J. Am. Chem. Soc., 1974, 96, 4555–4557.
9. C. F. Wilcox and C. Leung, J. Am. Chem. Soc., 1968, 90, 336–341.
10. S. Marriott and R. D. Topsom, J. Am. Chem. Soc., 1984, 106, 7–10.
11. C. Jinfeng and R. D. Topsom, J. Mol. Struct.: THEOCHEM, 1990, 204, 353–359.
12. C.-T. Cao and C. Cao, J. Chem. Educ., 2023, 100, 2680–2685.
13. W. L. Jolly and W. B. Perry, J. Am. Chem. Soc., 1973, 95, 5442–5450.
14. G. Bianchi, O. W. Howarth, C. J. Samuel and G. Vlahov, J. Chem. Soc., Perkin Trans. 2, 1995, 1427–1432.
15. S. Sakakibara and N. Inukai, Bull. Chem. Soc. Jpn., 1965, 38, 1979–1984.
16. G. Zheng, S. M. Eick and A. Salamova, Environ. Sci. Technol., 2023, 57, 15782–15793.
17. R. C. Buck, J. Franklin, U. Berger, J. M. Conder, I. T. Cousins, P. de Voogt, A. A. Jensen, K. Kannan, S. A. Mabury and S. P. van Leeuwen, Integr. Environ. Assess. Manage., 2011, 7, 513–541.
18. L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582.
19. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
20. The Organic Chemistry Tutor, Inductive Effect – Acids and Bases, 2023, https://www.youtube.com/watch?v=F7mbfPmOugY, accessed on 21/01/2024.
21. Chem Help ASAP, The inductive effect, 2019, https://www.youtube.com/watch?v=umNZHFbQ7SY, accessed on 21/01/2024.
22. Leah4sci, Inductive Effect on Acidity in Organic Chemistry Vid 6, 2015, https://www.youtube.com/watch?v=KoC-PinXWCA, accessed on 21/01/2024.
23. Khan Academy, Stabilization of a conjugate base: induction, 2015, https://www.khanacademy.org/science/organic-chemistry/organic-structures/acid-base-review/v/stabilization-of-a-conjugate-base-induction-new, accessed on 21/01/2024.
24. Master Organic Chemist and J. Ashenhurst, Five Key Factors That Influence Acidity, 2022, https://www.masterorganicchemistry.com/2010/09/22/five-key-factors-that-influence-acidity/, accessed on 21/01/2024.
25. LibreTextsChemistry, 20.4: Substituent Effects on Acidity, 2015, https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_(Morsch_et_al.)/20%3A_Carboxylic_Acids_and_Nitriles/20.04%3A_Substituent_Effects_on_Acidity, accessed on 31/01/2024.
26. K. P. Gregory, E. J. Wanless, G. B. Webber, V. S. J. Craig and A. J. Page, Chem. Sci., 2021, 12, 15007–15015.
27. C. Ni and J. Hu, Chem. Soc. Rev., 2016, 45, 5441–5454.
28. C. Ni, Y. Li and J. Hu, J. Org. Chem., 2006, 71, 6829–6833.
29. D. Cahard and V. Bizet, Chem. Soc. Rev., 2014, 43, 135–147.
30. C. Thiehoff, Y. P. Rey and R. Gilmour, Isr. J. Chem., 2017, 57, 92–100.
31. P. Kirsch and M. Bremer, ChemPhysChem, 2010, 11, 357–360.
32. L. Samuelsen, R. Holm, A. Lathuile and C. Schönbeck, Int. J. Pharm., 2019, 560, 357–364.
33. F. Rived, I. Canals, E. Bosch and M. Rosés, Anal. Chim. Acta, 2001, 439, 315–333.
34. A. Kütt, S. Tshepelevitsh, J. Saame, M. Lõkov, I. Kaljurand, S. Selberg and I. Leito, Eur. J. Org Chem., 2021, 2021, 1407–1419.
35. M. Gupta, E. F. da Silva and H. F. Svendsen, J. Phys. Chem. B, 2013, 117, 7695–7709.
36. F. Millero, F. Huang, T. Graham and D. Pierrot, Geochim. Cosmochim. Acta, 2007, 71, 46–55.
37. H. S. Harned and F. C. Hickey, J. Am. Chem. Soc., 1937, 59, 1284–1288.
38. V. Mandalaparthy, M. Tripathy and N. F. A. van der Vegt, J. Phys. Chem. Lett., 2023, 14, 9250–9256.
39. E. C. Johnson, J. D. Willott, W. M. de Vos, E. J. Wanless and G. B. Webber, Langmuir, 2020, 36, 5765–5777.
40. V. Bütün, S. P. Armes and N. C. Billingham, Polymer, 2001, 42, 5993–6008.
41. J. Makowska, M. Makowski, A. Liwo and L. Chmurzyński, J. Comput. Chem., 2005, 26, 235–242.
42. Z. Pawelka and M. C. Haulait-Pirson, J. Phys. Chem., 2002, 85, 1052–1057.
43. E. Grubbs, R. Fitzgerald, R. Phillips and R. Petty, Tetrahedron, 1971, 27, 935–944.
44. K. P. Gregory, G. R. Elliott, H. Robertson, A. Kumar, E. J. Wanless, G. B. Webber, V. S. J. Craig, G. G. Andersson and A. J. Page, Phys. Chem. Chem. Phys., 2022, 24, 12682–12718.
45. D. K. Eggers and J. S. Valentine, J. Mol. Biol., 2001, 314, 911–922.
46. H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014.
47. K. B. Rembert, J. Paterová, J. Heyda, C. Hilty, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2012, 134, 10039–10046.
48. G. V. Barnett, V. I. Razinkov, B. A. Kerwin, A. Hillsley and C. J. Roberts, J. Pharm. Sci., 2016, 105, 1066–1073.
49. Y. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, J. Am. Chem. Soc., 2005, 127, 14505–14510.
50. S. Z. Moghaddam and E. Thormann, J. Colloid Interface Sci., 2019, 555, 615–635.
51. H. Robertson, I. J. Gresham, A. R. J. Nelson, K. P. Gregory, E. C. Johnson, J. D. Willott, S. W. Prescott, G. B. Webber and E. J. Wanless, Langmuir, 2024, 40, 335–347.
52. H. Robertson, J. D. Willott, K. P. Gregory, E. C. Johnson, I. J. Gresham, A. R. J. Nelson, V. S. J. Craig, S. W. Prescott, R. Chapman, G. B. Webber and E. J. Wanless, J. Colloid Interface Sci., 2023, 634, 983–994.
53. K. P. Gregory, G. B. Webber, E. J. Wanless and A. J. Page, J. Phys. Chem. A, 2019, 123, 6420–6429.
54. E. E. Bruce, P. T. Bui, B. A. Rogers, P. S. Cremer and N. F. A. van der Vegt, J. Am. Chem. Soc., 2019, 141, 6609–6616.
55. J. Heyda, H. I. Okur, J. Hladílková, K. B. Rembert, W. Hunn, T. Yang, J. Dzubiella, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2017, 139, 863–870.
56. H. Robertson, I. J. Gresham, S. W. Prescott, G. B. Webber, E. J. Wanless and A. Nelson, SoftwareX, 2022, 20, 101225.
57. T. Patel, G. Ghosh, S. ichi Yusa and P. Bahadur, J. Dispersion Sci. Technol., 2011, 32, 1111–1118.
58. B. A. Humphreys, J. D. Willott, T. J. Murdoch, G. B. Webber and E. J. Wanless, Phys. Chem. Chem. Phys., 2016, 18, 6037–6046.
59. Y. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10, 658–663.
60. W. Kunz, J. Henle and B. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37.
61. V. Mazzini and V. S. Craig, Chem. Sci., 2017, 8, 7052–7065.
62. E. E. Bruce, H. I. Okur, S. Stegmaier, C. I. Drexler, B. A. Rogers, N. F. A. van der Vegt, S. Roke and P. S. Cremer, J. Am. Chem. Soc., 2020, 142, 19094–19100.
63. A. R. J. Nelson and S. W. Prescott, J. Appl. Crystallogr., 2019, 52, 193–200.
64. I. J. Gresham, T. J. Murdoch, E. C. Johnson, H. Robertson, G. B. Webber, E. J. Wanless, S. W. Prescott and A. R. J. Nelson, J. Appl. Crystallogr., 2021, 54, 739–750.
65. B. Zhou, U. Gasser and A. Fernandez-Nieves, Nat. Commun., 2023, 14, 3827.
66. B. A. Rogers, H. I. Okur, C. Yan, T. Yang, J. Heyda and P. S. Cremer, Nat. Chem., 2022, 14, 40–45.
67. E. Pretsch, P. Buhlmann and M. Badertscher, Structure Determination of Organic Compounds: Tables of Spectral Data, 4th edn, Springer, 2009.
68. P. R. Wells, in Group Electronegativities, Wiley, 1968, ch. 3, pp. 111–145.
69. R. V. Viesser, L. C. Ducati, C. F. Tormena and J. Autschbach, Phys. Chem. Chem. Phys., 2018, 20, 11247–11259.
70. A. C. Neto, L. C. Ducati, R. Rittner, C. F. Tormena, R. H. Contreras and G. Frenking, J. Chem. Theory Comput., 2009, 5, 2222–2228.
71. K. B. Wiberg, W. E. Pratt and W. F. Bailey, J. Org. Chem., 1980, 45, 4936–4947.
72. R. C. Bingham, J. Am. Chem. Soc., 1975, 97, 6743–6746.
73. I. V. Alabugin and T. A. Zeidan, J. Am. Chem. Soc., 2002, 124, 3175–3185.
74. W. Wang and P. Hobza, J. Phys. Chem. A, 2008, 112, 4114–4119.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04832f

---