Insights into the role of hierarchical porosity in zeolite architectures for selective uptake of metal ions in solution

Abstract

The ability to match two levels of porosity in hierarchical structures obtained via the top-down approach greatly enhances the adsorption capacity of zeolites. The effect of top-down desilication treatment on different topological frameworks (MFI, FAU and natural HEU) was evaluated by varying the pH (from 8 to 13.3) of alkaline solutions to minimize the loss of crystallinity and acidity. The structural, textural and acidity properties of the hierarchical zeolites were examined using a range of physicochemical characterization tools. In particular, the amount, location and accessibility of the Brønsted acid sites, the locus for cation exchange, processes were studied by FTIR spectroscopy using basic probe molecules with different kinetic diameters, and the accessibility factor (AF) was calculated. Finally, an improvement in the uptake capacity of Cu²⁺ and Co²⁺ cations from aqueous solutions, with different affinities and selectivities depending on the topological structures, was observed.

---

Introduction

Zeolites are extremely interesting and versatile microporous crystalline materials, owing to their unique chemical and structural properties that find extensive utility across various applications in both research and industrial domains, including: (i) regular microporosity, promoting molecular sieve behaviour with exceptional shape selectivity; (ii) notable ion exchange capacity; (iii) a significant number of acid sites exhibiting diverse strengths; (iv) exceptional thermal stability and high specific surface area (SSA).¹ Notably, they serve as effective dehydrating agents in liquid and gas treatment systems, cation exchangers in water-softening plants,^2,3 molecular sieves³ and they play pivotal roles as heterogeneous catalysts.^3,4

Among the distinctive properties of zeolites, the existence of acid sites belonging to the crystalline structure plays a prominent role, especially in catalysis applications.^5–7 In zeolites, acidity is predominantly attributed to the presence of Brønsted acid sites (BAS), which arise from trivalent aluminum within the framework.^5,8 Specifically, the bridging of an oxygen atom between a silicon(IV) atom and an aluminum(III) atom induces a net negative charge on oxygen, which can be balanced by the presence of H⁺ ions,^5,8 with the formation of Brønsted (Si–OH–Al) surface sites, namely BAS sites.⁹

Although microporosity is a primary characteristic of zeolites, it introduces notable limitations, particularly concerning catalytic applications. Specifically, the exclusive presence of micropores at the molecular scale within the crystalline structure may pose significant challenges to the internal diffusion of chemical species.^1,10,11 This limitation restricts the range of selectivity of achievable products and increases the susceptibility of the material to coke deposition phenomena. These factors not only contribute to the gradual decline in pore accessibility, leading to material deactivation, but also promote the formation of undesired by-products.¹

To overcome the limitations associated with the microporous nature of conventional zeolites, hierarchical zeolites, defined as such when they possess at least two interconnected classes of pores of different sizes,^10,12 have been developed. Mesopores, which range in size from 2 to 50 nm, are the most representative form of secondary porosity in hierarchical zeolites.^1,13 They provide significant advantages in terms of access to the internal surface area of the material without causing an excessive decrease in the specific surface area, which would otherwise result in a drastic alteration of the catalytic properties.¹

There are several synthetic paths to obtain hierarchical materials. A potential route is represented by top-down approaches, according to which mesoporosity is introduced through post-synthetic dealumination (acidic environment) or desilication (basic environment) treatments of pre-formed microporous materials.^10–18 The concept behind these methodologies lies in the partial degradation of the initial microporous material's structure, creating intracrystalline porosity with larger cavity sizes. However, these treatments act non-specifically on the entire surface of the material; consequently, the resulting porosity lacks long-range order and defined dimensions and is characterized by its heterogeneity.^19,20

In desilication processes, the partial instability of the zeolitic framework under basic conditions is exploited to extract silicon atoms from the crystalline structure.^17,21–26 The procedure involves contacting the microporous material with a diluted sodium hydroxide (NaOH) solution; contact time, temperature and initial concentration of the NaOH solution are the key parameters as they significantly influence the final properties of the hierarchical material. Thus, excessively low or excessively high values of those parameters lead to a lack of alteration of the starting structured material or its total disintegration, respectively.^26,27 The necessity for direct contact between hydrolysable bonds and OH⁻ ions means that the physicochemical properties of the zeolite, which can affect this interaction, play a crucial role in defining the treatment's effectiveness and, consequently, the controlled introduction of mesoporosity into the microporous material.^17,19,23,28 Among these properties, the aluminum content within the crystalline lattice and its distribution therein is particularly critical;^1,23,29 indeed, the occurrence of negative charges in the framework generated by the presence of Al³⁺ can partially hinder the hydrolytic action of OH⁻ species.²⁹ Thus, aluminum is considered a moderating agent in this process, and as a consequence, zeolites react differently to the treatment according to their respective Si/Al ratios.^17,29,30

During the desilication process, both inorganic and organic bases can be used; however, inorganic bases like NaOH are more selective for silicon removal and more cost-effective.^1,19 The removal of silicon atoms from the zeolite framework perturbs the microporous network, leading to mesopore formation and concurrently increasing the concentration of structural defects together with significant alterations in the population of acidic sites on zeolite surfaces.^16,31 This has notable implications on the accessibility of surface silanols (Si–OH) and Brønsted acid sites;³¹ consequently, the properties of zeolitic materials can be significantly improved once their hierarchical form is obtained.^17,25,32,33

The position of Brønsted acid sites in the material framework is an important feature of hierarchical zeolites. Accurately identifying and quantifying BAS within the interconnected dual-porosity structure is essential to better comprehend the acid properties and catalytic behaviour of these systems.²⁷ Fourier Transform Infrared (FTIR) spectroscopy, enhanced by the use of probe molecules adsorbed onto the material surface, is a highly effective technique for this purpose. The interaction between the probe molecules and the zeolitic surface groups induces perturbations in the IR signals of both entities, thus allowing both qualitative and semi-quantitative insights into the present acid sites.⁵ In this context, a critical parameter is represented by the accessibility of these sites, which is intrinsically related to their distribution within the micro-, meso-, or macroporous cavities.^31,34 This type of analysis involves a comparison between the FTIR spectra obtained before and after the adsorption of a probe molecule with basic properties and evaluating any potential discrepancies in the position or shape of the vibrational signals.^11,31,35,36 Specifically, the ion-pair method relies on the protonation of strong bases, typically ammonia or pyridine. The interaction between these bases and the surface species of the material generates new bands in the FTIR spectrum, which are then monitored.^22,37 The main advantage of this approach is that the appearance of the protonated base signals in the FTIR spectrum provides unequivocal evidence of the presence of BAS.^5,38 On the other hand, the lack of a characteristic spectral feature directly proportional to the strength of the probe-substrate interaction means that this methodology does not allow the direct measurement of acidic strength. To isolate the signals associated with the protonated probe molecule and eliminate those associated with weak interactions between the probe and surface species for a semi-quantitative determination of the Brønsted acid sites, variable-temperature desorption experiments are necessary.^31,34,39,40 For the evaluation of acid site accessibility, as well as the actual presence of larger porous structures, basic probes of varying kinetic diameters are employed.^33,41–43 To this purpose, substituted pyridines are particularly useful as they can selectively interact with acid sites located within meso- and macropores due to their large kinetic diameter, which prevents them from entering micropores.^22,26,31,40

A detailed study of the acid properties of hierarchical zeolites is fundamental for their application in metal removal because the Si/Al ratio, which is correlated to their acidity, directly influences the interaction mechanisms involved.⁴⁴ The uptake of metal ions by zeolitic systems occurs through multiple processes, including interactions with surface hydroxyl species, cation exchange, and adsorption.^44–46 In this context, the number, spatial distribution, and positioning of BAS, which are the most readily deprotonatable acidic sites, play key roles in determining the uptake performance of the studied materials. This aspect is particularly significant for synthetic zeolites, which lack the typical exchangeable cations (e.g., Ca²⁺, Mg²⁺, Na⁺) that are commonly present in natural zeolites.

Transition metals and their complexes play a crucial role in technological applications because of their distinctive optical and catalytic properties.^47–49 However, their increasing use has led to a rising accumulation of waste containing these metals. Industrial discharge and electronic waste contribute to the release of transition metals into the environment, categorizing them as emerging contaminants with largely uncharacterized ecological effects.⁵⁰ While mineral ore extraction remains the primary source of these metals, recycling strategies are gaining attention.⁵¹ Among them, solid–liquid extraction (SLE) and liquid–liquid extraction (LLE) represent two viable approaches for this purpose. SLE, which relies on ion exchange, adsorption, and complexation, presents several advantages over LLE, including a lower number of operational steps, reduced solvent consumption and the utilization of reusable solid supports, making it a more sustainable and efficient alternative.⁵²

In this context, zeolites are suitable systems for the adsorption of metal pollutants from aqueous solutions because they can effectively remove metal ions due to their adsorption and exchange properties.⁴⁶ Moreover, a desilication treatment could be useful for conferring a greater mesoporous character to these materials, addressing common limitations such as restricted diffusion and low accessibility of BAS.^20,53 This modification can enhance their overall performance, offering more efficient pollutant removal thanks to increased accessibility and improved interaction with metal ions.

Based on the considerations made thus far, this study investigated the top-down desilication of three different microporous zeolites in a basic environment to develop their hierarchical variants. The selected zeolites included two commercial synthetic zeolites, ZSM5 and USY (Ultra Stable Y), both with a SiO₄/Al₂O₃ ratio of 80 and exhibiting MFI and FAU crystalline lattices, respectively, as well as a natural clinoptilolite with an HEU-type lattice. The ZSM-5 zeolite featured an MFI-type framework composed of pentasil structural building units (SBUs), each consisting of eight five-membered rings. The spatial arrangement of multiple SBUs produces a crystalline lattice characterized by a bidirectional 10-membered ring channel system. One channel runs parallel to the crystallographic [010] axis and is defined by an elliptical pore aperture of 5.3 × 5.6 Å. The second channel system consists of sinusoidal elliptical channels running parallel to the (100) axis with an aperture of 5.1 × 5.5 Å. The intersectional voids between the two orthogonal channel systems form approximately spherical cavities with a diameter of 6.4 Å.^54,55 The USY zeolite exhibits a FAU crystal framework formed by the interconnection of sodalite cages (also referred to as β-cages), which are connected through their 6-membered rings (D6R, hexagonal prisms). This three-dimensional network presents micropores composed of 12-membered rings (7.4 × 7.4 Å) and larger supercages with a diameter of 11.24 Å, which are accessible in all three dimensions through 12-membered ring windows.⁵⁶ In contrast, Clinoptilolite exhibits a HEU type framework, characterized by a two-dimensional porous system consisting of three different families of microporous channels. Two of these families run parallel to the crystallographic axis [001] and are formed by elliptical channels delimited by 8- and 10-membered rings with dimensions of 4.1 × 4.7 Å and 4.4 × 7.2 Å, respectively. The third family, consisting of 8-membered ring channels with dimensions of 4.0 × 5.5 Å, runs perpendicular to the first two along the crystallographic axis [100].^57,58

The obtained hierarchical zeolites were then subjected to multi-technique characterization to determine their physicochemical properties, with a particular focus on their acidic properties. The characterization techniques included X-ray powder diffraction (XRPD), textural and thermogravimetric analysis (TGA), field emission scanning electron microscopy (FESEM), energy-dispersive X-ray spectrometry (EDX) and Fourier-transform infrared (FT-IR) spectroscopy enhanced by the use of probe molecules.⁵⁹ Finally, the developed hierarchical zeolites together with their microporous counterparts were evaluated as adsorbent materials for Cu²⁺ and Co²⁺ ions in an aqueous solution to compare their efficiency in metal removal before and after desilication treatment.

Results and discussion

The three microporous zeolites (HUSY-P, HCLI-P, and HZSM5-P) investigated in this study underwent alkaline desilication treatment to generate their respective hierarchical variants. Specifically, three NaOH solutions at different pH values (8, 9, and 13.3) were employed to assess the resilience of the distinct zeolitic frameworks to varying concentrations of OH⁻ hydrolytic species; the resulting hierarchical zeolites samples are labelled with the pH values used in the desilication process. The structural organization of each zeolite is crucial in defining the extent of modification following exposure to a basic environment because it influences the material's response to the treatment.^14,23 Therefore, a comprehensive analysis of the treatment effectiveness under different pH conditions is essential for optimizing the desilication process for each material. The alkaline treatment, while increasing the defect concentration within the framework and introducing intracrystalline mesoporosity, is also able to perturb the distribution and concentration of Brønsted acid sites (BAS) in the material. Consequently, the resulting hierarchical zeolites were thoroughly characterized using structural, volumetric, and spectroscopic physicochemical techniques.

X-ray powder diffraction (XRPD) analyses were performed to assess the maintenance of the crystalline structure in hierarchical zeolites (Fig. 1 and S1). The diffraction patterns of all desilicated HZSM5 zeolite samples exhibit the characteristic peaks associated with the MFI structure (Fig. 1A); a decrease in peak intensity was observed only for HZSM5-13.3. These results demonstrate the strong resistance of the MFI framework in an alkaline environment, as previously documented in the literature.^{22–24,26,29,60} On the other hand, the large-pore faujasite (FAU) structure of zeolite Y demonstrates increased sensitivity to treatment conditions (Fig. 1B).^27,61 While the HUSY-8 sample maintains visible high-intensity peaks, further increases in pH result in a significant reduction of the latter, leading to total amorphization in the case of the HUSY-13.3 sample. In the context of natural clinoptilolite, X-ray diffraction (XRD) analysis is particularly valuable for identifying impurities within the parent sample (Fig. S1C†). The XRD pattern of the parent material reveals not only the characteristic reflections of the heulandite structure (main peaks of HEU structure at 2θ angles of 9.8°, 11.2°, 13.1°, 17.3°, 22.5°, 30.2°), but also the presence of additional phases, specifically mordenite and albite.⁶² Samples HCLI-8, HCLI-9, and HCLI-13.3 were further analysed using the X-ray powder diffraction (XPRD) technique, and the results indicate that this zeolite exhibits resistance to alkaline treatments (Fig. 1C). To further elucidate the impact of the basic treatments on the different zeolitic materials, the relative crystallinity index (RC%) of each sample was determined (Table 1) following the procedure described in the experimental section.

Fig. 1 XRD patterns of (A) HZSM5, (B) HUSY and (C) HCLI samples desilicated under different pH conditions.

Table 1 Relative crystallinity indexes (RC %) for each sample, calculated as reported in the experimental section

Sample	RC%
HZSM5-P	100
HZSM5-8	92
HZSM5-9	92
HZSM5-13.3	74
HUSY-P	100
HUSY-8	96
HUSY-9	38
HUSY-13.3	—
HCLI-P	72
HCLI-8	81
HCLI-9	100
HCLI-13.3	93

---

Alkaline treatment typically induces a reduction in the crystallinity degree of zeolites, which is attributable to the extraction of Si atoms and a lesser extent, Al from the zeolitic framework. The magnitude of this reduction is generally correlated with the basicity of the desilicating solution.^{26,33,63–65} In contrast, clinoptilolite samples exhibit two distinct behaviors: (i) modification with highly diluted alkaline solutions results in a progressive enhancement of RC%, reaching a maximum in the HCLI-9 sample; (ii) conversely, when the pH of the desilication process is elevated (up to 13.3), a significant decrease, up to 93%, is observed. This phenomenon can be attributed to the ability of the diluted alkaline solution to selectively dissolve amorphous silicon deposits while preserving the structurally resilient clinoptilolite particles with a low Si/Al ratio, thus minimally affecting the material's structural integrity.⁶⁶

Consequently, moderate treatment conditions resulted in a purification effect on the natural zeolite. In contrast, when a solution with a pH of 13.3 is employed, the increased basicity promotes a partial amorphization process that prevails over the ‘purification’ effect associated with impurity removal, resulting in a pronounced decrease in relative crystallinity.^63,66 Comparative analysis of the X-ray diffraction (XRD) patterns of desilicated samples reveals a notable distinction among the three zeolites studied. Specifically, the HUSY zeolite exhibits the most significant susceptibility to treatment, indicating a marked instability of its crystal structure under alkaline conditions.

The effective introduction of secondary mesoporosity into the zeolitic samples was studied by N₂ adsorption/desorption analyses at 77 K. The N₂ adsorption/desorption isotherms and the corresponding pore size distributions, obtained by the NLDFT method, of the analyzed samples are reported in Fig. 2 and S2,† respectively; specific surface area (SSA), pore volume and pore size data are presented in Table 2. Data for HZSM5, HUSY and HCLI samples subjected to the harshest tested desilication conditions they could endure without structural collapse (HZSM5-13.3. HUSY-9 and HCLI-13.3, respectively), are reported; these samples are the most representative for understanding the effects induced by desilication.

Fig. 2 N₂ adsorption/desorption isotherms at 77 K of (A) HZSM5, (B) HUSY and (C) HCLI desilicated under different pH conditions.

Table 2 Textural properties of the analyzed zeolitic samples. Si/Al ratios of samples are also reported

Sample	RC%	SSABET (m^2 g^−1)	Vtot DFT (cm^3 g^−1)	Vmicro (cm^3 g^−1)	Vmeso (cm^3 g^−1)	Relative mesoporous volume (%)	Si/Al ratio^a
a Calculated using FESEM-EDX analyses.
HZSM5-P	100	397	0.24	0.13	0.11	46	42
HZSM5-13.3	74	435	0.49	0.11	0.38	78	19
HUSY-P	100	684	0.44	0.19	0.25	57	57
HUSY-9	38	705	0.47	0.19	0.28	60	46
HCLI-P	72	120	0.21	—	0.18	86	6
HCLI-13.3	93	91	0.16	—	0.16	100	4

---

The specific surface area (SSA) increased moderately upon desilication for both HZSM5 and HUSY, as expected, whereas an opposite trend was observed for HCLI. Similarly, the total pore volume and mesoporous volume, estimated via NLDFT calculations, showed a significant increase for HZSM5 and a moderate increase for HUSY, while both parameters decreased in the case of HCLI (Table 2).

The increases in SSA, V_tot and V_meso are consistent with the expected effects of desilication, which aims to enhance the mesoporous character of the modified materials. The inverse trend observed for the HCLI sample may be attributed to partial pore occlusion following desilication, a phenomenon previously reported for zeolites with small pore openings (10-membered rings (MR) or fewer) and with low Si/Al ratio.¹⁷ Finally, it is important to note that all desilicated samples, including HCLI-13.3, exhibit an increase in the relative mesoporous volume percentage, confirming the effectiveness of the alkaline treatment applied to the selected materials. Moreover, energy-dispersive X-ray spectrometry (EDX) coupled with field emission scanning electron microscopy (FESEM) was employed to determine the Si/Al ratios of the studied materials before and after desilication (Table 2 and Fig. S3†).⁵ This parameter and its variation upon treatment are crucial to both confirm the success of the process and assess the extent of compositional modification as a function of the initial material characteristics. As expected, this parameter decreases because of silicon atoms removal in the basic environment.

These results were further supported by thermogravimetric analysis (Fig. S4†). Specifically, all the TGA curves of the desilicated samples exhibited a greater percentage of weight loss, which can be attributed to the removal of adsorbed water (in the 25–350 °C range). This finding aligns with the observed decrease in the Si/Al ratio, which is associated with an increase in the hydrophilicity of the zeolitic framework.³²

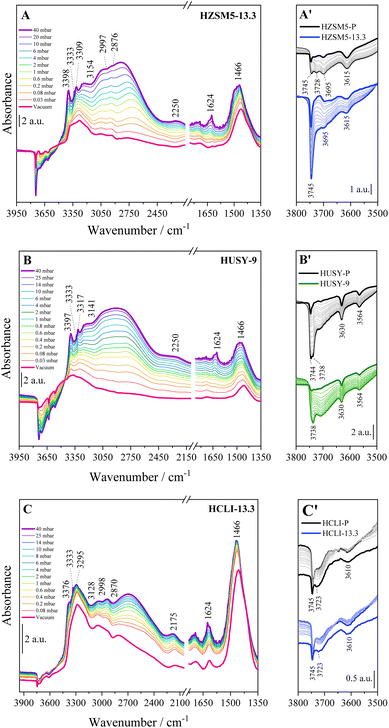
Considering the high heterogeneity of the hydroxyl sites present in hierarchical zeolites, to assess the influence of the post-synthetic desilication process on their distribution, FTIR spectroscopy was used to establish the nature of the acid sites located on the zeolitic surface (Fig. 3).^{5,11,31,67,68} In all the analysed zeolites, a characteristic stretching band related to the isolated silanol groups located on the outer surface (Si–OH_ext) and in the mesoporous cavities can be observed at 3745 cm⁻¹. For the HZSM5 and clinoptilolite samples (Fig. 3A and C), an increase in this signal was evident after alkaline treatment at pH 13.3, consistent with the increased mesoporous surface area observed for the HZSM5-13.3 and HCLI-13.3 samples. On the other hand, for the HUSY-9 and HUSY-13.3 samples (Fig. 3B), the same treatment resulted in a decrease in band intensity, likely due to the deposition of Al-rich debris on the surface of HUSY. This debris may interact with the Si–OH external groups, reducing their band contribution in the OH stretching region.^20,69 In the HZSM5 samples (Fig. 3A), the FTIR bands corresponding to silanols located within the microporous cavities appeared at 3728 cm⁻¹ and 3695 cm⁻¹ (Fig. S5†). The former signal, attributable to internal silanols Si–OH_int, remains observable after desilication, appearing as a shoulder of the peak associated with isolated silanol, while the latter, attributable to vicinal silanols interacting with each other through H-bonding, disappears following desilication at pH 13.3.^22,26,70,71 The Brønsted acid sites (BAS) band at 3615 cm⁻¹ shows minimal alteration after desilication treatment. In contrast, the hydrolytic action of OH⁻ ions at higher concentrations significantly destabilizes the silanols involved in hydrogen bonding (Si–OH⋯O) within crystal lattice defects, commonly named “nest silanols”, as indicated by the disappearance of the corresponding absorption band around 3500 cm⁻¹.^11,26,72,73 These findings align with previous literature studies reporting that Si–OH species involved in nest silanol defects are particularly unstable and can be removed even with diluted NaOH solutions.^22,26

Fig. 3 FTIR spectra in the OH stretching region of (A) HZSM5, (B) HUSY (C) and HCLI samples desilicated under different pH conditions.

The FTIR spectra of the HUSY zeolite samples (Fig. 3B) reveal the presence of specific characteristic bands associated with the faujasite structure: (i) at 3738 cm⁻¹, corresponding to Si–OH_int. The band remains largely unchanged in the spectrum of the HUSY-9 sample, in contrast to the signal at 3745 cm⁻¹, which is attributed to Si–OH_ext. This observation further supports the hypothesis of Al-rich debris deposition on the external surface of HUSY. In contrast, the HUSY-13.3 sample exhibits a significant reduction in the Si–OH_int signal, which correlates well with the complete amorphization observed in the XRD measurements; (ii) at 3630 cm⁻¹, attributed to Si–O₁H–Al BAS located within the supercage structure. These sites exhibit particularly high acidity due to the specific geometric configuration of the Si–O₁H–Al bridge within the FAU framework and present a narrow IR band, resulting from their high homogeneity;^27,74 (iii) at 3565 cm⁻¹, associated with Si–O₃H–Al BAS situated within the hexagonal prism β-cage structure.⁷⁴ The reduced resistance of the HUSY zeolite to the hydrolytic action of OH⁻ ions is evidenced by the complete disappearance of signals corresponding to BAS after desilication treatment at pH 13.3 (Fig. 3B). In contrast, it is noteworthy that the HUSY-9 sample retained the signals corresponding to surface BAS, despite a significant reduction in crystallinity, as confirmed by X-ray powder diffraction (XRPD) analysis (Table 1). The desilicated clinoptilolite samples (Fig. 3C) exhibit a prominent absorption band at 3610 cm⁻¹, indicative of BAS.⁶⁸ The enhanced intensity of this band observed in the HCLI-8 sample suggests that alkaline treatment may facilitate the removal of impurities, such as amorphous silica, from the clinoptilolite surface.⁶⁶ This behaviour is consistent with previously reported relative crystallinity values (Table 1), providing additional evidence for the purification effect of desilication under mild treatment conditions.

Adsorption of basic probe molecules monitored by FTIR spectroscopy

Given the pronounced heterogeneity of the surface sites of hierarchical zeolites, which is attributable to the presence of various types of acidic centers distributed within primary and secondary porosity systems, an in-depth characterization was carried out using FTIR spectroscopy enhanced by the use of specific basic probe molecules of different kinetic diameters. This approach provides a deeper understanding of the concentration, distribution, and accessibility of BAS.

Determination of the total acidity by NH₃ adsorption

Ammonia (NH₃), a strong base (pK_a = 9.24), was the first probe molecule adsorbed. NH₃ interacts through its lone electron pair with silanol groups and BAS, and in the latter case, ammonium ions (NH₄⁺) are formed through proton transfer phenomena.³⁸ These species, whose spectral properties are well-documented, can be employed to provide critical insights into the density of BAS during the spectroscopic characterization of aluminosilicates.⁷⁵ Specifically, NH₃ was employed to assess the total concentration of BAS, as its small kinetic diameter (2.6 Å) enables efficient penetration into both the micropores and mesopores of hierarchical zeolites.^35,76,77 Fig. 4 shows the FTIR spectra of the most representative samples reported to understand the effects induced by desilication.

Fig. 4 FTIR difference spectra of NH₃ adsorbed (max pressure 40 mbar) on hierarchical (A) HZSM5-13.3, (B) HUSY-9 and (C) HCLI-13.3 samples at room temperature. The intermediate pressures at which spectra are collected during desorption are reported in the figure. On the right, a comparison between the spectra of the desilicated samples and their corresponding parent samples in the OH stretching region (A′–C′) is provided.

The FTIR analysis of NH₃ adsorption at room temperature on hierarchical zeolites, specifically HZSM5-13.3 (Fig. 4A), HUSY-9 (Fig. 4B), and HCLI-13.3 (Fig. 4C), was conducted over both high- and low-frequency regions. This analysis aimed to evaluate the impact of the probe molecule's interaction on the hydroxyl group bands and to detect the characteristic bands associated with ammonium ions.

Within the zeolite framework, upon exposure to 40 mbar of NH₃ (violet curves), distinct bands corresponding to the presence of the probe were observed, indicating both its unbound form and its interaction with the OH sites of the materials. In the 3750–3600 cm⁻¹ spectral range, bands associated with surface hydroxyl groups are observed (Fig. 4A′–C′). These bands were completely reduced following the interaction with the ammonia probe, appearing as negative signals in the difference spectra. The observed evolution of the bands intensity is consistent with the observations from prior FTIR analysis performed in the absence of a probe (Fig. 2): for the ZSM5 zeolite, the band at 3745 cm⁻¹ due to free silanols becomes notably more negative in the spectrum of the HZSM5-13.3 sample (Fig. 4A′), indicating a higher concentration of silanols in the sample that underwent desilication. This result is consistent with the expected increase in the number of defect sites introduced by the alkaline treatment. In contrast, when comparing the spectra of the HUSY-9 (Fig. 4B′) samples before and after desilication, the band at 3744 cm⁻¹ corresponding to Si–OH_ext species, is less pronounced, while the band at 3738 cm⁻¹ exhibits a similar intensity. The reduction in the Si–OH_ext signal suggests a significant exclusion from interaction with the NH₃ probe, further supporting the hypothesis of Al-rich debris deposition on the material's external surface.⁶⁹

A distinct behaviour is observed in the HCLI samples (Fig. 4C′). Specifically, a comparison of the FTIR spectra between the parent and HCLI-13.3 reveals that the intensities of the bands at 3745 and 3723 cm⁻¹, corresponding to Si–OH_ext and Si–OH_int, show minimal variation following desilication. This observation is consistent with the observed trend of the RC% parameter (Table 1), where, unlike the HZSM-5 and HUSY zeolites, the natural clinoptilolite exhibits a nonlinear pattern, reaching a maximum for the HCLI-9 sample. The observed minimal changes in the FTIR bands could reasonably arise from the fact that, in the case of the HCLI zeolite, it appears necessary to remove impurities before its structure can be significantly altered through desilication.

Following NH₃ outgassing at room temperature, the silanol groups, which exhibit only weak interactions with the probe molecule, were almost entirely restored, as demonstrated by the significant reduction in the difference signals (Fig. 4). In contrast, for all zeolites, the bands corresponding to the acidic BAS (at 3615 cm⁻¹, 3630/3564 cm⁻¹ and 3610 cm⁻¹ for HZSM5-13.3, HUSY-9 and HCLI-13.3 materials respectively) remained almost unaffected during outgassing due to the proton transfer mechanism that leads to the formation of NH₄⁺ ions. The presence of ammonium can be identified at lower frequencies, notably by the appearance of a band at 1466 cm⁻¹ (δ_as N–H). Furthermore, the formation of these ammonium species is accompanied by the emergence of several characteristic bands in the higher-frequency region of the FTIR spectrum, with their specific positions depending on the material involved in the interaction. The bands are assigned as follows: (i) two signals at 3398 and 3309 cm⁻¹ in the HZSM5-13.3 sample (Fig. 3A), at 3397 and 3317 cm⁻¹ in the HUSY-9 (Fig. 3B), and at 3376 cm⁻¹ in the HCLI-13.3 (Fig. 3C), corresponding to the stretching vibrational modes of N–H groups not involved in hydrogen bonding; (ii) a broad composite band, extending over the range of 3250–2400 cm⁻¹, attributed to the stretching modes of N–H groups shifted to lower frequencies due to hydrogen bonding interactions.⁷⁵ This band is also significantly influenced by a strong Fermi resonance, resulting in the appearance of three Evans windows, which are distinguishable in the HZSM5-13.3 and HCLI-13.3 samples.^39,75,78 (Fig. 4); (iii) a slightly broadened band at 2250 cm⁻¹ in the HZSM5-13.3 and HUSY-9, and at 2175 cm⁻¹ in the HCLI-13.3 sample due to the combination of the vibrational bending modes δ(NH) of NH₄⁺ and a frustrated rotation localized at low wave numbers (550–100 cm⁻¹).⁷⁵

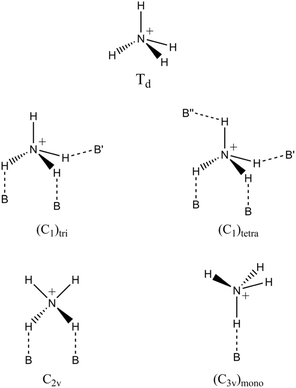
Depending on the type of crystal structure, the negatively charged walls of zeolites can stabilize different coordination structures of the ammonium ion, each with specific local symmetries, leading to variations in the distribution of FTIR bands.⁷⁵ In the case of the HCLI-13.3 sample, an intense band appeared at 3295 cm⁻¹ (Fig. 3C).

The appearance of this band can be explained by considering the most probable local symmetries adopted by NH₄⁺ ions, depending on their interaction with different zeolite frameworks (Scheme 1).⁷⁵ The C₂v and (C₃v)_mono geometries involve interactions with oxygen atoms of the same AlO₄⁻ tetrahedron (indicated with B in Scheme 1). In contrast, the less symmetrical geometries (C₁)_tri and (C₁)_tetra also exhibit NH bonds that participate in slightly weaker hydrogen bonds with less basic framework oxygens (B′ and B′′ in Scheme 1) that do not belong to the same tetrahedral unit. Specifically, these weaker basic sites may be associated with both more distant AlO₄⁻ and SiO₄ tetrahedra.⁷⁵ These distinct coordination modes of ammonium within the zeolitic environment can be identified by the appearance of characteristic signals in the FTIR spectra. Notably, the signal at 3295 cm⁻¹ observed in the spectrum of HCLI-13.3 is present exclusively when the ammonium ion is in a tridentate or tetradentate coordination state with C₁ symmetry. The greater intensity of this peak compared to those observed for the HZSM5 and HUSY zeolites is consequently associated with an increased presence of ammonium ions exhibiting (C₁)_tri and (C₁)_tetra coordination (Fig. 4A and B). Furthermore, considering that the band at 3376 cm⁻¹, associated with the unperturbed NH groups, appears as a shoulder to the signal at 3295 cm⁻¹, it is reasonable to hypothesize that among the two ammonium species with C₁ symmetry, the tetradentate species is present in greater abundance, as it does not possess any unperturbed NH groups. This hypothesis is further supported by literature indicating that this type of ammonium coordination structure is favored in the presence of microporous channels with particularly small diameters, where the NH₄⁺ ion is unlikely to maintain an unperturbed N–H bond due to high steric constraints.⁷⁵ Such conditions are consistent with the clinoptilolite HEU lattice.⁷⁹

Scheme 1 Most probable coordination geometries of ammonium ions in zeolite environments.

Finally, in the FTIR spectra of all materials, two signals at 3333 and 1624 cm⁻¹ are observed, corresponding respectively to ν(NH) and δ(NH) of the non-protonated probe with weak interaction with the surface. This assignment is further supported by the rapid decrease in the ion concentration during the outgassing procedure.^31,80

To determine the concentration of BAS within the parent and hierarchical materials, the ammonium band at 1466 cm⁻¹ was used to calculate the total number of Brønsted acid sites in the different zeolitic samples (Table 3). The BAS concentration was estimated using the Lambert–Beer law adapted for solids:

A = εNρ (1)

where A is the integrated area of the δ_as N–H band (mm⁻¹), ε is the molar extinction coefficient (mm μmol⁻¹), N is the concentration of the vibrating species (μmol mg⁻¹) and ρ is the density of the sample pellet (mass/area ratio, mg mm⁻²). For the calculations, a value of 130.0 mm μmol⁻¹ was used for ε.⁸¹

Table 3 Integrated area (A) of the ammonium δ_as NH (1466 cm⁻¹) band and concentration of total Brønsted sites (N_tot), expressed as μmol g⁻¹

Sample	A^a (cm^−1)	Ntot (μmol g^−1)
a The integrated area A of the 1466 cm^−1 band was obtained from the spectra of the materials outgassed for 30 minutes in a vacuum at room temperature.
HZSM5-P	283	218
HZSM5-9	440	338
HZSM5-13.3	603	464
HUSY-P	162	124
HUSY-8	174	134
HUSY-9	170	131
HCLI-P	679	522
HCLI-9	886	681
HCLI-13.3	718	552

---

Among the three investigated materials, only the zeolite ZSM5 exhibited a progressive increase in the BAS concentration with increasing treatment basicity. A significant increase in BAS concentration upon desilication at a pH of 13.3 was observed, reaching 464 μmol g⁻¹, over twice with respect to the parent sample (218 μmol g⁻¹). This phenomenon is likely attributed to the presence of aluminum atoms, which are extracted during the desilication process and remain in extra framework positions as amorphous Al-species, thus contributing to the formation of new protonic sites.^33,37,82 Reinsertion of Al, sometimes called ‘realumination’, was first proposed by Sulikowski et al. for ZSM5 zeolite⁸³ and subsequently studied in relation to desilication processes for other zeolitic materials.^{23,25,26,33,37,64,84–86} Furthermore, as illustrated in Fig. 3, the FTIR band at 3615 cm⁻¹ does not exhibit a significant increase following basic treatment. This observation suggests that the reintroduced Al atoms are only partially integrated into the zeolitic framework and do not exhibit the characteristic tetrahedral coordination typically associated with Si–OH–Al groups.^33,82

In contrast, Zeolite Y exhibited no significant increase in BAS concentration after exposure to an alkaline environment. Based on the FTIR and XRD analyses, it can be hypothesized that the faujasite structure simply dissolves upon contact with the alkaline solution without altering the distribution of tetrahedral aluminum sites.

The HCLI-P sample exhibited a significantly higher concentration of acidic sites than the synthetic zeolites, which was correlated with its lower Si/Al ratio (refer to the Experimental section). The increase in the number of BAS in the HCLI-9 sample was accompanied by an enhancement of the IR band at 3610 cm⁻¹ (Fig. 3C), indicating a greater abundance of Si–OH–Al groups per unit weight. This result confirms the efficacy of mild desilication conditions for sample purification, as previously reported. In contrast, after treatment at higher pH, the HCLI-13.3 sample exhibited a notable decrease in the number of BAS, accompanied by a reduction in the intensity of the corresponding FTIR signal. In this alkaline environment, the disruption of the microporous structure may become more relevant, leading to the subsequent removal of a higher amount of Al from Si–OH–Al bridging groups.^26,68

Secondary porosities acidity: substituted pyridines adsorption

To accurately assess the degree of hierarchization in zeolitic structures, it is essential to distinguish between acid sites within micropores and those on mesopore surfaces. Larger basic probe molecules are critical for this purpose. Substituted pyridines have been widely exploited to assess and quantify the enhanced accessibility of acid sites in hierarchical zeolites because their restricted diffusion through small micropores allows for selective analysis.^{22,33,34,40,42,87–89} Among them, 2,4,6-trimethylpyridine (2,4,6-TMPy, also known as collidine), which has a kinetic diameter of approximately 0.74 nm, is sterically hindered from penetrating the micropores of HZSM5 and HCLI. Consequently, it interacts exclusively with acid sites located on mesopore surfaces or at the mouths of micropores in hierarchical zeolites.^22,31,33 Conversely, for the HUSY zeolite, which features larger micropores (∼0.73 nm), an even larger probe molecule, such as 2,4,6-tritertbutylpyridine (2,4,6-TTBPy, with a diameter of 1.1 nm), is required to ensure selective probing.^40,90,91 The interaction of these probe molecules with zeolitic BAS is readily identifiable by FTIR spectroscopy. This identification is achieved both through the characteristic vibrational modes of the probe's aromatic ring and, due to their basic nature, via their conjugate acids (2,4,6-TMPyH⁺, and 2,4,6-TTBPyH⁺), which form through proton transfer mechanisms upon interaction with a BAS.^35,90

2,4,6-Trimethylpyridine (2,4,6-TMPy) adsorption

All analyzed zeolites exhibited an erosion of silanol and BAS signals following 2,4,6-TMPy (collidine) adsorption, which appeared as negative peaks in the difference spectrum (Fig. S6†). Additionally, two distinct bands emerged at 3300 cm⁻¹ and 3230 cm⁻¹, corresponding to the ν(NH) stretching vibration of the 2,4,6-TMPH⁺ ion (Fig. S6†).⁴⁰ Notably, these two bands are more pronounced for the samples desilicated at pH 13.3, especially in the case of the HZSM5 zeolite, indicating that the basic treatment enhanced the accessibility of Brønsted acid sites to 2,4,6-TMPy through the formation of mesopores. Furthermore, in this spectral region, a broader band around 2925 cm⁻¹ is observed, which is attributed to the various stretching modes of the aromatic ring of the 2,4,6-TMPy molecule.

Fig. 5 shows the difference in the FTIR spectra collected after outgassing at 423 K in the stretching region of C–C ring vibration of adsorbed 2,4,6-TMPy on the HZSM5 (Fig. 5A) and HCLI (Fig. 5B) samples. In each case, based on previous analyses, the samples treated at pH 8 were excluded from consideration because they exhibited negligible differences compared with the parent samples. The bands at 1617 cm⁻¹ and 1573 cm⁻¹ correspond to the ν_8a and ν_8b vibrational modes, respectively, which are characteristic of collidine molecules interacting via hydrogen bonds with isolated Si–OH groups. In contrast, the band at 1638 cm⁻¹ accompanied by a shoulder at 1649 cm⁻¹, originates from the ν_8a vibration of the 2,4,6-TMPyH⁺ ion, formed through proton transfer with BAS.^22,31,90 As reported in Table 4, the total number of accessible BAS (N_2,4,6-TMPy) was estimated by eqn (1) using the intensity of the 1638 cm⁻¹ band. For these calculations, a value of 10.1 cm μmol⁻¹ was used for ε.⁸⁸ To isolate the contribution of the desired band from the adjacent ones, a deconvolution of the signals in the C–C ring stretching region was performed (Fig. S7†). In the case of the HZSM5 zeolite, the accessible BAS concentration was negligible for samples HZSM5-P and HZSM5-9 but increased significantly following the more severe treatment at pH 13.3, confirming a higher degree of structural hierarchization. A similar trend is observed for natural clinoptilolite samples in response to desilication; however, in this case, a measurable concentration of accessible BAS is already present in the HCLI-P sample (32 μmol g⁻¹), likely due to the intrinsic intracrystalline mesoporosity characteristic of this material.⁵⁷ The ineffectiveness of pH 9 treatment in altering the clinoptilolite crystalline structure and consequently in contributing to secondary porosity further supports the conclusion that the increase in the total number of BAS detected via ammonia adsorption does not stem from structural alterations of the zeolite framework. Instead, it is more reasonably attributable to a purification process induced by the basic treatment.

Fig. 5 FTIR difference spectra of 2,4,6-TMPy adsorbed on (A) HZSM5 and (B) HCLI samples at room temperature. Spectra were collected after desorption at 423 K for 1 hour to isolate the contribution of irreversibly adsorbed TMPyH⁺ ions.

Table 4 Integrated area (A) of the 2,4,6-TMPH⁺ ion ν_8a (1638 cm⁻¹) band and concentration of BAS accessible to 2,4,6-TMPy molecule (N_2,4,6-TMPy), expressed as μmol g⁻¹. Accessibility factor relative to 2,4,6-TMPy molecule (AF_2,4,6-TMPy) was also calculated

Sample	A (cm^−1)	N(2,4,6-TMPy μmol g^−1)	AF2,4,6-TMPy^a
a AF2,4,6-TMPy calculated as
HZSM5-P	17	17	0.078
HZSM5-13.3	199	197	0.425
HCLI-P	32	32	0.061
HCLI-9	44	43	0.063
HCLI-13.3	64	64	0.116

---

To better evaluate the hierarchical structure of the hierarchical samples, the accessibility factor (AF) for 2,4,6-TMPy was calculated, which was defined as the number of sites detected by adsorption of the alkylpyridine (N_2,4,6-TMPy) divided by the total number of BAS detected by NH₃ adsorption (N_tot). As shown in Table 4, the AF values increased with the pH of the desilication treatment, in agreement with the increased mesoporous volumes (Table 2).

2,4,6-Tri-tert-butylpyridine (2,4,6-TTBPy) adsorption

To investigate mesopore formation in the HUSY samples, 2,4,6-tri-tert-butylpyridine (2,4,6-TTBPy, kinetic diameter of 1.1 nm) was adsorbed onto the zeolite surface at room temperature following the same procedure outlined for 2,4,6-TMPy. However, due to the solid state of 2,4,6-TTBPy at room temperature (T_m = 67 °C) and its lower vapor pressure (0.02 mbar), the contact time was extended to 2 hours to ensure saturation of the accessible surface area of the material⁴⁰ (see Experimental section).

Fig. 6B illustrates the FTIR difference spectra of 2,4,6-TTBPy adsorbed on the HUSY samples, emphasizing the regions associated with the aromatic ring and CH₃ deformation vibrations. The ν_8a vibration bands of the aromatic ring appear at 1611 and 1599 cm⁻¹, which are attributed to the 2,4,6-TTBPyH⁺ protonated species formed upon interaction with Brønsted acid sites (BAS) and the physisorbed 2,4,6-TTBPy on the material surface, respectively.

Fig. 6 FTIR difference spectra of 2,4,6-TTBPy adsorbed on (A) HUSY samples at room temperature in the N–H stretching region and (B) aromatic stretching region. Spectra were collected upon outgassing the samples at 298 K (for 30 min) and 423 K (for 2 h) to isolate the contribution of irreversibly adsorbed 2,4,6-TTBPyH⁺ ions.

Compared with 2,4,6-TMPy, these bands show a redshift, which is a direct result of the substitution of the three methyl groups with bulkier tert-butyl groups.⁹⁰ Furthermore, two additional bands, located at 1561 and 1545 cm⁻¹, are observed exclusively in the spectrum recorded upon outgassing the samples at 298 K and can thus be assigned to the aromatic ring vibrations of the unprotonated probe molecule. The δ CH_3,as signals, located at 1479, 1461, and 1407 cm⁻¹, and the δ CH_3,sym band at 1363 cm⁻¹ can also be attributed to this species. The contribution of the latter vibration mode is still visible in the spectrum collected after the outgassing at 423 K; however, in this case, only the blue-shifted component at 1375 cm⁻¹, associated with 2,4,6-TTBPyH⁺ cations, remains visible.⁹⁰

The significant decrease in the intensity of the signals associated with the physisorbed probe demonstrates the effectiveness of the adopted outgassing method, as further confirmed by the complete disappearance of the signals corresponding to the vibrational modes ν CH_3,as (2963 and 2905 cm⁻¹) and ν CH_3,sym (2872 cm⁻¹) (Fig. S8†). Notably, after thermal treatment, the 2,4,6-TTBPyH⁺ ν CH_3,as band emerges at 2975 cm⁻¹. The protonation of the probe was further confirmed by the presence of the band at 3364 cm⁻¹, which is characteristic of the N–H stretching vibration (Fig. 6A).⁴⁰

Due to its size, 2,4,6-TTBPy can only undergo protonation on the external zeolite surface or within meso- and macroporous cavities. As a result, the band at 3364 cm⁻¹, corresponding to the 2,4,6-TTBPyH⁺ ion, was used to quantify the BAS located outside the microporous framework.

Table 5 presents the concentrations of BAS in the HUSY zeolite samples, calculated using an extinction coefficient (ε) of 5.74 cm μmol⁻¹,⁴⁰ along with the corresponding accessibility factor (AF) values. The HUSY-8 sample exhibited only a slight increase in the number of BAS accessible to 2,4,6-TTBPy compared with the pristine HUSY-P zeolite. This finding is consistent with the minimal structural modifications detected by FTIR and XRD analysis. Consequently, the accessibility factor (AF) was marginally higher than that of the unmodified zeolite.

Table 5 Integrated area (A) of the 2,4,6-TTBPyH⁺ ν_N–H band (3364 cm⁻¹) and concentration of BAS accessible to 2,4,6-TTBPy molecule (N_2,4,6-TTBPy), expressed as μmol g⁻¹. Accessibility factor relative to 2,4,6-TTBPy molecule (AF_2,4,6-TTBPy) was also calculated

Sample	A (cm^−1)	N2,4,6-TTBPy (μmol g^−1)	AF2,4,6-TTBPy^a
a AF2,4,6-TTBPy calculated as
HUSY-P	19	32	0.26
HUSY-8	21	36	0.27
HUSY-9	27	47	0.36

---

For these materials, the number of detected acid sites aligns with values generally reported for commercial HUSY zeolites with similar Si/Al ratios (e.g. CBV760, CBV720) and is attributable to the presence of intracrystalline mesoporosity introduced during dealumination.⁹²

In contrast, following desilication at pH 9, a significant increase in the number of BAS accessible to 2,4,6-TTBPy was observed, with the AF increasing by approximately 33%.

The use of this basic probe therefore allowed for confirmation of the greater structural alteration of the zeolitic framework following the increase in the treatment pH, as previously suggested by the XRD and volumetric analyses (Fig. 1 and 2).

Adsorption of Cu²⁺ and Co²⁺ ions from aqueous solutions

Cu²⁺ and Co²⁺ ions were selected as transition metals to assess the uptake performance of the developed zeolitic materials in metal-polluted aqueous solutions. Because these metal ions exhibit specific absorption bands in the UV-vis region of the electromagnetic spectrum, UV-vis spectroscopy was selected to determine the concentration of captured metal ions under controlled experimental conditions (298 K, pH = 4.5). The selected metal ions differ in their ionic radii and coordination numbers (Cu²⁺ = 0.73 Å, C.N. = VI; Co²⁺ = 0.65 Å, C.N. = VI).⁹³ The uptake mechanism is based on a multitude of processes: interaction with surface hydroxyl species, cation exchange, and adsorption.^44–46 The experiments were conducted at pH 4.5 to prevent the formation of metal hydroxide precipitates.^94,95 Acidic conditions are commonly employed in industrial applications for the extraction of heavy metals from contaminated wastewater and electronic waste.⁹⁶

The two metal ions exhibited distinct absorption peaks in different regions of the UV-vis spectrum, with maxima at 809 nm for Cu²⁺ and 512 nm for Co²⁺ ions, respectively (Fig. 7).

Fig. 7 UV-vis spectra of (A) Cu²⁺ and (B) Co²⁺ aquo complexes in solution. The spectra correspond to the stock solutions of the two metal ions (∼10 mM concentration) and are presented over the 400–900 nm range for Cu²⁺ and the 350–700 nm range for Co²⁺, respectively.

From an instrumental perspective, a calibration curve was first established to determine the molar extinction coefficient (ε) of each species at their respective wavelengths of maximum absorbance (Fig. S9†), as described in the experimental section. The concentration of each metal ion in the solution was measured before and after the uptake tests performed using the hierarchical materials. These were obtained using Lambert–Beer equation (eqn (2)):

where A represents the absorbance measured at the wavelength of maximum absorption, ε is the previously determined molar extinction coefficient at the same wavelength, b corresponds to the optical path length of the cuvette (1 cm) and C is the unknown concentration of the metal species in solution. Using this approach, the residual concentration of each metal species in the solution was determined. The amount of metal captured by each analyzed sample was then calculated by subtracting the residual metal concentration from the initial concentration in the stock solution (10 mM). For each analyzed sample, two distinct aliquots of the material were taken and subjected to uptake tests. Each aliquot was then analyzed in triplicate.

Quantitative uptake data are reported in Fig. 8 and Table 6. Additionally, UV-vis spectra recorded after the uptake tests from each metal ion solution are reported for the HZSM5-13.3 sample as a representative example (Fig. S10†).

Fig. 8 Amounts of Cu²⁺ and Co²⁺ captured by the studied zeolites from their respective aqueous solutions after 24 hours, expressed as (A and B) μmol g⁻¹ and (A′ and B′) percentage of the captured metal ion. The amount of BAS in 60 mg of material is also provided (the bars represent the mean values; the error bars indicate the standard deviations, calculated considering, for each sample, the triplicate sets of analyses performed on the two aliquots).

Table 6 Amounts of Cu²⁺ and Co²⁺ contents captured by the studied zeolites from their respective aqueous solutions after 24 hours. The amount of BAS per gram of material is also provided (standard deviations were calculated considering, for each sample, the triplicate sets of analyses performed on the two aliquots)

Metal ion	Sample	μmol M^n+ g^−1 material	Adsorbed^a M^n+ (%)	mg M^n+ g^−1 material	[BAS] (μmol g^−1)
a Calculated with respect to the initial metal concentration in the solution (10 mM).
Cu^2+	HZSM5-P	57 ± 8	9 ± 1	3.6 ± 0.5	218
	HZSM5-13.3	84 ± 9	13 ± 1	5.3 ± 0.6	464
	HUSY-P	53 ± 3	8.0 ± 0.5	3.3 ± 0.2	124
	HUSY-9	56.5 ± 0.7	8.6 ± 0.1	3.59 ± 0.05	131
	HCLI-P	22 ± 1	3.3 ± 0.2	1.38 ± 0.06	522
	HCLI-13.3	26.0 ± 0.8	3.9 ± 0.1	1.65 ± 0.05	552
Co^2+	HZSM5-P	36.3 ± 0.8	5.9 ± 0.2	2.14 ± 0.05	218
	HZSM5-13.3	63 ± 2	10.2 ± 0.3	3.7 ± 0.1	464
	HUSY-P	70.2 ± 0.2	11.5 ± 0.1	4.13 ± 0.01	124
	HUSY-9	70.7 ± 0.4	11.5 ± 0.1	4.16 ± 0.02	131
	HCLI-P	39.1 ± 0.6	6.3 ± 0.1	2.30 ± 0.03	522
	HCLI-13.3	48 ± 3	7.7 ± 0.5	2.8 ± 0.2	552

---

As shown in Fig. 8A, A′ and Table 6, HZSM5 demonstrates the highest uptake capacity for Cu²⁺ ion, with values of 57 ± 8 μmol g⁻¹ and 84 ± 9 μmol g⁻¹ for samples HZSM5-P and HZSM5-13.3, respectively. The percentage of captured metal, calculated with respect to the initial metal concentration in solution (10 mM), increased from 9% ± 1% to 13% ± 1%. These findings indicate that desilication significantly enhances the adsorption performance of this zeolitic system by approximately 47%. In contrast, the other zeolitic systems exhibit only a marginal increase in metal uptake. This result is consistent with the varying sensitivities of the studied zeolites to the basic treatments applied in this work. Among the three investigated zeolites, HZSM5 exhibited remarkable resistance to desilication treatment and was the only material to undergo realumination, as evidenced by the FTIR analysis. This phenomenon is closely associated with a substantial increase in the concentration of BAS within the material (rising from 218 μmol g⁻¹ to 464 μmol g⁻¹, Table 3), which accounts for its significantly enhanced ability to capture Cu²⁺ ions (Table 6).

In contrast, the HUSY zeolite demonstrated pronounced sensitivity to the basic treatment, likely undergoing partial dissolution of its faujasite framework without any notable alteration in the distribution or concentration of BAS (which remained nearly unchanged, from 124 μmol g⁻¹ to 131 μmol g⁻¹, Table 3). Therefore, the HUSY-9 sample did not exhibit a substantial improvement in Cu²⁺ uptake performance (53 ± 3 μmol g⁻¹ and 56.5 ± 0.7 μmol g⁻¹ for HUSY and HUSY-9, respectively, Table 6). On the other hand, the natural zeolite HCLI displayed good resistance to desilication, accompanied by a modest increase in the BAS concentration in the HCLI-13.3 sample (from 522 μmol g⁻¹ to 552 μmol g⁻¹, Table 3). This trend correlates well with the observed enhancement in Cu²⁺ uptake (rising from 22 ± 1 μmol g⁻¹ to 26.0 ± 0.8 μmol g⁻¹, Table 6).

Despite exhibiting the highest concentration of BAS sites among the tested materials before and after desilication, natural clinoptilolite exhibited the lowest Cu²⁺ uptake efficiency. This behavior can be rationalized by considering several key factors: (i) HCLI-P and HCLI-13.3 samples possess the lowest specific surface area (Table 2), thereby offering a considerably reduced accessible surface per unit mass; (ii) the HEU framework is characterized by a two-dimensional (2D) topological structure, in contrast to the three-dimensional (3D) frameworks exhibited by the other studied zeolites.⁵⁸ This structural distinction, coupled with the fact that HCLI has the smallest pore diameter among the investigated materials, suggests a more pronounced diffusional constraint in this system. This aspect gains further relevance when considering that the selected metal ions exist in solution as solvated species, forming aquo complexes whose dimensions closely approximate the pore diameter of natural clinoptilolite.^46,97 As a result, the higher number and denser BAS of the HCLI samples may be less accessible and consequently less active during the ion capture process, with respect to those in the other zeolitic systems. Upon transitioning to the desilicated sample HCLI-13.3, this constraint is partially mitigated, leading to a slight improvement in the uptake performance.

The desilication process implemented across the studied zeolites led to an observable enhancement in Cu²⁺ uptake capacity; the magnitude of the improvement was directly correlated with the increase in BAS concentration induced by the alkaline treatment. Moreover, the development of a more mesoporous architecture within the modified materials is expected to facilitate the diffusion of metal ions in solutions into the porous network, thereby further optimizing the capture efficiency.

When evaluating the Co²⁺ ion uptake performance of the investigated materials, the previously established considerations remain valid (Fig. 8B, B′ and Table 6). Among the tested zeolites, hierarchical HZSM5 exhibited the most pronounced enhancement in the capture efficiency. Specifically, the concentration of adsorbed Co²⁺ increased from 36.3 ± 0.8 μmol g⁻¹ to 63 ± 2 μmol g⁻¹ (Table 6), representing an improvement of approximately 74%. This result further confirms the effectiveness of alkaline treatment in enhancing the adsorption capacity of this zeolitic system. The HUSY-P and HUSY-9 samples exhibited the highest Co²⁺ ion uptake efficiency among the investigated materials. However, the adsorption capacity remained largely unchanged before and after desilication, with the value shifting only marginally from 70.2 ± 0.2 μmol g⁻¹ to 70.7 ± 0.4 μmol g⁻¹ (Table 6). This observation is consistent with previous findings concerning the uptake of Cu²⁺ ions. The HCLI zeolite samples exhibited a trend consistent with that previously observed in the capture of Cu²⁺ ions; the concentration of adsorbed Co²⁺ increased from 39.1 ± 0.6 μmol g⁻¹ to 48 ± 3 μmol g⁻¹ (Table 6). Notably, this increase seems to be proportional to the rise in BAS concentration, as previously observed.

A comparative analysis of the uptake capacities for Cu²⁺ and Co²⁺ ions provides further insight. In the case of the HUSY and HCLI zeolites, the adsorption capacity for Co²⁺ was significantly higher than that for Cu²⁺ (third column, Table 6), indicating a stronger affinity of these systems for Co²⁺ ions. This preferential adsorption behavior translates into superior uptake performance in single-metal-ion adsorption experiments in solution. However, this trend did not extend to the HZSM5 zeolite, which exhibited the opposite behavior: the amount of adsorbed Co²⁺ was lower than that of Cu²⁺ (third column, Table 6). This suggests that HZSM5 possesses a greater intrinsic affinity for Cu²⁺ than other developed materials.

To further investigate the different adsorption behaviors of HZSM5 compared with those of other zeolitic systems, selectivity tests for metal ion uptake were performed.

Selectivity tests of Cu²⁺ and Co²⁺ ions uptake from aqueous solutions

Considering that the differences in the materials' affinity for the tested metal ions were already evident in the parent samples of the zeolites, selectivity tests were conducted using the HZSM5-P, HUSY-P, and HCLI-P samples. This approach allows the evaluation of the intrinsic affinities of zeolitic systems to metal ions, independent of any changes to the framework or porosity induced by the desilication process. Selectivity tests were conducted using the same experimental conditions previously described for the uptake experiments of single metal ions in solution; in this case, however, the materials were exposed to a solution containing both metal ions at a concentration of 10 mM each (see Experimental section). This approach enabled the evaluation of the selectivity of zeolitic systems toward the metal ions considered in this study. By contacting the materials to solutions containing both metal ions, the samples were subjected to a competitive environment for the capture process within the material's porous structure.

Quantitative uptake data are reported in Fig. 9 and Table 7. Additionally, the UV-vis spectrum recorded after the uptake test from the solution containing both metal ions is reported for the HZSM5-13.3 sample as a representative example (Fig. S11†). As shown in Fig. 9A and Table 7, HZSM5-P demonstrates the highest total uptake capacity (122 ± 3 μmol g⁻¹), followed by HUSY-P (102 ± 3 μmol g⁻¹) and HCLI-P (76 ± 6 μmol g⁻¹). To contextualize these results, the previously discussed considerations regarding the distinct structural characteristics of the zeolitic frameworks remain applicable; therefore, clinoptilolite emerges again as the zeolite with the lowest overall uptake performance.

Fig. 9 Amount of Cu²⁺ and Co²⁺ concentrations captured by the studied zeolites from the multi-ion aqueous solution after 24 hours, expressed as (A) μmol g⁻¹ and (A′) χ_Mⁿ⁺. The amount of BAS in 60 mg of material is also provided.

Table 7 Amounts of Cu²⁺ and Co²⁺ content captured by the studied zeolites from multi-element aqueous solutions after 24 hours. The amount of BAS per gram of material is also provided (standard deviations were calculated considering, for each sample, the triplicate sets of analyses performed on the two aliquots)

	HZSM5-P		HUSY-P		HCLI-P
a Calculated: (i) with respect to the initial metal concentration in solution (10 mM each); (ii) by summing the concentrations of the two captured metal ions.b Calculated by summing the concentrations of the two captured metal ions.c Mole fraction of the captured metal ion relative to the total captured amount.
[BAS] (μmol g^−1)	218		124		522
Total adsorbed M^n+ %^a	9.2 ± 0.2		7.7 ± 0.3		5.7 ± 0.4
Total μmol M^n+ g^−1 material^b	122 ± 3		102 ± 3		76 ± 6
Total mg M^n+ g^−1 material^b	7.5 ± 0.2		6.1 ± 0.1		4.5 ± 0.2
	Cu^2+	Co^2+	Cu^2+	Co^2+	Cu^2+	Co^2+
μmol M^n+ g^−1 material	58.1 ± 0.4	64 ± 2	27 ± 2	75 ± 1	12 ± 3	64 ± 3
mg M^n+ g^−1 material	3.69 ± 0.03	3.8 ± 0.2	1.7 ± 0.1	4.41 ± 0.08	0.7 ± 0.2	3.8 ± 0.1
χM^n+^c	0.48	0.52	0.27	0.73	0.15	0.85

---

Notably, the total amount of metal captured in the parent samples (fourth row, Table 7) increased under competitive conditions compared with the uptake observed in single-metal-ion experiments (third column, Table 6). This outcome is reasonable, as the initial solution in the selectivity tests contained 10 mM of each metal ion, effectively subjecting the material to twice the molar concentration of total metal ions relative to the single-metal experiments.

Moreover, data from these competition experiments indicate that, in the presence of both metal ions, the HUSY-P and HCLI-P samples exhibit pronounced selectivity for Co²⁺ (last row, Table 7). Conversely, in the case of HZSM5, no preferential uptake was observed between the two metals, as the molar fractions (χ) for Cu²⁺ and Co²⁺ were 0.48 and 0.52, respectively. This suggests that the MFI framework of HZSM5 exhibits no intrinsic preference for either metal ion when exposed to both simultaneously. Nevertheless, HZSM5 exhibited a greater affinity for Cu²⁺ than the other two zeolitic systems for the same metal ion. This behavior correlates well with the trends observed in the single-metal uptake experiments, further corroborating the previously developed hypotheses regarding the different affinities of the investigated zeolitic frameworks for the tested metal ions.

The selectivity exhibited by distinct zeolitic frameworks can also be modulated by several factors. These include: (i) hydration enthalpy; (ii) ionic and hydrated ionic radii; (iii) framework topology and (iv) spatial arrangement of anionic sites within the structure.⁹⁸ Among these, hydration enthalpy and hydrated ionic radius appear to exert the most pronounced influence. Considering that metal cations are solvated in an aqueous solution to form hexaaqua complexes whose dimensions are comparable to those of zeolitic channels, partial desolvation is a prerequisite for successful ion exchange.⁴⁶ The ΔH_hyd values for Co²⁺ and Cu²⁺ are −2000 and −2100 kJ mol⁻¹, respectively.⁹⁹ A lower negative hydration enthalpy implies a lower energetic cost for water ligand dissociation, thereby facilitating ion access to and interaction with the zeolitic lattice.⁹⁸ Additionally, the smaller effective size of hydrated Co²⁺ (r_Co < r_Cu)^46,99 promotes its diffusion into the microporous environment, ultimately enhancing its accessibility to active sites within the zeolitic matrix.

Another critical set of parameters includes the relative mesoporous volume of the zeolites and the distribution of Al³⁺ atoms within their respective frameworks. The Al³⁺ sites that generate Brønsted acid sites (BAS) serve as the principal locus for cation exchange. HUSY and HCLI exhibit relatively high mesoporous volumes, representing 57% and 86% of the total pore volume, respectively (Table 2). The Al³⁺ atoms in their framework are located in accessible positions: (i) within the channels of the sodalite cage in the case of zeolite HUSY¹⁰⁰ and (ii) within the 10-membered elliptical channels in the case of HCLI (Scheme 2B and C).¹⁰¹

Scheme 2 Spatial distribution of Al³⁺ atoms within the crystallographic unit cells of the zeolites (A) HZSM5; (B) HUSY and (C) HCLI.⁵⁸

In contrast, HZSM5 possesses a more compact architecture, with a lower relative mesoporous volume (46%, Table 2) and a three-dimensional network of narrow, intersecting channels. Furthermore, the Al³⁺ framework atoms in HZSM5 occupy sterically constrained regions such as channel intersections or tight microporous cavities (Scheme 2A),¹⁰² thus restricting ion accessibility and hampering cation exchange processes.

These structural and energetic considerations help rationalize the observed experimental results. HUSY and HCLI, which have higher mesoporous volumes and favorable exchange sites, provide enhanced diffusion pathways and more accessible active sites. The observed preferential selectivity toward Co²⁺ likely arises from its less negative hydration enthalpy and smaller hydrated radius, which together confer a competitive advantage to Co²⁺ over Cu²⁺ in accessing and interacting with the zeolitic framework.

Conversely, HZSM5 exhibited no clear selectivity toward metal ions. In our hypothesis, this is due to the specific structural features of the HZSM5 framework coupled with the unique coordination chemistry of Cu²⁺. The narrow, three-dimensional pore system and its poorly accessible BAS hinder both Cu²⁺ and Co²⁺ ions similarly. However, Cu²⁺ exhibits distinctive coordination dynamics due to the Jahn–Teller effect.¹⁰³ In an aqueous solution, its aqua complex fluctuates between octahedral, square planar, and square pyramidal geometries.^103,104 In this scenario, the topological development and specific spatial distribution of Al³⁺ atoms within the HZSM5 framework may stabilize these geometrically distorted species,¹⁰⁵ potentially counterbalancing the intrinsic energetic disadvantage of Cu²⁺ with respect to Co²⁺. Thus, although Co²⁺ is generally more favorable for zeolitic interactions, the ability of HZSM5 to accommodate multiple Cu²⁺ geometries may explain the absence of marked selectivity. This suggests that both steric constraints and coordination flexibility play critical roles in determining HZSM5 ion exchange behavior under the investigated conditions.

Conclusions

Hierarchical porous architectures were obtained from a top-down approach in alkaline media starting from microporous zeolites with different topological frameworks (MFI, FAU and natural HEU). The impact of the desilication treatment on the different structures was carefully investigated by varying the pH of the alkaline solutions from 8 to 13.3. In particular, FAU framework revealed a great susceptibility to alkaline treatment at the highest pH value (13.3). The enhancement of the specific surface areas and mesopore formation in the hierarchical zeolites was documented by volumetric analysis. The effect of the desilication process on the amount, location and accessibility of Brønsted acid sites (BAS) in the hierarchical frameworks was evaluated by the adsorption of basic probe molecules with increasing kinetic diameters (NH₃, 2,4,6-trimethylpyridine, 2,4,6-tri-tert-butylpyridine) monitored by FTIR spectroscopy. The accessibility factor (AF), the number of BAS sites detected by alkylpyridine adsorption divided by the total number of BAS detected by NH₃ adsorption, increased in all the hierarchical structures; however, the increase was more pronounced in the case of the MFI framework. The increased accessibility of BAS sites, the locus for cation exchange processes, observed in the hierarchical structures, is responsible for the improved efficiency of removing cations from metal-polluted aqueous solutions. Uptake tests of Cu²⁺ and Co²⁺ cations from aqueous solutions revealed that, among the hierarchical zeolites, ZSM5 (MFI) exhibited an improvement in metal uptake with respect to its microporous counterpart. Nevertheless, natural clinoptilolite (HEU), which showed the highest BAS amount upon desilication, demonstrated the lowest Cu²⁺ uptake efficiency due to its 2D topological structure and low specific surface area. The affinity and selectivity of the zeolite architectures toward Cu²⁺ and Co²⁺ cations were also evaluated by exposing the materials to solutions containing both metal ions. These results indicate that the interplay between the porosity evolution and the enhanced accessibility of Brønsted acid sites in the production of hierarchical zeolites strongly affects the removal efficiency of metal ions from aqueous solutions.

Experimental

Desilication process of the studied zeolites

Commercial NH₄-ZSM5 (CBV 8014) and HUSY (CBV 780) zeolites were obtained from Zeolyst International, both featuring a SiO₂/Al₂O₃ ratio of 80. The natural clinoptilolite used in this study was supplied by Energom (Mantova, Italy) with a Si/Al ratio of 6.

The as-received zeolites were subjected to alkaline desilication treatments. Specifically, the starting materials were treated with NaOH solutions of varying pH values (8, 9, and 13.3) at a solid/liquid ratio of 22 g L⁻¹. The solutions were prepared using ultrapure water following two different protocols: solutions at pH 8 and 9 were adjusted to the target pH using a pH meter, whereas the pH 13.3 solution corresponded to a 0.2 M NaOH solution.

The alkaline treatment was conducted in a glass reactor at 65 °C. The zeolite samples were introduced into the preheated basic solution and maintained under continuous stirring for 3 hours. Following treatment, the suspension was rapidly cooled in an ice bath and thoroughly washed with deionized water until a neutral pH (7) was reached. The resulting materials were dried overnight at 60 °C. To convert the hierarchical materials into acidic forms, an ion-exchange process was carried out using an NH₄NO₃ solution at 80 °C with a solid/liquid ratio of 6.7 g L⁻¹. Subsequently, the materials underwent calcination in air at 600 °C for 6 hours. To isolate the effect of alkaline treatment, untreated commercial zeolite samples were subjected to calcination and designated as HZSM-5-P and HUSY-P. For clinoptilolite, the parent sample (HCLI-P) was prepared via an ion-exchange procedure with NH₄NO₃ under the same conditions as the hierarchical samples, followed by a calcination step.

FTIR characterization

FTIR measurements were performed on self-supporting pellets prepared by compressing the zeolite powders using a mechanical press at a pressure of 6 tons cm⁻². The pellets were then placed in a suitable IR cell equipped with KBr windows, permanently connected to a vacuum line (residual pressure ≤1 × 10⁻⁴ mbar) to facilitate the analyses. All IR spectra were recorded at room temperature (rt) and, before measurement, the samples were pre-activated at 350 °C for 2 hours under vacuum to eliminate any residual physisorbed water. To ensure accurate comparisons among the samples, absorbance values in the spectra were normalized to the density of each pellet.

Adsorption of the basic probe molecules monitored by FTIR spectroscopy

FTIR spectroscopy measurements were conducted using basic probe molecules on self-supporting pellets prepared following the same procedure as those used for primary characterization. The pellets were then placed in a suitable IR cell permanently connected to a vacuum line (residual pressure ≤1 × 10⁻⁴ mbar) to facilitate the analyses. All IR spectra were recorded at room temperature (rt), and before both measurement and probe molecule introduction, the samples were pre-activated at 350 °C for 2 hours under vacuum to remove any residual physisorbed water.

The procedure for probe molecule introduction, outgassing, and spectral acquisition varied depending on the specific adsorbed probe. As in previous analyses, absorbance values in the spectra were normalized based on the density of each pellet to ensure accurate comparisons among samples.

NH₃ adsorption

The probe was introduced to the sample at an initial pressure of 40 mbar, followed by the acquisition of FTIR spectra under progressively increasing outgassing conditions until vacuum was achieved. The outgassing procedure was carried out at room temperature. Difference spectra were generated by subtracting the initial vacuum spectrum of the sample from each spectrum obtained during outgassing.

2,4,6-Trimethylpyridine (2,4,6-TMPy) adsorption

2,4,6-TMPy adsorption was conducted by exposing the samples to the probe's vapor pressure (∼2 mbar) for 30 minutes at room temperature. Afterwards, desorption was carried out at room temperature for 30 minutes to remove weakly interacting species, followed by a second desorption step at 423 K for 1 hour to isolate the contribution of irreversibly adsorbed TMPyH⁺ ions. Difference spectra were generated by subtracting the initial vacuum spectrum of the sample from each spectrum obtained during outgassing.

2,4,6-Tri-tert-butylpyridine (2,4,6-TTBPy) adsorption

The 2,4,6-TTBPy adsorption was carried out following the same procedure described for 2,4,6-TMPy. However, due to the low vapor pressure of the probe (∼0.02 mbar), the contact time was extended from 30 minutes to 2 hours.

Cu²⁺ solution (10 mM): 85.3 mg of copper(II) chloride dihydrate (CuCl₂·2H₂O, ≥99.0%; Merck KGaA) was dissolved in 50 mL of an aqueous HCl solution at pH = 4.5.

Co²⁺ solution (10 mM): 64.9 mg of anhydrous cobalt(II) chloride (CoCl₂, ≥98.0%; Merck KGaA) was dissolved in 50 mL of an aqueous HCl solution at pH = 4.5.

Uptake tests of Cu²⁺ and Co²⁺ ions from aqueous solutions

The experimental procedure was as follows: 60 mg of each zeolitic material was introduced into a glass vial, followed by the addition of 4 mL of a 10 mM aqueous stock solution of Cu²⁺ or Co²⁺ ions at pH 4.5. Uptake tests were performed under stirring at room temperature for 24 hours. The suspension was also transferred to a Falcon tube for centrifugation to separate the powder from the metal solution. The supernatant was then removed and filtered through a 0.40 μm cellulose acetate filter to eliminate any residual particles that could affect UV-vis analysis. At this stage, the solution was ready for measurement using the UV-vis spectroscopy technique. For each analyzed sample, two distinct aliquots of the material were taken and subjected to uptake tests. Each aliquot was then analyzed in triplicate.

Calibration curves were constructed using two single-element standard solutions for the target metal ions: the Cobalt Standard for AAS TraceCERT (Fluka) and the Copper Standard for AAS TraceCERT (Fluka), both at a known concentration of 1000 ppm. Calibration measurements were performed using five solutions prepared by serial dilution of the standard solution, at the following concentrations: 1000, 800, 600, 400, and 200 ppm. Each solution was then analyzed in triplicate.

Selectivity tests of Cu²⁺ and Co²⁺ ions uptake from aqueous solutions

Selectivity tests were conducted using the same experimental conditions previously described for the uptake experiments of single metal ions in solution (60 mg of sample in contact with 4 mL of solution, 298 K, pH = 4.5). In this case, a stock solution containing both metal ions at an initial concentration of 10 mM each was used. The residual concentrations of metal ions in the solution were determined using the Lambert–Beer equation (eqn (2)). The absorbance values at the absorption maxima of the respective species (809 nm for Cu²⁺ and 512 nm for Co²⁺, Fig. 8) were used. The corresponding molar extinction coefficients (ε) were obtained from the previously established calibration curves. As illustrated in Fig. 8, the two metal ions exhibit distinct absorption peaks in different regions of the UV-vis spectrum, with the absorbance values at these maxima remaining unaffected by the presence of the other UV-vis active species. The amount of each metal ion captured by the analyzed samples was calculated by subtracting the residual concentration from the initial concentration of the stock solution (10 mM for each metal ion). For each sample, two separate aliquots were collected and subjected to uptake tests, with each aliquot analyzed in triplicate.

Instrumentation and operating conditions

- X-ray powder diffractograms (XRPD) were collected on powder samples on a Bruker D8 Advance powder diffractometer (Karlsruhe, Germany), operating in Bragg–Brentano geometry, with a Cu anode target equipped with a Ni filter (used as an X-ray source) and with a Linxeye XE-T high-resolution position-sensitive detector. Trio and twin/twin optics are equipped on the DaVinci design modular XRD system. The X-ray tube of the instrument operates with Cu-K_α1 monochromatic radiation (λ = 1.54062 Å), with the current intensity and operative electric potential difference set to 40 mA and 40 kV, respectively, and with automatic variable primary divergent slits and primary Soller slits of 2.5°. The X-ray profiles were recorded at room temperature in the 2°–80° 2θ range with a coupled 2θ–θ method, continuous PSD fast scan mode, time per step (rate or scan speed) of 0.100 s per step, and 2θ step size (or increment) of 0.02°, with automatic synchronization of the air scatter (or anti-scatter) knife and slits and with a fixed illumination sample set at 17 mm. Following XRD analysis, the relative crystallinity index of the zeolitic samples was determined from the sum of the intensities of the principal crystallographic reflection of each zeolite, using the sample with the highest value as a reference. The characteristic peaks used for the different zeolites are: (i) 23°, 23.2°, 23.7°, 23.9° and 24.4° for the HZSM5 zeolite;¹⁰⁶ (ii) 15.9°, 19°, 20.7°, 24°, 27.5°, 31.9° e 34.7° for the HUSY samples;¹⁰⁷ and (iii) 9.88°, 11.2°, 13.1°, 17.3°, 22.5°, 27.9° e 30.2° for the HCLI zeolites.⁶³

- Nitrogen N₂ physisorption measurements were conducted at the N₂ cryogenic temperature (77 K) under relative pressure from 1 × 10⁻⁶ to 1.0 P/P₀ using a Quantachrome Autosorb 1 MP/TCD instrument (Florida, USA). Before the analysis, the samples were thermally treated under the following conditions: 353 K for 30 min, 423 K for 3 h, 523 K for 3 h, and then treated in vacuum for 6 h (residual pressure lower than 10⁻⁵ Torr). Specific surface areas (SSAs) were determined using the Brunauer–Emmett–Teller (BET) equation within the relative pressure range of 0.01–0.1 P/P₀. Pore-size distributions were obtained by applying the non-localized density functional theory (NLDFT) method (N₂ silica kernel based on a cylindrical pore model applied to the desorption branch).

- SEM images were acquired on a GeminiSEM 360 scanning electron microscope (Zeiss, Oberkochen, Germany) equipped with a Schottky-type field effect emitter as the electron source. Before the analysis, to prevent the insulating particles from becoming electronically charged under the electron beam, a conductive coating of platinum (30 nm) was deposited on the samples by chemical vapor deposition (CVD) using the Desk Sputter Coater DSCT1-F (Vac Coat, Golders Green, London, UK.)

- Infrared spectra were collected using a Thermo Electron Corporation FT Nicolet 5700 spectrometer (Waltham, MA, USA) operating in the 4000–400 cm⁻¹ range with a 4 cm⁻¹ resolution.

- Thermogravimetric analyses were performed using the Setaram SETSYS evolution thermobalance. The data were collected in the range of 30–800 °C with a scan rate of 5 °C min⁻¹ under argon flow (20 mL min⁻¹).

- UV-vis-NIR spectra were recorded at room temperature in the range 340–900 nm with a resolution of 1 nm using a double-beam PerkinElmer Lambda 900 spectrophotometer.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†

Author contributions

All authors contributed to the experimental design, scientific discussion, data analysis and curation, and manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to Dr Vanessa Miglio (DiSIT, Università del Piemonte Orientale, Alessandria, Italy) for the FESEM-EDX analyses, to Dr Stefano Marchesi for the TGA analyses and to Dr Giorgio Celoria for the volumetric analyses. The authors thank the NODES project (Nord Ovest Digitale e Sostenibile; Spoke 2 “Green Technologies and Sustainable Industries”) for its financial support. The financial support by Syensqo to Centro RiSPA is gratefully acknowledged.

References

1. X. Jia, W. Khan, Z. Wu, J. Choi and A. C. K. Yip, Adv. Powder Technol., 2019, 30, 467–484.
2. E. M. Flanigen, Stud. Surf. Sci. Catal., 2001, 137, 11–35.
3. A. F. Masters and T. Maschmeyer, Microporous Mesoporous Mater., 2011, 142, 423–438.
4. J. A. Rabo and M. W. Schoonover, Appl. Catal., A, 2001, 222, 261–275.
5. A. Palčić and V. Valtchev, Appl. Catal., A, 2020, 606, 117795.
6. G. Busca, Microporous Mesoporous Mater., 2017, 254, 3–16.
7. S. Kulprathipanja, Zeolites in Industrial Separation and Catalysis, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2010.
8. G. Li and E. A. Pidko, ChemCatChem, 2019, 11, 134–156.
9. J. Sun, H. Fang, P. I. Ravikovitch and D. S. Sholl, J. Phys. Chem. C, 2020, 124, 668–676.
10. J. Pérez-Ramírez, C. H. Christensen, K. Egeblad, C. H. Christensen and J. C. Groen, Chem. Soc. Rev., 2008, 37, 2530–2542.
11. C. Fernandez, I. Stan, J. P. Gilson, K. Thomas, A. Vicente, A. Bonilla and J. Pérez-Ramírez, Chem.–Eur. J., 2010, 16, 6224–6233.
12. R. Lakes, Nature, 1993, 361, 511–515.
13. D. P. Serrano, J. M. Escola and P. Pizarro, Chem. Soc. Rev., 2013, 42, 4004–4035.
14. J. C. Groen, L. A. A. Peffer, J. A. Moulijn and J. Pérez-Ramírez, Microporous Mesoporous Mater., 2004, 69, 29–34.
15. A. Maghfirah, M. M. Ilmi, A. T. N. Fajar and G. T. M. Kadja, Mater. Today Chem., 2020, 17, 100348.
16. K. Möller and T. Bein, Chem. Soc. Rev., 2013, 42, 3689–3707.
17. D. Verboekend and J. Pérez-Ramírez, Catal. Sci. Technol., 2011, 1, 879–890.
18. S. Mardiana, N. J. Azhari, T. Ilmi and G. T. M. Kadja, Fuel, 2022, 309, 122119.
19. D. Kerstens, B. Smeyers, J. Van Waeyenberg, Q. Zhang, J. Yu and B. F. Sels, Adv. Mater., 2020, 32, 1–47.
20. S. Mitchell, A. B. Pinar, J. Kenvin, P. Crivelli, J. Kärger and J. Pérez-Ramírez, Nat. Commun., 2015, 6, 104.
21. J. C. Groen, L. A. A. Peffer, J. A. Moulijn and J. Pérez-Ramírez, Colloids Surf., A, 2004, 241, 53–58.
22. M. S. Holm, S. Svelle, F. Joensen, P. Beato, C. H. Christensen, S. Bordiga and M. Bjørgen, Appl. Catal., A, 2009, 356, 23–30.
23. L. Sommer, D. Mores, S. Svelle, M. Stöcker, B. M. Weckhuysen and U. Olsbye, Microporous Mesoporous Mater., 2010, 132, 384–394.
24. J. C. Groen, J. C. Jansen, J. A. Moulijn and J. Pérez-Ramírez, J. Phys. Chem. B, 2004, 108, 13062–13065.
25. M. Gackowski, K. Tarach, L. Kuterasiński, J. Podobiński, S. Jarczewski, P. Kuśtrowski and J. Datka, Microporous Mesoporous Mater., 2018, 263, 282–288.
26. K. Sadowska, A. Wach, Z. Olejniczak, P. Kuśtrowski and J. Datka, Microporous Mesoporous Mater., 2013, 167, 82–88.
27. J. Van Aelst, D. Verboekend, A. Philippaerts, N. Nuttens, M. Kurttepeli, E. Gobechiya, M. Haouas, S. P. Sree, J. F. M. Denayer, J. A. Martens, C. E. A. Kirschhock, F. Taulelle, S. Bals, G. V. Baron, P. A. Jacobs and B. F. Sels, Adv. Funct. Mater., 2015, 25, 7130–7144.
28. C. J. Heard, L. Grajciar, F. Uhlík, M. Shamzhy, M. Opanasenko, J. Čejka and P. Nachtigall, Adv. Mater., 2020, 32, 1–29.
29. J. C. Groen, L. A. A. Peffer, J. A. Moulijn and J. Pérez-Ramírez, Chem.–Eur. J., 2005, 11, 4983–4994.
30. D. Verboekend, M. Milina, S. Mitchell and J. Pérez-Ramírez, Cryst. Growth Des., 2013, 13, 5025–5035.
31. A. Erigoni, S. H. Newland, G. Paul, L. Marchese, R. Raja and E. Gianotti, ChemCatChem, 2016, 8, 3161–3169.
32. M. Akgül and A. Karabakan, Microporous Mesoporous Mater., 2011, 145, 157–164.
33. K. A. Tarach, K. Góra-Marek, J. Martinez-Triguero and I. Melián-Cabrera, Catal. Sci. Technol., 2017, 7, 858–873.
34. F. Thibault-Starzyk, I. Stan, S. Abelló, A. Bonilla, K. Thomas, C. Fernandez, J. P. Gilson and J. Pérez-Ramírez, J. Catal., 2009, 264, 11–14.
35. I. Miletto, G. Paul, S. Chapman, G. Gatti, L. Marchese, R. Raja and E. Gianotti, Chem.–Eur. J., 2017, 23, 9952–9961.
36. C. J. Van Oers, K. Góra-Marek, K. Sadowska, M. Mertens, V. Meynen, J. Datka and P. Cool, Chem. Eng. J., 2014, 237, 372–379.
37. K. Sadowska, K. Góra-Marek, M. Drozdek, P. Kuśtrowski, J. Datka, J. Martinez Triguero and F. Rey, Microporous Mesoporous Mater., 2013, 168, 195–205.
38. M. Boronat and A. Corma, ACS Catal., 2019, 9, 1539–1548.
39. M. Che and J. C. Védrine, Characterization of Solid Materials and Heterogeneous Catalysts, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2012.
40. L. Lakiss, A. Vicente, J. P. Gilson, V. Valtchev, S. Mintova, A. Vimont, R. Bedard, S. Abdo and J. Bricker, ChemPhysChem, 2020, 21, 1873–1881.
41. J. Datka, M. Kawałek and K. Góra-Marek, Appl. Catal., A, 2003, 243, 293–299.
42. J. Ding, J. Hu, T. Xue, Y. Wang, H. Wu, P. Wu and M. He, RSC Adv., 2016, 6, 38671–38679.
43. L. Gao, I. Miletto, C. Ivaldi, G. Paul, L. Marchese, S. Coluccia, F. Jiang, E. Gianotti and M. Pera-Titus, J. Catal., 2021, 397, 75–89.
44. Z. Yuna, Environ. Eng. Sci., 2016, 33, 443–454.
45. L. Velarde, M. S. Nabavi, E. Escalera, M. L. Antti and F. Akhtar, Chemosphere, 2023, 328, 138508.
46. E. Erdem, N. Karapinar and R. Donat, J. Colloid Interface Sci., 2004, 280, 309–314.
47. E. P. Beaumier, A. J. Pearce, X. Y. See and I. A. Tonks, Nat. Rev. Chem., 2019, 3, 15–34.
48. M. Halka and B. Nordstrom, Transition Metal, Infobase Holdings, New York, 2019.
49. E. Boros and A. B. Packard, Chem. Rev., 2019, 119, 870–901.
50. V. Balaram, Geosci. Front., 2019, 10, 1285–1303.
51. N. Swain and S. Mishra, J. Clean. Prod., 2019, 220, 884–898.
52. N. N. Hidayah and S. Z. Abidin, Miner. Eng., 2017, 112, 103–113.
53. M. Hartmann, Angew. Chem., Int. Ed., 2004, 43, 5880–5882.
54. B. Bensafi, N. Chouat and F. Djafri, Coord. Chem. Rev., 2023, 496, 215397.
55. H. Sharbini Kamaluddin, X. Gong, P. Ma, K. Narasimharao, A. Dutta Chowdhury and M. Mokhtar, Mater. Today Chem., 2022, 26, 101061.
56. G. Sethia, R. S. Somani and H. Chand Bajaj, RSC Adv., 2015, 5, 12773–12781.
57. N. Mansouri, N. Rikhtegar, H. Ahmad Panahi, F. Atabi and B. K. Shahraki, Environ. Prot. Eng., 2013, 39, 139–152.
58. International zeolite association (IZA), https://www.iza-structure.org/databases, accessed May 2025.
59. M. Hartmann, M. Thommes and W. Schwieger, Adv. Mater. Interfaces, 2021, 8, 2001841.
60. J. Pérez-Ramírez, S. Abelló, A. Bonilla and J. C. Groen, Adv. Funct. Mater., 2009, 19, 164–172.
61. D. Verboekend, N. Nuttens, R. Locus, J. Van Aelst, P. Verolme, J. C. Groen, J. Pérez-Ramírez and B. F. Sels, Chem. Soc. Rev., 2016, 45, 3331–3352.
62. M. M. J. Treacy and J. B. Higgins, The International Zeolite Association, 2001, pp. 3–383.
63. K. Wojciechowska, Clay Miner., 2019, 54, 111–119.
64. H. Sammoury, J. Toufaily, K. Cherry, T. Hamieh, Y. Pouilloux and L. Pinard, Microporous Mesoporous Mater., 2018, 267, 150–163.
65. K. P. De Jong, J. Zečević, H. Friedrich, P. E. De Jongh, M. Bulut, S. Van Donk, R. Kenmogne, A. Finiels, V. Hulea and F. Fajula, Angew. Chem., Int. Ed., 2010, 49, 10074–10078.
66. H. Lin, Q. L. Liu, Y. B. Dong, Y. H. He and L. Wang, Microporous Mesoporous Mater., 2015, 218, 174–179.
67. M. Gackowski, Ł. Kuterasiński, J. Podobiński and J. Datka, ChemPhysChem, 2018, 19, 3372–3379.
68. D. Verboekend, T. C. Keller, M. Milina, R. Hauert and J. Pérez-Ramírez, Chem. Mater., 2013, 25, 1947–1959.
69. D. Verboekend, G. Vilé and J. Pérez-Ramírez, Adv. Funct. Mater., 2012, 22, 916–928.
70. O. A. A. Zecchina, S. Bordiga, G. Spoto, D. Scarano and M. Padovan, J. Chem. Soc. Trans., 1992, 88, 2959–2969.
71. R. Wei, H. Yang, J. A. Scott, K. F. Aguey-Zinsou and D. Zhang, Mater. Today Chem., 2018, 8, 1–12.
72. H. Hattori, P. Arudra, A. Abdalla, A. M. Aitani and S. S. Al-Khattaf, Catal. Lett., 2020, 150, 771–780.
73. D. Verboekend and J. Pérez-Ramírez, Chem.–Eur. J., 2011, 17, 1137–1147.
74. Y. Wang, A. Zhang, Q. Xu and R. Chen, Appl. Catal., A, 2001, 214, 167–177.
75. A. Zecchina, L. Marchese, S. Bordiga, C. Pazè and E. Gianotti, J. Phys. Chem. B, 1997, 101, 10128–10135.
76. L. M. Kustov, Top. Catal., 1997, 4, 131–144.
77. J. Cejka, H. van Bekkum, A. Corma and F. Schueth, Infrared and Raman Spectroscopy for Charaterizing Zeolites, Elsevier B.V., Amsterdam, 2007.
78. J. C. Evans, Spectrochim. Acta, 1962, 18, 507–512.
79. H. Kurama, A. Zimmer and W. Reschetilowski, Chem. Eng. Technol., 2002, 25, 301–305.
80. S. Coluccia, S. Lavagnino and L. Marchese, J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases, 1987, 83, 477–486.
81. O. Bortnovsky, Z. Melichar, Z. Sobalík and B. Wichterlová, Microporous Mesoporous Mater., 2001, 42, 97–102.
82. M. Gackowski, K. Tarach, Ł. Kuterasiński, J. Podobiński, B. Sulikowski and J. Datka, Microporous Mesoporous Mater., 2019, 281, 134–141.
83. B. Sulikowski, J. Rakoczy, H. Hamdan and J. Klinowski, J. Chem. Soc. Chem. Commun., 1987, 20, 1542–1543.
84. C. Pagis, A. R. Morgado Prates, N. Bats, A. Tuel and D. Farrusseng, CrystEngComm, 2018, 20, 1564–1572.
85. Y. Oumi, J. Takahashi, K. Takeshima, H. Jon and T. Sano, J. Porous Mater., 2007, 14, 19–26.
86. T. Farías, A. R. Ruiz-Salvador, L. Velazco, L. C. de Ménorval and A. Rivera, Mater. Chem. Phys., 2009, 118, 322–328.
87. K. Mlekodaj, K. Sadowska, J. Datka, K. Góra-Marek and W. Makowski, Microporous Mesoporous Mater., 2014, 183, 54–61.
88. N. S. Nesterenko, F. Thibault-Starzyk, V. Montouilliout, V. V. Yushchenko, C. Fernandez, J. P. Gilson, F. Fajula and I. I. Ivanova, Kinet. Catal., 2006, 47, 40–48.
89. N. Rajić, N. Z. Logar, A. Rečnik, M. El-Roz, F. Thibault-Starzyk, P. Sprenger, L. Hannevold, A. Andersen and M. Stöcker, Microporous Mesoporous Mater., 2013, 176, 162–167.
90. T. W. Beutel, A. M. Willard, C. S. Lee, M. S. Martinez and R. Dugan, J. Phys. Chem. C, 2021, 125, 8518–8532.
91. H. K. Heinichen and W. F. Hölderich, J. Catal., 1999, 185, 408–414.
92. Y. Han, K. Larmier, M. Rivallan and G. D. Pirngruber, Microporous Mesoporous Mater., 2024, 365, 112906.
93. P. Atkins, T. Overtone, J. Rourke, M. Weller and F. Armstrong, Inorganic Chemistry, Oxford University Press, Oxford, 2010.
94. B. Yang, X. Tong, Z. Deng and X. Lv, J. Chem., 2016, 2016, 2–8.
95. K. A. Krishnan and T. S. Anirudhan, Chem. Eng. J., 2008, 137, 257–264.
96. R. W. Gaikwad and D. V. Gupta, Appl. Ecol. Environ. Res., 2008, 6, 79–96.
97. M. Sprynskyy, B. Buszewski, A. P. Terzyk and J. Namieśnik, J. Colloid Interface Sci., 2006, 304, 21–28.
98. O. Oter and H. Akcay, Water Environ. Res., 2007, 79, 329–335.
99. D. T. Richens, The Chemistry of Aqua Ions: Synthesis, Structure and Reactivity: A Tour through the Periodic Table of the Elements, Wiley-VCH Verlag GmbH & Co. KGaA, 1997.
100. N. Wang, M. Zhang and Y. Yu, Microporous Mesoporous Mater., 2013, 169, 47–53.
101. A. R. Ruiz-Salvador, D. W. Lewis, J. Rubayo-Soneira, G. Rodríguez-Fuentes, L. R. Sierra and C. R. A. Catlow, J. Phys. Chem. B, 1998, 102, 8417–8425.
102. C. W. Kim, N. H. Heo and K. Seff, J. Phys. Chem. C, 2011, 115, 24823–24838.
103. D. H. Powell, L. Helm and A. E. Merbach, J. Chem. Phys., 1991, 95, 9258–9265.
104. J. Chaboy, A. Muñoz-Páez, P. J. Merkling and E. S. Marcos, J. Chem. Phys., 2006, 124, 064509.
105. M. H. Groothaert, K. Pierloot, A. Delabie and R. A. Schoonheydt, Phys. Chem. Chem. Phys., 2003, 5, 2135–2144.
106. S. J. You and E. D. Park, Microporous Mesoporous Mater., 2014, 186, 121–129.
107. I. S. Golubev, P. P. Dik, M. O. Kazakov, V. Y. Pereyma, O. V. Klimov, M. Y. Smirnova, I. P. Prosvirin, E. Y. Gerasimov, D. O. Kondrashev, V. A. Golovachev, O. S. Vedernikov, A. V. Kleimenov and A. S. Noskov, Catal. Today, 2021, 378, 65–74.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra03012a

---