Open Access Article
Open Access ArticleTwo-dimensional Janus α-Au2XY (X, Y = S/Se/Te) semiconductors with favourable band gaps and high carrier mobilities predicted by first-principles investigations†
Nguyen T. Hiep ab,
Quach K. Quangc,
Mai T. V. Nhanc,
Khanh V. Hoangd,
Cuong Q. Nguyen
ab,
Quach K. Quangc,
Mai T. V. Nhanc,
Khanh V. Hoangd,
Cuong Q. Nguyen ab,
Bui D. Hoi
ab,
Bui D. Hoi *e and
Nguyen N. Hieu
*e and
Nguyen N. Hieu ab
ab
aInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam. E-mail: hieunn@duytan.edu.vn
bFaculty of Natural Sciences, Duy Tan University, Da Nang 550000, Vietnam
cDivision of Physics, School of Education, Dong Thap University, Cao Lanh 870000, Vietnam
dPhenikaa Institute for Advanced Study (PIAS), Phenikaa University, Hanoi 12116, Vietnam
eFaculty of Physics, University of Education, Hue University, Hue 530000, Vietnam. E-mail: buidinhhoi@hueuni.edu.vn
First published on 30th May 2025
Abstract
In this work, two-dimensional Janus α-Au2XY (X, Y = S/Se/Te) monolayers are designed and their structural stabilities and fundamental properties are investigated using first-principle calculations. We find that the three α-Au2SSe, α-Au2STe, and α-Au2SeTe structures have high energetic, thermodynamic and mechanical stabilities, indicating that experimental fabrication is feasible. In addition, the proposed systems have anisotropic Young’s modulus and Poisson’s ratio values. According to the electronic structure calculations, the α-Au2XY monolayers are indirect semiconductors with appropriate band gaps for sunlight absorption of 1.06 to 1.33 eV at the Perdew–Burke–Ernzerhof level. The calculation results from the Heyd–Scuseria–Ernzerhof method for the α-Au2XY monolayers also show indirect band gap semiconductor behavior. Moreover, we utilize the deformation potential technique to analyze the electron and hole mobilities of the α-Au2XY materials to determine their transport properties. Interestingly, α-Au2SSe shows an impressive hole carrier mobility of 6258.42 cm2 V−1 s−1 along the y-axis. α-Au2STe and α-Au2SeTe also have high electron mobilities (μe) of 642.21/584.96 cm2 V−1 s−1 and 676.56/760.39 cm2 V−1 s−1 in the x/y directions, respectively. In view of the remarkable electronic and transport properties, the α-Au2XY materials are expected to be promising Janus materials for next-generation optical, electronic, and photovoltaic devices.
1 Introduction
In order to meet the demand for innovative materials in advanced technologies, many scientists around the world have been researching and developing new materials for next-generation devices. In the last two decades, two-dimensional (2D) nanomaterials have attracted much attention due to their unique structures with outstanding electronic,1,2 magnetic,3,4 catalytic,5,6 optoelectronic,7,8 thermodynamic,9,10 and photovoltaic11 properties, which are superior to those of their bulk counterparts. The 2D material library has expanded since the discovery of graphene with the appearance of antinonene,12 phosphorene,13 transition-metal chalcogenides,14 transition-metal oxides,15,16 and MXenes.17 In particular, 2D Janus monolayers are emerging as novel 2D materials with remarkable properties derived from their asymmetric structures.18–20 In studies of 2D Janus materials, investigations using density functional theory (DFT) have proven to be an effective method and have proposed many novel Janus structures with intriguing physical properties.21,22 In addition to theoretical studies, 2D Janus MoSSe materials were first successfully synthesized using the chemical vapor deposition technique.23 This has led to Janus materials undergoing more intensive study.For applications in electronics, photonics, and photovoltaics, the band-gap energy and carrier mobility are very important factors affecting the material properties. The potential materials require favorable band gaps for solar spectrum absorption, as well as good charge transport with high carrier mobility. As a result, research teams have concentrated on exploring new Janus materials with these intriguing properties. For example, based on first-principles simulations, Bouziani et al. found Janus SnGeS2 and Sn2SSe to be potential absorbers with promising optical and electronic properties for solar energy conversion systems. They are indirect semiconductors with moderate band-gap energies of 1.61 eV for SnGeS2 and 1.60 eV for Sn2SSe. Moreover, the SnGeS2 and Sn2SSe monolayers showed a maximum optical conductivity of 4513 Ω−1 cm−1 with low reflectivity of less than 38.5% in the visible spectrum. In addition, the monolayers also had a large absorption coefficient of more than 49.7 μm−1. Consequently, the single-junction solar cells based on these monolayers reached high photovoltaic efficiencies of 27.47% for SnGeS2 and 28.12% for Sn2SSe.24 Ge and co-workers used density functional theory to investigate the structural and electronic properties of PtX2 and Janus PtXY monolayers with X/Y = S/Se/Te. They confirmed that these monolayers were stable and highly flexible from the phonon spectra, elastic constants, and the Young’s modulus results. At the Perdew–Burke–Ernzerhof level, PtX2 and Janus PtXY had indirect band gaps varying from 0.76 to 1.81 eV. The electronic properties of these monolayers were tunable under applied strains. They observed that with increasing tensile strain, there was a presence of an indirect band gap to a quasi-direct band-gap transition. These results revealed potential semiconductors for optoelectronic and nanoelectronic applications.25 Based on MoSi2N4, Ding and co-workers designed 2D Janus XMoSiN2 semiconductors with X = S/Se/Te. From the calculation results, the XMoSiN2 exhibited metal-like electrical conductivity due to its extremely high carrier mobility, which reached 4640 cm2 V−1 s−1.26 Yin et al. studied the fundamental behaviors of Janus MoSSe/GaN heterostructures using first-principles calculations. They reported that the proposed structures showed a high hole mobility of 3951.2 cm2 V−1 s−1 and electron mobility of 281.28 cm2 V−1 s−1. Specifically, stacking modes of the heterostructure and Janus structure could adjust the carrier mobility. In addition, the deformation potential contributed to the varied electron and hole mobilities, and the elastic moduli and equivalent mass also influenced the carrier mobility of the heterostructure.27 Recently, by using first-principles investigations, Janus group-III chalcogenide MX monolayers with M = Ga/In and X = S/Se were reported to exhibit semiconducting behavior with optimal band gaps of 1.295 eV for Se–In–Ga–S and 1.752 eV for S–In–Ga–Se. Notably, type I and II band alignment transitions could be realized through surface termination at the interface and various stacking configurations because of the interlayer interaction. The heterostructures based on these MX monolayers possessed a maximum power conversion efficiency of 16.2%.28
2D gold chalcogenides are predicted to hold great promise for applications in nanoelectronics, thanks to their exceptional physical and mechanical properties. The carrier mobility in gold-based 2D structures is very high,29 making them suitable for applications in nanoelectronics. Also, gold chalcogenides have been explored for a wide range of applications in various fields, including catalysis,30 and photoluminescence.31 In particular, gold chalcogenides have been successfully fabricated experimentally.32 Herein, we theoretically design 2D Janus α-Au2XY (X; Y = S/Se/Te) monolayers and explore their fundamental characteristics using first-principles calculations. After optimizing the crystal α-Au2XY structures, we elucidate their stabilities by calculating cohesive energies and elastic constants, and by performing ab initio molecular dynamics simulations. The Young’s modulus and Poisson’s ratio of the three proposed systems are also examined. Additionally, the electronic structures of the α-Au2SSe, α-Au2STe, and α-Au2SeTe monolayers are investigated by using both the Perdew–Burke–Ernzerhof and Heyd–Scuseria–Ernzerhof methods. We also calculate the work functions of the α-Au2XY configurations to indicate the ability of electrons to leave the material’s surfaces. Notably, we use the deformation potential technique to analyze the carrier mobilities and related parameters of the α-Au2XY for their transport properties.
2 Computational methods
With the Vienna ab initio simulation program,33,34 we apply the projector augmented wave (PAW) approach35,36 to construct the crystal structures and explore the properties of α-Au2XY (X; Y = S/Se/Te) monolayers based on density functional theory (DFT). To verify thermal stability, a canonical ensemble is used for the ab initio molecular dynamics (AIMD) simulation with a canonical ensemble at room temperature (300 K). The exchange–correlation potential is estimated from the Perdew–Burke–Ernzerhof (PBE) functional using a generalized gradient approximation (GGA).37 In addition, the band gap energy is computed from the electronic band structures using the Heyd–Scuseria–Ernzerhof (HSE06)38 hybrid functional. To integrate a supercell’s Brillouin zone (BZ), a 12 × 12 × 1 k grid is used with the Monkhorst technique.39 Along the z-axis, a vacuum space of 30 Å is applied to prevent interactions between the periodic slabs. We use a cut-off of 650 eV for the kinetic energy.35,36 The density functional perturbation theory (DFPT) approach is employed to estimate the elastic constants based on the strain–stress connection. The convergence of the Hellmann–Feynman force and the total energy criteria are determined to be 10−3 eV Å−1 and 10−6 eV, respectively. To correct the dipole moment resulting from the asymmetric Janus structures, we utilize the dipole layer technique for electrostatic potential computations. For the carrier mobilities, the deformation potential (DP) technique is used to analyze the transport characteristics.403 Results and discussion
3.1 Structural parameters and stability
We initially build the geometric configuration of the α-Au2SSe, α-Au2STe, and α-Au2SeTe monolayers. As shown in Fig. 1(a), the black rectangle primitive cell of the three α-Au2XY structures contains four atoms including two Au atoms, one X atom, and one Y atom. In this case, one Au atom bonds with one X atom and one Y atom, and the second Au atom tetra-coordinates with two X atoms and two Y atoms. The atomic positions of the proposed Janus structures are shown in Table S1 of the ESI.† It should also be mentioned that several 2D Janus materials have also been successfully fabricated experimentally, including Janus MoSSe23,41 and PtSSe.42 Table 1 summarizes the optimized lattice parameters of the proposed configurations. The calculated lattice constants a/b of α-Au2SSe, α-Au2STe, and α-Au2SeTe are, respectively, 3.58/6.02, 3.72/6.14, and 3.81/6.08 Å. Along the z-axis, the α-Au2XY structures are formed from three atomic layers of X–Au–Y, as depicted in Fig. 1(b). Their monolayer thickness Δd increases from 2.59 Å for α-Au2SSe to 2.73 and 2.90 Å for, respectively, α-Au2STe and α-Au2SeTe monolayers. This is due to the increasing of the bond lengths between Au and X/Y atoms. Since the α-Au2SSe has the lowest dAu-X/dAu-Y of 2.39/2.49 Å, the α-Au2STe and α-Au2SeTe monolayers have the higher dAu-X/dAu-Y values of 2.43/2.64 Å and 2.54/2.65 Å, respectively. Accordingly, the monolayer thickness and the increased bond lengths of the α-Au2XY are in good agreement with the increasing of the atomic radii of X and Y from 1.84 Å for the S atom to 1.98 Å for Se and 2.21 Å for the Te atom.43,44 Compared with their corresponding symmetric structures, i.e., α-AuX, we find that the Janus α-Au2SSe has a lattice constant a = 3.58 Å, which is larger than that of α-AuS (3.54 Å)29 but smaller than that of α-AuSe (3.65 Å).45 In contrast, the lattice constant b of Janus α-Au2SSe (6.02 Å) is smaller than that of α-AuS (6.18 Å)29 but larger than that of α-AuSe (5.95 Å).45 It is also noted that the 2D α-AuSe has been experimentally fabricated for a long time and its lattice constants are a = 3.690(7), b = 8.355(2), and c = 3.663(1) Å.46| a | b | Δd | dAu-X | dAu-Y | Ecoh | C11 | C12 | C22 | C66 | EPBEg | EHSE06g | Φ1 | Φ2 | ΔΦ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α-Au2SSe | 3.58 | 6.02 | 2.59 | 2.39 | 2.49 | −3.75 | 38.91 | 2.81 | 9.57 | 3.68 | 1.33 | 1.99 | 6.21 | 5.78 | 0.43 |
| α-Au2STe | 3.72 | 6.14 | 2.73 | 2.43 | 2.64 | −3.64 | 36.12 | 2.20 | 7.38 | 2.29 | 1.09 | 1.63 | 6.10 | 5.19 | 0.91 |
| α-Au2SeTe | 3.81 | 6.08 | 2.90 | 2.54 | 2.65 | −3.52 | 36.88 | 1.39 | 5.77 | 1.33 | 1.06 | 1.60 | 5.66 | 5.08 | 0.58 |
Next, to indicate the bonding strength for the energetic stability of the materials, the cohesive energy (Ecoh) of the α-Au2XY systems are estimated as follows:
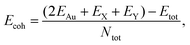 | (1) |
We also evaluate the dynamic stability of the proposed structures by calculating their phonon spectra. Dynamic stability is indicated by the presence of only real phonon frequencies (where the square of the vibrational frequency is positive). Conversely, the appearance of imaginary frequencies in the phonon spectrum signifies a lack of restoring force against atomic displacements, implying structural instability. The phonon spectra of the Janus α-Au2XY materials are shown in Fig. 2(a). It is demonstrated that there are no imaginary frequencies in the phonon spectra of all three proposed structures, implying that the they are dynamically stable.
AIMD simulations are also conducted to evaluate the thermal stability of the α-Au2XY configurations. The dependence of total energy with simulation time (7 ps) at 500 K of the α-Au2SSe, α-Au2STe, and α-Au2SeTe monolayers are illustrated in Fig. 2(b). During the AIMD simulations, we only observe small energy fluctuations, meaning the total energies of three monolayers are quite stable. From the inset atomic structures after the simulations, the bonding of the α-Au2XY structures is well maintained without any reconstruction/fracture, suggesting that the three α-Au2XY systems are thermodynamically stable.
3.2 Mechanical properties
Moreover, we analyse the mechanical properties of the α-Au2XY monolayers by determining their elastic constants of C11, C12, C22, and C66. To estimate the elastic constants, we apply a strain between −1.5 to 1.5% to the x/y-axis. The elastic constant values are then obtained by fitting the applied strains with the varying energies.50 As shown in Table 1, all four obtained elastic constants are positive. The α-Au2SSe has higher elastic constant values than those of the other α-Au2STe and α-Au2SeTe monolayers. This may relate to the larger electronegativity of S (2.58) and Se (2.55) atoms compared with the Te atom (2.1), resulting in a larger elastic modulus with shorter bond lengths. The C11 and C12 values vary from 36.88 to 38.91 N m−1 and 1.39 to 2.81 N m−1, respectively. Thus, the elastic constants of the α-Au2XY monolayers obey the Born and Huang criterion of C11 − C12 > 0 and C66 > 0 for mechanical stability.51,52 This confirms that the α-Au2SSe, α-Au2STe, and α-Au2SeTe materials are mechanically stable for laboratory fabrication.From the attained elastic constants, the material stiffness and deformation are evaluated by analyzing the Young’s modulus Y2D(θ) and Poisson’s ratio ν2D(θ) with polar coordinates using the following equations:52,53
 | (2) |
 | (3) |
The Young’s modulus values of the α-Au2XY configurations are highly anisotropic, as shown by the Young’s modulus diagram in Fig. 3(a). All three monolayers have the maximum Y2D(θ) values at θ = 0° of 38.09 N m−1 for α-Au2SSe, 35.46 N m−1 for α-Au2STe, and 36.54 N m−1 for α-Au2SeTe. Thus, at θ = 0°, the α-Au2SSe structure is slightly stiffer than the other two structures. This is consistent with its having the largest cohesive energy as mentioned above. After reaching the maximum, the Y2D(θ) values steadily decrease and reach much lower values of 9.37, 7.25, and 5.71 N m−1 for α-Au2SSe, α-Au2STe, and α-Au2SeTe, respectively. These attained Y2D(θ) values of α-Au2XY are smaller than those of some other 2D materials, such as Al2SO (Y2D = 90.23 N m−1),54 MoS2 (123 N m−1),55 and graphene (336 N m−1).56 Thus the three proposed α-Au2XY structures have quite similar anisotropic Young’s modulus values and high mechanical flexibility.
 | ||
| Fig. 3 (a) Young’s modulus and (b) Poisson’s ratio diagrams as a function of the in-plane angle θ of α-Au2XY monolayers. | ||
The polar Poisson’s ratio diagrams of the α-Au2XY materials are illustrated in Fig. 3(b). It is easy to observe that the Poisson’s ratio diagrams of the three monolayers also have quite similar shapes with anisotropic behaviors. At θ = 0°, the ν2D(θ) values of α-Au2SSe, α-Au2STe, and α-Au2SeTe are, respectively, 0.29, 0.30, and 0.24. The Poisson’s ratios of the three monolayers spatially increase and reach the maximum values at about θ = 30°, then they steadily decrease to the minimum ν2D(θ) values at θ = 90°. The maximum ν2D(θ) of values of 0.44 for α-Au2SS, 0.54 for α-Au2STe, and 0.65 for α-Au2SeTe at about θ = 30°are higher than the Poisson’s ratios of other reported materials, such as 2D PtSeTe (ν2D = 0.27),25 ZrSeTe (ν2D = 0.26),57 and Sn2PAs (ν2D = 0.24).54
3.3 Electronic properties
In this section, we study the electronic properties of the α-Au2XY monolayers by calculating their band structures in the BZ along the Γ–X–S–Y–Γ point path. As displayed in Fig. 4, the three α-Au2SSe, α-Au2STe, and α-Au2SeTe systems are found to have semiconductor characteristics. At the PBE level, the α-Au2SSe exhibits an indirect band gap of 1.33 eV with the conduction-band minimum (CBM) located between the Γ–X-points, and the valence-band maximum (VBM) located at the S-point. Meanwhile, the α-Au2STe and α-Au2SeTe structures have lower indirect band gaps of 1.09 and 1.06 eV, with the CBM and VBM located at the Γ–X/S–Y and Γ–X/Y point paths, respectively. These obtained band gaps of about 1.0 eV for the α-Au2XY materials are appropriate for sunlight absorption, making them promising semiconductors for photovoltaic systems. PBE systematically underestimates the band gap because it suffers from self-interaction errors and delocalization errors, and it lacks the correct treatment of exchange interactions. Meanwhile, HSE06 partially corrects these problems by mixing in a fraction of exact Hartree–Fock exchange with the PBE exchange–correlation energy, and by screening the Coulomb potential to focus on short-range interactions. The calculated results for the band structures of α-Au2XY using the HSE06 functional are also shown in Fig. 4. Similar to the results from the PBE approach, the band structures from the HSE06 method also show indirect semiconductor behavior for all three α-Au2XY monolayers. The calculated band gaps at the HSE06 level for α-Au2SSe, α-Au2STe, and α-Au2SeTe are 1.99, 1.63, and 1.60 eV, respectively, as presented in Table 1. | ||
| Fig. 4 Electronic band structures from PBE and HSE06 approaches of (a) α-Au2SSe, (b) α-Au2STe, and (c) α-Au2SeTe systems. | ||
Furthermore, to determine the required energy for the electrons to escape the material’s surface, we estimate their work functions Φ from the Fermi (EF) and vacuum (Evac) levels according to the following formula:
| Φ = Evac − EF. | (4) |
A dipole adjustment is necessary for electrostatic potential calculations due to the existence of intrinsic electric fields caused by the asymmetry of Janus α-Au2XY structures.58 The electrostatic potential diagrams of the α-Au2XY configurations are depicted in Fig. 5. All three monolayers have a work function Φ1 on the X side that is higher than the work function Φ2 on the Y side. This can be related to the higher electronegativity of the X atoms compared with the Y atoms. As tabulated in Table 1, the Φ1/Φ2 values decrease from 6.21/5.78 eV for α-Au2SSe to 6.10/5.19 eV for α-Au2STe, and 5.66/5.08 eV for the α-Au2SeTe monolayer. It is more difficult for the electrons to escape from the surface at higher energy. According to these obtained Φ1/Φ2 values, the calculated electrostatic potential difference ΔΦ of the α-Au2XY materials are 0.43, 0.91, and 0.58 eV for α-Au2SSe, α-Au2STe, and α-Au2SeTe, respectively.
 | ||
| Fig. 5 Electrostatic potentials of α-Au2XY monolayers with the dashed green line indicating the Fermi level. | ||
3.4 Transport properties
Finally, the transport properties of the α-Au2XY monolayers are explored to elucidate their potential applications in the electronic fields. The carrier mobilities μ2D are estimated based on the deformation potential method, which can be expressed as follows:40,59
 | (5) |
 denotes the average effective mass. kB and ħ, respectively, relate to the Boltzmann and reduced Planck constants. Ed is the deformation potential. e refers to the elementary charge. C2D indicates the elastic modulus and T is room temperature of 300K. Before getting μ2D, we need to calculate m*, a significant parameter that strongly affects the mobility of carriers. m* can be expressed by the following calculation:
denotes the average effective mass. kB and ħ, respectively, relate to the Boltzmann and reduced Planck constants. Ed is the deformation potential. e refers to the elementary charge. C2D indicates the elastic modulus and T is room temperature of 300K. Before getting μ2D, we need to calculate m*, a significant parameter that strongly affects the mobility of carriers. m* can be expressed by the following calculation:
 | (6) |
 and
and  are defined relative to that band’s extremum point.
are defined relative to that band’s extremum point.  is the effective mass along the Γ–X direction, which is the direction along the conduction band valley (i.e., longitudinal effective mass) and
is the effective mass along the Γ–X direction, which is the direction along the conduction band valley (i.e., longitudinal effective mass) and  is the effective mass in the direction perpendicular to Γ–X, i.e., the Γ–Y direction (transverse effective mass). Generally, the electron effective masses
is the effective mass in the direction perpendicular to Γ–X, i.e., the Γ–Y direction (transverse effective mass). Generally, the electron effective masses  along the x direction are quite low, ranging from 0.21 to 0.26 m0, which are lower than the
along the x direction are quite low, ranging from 0.21 to 0.26 m0, which are lower than the 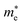 values in the y direction and the hole effective masses
values in the y direction and the hole effective masses  . The α-Au2XY monolayers have quite high
. The α-Au2XY monolayers have quite high  values in the x direction of 4.70 m0 for α-Au2SSe, 1.07 m0 for α-Au2STe, and 1.16 m0 for α-Au2SeTe. This may affect their μ2D values because the high effective masses lead to the low response of carriers, resulting in lower carrier mobilities.
values in the x direction of 4.70 m0 for α-Au2SSe, 1.07 m0 for α-Au2STe, and 1.16 m0 for α-Au2SeTe. This may affect their μ2D values because the high effective masses lead to the low response of carriers, resulting in lower carrier mobilities.
| C2Dx | C2Dy | Edx | Edy | μx | μy | ||||
|---|---|---|---|---|---|---|---|---|---|
| Electron | α-Au2SSe | 0.26 | 0.57 | 78.06 | 73.14 | −6.20 | −3.75 | 431.55 | 504.17 |
| α-Au2STe | 0.21 | 0.48 | 68.89 | 64.40 | −5.85 | −3.92 | 642.21 | 584.96 | |
| α-Au2SeTe | 0.24 | 0.38 | 69.99 | 56.77 | −5.51 | −3.72 | 676.56 | 760.39 | |
| Hole | α-Au2SSe | 4.70 | 0.26 | 78.06 | 73.14 | −6.88 | −0.93 | 6.75 | 6258.42 |
| α-Au2TSe | 1.07 | 0.59 | 68.89 | 64.40 | −2.44 | −4.44 | 289.51 | 148.23 | |
| α-Au2SeTe | 1.16 | 0.63 | 69.99 | 56.77 | −7.46 | −3.21 | 26.97 | 217.60 |
For the calculation of the elastic modulus C2D and DP constant Ed, we apply uniaxial strains (εunix/y) ranging from −0.4 to 0.4% along the two in-plane axes, and estimate the C2D and Ed by using the following equations:
 | (7) |
 | (8) |
As shown in Fig. 6(a), the α-Au2STe and α-Au2SeTe monolayers have quite different band-edge energies along the two in-plane directions under various applied strains from −0.4 to 0.4%. Whereas, the band-edge changing energies of the α-Au2SSe and the CBM/VBM positions of the α-Au2XY monolayers are not much different along the x/y directions. Ed and C2D can be obtained from the fitting curves of the positions and energies of the band edges with the band-edge energies/positions under applied strains.59,60 It can be seen that the calculated C2D and Ed values in Table 2 are quite different along the two in-plane transport directions. α-Au2SSe has the highest C2D of 78.06 Nm−1 in the x direction, and the α-Au2SeTe exhibits the lowest C2D of 56.77 Nm−1 in the y direction. Some other reported 2D materials, such as Ga2SX2,61 Ga2Te3,58 and STiSiAs2 (ref. 62) also exhibited anisotropic Ed values. Similarly, the highest Ed of −0.93 eV is obtained for α-Au2SSe and the lowest Ed of −7.46 eV is obtained for α-Au2SeTe. This directional anisotropy of the elastic modulus and DP constants may cause the anisotropic carrier mobilities of the α-Au2XY monolayers.
 | ||
| Fig. 6 (a) The shifting of the total energies and (b) CBM/VBM positions with the uniaxial strain of α-Au2XY systems along the two in-plane axes. The solid lines are fitting curves. | ||
Consequently, the carrier mobilities μ2D of the α-Au2XY monolayers can be estimated from the obtained C2D, Ed, and m* values according to eqn (5). As expected from the high hole effective masses in the x direction, all three α-Au2XY monolayers exhibit quite low hole mobilities (μh) of 6.75 to 289.51 cm2 V−1 s−1 along the x-axis. However, α-Au2SSe shows the highest μh values of 6258.42 cm2 V−1 s−1 along the y-axis. α-Au2STe and α-Au2SeTe also have high electron mobilities (μe) of 642.21/584.96 cm2 V−1 s−1 and 676.56/760.39 cm2 V−1 s−1 along the x/y axes, respectively. These attained electron mobilities of the α-Au2STe and α-Au2SeTe systems are comparable with the μe values of the reported 2D Si2STe (μe = 530.98 cm2 V−1 s−1),63 ZrSSe (μe = 682.14 cm2 V−1 s−1),64 and WSiP3H (μe = 403.21 cm2 V−1 s−1) materials.65 Meanwhile, the hole mobility value of the α-Au2SSe monolayer along the y-axis is much higher. This indicates that the α-Au2SSe, α-Au2STe, and α-Au2SeTe materials are potential candidates for electronic transport. It is clear that in the DP theory, the carrier mobility depends not only on the mass but also on the DP constant and C2D. Therefore, despite the small effective masses of the α-Au2XY materials, their carrier mobilities are not very high because they have large DP constants (absolute value) and small elastic moduli.
4 Conclusions
By using first-principles simulations, we have designed and explored the fundamental characteristics of the Janus α-Au2XY monolayers. We find that the monolayer thickness and bond lengths of the proposed α-Au2SSe, α-Au2STe, and α-Au2SeTe configurations increase with the increasing of the X and Y atomic radii. From the AIMD simulations, the α-Au2XY structures are thermodynamically stable without any reconstruction/fracture during the heating at 300 K. In addition, the cohesive energy and elastic constant results confirm the high energetic and mechanical stabilities for experimental fabrications of the α-Au2SSe, α-Au2STe, and α-Au2SeTe materials. Anisotropic behavior is found for the Young’s modulus and Poisson’s ratio of the proposed systems. According to the electronic structure calculations, the α-Au2XY monolayers are indirect semiconductors with appropriate band gaps for sunlight absorption of 1.06 to 1.33 eV at the PBE level. The calculation results from the HSE06 approach of the α-Au2XY monolayers also indicate indirect band gap semiconductor behavior. Notably, the transport properties of the α-Au2XY configurations are explored by calculating their carrier mobilities and related parameters. The α-Au2SSe, α-Au2STe, and α-Au2SeTe materials have anisotropic carrier mobilities. Interestingly, α-Au2SSe shows an impressive hole carrier mobility of 6258.42 cm2 V−1 s−1 along the y-axis. α-Au2STe and α-Au2SeTe also have high electron mobilities (μe) of 642.21/584.96 cm2 V−1 s−1 and 676.56/760.39 cm2 V−1 s−1 in the x/y axes, respectively. From the remarkable electronic and transport properties, α-Au2XY structures are expected to be promising Janus materials for next-generation optical, electronic, and photovoltaic devices.Data availability
All data that support the findings of this study are included within the article.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Khanh V Hoang acknowledges Phenikaa University for providing HPC computational resources.References
- H. R. Banjade, J. Pan and Q. Yan, Phys. Rev. Mater., 2021, 5, 014005 CrossRef CAS.
- N. D. Hien, D. V. Lu and L. C. Nhan, Nanoscale Adv., 2023, 5, 4546–4552 RSC.
- D. Muoi, N. N. Hieu, C. V. Nguyen, B. D. Hoi, H. V. Nguyen, N. D. Hien, N. A. Poklonski, S. S. Kubakaddi and H. V. Phuc, Phys. Rev. B, 2020, 101, 205408 CrossRef CAS.
- C. Zhang, Y. Nie, S. Sanvito and A. Du, Nano Lett., 2019, 19, 1366–1370 CrossRef CAS PubMed.
- Y. Zhu, L. Peng, Z. Fang, C. Yan, X. Zhang and G. Yu, Adv. Mater., 2018, 30, 1706347 CrossRef PubMed.
- N. N. Som and P. K. Jha, Int. J. Hydrogen Energy, 2020, 45, 23920 CrossRef CAS.
- M. J. Varjovi, M. E. Kilic and E. Durgun, Phys. Rev. Mater., 2023, 7, 034002 CrossRef CAS.
- M. Zhao, Y. Hao, C. Zhang, R. Zhai, B. Liu, W. Liu, C. Wang, S. H. M. Jafri, A. Razaq, R. Papadakis, J. Liu, X. Ye, X. Zheng and H. Li, Crystals, 2022, 12, 1087 CrossRef CAS.
- Y.-S. Lan, Q. Lu, C.-E. Hu, X.-R. Chen and Q.-F. Chen, Appl. Phys. A, 2019, 125, 33 CrossRef.
- N. Wang, C. Shen, Z. Sun, H. Xiao, H. Zhang, Z. Yin and L. Qiao, ACS Appl. Energy Mater., 2022, 5, 2564–2572 CrossRef CAS.
- F. Zhang, J. Qiu, H. Guo, L. Wu, B. Zhu, K. Zheng, H. Li, Z. Wang, X. Chen and J. Yu, Nanoscale, 2021, 13, 15611–15623 RSC.
- D. Singh, S. K. Gupta, Y. Sonvane and I. Lukačević, J. Mater. Chem. C, 2016, 4, 6386–6390 RSC.
- V. Chaudhary, P. Neugebauer, O. Mounkachi, S. Lahbabi and A. E. Fatimy, 2D Mater., 2022, 9, 032001 CrossRef CAS.
- Y. Dahiya, M. Hariram, M. Kumar, A. Jain and D. Sarkar, Coord. Chem. Rev., 2022, 451, 214265 CrossRef CAS.
- F. Song, L. Bai, A. Moysiadou, S. Lee, C. Hu, L. Liardet and X. Hu, J. Am. Chem. Soc., 2018, 140, 7748–7759 CrossRef CAS PubMed.
- M. J. Varjovi, M. Yagmurcukardes, F. M. Peeters and E. Durgun, Phys. Rev. B, 2021, 103, 195438 CrossRef CAS.
- Y. Gogotsi and B. Anasori, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS PubMed.
- J. Schmeink, J. Osterfeld, O. Kharsah, S. Sleziona and M. Schleberger, npj 2D Mater. Appl., 2024, 8, 67 CrossRef CAS.
- V. Q. Nha, N. Q. San, H. T. T. Linh, T. V. Vu and N. D. Hien, Nanoscale Adv., 2025, 7, 2301–2308 RSC.
- T. V. Vu, A. Kartamyshev, M. D. Nguyen, K. D. Pham, T. T. Trinh, N. P. Nhuan and N. D. Hien, Mater. Sci. Semicond.Process., 2024, 181, 108590 CrossRef CAS.
- T. V. Vu, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Appl. Phys. Lett., 2023, 122, 061601 CrossRef CAS.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Phys. Rev. B, 2021, 104, 115410 CrossRef CAS.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744 CrossRef CAS PubMed.
- I. Bouziani, M. Kibbou, Z. Haman, N. Khossossi, I. Essaoudi, A. Ainane and R. Ahuja, Phys. E, 2021, 134, 114900 CrossRef CAS.
- X. Ge, X. Zhou, D. Sun and X. Chen, ACS Omega, 2023, 8, 5715–5721 CrossRef CAS PubMed.
- C.-H. Ding, Z.-F. Duan, Z.-K. Ding, H. Pan, J. Wang, W.-H. Xiao, W.-P. Liu, Q.-Q. Li, N.-N. Luo, J. Zeng, W. Ren, L.-M. Tang and K.-Q. Chen, Europhys. Lett., 2023, 143, 16002 CrossRef CAS.
- W.-J. Yin, X.-L. Zeng, B. Wen, Q.-X. Ge, Y. Xu, G. Teobaldi and L.-M. Liu, Front. Phys., 2021, 16, 33501 CrossRef.
- Y. Zhao, Q. Tan, H. Li, Z. Li, Y. Wang and L. Ma, Sci. Rep., 2024, 14, 10698 CrossRef CAS PubMed.
- Q. Wu, W. W. Xu, D. Lin, J. Wang and X. C. Zeng, J. Phys. Chem. Lett., 2019, 10, 3773–3778 CrossRef CAS PubMed.
- R. Meyer, C. Lemire, S. K. Shaikhutdinov and H. J. Freund, Gold Bull., 2004, 37, 72–124 CrossRef CAS.
- F. K.-W. Hau, T. K.-M. Lee, E. C.-C. Cheng, V. K.-M. Au and V. W.-W. Yam, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 15900–15905 CrossRef CAS PubMed.
- G. Palyanova, Y. Mikhlin, V. Zinina, K. Kokh, Y. Seryotkin and T. Zhuravkova, J. Phys. Chem. Solids, 2020, 138, 109276 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef CAS.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198 CrossRef CAS PubMed.
- R. Sant, M. Gay, A. Marty, S. Lisi, R. Harrabi, C. Vergnaud, M. T. Dau, X. Weng, J. Coraux, N. Gauthier, O. Renault, G. Renaud and M. Jamet, npj 2D Mater. Appl., 2020, 4, 41 CrossRef CAS.
- D. Ghosh and R. Biswas, Int. J. Mol. Sci., 2003, 4, 379–407 Search PubMed.
- S. Gao, T. Broux, S. Fujii, C. Tassel, K. Yamamoto, Y. Xiao, I. Oikawa, H. Takamura, H. Ubukata, Y. Watanabe, K. Fujii, M. Yashima, A. Kuwabara, Y. Uchimoto and H. Kageyama, Nat. Commun., 2021, 12, 201 CrossRef CAS PubMed.
- C. Tang, L. Zhang, C. Zhang, J. MacLeod, K. K. Ostrikov and A. Du, Nanoscale Horiz., 2020, 5, 366–371 Search PubMed.
- A. Rabenau and H. Schulz, J. Less-Common Met., 1976, 48, 89–101 CrossRef CAS.
- L. Zhang, Y. Gu and A. Du, ACS Omega, 2021, 6, 31919–31925 CrossRef CAS PubMed.
- D. Bezzerga, E.-A. Haidar, C. Stampfl, A. Mir and M. Sahnoun, Nanoscale Adv., 2023, 5, 1425–1432 RSC.
- Y. Liu, C. Shao, W. Yu, Q. Gui, J. Robertson and Y. Guo, Appl. Phys. Lett., 2022, 121, 244105 Search PubMed.
- K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876 CrossRef CAS.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- N. T. Hung, A. R. T. Nugraha and R. Saito, J. Phys. D: Appl. Phys., 2018, 51, 075306 CrossRef.
- P. Xiang, S. Sharma, Z. M. Wang, J. Wu and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2020, 12, 30731 CrossRef CAS PubMed.
- A. Mallah, M. Debbichi, M. H. Dhaou and B. Bellakhdhar, Crystals, 2023, 13, 126 CrossRef CAS.
- K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou, S. Tongay, J. Ji, J. B. Neaton and J. Wu, Nano Lett., 2014, 14, 5097–5103 CrossRef CAS PubMed.
- O. Leenaerts, H. Peelaers, A. D. Hernández-Nieves, B. Partoens and F. M. Peeters, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 195436 CrossRef.
- Dimple, N. Jena, A. Rawat, R. Ahammed, M. K. Mohanta and A. De Sarkar, J. Mater. Chem. A, 2018, 6, 24885–24898 RSC.
- C.-F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312–6317 CrossRef CAS PubMed.
- W. Wan, S. Zhao, Y. Ge and Y. Liu, J. Phys.:Condens. Matter, 2019, 31, 435501 CrossRef CAS PubMed.
- S.-D. Guo, W.-Q. Mu, Y.-T. Zhu, R.-Y. Han and W.-C. Ren, J. Mater. Chem. C, 2021, 9, 2464–2473 RSC.
- N. N. Hieu, H. V. Phuc, A. I. Kartamyshev and T. V. Vu, Phys. Rev. B, 2022, 105, 075402 CrossRef CAS.
- Z. Gao, X. He, W. Li, Y. He and K. Xiong, Dalton Trans., 2023, 52, 8322–8331 RSC.
- N. T. Hiep, C. Q. Nguyen and N. N. Hieu, Appl. Phys. Lett., 2023, 123, 092102 CrossRef CAS.
- S.-Z. Huang, C.-G. Fang, Q.-Y. Feng, B.-Y. Wang, H.-D. Yang, B. Li, X. Xiang, X.-T. Zu and H.-X. Deng, Langmuir, 2023, 39, 2719–2728 CrossRef CAS PubMed.
- T. V. Vu, B. D. Hoi, A. I. Kartamyshev and N. N. Hieu, J. Appl. Phys., 2024, 135, 074301 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01319d |
| This journal is © The Royal Society of Chemistry 2025 |