ANSYS simulation and experimental analysis of an RDX/Al/NC composite explosive prepared via an electrostatic spraying method

Abstract

In order to explore the effect of aluminum (Al) on the performance of 1,3,5-trimethylene trinitramine (RDX), the process of RDX/Al/NC composite explosives prepared via an electrostatic spraying method was simulated using ANSYS software, and the simulation data such as the velocity profile and particle size distribution were obtained. RDX/Al/NC composite explosives with different ratios were experimentally prepared, and the morphology, structure, thermal properties, combustion properties and impact sensitivity of the samples were measured. The simulated particle sizes of the RDX/Al/NC composite explosives with 15%, 35% and 55% Al contents were concentrated at 1427 nm, 3250 nm and 5428 nm, respectively. Experimental results showed that the experimentally prepared particles were slightly smaller than their simulated counterparts, yet both datasets revealed the same trend. The physical recombination of RDX, Al and NC was observed in composite explosives. Compared with the raw material RDX, the activation energy of the RDX/Al/NC composite explosives decreased, the critical temperature of thermal explosion increased, the impact sensitivity decreased, and the combustion performance improved. The activation energies of the RDX/Al/NC composite explosives with 15%, 35% and 55% Al contents reduced by 45 kJ mol⁻¹, 48 kJ mol⁻¹, and 67 kJ mol⁻¹, respectively, and the critical temperature of thermal explosion of the RDX/Al/NC composite explosives with 15%, 35% and 55% Al contents improved by 9 K, 3 K and 4 K, respectively.

---

1 Introduction

RDX is widely used in mixed explosive charges and propellants owing to its low cost, high energy density and excellent detonation performance.^1,2 Explosion velocity, explosion heat, and metal acceleration capacity are important indicators for evaluating the charge performance of RDX. In order to optimize them, the most commonly used method is to optimize RDX-based aluminized explosives.^3,4 The addition of Al to RDX-based explosives results in a significant improvement in the explosion temperature, explosion heat and other energy release characteristics, which substantially improves the work capacity and destructive effectiveness of the combatant charge. Therefore, aluminized explosives have been widely used in various munition systems, such as air-to-air and underwater weapons.^5–7

In recent years, many scholars have conducted extensive research on aluminized explosives, which demonstrated the synergistic effect of Al and explosives.^8,9 On the one hand, Al has a catalytic effect on the thermal decomposition of explosives.¹⁰ On the other hand, the pressure generated by the decomposition of explosives can significantly enhance convection-controlled flame propagation.¹¹ Huang¹² et al. studied the effect of Al with different particle sizes on the thermal decomposition of RDX. Their results show that 10.7 μm and 2.6 μm Al have no significant effect on the thermal decomposition kinetics of RDX, but 40 nm Al actually reduces the activation energy of RDX from 130 kJ mol⁻¹ to 94 kJ mol⁻¹. Zeng¹³ et al. reported core–shell HMX@(Al@GAP) aluminized explosives, which exhibit a longer combustion time and stronger flame compared with physically mixed samples. Currently, the main obstacle to the achievement of synergy between Al and explosives is the assurance of uniformity during the molding process.

Electrostatic spraying technique is a spraying method used to obtain microsphere samples with more homogeneous mixing of components as well as micro- and nanosized particle sizes and is less prone to agglomeration; therefore, several theoretical and experimental results based on this technique are available.^14,15 A novel method for estimating droplet charge in numerical simulations of conductively and inductively charged sprays has been presented by Brentjes Antoni et al.¹⁶ Yu¹⁷ et al. used the Lagrangian method to study the flow field and deposition characteristics of charged droplets in electrostatic spraying and explored the influence of particle velocity, spray cone angles, deposition morphology and other parameters. Chen¹⁸ et al. used COMSOL Multiphysics to establish a two-dimensional simulation model that fully couples electrostatics, laminar flow, and droplet atomization. The model revealed the process of droplet fragmentation and motion under the combined effects of electric field, gravitational field, and airflow. This model provides a more realistic representation of the electrostatic spraying process.

In this study, the electrostatic spraying process for the preparation of RDX/Al/NC composite explosives was simulated using ANSYS software to simulate the electric field distribution of the electrostatic field, the velocity and residence time of the droplets in the electrostatic field, and the particle size distribution of the RDX/Al/NC composite explosives under the same process conditions. On this basis, experiments were carried out to prepare RDX/Al/NC composite explosives with different ratios using an electrostatic spraying method, and the results were compared with the simulation result to shed light on the design of high-performance aluminized explosives.

2 Geometric and numerical model design of electrostatic spray

2.1 Geometric modeling

The geometric model was established according to the entity of the electrostatic spraying device. The model was a two-dimensional plane model, which included 1 radiation source, 1 outlet, 1 axis, 1 wall, 1 region with positive electric potential, and 1 region with negative electric potential. The model is shown in Fig. 1.

Fig. 1 Two-dimensional geometric model of electrostatic spraying.

2.2 Numerical modeling

After the geometric model was established, ANSYS software was used for numerical analysis. Before that, the principle of the electrostatic spraying process was analyzed as a way to select a suitable model for this process. The electrostatic spraying device created an electrostatic field, and the droplets in the electrostatic field were subjected to a variety of forces, including electric field force, surface tension, gravity, coulomb force, and electrostatic repulsion between the droplets. When the resultant force in a certain direction exceeded the surface tension, the droplets ruptured. In this study, only two dominant forces in the whole electric field were considered: electric field force and surface tension. When a droplet moved in an electric field, there was an interaction between the droplet's inherent surface tension and the electric field force present in the electric field. When the electric field force reached a certain strength, the droplet began to break, and internal electrostatic repulsion enhanced, resulting in further breakage, and finally, the droplet completely broke. Currently, there are various models to describe the droplet fragmentation process, such as the Kelvin–Helmholtz (KH) model, the Rayleigh–Taylor droplet breakup model, the Plateau–Rayleigh droplet breakup model, the gravitational droplet breakup model, and the Taylor–Culick droplet breakup model. Among these, the Rayleigh–Taylor model is suitable for describing the above process. The Rayleigh model assumes that the droplet is a uniformly charged conductive sphere. Under the influence of an electric field, the charge distribution on the droplet surface is uneven. According to this model, when the electric field strength exceeds the critical field strength of the droplet, the droplet ruptures. During the breakup process, the internal charge of the droplet is affected by the electric field force, resulting in the deformation and breakup of the droplet. The Rayleigh model can be described by the following equations, which represent the conditions and characteristics of droplet breakup.

Expression for the critical field strength:¹⁹

E_c = 2σ/Rρ (1)

Expression for the minimum droplet radius required for the breakup:¹⁹

R_min = 2σ/E (2)

Expression for the breakup time:¹⁹

t = 2ηR/3σ (3)

In the above equations, E_c is the critical field strength, σ is the surface tension of the droplet, R is the droplet radius, ρ is the density of the droplet material, E is the applied electric field strength, η is the viscosity of the droplet material, and t is the breakup time.

The Rayleigh–Taylor model is based on the Rayleigh–Taylor instability theory, which describes the instability phenomena that occur at the interface between two fluids of different densities under the influence of gravity or other external forces. The Rayleigh–Taylor model employs fundamental equations to describe the evolution of the fluid interface and the process of droplet breakup: the mass conservation equation, momentum conservation equation, motion equation, surface tension equation, and energy conservation equation.

According to the mass conservation equation:²⁰

∂ρ/∂t + ∇·(ρv) = 0, (4)

where ρ is fluid density, v is the velocity vector of the fluid.

In the Rayleigh–Taylor model, the mass of the droplets does not change during the droplet crushing process. Therefore, the mass conservation equation can be reduced to as follows:

∇·v = 0. (5)

According to the momentum conservation equation:²⁰

ρ(∂v/∂t + v·∇v) = −∇p + ∇·τ + ρg, (6)

where ∇ is the gradient operator, p is the pressure of the fluid, τ is the viscous stress tensor of the fluid, g is the gravitational acceleration vector.

According to the surface tension equation,

ΔP = γ(1/R₁ + 1/R₂), (7)

where γ is interfacial coefficient tension, ΔP is the pressure difference at the liquid interface, and R₁ and R₂-the radii of the principal curvature at the liquid interface.

In the interfacial tension equation, the Young–Laplace equation is often used to describe the effect of surface tension on droplets or bubbles.

According to the conservation of energy equation,

∂(ρE)/∂t + ∇·(ρEu) = ∇·(κ∇T) + ∇·q + ∇·(τu), (8)

where E is the total energy per unit mass, u is the velocity vector of the fluid, κ is thermal conductivity, and q is the volume source item.

After analyzing the above equations, the experimental parameters required to simulate the process were obtained through measurement or experimentation, as shown in Table 1.

Table 1 Electrostatic spraying related parameter settings

Parameter/unit	Symbol	Value
Cabin temperature/°C	T	18
Humidity/%	ω	48
Free space permittivity	ε0	8 × 10^−12
Aperture/G	d	25
Inlet speed/ml min^−1	V	0.02
Positive voltage/kV	U−	10
Negative voltage/kV	U+	−10
Distance/mm	L	25
High/mm	H	25

---

3 Experimental work

3.1 Materials

RDX and NC were obtained from Luzhou North Chemical Industries Co., Ltd, China. Al was provided by Liao Ning Qing An Chemical Co., Ltd, China. Acetone (99.5%) was purchased from Chengdu Kelong Chemical Co., Ltd, China.

3.2 Preparation of samples

A schematic of the fabrication of the RDX/Al/NC composite explosive through electrostatic spraying is displayed in Fig. 2. For the fabrication process, certain amounts of RDX and NC were dissolved in 4 mL of acetone to form a clear solution. Then, a specific amount of Al was added to the above NC/RDX solution in an appropriate ratio (as shown in Table 2). The mixture was ultrasonically mixed for 60 min to allow the nanoparticles to disperse homogeneously. This was followed by an additional 24 h of magnetic stirring at room temperature. Finally, the precursor solution was loaded into a syringe and secured for electrostatic spraying. In the electrostatic spraying process, 10 kV potential was attached to the needle using a high-voltage–power supply. The flow was set at 0.06 mL min⁻¹. The composite materials were collected on an aluminum foil situated at 10 cm from the needle.

Fig. 2 Schematic of RDX/Al/NC composite explosive preparation via electrostatic spraying.

Table 2 Mass ratio and number of three types of composite explosives

Samples	m (RDX)/%	m (Al)/%	m (NC)/%
A	80	15	5
B	60	35	5
C	40	55	5

---

3.3 Characterization

The morphology of the RDX/Al/NC composite explosives was characterized using scanning electron microscopy (SEM, Hitachi regulus 8100). The particle size of the RDX/Al/NC composite explosives was measured through a laser particle size analyzer (Mastersizer 3000). Fourier transform infrared spectroscopy (FTIR, Nicholson Tenser 27) and X-ray diffractometry (XRD, DX-2700) were used to further characterize the composition of the samples. Thermogravimetry-differential scanning calorimetry (TG-DSC, Netzsch STA 449F5) was used to evaluate the thermal properties of the samples, conducted from 50 °C to 500 °C with a nitrogen atmosphere of 60 mL min⁻¹ at a heating rate of 5, 10, 15 and 20 K min⁻¹, respectively. The combustion performances were investigated by employing open combustion behavior tests, and about 30 mg of the sample was placed in an inverted cylindrical crucible and ignited with a nichrome wire (0.25 mm in diameter). The loaded wire was connected with a direct current power supply operated at 5.0 A. The combustion process was recorded using a high-speed camera (PHANTOM v 12.0 UX50) with a sampling rate of 2000 frames per second to further estimate the ignition delay time and burning time. An impact sensitivity meter (WL-1) was used to test the characteristic drop height of the samples. The weight of the drop hammer was 2.5 kg, the sample size was 35 mg, and the test was repeated for 25 cycles.

4 Results and discussion

4.1 Simulation results

The results of the electrostatic spraying preparation of three different ratios of RDX/Al/NC composite explosives were simulated using ANSYS software as follows. The simulation results of the particle size distribution, velocity profile and residence time distribution are given in Fig. 3–5, respectively.

Fig. 3 The particle size distribution of RDX/Al/NC composite explosives.

Fig. 4 The velocity profile of RDX/Al/NC composite explosives.

Fig. 5 The residence time distribution of RDX/Al/NC composite explosives.

As shown in Fig. 3, the simulated particle size of sample A ranged from 600 to 2200 nm, with the highest proportion (17.11% of the total) observed at 1427 nm. Furthermore, particles smaller than 1427 nm constituted a larger proportion compared with those larger than 1427 nm, indicating effective droplet fragmentation and yielding smaller particle sizes in the composite explosive. For sample B, the simulated particle sizes spanned 1500–5000 nm, peaking at 3250 nm (24.36% of the total). Notably, the distribution curve of sample B closely approximated a normal distribution, aligning with the experimental results. In contrast, sample C exhibited simulated particle sizes within 4000–8000 nm, with the highest frequency (22.78% of the total) at 5428 nm. In summary, sample C demonstrated the largest simulated particle size, followed by sample B, while sample A achieved the smallest particle size distribution.

As shown in Fig. 4 and 5, within the electrostatic field, the droplet velocities of sample A predominantly ranged from 60 to 200 m s⁻¹, with the highest proportion (21.28% of the total) observed at 111 m s⁻¹. The residence time of sample A droplets in the electrostatic field spanned 6 × 10⁻⁴–2 × 10⁻³ s, peaking at 1.25 × 10⁻³ s (20.41% of the total). Notably, the velocity distribution of sample A exhibited an inverse correlation with its residence time distribution: lower velocities corresponded to longer residence times, demonstrating strong data consistency and reliability. Within the electrostatic field, the droplet velocities of sample B ranged from 70 to 105 m s⁻¹, with the highest proportion (22% of the total) observed at 88 m s⁻¹. The residence time of sample B droplets in the electrostatic field peaked at 1.25 × 10⁻⁴ s, accounting for 20.41% of the total population. Notably, the Gaussian fitting curve of sample B closely approximated a normal distribution, indicating strong alignment with real-world experimental processes. For sample C, droplets with a velocity of 95 m s⁻¹ and a residence time of 1.25 × 10⁻⁴ s were predominantly observed.

4.2 Analysis of experimental results

4.2.1 Morphology and chemical composition. The SEM images and particle size distribution of RDX/Al/NC composite explosives with different ratios is shown in Fig. 6. Sample B and sample C prepared via the electrostatic spraying method demonstrated hollow microsphere-like structures, and sample A remained in granular form. Each component of the composite explosives was tightly combined, and the filamentary NC fibers on the surface of the microspheres were tightly connected with the explosives to form a mesh structure. Sample A exhibited the smallest particle size among the three samples, ranging from 0.5 to 1.2 μm with an average of 0.78 μm, while sample C demonstrated the largest particle size (1–4 μm) and an average of 1.92 μm. Sample B exhibited an intermediate average particle size of 1.26 μm. The experimentally prepared RDX/Al/NC composite explosive particles were slightly smaller than their simulated counterparts, yet both datasets revealed the same trend: a higher Al content in the composite explosive correlated with larger particle sizes. This phenomenon was attributed to the enhanced structural support provided by Al aggregation during the formation of the composite explosives.

Fig. 6 SEM images and particle size distribution of RDX/Al/NC composite explosives with different ratios.

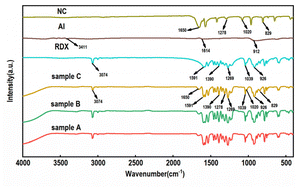
The FT-IR spectra of the raw materials RDX, Al, NC and RDX/Al/NC composite explosives are shown in Fig. 7. In the infrared spectrum of RDX, the absorption peak at 3074 cm⁻¹ is the absorption peak of the C–H group, the absorption peaks at 1591 cm⁻¹ and 1269 cm⁻¹ are the antisymmetric stretching peak and symmetric stretching peak of –NO₂, respectively, and the characteristic peak of –NO₂ is at 1390 cm⁻¹. In the NC infrared spectrum the asymmetric stretching vibration peak, symmetric stretching vibration peak and –CONO₂ deformation vibration peak of the –ONO₂ group are located at 1651 cm⁻¹, 1278 cm⁻¹ and 829 cm⁻¹, respectively. From their comparison, the absorption peak of the RDX/Al/NC composite explosives remained unchanged, and no new absorption peak was generated, indicating that the combination of RDX, Al and NC, was a physical recombination and did not undergo a chemical reaction.

Fig. 7 FT-IR spectra of the raw materials RDX, Al, NC and RDX/Al/NC composite explosives.

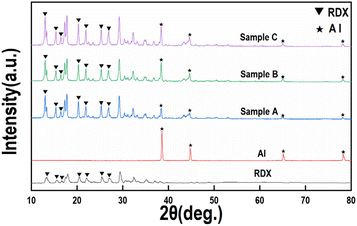
The XRD spectra of the raw materials RDX, Al and RDX/Al/NC composite explosives are shown in Fig. 8. Fig. 8 shows that the diffraction peaks of Al are located at 38.56°, 44.80°, 65.14°, and 78.28°, which correspond to the (111), (200), (220), and (311) crystal planes of the face-centered cubic (fcc) structure, respectively. In the composite explosive, the diffraction peaks of Al match those of the Al raw material, but with weaker diffraction peak intensities, which can be attributed to the lower content of Al in the composite. Compared with the standard reference card, the raw RDX was identified as α-RDX. The diffraction peaks of RDX in samples A, B, and C show no changes compared with those of the raw RDX, indicating that the crystal phase of RDX remains unchanged during the electrostatic spray process.

Fig. 8 XRD patterns of the raw materials RDX, Al and RDX/Al/NC composite explosives.

4.2.2 Thermal decomposition performance. The TG curves of the RDX/Al/NC composite explosives with different ratios at a heating rate of 10 K min⁻¹ are shown in Fig. 9. Under a heating rate of 10 K min⁻¹, the thermal degradation process of the RDX/Al/NC composite explosive exhibited a single-stage weight loss within the temperature range of 180–260 °C, with the maximum weight loss rate occurring near 240 °C. Sample A showed the largest weight loss, which was 97.5%, followed by sample B with a weight loss of approximately 93.8%, while sample C exhibited the smallest weight loss, which was 80.2%. It can be found that the lower the RDX content and the higher the Al content, the smaller the weight loss of the composite explosives. This is because, as the main energetic component, RDX undergoes a violent weight loss within its thermal decomposition temperature range, generating gaseous products. As a metallic fuel, Al undergoes an oxidation reaction at high temperatures, producing stable Al₂O₃ residues. As the RDX proportion decreases and the Al content increases, the total amount of decomposable energetic substances decreases, and the proportion of residual solid-phase products increases, resulting in a decrease in the weight loss.

Fig. 9 TG curves of RDX/Al/NC composite explosives at a heating rate of 10 K min⁻¹.

Fig. 10 shows the DSC and fitting curves of the RDX/Al/NC composite explosive at different heating rates. From Fig. 10 it can be seen that the thermal decomposition of composite explosives is divided into two stages. The first stage occurred at around 205 °C, when RDX underwent a molten phase transition. It can be observed that different heating rates and the Al content had little effect on the melting peak of RDX. At different heating rates, the second stage occurred from 220 °C to 260 °C, and there existed a violent exothermic peak, which is the exothermic peak of thermal decomposition of RDX. Overall, under different heating rates, sample A exhibited the highest thermal decomposition peak temperature, while sample C shows the lowest. Within a certain range, as the Al content increased, the thermal decomposition peak temperature of the composite explosive decreased. Firstly, with the reduction in the RDX proportion, the proportion of high-energy substances in the system significantly decreased, leading to a lower overall energy required for thermal decomposition and a shift in the peak temperature toward lower temperatures. Additionally, Al could react with oxidative gases, such as NO₂ generated during RDX decomposition, forming Al₂O₃ and releasing heat. This reaction further promoted the premature decomposition of RDX.^21,22 Furthermore, the increase in Al content enhanced the thermal conductivity of the system, accelerating heat transfer within the composite. This allows localized temperatures to rapidly reach the RDX decomposition threshold thereby reducing the apparent decomposition temperature.

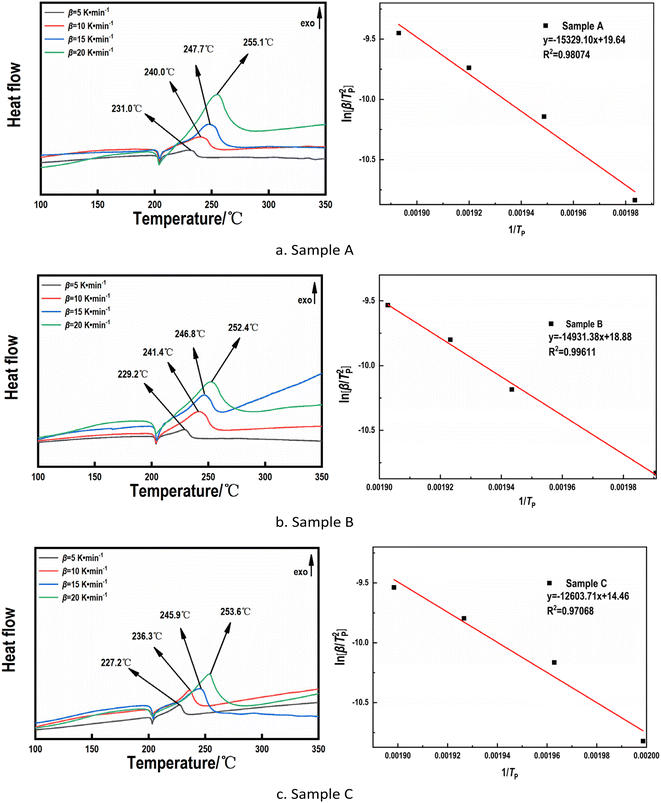Fig. 10 DSC and fitting curves of sample A (a), sample B (b) and sample C (c) at different heating rates.

In addition, it can be found from Fig. 10 that the peak and peak height of the DSC curve had a certain regularity at different heating rates. The peak temperature gradually increased with an increase in heating rate, and the peak width gradually widened with an increase in the heating rate. According to the exothermic peak temperature data given in the diagram, the thermal decomposition kinetic parameters of different samples were calculated according to the formulae (9)–(11).²³ The kinetic parameters for thermal decomposition of different samples are tabulated in Table 3.

T_p = T_p0 + bβ + cβ², (10)

In the above equations, β is the heating rate (K min⁻¹), T_p is the maximum exothermic peak temperature (K), A is the pre-exponential factor (s⁻¹), R = 8.314 J (mol K⁻¹)⁻¹ is the gas constant, E_a is the activation energy (K min⁻¹), T_p0 is the decomposition peak temperature (K) when the heating rate approaches 0, and T_b is the critical temperature of thermal explosion (K).

Table 3 Thermal decomposition kinetic performance parameters of RDX and RDX/Al/NC composite explosives

Sample	A/s^−1	Ea/kJ mol^−1	Tp0/K	Tb/K
Raw RDX	1.2 × 10^13	172	486	498
A	3.4 × 10^8	127	495	512
B	1.6 × 10^8	124	489	506
C	1.9 × 10^6	105	490	511

---

As can be seen from Table 3, compared with the raw material RDX, the activation energies of samples A, B, and C were reduced by 45 kJ mol⁻¹, 48 kJ mol⁻¹, and 67 kJ mol⁻¹, respectively. This indicates that the addition of Al reduced the apparent activation energy of explosives and promoted the decomposition reaction rate of explosives, proving that Al had an obvious catalytic effect on the thermal decomposition of explosives. Compared with the raw material RDX, the thermal explosion critical temperatures of the RDX/Al/NC composite explosives improved to a certain extent, among which the samples A, B and C improved more obviously by 9 K, 3 K and 4 K, respectively, and the thermal stability at high temperature significantly improved.

4.2.3 Combustion performance. The combustion experiment for raw material RDX was carried out. The raw material RDX was heated using a resistance tungsten wire. RDX did not burn and was only accompanied by a large amount of white smoke. This is because of the high ignition point of RDX, and it is difficult to ignite it under open conditions using a resistance wire. The combustion test was performed on each sample, and the combustion process is shown in Fig. 11. As shown in Fig. 11a, under the heating of the resistance wire, sample A could be easily ignited compared with the raw material RDX, and the combustion duration was about 725 ms, and the combustion speed was 0.041 g s⁻¹. The flame produced by the combustion of sample A was bright, relatively smooth, and in the form of a spindle shape with a large lower and small upper part and accompanied by a small amount of sparks, which suggests that the incorporation of nano-Al can improve the combustion performance of RDX. This is due to the small particle size and large specific surface area of nano-Al, with the small size and surface boundary effects. There are many surface active points, greatly increasing the exothermic heat and gas of the composite explosives. From Fig. 10b and c, it can be seen that the combustion process of sample B and sample C was similar to that of sample A. However, compared with sample A, the flames produced by the combustion of sample B and sample C were larger and higher, among which the combustion of sample C produced the highest maximum flames and generated the most sparks. The combustion speeds of sample B and sample C are 0.025 g s⁻¹ and 0.035 g s⁻¹, respectively. It can be seen that Al significantly improved the combustion performance of RDX, and the combustion performance of the composite explosives enhanced with an increase in the aluminum content.

Fig. 11 Combustion process diagram of RDX/Al/NC composite explosives with different ratios.

4.2.4 Impact sensitivity. The impact sensitivity test results of raw RDX and each sample are as follows (Table 4). The results show that the characteristic drop height of each sample was greater than that of the raw material RDX, the impact sensitivity of the composite explosive was significantly reduced, and the safety improved. The reasons for the decrease in sensitivity are outlined below. Firstly, the RDX/Al/NC composite explosives prepared via the electrostatic spraying method have smooth surfaces and small particle sizes. Moreover, the crystal defects of the sample were reduced, resulting in a lower probability of hot spot formation when subjected to impact and other effects. Secondly, NC acted as a binder and formed a network structure with explosives, which exhibited a certain shock mitigation effect. Moreover, the addition of nano-Al increased the contact point with the drop hammer surface, dispersed the force, and the energy could not be concentrated effectively, which reduced the probability of hot spot generation to a certain extent. Furthermore, the addition of Al powder led to the enhancement of the thermal conductivity of the explosive, which is not conducive to the formation of hot spots.²⁴

Table 4 Characteristics fall heights of the different samples

Samples	Characteristic drop height/cm
Raw RDX	36
A	48
B	62
C	>75

---

5 Conclusions

The electrostatic spraying process of three types of RDX/Al/NC composite explosives with different mass ratios was simulated using ANSYS software, and the simulation data of the composite explosives were obtained. Three types of RDX/Al/NC composite explosives were successfully prepared via the electrostatic spraying method through experiments.

The simulated particle sizes of RDX/Al/NC composite explosives with 15%, 35% and 55% Al contents were concentrated at 1427 nm, 3250 nm and 5428 nm, respectively. The experimental average diameters of the RDX/Al/NC composite explosives with 15%, 35%, and 55% Al contents were 780 nm, 1260 nm and 1920 nm, respectively. The composite explosives with 35% and 55% Al contents were hollow microsphere-like structures, and the composite explosives with a 15% Al content remained in granular form. The experimentally prepared RDX/Al/NC composite explosive particles were slightly smaller than their simulated counterparts, yet both datasets revealed the same trend: higher Al content in the composite explosive correlated with larger particle sizes.

Compared with the activation energy of the raw material RDX, the activation energies of the composite explosives were reduced, and the thermal explosion critical temperatures were increased. The activation energies of RDX/Al/NC composite explosives with 15%, 35% and 55% Al contents were reduced by 45 kJ mol⁻¹, 48 kJ mol⁻¹, and 67 kJ mol⁻¹, respectively, and the critical temperature of thermal explosion of the RDX/Al/NC composite explosives with 15%, 35% and 55% Al contents were improved by 9 K, 3 K and 4 K, respectively.

Compared with the raw material RDX, the impact sensitivity decreased and the combustion performance of RDX/Al/NC composite explosives improved. The RDX/Al/NC composite explosives with a 55% Al content showed the most significant increase in impact sensibility.

Data availability

The datasets generated and analyzed in this current study are available from the corresponding author upon reasonable request.

Author contributions

Wei Ji and Yilong Duan contributed equally to this work.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 22275150).

Notes and references

1. B. Liu, W. Li, S. Chen, H. Qian and D. Liu, ChemistrySelect, 2022, 7, e202201459.
2. L. Xiao, Y. Zhang, X. Wang, G. Hao, J. Liu, X. Ke, T. Chen and W. Jiang, RSC Adv., 2018, 8, 38047–38055.
3. C. Chang, X. Wei, J. Peng, M. Yao, D. Wang and X. Qian, J. Loss Prev. Process Ind., 2023, 83, 105070.
4. V. Bagheri, M. H. Keshavarz and A. Mousaviazar, J. Energ. Mater., 2023, 41, 144–156.
5. H. Yang, Y. Liu, H. Huang, Y. Zhao, K. Song, H. Wang, W. Xie, Y. Cheng and X. Fan, J. Therm. Anal. Calorim., 2019, 137, 1615–1620.
6. W. Wang, H. Li, Y. Yang, F. Zhao, H. Li and K. Xu, Cellulose, 2021, 28, 6089–6105.
7. G. Young, D. P. Wilson, M. Kessler, J. B. DeLisio and M. R. Zachariah, Combust. Sci. Technol., 2021, 193, 2259–2275.
8. J. Zhou, B. Wu, R. Zhu, Y. Guo, J. Shi, C. An and J. Wang, Energ. Mater. Front., 2022, 3, 219–225.
9. D. Liu, P. Zhao, S. Hay-Yee Chan, H. H. Hng and L. Chen, Def. Technol., 2021, 17, 327–337.
10. B. Yao, X. Zheng, Y. Lv, W. Tang, J. Jiang and S. Qiu, Chin. J. Energetic Mater., 2019, 27, 616–621.
11. B. Ye, C. Feng, C. An, J. Wang, F. Zhao and J. Zhao, Chin. J. Explos. Propellants, 2022, 45, 60–66.
12. H. Huang, Q. Jiao, J. Li, X. Zhu and C. Zang, Chin. J. Explos. Propellants, 2011, 34, 48–52.
13. C. Zeng, Z. Yang, Y. Wen, W. He, J. Zhang, J. Wang, C. Huang and F. Gong, Chem. Eng. J., 2021, 407, 126360.
14. W. Ji and Y. Xu, Chin. J. Energetic Mater., 2022, 30, 528–534.
15. Y. Bayat, M. Eghdamtalab and V. Zeynali, J. Energ. Mater., 2010, 28, 273–284.
16. A. Brentjes, A. K. Pozarlik and G. Brem, J. Electrost., 2021, 112, 103591.
17. H. Yu, H. Wang, X. Zhu, Y. Ding, R. Chen and Q. Liao, J. Eng. Thermophys., 2021, 42, 2004–2009.
18. F. Chen and X. Deng, Adv. Powder Technol., 2022, 33, 103842.
19. H. Huang, H. Liang and J. Xu, Acta Phys. Sin., 2021, 70, 114701.
20. R. Jazaei, Fluid Mechanics Experiments, Morgan & Claypool, San Rafael, CA, 2020.
21. Q. Luo, X. Long, F. Nie, G. Liu and M. Zhu, Materials, 2018, 11, 1930.
22. L. Xiao, L. Zhao, X. Ke, T. Zhang, G. Hao, Y. Hu, G. Zhang, H. Guo and W. Jiang, Chem. Eng. Sci., 2021, 231, 116302.
23. Z. Liu, Thermal Analysis of Energetic Material, National Defense Industry Press, Beijing, China, 2008.
24. C. Wang, S. Chen, S. Zhao, S. Wang, X. Diao and J. Dong, Initiators Pyrotech., 2010, 132, 32–34.

---

Footnote

† These authors contributed equally to this work.

---