Reaction mechanism study of Al/Ti alloy thin films under thermal stimulation

Abstract

Alloy films are widely used in energy-containing materials to enhance combustion efficiency and heat release, and to improve explosive or propulsive performance. However, studies on the reaction mechanism under thermal stimulation are scarce. In this study, the reaction properties of Al/Ti nanolayers under different conditions are systematically investigated using molecular dynamics simulations (NVT and NVE) and atomic embedding potentials. By constructing accurate atomic models ((Al/Ti)_II, (Al/Ti)_III, and (Al/Ti)_IV) and using appropriate potential energy functions, the reaction was firstly relaxed at 1500 K for 20 ps, followed by reaction simulations under adiabatic conditions for 6 ns. The study reveals the microscopic mechanism of the Al/Ti nanolayer reaction, covering the key processes of reaction triggering, interfacial evolution and temperature change. The main results are as follows: at the junction of the Al and Ti layers, Ti atoms are exfoliated from the solid state and migrate to the Al liquid phase, triggering the reaction. In the “liquid-like” structure (reaction temperature in the range of 1840–1900 K), the interface atoms alloy with the Ti surface, and as the temperature increases, the Ti atoms absorb heat and transform from solid to liquid, and contact with the Al melt to drive the reaction. With the increase of the reaction period, the alloying of the transition layer is completed in advance, and the shorter the period ((Al/Ti)_II, (Al/Ti)_III, and (Al/Ti)_IV), the faster the reaction rate (0.203, 0.398, and 0.707 K ps⁻¹). In the adiabatic stage, the Al/Ti system exhibits self-sustained reaction properties, and the temperature increase promotes the alloying reaction. Eventually, the system reaches equilibrium. This study provides an important theoretical reference for alloy film design and reaction energy control. Simulations provide insight into the high-temperature properties, while experiments demonstrate the behavior of the alloy at lower temperatures, providing a basis for the practical application of the material in industry, and together the two studies build a more comprehensive picture of the material's behavior.

---

1. Introduction

The study of reactive multilayer films¹ (RMFs), especially those composed of aluminium (Al) and titanium (Ti), and the relationship between them and the ignition materials is a complex and tightly interconnected system that involves a number of aspects, such as ignition sensitivity, reaction propagation, energy release, material compatibility and specific application scenarios. The selection and design of suitable ignition materials are crucial to achieve the best performance of RMFs. For example, Jianbing Xu et al.² investigated three types of energy-containing semiconductor bridges (ESCBs) by integrating different Al/MoO_x energetic multilayer nanofilms on the semiconductor bridges, and the results showed that by shortening the modulation period of the nanofilms, the output energies of the ESCBs could be significantly improved. The exothermic reaction between the aluminium and titanium layers in nanoscale RMFs can produce high energy outputs, making them ideal candidates for various technological advances.

In recent years, molecular dynamics is often applied in the study of the properties of binary alloys, such as Cu/Ni,³ Ti/Ni⁴ and Fe/Cr⁵ alloys. For example, Jung G. Y. et al.⁶ used molecular dynamics simulations to investigate the law of stoichiometry influence on the reaction mechanism of Ni/Al nanolayers and explored the reaction properties by varying the ignition temperature and the thickness of the material layer, and the reaction time was shortened as the ignition temperature increased or the thickness of the material layer was reduced. The results of MD simulations showed that the critical temperature for diffusion and direct alloying between W and Cu was about 1000 K. As the temperature increases, the diffusive flux for W/Cu diffusion increases while the interfacial structure becomes more disordered.⁷ S. Li et al.⁸ showed through molecular dynamics simulations that higher temperatures are favourable for the migration of twin boundaries (TBs), and that the softening effect of elemental Y on the migration of TB in magnesium alloys diminishes as the temperature increases. In addition, the migration mechanism of TB in magnesium alloys was analysed in detail. This study provides a theoretical basis for the design and preparation of high-performance magnesium alloys. S. Yazdani et al.⁹ used molecular dynamics simulations and radial distribution functions to evaluate atomic bias in grain boundaries, and the results showed that the highest density of Shockley dislocations and stacking dislocations were formed in the equimolar Cu–Ni alloys, which resulted in a huge sliding phase in the stress–strain curve.

In their study, S. K. Maurya et al.¹⁰ carried out atomic simulations to examine the role of interfacial characteristics, layer thickness and heating rate on the microstructural transformation of Al/Ti multilayers. The results of the study concluded that the structural transformation of Ti from HCP to FCC occurs by generating a series of consecutive prismatic stacking faults in the Ti layer. Peng Yao et al.¹¹ used molecular dynamics to simulate the nanocutting and stress relief annealing of single-crystal γ-TiAl alloys and to analyse the microscopic defects and residual stress distributions after nanocutting of single-crystal γ-TiAl alloys. Y. F. Zhang et al.¹² showed that nano-Al/Ti multilayers have excellent mechanical properties at room temperature, and that, after annealing at 400 °C, the nano-twinned Al/Ti multilayers exhibit excellent thermal properties when the thickness of the monolayer exceeds 22 nm exhibited excellent thermal stability and limited mixing. Rizal Arifin et al.¹³ investigated the structural changes occurring in titanium based alloys (i.e., Ti_X%Al_(100−X)% and Ti_X%Ni_(100−X)%) subjected to compressive and tensile loading using molecular dynamics simulations and found that the atomic composition of equal (50 : 50) Ti_X%Al_(100−X)% and Ti_X%Ni_(100−X)% alloys with equal atomic composition (50 : 50) were found to have higher mechanical strength than alloys with different atomic compositions.

B. Zhai et al.¹⁴ used molecular dynamics simulations to study the local structure and nucleation process of liquid Ti–48%Al and Ti–52%Al (atomic percentage) alloys from the normal to the supercooled state. TiAl₃ is the only intermetallic compound layer formed along the Al/Ti metal layer interface at the processing temperature, and in the diffusion-controlled growth process the growth of the TiAl₃ layer is mainly controlled by the diffusion rates of Ti and Al atoms. Growth kinetics studies have shown that the layer growth rate is higher during the diffusion-controlled growth phase, which is mainly due to faster Al diffusion and higher TiAl₃ nucleation rate at the Ti/TiAl₃ interface.¹⁵

Although MD simulations have been widely used in the study of mechanical and other properties of Al/Ti materials, relatively few studies have been conducted on the reaction properties of high-energy materials such as Al/Ti nanolayers, and they face various challenges, such as the accurate selection of the potential energy function, the computational efficiency of large-scale atomic systems, and the analysis of complex reaction pathways. Therefore, through the comprehensive application of computational simulation technology and theoretical analysis methods, molecular dynamics simulation technology and the Large Scale Atomic/Molecular Massively Parallel Simulator¹⁶ (LAMMPS) were used to deeply explore the reaction performance of Al/Ti nanolayers under different conditions, including reaction triggering mechanism, reaction rate, heat release, etc., in order to reveal the micro-regulation mechanism of the reaction performance of Al/Ti nanolayers. The simulation results, combined with related experiments, provide theoretical guidance for the design and preparation of composites with better performance.

2. Experiment

2.1 Modelling of Al/Ti nano-alloy layered system

In order to elucidate the reaction properties of Al/Ti nanolayers from a microscopic point of view, a modelling system of Al/Ti nanolayers for MD simulations (Fig. 1) was established based on the LAMMPS package, which was investigated in conjunction with the atomic embedding potential (EAM).

Fig. 1 Schematic diagram of modelling of Al/Ti layered nanosystems: (1) (Al/Ti)_II layered nanosystem, (2) (Al/Ti)_III layered nanosystem, (3) (Al/Ti)_IV layered nanosystem; the orange particles are Al atoms and the green particles are Ti atoms.

Two supercells of Ti and Al were firstly built and layered together to minimise lattice mismatch. Then, three different modulation period systems (i.e. (Al/Ti)_II, (Al/Ti)_III and (Al/Ti)_IV) are modelled to have the same thickness value (i.e., ∼57.2 nm) in the z-direction, containing a total of 24 000 atoms, by controlling the ratio of the number of Al/Ti atoms to be 1 : 1, with Ti atoms in the green part and Al atoms in the orange part.

For simulations, the EAM potential developed by R. R. Zope and Y. Mishin¹⁷ was used in the LAMMPS programme package.^18,19 Successive applications of the canonical systematic (NVT)²⁰ and microcanonical systematic (NVE)²¹ ensembles were applied in MD simulations to simulate the heating and ignition processes. Detailed procedure: (1) each of the above three models is subjected to NVT conditions and relaxation at an initial 20 ps of 1500 K²² to reach the equilibrium state. This step can be considered as a thermal shock and no mixing occurs at the interface. A Nose–Hoover thermostat with a coupling constant of 0.1 ps was used to control the temperature; (2) the NVE condition was run for 6 ns, during which the temperature and pressure values converged, indicating the completion of the alloying reaction. During the calculations, the thermal energy accumulated in the Ti and Al atoms during the (NVT-MD) heating process was converted into kinetic energy, which in turn triggered the mixing of the Ti and Al atoms, thus saving the total energy. The time step for all MD simulations was set to 1 fs. When a thermal shock is applied to the Al/Ti nanolayer, the mixing of Ti and Al causes the temperature to increase and undergo a phase transition from solid to liquid.

2.2 Preparation and experiments of Al/Ti alloy thin films

Al/Ti alloy films with three modulation cycles were prepared using RF magnetron sputtering. The growth thickness was controlled according to the sputtering rate, and the Al and Ti films were deposited alternately on K9 glass substrates (the diameter of metallic Al and Ti targets were both 50 mm, the thickness was 4 mm, and the purity was 99.999%). Fig. 2 shows the magnetron sputtering setup used for Ti–Al alloy thin film deposition. Radio-frequency (RF) magnetron sputtering was used to sputter Ti and Al targets at power settings of 172 W and 158 W, respectively, to obtain films with optimum quality. The base pressure of the vacuum chamber (gas flow rate of 1.8 × 10⁻³ m³ h⁻¹) was 5 × 10⁻³ Pa and the working pressure of argon (99.999%) was 0.4 Pa. Multiple alternating operations were performed using a substrate turntable. Deposition and deposition times were used to adjust the thickness of the alloy films. For the alloy film modulation cycle, the total thickness was kept consistent.

Fig. 2 Magnetron sputtering flow and sample diagram.

The composition and structure of the multilayer Al/Ti alloy films were determined using an X-ray diffractometer²³ (XRD, D8ADVANCE) and an energy dispersive spectrometer²⁴ (EDS, S-4800 II). The cross-sectional structure of the samples was characterised microscopically using a field emission scanning electron microscope²⁵ (FESEM, S-4800 II). A NETZSCH STA 449C power-compensated DSC-TG coupler was used for testing to obtain the thermal effects of chemical reactions, and the DSC test conditions for the Al/Ti nanoenergy-containing thin films were as follows: protective gas (N₂) with a gas flow rate of 20 mL min⁻¹, an Al₂O₃ crucible with a lid, a temperature increase rate of 10 °C min⁻¹, and a temperature increase range of 100–1000 °C.

The LIBS experimental setup is shown in Fig. 3, and the Nd:YAG (1064 nm, 6.5 ns) pulsed laser was focused on the surface of Al/Ti alloy film through a convex lens. After focusing the convex lens (focal length of 120 mm, diameter of the laser focus is 0.6 mm), the laser beam generates plasma on the surface of the Al/Ti alloy film, and the plasma spectra are collected using an ICCD spectrometer (DH720-18F-03), and the plasma emission spectrum of the Al/Ti alloy film is captured in parallel three times at the same laser energy. The spectrometer had a time resolution of 2 ns and a gate width of 20 ns, using a holographic grating with 300 notches per mm. Prior to testing, the laser pulse energy was recorded using a laser pulse energy meter (Ophir, model 30A).

Fig. 3 Schematic diagram of the experimental setup for laser-induced breakdown spectroscopy (LIBS).

3. Results and discussion

3.1 MD simulation analysis of Al/Ti layer system

3.1.1 Simulation of thermal behaviour of Al/Ti layered system. The variation of reaction temperature with simulation time for three different modulation cycles of Al/Ti layered nanosystems simulated by NVE system at an initial temperature of 1500 K is given in Fig. 4. From the figure, it can be seen that the relaxation of Al/Ti layered nanosystems under NVT conditions for 20 ps is stabilised at a temperature of 1500 K. The self-sustained exothermic reaction of Al/Ti starts under adiabatic conditions and the temperature of the system continues to increase and finally reaches a convergence temperature, T_ad (i.e., the adiabatic temperature).

Fig. 4 (a) Variation of reaction temperature with simulation time for three modulation cycle (Al/Ti)_II, (Al/Ti)_III and (Al/Ti)_IV thin film systems at an initial temperature of 1500 K. (b) Variation of reaction enthalpy with simulation time for (Al/Ti)_II, (Al/Ti)_III and (Al/Ti)_IV thin film systems.

As can be seen from Table 1, the differences in the adiabatic temperatures T_ad after the system reaches equilibrium are small at an initial temperature of 1500 K, which are 2376 K, 2371 K, and 2356 K. The corresponding reaction times are 4.32 ns, 2.19 ns, and 1.21 ns, and the self-heating rates are calculated to be 0.203, 0.398, and 0.707 K ps⁻¹, respectively. Table 1 shows that as the number of model cycles increases, the reaction time is shortened and the self-heating rate is subsequently enhanced. This is due to the fact that increasing the number of cycles leads to a decrease in the thickness of a single cycle at a constant total thickness. When the Al/Ti system is alloyed, a Ti–Al diffusion barrier layer is formed at the interface of Ti and Al. The thinner the barrier layer, the shorter the reaction time and the higher the self-heating rate. Therefore, the thickness of the interfacial diffusion barrier layer directly affects the self-heating rate in the alloying reaction.

Table 1 Adiabatic temperatures and reaction times for the reactions of three modulation cycle (Al/Ti)_II, (Al/Ti)_III and (Al/Ti)_IV film systems

System	Initial temp. T0/K	Adiabatic temp. Tad/K	Response time/ns	Self-heating rate/K ps^−1
(Al/Ti)II	1500	2376	4.32	0.203
(Al/Ti)III	1500	2371	2.19	0.398
(Al/Ti)IV	1500	2356	1.21	0.707

---

The enthalpy changes of the three modulation cycle (Al/Ti)_II, (Al/Ti)_III and (Al/Ti)_IV film systems were extracted and analysed for the time from 0 to 6 ns. As shown in Fig. 4(b), the enthalpy changes of the three systems are 11 800.4 eV, 11 343.8 eV and 10 986.9 eV, and the enthalpy changes are all positive indicating that the Ti–Al alloying reaction is a heat-absorbing reaction, and the smaller enthalpy changes usually indicate that the energy change during the reaction is small, which is due to the fact that the higher the period is, the alloying reaction of the transition layer finishes in advance, and the amount of the available Al/Ti The amount of substance becomes less, then the degree of the final reaction of the three systems is (Al/Ti)_IV, (Al/Ti)_III, (Al/Ti)_II in the order from easy to difficult.

3.1.2 Atomic migration analysis of the Al/Ti layer system. In order to gain a deeper understanding of the thermal reaction process in the Al/Ti layer, a radial distribution function (RDF)^26,27 analysis was carried out for the distances between atoms at 1500 K. The RDF is an example of a correlation function that describes how the particle correlation in the substance in the average case decays with an increase in the separation rate and reflects the microstructural characteristics of the system. The radial distribution function can be understood as the ratio of the regional density to the average density of the system. Near a reference molecule (smaller value), the areal density is different from the mean density of the system, but at a distance from the reference molecule (larger value) the areal density is the same as the mean density of the system, i.e., the radial distribution function is close to 1 (g(r) → 1). Molecular dynamics calculates the radial distribution function with the formula:where N is the total number of molecules, T is the total time of the calculation, δr is the set distance difference, and ΔN is the number of atoms between r → r + δr.

As can be seen from Fig. 5, g_Al–Ti(r) represents the ratio of the regional density of Ti atoms to the average density of the system with Al atoms as the central atoms, and the three models of (Al/Ti)_II, (Al/Ti)_III, and (Al/Ti)_IV reach a complete mixing state of the Al atoms and Ti atoms at t = 4.32, 2.19, and 1.21 ns, respectively, when the alloying reaction is the alloying reaction is completed at this time. This further proves that in the case of the same thickness and modulation ratio, the smaller the modulation period, the higher the reaction rate.

Fig. 5 (a)–(c) represent the correspondence between g_Al–Ti(r) and atomic migration snapshots for different modulation cycles of Al/Ti, respectively.

From Fig. 6, it can be further found that when the system reaches equilibrium, i.e., the reaction time is 6 ns: (a) the radial distribution function is zero when r < 1.55 Å, indicating that the nearest distance between Al atoms in the system will not be less than 1.55 Å. When 1.55 Å ≤ r ≤ 3.75 Å, a sharp peak appears, and the density near the peak is greater than the average density, reflecting the aggregation nature of Al atoms; (b) when r < 2.15 Å, the radial distribution function is zero, indicating that the closest distance between Al atoms and Ti atoms in the system will not be less than 2.15 Å. When 2.15 Å ≤ r ≤ 3.85 Å, a sharp peak appears, and the density near the peak is greater than the average density, reflecting the nature of Ti atom aggregation around Al atoms; (c) when r < 1.95 Å, the radial distribution function is zero, indicating that the closest distance between Ti atoms in the system will not be less than 1.95 Å. When 1.95 Å ≤ r ≤ 3.85 Å, a sharp peak appears, and the density near the peak is greater than the average density, reflecting the aggregation nature of Ti atoms. And the following information can be further derived from Fig. 6: the order of peak size at the first peak of RDF is g_Al–Ti(r) = 2.928 (B₂) > g_Ti–Ti(r) = 2.394 (C₂) > g_Al–Al(r) = 2.097 (A₂), which indicates that the Al–Ti atoms have the most compact arrangement, followed by Ti–Ti, and Al–Al has the sparsest arrangement. The most sparsely arranged; at the same time, since the width of the first peak of the RDF of the Ti atom group (1.9 Å) is smaller than the width of the first peak of the RDF of the Al atom group (2.2 Å), it indicates that the Ti atoms have stronger interactions with each other, which require more energy to break this bond, and thus the diffusion rate is slower, and that the Al atoms have interactions are weaker and diffusion can easily occur, thus the diffusion rate is faster.

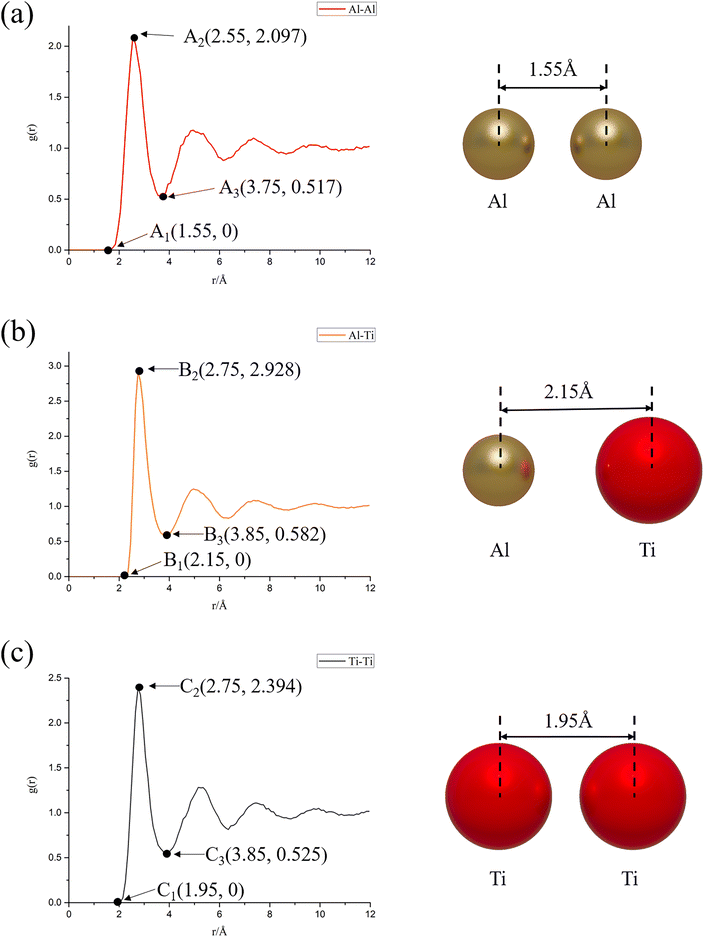Fig. 6 Radial distribution function plots at 6 ns reaction time under NVE system: (a) Al–Al; (b) Al–Ti; (c) Ti–Ti.

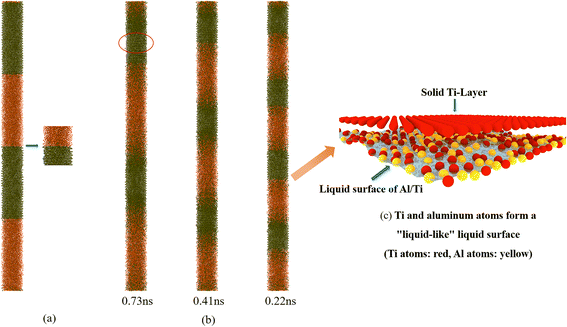
The initial simulation temperature of the system was set at 1500 K, which is higher than the melting point of aluminum (933.47 K) and lower than the melting point of titanium (1905.15 K); therefore, theoretically, the aluminum should be completely melted into the liquid state at the initial stage of the simulation, while the titanium should remain in the solid state. However, it was found during the study that at the initial stage of the NVE simulation, the phenomenon of titanium atoms peeling off from the solid layer and migrating to the aluminum liquid appeared at the junction of the aluminum and titanium layers, indicating that at this time, the temperature at the junction had exceeded the melting point of titanium, while the temperature inside the titanium layer was still lower than the melting point, and it remained in the solid state (as shown in Fig. 7(a)). In addition, it can be observed from the temperature profile in Fig. 4(a) that the temperature rise appears to slow down significantly at 1840 K (corresponding to reaction times of 0.73 ns, 0.41 ns, and 0.22 ns, respectively), as shown in Fig. 7(b), and at this time, the atoms of the titanium surface layer (at the junction) show a high degree of disorder and possess a certain degree of mobility, whereas the atoms of the inner layer still remain in the solid state and make a thermal vibration (see the red circle in Fig. 7(b)). We call the structures in the temperature range of 1840–1900 K “liquid-like” structures.²⁸ In this “liquid-like” structure (e.g., Fig. 7(c)), self-diffusion occurs mainly in a direction parallel to the surface: some diffusion occurs in the outermost layer, and more solids are transformed into liquids as the temperature increases. This “liquid-like” structure causes the flowing atoms at the interface to alloy with the titanium surface, which triggers a further increase in system temperature. As the temperature continues to rise, the atoms inside the titanium layer gradually absorb heat, leading to a transition from solid titanium to liquid, and the uniformly distributed aluminum and titanium melts begin to come into close contact, further promoting the alloying reaction between aluminum and titanium, and ultimately bringing the aluminum–titanium system to equilibrium.

Fig. 7 NVE adiabatic reaction: (a) atomic migration at the interface of the Al/Ti layer system at 0 ns (after relaxation is completed); (b) snapshots of the Al/Ti layer system for different modulation periods with reaction times of 0.73, 0.41 and 0.22 ns, respectively; (c) schematic diagram of the ‘liquid-like’ state.

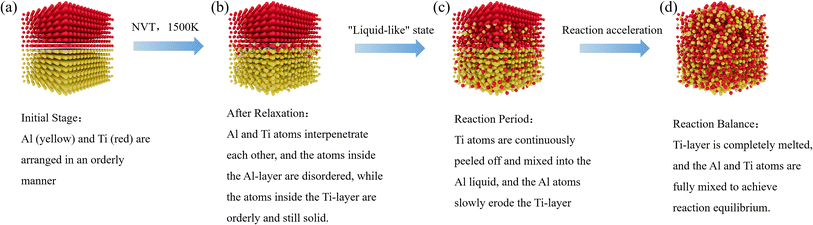
In summary, the process can be simplified as follows: after 20 ps of relaxation simulation at 1500 K temperature, the migration of Ti atoms into the Al liquid phase (Fig. 8(b)) occurs at the junction of the Al/Ti layer system (Fig. 8(a)). At this point, the Ti atoms at the interface show a high degree of disorder and some mobility, while the inner layer remains solid. In this ‘liquid-like’ structure, self-diffusion occurs mainly in the surface-parallel direction. As the temperature increases, the liquid-like structure gradually expands to the interior of the Ti layer, leading to the conversion of more Ti atoms into the liquid phase (Fig. 8(c)), which further promotes the alloying reaction between Al and Ti. Eventually, the system reaches equilibrium (Fig. 8(d)).

Fig. 8 Mechanism of simulated processes in the Al/Ti layer system (Al atoms: yellow, Ti atoms: red): (a) initial stage; (b) after relaxation; (c) reaction period; (d) reaction balance.

3.2 Preparation and experimentation of Al/Ti alloy thin films

3.2.1 Layer structure and morphological analysis of Al/Ti alloy thin films. The 3D schematic and FESEM images of different cross sections of the Al/Ti alloy films are shown in Table 2, respectively. The modulation periods of the Al/Ti alloy films are 2100 nm (Al/Ti: 1310/790 nm, 2 cycles, Φ = 0.7), 1450 nm (Al/Ti: 910/540 nm, 3 cycles, Φ = 0.7) and 1200 nm (Al/Ti: 700/500 nm, 4 cycles, Φ = 0.7). The total thickness of the RMFs composite film was 4.0 μm. The modulation period of the composite film is a very important parameter because it is one of the most important factors affecting the rate of the chemical reaction in Al/Ti alloy films. In addition, by controlling the modulation period of Al/Ti alloy films based on the theory of fixed thickness and stoichiometric ratio, the heat transfer rate and chemical reaction rate can be directly changed. Therefore, the nanosecond laser-induced plasma properties were observed and regulated for three different modulation periods of Al/Ti alloy films. The cross-sectional FESEM images of the Al/Ti alloy films show that the Al/Ti layer has a distinct boundary layer, as shown in Table 2.

Table 2 Schematic representation of Al/Ti films with three modulation cycles

Films	Layer structure	FESEM image
(Al/Ti)II film
Al/Ti: 1310/790 nm
Thickness: 4.20 μm
Φ = 0.77
(Al/Ti)III film
Al/Ti: 910/540 nm
Thickness: 4.35 μm
Φ = 0.7
(Al/Ti)IV film
Al/Ti: 700/500 nm
Thickness: 4.80 μm
Φ = 0.71

---

3.2.2 Chemical reaction properties of Al/Ti alloy films. Fig. 9 shows the DSC curves of Al/Ti nanoenergy-containing thin films with three different modulation cycles ((Al/Ti)_II, (Al/Ti)_III, (Al/Ti)_IV) under the condition of 10 °C min⁻¹ heating rate.

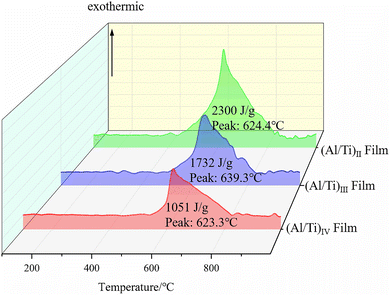Fig. 9 DSC curves of Al/Ti nanoenergy-containing films with three different modulation cycles ((Al/Ti)_II, (Al/Ti)_III, (Al/Ti)_IV).

From Fig. 9, it can be seen that the DSC curves of (Al/Ti)_II, (Al/Ti)_III and (Al/Ti)_IV are basically the same, and a main exothermic peak appears in all three curves, corresponding to the temperature range of 550–800 °C, and each exothermic peak temperature shows an upward trend with the increase of the modulation period. The melting heat absorption peak of Al does not appear because the alloying reaction of the multilayer Al/Ti film emits a large amount of heat, which masks the melting heat absorption peak of Al. There are two stages in the reaction process of the Al/Ti nanoenergy-containing thin films: the first stage is the slow solid-phase reaction of Al and Ti at the interfaces of the energy-containing nano-films, which leads to the formation of nuclei at the interfaces and the formation of a continuous layer gradually; in the second stage, the continuous layer at the interface continues to react in the vertical direction along the Al/Ti nanoenergy-containing film interface, and once the reaction temperature (600 °C) approaches the melting point of Al (660 °C), the alloying reaction rate accelerates drastically and produces a large exothermic peak.

The exotherms of the three modulation cycles are shown in Fig. 9, and the exotherms of the nanoenergy-containing films with modulation cycles (Al/Ti)_II, (Al/Ti)_III, and (Al/Ti)_IV are 2300 J g⁻¹, 1732 J g⁻¹, and 1051 J g⁻¹, respectively, where the exotherms of the reactions (Al/Ti)_II > (Al/Ti)_III > (Al/Ti)_IV, which are derived from the results of the tests.

3.2.3 Laser induced breakdown spectroscopic properties of Al/Ti Alloy thin films. S. S. Harilal et al.²⁹ studied that the kinetic reaction rate depends directly or indirectly on the magnitude of electron temperature and density values. Based on the Atomic Emission Spectroscopy (AES) method, using Laser Induced Breakdown Spectroscopy (LIBS) test method, the laser pulse energy density was set to 55.14 J cm⁻², and the variation rule of the electron temperature and density with time was changed under the conditions of different delay times after the laser pulse.

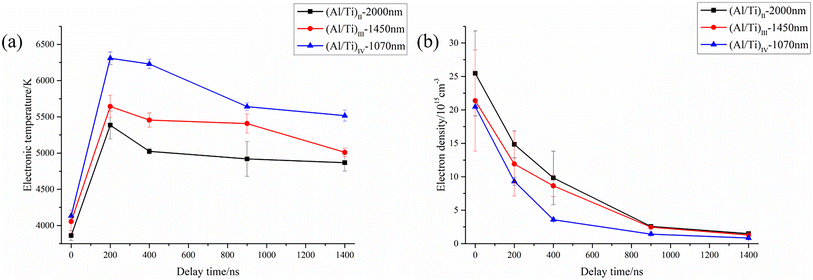
Fig. 10(a) and (b) show the variation of electron temperature and density with time when the laser pulse energy is 55.14 J cm⁻². As the time increases from 0 to 200 ns, the temperature of (Al/Ti)_II increases from 3860.3 to 5385.9 K and then decreases to 4867.8 K, while the density decreases from 25.46 × 10¹⁵ to 6.36 × 10¹⁵ cm⁻³ before reaching a steady state. The temperature of (Al/Ti)_III increases from 4055.3 to 5643.6 K and then decreases to 5010.4 K while the density decreases from 21.37 × 10¹⁵ to 11.91 × 10¹⁵ cm⁻³ before reaching a steady state. The temperature of (Al/Ti)_IV increases from 4133.3 to 6308.7 K and then decreases to 5516.1 K, while the density decreases from 20.47 × 10¹⁵ to 9.32 × 10¹⁵ cm⁻³ before reaching a steady state. The peak in electron temperature is due to the energy released from the Ti–Al chemical reaction. The electron density decreases during the lifetime of the nanosecond laser-induced plasma. The electron density exhibits an anomaly in which (Al/Ti)_IV decreases more rapidly, with the electron density decreasing from close to (Al/Ti)_III to significantly less than (Al/Ti)_III. The plasma electron temperature (Al/Ti)_IV > (Al/Ti)_III > (Al/Ti)_II, but the plasma electron density (Al/Ti)_II > (Al/Ti)_III > (Al/Ti)_IV. This is due to the smaller modulation period and higher reactivity, which contributes to the chemical reaction between Ti–Al films. Faster reaction rate leads to higher temperature and lower density.

Fig. 10 0, 200, 400, 900, 1400 ns delay time: (a) electron temperature variation curves of Al/Ti alloy thin films; (b) electron density variation curves of Al/Ti alloy thin films.

4. Conclusion

In this study, the reaction characteristics of Al/Ti nanolayers under different environmental conditions, including the reaction temperature change, atomic migration and energy release, were deeply investigated by molecular dynamics simulation. The results reveal the significant effect of Al/Ti modulation periodonas on the reaction properties of Al/Ti nanolayers, which provides a new perspective to understand the reaction mechanism of this type of high-energy composites. The MD simulations focus on high temperature scenarios, and the simulations address the atomic-level mechanisms that occur when these alloys are heated to very high temperatures. The experimental studies involve lower temperatures and investigate the exotherm and reaction rates of Al/Ti alloy films. Also supplemented by DSC tests and LIBS experiments on Al/Ti alloy films, the following conclusions can be drawn:

(1) It was found by MD simulations that the Al/Ti layered nanosystems release more energy with a larger modulation period for the same thickness and modulation ratio, and this behavior matches the trend observed in the DSC tests;

(2) It was found by MD simulations that the larger the number of modulation cycles, i.e., the smaller the modulation period (increasing the number of cycles leads to a decrease in the thickness of a single cycle), the shorter the reaction time, and the consequent increase in the rate of self-heating of the Al/Ti layered nanosystems for the same thickness and modulation ratio, a trend that correlates with the results of the LIBS experiment;

(3) In the “liquid-like” structure (reaction temperature in the range of 1840–1900 K), the self-diffusion mainly takes place along the surface parallel direction, and as the temperature rises, the liquid-like structure expands to the interior of the Ti layer, which converts more Ti into the liquid phase and promotes the further alloying reaction between Al and Ti to reach equilibrium.

Data availability

The data that support the findings of this study are available on request from the corresponding author, [Lizhi Wu],upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

References

1. W. Guo, L. Wu, N. Meng, Y. Chen, Z. Ma and X. Zhou, et al., Optimisation of modulation period of TiO2/Al reactive multilayer films for laser-driven flyer plates, Chem. Eng. J., 2019, 360, 1071–1081,  DOI:10.1016/j.cej.2018.10.175.
2. J. Xu, Y. Tai, C. Ru, J. Dai, Y. Shen and Y. Ye, et al., Characteristic of energetic semiconductor bridge based on Al/MoOx energetic multilayer nanofilms with different modulation periods, J. Appl. Phys., 2017, 121(11), 113301.
3. A. Zhou, X.-B. Liu, Q. Wang, S.-Y. Zhang, Y. Meng and H.-B. Zhou, et al., Investigation of nano-tribological behaviors and deformation mechanisms of Cu-Ni alloy by molecular dynamics simulation, Tribol. Int., 2023, 180, 108258.
4. B. Liu, Z. Li, W. Li, Y. Pan and W. Wu, Molecular dynamics simulation of the porosity effect on transformation mechanism of nanocrystalline porous NiTi shape memory alloy, Mater. Today Commun., 2023, 34, 105320.
5. X. Zhu, Y. Luo, Y. Liu, X. Wang, H. Zhang and X. Zhao, Understanding the effect of oil-based lubricants on the tribological behavior of Fe–Cr alloys from reactive molecular dynamics, Langmuir, 2023, 39(14), 5145–5155.
6. G. Y. Jung, W. C. Jeon, S. Lee, S.-H. Jung, S. G. Cho and S. K. Kwak, Reaction characteristics of Ni–Al nanolayers by molecular dynamics simulation, J. Ind. Eng. Chem., 2018, 57, 290–296,  DOI:10.1016/j.jiec.2017.08.035.
7. K. Wang, X. Chen, S. Huang, X. Chen, Z. Wang and Y. Huang, Diffusion behavior determined by the new n-body potential in highly immiscible W/Cu system through molecular dynamics simulations, J. Mater. Res. Technol., 2023, 24, 3731–3745.
8. S. Li, H. Song, L. Han and W. Su, Effect of rare earth element yttrium on migration behavior of twin boundary in magnesium alloys: a molecular dynamics study, J. Mater. Res. Technol., 2023, 24, 5991–5999.
9. S. Yazdani and V. Vitry, Using molecular dynamic simulation to understand the deformation mechanism in Cu, Ni, and equimolar Cu-Ni polycrystalline alloys, Alloys, 2023, 2(1), 77–88.
10. S. K. Maurya, J. F. Nie and A. Alankar, Atomistic analyses of HCP-FCC transformation and reorientation of Ti in Al/Ti multilayers, Comput. Mater. Sci., 2021, 192, 1–14,  DOI:10.1016/j.commatsci.2021.110329.
11. P. Yao, R. Feng, H. Cao, Y. Liu, H. Li and C. Lei, et al., Atomic simulation of effect of stress-relief annealing on the regulation of residual stress in nano-cutting of γ-TiAl alloy, J. Mater. Eng. Perform., 2023, 32(14), 6380–6392.
12. Y. F. Zhang, R. Su, T. J. Niu, N. A. Richter, S. Xue and Q. Li, et al., Thermal stability and deformability of annealed nanotwinned Al/Ti multilayers, Scr. Mater., 2020, 186, 219–224,  DOI:10.1016/j.scriptamat.2020.04.015.
13. R. Arifin, D. R. P. Setiawan, D. Triawan, A. F. S. Putra and W. Y. Munaji, et al., Structural transformation of Ti-based alloys during tensile and compressive loading: An insight from molecular dynamics simulations, MRS Commun., 2023, 13(2), 225–232.
14. B. Zhai and H. Wang, Accurate interatomic potential for the nucleation in liquid Ti-Al binary alloy developed by deep neural network learning method, Comput. Mater. Sci., 2023, 216, 111843.
15. N. Thiyaneshwaran, K. Sivaprasad and B. Ravisankar, Characterization based analysis on TiAl3 intermetallic phase layer growth phenomenon and kinetics in diffusion bonded Ti/TiAl3/Al laminates, Mater. Charact., 2021, 174, 1–9,  DOI:10.1016/j.matchar.2021.110981.
16. S. Gowthaman, A review on mechanical and material characterisation through molecular dynamics using large-scale atomic/molecular massively parallel simulator (LAMMPS), Funct. Compos. Struct., 2023, 5(1), 012005.
17. R. R. Zope and Y. Mishin, Interatomic potentials for atomistic simulations of the Ti-Al system, Phys. Rev. B, 2003, 68(2), 024102.
18. M. Jalalvand, M. A. Charsooghi and S. Mohammadinejad, Smoothed Dissipative Particle Dynamics package for LAMMPS, Comput. Phys. Commun., 2020, 255, 107261.
19. J. Guénolé, W. G. Nöhring, A. Vaid, F. Houllé, Z. Xie and A. Prakash, et al., Assessment and optimization of the fast inertial relaxation engine (fire) for energy minimization in atomistic simulations and its implementation in lammps, Comput. Mater. Sci., 2020, 175, 109584.
20. X.-X. Guo, J.-L. Shao and G. Lu, Reversibility of the structural transition in single crystal iron driven by uniaxial and triaxial strains: Atomistic study, Int. J. Mech. Sci., 2021, 191, 1–9,  DOI:10.1016/j.ijmecsci.2020.106064.
21. K. Lee, K. Joshi, S. Chaudhuri and D. Scott Stewart, Mirrored continuum and molecular scale simulations of deflagration in a nano-slab of HMX, Combust. Flame, 2020, 215, 352–363,  DOI:10.1016/j.combustflame.2020.01.043.
22. M. Fathollahi and H. Azizi-Toupkanloo, Thermal characterization and kinetic analysis of nano- and micro-Al/NiO thermites: Combined experimental and molecular dynamics simulation study, J. Chin. Chem. Soc., 2019, 66(8), 909–918,  DOI:10.1002/jccs.201800371.
23. F. Fabian, C. Barbosa, J. Santos, R. Caraballo-Vivas, F. Garcia and J. Duque, et al., In-situ XANES and XRD studies of the phase transition of RCrO3+ γ (R= Y, Pr, Nd, Gd and Dy; γ= 0 or 1) compounds, J. Alloys Compd., 2020, 815, 152427.
24. T.-L. Tsai, Y.-H. Shih, L.-C. Chen, S.-C. Tsai, I.-H. Lee and C.-P. Lee, et al., Preliminary evaluation of SEM/EDS technique for the determination of colloid diffusion coefficient in granite matrix, J. Radioanal. Nucl. Chem., 2019, 322(3), 1803–1808.
25. H.-q Dou, C.-z Yao, H. Liu, Y. Wan, R.-j Ding and X.-d Yuan, et al., Femtosecond laser ablation of Al-Mg alloy in vacuum and air, Appl. Surf. Sci., 2018, 447, 388–392.
26. I.-H. Lee and K. J. Chang, Crystal structure prediction in a continuous representative space, Comput. Mater. Sci., 2021, 194, 1–8,  DOI:10.1016/j.commatsci.2021.110436.
27. S. Maskey, B. H. Morrow, M. Z. Gustafson, D. J. Luning Prak, P. T. Mikulski and J. A. Harrison, Systematic examination of the links between composition and physical properties in surrogate fuel mixtures using molecular dynamics, Fuel, 2020, 261, 1–12,  DOI:10.1016/j.fuel.2019.116247.
28. F.-L. Tang, G.-B. Chen, Y. Xie and W.-J. Lu, Liquid-Like Structure and Self-Diffusion Channels on Al, Surfaces, 2011, 60 DOI:10.1088/1674-1056/20/2/028401.
29. S. S. Harilal, C. V. Bindhu, R. C. Issac, V. Nampoori and C. Vallabhan, Electron density and temperature measurements in a laser produced carbon plasma, J. Appl. Phys., 1997, 82(5), 2140–2146.

---