Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles study of the ground-state properties of ternary borides with the Ru3B2X (X = Th, U) type structure: a comparative analysis†
Md. Raihan
Islam
a,
Prianka
Mondal
a and
Arpon
Chakraborty
 *b
*b
aDepartment of Physics, Dhaka University of Engineering and Technology (DUET), Gazipur, Gazipur-1707, Bangladesh
bDepartment of Physics, Bangabandhu Sheikh Mujibur Rahman Science and Technology University, Gopalganj-8100, Bangladesh. E-mail: iamarpon07@gmail.com; arpon.phy@gstu.edu.bd
First published on 17th April 2025
Abstract
The distinctive structural, mechanical, electrical, and thermophysical characteristics of the hexagonal Ru3B2X (X = Th, U) compounds make them appropriate for high-temperature and cutting-edge technological applications. Their ground-state features are investigated in this work using density functional theory (DFT). Ru3B2U exhibits higher stability than Ru3B2Th, confirming mechanical stability and advantageous formation in both compounds. Both Ru3B2Th and Ru3B2U show covalent bonding, moderate hardness, and ductility, with Ru3B2Th exhibiting better machinability and greater ductility. Metallic behavior and the characteristic Fermi surface features are highlighted by electronic band structure investigation, with Ru3B2Th exhibiting increased electronic conductivity. Although both compounds show strong covalent connections, uranium and thorium have distinct effects on bonding. Both compounds have high Debye temperatures and melting points indicating their strong bonding and thermal stability. Between the two compounds, Ru3B2Th is preferable for thermal insulation. Optical properties show that these compounds behave in an anisotropic manner and have modest reflectivity, which is compatible with their metallic electronic structure. Due to their high optical reflectivity in the infra-red (IR) region, they are also candidates for IR-shielding applications. This thorough analysis emphasizes their potential for uses demanding robust thermal, mechanical, and optical characteristics.
1. Introduction
Metal borides, a subclass of refractory hard materials, are used in a variety of applications, including defense, the nuclear sector, and high-temperature industries.1 Metal borides constitute a nascent category of improved electrocatalysts for the oxygen evolution reaction (OER), while also presenting a promising opportunity to customize their electrochemical characteristics for potential application in energy storage and conversion technologies.2 The transition metals typically generate borides that are high in metal content. Metal-rich borides, collectively, exhibit inertness and possess elevated melting temperatures. A recent classification of ternary metal borides has been provided.3 Numerous well-defined ternary metal borides have been identified and characterized, especially by Russian researchers. Only a limited number of studies on physical and chemical properties are known. Measurements have primarily been conducted on full and terminal solid solutions of binary metal borides, which may also provide insights into the behavior of ternary borides in some instances.4 The crystal structures of the majority of ternary metal borides can be obtained from structural units that are assembled based on topochemical principles. A categorization of ternary metal borides can be established based on boron–boron aggregation, which is dependent on the boron to metal ratio.Numerous studies on ternary metal borides have been conducted in recent years. In the course of various experimental investigations on transition metal borides, J. M. Leitnaker observed anomalous behavior in heated mixtures of Group IV metal diborides with tungsten and molybdenum.5–7 Density functional theory simulations have been employed to discover stable layered crystal structure phases of Li–M–B, obtained from a recently reported binary metal-sandwich (MS) lithium monoboride superconductor. They demonstrate that the stability of MS lithium monoboride is enhanced when alloyed with electron-rich metal diborides.8 Another study observed superconductivity at approximately 8 K in the metal-rich Li–Pd–B ternary system. This is the inaugural detection of superconductivity in metal-rich ternary borides comprising alkaline metals and palladium as a late transition metal.9 A separate study examined the auto-ignition sol–gel method for synthesizing ternary transition metal boride (TTMB) powders and analyzed their magnetic properties. The synthesized TTMB powders exhibited varying degrees of crystallinity and magnetic properties, contingent upon the boron-to-metal ratio and the subsequent incorporation of dysprosium into one of the samples.10 This study employed semi-automated density functional theory (DFT) simulations to analyze transition metal diborides, focusing on their structural characteristics, phase stability, and mechanical properties. An intriguing aspect is the design of thin film materials, such as ternary or multilayer systems, enabling application-oriented coating development, aimed at concentrating experimental investigations on the most promising systems.11 Transition metal borides exhibit hardness characteristics. The most resilient boride (B12C3) is utilized as a wear-resistant polycrystalline material, in armor tiles, and within the nuclear business, among other applications. The transition metal integrates into the crystal lattice of B12C3, forming new superhard ternary borides B12−nC3 with a hardness ranging from 50 to 77 GPa.12
The RE–[Ru, Rh]–B systems have been partially investigated by Matthias et al., and also RE[Ru, Rh]4B4 compounds exhibiting notable magnetic and superconducting properties have been documented.13–15 Peter Rogl has synthesized novel ternary metal borides with the composition RET4B4 (where RE represents a rare earth metal and T denotes a transition metal) within the systems [La, Ce, Pr, Nd, Sm]–Os–B and [Y, La, Ce, Pr, Nd, Sm, Gd, Tb]–Ir–B. These compounds were seen to crystallize in the NdCo4B4-type structure.16 Ku et al. report four new ternary boride systems with the CeCo3B2-type structure, characterized by the general formulae MRu3B2 (M = La, Ce, Pr, Nd, Sm, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu, Y, Th, or U), MRh3B2 (M = La, Ce, Pr, Nd, Sm, Eu, or Gd), MOs3B2 (M = Lu or U), and MIr3B2 (M = La, Th, or U).17 The majority of members inside these systems were observed to exhibit either superconductivity or magnetic ordering. Superconductivity has been found in Ru3B2Th, where Th is a nonmagnetic element. The superconducting transition temperature ranges from 1.79 K to 1.6 K.17
The formula, lattice parameters, and powder intensities suggest a structural similarity between the new RERu3B2 family of compounds (space group P6/mmm, no. 191) and the structure type of CeCo3B2.18 The crystal structure of Ru3B2U was determined using single-crystal four-circle diffractometer data and revealed a low-symmetry, fourfold superstructure (a = 2a*, c = 2c*) of the CeCo3B2 unit cell,19 with a lower c/a ratio (∼0.54) compared to CeCo3B2 (∼0.55–0.57), indicating compressed axial stacking. This structural distortion in Ru3B2U arises from U's smaller ionic radius and stronger covalent interactions compared to that of Th or rare-earth elements in CeCo3B2. The magnetic properties and structural chemistry of the Ru-series compounds RERu3B2 were examined for an alternative space group, leading to a structural analogy with CeCo3B2, as determined from the single crystal analysis of ErRu3B2. A meticulous examination of the X-ray powder patterns of the uranium compounds U(Ru, Os)3B2, however, revealed a significantly different c/a ratio (0.542), prompting a comprehensive exploration of their structural type in a previous study. The little divergence from the higher symmetry atomic configuration in the CeCo3B2 subcell (P6/mmm20) is evident from a preliminary revision of the Ru3B2U structure in space group P63/mmc, resulting in a reliability factor as low as R ∼ 10%.19 While TiB2 and ZrB2 exhibit simple hexagonal AlB2-type structures with planar B layers, Ru3B2X incorporates actinide atoms (Th/U) in prismatic sites, introducing additional bonding complexity and reducing direct B–B bonding (B–B distances >3 Å vs. ∼1.8 Å in TiB2). The magnetic susceptibility of Y, Lu, Th, and U compounds was determined to be mostly temperature-independent, hence categorizing [Y, Lu, U, Th]Ru3B2 and UOs3B2 as Pauli paramagnets. The majority of the remaining RERu3B2 borides displayed typical paramagnetic behavior and closely followed the Curie–Weiss law over the significant temperature range of 300–1100 K.18
Our study focuses on Ru3B2X (X = Th, U) due to their unique structural stability with a unique combination of hexagonal symmetry, mechanical properties, and potential applications in high-temperature environments and IR shielding materials. Unlike other RERu3B2 compounds, Ru3B2X compounds exhibit a combination of strong covalent bonding and moderate ductility, making them particularly interesting for technological applications. Ru3B2Th and Ru3B2U are understudied compared to other RERu3B2 compounds. Additionally, experimental studies on these compounds are limited, making theoretical insights especially valuable.
2. Computational method
In this study, we employed the Cambridge serial total energy package (CASTEP) software to examine the characteristics of Ru3B2X (X = Th, U) utilizing density-functional theory (DFT).21,22 In order to calculate the exchange–correlation energy, we utilize the generalized gradient approximation (GGA) in conjunction with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.23 In the realm of electron–ion interactions, ultrasoft pseudopotentials are the defining characteristics.24 When it comes to Ru3B2X (X = Th, U), the electron wave function is represented by plane waves that have a cut-off energy of 500 eV. The Monkhorst–Pack technique25 is in charge of producing a consistent grid of k-points along the three axes in reciprocal space in order to sample the Brillouin zone. Within this grid, 5 × 5 × 8 special k-points were chosen for the purpose of optimizing the geometry of Ru3B2X. In order to determine the equilibrium crystal structure of Ru3B2X (X = Th, U), the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization algorithm26 was utilized. The following is a list of the criteria that were defined for the optimization of geometry. It was determined that the total energy of the atom was 1.0 × 10−6 eV, the maximum force was 0.03 eV Å−1, the greatest stress was 0.05 GPa, and the maximum atomic displacement was 0.001 Å.The bulk modulus, electronics characteristics, and elastic constants Cij were all computed directly by using the CASTEP code. The polycrystalline elastic constants are inferred from the computed Cij using the Voigt–Reuss–Hill (VRH) approximation approach.27 The Kleinman parameter (ζ), which evaluates a compound's resistance to stresses like stretching and bending, is another helpful metric. The thermal properties of crystalline materials are crucial for the direct explanation of many solid-state phenomena.28 Debye temperatures, specific heats, melting temperature, thermal conductivity, and thermal expansion coefficient have all been evaluated for our compounds.
The energy band structure of materials is directly proportional to the frequency-varying complex dielectric function, ε(ω). Drude damping29 is required for the study of optical constants in metallic materials. The optical constants of Ru3B2X were calculated using the CASTEP technique with a screened plasma energy of 3 eV and a Dude damping of 0.5 eV. We were able to correct the imaginary part of the dielectric function by using the momentum matrix components that fall between the wave functions of the occupied and unoccupied states. The imaginary component ε2(ω) of the dielectric function in this study is as follows:
 | (1) |
Here, i represents the initial state and j represents the final state. Also, Md denotes the dipole matrix, fi denotes the Fermi distribution function, and Ei represents the energy of the electron in the i-th state. We can obtain the real portion of the dielectric function with the help of the Kramers–Kronig relation and it can be represented as
 | (2) |
Ab initio molecular dynamics (AIMD) simulation was performed using the Vienna ab initio simulation package (VASP).31,32 The simulations were performed for 1000 femtoseconds. VASPKIT33 was used to analyze the output. To check the stability energetically, single-atom energies were computed, using the same pseudopotentials and functional (GGA-PBE) as for the bulk system.
3. Results and discussion
3.1 Structural properties
The crystal structure of Ru3B2X (X = Th, U) is hexagonal with space group P6/mmm (no. 191). The optimized unit cell is depicted in Fig. 1(a). We perform our calculation at zero external pressure and the results of the first principles calculations of structural properties are presented in Table 1. A high degree of reliability of the computational methods used is indicated by the good agreement between our estimated values of lattice constants and volume and the experimental data.17–19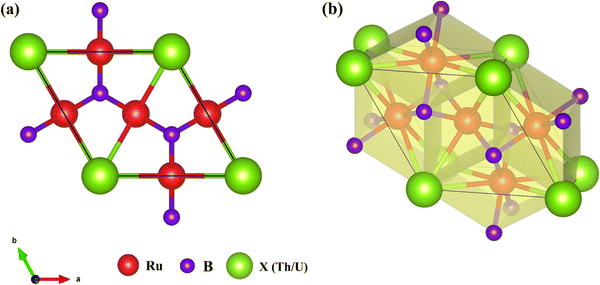 | ||
| Fig. 1 (a) Optimized crystal structure of the Ru3B2X (X = Th, U) unit cell and (b) structural building blocks of Ru3B2X (with polyhedra). | ||
X-Centered hexagonal prisms: the X atoms (Th or U) occupy the 1a Wyckoff position (0, 0, 0) and are coordinated by 12 Ru atoms forming a hexagonal prism. These prisms are arranged in a hexagonal pattern in the ab-plane and share faces along the c-axis.
B-Centered trigonal prisms: the B atoms occupy the 2c Wyckoff position (1/3, 2/3, 0) and are coordinated by 6 Ru atoms forming a trigonal prism. These B-centered trigonal prisms share edges with neighboring prisms, forming a continuous network in the ab-plane.
Ru coordination polyhedra: the Ru atoms, located at the 3g Wyckoff position (1/2, 0, 1/2), exhibit a complex coordination environment. Each Ru atom is bonded to 4 B atoms and 4 X atoms, forming a distorted square antiprism. The Ru atoms serve as the connective tissue between the X and B layers.
B coordination: each B atom is surrounded by 6 Ru atoms forming a trigonal prism. The B–Ru bond lengths are 2.21 Å for Ru3B2Th and 2.18 Å for Ru3B2U. Notably, the B atoms form a planar honeycomb-like network in the ab-plane, with no direct B–B bonds observed (B–B distances exceed 3 Å), distinguishing this structure from boron-rich borides.
Ru coordination: the Ru atoms exhibit a mixed coordination environment with 4 B neighbors and 4 X neighbors. The Ru–B bonds (2.18–2.21 Å) are significantly shorter than the Ru–X bonds (2.94–3.02 Å), reflecting the stronger covalent character of the Ru–B interaction compared to the more metallic Ru–X bonding.
| ΔHf(Ru3B2X) = Etotal(Ru3B2X) − 3E(Ru) − 2E(B) − E(X) | (3) |
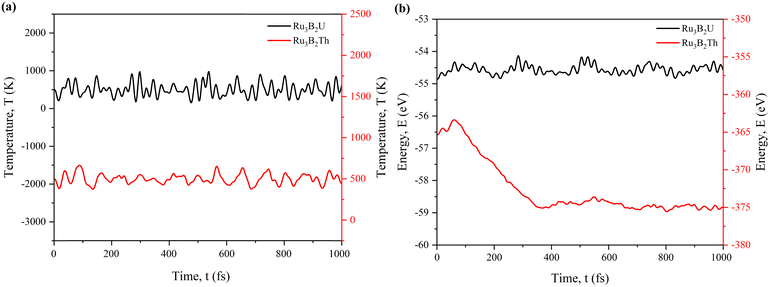
To check the structural stability more precisely, we have conducted ab initio molecular dynamics (AIMD) simulation for 1000 femtoseconds (fs). From Fig. 2(a), it can be seen that Ru3B2Th stabilizes at a lower average temperature. Ru3B2U maintains a higher temperature on average, with smaller amplitude fluctuations around that higher value. On the other hand, Fig. 2(b) indicates that Ru3B2Th starts at a higher total energy (around ∼355 eV) and relaxes over the first ∼200 fs to about ∼375 eV, after which it fluctuates only slightly. Ru3B2U (black curve) remains near ∼−58 eV the entire time with small fluctuations, suggesting that it was already close to an equilibrium state (or at least a shallow minimum) under the chosen simulation conditions.
So, it can be concluded that Ru3B2Th relaxes to a deeper potential-energy minimum and remains there with a lower thermal energy. In contrast, Ru3B2U appears stable in its own shallower energy minimum at a higher temperature.
3.2 Mechanical properties
The selection of materials capable of withstanding particular loads and stresses, by engineers and designers, is dependent on mechanical characteristics like tensile strength, elasticity, ductility, and toughness. Moreover, comprehensive knowledge of such properties facilitates the optimization of several heat treatment procedures. In the subsequent sub-sections, we will provide the computed mechanical properties that characterize the parameters of Ru3B2X (X = Th, U) compounds.| C11 > 0, C33 > 0, C44 > 0, C11 − |C12| > 0, C33(C11 + C12) − 2C132 > 0 | (4) |
| Compound | C 11 | C 12 | C 13 | C 33 | C 44 | C 66 | C′ |
|---|---|---|---|---|---|---|---|
| Ru3B2U | 464.86 | 166.56 | 147.35 | 451.97 | 107.88 | 149.15 | 149.15 |
| Ru3B2Th | 339.61 | 134.74 | 136.84 | 329.96 | 82.40 | 102.44 | 102.43 |
The computed values of Cij shown in Table 2 correspond to the aforementioned relationships and indicate that the Ru3B2X (X = Th, U) compounds we investigated exhibit mechanical stability. The superiority of C11 over C33 indicates more robust atomic interactions along the a-axis compared to the c-axis. The strong adhesion along the a-axis suggests increased resistance to distortion caused by the a-axis. The observation that C11 and C33 exhibit higher values compared to C44 implies that shear deformation is more readily accommodated than axial strain. The shear constant (C′ = (C11 − C12)/2) is a parameter that quantifies the stiffness of the crystal and also determines the dynamical stability of a crystalline material. The positive value of C′, as listed in Table 2, numerically equal to C66 for our examined crystal structure, indicates that Ru3B2X (X = Th, U) is dynamically stable.
 . The elastic moduli are linked with thermal conductivity (KL) as
. The elastic moduli are linked with thermal conductivity (KL) as  .36 Moreover, an essential factor in the design of materials for acoustic applications is the impact of the bulk modulus (B) on the speed of sound in a material. We calculated these parameters using the Voigt–Reuss–Hill (VRH) approximation,37–40 and our findings are tabulated in Table 3.
.36 Moreover, an essential factor in the design of materials for acoustic applications is the impact of the bulk modulus (B) on the speed of sound in a material. We calculated these parameters using the Voigt–Reuss–Hill (VRH) approximation,37–40 and our findings are tabulated in Table 3.
| Compound | Y | B | G | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Y V | Y R | Y H | B V | B R | B H | G V | G R | G H | |
| Ru3B2U | 343.03 | 334.72 | 338.88 | 256.02 | 255.78 | 255.90 | 134.34 | 130.56 | 132.45 |
| Ru3B2Th | 243.14 | 241.01 | 242.08 | 202.89 | 202.87 | 202.88 | 93.50 | 92.56 | 93.03 |
The higher Y values imply that Ru3B2X (X = Th, U) are stiffer compounds and the stiffness follows the order Ru3B2U > Ru3B2Th. Furthermore, the thermal shock resistance (R) is inversely related to Y, making it a crucial determinant for choosing compounds as thermal barrier coating (TBC) materials.41,42 The Y value suggests that the compounds Ru3B2X (X = Th, U) have the potential to be used as TBC materials,42 and Ru3B2Th is a more effective TBC material than Ru3B2U. The comparison of the thermal coating ability of our compounds with Y3Al5O12 (Y = 290 GPa)42 gives rise to the order Ru3B2Th > Y3Al5O12 > Ru3B2U.
The brittleness and ductility of a material can be characterized by two parameters, namely Poisson's (ν) and Pugh's ratio (B/G), which are derived from elastic moduli. Table 4 lists the values of these parameters. The criteria ν > 0.26 and B/G >1.75 determine the ductility of a material; otherwise, it is brittle.43,44 Consequently, the material Ru3B2X (X = Th, U) is predicted to be ductile. It is a rare feature in hard borides. In addition, it is observed that Ru3B2Th exhibits more ductility than Ru3B2U. Besides this, Poisson's ratio can also indicate the characteristics of the bonding of a molecule. Given that Ru3B2X (X = Th, U) meets the limiting condition 0.25 ≤ ν ≤ 0.50, the influence of central force interaction and ionic contribution is crucial in both compounds.45,46 Another significant stress property of materials that quantifies the ductility or brittleness of components is the Cauchy pressure (C′′ = C12 − C44),47 which is presented in Table 4. Ductility and the presence of an ionic bond in a compound are probable when the Cauchy pressure is positive, whereas negative values indicate brittleness.48 The positive nature of C′′ suggests the ductility and predominance of ionic bonding in Ru3B2X (X = Th, U).
| Compound | ν | B/G | C′′ | ξ | μ M | H macro | H micro | K IC |
|---|---|---|---|---|---|---|---|---|
| Ru3B2U | 0.279 | 1.93 | 58.68 | 0.501 | 2.372 | 13.136 | 19.489 | 2.824 |
| Ru3B2Th | 0.301 | 2.18 | 52.35 | 0.536 | 2.462 | 8.388 | 12.333 | 2.126 |
 | (5) |
The values of ξ of Ru3B2X (X = Th, U) are listed in Table 4 and are typically within the range of zero to one (0 ≤ ξ ≤ 1). These minimum and maximum limits represent the minimal impact of bond bending and the minimal impact of bond stretching/contraction, respectively, in resisting external force. The computed value of ξ for Ru3B2X (X = Th, U) demonstrates that the mechanical strength of Ru3B2X (X = Th, U) is substantially influenced by both bond bending and bond stretching/contraction contributions.
The machinability index, μM, of a material is a reliable measure of its effectiveness. It is an essential determinant of the elastic properties or characteristics of the working materials.50 Moreover, it is beneficial for quantifying the plasticity51,52 and lubricating characteristics of a substance. The assessment of μM is made using the equation B/C44, where B is the bulk modulus. Table 4 reports the μM of Ru3B2X (X = Th, U), and based on our findings, though Ru3B2Th exhibits great machinability compared to Ru3B2U, both compounds are equally appropriate for use in manufactured machines.
The hardness of Ru3B2X (X = Th, U) compounds was determined by the application of the following formulae:
 | (6) |
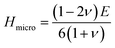 | (7) |
The relationship between hardness and crystalline elastic modulus is highly interdependent and directly impacts their resistance to notching forces. From Table 4, Ru3B2U is anticipated to exhibit higher hardness between the compounds considering the stated value (Hmacro = 13.136 GPa), whereas Ru3B2Th has a low hardness value (Hmacro = 8.388 GPa). Overall, Ru3B2X shows moderate hardness, lower than superhard borides like B12C3 (∼50–77 GPa) but higher than ductile borides such as Fe2B (∼8 GPa). The capacity of a material to withstand the spread of cracks and fractures under external forces is represented by fracture toughness KIC, which can be calculated using the formula published by Niu et al.:53
| KIC = V1/60G(B/G)0.5 | (8) |
The constant V0 represents the final volume per atom of the unit cell, and the obtained value of KIC of Ru3B2X (X = Th, U) is shown in Table 4. The superior fracture toughness of Ru3B2U compared to Ru3B2Th allows it to endure greater applied pressures without undergoing crack propagation, rendering it more appropriate for load-bearing structures. Moreover, KIC is related to the brittleness index (MB) and hardness (HV) by the equation MV = HV/KIC.
 | (9) |
 | (10) |
 | (11) |
The shear anisotropic factors for Ru3B2X (X = Th, U) have been computed and are presented in Table 5. The findings indicate that Ru3B2U exhibits a higher degree of anisotropy, whereas Ru3B2Th has a lower amount of anisotropy. The concept of the universal anisotropy index (AU) was introduced by Ranganathan and Ostoja-Starzewski,57 which offers a unidimensional measure of anisotropy, independent of the crystal symmetry. This also encompasses the impact of the bulk on the anisotropy of a solid and is measured solely as zero or positive. A value of AU equal to zero indicates that the crystal is isotropic, while any value other than zero suggests the existence and degree of anisotropy. The value of Aeq, the equivalent Zener anisotropy measure, for an isotropic crystalline material is 1. The conventional formulae for estimating the universal anisotropy index AU, equivalent Zener anisotropy measure Aeq, anisotropy in compressibility AB, and anisotropy in shear AG (or AC) for a material with any symmetry are as follows:58–60
 | (12) |
 | (13) |
 | (14) |
 | (15) |
| Anisotropy factors | Compound | ||
|---|---|---|---|
| Ru3B2U | Ru3B2Th | ||
| Shear anisotropy factors | A 1 | 0.694 | 0.833 |
| A 2 | 0.694 | 0.833 | |
| A 3 | 1.000 | 1.000 | |
| Universal and Zener anisotropy | A U | 0.146 | 0.051 |
| A eq | 1.091 | 1.032 | |
| Shear and compressibility anisotropy | A G | 0.014 | 0.005 |
| A B | 0.00047 | 0.00005 | |
| Linear compressibility | β a | 0.007 | 0.004 |
| β c | 0.008 | 0.005 | |
| β a /βc | 0.875 | 0.800 | |
Table 5 lists all the above mentioned anisotropic factors. The value of AU of Ru3B2X (X = Th, U) signifies that both compounds display anisotropy, but the anisotropy of Ru3B2Th is rather minimal (AU = 0.051). The predicted value of Aeq for Ru3B2X (X = Th, U) additionally suggests that the compounds are anisotropic. Moreover, the positive departure of AB and AG from zero indicates the level of anisotropy. Our findings indicate that Ru3B2U consistently displays a higher degree of anisotropy compared to Ru3B2Th. In Ru3B2X (X = Th, U), the difference between the values of AG and AB (Table 5) suggests that the anisotropy in shear is greater than the anisotropy in compressibility.
The linear compressibility of a hexagonal crystal along the a and c axes (βa and βc) can be determined using the following equations:61
 | (16) |
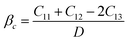 | (17) |
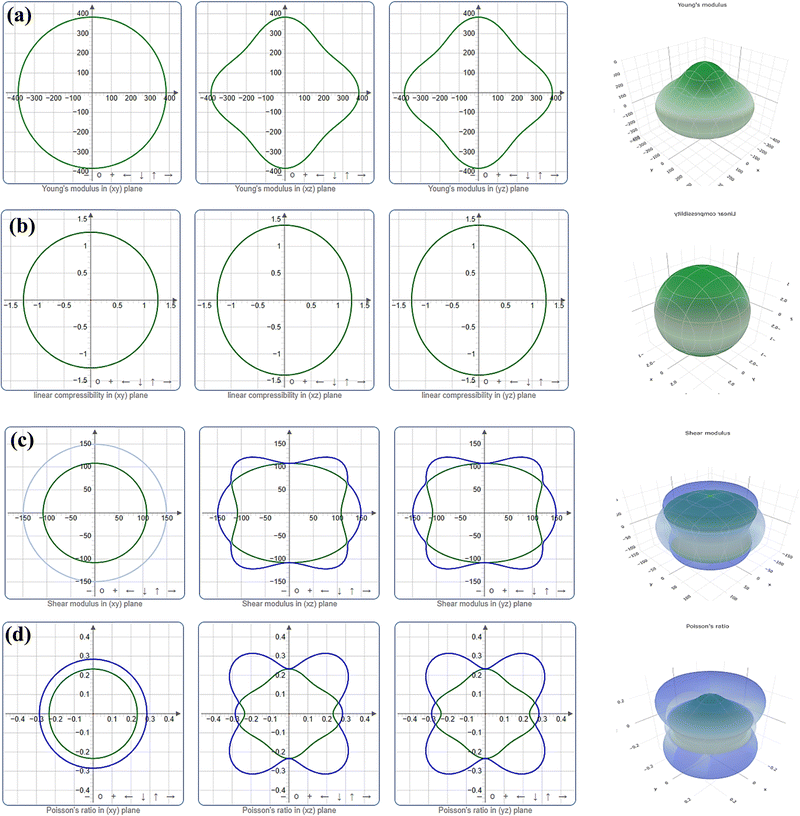
With the aid of the ELATE program,62 the directional dependence of Young's modulus (Y), linear compressibility (β), Shear modulus (G), and Poisson ratio (ν) of the crystal Ru3B2X (X = Th, U) is investigated using both 2D and 3D graphical projection. The necessary elastic stiffness matrices for this work are calculated using the CASTEP model. Uniform circular two-dimensional and spherical three-dimensional graphical representations are physical manifestations of the isotropic properties of crystals.
The level of anisotropy increases proportionally with the extent of departure from these ideal forms. Fig. 3 and 4 illustrate the 2D projection of the compound on the xy-, xz-, and yz-planes, as well as the 3D analysis of Y, β, G, and ν, for Ru3B2Th and Ru3B2U respectively. The curves in green and blue correspond to the minimum and maximum values for the parameters, respectively. Evidently, all four parameters exhibit isotropy in the xy-plane and anisotropy in other planes. Furthermore, the figures clearly show that the anisotropy in linear compressibility (β) is almost negligible for both compounds.
 | ||
| Fig. 3 Directional dependence of (a) Young's modulus (Y), (b) linear compressibility (β), (c) shear modulus (G), and (d) Poisson's ratio (ν) of Ru3B2Th. | ||
3.3 Electronic properties
Determining the electronic characteristics of materials is essential for developing technology and innovation in a variety of sectors. The design and functionality of electronic devices are influenced by electronic qualities including band structure, electronic charge density, density of states, bond population analysis, and Fermi surface topology, which have a direct impact on how materials react to electric fields and currents. In essence, investigating electronic characteristics results in the discovery of novel materials, expanding our knowledge of the physics of condensed matter and materials science.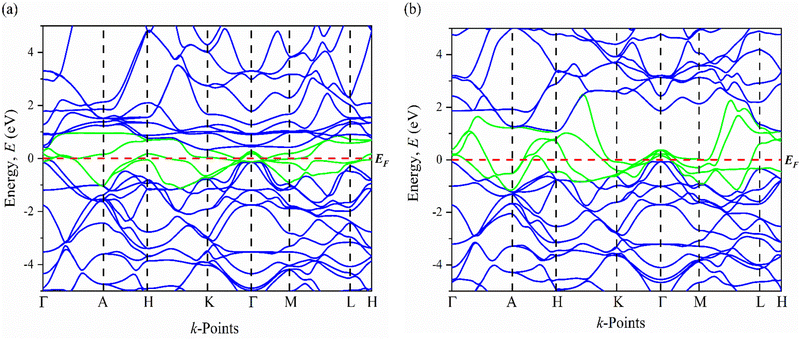 | ||
| Fig. 5 The electronic band structures of (a) Ru3B2U and (b) Ru3B2Th along the high symmetry directions. | ||
An important contribution of electronic states to electrical conductivity is indicated by the band dispersion close to the Fermi level. As evident from the band structures, several electronic bands marked by green lines cross the Fermi level, confirming the metallic character of Ru3B2X (X = Th, U). In contrast to Ru3B2U, Ru3B2Th shows more metallic behavior because its conductivity is enhanced by a higher density of states at EF, which is likely caused by the Fermi energy intersecting with more bands. Additionally seen is the topological nontrivial electronic band structure, which consists of slightly overlapping bands at specific places (K, Γ, and M points) in the Brillouin zone with several Dirac points. In some areas of the E(k) figure, nearly linear dispersive bands are visible. For instance, the quasi-linear electronic dispersions close to the Fermi level refer to a relatively high degree of mobility, which results from the effective masses of the charge carriers and the corresponding wave vectors being substantially tiny.
 | ||
| Fig. 6 The partial and total density of states (PDOS and TDOS, respectively) plots of (a) Ru3B2U and (b) Ru3B2Th as a function of energy. | ||
The presence of metallic electrical conductivity in Ru3B2X (X = Th, U) is implied by the non-zero value of TDOS at the Fermi level. The computed values of TDOS at the Fermi level for Ru3B2U and Ru3B2Th are 6.13 and 4.76 per eV per unit cell, respectively, from Fig. 6(a) and (b), suggesting that Ru3B2U exhibits better electrical conductivity than Ru3B2Th. In contrast, Ru3B2Th has greater stability than Ru3B2U. Although Ru3B2Th has more conduction channels intersecting the Fermi level (Section 3.3.1), Ru3B2U has a higher density of states, both of which contribute differently to conductivity. So, it can be concluded that both compounds have good electrical conductivity. Ru-4d orbitals are the source of most of the electronic states close to the Fermi level; however B-2p states play a role at lower energy levels. Additionally, the U-5f orbital clearly plays a major role in the TDOS of Ru3B2U. A high density of accessible states for conduction is shown by the steep peaks in the TDOS at 0 GPa in Fig. 6, which are located just below the Fermi level. The TDOS of Ru3B2U has significant peaks around EF at −1.37 and 1.02 eV. The hybridization of Ru-4d and U-5f orbitals results in the emergence of these bonding/anti-bonding peaks. The anti-bonding peaks of Ru3B2Th near EF are quite dissimilar to those in Ru3B2U. Furthermore, the presence of a deep valley in the TDOS plots of Ru3B2X (X = Th, U) near EF is known as a pseudogap or quasi-gap, which is associated with the electronic stability of a material and separates the bonding states from the anti-bonding states.64 Additionally, as the pseudogap position is extremely close to EF, covalent bonding is present in the crystals, indicating that the materials are very resilient and have excellent mechanical properties.
An essential factor in identifying electronic correlations in a system is the electron–electron interaction (EEI) caused by the Coulomb force, commonly referred to as the repulsive Coulomb pseudopotential. It gives us a sense of how strong the direct Coulomb repulsion between electrons is and can be calculated using the following formula:65
 | (18) |
In the ground state, the predicted Coulomb pseudopotential values for Ru3B2U and Ru3B2Th are 0.223 and 0.215, which are relatively high and suggest significant electronic correlations.
Conversely, in the case of Ru3B2Th, smaller Fermi surface pockets, perhaps at various energy bands, are indicated by the gray lobes spreading outward, while the larger, linked blue region shows massive electron or hole pockets centered around the Γ point. This complexity in the Fermi surface indicates a high carrier density, which implies metallicity and the possibility of charge density wave (CDW) production or superconductivity. Compared to the Fermi surface of Ru3B2U, which suggests conduction channels that are limited, the Fermi surface of Ru3B2Th supports better conductivity and enhanced electronic interactions, demonstrating the impact of band structure complexity on material performance.
 | ||
| Fig. 8 Electronic charge density distribution of Ru3B2U in (a) (100), (b) (101), and (c) (110) planes and Ru3B2Th in (d) (100), (e) (101), and (f) (110) planes. | ||
The distinctions between the bonding properties of Ru3B2U and Ru3B2Th, however, are visible in the (101) and (110) planes. Significant delocalization and overlap between Ru, U, and B atoms are evident in the charge density of Ru3B2U, especially in the (110) plane. On the other hand, there is less overlap and a more localized charge density surrounding the Th atoms in the charge density distribution of Ru3B2Th. According to this localization, more dispersed electronic orbitals and lower electronegativity of Th than U suggest that it contributes less to bonding interactions. Th and nearby Ru or B atoms have less charge density overlap in the (101) and (110) planes of Ru3B2Th, which suggests less Ru–Th and Th–B bonding interactions. While the electrical characteristics of Th are responsible for the decreased bonding strength in Ru3B2Th, our results demonstrate the crucial function that U plays in strengthening bonding contacts within Ru3B2U. From Fig. 8, it can be clearly seen that charge overlap occurs between Ru and B atoms as well as U/Th and B atoms. This charge sharing is an indication of covalent bonding. So, covalent bonding has greater significance than ionic bonding in both compounds.
3.4 Bond population analysis
In order to better understand the bonding nature and electric charge contribution from each atom in Ru3B2X (X = Th, U), the Mulliken bond population analysis67 technique was used. The Mulliken charge measures how the electronic structure varies with atomic displacement and is connected to the vibrational characteristics of molecules.68Table 6 shows the charge spilling parameter and atomic charges generated from these computations.| Compound | Charge spilling | Species | Mulliken atomic populations | Mulliken charge | Formal ionic charge | Effective valence | Hirshfeld charge | Effective valence | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s | P | d | f | Total | ||||||||
| Ru3B2U | 0.17 | Ru | 1.03 | −0.45 | 7.18 | 0 | 7.76 | 0.24 | +3 | 2.76 | 0.10 | 2.90 |
| B | 1.30 | 2.41 | 0 | 0 | 3.71 | −0.71 | −3 | 2.29 | −0.21 | 2.79 | ||
| U | 3.23 | 4.56 | 2.67 | 2.83 | 13.29 | 0.71 | +3 | 2.29 | 0.11 | 2.89 | ||
| Ru3B2Th | 0.20 | Ru | 0.95 | −0.60 | 7.25 | 0 | 7.6 | 0.40 | +3 | 2.60 | 0.11 | 2.89 |
| B | 1.31 | 2.37 | 0 | 0 | 3.68 | −0.68 | −3 | 2.32 | −0.18 | 2.82 | ||
| Th | 2.96 | 5.79 | 2.64 | 0.46 | 11.85 | 0.15 | +3 | 2.85 | 0.05 | 2.95 | ||
The computation shows that the overall charge of the U and Th atoms is greater than that of any other species present in the compounds Ru3B2U and Ru3B2Th, respectively. While thorium in Ru3B2Th exhibits significantly reduced f-orbital participation (0.46 electrons), resulting in weaker bonds, uranium in Ru3B2U has large f-orbital contributions (2.83 electrons), which enhance covalent bonding. Additionally, Ru3B2U exhibits superior charge localization and bonding stability, as evidenced by a lower charge spilling parameter (0.17%) than that of Ru3B2Th (0.20%). The formal charges that would be predicted for a purely ionic state are all different from these charges. As a result, charge transfers occur between the atoms, and this departure from the formal ionic charge indicates that covalent bonds with an ionic contribution are present.
The effective valence charge (EVC) of a species is the difference between the formal ionic charge and the Mulliken charge of an atom in that substance,69 which are listed in Table 6. It can be utilized to assess the level of ionicity and covalency. The deviation of EVC from zero refers to the prominent covalent bonding in the Ru3B2X (X = Th, U) system. The Hirshfeld population analysis (HPA)70 produces more significant results as it does not require a reference to the basis set or its location. Compared to those from the Mulliken population analysis, the Hirshfeld charges mentioned in Table 6 are substantially smaller.
The calculated bond overlap population and bond length in Ru3B2X (X = Th, U) are summarized in Table 7. The bond overlap population indicates how strong the covalent link is between atoms as well as how strong the bond is per unit volume. Ru–B bonds have a moderate covalent character, as indicated by their Mulliken overlap population of 0.67 for Ru3B2U, whereas the Ru–Ru bonds have a negative overlap population of −0.87, which suggests a net repulsive interaction or antibonding nature. In contrast to Ru3B2U, Ru3B2Th exhibits a higher negative Ru–Ru overlap population of −1.04, suggesting greater antibonding interactions71 between Ru atoms, and a somewhat lower Ru–B bond overlap population (0.60), suggesting weaker bonding. Ru3B2X exhibits strong covalent Ru–B bonds comparable to TiB2 (B–B covalent bonds). However, the inclusion of actinides introduces metallic Ru–X interactions (Th/U–Ru bond lengths: ∼2.94–3.02 Å), contrasting with purely covalent bonding in B-rich borides like B12C3. The compounds Ru3B2U and Ru3B2Th also differ in their bond lengths. Stronger Ru–B interactions are indicated by the shorter Ru–B bond length (2.17773 Å) in Ru3B2U compared to Ru3B2Th (2.22268 Å). Similarly, the Ru–Ru bond length in Ru3B2U (2.75411 Å) is slightly shorter than in Ru3B2Th (2.78527 Å), consistent with the reduced antibonding interactions in the former. The covalent bonding strength is described by Phillips's homopolar band gap (Eh = 39.74/d2.5),72 which is proportional to the dislocation glide activation energies in polar covalent crystals. d is the bond length and Eh represents the pure covalent contribution (eV) to hardness. The estimated values are displayed in Table 7.
| Compound | Bond | P μ | d μ | E h |
|---|---|---|---|---|
| Ru3B2U | Ru–B | 0.67 | 2.17773 | 5.678 |
| Ru–Ru | −0.87 | 2.75411 | 3.157 | |
| Ru3B2Th | Ru–B | 0.60 | 2.22268 | 5.395 |
| Ru–Ru | −1.04 | 2.78527 | 3.069 | |
3.5 Acoustic properties
The acoustic properties are an important concern that affects the thermal and electrical conductivity of a material. Effective sound management is essential in safeguarding against sound pollution, thereby requiring the use of a material that allows sound waves to be reflected.73 The second-order elastic constants provide insights into the propagation of acoustic waves within a substrate. The fundamental acoustic parameters investigated in this work include the velocity of sound and its anisotropy, the impedance of sound, and the coefficient of sound radiation.Acoustic velocity is the speed at which sound waves propagate when they pass through a solid material, which is determined by the elastic characteristics of the material and can be described using longitudinal velocity (P-wave velocity) and transverse velocity (S-wave velocity). In a crystalline material, the transverse, longitudinal, and mean sound velocities are calculated using the equations provided below:74
 | (19) |
 (m4 kg−1 s−1), and density (g cm−3)
(m4 kg−1 s−1), and density (g cm−3)
An essential factor that governs the transmission of acoustic energy between two media is the acoustic impedance (Z). The magnitude of sound received and reflected at the interface during the transmission of sound between two substances is determined by the acoustic impedance difference between the two materials. Hence, when the two impedances are approximately identical, the majority of the sound is conducted. The expression for the acoustic impedance of a solid is given by  where ρ and G, respectively, represent the density and shear modulus of the medium.75Table 8 reports the computed acoustic impedances for Ru3B2X (X = Th, U), suggesting that the speed of sound is higher in Ru3B2U than in Ru3B2Th.
where ρ and G, respectively, represent the density and shear modulus of the medium.75Table 8 reports the computed acoustic impedances for Ru3B2X (X = Th, U), suggesting that the speed of sound is higher in Ru3B2U than in Ru3B2Th.
An additional crucial design factor in acoustics is the intensity of sound radiation when designing acoustic insulation and soundproofing materials. For a given driving source, the radiation intensity, I, is directly proportional to the surface velocity. This relationship scales with the modulus of stiffness and density as76
 is the radiation factor. Instrument manufacturers typically use materials with high radiation factor values to incorporate into appropriately constructed soundboards. In addition, the acoustic conversion efficiency (ACE) of a medium is directly affected by this entity. Table 8 also provides the corresponding predicted radiation factor value for Ru3B2X (X = Th, U).
is the radiation factor. Instrument manufacturers typically use materials with high radiation factor values to incorporate into appropriately constructed soundboards. In addition, the acoustic conversion efficiency (ACE) of a medium is directly affected by this entity. Table 8 also provides the corresponding predicted radiation factor value for Ru3B2X (X = Th, U).
Each atom in a solid has three vibrational modes: two transverse and one longitudinal. Only along specific axes may the pure longitudinal and transverse modes exist in an anisotropic composite. However, in every other direction, the propagating modes are either quasi-longitudinal or quasi-transverse. Only the symmetry directions along [100] and [001] can have pure transverse and longitudinal modes due to the hexagonal symmetry of the compound. The single crystal elastic constants can be used to compute the acoustic velocities of Ru3B2X (X = Th, U) in three primary directions:77
In the [100] direction,
 | (20) |
In the [001] direction,
 | (21) |
| Propagation directions | Ru3B2U | Ru3B2Th | |
|---|---|---|---|
| [100] | [100]vl | 3532.87 | 3022.88 |
| [010]vt1 | 6237.02 | 5504.11 | |
| [001]vt2 | 3004.60 | 2711.19 | |
| [001] | [001]vl | 6149.94 | 5425.35 |
| [100]vt1 | 3004.60 | 2711.19 | |
| [010]vt2 | 3004.60 | 2711.19 | |
3.6 Thermophysical properties
Factors such as Debye temperature, melting temperature, thermal conductivity, and thermal expansion coefficient are utilized for assessing the thermal properties of a material. Studying these factors enables the prediction of possible solutions for the system. | (22) |
In this context, h represents Planck's constant, kB denotes Boltzmann's constant, V0 defines the volume of the unit cell, and n specifies the number of atoms in the cell. The high Debye temperature values reported in Table 10 for both Ru3B2U and Ru3B2Th indicate that certain properties such as high melting point, high thermal conductivity, low specific heat, and high stiffness are anticipated. Moreover, the value of ΘD is sensitive to temperature and decreases as temperature increases, owing to the temperature-dependent nature of elastic constants and sound velocity of the substance. At values below and over ΘD, the acoustic and optical phonon modes are anticipated to be more dominant in the lattice, respectively.
| Compound | Θ D | T m | α (×10−5) | ρC P (×106) | λ dom (×10−12) | γ | k min | k ph |
|---|---|---|---|---|---|---|---|---|
| a Measured at 300 K. | ||||||||
| Ru3B2U | 469.41 | 2426.53 | 1.21 | 3.18 | 155.34 | 1.65 | 0.925 | 26.579 |
| Ru3B2Th | 400.11 | 1867.77 | 1.72 | 3.01 | 134.71 | 1.78 | 0.774 | 14.071 |
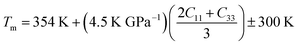 | (23) |
The calculated melting points for Ru3B2X (X = Th, U) are included in Table 10. Both compounds have extremely high melting temperatures, making them potentially suitable for use in environments with severe thermal conditions. Ru3B2U has a significantly greater melting point in comparison to Ru3B2Th. Hence, Ru3B2U will exhibit superior bonding and cohesive energy in comparison to Ru3B2Th. It is worth noting that the melting temperature rises in proportion to the bonding strength, enhanced cohesive energy, and reduced coefficient of thermal expansion.80
Another crucial thermophysical characteristic is the heat capacity per unit volume (ρCP), which is sometimes referred to as volumetric heat capacity. The alteration in heat energy per unit volume in a material due to a temperature change of one Kelvin is referred to as ρCP of the substance, and is calculated by ρCP = 3kB/Ω.81 Here, the number of atoms per unit volume is denoted as N = 1/Ω. The thermal energy storage capacity and thermal sensitivity to temperature variations of a material are quantified by this measurement. Table 10 also lists the calculated values of heat capacity per unit volume of Ru3B2X (X = Th, U).
 | (24) |
 | (25) |
 | (26) |
On the flip side, the contribution of phonons to the total thermal conductivity of a material is known as lattice thermal conductivity, kph. It illustrates how the propagation of phonons causes heat to be efficiently transferred through a material. The following empirical formula, developed by Slack,84 was used in this investigation to determine the kph of Ru3B2X (X = Th, U) compounds at room temperature and the results are shown in Table 10:
 | (27) |
 | (28) |
The low kph values of Ru3B2Th compared to that of Ru3B2U imply that Ru3B2Th can be employed more effectively for thermal insulation than Ru3B2U. The temperature variations of the lattice thermal conductivity of both compounds are listed in Table 11. Also, Fig. 9 shows that the bonding and atomic characteristics of U and Th have a considerable impact on lattice thermal conductivity. Because of the stronger covalent bonding involving U, which reduces phonon dispersion and improves heat transmission, Ru3B2U shows noticeably higher kph at any particular temperature than Ru3B2Th. As the temperature rises, the kph of Ru3B2X (X = Th, U) falls, which is consistent with normal phonon scattering behavior. These distinctions suggest that Ru3B2Th may be more appropriate for applications where thermal insulation is desired.
| Temperature (K) | Ru3B2U | Ru3B2Th |
|---|---|---|
| 100 | 79.738 | 42.213 |
| 200 | 39.869 | 21.107 |
| 300 | 26.579 | 14.071 |
| 400 | 19.935 | 10.553 |
| 500 | 15.948 | 8.443 |
| 600 | 13.290 | 7.036 |
| 700 | 11.391 | 6.030 |
| 800 | 9.967 | 5.277 |
| 900 | 8.860 | 4.690 |
| 1000 | 7.974 | 4.221 |
3.7 Optical properties
The optical properties are the result of interactions between the photons in light impacting the surface of a material and the charge carriers. The specifics of the electronic band structure of a material have a significant influence on the frequency- and energy-dependent factors that define the optical response of the material. For two distinct polarization orientations [100] and [001], the dielectric function ε(ω), absorption coefficient α(ω), reflectivity R(ω), refractive index n(ω), optical conductivity σ(ω), and energy loss function L(ω) of Ru3B2X (X = Th, U) were examined as a function of photon energies up to 40 eV. The necessary equations to calculate these optical properties can be found in the literature.86,87 The metallic character of the substance under investigation has led to the application of the Drude damping parameter of 0.5 eV88,89 with an energy smearing of 0.5 eV.The complex-valued dielectric function, ε(ω) = ε1(ω) + ε2(ω), represents how a material reacts to an external electric field. The real and imaginary components of ε(ω) are ε1(ω) and ε2(ω), respectively. The electric polarization that occurs when light passes through a medium is explained by the real part ε1(ω). With a strong Drude peak at low energy, the real part, ε1(ω) in Fig. 10(a), exhibits metallic characteristics. It has a prominent peak in the range of 0–0.6 eV and falls below zero at ∼0.6 eV for both compounds. It stays below the zero level until ∼30.5 eV and ∼29.2 eV are reached for Ru3B2U and Ru3B2Th, respectively. Conversely, the imaginary component, ε2(ω), corresponds to absorption characteristics and the electronic band structure of a material. As seen in Fig. 10(b), the value of ε2(ω) is highest at zero energy and decreases as photon energy increases, a behavior which is fairly frequent in metallic systems. An energy range where the imaginary part is nonzero indicates that the photons are absorbed by a material. The figures reveal that for Ru3B2U and Ru3B2Th, the value of ε2(ω) becomes zero at about 29.5 eV and 27.9 eV, respectively, indicating that the compounds will exhibit transparency above that energy value. In the low energy range, there is anisotropy in both real and imaginary components.
The absorption spectra α(ω) of Ru3B2X (X = Th, U) as a function of photon energy for [100] and [001] polarizations are shown in Fig. 10(c). The fact that the absorption begins at 0 eV in both situations is additional evidence of their metallic nature. As we can see from this figure, the absorption fluctuates significantly within the 5–20 eV energy range. For [001] and [100] polarization directions, the maximum light absorption of Ru3B2U occurs at approximately 26.8 eV and 25.3 eV, respectively, whereas the maximum light absorption of Ru3B2Th for the [001] and [100] polarization directions occurs at roughly 25.2 eV and 24.2 eV, respectively. A sharp decline in absorption occurs following the position of these peaks. Notably, the absorption coefficient of Ru3B2X (X = Th, U) is high enough for it to be used as a good solar absorber in photovoltaic device applications.
With respect to photon energy, the reflectivity spectra of Ru3B2X (X = Th, U) are shown in Fig. 10(d), which represent the ratio of photon energy that is incident to that is reflected. These spectra start from zero photon energy with 74% and 79% for Ru3B2X (X = Th, U), respectively. Reflectivity decreases sharply for all samples around 10 eV but shows a slight increase at higher energies (above 20 eV). Also, there is a clear optical anisotropy in the reflectivity spectra. Ru3B2X shows high IR reflectivity (>70%), outperforming traditional IR reflectors like Au or Al. This property aligns with metallic borides (e.g., ZrB2) but with improved anisotropy due to hexagonal symmetry.
An expression for the complex refractive index of a material is N(ω) = n(ω) + ik(ω), where k(ω) is the extinction coefficient which is an extensively researched parameter in the construction of optoelectronic devices. Fig. 10(e) and (f) show the refractive index of Ru3B2X (X = Th, U) as a function of photon energy, acquired in two polarization directions. The low energy IR and visible regions have a relatively high refractive index which refers to the compounds that can be used as a waveguide and in photonic engineering. Also, the extinction coefficient of both the compounds exhibits peaks in the same energy region. Comparable peaks in the imaginary component of the dielectric function can be detected in such low energy regions implying that both the refractive index and extinction coefficient are connected to photon energy loss.
In the presence of an alternating electric field, the optical conductivity of a material is another extensively researched property that indicates its ability to conduct electricity. Fig. 10(g) displays the photoconductivity σ(ω) of Ru3B2X (X = Th, U) for both [100] and [001] polarizations. Photoconductivity beginning with zero photon energy is a sign of the absence of an electronic band gap. Conductivity varies significantly across the energy range and several peaks occur at distinct energy values. These peaks might correspond to electronic transition or interaction between energy states which are affected by material types and their anisotropy. The conductivity of a material is also significantly influenced by the number of free charge carriers that have the ability to conduct electricity. Over 30 eV, the optical conductivity of Ru3B2X (X = Th, U) becomes isotropic for both the polarization directions.
Fig. 10(h) shows the electron energy loss spectrum as a function of frequency for Ru3B2X (X = Th, U), which is related to its absorption and reflection characteristics. It is evident from the figure that neither compound loses energy up to roughly 12 eV due to the comparatively high value of ε2(ω). The maximum energy loss is observed for Ru3B2U at around 33 eV whereas for Ru3B2Th, a similar peak is found at nearly the same position but with slightly lower energy. The compound Ru3B2U shows higher loss than Ru3B2Th, indicating greater energy dissipation in U-doped samples. The sharp peak in the loss factor corresponds to specific plasmon resonance energies and hence the bulk plasma frequency ωp can be found from the energy loss spectrum.86
4. Conclusion
The ground-state characteristics of ternary borides Ru3B2X (X = Th, U) are thoroughly examined in this work using first-principles density functional theory (DFT) computations. In agreement with experimental findings, our structural analysis showed that Ru3B2U and Ru3B2Th crystallize in a hexagonal configuration and also that the lattice constants and unit cell volumes closely resemble previously published experimental results, proving the accuracy of our methodology. Both structures are found to be stable. Higher values of elastic moduli reveal that Ru3B2U exhibits superior stiffness and resilience. Despite the fact that both materials are ductile, Poisson's and Pugh's ratios support the slightly higher ductility of Ru3B2Th. In contrast, Ru3B2U shows increased mechanical anisotropy, indicating direction-dependent mechanical behavior.The presence of bands that pass the Fermi level in electronic structure calculations supports that both compounds are metallic. Because Ru3B2Th has a greater density of states at the Fermi level, it demonstrated stronger metallic behavior. The bonding study of Ru3B2U demonstrated significant hybridization between Ru-4d states and B-2p states, indicating better covalent interactions. The mechanical strength of Ru3B2U is further highlighted by acoustic qualities obtained from elastic constants, which include higher sound velocities and acoustic impedance values. Its increased hardness and fracture toughness suggest potential uses in situations that can withstand wear.
Ru3B2U exhibits better thermal stability and performance in harsh environments because of its higher Debye temperature, melting temperature, and lower thermal expansion coefficient. Ru3B2Th, on the other hand, has the potential to be used as a thermal barrier coating material due to its reduced lattice thermal conductivity. High reflectivity in the visible spectrum was found when the optical characteristics of Ru3B2X (X = Th, U) were examined, indicating possible uses in optical coatings and display technology, especially in the IR region. Both Ru3B2U and Ru3B2Th can be used as efficient materials for optical devices, according to the computed dielectric function and refractive index, with Ru3B2Th showing somewhat higher reflectivity. These findings open the door for additional experimental research and technical developments in the fields of aerospace, thermal management, and superconducting materials by offering insightful information on the functional potential of Ru3B2X (X = Th, U) compounds.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors want to mention that “Bangabandhu Sheikh Mujibur Rahman Science and Technology University, Gopalganj” has been renamed as “Gopalganj Science and Technology University”. We gratefully acknowledge Md. Injamamul Haque of Department of Physics, Gopalganj Science and Technology University, Gopalganj-8105, Bangladesh, for helping to study the AIMD simulations.References
- I. P. Borovinskaya, A. A. Gromov, E. A. Levashov, Y. M. Maksimov, A. S. Mukasyan and A. S. Rogachev, Concise encyclopedia of self-propagating high-temperature synthesis: History, theory, technology, and products, Elsevier, Amsterdam, 2017, pp. 39–41 DOI:10.1016/B978-0-12-804173-4.00017-X.
- J. M. Nsanzimana, R. Dangol, V. Reddu, S. Duo, Y. Peng, K. N. Dinh, Z. Huang, Q. Yan and X. Wang, Facile synthesis of amorphous ternary metal borides–reduced graphene oxide hybrid with superior oxygen evolution activity, ACS Appl. Mater. Interfaces, 2018, 11, 846–855 CrossRef PubMed.
- H. Nowotny, Crystal chemistry of complex carbides and related compounds, Angew. Chem., Int. Ed. Engl., 1972, 11, 906–915 CrossRef CAS.
- S. Carenco, D. Portehault, C. Boissiere, N. Mezailles and C. Sanchez, Nanoscaled metal borides and phosphides: recent developments and perspectives, Chem. Rev., 2013, 113, 7981–8065 CrossRef CAS PubMed.
- J. M. Leitnaker, Thermodynamic properties of refractory borides: Evaporation behavior and vapor pressure of zirconium diboride. Phase studies in the tantalum-boron system between Ta and TaB, Los Alamos Scientific Laboratory of the University of California, 1960, vol. 2402 Search PubMed.
- J. M. Leitnaker, N. H. Krikorian and M. G. Bowman, High temperature poisons, Los Alamos Scientific Lab., N. Mex., 1961 Search PubMed.
- J. M. Leitnaker, N. H. Krikorian and M. C. Krupka, Unusual ternary behavior of transition metal borides, J. Electrochem. Soc., 1962, 109, 66 CrossRef CAS.
- A. N. Kolmogorov, M. Calandra and S. Curtarolo, Thermodynamic stabilities of ternary metal borides: an ab initio guide for synthesizing layered superconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 094520 CrossRef.
- K. Togano, P. Badica, Y. Nakamori, S. Orimo, H. Takeya and K. Hirata, Superconductivity in the metal rich Li–Pd–B ternary boride, Phys. Rev. Lett., 2004, 93, 247004 CrossRef CAS.
- V. Dhand, J. Lim, S. Bharadwaj, S. Kim and K. Rhee, Sol–gel combustion derived novel ternary transition metal boride-anisotropic magnetic powders and their magnetic property, J. Mater. Res. Technol., 2023, 24, 7219–7228 CrossRef CAS.
- A. Ch, Ceramic armor materials by design, J. Am. Ceram. Soc., 2002, 487–489 Search PubMed.
- Z. Zachariev, New superhard ternary borides in composite materials, Met., Ceram. Polym. Compos. Var. Uses, 2011, 61–78 CAS.
- B. T. Matthias, E. Corenzwit, J. M. Vandenberg and H. E. Barz, High superconducting transition temperatures of new rare earth ternary borides, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 1334–1335 CrossRef CAS.
- D. C. Johnston, Superconductivity in a new ternary structure class of boride compounds, Solid State Commun., 1977, 24, 699–702 CrossRef CAS.
- J. M. Vandenberg and B. T. Matthias, Crystallography of new ternary borides, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 1336–1337 CrossRef CAS PubMed.
- P. Rogl, Ternäre Metallboride. [La, Ce, Pr, Nd, Sm] Os4B4 und [Y, La, Ce, Pr, Nd, Sm, Gd, Tb] Ir4B4 mit NdCo4B4-Struktur, Monatsh. Chem., 1979, 110, 235–243 CrossRef CAS.
- H. C. Ku, G. P. Meisner, F. Acker and D. C. Johnston, Superconducting and magnetic properties of new ternary borides with the CeCo3B2-type structure, Solid State Commun., 1980, 35, 91–96 CrossRef CAS.
- K. Hiebl, P. Rogl, E. Uhl and M. J. Sienko, Magnetic behavior and structural chemistry of RERu3B2 borides, Inorg. Chem., 1980, 19, 3316–3320 CrossRef CAS.
- P. Rogl, The crystal structure of URu3B2, J. Nucl. Mater., 1980, 92, 292–298 CrossRef CAS.
- E. Burzo, Rare Earths-Transition Metals-Boron Compounds: Basic Properties to Technical Applications, Springer Nature, 2023 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567 CAS.
- R. G. Parr, Density functional theory, Electron Distributions and the Chemical Bond, Springer US, Boston, MA, 1982, pp. 95–100 DOI:10.1146/annurev.pc.34.100183.003215.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- T. H. Fischer and J. Almlof, General methods for geometry and wave function optimization, J. Phys. Chem., 1992, 96, 9768–9774 CrossRef CAS.
- J. P. Watt, Hashin–Shtrikman bounds on the effective elastic moduli of polycrystals with orthorhombic symmetry, J. Appl. Phys., 1979, 50, 6290–6295 CrossRef CAS.
- L. S. Combes, S. S. Ballard and K. A. McCarthy, Mechanical and thermal properties of certain optical crystalline materials, JOSA, 1951, 41, 215–222 CrossRef CAS.
- A. H. Reshak, V. V. Atuchin, S. Auluck and I. V. Kityk, First and second harmonic generation of the optical susceptibilities for the non-centro-symmetric orthorhombic AgCd2GaS4, J. Phys.: Condens. Matter, 2008, 20, 325234 CrossRef.
- S. Saha, T. P. Sinha and A. Mookerjee, Electronic structure, chemical bonding, and optical properties of paraelectric BaTiO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8828 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50, DOI:10.1016/0927-0256(96)00008-0.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, VASPKIT: a user-friendly interface facilitating high-throughput computing and analysis using VASP code, Comput. Phys. Commun., 2021, 267, 108033, DOI:10.1016/j.cpc.2021.108033.
- F. Mouhat and F. X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160–172 CrossRef CAS.
- W. Kim, Strategies for engineering phonon transport in thermoelectrics, J. Mater. Chem. C, 2015, 3, 10336–10348 RSC.
- W. Voigt, Lehrbuch der Kristallphysik: (mit Ausschluss der Kristalloptik), B.G. Teubner, 1910 Search PubMed.
- A. Reuß, Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle, J. Appl. Math. Mech., 1929, 9, 49–58 Search PubMed.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- R. Hill, Elastic properties of reinforced solids: some theoretical principles, J. Mech. Phys. Solids, 1963, 11, 357–372 CrossRef.
- M. T. Nasir, M. A. Hadi, M. A. Rayhan, M. A. Ali, M. M. Hossain, M. Roknuzzaman and K. Ostrikov, First-principles study of superconducting ScRhP and ScIrP pnictides, Phys. Status Solidi B, 2017, 254, 1700336 CrossRef.
- X. Zhan, Z. Li, B. Liu, J. Wang, Y. Zhou and Z. Hu, Theoretical prediction of elastic stiffness and minimum lattice thermal conductivity of Y3Al5O12, YAlO3, and Y4Al2O9, J. Am. Ceram. Soc., 2012, 95, 1429–1434 CrossRef CAS.
- P. Mondal, M. R. Islam, M. S. Khanom and F. Ahmed, The impact of hydrostatic pressure on the structural, mechanical, thermal, and optoelectronic characteristics of the RbV3Sb5 Kagome compound: ab initio approach, ChemistryOpen, 2024, e202400291 Search PubMed.
- M. W. Qureshi, X. Ma, G. Tang and R. Paudel, Structural stability, electronic, mechanical, phonon, and thermodynamic properties of the M2GaC (M = Zr, Hf) MAX phase: an AB initio calculation, Materials, 2020, 13, 5148 CrossRef CAS PubMed.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, Relaxation of crystals with the quasi-Newton method, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- O. L. Anderson and H. H. Demarest Jr, Elastic constants of the central force model for cubic structures: polycrystalline aggregates and instabilities, J. Geophys. Res., 1971, 76, 1349–1369 CrossRef CAS.
- M. E. Eberhart and T. E. Jones, Cauchy pressure and the generalized bonding model for nonmagnetic bcc transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134106 Search PubMed.
- W. Feng and S. Cui, Mechanical and electronic properties of Ti2AlN and Ti4AlN3: a first-principles study, Can. J. Phys., 2014, 92, 1652–1657 Search PubMed.
- L. Kleinman, Deformation potentials in silicon. I. Uniaxial strain, Phys. Rev., 1962, 128, 2614 Search PubMed.
- M. S. Sorker, M. R. Islam, A. Chakraborty and M. A. Razzak Sarker, First-principles and experimental study to investigate structural, elastic, electronic, thermal, and optical properties of KCdCl3 metal halide perovskite crystals, AIP Adv., 2024, 14, 4 Search PubMed.
- R. C. Lincoln, K. M. Koliwad and P. B. Ghate, Morse-potential evaluation of second-and third-order elastic constants of some cubic metals, Phys. Rev., 1967, 157, 463 Search PubMed.
- K. J. Puttlitz and K. A. Stalter, Handbook of lead-free solder technology for microelectronic assemblies, CRC Press, 2004 Search PubMed.
- H. Niu, S. Niu and A. R. Oganov, Simple and accurate model of fracture toughness of solids, J. Appl. Phys., 2019, 125, 6 CrossRef.
- M. A. Ali, M. M. Hossain, M. M. Uddin, M. A. Hossain, A. K. M. A. Islam and S. H. Naqib, Physical properties of new MAX phase borides M2SB (M = Zr, Hf, Nb) in comparison with conventional MAX phase carbides M2SC (M = Zr, Hf, Nb): comprehensive insights, J. Mater. Res. Technol., 2021, 11, 1000–1018 Search PubMed.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, Density functional theory for calculation of elastic properties of orthorhombic crystals: application to TiSi2, J. Appl. Phys., 1998, 84, 4891–4904 CrossRef CAS.
- H. Y. Yan, M. G. Zhang, D. H. Huang and Q. Wei, First-principles study of elastic and thermodynamic properties of orthorhombic OsB4 under high pressure, Solid State Sci., 2013, 18, 17–23 Search PubMed.
- S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101, 055504 Search PubMed.
- C. M. Kube and M. De Jong, Elastic constants of polycrystals with generally anisotropic crystals, J. Appl. Phys., 2016, 120, 165105 CrossRef.
- Anisotropy in Single-Crystal Refractory Compounds, ed. F. Vahldiek, Springer, 2013 Search PubMed.
- D. H. Chung and W. R. Buessem, The elastic anisotropy of crystals, J. Appl. Phys., 1967, 38, 2010–2012 CrossRef CAS.
- V. Milman and M. C. Warren, Elasticity of hexagonal BeO, J. Phys.: Condens. Matter, 2001, 13, 241 CrossRef CAS.
- R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: an open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28, 275201 CrossRef PubMed.
- S. Kerdsongpanya, B. Alling and P. Eklund, Effect of point defects on the electronic density of states of ScN studied by first-principles calculations and implications for thermoelectric properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195140 CrossRef.
- T. Hong, T. J. Watson-Yang, A. J. Freeman, T. Oguchi and J. H. Xu, Crystal structure, phase stability, and electronic structure of Ti–Al intermetallics: TiAl3, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 12462 CrossRef CAS.
- K. H. Bennemann and J. W. Garland, Theory for superconductivity in d-band metals, AIP Conf. Proc., 1972, 4, 103–137 Search PubMed.
- P. Cudazzo, G. Profeta, A. Sanna, A. Floris, A. Continenza, S. Massidda and E. K. U. Gross, Ab initio description of high-temperature superconductivity in dense molecular hydrogen, Phys. Rev. Lett., 2008, 100, 257001 CrossRef CAS PubMed.
- R. S. Mulliken, Electronic population analysis on LCAO–MO molecular wave functions. I, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- P. Mondal, K. Hossain, M. S. Khanom, M. K. Hossain and F. Ahmed, First-principles calculations to investigate structural, elastic, thermodynamic, electronic, and optical properties of AgXCl3 (X = Fe, Co & Mn), Comput. Condens. Matter, 2023, 37, e00860 CrossRef.
- M. A. Hadi, S. H. Naqib, S. R. Christopoulos, A. Chroneos and A. K. M. A. Islam, Mechanical behavior, bonding nature and defect processes of Mo2ScAlC2: a new ordered MAX phase, J. Alloys Compd., 2017, 724, 1167–1175 CrossRef CAS.
- F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- R. D. Harcourt, Diatomic antibonding σ* s orbitals as ‘metallic orbitals’ for electron conduction in alkali metals, J. Phys. B: At. Mol. Phys., 1974, 7, L41 CrossRef CAS.
- V. K. Srivastava, Ionic and covalent energy gaps of CsCl crystals, Phys. Lett. A, 1984, 102, 127–129 CrossRef.
- P. Mondal, S. Khanom, N. A. Shahed, M. K. Hossain and F. Ahmed, An ab initio insight into the structural, physical, thermodynamic and optoelectronic properties of superconducting Heusler-like LiGa2Rh, Phys. C, 2022, 603, 1354142 CrossRef CAS.
- E. Schreiber, O. L. Anderson and N. Soga, Elastic constants and their measurement, McGraw-Hill, 1974 Search PubMed.
- A. Chakraborty, M. N. H. Liton, M. S. I. Sarker, M. M. Rahman and M. K. R. Khan, Exploration of the structural, vibrational, electronic, mechanical and thermal properties of Ru4Al3B2 and Ru9Al3B8: a DFT study, RSC Adv., 2023, 13, 28912–28930 RSC.
- D. L. Schodek, P. Ferreira and M. F. Ashby, Nanomaterials, nanotechnologies and design: an introduction for engineers and architects, Butterworth-Heinemann, 2009 Search PubMed.
- L. Sun, Y. Gao, B. Xiao, Y. Li and G. Wang, Anisotropic elastic and thermal properties of titanium borides by first-principles calculations, J. Alloys Compd., 2013, 579, 457–467 CrossRef CAS.
- O. L. Anderson, A simplified method for calculating the Debye temperature from elastic constants, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS.
- M. E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18, 951–956 CrossRef CAS.
- M. I. Naher and S. H. Naqib, An ab initio study on structural, elastic, electronic, bonding, thermal, and optical properties of topological Weyl semimetal TaX (X = P, As), Sci. Rep., 2021, 11, 5592 CrossRef CAS PubMed.
- M. F. Ashby, P. J. Ferreira and D. L. Schodek, Material classes, structure, and properties, Nanomater., Nanotechnol. Des., 2009, 10, 113–116 Search PubMed.
- D. R. Clarke, Materials selection guidelines for low thermal conductivity thermal barrier coatings, Surf. Coatings Technol., 2003, 163, 67–74 CrossRef.
- Y. Liu, V. R. Cooper, B. Wang, H. Xiang, Q. Li, Y. Gao and B. Liu, Discovery of ABO3 perovskites as thermal barrier coatings through high-throughput first principles calculations, Mater. Res. Lett., 2019, 7, 145–151 CrossRef CAS.
- G. A. Slack, The thermal conductivity of nonmetallic crystals, Solid State Phys., 1979, 34, 1–71 CAS.
- C. L. Julian, Theory of heat conduction in rare-gas crystals, Phys. Rev., 1965, 137(1A), A128 CrossRef.
- T. K. Ghosh, M. N. H. Liton, A. Chakraborty, M. K. R. Khan and M. S. I. Sarker, Atomic position dependent structural, electronic, mechanical and optical properties of ZnSbF3 fluoroperovskites, Mater. Sci. Semicond. Process., 2025, 187, 109065, DOI:10.1016/j.mssp.2024.109065.
- A. Chakraborty, M. N. H. Liton, M. S. I. Sarker, M. M. Rahman and M. K. R. Khan, A comprehensive DFT evaluation of catalytic and optoelectronic properties of BaTiO3 polymorphs, Phys. B, 2023, 648, 414418, DOI:10.1016/j.physb.2022.414418.
- S. Li, R. Ahuja, M. W. Barsoum, P. Jena and B. Johansson, Optical properties of Ti3SiC2 and Ti4AlN3, Appl. Phys. Lett., 2008, 92(22), 221907, DOI:10.1063/1.2938862.
- M. Fox, Optical properties of solids, Oxford University Press, 2010, vol. 3 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ma00091b |
| This journal is © The Royal Society of Chemistry 2025 |