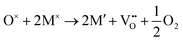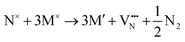Influence of anion ordering on defect diffusion anisotropy in layered perovskite Sr₂TaO₃N: implications for oxynitride stability

Abstract

The defect chemistry of heteroanionic semiconductors can have a large effect on ionic conductivity and optoelectronic properties. Of particular interest are oxynitrides, which have found broad interest recently in sunlight driven water splitting due to their favourable band edge positions while being more stable compared to pure nitrides. The mixed-anion content however creates challenges in terms of retaining nitrogen stoichiometry under the oxidizing conditions of the oxygen evolution reaction (OER), either through formation of a passivating oxide layer or bulk nitrogen loss. In comparison to ternary and perovskite oxynitrides, layered perovskites have potential for improved stability against critical performance limiting defects and present an avenue for improving theoretical water splitting efficiency. In this work, the layer and anion ordering specific O²⁻ and N³⁻ defect properties of Ruddlesden–Popper Sr₂TaO₃N perovskite oxynitride were extensively investigated using first-principles calculations. We screen anion orderings, then compare anion defect formation and model the e⁻ redistribution across the Sr²⁺ and Ta⁵⁺ sublattices with neutral V_O and V_N defects. Following this we map the vacancy-mediated anion diffusion pathway barriers with the nudged elastic band (NEB) of O²⁻/V_O and N³⁻/V_N both in the plane of and perpendicular to TaON layers of Sr₂TaO₃N. The findings of this study suggest that cis- to trans- shifts in the local N³⁻–Ta⁵⁺–N³⁻ anion ordering modulate the anisotropy of the vacancy-mediated N³⁻ and O²⁻ diffusion in and out of plane relative to the TaON layer. This work points to the potential of a novel avenue for defect engineering in layered mixed-anion materials and oxynitride photocatalysts.

---

Introduction

Multi-anion materials (also referred to as mixed-anion or heteroanionic materials) are an interesting class of solid-state compounds that by their nature afford tuneable functionalities by the assembly of anions with different sizes, charges and electronegativities.¹ Anion ordering in these materials has been shown to be associated with a plethora of structure–property relationships in this broad class of materials² and has been demonstrated to be a critical consideration in the modulation of optoelectronic,^3,4 electrochemical,^4–6 magnetic⁷ and thermal properties⁸.

Oxynitrides are a prominent class of heteroanionic semiconductors that have garnered research interest for photocatalytic/photochemical water splitting (WS), due to their favourable band gaps in comparison to oxides,^9,10 and can demonstrate more stable nitrogen reduction reaction (NRR) activity in comparison to nitrides.¹¹ However, nitrogen loss, non-stoichiometry or other nitrogen anion associated defects can often create challenges in terms of stability and reaching theoretical efficiency, which has been reported extensively in pursuit of better oxynitride photo(electro)catalysts.^12–14 A key issue limiting these materials from achieving their theoretical efficiencies in this application can be described as inhibiting defects formed during high temperature ammonolysis⁹ (N³⁻ vacancies and B-site cation reduction in perovskites),¹⁵ during operation.¹⁶ Emergent anion defect properties are also reported for mixed-anion oxyfluorides and oxysulphides.^17,18 So while greater possibilities for property optimisation can be afforded with a multi-anion composition, this also necessitates a more detailed understanding of the interplay of each anion with the emergent defect chemistry of the material.

Perovskite oxynitrides, AB(O,N)₂ (A^(III) = La with B^(IV) = Ti, Zr, Hf and A^(II) = Ca, Sr, Ba with B^(V) = Ta, Nb), exhibit a lack of long-range structural order in their crystal lattices, while maintaining local ordering of anions within individual MO_6−xN_x octahedra. Long-range structural order is lost due to the similarity between the Bⁿ⁺–O²⁻ and Bⁿ⁺–N³⁻ bond lengths, a feature unique to oxynitride mixed-anion semiconductors. The slightly larger Bⁿ⁺–N³⁻ bond length drives a predominantly cis-ordering in individual octahedra, giving rise to N³⁻–Bⁿ⁺–N³⁻ chains, with the alternate (unfavourable) trans-ordering (Fig. 1).¹⁹ This type of oxynitride anion ordering induces local distortions in the crystal lattice,²⁰ and subsequently bandgaps,^21,22 ferroelectricity^23,24 and effective charge carrier mobilities.^25–27 In recent years, several ATaO₂N perovskites in particular have been identified as promising candidate semiconductors for solar energy conversion owing to their broad absorption window for visible light.^28–33

Fig. 1 (a) Anion ordering in Ta–O₄N₂ octahedra. (b) Crystal structure of Sr₂TaO₃N used in this work with partial N³⁻ occupancy of anion sites in TaON layers.

Layered materials such as Ruddlesden–Popper (RP) phase perovskites have also attracted interest in sunlight driven water splitting due to enhancements to stability and anisotropic tuning of structural and optoelectronic properties.³⁴ RP phase perovskites possess a composition of A_n+1B_nX_3n+1 whereby for oxides, ABO₃ perovskite units are interspersed between SrO layers.

The RP phase perovskite Sr₂TaO₃N (n = 1) has been suggested to be good for photocatalytic water splitting based on its favourable band edge positions from high throughput screening³⁵ and experimental studies.^36,37 Recent computational studies of the Sr₂TaO₃N [001]³⁸ and [100]³⁹ surfaces suggest that both surfaces would be active for the oxygen evolution reaction (OER) to facilitate water splitting. Interestingly, the ridged [100] surface is predicted to be the most active with the lowest overpotential for the OER,³⁹ which opens new possibilities for facet-specific anion defect chemistry given this surface is perpendicular to the layered axis. Anion ordering for RP phase (n = 1) perovskite oxynitrides is innately 2D as it is confined exclusively to the TaON layer, unlike the ABO₂N and ABON₂ perovskites previously studied, which can have chains of N³⁻–B^x+–N³⁻ in 2D or 3D.

Recent studies have shown that doping the B-site cation with excess of A-site cations had the same protective effect of inhibiting the formation of reduced B-site cation defects as compared to shifting from cubic SrTaO₂N to a layered RP (n = 1) phase perovskite Sr₂TaO₃N.⁴ Additionally, in the synthesis of perovskite oxynitrides intergrowth of RP phases has been reportedly observed for tantalates,^36,37 whereas niobates formed defective surfaces.⁴⁰

Oxynitride perovskites additionally provide an accessible platform for using composition to drive shifts in the anion ordering. Dimensionality crossover of two-dimensional (2D) orderings to three dimensional (3D) orderings are reported for the series of Ba_1−xSr_xTaO₂N.⁴¹ Additionally, a pivotal report by Oka et al. demonstrated that in the Ca_1–xSr_xTaO₂N series, increased Sr²⁺ doping in CaTaO₂N stabilises a partial trans-N³–Ta⁵⁺–N³⁻ ordering with the corresponding fully cis-ordering becoming energetically inhibited due to strain.⁴² Computational studies have predicted that compressive strain larger than 4% would bias trans-ordering in bulk LaTiO₂N,⁴³ while also predicting surface polarisation in LaTiO₂N to favour a trans-ordering.⁴⁴ This demonstrates that while cis-ordering is preferred for d⁰ oxynitrides, the interconversion between cis- & partial trans-orderings is sensitive to strain and accessible via lattice substitutions and interfacial effects.

In previous density functional theory (DFT) studies we have investigated the charged vacancy-mediated anion diffusion in TaON and O:Ta₃N₅⁴⁵ and subsequently extended this to consider how anion ordering effects impact defect formation and mobility in BaNbO₂N and LaNbON₂,⁴⁶ since niobium oxynitrides are known to be more prone to defect formation and potentially amenable to tuning non-stoichiometry and defect engineering strategies.^47,48 Anion ordering and N:O composition was predicted to have a substantial impact on the defect formation energies and consequent charge redistribution to the cation sub-lattice (degree of e⁻ redistribution indicative of potential to form photocatalytically inhibitive reduced B-site cation defects).^45,46 From these prior computational results it is predicted that biasing the trans-configuration and controlling the local charge redistributed from defects is a possible strategy for longer term retention of N³⁻ lattice ions in an oxynitride water splitting catalyst.^13,46,49

Besides the reported effects on stability of the RP phase Sr₂TaO₃N (n = 1) relative to SrTaO₂N (n = ∞), a recent modelling effort looking at the dynamics of oxygen vacancy (V_O) formation and diffusion barriers of A²⁺B⁵⁺O₂N using Buckingham potentials and core–shell models predicts that SrTaO₂N has the most favourable defect chemistry for ionic conductivity amongst these oxynitrides.⁴⁵

In this work we are interested in probing the interplay between anion order and defect chemistry in the layered perovskite oxynitride Sr₂TaO₃N. Specifically we investigate the layer-specific neutral O²⁻ and N³⁻ vacancy defect formation, e⁻ redistribution to the cation sublattice and vacancy-mediated diffusion in Sr₂TaO₃N using accurate first-principles calculations. We screen cis- and trans-orderings and elucidate the subsequent impact on anion defect formation and e⁻ redistribution to the cation sub-lattice. We also investigate the vacancy-mediated diffusion barriers of O²⁻ and N³⁻ in and out of the TaON layer. Native migration pathways (O²⁻ → V_O, N³⁻ → V_N) are compared with what we designate as ‘anion crossing pathways’, whereby one anion migrates via the vacancy of the other anion: O²⁻ → V_N and N³⁻ → V_O.

Our results reveal the relationship between anion ordering and the degree of anisotropy of separate N³⁻ and O²⁻ diffusion pathways. In this regard, we believe this work is useful to understanding how to maintain N:O stoichiometry in oxynitride semiconductors under WS and NRR conditions.

Methods

All calculations reported here employ the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) exchange–correlation functional, revised for solids (i.e. PBEsol),⁵⁰ as implemented in the Vienna Ab initio Simulation Package (VASP) code^51,52 using the projector augmented wave (PAW) method.⁵³ All calculations employ (core)/valence configurations of Nb: ([Ne]3s)/3p3d4s; O: ([He])/2s2p N: ([He])/2s2p. Sr₂TaO₃N crystals (Fig. 1c) were constructed from I4/mmm Sr₂TiO₄ sourced from the Materials Project Database (ID mp-5532)⁵⁴ and fully relaxed with a planewave energy cut-off of 450 eV for each anion ordering constructed. Monkhorst–Pack meshes consisting of 6 × 6 × 4 k-points were used for the 56 atom 2 × 2 × 1 supercell, while 4 × 4 × 4 k-point meshes were used for the 126 atom 3 × 3 × 1 supercell.

Partial density of states (PDOS) and band structure calculations were conducted with Hubbard U corrections of U^d(Ta⁵⁺) = 3.10 eV, U^p(N³⁻) = 6.66 eV and U^p(O²⁻) = 8.87 eV based on band gap benchmarking for TaON reported by Kirchner-Hall et al.⁵⁵ The Hubbard U correction was applied in an attempt to minimize the underestimation of the band gap by uncorrected GGA-PBEsol, though it should be acknowledged that the choice of Hubbard U correction for materials with local anion ordering variations is non-trivial and requires further investigation.

Vacancy-mediated anion diffusion barriers were calculated with the nudged elastic band (NEB) method and forces were converged to within 0.05 eV per atom along the pathway.⁵⁶ We note for reference that changes in the migration enthalpy barrier of 0.4 eV have been reported to correspond to a difference of up to two orders of magnitude in oxide conductivity of perovskites.⁵⁷

For a neutral supercell, the anion vacancy formation energy, E_f,vac, can be obtained from the simplified expression:⁵⁸

E_f,vac = E_def − E_pris + μ_i

where E_def is the defective supercell, E_pris is the pristine supercell and μ_i is the chemical potential for the missing anion. In this work we are using the fitted elemental-phase reference energies (FERE) as the chemical potentials for oxygen and nitrogen respectively (μ_O = −4.76 eV and μ_N = −8.51 eV).⁵⁹ The formation of vacancies can be expressed according to the Kroger–Vink notation, whereby,
and
Additionally, depending on the reducibility of the M cation, the localization of e⁻ on the M site compared to the anion vacancy can exist within:
or
Then to analyse the e⁻ redistribution to the cation sublattice as a function of defect type and anion ordering we have conducted charge analysis using DDEC6 implemented with the Chargemol program.^60–62

Results and discussion

We begin our discussion by considering what cis- and trans-anion orderings are capturable in the 2 × 2 × 1 supercell, which is nominally the most computationally tractable supercell to probe anion orderings. This is since anion orderings in perovskite oxynitride materials are defined in terms of the chain orientations of the minority anion in the B-site metal octahedra (N³⁻–B^x+–N³⁻ chains in the case of Ta–O₄N₂ in Sr₂TaO₃N), meaning that fully cis-configurations cannot be constructed in periodic supercells containing an odd number of B-site octahedra in any axis. A challenge arises then however, as reports modelling defect migration in cubic perovskite materials indicate that a 3 × 3 supercell is required in the plane that the defect is moving, at a minimum.^46,63–65 For these reasons we use the 2 × 2 × 1 supercell to map possible cis- and trans-anion orders, changes in anion vacancy formation energy across these orderings and the subsequent e⁻ redistribution to the cation sublattice due to these neutral defects. Following this we map the lowest energy cis- and trans-orderings to a 3 × 3 × 1 supercell for NEB calculations of vacancy-mediated anion migration barriers.

For the layered material Sr₂TaO₃N it is possible to construct five different cis- (C1–C5) and 2 different trans-orderings (T1–T2) when considering the N³⁻–Ta⁵⁺–N³⁻ chain pattern and whether the chains were parallel or orthogonal between TaON layers (Fig. 2). Fig. 3a shows the relative energy in eV between these different anion orderings. The C1–C4 orderings are all within 0.2 eV of each other, while the ring chain orientation in C5 is 0.3 eV higher in energy than the most favourable ordering which was predicted to be C2. The trans-orderings are ∼2.0 eV higher than all the cis-orderings, with T1 being the lowest energy of these two.

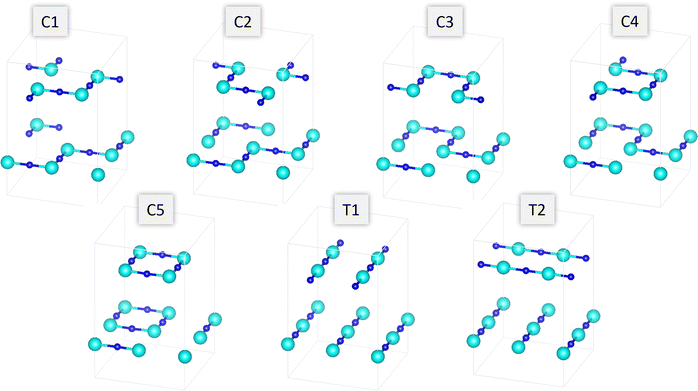Fig. 2 Series of five cis- and two trans-orderings able to be constructed in the 2 × 2 × 1 Sr₂TaO₃N supercell.

Fig. 3 (a) Relative formation energies of cis- and trans-anion orderings for the 2 × 2 × 1 Sr₂TaO₃N supercell. PBEsol+U calculated partial density of states for (b) C2 and (c) T1 anion orderings.

Fig. 3b and c depicts the calculated PDOS of the most stable cis- (C2) and trans-ordering (T1), which were calculated with a Hubbard U correction applied to the PBEsol DFT functional. Comparing the PDOS in Fig. 3b and c, the T1 ordering has significant orbital population shifted closer to the valence band maximum (VBM), whereas the C2 ordering VBM primarily consists of N-2p orbital density. The T1 ordering shows much more O-2p character around the VBM. In the conduction bands an upshift in the Ta-5d orbital population is observed in the T1 ordering, which is attributable to a change in crystal field splitting in going from cis- to trans-ordering. We have also included the full k-path band structures for these orderings of Sr₂TaO₃N in Fig. S1 and S2 in the ESI.† PBEsol+U predicted a direct bandgap of 1.425 eV for C2 and 1.871 eV for T1 at the gamma k-point.

In prior work by Bouri and Aschauer, they report the PBE and HSE06 bandgaps to be 1.128 eV and 2.005 eV respectively.³⁸ So while the Kirchner-Hall derived DFT+U corrections for TaON assist significantly with reducing the bandgap underestimation error from GGA functionals (exp. bandgap = 2.5 eV, DFT+U bandgap = 2.36 eV),⁵⁵ there is still significant underestimation of the Sr₂TaO₃N bandgap when comparing the PBEsol+U calculated bandgaps of this work (C2 = 1.425 eV, T1 = 1.871 eV) and the HSE06 bandgap (2.005 eV). Given the structural and anion ordering diversity of oxynitride perovskites in addition to their RP phase permutations, a more generalizable set of Hubbard U corrections for oxynitride perovskites is desirable to computationally explore the optoelectronic properties of these materials.

In terms of vacancy defects one can also look at charged defect sites, however, for relevance to photocatalytic applications where the scope of this work is probing the interactions of anion order and defect chemistry, we prefer to extend the study of neutral defects to analyze the degree of e⁻ redistribution to the A-site and B-site cation sublattices. This is because reduced B-site defects are quite common in perovskite photocatalysts and are a significant contribution to the reported ‘absorption tails’ in perovskite oxynitrides. To calculate the e⁻ redistribution to the A-site and B-site cation sublattice as we have done in previous work for BaNbO₂N and LaNbON₂, we take a common set of anion vacancy defects from the central Ta–O₄N₂ octahedra in the 2 × 2 × 1 Sr₂TaO₃N supercell (octahedra shifted to the cell center relative to the Fig. 1 illustration). This set of vacancy defects across C1–C5, T1 & T2 orderings for this material resulted in a general V_N defect in the TaON layer as well as a general V_O defect in each of the TaON and SrO layers. Fig. S3 (ESI†) summarizes the vacancy defect formation energies across the cis- and trans-orderings considered here. Interestingly, for the cis-orderings C1–C5, the V_O formation energy is quite consistent across orderings and between TaON and SrO layer locations, varying between 6.20–6.30 eV. The V_N defect formation energy is consistent for C1–C4, predicted to be from 3.60–3.67 eV, however the ring structure in C5 appears quite unfavourable for N³⁻ ions, in that the V_N defect formation energy shifts down to 2.98 eV, which is comparable to T1 and T2 (2.98–3.02 eV). Interestingly, the trans-orderings T1 and T2 create anisotropy in the V_O formation energies of approximately 0.4 eV. These results suggest that the trans-orderings induce anisotropy in the vacancy defect chemistry in the plane of the layer stacking, while the cis-orderings do not.

Table 1 summarizes the calculated e⁻ redistribution to the Sr²⁺ and Ta⁵⁺ cation sublattices and the total lattice for the defects in Fig. S3 (ESI†). From this analysis of the DFT calculated charge density with DDEC6 it is predicted that V_N–TaON defects redistribute 0.31–0.39 e⁻ to the Sr²⁺ cations and 1.71–1.75 e⁻ to the Ta⁵⁺ cations, respectively, while the V_O–TaON shifts back 0.30–0.32 e⁻ to Sr²⁺ cations and 1.38–1.39 e⁻ to Ta⁵⁺ cations. This difference in magnitude of shifted e⁻ correlates to the difference in relative charges of O²⁻ and N³⁻ anions. The V_O–SrO layer defects correspondingly shift an increased 0.55–0.57 e⁻ to the Sr²⁺ cations and 0.92–0.94 e⁻ to the Ta⁵⁺ cations respectively. We also analyzed the PBEsol predicted e⁻ delocalization from the vacancy defects by comparing the reduction of vacancy adjacent B-site (Ta⁵⁺) cations compared to non-adjacent lattice sites. Interestingly, for the V_O–SrO layer defects, while less e⁻ is redistributed to the Ta⁵⁺ sublattice in total, a larger proportion (0.44 e⁻ of 0.94 e⁻) is redistributed to defect non-adjacent Ta⁵⁺ cations.

Table 1 DDEC6 calculated average e⁻ redistribution to cation sublattices from vacancy defects for cis- and trans-orderings

		cis-Orderings (C1–C5)			trans-Orderings (T1 & T2)
		VO–TaON	VN–TaON	VO–SrO	VO–TaON	VN–TaON	VO–SrO
	Sr	1.35	1.34	1.33	1.34	1.34	1.33
Partial charge	Defect adjacent Ta	1.50	1.32	1.55	1.45	1.41	1.56
	Non-adjacent Ta	2.00	2.00	1.98	2.04	2.00	2.01
Charge	Sr	−0.32	−0.42	−0.57	−0.30	−0.34	−0.55
Redistribution	Defect adjacent Ta	−1.10	−1.43	−0.50	−1.22	−1.31	−0.51
	Non-adjacent Ta	−0.28	−0.33	−0.44	−0.17	−0.40	−0.41

---

In comparison, for V_N/O–TaON layer defects only approx. 20% of the total e⁻ redistributed reaches defect non-adjacent sites. These results suggest that the protective effect of excess A-site cation doping or the addition of an AO rock salt layer in RP phase perovskite oxynitrides (A_n+1B_nX_3n+1 → Sr_n+1Ta_nO_2n+1N_n here) is due to the AO layer associated V_O defects localizing less e⁻ on adjacent B-site cations. This suggests a more defect tolerant material with a lower concentration of photocatalytically inhibiting reduced B-site defects.

In terms of the effects of anion order, the largest effect is observed for DDEC6 calculated partial charges and e⁻ localization at V_N–TaON. Here we observe that a shift from a cis- to a trans-ordering is predicted to decrease the e⁻ sent to the Sr²⁺ and defect adjacent Ta⁵⁺ cations by 0.08 e⁻ and 0.12 e⁻ respectively, while an increase of 0.07 e⁻ is redistributed to the non-adjacent Ta⁵⁺ cations. While these effects are minor it is interesting to note that these shifts are reversed when going from cis- to trans-orderings for V_O defects.

Lastly, in comparing the total e⁻ redistributed from the vacancy defects, while we have primarily reported the e⁻ redistributed to Sr²⁺ and Ta⁵⁺ cations it is important to note that the difference between vacancy induced shifts in the partial charges of the cations and anions totals to the O²⁻ and N³⁻ partial charge shown in Table S1 (ESI†). We interpret this as indicative that the defect charge is indeed different from the defective supercell charge, where in fact and in Kroger–Vink notation. Following this distinction, in the next section we subsequently deem it necessary to use Kroger–Vink notation to discuss and compare the vacancy-mediated anion migration across native and anion crossing pathways ( and ).

When scaling up to a 3 × 3 × 1 supercell for the vacancy-mediated diffusion analysis, it is only feasible to build three different anion orderings in one TaON layer as there is an unavoidably uneven number of Ta–O₄N₂ octahedra in this plane. These orderings can be characterized by their varying amounts of cis-chains; 6/9, 4/9 0/9 (i.e. trans-). The 6/9 cis-ordering is 1.51 eV and 4.04 eV more stable than the 4/9 cis- and trans-orderings, respectively. The 6/9 cis-ordering and the trans-ordering were then used for further vacancy-mediated diffusion modelling. Fig. 4a and b illustrates a layer of the TaON anion ordering of the 6/9 cis- and trans-ordering configurations, and these orderings are consistent for each TaON layer in the 3 × 3 × 1 supercell.

Fig. 4 (a) Representation of anion ordering constructable with the most cis-character; 6/9 N³⁻–Ta⁵⁺–N³⁻ chains are cis- and 3/9 are trans- and (b) corresponding fully trans-ordering used for the 3 × 3 × 1 supercell. Insets depict anion/vacancy positions from the core of the structure used in this work, which also map to the 2 × 2 × 1 supercell.

Fig. 5a summarizes the O²⁻ and N³⁻ vacancy defect formation energies for the orderings shown in Fig. 4. The 6/9 cis-ordering V_O formation energy ranges from 6.09 to 6.12 eV, while the formation energy is 5.69 eV for the SrO layer compared to 6.31 eV for the TaON layer in the trans-ordering. The formation energy is also 1.26 eV lower for the trans-ordering. Comparing this data with Fig. 2c, the 6/9 cis-ordering exhibits comparable trends in defect formation energies and while this is a mixed ordering, it should be consistent with a fully cis-anion order.

Fig. 5 (a) Single vacancy defect formation energies in TaON and SrO layers and (b) anti-site + vacancy defect pairs of different anion orderings which characterize end points for the crossing vacancy-mediated anion migration pathways.

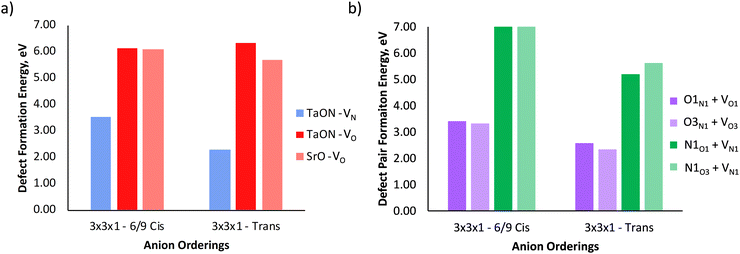
Fig. 5b depicts the defect pair formation energy for the end points of anion crossing diffusion pathways, where an O²⁻ or N³⁻ anion crosses into a or site and creates a defect pair comprising an anti-site defect and a vacancy. These end point defect pairs are necessary to calculate when considering vacancy-mediated anion diffusion pathways in a mixed-anion material, since there are now two types of vacancies via which an anion may diffuse. Fig. 5b shows that the 6/9 cis-ordering has a comparable formation energy regardless of whether the defect pair uses the O1 (TaON layer) or O3 (SrO layer) position, with 3.32–3.41 eV predicted for pairs and 7.06–7.21 eV for 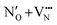defect pairs, respectively. However, a splitting occurs for the trans-ordering, where the two types of defect pairs are now 0.24 eV and 0.42 eV lower in energy when incorporating the O3 position. Additionally, the and defect pairs are ∼0.9 eV and ∼1.7 eV lower for the trans-ordering.

Fig. 6a depicts the pathways considered for the native vacancy-mediated anion migration pathways in the 3 × 3 × 1 supercell with the 6/9 cis- and trans-orderings and the resultant PBEsol NEB calculated migration energy barriers. The full NEB pathways are shown in Fig. S5 (ESI†). These pathways are denoted as the ‘native’ pathways, in that the N³⁻ and O²⁻ anions are diffusing via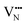 and defects, respectively, and the defect type is the same at both NEB end points. From Fig. 6b, the highest migration barrier occurs for N³⁻ diffusing in the TaON layer at 2.42 eV, while O²⁻ diffusion is predicted to have a lower barrier at 1.34 eV. The trans-ordering does not have adjacent or positions so only migration in the c-lattice vector is considered here. Diffusion of a TaON layer O²⁻ anion into a SrO layer vacancy is predicted to have the lowest barrier for both orderings (0.65–0.81 eV), and interestingly the main impact of the trans-ordering on these native diffusion pathways is a lower diffusion barrier for mediated O²⁻ migration between SrO–OSr layers . The same trends in barrier heights are predicted in the 2 × 2 × 1 supercell, which is summarized in Fig. S4 (ESI†). In comparing the barrier heights from the 3 × 3 × 1 supercell in Fig. 6b to the 2 × 2 × 1 supercell in Fig. S4 (ESI†), the TaON layer migration barriers are comparable across both supercells, and the barriers are 0.3–0.46 eV higher in the 2 × 2 × 1 supercell as compared to the 3 × 3 × 1 supercell. This highlights that separate anion diffusion barriers in mixed-anion materials are not uniformly sensitive to the supercell dimensions and further studies may be needed to elucidate the convergence of supercell size with different types of diffusing anions, defect charge states and pathways.

Fig. 6 (a) Native vacancy-mediated anion diffusion pathways around Ta–O₄N₂ octahedra core in 6/9 cis- and trans-3 × 3 × 1 supercells and (b) PBEsol calculated NEB defect migration barrier heights for each pathway.

Fig. 7a depicts the considered anion crossing vacancy-mediated diffusion pathways (where the end point of the diffusion path is the anion defect pairs whose defect formation energy is shown in Fig. 5b).

Fig. 7 (a) Anion crossing vacancy-mediated diffusion pathways around Ta–O₄N₂ octahedra core in 6/9 cis- and trans-3 × 3 × 1 supercells and (b) PBEsol calculated NEB defect migration barrier heights for each pathway and (c) defect states at the start and end points of the NEB pathways.

Fig. 7b correspondingly summarizes the PBEsol NEB calculated energy barriers and Fig. 7c provides a reference for the defect types at the NEB end points.

The anion crossing pathways enable a greater comparison between the 6/9 cis- and trans-anion orderings by considering a more exhaustive set of vacancy-mediated pathways and realistically must be considered in this case as these are likely mechanisms by which anion ordering is shifted in these materials. The pathway is characterized by either O1 (TaON layer) or O3 (SrO layer) migrating to a nitrogen vacancy. The O1 migration barrier to is 1.77 eV in the 6/9 cis-ordering and only drops by 0.19 eV for the trans-ordering. However, the O3 migration halves from 1.0 eV to 0.47 eV. Migration of the N1 atom to either the 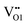or sites is highly sensitive to the anion ordering whereby planar migration in the transverse migration to drops from 1.56 eV to 0.24 eV from the 6/9 cis- to the trans-ordering respectively.

These NEB calculated migration barriers indicate that the anion ordering affects the anisotropy of the O²⁻ and N³⁻ anion diffusion to differing degrees. The diffusion barriers are primarily affected in the c-axis direction (perpendicular to the TaON layer) and within the SrO layer. Whereas for , the lower energy cis-orderings confine the diffusion to the TaON plane, the trans-orderings conversely promote competitive mobility in the transverse c-axis direction.

Conclusions

In summary, this work has used planewave DFT (PBEsol) to model the layer-dependent defect stability and migration energy barriers in the RP phase perovskite oxynitride Sr₂TaO₃N. We have specifically focused on anion vacancy defects in-plane and out-of-plane relative to the TaON layer. Several types of defects are considered in this work but arise from defective supercells with a neutral overall charge. Besides anion vacancies we consider e⁻ redistribution to Sr²⁺ and Ta⁵⁺ cations (the latter of which corresponds to photocatalytically inhibiting reduced B-site defects) and expand vacancy-mediated anion migration pathways to consider ‘anion crossing’ pathways whereby an anion diffuses by a vacancy positionally ascribed to the other anion type.

For Sr₂TaO₃N, PBEsol predicts the N³⁻ anion and SrO layer O²⁻ anion defect formation energy to be the most sensitive to increasing trans- character in the N³⁻–Ta⁵⁺–N³⁻ chains. SrO layer defects were predicted to delocalize e⁻ across defect non-adjacent Ta⁵⁺ cations to a larger degree than the TaON layer and 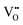defects, potentially explaining the protective effect of B-site Sr²⁺ doping in SrTaO₂N and RP phase Sr₂TaO₃N. Additionally, N³⁻ and O²⁻ vacancy-mediated anion diffusion was found to be highly sensitive to the local trans-ordering character, whereby a switch from cis- to trans-ordering is predicted to tune N³⁻ mobility from being confined to the TaON layer to enabling diffusion to the apical Ta–(O,N)₆ octahedra site in the SrO layer.

The present work highlights the potential of exploiting the anisotropy of anion defect chemistry in layered oxynitride materials as a tool for retaining N:O stoichiometry and approaching theoretical water splitting efficiencies. We also note that the constraint of using supercells computationally tractable for DFT studies does create limitations in investigating complimentary effects of anion ordering and defect engineering. As such there would be great utility in future studies expanding to molecular dynamics modelling of defect diffusion such that extended anion ordering effects and octahedral tilting variations may be captured.

Data availability

The data supporting this article have been included as part of the ESI.† This study was carried out using publicly available data from Materials Project Database at https://next-gen.materialsproject.org/, structure ID mp-5532.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was undertaken with the assistance of resources provided at the NCI National Facility systems at the Australian National University, through the National Computational Merit Allocation Scheme supported by the Australian Government. AJP acknowledges support from the Australian Research Council (INTERSECT, LE170100032). JJB acknowledges support from an Australian Government RTP Scholarship.

Notes and references

1. J. K. Harada, N. Charles, K. R. Poeppelmeier and J. M. Rondinelli, Adv. Mater., 2019, 31, 1805295.
2. N. Charles, R. J. Saballos and J. M. Rondinelli, Chem. Mater., 2018, 30, 3528–3537.
3. V. V. Atuchin, L. I. Isaenko, V. G. Kesler, Z. S. Lin, M. S. Molokeev, A. P. Yelisseyev and S. A. Zhurkov, J. Solid State Chem., 2012, 187, 159–164.
4. G. Pilania, A. Ghosh, S. T. Hartman, R. Mishra, C. R. Stanek and B. P. Uberuaga, Npj Comput. Mater., 2020, 6, 71.
5. J. T. Incorvati, L. F. Wan, B. Key, D. Zhou, C. Liao, L. Fuoco, M. Holland, H. Wang, D. Prendergast, K. R. Poeppelmeier and J. T. Vaughey, Chem. Mater., 2016, 28, 17–20.
6. K. Maeda, F. Takeiri, G. Kobayashi, S. Matsuishi, H. Ogino, S. Ida, T. Mori, Y. Uchimoto, S. Tanabe, T. Hasegawa, N. Imanaka and H. Kageyama, Bull. Chem. Soc. Jpn., 2022, 95, 26–37.
7. C. A. Crawford, C. I. Hiley, C. A. M. Scott, C. Ritter, M. R. Lees, N. C. Bristowe, R. I. Walton and M. S. Senn, Inorg. Chem., 2024, 63, 9184–9194.
8. Z. Hiroi, N. Kobayashi and M. Takano, Nature, 1994, 371, 139–141.
9. M. Ahmed and G. Xinxin, Inorg. Chem. Front., 2016, 3, 578–590.
10. Y. Subramanian, A. Dhanasekaran, L. A. Omeiza, M. R. Somalu and A. K. Azad, Catalysts, 2023, 13, 173.
11. P. Chukwunenye, A. Ganesan, M. Gharaee, K. Balogun, Q. Adesope, S. C. Amagbor, T. D. Golden, F. D’Souza, T. R. Cundari and J. A. Kelber, Phys. Chem. Chem. Phys., 2023, 25, 19540–19552.
12. J. Feng, H. Huang, T. Fang, X. Wang, S. Yan, W. Luo, T. Yu, Y. Zhao, Z. Li and Z. Zou, Adv. Funct. Mater., 2019, 29, 1808389.
13. J. J. Brown, Z. Ke, T. Ma and A. J. Page, ChemNanoMat, 2020, 6, 708–719.
14. Y. Zhu, X. Liu, S. Jin, H. Chen, W. Lee, M. Liu and Y. Chen, J. Mater. Chem. A, 2019, 7, 5875–5897.
15. Y.-I. Kim, P. M. Woodward, K. Z. Baba-Kishi and C. W. Tai, Chem. Mater., 2004, 16, 1267–1276.
16. Y. He, J. E. Thorne, C. H. Wu, P. Ma, C. Du, Q. Dong, J. Guo and D. Wang, Chem, 2016, 1, 640–655.
17. S. Chen and L. W. Wang, Appl. Phys. Lett., 2011, 99, 222103.
18. K. Motohashi, T. Sanada, T. Nakamura, Y. Kimura, Y. Uchimoto and K. Amezawa, Electrochemistry, 2022, 90, 127005.
19. M. Yang, J. Oró-Solé, J. A. Rodgers, A. B. Jorge, A. Fuertes and J. P. Attfield, Nat. Chem., 2010, 3, 47.
20. A. Fuertes, J. Mater. Chem., 2012, 22, 3293–3299.
21. N. Vonrüti and U. Aschauer, Phys. Rev. Mater., 2018, 2, 105401.
22. A. Ziani, C. Le Paven, L. Le Gendre, F. Marlec, R. Benzerga, F. Tessier, F. Cheviré, M. N. Hedhili, A. T. Garcia-Esparza, S. Melissen, P. Sautet, T. Le Bahers and K. Takanabe, Chem. Mater., 2017, 29, 3989–3998.
23. D. Oka, Y. Hirose, H. Kamisaka, T. Fukumura, K. Sasa, S. Ishii, H. Matsuzaki, Y. Sato, Y. Ikuhara and T. Hasegawa, Sci. Rep., 2014, 4, 4987.
24. Y. Hinuma, H. Moriwake, Y.-R. Zhang, T. Motohashi, S. Kikkawa and I. Tanaka, Chem. Mater., 2012, 24, 4343–4349.
25. A. P. Black, H. Suzuki, M. Higashi, C. Frontera, C. Ritter, C. De, A. Sundaresan, R. Abe and A. Fuertes, Chem. Commun., 2018, 54, 1525–1528.
26. A. Kubo, G. Giorgi and K. Yamashita, Chem. Mater., 2017, 29, 539–545.
27. P. J. Camp, A. Fuertes and J. P. Attfield, J. Am. Chem. Soc., 2012, 134, 6762–6766.
28. B. Siritanaratkul, K. Maeda, T. Hisatomi and K. Domen, ChemSusChem, 2011, 4, 74–78.
29. D. Y. Wan, Y. L. Zhao, Y. Cai, T. C. Asmara, Z. Huang, J. Q. Chen, J. Hong, S. M. Yin, C. T. Nelson, M. R. Motapothula, B. X. Yan, D. Xiang, X. Chi, H. Zheng, W. Chen, R. Xu, A. Ariando, A. Rusydi, A. M. Minor, M. B. H. Breese, M. Sherburne, M. Asta, Q.-H. Xu and T. Venkatesan, Nat. Commun., 2017, 8, 15070.
30. X. Xu, C. Randorn, P. Efstathiou and J. T. S. Irvine, Nat. Mater., 2012, 11, 595–598.
31. K. Maeda, M. Higashi, B. Siritanaratkul, R. Abe and K. Domen, J. Am. Chem. Soc., 2011, 133, 12334–12337.
32. Z. Lan, T. Vegge and I. E. Castelli, Chem. Mater., 2021, 33, 3297–3303.
33. M. Hojamberdiev, R. Vargas, Z. C. Kadirova, K. Kato, H. Sena, A. G. Krasnov, A. Yamakata, K. Teshima and M. Lerch, ACS Catal., 2022, 12, 1403–1414.
34. H. Xiao, P. Liu, W. Wang, R. Ran, W. Zhou and Z. Shao, Energy Fuels, 2020, 34, 9208–9221.
35. I. E. Castelli, J. M. García-Lastra, F. Hüser, K. S. Thygesen and K. W. Jacobsen, New J. Phys., 2013, 15, 14.
36. Y. Suemoto, Y. Masubuchi, Y. Nagamine, A. Matsutani, T. Shibahara, K. Yamazaki and S. Kikkawa, Inorg. Chem., 2018, 57, 9086–9095.
37. J. Seo, M. Nakabayashi, T. Hisatomi, N. Shibata, T. Minegishi and K. Domen, ACS Appl. Energy Mater., 2019, 2, 5777–5784.
38. M. Bouri and U. Aschauer, Phys. Chem. Chem. Phys., 2018, 20, 2771–2776.
39. M. Bouri and U. Aschauer, Chem. Mater., 2020, 32, 75–84.
40. J. Seo, M. Nakabayashi, T. Hisatomi, N. Shibata, T. Minegishi, M. Katayama and K. Domen, J. Mater. Chem. A, 2019, 7, 493–502.
41. H. Johnston, A. P. Black, P. Kayser, J. Oró-Solé, D. A. Keen, A. Fuertes and J. P. Attfield, Chem. Commun., 2018, 54, 5245–5247.
42. D. Oka, Y. Hirose, F. Matsui, H. Kamisaka, T. Oguchi, N. Maejima, H. Nishikawa, T. Muro, K. Hayashi and T. Hasegawa, ACS Nano, 2017, 11, 3860–3866.
43. N. Vonrüti and U. Aschauer, Phys. Rev. Lett., 2018, 120, 046001.
44. S. Ninova and U. Aschauer, J. Mater. Chem. A, 2017, 5, 11040–11046.
45. A. Kousika and T. Thomas, Solid State Ion., 2023, 399, 116300.
46. J. J. Brown, Y. Shao, Z. Ke and A. J. Page, Mater. Adv., 2021, 2, 2398–2407.
47. J. Liu, Z. Wei and W. Shangguan, ChemCatChem, 2019, 11, 6177–6189.
48. S. Bai, N. Zhang, C. Gao and Y. Xiong, Nano Energy, 2018, 53, 296–336.
49. J. J. Bown and A. J. Page, J. Mater. Chem. A, 2019, 7, 13029–13035.
50. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
51. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
52. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
53. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
54. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
55. N. E. Kirchner-Hall, W. Zhao, Y. Xiong, I. Timrov and I. Dabo, Appl. Sci., 2021, 11, 2395.
56. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
57. Y. Cao, M. J. Gadre, A. T. Ngo, S. B. Adler and D. D. Morgan, Nat. Commun., 2019, 10, 1346.
58. M. Pavone, A. M. Ritzmann and E. A. Carter, Energy Environ. Sci., 2011, 4, 4933–4937.
59. V. Stevanović, S. Lany, X. Zhang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115104.
60. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
61. N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747.
62. N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707.
63. L. Zhang, B. Liu, H. Zhuang, P. R. C. Kent, V. R. Cooper, P. Ganesh and H. Xu, Comput. Mater. Sci., 2016, 118, 309–315.
64. J. J. Brown, Z. Ke, W. Geng and A. J. Page, J. Phys. Chem. C, 2018, 122, 14590–14597.
65. J. J. Brown and A. J. Page, J. Chem. Phys., 2021, 154, 124121.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma01137f

---