Optical nonlinear refractive index measurements of Cr₂Te₃ with an immense photothermal effect

Abstract

In this work, the optical nonlinearity of PVD-grown Cr₂Te₃ thin films of 33- and 100-nm thickness with an immense thermal optical effect was investigated. By removing the thermally induced background signal, the n₂ value without accumulated heat could then be estimated to be of the order of magnitude of around 10⁻⁸ cm² W⁻¹. A decrease in the n₂ value with the pump power was observed, leading to increased absorption. In addition, the changing sign for the 100-nm-thick thin film as the pump power exceeded 450 mW was investigated, exhibiting good agreement with the observed additional increasing temperature resulting from the anomalous increasing absorption. This work paves the way to not only characterize the optical nonlinearity of samples with initiable thermal effects but also to evaluate materials with potential for real applications through the methodology provided.

---

1. Introduction

Transition metal chalcogenides (TMCs), which are composed of the group VI transition metals (Cr, Mo, W) and chalcogenides (S, Se, Te), have been used extensively to realize nonlinear photonic devices, owing to their superb nonlinear optical responses, electron mobilities, and broadband absorption.^1,2 In particular, two-dimensional (2D) Cr₂Te₃ has attracted attention recently in the field of spintronics owing to its superb ferromagnetism properties, including a unique skyrmion state and topological Hall effect³ and highly tunable magnetic anisotropy.⁴ The layer-dependent ferromagnetic properties of Cr₂Te₃ films have also been investigated, demonstrating that even monolayer Cr₂Te₃ exhibits ferromagnetic behavior.⁵ Additionally, advanced film growth techniques for Cr₂Te₃ have been studied, highlighting the reproducible and high-quality film.⁶ Furthermore, the recent experimental work by I. Kariper et al. explored the linear optical absorption and refraction properties of Cr₂Te₃.⁷ Although a variety of investigations have been conducted to determine its unique physical properties,^4,8–15 only a few studies regarding optical nonlinearity have been conducted.¹⁶ Recently, research on the nonlinear refractive index n₂ and its application for pulsed lasers has been reported, revealing the potential of Cr₂Te₃-based optical applications and leading to the requirement for detailed investigations.¹⁶ To understand the feasibility for photonic application at a wavelength of 1 μm, the nonlinear characterizations at this wavelength region is therefore desired. In this work, the optical nonlinear coefficients of PVD-grown Cr₂Te₃ thin films were investigated. An immense thermal effect due to heat accumulation was observed. By subtracting the contribution of the thermal optical effect within the thin films, the n₂ value of Cr₂Te₃ thin films under various excitation peak intensities ranging from 1.17 to 20.93 MW cm⁻² was characterized. In addition, the thickness dependence of n₂ was investigated and discussed. These results not only provide relevant information regarding Cr₂Te₃ thin films for applications but also pave the way for investigating the optical nonlinearity of materials with inevitable thermal effects.

2. Sample preparation and experimental setup for optical nonlinearity

In general, z-scan measurements are popular for studying the nonlinear properties of thin films. Therefore, here, a conventional z-scan system utilizing a fiber pulsed laser with a wavelength, pulse width, and repetition rate of 1030 nm, 130 fs, and 28 MHz, respectively, was first constructed to investigate the n₂ value of Cr₂Te₃. Fig. 2(a) shows the experimental setup of our z-scan system. By using a lens with a focal length of 50 mm, the peak intensity of the focusing spot ranging from 2 to 207 MW cm⁻² can be adjusted.

In this work, Cr₂Te₃ thin films of 33- and 100-nm thickness were prepared. The nanoscale-layered Cr₂Te₃ thin films were prepared by physical vapor deposition (PVD) with a high vacuum (<5 × 10⁻⁸ Torr) and a co-evaporation system (Cr: 99.995%; Te: 99.999%). The nanoscale-layered Cr₂Te₃ thin films were grown on sapphire substrates (0001) at a growth temperature of 350 °C. The Cr and Te fluxes were set to 0.03 and 0.7 Å s⁻¹, respectively. Considering that the vaporization temperature of Te at a high vacuum is lower than 350 °C, the Te flux was set to be sufficiently higher than the Cr flux. Then, the deposition rate of Cr₂Te₃ thin film was controlled by the Cr flux. The films were post-annealed at 400 °C for 30 min after film growth. Further details on the film fabrication process are fully described in ref. 16. The high-resolution transmission electron microscopy (HR-TEM) image in Fig. 1(a) shows the high quality of the Cr₂Te₃ film. The dark region on the left side of Fig. 1(a) indicates the well-grown Cr₂Te₃ film along the c-axis of the sapphire substrate on the right side of the Fig. 1(a). Fig. 1(b) shows the X-ray photoelectron spectroscopy (XPS) peaks of Cr 2p and Te 3d overlapped at 571 and 581 eV, which are characteristic peaks observed in the XPS spectrum of Cr₂Te₃.¹⁷Fig. 1(c) shows the measured Raman spectrum of the Cr₂Te₃ film with peaks at 99.7, 122.0, and 139.8 eV, which correspond to the values reported in a previous study.¹⁸Fig. 1(d) shows the measured linear absorbance of the 100-nm-thick Cr₂Te₃ film in the 1.0 μm wavelength region.

Fig. 1 (a) High-resolution TEM image, (b) XPS spectrum, (c) Raman spectrum, and (d) linear absorption spectrum of the Cr₂Te₃ film.

Fig. 2(a) shows the typical z-scan measurement setup. Here, an open aperture was used to conduct OA profiles, and the CA curve was recorded by suitably adjusting the aperture. The OA and CA curves were recorded separately, and the CA/OA curves could be accordingly obtained to derive the n₂ value. Fig. 2(b) and (c) show the z-scan measurement results of the 100-nm-thick Cr₂Te₃ film under focusing optical intensities ranging from 2.07 MW cm⁻² to 207 MW cm⁻². Clearly, the open aperture (OA) curves reveal fruitful behavior; see Fig. 2(b). When the focusing optical peak intensity was adjusted to 2.07 MW cm⁻², the transmittance experienced reversed saturation absorption (RSA) first and changed to saturation absorption (SA) as the Cr₂Te₃ thin film was moved toward the focusing spot. Finally, the absorption exhibits RSA again. This indicates that Cr₂Te₃ possesses strong high-order nonlinear absorption, leading to the fruitful nature of the band structure within Cr₂Te₃.³ In addition, the curve shows SA directly for stronger focusing peak intensity instead of RSA. This can be attributed to the stronger peak intensity at the same position. One can note that the OA curves of three different focusing conditions all exhibit an “M”-shaped profile. Moreover, the curves exhibit clear asymmetry around the focal point at z = 0. In the past, these asymmetry phenomena have been discussed and can be attributed to heat accumulation during long-term laser illumination, given the high repetition rate of the applied pulsed laser.^19–23 Regarding the CA/OA curve, as expected for the z-scan measurement under thermal accumulation, these curves appear significantly distorted, leading to remarkable difficulty for z-scan analysis.

Fig. 2 (a) Diagram of the femtosecond pump z-scan setup; (b) OA and (c) CA/OA z-scan results under a peak intensity ranging from 2.07 MW cm⁻² to 207 MW cm⁻².

3. Photothermal nonlinearity

In the past, several approaches have been proposed for investigating the z-scan result under thermal effects.^21–25 Among various approaches, reducing the repetition rate is popular and widely used. In general, by reducing the laser repetition rate of the z-scan measurement, heat accumulation can be efficiently reduced. However, it should be noted that the remarkable decreasing average power will be inevitable. In this work, Fig. 2 exhibits a clear thermal effect while using a pump power of 1, 10, and 100 mW. One can estimate that the average power will be down to the μW level once a laser of 1 kHz repetition rate is used to replace the laser with a repetition rate of 28 MHz. Considering the measurement limits of typical experimental detectors, accurately distinguishing output power at such low average power levels is difficult. Recently, an alternative method was proposed for dealing with the optical nonlinearity measurement with the photothermal effect.²⁶ The approach has successfully been applied for characterizing the optical nonlinear coefficient of 2D materials, such as graphene and Bi₂Te₃. This method is based on the process that removes the contribution of thermally induced nonlinearity from both the substrate and the sample. Fig. 3(a) illustrates the flowchart of the process for estimating n₂ values. In step 1, a pulsed laser is used as the pump beam source to induce the photothermal nonlinearity at various pump beam powers, and the power-dependent NPT value is then determined. In step 2, a thermal camera is used to visualize the sample temperature under excitation at each pump beam power, and NPT can be redrawn with its corresponding temperature. Next, to determine the purely thermally induced nonlinearity n_TI over the same temperature range in step 2, a heater is applied to the sample to adjust and increase the background temperature. In step 4, the thermally induced signal is removed by subtracting n_TI from NPT, and the purely photon-induced nonlinearity n₂I is then obtained. Finally, n₂I is divided by the peak intensity of the pump beam to obtain the estimated n₂ value. Three different experiments were used to record the data required for analysis. The photothermal effect was initially verified by monitoring the surface temperature of our sample using a thermal camera. Fig. 3(b) shows the experimental setup for visualizing the sample temperature under excitation at each pump beam power. Regarding the values of n_TI and NPT, pump–probe spectroscopy was then used to assess the degree of the photothermal nonlinearity, and the experimental setup is shown in Fig. 3(c). The same pulsed laser utilized in Fig. 3(b) was used as the pump beam source to induce photothermal nonlinearity at varying average powers. A continuous-wave He–Ne laser was used as the probe beam source for detecting the optical responses of the sample. The pump beam spot size was 1.6 mm, and the sample was fixed onto a heater stage. A polarizing beam splitter (PBS), a half-waveplate, and a mechanical shutter were used to control the average power and illumination time of the pump beam, respectively. In addition, a black baffle and a low-pass filter were placed in front of the photodetector to prevent any scattering pump light from reaching the photodetector.

Fig. 3 (a) Flowchart of the process for estimating n₂ values. (b) Experiment setup of the thermal camera system. (c) Pump–probe spectroscopy for assessing the degree of the photothermal nonlinearity. (d) Pump–probe setup for thermally induced nonlinearity.

To measure the thermally induced optical responses, the heater was used to create different background temperature conditions. As shown in Fig. 3(d), the heater temperature was adjusted precisely using a temperature controller (Model 335, Lake Shore Cryotronics, OH, USA). A thermal camera (TVX 100EX, Nippon Avionics Co., Ltd, Yokohama, Japan) was then used to monitor the sample's surface temperature. The same as for detecting photothermally induced nonlinearity, a continuous-wave He–Ne laser was used as the probe beam source for detecting the optical responses of the sample.

4. Results and discussion

The change in temperature ΔT at various pump beam powers ranging from 50 mW to 800 mW was recorded, as depicted in Fig. 4. The surface temperature of 33- and 100-nm-thick Cr₂Te₃ thin films exhibits an increasing tendency with the pump beam power, and variations of 15 and 33 K were obtained while pumping with a power of 800 mW, respectively. This indicates a significant photothermal effect within Cr₂Te₃ thin films and echoes the results of the asymmetric OA curve shown in Fig. 2(b) and the distortion CA/OA curve shown in Fig. 2(c), which represent the heat accumulation rate within the samples. Following the procedure sketched in Fig. 3(a), pump–probe spectroscopy was then used to assess the degree of the photothermal nonlinearity. In addition, to ascertain the purely thermally induced nonlinearity over the same temperature range in Fig. 4, a heater was applied to the sample to adjust and increase the background temperature. The temperature-dependent reflections and transmittances were subsequently obtained. Moreover, in this work, the primary source of error stems from the instability of the probe beam. To quantify this error, the instability of the He–Ne laser was measured over a 10-minute period and determined to be 2.3%. We can therefore determine the power-dependent reflections and transmittances resulting from photothermal nonlinearity and the thermally induced reflections and transmittances at various heater temperatures for 33- and 100-nm-thick Cr₂Te₃ thin films, as shown in Fig. 5. Fig. 5(a) and (c) show the power-dependent reflections and transmittances that resulted from photothermal nonlinearity of the samples. Meanwhile, the thermally induced reflections and transmittances at various heater temperatures were also plotted, as shown in Fig. 5(b) and (d). All the plots show an error bar by considering the instability. Clearly, photothermal nonlinearity measurements show that the transmittance of the 100-nm-thick thin film, ranging from 9 to 12%, is smaller than that of the 33-nm-thick thin film, ranging from 31.5 to 37.5%. This can be due to the thickness being three times longer. An interesting point is that the transmittance of the 100-nm-thick thin film begins to decrease after 300–400 mW, unlike the monotonic increasing behavior of the 33-nm-thick thin film. Similar behavior was also observed within the plots of thermally induced measurements; see Fig. 5(b) and (d). This might be the additional absorption for the 100-nm-thick thin film and agrees quite well with the variation of increasing temperature under various pump powers; see the green dashed line in Fig. 4.

Fig. 4 Temperature variation ΔT of Cr₂Te₃ thin films under various pump powers due to the photothermal effect.

Fig. 5 (a) Power-dependent reflections and transmittances resulted from photothermal nonlinearity for 33 nm Cr₂Te₃ thin film. (b) Thermally induced reflections and transmittances at various heater temperature for 33 nm Cr₂Te₃ thin film. (c) Power-dependent reflections and transmittances resulted from photothermal nonlinearity for 100 nm Cr₂Te₃ thin film. (d) Thermally induced reflections and transmittances at various heater temperature for 100 nm Cr₂Te₃ thin film.

After recording the power-dependent reflections and transmittances resulting from photothermal nonlinearity and the thermally induced reflections and transmittances at various heater temperatures for 33- and 100-nm-thick Cr₂Te₃ thin films (see Fig. 5), the refractive index n and extinction coefficient κ resulting from photothermal and thermally induced nonlinearity could be accordingly calculated based on the equation below²⁶:

where λ is the wavelength of the probe beam.

Fig. 6 shows the power-dependent refractive index (NPT) and extinction coefficient (κ_PT) with error bars for the 33- and 100-nm-thick Cr₂Te₃ thin films. Clearly, these two optical parameters for the two samples show similar tendencies. For the 33-nm-thick Cr₂Te₃ thin film, the initial κ_PT value is 1.3, and it decreases to 1.15 at a pump beam power of 700 mW. After 700 mW, κ_PT slightly increases. As for the refractive index NPT, the initial value of NPT is 6.15, but it decreases drastically to 5.25 at a pump beam power of 800 mW. In addition, we have to note that NPT shows a tremendous increase for the 100-nm-thick thin film. In the past, layered Cr₂Te₃ has been reported to possess a hexagonal NiAs structure based on a space group of P3̄1 with metallic conductivity.³ Therefore, this might reflect the metallic state tendency as thickness increases. Furthermore, NPT and κ_PT for the 100-nm-thick thin film also reveal a power-dependent change from decreasing to increasing at around 400 mW. This again reflects the characteristic of the increasing temperature shown in Fig. 4 and the decreasing transmittance shown in Fig. 5. To further characterize this, one can estimate the merit of absorption using the equation below:

κ × d × (1 − R)

where κ, d, and R are the extinction coefficient, thickness, and reflection, respectively. This is semi-quantitatively related to the absorption since (1 − R), and κ and d are the percentage and absorption when entering the thin film, respectively. Fig. 6(c) shows the merit for 33- and 100-nm-thick thin films. For the 100-nm-thick thin film, a merit of nearly three times that of the 33-nm-thick sample was obtained. Recalling the increasing temperature shown in Fig. 4, the proposed merit provides a reasonable and good evaluation. In addition, this exhibits the reliability of the retrieved parameter. Since the photothermal nonlinearity comprises both thermally induced and photo-induced optical responses, the thermally induced signal can therefore be removed by subtracting n_TI from NPT. This subtraction yields the purely photo-induced nonlinearity n₂I. Here, using the equations mentioned above, the refractive index n_TI resulting from thermally induced nonlinearity can be calculated accordingly. Fig. 7(a) and (b) show the temperature-dependent refractive index due to photothermally and thermally induced nonlinearity of 33- and 100-nm-thick thin films. Clearly, the variations of refractive index exhibit different behavior with photothermal effect or thermally induced nonlinearity. Additionally, the extinction coefficient for 33- and 100-nm-thick thin film samples all exhibit the increasing trend with power while the pump power exceeds 400 mW, leading to the extra absorption.

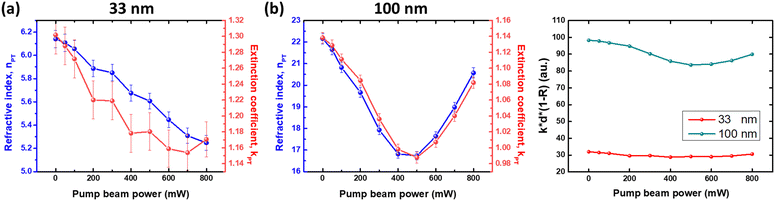Fig. 6 (a) Power-dependent refractive index and extinction coefficient for 33-nm-thick and (b) 100-nm-thick Cr₂Te₃ thin films; (c) estimated merit of absorption for the Cr₂Te₃ thin films.

Fig. 7 (a) Refractive indices due to photothermally and thermally induced nonlinearity of 33-nm-thick and (b) 100-nm-thick thin films. (c) Estimated n₂ value of Cr₂Te₃.

Finally, the n₂ value of Cr₂Te₃ can therefore be estimated by dividing the obtained n₂I by the peak intensity of the pump beam. The n₂ values are shown in Fig. 7(c). The n₂ values all reveal a decreasing tendency with pump power. For example, n₂ of the 33-nm-thick thin film decreases from 10.32 to 0.38 × 10⁻⁸ cm² W⁻¹. In addition, n₂ of the 100-nm-thick Cr₂Te₃ thin film becomes negative while the peak intensity exceeds 12 MW cm⁻², corresponding to a power of 450 mW. Typically, the absorption will result in a decreasing n₂ value, and the sign of n₂ might change with the additional absorption.^20,21,27 This can be used to interpret the decreasing tendency observed since the temperature of thin film increases monotonically with the pump power. Furthermore, the changing sign of n₂ for the 100-nm-thick thin film will also be expectable as the pump power exceeds 450 mW. Meanwhile, the phenomenon caused by this additional absorption corresponds to the decreasing transmittance trend observed for the 100 nm sample in Fig. 5 and the increasing trend of NPT and κ_PT in Fig. 6. Similarly, the extra increase in temperature variation observed in Fig. 4 also aligns with this result.

Typically, z-scan measurements, which are a popular approach for characterizing optical nonlinearity, have been widely used to evaluate the feasibility of various applications, such as optical limiters or saturable absorbers for pulsing lasers.^28,29 However, the distortion of the z-scan profile resulting from the thermal effect leads to difficulties in investigation. Despite this, the thermal effects can be ignored by reducing the repetition rate of the pump laser. The remarkable reduced average power results in the detection limit when recording the z-scan profile with lasers of low repetition rates. In this work, an immense photothermal effect within Cr₂Te₃ thin films was observed. By removing the thermally induced nonlinearity, the n₂ value could therefore be estimated. In addition, the clear thickness dependency of optical nonlinearity was investigated. The strong thickness and power-dependent absorption revealed a direct relationship with the optical nonlinearity, providing an alternative method to handle optical nonlinearity measurements that are subject to the photothermal effect. In the last decade, 2D materials have attracted considerable attention due to their fruitful potential for application.^30–37 However, the inevitable thermal effects, such as thermal electric properties, limit their optical applications. This work paves the way for more reliable applications by directly understanding the role of the thermal effect and the nature of the optical nonlinearity.

5. Conclusions

In this work, the optical nonlinearity of PVD-grown Cr₂Te₃ thin films of 33 and 100 nm thickness with an immense thermal optical effect was investigated. A decreasing n₂ value with the pump power was observed, leading to increasing absorption. The changing sign for the 100-nm-thick thin film as the pump power exceeded 450 mW was characterized. This agrees quite well with the observed additional increasing temperature resulting from the anomalous increasing absorption. Moreover, the merit of absorption was proposed, exhibiting the reasonable guide about the thermal effect. As a summary, this work provides a way to characterize the optical nonlinearity of the sample with initiable thermal effect.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by various grants from Taiwan and Korea. For Prof. Chao-Kuei Lee, the research was supported by the National Science and Technology Council, Taiwan (NSTC), under Contract No. NSTC-112-2112-M-110-016 and NSTC 113-2112-M-110-017. For Prof. Ju-Han Lee, this work was supported by the Basic Study and Interdisciplinary R&D Foundation Fund of the University of Seoul (2024). In addition, for Prof. Young Jun Chang, this work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (NRF-2020R1A2C200373211, RS-2023-00220471, RS-2024-00334854) and MOLIT [Innovative Talent Education Program for Smart City]. This work was also supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (RS-2021-NR060086) for Kyungtaek Lee. The corresponding authors of this article are Chao-Kuei Lee and Ju Han Lee.

References

1. S. Wang, H. Yu, H. Zhang, A. Wang, M. Zhao, Y. Chen, L. Mei and J. Wang, Broadband few-layer MoS₂ saturable absorbers, Adv. Mater., 2014, 2, 3538–3544.
2. P. Ranjan, S. Gaur, H. Yadav, A. B. Urgunde, V. Singh, A. Patel, K. Vishwakarma, D. Kalirawana, R. Gupta and P. Kumar, 2D materials: increscent quantum flatland with immense potential for applications, Nano Convergence, 2022, 9, 26.
3. M. Bian, A. N. Kamenskii, M. Han, W. Li, S. Wei, X. Tian, D. B. Eason, F. Sun, K. He, H. Hui, F. Yao, R. Sabirianov, J. P. Bird, C. Yang, J. Miao, J. Lin and S. A. Crooker, Covalent 2D Cr₂Te₃ ferromagnet, Mater. Res. Lett., 2021, 9, 205–212.
4. I. H. Lee, Y. G. Khim, J. Eom, J. Y. Kee, B. K. Choi, H. J. Kim, R. Kim, M. Y. Jung, K. J. Lee, Y. Kim, W.-S. Noh, B.-H. Lee, H. Suh, H. J. Chang, S. O. Won, C. Jang, H. Ryu, D. R. Lee, S. H. Chang, H. H. Lee, Y. J. Chang and J. W. Choi, Controlling the magnetic properties of layered Cr₂Te₃ thin films via ex-situ annealing, Appl. Surf. Sci., 2024, 648, 159057.
5. Y. Zhong, C. Peng, H. Huang, D. Guan, J. Hwang, K. H. Hsu, Y. Hu, C. Jia, B. Moritz, D. Lu, J.-S. Lee, J.-F. Jia, T. P. Devereaux, S.-K. Mo and Z.-X. Shen, From Stoner to local moment magnetism in atomically thin Cr₂Te₃, Nat. Commun., 2023, 14, 5340.
6. I. H. Lee, B. K. Choi, H. J. Kim, M. J. Kim, H. Y. Jeong, J. H. Lee, S.-Y. Park, Y. Jo, C. Lee, J. W. Choi, S. W. Cho, S. Lee, Y. Kim, B. H. Kim, K. J. Lee, J. E. Heo, S. H. Chang, F. Li, B. L. Chittari, J. Jung and Y. J. Chang, Modulating Curie Temperature and Magnetic Anisotropy in Nanoscale-Layered Cr₂Te₃ Films: Implications for Room-Temperature Spintronics, ACS Appl. Nano Mater, 2021, 4(5), 4810–4819.
7. I. A. Kariper, Optical and structural properties of chromium telluride (Cr₂Te₃) thin film produced via chemical bath deposition, Optoelectron. Adv. Mater., Rapid Commun., 2016, 10, 541–546.
8. H. Li, L. Wang, J. Chen, T. Yu, L. Zhou, Y. Qiu, H. He, F. Ye, I. K. Sou and G. Wang, Molecular Beam Epitaxy Grown Cr₂Te₃ Thin Films with Tunable Curie Temperatures for Spintronic Devices, ACS Applied Nano Materials, ACS Appl. Nano Mater., 2019, 2(11), 6809–6817.
9. K. Zberecki, Magnetic properties of two-dimensional M₂N₃ (M-metal, N = S, Se, Te) compounds, arXiv, 2020, preprint, https://doi.org/10.48550/arXiv.2006.09757.
10. L. Zhou, J. Chen, X. Chen, B. Xi, Y. Qiu, J. Zhang, L. Wang, R. Zhang, B. Ye, P. Chen, X. Zhang, G. Guo, D. Yu, J.-W. Mei, F. Ye, G. Wang and H. He, Topological Hall effect in bulk ferromagnet Cr₂Te₃ embedded with black-phosphorus-like bismuth nanosheets, https://doi.org/10.1021/acsami.0c04447.
11. Y. Kubota, Y. Okamoto, T. Kanematsu, T. Yajima, D. Hirai and K. Takenaka, Large magnetic-field-induced strains in sintered chromium tellurides, Appl. Phys. Lett., 2023, 122, 042404.
12. Y. Ou, M. Mirzhalilov, N. M. Nemes, J. L. Martinez, M. Rocci, A. Duong, A. Akey, W. Ge, D. Suri, Y. Wang, H. Ambaye, J. Keum, M. Randeria, N. Trivedi, K. S. Burch, D. C. Bell, W. Wu, D. Heiman, V. Lauter, J. S. Moodera and H. Chi, Enhanced Ferromagnetism in Monolayer Cr₂Te₃via Topological Insulator Coupling, https://doi.org/10.48550/arXiv.2312.15028.
13. Q. Guillet, H. Boukari, F. Choueikani, P. Ohresser, A. Ouerghi, F. Mesple, V. T. Renard, J.-F. Jacquot, D. Jalabert, C. Vergnaud, F. Bonell, A. Marty and M. Jamet, Magnetic evolution of Cr₂Te₃ epitaxially grown on graphene with post-growth annealing, https://doi.org/10.48550/arXiv.2405.05689.
14. C. C. Gowda, A. Kartsev, N. Tiwari, A. A. Safronov, P. Pandey, A. K. Roy, P. M. Ajayan, D. S. Galvao and C. S. Tiwary, Non-thermal Magnetic Deicing Using Two-Dimensional Chromium Telluride, https://doi.org/10.48550/arXiv.2406.14381.
15. A. L. Coughlin, D. Xie, X. Zhan, Y. Yao, L. Deng, H. Hewa-Walpitage, T. Bontke, C.-W. Chu, Y. Li, J. Wang, H. A. Fertig and S. Zhang, van der Waals Superstructure and Twisting in Self-Intercalated Magnet with Near Room-Temperature Perpendicular Ferromagnetism, Nano Lett., 2021, 21(22), 9517–9525.
16. K. Lee, I. H. Lee, Y. G. Khim, S.-Y. Kwon, G. Lim, J. Jung, Y. J. Chang and J. H. Lee, Nonlinear optical properties of PVD-grown Cr₂Te₃ film and its nonlinear switching application, J. Alloys Compd., 2023, 956, 170308.
17. H. Yang, F. Wang, H. Zhang, L. Guo, L. Hu, L. Wang, D.-J. Xue and X. Xu, Solution Synthesis of Layered van der Waals (vdW) Ferromagnetic CrGeTe₃ Nanosheets from a Non-vdW Cr₂Te₃ Template, J. Am. Chem. Soc., 2020, 142, 4439–4444.
18. J. Zhong, M. Wang, T. Liu, Y. Zhao, X. Xu, S. Zhou, J. Han, L. Gan and T. Zhai, Strain-sensitive ferromagnetic two-dimensional Cr₂Te₃, Nano Res. 15, 2022, 1254–1259.
19. T. Kawazoe, H. Kawaguchi, J. Inoue, O. Haba and M. Ueda, Measurement of nonlinear refractive index by time-resolved z-scan technique, Opt. Commun., 1999, 160, 125e9.
20. T.-H. Wei, T.-H. Huang, T.-T. Wu, P.-C. Tsai and M.-S. Lin, Studies of nonlinear absorption and refraction in C60/toluene solution, Chem. Phys. Lett., 2000, 318, 53e7.
21. A. Gnoli, L. Razzari and M. Righini, Z-scan measurements using high repetition rate lasers: how to manage thermal effects, Opt. Exp., 2005, 13(20), 7976–7981.
22. I. Severiano-Carrillo, E. Alvarado-Mendez, M. Trejo-Duran and M. M. Mendez-Otero, Improved Z-scan adjustment to thermal nonlinearities by including nonlinear absorption, Opt. Commun., 2017, 397, 140e6.
23. A. S. Gomes, E. L. Falcão Filho, C. B. de Araújo, D. Rativa, R. E. De Araujo, K. Sakaguchi, F. P. Mezzapesa, I. Carvalho and P. G. Kazansky, Third-order nonlinear optical properties of bismuth-borate glasses measured by conventional and thermally managed eclipse Z scan, J. Appl. Phys., 2007, 101, 033115.
24. N. Wickremasinghe, X. Wang, H. Schmitzer and H. P. Wagner, Eliminating thermal effects in z-scan measurements of thin PTCDA films, Opt. Express, 2014, 22, 23955e64.
25. M. S. Z. Abidin, A. S. M. Noor, S. A. Rashid and M. A. Mahdi, Frequency and duty cycle modulation optimization in minimizing thermal accumulation effect in Z-scan measurement with highrepetition-rate laser, Jpn. J. Appl. Phys., 2014, 53, 112702.
26. J.-C. Lan, T.-Y. Chung, C.-M. Cheng, J.-C.-A. Huang and C. Lee, Determination of optical nonlinearity with photothermal effect within a layered bismuth telluride, J. Mater. Res. Technol., 2023, 26, 176–185.
27. P. Burkins, R. Kuis, I. Basalua, A. M. Johnson, S. R. Swaminathan, D. Zhang and S. Trivedi, Thermally managed Z-scan methods investigation of the size-dependent nonlinearity of graphene oxide in various solvents, JOSA B, 2016, 33(11), 2395–2401.
28. M. Sheik-Bahae, A. A. Said, T. H. Wei, D. J. Hagan and E. W. Van Stryland, Sensitive measurements of optical nonlinearities using a single beam, IEEE J. Quantum Electron., 1990, 26, 760e9.
29. J. Qiao, M.-Y. Chuang, J.-C. Lan, Y.-Y. Lin, W.-H. Sung, R. Fan, M.-Y. Wu, Q.-Y. Lee, C.-H. Chen, W. Qiao, S. Zhao, H. Liu and C.-K. Lee, Two-Photon Absorption within the Layered Bi₂Te₃ Topological Insulators and Role for Nonlinear Transmittance Therein, J. Mater. Chem. C, 2019, 7, 7027–7034.
30. B. Zhang, J. Liu, C. Wang, K. Yang, C. Lee, H. Zhang and J. He, Recent Progress in 2D Material-Based Saturable Absorbers for All Solid-State Pulsed Bulk Lasers, Laser Photonics Rev., 2019, 1900240.
31. J. Qiao, W.-H. Sung, J.-C. Lan, Y.-Y. Lin, M.-Y. Wu, R. Fan, Y. Li, W. Qiao, H. Liu, S. Zhao and C.-K. Lee, Are graphene Bi₂Te₃ van der Waals heterostructure-based saturable absorbers promising for solid-state Q-switched lasers?, Opt. Lett., 2019, 44(5), 1072–1075.
32. G. Sobon, J. Sotor, I. Pasternak, A. Krajewska, W. Strupinski and K. M. Abramski, Thulium-doped all-fiber laser mode-locked by CVD-graphene/PMMA saturable absorber, Opt. Mater. Express, 2015, 5, 2884–2894.
33. G. Xing, H. Guo, X. Zhang, T. C. Sum and C. Hon Alfred Huan, The Physics of ultrafast saturable absorption in graphene, Opt. Express, 2010, 18, 4564–4573.
34. Y.-R. Wang, P. Lee, B.-T. Zhang, Y.-H. Sang, J.-L. He, H. Liu and C.-K. Lee, Optical nonlinearity engineering of a bismuth telluride saturable absorber and application of a pulsed solid state laser therein, Nanoscale, 2017, 9, 19100–19107.
35. S. Chen, C. Zha, Y. Li, H. Huang, S. Lu, H. Zhang and S. Wen, Broadband optical and microwave nonlinear response in topological insulator, Opt. Mater. Express, 2014, 4, 587–596.
36. K. Wang, J. Wang, J. Fan, M. Lotya, A. O’Neill, D. Fox, Y. Feng, X. Zhang, B. Jiang, Q. Zhao, H. Zhang, J. N. Coleman, L. Zhang and W. Josef Blau, Ultrafast saturable absorption of two-dimensional MoS₂ nanosheets‘, ACS Nano, 2013, 10, 9260–9267.
37. J. Moore, The birth of topological insulators, Nature, 2010, 464, 194–198.

---