Atomic structures and energetics of heterophase interfaces among Fe(100), TiC(110) and Mo₂C(001) surfaces: insights from first-principles calculations

Abstract

Atomic structures and interfacial energies of Fe(100)/TiC(110), Fe(100)/Mo₂C(001) and TiC(110)/Mo₂C(001) interfaces were studied by using first-principles calculations. Convergence testing of surface energy demonstrates that Fe(100) and TiC(110) slabs with more than five atomic layers, and Mo- and C-terminated Mo₂C(001) slabs with six and seven atomic layers, exhibit bulk-like properties inside the interface models. Slab supercells of five different heterophase interfaces composed of any two surfaces among Fe(100), TiC(110) and Mo₂C(001) with Mo- and C-terminations were constructed with low lattice mismatches below 6%, and their atomistic relaxations were carried out. Our calculations for interfacial work of adhesion, interface binding energy and interfacial energy demonstrate that the Fe/Mo₂C interface has stronger interfacial binding and higher thermodynamic stability than the Fe/TiC interface, while the TiC/Mo₂C interface exhibits stronger interfacial binding but lower stability than the Fe/TiC interface. The reason is that the interfacial Fe–C chemical bonds are weaker than the Mo–C and Ti–C bonds as revealed by analysis of electronic charge density difference. The present work can provide guidelines to improve the performance of Fe-based composites.

---

1 Introduction

During the past decades, ceramics-reinforced metal matrix composites (MMCs) have attracted significant research and technological interest in modern industries.^1–3 In general, MMCs are composed of a ductile metal matrix and high-strength ceramic particles to combine the advantages of metal and ceramics, thereby exhibiting better performance than ordinary alloys.^4,5 Typically, iron matrix composites reinforced with TiC ceramic particles have shown higher hardness and remarkably improved wear resistance when compared to the traditional wear-resistant iron alloys.^6–8 This is due to the unique properties of TiC ceramic particles, such as high hardness, high melting temperature, good thermal stability and low density.^9–13 Through extensive experimental studies, it has become clear that the content, morphology and size of TiC particles have a great influence on the performance of TiC/Fe composites.^14–21

In the preparation of TiC/Fe composites, the iron melt provides a liquid environment, which is favourable for the formation of TiC particles.²² Jin et al.²³ found that the variance of melting point between different metal matrices may result in different heat release of ceramic synthesis and thus affect the size and morphology of ceramic particles corresponding to the exposure of different crystalline planes. Furthermore, the lattice mismatch and interface energy between the TiC particle and Fe matrix decisively exert influence on the mechanical and physical properties of TiC/Fe composites.⁸ To obtain better mechanical properties of MMCs, the higher interfacial binding between the ceramics and metal matrix is more desirable. However, the interfacial energy between TiC particle and Fe matrix was found to be relatively high, leading to the low interfacial bonding and thus the poor wettability between the metallic binder phase and the TiC hard phase.²⁴ To address the issue of poor wettability, Mo₂C has been used generally as a sintering aid.^25–27 Moreover, the addition of Mo₂C to TiC-based MMCs has been found to be beneficial to the higher fracture toughness, finer microstructure and better mechanical properties.²⁸ From these experimental findings, one can expect higher interfacial bonding between the Mo₂C phase and Fe binder phase and the formation of a Mo₂C middle layer between the TiC and Fe phases. However, the interfacial bonding characteristics and energetics between these three phases, which are difficult to determine in experiments, have not yet been reported in the literature.

Although there are some theoretical studies based on density functional theory (DFT) calculations for the Fe/TiC interface,^29–32 TiC surface^9,33–35 and Mo₂C bulk,^36,37 a systematic study of Fe/TiC, Fe/Mo₂C and TiC/Mo₂C interfaces has not yet been provided. Thus, the mechanism of wettability enhancement in the Fe/TiC composite by the addition of a Mo₂C phase remains unrevealed. In this work, we report a theoretical study on the interfaces among the TiC, Mo₂C and Fe matrixes using first-principles calculations within the DFT framework. After selecting the appropriate surface indexes to minimize the lattice mismatch, we construct the slab supercell models for the selected interfaces and perform the atomistic relaxations. For the relaxed interfaces, the atomic structures and energetics are analyzed to obtain insight into interfacial properties.

2 Computational methods

All the DFT calculations in this work were performed by applying the pseudopotential plane wave method, as implemented in the Quantum ESPRESSO (QE) package (version 7.2).^38,39 The Coulomb interactions between the ionic cores and the valence electrons were described by the ultrasoft pseudopotentials,⁴⁰ as provided in the GBRV library of the package,⁴¹ where the valence electron configurations were Fe-3s²3p⁶3d⁶4s², Ti-3s²3p⁶3d²4s², Mo-4s²4p⁶4d⁵5s¹ and C-2s²2p². The Perdew–Burke–Ernzerhof (PBE) functional⁴² within the generalized gradient approximation (GGA) was used to treat the exchange–correlation interaction between the valence electrons. The kinetic cut-off energies were set as 50 Ry for wave functions and 400 Ry for electron density. The Brillouin zone integration was performed by using the k-point samplings of 8 × 8 × 8 and 2 × 3 × 1 for the bulk unit cell and surface or interface supercell, respectively.

Surfaces and interfaces were simulated using the slab supercell models with 3-dimensional (3D) periodic boundary conditions. As the slab model consists of atomic and vacuum layers, the suitable numbers of atomic layers were determined for TiC, Mo₂C and Fe surface slabs by performing the convergence test, and the thickness of the vacuum layer was set as 15 Å to inhibit the artificial interaction between the top and bottom atoms of neighbouring cells. For the bulk optimization and surface or interface relaxations, the atoms were relaxed until the maximum force was 5 × 10⁻⁴ Ry bohr⁻¹. To calculate the elastic constants of the bulk, the stress–strain method was used, as implemented in the ElaStic code⁴³ in connection with QE.

3 Results and discussion

3.1 Bulk properties

As a preliminary step towards interface calculations, the lattice constants, elastic properties and cohesive energies for the bulk Fe, TiC and Mo₂C unit cells were determined to have confidence in the reliability of the calculation. In this work, it was supposed that iron crystallized in the body-centered cubic (bcc) phase (α-Fe, space group Im3m), titanium carbide in the cubic phase (space group Fm3̄m), and molybdenum hemicarbide in the orthorhombic phase (α-Mo₂C, space group Pbcn) among various polymorphs.⁴⁴Fig. 1 shows the structures of the unit cells for the three substances. For the structural optimization of the bcc-Fe unit cell, spin-polarization was considered with a ferromagnetic (FM) configuration to obtain a more reliable lattice constant. The cohesive energy was calculated as E_c = (E_bulk − Σ_iE^atom_i)/N_a, where E_bulk is the total energy of the bulk unit cell, E^atom_i is the energy of the isolated i-th atom, and N_a is the number of atoms in the unit cell.

Fig. 1 Ball-and-stick view of unit cells for (a) iron in the bcc phase (α-Fe), (b) titanium carbide (TiC) in the cubic phase, and (c) molybdenum hemicarbide in the orthorhombic phase (α-Mo₂C).

Table 1 lists the calculated values of lattice constants, bulk moduli, Poisson's ratios, mass densities and cohesive energies in comparison with the available experimental data. Details of elastic properties, calculated with the strain–stress method,⁴³ are given in Table S1 in the ESI.† As shown in the table, the calculated lattice constants well agree with the experimental values^45,46 within the small relative errors (REs) below 1%. For the case of Mo₂C, the atomic fractional coordinates, Mo (0.246, 0.121, and 0.080) and C (0, 0.375, and 0.25), were also in good agreement with the previous calculation.³⁷

Table 1 Lattice constant, bulk modulus (B), Poisson's ratio (ν), density (ρ) and cohesive energy (E_c) for Fe, TiC and Mo₂C crystals in comparison with the available experimental data. In the case of the lattice constant, the value in parenthesis is the relative error compared to the experimental ones

Phase		Lattice constant (Å)	B (GPa)	ν	ρ (g cm^−3)	E c (eV per atom)
a Ref. 45. b Ref. 47. c Ref. 48–50. d Ref. 46. e Ref. 44.
Fe	This	2.841 (−0.65)	165	0.28	8.085	−4.49
	Exp.	2.866^a	168^b	0.29^b	7.87^a	−4.28^b
TiC	This	4.334 (0.17)	247	0.21	4.888	−7.53
	Exp.	4.327^a	242^c	0.20^c	4.94^a	−7.04^c
Mo2C	This	4.772 (0.67), 6.050 (0.33), 5.215 (0.09)	295	0.28	8.995	−8.70
	Exp.	4.74, 6.03, 5.21^d	289^e	0.28^e	9.18^a

---

To confirm the good agreement between the calculated elastic moduli and the experimental data,^47–50 it is worth comparing them. Among the three crystals, the ferrite has the smallest bulk modulus of 165 GPa, indicating that it is a soft material used as a ductile metallic matrix. Meanwhile, the orthorhombic Mo₂C crystal has a larger bulk modulus (295 GPa) than the cubic TiC crystal (247 GPa), implying that the former is harder than the latter, although the shear and Young's moduli of Mo₂C (156 and 398 GPa) are slightly smaller than those of TiC (179 and 431 GPa, see Table S1, ESI†). Therefore, the addition of Mo₂C to Fe/TiC composite may not degrade the mechanical properties of the composite but rather enhance the mechanical strength. Moreover, the Poisson's ratio of Mo₂C was found to be 0.28 like bcc-Fe, which is larger than the threshold value of 0.26 for ductility according to the Frantsevich rule,^51–53 thereby indicating that the Fe/Mo₂C composite should be ductile. However, the cubic TiC ceramic is brittle, since its Poisson's ratio of 0.21 is smaller than the threshold value. On the other hand, the density of TiC (4.888 g cm⁻³) is much smaller than those of bcc-Fe (8.085 g cm⁻³) and Mo₂C (8.995 g cm⁻³), indicating that the Fe/TiC composite is lighter than the Fe/Mo₂C composite. For all three crystals, the cohesive energies were found to be negative, giving an implication of cohesive attraction in these bulk materials.

3.2 Surface energetics

In this work, the interfacial properties of three kinds of binary composites among Fe, TiC and Mo₂C were considered, and therefore the indexes of Fe, TiC and Mo₂C surfaces should be selected to minimize the lattice mismatch. According to Bramfitt's theory,⁵⁴ the lattice distortion energy affects the solidification interface. In fact, the interface with small lattice mismatch shows the great possibility of formation with acceptable stability. Therefore, it is reasonable to select the representative Fe/TiC, Fe/Mo₂C and TiC/Mo₂C interfaces with a small lattice mismatch among the low index surfaces. With the calculated lattice constants of the bulk unit cells, the Fe(100) (3 × 2), TiC(110) (2 × 1) and Mo₂C (2 × 1) surface supercells have dimensions of (8.524, 5.683) Å, (8.668, 6.130) Å and (9.544, 6.050) Å, respectively. Then, the lattice mismatches, defined as δ_a = |a₁ − a₂|/(a₁ + a₂) × 100%, were determined to be (δ_a, δ_b) = (0.84, 3.78)%, (5.64, 3.13)% and (4.81, 0.65)% for the Fe/TiC, Fe/Mo₂C and TiC/Mo₂C interfaces, respectively. These values of lattice mismatch are below 6%, and thus can be acceptable for the formation of an interface. When choosing the Fe(110) surface, the lattice mismatches can also be lower than 6%, but the numbers of atoms included in the interface models are much larger than those with the Fe(100) surface.

Before constructing the interface models, the surface models should be constructed for each surface. Since the surface can be created by cutting the crystal along the plane with certain index, different terminations might be possible. In the Fe(100) and TiC(110) surfaces, there is only one termination, but in the Mo₂C(001) surface, there are two different terminations, i.e., Mo- and C-terminations, as shown in Fig. 2. Here, we adopted the 3D periodic slab models with two equivalent top and bottom surfaces, which consist of a certain number of atomic layers and a vacuum layer. The thickness of the vacuum layer was set to be 15 Å, which was proved to be long enough to prevent artificial interaction, as adopted in numerous DFT studies of surfaces.

Fig. 2 Optimized structures of slab supercells for (a) Fe(100) (3 × 2), (b) TiC(110) (2 × 1), and (c) and (d) Mo₂C(001) (2 × 1) Mo- and C-terminated surfaces.

Then, the minimum number of atomic layers should be determined to ensure that the slabs comprising the interface are sufficiently thick to represent the bulk-like features. This task can be achieved by checking the convergence of surface energy while gradually increasing the number of atomic layers. For the stoichiometric Fe(100) and TiC(110) surfaces, the surface energy can be readily calculated as follows,

where E^slab_surf is the total energy of the slab supercell of the surface, E^uc_bulk is the total energy of the bulk unit cell (uc) per formula unit (fu), N_fu is the number of formula units contained in the slab supercell, and A_s is the surface area, respectively.

For the non-stoichiometric Mo₂C(001) surface slabs, the surface energy can be rewritten using the chemical potentials of the constituent species (μ_Mo and μ_C) as follows,

where N_Mo and N_C are the numbers of Mo and C atoms in the surface slab, respectively. Assuming that the surface is in equilibrium with the bulk, the chemical potentials satisfy the following relationship,where the chemical potential of the Mo₂C bulk can be approximated as the total energy of the unit cell of bulk Mo₂C, i.e., . The formation enthalpy of bulk Mo₂C at 0 K is determined as follows,where μ^bulk_Mo ≈ E^bcc_Mo and μ^bulk_C ≈ E^gr_C are the total energies of the unit cells per atom for Mo metal in the bcc phase and graphite. If the chemical potential differences are defined as follows,

Δμ_Mo = μ_Mo − μ^bulk_Mo, Δμ_C = μ_C − μ^bulk_C, (5)

the formation enthalpy, eqn (4), can be rewritten as follows,By using eqn (3) and (5), the surface energy, eqn (2), can be formulated with Δμ_C as follows,Since the Mo₂C bulk cannot be decomposed into simple substances, the chemical potential μ_Mo (or μ_C) must be lower than μ^bulk_Mo (or μ^bulk_C). Together with eqn (6), therefore, the ranges of chemical potential differences are expressed as follows,In a similar way, the surface energy of the non-stoichiometric (i.e., defective) TiC(110) surface can be expressed as follows,with the chemical potential ranges provided as follows,

ΔH^f_TiC ≤ Δμ_Ti ≤ 0, ΔH^f_TiC ≤ Δμ_C ≤ 0 (10)

Table 2 shows the convergence of surface energy with respect to the atomic layers for the Fe(100), TiC(110), and Mo₂C(001) Mo-terminated surfaces, which are all the stoichiometric surfaces. For the Fe(100) and TiC(110) surfaces, the 5 atomic layers were found to give reliable surface energies of 2.36 and 3.46 J m⁻², which are in good agreement with the previous calculations of 2.27–2.34⁵⁵ and 3.53–3.58 J m⁻²,^56,57 respectively. For the Mo₂C(001) surface with Mo termination, the converged surface energy was found to be 3.04 J m⁻² at the 6 atomic layers in reasonable agreement with the previous value of 3.16–3.32 J m⁻².⁵⁸ Therefore, the minimum numbers of atomic layers were set to be 5, 5 and 6 for the Fe(100), TiC(110) and Mo₂C(001)–Mo terminated surfaces to construct the interface models.

Table 2 Surface energy (γ) of stoichiometric Fe(100), TiC(110), and Mo₂C(001) Mo-terminated surfaces with an increase in the atomic layers n

Layers n	γ (J m^−2)
	Fe(100)	TiC(110)	Mo2C(001)–Mo
a Ref. 55. b Ref. 56. c Ref. 58.
3	2.40	3.57	3.05
5	2.36	3.46	—
6	—	—	3.04
7	2.37	3.45	—
9	2.37	3.46	3.06
11	2.39	3.47	—
12	—	—	3.07
13	2.35	3.47	—
Prev Cal. (GGA)	2.27–2.34^a	3.53–3.58^b	3.16–3.32^c

---

It is known that the intrinsic point defects, especially vacancies, can be readily created on the solid surface. Accordingly, we considered defective TiC(110) surfaces with a surface Ti (V_Ti) or C vacancy (V_C) and defective Mo₂C(001) surfaces with a surface Mo (V_Mo) or C vacancy. The surface energy of the Mo₂C(001) C-terminated surface was calculated as a function of the carbon chemical potential difference Δμ_C. The structural optimizations of bulk Mo in the bcc phase, Ti in the hcp phase and graphite were performed, producing the lattice constants of a = 3.163 Å (RE = −0.09%) for bcc-Mo, a = 2.945 Å (RE = −0.20%) and c = 4.712 Å (RE = 0.71%) for hcp-Ti, and a = 2.466 (RE = 0.20%) and c = 6.624 Å (RE = −1.21%) for graphite in good agreement with the experimental data. We note that van der Waals (vdW) correction was considered for the graphite using the vdW-DF-ob86 functional.⁵⁹ Using eqn (4), the formation enthalpy of bulk Mo₂C was calculated to be −0.48 eV, and thus −0.48 eV ≤ Δμ_C ≤ 0. For bulk TiC, the formation enthalpy was obtained to be −1.63 eV, which is in good agreement with the previous computational data of −1.76 eV⁵⁷ and −1.78 eV.⁶⁰

Fig. 3 shows the calculated surface energies of the Mo- and C-terminated Mo₂C(001) surface without and with V_Mo or V_C and the TiC(110) surface without and with V_Ti or V_C as a function of Δμ_C (see Fig. S1 for the optimized structures, ESI†). Although the lower limit of Δμ_C for the TiC surface (−1.80 eV) is lower than that for the Mo₂C surface (−0.48 eV), the lower limit of Δμ_C for both the surfaces is set to be −0.48 eV since they form the interface. It is natural to see that the relative stability of the surfaces varies with the chemical potential change of carbon. In general, the surfaces with C vacancies show increasing surface energy while the surfaces with metal vacancy show decreasing surface energy as the carbon chemical potential is increased from −0.48 eV (C-poor condition) to 0 (C-rich condition). From Fig. 3(a) for the TiC(110) surfaces, it can be seen that the surface with C (Ti) vacancy is more (less) stable than the perfect surface within the whole range of carbon chemical potential in agreement with the previous calculation.⁵⁷ For the Mo₂C(001) surfaces, the perfect Mo-terminated surface was found to be the most stable while the C-terminated surface with Mo vacancies was the least stable within the whole range of Δμ_C, as shown in Fig. 3(b). Under the C-poor condition (−0.48 eV ≤ Δμ_C ≤ −0.42 eV), the surfaces with C vacancies were found to be more stable than those with Mo vacancies. Meanwhile, the Mo-terminated surface with Mo vacancies became the second most stable under the C-rich condition (−0.13 eV ≤ Δμ_C ≤ 0). This variation in the relative stability of surfaces with carbon chemical potential will have an effect on the interface energies.

Fig. 3 Surface energy (γ) as functions of carbon chemical potential difference (Δμ_C) for (a) TiC(110) surfaces and (b) Mo₂C(001) Mo- and C-terminated surfaces, without and with a surface vacancy.

To sum up so far, it is concluded that the calculated data of the bulk and surface properties for Fe, TiC and Mo₂C agreed well with the available data of previous experiments and calculations. Therefore, our calculation settings were validated as feasible for investigating the interfacial properties.

3.3 Interface properties

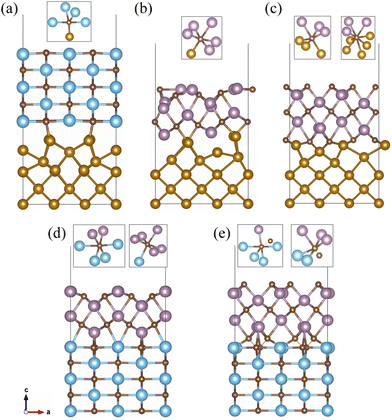
The interface slab models were constructed using the Fe(100) (3 × 2), TiC(110) (2 × 1) and Mo₂C(001) Mo- and C-terminated (2 × 1) surface supercells. The 5-layer TiC(110), 6-layer Mo-terminated and 7-layer C-terminated Mo₂C(001) surfaces were placed on the 5-layer Fe(100) surface to construct the supercells for the Fe(100)/TiC(110), Fe(100)/Mo₂C(001)–Mo and Fe(100)/Mo₂C(001)–C interfaces. Also, the 6-layer Mo-terminated and 7-layer C-terminated Mo₂C(001) surfaces were located on the 5-layer TiC(110) surface to build the supercells for the TiC(110)/Mo₂C(001)–Mo and TiC(110)/Mo₂C(001)–C interfaces. It should be noted that in the previous DFT studies the Fe(100)/TiC(100) interface models were also composed of 5 Fe layers and 5 TiC layers.^30,31 Like the surface slab, a vacuum layer with a thickness of 15 Å was added to the top of the interface to eliminate the interaction between the interface film layers. The relatively small lattice mismatches between the constituent surfaces (below 5.64%) indicate that the constructed interfaces are a typical coherent interface. The atomistic relaxations were performed on these interface supercells, where the atoms in the middle layer of each surface side were fixed at the bulk positions. Fig. 4 shows the optimized structures of the slab supercells for the 5 interface models constructed with the perfect surfaces (see Fig. S2 for the interfaces with defective surfaces, ESI†).

Fig. 4 Optimized structures of the slab supercells for interfaces of (a) Fe(100)/TiC(110), (b) and (c) Fe(100)/Mo₂C(001) Mo- and C-terminations, and (d) and (e) TiC(110)/Mo₂C(001) Mo- and C-terminations. The insets show all-metal or metal–carbon hybrid polyhedra centered at the C atom around the interface region.

At a glance, one can find the significant atomic relaxations around the interface region for all the interfaces. Such atomic relaxations resulted in the formation of new interfacial chemical bonds between the transition metal atoms (Fe, Ti, and Mo) and carbon atoms, and repulsion between the metal atoms at the opposite sides of the interface. For the case of the Fe(100)/TiC(110) interface shown in Fig. 4(a), the interfacial Fe–C chemical bond with a bond length of 1.76 Å was found to be newly formed, resulting in the increase in coordination number (CN) of the interface C atom from 4 to 5 ({Ti₄FeC}), which is however still lower than that of the bulk C atom (6, {Ti₆C}). Meanwhile, the distances (2.62 Å) between the top and next layer Fe atoms were enlarged compared to the Fe–Fe distance (2.45 Å) in the bulk.

At the Fe(100)/Mo₂C(001) interfaces, the interfacial Fe–C chemical bonds with bond lengths of 1.91–1.94 Å were also observed, as shown in Fig. 4(b) and (c). With these interfacial chemical bonds, the metal octahedra around the C atom with the 6 CN were formed, but the compositions of the octahedra were different according to the termination, such as {Mo₅FeC} and {Mo₃Fe₃C} for the Mo- and C-terminations, respectively. That is, for the C-terminated Mo₂C surface, more Fe atoms were bound chemically to the C atom than for the Mo-terminated surface. Moreover, the shortest Fe–C bond length (1.91 Å) in the Fe(100)/Mo₂C(001)–C interface was slightly shorter than that in the Fe(100)/Mo₂C(001)–Mo interface (1.94 Å), although the longer Fe–C bond (2.03 Å) exists in the former case. In addition, one can find another interface C atom with larger CN of 8, {Mo₃Fe₅C}, at the Fe(100)/Mo₂C(001)–C interface. From these findings, it can be concluded that the interface binding in the C-terminated Mo₂C(001) interface is stronger than in the Mo-terminated interface.

For the TiC(110)/Mo₂C(001) interfaces, the top Ti atoms reacted with the C atoms of the Mo₂C side to form interfacial Ti–C chemical bonds, while the bottom Mo atoms made the Mo–C chemical bonds with the C atoms of the TiC side. As shown in Fig. 4(d) for the case of the Mo-terminated interface, the C atoms at both sides of the interface were found to fully recover the bulk environments with 6 CN, like {Ti₄Mo₂C} for the C atom in the TiC side and {Mo₅TiC} for the C atom in the Mo₂C side, implying strong interface binding. In this case, the Ti–C and Mo–C bond lengths were found to be 2.11 and 2.37 Å, respectively. In the case of the C-terminated interface shown in Fig. 4(e), the C atoms at the opposite sides of the interface reacted with each other to form a C_Ti–C_Mo bond (1.49 Å) in addition to the interfacial Ti–C (2.11 Å) and Mo–C (2.11 Å) bonds, resulting in the formation of metal–carbon hybrid octahedra such as {Ti₄MoCC} in the TiC side and {Ti₂Mo₃CC} in the Mo₂C side. These metal–carbon hybrid octahedra might be thought of as being weaker than the all-metal octahedra, thereby indicating that the C-terminated interface has relatively weaker interfacial binding than the Mo-terminated ones.

In order to quantitatively evaluate the binding strength between the interfacial layers, we calculated the ideal work of adhesion, W_ad, using the following equation,

where E^fix_surf and E^fix_int are the total energies of the slab supercells for the isolated surface and the interface with fixed atomic positions, d is the interfacial distance (or separation), and A_i is the interface area. For the interfaces, the interface separation d was gradually changed while fixing the atomic positions at those in the fully relaxed interface slab. For the isolated surfaces, we used the same supercell at the interface, where one side was occupied by the surface layer and the other side was replaced by a vacuum layer. Here, the atomic positions were fixed as being in the interface slab, and thus the isolated surface slabs were still in strained states as in the interface slab.

The work of adhesion W_ad(d) can be described by the universal binding energy relation (UBER) curve proposed by Rose et al.,^61–63

where W⁰_ad is the depth of the adhesion work well at the equilibrium interfacial distance d₀, and λ is the Thomas-Fermi screening length, which is specific to materials. The equilibrium values of W⁰_ad, d₀ and λ were determined by fitting the (W_ad, d) data obtained without relaxation into the UBER, eqn (12). The larger value of W⁰_ad indicates stronger interaction between the interface atoms and thus stronger interface binding strength between the interfacial layers. Fig. 5 shows the calculated work of adhesion as a function of interfacial distance in all the interface systems, together with the fitting curves (see Table S2 for the fitting results, ESI†). Table 3 lists the determined interfacial distance d₀ and the work of adhesion W⁰_ad for the interface systems.

Fig. 5 Work of adhesion as a function of interfacial distance in the interface systems. The filled circles indicated the calculated values and the solid lines represent the fitting curves into the UBER equation. Insets show the magnified view around the minimum of the UBER fitting curves.

Table 3 Interfacial distance d₀, work of adhesion determined from UBER fitting W⁰_ad and from the fully relaxed structures W^r_ad

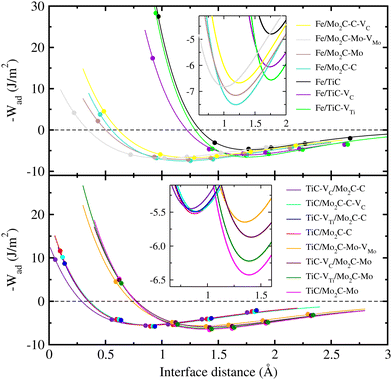
Interface	d 0 (Å)	Work of adhesion (J m^−2)
		W ^0ad	W ^rad
Fe/TiC	1.761	4.779	5.099
Fe/TiC–VC	1.759	6.056	4.723
Fe/TiC–VTi	1.739	6.560	5.043
Fe/Mo2C–C	1.190	7.506	5.995
Fe/Mo2C–C–VC	1.290	6.672	4.412
Fe/Mo2C–Mo	1.192	7.150	5.728
Fe/Mo2C–Mo–VMo	1.065	6.819	4.656
TiC/Mo2C–C	0.879	5.522	4.435
TiC/Mo2C–C–VC	0.901	5.491	4.509
TiC–VC/Mo2C–C	0.843	5.450	4.232
TiC–VTi/Mo2C–C	0.883	5.495	4.400
TiC/Mo2C–Mo	1.389	6.428	5.960
TiC/Mo2C–Mo–VMo	1.350	5.647	5.092
TiC–VC/Mo2C–Mo	1.409	5.870	5.334
TiC–VTi/Mo2C–Mo	1.390	6.223	5.719

---

The cohesive properties for the relaxed surface were not accurately captured by this UBER-based approach. Therefore, we used the relaxation approach as well, in which the relaxed (or real) work of adhesion W^r_ad is determined as follows:

where E^relax_surf and E^relax_int are the total energies of the surface and interface slabs with fully relaxed atomic positions, respectively. Therefore, the work of adhesion is the reversible work required to split an interface into two isolated free surfaces.³¹

As shown in Fig. 5 and Table 3, the Fe(100)/TiC(110) interface was found to have the lowest value of W⁰_ad (4.78 J m⁻²) and the largest value of d₀ (1.761 Å) among the studied interface models, indicating the weakest interface binding strength. When creating a vacancy such as V_C and V_Ti on the TiC side, we observed the enhancement of the interface binding strength, which was slightly more highlighted by V_Ti formation than V_C. One can find the larger values of W⁰_ad and smaller values of d₀ in the Fe(100)/Mo₂C(001) interfaces than those in the Fe(100)/TiC(110) interfaces, indicating that iron can make composites more favourably with Mo₂C than with TiC. For the case of the Fe/Mo₂C interface, the C-terminated Mo₂C(001) surface showed a slightly larger value of W⁰_ad (7.51 J m⁻²) and smaller value of d₀ (1.190 Å) than the Mo-terminated surface (7.15 J m⁻² and 1.192 Å), revealing that the interface binding in the former case is stronger than in the latter case, as mentioned above. In contrast to the Fe/TiC interface, the vacancy formation on the Mo₂C side (V_C or V_Mo) was found to decrease the work of interface adhesion (6.67 and 6.82 J m⁻²). Meanwhile, the TiC(110)/Mo₂C(001) interfaces had higher and lower values of 5.52 and 6.43 J m⁻² for the C- and Mo-terminated Mo₂C(001) surfaces compared with the Fe/TiC and Fe/Mo₂C interfaces, respectively. For the case of the TiC/Mo₂C interface, the Mo-terminated surface exhibited large values of W⁰_ad compared with the C-terminated counterparts, although their interfacial distances were found to be larger than those in the latter cases. In accordance with the Fe/Mo₂C interfaces, when creating the vacancy defect on either the TiC or Mo₂C side, the W⁰_ad values were found to be decreased compared with the perfect surface cases. In all the cases, the interfaces with a metal vacancy (V_Ti or V_Mo) showed slightly larger values of W⁰_ad than those with a carbon vacancy. Through the work, the relaxed work of adhesion W^r_ad was found to be slightly reduced, but similar findings to those from W⁰_ad were obtained.

From the above analysis, it can be concluded that the interfacial binding strengths between the Fe matrix and TiC ceramics are weaker than those between the Fe matrix and Mo₂C hard phase, and the interfaces between TiC and Mo₂C phases have moderated interface binding strengths. This is in good agreement with the experimental result showing that the Fe/TiC composite has poor wettability, which can be enhanced by adding an Mo₂C phase.²⁴ To increase the interface binding and improve the wettability, it is suggested that the Mo₂C layer can be inserted between the Fe matrix and TiC ceramic phases. The formation of interfacial vacancy defects can slightly reduce the interfacial binding strength.

In order to estimate the stability of the interface, we calculated the interface formation energy γ_int using the determined surface energies and the work of adhesion as follows,⁶⁴

γ_int = 2(γ_surf1 + γ_surf2) − W^r_ad, (14)

where γ_surf is the surface energy of the constituent surface and W^r_ad is the relaxed work of interface adhesion. For the cases of the non-stoichiometric C-terminated Mo₂C(001) surface and the defective surfaces, the surface energy depends on the chemical potential of C, and therefore the interface energy also depends on Δμ_C. The lower value of γ_int indicates more stability.

Fig. 6 shows the calculated interface energies of all the interface systems under study in this work (see Table S3 for values, ESI†). In accordance with the analysis of the interfacial binding strength, the Fe/TiC interface showed higher values of interface energy (6.54 J m⁻²) than the Fe/Mo₂C interfaces (4.84–5.37 and 5.08 J m⁻² for the C- and Mo-termination), indicating that the former interface is thermodynamically less stable than the latter interfaces. Due to the higher values of γ_int, the TiC/Mo₂C interfaces were found to be less stable than the Fe/TiC and Fe/Mo₂C interfaces. When considering the effect of interfacial vacancy formation, the effect was found to be positive (improving stability) or negative (decreasing stability) according to interfaces and carbon chemical potential. In the case of the Fe/TiC interface, V_C improved but V_Ti deteriorated the stability. For the Fe/Mo₂C interface, both the C-terminated interface with V_C and the Mo-terminated interface with V_Mo became less stable. In the case of the TiC/Mo₂C–C interface, the V_C (V_Ti) formation on the TiC side improved (decreased) the stability, while the V_C formation on the Mo₂C side improved it within the range of carbon chemical potential −0.48 eV ≤ Δμ_C ≤ −0.06 eV but decreased it within the range of −0.06 eV ≤ Δμ_C ≤ 0 eV. For the TiC/Mo₂C–Mo interface, the metal vacancy (V_Mo or V_Ti) decreased the stability, while the V_C formation on the TiC side improved it in the range of −0.48 eV ≤ Δμ_C ≤ −0.06 eV but decreased it in the range of −0.06 eV ≤ Δμ_C ≤ 0 eV. In conclusion, the Fe/Mo₂C interface without interfacial vacancy defect is the most stable while the TiC/Mo₂C–C interface with a Ti vacancy is the most unstable within the whole range of carbon chemical potential.

Fig. 6 Interface energy as a function of the chemical potential of carbon (Δμ_C) varying from −0.48 eV to 0 for the interface systems.

In order to analyze the interface atomic interaction, the electron density difference was calculated as follows:

Δρ(r) = ρ_int(r) − ρ^fix_surf1(r) − ρ^fix_surf2(r), (15)

where ρ_int and ρ^fix_surf are the electron densities of the interface and the constituent surface with fixed atomic positions, respectively. Fig. 7 presents the isosurface plot of the electron density difference around the interface region for the interfaces without interfacial vacancy (see Fig. S3 for those with vacancy, ESI†). In this work, a positive value of Δρ (red colour) means electron gain, while a negative value (blue colour) means electron loss. It becomes clear that upon the formation of an interface the electron transfer occurs mainly in the vicinity of the interface. One can find a strong charge accumulation (electron gain) around the C atoms and a strong charge depletion around the transition metal Fe, Ti and Mo atoms for all the studied interfaces. This indicates that a number of electrons are transferred from the interface metal atoms to the interface carbon atoms, thereby forming new interfacial M–C (M = Fe, Ti, Mo) chemical bonds. These chemical bonds are obviously polar covalent bonds. Interestingly, the charge accumulation was also observed in the middle space between the interface metal atoms, indicating some chemical bonds between interface metallic atoms. When the interfacial vacancy formation occurs, the degree of electron density difference looks like reducing due to the absence of interfacial atoms, which might be associated with the slight decrease in interfacial binding strength for the defective interfaces as discussed above.

Fig. 7 Isosurface view of electron density difference (Δρ) around the interface region in (a) Fe(100)/TiC(110), (b) Fe(100)/Mo₂C(001)–Mo, (c) Fe(100)/Mo₂C(001)–C, (d) TiC(110)/Mo₂C(001)–Mo, and (e) TiC(110)/Mo₂C(001)–C interfaces. Isosurface is plotted on the (010) plane in the depth of 0.5b of the supercell for (a)–(c) and (e), while on the (100) plane in the depths of 0.75a and 0.5a for (d). Here, a and b are the lattice constants of the supercell. A positive (negative) value means electron gain (loss).

To further analyze the interfacial binding characteristics, the atom-projected partial density of states (PDOS) were calculated (see Fig. S4–S8, ESI†). It was found that all the interfaces exhibit metallic properties due to their non-zero values of PDOS at the Fermi level. It should be noted that for the Fe/TiC and Fe/Mo₂C interfaces PDOS shows the asymmetrical characteristics between the spin-up and spin-down orbitals, implying the existence of magnetism that comes mainly from the Fe atoms. Meanwhile, a symmetrical PDOS was observed for the TiC/Mo₂C interfaces, which thus do not exhibit magnetism. In fact, the magnetic moment of Fe atoms was found to be about 0.8–1.4μ_B while those of Mo, Ti and C atoms were negligibly small, being below 0.01μ_B in the present calculations. As mentioned above for the interface energy analysis, the higher stabilities of Fe-based interfaces compared with the TiC/Mo₂C interfaces might be ascribed to such magnetism. The orbital hybridization between transition metal d states and C 2p states was observed around the Fermi level. Fig. 8 presents the electron density calculated by squaring the wave functions with the energy levels from the Fermi level to ±1 eV for all the interfaces. One can observe that the Fe 3d, Ti 3d and Mo 4d states dominate the electronic states around the Fermi level while C atoms have negligible influence.

Fig. 8 Isosurface view of electron density calculated using the wave functions with energy levels from the Fermi level to +1 eV (top panel) and to −1 eV (bottom panel) in (a) Fe(100)/TiC(110), (b) Fe(100)/Mo₂C(001)–Mo, (c) Fe(100)/Mo₂C(001)–C, (d) TiC(110)/Mo₂C(001)–Mo, and (e) TiC(110)/Mo₂C(001)–C interfaces.

Upon the formation of an interface, the interface metal atoms lost the valence electrons, and some of electrons accumulate in the middle space, leading to formation of interfacial Fe–Mo, Fe–Ti and Ti–Mo metallic bonds. However, the binding strength of these metallic bonds might be weaker than that of the covalent bonds, considering that the amount of charge accumulation in the former bonds is smaller than that in the latter bonds. Furthermore, the binding strength of Fe–Mo metallic bonds is stronger than that of Fe–Ti metallic bonds, leading to a weaker interaction in the case of the Fe/TiC interface.

4 Conclusions

In this work, we have systematically investigated the Fe/TiC, Fe/Mo₂C and TiC/Mo₂C interfaces using the first-principles calculations, aiming to obtain an atomistic insight into the performance enhancement of Fe-based metal matrix composites. Through the calculation of bulk properties and convergence test of surface energies, which were in good agreement with the available experimental and previous calculation data, our computational settings were validated to be feasible for investigating the interfaces. Using the Fe(100) (3 × 2), TiC(110) (2 × 1) and Mo₂C(001) Mo- and C-terminated (2 × 1) surface supercells without and with vacancy defects, the slab supercells for Fe(100)/TiC(110), Fe(100)/Mo₂C(001)–Mo and –C, TiC(110)/Mo₂C(001)–Mo and –C interfaces without and with interfacial vacancy defects were constructed with low lattice mismatches below 6% and their atomic relaxations were performed with the analysis of detailed atomistic structures around the interfaces. Our calculations for interface energetics revealed that the Fe/Mo₂C interface showed stronger interface binding and higher thermodynamic stability than the Fe/TiC interface, while the TiC/Mo₂C interface exhibited stronger interface binding but lower stability than the Fe/TiC interface. The reason for such interface binding and stability characteristics was described by the interactions between the interface metal atoms and carbon atoms to form highly polar covalent M–C (M = Fe, Ti, Mo) chemical bonds. The formation of interfacial vacancies was found to reduce the interfacial binding for the Fe/Mo₂C and TiC/Mo₂C interfaces, while the effect of vacancy formation on the stability was different according to the interface and carbon chemical potential. With these findings, we believe that this work provides a useful atomistic understanding of interfacial properties and guidelines on performance improvement of Fe-based MMCs.

Author contributions

Chol-Jun Yu and Chol-Song Pang developed the original project. Chol-Jun Yu and Kyong-A Rim performed the calculations and drafted the first manuscript. Chol Ryu, Hyok-Bom Yun, and Jang-Il Rim assisted with the post-processing of calculation results, and contributed to useful discussions. Chol-Song Pang supervised the work. All authors reviewed the manuscript.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported as part of the basic research project “Design of New Energy Materials” (no. 2021-12) funded by the State Commission of Science and Technology, DPR Korea. Computations have been performed on the HP Blade System C7000 managed by the Faculty of Materials Science, Kim Il Sung University.

References

1. K. Das, T. K. Bandyopadhyay and S. Das, J. Mater. Sci., 2002, 37, 3881–3992.
2. Y. S. Suh, S. P. Joshi and K. T. Ramesh, Acta Mater., 2009, 57, 5848–5861.
3. G. Sozhamannan, S. B. Prabu and R. Paskaramoorthy, Mater. Des., 2010, 31, 3785–3790.
4. D. Y. Chen, Y. Liu, R. Q. Wang and J. W. Ye, Int. J. Miner., Metall. Mater., 2021, 28, 1215–1223.
5. S. Wei and L. Xu, Acta Metall. Sin., 2020, 56, 523–538.
6. Z. Wang, M. Zhou, M. Zhu, Y. Jiang and Y. Sui, Ceram. Int., 2023, 49, 18925–18936.
7. A. Perminov, G. Bartzsch, A. Asgarian, K. Chattopadhyay and O. Volkova, J. Alloys Compd., 2022, 166281.
8. I. W. M. Brown and W. R. Owers, Curr. Appl. Phys., 2004, 4, 171–174.
9. B. X. Dong, H. Y. Yang, F. Qiu, Q. Li, S. L. Shu, B. Q. Zhang and Q. C. Jiang, Mater. Des., 2019, 181, 107951.
10. B. AlMangour, D. Grzesiak and J. Yang, J. Alloys Compd., 2017, 706, 409–418.
11. A. Levy, A. Miriyev, A. Elliott, S. S. Babu and N. Frage, Mater. Des., 2017, 118, 198–203.
12. M. B. Rahaei, R. Y. Rad, A. Kazemzadeh and T. Ebadzadeh, Powder Technol., 2012, 217, 369–376.
13. F. Akhtar, J. Alloys Compd., 2008, 459, 491–497.
14. H. Zhang, H. Chen, Y. Lai, G. Xiao, W. Zhao, Y. Zhang and X. Cha, Ceram. Int., 2023, 49, 16089–16098.
15. Z.-B. Xu, S.-Q. Kou, H.-Y. Yang, B.-X. Dong, Y. Han, L.-Y. Chen, F. Qiu and Q.-C. Jiang, Ceram. Int., 2022, 48, 30418–30429.
16. X. Chen, L. Chen, H. Chen, B. Song, Y. Zhao, T. Yu and J. Zhao, Ceram. Int., 2022, 48, 12299–12310.
17. X. Wei, A. Perminov, M. O. Ilatovskaia, S. Dudczig, E. Storti and O. Volkova, Ceram. Int., 2022, 48, 34976–34986.
18. D. Deng, T. Li, Z. Huang, H. Jiang, S. Yang and Y. Zhang, Opt. Laser Technol., 2022, 153, 108259.
19. M. Zhu, Y. Jiang, Y. Sui and M. Zhou, Mater. Res. Express, 2022, 9, 036517.
20. A. Perminov, G. Bartzsch, A. Franke, H. Biermann and O. Volkova, Adv. Eng. Mater., 2020, 2000717.
21. A. Perminov, M. Jurisch, G. Bartzsch, H. Biermann, T. Weißgärber and O. Volkova, Mater. Sci. Eng., 2021, 813, 141130.
22. Y. Zheng, Y. Zhou, Y. D. Feng, X. Y. Teng, S. T. Yan, R. F. Li, W. B. Yu, Z. Y. Huang, S. B. Li and Z. W. Li, Ceram. Int., 2018, 44, 21742–21749.
23. S. B. Jin, P. Shen, D. S. Zhou and Q. C. Jiang, Nanoscale Res. Lett., 2011, 6, 515.
24. H. Qiu, X. Li, C. Pan and J. Fan, Materials, 2023, 16, 5645.
25. R. Chang, J. Zang, Y. Wang, Y. Yu, J. Lu and X. Xu, Mater. Chem. Phys., 2018, 204, 154–162.
26. L. Huang, X. Deng, Y. Jia, C. Li and Z. Wang, Wear, 2018, 410, 119–126.
27. X. H. Wang, M. Zhang and S. Y. Qu, Opt. Laser Eng., 2010, 48, 893–898.
28. Q. Xu, J. Zhao, X. Ai, W. Qin, D. Wang and W. Huang, J. Alloys Compd., 2015, 649, 885–890.
29. S. Liu, Y. K. Gao, Z. J. Wang, Z. J. Shi, Y. F. Zhou, X. J. Ren and Q. X. Yang, J. Alloys Compd., 2018, 731, 822–830.
30. S. Lu, J. Ågren and L. Vitos, Acta Mater., 2018, 156, 20–30.
31. J. Yang, P. Zhang, Y. Zhou, J. Guo, X. Ren, Y. Yang and Q. Yang, J. Alloys Compd., 2013, 556, 160–166.
32. Z. G. Zou, K. Liu, Y. F. Shen, Z. G. Xiao, F. Long and Y. Wu, Adv. Mater. Res., 2012, 415–417, 368–371.
33. W. Sun, H. Ehteshami, P. R. C. Kent and P. A. Korzhavy, Acta Mater., 2018, 165, 381–387.
34. V. V. Ilyasov, K. D. Pham, I. V. Ershov, C. V. Nguyen and N. N. Hieu, Comput. Mater. Sci., 2016, 124, 344–352.
35. Z. Dridi, B. Bouhafs, P. Ruterana and H. Aourag, J. Phys.: Condens. Matter, 2002, 43, 10237–10249.
36. H. Liang, R. He, L. Liu, W. Zhang and L. Fang, Ceram. Int., 2023, 49, 7341–7349.
37. Y. Liu, Y. Jiang, R. Zhou, X. Liu and J. Feng, Ceram. Int., 2015, 41, 5239–5246.
38. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
39. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901.
40. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
41. K. F. Garrity, J. W. Bennet, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
43. R. Golesorkhtabar, P. Pavone, J. Spitaler, P. Puschnig and C. Draxl, Comput. Phys. Commun., 2013, 184, 1861–1873.
44. M. Cankurtaran, S. P. Dodd and B. James, J. Mater. Sci., 2004, 39, 1241–1248.
45. CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 2005, https://www.hbcpnetbase.com.
46. T. Epicier, J. Dubois, C. Esnouf, G. Fantozzi and P. Convert, Acta Metall., 1988, 36, 1903–1921.
47. C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, New York, 1996.
48. L. E. Toth, Transition Metal Carbides and Nitrides, Academic Press, New York, 1971.
49. J. J. Gilman and B. W. Roberts, J. Appl. Phys., 1961, 32, 1405.
50. R. Chang and L. J. Graham, J. Appl. Phys., 1966, 37, 3778.
51. I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Naukova Dumka, Kiev, 1990, pp. 60–180.
52. J.-H. Jang, K.-C. Ri, S.-J. Kim, S.-H. Jon and C.-J. Yu, Appl. Phys. Lett., 2024, 124, 161601.
53. C.-J. Yu, J.-H. Jang, K.-C. Ri, S.-M. Kim, C.-H. Pak and R.-J. Kim, Phys. Rev. B, 2024, 109, 075426.
54. B. L. Bramfitt, Metall. Trans., 1970, 1, 1987–1995.
55. J. Radilla, G. E. Negrón-Silva, M. Palomar-Pardavéb, M. Romero-Romo and M. Galván, Electrochim. Acta, 2013, 112, 577–586.
56. L. Wang, L. Fang and J. Gong, Trans. Nonferrous Met. Soc. China, 2012, 22, 170–174.
57. J. Mao, S. Li, Y. Zhang, X. Chu and Z. Yang, Appl. Surf. Sci., 2016, 386, 201–209.
58. T. Wang, X. Tian, Y. Yang, Y.-W. Li, J. Wang, M. Beller and H. Jiao, Surf. Sci., 2016, 651, 195–202.
59. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
60. J. Li, Y. Yang, G. Feng, X. Luo, Q. Sun and N. Jin, Appl. Surf. Sci., 2013, 286, 240.
61. J. H. Rose, J. R. Smith and J. Ferrante, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1835–1845.
62. B. Wang, J. Dai, X. Wu, Y. Song and R. Yang, Intermetallics, 2015, 60, 58–65.
63. A. Hung, I. Yarovsky, J. Muscat, S. Russo, I. Snook and R. O. Watts, Surf. Sci., 2002, 501, 261–269.
64. M. Christensen, S. Dudiy and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 045408.

---

Footnote

† Electronic supplementary information (ESI) available: Tables for elastic constants, elastic moduli and Poisson's ratio for bulk Fe, TiC and Mo₂C, and figures for DOS in various interfaces. See DOI: https://doi.org/10.1039/d4ma00901k

---