 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computation-guided exploration of the reaction parameter space of N,N-dimethylformamide hydrolysis†
Ignas
Pakamorė
* and
Ross S.
Forgan

WestCHEM, School of Chemistry, University of Glasgow, Joseph Black Building, University Avenue, Glasgow G12 8QQ, UK. E-mail: ignas.pakamore.research@gmail.com
First published on 29th May 2025
Abstract
Navigating the reaction parameter space can pose challenges, especially considering the exponential growth in the number of parameters even in seemingly straightforward chemical reactions or formulations. Consequently, recent research efforts have been increasingly dedicated to the development of computational tools aimed at facilitating the exploration process. Herein, we introduce ChemSPX, a Python-based program specifically crafted for exploring the complex landscape of reaction parameter space. We propose the use of the inverse distance function to map reaction parameter space and efficiently sample sparse regions. This is implemented in ChemSPX to allow the user to simply generate sets of reaction conditions that efficiently sample wide parameter spaces. In addition, the program includes tools necessary for the analysis and comprehension of the multidimensional parameter space landscape. The developed algorithms were utilized to experimentally investigate the hydrolysis of N,N-dimethylformamide (DMF), a commonly employed solvent, in the specific context of metal–organic framework synthesis. We use ChemSPX to generate batches of experiments to sample parameter space, starting from an empty space, but subsequently assessing under-sampled regions. We use statistical analysis and machine learning models to show that addition of strong acids induces hydrolysis, generating up to 1.0% (w/w) formic acid. The results show that ChemSPX can generate datasets that efficiently sample parameter space, in this case allowing the user to distinguish the individual effects of five different physical and chemical variables on reaction outcome.
Introduction
The integration of advanced computational tools, driven by machine learning, artificial intelligence, and data science, has become pivotal in modern chemical research.1–3 The synergy between computational and experimental approaches facilitates a deeper understanding of the relationship between reaction parameter and chemical spaces.4 As the volume of synthetic and physical/chemical data burgeons, sophisticated computational tools equipped with machine learning algorithms play a crucial role in navigating and processing this information.5–12 The data-driven approach not only boosts research efficiency but also fosters innovation, steering the field towards more precise and accelerated methodologies.13,14 From an experimental perspective, a time- and resource-efficient method for exploring the vast reaction parameter space involves utilising a high-throughput synthesis approach.15,16 This technique allows for simultaneously testing multiple reaction conditions, significantly accelerating the exploration process and reducing the required resources. Manual strategies for probing parameter space typically follow the one-variable-at-a-time approach, by iteratively changing individual parameters.17Over the past decade, algorithms for exploring reaction parameter space have emerged, encompassing machine learning-driven approaches or various alternative strategies.15,18,19 Machine learning algorithms thrive with ample data, but the challenge lies in acquiring and ensuring the quality of such datasets. For example, literature-based synthesis databases suffer from inherent biases, where published research is not representative of all studies.20 This bias arises from factors such as the fear of journal rejection for negative results. Additionally, the presence of fraudulent manuscripts, as seen in cases of counterfeit publications in the field of metal–organic frameworks (MOFs), raises concerns about the reliability of data.21,22 Anthropogenic biases, such as heuristics and social influences in chemical reactions, further impact data-driven planning efforts, hindering the objectivity of literature-based synthesis databases.23 Additionally, compiling such extensive databases can be complex and, at times, seemingly impossible.
In this study, we introduce the ChemSPX program, which facilitates the analysis and exploration of a predefined reaction parameter space autonomously, without dependence on prior knowledge or experimental outcomes. The search algorithm employs an inverse distance function to maximise the separation between sampled reaction condition vectors in n-dimensional parameter space, thereby enhancing exploration. The algorithm aims to methodically navigate through the parameter space, sampling a minimum number of unique reaction formulations that have not been explored before. Sequential sampling is focused on sparse regions of the parameter space with the highest potential for yielding novel and unexplored reaction conditions. This strategic approach aims to efficiently provide human researchers with a feasible number of experiments, streamlining the experimental process and maximising the information gained from each iteration. The primary motivation behind developing the ChemSPX program is to create a user-centric application that aids researchers working on small or medium-scale projects, especially in the absence of experiment automation.
We demonstrate the application of ChemSPX code by exploring the parameter space of N,N-dimethylformamide (DMF) hydrolysis. DMF is a widely used aprotic solvent with a high boiling point (152.85 °C) and is miscible with water and other solvents.24,25 Its versatile physical and chemical properties make it a common choice in both small-scale and industrial chemical processes; it has been widely applied to the synthesis of MOFs, for example. A key characteristic of DMF is its decomposition under certain conditions. Upon heating, DMF undergoes decarbonylation, producing carbon monoxide (CO) and dimethylamine (DMA).26 Additionally, in the presence of water, DMF undergoes gradual hydrolysis, resulting in the formation of formic acid (FA) and DMA.27,28 Therefore, these two byproducts, DMA in particular, serve as predominant impurities in DMF, contributing to its distinct amine odour.
Aqueous DMF hydrolysis can be accelerated with an acid or base catalyst.29–31 MOF syntheses typically employ neat DMF, but commonly used additives like acidic modulators and co-solvents, such as water,32 are expected to promote DMF hydrolysis. The resulting products play crucial roles in influencing the kinetics of MOF formation: FA acts as a modulator and/or a source of protons, while DMA serves as a Brønsted base, deprotonating carboxylate ligands.33 The slow release of base upon gentle heating allows pH control in solvothermal reactions, which are widely utilised in synthesising various MOF materials, for example, the well-known MOF-5.34
The hydrolysis mechanism of DMF under acidic conditions has been thoroughly studied and understood.30,35–37 Typically, DMF hydrolysis is qualitatively assessed in the literature through NMR spectroscopy. However, only a limited number of studies have specifically tackled the quantification of the generated products, formic acid and dimethylamine.38,39 The complexity of this reaction, influenced by numerous parameters, necessitates a comprehensive investigation to identify optimum conditions that minimise byproduct yield. Herein, we exemplify the power of the ChemSPX program to analyse and sample parameter space in the hydrolysis of DMF under conditions relevant to MOF synthesis.
ChemSPX design and implementation
The design of the ChemSPX program necessitates methodology to parse information about reaction parameter spaces into mathematical functions which become key features of the software, all of which are detailed below.Distance function
Chemical reactions can be conceptualised within a mathematical function space, where a set of parameters x is considered. Within the defined domain (x ∈ Xn) for each parameter choice, there exists an associated experimental response f(x). The mapping of f(x) affords the analytical assessment of reaction coordinates. In the context of optimization, the response f(x) can be minimised or maximised by varying a set of parameters x. Algorithms such as Bayesian optimizers (BOs) or genetic algorithms (GAs) can explore the landscape of f(x) and determine optimal reaction parameters.15,19,40,41 The majority of algorithms reported in the literature depend on experimental responses to serve as targets (f(x)). In contrast, in this study we utilize mathematical assessments of reaction parameter coordinates as the target for the optimisation algorithm.The diverse reaction conditions can be visualized in an n-dimensional parameter space through multidimensional vectors. The mathematical distance between vectors (eqn (1)), signifies the difference between two sets of reaction conditions. This distance metric quantifies the dissimilarity or separation between the multidimensional vectors 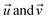 , providing a measure of how distinct or similar the corresponding reaction conditions are.
, providing a measure of how distinct or similar the corresponding reaction conditions are.
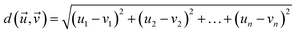 | (1) |
Therefore, the probability of two reaction conditions producing identical results is proportional to the inverse of the distance between their respective multidimensional vectors (eqn (2)).
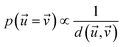 | (2) |
This mathematical relationship underscores the concept that closely positioned points in the parameter space are associated with more comparable reaction conditions, while greater distances suggest greater dissimilarity or divergence in the outcomes. Therefore, to select reaction conditions from the parameter space with the lowest likelihood of producing identical or similar outcomes, it is crucial to maximise the spatial distance between the corresponding vectors.
Inverse distance function
In this work, we propose the use of an inverse distance function, denoted as ϕ, which assesses the average distance between vector and its N nearest neighbours within the defined reaction parameter space (eqn (3)).
and its N nearest neighbours within the defined reaction parameter space (eqn (3)).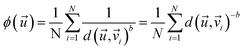 | (3) |
Applying this concept, we sample new reaction conditions from regions characterized by the lowest ϕ values, which indicate the highest probability of producing diverse reaction outcomes.
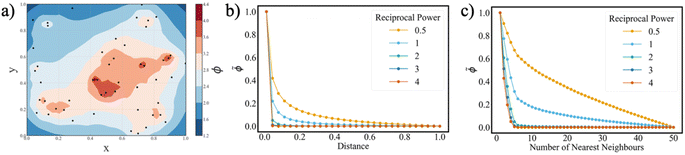
The magnitude of the inverse distance measure is determined by two variables: the number of nearest neighbours, considered N; and the exponent, b. Adjusting these two parameters alters the distribution landscape of ϕ in the parameter space (Fig. 1a).
The reciprocal power b serves as a critical factor in determining the proximity threshold between the reaction vectors. As the reciprocal power increases, the sharpness of the change in ϕ values at low distances diminish (Fig. 1b). This implies that at higher values of b, reaction condition vectors can be sampled at closer proximities. Furthermore, increasing the number of nearest neighbours N results in a reduction of ϕ values (Fig. 1c). In other words, as N increases, the impact of nearby neighbours on the inverse distance function ϕ diminishes. Therefore, to evaluate unexplored local regions effectively, careful tuning of the N parameter is essential. Overall, while reciprocal power allows control over the proximity of vectors, the number of nearest neighbours steers ϕ towards local minima in the parameter space.
Parameter space exploration algorithm
To initially populate the parameter space, ChemSPX samples M reaction parameter vectors within the designated parameter space, employing user-selected techniques such as Latin Hypercube Sampling (LHS) or random sampling methods. Subsequently, the average inverse distance function, 〈ϕ〉, is calculated to assess the distribution of the sampled vectors across the space. To refine this distribution, the algorithm optimises the vector coordinates to minimise the global 〈ϕ〉 value, thus encouraging convergence of the sampled data points and maximising the overall spacing in the parameter space. To achieve this, a stepwise strategy is implemented in the iterative process of exploration. Every move is governed by the step size parameter χ. In each move, a subspace B of a reaction vector A is constructed. The upper and lower boundaries of this subspace are defined by adding and subtracting the step size χ value (eqn (4)).| B = [A − Aχ,A + Aχ] | (4) |
After constructing the subspace hyperrectangle, an optimisation algorithm is employed to minimise ϕ within the vicinity of B and identify a new vector with the minimum ϕ value.
The implemented optimization algorithm, as illustrated in Fig. 2, iteratively focuses on optimizing the coordinates of individual vectors within the sampled set. By systematically refining each vector's coordinates, the algorithm gradually improves the overall distribution and convergence of the sampled data points, leading to enhanced representation and effectiveness within the parameter space. At each algorithm iteration step, the average ensemble properties (denoted in 〈ϕ〉) of sample parameter vectors are calculated.
The success of the search of sparse regions is defined by three convergence criteria: the average inverse distance function; the average change in inverse distance function; and the average sample vector change (eqn (5)–(7)).
 | (5) |
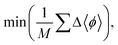 | (6) |
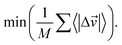 | (7) |
The vector change is determined by computing the difference between vectors at iteration i and i + 1 and expressed as the modulus of the resultant (eqn (8)).
 | (8) |
This parameter enables the assessment of whether the vector has converged in specific coordinates, and hence if the algorithm can be terminated. The convergence of the vector occurs when its coordinates either remain unchanged or exhibit minimal changes between successive iteration steps. It is also possible to use ChemSPX to search and optimise an existing parameter space that has been populated manually or by alternative computational methods. When employing a pre-populated parameter space for analysis and sampling, the existing reaction vectors remain static while the sampled vectors are optimised in relation to each other and the static vectors. This optimization process aims to enhance the coherence and distribution of the sampled vectors within the parameter space, ensuring that they align effectively with the existing data points while also maintaining appropriate spacing and coverage across the entire space.
Algorithm performance analysis
To investigate the impact of step size on the convergence behaviour of three distinct mathematical functions – Ackley, Matyas, and Himmelblau – the parameter χ was systematically varied across four values: 0.01, 0.1, 0.5, and 1 (see ESI Section S1†). For each configuration, 150 parameter space exploration iterations were conducted to allow sufficient opportunity for convergence. An initial set of 10 data points was generated using the Latin Hypercube Sampling (LHS) method, chosen for its ability to provide a well-distributed representation of the input space. The primary objective was to evaluate whether all sampled points converged to a consistent minimum. For the Himmelblau function, particular attention was given to assessing the algorithm's capacity to simultaneously identify all four known global minima.The plots presented in Fig. 3, illustrating the minimization of the test functions, reveal the significant influence of the step size parameter χ on the convergence behaviour. In particular, for the Ackley function – known for its complex landscape with numerous local minima – the Genetic Algorithm optimizer exhibits difficulty in locating the global minimum when smaller χ values are used. In contrast, for the Matya's and Himmelblau functions, convergence to the global minimum is consistently achieved when the step size is greater than or equal to 0.1. These observations highlight the critical role of appropriately tuning the χ parameter to guide the optimization process toward either local or global convergence.
Boundary conditions of the search space
While the proposed reaction parameter space sampling algorithm operates without explicit boundary conditions by default, it is advisable to establish constraints on vector sampling to facilitate convergence. Setting boundary conditions is recommended; aligning them with the permissible maximum and minimum values of the parameters is particularly crucial. With boundaries set, any parameter vector surpassing the predefined limits undergoes correction by relocating it within the proximity of the boundary conditions. This correction involves adjusting values that exceed the specified limits to the maximum allowable values for the respective parameter.Void search algorithm
An additional feature of the ChemSPX program is the ability to search existing datasets for large sparse regions, or voids, which can form due to the sampling approach or data point distribution. To identify and explore these regions, a void search algorithm was designed. The backbone of this method is a genetic algorithm that operates within the boundaries of the defined parameter space. In this case, the objective function constructs an n-dimensional hypersphere (SN) of radius r around centre point Z and counts the number of reaction vectors A inside it. The genetic algorithm optimizer will search for a minimum of data points falling within the defined hypersphere (eqn (9)).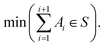 | (9) |
The new sampled reaction vector is the centre point Z of a hypersphere S, encompassing the smallest number of reaction vectors A. In the consecutive sampling, all parameter space is explored with new data points considered. The search radius can be manually controlled and is defined by eqn (10):
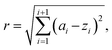 | (10) |
| Zi = {z0,z1,…,zn} | (11) |
The radius of the hypersphere can be tuned based on the previously discussed vector change factor  (eqn (8)). The size of the defined hypersphere affords control over the regions that are explored within the parameter space. The more vacant regions will fit a larger hypersphere and vice versa.
(eqn (8)). The size of the defined hypersphere affords control over the regions that are explored within the parameter space. The more vacant regions will fit a larger hypersphere and vice versa.
When compared to the aforementioned inverse distance function method, the void search algorithm exhibits a higher level of stochasticity. As the initial positions for the genetic algorithm are randomly determined, there is no guarantee of convergence to identical coordinates between iterations. Therefore, the void search algorithm proves effective in discovering unsampled regions while retaining a stochastic nature that reduces bias in parameter selection. The void search algorithm can be seen as an extension of the inverse distance function, facilitating the rapid identification of large unpopulated parameter space regions.
The ChemSPX package
The parameter space sampling algorithm using the inverse distance function has been integrated into the ChemSPX (Chemical Space Explorer) Python package. ChemSPX has a user-friendly interface for both the analysis and sampling of the reaction parameter space. The package encompasses a variety of implemented functionalities (see ESI, Section S2†), making it suitable for straightforward applications. This integration enhances the package's accessibility, allowing researchers to efficiently explore reaction conditions. In addition, the ChemSPX package includes LHS and LHSEQ initial sampling algorithms, the void exploration algorithm, and tools for parameter space analysis (see ESI, Section S4†).Reaction parameter space exploration of DMF hydrolysis
To validate the ChemSPX program, the hydrolysis of DMF was selected as a model reaction, being of specific interest to our program of research examining the self-assembly of MOFs.32 In the context of MOF synthesis, DMF hydrolysis can be influenced by five key chemical and physical parameters: water content, quantity of catalyst (in this case acid), pKa of the catalyst, reaction temperature, and reaction time (see ESI, Section S6†). These were used as variables in the exploration of the reaction parameter space. To quantify the extent of how much formic acid is generated in this reaction and establish reliable quantification methods, initial experiments were manually selected, using concentrated (37%) hydrochloric acid as a catalyst. Two distinct temperature modes were investigated, each subjected to evaluation across four different time intervals. 1H NMR spectroscopy was shown to be feasible for the quantification of formed formic acid, which reached a maximum of 0.5% (w/w) under these conditions, and therefore used as a measurement of DMF hydrolysis (see ESI, Section S7†). Plots of formic acid against reaction time exhibit logarithmic behaviour, allowing the identification of a cut-off point for the investigated time range (see ESI, Section S8†).Parameter space description and sampling
Having established proof-of-principle manually, we comprehensively explored the broader impact of reaction parameters on DMF hydrolysis reaction by using ChemSPX to undertake an in-depth study of the parameter space. The choice of primary parameters, and their respective ranges, were influenced by commonly employed solvothermal synthesis procedures in the realm of metal–organic frameworks (Table 1).32 In particular, it is reflected in the choice of DMF/acid and DMF/water volume ratios, spanning from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 to 1
0 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5. The acid catalysts selected are common modulators used in MOF synthesis: hydrochloric acid, sulfuric acid, nitric acid, trifluoroacetic acid, dichloroacetic acid, chloroacetic acid and formic acid. Each acid is characterized by its pKa value in the parameter space calculations, covering a range between −6.3 and 4.76.
0.5. The acid catalysts selected are common modulators used in MOF synthesis: hydrochloric acid, sulfuric acid, nitric acid, trifluoroacetic acid, dichloroacetic acid, chloroacetic acid and formic acid. Each acid is characterized by its pKa value in the parameter space calculations, covering a range between −6.3 and 4.76.
The DMF hydrolysis parameter space was sampled using the developed ChemSPX package. Two sampling methods were employed to search the parameter space: discrete and uniform (outlined in Table 1). For experimental simplicity, the DMF volume was kept constant. For the time parameter, a mixed sampling method was used, obtaining data in short (1–12 h, uniform) and long (24–168 h, discrete) periods. Additionally, a uniform method was applied to sample continuous parameters of moles of an acid catalyst and water volume. Taking all parameters into account, there are approximately 672![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible reaction conditions. Hence, in silico reaction condition sampling proves instrumental for a more efficient and focused examination of the parameter space.
000 possible reaction conditions. Hence, in silico reaction condition sampling proves instrumental for a more efficient and focused examination of the parameter space.
The reaction formulations were systematically sampled within the specified bounds, as outlined in Table 1. The complete reaction parameter space sampling was executed in five batches (Table 2). Variations in batch sizes were employed to track improvements in both the correlation between generated formic acid and reaction parameters, as well as enhancements in machine learning model performance (vide infra). The first batch of 50 experiments were selected using LHS and kept exempt from equilibration by the inverse distance function, thus creating a pre-populated parameter space. To exemplify the features of ChemSPX, the subsequent batches 2–5 were samples by both the LHS method (batches 2 and 3) and the void search algorithm (batches 4 and 5). Every successive set of reaction conditions generated by ChemSPX was added to the pre-existing reference dataset, thereby blocking already explored regions. The initial formulations acquired in batches 2–5 were refined through additional iterations utilising the inverse distance function ϕ, aiming to identify its minimum. The ϕ values for individual data points were calculated by considering their four nearest neighbours. The reciprocal power b was set to 1 aiming to maintain a larger distance between sampled reaction parameter vectors. A genetic algorithm optimiser, configured with optimisation step size χ set to 0.01, was employed to locate the minima of the ϕ function. Genetic algorithm optimizations consisted of 80 cycles with a population size of 100, while other parameters were maintained at default program settings (see ESI, Section S3†). A total of 120 inverse distance function optimisation cycles were performed, with ϕ, Δϕ, and  parameters achieving convergence.
parameters achieving convergence.
| Batch | Size | ChemSPX initial sampling method | ϕ minimisation applied |
|---|---|---|---|
| 1 | 50 | LHS | No |
| 2 | 20 | LHS | Yes |
| 3 | 21 | LHS | Yes |
| 4 | 21 | Void | Yes |
| 5 | 40 | Void | Yes |
To evaluate the extent of exploration within the defined parameter space, we employ the Monte Carlo integration algorithm (refer to ESI, Section S8† for detailed methodology). The computed exploration fraction quantifies how much of the parameter space has been covered, varying between 0 (entirely unexplored) and 1 (fully explored). In the consecutive sampling of the parameter space, from batches 1 to 3, the fraction of the explored parameter space increases sharply to 0.55 with 91 sampled reaction conditions (Fig. 4). Furthermore, the exploration rate drops sharply with the addition of an extra 61 reaction formulations. These observations indicate that most of the reaction parameter space is explored with batches 1 to 3. The reduced exploration rate implies that beyond batch 4, there is a transition from exploration to exploitation of the parameter space. The Monte Carlo calculations reveal that 57% of the parameter space has been explored and showcase the effectiveness of the ChemSPX algorithm in uncovering under-sampled regions of the parameter space.
Collection of experimental data
All in silico generated reaction formulations were tested manually in the laboratory (see ESI, Sections S6†). All reactions were carried out in glass vials, or hydrothermal reactors for temperatures larger than 100 °C. The content of the formic acid formed (% FA, w/w) was measured using quantitative 1H NMR spectroscopy, by comparison of integral ratios from signals from a known amount of tetramethylsilane (TMS) reference. The amount of formic acid per sample was determined using eqn (12). | (12) |
Each experiment was carried out in triplicate to obtain the standard deviation of the measurement.
Prior to analysis of the data, a systematic assessment of the impact of 1H NMR spectroscopic measurement errors on the entirety of our experimental data was carried out. The analysis procedure demanded a meticulous level of precision in both the preparation of the deuterated solvent containing the standard reference (TMS) and the analyte. Despite the potential for errors during sample preparation and measurement, the error distribution across the entire dataset reveals a remarkably high level of measurement accuracy. As depicted in Fig. 5a, a significant proportion of the samples exhibit low standard deviation values, underscoring the precision of our measurements.
For a more nuanced measurement error analysis, we computed fractional errors by dividing standard deviation values by the average % FA values of a single experiment (Fig. 5b). The obtained data revealed a discernible trend: as the % FA amount in the measured samples decreases, fractional errors exhibit an increasing pattern. Notably, most samples demonstrate fractional values around 0.2, indicating a higher level of accuracy (Fig. 5c). However, a small subset of samples, found in the lower % FA range, exhibit higher fractional error values due to limitations in the detection of small quantities of material by 1H NMR spectroscopy. This observation is attributed to peak merging, coupled with low signal intensities, leading to reduced accuracy in peak integration (see ESI Section S8†). Importantly, these samples constitute a minor proportion of the overall dataset: approximately 5%.
Analysis of experimental data
A total of 152 experiments, as selected across five batches by ChemSPX, were conducted in triplicate, encompassing 456 1H NMR spectroscopic measurements. The complete dataset consists of 7 parameters (features), making it challenging for straightforward analysis. Therefore, several methods were used to determine underlying trends in DMF hydrolysis reactions.The influence of each batch, and consequently the sample size, on the overall dataset was assessed using Pearson's R correlation measure. The extended Pearson's correlation matrix and parameter pair plot can be found in the ESI, Section S9.† Initially, it was noted that the water parameter exhibited a relatively low correlation coefficient, which was counterintuitive. Further examination of the data revealed the need to account for water originating from aqueous acid solutions, which was not captured by the initial parameter space generation. Corrections were specifically applied to reactions involving 37% HCl and 70% HNO3 acid catalysts to account for the water in these solutions. The post-correction correlation analysis on the overall data demonstrated a significant improvement in the R factor, increasing from 0.16 to 0.37 for all data.
Machine learning assisted data analysis
To gain deeper insights into the feature role in our DMF hydrolysis dataset, various machine learning (ML) models have been evaluated to determine their ability to capture chemical intuition. Herein, the data obtained from the initial experiments was combined with the overall data set, yielding a total of 177 samples in triplicate. In this dataset, tree-based machine learning models have displayed superior performance compared to linear regression and support vector regressor model (see ESI, Section S10†). The selected models were tested using a leave-one-out cross-validation strategy to assess prediction accuracy (for more detailed model assessment, please see the ESI Section S10†). LightGBM exhibited the highest prediction accuracy, achieving an R2 value of 0.73 and a mean absolute error of 0.08 (Fig. 6a). The performance of the LightGBM model tends to decrease in regions of low certainty (% FA ≥ 0.6) and can be attributed to the lower number of data points available to train the model. This is notable for the outlier lying beyond 1% (w/w) FA in the residual plot.SHAP analysis was conducted to deepen our understanding of the resultant model. This method provides insights into feature contribution towards the machine learning model predictions, offering a nuanced understanding of its behaviour.42 Positive SHAP values indicate a feature's contribution to increasing the prediction output, negative values indicate a contribution to decreasing the prediction output, and values close to zero signify minimal influence on the prediction. SHAP values correlate with real processes by revealing the impact magnitude of each feature on the model's predictions, helping to understand how changes in input variables affect the outcome, which can align with actual mechanisms or behaviours observed in the real-world process.6
Upon analysing the data, it becomes evident that the concentration of acid moles and the pKa value emerge as pivotal factors shaping the predictions (Fig. 6b). In contrast, water volume, temperature, and duration exhibit diminished significance in influencing the outcomes. These observations align with findings from Pearson's correlation analysis (see ESI, Section S9†), which indicated significant correlations between acid moles and pKa values and the percentage of formic acid (% FA). In contrast, water volume, temperature, and time features exhibit a relatively minor influence on the model's predictions. Notably, the removal of these parameters does not alter the accuracy of the model, underscoring their limited significance in the predictive framework.
Furthermore, the calculated SHAP values were analysed for each model input or feature individually (Fig. 6c and d; other plots are given in ESI, Section S10†). As anticipated, all features demonstrate consistency with the correlations observed between the generated formic acid and the various reaction parameters. In addition, the obtained LightGBM regression model was utilised to predict the distribution of formic acid in the parameter space. By evaluating the determined principal parameters, discrete regions can be identified for estimating the yield of % FA (see ESI, Section S10†). Again, the ability to unveil these subtle effects of modifying specific variables on the outcome of the DMF hydrolysis reaction underpin the utility of ChemSPX in efficiently searching parameter space.
Conclusions
In this study, we introduce an inverse distance function, ϕ, as a metric for evaluating the novelty of sampled reaction condition vectors. We have demonstrated the sensitivity of the proposed ϕ function in locating new reaction vectors within under-sampled regions of the reaction parameter space, and used it to underpin the ChemSPX program, which is tailored for user-targeted needs, facilitating straightforward applications in research. Within the context of our study, we illustrated the practical applications of the developed code by employing it to sample the parameter space of the DMF hydrolysis reaction. By analysing the data collected from the hydrolysis experiments put forward by ChemSPX, we were able to construct a sophisticated ML model that enhances our comprehension of how five individual parameters impact the reaction. Notably, the pivotal parameters influencing the hydrolysis reaction include the acid catalyst amount and its pKa. The models derived indicate that the percentage of formic acid (%FA) can be diminished by minimizing the quantity of water and acid present, as well as by increasing the pKa value of the acid catalyst. These findings have significant implications for the solvothermal synthesis of metal–organic frameworks, where formic acid can play a significant role (both positive and negative) in formation of desired phase and/or control of physical properties such as particle size. Moreover, our demonstration of the machine learning capability to capture chemical intuition implies that obtaining a more robust model with enhanced predictive accuracy for % FA generated during the DMF hydrolysis reaction is achievable with a larger dataset. We hope that the ChemSPX program – available freely for the chemical community – will become another useful resource in the ongoing digitisation of the field.Data availability
The developed ChemSPX code is publicly available on the GitHub repository: https://github.com/ignaspakamore/ChemSPX. The code and data used for DMF hydrolysis experiment analysis and machine learning modelling are available on the GitHub repository: https://github.com/ignaspakamore/dmf_hydrolysis. All of the data collected for this work is deposited within the University of Glasgow and can be accessed using the following DOI https://doi.org/10.5525/gla.researchdata.1977. In addition, we attach data files as ESI.†Conflicts of interest
We do not have any conflicts of interest to declare.Acknowledgements
RSF and IP thank the University of Glasgow for funding. We extend our gratitude to Dr Daniel Kowalski for insightful discussions during the development of the ChemSPX program.References
- Z. J. Baum, X. Yu, P. Y. Ayala, Y. Zhao, S. P. Watkins and Q. Zhou, J. Chem. Inf. Model., 2021, 61, 3197–3212 CrossRef CAS PubMed.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 Search PubMed.
- J. Yano, K. J. Gaffney, J. Gregoire, L. Hung, A. Ourmazd, J. Schrier, J. A. Sethian and F. M. Toma, Nat. Rev. Chem., 2022, 6, 357–370 CrossRef PubMed.
- P. S. Gromski, A. B. Henson, J. M. Granda and L. Cronin, Nat. Rev. Chem., 2019, 3, 119–128 Search PubMed.
- S. Park, H. Han, H. Kim and S. Choi, Chem.–Asian J., 2022, 17, e202200203 CrossRef CAS PubMed.
- S. Diab and D. I. Gerogiorgis, Pharmaceutics, 2020, 12, 235 Search PubMed.
- S. Stocker, G. Csányi, K. Reuter and J. T. Margraf, Nat. Commun., 2020, 11, 5505 CrossRef CAS PubMed.
- D. Jha, L. Ward, A. Paul, W. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593 Search PubMed.
- P.-P. De Breuck, G. Hautier and G.-M. Rignanese, npj Comput. Mater., 2021, 7, 83 Search PubMed.
- R. E. A. Goodall and A. A. Lee, Nat. Commun., 2020, 11, 6280 CrossRef CAS PubMed.
- A. Davariashtiyani, Z. Kadkhodaie and S. Kadkhodaei, Commun., Mater., 2021, 2, 115 Search PubMed.
- Y. Ding, B. Qiang, Q. Chen, Y. Liu, L. Zhang and Z. Liu, J. Chem. Inf. Model., 2024, 8, 2955–2970 Search PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 Search PubMed.
- E. O. Pyzer-Knapp, J. W. Pitera, P. W. J. Staar, S. Takeda, T. Laino, D. P. Sanders, J. Sexton, J. R. Smith and A. Curioni, npj Comput. Mater., 2022, 8, 84 Search PubMed.
- Y. Xie, C. Zhang, H. Deng, B. Zheng, J.-W. Su, K. Shutt and J. Lin, ACS Appl. Mater. Interfaces, 2021, 13, 53485–53491 Search PubMed.
- I. G. Clayson, D. Hewitt, M. Hutereau, T. Pope and B. Slater, Adv. Mater., 2020, 32, 2002780 CrossRef CAS PubMed.
- P. M. Murray, F. Bellany, L. Benhamou, D.-K. Bučar, A. B. Tabor and T. D. Sheppard, Org. Biomol. Chem., 2016, 14, 2373–2384 Search PubMed.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Appl. Phys. Rev., 2021, 8, 3 Search PubMed.
- L. Porwol, D. J. Kowalski, A. Henson, D.-L. Long, N. L. Bell and L. Cronin, Angew. Chem., Int. Ed., 2020, 59, 11256–11261 CrossRef CAS PubMed.
- H. A. Carroll, Z. Toumpakari, L. Johnson and J. A. Betts, PLoS One, 2017, 12, 1–19 Search PubMed.
- H. Else and R. Van Noorden, Nature, 2021, 591, 516–519 Search PubMed.
- D. Bimler, Research Square, 2022 DOI:10.21203/rs.3.rs-1537438/v1.
- X. Jia, A. Lynch, Y. Huang, M. Danielson, I. Langat, A. Milder, A. E. Ruby, H. Wang, S. A. Friedler, A. J. Norquist and J. Schrier, Nature, 2019, 573, 251–255 Search PubMed.
- M. M. Heravi, M. Ghavidel and L. Mohammadkhani, RSC Adv., 2018, 8, 27832–27862 Search PubMed.
- P. Linstrom, NIST Chemistry WebBook, NIST Standard Reference Database 69, http://webbook.nist.gov/chemistry/ Search PubMed.
- Y. Wan, M. Alterman, M. Larhed and A. Hallberg, J. Org. Chem., 2002, 67, 6232–6235 Search PubMed.
- J. K. Magtaan, M. Devocelle and F. Kelleher, J. Pept. Sci., 2019, 25, e3139 Search PubMed.
- J. Julliard, Pure Appl. Chem., 1977, 49, 885–892 Search PubMed.
- P. G. Gassman, P. K. G. Hodgson and R. J. Balchunis, J. Am. Chem. Soc., 1976, 98, 1275–1276 CrossRef CAS.
- D. Zahn, J. Phys. Chem. B, 2003, 107, 12303–12306 Search PubMed.
- E. Buncel and E. A. Symons, J. Chem. Soc. D, 1970, 164–165 RSC.
- R. S. Forgan, Chem. Sci., 2020, 11, 4546–4562 Search PubMed.
- R. Seetharaj, P. V. Vandana, P. Arya and S. Mathew, A. J. Chem., 2019, 12, 295–315 Search PubMed.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS.
- R. S. Brown, A. J. Bennet and H. Slebocka-Tilk, Acc. Chem. Res., 1992, 25, 481–488 CrossRef CAS.
- A. J. Kresge, P. H. Fitzgerald and Y. Chiang, J. Am. Chem. Soc., 1974, 96, 4698–4699 CrossRef CAS.
- T. Cottineau, M. Richard-Plouet, J.-Y. Mevellec and L. Brohan, J. Phys. Chem. C, 2011, 115, 12269–12274 Search PubMed.
- V. A. Meglitskii and N. M. Kvasha, Fibre Chem., 1972, 327–329 CrossRef.
- A. Paul, D. Connolly, M. Schulz, M. T. Pryce and J. G. Vos, Inorg. Chem., 2012, 51, 1977–1979 Search PubMed.
- V. Duros, J. Grizou, W. Xuan, Z. Hosni, D.-L. Long, H. N. Miras and L. Cronin, Angew. Chem., Int. Ed., 2017, 56, 10815–10820 CrossRef CAS PubMed.
- M. Fitzner, A. Šošić and A. Hopp, BayBe, Merck KGaA, Dramstadt Germany, 2022 Search PubMed.
- S. M. Lundberg and S.-I. Lee, in Advances in Neural Information Processing Systems, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, vol. 30 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00200a |
| This journal is © The Royal Society of Chemistry 2025 |

![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif)




