Digital flow platform for the synthesis of high-quality multi-material perovskites

Abstract

Perovskite materials have demonstrated great potential for a wide range of optoelectronic applications due to their exceptional electronic and optical properties. However, synthesising high-quality perovskite films remains a significant challenge, often hindered by batch-wise processes that suffer from limited control over reaction conditions, scalability and reproducibility. In this study, we present a novel approach for synthesising single-crystal perovskites with an optimised continuous-flow reactor. Our methodology utilises a 3D printed system that enables precise control over reactant concentrations, reaction times, and temperature profiles. The reaction chamber was designed and optimised by combining residence time distribution (RTD) studies and computational fluid dynamics (CFD) simulations. High-quality single-crystal perovskites with different formulations were obtained employing seeding and seedless conditions. The possibility of synthesising mixed halide single crystal perovskites with different compositions along its structure was demonstrated by simply shifting the feedstock solution during the crystallisation, demonstrating the versatility of this technology.

---

1 Introduction

Over the recent decade, the interest in hybrid organic–inorganic perovskites has greatly risen. Thanks to their widely tuneable semiconductive and optoelectronic properties, this family of materials has seen great developments in fields like solar cells,¹ X-ray sensors,² LEDs³ or memristors.⁴ Part of the interest is due to the possibility of their synthesis under mild conditions using solution-based approaches. Most applications using these materials employ polycrystalline thin films, but the boundaries between grains hinder the maximum performance of the resulting devices and can induce material degradation paths.⁵ In this regard, the use of monocrystalline perovskites offers superior properties in terms of lower trap density, longer carrier diffusion lengths, and resistance to degradation by moisture.⁶

Perovskite single crystals have been classically grown in batch with techniques like antisolvent crystallisation,⁷ solvent evaporation⁸ or solution temperature lowering.⁹ Achieving millimetre-sized crystals with these methods required days. In contrast, the inverse temperature crystallisation method (ITC), based on the retrograde solubility of the perovskite (solubility decreases as temperature is increased), allows it to grow crystals in a matter of hours.¹⁰ One of the main problems derived from its use is the loss of control over nucleation, as the increase in temperature also accelerates crystallisation kinetics, resulting in a decrease in crystal quality and reproducibility between experiments.¹¹ This is reflected in the range of electronic defect concentrations reported, even for the monocrystalline structures.¹² Different strategies have been used to overcome these issues, including control over precursor quality,¹³ slow ramped heating of solution, use of seeds¹⁴ or localised heating.¹⁵ Nevertheless, batch synthesis has limitations since the maximum crystal size is dependent on the volume and concentration of the starting solution, and the inhomogeneous distribution of temperature and precursor concentration within the crystallisation chamber might affect the quality of the crystals.

Continuous flow synthesis has become an important asset in the transition to more sustainable processes. In complex processes like crystallisation, the use of continuous flow reduces mass and heat transfer limitations, resulting in more homogeneous product distribution compared to batch, improving the overall reproducibility.^16,17 In the field of perovskites, there are numerous reports of their application for the synthesis of crystalline materials, often upgrading the properties of their batch-synthesised counterparts.^18,19 The synthesis of nanostructured perovskite materials is typically carried out in coil reactors with cross sections under 1 mm.²⁰ In the case of higher lateral area materials, like millimetre-sized monocrystalline perovskites, the cross-section of the tubing severely limits their growth. Meanwhile, as the cross-section increases, mass and heat transfer limitations present in batch might arise.¹⁶ Therefore, there is a need for developing new geometries where crystals have sufficient space for their growth while maintaining the advantages of continuous flow.

Digital reactor design combines computer-aided design (CAD), computational fluid dynamics (CFD) and additive manufacturing to produce advanced reactors with tailored geometries and advanced mixing features.^21,22 Modelled geometries can be used for simulating the resulting flow pattern with CFD, calculating parameters like flow streamlines, velocity and temperature fields, or tracer transport to validate the model. The analysis of CFD permits the detection of flow maldistributions (short-circuits, dead volumes, etc.) to optimise the CAD geometry.²³ Finally, thanks to 3D printing (3DP), validated reactors can be swiftly manufactured onsite for their experimental application.^24,25 Another significant step towards highly controlled and reproducible synthetic platforms is the development of digital flow platforms. Reaction conditions can be transformed into digital inputs; therefore, solution delivery or reactor temperature can be controlled through an interface for setting up experiments. Additionally, the implementation of in-line analytics allows recording data, like absorbance²⁶ or photoluminescence,²⁷ for monitoring crystal growth in real time. With this, variability caused by human intervention is minimised, and products obtained can be directly correlated with acquired data to better understand the process. It could even be possible to implement self-optimisation algorithms for achieving synthesis by selecting target properties directly.^20,28,29 Flow platforms have been successfully used for the synthesis of crystalline materials,^27,30,31 and very recently, the growth of high-quality perovskites has been monitored by employing in situ video imaging.³² In this work, a PID feedback control loop was employed with an imaging algorithm to monitor crystal growth to produce single crystals with fewer defects.

We introduced in previous work the possibility of employing 3D printing to create flow reactors for the synthesis of perovskite single crystals, albeit further developments were required to better control the number of crystals synthesised and to improve their quality.¹⁹ Here, we developed a digital platform that achieved a high degree of reproducibility, allowing for the synthesis of perovskite single crystals with consistent properties and minimal batch-to-batch variations. Compared to the work of Haruta et al.³² the key innovation here is the integration of flow chemistry with digitally engineered reactors, optimized through RTD studies and CFD simulations. This enables precise control of inverse temperature crystallization (ITC), improving crystal quality, while in situ monitoring provides insight into growth kinetics and temperature–composition relationships. Moreover, the continuous-flow approach offers improved reaction kinetics, leading to enhanced crystallinity, homogeneity and reduced defect density in the resulting perovskite films. We also investigate the impact of various reaction parameters, such as precursor flow rates, reaction temperatures, and solvent compositions, on the properties of the resulting films and device performance. Furthermore, we use the same platform for the synthesis of different perovskite materials, and its design enables the change of material without interrupting the process. XPS and X-ray diffraction (XRD) have confirmed that the successive perovskite films obtained are stoichiometrically and structurally homogeneous. Hence, our study demonstrates the successful synthesis of high-quality perovskite films under continuous-flow conditions, offering a scalable and reproducible method to produce perovskite-based optoelectronic devices.

2 Results and discussion

2.1 Design of flow platform

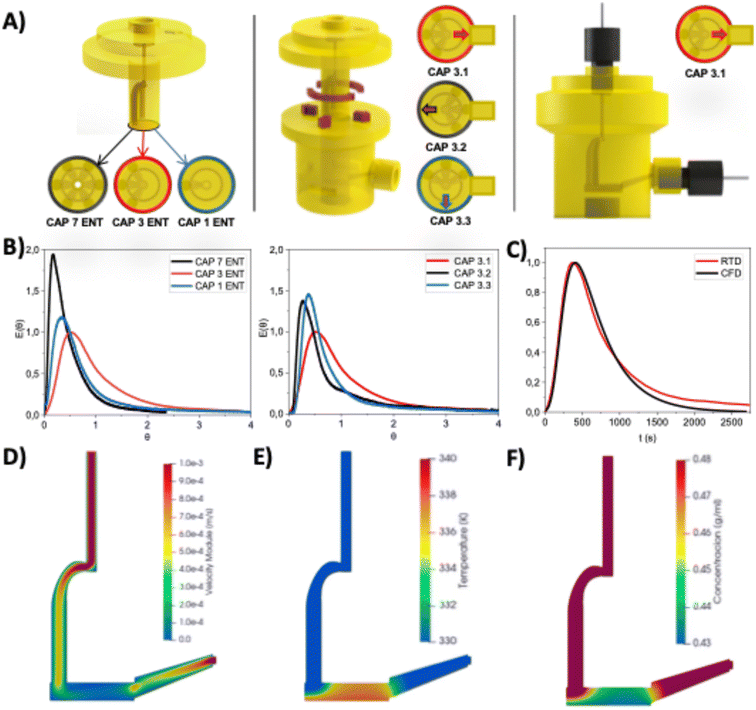
The main aim of the work was to build a low-cost platform for consistently producing perovskite single crystals with improved properties. In this regard, a strategy addressing multiple fronts for controlling the crystallisation process was developed. As a starting point, we used the combination of flow and a 3D-printed reactor to develop a system capable of yielding perovskite single crystals based on previous work.¹⁹ However, further developments of the technique were required to demonstrate an optimised control over the crystallisation processes. To achieve this, a platform was designed (Fig. 1) with an optimised flow diffuser to generate a pattern for homogeneous precursor distribution in the crystallisation chamber. The localised homogeneous heating of the surface of the crystallisation chamber aimed to improve control over nucleation and crystallisation.

Fig. 1 General overview of the digital flow platform developed in this work.

In parallel, the implementation of a vision control algorithm allows the monitoring of growth kinetics in real-time. Finally, the implementation of flow control methodologies with multiple programmable pumps was developed to dynamically control the composition of the crystallisation environment, thus enabling the development of innovative single-crystal multi-materials.

The core reactor was designed as a two-bodied system, plus additional accessories for controlling flow, monitorisation, and heating. The bottom part featured a 10.5 mm diameter circular hole for introducing glass substrates and an outlet to maintain steady state flow conditions. The top part was designed as a cylinder, featuring flow channels to act as an inlet, that was inserted into the reactor body. Once both parts were connected and the system closed using a clamp, a small chamber of 1.5 mm height was created to grow crystals with a volume of 0.13 mL (more detailed measurements can be seen in Fig. S1†). The pieces were manufactured using 3D printing techniques based on stereolithography, which is based on the focused polymerisation of a thin layer of ink inside the vat using a laser beam.³³ The photopolymerisable resin selected was High Temp Resin (HRT) from Formlabs, as we previously demonstrated its compatibility with conditions used for the Inverse Temperature Crystallisation (ITC) of the MAPbBr₃ perovskite.¹⁹

2.2 Optimised design based on flow dynamics

The first step was the study of the flow inlet configuration to achieve a more homogeneous flow distribution in the crystallisation chamber compared to the previous model of the designed reactor. In the original iteration, the flow diffusor, which includes the flow inlet and the diffuser, was designed as a cylinder featuring a flow line divided into seven channels to distribute the flow homogeneously into the reactor.¹⁹ Different flow diffusers for the reactor were fabricated with a varying number of holes and orientations relative to the reactor's lower outlet. An orienting arrow was added to the upper design to aid positioning, as shown in Fig. 2A.

Fig. 2 (A) Flow diffuser development studied by residence time distribution (RTD) and CFD. (B) Left: analyses of multiple inlet flow diffuser geometries. Right: geometry orientations are studied as a function of the angle between the inlet and outlet orientations. (C) Comparison of RTD study and CFD simulation for the optimal flow diffuser geometry. CFD simulations of: (D) velocity profile inside the reactor; (E) temperature distribution field; (F) solubility field of MAPbBr₃ in dimethylformamide (DMF).

To evaluate the impact of different flow diffusor configurations, pulse tracer-based residence time distribution (RTD) studies were conducted as a quantitative measure of the internal mixing within the reactor.³⁴ Here, an inert tracer pulse was injected into the reactor, and the output was constantly recorded with a UV-VIS spectrophotometer. With this, the residence time distribution function (E(θ)) can be calculated to evaluate differences in residence time of fluid particles. Fig. 2B shows the E(θ) curves of the different geometries studied. Initially, the number of inlets in the reactor's flow diffusor was evaluated (1, 3, 7 inlets), all oriented in an initial 180° configuration to the outlet, using a liquid flow rate of 50 μL min⁻¹. The curve corresponding to the flow diffusor with three inlets, referred to as CAP 3 ENT, presents a distribution closer to the ideal normalised distribution time of 1, while the other two show premature tracer breakthrough, suggesting issues such as channelling or short-circuiting.

Once it was established that the configuration with three inlets (CAP 3 ENT) offers better flow distribution compared to the 1 and 7 inlet designs, the orientation of the inlets was studied. The orientation CAP 3.1, in which the three inlets of the reactor's upper part are situated opposite the outlet, showed a more homogeneous flow distribution compared to the other inlet angles studied, which showed a less homogeneous tracer concentration. To validate these results, a CFD simulation of the system was performed. As shown in Fig. 2C, an overall agreement between the RTD experimental curve and validated the CFD simulations performed. The experimental curve experiences a slightly longer tail associated with wall effects and inhomogeneities of the structured reactor.

The heating system was designed to provide heat specifically directed towards the crystallisation surface, thus avoiding undesired secondary nucleation and crystal growth. An aluminium block connected to a heating resistance controlled by a PID (Proportional-Integral-Derivative) temperature controller was fabricated featuring a little pivot connected with the cavity of the bottom part of the main body of the reactor. A thin wall of 1.8 mm separated the glass substrate and the heating block pivot. The rest of the reactor and heating block were adequately insulated from the environment using thick polymer walls. A calibration of the relationship between the nominal temperature of the PID controller and the inside of the chamber was performed (Fig. S2†).

The flow and temperature gradients within the crystallisation chamber play a key role in the uniformity of the perovskite concentration and uniformity during the crystallisation process. Therefore, using the values previously validated at the RTD, heat exchange and velocity profiles at the interior of the crystallisation chamber were modelled using CFD. A flow of precursor solution through the reactor passing through the crystallization chamber was simulated while simultaneously, the bottom section of the reactor was constantly heated. In Fig. 2D, it can be noticed that the orientation of the inlets promotes a smooth transition from high to low velocities, allowing the solution to homogenise near the bottom where crystallisation starts occurring, also promoting steady, regular crystal growth. Regarding temperature, the contour in Fig. 2E shows the formation of a steady gradient of temperature in the chamber that decreases with the distance to the heating wall, as expected. Also, it can be noticed the effect due to the entrance of the cold stream at the rear part of the chamber. The temperature increases as the flow advances through the chamber, promoting nucleation in the middle/frontal region of the reactor. This temperature distribution (T) has a direct effect on the solubility concentration (C) of MAPbBr₃ in dimethylformamide (DMF) (eqn (1)).¹⁴

Fig. 2F clearly shows that lower solubilities are observed at the bottom of the reactor, suggesting that saturation will occur in this area, leading to crystal nucleation near the bottom. Additionally, even if some nucleation occurs near the chamber entrance, significant crystal growth is unlikely due to the higher solubility in that region.

2.3 Vision control of growth kinetics of perovskite single crystals

Once the optimal reactor configuration was selected, the platform was ready for the growth of perovskite single crystals. MAPbBr₃ was used as the case model, as we previously demonstrated the possibility of its growth using continuous flow and the ITC method.¹⁹ The monitoring was conducted using the setup illustrated in Fig. 3A. The system features a 3D-printed platform that supports the heating block of the crystalliser, along with two perpendicular mounts that house cameras. These cameras capture images at specified time intervals, which are subsequently processed using the OpenCV library³⁵ for image recognition and Python scripts for data analysis. The reactor is equipped with two 33 mm² rectangular windows, perpendicular to the substrate, that allow for the observation of perovskite crystal growth. During the analysis, the crystal size is normalised using these windows as a reference, ensuring precise and consistent measurement of crystal growth. The analysis software developed for this purpose is available on a supplementary GitHub repository.³⁶ The methodology was validated by conducting analyses of the vision computing area (VCA), comparing them to the experimental determination of the size of the perovskites, which was measured outside the crystallisation chamber with a calliper. A good experimental correlation was found (Fig. 3A). It is important to mention that a negative x0 indicates that the VCA system cannot reliably measure very small perovskites (<1 mm²). Hence, the system can assess the growth of perovskites, yet the nucleation processes can only be qualitatively evaluated.

Fig. 3 (A) Control setup of the growth of perovskite single crystals. The correlation between the vision computing area (VCA) and the experimental area of the perovskites was y = −0.93 + 0.88x. R² = 0.976. (B) Temperature-dependent perovskite growth kinetics for unseeded perovskites. Crystallization conditions: 1.2 M MABr and PbBr₂ solutions both pumped at 25 μL min⁻¹. Crystallisation kinetics for (C) seeded growth crystals; (D) unseeded growth crystals. Crystallization conditions: 1.2 M MABr and PbBr₂ solutions both pumped at 25 μL min⁻¹, Reactor temperature: 61 °C.

A series of experiments were conducted to monitor the growth of MAPbBr₃ perovskite single crystals under varying conditions. The concentration of reagents (methylammonium bromide and lead(II) bromide in dimethyl formamide) remained constant at 1.2 mol L⁻¹, while other parameters were systematically varied. Initially, experiments were conducted without the use of seed crystals, focusing on evaluating the influence of key parameters such as flow rate and temperature on single crystal growth. Growth temperatures were kept as low as possible to minimise the apparition of secondary crystal nuclei while enabling stable crystal growth. A summary of the experimental conditions is provided in Table S1,† while Fig. 3B illustrates the differences in growth kinetics for different temperatures under the same conditions. The crystal growth kinetics presented a direct dependence on the solution temperature. At 58 °C, no nucleation was observed until 200 minutes, followed by slow growth. Alternatively, by selecting a temperature of 68 °C, nucleation started at 50 minutes, and the slope was notably more pronounced. This behaviour was expected since, at higher temperatures, it's easier for an oversaturated system to overcome the nucleation energy for the subsequent formation of nuclei, and the growth kinetics are also favoured at higher temperatures.¹¹

While nucleation time decreases at higher temperatures, the probability of uncontrolled nucleation increases. Seed-assisted growth is a way to enable growth at lower temperatures. Here, previously grown and harvested MAPbBr₃ single crystals are introduced into the saturated solution to be used as nucleation centres for further growth. For the case of a 1.2 mol L⁻¹ MAPbBr₃ precursor solution at a 61 °C temperature, with a 25 μL min⁻¹ flowrate, seeded and unseeded experiments were monitored (Fig. 3C and D). Seeded experiments presented a 30 minutes induction time where growth was not observed. On the other hand, non-seeded experiments typically present a time of approximately 150 minutes of induction time before crystals are observed. At selected conditions, the solution presents a low supersaturation level. Hence, further nucleation is unlikely,¹¹ thus inhibiting the appearance of secondary crystals. However, this makes seedless growth challenging. Another difference observed is the aspect ratio of crystals, as also seen in Fig. 3C. Seeded crystals present more similar growth speeds in both horizontal and horizontal directions, while unseeded crystals favour horizontal growth (Fig. 3D), resulting in a higher area-to-thickness ratio. It should be considered that partial redissolution of the seed during the initial minutes increased the supersaturation level in all the surroundings of the crystal. This would cause an acceleration of growth in all directions, as observed in Fig. 3C. Alternatively, in seedless experiments, crystals remained thinner, possibly due to a combination of factors that need further exploration, like the temperature difference between the top and bottom of the effect of the flow parallel to the crystal surface.

Additionally, the platform was tested for the synthesis of MAPbCl₃ crystals, as it also presented retrograde solubility when precursors were dissolved into a mixture of dimethyl formamide and dimethyl sulfoxide (1 : 1). In this case, different solution concentrations were tested at the same conditions used for the previous bromide experiments (61 °C and 25 μL min⁻¹ flowrate). MAPbCl₃ crystals were obtained successfully using a 0.8 M solution concentration, demonstrating the possibility of extending the principles of the platform to other systems that can be grown via the ITC of the platform. However, MAPbCl₃ appeared to be more prone to secondary nucleation, something that can be controlled by a more exhaustive adjustment of crystallisation conditions. Moreover, due to the colourless look of the crystals, growth could not be monitored by the existing setup. Further developments of the platform could implement photoluminescence measurements or other methodologies for overcoming this issue.

2.4 Characterisation of perovskite single crystals

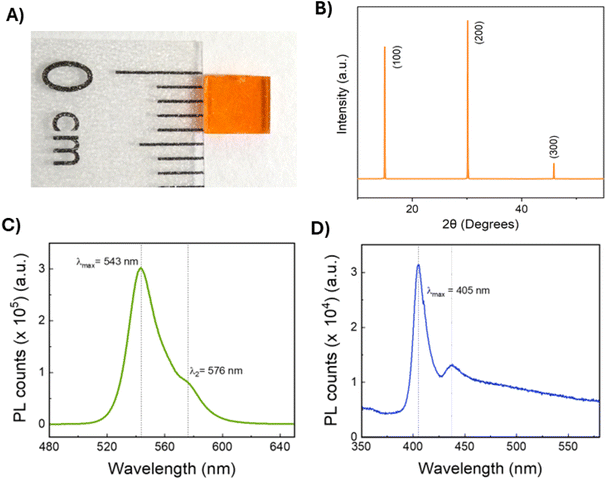
Selected crystals synthesised with the previously discussed methodology were characterised to evaluate their properties. Seedless-grown crystals showed a clear and homogenous structure, as seen in Fig. 4A, with no observable morphological defects, while seeded crystals presented a comparable appearance but with the initial seed embedded in the centre. The XRD spectra (Fig. 4B) showed diffraction peaks at 14.97°, 30.14° and 45.90°, which can be attributed to the (100), (200), and (300) facets, confirming the growth of the monocrystalline cubic MAPbBr₃ perovskite.³⁷ An analysis of the FWHM and lattice strain using Williamson–Hall plot indicates a low compressive strain value of −0.014%, suggesting a high-quality crystal (see ESI, Table S2 and Fig. S3.†³⁸) Atomic force microscopy of the crystal revealed a surface roughness of 2.93 nm for the seedless-grown crystal and 1.46 nm for the seeded crystal (Fig. S4†), greatly improving the surface smoothness compared to the literature.¹⁹

Fig. 4 (A) Image of a seedless synthesised MAPbBr₃ single crystal. (B) X-ray diffraction spectra of the seedless-grown MAPbBr₃ crystal. (C) and (B) X-ray diffraction spectra of the seedless-grown MAPbBr₃ crystal. (D) Photoluminescence measurements of a seed containing MAPbCl₃ single crystal.

The photoluminescence (PL) properties of the seedless crystals were also evaluated (Fig. 4C). Crystal presented an intense peak at 543 nm, corresponding to MAPbBr₃ perovskite. A minor secondary peak can be observed at 576 nm, which may be due to reabsorption phenomena observed in monocrystalline materials.³⁹ Time-resolved photoluminescence (TRPL) decay revealed a τ_F of 181.7 ns (Fig. S5A, Table S3†), shorter than the values we observed in the previous iteration of the platform.¹⁹ Crystals grown using an initial seed presented higher photoluminescence intensity and a less pronounced shoulder, which indicates lower defect concentration (Fig. S5B†). Interestingly, τ_F was noticeably shorter, with a value of 91.3 ns (Table S3†). It has been reported that the shortening of photoluminescence decay can be related to an increase in crystallinity quality and decreased surface roughness in bulk single crystals.⁴⁰ However, there are also reports about how this is linked to a decrease in photoluminescence intensity, as surface defects play a key role in PL emission. Paradoxically, crystals grown in flow with the seed-assisted method presented shorter decay times but higher emission intensity. It can be considered that flow might have a further influence on crystal morphology and their properties, but the complexity of the underlying mechanisms would require extensive exploration. In the case of MAPbCl₃ crystals, the maximum PL intensity peak is expected at 405 nm. However, a secondary peak at 440 nm can also be observed (Fig. 4D), and, compared to MAPbBr₃, it presents a higher relative intensity compared to the main peak. This corroborated that further optimisation of the conditions of the chloride crystals would be required to yield optimal PL properties.

2.5 Growth of mixed halide perovskite single crystals

The possibility to adjust the flow rate and composition by employing multiple pumps during the experiment enables the dynamic modification of the crystallization conditions. This is a clear advantage over conventional batch processes, where a change of solution requires stopping the process and the transfer of the crystal to another vessel or diluting the mother liquor by the addition of a new substrate solution. These actions inevitably disturb the growth, as crystals might redissolve partially until supersaturation temperature is reached again, and the manipulation of the crystal might generate surface-level irregularities. In that sense, the use of multiple pumps allows the introduction of different solutions without manipulating the reactor, making this transition smoother. Hence, novel single-crystal multi-materials can be generated with this approach. As a proof of concept, a mixed halide methylammonium lead-based perovskite was synthesised.

Selected materials for the experiments were MAPbCl₃ and MAPbBr₃, as they share a cubic structure with the same space group⁴¹ and they were both successfully synthesised in the reactor. The first step was the seed-based growth of a crystal of MAPbCl₃ using a 0.8 M solution of precursors in a mixture of DMF and dimethylsulfoxide (DMSO) (1 : 1 (v/v)) at 65 °C with a flow rate of 25 μL min⁻¹ since we already used these conditions successfully. After a selected growth time of 2 h, a step change of feedstock solution to a 1.2 mol L⁻¹ of precursors in DMF was performed with a second programmable pump, maintaining the overall flow rate constant at 25 μL min⁻¹. Growth of the coloured bromide containing perovskite was constantly monitored with the vision computing platform (Fig. S6†). The resulting crystals (Fig. 5A) are multi-component, with a clear colour gradient across the surface. The crystals were not flat on the surface, they presented a trapezoidal shape, presumably due to the bigger lattice structure of Br-containing crystals versus the smaller Cl-containing ones. The experiment was repeated 3 times to test the reproducibility of the synthetic procedure. Even though the MAPbCl₃ seeds were not identical, the final dimensions were found to have a crystal area of 14.9 ± 2.5 mm². The area of the crystals were measured and a reproducibility of a it is noteworthy that growth experiments in reverse order, starting from a MAPbBr₃ and then introducing MAPbCl₃ solution, were not possible, as the crystal was swiftly dissolved once the solution reached the inside of the crystallisation chamber. MAPbCl₃ growth requires a DMF/DMSO 1 : 1 solution, but MAPbBr₃ shows very small retrograde solubility in DMSO, and its solubility is over ten times higher at selected conditions.⁴² Thereby, the continuous growth of multiple material single crystals requires a thorough revision of the solvent compatibility for each step.

Fig. 5 (A) Picture of a mixed halides perovskite single crystal and diagram of crystal composition (B) Raman shift spectra of selected points. (C) Photoluminescence of crystal faces (D) confocal photoluminescence microscope picture of the mixed composition perovskite single crystal.

Raman spectroscopy was employed to probe the composition of the crystal at different points (Fig. 5B). The C–N stretching Raman band of the methylammonium (MA) varies as a function of the halide of the corresponding perovskite in the series MAPbCl_xBr_y.⁴¹ In Fig. 5, point 1 was measured in the centre of the crystal at 5 μm depth (Fig. S7†), showing a Raman shift of 977 cm⁻¹ (MAPbCl₃). However, at the same point, but at the surface, the Raman shift observed was 974 cm⁻¹ (MAPbCl₂Br), thus indicating a compositional from the initial MAPbCl₃ perovskite. Furthermore, point 2 at the surface showed a Raman shift of 971 cm⁻¹ (MAPbClBr₂) points 3 and 4 clearly correlate to the growth of the crystal under predominantly PbBr₂ stock solution. Here, a Raman shift of 968 cm⁻¹ confirmed the presence of MAPbBr₃ on the surface of the crystal. Interestingly, X-ray photoelectron spectroscopy (XPS) probed at similar points than shown in Fig. 5B showed that on the surface (1–10 nm) were bands consistent with MAPbBr₃, showing no detectable signals of chlorine (Fig. S8 and S9†). The core levels of Pb, C, Br, N, and O confirm the spectroscopic homogeneity of the top perovskite film, MAPbBr₃.

The photoluminescence properties of the crystal were recorded, and a difference in behaviour between the two faces was observed (Fig. 5C and S10, Table S4†). Both faces presented a maximum emission at 543 nm, attributed to MAPbBr₃, but then different secondary peaks appeared. The 560 nm and 576 nm correspond, presumably, to reabsorption processes and are more noticeable in the top layer, where they might be related to the height differences observed in the surface. On the other hand, the contribution of MAPbCl₃ can be detected in the bottom layer at 418 and 443 nm, where MAPbBr₃ growth was restricted due to physical limitations of space. To give further insight into this observation, confocal photoluminescence microscopy images were taken with selected wavelengths to detect the perovskites studied (Table S5†). Fig. 5D reveals an outer shell of MAPbBr₃ that corresponds to the transparent orange sections (Fig. 5A). Meanwhile, the central section of the crystal features different species that have mixed halide compositions. There is a gradient where proximity to the core of the crystal corresponds to lower wavelengths, signalling species with increasing proportions of chloride. This indicated the growth of perovskite layer by layer with a gradual change of compositions, as the initial medium containing chloride solution is replaced by the bromide.

Interestingly, MAPbBr₃ preferentially grew in the horizontal direction towards the outer edges of the crystal, while it did not cover the central area for the top layers. Also, bromide ion has a higher radius than chloride, and therefore, as bromide content is increased, cell size presents higher values. The combination of these factors could explain the observed difference in behaviour between faces and the height difference existing between the inner and outer areas (Fig. S11†).

3 Conclusions

The development of a novel digital flow platform for the controlled synthesis of perovskite single crystals enables the fabrication of advanced high-quality materials in a controlled and reproducible fashion. The optimisation of the heating chamber and flow conditions offered enhances control over the temperature profile within the crystallisation chamber and offers great potential for future scaling up of the process. Vision control can help in the understanding of growth kinetics, allowing a better selection of reaction conditions.

Single crystals with improved surface smoothness were generated with this platform employing seeded and interestingly highly challenging unseeded conditions. The capabilities of the digital and programmable platform were demonstrated by synthesizing novel single-crystal perovskites as individual highly stoichiometric films, even at thicknesses of just a few nanometers. These films could exhibit various halide compositions (MAPbCl₃, MAPbBrCl₂, MAPbBr₂Cl, and MAPbBr₃) by simply dynamically switching the precursor solution during a single-crystal growth experiment. A total of four different perovskites were integrated into a single crystal material, thus opening the possibility to the discovery of new materials, especially new combinations of multi-material single-crystal perovskites with advanced optoelectronic properties.

4 Methodology

4.1 Materials

CH₃NH₃Br (>99 wt%) and CH₃NH₃Cl (>99 wt%) were purchased from Great Cell Solar Materials. PbBr₂ (>98 wt%), PbCl₂ (>98 wt%), DMF (>99.8 wt%, anhydrous) and DMSO (>99.9 wt%, anhydrous) were purchased from Merck. Salts and solvents were used as received without any further purification.

4.2 Precursor solution preparation

In the typical synthesis used for this work, 1.34 g of CH₃NH₃Br (>99 wt%, Great Cell Solar Materials) and 4.404 g of PbBr₂ (>98 wt%, Merck) were dissolved at 1 : 1 molar ratio in 10 mL of DMF (>99.8 wt%, anhydrous, Merck) under nitrogen atmosphere to produce a 1.2 mol L⁻¹ solution of MAPbBr₃ and 0.54 g of CH₃NH₃Cl (>99 wt%, Great Cell Solar Materials) and 2.22 g of PbCl₂ (>98 wt%, Merck) were dissolved at 1 : 1 molar ratio in 5 mL of DMF (>99.8 wt%, anhydrous, Merck) and in 5 mL of DMSO (>99.9 wt%, anhydrous, Merck) under nitrogen atmosphere to produce a 0.8 mol L⁻¹ solution of MAPbCl₃. Solutions were kept at room temperature under stirring and filtered before starting the crystallisation with a 0.2 μm pore size PTFE filter.

4.3 3D printed reactor production

The reactor was modelled using Solidworks CAD software and converted to standard tessellation language (STL) format. It was printed using a Formlabs 3 low-force stereolithography printer loaded with off-the-self Formlabs High Temp resin. STL files were sliced using Formlabs slicing software, Preform, and printed with a layer height of 50 μm using the settings recommended by the manufacturer. EPDM O-rings were purchased from RTC Couplings. Clamps were purchased from Leybold.

4.4 Heat and temperature control

A homemade setup consisting of a PID temperature controller connected to a cartridge heater was produced. The cartridge was introduced into a bespoken aluminium block, and its temperature was monitored by a thermocouple connected to the PID temperature controller. The temperature at the base of the crystallisation chamber was measured with a high-resolution contact thermometer after waiting for two hours. A calibration for the correlation between the temperature of the block and the temperature at the surface of the crystallisation chamber was done (eqn (S1)†).

4.5 RTD studies

The experimental procedure utilized a setup consisting of two syringe pumps: one for controlling the primary flow rate and the other for loading a 50 μL loop into an automated 6-way Rheodyne valve. This valve facilitated the injection of a tracer pulse into the flow stream, simplifying the process. The valve was connected to a commercial flow cell, allowing a light beam to pass through and be detected by a UV-visible spectrometer operating at a fixed wavelength. All components were connected using 1/16-inch PEEK capillary tubing. The experiments were conducted with isopropanol as the solvent and a Methyl Red tracer solution (1 mg L⁻¹) in the same solvent, with a flow rate of 50 μL min⁻¹. The change in tracer concentration over time was monitored by measuring the absorbance peak at 525 nm in the UV-VIS spectra.

4.6 CFD studies

The CFD validation for the RTD was performed using OpenFOAM 2112. The 3D geometry was meshed using snappyHexMesh to obtain a mostly tetrahedral non-deformed mesh composed of 400k nodes. The simpleFoam solver was employed to obtain the steady-state resolution of the flow in similar conditions to the RTD study with a flow rate of 50 mL min⁻¹. The fluid was considered Newtonian and incompressible (kinematic viscosity of 4.9 × 10⁻⁶ m² s⁻¹ and base density of 1425 kg m⁻³) while the temperature was set to 20 °C (the heating plate was off in this case). Then, a laminar transient simulation with frozen hydrodynamics was performed by using the scalarTransportFoam solver with a kinematic diffusivity of 10⁻⁸ m² s⁻¹. The tracer pulse was injected with a concentration of 1 mg L⁻¹ for 60 s, and its evolution was solved over 2700 s.

CFD simulations for the heat transfer analysis were performed employing the chtMultiRegionSimpleFoam solver from OpenFOAM 2112, in addition to the conditions previously described for the RTD curve validation. Inlet flow was fixed at a temperature of 20 °C, while the bottom area of the reactor was fixed at 65 °C (this temperature was determined from the steady-state temperature of the heating plate). Reactor walls were modelled with an experimentally determined thermal conductivity coefficient of 0.282 kg m s⁻³ K⁻¹, while the external temperature was set at 20 °C to model the heat exchange with the surrounding air in the room.

4.7 XPS studies

High-energy resolution X-ray photoelectron spectroscopy (XPS) measurements were conducted using a SPECS GmbH system, with a base pressure of 1.0 × 10⁻¹⁰ mbar. The system featured a PHOIBOS 150 2D CMOS hemispherical analyzer. Photoelectrons were excited using the Al-Kα line (1486.7 eV). Measurements were performed at room temperature with a pass energy of 20 eV. For all HR-XPS measurements, the samples were placed under ultrahigh vacuum (UHV) conditions, with the analysis chamber achieving a base pressure lower than 1.0 × 10⁻¹⁰ mbar.

5 Continuous-flow single and multimaterial crystal growth experiments

Continuous-flow single crystal growth experiments were conducted using two programmable Tricontinent C3000 pumps, each equipped with a 5 mL syringe. These pumps operated in sequence to maintain a continuous flow of the previously prepared precursor solution into the reactor. The pumps were controlled via an interface developed in Visual Studio with Python scripts. The reactor's internal temperature was adjusted between 58 °C and 68 °C and the flow rate between 12 μL min⁻¹ and 50 μL min⁻¹ for the experiments.

Multi-material crystal growth experiments were conducted similarly to the previous ones, with one key modification: each of the two pumps introduced a different solution, with the first pump delivering a 0.8 M solution of MAPbCl₃ in DMF/DMSO 1 : 1, followed by the second pump, which delivered a 1.2 M solution of MAPbBr₃ in DMF.

The procedure was similar to the previous one, with continuous-flow growth experiments were conducted using two programmable Tricontinent C3000 pumps, each equipped with a 5 mL syringe. These pumps operated in sequence to maintain a continuous flow of different solutions into the reactor. The first one pumped a solution of 0.8 M MAPbCl₃ in DMF/DMSO 1 : 1 v/v, followed by the second pump, which delivered a 1.2 M MAPbBr₃ solution in DMF. The pumps were controlled via an interface developed in Visual Studio with Python scripts. The reactor's internal temperature was kept constant at 67 °C, and the flow rate was adjusted between 6 μL min⁻¹ and 25 μL min⁻¹ for the experiments.

6 Vision control of growth kinetics of perovskite single crystals

For the monitoring and analysis of perovskite crystal growth in continuous flow, a specialised algorithm was developed in Python, utilizing the OpenCV library for image processing. This algorithm facilitates automated and precise analysis of the images captured from the reactor during the experiments.

The camera system captures images of the reactor at predetermined time intervals, which are automatically loaded for processing. A Region of Interest (ROI) is defined in each image using a polygon with predefined coordinates, delineating the area where perovskite crystal growth is expected to be observed. This polygon is superimposed on the image to facilitate visualisation and analysis of the target area.

The images, originally in BGR format, are converted to the HSV (Hue, Saturation, Value) colour space to improve colour segmentation, thereby aiding in the identification of perovskite crystals. In this case, a specific colour range in the orange spectrum is used to detect lead perovskite. This colour range can be adjusted according to experimental needs, allowing for flexible adaptation to different lighting conditions or variations in sample composition.

Once the regions of interest are segmented based on colour, contours within these regions are detected. Each contour is analysed to determine its area, with those below a predefined threshold being discarded to avoid noise or irrelevant elements. Valid contours are highlighted in the original image to facilitate visual review.

The total area of the crystals detected within the ROI is calculated and stored for subsequent analysis. These area values are normalised based on the known size of the ROI, enabling accurate comparisons over time. Each area measurement is associated with the corresponding image capture time, creating a time series of data.

To improve data interpretation, a smoothing technique using a moving average with a three-point window is applied, reducing variability and highlighting trends in crystal growth. The results are presented in a graph showing the detected area over time, which is saved as a PDF for documentation. Additionally, the processed images are stored in a specific folder for further review.

This automated approach allows for continuous and detailed monitoring of perovskite crystal growth, providing valuable data for process optimisation and scientific research.

7 Characterisation

XRD spectra were measured in a Bruker D8-Advance diffractometer. CuKα radiation (λ = 1.5406 Å) was used for the direct recording of the signal by mounting the crystal in a sample holder.

Atomic force microscopy images were made using a JSPM-5200 Scanning Probe Microscope from Jeol. Images were taken in contact mode for an area of 2 × 2 μm with a pixel resolution of 256 × 256.

PL and TRPL measurements were performed with the use of Edinburgh Instrument FLS 1000 fluorimeter with a picosecond pulsed diode laser EPL 375 nm as the excitation source. The pulse period was settled at 200 ns for steady-state PL and increased up to 500 ns for the TRPL performance with a time scale of 500 ns.

Raman spectra measurements were performed using a WITec Apyron confocal Raman microscope. A 785 nm laser with a laser power of 9.62 mW was used as an excitation source with a Zeiss EC Epiplan-Neofluar Dic 100× objective.

Confocal fluorescence pictures were taken using a Leica TCS SP8 microscope using a 405 nm laser as the excitation source. Photoluminescence was acquired by using a series of PMT detectors with wavelength ranges described in Table S5,† with a 53.1 μm pinhole and a Leica HC PL APO ×10 objective.

Data availability

The datasets and figures generated in this manuscript can be found in Zenodo: 10.5281/zenodo.15000698. The CAD files in solidworks and.stl format and the code developed in this work can be found in GitHub. https://www.github.com/catm542-ai/PerovskiteGrowthDetection and in Zenodo: 10.5281/zenodo.15552360. All the relevant information on the code can be found in a README file.

Author contributions

Conceptualization VS; Methodology VS, MZ, RAB, PB; Software programming CT, J. L-G.; Validation DI, SM, JMX; Formal analysis DI, CT, VS; Investigation DI, SM, CAA, AMS, MCA; Resources; Data Curation DI, SM, MZ; Writing – original draft DI, MZ, CT; Writing – review & editing all authors; Visualisation; Supervision VS, MZ, RMC; Project administration VS; Funding acquisition VS, PB, RAB, MCA, MZ.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been funded by the project (PID2020-119628RB-C33, PID2020-119628RB-C32 and PID2020-119628RB-C31), MCIN/AEI/10.13039/501100011033 and (CNS2023-144752) funded by MCIN/AEI/10.13039/501100011033 and the Unión Europea NextGenerationEU/PRTR. CT thanks the Generalitat Valenciana (CIGRIS/2021/075) for funding. The authors are grateful to the SCIC of the Universitat Jaume I for Technical support. J. L-G. is supported by an FPU21/03740 Doctoral grant from the Spanish MCIU. CAA thanks the Spanish Ministry of Science and Innovation under contract number (TED2021-129758B-C33) MCIN/AEI/10.13039/501100011033/European Union NextGeneration EU/PRTR provided gratefully acknowledged financial support. MZ thanks the funding received from the “la Caixa” Foundation (ID 100010434) under the fellowship number LCF/BQ/PR24/12050016.

References

1. A. Y. Alsalloum, B. Turedi, K. Almasabi, X. Zheng, R. Naphade, S. D. Stranks, O. F. Mohammed and O. M. Bakr, Energy Environ. Sci., 2021, 14, 2263–2268.
2. H. Wei, Y. Fang, P. Mulligan, W. Chuirazzi, H.-H. Fang, C. Wang, B. R. Ecker, Y. Gao, M. A. Loi, L. Cao and J. Huang, Nat. Photonics, 2016, 10, 333–339.
3. V.-C. Nguyen, H. Katsuki, F. Sasaki and H. Yanagi, Jpn. J. Appl. Phys., 2018, 57, 04FL10.
4. I. Fernandez-Guillen, C. A. Aranda, P. F. Betancur, M. Vallés-Pelarda, C. Momblona, T. S. Ripolles, R. Abargues and P. P. Boix, Adv. Electron. Mater., 2024, 10, 2300475.
5. Y. Liu, Z. Yang and S. Liu, Advanced Science, 2018, 5, 1700471.
6. Q. Wang, B. Chen, Y. Liu, Y. Deng, Y. Bai, Q. Dong and J. Huang, Energy Environ. Sci., 2017, 10, 516–522.
7. D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522.
8. Z. Gu, Z. Huang, C. Li, M. Li and Y. Song, Sci. Adv., 2018, 4, eaat2390.
9. Z. Lian, Q. Yan, T. Gao, J. Ding, Q. Lv, C. Ning, Q. Li and J.-l. Sun, J. Am. Chem. Soc., 2016, 138, 9409–9412.
10. M. I. Saidaminov, A. L. Abdelhady, G. Maculan and O. M. Bakr, Chem. Commun., 2015, 51, 17658–17661.
11. W. Zia, C. A. Aranda, J. Pospisil, A. Kovalenko, M. Rai, C. Momblona, S. Gorji, G. Muñoz-Matutano and M. Saliba, Chem. Mater., 2023, 35, 5458–5467.
12. S. Kumar, G. Hodes and D. Cahen, MRS Bull., 2020, 45, 478–484.
13. J. T. Tisdale, T. Smith, J. R. Salasin, M. Ahmadi, N. Johnson, A. V. Ievlev, M. Koehler, C. J. Rawn, E. Lukosi and B. Hu, CrystEngComm, 2018, 20, 7818–7825.
14. S. Amari, J.-M. Verilhac, E. Gros D'Aillon, A. Ibanez and J. Zaccaro, Cryst. Growth Des., 2020, 20, 1665–1672.
15. S. Kumar, A. Rukban, J. Sinisi, V. H. Damle and D. Cahen, Cryst. Growth Des., 2022, 22, 7160–7167.
16. V. Sebastian, Nanoscale, 2022, 14, 4411–4447.
17. D. Iglesias, D. Haddad and V. Sans, Chem. Methodol., 2022, 2, e202200031.
18. S. Das Adhikari, S. Masi, C. Echeverría-Arrondo, S. Miralles-Comins, R. S. Sánchez, J. A. Fernandes, V. Chirvony, J. P. Martínez-Pastor, V. Sans and I. Mora-Seró, Adv. Opt. Mater., 2021, 9, 2101024.
19. D. Iglesias, C. Tinajero, J. Luis-Gómez, C. A. Aranda, R. Martinez Cuenca, M. Zanatta and V. Sans, Mater. Today Energy, 2024, 39, 101476.
20. R. W. Epps, M. S. Bowen, A. A. Volk, K. Abdel-Latif, S. Han, K. G. Reyes, A. Amassian and M. Abolhasani, Adv. Mater., 2020, 32, 2001626.
21. T. Savage, N. Basha, J. McDonough, J. Krassowski, O. Matar and E. A. del Rio Chanona, Nature Chemical Engineering, 2024, 1, 522–531.
22. C.-Y. Lee, W.-T. Wang, C.-C. Liu and L.-M. Fu, Chem. Eng. J., 2016, 288, 146–160.
23. S. Bettermann, F. Kandelhard, H.-U. Moritz and W. Pauer, Chem. Eng. Res. Des., 2019, 152, 71–84.
24. G. Gonzalez, I. Roppolo, C. F. Pirri and A. Chiappone, Addit. Manuf., 2022, 55, 102867.
25. C. Parra-Cabrera, C. Achille, S. Kuhn and R. Ameloot, Chem. Soc. Rev., 2018, 47, 209–230.
26. J. Yue, F. H. Falke, J. C. Schouten and T. A. Nijhuis, Lab Chip, 2013, 13, 4855–4863.
27. R. W. Epps, K. C. Felton, C. W. Coley and M. Abolhasani, Lab Chip, 2017, 17, 4040–4047.
28. B. Pinho and L. Torrente-Murciano, Adv. Energy Mater., 2021, 11, 2100918.
29. F. Bateni, S. Sadeghi, N. Orouji, J. A. Bennett, V. S. Punati, C. Stark, J. Wang, M. C. Rosko, O. Chen, F. N. Castellano, K. G. Reyes and M. Abolhasani, Adv. Energy Mater., 2024, 14, 2302303.
30. I. Lignos, R. M. Maceiczyk, M. V. Kovalenko and S. Stavrakis, Chem. Mater., 2020, 32, 27–37.
31. O. Okafor, A. Weilhard, J. A. Fernandes, E. Karjalainen, R. Goodridge and V. Sans, React. Chem. Eng., 2017, 2, 129–136.
32. Y. Haruta, H. Ye, P. Huber, N. Sandor, A. Pavesic Junior, S. Dayneko, S. Qiu, V. Yeddu and M. I. Saidaminov, Nat. Synth., 2024, 3, 1212–1220.
33. A. Salas, M. Zanatta, V. Sans and I. Roppolo, ChemTexts, 2023, 9, 4.
34. V. Sans, N. Karbass, M. I. Burguete, E. García-Verdugo and S. V. Luis, RSC Adv., 2012, 2, 8721–8728.
35. Open CV Library, (https://www.opencv.org).
36. C. Tinajero, VCA Algorithm, (https://www.github.com/catm542-ai/PerovskiteGrowthDetection/blob/main/LICENSE).
37. K. M. Boopathi, B. Martín-García, A. Ray, J. M. Pina, S. Marras, M. I. Saidaminov, F. Bonaccorso, F. Di Stasio, E. H. Sargent, L. Manna and A. L. Abdelhady, ACS Energy Lett., 2020, 5, 642–649.
38. Y. Chen, Y. Lei, Y. Li, Y. Yu, J. Cai, M.-H. Chiu, R. Rao, Y. Gu, C. Wang, W. Choi, H. Hu, C. Wang, Y. Li, J. Song, J. Zhang, B. Qi, M. Lin, Z. Zhang, A. E. Islam, B. Maruyama, S. Dayeh, L.-J. Li, K. Yang, Y.-H. Lo and S. Xu, Nature, 2020, 577, 209–215.
39. K. Schötz, A. M. Askar, W. Peng, D. Seeberger, T. P. Gujar, M. Thelakkat, A. Köhler, S. Huettner, O. M. Bakr, K. Shankar and F. Panzer, J. Mater. Chem. C, 2020, 8, 2289–2300.
40. J. Ding, Z. Lian, Y. Li, S. Wang and Q. Yan, J. Phys. Chem. Lett., 2018, 9, 4221–4226.
41. R. G. Niemann, A. G. Kontos, D. Palles, E. I. Kamitsos, A. Kaltzoglou, F. Brivio, P. Falaras and P. J. Cameron, J. Phys. Chem. C, 2016, 120, 2509–2519.
42. A. A. Petrov, A. A. Ordinartsev, S. A. Fateev, E. A. Goodilin and A. B. Tarasov, Molecules, 2021, 26, 7541.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00099h

---