Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assessing data-driven predictions of band gap and electrical conductivity for transparent conducting materials†
Federico
Ottomano
 a,
John Y.
Goulermas‡
a,
Vladimir
Gusev
a,
John Y.
Goulermas‡
a,
Vladimir
Gusev
 ab,
Rahul
Savani
ab,
Rahul
Savani
 *ac,
Michael W.
Gaultois
*ac,
Michael W.
Gaultois
 b,
Troy D.
Manning
b,
Troy D.
Manning
 b,
Hai
Lin
b,
Hai
Lin
 b,
Teresa Partida
Manzanera
b,
Teresa Partida
Manzanera
 b,
Emmeline G.
Poole
b,
Matthew S.
Dyer
b,
Emmeline G.
Poole
b,
Matthew S.
Dyer
 b,
John B.
Claridge
b,
Jon
Alaria
bd,
Luke M.
Daniels
b,
John B.
Claridge
b,
Jon
Alaria
bd,
Luke M.
Daniels
 b,
Su
Varma
e,
David
Rimmer
e,
Kevin
Sanderson
e and
Matthew J.
Rosseinsky
b,
Su
Varma
e,
David
Rimmer
e,
Kevin
Sanderson
e and
Matthew J.
Rosseinsky
 *b
*b
aDepartment of Computer Science, University of Liverpool, Ashton Street, L69 3BX Liverpool, UK. E-mail: rahul.savani@liverpool.ac.uk
bMaterials Innovation Factory, Department of Chemistry, University of Liverpool, 51 Oxford Street, L7 3NY Liverpool, UK. E-mail: rossein@liverpool.ac.uk
cThe Alan Turing Institute, British Library, 96 Euston Rd., London NW1, UK
dDepartment of Physics, University of Liverpool, Oxford Street, Liverpool L69 7ZE, UK
ePilkington Technology Management Ltd., NSG Group European Technical Centre Hall Lane, Lathom Ormskirk L40 5UF, UK
First published on 28th May 2025
Abstract
Machine Learning (ML) has offered innovative perspectives for accelerating the discovery of new functional materials, leveraging the increasing availability of material databases. Despite the promising advances, data-driven methods face constraints imposed by the quantity and quality of available data. Moreover, ML is often employed in tandem with simulated datasets originating from density functional theory (DFT), and assessed through in-sample evaluation schemes. This scenario raises questions about the practical utility of ML in uncovering new and significant material classes for industrial applications. Here, we propose a data-driven framework aimed at accelerating the discovery of new transparent conducting materials (TCMs), an important category of semiconductors with a wide range of applications. To mitigate the shortage of available data, we create and validate unique experimental databases, comprising several examples of existing TCMs. We assess state-of-the-art (SOTA) ML models for property prediction from the stoichiometry alone. We propose a bespoke evaluation scheme to provide empirical evidence on the ability of ML to uncover new, previously unseen materials of interest. We test our approach on a list of 55 compositions containing typical elements of known TCMs. Although our study indicates that ML tends to identify new TCMs compositionally similar to those in the training data, we empirically demonstrate that it can highlight material candidates that may have been previously overlooked, offering a systematic approach to identify materials that are likely to display TCMs characteristics.
1 Introduction
Data-driven approaches have proposed a valuable change of perspective in the discovery of new functional materials, assisting traditional methods based on experimental investigation and density functional theory (DFT) calculations.1,2 This has been made possible by the consistent growth of available material repositories (Materials Project,3 Materials Platform for Data Science,4 Open Quantum Materials Database,5etc.). In recent years, computational methods driven by Machine Learning (ML) have proven effective in accelerating the exploration of the chemical space, assisting in the identification of dielectric materials,6 nickel-based superalloys7 and superhard materials.8 Despite the broad perspectives opened up by data-driven methods, the horizon of available properties to leverage ML towards the discovery of specific material classes is still quite narrow due to the scarcity and dispersity of available data to train ML models. Many data-driven approaches are based on computed data and thus subject to the approximations and limitations of the calculation themselves. Experimental data are generally not available at scale. Industrial applications frequently require exceptional compounds,9 often exhibiting a counterintuitive combination of two or more chemical properties. This poses significant challenges to current data-driven frameworks, as conventional material databases may lack the necessary information to effectively guide ML in discovering materials tailored at specific applications.Transparent conducting materials (TCMs) fully exemplify the category of exceptional compounds. These represent a class of semiconductors showing simultaneously high electrical conductivity, and low absorption in the range of visible light. This unique behaviour is often enforced in practice by a process known as doping, where additional components are introduced into an intrinsic semiconductor to modulate its optoelectronic properties. Conventional transparent conductors are typically achieved by doping metal oxide semiconductors like In2O3, SnO2, CdO and ZnO. Among various classes of TCMs, tin-doped indium oxide (ITO) stands out as the most common one typically used in high value applications such as displays due to the scarcity of indium, while fluorine-doped tin oxide (FTO) has been widely adopted in larger area applications such as solar control glazing and transparent electrodes for solar cells.10 Although the existing set of TCMs currently addresses the demands imposed by modern optoelectronic applications, the scarcity of raw materials, together with the high costs of vapour deposition techniques, drive researchers to look for alternative solutions.11,12 Previous literature using ML in the TCMs field has investigated the optimization of existing semiconductors,13 or focused on well-defined phase-fields,14,15 and progress has been hindered due to the absence of adequate datasets of experimental optoelectronic properties.
In this work, we propose a data-driven framework to accelerate the discovery of new TCMs. To address the shortage of available data, we create and validate databases of chemical formulas reporting experimental room-temperature conductivity and band gap measurements. We utilize the obtained data to train state-of-the-art (SOTA) ML models that leverage the stoichiometry of input materials, taking into account that composition and the presence of dopants are important for conductivity and band gap, given the typical absence of structural information in materials discovery tasks. Furthermore, we assess the performance of trained models using a custom evaluation framework, designed to determine whether ML can identify previously unseen classes of TCMs. To test the proposed framework, we further utilize a list of 55 experimentally-reported chemical compositions sourced from entries across MPDS,4 Pearson,16 and ICSD databases.17 We use this list to empirically demonstrate the effectiveness of ML in accelerating the identification of new materials that are likely to display TCMs characteristics. The main contributions of this study can be summarized as follows:
• We create two datasets of experimentally-reported optoelectronic properties, (1) a dataset of electrical conductivity is collated and curated from data residing in the MPDS and (2) we augment a published band gap dataset. Both datasets serve as a foundation for training ML models aimed at the identification of TCMs.
• We evaluate SOTA ML models for property-prediction on the proposed experimental datasets.
• We empirically measure the ability of ML models to identify new classes of TCMs through a bespoke evaluation method.
• We compile a list of 55 compositions across various databases and we empirically demonstrate the potential of ML in accelerating the identification of materials that are likely to exhibit TCMs characteristics.
2 Related work
2.1 Computationally-guided search for new TCMs
DFT has primarily enabled a computational exploration of various material classes, including TCMs. Notably, Woods-Robinson et al.13 curated an experimental dataset comprising 74 bulk structures of well-known TCMs with the goal of computing a set of DFT-based descriptors that would capture essential features of these materials for computational screening purposes. Hautier et al.18 employed a high-throughput computational approach to identify oxides with low electron effective mass. They also assessed the band gap of the most promising candidates and proposed potentially novel n-type transparent conducting oxides. The increasing accessibility of materials data has also facilitated data-driven frameworks for ML-guided search for new materials. Sun et al.19 conducted a study that explored the application of ML to predict new TCMs. They utilized data on formation energy and band gap obtained from a Kaggle competition focused on TCMs discovery.19 Despite the promises established by computational modelling, challenges such as high computational cost and systematic errors in DFT-based approaches, along with the scarcity of suitable datasets in the realm of ML, have posed important obstacles to the search for new such materials.2.2 Data-driven identification of optoelectronic properties
Electronic transport and optical data on semiconductors have been gathered and evaluated in the context of thermoelectrics20,21 and of band gap.22,23 Studies have then evaluated different ML approaches in combination with data extracted from the University of California Santa Barbara (UCSB) dataset to predict the electrical conductivity of materials.24,25 Furthermore, DFT-calculated datasets for electron transport properties have also been proposed26–29 and utilized for different tasks ranging from data visualization, to ML property prediction. The availability of experimental datasets has remained rather limited,21,30–32 with most available datasets reaching the order of ∼102 entries. Furthermore, experimental data often encompass minimal chemical diversity, primarily due to the difficulties in obtaining reliable measurements. These two crucial issues (limited datasets size and narrow chemical diversity) heavily limit the application of data-driven methods for the prediction of electronic properties. In the case of band gap, the extensive availability of entries derived from DFT calculations3,5,33 has, in part, mitigated the problem of data scarcity, specifically because this property is more feasible to theoretical simulations compared to electron transport properties. However, significant challenges persist in the prediction of experimental band gaps due to the underestimation of band gaps calculated using the high-throughput DFT approaches of large databases34 and imbalance between metals and non-metals in the available datasets.63 Databases overview
A well-established figure of merit for TCMs can be identified as the ratio of electrical conductivity (σ) to the optical absorption coefficient (α):35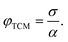 | (1) |
A well-performing TCM should combine high electrical conductivity with low absorption of visible light. Therefore, to accommodate φTCM within a data-driven perspective, it would be necessary to rely on abundance of data in terms of σ and α. Typically, datasets containing these properties are scarce and fragmented across numerous sources in the literature. To address the limitation of optical property data, we adopt the band gap (Eg) as a proxy for optical transparency, motivated by the abundance of this information in the existing literature.3,5 The band gap is a crucial parameter that influences materials' optical properties. A material with a band gap exceeding the energy of visible light (approximately 3 eV) appears generally transparent, as photons within this range lack the energy to excite electrons across the band gap. Thus, by choosing materials with band gaps greater than 3 eV, we can identify materials that are likely to exhibit transparency in the visible spectrum. To enable a ML approach, we have created and validated two experimental datasets of room-temperature conductivity and band gap measurements, to be used as foundation for training SOTA ML models for the discovery of new TCMs. Below, we detail the creation of these databases, a key contribution of this work. Both datasets were tailored to remove unphysical entries by expert assessment and to ensure that a wide range of chemistries were included, resulting in datasets well-balanced between metals and non-metals as discussed below.
3.1 Electrical conductivity dataset
The electrical conductivity dataset was constructed using two primary data sources. Initially, data on conductivity and resistivity, along with associated chemical formulas, were gathered from the Materials Platform for Data Science (MPDS),4 with 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068 entries available as of December 2024. This source was supplemented with the UCSB dataset21 (1794 entries), which provides a range of experimental thermoelectric properties, including electrical conductivity. In total, we compiled a raw dataset comprising 39
068 entries available as of December 2024. This source was supplemented with the UCSB dataset21 (1794 entries), which provides a range of experimental thermoelectric properties, including electrical conductivity. In total, we compiled a raw dataset comprising 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862 material entries with associated conductivity measurements at various temperatures. Several preprocessing steps were conducted on the raw data. Initially, we excluded all pure elements and noble gases and selected all chemical formulas reported within a window of room temperature (298 ± 5 K), reducing the dataset to 14
862 material entries with associated conductivity measurements at various temperatures. Several preprocessing steps were conducted on the raw data. Initially, we excluded all pure elements and noble gases and selected all chemical formulas reported within a window of room temperature (298 ± 5 K), reducing the dataset to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307 entries. Given the experimental nature of utilized data, it is common to encounter several material entries where different measurements are documented for identical chemical formulas at the same temperatures. This variance is inherently linked to the different experimental conditions under which these measurements were conducted. To process raw data in view of statistical estimation, we initially considered the distributions of measurements corresponding to duplicated chemical formulas, discarding those groups associated to a standard deviation exceeding 10 S cm−1.
307 entries. Given the experimental nature of utilized data, it is common to encounter several material entries where different measurements are documented for identical chemical formulas at the same temperatures. This variance is inherently linked to the different experimental conditions under which these measurements were conducted. To process raw data in view of statistical estimation, we initially considered the distributions of measurements corresponding to duplicated chemical formulas, discarding those groups associated to a standard deviation exceeding 10 S cm−1.
Furthermore, we excluded entries with conductivity measurements falling outside of 4 standard deviations from the mean, resulting in a processed dataset containing 8034 material entries. At this stage, we performed a meticulous validation, which involved a line-by-line review of the obtained data by domain experts, referring back to the original literature on suspicious entries, to ensure the accuracy of the reported conductivity measurements, alongside the correctness of the corresponding chemical formulas. To facilitate the validation process, automated nonsense-detection strategies were implemented to systematically identify anomalous conductivity measurements associated to the reported material entries. This involved inferring the oxidation states of the chemical elements in each composition, to ensure the feasibility of different chemical species, in accordance with their corresponding conductivity measurements. First, Comgen36 was used to infer the oxidation states of chemical elements in each composition. These were used to verify the feasibility of the chemical species in the composition, in accordance with the reported conductivity measurement. For example, closed-shell, i.e. fully stoichiometric and undoped, oxides are expected to exhibit low conductivities. Therefore, reported entries corresponding to closed-shell oxides with a conductivity higher than a threshold set to 10−6 S cm−1 were automatically flagged by the nonsense-detection tool for further expert consideration. Additionally, we incorporated experimental conductivities for several chemical families that were absent, such as the alkaline earth oxides, binary and ternary oxides including materials selected to represent each integer transition metal oxidation state as far as available data allow, as well as known TCMs (reported in Table 1). We end up with a final, validated database comprising 8231 material entries, with a mean ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) of 1.09 (log10 (S cm−1)), a median
of 1.09 (log10 (S cm−1)), a median ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) of 2.44 (log10 (S cm−1)) and an interquartile range (50% of data; materials from the 25th to the 75th percentile of log10(σ)) spanning from −0.18 to 3.60 (log10 (S cm−1)). The data distribution of conductivity dataset is shown on the left of Fig. 1. To understand the distribution of metals and non-metals in our conductivity dataset, we utilize the theoretical notion of minimum metallic conductivity (MMC), as introduced in ref. 37. This indicates a threshold below which materials exhibit semiconductor-like behavior. Thus, compounds with conductivity above this threshold display metallic characteristics, while those below it show a non-metallic behavior. For our analysis, we adopt a threshold value of σmin = 103 S cm−1, represented by the purple dotted line in Fig. 1 (left), which has been experimentally observed for many transition metal compounds near the metal–insulator transition.38 Applying this criterion, we identified 3187 metals in the dataset (≈39%), and 5044 materials (≈61%) exhibiting non-metallic conductivity.
of 2.44 (log10 (S cm−1)) and an interquartile range (50% of data; materials from the 25th to the 75th percentile of log10(σ)) spanning from −0.18 to 3.60 (log10 (S cm−1)). The data distribution of conductivity dataset is shown on the left of Fig. 1. To understand the distribution of metals and non-metals in our conductivity dataset, we utilize the theoretical notion of minimum metallic conductivity (MMC), as introduced in ref. 37. This indicates a threshold below which materials exhibit semiconductor-like behavior. Thus, compounds with conductivity above this threshold display metallic characteristics, while those below it show a non-metallic behavior. For our analysis, we adopt a threshold value of σmin = 103 S cm−1, represented by the purple dotted line in Fig. 1 (left), which has been experimentally observed for many transition metal compounds near the metal–insulator transition.38 Applying this criterion, we identified 3187 metals in the dataset (≈39%), and 5044 materials (≈61%) exhibiting non-metallic conductivity.
| TCMs family | N | σ (log10 (S cm−1)) (μ ± s) | E g (eV) (μ ± s) |
|---|---|---|---|
| SnO2: Ga43 | 3 | 2.52 ± 0.03 | 3.77 ± 0.03 |
| SnO2: In42 | 4 | 2.26 ± 0.75 | 3.83 ± 0.09 |
| SnO2: Mn44 | 3 | 2.07 ± 0.01 | 4.07 ± 0.03 |
| SnO2: Ta45 | 3 | 2.52 ± 0.54 | 4.16 ± 0.11 |
| SnO2: Ti46 | 5 | 2.73 ± 0.06 | 3.80 ± 0.06 |
| SnO2: W47 | 4 | 2.23 ± 0.22 | 4.23 ± 0.68 |
| In2O3: Sn50–52 (ITO) | 3 | 2.65 ± 0.64 | 3.73 ± 0.29 |
| ZnO: Al–Sn53 | 4 | 2.58 ± 0.18 | 3.80 ± 0.16 |
| ZnO: Al48 | 3 | 3.43 ± 0.57 | 3.61 ± 0.05 |
| ZnO: Ga49 | 6 | 3.93 ± 0.29 | 3.64 ± 0.05 |
3.2 Band gap dataset
The initial band gap data was sourced from a well-known experimental dataset proposed by ref. 22. The original dataset comprises 6354 material entries with experimental band gap measurements determined from optical and transport measurements. Preprocessing steps were applied to the raw data. Specifically, we excluded groups of duplicated formulas with band gap measurements having a standard deviation greater than 0.1 eV. This preprocessing approach is similar to the one used for creating the matbench_expt_gap dataset, available on the Matbench platform.39 All the entries associated with noble gases and pure elements have been discarded. Additionally, entries with band gap measurements exceeding 4 standard deviations from the mean have been excluded, leading to a processed dataset of 4732 material entries. As in the case of conductivity, the obtained pool of data has been expanded by including experimental band gap measurements of binary and ternary oxides not already in the dataset, along with known TCMs, reported in Table 1. The additional data was taken from the primary literature40–49 after identifying the gaps in the original dataset. These preprocessing steps resulted in a final dataset comprising 4767 material entries, with a mean![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) of 1.04 (eV), a median
of 1.04 (eV), a median ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) of 0.00 (eV), and an interquartile range spanning from 0.00 to 1.93 eV. The data distribution of the band gap dataset is shown on the right in Fig. 1. We observe a balanced representation of metals (Eg = 0) and non-metals (Eg > 0) in the created dataset. The group of metals comprises 2426 material entries (≈51%), while non-metals encompass 2341 entries (≈49%).
of 0.00 (eV), and an interquartile range spanning from 0.00 to 1.93 eV. The data distribution of the band gap dataset is shown on the right in Fig. 1. We observe a balanced representation of metals (Eg = 0) and non-metals (Eg > 0) in the created dataset. The group of metals comprises 2426 material entries (≈51%), while non-metals encompass 2341 entries (≈49%).
4 Methods
In this section, we introduce both the ML models and the evaluation methods considered in this study.4.1 Representation of stoichiometry for Machine Learning approaches
A central aspect in composition-based ML is selecting suitable representations of input stoichiometry that reflect the underlying chemical principles. Given a compound containing elements , where
, where  denotes the (abstract) set of all chemical elements, it is common to consider a mapping
denotes the (abstract) set of all chemical elements, it is common to consider a mapping  that represents a chemical element ai with a vector
that represents a chemical element ai with a vector  . The choice of
. The choice of  determines the nature of the representation and is often tailored to the ML model being employed. In our study, we utilize two distinct representations: Magpie descriptors54 and Mat2vec embeddings.55 Each reflects a different approach to encoding element information, the former being manually crafted, the latter learned from data. To use these element-level features in ML models, a global representation of the compound must be derived. For traditional ML models like linear regression or tree-based algorithms, it is common to construct a composition-based feature vector (CBFV) by aggregating element vectors:
determines the nature of the representation and is often tailored to the ML model being employed. In our study, we utilize two distinct representations: Magpie descriptors54 and Mat2vec embeddings.55 Each reflects a different approach to encoding element information, the former being manually crafted, the latter learned from data. To use these element-level features in ML models, a global representation of the compound must be derived. For traditional ML models like linear regression or tree-based algorithms, it is common to construct a composition-based feature vector (CBFV) by aggregating element vectors: | (2) |
 that represents the entire compound. In our experiments, we apply this aggregation to Magpie descriptors,54 which are handcrafted vectors (df = 132) incorporating physical and chemical attributes (e.g. atomic number, electronegativity etc.), along with statistical operations such as mean and standard deviation. In contrast, Mat2vec embeddings55 are not aggregated via CBFV. Instead, they have been used in tandem with attention-based deep learning architectures to learn relationships between the elements in a compound.56 Mat2vec embeddings are data-driven representations, where each chemical element is assigned to a vector (df = 200) trained from co-occurrence patterns in materials science literature. Mat2vec embeddings have proven particularly effective when paired with deep learning models for property prediction.56,57 This is likely due to the incorporation of a broader material science knowledge learned from scientific literature. As a result, the embeddings can adapt flexibly to specific material–property relationships through nonlinear transformations in neural network models. Specifically, in our experiments we adopt Random Forest (RF)58 with CBFVs obtained from Magpie descriptors, and CrabNet56 paired with Mat2vec embeddings.
that represents the entire compound. In our experiments, we apply this aggregation to Magpie descriptors,54 which are handcrafted vectors (df = 132) incorporating physical and chemical attributes (e.g. atomic number, electronegativity etc.), along with statistical operations such as mean and standard deviation. In contrast, Mat2vec embeddings55 are not aggregated via CBFV. Instead, they have been used in tandem with attention-based deep learning architectures to learn relationships between the elements in a compound.56 Mat2vec embeddings are data-driven representations, where each chemical element is assigned to a vector (df = 200) trained from co-occurrence patterns in materials science literature. Mat2vec embeddings have proven particularly effective when paired with deep learning models for property prediction.56,57 This is likely due to the incorporation of a broader material science knowledge learned from scientific literature. As a result, the embeddings can adapt flexibly to specific material–property relationships through nonlinear transformations in neural network models. Specifically, in our experiments we adopt Random Forest (RF)58 with CBFVs obtained from Magpie descriptors, and CrabNet56 paired with Mat2vec embeddings.
4.2 Models
In the context of materials science, the input tokens can be viewed as elements of a chemical composition. Attention scores, computed via self-attention, can then be utilized to adjust the overall material representation for predicting a specific property of interest. CrabNet has delivered remarkable outcomes in predicting chemical and physical properties of materials when only the composition is available.39 It frequently serves as a SOTA model in scenarios where property predictions are solely reliant on the chemical composition of materials.64–67 For further details regarding the underlying architecture, we refer to the original paper.56
4.3 Evaluation
In our goal of identifying the constitutive properties of the materials of interest, we stay aligned to previous work23,24,65,68 and adopt a regression task. In this context, the goal is to train ML models to predict numerical values associated to the corresponding material properties. It is worth mentioning that a classification task may be considered too, directly determining whether the predicted material meets the specified criteria or not and thus falls into the category of TCMs. However, we argue that adopting a classification approach in this context might sacrifice valuable interpretability. Rather than simply classifying materials as TCMs or non-TCMs, regression models provide continuous numerical predictions for properties like conductivity and band gap. This granularity offers a more precise understanding of each material's performance, allowing us to evaluate how close each material is to meeting the TCM criteria. To assess the performance of trained ML models, we utilize different evaluation schemes: K-fold, a conventional method deeply rooted in statistical learning theory,69 is commonly employed; additionally, Leave-One-Cluster-Out Cross-Validation (LOCO-CV)70 stands as an alternative method targeting the assessment of chemical extrapolation, crucial for discovering new materials, absent in the training data. Furthermore, we introduce a third evaluation method designed to offer nuanced interpretability within the task at hand, namely the discovery of novel TCMs. Details outlining each of these methods are provided in the following. | (3) |
 | (4) |
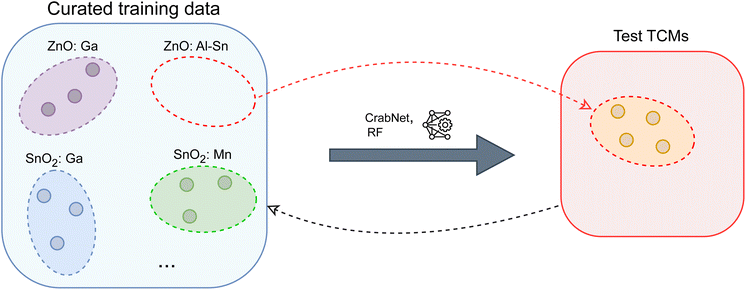
 is the count of correctly predicted families. In Fig. 2, we provide a visual overview of the proposed evaluation scheme.
is the count of correctly predicted families. In Fig. 2, we provide a visual overview of the proposed evaluation scheme.
5 Results
Since the primary task can be formulated as a regression problem, we utilize mean absolute error (MAE) and coefficient of determination (R2) as evaluation metrics to assess models' performance. For band gap prediction, CrabNet undergoes pre-training on a dataset of DFT-computed band gaps sourced from the Materials Project.3 This pre-trained model is then fine-tuned on the curated experimental band gap dataset (results for CrabNet's band gap predictions, shown in Table 3, pertain to this fine-tuned model). During fine-tuning, we choose to retrain all model weights rather than freezing earlier layers. This approach retains knowledge from the larger DFT dataset while allowing the model to fully adapt to experimental trends. We adopt this transfer learning strategy to help mitigate well-known ML limitations in band gap prediction, which often lead to metallic materials being incorrectly classified as semiconductors or insulators.65.1 KFold & LOCO-CV
In Tables 2 and 3 we report evaluation results for ML prediction on both the properties considered. Fig. 3 illustrates the distinct material clusters obtained for the LOCO-CV evaluation setting, projected onto a two-dimensional space for visualization using Principal Component Analysis (PCA). Specific chemical elements included in each cluster are provided in the ESI.† In Fig. 4, we show parity plots related to the K-fold evaluation scheme. | ||
| Fig. 3 LOCO-CV material clusters obtained separately for the conductivity dataset (left) and for the band gap dataset (right), projected onto a two-dimensional space for visualization using Principal Component Analysis (PCA). More details on the compositions included in each cluster can be found in the ESI.† | ||
5.2 Identification of metals and non-metals
Accurate band gap prediction is critical for our ML pipeline. However, challenges arise due to the imbalance between metals and non-metals in material datasets, leading to frequent misclassification of metals as semiconductors or insulators, which can undermine prediction reliability.6 Various strategies have been explored to mitigate this issue. A first attempt might be partitioning the task into two stages. The initial stage entails training a classifier to discriminate materials into metals and non-metals, eventually using loss-weighting schemes to limit the impact of class imbalances. The next stage would involve a regression task on the subset of non-metals by the preceding classification step. These methods have shown a limited effectiveness in practice.6 We believe that an interesting alternative may involve foundation models pre-trained on large multi-domain datasets,77 to be then fine-tuned for specific tasks with limited data.78 However, we argue that a key concern with foundation models is potential data leakage during pre-training, which can lead to overly optimistic results in downstream tasks.In our study, to enhance the accuracy of band gap identification, and thus minimizing the number of false negatives (in our definition, metals that are wrongly predicted as semiconductors or insulators), we have utilized a transfer learning approach. This involved pre-training CrabNet on an extensive dataset sourced from the Materials Project,3 encompassing all entries with chemical formulas and associated band gap information. At the time of data retrieval, 153![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224 material entries with their corresponding band gaps were present in the Materials Project v2023.11.1 database. From this initial dataset, we filtered out chemical formulas that were deemed equivalent in our experimental band gap dataset, encompassing 4767 material entries. We have used the reduced chemical formula as criterion to establish equivalent entries, as atomic proportions are utilized when creating inputs to ML models. To ensure a fair evaluation we have discarded all such entries, ending up with a pretraining dataset consisting of 149
224 material entries with their corresponding band gaps were present in the Materials Project v2023.11.1 database. From this initial dataset, we filtered out chemical formulas that were deemed equivalent in our experimental band gap dataset, encompassing 4767 material entries. We have used the reduced chemical formula as criterion to establish equivalent entries, as atomic proportions are utilized when creating inputs to ML models. To ensure a fair evaluation we have discarded all such entries, ending up with a pretraining dataset consisting of 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714 data points. Further processing is conducted on the resulting data to handle duplicates. We utilize a similar strategy akin to that employed for the experimental Eg dataset. Once duplicated material groups are identified, we eliminate those with a standard deviation exceeding 0.1 eV in terms of the corresponding band gaps. We have used this pool of data to pretrain CrabNet on DFT-calculated band gaps. This is later fine-tuned on our experimental Eg dataset.
714 data points. Further processing is conducted on the resulting data to handle duplicates. We utilize a similar strategy akin to that employed for the experimental Eg dataset. Once duplicated material groups are identified, we eliminate those with a standard deviation exceeding 0.1 eV in terms of the corresponding band gaps. We have used this pool of data to pretrain CrabNet on DFT-calculated band gaps. This is later fine-tuned on our experimental Eg dataset.
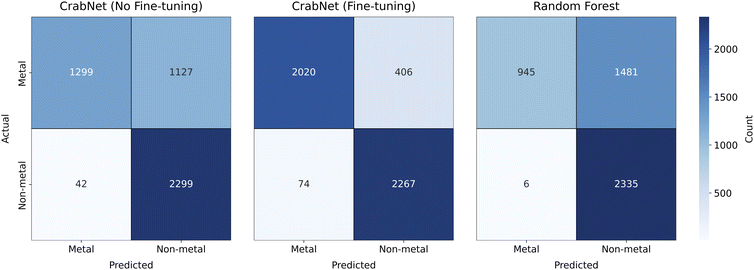
In terms of regression metrics, the fine-tuned model demonstrates enhancements of roughly ≈20% in MAE and ≈10% in terms of R2. To better evaluate the fine-tuned model's effectiveness in reducing false negatives, we investigate the predictions from both the original and fine-tuned models from a classification perspective. For a comprehensive assessment, we also include RF predictions within this evaluation. First, a simple rounding scheme is applied to all the obtained predictions. Specifically, predicted band gaps that are zero when rounded to two decimal places (i.e., values less than 0.005) are assigned a label of 0, indicating metals. Predicted band gaps that round to non-zero values (i.e., 0.005 or greater) are assigned a label of 1, indicating non-metals.
In Fig. 5 we report the confusion matrices related to the different models considered. In terms of CrabNet, a significant decrease is observed in the count of false negatives, from the initial model (1127) to the fine-tuned one (406). This improvement comes with a slight increase in false positives (instances where semiconductors or insulators are incorrectly predicted as metals), rising from 42 in the model without fine-tuning to 74 in the fine-tuned model. For RF, we note a significant tendency to overestimate band gaps, resulting in a large number of metals being incorrectly predicted as non-metals (1481). Interestingly, in terms of false positives, only 6 non-metals are misclassified as metals. Further investigation on this aspect is deferred to future research. Additionally, we utilize Matthews correlation coefficient (MCC)79 as a robust metric to quantify models' performance on binary classification, given its suitability for imbalanced data. It is defined as follows:
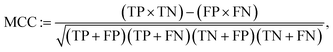 | (5) |
5.3 Leave-one-TCM-family-out
We have discussed the results of two classic evaluation schemes, which carry intrinsic limitations. On the one hand, K-fold provides limited insights on the real possibilities of identifying materials outside the training distribution, frequently yielding overestimated results. On the other hand, LOCO-CV often leads to a noisy evaluation, due to the different size of the obtained material clusters. In Fig. 6, we present the results obtained from the proposed leave-one-TCM-family-out benchmark, showcasing the joint predictions of both RF and CrabNet and for both properties under consideration (σ and Eg). We notice that CrabNet is the only model capable of identifying the majority of TCMs families in the test set, achieving an FDR of 90%, compared to 20% obtained by RF. The main challenge results in the identification of electrical conductivity in these materials. As shown in Fig. 6, RF significantly underestimates this property. However, in the case of band gap prediction, both models correctly identify over 90% of the total materials. We believe this is primarily due to the smoother relationship between stoichiometry and band gap, which simplifies the out-of-distribution evaluation. Overall, our analysis shows a superior robustness of CrabNet in identifying novel stoichiometric combinations that were not present in the training distribution.5.4 Predictions explainability via attention scores
Although the significant breakthroughs enabled by deep learning in materials informatics, the interpretability of these methods still remains severely limited, giving rise to entire branches of research which aim to improve human understanding of ML models (explainable AI).80 The interpretability of ML is indeed a crucial aspect, that acquires further importance in scientific applications, often characterized by collaboration among researchers from various fields, and with different backgrounds. However, current approaches often rely on black-box functions, which offer limited insights into the decision-making process. Notably, the transformer architecture63 provides an inherent mechanism for interpreting its decision-making process through the use of self-attention. The analysis of the underlying attention scores can indeed offer insights about tokens' significance with respect to the surrounding context.To investigate the superior predictive accuracy achieved by CrabNet in conductivity prediction, we examined the corresponding attention scores generated during the leave-one-TCM-family-out evaluation scheme. Specifically, we extracted attention scores from the last layer of the CrabNet encoder, averaged by the corresponding number of attention heads. In this context, we aim to understand whether the model captures complex chemical phenomena related to doping. In this context, we indicate with B = {b1, …, bn} the base elements, i.e. those which are present in the pristine form of the material, while with D = {d1, …, dk} we indicate the dopant elements in the chemical formula. For example, for Zn0.95Al0.05O we have B = {Zn, O} and D = {Al} while for Zn0.97Al0.02Sn0.01O2 we have B = {Zn, O} and D = {Al, Sn}. We categorize entries of the attention matrices into four interaction groups:
• ABB = [Aij] with ei, ej ∈ B for base–base interactions;
• ABD = [Aij] with ei ∈ B, dj ∈ D for base–dopant interactions;
• ADD = [Aij] with di, dj ∈ D for dopant–dopant interactions;
• ADB = [Aij] with di ∈ D, ej ∈ B for dopant–base interactions.
The interactions involving base elements, IB: = ADB ∪ ABB, and those involving dopants, ID: = ABD ∪ ADD, reveal distinct patterns in the attention scores. As shown in Fig. 7 (left), the distribution of ID exhibits a clear shift towards higher attention scores compared to IB, with the medians indicated by dotted lines. This suggests that the model assigns a greater importance to the interactions involving dopants, effectively capturing their critical role in shaping material representations for conductivity prediction.
6 Testing the search for new TCMs
To assess ML models' effectiveness in identifying TCMs, a search was conducted in the Pearson's Crystallographic Database,16 MPDS4 and ICSD17 (based on available data as of December 2024) for compounds containing elements commonly found in known classes of TCMs. Predicting their properties with ML could reveal materials previously overlooked as TCMs. For this experiment, we utilize CrabNet, given its good performance in the proposed leave-one-TCM-family-out evaluation method.We conducted a search for oxide compounds containing combinations of three cations from Zn, Ga, Sn, Al, and In. We also include a small selection of five compositions across MPDS and ICSD of doped binary oxides (ZnO, SnO2 and In2O3), with dopants not present in the training dataset. We end up with a final list comprising 55 compositions shown in Table 4.
We utilize the same TCMs criteria established for the leave-one-TCM-family-out evaluation. Specifically, we are targeting materials with band gap Eg > 3 eV and with conductivity σ > 102 S cm−1. Compositions meeting these criteria are highlighted in Table 4. To provide a global assessment of ML-predicted materials, we define a figure of merit ΦM as:
ΦM = Êg × ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) , , | (6) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) denote the predicted band gap and conductivity (as log10) from ML models' ensembles, respectively. In essence, ΦM will prioritize an optimal trade-off between the two properties. We further utilize a risk-adjusted figure of merit Φstd-adjM,6 defined as
denote the predicted band gap and conductivity (as log10) from ML models' ensembles, respectively. In essence, ΦM will prioritize an optimal trade-off between the two properties. We further utilize a risk-adjusted figure of merit Φstd-adjM,6 defined as| Φstd-adjM: = ΦM − ΦstdM, | (7) |
 is obtained by uncertainty propagation rules for multiplication, and sP denotes the uncertainty produced by an ensemble of ML models (standard deviation corresponding to the predictive mean, see ESI†) for a predicted property P. The risk-adjusted figure of merit Φstd-adjM is essentially defined by subtracting one standard deviation from the original figure of merit ΦM. Compositions with high figure of merit and low uncertainty in their prediction are prioritised over compositions with large uncertainty in their prediction.
is obtained by uncertainty propagation rules for multiplication, and sP denotes the uncertainty produced by an ensemble of ML models (standard deviation corresponding to the predictive mean, see ESI†) for a predicted property P. The risk-adjusted figure of merit Φstd-adjM is essentially defined by subtracting one standard deviation from the original figure of merit ΦM. Compositions with high figure of merit and low uncertainty in their prediction are prioritised over compositions with large uncertainty in their prediction.
From the analysis of the model outputs of the 55 materials selected above, the compositions with the highest Φstd-adjM are, as expected, those most similar to the training dataset; we discuss the results for a selection of the other compositions here. Doped binary oxides are ranked high by ΦM and their band gaps are accurately predicted. Na0.025Zn0.975O0.988 (entry 2) is predicted to have a conductivity of 3.14 (log10(S cm−1)), although measurements reported in the literature are much lower, due to the low concentration of p-type carriers.82 The band gap prediction of Na0.025Zn0.975O0.988 (3.74 eV), compares to the reported experimental measurement of 3.26 eV.101 Thin films of Ca0.04Zn0.96O (entry 3) exhibit a band gap of 3.40 eV and a conductivity of 1.3(log10(S cm−1)),83 though the nature of the conductivity is not discussed in the report and Ca2+ doped ZnO would not be expected to display electrical conductivity. CrabNet predicts a band gap of 4.02 eV and a conductivity of 3.12(log10(S cm−1)) for this composition. Both the band gap and conductivity predictions show consistency with the expected error ranges outlined in Tables 2 and 3. The higher deviation in conductivity predictability is considered acceptable given the inherent complexity of predicting conductivity solely from stoichiometry. Notably, neither {Ca, Zn, O} nor {Na, Zn, O} phase fields are present in the training dataset. For materials containing three cations, indium-containing phase fields rank near the top (Table 4). This is expected, given the well-established significance of In2O3 in the TCMs literature. Materials in the Ga2O3–In2O3–SnO2 phase field102 have been explored as transparent conductors,99 with the highest-ranking material in the phase field Ga0.06In1.92Sn0.02O3.01 (entry 6) having a reported conductivity of 3.43(log10(S cm−1)) and a band gap of 3.04 eV (ref. 84) which the model does well at predicting with 2.92(log10(S cm−1)) for conductivity and 3.52 eV for band gap. The highest Φstd-adjM-ranked material, Al0.67Ga1.33Zn37O40 (entry 1) is a homologous phase ((Ga1−αAlα)2O3(ZnO)m) in the pseudo-ternary Ga2O3–Al2O3–ZnO phase field and has been postulated as a potential thermoelectric81 but not as a TCM, and its band gap and electrical conductivity were not reported. Given that other materials in the Ga2O3–Al2O3–ZnO phase field have very high conductivity (1.0 × 104 to 1.6 × 104 S cm−1)81 it could be expected that the composition Al0.67Ga1.33Zn37O40 could also show high conductivity and an appropriate band gap. The Al doped Zn2SnO4 spinel, Al0.04Sn0.98Zn1.98O4 (entry 32 in Table 4) has been explored as TCM for CIGS solar cells,91 and has a measured band gap of >3.5 eV but low conductivity (12.9(log10(S cm−1))). Other spinel materials have had their conductivity measured, for example GaInZnO4 (entry 54) has a measured conductivity of 2.7 (log10(S cm−1)) which is much higher than predicted (−6.53 (log10(S cm−1))), and a band gap of 3.5 eV (ref. 103) which is predicted very closely (3.26 eV). These two examples show that the model recognizes that doping small amounts of elements into structures can induce conductivity (Al0.04Sn0.98Zn1.98O4) and more stoichiometric closed shell materials are less likely to display conductivity (GaInZnO4). In fact, the measured conductivity in GaInZnO4 results from Ga anti-site defects, GaZn, as the major electron donor in GaInZnO4 (ref. 104) which would be difficult for an ML model to capture, when trained on composition only. This is because the oxidation states present would correspond to filled bands and thus to a low conductivity in terms of electron count, while the model is unable to recognise the self-doping that produces the experimentally observed conductivity.
7 Limitations
While we believe our analysis has provided valuable insights into leveraging data-driven methods for accelerating the discovery of new TCMs, it is important to acknowledge certain limitations inherent in our approach. As with all ML models, they should be used and the outputs assessed by a domain expert for the full benefits to be realised.The first challenge stems from the inherently limited pool of existing TCMs. Given the scarcity of such materials in current databases or literature, our data-driven pipeline is inevitably constrained, impacting the breadth and depth of the proposed analysis.
A second limitation relates to the specific mechanisms underlying the properties of the materials of interest. If the goal is to identify TCMs similar to those in the training dataset, the proposed framework is indeed promising, as shown in Table 4. However, when seeking materials that achieve the desired properties through different mechanisms, our approach is less likely to provide new insights into the underlying chemistry. For example, the model reported here will not distinguish between n-type and p-type conductivity, as highlighted in Section 6, and the outputs will need to be interpreted by the expert user. This is because data-driven frameworks largely depends on the patterns reflected in the training dataset, which may not capture the diversity of mechanisms outside the established categories. This limitation was already highlighted in previous work.9,105
Another limitation arises from the nature of the input data used in this study, which focuses solely on the stoichiometry of materials. In exploratory settings, stoichiometry-based methods provide a valuable and natural baseline since structural information is typically unavailable. However, when additional information is available, it becomes essential to incorporate it effectively. Moving forward, we foresee the integration of more detailed prior knowledge as an important next step. This could involve leveraging recent developments in Large Language Models (LLMs) to encode domain knowledge in chemistry, as suggested by ref. 106 and 78, or incorporating structural data via representation learning schemes.67,107
8 Conclusions
We have proposed a bespoke data-driven framework aimed at leveraging data-driven methods to accelerate the discovery of new TCMs. To address the challenge of limited and sparse material data, we created two experimental datasets of room-temperature conductivity and band gap. This involved the collection of raw data, followed by the application of a meticulous, line-by-line validation to verify the correctness of the reported chemical formulas, alongside the corresponding measurements of electrical conductivity and band gap. The validated datasets were used as foundation for evaluating SOTA ML models for property-prediction from the stoichiometry alone. We have proposed a bespoke evaluation method to empirically measure the potential of ML in identifying new classes of TCMs. Finally, we have compiled a list of 55 compositions sourced across various material databases, to test the effectiveness of ML in accelerate the identification of new TCMs. Overall, our results suggest that ML has the potential to identify new TCMs that are compositionally similar to the ones in the training dataset. Nonetheless, we argue that this holds significant value, as it enables an accelerated identification of compounds that may have been previously overlooked as TCMs.9 Implementation details
CrabNet has been implemented with a batch size of 512, a RobustL1 loss function, a Lamb Lookahead optimizer with stochastic weight averaging, a cyclic learning rate from 1 × 10−4 to 6 × 10−3. For RF, we used a modified scikit-learn implementation to estimate aleatoric and epistemic contributions to uncertainties.60 This involved fitting two RF models: one for point predictions and epistemic uncertainty, quantified as the standard deviation across predictions within trees in the ensemble (n_estimators = 500, min_samples_split = 2, min_samples_leaf = 1), and another for aleatoric uncertainty, which was identical except for min_samples_leaf = 10, as suggested in ref. 60.Code availability
The code supporting the main results of this study is available on GitHub at https://github.com/fedeotto/tcms. Code repository has been archived on Zenodo at https://doi.org/10.5281/zenodo.15366904. Instructions for obtaining representative datasets to run the pipeline are included in the repository.Data availability
The electrical conductivity dataset used in this work was compiled from two primary sources: the UCSB Thermoelectric Database and the Materials Platform for Data Science (MPDS). The original UCSB dataset, consisting of approximately 1100 entries, was expanded as part of ongoing work by the original authors. This updated version, which was used in our study, is available at https://zenodo.org/records/15365345 (DOI: 10.5281/zenodo.15365345). Due to licensing restrictions associated with MPDS data and confidentiality agreements tied to funding, we are unable to publicly release the full experimental conductivity dataset used in this study. Access to raw MPDS data requires a commercial API license, which can be obtained from https://mpds.io/.The original, unmodified band gap dataset, used as the basis for the enriched version proposed in this study, is available through the original publication https://pubs.acs.org/doi/10.1021/acs.jpclett.8b00124 (DOI: 10.1021/acs.jpclett.8b00124). Due to confidentiality agreements tied to funding, we are unable to publicly release the modified band gap dataset used in this study.
Additional band gap data used for pre-training CrabNet were obtained from the Materials Project (version 2023.11.1), accessible via their API at https://materialsproject.org. Data from Pearson's Crystallographic Database are available through institutional or commercial subscription. Access to the Inorganic Crystal Structure Database (ICSD) similarly requires a commercial API license, available at https://www.fiz-karlsruhe.de/icsd.html.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank EPSRC for support under EP/V026887/1 and the Impact Acceleration Account, Pilkington (NSG Group) and Leverhulme Trust through the Leverhulme Research Centre for Functional Materials Design (RC-2015-036).References
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, J. Phys.: Mater., 2019, 2(3), 032001 Search PubMed.
- R. Pollice, G. dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn and C. Lavigne, et al., Data-Driven Strategies for Accelerated Materials Design, Acc. Chem. Res., 2021, 54(4), 849–860 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards and S. Dacek, et al., The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- E. Blokhin and P. Villars, The PAULING FILE Project and Materials Platform for Data Science: From Big Data Toward Materials Genome, Handbook of Materials Modeling: Methods: Theory and Modeling, 2018, pp. 1–26 Search PubMed.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak and M. Aykol, et al., The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1(1), 15010 CrossRef.
- J. Riebesell, T. W. Surta, R. E. A. Goodall, M. W. Gaultois and A. A. Lee, Discovery of high-performance dielectric materials with machine-learning-guided search, Cell Rep. Phys. Sci., 2024, 5(10), 102241 CrossRef.
- B. D. Conduit, T. Illston, S. Baker, D. V. Duggappa, S. Harding and H. J. Stone, et al., Probabilistic neural network identification of an alloy for direct laser deposition, Mater. Des., 2019, 168, 107644 CrossRef.
- T. A. Mansouri, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper and F. Lin, et al., Machine Learning Directed Search for Ultraincompressible, Superhard Materials, J. Am. Chem. Soc., 2018, 140(31), 9844–9853 CrossRef PubMed.
- J. Schrier, A. J. Norquist, T. Buonassisi and J. Brgoch, In Pursuit of the Exceptional: Research Directions for Machine Learning in Chemical and Materials Science, J. Am. Chem. Soc., 2023, 145(40), 21699–21716 CrossRef PubMed.
- A. Way, J. Luke, A. D. Evans, Z. Li, J. S. Kim and J. R. Durrant, et al., Fluorine doped tin oxide as an alternative of indium tin oxide for bottom electrode of semi-transparent organic photovoltaic devices, AIP Adv., 2019, 9(8), 085220 CrossRef.
- S. K. Maurya, H. R. Galvan, G. Gautam and X. Xu, Recent Progress in Transparent Conductive Materials for Photovoltaics, Energies, 2022, 15(22), 8698 CrossRef.
- M. Morales-Masis, S. De Wolf, R. Woods-Robinson, J. W. Ager and C. Ballif, Transparent Electrodes for Efficient Optoelectronics, Adv. Electron. Mater., 2017, 3(5), 1600529 CrossRef.
- R. Woods-Robinson, D. Broberg, A. Faghaninia, A. Jain, S. S. Dwaraknath and K. A. Persson, Assessing High-Throughput Descriptors for Prediction of Transparent Conductors, Chem. Mater., 2018, 30(22), 8375–8389 CrossRef.
- X. Xiong, Y. Sun, Y. Xing and T. Hato, Investigate Machine Learning Methods for Transparent Conductors Prediction, 2018, http://noiselab.ucsd.edu/ECE228_2018/ Search PubMed.
- C. Sutton, C. Bartel, X. Liu, M. Boley, M. Rupp, L. Ghiringhelli, et al., Evaluation of Machine Learning Methods for the Prediction of Key Properties for Novel Transparent Semiconductors, in APS March Meeting Abstracts, 2018, vol. 2018, p. E34.012 Search PubMed.
- P. Villars, K. Cenzual and W. B. Pearson, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds, 2007 Search PubMed.
- D. Zagorac, H. Müller, S. Ruehl, J. Zagorac and S. Rehme, Recent developments in the Inorganic Crystal Structure Database: theoretical crystal structure data and related features, J. Appl. Crystallogr., 2019, 52(5), 918–925 CrossRef PubMed.
- G. Hautier, A. Miglio, D. Waroquiers, G. M. Rignanese and X. Gonze, How Does Chemistry Influence Electron Effective Mass in Oxides? A High-Throughput Computational Analysis, Chem. Mater., 2014, 26(19), 5447–5458 CrossRef.
- Y. Sun, Y. Xing, X. Xiong and T. Hao, Investigate Machine Learning Methods for Transparent Conductors Prediction, 2018, http://noiselab.ucsd.edu/ECE228_2018/Reports/Report3.pdf Search PubMed.
- L. M. Antunes, V. Vikram, J. J. Plata, A. V. Powell, K. T. Butler and R. Grau-Crespo, Machine learning approaches for accelerating the discovery of thermoelectric materials, in Machine Learning in Materials Informatics: Methods and Applications, ACS Publications, 2022, pp. 1–32 Search PubMed.
- M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Data-Driven Review of Thermoelectric Materials: Performance and Resource Considerations, Chem. Mater., 2013, 25(15), 2911–2920 CrossRef.
- Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, Predicting the Band Gaps of Inorganic Solids by Machine Learning, J. Phys. Chem. Lett., 2018, 9(7), 1668–1673 CrossRef PubMed.
- T. Wang, K. Zhang, J. Thé and H. Yu, Accurate prediction of band gap of materials using stacking machine learning model, Comput. Mater. Sci., 2022, 201, 110899 CrossRef.
- M. Mukherjee, S. Satsangi and A. K. Singh, A Statistical Approach for the Rapid Prediction of Electron Relaxation Time Using Elemental Representatives, Chem. Mater., 2020, 32(15), 6507–6514 CrossRef.
- G. S. Na, S. Jang and H. Chang, Predicting thermoelectric properties from chemical formula with explicitly identifying dopant effects, npj Comput. Mater., 2021, 7(1), 106 CrossRef.
- F. Ricci, W. Chen, U. Aydemir, G. J. Snyder, G. M. Rignanese and A. Jain, et al., An ab initio electronic transport database for inorganic materials, Sci. Data, 2017, 4(1), 170085 CrossRef CAS PubMed.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi and A. R. Hight Walker, et al., The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design, npj Comput. Mater., 2020, 6(1), 173 CrossRef.
- M. Yao, Y. Wang, X. Li, Y. Sheng, H. Huo and L. Xi, et al., Materials informatics platform with three dimensional structures, workflow and thermoelectric applications, Sci. Data, 2021, 8(1), 236 CrossRef CAS.
- H. Miyazaki, T. Tamura, M. Mikami, K. Watanabe, N. Ide and O. M. Ozkendir, et al., Machine learning based prediction of lattice thermal conductivity for half-Heusler compounds using atomic information, Sci. Rep., 2021, 11(1), 13410 Search PubMed.
- Y. Katsura, M. Kumagai, T. Kodani, M. Kaneshige, Y. Ando and S. Gunji, et al., Data-driven analysis of electron relaxation times in PbTe-type thermoelectric materials, Sci. Technol. Adv. Mater., 2019, 20(1), 511–520 Search PubMed.
- P. Priya and N. R. Aluru, Accelerated design and discovery of perovskites with high conductivity for energy applications through machine learning, npj Comput. Mater., 2021, 7(1), 90 CrossRef CAS.
- G. S. Na and H. Chang, A public database of thermoelectric materials and system-identified material representation for data-driven discovery, npj Comput. Mater., 2022, 8(1), 214 CrossRef.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii and R. H. Taylor, et al., AFLOW: An automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Insights into Current Limitations of Density Functional Theory, Science, 2008, 321(5890), 792–794 CrossRef CAS.
- R. G. Gordon, Criteria for Choosing Transparent Conductors, MRS Bull., 2000, 25(8), 52–57 CrossRef CAS.
- J. Clymo, C. M. Collins, K. Atkinson, M. S. Dyer, M. W. Gaultois, V. V. Gusev, M. J. Rosseinsky and S. Schewe, Exploration of chemical space through automated reasoning, Angew. Chem., Int. Ed., 2025, 64(6), e202417657 CrossRef CAS PubMed.
- N. F. Mott, Is there ever a minimum metallic conductivity?, Solid-State Electron., 1985, 28(1), 57–59 CrossRef CAS.
- F. A. Chudnovskii, The minimum conductivity and electron localisation in the metallic phase of transition metal compounds in the vicinity of a metal-insulator transition, J. Phys. C: Solid State Phys., 1978, 11(3), L99 CrossRef CAS.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm, npj Comput. Mater., 2020, 6(1), 138 CrossRef.
- J. Portier, G. Campet, C. W. Kwon, J. Etourneau and M. A. Subramanian, Relationships between optical band gap and thermodynamic properties of binary oxides, Int. J. Inorg. Mater., 2001, 3(7), 1091–1094 CrossRef CAS.
- F. Di Quarto, C. Sunseri, S. Piazza and M. C. Romano, Semiempirical Correlation between Optical Band Gap Values of Oxides and the Difference of Electronegativity of the Elements. Its Importance for a Quantitative Use of Photocurrent Spectroscopy in Corrosion Studies, J. Phys. Chem. B, 1997, 101(14), 2519–2525 CrossRef CAS.
- B. Teldja, B. Noureddine, B. Azzeddine and T. Meriem, Effect of indium doping on the UV photoluminescence emission, structural, electrical and optical properties of spin-coating deposited SnO2 thin films, Optik, 2020, 209, 164586 CrossRef CAS.
- P. Sivakumar, H. S. Akkera, T. Ranjeth Kumar Reddy, G. Srinivas Reddy, N. Kambhala and N. Nanda Kumar Reddy, Influence of Ga doping on structural, optical and electrical properties of transparent conducting SnO2 thin films, Optik, 2021, 226, 165859 Search PubMed.
- I. Arora, K. Malhotra, A. Mahajan and P. Kumar, Structural, optical and electrical characterization of spin coated SnO2:Mn thin films, Mater. Today: Proc., 2021, 36, 697–700 Search PubMed.
- V. Uwihoreye, Z. Yang, J. Y. Zhang, Y. M. Lin, X. Liang and L. Yang, et al., Transparent conductive SnO2 thin films via resonant Ta doping, Sci. China Mater., 2023, 66(1), 264–271 CrossRef CAS.
- P. Sivakumar, H. S. Akkera, T. R. Kumar Reddy, Y. Bitla, V. Ganesh and P. M. Kumar, et al., Effect of Ti doping on structural, optical and electrical properties of SnO2 transparent conducting thin films deposited by sol-gel spin coating, Opt. Mater., 2021, 113, 110845 CrossRef CAS.
- M. Wang, Y. Gao, Z. Chen, C. Cao, J. Zhou and L. Dai, et al., Transparent and conductive W-doped SnO2 thin films fabricated by an aqueous solution process, Thin Solid Films, 2013, 544, 419–426 CrossRef CAS.
- R. K. Shukla, A. Srivastava, A. Srivastava and K. C. Dubey, Growth of transparent conducting nanocrystalline Al doped ZnO thin films by pulsed laser deposition, J. Cryst. Growth, 2006, 294(2), 427–431 CrossRef CAS.
- R. S. Ajimsha, A. K. Das, P. Misra, M. P. Joshi, L. M. Kukreja and R. Kumar, et al., Observation of low resistivity and high mobility in Ga doped ZnO thin films grown by buffer assisted pulsed laser deposition, J. Alloys Compd., 2015, 638, 55–58 CrossRef.
- L. Shen, Y. An, R. Zhang, P. Zhang, Z. Wu and H. Yan, et al., Enhanced room-temperature ferromagnetism on (In0.98−xCoxSn0.02)2O3 films: magnetic mechanism, optical and transport properties, Phys. Chem. Chem. Phys., 2017, 19, 29472–29482 RSC.
- H. R. Fallah, M. Ghasemi, A. Hassanzadeh and H. Steki, The effect of annealing on structural, electrical and optical properties of nanostructured ITO films prepared by e-beam evaporation, Mater. Res. Bull., 2007, 42(3), 487–496 CrossRef.
- A. Ambrosini, A. Duarte, K. R. Poeppelmeier, M. Lane, C. R. Kannewurf and T. O. Mason, Electrical, Optical, and Structural Properties of Tin-Doped In2O3–M2O3 Solid Solutions (M=Y, Sc), J. Solid State Chem., 2000, 153(1), 41–47 CrossRef.
- H. Guendouz, A. Bouaine and N. Brihi, Biphase effect on structural, optical, and electrical properties of Al-Sn codoped ZnO thin films deposited by sol-gel spin-coating technique, Optik, 2018, 158, 1342–1348 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2(1), 16028 CrossRef.
- V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong and O. Kononova, et al., Unsupervised word embeddings capture latent knowledge from materials science literature, Nature, 2019, 571(7763), 95–98 CrossRef PubMed.
- A. Y. T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, Compositionally restricted attention-based network for materials property predictions, npj Comput. Mater., 2021, 7(1), 77 CrossRef.
- R. E. A. Goodall and A. A. Lee, Predicting materials properties without crystal structure: deep representation learning from stoichiometry, Nat. Commun., 2020, 11(1), 6280 CrossRef PubMed.
- L. Breiman, Random Forests, Mach. Learn., 2001, 45(1), 5–32 CrossRef.
- V. Venkatraman, The utility of composition-based machine learning models for band gap prediction, Comput. Mater. Sci., 2021, 197, 110637 CrossRef.
- J. Riebesell, Probabilistic Data-Driven Discovery of Thermoelectric Materials, MPhil thesis, University of Cambridge, 2019, https://github.com/janosh/thermo.
- S. J. S. Chelladurai, K. Upreti, M. Verma, M. Agrawal, J. Garg and R. Kaushik, et al., Prediction of Mechanical Strength by Using an Artificial Neural Network and Random Forest Algorithm, J. Nanomater., 2022, 2022, 7791582 CrossRef.
- A. Sonpal, M. A. F. Afzal, Y. An, A. Chandrasekaran and M. D. Halls, Benchmarking Machine Learning Descriptors for Crystals, American Chemical Society, 2022. vol. 1416 of ACS Symposium Series, pp. 111–126 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, et al., Attention is All you Need, in Advances in Neural Information Processing Systems, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, et al., Curran Associates, Inc., 2017, vol. 30, https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf Search PubMed.
- S. G. Baird, T. Q. Diep and T. D. Sparks, DiSCoVeR: a materials discovery screening tool for high performance, unique chemical compositions, Digital Discovery, 2022, 1, 226–240 RSC.
- C. J. Hargreaves, M. W. Gaultois, L. M. Daniels, E. J. Watts, V. A. Kurlin and M. Moran, et al., A database of experimentally measured lithium solid electrolyte conductivities evaluated with machine learning, npj Comput. Mater., 2023, 9(1), 9 CrossRef CAS.
- L. M. Antunes, K. T. Butler and R. Grau-Crespo, Predicting thermoelectric transport properties from composition with attention-based deep learning, Mach. Learn.: Sci. Technol., 2023, 4(1), 015037 Search PubMed.
- J. Lee, C. Park, H. Yang, S. Han and W. Lim, CLCS: Contrastive Learning between Compositions and Structures for practical Li-ion battery electrodes design, in AI for Accelerated Materials Design – NeurIPS 2023 Workshop, 2023, https://openreview.net/forum?id=FfvByyoVAO Search PubMed.
- T. Nguyen-Sy, Q. D. To, M. N. Vu, T. D. Nguyen and T. T. Nguyen, Predicting the electrical conductivity of brine-saturated rocks using machine learning methods, J. Appl. Geophys., 2021, 184, 104238 CrossRef.
- T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Springer Series in Statistics, Springer New York Inc., New York, NY, USA, 2001 Search PubMed.
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling and S. Paradiso, et al., Can machine learning identify the next high-temperature superconductor? Examining extrapolation performance for materials discovery, Mol. Syst. Des. Eng., 2018, 3, 819–825 RSC.
- F. Ottomano, G. De Felice, V. V. Gusev and T. D. Sparks, Not as simple as we thought: a rigorous examination of data aggregation in materials informatics, Digital Discovery, 2024, 3(2), 337–346 RSC.
- K. Li, B. DeCost, K. Choudhary, M. Greenwood and J. Hattrick-Simpers, A critical examination of robustness and generalizability of machine learning prediction of materials properties, npj Comput. Mater., 2023, 9(1), 55 CrossRef.
- S. S. Omee, N. Fu, R. Dong, M. Hu and J. Hu, Structure-based out-of-distribution (OOD) materials property prediction: a benchmark study, npj Comput. Mater., 2024, 10(1), 144 CrossRef.
- S. P. Lloyd, Least squares quantization in PCM, IEEE Trans. Inf. Theory, 1982, 28, 129–136 CrossRef.
- S. Durdy, M. W. Gaultois, V. V. Gusev, D. Bollegala and M. J. Rosseinsky, Random projections and kernelised leave one cluster out cross validation: universal baselines and evaluation tools for supervised machine learning of material properties, Digital Discovery, 2022, 1, 763–778 RSC.
- T. Hofmann, B. Schölkopf and A. J. Smola, Kernel methods in machine learning, Ann. Stat., 2008, 36(3), 1171–1220 Search PubMed.
- N. Shoghi, A. Kolluru, J. R. Kitchin, Z. W. Ulissi, C. L. Zitnick and B. M. Wood, From Molecules to Materials: Pre-training Large Generalizable Models for Atomic Property Prediction, 2023 Search PubMed.
- K. Jablonka, P. Schwaller, A. Ortega-Guerrero and B. Smit, Leveraging large language models for predictive chemistry, Nat. Mach. Intell., 2024, 6, 1–9 CrossRef.
- D. Chicco and G. Jurman, The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation, BMC Genomics, 2020, 21(1), 6 CrossRef.
- P. Linardatos, V. Papastefanopoulos and S. Kotsiantis, Explainable AI: A Review of Machine Learning Interpretability Methods, Entropy, 2021, 23(1), 18 CrossRef.
- Y. Michiue, H. W. Son and T. Mori, Utilizing a unified structure model in (3+1)-dimensional superspace to identify a homologous phase (Ga1−αAlα)2O3(ZnO)m in ZnO-based thermoelectric composites, J. Appl. Crystallogr., 2020, 53(6), 1542–1549 CrossRef CAS.
- N. Erdogan, T. Kutlu, N. Sedefoglu and H. Kavak, Effect of Na doping on microstructures, optical and electrical properties of ZnO thin films grown by sol-gel method, J. Alloys Compd., 2021, 553, 160554 CrossRef.
- H. Mahdhi, K. Djessas and Z. B. Ayadi, Synthesis and characteristics of Ca-doped ZnO thin films by rf magnetron sputtering at low temperature, Mater. Lett., 2018, 214, 10–14 CrossRef CAS.
- A. Dolgonos, S. A. Wells, K. R. Poeppelmeier and T. O. Mason, Phase stability and optoelectronic properties of the bixbyite phase in the gallium–indium–tin–oxide system, J. Am. Ceram. Soc., 2015, 98(2), 669–674 CrossRef CAS.
- A. Ahmad, M. Umer, X. Tan, R. Liu, F. Mohmad, M. Hussain, G. K. Ren and Y. H. Lin, High-temperature electrical and thermal transport behaviors of In2O3-based ceramics by Zn–Sn co-substitution, J. Appl. Phys., 2018, 123(24), 245108 CrossRef.
- R. K. Sahu, R. Vispute, S. Dhar, D. Kundaliya, S. S. Manoharan and T. Venkatesan, et al., Enhanced conductivity of pulsed laser deposited n-InGaZn6O9 films and its rectifying characteristics with p-SiC, Thin Solid Films, 2009, 517(5), 1829–1832 CrossRef CAS.
- S. Préaud, C. Byl, F. Brisset and D. Berardan, SPS-assisted synthesis of InGaO3 (ZnO) m ceramics, and influence of m on the band gap and the thermal conductivity, J. Am. Ceram. Soc., 2020, 103(5), 3030–3038 CrossRef.
- Y. S. Lee, C. H. Chang, Y. C. Lin, R. J. Lyu, H. C. Lin and T. Y. Huang, Effects of Ga2O3 deposition power on electrical properties of cosputtered In–Ga–Zn–O semiconductor films and thin-film transistors, Jpn. J. Appl. Phys., 2014, 53(5S3), 05HA02 CrossRef.
- M. Nakamura, N. Kimizuka and T. Mohri, The phase relations in the In2O3-Ga2ZnO4-ZnO system at 1350 °C, J. Solid State Chem., 1991, 93(2), 298–315 Search PubMed.
- A. Suresh, P. Gollakota, P. Wellenius, A. Dhawan and J. F. Muth, Transparent, high mobility InGaZnO thin films deposited by PLD, Thin Solid Films, 2008, 516(7), 1326–1329 CrossRef.
- H. Jung, Y. Park, S. Gedi, V. R. M. Reddy, G. Ferblantier and W. K. Kim, Al-doped zinc stannate films for photovoltaic applications, Korean J. Chem. Eng., 2020, 37, 730–735 CrossRef.
- M. Orita, H. Ohta, M. Hirano, S. Narushima and H. Hosono, Amorphous transparent conductive oxide InGaO3 (ZnO) m (mle 4): a Zn4s conductor, Philos. Mag. B, 2001, 81(5), 501–515 CrossRef.
- E. S. Anannikov, T. A. Markin, I. A. Solizoda, G. M. Zirnik, D. A. Uchaev and A. S. Chernukha, et al., Synthesis and research of physical and chemical properties of InGaZn2O5 prepared by nitrate-glycolate gel decomposition method. Nanosystems: Physics, Chemistry, Mathematics, 2024, 15(6), 806–813 Search PubMed.
- K. Rickert, A. Huq, S. H. Lapidus, A. Wustrow, D. E. Ellis and K. R. Poeppelmeier, Site Dependency of the High Conductivity of Ga2In6Sn2O16: The Role of the 7-Coordinate Site, Chem. Mater., 2015, 27(23), 8084–8093 Search PubMed.
- Q. Li, L. Zhang, C. Tang, P. Zhao, C. Yin and J. Yin, Synthesis of Zn (InxGa1−x)2O4 solid-solutions with tunable band-gaps for enhanced photocatalytic hydrogen evolution under solar-light irradiation, Int. J. Hydrogen Energy, 2020, 45(11), 6621–6628 CrossRef.
- J. Rezek, J. Houška, M. Procházka, S. Haviar, T. Kozák and P. Baroch, In-Ga-Zn-O thin films with tunable optical and electrical properties prepared by high-power impulse magnetron sputtering, Thin Solid Films, 2018, 658, 27–32 Search PubMed.
- J. Grover, S. Arrasmith and D. D. Edwards, Thermoelectric properties and impedance spectroscopy of polycrystalline samples of the beta-gallia rutile intergrowth, (Ga,In)4 (Sn,Ti)5O16, J. Solid State Chem., 2012, 191, 129–135 CrossRef.
- E. Finley and J. Brgoch, Deciphering the loss of persistent red luminescence in ZnGa2O4: Cr3+ upon Al3+ substitution, J. Mater. Chem. C, 2019, 7(7), 2005–2013 RSC.
- D. Edwards, T. Mason, F. Goutenoire and K. Poeppelmeier, A new transparent conducting oxide in the Ga2O3-In2O3-SnO2 system, Appl. Phys. Lett., 1997, 70(13), 1706–1708 CrossRef.
- K. Sakoda and M. Hirano, Formation of complete solid solutions, Zn(AlxGa1−x)2O4 spinel nanocrystals via hydrothermal route, Ceram. Int., 2014, 40(10), 15841–15848 Search PubMed.
- M. A. Basyooni, M. Shaban and A. M. El Sayed, Enhanced gas sensing properties of spin-coated Na-doped ZnO nanostructured films, Sci. Rep., 2017, 7(1), 41716 CrossRef PubMed.
- D. D. Edwards and T. O. Mason, Subsolidus Phase Relations in the Ga2O3-In2O3-SnO2 System, J. Am. Ceram. Soc., 1998, 81(12), 3285–3292 CrossRef.
- M. Orita, H. Tanji, M. Mizuno, H. Adachi and I. Tanaka, Mechanism of electrical conductivity of transparent InGaZnO4, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(3), 1811 CrossRef.
- A. Murat, A. U. Adler, T. O. Mason and J. E. Medvedeva, Carrier generation in multicomponent wide-bandgap oxides: InGaZnO4, J. Am. Chem. Soc., 2013, 135(15), 5685–5692 CrossRef PubMed.
- S. K. Kauwe, J. Graser, R. Murdock and T. D. Sparks, Can machine learning find extraordinary materials?, Comput. Mater. Sci., 2020, 174, 109498 CrossRef.
- T. Xie, Y. Wan, Y. Zhou, W. Huang, Y. Liu, Q. Linghu, et al., Large Language Models as Master Key: Unlocking the Secrets of Materials Science, 2023 Search PubMed.
- N. Lee, H. Noh, G. S. Na, T. Fu, J. Sun and C. Park, Stoichiometry Representation Learning with Polymorphic Crystal Structures, arXiv, 2023, preprint, arXiv:2312.13289, DOI:10.48550/arXiv.2312.13289.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00010f |
| ‡ Deceased in May 2022. |
| This journal is © The Royal Society of Chemistry 2025 |