Evolutionary machine learning of physics-based force fields in high-dimensional parameter-space

Abstract

This work presents the Alexandria Chemistry Toolkit (ACT), an open-source software for machine learning of physics-based force fields (FFs) from scratch, based on user-specified potential functions. In this approach, a set of FF parameters for molecular simulation is described as a chromosome consisting of atom and bond genes. The accuracy of a FF, that is how well quantum chemical training data are reproduced, determines the fitness of the chromosome. The ACT implements a hierarchical parallel scheme that iterates between a genetic algorithm and Monte-Carlo steps for global and local search, to find “genomes” with high fitness. As a sample application, genome evolution is performed to create physical models that allow the prediction of properties of organic molecules in the gas and liquid phases. Evaluation of the prediction accuracy of different models showcases how force field science can contribute to systematically improve prediction accuracy of physicochemical observables.

---

The recent revolution in data-driven modeling has encouraged some to proclaim “the end of theory in science” but the notion that data should be considered more important than theory was introduced by Francis Bacon already in the 1600s.³⁵ In chemistry, it is clear that the advent of high-accuracy quantum chemical databases²⁹ holds opportunities as well as challenges for physics-based models. Opportunities, since richer and more complete data sets allow the refinement of models.⁵⁴ Challenges, since large data sets may help to uncover flaws in existing models through systematic benchmarks.⁶ Are existing models sufficiently accurate to explain the complexity of the chemical data? Do the underlying mathematical formulae and physical assumptions impose limitations? On the other hand, does the lack of pre-specified structure and chemical concepts in data-driven models enable them to discover patterns from data, with the promise of automating and speeding up developments rather than hoping for serendipitous discoveries?.^1,8 As important as these semantic arguments, is the practical desire to simultaneously enhance and understand discoveries in molecular sciences in terms of a comprehensive model. As it happens, chemical big data²⁹ is being used to guide development of physics-based models and vice versa^39,40,49 even though artificial intelligence-based methods struggle to capture the complex physics in biomolecular interactions.² This strongly suggests that theory and data should be used in conjunction to speed up progress in, for instance, drug or material design.¹

The lack of software infrastructure for systematic global/local optimization is a key reason that physics-based models have not been able to make efficient use of big data in chemistry.⁵⁴ Despite effort for systematic force field parametrization,⁶⁵ almost all widely-used molecular models that are based on the principles of molecular mechanics have been developed based on small data sets through iterative trial-and-error procedures, often manually.¹⁰ Nevertheless, the chemical and physical intuition that has been put into these models during “training” should neither be forgotten nor neglected.¹⁸ Indeed, the usage of machine learning and artificial intelligence methods does not invalidate the laws of physics.⁶⁷ It is therefore the combination of physics, big data, and training of large parameter sets that will help us move toward chemical accuracy in molecular models. Very recently, two new force fields were derived from large quantum chemistry datasets, but just to model the bonded energy terms.^48,50 Here, we focus on training the non-bonded forces from scratch.

With this paper, the open-source Alexandria Chemistry Toolkit (ACT, Fig. 1) is released to the research community as an extensible and scalable software suite for rapid development of force field models using large databases of molecular properties.⁵⁹ The ACT includes pipelines to work with multiple databases of quantum chemistry calculations^5,12,17,53 and experimental data such as electric moments or vibrational frequencies. Data from other force fields can be used as well. As insights progressed during the development of ACT^30,31 we decided to focus on training intermolecular FF parameters on energy components derived using symmetry adapted perturbation theory²³ (SAPT) calculations of dimeric compounds, although total intermolecular energies from other methods can be used as well.^12,53 Intramolecular forces are derived from quantum-chemistry calculations of out-of-equilibrium conformations of compounds. For both inter- and intramolecular forces extensive sampling of the potential energy surface is needed (see Methods). The functionality that the ACT provides has been termed “force field science” in a recent review of the open force field project, and it was noted that this is in fact “nearly unexplored”,⁶⁶ emphasizing the need for such tools in the research community.

Fig. 1 Gene pool containing N copies of force field genomes and flowchart of the training of FF genomes in the ACT. (A) Each genome consists of atom genes, including the atomic polarizability α (in case of polarizable models), the Gaussian charge-spreading width ζ, charge q, the van der Waals parameters σ, ε and more (depending on van der Waals function used) and, finally, the electronegativity χ and hardness η. For bonds, the parameters are listed for a Morse potential³⁸ namely the equilibrium bond length b₀, the steepness β and the well-depth D₀ and, in addition, the bond electronegativity Δχ and bond hardness Δη. Three out of N individuals in the population are plotted, colors indicating that parameters have different values (“genes”) in different individuals. (B) Flowchart for the Alexandria Chemistry Toolkit. Starting from quantum chemistry data and a physical model, parameters can be trained to reproduce the data and evaluated using a test set. The resulting force field can be evaluated on experimental data using both ACT and OpenMM.¹⁴

Three training algorithms are implemented in the ACT⁵⁹ for global as well as local navigation in a high-dimensional parameter space of molecular-mechanics force fields, to reproduce properties of a large set of either monomers or non-covalent dimers. The parameters of a force field can be arranged as a vector of floating point numbers and thus it may be ordered like a genome consisting of atom and bond genes. That is, parameters dependent on atoms only for non-bonded interactions, or parameters describing bonded forces (including angular and torsional forces) are ordered in a linear array (Fig. 1A). This analogy suggests that a force field genome can be improved using evolutionary operators such as chromosomal crossover and point mutations and therefore a genetic algorithm (GA) or a Markov Chain Monte Carlo (MCMC) can be used for this purpose. GA operates using crossovers and completely random point mutations while MCMC induces point mutations according to a Metropolis criterion, with the aim to achieve local improvement of the gene. In a real chromosome, related genes are often located close to each other to make sure that they are inherited together. We try to mimic this (Fig. 1A) but we note that it is not a priori clear what FF genes are related to each other. Finally, a hybrid GA/MCMC algorithm is implemented, combining the strengths of both these algorithms. Here, GA performs chromosomal crossovers at the top level and MCMC induces point mutations which together promote diversity in the FF gene pool. The software will typically train parameters on one (“train”) subset of compounds or compound dimers and evaluate convergence on another (“test”) subset.

The fitness function for model training is given by

F(Θ) = ΩX²(Θ) + Λ(Θ) (1)

where Θ is the force field genome of parameters and X² a vector representation of residuals in the least-squares form weighted by vector Ω. The elements of X² are the intermolecular SAPT energy components (Section S2†) or total intermolecular energies from either SAPT or other sources.²⁹ In addition, the valence bond FF parameters can be trained on intramolecular energies and forces from quantum-chemistry calculations of out-of-equilibrium compounds, but that was not applied in this work. Λ in eqn (1) adds a penalty to keep observables that are not trained directly within reasonable bounds. This can be applied, for instance, to the charge on hydrogen atoms which can in this manner be prevented from becoming negative.

It was estimated that a biomolecular force field like Amber99 employs around 1500 parameters, including the tabulated charges.⁵⁴ While the number of parameters to be trained by the ACT depends on the functional form used (see ACT manual⁵⁸), it will usually be somewhat fewer than Amber99; the main reason being that charges are not tabulated but generated based on either the charge equilibration method⁴⁵ or the split-charge equilibration method.⁶² For completeness, it should be noted that charges can be provided by the user of the ACT software as well. Nevertheless, the optimization of so many parameters still is a formidable task. To make this tractable, the complete process is divided into two steps (Fig. 1B). First, parameters for models of user-defined complexity are trained to reproduce intermolecular energies from quantum chemistry, either the total interaction energy or SAPT energy components and, second, to reproduce intramolecular energies from quantum chemistry (see Methods). The use of SAPT energy components facilitates independent training of groups of parameters which is known to lead to better transferability.³³ It also reduces the search space, since parameters can be trained independently to the energy components which should lead to faster convergence. Since parameters governing intermolecular forces are trained first, the intramolecular potentials such as bond, angle and dihedrals effectively provide the remainder of the total energy of a compound. The training of intramolecular parameters aims to yield a molecular potential energy surface to reproduce enthalpies of formation and, through this, frequencies and thermochemical properties.⁵⁶ Once training has converged, validation should be performed using independent experimental data from both the gas phase, e.g. second virial coefficients, and the condensed phase, e.g. using liquid density and vaporization enthalpies.³¹

Results

Comparison of training algorithms

The three algorithms were tested on hydrogen halides, which may serve as an example of small molecules that are used extensively in both industry and laboratory settings. A SAPT dataset of hydrogen halides (HF, HCl, HBr, HI) dimers was created (see Methods, Table S1†) and two different van der Waals potentials were trained to reproduce the SAPT energies. Since the training set only contains the homodimers, the test set of heterodimers is a challenge for force field transferability. For the 12-6 Lennard-Jones potential, all algorithms yield similar RMSDs (Table S2†). For the 14-7 potential¹⁹ (Section S1†), the MCMC and HYBRID algorithms yield the same RMSD from the SAPT reference data (total interaction energy) for both train and test sets while the GA is somewhat more variable. Interestingly, the GA locates a solution for the 14-7 potential in the training with 512 individuals that has slightly higher RMSD than the best HYBRID or MCMC, but a much lower RMSD for the test set than either HYBRID or MCMC (Table S2†). This suggests on the one hand that training of the 14-7 potential for these simple molecules may lead to over-fitting (HYBRID, MCMC, Table S2†), but on the other hand that with prudent management of the training samples it should be possible to obtain predictive power beyond the training data set (GA, Table S2†). It may be that some potentials are more prone to overfitting than others, but this needs further studies. Alternatively, since the training set used homodimers and the test set used heterodimers, it could be that the combination rules used for the 14-7 potential that worked well for noble gases³¹ do not work as well for halogen atoms. It is also clear that the 14-7 potential provides a much lower RMSD from SAPT than the 12-6 potential, which may serve as a first example of the force field science that is possible with the ACT.

Training becomes more challenging when increasing the number of parameters. To evaluate the raw optimization power of the three algorithms a system of sixteen dimers consisting of eight compounds (water, alcohols, diethylene-glycol, Table S3†) was used with 70 parameters to train. No test set was used here, which is not recommended for real model training, but that was not the purpose here. We performed each of 10 trainings with the HYBRID, GA and MCMC algorithms and the algorithms were used in such a way that the total number of energy evaluations was identical. We found the HYBRID algorithm produced an average RMSD of 0.92 kJ mol⁻¹, MCMC 1.03 kJ mol⁻¹ and the GA algorithm yielded an average RMSD of 2.1 kJ mol⁻¹ (Fig. 2A) suggesting the HYBRID algorithm is more likely to find good parameter sets than the other algorithms. This is corroborated by the tests on hydrogen halides where GA does not reproducibly yield the same low fitness values for the 14-7 potentials as do HYBRID and MCMC (Table S2†). However, care should be taken to prevent over-fitting and further meta-parameter studies are needed.³⁴

Fig. 2 Properties of the ACT algorithms. (A) Histogram of RMSD produced by the three algorithms in ACT after training a polarizable force field for 16 dimers (Table S3†). The same number of fitness evaluations is used for both algorithms and each training was run ten times starting from random parameters with different random number seeds. The 14-7 potential was used and virtual sites corresponding to σ-holes on water.³⁰ In these trainings just 1 bonded neighbor was excluded. (B) Strong scaling for trainings using the GA, HYBRID and MCMC algorithms on the same dataset (except water–water) and a total of 466 dimer structures. Benchmarking was performed on a Cray with 1–8 nodes consisting of dual AMD EPYC 7742 64-core processors. For these training a non-polarizable model was used with the 14-7 potential¹⁹ and Gaussian charge distributions,¹⁶ both with 2 excluded neighbors.

Fig. S1† explain the parallellization scheme used in force field training in the ACT. Parallel scaling is limited by the amount of global communication, which happens once per generation in the GA but never in the MCMC algorithm (see Section S3† for details). Scaling for the HYBRID method is therefore in-between GA and MCMC (Fig. 2B). MCMC, that uses no communication at all during training even shows superlinear scaling, likely due to favorable memory caching. Table S12† confirms that GA scales less well than the other two methods (cf.Fig. 2B). The results also confirm that GA does not reproducibly find the genome with the lowest RMSD.

Application to organic compounds

The ultimate goal of the development of the ACT is to produce, phase-transferable⁶³ physics-based force fields, in a systematic manner.⁵⁴ Before doing so, it is important to validate that the software can reproduce an existing force field. Therefore, a data set consisting of water, alcohols and alkanes was created with over 2000 SAPT calculations (see Methods). Then, an ACT force field file corresponding to OPLS2020 (ref. 26) including the TIP4P water model²⁵ was created and the energies and energy components were computed using the same dimer conformations. The correlation between SAPT and OPLS2020 energies are shown in Fig. 3. The electrostatic energies due to OPLS2020 are too high and the exchange energies are too low. However, the total interaction energy is reproduced quite well, due to a significant compensation of errors between the two terms that is common for non-polarizable pairwise-additive force fields.⁶⁸

Fig. 3 Correlation between SAPT and force field energy components. Comparison with the OPLS2020 force field²⁶ and the TIP4P²⁵ water model and model BC derived here, that was trained on SAPT energy components (see Table 1). (A) Coulomb (electrostatics), (B) dispersion, (C) exchange and (D) total energy. Data set consisting of 2114 dimers of water, alcohols and alkanes (Table S4†). RMSD and Pearson correlation coefficient r² are indicated in each plot. The black line in all plots indicates y = x.

We then proceed to try and “rediscover” the OPLS2020 force field by training a model with the same features (Lennard-Jones or LJ 12-6 potential,²⁴ point charges) and restrictions (see Methods). Training targeted either the total interaction energies produced by OPLS2020 (model AT) or the electrostatics, dispersion and exchange energy components (model AC). Note, that the T indicates training on total interaction energy, and C indicates training on interaction energy components, for an overview of models used in this section, see Table 1. The training data set is given in Table S4.† The ACT can reproduce the OPLS2020 energies with a RMSD of <0.01 kJ mol⁻¹ (models AT, AC) starting from random initial values, and as a result, the deviation from SAPT energies is virtually identical to that computed directly with the original OPLS2020 (Fig. 3). Whether training targets the total interaction energies (AT) or its components (AC) does not make a difference in this case, since in both scenarios the energies can be reproduced exactly by the models that share the atom types of the OPLS2020 force field. It should be pointed out here, that training can employ a combination of total energy and components as well. Table S5† summarizes the force field parameters resulting from trainings AT for alcohols and alkanes, Table S6† gives the parameters for water. The mean percent error (MPE) for the 24 parameters listed is less than 1 (since the charge on water oxygen in TIP4P is 0, this parameter was excluded to avoid biasing the MPE by a 100% deviation in this case).

Table 1 Root mean square deviation (kJ mol⁻¹) from reference interaction energies from either SAPT or OPLS2020 for a data set (N = 2114) consisting of dimers of water, alcohols and alkanes. The use of point charges (PC) or Gaussian charges (GC) is indicated in the FF column and the potential form is either Lennard-Jones 12-6 or Halgrens 14-7 potential (Section S1). N indicates the number of parameters trained, including those for the charge generation algorithm. AT indicates what atom types are used, O (OPLS) or A (ACT, see Methods). The TC column indicates whether training used the total interaction energy (T) or its components (C)

Model	Force field	N	AT	Training energy	Target TC	Reference
						SAPT	OPLS2020
	OPLS2020		O	Liquid, QM		2.1	0
AT	LJ12-6 + PC	20	O	OPLS2020	T	2.1	0.005
AC	LJ12-6 + PC	20	O	OPLS2020	C	2.1	0.006
BT	LJ12-6 + PC	36	A	SAPT	T	1.2	1.7
BC	LJ12-6 + PC	36	A	SAPT	C	5.0	4.5
C	LJ12-6 + GC	43	A	OPLS2020	T	2.1	0.14
D	LJ12-6 + GC	43	A	SAPT	T	1.1	1.8
E	14-7 + GC	42	A	OPLS2020	T	2.2	0.42
F	14-7 + GC	42	A	SAPT	T	1.3	1.9

---

In addition, a model (BT) with chemistry-based atom types (see Methods) was trained on the SAPT energies and the force fields are compared to both sets of reference energies (Table 1). Unsurprisingly, the BT model trained on the total SAPT energies yields energies closer to the SAPT reference than does OPLS2020 and vice versa. Neither of the two parameterizations AT or BT can reproduce both reference energy data sets with the same accuracy. The BC model was trained on the SAPT energy components and reproduction of the total SAPT energy as well as the OPLS2020 total energy is a lot worse than for BT that was trained on the total energy (Table 1). This means the BC model, which is based on a 12-6 Lennard-Jones potential and point charges derived through the split-charge equalization method,⁶² is not sufficiently “physical” to reproduce the total SAPT energies. However, as shown in Fig. 3, the energy components are reproduced more accurately by the BC model than by OPLS2020. On the other hand, training model BT on the total energy introduces a large compensation of errors⁶⁸ (see Table S7†).

In a subsequent step, the ACT was used to derive force fields for the same data set (Table S4†) based on both OPLS2020 and SAPT with two different potentials. Both the LJ12-6 and the 14-7 potential due to Halgren¹⁹ were combined with Gaussian-distributed charges¹⁶ (models C–F). Fixed γ and δ parameters (eqn (S1)†) were used for the water/alcohol/alkane models E and F, according to the original model due to Halgren.¹⁹ The RMSD of the total interaction energies with respect to both data sets are given in Table 1. Moving from point to Gaussian charges (model C) slightly increases the RMSD from the OPLS2020 data set, but both liquid and gas-phase properties are reasonably close to experiment (Fig. 4) for a model with fewer atom types than OPLS2020. From this result it is not obvious that the use of Gaussian charge yields a better model than point charges, but further research is needed. The use of a 14-7 potential (model E) increases the RMSD somewhat further. Models D (12-6 + GC) and F (14-7 + GC), trained on SAPT data have similar deviation from SAPT as model BT (12-6 + PC). The reason why the 14-7 is not better than 12-6 in this case, is likely that γ and δ were kept constant rather than variable like we did for the hydrogen halides (Table S2†), and previously for noble gases.³¹

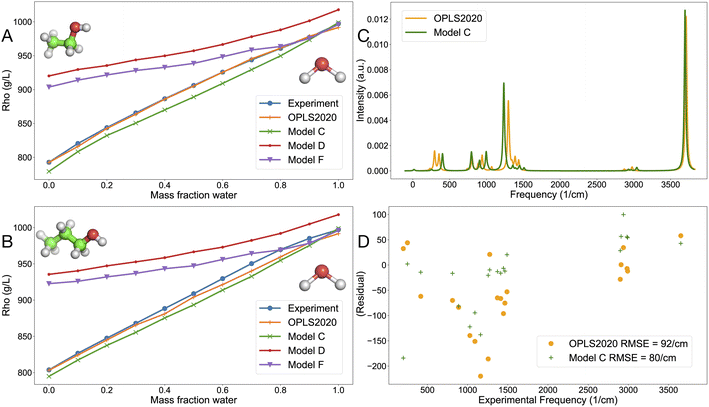Fig. 4 Liquid density for alcohol–water mixture as a function of water mass-fraction and vibrational properties. (A) Density of water–ethanol mixture, (B) density of water-1-propanol mixture, (C) simulated IR gas-phase spectrum of ethanol using the OPLS2020 FF and model C computed with the ACT, with a linewidth of 24 cm⁻¹ and (D) residual plot for the correlation between experimentally determined frequencies for ethanol⁹ and FF-based frequencies.

The promise of physics-based models is that they should be applicable to both the gas and condensed phases, like our earlier models for alkali-halides⁶³ and noble gases.³¹ Here, we evaluated the liquid density of an ethanol–water mixture (Fig. 4A) and a 1-propanol-water mixture (Fig. 4B), numbers are given in Tables S8 and S9.† OPLS2020 reproduces the liquid density very well, which is expected since the model was designed for that purpose. Model C, trained on OPLS2020 interaction energies is very close to experiment as well. The two models D and F that were trained on SAPT data overestimate the alkane density. Interestingly, the 14-7 potential (model F) reproduces the liquid density of alcohol-water mixtures somewhat better than the LJ12-6 potential (model D), see Fig. 4A and B. Simulated gas-phase infrared spectra for ethanol are rather similar for OPLS2020 and model C (Fig. 4C), but there are some differences in the region around 1400 cm⁻¹, which are related to the methyl group vibrations.⁹ The intramolecular forces in model C were trained on MP2 quantum chemistry (see Methods) which could explain the somewhat lower RMSD from experimental frequencies (Fig. 4D).

In a further evaluation of compounds in the liquid state, eleven pure alkanes, including some larger compounds not involved in training, were simulated using OPLS2020 as well as models C, D and F. Table S10† shows that the RMSD from experiment of the liquid density is about 20 g L⁻¹ for both OPLS2020 and model C, whereas models D and F significantly overestimate the density, in line with Fig. 4A and B.

An important result from these evaluations is that there is a large error compensation between exchange and the electrostatic terms (Table S7†). Most classical force fields are trained to reproduce total energies and it has been shown that such error compensation occurs there as well.^5,68 Since the distance dependence of exchange energy is very different from the electrostatic energy, it is likely that this error compensation will lead to incorrect forces. In the trainings presented here (Table S7†) the exchange energy typically has the highest RMSD but, as it is discussed below, this can be addressed by adding additional virtual sites corresponding to, for instance, σ-holes on the OH bonds. It should be noted that virtual site hitherto have been mainly used for modeling charge distributions (as in e.g. the TIP4P water model²⁵). However, as may be evident from model BC, more accurate potential functions are needed to accurately reproduce total interaction energies based on SAPT.³⁶ The ACT supports a large number of potentials (see e.g. ref. 31) including terms to model polarisation and induction, but application to larger organic or biomolecular systems is beyond the scope of this work.

Application to exchange interactions

In a recent paper we demonstrated that the exchange interactions around a water molecule are highly anisotropic.³⁰ This was found by doing a scan of a helium probe around a water molecule and computing SAPT interaction energy components. It was shown that the exchange energy is high for a probe close to the lone-pair positions and low close to positions corresponding to where σ-holes could be expected, in the extension of the OH bonds. Using the ACT, a model can be designed with virtual sites at the lone-pairs (LP) and/or σ-hole (SH) positions to correct the otherwise purely spherical exchange from the oxygen atom (Fig. 5A). The ACT simultaneously derived the parameters for the Buckingham exchange potential (Ae^−br) and the optimal positions of the virtual sites, where the lone-pairs added exchange (ALP > 0) and the σ-holes reduced it (ASH < 0). In this manner the relative importance of the LP and SH sites could be evaluated. Intriguingly, modeling the σ-holes reduced the RMSD from SAPT exchange by about 70%, whereas modeling the lone-pairs only reduced the RMSD by about 30% (Fig. 5B). The combination of both leads to more than 80% reduction of the RMSD. It should be emphasized that each set of virtual sites adds additional parameters increasing the risk of overfitting. In the case where only LP were used, they were positioned on a line perpendicular through the oxygen atom, at a distance of 0.27 Å. When both LP and SH were used, the optimal position of the lone-pairs was tetrahedral at a distance of 0.22 Å from the oxygen atom. The position of the σ-hole was on the vector through the OH bond at a distance of 0.53 Å from the oxygen (Fig. 5A). This example shows how the ACT can be used to perform detailed comparisons of physical models, to fine-tune models, and how new chemical insights can be deduced from the results.³⁰

Fig. 5 (A) Model for exchange interactions between water and helium produced using ACT including virtual sites for both lone-pair (LP) particles and σ-holes (SH). × denotes that virtual sites for exchange were included in the model. Note that these models are entirely different from the TIP4P model²⁵ and ACT variants used in Table 1 and Fig. 4. (B) Root mean square deviation (RMSD, kJ mol⁻¹) from SAPT exchange for four different water models with lone-pair (LP) and/or σ-hole (SH) virtual sites. N is the total number of particles in the water model. Training done using the ACT based on a systematic scan of a helium probe around a water molecule in the plane of the molecule and perpendicular to it.³⁰

Discussion

Free and open-source software libraries such as TensorFlow¹¹ and PyTorch⁴³ have facilitated the use of big data for the development of machine learning models in molecular science. For example, they have made it possible to derive both neural-network potential energy functions⁸ as well as parts of empirical potential functions.^28,48,50 However, the complexity of the chemical space makes it difficult to design general neural network models for intermolecular interactions.²

In this paper, the Alexandria Chemistry Toolkit is presented as open-source software that implements machine learning of complete force fields from scratch based on a user-specified physical model.⁵⁸ Three parameter training algorithms are implemented: MCMC, GA, and HYBRID. Our analyses (Fig. 2A) show that HYBRID is somewhat more efficient than the other two algorithms. Using this algorithm, ACT can evolve FF genomes that best reproduce reference data by combining a global optimization through a genetic algorithm with a local optimization through MCMC in an iterative fashion. The code is compatible with multiple existing quantum chemistry databases^5,12,17,53 as well as new quantum chemistry calculations.⁵⁸ It should be noted that genetic algorithms have been used for parameter optimization for water⁷ as well as for the ReaxFF¹⁵ but, it was shown later that local optimization of the same ReaxFF with gradient-based methods was more efficient.²⁷ Gradient optimization is also at the core of the ForceBalance algorithm⁶⁵ that is routinely used in the Open Force Field project.⁶⁶ Betz and Walker proposed a combination of a GA with a local minimizer to tune bonded-force parameters.³ The combination of GA for global optimization with MCMC for local refinement has been used in many fields of science, for instance, for protein structure prediction,⁵² for a review see ref. 46. For the case of force field training proposed in this work, the HYBRID algorithm has the potential to determine parameters rapidly and reproducibly, but further parameter and algorithm investigations are needed.³⁴

The ACT is effective in generating force fields that reproduce intermolecular interaction energies from quantum chemistry. However, much work remains to be done to further refine these models, including a critical review of the method for generating charges,^22,62 potential functions³¹ and treatment of electrostatics and induction.³⁶ Simple models that adequately describe the gas-phase, do not at the same time reproduce the condensed phases very well (Table 1 and Fig. 4) and vice versa. Takaba and co-workers,⁵⁰ avoided this issue by restricting their training to intramolecular energies and by relying on the TIP3P water model²⁵ and the OpenFF 2.0 for the non-bonded parameters.⁴ Likewise, the intramolecular FF due to Seute et al.⁴⁸ uses the TIP3P water model and the Amber99SB force field³² to describe non-bonded forces. Both these models are therefore limited by the accuracy that can be provided by the Lennard-Jones/point charge model.^18,31,63

It has been argued for a long time that the addition of polarizability will make force fields more phase-transferable.^54,63 However, as pointed out by McDaniel and Schmidt,³⁶ additional energy terms may be needed to correctly model induction. Further research will have to evaluate whether the purely attractive exponential term proposed by those authors is the solution to this problem. Finally, it should be emphasized that extensive validation of any future FF is needed,⁴⁴ including analysis of vibrational spectroscopy^20,60 and thermochemistry⁵⁶ for monomers, second virial coefficients for dimers,³¹ liquid properties,⁶ free energies of solvation⁶⁹ and stability of crystals.^21,31,47 We believe that the Alexandria Chemistry Toolkit, in conjunction with OpenMM,¹⁴ can make substantial contributions toward this goal.

Methods

Quantum chemical data collection

Multiple datasets of dimer structures and corresponding interaction energy components were constructed at the SAPT2 + (ccd)δMP2 level of theory⁴² with an augmented triple-zeta basis set¹³ and calculations were performed using the Psi4 software suite.⁵¹ For this purpose a series of Python scripts were created and made available to the community on GitHub.⁵⁵ Usage of the scripts is described in the ACT manual.⁵⁸ Tables S1, S3 and S4† list the compound dimers used for the SAPT calculations reported in this paper. MP2 calculations³⁷ were performed using Psi4 of 100 high energy structures for monomeric compounds corresponding to Tables S1, S3 and S4.† The structures were generated in a short classical molecular dynamics simulation using the Generalized Amber FF.⁶⁴ Although 100 is a relatively small number, many interactions such as e.g. a C–H bond occur in multiple compounds, providing independent data.

Determination of atom types

In the derivation of force field parameters, the physical models use simple atom types corresponding to the element and its hybridization state. That is, three atom types are employed for carbon corresponding to sp³, sp² and sp¹ hybridizations, named c3, c2 and c1, respectively. The other elements are treated in the same manner, except for hydrogen atoms for which multiple different atom types derived from the General Amber FF⁶⁴ are used (Table S5†). Water–oxygen is, due to its importance in biological systems, treated separately from other sp³ oxygen atoms as well (Table S6†). Code to determine atom types based on the elemental composition and atomic coordinates is present in OpenBabel.⁴¹ For this work, the OpenBabel code was adapted, and this is available on GitHub.⁵⁸ It should be noted that the number of atom types defined in the Alexandria force field is typically less than what is commonly used in general force fields.^61,64 This is based on the premise that an improved description of the physics will limit the need for large numbers of nearly-identical atom types. The exact atom types to be used for generating a force field can be decided upon by the user of the ACT.

Model training using the ACT

Training using a genetic algorithm started from a population of 256 individuals where parameters were generated from a uniform random distribution within a user-defined interval. It is important to have a range for each parameter that is not too large in order not to complicate training unnecessarily, but not too small either, so that optimal values fall within the range. This is relatively simple for e.g. the van der Waals radius σ of particles where we can use existing force fields for reference. However, for some other parameters the ranges were determined based on experience built-up during the development of the ACT. It happens that parameters end up at one of the bounds that are used as input. For instance, for the Gaussian screening widths, a large ζ will effectively turn a Gaussian charge into a point charge. When capping ζ to not allow values larger than 10 nm⁻¹, some atom types will end up at ζ = 10 nm⁻¹. In this case the user has to decide whether to increase the range. However this has to be balanced with the risk of premature convergence of the training and ending up with a sub-optimal parameter set. The range of parameters needed for effective training also depends on the physical model (point charges versus Gaussian charges, van der Waals potential used) and on whether training is done on components or total interaction energy.

Meta parameters for the training are based on an evaluation of a beta version of the ACT.³⁴ Typically, five cross-over points are used in the genetic algorithm, selected randomly. 20 generations of evolution were performed in the GA, combined with 40 iterations per parameter in the Monte Carlo mutation algorithm. Simulated annealing was applied in the Monte Carlo algorithm, linearly reducing the temperature to zero from the 30th iteration. The number of energy evaluations equaled 20 × 40 × the number of parameters × 2114 dimers per individual. For the case of the alcohol/water/alkane data set (Table S4†), this amounts to ≈34 million dimer energy evaluations. The training took one to three hours on AMD EPYC 7763 processors.

To reproduce the OPLS2020 force field for alcohols, alkanes and water, OPLS2020 energies were computed using 2114 SAPT dimer conformations (Table S4†). These were then used to train the intermolecular part of the OPLS2020 FF with limitations of that FF (e.g. identical charge on all aliphatic hydrogen atoms). The original parameters were retained for the intramolecular energy terms. For models B–F (Table 1) ACT atom types were used (see above) and the intermolecular potential functions were trained on either OPLS2020 or SAPT energies. The intramolecular forces were trained on MP2 energies and forces, which means that these models are derived from scratch.

In general, a data set should be split into a training and a test set and the convergence of both should be monitored. If the fitness of the test set does not improve for several GA iterations, training should be terminated to prevent over-fitting (see Table S2† for an example of the latter).

Molecular dynamics simulations

A utility within the ACT can convert an ACT force field file with a user-defined molecular system to an input for the OpenMM simulation engine.¹⁴ The ACT includes middleware in the form of a Python interface to OpenMM, that implements the custom potential functions described in the ACT manual⁵⁸ and the OpenMM code is able to execute these efficiently on graphical processing units (GPUs). This middleware was used for performing simulations with a range of potentials in our studies on noble gases.³¹ Here, this interface was validated once more by reproducing simulations of alkali-halide crystals at room temperature from our previous work⁶³ (Table S11†). The results listed in Tables 1, S8–S11† were derived from simulations on GPUs using the ACT-OpenMM interface as well. Table S8† lists further simulation details.

Code availability

The ACT is available as free and open source on GitHub.⁵⁹

Data availability

The data from both SAPT and MP2 calculations are stored in machine-readable extensible markup language (XML) files. XML is used for storing and transferring force field parameters as well. All data is available without restriction on Zenodo.⁵⁷

Author contributions

DvdS designed the software, implemented most of it, performed validations and simulations and wrote the draft of the manuscript. JM implemented the evolution algorithms and contributed to writing. KK contributed to code and writing. ANH contributed to code and writing. ATN contributed to the OpenMM interface. JPAM contributed to quantum chemistry data collection. MMW proposed the evolutionary algorithm and contributed to coding and writing. PJvM contributed chemical insights in software design and to writing. MMG contributed to the software design of the ACT and implemented parts of it. He also contributed to finalizing the manuscript.

Conflicts of interest

Authors declare no competing interests.

Acknowledgements

This research was supported financially by the project AI4Research at Uppsala University, Sweden, and by the Swedish Research Council (grants 2020-05059, 2024-04314). Funding from eSSENCE – The e-Science Collaboration (Uppsala-Lund-Umeå, Sweden) is gratefully acknowledged. Computer resources provided by the National Academic Infrastructure for Supercomputing Sweden at the national supercomputing center in Linköping, Sweden, the PDC Center for High Performance Computing, KTH Royal Institute of Technology, Sweden, partially funded by the Swedish Research Council through (grant 2022-06725). We acknowledge NAISS-Sweden for awarding this project access to the LUMI supercomputer, owned by the EuroHPC Joint Undertaking, hosted by CSC (Finland) and the LUMI consortium.

References

1. A. Aspuru-Guzik, R. Lindh and M. Reiher, The matter simulation revolution, ACS Cent. Sci., 2018, 4(2), 144–152.
2. M. Baek, Towards the prediction of general biomolecular interactions with AI, Nat. Methods, 2024, 21, 1382–1383.
3. R. M. Betz and R. C. Walker, Paramfit: Automated optimization of force field parameters for molecular dynamics simulations, J. Comput. Chem., 2015, 36, 79–87.
4. B. Simon, L.-P. Wang, D. L. Mobley, J. D. Chodera and M. R. Shirts, Open force field evaluator: An automated, efficient, and scalable framework for the estimation of physical properties from molecular simulation, J. Chem. Theory Comput., 2022, 18(6), 3566–3576.
5. L. A. Burns, J. C. Faver, Z. Zheng, M. S. Marshall, D. G. A. Smith, K. Vanommeslaeghe, A. D. MacKerell, K. M. Merz and C. David Sherrill, The BioFragment Database (BFDb): An open-data platform for computational chemistry analysis of noncovalent interactions, J. Chem. Phys., 2017, 147, 161727.
6. C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, Force field benchmark of organic liquids: Density, enthalpy of vaporization, heat capacities, surface tension, compressibility, expansion coefficient and dielectric constant, J. Chem. Theory Comput., 2012, 8, 61–74.
7. A. V. C. Camposano, E. Marius Nordhagen, H. Andersen Sveinsson and A. Malthe-Sørenssen, Genetic algorithm workflow for parameterization of a water model using the vashishta force field, J. Phys. Chem. B, 2025, 129(4), 1331–1342.
8. C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nature Comput. Sci., 2022, 2, 718–728.
9. S. Coussan, Y. Bouteiller, J. P. Perchard and W. Q. Zheng, Rotational isomerism of ethanol and matrix isolation infrared spectroscopy, J. Phys. Chem. A, 1998, 102, 5789–5793.
10. P. Dauber-Osguthorpe and A. T. Hagler, Biomolecular force fields: where have we been, where are we now, where do we need to go and how do we get there?, J. Comput. Aid. Mol. Des., 2019, 33(2), 133–203.
11. J. V. Dillon, I. Langmore, D. Tran, E. Brevdo, S. Vasudevan, D. Moore, B. Patton, A. Alemi, M. Hoffman, and R. A. Saurous, Tensorflow distributions, arXiv, 2017, preprint, arXiv:1711.10604,  DOI:10.48550/arXiv.1711.10604.
12. A. G. Donchev, A. G. Taube, E. Decolvenaere, C. Hargus, R. T. McGibbon, K.-H. Law, B. A. Gregersen, J.-L. Li, K. Palmo, K. Siva, M. Bergdorf, J. L. Klepeis and D. E. Shaw, Quantum chemical benchmark databases of gold-standard dimer interaction energies, Sci. Data, 2021, 8(1), 55.
13. T. H. Dunning Jr and K. A. Peterson, Approximating the basis set dependence of coupled cluster calculations: Evaluation of perturbation theory approximations for stable molecules, J. Chem. Phys., 2000, 1113, 7799–7808.
14. P. Eastman, R. Galvelis, R. P. Peláez, C. R. A. Abreu, S. E. Farr, E. Gallicchio, A. Gorenko, M. M. Henry, F. Hu, J. Huang, A. Krämer, J. Michel, J. A. Mitchell, V. S. Pande, J. P. G. L. M. Rodrigues, J. Rodriguez-Guerra, A. C. Simmonett, S. Singh, J. Swails, P. Turner, Y. Wang, I. Zhang, J. D. Chodera, G. De Fabritiis and T. E. Markland, Openmm 8: Molecular dynamics simulation with machine learning potentials, J. Phys. Chem. B, 2024, 128, 109–116.
15. D. Fantauzzi D. Gaissmaier, M. van den Borg and T. Jacob, KVIK optimiser - an enhanced ReaxFF force field training approach, ChemRxiv, 2022, preprint,  DOI:10.26434/chemrxiv-2022-lrsjd-v2.
16. M. M. Ghahremanpour, P. J. van Maaren, C. Caleman, G. R. Hutchison and D. van der Spoel, Polarizable drude model with s-type gaussian or slater charge density for general molecular mechanics force fields, J. Chem. Theory Comput., 2018, 14, 5553–5566.
17. M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, The Alexandria library: a quantum chemical database of molecular properties for force field development, Sci. Data, 2018, 5, 180062.
18. A. T. Hagler, Force field development phase II: Relaxation of physics-based criteria…or inclusion of more rigorous physics into the representation of molecular energetics, J. Comput.-Aided Mol. Des., 2019, 33, 205–264.
19. T. A. Halgren, The representation of van der Waals (vdW) interactions in molecular mechanics force fields: potential form, combination rules, and vdW parameters, J. Amer. Chem. Soc., 1992, 114, 7827–7843.
20. H. Henschel and D. van der Spoel, An intuitively understandable quality measure for theoretical vibrational spectra, J. Phys. Chem. Lett., 2020, 11, 5471–5475.
21. A. Najla Hosseini and D. van der Spoel, Simulations of amyloid-forming peptides in the crystal state, Prot. J., 2023, 42, 192–204.
22. F. Jensen, Unifying charge-flow polarization models, J. Chem. Theory Comput., 2023, 19, 4047–4073.
23. B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation theory approach to intermolecular potential energy surfaces of van der waals complexes, Chem. Rev., 1994, 94(7), 1887–1930.
24. J. E. Jones, On the determination of molecular fields. -II. From the equation of state of a gas, Proc. Royal Soc. Lond. Ser. A, 1924, 106, 463–477.
25. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
26. W. L. Jorgensen, M. M. Ghahremanpour, A. Saar and J. Tirado-Rives, OPLS/2020 force field for unsaturated hydrocarbons, alcohols, and ethers, J. Phys. Chem. B, 2023, 128, 250–262.
27. M. Cagri Kaymak, R. Ali, K. A. O'Hearn, A. C. T. van Duin, K. M. Merz and H. M. Aktulga, JAX-ReaxFF: A gradient-based framework for fast optimization of reactive force fields, J. Chem. Theory Comput., 2022, 18, 5181–5194.
28. A. Kumar, P. Pandey, P. Chatterjee and A. D. MacKerell, Deep neural network model to predict the electrostatic parameters in the polarizable classical drude oscillator force field, J. Chem. Theory Comput., 2022, 22, 1711–1725.
29. K. Kříž, L. Schmidt, A. T. Andersson, M.-M. Walz and D. van der Spoel, An imbalance in the force: The need for standardised benchmarks for molecular simulation, J. Chem. Inf. Model., 2023, 63, 412–431.
30. K. Kříž and D. van der Spoel, Quantification of anisotropy in exchange and dispersion interactions: A simple model for physics-based force fields, J. Phys. Chem. Lett., 2024, 15, 9974–9978.
31. K. Kříž and J. Paul, van Maaren, and David van der Spoel. Impact of combination rules, level of theory and potential function on the modelling of gas and condensed phase properties of noble gases, J. Chem. Theory Comput., 2024, 20, 2362–2376.
32. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Improved side-chain torsion potentials for the amber ff99sb protein force field, Proteins:Struct., Funct., Bioinf., 2010, 78, 1950–1958.
33. C. Liu, J.-P. Piquemal and P. Ren, Amoeba+ classical potential for modeling molecular interactions, J. Chem. Theory Comput., 2019, 15, 4122–4139.
34. J. R. Marrades Furquet, Data-driven Parameterization of Molecular Force Fields, Master's thesis, Uppsala University, Dept. of Information Technology, 2022.
35. F. Mazzocchi, Could big data be the end of theory in science?, EMBO reports, 2015, 16(10), 1250–1255.
36. J. G. McDaniel and J. R. Schmidt, Physically-motivated force fields from symmetry-adapted perturbation theory, J. Phys. Chem. A, 2013, 117(10), 2053–2066.
37. C. Møller and M. S. Plesset, Note on an approximation treatment for many-electron systems, Phys. Rev., 1934, 46, 618–622.
38. P. M. Morse, Diatomic molecules according to the wave mechanics. II. Vibrational levels, Phys. Rev., 1929, 34, 57–64.
39. T. Mueller, A. Hernandez and C. Wang, Machine learning for interatomic potential models, J. Chem. Phys., 2020, 152, 050902.
40. F. Noe, A. Tkatchenko, K.-R. Mueller and C. Clementi, Machine learning for molecular simulation, Annu. Rev. Phys. Chem., 2020, 71, 361–390.
41. N. O’Boyle, T. Vandermeersch, C. Flynn, A. Maguire and G. Hutchison, Confab - systematic generation of diverse low-energy conformers, J. Cheminf., 2011, 3, 8.
42. T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. David Sherrill, Levels of symmetry adapted perturbation theory (sapt). I. efficiency and performance for interaction energies, J. Chem. Phys., 2014, 140(9), 094106.
43. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, et al., Pytorch: An imperative style, high-performance deep learning library, NeurIPS, 2019, vol. 32.
44. M. D. Polêto and J. A. Lemkul, Integration of experimental data and use of automated fitting methods in developing protein force fields, Commun. Chem., 2022, 5, 38.
45. A. K. Rappé and W. A. Goddard III, Charge Equillibration for Molecular Dynamics Simulations, J. Phys. Chem., 1991, 95, 3358–3363.
46. J.-M. Renders and S. P. Flasse, Hybrid methods using genetic algorithms for global optimization, IEEE Trans. Syst. Man. Cybern. B Cybern., 1996, 26(2), 243–258.
47. L. Schmidt, D. van der Spoel and M.-M. Walz, Probing phase transitions in organic crystals using atomistic md simulations, ACS Phys. Chem. Au, 2023, 3, 84–93.
48. L. Seute, E. Hartmann, J. Stühmer and F. Gräter, Grappa – a machine learned molecular mechanics force field, Chem. Sci., 2025, 16, 2907–2930.
49. J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: an extensible neural network potential with dft accuracy at force field computational cost, Chem. Sci., 2017, 8, 3192–3203.
50. K. Takaba, A. J. Friedman, C. E. Cavender, P. Kumar Behara, I. Pulido, M. M. Henry, H. MacDermott-Opeskin, C. R. Iacovella, A. M. Nagle, A. M. Payne, M. R. Shirts, D. L. Mobley, J. D. Chodera and Y. Wang, Machine-learned molecular mechanics force fields from large-scale quantum chemical data, Chem. Sci., 2024, 15, 12861–12878.
51. J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. David Sherrill and T. Daniel Crawford, Psi4: an open-source ab initio electronic structure program, WIREs Comput. Mol. Sci., 2011, 2, 556–565.
52. R. Unger and J. Moult, Genetic algorithms for protein folding simulations, J. Mol. Biol., 1993, 231, 75–81.
53. J. Řezác, Non-covalent interactions atlas benchmark data sets: Hydrogen bonding, J. Chem. Theory Comput., 2020, 16, 2355–2368.
54. D. van der Spoel, Systematic design of biomolecular force fields, Curr. Opin. Struct. Biol., 2021, 67, 18–24.
55. D. van der Spoel, SaptACT, 2025, https://github.com/AlexandriaChemistry/SaptACT, date accessed: 2025-03-08.
56. D. van der Spoel, M. M. Ghahremanpour and J. Lemkul, Small molecule thermochemistry: A tool for empirical force field development, J. Phys. Chem. A, 2018, 122, 8982–8988.
57. D. van der Spoel, J. Marrades, K. Kříž, A. Najla Hosseini, A. T. Nordman, J. P. A. Martins, M.-M. Walz, P. J. van Maaren, and M. M. Ghahremanpour, Supporting information for the paper ‘Evolutionary Machine Learning of Physics-Based Force Fields in High-Dimensional Parameter-Space’, 2025, https://zenodo.org/records/15037854.
58. D. van der Spoel, P. J. van Maaren, and M. M. Ghahremanpour, Alexandria Chemistry Toolkit Reference and User Manual Version 1.0, The Alexandria Chemistry Project, Uppsala, Sweden, 2025, https://zenodo.org/records/15020366.
59. D. van der Spoel, P. J. van Maaren, and M. Mehdi Ghahremanpour, Alexandria chemistry toolkit, 2025, https://github.com/AlexandriaChemistry/ACT, date accessed: 2025-03-08.
60. P. J. van Maaren and D. van der Spoel, Quantitative evaluation of anharmonic bond potentials for molecular simulations, Digit. Discov., 2025, 4, 824–830.
61. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr, Charmm general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690.
62. T. Verstraelen, V. V. Speybroeck and M. Waroquier, The electronegativity equalization method and the split charge equilibration applied to organic systems: Parametrization, validation, and comparison, J. Chem. Phys., 2009, 131, 044127.
63. M.-M. Walz, M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, Phase-transferable force field for alkali halides, J. Chem. Theory Comput., 2018, 14, 5933–5948.
64. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general AMBER force field, J. Comput. Chem., 2004, 25, 1157–1174.
65. L.-P. Wang, J. Chen and T. Van Voorhis, Systematic Parametrization of Polarizable Force Fields from Quantum Chemistry Data, J. Chem. Theory Comput., 2013, 9(1), 452–460.
66. L. Wang, P. Kumar Behara, M. W. Thompson, T. Gokey, Y. Wang, J. R. Wagner, D. J. Cole, M. K. Gilson, M. R. Shirts and D. L. Mobley, The open force field initiative: Open software and open science for molecular modeling, J. Phys. Chem. B, 2024, 128(29), 7043–7067.
67. K. E. Willcox, O. Ghattas and P. Heimbach, The imperative of physics-based modeling and inverse theory in computational science, Nat. Comput. Sci., 2021, 1, 166–168.
68. M. Zgarbova, M. Otyepka, J. Sponer, P. Hobza and P. Jurecka, Large-scale compensation of errors in pairwise-additive empirical force fields: comparison of AMBER intermolecular terms with rigorous DFT-SAPT calculations, Phys. Chem. Chem. Phys., 2010, 12, 10476–10493.
69. J. Zhang, B. Tuguldur and D. van der Spoel, Force field benchmark II: Gibbs energy of solvation of organic molecules in organic liquids, J. Chem. Inf. Model., 2015, 55, 1192–1201.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00178a

---