Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using machine learning to map simulated noisy and laser-limited multidimensional spectra to molecular electronic couplings†
Jonathan D.
Schultz
 *a,
Kelsey A.
Parker
*a,
Kelsey A.
Parker
 *a,
Bashir
Sbaiti
*a,
Bashir
Sbaiti
 ab and
David N.
Beratan
ab and
David N.
Beratan
 abc
abc
aDepartment of Chemistry, Duke University, Durham, NC 27708, USA. E-mail: jonathan.schultz@duke.edu; kelsey.parker@duke.edu
bDepartment of Physics, Duke University, Durham, NC 27708, USA
cDepartment of Biochemistry, Duke University, Durham, NC 27710, USA
First published on 25th June 2025
Abstract
Two-dimensional electronic spectroscopy (2DES) has enabled significant discoveries in both biological and synthetic energy-transducing systems. Although deriving chemical information from 2DES is a complex task, machine learning (ML) offers exciting opportunities to translate complicated spectroscopic data into physical insight. Recent studies have found that neural networks (NNs) can map simulated multidimensional spectra to molecular-scale properties with high accuracy. However, simulations often do not capture experimental factors that influence real spectra, including noise and suboptimal pulse resonance conditions, bringing into question the experimental utility of NNs trained on simulated data. Here, we show how factors associated with experimental 2D spectral data influence the ability of NNs to map simulated 2DES spectra onto underlying intermolecular electronic couplings. By systematically introducing multisourced noise into a library of 356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulated 2D spectra, we show that noise does not hamper NN performance for spectra exceeding threshold signal-to-noise ratios (SNR) of ca. 12.4, 2.5, and 5.1 if uncorrelated additive, correlated additive, or intensity-dependent noise sources dominate, respectively. In stark contrast to human-based analyses of 2DES data, we find that the NN accuracy improves significantly (ca. 84% → 96%) when the data are constrained by the bandwidth and center frequency of the pump pulses. This result is consistent with the NN learning the optical trends described by Kasha's theory of molecular excitons. Our findings convey positive prospects for adapting simulation-trained NNs to extract molecular properties from inherently imperfect experimental 2DES data. More broadly, we propose that machine-learned perspectives of nonlinear spectroscopic data may produce unique and perhaps counterintuitive guidelines for experimental design.
000 simulated 2D spectra, we show that noise does not hamper NN performance for spectra exceeding threshold signal-to-noise ratios (SNR) of ca. 12.4, 2.5, and 5.1 if uncorrelated additive, correlated additive, or intensity-dependent noise sources dominate, respectively. In stark contrast to human-based analyses of 2DES data, we find that the NN accuracy improves significantly (ca. 84% → 96%) when the data are constrained by the bandwidth and center frequency of the pump pulses. This result is consistent with the NN learning the optical trends described by Kasha's theory of molecular excitons. Our findings convey positive prospects for adapting simulation-trained NNs to extract molecular properties from inherently imperfect experimental 2DES data. More broadly, we propose that machine-learned perspectives of nonlinear spectroscopic data may produce unique and perhaps counterintuitive guidelines for experimental design.
1 Introduction
Coherent multidimensional spectroscopies (CMDS) afford rich insight into the mechanisms of light-driven molecular processes.1–7 For example, studies using two-dimensional electronic spectroscopy (2DES) in the last two decades exposed the central role that electron–vibrational (vibronic) coupling plays in the excited-state photophysics of chemical and material systems, including natural photosynthetic complexes,8–11 organic semiconductors,12–16 and quantum dots.17,18 The abundance of information within 2DES spectra, as with spectra from other CMDS techniques, comes at the expense of interpretability; results of early 2DES measurements sparked decade-long debates of their physical interpretation.7,19–22 Developing robust methods to derive accurate chemical information from 2DES will be indispensable as this technique is used increasingly to probe complex, device-relevant condensed-phase systems.Spectroscopy is often used to solve inverse problems, where physical insight about a chemical system is sought from spectroscopic data. Machine learning (ML) models are uniquely suited to solve inverse problems,23,24 and ML has already been applied to many inverse chemical problems in spectroscopy.25–40 For example, Lansford et al.27 and Enders et al.28 used ML to extract surface microstructure and functional group information, respectively, from infrared spectra. Cui et al.41 demonstrated an ML method that relates infrared and Raman spectra to the electrocatalytic properties of CO2 reduction. Despite recent progress in joint ML-spectroscopic approaches, time-evolving nonlinear spectra are vastly more complicated than steady-state linear spectra, and this is especially true for spectra derived from multidimensional methods like 2DES. As a result, few studies29,31–36 have demonstrated how ML can be used to map the properties of molecular systems directly from their multidimensional spectra. However, innovations enabled by ML applied to linear spectroscopy27,28,38,41,42 and magnetic resonance spectroscopies37,43,44 clearly indicate the potential of using ML to transform the interpretation of complicated spectroscopic data.
The data requirements of ML pose a significant challenge in applying ML to spectroscopy.24,29,43,45 There is currently no public repository for experimental 2DES data. Of the experimental data that accompany journal publications, factors such as low molecular diversity, variation in data processing methods, and insufficient sample characterization hinder the prospects for training neural networks (NNs) with purely experimental 2DES datasets. A viable and precedented alternative is to use simulated data to train NNs for experimental applications.27,29,46–52 Simulated data offer the unique advantages of practically infinite availability and complete knowledge of the underlying physical properties, which enabled several recent studies29,31,33–36 that leverage ML to solve inverse problems with multidimensional spectra. Simulated data are, however, pristine: they do not typically include the influence of experimental features in CMDS spectra, such as noise, finite pulse bandwidths, and imperfect laser-sample resonance conditions.2,51,53–55 It remains unknown how such experimental aspects of 2DES might influence the performance of ML-based interpretation tools. This gap in knowledge contributes to the already considerable challenge of adapting simulation-trained NNs to experimental applications.
Here, we develop an expansive database of 356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 vibronic dimer 2DES spectra and use it to identify how experimental constraints influence inverse problem solving with a feed-forward NN. When trained and evaluated on pristine simulated data, the NN classifies unseen spectra to one of 33 electronic coupling categories with ∼84% accuracy. By systematically introducing experimental constraints, or “data pollutants,” into the spectra and performing repeated training and evaluation, we find how the pollutants influence the testing performance of the NN. We find that the simulation-trained NNs are relatively robust to additive noise sources with correlations along the probe axis (e.g., intensity jitter of the local oscillator) and sources that depend on the signal magnitude (e.g., fluctuations in the pump power or beam alignment). The NN performance appears to be most susceptible to uncorrelated additive noise sources, such as detector dark current or the readout electronics. We also find that NN performance increases significantly (up to ∼96% accuracy) when the effects of pump bandwidth and center frequency are accounted for in the spectral dataset. We find that this counterintuitive result provides fundamental insight into the machine learnability of electronic coupling information in multidimensional optical spectra. Ultimately, our study clarifies how the performance of simulation-trained NNs may vary, potentially in a positive or negative direction, as they are adapted for experimental applications. These findings encourage the use of ML to derive chemical insight directly from multidimensional spectroscopy experiments.
000 vibronic dimer 2DES spectra and use it to identify how experimental constraints influence inverse problem solving with a feed-forward NN. When trained and evaluated on pristine simulated data, the NN classifies unseen spectra to one of 33 electronic coupling categories with ∼84% accuracy. By systematically introducing experimental constraints, or “data pollutants,” into the spectra and performing repeated training and evaluation, we find how the pollutants influence the testing performance of the NN. We find that the simulation-trained NNs are relatively robust to additive noise sources with correlations along the probe axis (e.g., intensity jitter of the local oscillator) and sources that depend on the signal magnitude (e.g., fluctuations in the pump power or beam alignment). The NN performance appears to be most susceptible to uncorrelated additive noise sources, such as detector dark current or the readout electronics. We also find that NN performance increases significantly (up to ∼96% accuracy) when the effects of pump bandwidth and center frequency are accounted for in the spectral dataset. We find that this counterintuitive result provides fundamental insight into the machine learnability of electronic coupling information in multidimensional optical spectra. Ultimately, our study clarifies how the performance of simulation-trained NNs may vary, potentially in a positive or negative direction, as they are adapted for experimental applications. These findings encourage the use of ML to derive chemical insight directly from multidimensional spectroscopy experiments.
2 Methods
2.1 Spectral database for machine learning
We performed nonlinear response simulations in Python to generate our training and testing datasets. Because of computational costs and storage limitations, we limited the scope of the current study to models for molecular dimers. Studies from the last two decades found that simple molecular models, such as the harmonic oscillator or purely electronic dimer models, are often insufficient to describe sub-picosecond photophysics.8,10,56,57 Hence, we used a Holstein-like vibronic exciton Hamiltonian, which was shown to be accurate for predicting features in experimental 2DES spectra of light-harvesting systems.8,12,13,58–60 The system Hamiltonian is| Hsys = Hel + Hvib + Hel−vib, | (1) |
 | (2) |
 and cn are the electronic creation and annihilation operators, respectively, such that
and cn are the electronic creation and annihilation operators, respectively, such that  represents an exciton on site n, and JCoul is the coulombic coupling. The vibrational and vibronic Hamiltonians are:
represents an exciton on site n, and JCoul is the coulombic coupling. The vibrational and vibronic Hamiltonians are: | (3) |
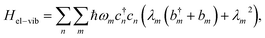 | (4) |
 creates (annihilates) vibrational quanta for vibration m with frequency ℏωm and Huang–Rhys factor λm2.
creates (annihilates) vibrational quanta for vibration m with frequency ℏωm and Huang–Rhys factor λm2.
In generating the spectral database with the vibronic exciton Hamiltonian (eqn (1)), we set ranges for all Hamiltonian parameters so that the simulated spectra correspond to molecular systems that are typically studied with 2DES. Fig. 1 shows the parameter distributions for the coulombic couplings and the nuclear displacements. We varied the coulombic coupling from JCoul = −800 to +800 cm−1 (Fig. 1a), which corresponds to strong J- and H-type coupling interactions, respectively.61 We previously found that NNs disproportionately misclassify the value of JCoul that underpins the 2DES spectra of J-type dimers.33,34 Thus, while we primarily used a 50 cm−1 increment as JCoul was varied, we used smaller increments in varying JCoul < −550 cm−1 (see Fig. 1a).
 | ||
Fig. 1 Values of the (a) coulombic coupling (JCoul) and nuclear displacements (λi) of the (b) i = 1300 and (c) i = 200 cm−1 modes (eqn (2) through (4)) used in generating the spectral database. There are 356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 unique 2DES spectra in the full dataset, reflecting 1424 unique homodimers. Slice areas in each hollowed circle are proportional to the amount of data they represent. Outward-facing ticks in (a) indicate the boundaries of the 33 classes reflected in the output of the neural network (vide infra). See Table S1† for further details. 000 unique 2DES spectra in the full dataset, reflecting 1424 unique homodimers. Slice areas in each hollowed circle are proportional to the amount of data they represent. Outward-facing ticks in (a) indicate the boundaries of the 33 classes reflected in the output of the neural network (vide infra). See Table S1† for further details. | ||
We made two compromises to balance storage costs with the generality of our data space. First, we considered only homodimers (i.e., ε1 = ε2 = ε in eqn (2)). We chose the specific value of ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to align with the approximate transition energy of terrylenediimide, a prototypical organic chromophore with extensive prior 2DES characterization.13,59,62–64 Second, we constrained eqn (3) and (4) to include two independent vibrational modes. In a previous study, we considered systems with up to three vibrational modes and analyzed how the number and frequency of the modes impacted the machine learning.33 Here, we prioritize the inclusion of one high-frequency (1300 cm−1) and one low-frequency (200 cm−1) mode. This is because high-frequency modes, especially C
500 cm−1 to align with the approximate transition energy of terrylenediimide, a prototypical organic chromophore with extensive prior 2DES characterization.13,59,62–64 Second, we constrained eqn (3) and (4) to include two independent vibrational modes. In a previous study, we considered systems with up to three vibrational modes and analyzed how the number and frequency of the modes impacted the machine learning.33 Here, we prioritize the inclusion of one high-frequency (1300 cm−1) and one low-frequency (200 cm−1) mode. This is because high-frequency modes, especially C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretches, often exhibit significant Franck-Condon (FC) activity in organic chromophores.61 Also, low-frequency modes are found to play significant roles in non-adiabatic excited-state dynamics.65–68 Further details of the spectral database are provided in the ESI.†
C stretches, often exhibit significant Franck-Condon (FC) activity in organic chromophores.61 Also, low-frequency modes are found to play significant roles in non-adiabatic excited-state dynamics.65–68 Further details of the spectral database are provided in the ESI.†
2.2 2DES simulations
We simulated absorptive 2DES signals (e.g., Fig. 3a) for each model Hamiltonian using in-house Python codes (freely available in ref. 69). We calculated the third-order optical response functions (ground-state bleach and stimulated emission pathways) as a function of the t1, t2, and t3 interpulse time delays (Fig. 2a). We applied a phenomenological lineshape function70 to each dimension of the time-domain signals to account for phenomenological system–bath interactions and to realize finite linewidths. The final absorptive 2DES spectra are computed by fast Fourier transformation of the signal to the pump (ω1/(2πc)) and probe (ω3/(2πc)) frequency domains (abbreviated herein for clarity as ω1 and ω3, respectively). Table S2† shows the parameters that were used in our nonlinear response simulations. We selected parameters that reflect common scenarios encountered in 2DES experiments (e.g., spectral linewidths, time and frequency resolutions, etc.). Further details of the simulations are described in the ESI.† | ||
| Fig. 2 Schematic workflow of the spectral simulations, data processing, and machine learning trial employed here. (a) We used nonlinear response function simulations to generate a spectral database for all systems within the parameter space portrayed in Fig. 1. (b) For each type of data pollutant, we operated on a copy of the clean spectral database and sent the polluted spectra to the ML algorithm. (c) We used 80% of the data to train a categorical feed-forward neural network and the remaining 20% for testing. | ||
2.3 Data pollution
The simulations described above provide “clean” spectra, which do not capture many features of experimentally measured 2DES spectra. Noise and pulse properties can significantly influence the results of 2DES experiments,2,53–55 yet such factors are commonly neglected in simulations. To explore: (i) how experimental effects (i.e. noise and laser-sample resonance constraints) influence the machine-learnability of 2D data and (ii) bridge simulation-trained NNs toward applications to experimental data, we “polluted” our ML datasets prior to both training and testing and examined the resulting effects on NN performance. Fig. 2b shows the strategy for introducing each kind (vide infra) of pollutant; we applied the pollution operation to a copy of the pristine dataset, trained the ML model on the polluted data (Fig. 2c), and then computed the performance on a test set of the polluted data.Noise signatures, and the spectral characteristics of the pump pulses, are key factors that augment experimental 2DES spectra compared to their simulated counterparts. In nonlinear spectroscopy experiments, noise manifests in numerous ways that can vary depending on the signal acquisition geometry and any procedures used for background removal (e.g., chopping and phase cycling).51,55,71–73 Noise signatures are commonly categorized as either “additive” or “multiplicative” in nature (Fig. 3b). Additive noise refers to signal-independent fluctuations arising from sources such as local-oscillator intensity jitter, detector dark current, and readout electronics.55,71,74 In contrast, multiplicative or “convolutional” noise sources are proportional to the analyte signal (∝ χ(3)).71,72 Examples of multiplicative noise, which we will denote as “intensity-dependent” noise herein, are shot noise in the pump pulses and fluctuations in the beam overlap at the sample.73
Additive noise typically dominates the total noise present in a 2DES experiment, and it is instructive to distinguish between two unique scenarios. In most set-ups, intensity jitter in the local oscillator pulses leads to constant baseline offsets along ω3 that fluctuate along ω1 (e.g., the left-most panel of Fig. 3b).51,71–73 We refer to this class of noise as correlated additive noise herein. In contrast, detector dark current and read-out electronics contribute noise that is uncorrelated between pixels, or Gaussian pixel noise (e.g., the middle panel of Fig. 3b).
For each unique system Hamiltonian, we modeled noise at every ω1 × ω3 × t2 data point using a normal distribution centered around zero and with a standard deviation of σ. Unlike intensity-dependent noise and uncorrelated additive noise, which are normally distributed along all dimensions, we constructed correlated additive noise profiles that are Gaussian distributed only along ω1 × t2. All 2DES spectra associated with a given model Hamiltonian were normalized to the maximum signal magnitude at t2 = 0 prior to noise injection. As such, a value of σ = 1 corresponds to random noise comparable to the signal magnitude (or SNR ≈ 1 at t2 = 0). Table 1 provides the values of σ that we considered in this study, divided into additive (σadd) and intensity-dependent (σint) categories. Both correlated and uncorrelated additive noise profiles are simply added to the 2D spectral data. In contrast, for intensity-dependent noise, we multiply each 2D noise profile (size nω1·nω3, where nω1 and nω3 are the number of “pixels” in the pump and probe frequency dimensions, respectively) element-wise by the corresponding 2D spectrum prior to addition. Note that for a given value of σadd, the SNR of the noised spectra may differ slightly between correlated and uncorrelated additive noise (Fig. S3†). See the ESI† for details of the noise injection procedures.
| Data pollutant | Parameter (units) | Values |
|---|---|---|
| Additive noise | σ add (unitless) | 0, 1 × 10−5, 2.5 × 10−5 |
| 5 × 10−5, 7.5 × 10−5 | ||
| 1 × 10−4, 2.5 × 10−4 | ||
| 5 × 10−4, 7.5 × 10−4 | ||
| 0.001, 0.0025, 0.005 | ||
| 0.0075, 0.01, 0.025 | ||
| 0.05, 0.075, 0.1, 0.25 | ||
| Intensity-dependent noise | σ int (unitless) | 0, 0.001, 0.0025, 0.005 |
| 0.0075, 0.01, 0.025 | ||
| 0.05, 0.075, 0.1, 0.25 | ||
| 0.5, 0.75, 1, 2.5, 5 | ||
| 7.5, 10, 25, 50 | ||
| Pump spectrum | Δω (cm−1) | 100, 250, 500, 1000, 1500 |
| 2000, 2500, 3000, 3500 | ||
4000, 5000, 7500, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||
| ω c (cm−1) | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 12 000, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250, 12 250, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
|
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750, 13 750, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 13 000, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
||
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 13 500, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750, 14 750, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250, 14 250, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 14 500, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
||
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 15 000, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250, 15 250, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
||
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750, 16 750, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 16 000, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
||
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 16 500, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750, 17 750, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2DES signals depend critically on the spectral overlap between the pump pulses and the sample absorption. Both the spectral bandwidth (Δω) and center frequency (ωc) of the pump pulses determine the spectral overlap. To introduce pump pulse characteristics to our ML dataset, we convoluted the simulated 2DES spectra with Gaussian pulses (eqn (S9)†) parameterized with realistic values of ωc and Δω (Table 1). We defined the former to span the excited-state transition energies of the molecular systems represented in our spectral database (ca. 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 18
000 to 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1). Depending on the experimental apparatus, the Δω of the pump pulses in conventional 2DES experiments typically ranges between 1000 and 6000 cm−1.64,75,76 See the ESI† for further information.
500 cm−1). Depending on the experimental apparatus, the Δω of the pump pulses in conventional 2DES experiments typically ranges between 1000 and 6000 cm−1.64,75,76 See the ESI† for further information.
2.4 Machine learning
The machine-learning protocols used here are based on earlier workflows of Parker and coworkers33 that use the PyTorch library77 in Python. Our codes are freely available to the public in ref. 78. Here, we examined an inverse problem where we trained feed-forward NNs (Fig. 2c) to classify 2DES spectra based on the electronic couplings in the underlying model Hamiltonians. The NN uses flattened 2DES spectra (1D arrays of length nω1·nω3) as inputs. We used an automated trimming algorithm on all spectra (see the ESI† for details) to remove outer low-intensity signals and to ensure that all final spectra (i.e. NN inputs) have size: nω1 = nω3 = 151. The NN applies linear transformations and rectified linear unit (ReLU) activation functions to connect the input layer (consisting of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 801 neurons from the spectra of size 151 × 151) to a single hidden layer with 300 neurons. Additional hidden layers produced marginal performance gains, as discussed in the ESI.† We apply a dropout operation on hidden layer neurons for regularization. Linear transformations and softmax activation functions connect the hidden layer and output layer neurons. Each of the 33 neurons in the output layer corresponds to a single class of electronic coupling JCoul (see Fig. 1a for the class bounds in the JCoul parameter space).
801 neurons from the spectra of size 151 × 151) to a single hidden layer with 300 neurons. Additional hidden layers produced marginal performance gains, as discussed in the ESI.† We apply a dropout operation on hidden layer neurons for regularization. Linear transformations and softmax activation functions connect the hidden layer and output layer neurons. Each of the 33 neurons in the output layer corresponds to a single class of electronic coupling JCoul (see Fig. 1a for the class bounds in the JCoul parameter space).
We conducted independent ML trials for each polluted dataset (i.e., the NN was trained and tested on each polluted dataset). For simplicity, we determined a set of hyperparameters (Table 2) that optimizes NN performance when trained and tested on clean data. We then kept the hyperparameters constant for all ML trials with the polluted datasets. We also used the same initializations for the trainable parameters (e.g., weights and biases) in each trial and kept the training and testing subsets consistent by seeding data shuffling and splitting operations. See the ESI† for additional details of our ML procedures and hyperparameter optimization (Fig. S2†).
In addition to the conventional accuracy metric that assesses NN performance, we used the scikit-learn module79 in Python to calculate F1 scores and top-k accuracies. Compared to accuracy, the F1 score provides better accounting of false positives and false negatives, as well as more robustness to class imbalances.80 The top-k accuracy examines whether the true classification is in the top k most probable classifications predicted by the NN. Thus, the top-k accuracy provides additional insight into the precision of NN classifications (e.g., how far the misclassifications are from ground truth).
3 Results and discussion
The quality of NN classifications when trained and tested on clean (not polluted) spectra is a key reference point for this study. We found that the NN classifies clean 2DES spectra in their correct JCoul category with an accuracy of 83.99% and an F1 score (macro-averaged) of 0.845. This high performance is consistent with our previous study,33 in which we found an accuracy of ca. 92% for a similar JCoul range subdivided into five categories (as opposed to the 33 used here). Note that, in general, we observed that the accuracy and F1 scores were approximately equal (within about one percentage point, as shown in Fig. S8†). For clarity, we only report the F1 scores.Fig. 4 shows the performance of the NN trained and tested using clean spectra through the lens of a confusion matrix. In the confusion matrix representation, correct and incorrect NN classifications are reflected by on- and off-diagonal values, respectively. We observe that while 16% of the NN classifications are incorrect, the majority of misclassifications occur only one category away from the ground truth. This observation is consistent with the calculated 99.04% top-2 accuracy.
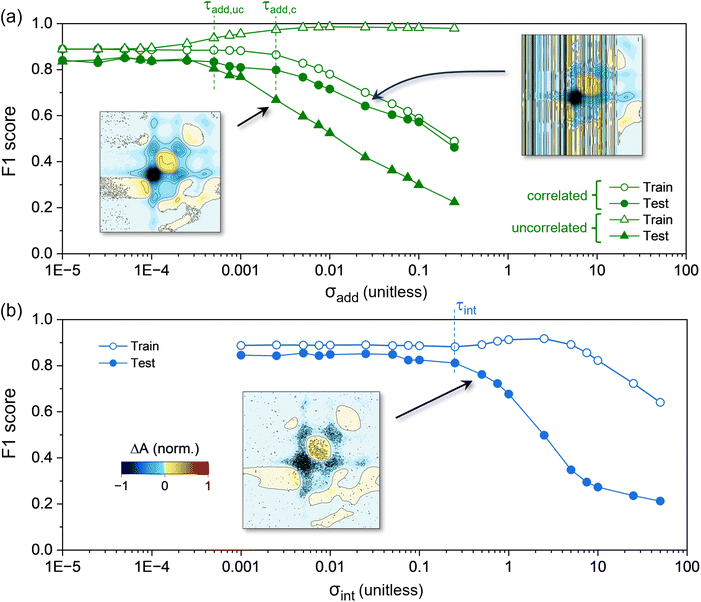
3.1 Influence of noise on NN performance
The dependence of the NN performance on the amount of additive noise in the dataset is shown in Fig. 5a (see the insets for representative 2DES spectra). We find that training and testing F1 scores are relatively unaffected (remaining within 5% of the F1 ≈ 0.845 observed on the clean dataset) by both types of additive noise until σadd exceeds a threshold value, τadd. The threshold level of uncorrelated additive noise, or τadd,uc, is 0.0005 (corresponding to SNR ≈ 12.4). In contrast, the threshold for correlated additive noise (τadd,c) is 0.0025, or SNR ≈ 2.5. This indicates that, with respect to additive noise, the NN performance is more robust to correlated sources than it is to uncorrelated sources. This is further supported by the testing F1 scores at increasingly large values of σadd, which drop exponentially for datasets with uncorrelated additive noise. The testing scores also decrease with increasing σadd for models trained on data with correlated noise, but at a significantly slower rate.Comparing the models' F1 scores on the training versus the testing datasets provides information about over-fitting.81 For both correlated and uncorrelated sources, we observe small amounts of over-fitting to the training data when σadd is less than the respective τadd, as indicated by the slightly higher training F1 scores compared to the testing scores (Fig. 5a). However, as σadd increases beyond the respective τadd, the extent of over-fitting substantially increases solely in the case of uncorrelated additive noise. This result suggests that the NNs ‘memorize’ the uncorrelated noise signatures in the training dataset. In ML approaches applied to other types of datasets, noise injection is commonly performed82–85 to improve the generalizability of NNs (e.g., to mitigate over-fitting81). Still, previous studies86–88 found that deep neural networks (DNNs) tend to over-fit when trained on data with noisy labels. This tendency was shown to evince a shift in the DNN from learning general features of the training data to memorizing the noise patterns.88 The trends in Fig. 5a, as well as Fig. S7,† suggest a similar effect when the feed-forward NN here is trained on spectra with uncorrelated additive noise. Still, even for σadd = 0.25, the NN significantly outperforms random guessing.
As in the case of additive noise, we find that the training and testing F1 scores are invariant with increasing intensity-dependent noise (Fig. 5b) until a threshold is exceeded, i.e. σint > τint = 0.25 (corresponding to SNR ≈ 5.1). The intensity-dependent threshold is thus significantly higher than the thresholds for both types of additive noise (i.e. τint > τadd,c > τadd,uc). This makes sense, as increasing σadd leads to an increase in SNR more quickly than increasing σint (see Fig. S3†). With respect to SNR, the impact of intensity-dependent noise on NN performance falls between that of correlated and uncorrelated additive noise (SNR ≈ 5.1 vs. 2.5 and 12.4, respectively). Fig. 5b also shows that, for σint > τint, the NN performance exhibits a logistic-like decay with increasing intensity-dependent noise (compared to the exponential decay found for additive noise). In contrast, the training F1 score shows a slight growth from 0.882 to 0.913 between σint = 0.5 and 5, respectively, followed by an exponential decay for σint > 5. Aside from indicating over-fitting, this result suggests fundamental differences between the nature of over-fitting for spectral datasets with uncorrelated additive vs. intensity-dependent noise.
The results in Fig. 5 show that each category of noise explored here exhibits clear and distinct influences on NN classifications of 2D spectra based on electronic couplings. We find that the NN performance is generally robust up to certain threshold amounts of noise (τadd,uc = 0.0005, τadd,c = 0.0025, and τint = 0.25). These thresholds predict reductions in NN performance for spectra with SNR < 12.4, 2.5, and 5.1 if the total noise is dominated by uncorrelated additive, correlated additive, or intensity-dependent noise, respectively. For σ > τ, the NNs generally exhibit a mixture of learning and memorizing, with memorization being particularly evident for datasets with uncorrelated additive or intensity-dependent noise. Many of the misclassifications when σ > τ, as shown in Fig. S9,† occur more than one category away from the true class. This is especially the case for spectra from Hamiltonians that have weak-to-intermediate electronic coupling values.
3.2 Influence of pump characteristics on NN performance
Resonance between the pump pulses and the absorption spectrum of the sample in a 2DES experiment critically determines the magnitude and shape of features in the 2DES spectra. As described above and shown in Fig. 3c, we varied the spectral bandwidth (Δω) and center frequency (ωc) of the pump pulses to simulate experiments with varied resonance conditions. The heatmap in Fig. 6a shows the testing F1 score after training and testing the NNs with datasets spanning each combination of the Δω and ωc parameters. We observe rich variation in the NN performance as Δω and ωc are varied. For all ωc, the F1 scores when Δω = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are similar to those obtained from the clean dataset (ca. 0.845). As Δω decreases, we observe that the F1 scores increase and subsequently decrease. The values of Δω that yield the maximum F1 score depend strongly on ωc. Several combinations of Δω and ωc yield F1 scores above 0.95 (dark red regions). Within the range 500 ≤ Δω ≤ 5000 cm−1, the F1 scores are bi-modal with respect to ωc. For ωc ≤ 14
000 cm−1 are similar to those obtained from the clean dataset (ca. 0.845). As Δω decreases, we observe that the F1 scores increase and subsequently decrease. The values of Δω that yield the maximum F1 score depend strongly on ωc. Several combinations of Δω and ωc yield F1 scores above 0.95 (dark red regions). Within the range 500 ≤ Δω ≤ 5000 cm−1, the F1 scores are bi-modal with respect to ωc. For ωc ≤ 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and ≥15
000 cm−1 and ≥15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, small values of Δω result in F1 scores below the 0.845 score obtained with the clean dataset (blue regions). All trends noted in Fig. 6a are also found in the training F1 scores (Fig. S10†).
000 cm−1, small values of Δω result in F1 scores below the 0.845 score obtained with the clean dataset (blue regions). All trends noted in Fig. 6a are also found in the training F1 scores (Fig. S10†).
The dependencies of the F1 score on Δω and ωc are counter-intuitive for two reasons. First, 2DES experiments are typically designed with maximal pulse bandwidth.53,75 This is because lower values of Δω constrain the shape of the 2DES signal along the pump axis, in turn obscuring information about the molecular system. For example, compare the upper and middle spectra in Fig. 6b to 3a. In contrast, we find that smaller Δω values improve NN performance (to a limit). Second, we might expect better NN performance when the pump pulse spectra are resonant with the excited-state energy of the monomers in the site basis (i.e., ωc = ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 in eqn (2)). Instead, we find that, for almost all Δω values, the F1 scores increase when the pump spectra are significantly red- or blue-shifted away from the monomer transition energy.
500 cm−1 in eqn (2)). Instead, we find that, for almost all Δω values, the F1 scores increase when the pump spectra are significantly red- or blue-shifted away from the monomer transition energy.
Kasha's theory61,89,90 for the optical responses of molecular aggregates predicts two exciton classifications based on the sign of the coulombic coupling. The theory predicts that the absorption spectrum of a dimer with JCoul < 0 (J-type) will be red-shifted compared to that of the isolated monomer (illustrated in the upper portion of Fig. 6a). In contrast, dimers with JCoul > 0 (H-type) yield blue-shifted absorption spectra. The qualitative predictions of Kasha's theory correlate well with both (i) the bimodal dependence of NN accuracy on ωc and (ii) the symmetry of the bimodal trend about ωc = ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. Such a correlation makes sense since, for all pump spectra except those with ωc = 14
500 cm−1. Such a correlation makes sense since, for all pump spectra except those with ωc = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, the pump biases the spectral dataset toward one exciton response regime and, in turn, influences how the NN learns about the underlying electronic couplings. From the trends in the F1 score as Δω is varied, we posit that, for sufficiently large Δω, biasing one exciton regime over the other boosts NN performance by emphasizing the differences in the 2DES signatures of H- vs. J-type aggregates. However, as Δω is decreased, the performance gains from biasing one exciton regime should eventually be overcome by the erasure of information contained in off-resonant regions of the 2DES spectra. We observe this behavior for all ωc, as the NN performance drops substantially when Δω drops below threshold values (e.g., for Δω < 1500 cm−1 when ωc = 12
500 cm−1, the pump biases the spectral dataset toward one exciton response regime and, in turn, influences how the NN learns about the underlying electronic couplings. From the trends in the F1 score as Δω is varied, we posit that, for sufficiently large Δω, biasing one exciton regime over the other boosts NN performance by emphasizing the differences in the 2DES signatures of H- vs. J-type aggregates. However, as Δω is decreased, the performance gains from biasing one exciton regime should eventually be overcome by the erasure of information contained in off-resonant regions of the 2DES spectra. We observe this behavior for all ωc, as the NN performance drops substantially when Δω drops below threshold values (e.g., for Δω < 1500 cm−1 when ωc = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1).
250 cm−1).
The findings of Fig. 6 show that feed-forward NNs more accurately map 2DES spectra to electronic couplings when the datasets are spectrally constrained (polluted by pump resonance). This result marks a significant departure from human-based designs and analyses of 2DES experiments. With few exceptions,91 spectrally broadband and on-resonance pump pulses are desired for 2DES experiments. Heisler and coworkers54 showed that limited resonance between the pump pulses in a 2DES experiment and the absorption spectrum of the molecular monomer can artificially manifest signatures of electronic coherences in the spectra, which are physically impossible for monomeric samples. While such unphysical information may mislead human analysis of 2DES data, our findings show that some constraints on spectral resonance can positively influence the ability of NNs to learn about spectral signatures of electronic coupling.
3.3 Implications for applications to 2DES experiments
ML presents revolutionary opportunities for decoding information from optical data.25,26 The results of our study suggest that, despite the signal complexity of nonlinear multidimensional spectroscopy, simple ML approaches like the feed-forward NNs can learn information about the underlying molecular properties in the face of experimental realities (noise and pulse resonance conditions). Although each category of noise investigated here degrades NN performance, this is only the case for noise widths that exceed some threshold (σ > τ). For additive noise, the thresholds vary significantly depending on whether the source adds correlated or uncorrelated noise in the ω1 × ω3 dataspace. For uncorrelated additive sources, noise levels exceeding σadd > τadd,uc = 0.0005, or SNR <12.4, yield NN performance loss. This is compared to the case of correlated additive sources, where τadd,c = 0.0025 (SNR ≈ 2.5). For noise sources that scale with the intensity of the analyte signal, we find NN performance is unaffected until σint > τint = 0.5 (SNR < 5.1). We infer from these results that sources of correlated additive and intensity-dependent noise pose limited risk of obscuring coupling information in experimental 2DES spectra.In practice, the relative influence of different noise sources in CMDS experiments depends critically on factors such as the experimental geometry, detection mechanism, and approaches for background removal. Still, it is generally the case that intensity-dependent noise sources are least problematic.71–73 In contrast, power fluctuations of the local oscillator, modeled here as correlated additive noise, are often the dominant noise source.51 In this work, we find that NN performance is less susceptible to correlated additive noise in the training data compared to uncorrelated noise (Fig. 5a). We thus anticipate that noise sources such as the detector (i.e., dark current) and read-out electronics, which contribute uncorrelated additive noise, may be most disruptive to NN-based analyses of CMDS data. Taken together, our findings suggest that NN-based approaches to extracting couplings from experimental data should be robust to noise if the SNR is sufficiently high. Increased reliance on noise-reduction methods, including standard averaging and phase cycling procedures92 or post-processing algorithms,93 may be warranted in experimental scenarios prone to excessive noise.
The counterintuitive behavior revealed in Fig. 6 highlights that NNs interface with spectroscopic signals in a fundamentally different way compared to humans. We hypothesize that ML tools may provide opportunities to leverage subtle properties of multidimensional spectra that are overlooked by traditional interpretation methods. For example, the traditional workflow to interpret 2DES spectra for complex molecular systems follows insights gained from nonlinear optical response theories.1,94,95 Theoretical models predict that cross-peaks in rephasing 2DES spectra are particularly sensitive to electronic and vibronic couplings.11,56,58,96 In turn, cross-peaks are of central focus in the analysis of experimental 2DES data.11,97–99 The salient trends in the predictions from nonlinear optical response theories tend to guide human-based analyses of spectra, but there may be a wealth of information contained in the more fleeting trends in the theoretical spectra. Our observation that the NN-interpretability of 2DES data is maximized by sub-optimal (by human standards) resonance conditions supports our hypothesis.
NNs elicit an information-centric perspective of spectroscopic signals during training. In a recent study of Flores and coworkers,38 the authors trained a CNN to classify linear infrared spectra based on functional group information. In addition to spectral features from fundamental vibrational frequencies, they found that the model uses non-intuitive features, such as the absence of specific peaks or peaks from anharmonic modes, in its classifications. Such findings emphasize the potential usefulness of traditionally overlooked properties of spectra in enabling accurate spectral interpretations. Our findings prompt further explorations of how property-specific information is distributed throughout 2DES datasets. Indeed, a recent study of Jakobsson and coworkers100 found patterns of Fisher information distribution in simulated 2DES spectra that differ from the typical spectral regions that nonlinear response theories suggest for analysis.11,56,58,96 Information-based (machine-learned in our case) approaches may guide experimental designs or spectral analyses that most efficiently lead to molecular insight from multidimensional spectra.
4 Conclusions
2DES spectroscopy is an increasingly accessible and powerful tool that can probe ultrafast dynamics. Chemically meaningful information is traditionally inferred from 2DES spectra through extensive signal analysis, theoretical modeling, and human-led comparisons of simulated and experimental spectra.58,98,99 Despite the time and effort required to perform such tasks, misinterpretations of 2DES spectra are still possible and are historically precedented.7,19–22 Misinterpretations pose a concern, especially as 2DES is used to study increasingly complicated condensed-phase systems. Being agnostic to traditional strategies for interpreting spectra, ML offers a promising route to translate experimental spectra to chemical insight in a robust and data-driven manner. Indeed, there are few studies29 that use ML as an inverse problem solving tool to address experimental 2DES data.We have shown that even when practical limitations such as noise and pulse resonance conditions are included in the spectral data, feed-forward NNs match simulated 2DES spectra to electronic coupling strengths with high accuracy. We found that uncorrelated additive (e.g., detector dark noise), correlated additive (e.g., intensity fluctuations in the local oscillator), and intensity-dependent (e.g., laser power fluctuations) noise signatures degrade NN performance after threshold amounts of noise are exceeded. The threshold for the latter two categories of noise is significantly higher than for uncorrelated additive noise, suggesting that correlated additive and intensity-dependent noise sources pose a smaller risk of obscuring information about electronic couplings in experimental 2DES spectra. We also found that uncorrelated additive and intensity-dependent noise lead to substantial over-fitting, which aligns with findings of earlier studies of noise with deep neural networks.85–88 Our results suggest that methods to mitigate the presence of uncorrelated additive noise in 2DES experiments may be necessary to enable ML-driven extractions of molecular properties from measured spectra.
The results presented here convey positive prospects for adapting ML-based tools to analyze and interpret complex experimental 2DES data. Future directions toward ML-guided analyses of experimental spectra may combine polluted simulated data with established transfer learning techniques.31,35,36,50,101,102 A potential approach could start with pretraining on polluted simulated spectra to produce a general ML model. Other research groups could then retrain the final layers of the general model (i.e., fine-tune)50,101,102 with local, smaller experimental datasets. This fine-tuning would allow the model to adapt to the molecular diversity, postprocessing techniques, and noise sources represented in the experimental dataset of interest. Transfer learning techniques have shown promising results in other multidimensional spectroscopy studies focused on protein structure classification.31,35,36
Finally, this study reveals significant differences between the human- and machine-based interpretation of 2DES signals. In contrast to human-based analysis, we found that NNs exhibit enhanced performance (exceeding an F1 score of 0.96) when the data are constrained by the bandwidth and center-frequency of the pump. We attribute such counterintuitive behavior to the pulse resonance changing how the NN learns the optical properties of molecular excitons. In other words, biasing the spectral data in either of the exciton absorption regimes (J- or H-type) helps the NN learn how couplings manifest in the spectra. This observation provides evidence that NNs accrue a radically different, more information-centric perspective of electronic coupling signatures in 2DES spectra. Further studies of the machine learnability of CMDS spectra may afford guidelines for experimental design as well as approaches to interpret experimental datasets.
Data availability
The codes used for this work are freely available at two public repositories. The machine learning code, iterative data pollution workflow, and a subset of the training/testing dataset are available at https://doi.org/10.5281/zenodo.15041004.78 The spectral simulation code that we used to generate the machine learning dataset is available at https://doi.org/10.5281/zenodo.6757663.69Author contributions
The authors confirm contributions to this work as follows: study conceptualization: JDS, KAP; simulation software: JDS, KAP; machine learning infrastructure: JDS, KAP, BS; analysis and interpretation: JDS, KAP, BS; resources: DNB; manuscript preparation: all authors; project administration: JDS, KAP, DNB; All authors approve the final version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
J. D. S. gratefully acknowledges support from an Arnold O. Beckman Postdoctoral Fellowship in the Chemical Sciences (https://doi.org/10.13039/100000997). Support to K. A. P., B. S., and D. N. B. from the Department of Energy (DE-SC0019400) is acknowledged gratefully.References
- S. Biswas, J. W. Kim, X. Zhang and G. D. Scholes, Coherent two-dimensional and broadband electronic spectroscopies, Chem. Rev., 2022, 122(3), 4257–4321 CrossRef CAS PubMed.
- F. D. Fuller and J. P. Ogilvie, Experimental implementations of two-dimensional Fourier transform electronic spectroscopy, Annu. Rev. Phys. Chem., 2015, 66, 667–690 CrossRef CAS PubMed.
- C. Elisabetta, 2D electronic spectroscopic techniques for quantum technology applications, J. Phys. Chem. C, 2021, 125(24), 13096–13108 CrossRef PubMed.
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. Birgitta Whaley and X. Zhu, Using coherence to enhance function in chemical and biophysical systems, Nature, 2017, 543(7647), 647–656 CrossRef CAS PubMed.
- J. C. Dean and G. D. Scholes, Coherence spectroscopy in the condensed phase: Insights into molecular structure, environment, and interactions, Acc. Chem. Res., 2017, 50(11), 2746–2755 CrossRef CAS PubMed.
- E. Fresch, F. V. A. Camargo, Q. Shen, C. C. Bellora, T. Pullerits, G. S. Engel, G. Cerullo and E. Collini, Two-dimensional electronic spectroscopy, Nat. Rev. Methods Primers, 2023, 3(1), 84 CrossRef CAS.
- J. D. Schultz, J. L. Yuly, E. A. Arsenault, K. Parker, S. N. Chowdhury, R. Dani, S. Kundu, H. Nuomin, Z. Zhang and J. Valdiviezo, et al., Coherence in chemistry: Foundations and frontiers, Chem. Rev., 2024, 124(21), 11641–11766 CrossRef CAS PubMed.
- R. Tempelaar, T. L. C. Jansen and J. Knoester, Vibrational beatings conceal evidence of electronic coherence in the fmo light-harvesting complex, J. Phys. Chem. B, 2014, 118(45), 12865–12872 CrossRef CAS PubMed.
- A. Chenu and G. D. Scholes, Coherence in energy transfer and photosynthesis, Annu. Rev. Phys. Chem., 2015, 66, 69–96 CrossRef CAS PubMed.
- F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Vibronic coherence in oxygenic photosynthesis, Nat. Chem., 2014, 6(8), 706–711 CrossRef CAS PubMed.
- J. C. Dean, T. Mirkovic, Z. S. D. Toa, D. G. Oblinsky and G. D. Scholes, Vibronic enhancement of algae light harvesting, Chem, 2016, 1(6), 858–872 CAS.
- A. A. Bakulin, S. E. Morgan, T. B. Kehoe, M. W. B. Wilson, A. W. Chin, D. Zigmantas, D. Egorova and A. Rao, Real-time observation of multiexcitonic states in ultrafast singlet fission using coherent 2D electronic spectroscopy, Nat. Chem., 2016, 8(1), 16–23 CrossRef CAS PubMed.
- J. D. Schultz, J. Y. Shin, M. Chen, J. P. O'Connor, R. M. Young, M. A. Ratner and M. R. Wasielewski, Influence of vibronic coupling on ultrafast singlet fission in a linear terrylenediimide dimer, J. Am. Chem. Soc., 2021, 143(4), 2049–2058 CrossRef CAS PubMed.
- A. De Sio, F. Troiani, M. Maiuri, J. Réhault, E. Sommer, J. Lim, S. F. Huelga, M. B. Plenio, C. A. Rozzi and G. Cerullo, et al., Tracking the coherent generation of polaron pairs in conjugated polymers, Nat. Commun., 2016, 7(1), 13742 CrossRef CAS PubMed.
- Y. Song, S. N. Clafton, R. D. Pensack, T. W. Kee and G. D. Scholes, Vibrational coherence probes the mechanism of ultrafast electron transfer in polymer-fullerene blends, Nat. Commun., 2014, 5, 4933 CrossRef PubMed.
- A. De Sio, E. Sommer, X. T. Nguyen, L. Groß, D. Popović, B. T. Nebgen, S. Fernandez-Alberti, S. Pittalis, C. A. Rozzi and E. Molinari, et al., Intermolecular conical intersections in molecular aggregates, Nat. Nanotechnol., 2021, 16(1), 63–68 CrossRef CAS PubMed.
- J. R. Caram, H. Zheng, P. D. Dahlberg, B. S. Rolczynski, G. B. Griffin, D. S. Dolzhnikov, D. V. Talapin and G. S. Engel, Exploring size and state dynamics in CdSe quantum dots using two-dimensional electronic spectroscopy, J. Chem. Phys., 2014, 140(8), 084701 CrossRef PubMed.
- E. Collini, H. Gattuso, R. D. Levine and F. Remacle, Ultrafast fs coherent excitonic dynamics in CdSe quantum dots assemblies addressed and probed by 2D electronic spectroscopy, J. Chem. Phys., 2021, 154(1), 014301 CrossRef CAS PubMed.
- J. Cao, R. J. Cogdell, D. F. Coker, H.-G. Duan, J. Hauer, K. Ulrich, T. L. C. Jansen, T. Mančal, R. J. D. Miller and J. P. Ogilvie, et al., Quantum biology revisited, Sci. Adv., 2020, 6(14), eaaz4888 CrossRef CAS PubMed.
- H. G. Duan, V. I. Prokhorenko, R. J. Cogdell, K. Ashraf, A. L. Stevens, M. Thorwart and R. J. D. Miller, Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(32), 8493–8498 CrossRef CAS PubMed.
- T. Mančal, A decade with quantum coherence: How our past became classical and the future turned quantum, Chem. Phys., 2020, 532, 110663 CrossRef.
- E. Z. Harush and Y. Dubi, Do photosynthetic complexes use quantum coherence to increase their efficiency? Probably not, Sci. Adv., 2021, 7(8), eabc4631 CrossRef CAS PubMed.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang and L. Yang, Physics-informed machine learning, Nat. Rev. Phys., 2021, 3(6), 422–440 CrossRef.
- B. Sridharan, M. Goel and U. Deva Priyakumar, Modern machine learning for tackling inverse problems in chemistry: molecular design to realization, Chem. Commun., 2022, 58(35), 5316–5331 RSC.
- C. A. M. Ramirez, M. Greenop, L. Ashton and I. U. Rehman, Applications of machine learning in spectroscopy, Appl. Spectrosc. Rev., 2021, 56(8–10), 733–763 CrossRef.
- J. Fang, A. Swain, R. Unni and Y. Zheng, Decoding optical data with machine learning, Laser Photonics Rev., 2021, 15(2), 2000422 CrossRef CAS PubMed.
- J. L. Lansford and D. G. Vlachos, Infrared spectroscopy data-and physics-driven machine learning for characterizing surface microstructure of complex materials, Nat. Commun., 2020, 11(1), 1513 CrossRef CAS PubMed.
- A. A. Enders, N. M. North, C. M. Fensore, J. Velez-Alvarez and H. C. Allen, Functional group identification for ftir spectra using image-based machine learning models, Anal. Chem., 2021, 93(28), 9711–9718 CrossRef CAS PubMed.
- S. Namuduri, M. Titze, S. Bhansali and H. Li, Machine learning enabled lineshape analysis in optical two-dimensional coherent spectroscopy, J. Opt. Soc. Am. B, 2020, 37(6), 1587–1591 CrossRef CAS.
- P. Kollenz, D.-P. Herten and T. Buckup, Unravelling the kinetic model of photochemical reactions via deep learning, J. Phys. Chem. B, 2020, 124(29), 6358–6368 CrossRef CAS PubMed.
- H. Ren, Q. Zhang, Z. Wang, G. Zhang, H. Liu, W. Guo, S. Mukamel and J. Jiang, Machine learning recognition of protein secondary structures based on two-dimensional spectroscopic descriptors, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(18), e2202713119 CrossRef CAS PubMed.
- M. Rodríguez and T. Kramer, Machine learning of two-dimensional spectroscopic data, Chem. Phys., 2019, 520, 52–60 CrossRef.
- K. A. Parker, J. D. Schultz, N. Singh, M. R. Wasielewski and D. N. Beratan, Mapping simulated two-dimensional spectra to molecular models using machine learning, J. Phys. Chem. Lett., 2022, 13(32), 7454–7461 CrossRef CAS PubMed.
- B. Sbaiti, J. D. Schultz, K. A. Parker and D. N. Beratan, Machine learning for video classification enables quantifying intermolecular couplings from simulated time-evolved multidimensional spectra, J. Phys. Chem. Lett., 2025, 16(19), 4707–4714 CrossRef CAS PubMed.
- F. Wu, Y. Huang, G. Yang, S. Ye, S. Mukamel and J. Jiang, Unraveling dynamic protein structures by two-dimensional infrared spectra with a pretrained machine learning model, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(27), e2409257121 CrossRef CAS PubMed.
- S. Ye, L. Zhu, Z. Zhao, F. Wu, Z. Li, B. B. Wang, K. Zhong, C. Sun, S. Mukamel and J. Jiang, Ai protocol for retrieving protein dynamic structures from two-dimensional infrared spectra, Proc. Natl. Acad. Sci. U. S. A., 2025, 122(7), e2424078122 CrossRef CAS PubMed.
- D. Lemm, G. Falk von Rudorff and O. Anatole von Lilienfeld, Impact of noise on inverse design: the case of nmr spectra matching, Digital Discovery, 2024, 3(1), 136–144 RSC.
- L. H. Rieger, M. Wilson, T. Vegge and E. Flores, Understanding the patterns that neural networks learn from chemical spectra, Digital Discovery, 2023, 2(6), 1957–1968 RSC.
- T. David, N. K. N. Aznan, K. Garside and T. Penfold, Towards the automated extraction of structural information from x-ray absorption spectra, Digital Discovery, 2023, 2(5), 1461–1470 RSC.
- J. Liu, M. Osadchy, L. Ashton, M. Foster, C. J. Solomon and S. J. Gibson, Deep convolutional neural networks for Raman spectrum recognition: a unified solution, Analyst, 2017, 142(21), 4067–4074 RSC.
- C.-X. Cui, Y. Shen, J.-R. He, Y. Fu, X. Hong, S. Wang, J. Jiang and Y. Luo, Quantitative insight into the electric field effect on CO2 electrocatalysis via machine learning spectroscopy, J. Am. Chem. Soc., 2024, 146(50), 34551–34559 CrossRef CAS PubMed.
- S. B. Torrisi, M. R. Carbone, B. A. Rohr, J. H. Montoya, Y. Ha, J. Yano, S. K. Suram and L. Hung, Random forest machine learning models for interpretable x-ray absorption near-edge structure spectrum-property relationships, npj Comput. Mater., 2020, 6(1), 109 CrossRef.
- E. Jonas, Deep imitation learning for molecular inverse problems, in Advances in Neural Information Processing Systems, ed. H. Wallach, H. Larochelle, A. Beygelzimer, F. d’ Alché-Buc, E. Fox and R. Garnett, Curran Associates, Inc., 2019, vol. 32 Search PubMed.
- M. Khosravian, R. Koch and J. L. Lado, Hamiltonian learning with real-space impurity tomography in topological moiré superconductors, J. Phys. Mater., 2024, 7(1), 015012 CrossRef CAS.
- J. Schuetzke, N. J. Szymanski and M. Reischl, Validating neural networks for spectroscopic classification on a universal synthetic dataset, npj Comput. Mater., 2023, 9(1), 100 CrossRef.
- S. Jan, A. Benedix, R. Mikut and M. Reischl, Enhancing deep-learning training for phase identification in powder X-ray diffractograms, IUCrJ, 2021, 8(3), 408–420 CrossRef PubMed.
- H. Wang, Y. Xie, D. Li, H. Deng, Y. Zhao, M. Xin and J. Lin, Rapid identification of x-ray diffraction patterns based on very limited data by interpretable convolutional neural networks, J. Chem. Inf. Model., 2020, 60(4), 2004–2011 CrossRef CAS PubMed.
- D. Chen, Z. Wang, D. Guo, V. Orekhov and X. Qu, Review and prospect: deep learning in nuclear magnetic resonance spectroscopy, Chem.–Eur. J., 2020, 26(46), 10391–10401 CrossRef CAS PubMed.
- L. Yang, Z. Zhao, T. Yang, D. Zhou, X. Yue, X. Li, Y. Huang, X. Wang, R. Zheng and T. Heine, et al., Monitoring C–C coupling in catalytic reactions via machine-learned infrared spectroscopy, Natl. Sci. Rev., 2025, 12(2), nwae389 CrossRef PubMed.
- H. Han and S. Choi, Transfer learning from simulation to experimental data: NMR chemical shift predictions, J. Phys. Chem. Lett., 2021, 12(14), 3662–3668 CrossRef CAS PubMed.
- M. L. Valentine, G. D. Wiesehan and W. Xiong, An evaluation of maximum determination methods for center line slope analysis, J. Phys. Chem. B, 2023, 127(19), 4268–4276 CrossRef CAS PubMed.
- X. Chen, Y. Sun, E. Hruska, V. Dixit, J. Yang, Y. He, Y. Wang and F. Liu, Detecting thermodynamic phase transition via explainable machine learning of photoemission spectroscopy, Newton, 2025, 1(3), 100066 CrossRef.
- N. M. Kearns, R. D. Mehlenbacher, A. C. Jones and M. T. Zanni, Broadband 2D electronic spectrometer using white light and pulse shaping: noise and signal evaluation at 1 and 100 kHz, Opt. Express, 2017, 25(7), 7869–7883 CrossRef CAS PubMed.
- F. V. d. A. Camargo, L. Grimmelsmann, H. L. Anderson, S. R. Meech and I. A. Heisler, Resolving vibrational from electronic coherences in two-dimensional electronic spectroscopy: the role of the laser spectrum, Phys. Rev. Lett., 2017, 118(3), 033001 CrossRef PubMed.
- G. Bressan, I. A. Heisler, G. M. Greetham, A. Edmeades and S. R. Meech, Half-broadband two-dimensional electronic spectroscopy with active noise reduction, Opt. Express, 2023, 31(25), 42687–42700 CrossRef CAS PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203 CrossRef CAS PubMed.
- A. Chenu, N. Christensson, H. F. Kauffmann and T. Mancal, Enhancement of vibronic and ground-state vibrational coherences in 2D spectra of photosynthetic complexes, Sci. Rep., 2013, 3, 2029 CrossRef PubMed.
- A. Halpin, P. J. M. Johnson, R. Tempelaar, R. Scott Murphy, J. Knoester, T. L. C. Jansen and R. J. D. Miller, Two-dimensional spectroscopy of a molecular dimer unveils the effects of vibronic coupling on exciton coherences, Nat. Chem., 2014, 6(3), 196–201 CrossRef CAS PubMed.
- J. D. Schultz, T. Kim, J. P. O'Connor, R. M. Young and M. R. Wasielewski, Coupling between harmonic vibrations influences quantum beating signatures in two-dimensional electronic spectra, J. Phys. Chem. C, 2022, 126(1), 120–131 CrossRef CAS.
- R. Tempelaar and D. R. Reichman, Vibronic exciton theory of singlet fission. II. Two-dimensional spectroscopic detection of the correlated triplet pair state, J. Chem. Phys., 2017, 146(17), 174704 CrossRef PubMed.
- N. J. Hestand and F. C. Spano, Expanded theory of H- and J-molecular aggregates: the effects of vibronic coupling and intermolecular charge transfer, Chem. Rev., 2018, 118(15), 7069–7163 CrossRef CAS PubMed.
- X. Zhao, J. P. O’Connor, J. D. Schultz, Y. J. Bae, C. Lin, R. M. Young and M. R. Wasielewski, Temperature tuning of coherent mixing between states driving singlet fission in a spiro-fused terrylenediimide dimer, J. Phys. Chem. B, 2021, 125(25), 6945–6954 CrossRef CAS PubMed.
- A. Mandal, M. Chen, E. D. Foszcz, J. D. Schultz, N. M. Kearns, R. M. Young, M. T. Zanni and M. R. Wasielewski, Two-dimensional electronic spectroscopy reveals excitation energy-dependent state mixing during singlet fission in a terrylenediimide dimer, J. Am. Chem. Soc., 2018, 140(51), 17907–17914 CrossRef CAS PubMed.
- L. Mewes, R. A. Ingle, A. A. Haddad and M. Chergui, Broadband visible two-dimensional spectroscopy of molecular dyes, J. Chem. Phys., 2021, 155(3), 034201 CrossRef CAS PubMed.
- Y. Hong, F. Schlosser, W. Kim, F. Würthner and D. Kim, Ultrafast symmetry-breaking charge separation in a perylene bisimide dimer enabled by vibronic coupling and breakdown of adiabaticity, J. Am. Chem. Soc., 2022, 144(34), 15539–15548 CrossRef CAS PubMed.
- J. W. Kim, Tu C. Nguyen-Phan, A. T. Gardiner, R. J. Cogdell, G. D. Scholes and M. Cho, Low-frequency vibronic mixing modulates the excitation energy flow in bacterial light-harvesting complex II, J. Phys. Chem. Lett., 2021, 12(27), 6292–6298 CrossRef CAS PubMed.
- C. Lin, T. Kim, J. D. Schultz, R. M. Young and M. R. Wasielewski, Accelerating symmetry-breaking charge separation in a perylenediimide trimer through a vibronically coherent dimer intermediate, Nat. Chem., 2022, 14, 786–793 CrossRef CAS PubMed.
- T. Kim, C. Lin, J. D. Schultz, R. M. Young and M. R. Wasielewski, π-stacking-dependent vibronic couplings drive excited-state dynamics in perylenediimide assemblies, J. Am. Chem. Soc., 2022, 144(25), 11386–11396 CrossRef CAS PubMed.
- J. D. Schultz and K. A. Parker, Optical Response Simulator, 2025, DOI:10.5281/zenodo.6757663.
- R. Kubo, A Stochastic Theory of Line Shape and Relaxation, Fluctuation, Relaxation, and Resonance in Magnetic Systems, Oliver & Boyd, 1962 Search PubMed.
- Y. Feng, I. Vinogradov and N.-H. Ge, Optimized noise reduction scheme for heterodyne spectroscopy using array detectors, Opt. Express, 2019, 27(15), 20323–20346 CrossRef CAS PubMed.
- Y. Feng, I. Vinogradov and N.-H. Ge, General noise suppression scheme with reference detection in heterodyne nonlinear spectroscopy, Opt. Express, 2017, 25(21), 26262–26279 CrossRef CAS PubMed.
- K. C. Robben and C. M. Cheatum, Edge-pixel referencing suppresses correlated baseline noise in heterodyned spectroscopies, J. Chem. Phys., 2020, 152(9), 094201 CrossRef CAS PubMed.
- M. J. Sáiz-Abajo, B.-H. Mevik, V. H. Segtnan and T. Næs, Ensemble methods and data augmentation by noise addition applied to the analysis of spectroscopic data, Anal. Chim. Acta, 2005, 533(2), 147–159 CrossRef.
- M. Son, S. Mosquera-Vázquez and G. S. Schlau-Cohen, Ultrabroadband 2D electronic spectroscopy with high-speed, shot-to-shot detection, Opt. Express, 2017, 25(16), 18950–18962 CrossRef CAS PubMed.
- D. Timmer, D. C. Lünemann, S. Riese, A. De Sio and C. Lienau, Full visible range two-dimensional electronic spectroscopy with high time resolution, Opt. Express, 2023, 32(1), 835–847 CrossRef PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, et al., Pytorch: an imperative style, high-performance deep learning library, in Proc. 33rd Conference on Neural Information Processing Systems, 2019, vol. 32, pp. 8026–8037 Search PubMed.
- J. D. Schultz, K. A. Parker, S. Bashir, and D. N. Beratan, Repository: Bridge-to-experiment-manuscript, 2025, DOI:10.5281/zenodo.15041004.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. Grandini, E. Bagli and G. Visani, Metrics for multi-class classification: an overview, arXiv, 2020, preprint, arXiv:2008.05756, DOI:10.48550/arXiv.2008.05756.
- H. Noh, T. You, J. Mun and B. Han, Regularizing deep neural networks by noise: Its interpretation and optimization, Proceedings of the 31st International Conference on Neural Information Processing Systems, 2017, vol. 30, pp. 5115–5124 Search PubMed.
- Y. Grandvalet, S. Canu and S. Boucheron, Noise injection: Theoretical prospects, Neural Comput., 1997, 9(5), 1093–1108 CrossRef.
- M. Eren Akbiyik, Data augmentation in training CNNs: injecting noise to images, arXiv, 2023, preprint, arXiv:2307.06855, DOI:10.48550/arXiv.2307.06855.
- L. Holmstrom and P. Koistinen, et al., Using additive noise in back-propagation training, IEEE Trans. Neural Netw., 1992, 3(1), 24–38 CrossRef CAS PubMed.
- S. Yin, C. Liu, Z. Zhang, Y. Lin, D. Wang, J. Tejedor, T. F. Zheng and Y. Li, Noisy training for deep neural networks in speech recognition, EURASIP J. Audio Speech Music Process., 2015, 1–14 Search PubMed.
- B. Han, Q. Yao, T. Liu, G. Niu, I. W. Tsang, J. T. Kwok and M. Sugiyama, A survey of label-noise representation learning: Past, present and future, arXiv, 2020, preprint, arXiv:2011.04406, DOI:10.48550/arXiv.2011.04406.
- X. Tong, T. Xia, Y. Yang, C. Huang and X. Wang, Learning from massive noisy labeled data for image classification, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 2691–2699 Search PubMed.
- Y. Bae, Y. Song and H. Jeong, Stochastic restarting to overcome overfitting in neural networks with noisy labels, arXiv, 2024, preprint, arXiv:2406.00396v1, DOI:10.48550/arXiv.2406.00396.
- M. Kasha, Energy transfer mechanisms and the molecular exciton model for molecular aggregates, Radiat. Res., 1963, 20(1), 55–70 CrossRef CAS PubMed.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, The exciton model in molecular spectroscopy, Pure Appl. Chem., 1965, 11(3–4), 371–392 CAS.
- S. Seckin Senlik, V. R. Policht and J. P. Ogilvie, Two-color nonlinear spectroscopy for the rapid acquisition of coherent dynamics, J. Phys. Chem. Lett., 2015, 6(13), 2413–2420 CrossRef PubMed.
- Z. Zhang, K. Lewis Wells, E. W. J. Hyland and H.-S. Tan, Phase-cycling schemes for pump–probe beam geometry two-dimensional electronic spectroscopy, Chem. Phys. Lett., 2012, 550, 156–161 CrossRef CAS.
- Z. A. Al-Mualem and C. R. Baiz, Generative adversarial neural networks for denoising coherent multidimensional spectra, J. Phys. Chem. A, 2022, 126(23), 3816–3825 CrossRef CAS PubMed.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy. Oxford Series in Optical and Imaging Sciences, Oxford University Press, 1995 Search PubMed.
- M. Cho, Coherent two-dimensional optical spectroscopy, Chem. Rev., 2008, 108(4), 1331–1418 CrossRef CAS PubMed.
- V. Perlik, C. Lincoln, F. Sanda and J. Hauer, Distinguishing electronic and vibronic coherence in 2D spectra by their temperature dependence, J. Phys. Chem. Lett., 2014, 5(3), 404–407 CrossRef CAS PubMed.
- L. Wang, G. B. Griffin, A. Zhang, F. Zhai, N. E. Williams, R. F. Jordan and G. S. Engel, Controlling quantum-beating signals in 2D electronic spectra by packing synthetic heterodimers on single-walled carbon nanotubes, Nat. Chem., 2017, 9(3), 219–225 CrossRef CAS PubMed.
- E. Thyrhaug, R. Tempelaar, M. J. P. Alcocer, K. Zidek, D. Bina, J. Knoester, T. L. C. Jansen and D. Zigmantas, Identification and characterization of diverse coherences in the fenna-matthews-olson complex, Nat. Chem., 2018, 10(7), 780–786 CrossRef CAS PubMed.
- V. R. Policht, A. Niedringhaus, R. Willow, P. D. Laible, D. F. Bocian, C. Kirmaier, D. Holten, T. Mančal and J. P. Ogilvie, Hidden vibronic and excitonic structure and vibronic coherence transfer in the bacterial reaction center, Sci. Adv., 2022, 8(1), eabk0953 CrossRef CAS PubMed.
- L. Bolzonello, N. F. van Hulst and A. Jakobsson, Fisher information for smart sampling in time-domain spectroscopy, J. Chem. Phys., 2024, 160(21), 214110 CrossRef CAS PubMed.
- B. Han, R. Okabe, A. Chotrattanapituk, M. Cheng, M. Li and Y. Cheng, AI-powered exploration of molecular vibrations, phonons, and spectroscopy, Digital Discovery, 2025, 4, 584–624 RSC.
- M. Alberts, T. Laino and A. C. Vaucher, Leveraging infrared spectroscopy for automated structure elucidation, Commun. Chem., 2024, 7(1), 268 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00125k |
| This journal is © The Royal Society of Chemistry 2025 |