RedCat, an automated discovery workflow for aqueous organic electrolytes

Abstract

Developing cost-effective organic molecules with robust redox activity and high solubility is crucial for widespread acceptance and deployment of aqueous organic redox flow batteries (AORFBs). We present RedCat, an automated workflow designed to accelerate the discovery of redox-active organic molecules from extensive molecular databases. This workflow employs structure-based selection, machine learning models for predicting redox reaction energy and aqueous solubility, and dynamically integrates up-to-date pricing data to prioritize candidates. Applying this workflow to 112 million molecules from the PubChem database, we identified 261 promising anolyte candidates. We validated their battery-related properties through first-principles and molecular dynamics calculations and experimentally tested two electrochemically active molecules. These molecules demonstrated higher energy densities than previously reported compounds, confirming the robustness of our workflow in discovering electrolytes. With its open-access code repository and modular design, RedCat is well-suited for integration into self-driving labs, offering a scalable framework for autonomous, data-driven electrolyte discovery.

---

1 Introduction

Redox flow batteries (RFBs) are an emerging energy storage technology characterized by decoupled power and energy components, rendering them particularly suitable for long-duration storage.^1–3 However, the availability, cost, and environmental burden associated with mining of the metal ore have impelled the search of new electroactive energy storage materials.⁴ Electroactive organic molecules, like quinones, alloxazines, and phenazines, have been extensively screened for high-performance candidates in advanced aqueous organic redox flow batteries (AORFBs) due to their potential advantage toward achieving low-cost synthesis at scale, structural diversity, and tailorability.^5–7

Data-driven workflows, empowered by algorithms, computational tools, and machine learning (ML) models, have been comprehensively applied in material discovery.^8–10 The design of a workflow, including the selection of applied methods and tools, needs to be tailored to align with the material class and its intended application.¹¹ For the discovery of AORFB electrolyte materials, customized workflows that account for electrolyte-related properties have been designed in previous studies.^12,13 With the rapid advancement of ML in battery materials research, ML-assisted DFT and molecular dynamics simulations are increasingly integrated into data-driven workflows to predict physicochemical properties and understand kinetic behavior,^14,15 thereby shifting electrolyte materials design from trial-and-error to rational strategies. Library generation has been frequently integrated into the data-driven workflows as the starting point of the discovery process, focusing on a subset of core structures within a known organic family and their substituents, which are enumerated using selected electron-withdrawing or donating groups. Therefore, screenings by the workflows based on virtual library generation confined to predefined or localized chemical spaces. Furthermore, the molecules identified through this approach may either be commercially unavailable or exist only virtually, and thus have not yet been synthesized. For example, simple functional groups such as –NH₂, –OH, –F, –COOH, –SO₃H, and –PO₃H₂ are widely chosen in library design. The introduction of intricate chemical groups such as –O(CH₂)₃COOH, –O(CH₂)₃PO₃H₂, –C(CH₃)₂CH₂COOH, –(CH₂)₂SO₃H₂, –(CH₂)₂COOH, and –(CH₂)₂PO₃H₂ was not considered until recent experimental findings^16,17 demonstrated their potential to enhance the stability and solubility of quinone-based electrolytes in AORFBs. Consequently, breakthroughs in data-driven discovery have been largely driven by chemical intuition and experimental knowledge.

Publicly available chemical databases contain repositories of millions of unique molecules, offering an extensive spectrum of molecular diversity in redox moieties and functional groups. However, identifying suitable electroactive molecules from such an extensive dataset is akin to searching for a needle in a haystack and requires intelligent strategies to efficiently screen the entire database.

Recent advancements in materials science and electrochemistry have highlighted the transformative potential of self-driving laboratories (SDLs) in accelerating discovery.^18,19 Despite their potential, current SDLs face significant challenges. Many existing systems are designed for specific tasks and lack the flexibility needed to coordinate complex, multi-component workflows in fully autonomous labs.^20,21 To realize the full capabilities of SDLs, it is essential to develop a modular, scalable infrastructure that can seamlessly integrate AI, DTs, and orchestration systems for efficient and autonomous lab operations. In this study, we propose an SDL-compatible automated workflow, RedCat, to screen large databases for potential AORFB electrolytes without human intervention.

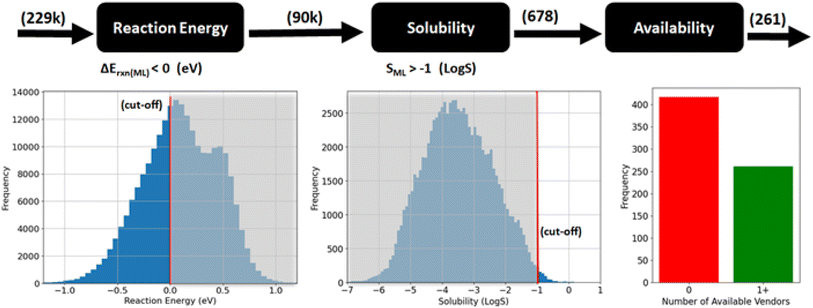
In the following sections, we present the results of applying our proposed RedCat workflow to the PubChem²² database. We begin by detailing the workflow's filtering steps, which include similarity-based, property-based, and availability-based filtering, followed by physics-based simulations. These filtering stages along with the number of molecules selected at each step are illustrated in Fig. 1. Finally, we discuss the experimental results of the two top-ranking molecules.

Fig. 1 Schematic overview of the study. The numbers within the blue circles represent each distinct filtering step, while the numbers in parentheses next to the arrows indicate the number of remaining molecules after each filtering stage.

2 Results

2.1 Similarity-based filtering

The objective of this step is to identify molecules in PubChem that are similar to those in the reference database, RedDB,²³ which contains electroactive compounds. Fig. 2 shows the similarity-based filtering process of the RedCat workflow. We established three criteria for filtering PubChem molecules based on their similarity to RedDB molecules:

Fig. 2 Screening of organic electroactive molecules from the PubChem database based on their similarity to molecules in the reference database, RedDB.

• Chemical elements present in the structure

• Redox-active substructure match

• Structural similarity

Our reference database, RedDB, consists of molecules containing only carbon (C), hydrogen (H), oxygen (O), fluorine (F), nitrogen (N), and sulfur (S). Therefore, we excluded any PubChem molecules that contained elements outside of this set. Additionally, we removed compounds identified as mixtures, which are indicated by the presence of “.” character in the SMILES notation. This filtering reduced the dataset from 112 million to approximately 78 million molecules.

Next, we eliminated molecules that have no matching redox-active substructure from the substructure list derived from RedDB. We used 52 core structures from RedDB to extract these redox-active substructures, as detailed in the Data section. Two sets of substructures were used for filtering:

• Set-1: Minimum substructure. These are substructures associated with potential redox activity.

• Set-2: Minimum full ring substructure. These are substructures that include the complete redox-active ring.

As a result of filtering based on substructure matching, approximately 40M molecules remained in set-1 and 6M in set-2.

Then, we filtered molecules based on their structural similarity to RedDB molecules using the Tanimoto similarity of ECFP²⁴ fingerprints (see eqn (1) in the Methods section). The process involved several key steps. First, for each PubChem molecule that remained after substructure filtering, the Tanimoto similarity was calculated against every RedDB molecule individually. Next, each PubChem molecule was assigned with the highest similarity value obtained from these comparisons. Molecules with similarity values below the chosen cut-off thresholds were then excluded. The cut-off values were selected to balance the number of selected molecules with their similarity to the reference database, favoring a looser threshold to maintain diversity. For set-1, which focused on minimum substructure matching, a Tanimoto similarity cut-off of 0.5 was applied. For set-2, which required minimum full ring substructure matching, a cut-off of 0.4 was used, as stricter filtering had already ensured the presence of complete redox-active ring structures. After this structural similarity filtering, approximately 60k molecules remained in set-1, and 217k molecules in set-2. Finally, we combined the two sets of molecules and removed any duplicates, resulting in a dataset of nearly 229k molecules.

2.2 Property-based filtering using machine learning predictions

In this step, we filtered the molecules based on two key properties, namely reaction energy, which is used as a proxy for redox potential, and solubility in water. These properties significantly influence the energy density of AORFBs. Fig. 3 shows the property-based filtering process, and the data distribution based on these properties. To obtain the reaction energy and solubility values, we used two ML models developed in previous studies, namely RedPred²⁵ and AqSolPred.²⁶ Detailed information about these ML models integrated into the RedCat workflow is provided in the Methods section. We selected molecules that have reaction energy less than 0 eV and solubility in water in terms of log S higher than −1 (i.e., greater than 0.1 mol L⁻¹). Applying these criteria resulted in 678 molecules.

Fig. 3 Selection of molecules based on predicted properties and vendor availability. Reaction energy and solubility were predicted using the RedPred and AqSolPred ML models, respectively. Shaded areas in the histograms indicate molecules excluded due to the applied cut-off for ML-predicted properties. The bar chart illustrates the proportion of molecules that are either unavailable or available with pricing information from vendors.

2.3 Availability-based filtering

The goal of this step is to identify molecules that are commercially available. To achieve this, we integrated ChemPrice,²⁷ a Python library designed to programmatically collect information on molecule availability and pricing, into the RedCat workflow. ChemPrice aggregates data from ChemSpace, Mcule, and Molport which collectively source information from over 100 suppliers. We conducted a price search for the 678 molecules obtained from the property-based filtering step. For these molecules, 1248 price instances were collected from various vendors. Molecules without available price information were then filtered out, narrowing the selection to 261 commercially available molecules.

2.4 Validation of selected molecules by physics-based simulations

Physics-based simulations were performed using the Schrödinger Materials Science Suite (SMSS) to rank the 261 selected molecules. By visualizing the molecular geometries in SMSS, we identified and removed 12 redox-inactive molecules. Although these 12 molecules contained the same substructure (O=C–C=C–C=O) as quinones, their moieties featured dual carboxyl groups in the ortho position of a ring, resulting in reversible redox-inactivity. Additionally, we excluded 27 steric conformers using the Filter Duplicates tool in SMSS. This process left us with 222 electroactive molecules, which were then subjected to density functional theory (DFT) simulations.

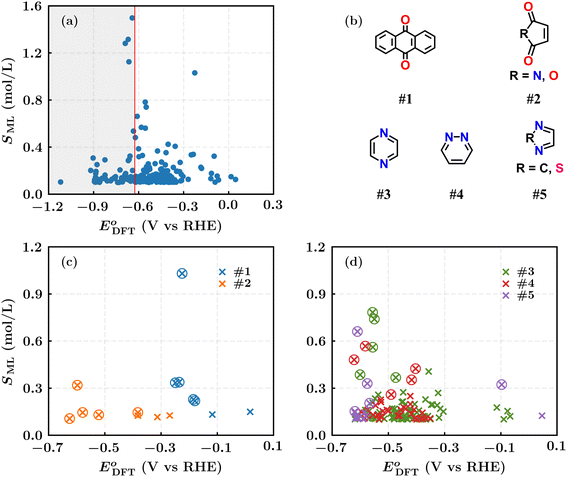
We calculated the DFT-level reaction energies of these molecules and further determined the DFT-based redox potentials using eqn (2), as described in the Methods section. The scatter plot in Fig. 4a shows the distribution of the 222 molecules based on the calculated redox potential values (E⁰_DFT) and the ML-predicted solubility (S_ML) values. The same cut-off criterion applied to the ML-predicted reaction energy values (Fig. 3) was used for the DFT-computed reaction energies. Applying eqn (2) with a cut-off criterion of E⁰_DFT < −0.63 V vs. RHE, we selected 160 molecules located to the right of the vertical line in Fig. 4a.

Fig. 4 Computational screening and analysis of 222 organic molecules. (a) Distribution of molecules based on ML-predicted solubility (S_ML) and DFT-calculated redox potential (E⁰_DFT). The vertical line marks the ΔE_rxn = 0 eV cut-off applied in the current study, and the shaded rectangle denotes the region of filtered-out molecules. (b) Representative structures of five redox moiety types identified among the 160 retained molecules. (c) Distribution of carbonyl-based moieties (#1 and #2). (d) Distribution of aza-aromatic moieties (#3, #4, and #5). Colored circles denote the top five molecules per moiety type, ranked by theoretical energy density.

To evaluate the thermodynamic stability of the selected 160 electroactive molecules and their corresponding hydrogenated (e.g., electrochemically reduced) products, we performed molecular dynamics (MD) simulations. We used the average root mean square deviation (RMSD) of all atoms and the maximum root mean square fluctuation (RMSF) of heavy atoms as proxies for stability.²⁸ The scatter plot showing the distribution of the 160 molecules based on these metrics is provided in ESI Fig. S1.† The results show that the average RMSD values for all reactant and product molecules are below 1.5 Å, and the maximum RMSF values are under 2.4 Å, indicating favorable molecular stability at 300 K and 1 atm.

The selected 160 molecules comprise five types of redox moieties, with types #1 and #2 being carbonyl-based and the remaining being aza-aromatic (Fig. 4b). These moieties are distributed as follows: seven molecules for type #1, eight for type #2, ninety-two for type #3, thirty-seven for type #4, and sixteen for type #5. The distributions of these moiety groups based on their ML-predicted solubility values and DFT-calculated redox potential values are given in Fig. 4c and d.

2.5 Experimental validation of top-ranking molecules

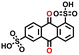
In the final step, we analyzed the top five molecules for each type of redox moiety, ranked based on their predicted energy density as detailed in the Methods. These molecules are marked by circled dots in Fig. 4c and d, and their 2D structural representations and numerical data, including predicted redox potential, solubility, energy density, average RMSD, maximum RMSF, and available experimental values are listed in Table 1.

Table 1 Details of the top five molecules in each compound group, including PubChem CID, 2D molecular structures, DFT-computed redox potential (E⁰_DFT), ML-predicted solubility (S_ML), predicted energy density (W_pre), average RMSD and maximum RMSF for both reactant and product molecules, and available experimental data (E⁰_exp). Experimental redox potentials are provided at pH = 7

#	PubChem CID	2D representation	E ^0DFT (V vs. RHE)	S ML (mol L^−1)	W pre (Wh L^−1)	Average RMSD (Å)	Maximum RMSF (Å)	E ^0exp (V vs. RHE)
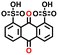
#1	6712		−0.23	1.03	32.3	0.2	1.0	−0.21 (ref. 29)
						0.3	0.9
	412447		−0.25	0.33	10.9	0.7	1.3	−0.30 (ref. 29)
						0.5	1.5
	8329		−0.24	0.34	10.8	0.2	0.4	−0.18 (ref. 29)
						0.8	1.4
	84406		−0.18	0.23	6.7	0.6	1.5
						0.6	1.5
	84473		−0.18	0.22	6.3	0.6	1.6
						0.5	1.5
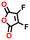
#2	136476		−0.60	0.32	16.3	0.1	0.1
						0.1	0.1
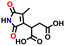
	44718968		−0.58	0.14	7.3	0.3	0.8
						0.3	0.5
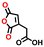
	65163		−0.52	0.13	6.1	0.4	0.8
						0.5	0.9
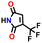
	21399352		−0.38	0.14	5.7	0.2	1.3
						0.3	1.3
	44718969		−0.63	0.11	5.6	1.2	1.7
						1.1	1.7
#3	20389456		−0.56	0.78	38.4	0.7	1.0
						0.7	0.8
	13910894		−0.55	0.74	36.1	1.0	1.1	−0.48
						0.8	1.2
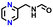
	292282		−0.56	0.56	27.5	0.8	0.9	−0.47
						0.7	0.9
	104277027		−0.60	0.39	19.8	0.5	0.9
						1.3	1.2
	19797048		−0.47	0.37	16.4	0.8	1.3
						0.6	1.0
#4	23498776		−0.58	0.57	28.6	0.7	0.9
						0.8	0.7
	67291481		−0.62	0.48	25.3	0.4	0.8
						0.7	1.1
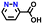
	269369		−0.40	0.42	17.3	0.2	0.6
						0.3	0.6
	82418574		−0.42	0.35	14.7	0.2	0.5
						0.3	0.9
	115736040		−0.49	0.26	11.8	0.3	0.5
						0.3	0.3
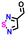
#5	12649778		−0.61	0.66	34.3	0.1	0.1
						0.5	0.6
	88038927		−0.57	0.33	16.5	0.6	0.9
						0.7	0.9
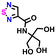
	107845553		−0.57	0.20	10.1	0.9	1.7
						0.9	1.8
	70140281		−0.10	0.32	8.0	0.1	0.2
						0.4	1.0
	81964837		−0.62	0.15	7.9	0.7	1.4
						1.0	1.8

---

Among the 25 molecules, those containing the #1 redox moiety exhibited high redox potential, while those with the #3 redox moiety demonstrated high energy density due to their elevated solubility. The average RMSD and maximum RMSF values for all 25 molecules and their product molecules were below 1.40 Å and 1.80 Å, respectively. In addition, vibrational frequency calculations for the optimized geometries of these molecules showed no imaginary frequencies, confirming that the structure optimizations converged to stable minima. Given the goal of identifying candidate compounds for energy-dense AORFB electrolytes, we selected two diaza compounds (group #3), (2-aminoethyl)[(pyrazin-2-yl)methyl]amine and N-[(pyrazin-2-yl)methyl]formamide, based on their predicted energy density, cost, and availability, and then experimentally tested them to validate the workflow's output.

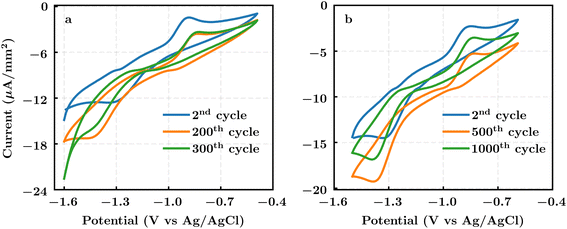
Redox activity was measured via cyclic voltammetry (CV) using 1 mmol L⁻¹ pyrazine solutions in 1 mol L⁻¹ KCl, whereby oxidation and reduction waves pertaining to the molecule were observed compared to the background current (Fig. S2†). Fig. 5 shows the CVs recorded for the two pyrazines. It is worthwhile noting that heterogeneous electron transfers for pyrazines can occur at potentials outside the thermodynamic stability for water, resulting in reactions at carbon surfaces (e.g., partial reduction of oxidized species, hydrogen adsorption and evolution^30,31) that produce background currents overlapping with the CV response of the pyrazines. This effect is seen in Fig. 5, where both oxidation and reduction peaks for the two pyrazines appear exclusively in the cathodic (i.e., negative) current range. Additionally, a peak separation greater than 0.4 V is observed in the CV, indicating sluggish electron transfer, which could lead to lower voltaic efficiencies in an AORFB. However, for the purpose of validating the RedCat workflow, the calculated redox potentials align well with the experimentally determined values, with differences of less than 0.1 V (Table 1).

Fig. 5 Electrochemical characterization of two selected organic molecules. (a) Cyclic voltammogram of 1 mM (2-aminoethyl)[(pyrazin-2-yl)methyl]amine in 1 M KCl aqueous solution. (b) Cyclic voltammogram of N-[(pyrazin-2-yl)methyl]formamide under the same conditions. Both voltammograms were recorded at a scan rate of 20 mV s⁻¹.

Extended voltametric cycling provides a cursory indication of reversibility, as the pyrazine's redox waves persist, suggesting that battery electrolytes using the molecules could undergo several charging and discharging cycles. Nonetheless, a slight increase in peak separation for both species and a tendency toward hydrogen gas evolution (particularly for (2-aminoethyl)[(pyrazin-2-yl)methyl]amine) may result in lower round-trip efficiency in a working AORFB system. Visual inspection at the end of the cycling regime did not reveal coloration of the solution or film formation on the electrode surface, suggesting that the electrochemical changes observed in the CVs are likely due to alterations in functional groups at the glassy carbon electrode surface. Precisely quantifying energy storage characteristics, including any evolution in overpotentials or hydrogen gas, is beyond the scope of this study and will require further analysis in a flow cell configuration under appropriate conditions.

In addition to redox potential, the concentration of the dissolved molecule in the electrolyte determines its volumetric capacity (Ah L⁻¹). Solubility was determined using UV-vis spectroscopy by constructing a calibration curve based on serial dilution of stock solutions. Using this method, the solubility for N-[(pyrazin-2-yl)methyl]formamide was measured to be 10.4 ± 0.1 mol L⁻¹, translating to an anolyte with a theoretical capacity of 557 Ah L⁻¹, which is more than ten times higher than the incumbent vanadium(II/III) system. In contrast, (2-aminoethyl)[(pyrazin-2-yl)methyl]amine is a liquid at room temperature and fully miscible with water. An anolyte composed solely of this pyrazine³² (without additional solvent) would have a volumetric capacity of approximately 400 Ah L⁻¹, significantly higher than that of current systems. In comparison to other aqueous organic anolytes, a recent review by P. Fischer and co-workers provides a graphical summary of indicative volumetric capacities based on solubility for commonly used compounds in flow battery electrolytes. Therein, most reported values fall between 10 and 100 Ah L⁻¹.³³ Additional recent examples include 2,6-D2PEAQ, a substituted anthraquinone with a theoretical capacity of 107 Ah L⁻¹,³⁴ AZON3, an N-alkylated fluorenone (46.4 Ah L⁻¹ (ref. 35)), 2,3-O-DBAP, a phenazine derivative (32 Ah L⁻¹ (ref. 36)) and MBPE-Vi, a bisphosphonated viologen (38.9 Ah L⁻¹ (ref. 37)). However, the volumetric capacities reported for the two pyrazines studied here may be overly optimistic. In practical flow cell operation, factors such as overpotentials, cell configuration, and electrolyte viscosity are likely to reduce the accessible capacity and overall round-trip efficiency. Nonetheless, the estimated capacity values for pyrazine-based anolytes are notable and warrant continued investigation into this class of materials. Furthermore, the high solubility and miscibility observed in a near pH-neutral medium have practical implications for flow batteries, as strongly acidic or alkaline electrolytes require special considerations in terms of battery materials and electrolyte handling procedures. Near-neutral pH electrolytes simplify several of these constraints.

3 Discussion

In this study, we propose RedCat, an SDL-compatible automated workflow for identifying promising organic electroactive molecules for AORFBs. As a proof of concept, we implemented this workflow using two databases: PubChem as the search database and RedDB as the reference database. However, this workflow is highly adaptable and can be used with other databases. For example, the search databases are represented as lists of molecules in SMILES notation, a universally recognized format used in nearly all molecular databases. Thus, by simply substituting the search database (the list of SMILES), the same screening process can be applied to different chemical search spaces. Additionally, the set of target structures can be expanded by adding new redox-active core structures, represented by SMARTS notations, to the reference database. This modular approach allows the workflow to be used for screening new databases and reevaluating previously screened databases in search of new chemical motifs.

Through screening the PubChem database, we identified two molecules for potential use as AORFB electrolytes. We experimentally validated their electrochemical activity and solubility. Notably, (2-aminoethyl)[(pyrazin-2-yl)methyl]amine is liquid at room temperature and fully miscible with water. From an application perspective, identification of (2-aminoethyl)[(pyrazin-2-yl)methyl]amine could be immensely useful as the electrochemically active liquid can be used directly as a flow battery anolyte with minimal or no solvent, resulting in a highly energy-dense electrolyte.³² However, in general, deploying highly concentrated solutions may not be practical, as electrochemical side reactions can be exacerbated, reducing the lifetime of the electrolyte. Additionally, high electrolyte viscosity or low ionic conductivity can lead to lower roundtrip efficiency of the battery system.^32,38,39

Our workflow successfully identified two high-potential molecules, and several others may also be worth exploring. To understand why some known molecules were excluded, we retrospectively analyzed a dataset of 64 AORFB molecules (see Table S1†) previously reported in the literature.^29,40–44 Out of these, only three molecules passed the full screening workflow, as shown in Fig. S4.† This analysis revealed that most exclusions resulted from the strict filtering thresholds applied. However, these thresholds are not fixed and can be easily customized based on research needs. For example, adjusting the Tanimoto similarity threshold could allow structurally distinct molecules, such as benzoquinones, to advance to later stages. Similarly, relaxing the solubility cut-off from −1 to −2 log S, would increase the number of retained candidates from six to sixteen. The extent to which literature-reported molecules are retained can serve as a useful guide for calibrating threshold values. All relevant parameters are accessible through a configuration file included with the code, allowing users to re-screen the molecular dataset using customized settings tailored to their objectives.

The property filtering phase relies on ML predictions, making the accuracy of these predictions crucial for molecule selection. While the accuracies of ML models have been reported for specific test sets,^25,26 their predictions may not be as robust for chemical spaces that are less familiar to these models. Therefore, it is recommended to consider the trade-off between the coverage of the applied chemical spaces and the determined cut-off values. This requires a prior analysis by comparing the diversity between the chemical space coverage of the training data sets (ML models) and the screened molecules.⁴⁵ Another limitation arises from solubility models, particularly for predictions of extremely large values. This stems from the fact that experimental values for highly soluble molecules used in training are often reported as “higher than” indications rather than exact values, which constrains the prediction range of the model. For example, the predicted solubility values of the two proposed molecules were 0.74 mol L⁻¹ and 0.56 mol L⁻¹, while their experimental measurements were 10.4 mol L⁻¹ and fully miscible in water, respectively. Despite these apparent discrepancies, the predicted solubility values ranked among the top 0.1% soluble molecules within the screened set (Fig. 3). Given this limitation, it is important to evaluate a molecule's predicted solubility relative to the predicted solubilities of other molecules rather than relying on standalone values.

When evaluating electrochemical redox potentials, we conducted a literature survey for experimental redox potentials and identified three of the 25 highest-performing molecules that had been previously evaluated experimentally. This provided a means of validating our DFT calculations. Comparing the calculated redox potentials with those reported in the literature revealed differences of only 0.02, 0.05, and 0.06 V, for 1,8-anthraquinonedisulfonic acid, 1,5-dihydroxy-9,10-anthraquinone-2,6-disulfonic acid and 1,5-anthraquinonedisulfonic acid, respectively.²⁹ Additionally, the differences between the calculated and experimental redox potentials for the two proposed molecules, (2-aminoethyl)[(pyrazin-2-yl)methyl]amine and N-[(pyrazin-2-yl)methyl]formamide, were 0.07 and 0.09 V, respectively. These minor discrepancies underscore the reliability of the DFT calculated redox potentials. In this study, three descriptors were used for high throughput screening: reaction free energy (a proxy for redox potential), aqueous solubility, and structural stability derived from molecular dynamics simulations. While this triage captures the key thermodynamic prerequisites for high energy density anolytes, practical performance also depends on kinetic parameters such as electron transfer rates and diffusion coefficients, membrane crossover, and overall round trip efficiency. Incorporating these additional descriptors into future versions of RedCat, along with flow cell validation, will further accelerate the discovery of commercially viable aqueous organic electrolytes.

4 Method

4.1 Data

4.1.1 PubChem. We used the PubChem²² database as the primary resource for our search for candidate electroactive compounds. PubChem serves as a data aggregator, gathering chemical information from an extensive array of data sources, making it invaluable for screening previously synthesized molecules for application in AORFBs. For this study, we downloaded the complete set of molecules represented by their SMILES notations from the PubChem File Transfer Protocol (FTP) server.⁴⁶ It is important to note that PubChem is continuously updated, hence, our study reflects the state of the database on the access day.

4.1.2 RedDB. We used the RedDB²³ database version 1.0 as a reference source for electroactive compounds suitable for AORFBs. RedDB contains 15 932 reversible two-electron two-proton redox reaction pairs, with their reaction energies calculated by quantum chemical methods. The database is built on 52 core structures, and all molecules within RedDB are derived through the R-group functionalization of these core structures. We extracted redox-active substructures from these 52 core structures to use as reference structures when screening the PubChem database.

4.2 Similarity-based filtering methods

4.2.1 Substructure matching. To filter molecules based on their substructures, we extracted redox-active substructures from the core structures within the RedDB database. These target substructures were represented using SMARTS notations, and we employed the RDKit⁴⁷ library to perform substructure matching. Molecules were retained in the selection if they contained at least one of these target substructures; those that did not were excluded.

4.2.2 Similarity calculation. To assess the structural similarity of the molecules, we converted their SMILES notations into Extended-Connectivity Fingerprints (ECFPs).²⁴ ECFPs are binary vectors where each bit corresponds to the presence or absence of a specific substructure. The algorithm works by extracting substructures from the primary molecular structure, starting from each non-hydrogen atom and extending to neighboring atoms up to a specified radius. These substructures are then hashed and mapped to a fixed-sized bit-vector. In this study, we used the RDKit implementation of ECFP with a vector length of 2048 and a radius encompassing two adjacent atoms. We quantified the similarity between two molecules using the Tanimoto similarity metric, calculated by dividing the intersection of their ECFP binary vectors by their union, as expressed in eqn (1):where U and V are the binary vector representations of two molecules.

4.3 Machine learning predictions

For the prediction of reaction energy values, we used RedPred²⁵ model, trained on RedDB²³ data. This model was tested on two separate datasets based on chemical space coverage calculated by ChemPlot,⁴⁵ achieving a mean absolute error of 0.99 eV within the training chemical space and 1.16 eV outside it. For the prediction of solubility values, we used AqSolPred²⁶ model, trained using AqSolDB,⁴⁸ which contains nearly 10 000 molecules with curated experimental aqueous solubility values. This model comprises a consensus of three different ML models and achieved a mean absolute error of 0.348 log S on a widely accepted dataset.⁴⁹

4.4 Physics-based simulations

4.4.1 DFT simulations. All simulations were performed using the Schrödinger Materials Science Suite (SMSS). Molecular geometries were generated from the SMILES notations in SMSS, and the lowest-energy conformers were identified using the OPLS4⁵⁰ Force Field. Subsequently, density functional theory (DFT) based structure optimizations, and single-point energy calculations were conducted on these lowest-energy conformers. The conformational search was performed using the MacroModel⁵¹ module, while DFT calculations were executed using the Jaguar⁵² package within SMSS. For DFT calculations, the PBE⁵³ exchange–correlation functional was employed in conjunction with the LACVP⁺⁺** basis set,⁵⁴ which includes polarization and diffuse functions. Convergence criteria were set at 5.0 × 10⁻⁵ hartree for energy change and 5.0 × 10⁻⁶ hartree for root mean squared (RMS) density matrix change. The ‘medium’ grid density and ‘quick’ accuracy level were applied for DFT-based optimizations, while ‘fine’ grid density and ‘accurate’ accuracy level were used for DFT single-point calculations. For the latter, an implicit aqueous environment was modeled using the standard Poisson–Boltzmann Formalism (PBF).⁵⁵ Additionally, vibrational frequencies of the top 25 molecules were calculated using the same basis set and functional.

4.4.2 Molecular dynamics simulations. All molecular dynamics (MD) simulations were performed using the Desmond⁵⁶ package, within SMSS. Each molecule was placed in a cubic box with an edge length of 50 Å, and the OPLS4⁵⁰ force field was applied to calculate the atomistic interactions. The simulations were performed in the canonical NVT⁵⁷ ensemble at a temperature of 300 K and a pressure of 1 atm. Temperature control was managed using the Nose–Hoover chain thermostat⁵⁸ with a relaxation time of 1.0 ps. A cut-off radius of 9 Å was set for Coulomb interactions. Each system underwent 100 ns of MD simulations, with trajectory frames saved at 100 ps intervals. MD data analysis was performed using the Simulation Interactions Diagram tool in SMSS, calculating the root mean square deviation (RMSD) of all atoms and the root mean square fluctuation (RMSF) of heavy (non-hydrogen) atoms in the molecules. The average RMSD values were obtained from 1000 frames of each MD trajectory.

4.5 Energy-related performance calculations

4.5.1 Redox potential. Previous studies^12,59 have demonstrated that the reaction energy (ΔE_rxn) during the charge–discharge process serves as an effective descriptor (R² = 0.977, RMSE = 0.051 V) for predicting the redox potential of quinone-based molecules. Further details on reaction energy as a chemical descriptor are provided in the ESI.† To develop a generalized linear regression (LR) equation for the electroactive molecules in the PubChem database, we converted all experimental redox potentials^29,40–44 to neutral pH and used ΔE_rxn as the descriptor. The resulting LR equation is shown below.

E⁰_DFT (V vs. RHE, pH = 7) = [−0.41 × ΔE_rxn (eV)] − 0.63 (2)

where E⁰_DFT represents the predicted redox potential of the organic electroactive molecule using the PBE functional.

4.5.2 Energy density. The theoretical energy density of a redox flow battery can be expressed as:⁶⁰

W_pre (Wh L⁻¹) = nCFV/μ_v (3)

where n is the number of transferred electrons per electrolyte molecule, C is the concentration of redox-active molecules dissolved in water, F is Faraday's constant (26.8 Ah mol⁻¹), V is the working voltage of the cell, and μ_v is the volume factor. In this study, ferri/ferrocyanide, which exhibits a redox potential of 0.36 V vs. SHE at neutral pH, was used in conjunction with candidate organic anolyte materials. Assuming μ_v = 1, the theoretical energy density of the anolyte simplifies to:

W_pre (Wh L⁻¹) = 26.8 × n × S_ML × (0.36 − E⁰_DFT) (4)

where n = 2 for the current study, and S_ML represents the solubility (in mol L⁻¹) of the electroactive molecules as predicted by the ML model.

4.6 Experimental methods

4.6.1 Materials. Potassium hydroxide (Supelco, EMSURE) and potassium chloride (≥99.0%, Bioreagent) were purchased from Merck. N-[(pyrazin-2-yl)methyl]formamide (95%) and (2-aminoethyl)[(pyrazin-2-yl)methyl]amine dihydrochloride (95%) were obtained from Enamine Ltd. Chloroform (99.8%) and Na₂SO₄ (Anhydrous, EMPROVE® ESSENTIAL) were sourced from Biosolve and Merck, respectively.

4.6.2 Neutralization of (2-aminoethyl)[(pyrazin-2-yl)methyl]amine dihydrochloride. To neutralize (2-aminoethyl)[(pyrazin-2-yl)methyl]amine dihydrochloride, 3 grams of the solute were dissolved in 30 mL of distilled water. Five equivalents of potassium hydroxide (KOH) were added to the solution in a 100 mL glass round-bottom flask and stirred overnight. Chloroform was added to the solution and the solute was extracted twice with 100 mL of organic solvent. To improve the extraction efficiency, potassium chloride (KCl) was added to the water phase until saturation, and the extraction was repeated two more times until no coloration was observed in the organic phase. The organic phase was then dried using anhydrous Na₂SO₄, filtered, and the solvent was removed using rotary evaporator at 40 °C and 20 mbar. The resulting brown liquid was used without further purification (yield = 52%).

4.6.3 Cyclic voltammetry and UV-vis spectroscopy. Before conducting any experiments, all equipment was thoroughly cleaned with ultra-pure water (Type 1, 18.2 MΩ cm at 25 °C, Ultrapure water system A series, Avantor) using ultrasonication (Branson 5510) for 20 minutes. Electrodes were polished to a mirror finish with diamond and alumina slurries (PK-4, BASMF2060, Bioanalytical Systems Inc.), followed by an additional 10 minutes of ultrasonication. All components were then dried at room temperature for one day.

4.6.4 Cyclic voltammetry. Electrochemical tests were conducted using an Ivium Octostat 200 (Ivium Technologies) under a nitrogen (N₂) atmosphere with a gas bubbler filled with water, maintained at 22.7 °C. Cyclic voltammetry (CV) measurements were performed at a scan rate of 20 mV s⁻¹ using a glassy carbon working electrode (2 mm active diameter, PEEK body 6 mm diameter, Redoxme AB), a platinum sheet counter electrode (10 × 10 × 0.1 mm, Dek Research Instrumentation) and an Ag/AgCl reference electrode (6 mm body diameter, Redox.me AB). The electrochemical cells had a glass chamber with a total volume of 50 mL, equipped with a PEEK lid, gas inlet/outlet, and three terminals for electrodes (Redox.me AB). Electrolyte solutions were prepared with ultra-pure water (Type 1, 18.2 MΩ cm at 25 °C, Ultrapure water system A series, Avantor). All experiments were conducted with 30 mL of 1 mM solute in 1 M KCl electrolytes, with solutions sparged with wet N₂ for 30 minutes before initiating any experiments.

4.6.5 UV-vis spectroscopy. UV-vis measurements were conducted using a UV-vis spectrophotometer P9 (Avantor) at 22.7 °C. Quartz cuvettes (10 mm, Avantor) were cleaned with ethanol (absolute, ≥99.5%, Merck) and dried with an N₂ flow. Calibration curves were constructed by preparing stock solutions of 1 mM solute in three different electrolytes. From each stock solution, 0.1, 0.2, 0.3, 0.4, and 0.5 mL were aliquoted into new samples and diluted with 3 mL of the corresponding electrolyte. These diluted solutions were measured with the UV-vis spectrophotometer, and calibration curves were plotted based on maximum absorbance as a function of concentration. For saturated solutions, 1–2 mL of each electrolyte was used, and solutes were gradually added and left to stir overnight. The following day, any remaining solid indicated saturation. 0.1 mL of these solutions were filtered using hydrophilic PTFE filters (0.22 μm, Avantor) and diluted until their maximum absorbance fell within the calibration curve range.

Data availability

The reproducibility of the automated RedCat workflow can be verified by executing the provided scripts on Code Ocean (https://codeocean.com/capsule/8660050/tree).

Author contributions

M. C. S. and X. Z. contributed equally to this work. Conceptualization, S. E.; methodology, S. E., M. C. S., and X. Z.; algorithm-based programming and validation, M. C. S., J. M. and A. K. N.; physics-based modeling and validation, X. Z.; experiments and validation, E. B. and N. M.; formal analysis and discussion, M. C. S., X. Z., S. E., S. S., A. K. N., K. K., N. M., and P. A. A. K.; writing – original draft preparation, M. C. S. and X. Z. (computational part), N. M. and E. B. (experimental part); writing – review and editing, M. C. S., X. Z., S. E. S. S., A. K. N., K. K., N. M., P. A. A. K., and E. B.; supervision, S. E.; project administration, S. E.; funding acquisition, S. E. All the authors have read and agreed to the published version of the manuscript.

Conflicts of interest

Patent application has been submitted based on the results reported in this paper.

Acknowledgements

DIFFER is part of the institute organization of NWO. This work was sponsored by NWO Exact and Natural Sciences for the use of supercomputer facilities. The authors acknowledge funding from Shell Global Solutions International B.V.

References

1. Z. X. Zhu, et al., Rechargeable batteries for grid scale energy storage, Chem. Rev., 2022, 122, 16610–16751.
2. A. A. Kebede, T. Kalogiannis, J. Van Mierl and M. Berecibar, A comprehensive review of stationary energy storage devices for large scale renewable energy sources grid integration, Renewable Sustainable Energy Rev., 2022, 159, 112213.
3. E. Sánchez-Díez, et al., Redox flow batteries: Status and perspective towards sustainable stationary energy storage, J. Power Sources, 2021, 481, 228804.
4. J. Winsberg, T. Hagemann, T. Janoschka, M. D. Hager and U. S. Schubert, Redox-flow batteries: From metals to organic redox-active materials, Angew. Chem., 2017, 56, 686–711.
5. J. Kim, et al., Organic batteries for a greener rechargeable world, Nat. Rev. Mater., 2023, 8, 54–70.
6. G. J. Yang, et al., Organic electroactive materials for aqueous redox flow batteries, Adv. Mater., 2023, 35, 2301898.
7. Q. R. Chen, et al., Organiac electrolytes for pH-neutral aqueous organic redox flow batteries, Adv. Funct. Mater., 2022, 32, 2108777.
8. Z. Wang, et al., Data-driven materials innovation and applications, Adv. Mater., 2022, 34, 35451528.
9. R. Pollice, et al., Data-driven strategies for accelerated materials design, Acc. Chem. Res., 2021, 54, 849–860.
10. L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Data-driven materials science: Status, challenges, and perspectives, Adv. Sci., 2019, 6, 1900808.
11. J. Schaarschmidt, et al., Workflow engineering in materials design within the battery 2030+ project, Adv. Energy Mater., 2022, 12, 2102638.
12. Q. Zhang, et al., Data-driven discovery of small electroactive molecules for energy storage in aqueous redox flow batteries, Energy Storage Mater., 2022, 47, 167–177.
13. Q. Zhang, A. Khetan, E. Sorkun and S. Er, Discovery of aza-aromatic anolytes for aqueous redox flow batteries via high-throughput screening, J. Mater. Chem. A, 2022, 10, 22214–22227.
14. X. Chen, X. Y. Liu, X. Shen and Q. Zhang, Applying machine learning to rechargeable batteries: From the microscale to the macroscale, Angew. Chem., Int. Ed., 2021, 60, 24354–24366.
15. N. Yao, X. Chen, Z. H. Fu and Q. Zhang, Applying classical, ab initio, and machine-learning molecular dynamics simulations to the liquid electrolyte for rechargeable batteries, Chem. Rev., 2022, 122, 10970–11021.
16. F. Hasan, V. Mahanta and A. A. Abdelazeez, Quinones for aqueous organic redox flow battery: A prospective on redox potential, solubility, and stability, Adv. Mater. Interfaces, 2023, 10, 2300268.
17. J. C. Xu, S. Pang, X. Y. Wang, P. Wang and Y. L. Ji, Ultrastable aqueous phenazine flow batteries with high capacity operated at elevated temperatures, Joule, 2021, 5, 2437–2449.
18. F. Delgado-Licona and M. Abolhasani, Research acceleration in self-driving labs: Technological roadmap toward accelerated materials and molecular discovery, Adv. Intell. Syst., 2023, 5, 2200331.
19. M. Abolhasani and E. Kumacheva, The rise of self-driving labs in chemical and materials sciences, Nat. Synth., 2023, 2, 483–492.
20. G. Tom, et al., Self-driving laboratories for chemistry and materials science, Chem. Rev., 2024, 124, 9633–9732.
21. Y. Xie, K. Sattari, C. Zhang and J. Lin, Toward autonomous laboratories: Convergence of artificial intelligence and experimental automation, Prog. Mater. Sci., 2023, 132, 101043.
22. S. Kim, et al., PubChem substance and compound databases, Nucleic Acids Res., 2016, 44, D1202–D1213.
23. E. Sorkun, Q. Zhang, A. Khetan, M. C. Sorkun and S. Er, RedDB, a computational database of electroactive molecules for aqueous redox flow batteries, Sci. Data, 2022, 9, 718.
24. D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model., 2010, 50, 742–754.
25. M. C. Sorkun, E. N. Ghassemi, C. Yatbaz, J. V. A. Koelman and S. Er, RedPred, a machine learning model for the prediction of redox reaction energies of the aqueous organic electrolytes, Artif. Intell. Chem., 2024, 2, 100064.
26. M. C. Sorkun, J. M. A. Koelman and S. Er, Pushing the limits of solubility prediction via quality-oriented data selection, iScience, 2021, 24, 101961.
27. M. C. Sorkun, B. Saliou and S. Er, ChemPrice, a Python package for automated chemical price search, Chem. Methods, 2025, 5, e202400005.
28. X. Zhou, R. A. Janssen and S. Er, Virtual screening of organic quinones as cathode materials for sodium-ion batteries, Energy Adv., 2023, 2, 820–828.
29. D. P. Tabor, et al., Mapping the frontiers of quinone stability in aqueous media: Implications for organic aqueous redox flow batteries, J. Mater. Chem. A, 2019, 7, 12833–12841.
30. F. Hine, M. Yasuda and M. Iwata, Chlorine and oxygen electrode processes on glasslike carbon, pyrolytic graphite, and conventional graphite anodes, J. Electrochem. Soc., 1974, 121, 749.
31. M. Noel and P. N. Anantharaman, Voltammetric studies on glassy carbon electrodes i: Electrochemical behaviour of glassy carbon electrodes in H₂SO₄, Na₂SO₄ and NaOH media, Surf. Coat. Technol., 1986, 28, 161–179.
32. J. H. Huang, et al., Liquid catholyte molecules for nonaqueous redox flow batteries, Adv. Energy Mater., 2014, 5, 1401782.
33. P. Fischer, P. Mazúr and J. Krakowiak, Family tree for aqueous organic redox couples for redox flow battery electrolytes: a conceptual review, Molecules, 2022, 27, 560.
34. E. F. Kerr, et al., High energy density aqueous flow battery utilizing extremely stable, branching-induced high-solubility anthraquinone near neutral ph, ACS Energy Lett., 2023, 8, 600–607.
35. M. Artault, et al., Azoniafluorenones: A new family of two-electron storage electrolytes for sustainable near-neutral pH aqueous organic flow battery, Adv. Energy Mater., 2024, 14, 2401635.
36. T. Y. Kong, et al., Enabling long-life aqueous organic redox flow batteries with a highly stable, low redox potential phenazine anolyte, ACS Appl. Mater. Interfaces, 2024, 16, 752–760.
37. G. Gonzalez, et al., Redox-active bisphosphonate-based viologens as negolytes for aqueous organic flow batteries, Chem.–Eur. J., 2025, 31, e202404122.
38. D. G. Kwabi, Y. L. Ji and M. J. Aziz, Electrolyte lifetime in aqueous organic redox flow batteries: A critical review, Chem. Rev., 2020, 120, 6467–6489.
39. V. Singh, S. Kim, J. Kang and H. R. Byon, Aqueous organic redox flow batteries, Nano Res., 2019, 12, 1988–2001.
40. K. X. Lin, et al., A redox-flow battery with an alloxazine-based organic electrolyte, Nat. Energy, 2016, 1, 16102.
41. M. R. Gerhardt, et al., Anthraquinone derivatives in aqueous flow batteries, Adv. Energy Mater., 2017, 7, 1601488.
42. K. Wedege, E. Dražević, D. Konya and A. Bentien, Organic redox species in aqueous flow batteries: Redox potentials, chemical stability and solubility, Sci. Rep., 2016, 6, 39101.
43. J. R. T. J. Wass, E. Ahlberg, I. Panas and D. J. Schiffrin, Quantum chemical modeling of the reduction of quinones, J. Phys. Chem. A, 2006, 110, 2005–2020.
44. J. J. Hasford and C. J. Rizzo, Linear free energy substituents effect on flavin redox chemistry, J. Am. Chem. Soc., 1998, 120, 2251–2255.
45. M. Cihan Sorkun, D. Mullaj, J. M. V. A. Koelman and S. C. Er, a python library for chemical space visualization, Chem. Methods, 2022, 2, e202200005.
46. PubChem FTP Server, URL https://ftp.ncbi.nlm.nih.gov/pubchem, accessed 2022-08-14.
47. RDKit: Open-Source cheminformatics software, URL http://www.rdkit.org.
48. M. C. Sorkun, A. Khetan and S. Er, AqSolDB, a curated reference set of aqueous solubility and 2D descriptors for a diverse set of compounds, Sci. Data, 2019, 6, 143.
49. J. Huuskonen, Estimation of aqueous solubility for a diverse set of organic compounds based on molecular topology, J. Chem. Inf. Comput. Sci., 2000, 40, 773–777.
50. C. Lu, et al., OPLS4: Improving force field accuracy on challenging regimes of chemical space, J. Chem. Theory Comput., 2021, 17, 4291–4300.
51. F. Mohamadi, et al., Macromodel – an integrated software system for modeling organic and bioorganic molecules using molecular mechanics, J. Comput. Chem., 1990, 11, 440–467.
52. S. M. Bachrach, Jaguar 5.5, J. Am. Chem. Soc., 2004, 126, 5018.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310.
55. B. Marten, et al., New model for calculation of solvation free energies: correction of self-consistent reaction field continuum dielectric theory for short-range hydrogen-bonding effects, J. Phys. Chem., 1996, 100, 11775–11788.
56. K. J. Bowers et al., Scalable algorithms for molecular dynamics simulations on commodity clusters, Proceedings of the 2006 ACM/IEEE Conference on Supercomputing 84–es, 2006.
57. H. C. Andersen, Molecular dynamics simulations at constant temperature and pressure, J. Chem. Phys., 1980, 72, 2384.
58. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697.
59. Q. Zhang, A. Khetan and S. Er, Comparison of computational chemistry methods for the discovery of quinone-based electroactive compounds for energy storage, Sci. Rep., 2020, 10, 22149.
60. J. Luo, B. Hu, M. W. Hu, Y. Zhao and T. L. Liu, Status and prospects of organic redox flow batteries toward sustainable energy storage, ACS Energy Lett., 2019, 4, 2220–2240.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00111k

‡ These authors contributed equally to this work.

---