Mutual information informed novelty estimation of materials along chemical and structural axes

Abstract

Assessing the novelty of computationally or experimentally discovered materials against vast databases is crucial for efficient materials exploration, yet robust, objective methods are lacking. This paper introduces a parameter-free approach to quantify material novelty along chemical and structural axes. Our method leverages mutual information (MI), analyzing how it changes with calculated inter-material distances (e.g., using EIMD for chemistry, LoStOP for structure) to derive data-driven weight functions. These functions define meaningful similarity neighborhoods without preset cutoffs, yielding quantitative novelty scores based on local density. We validate the approach using synthetic data and demonstrate its effectiveness across diverse materials datasets, including perovskites with controlled subgroups, a collection with varied structure types, and predicted lithium compounds from the GNOME database compared against materials in the materials project. The MI-informed framework successfully identifies and differentiates chemical and structural novelty, offering an interpretable tool to guide materials discovery and assess new candidates within the context of existing knowledge.

---

1 Introduction

The materials science field has witnessed an expansion of computational and experimental data, with significant resources devoted to developing and maintaining comprehensive data repositories.^1–4 These databases, which now contain several million materials, have enabled rapid computational screening for high performing materials using machine learning.^5–7 While claims of “new” materials frequently appear in the literature, the field lacks robust methods to quantify and assess the novelty of these new materials relative to what is known. It is likely that much of the low hanging fruit in the materials space has been picked and that future, high-performing materials will need to be sought after in less explored regions of materials space. This necessitates the development of methods to assess and quantify relative novelty in materials databases.

Novelty in the materials science space can take on a variety of meanings depending on the subfield and the specific chemical and structural features that define differentiation therein. In thermoelectric materials, for example, the type, concentration, and spatial distribution of dopants serve as key differentiating features between compounds. At a general level, one can define material novelty along chemical and structural axes. Chemical differentiation is expressed in the use of different elements and formula templates. Structural differences are then drawn from the arrangement of these elements. Distinction can be quantified as a distance between materials along these axes. Two prominent approaches for computing chemical and structural distance are the element mover's distance (ElMD)⁸ and differences between compounds' local structure order parameters (LoStOP),⁹ respectively. The ElMD computes the Wasserstein distance between compounds on a modified Pettifor scale,¹⁰ a one-dimensional representation of the periodic table, which was derived by analyzing substitutional patterns in the Inorganic Crystal Structure Database (ICSD). This scale places chemically similar elements (such as sodium and potassium) next to each other, reflecting their tendency to substitute for one another in crystal structures. The Wasserstein distance quantifies the minimum energy required to transform one chemical composition, represented as a distribution on the modified Pettifor scale, into another. On the structural side, LoStOPs quantify the degree to which atomic sites in a crystal structure display affinity for specific coordination environments. For example, LoStOPs can measure the degree to which a distorted, 4-fold coordinated site shows similarity to both an ideal tetrahedral and square planar geometry. Structural similarity is then calculated as the Euclidean distance between vectors containing the mean, standard deviation, minimum, and maximum LoStOP values across all sites in compared structures. The reader is referred to the relevant publications for further information on these distance metrics. While ongoing research continues to advance materials distance representations,^11,12 this analysis employs the widely-adopted ElMD and LoStOP metrics.

Previous work in materials novelty estimation has explored various methodological approaches, each with distinct limitations. Baird et al. previously used ElMD with a density-based approach to quantify chemical novelty in active learning campaigns.¹³ This approach, however, omitted structure and thus could not distinguish between polymorphs (same formula, different structure), which are an important axis of novelty. Additionally, their method computed material densities from multivariate Gaussian density functions over UMAP¹⁴ projections, which makes assumptions of the local structure of the data and introduces stochasticity. This stochasticity leads to inconsistent density calculations that vary with the chosen random seed. Other approaches using variational autoencoders have shown promise in learning structural patterns from X-ray diffraction data and identifying materials outside the training distribution.¹⁵ However, these methods require large training datasets that limit the method's applicability to small, specialized datasets. Xie et al. used the pairwise distances between composition features and LoStOPs to define the chemical and structural novelty of generated materials.¹⁶ Gruver et al. recently adopted this same approach to assess the novelty of materials generated by large language models.¹⁷ In both cases, differentiation along chemical and structural axes was successfully assessed, but their approaches relied on fixed, arbitrary cutoff values that may not reflect the natural distance distributions in materials datasets.

A variety of statistical approaches for novelty and outlier estimation methods exist within the literature.^18–20 While these offer convenient statistical interpretations, they are found to rely on user selected parameters that drastically influence novelty classification outcomes. Additionally, they often make distribution assumptions that are not guaranteed in materials datasets and may not reflect the local structure of the data. The recent AUTOGLOSH²¹ approach attempts to remedy this by providing a data-driven method for selecting optimal parameters. This involves sampling a range of parameters and looking for regions where the metric stabilizes. However, this method was found to perform poorly when sharp distinctions between points or groups are not present in the data.

In this work, we present a simple, parameter-free method of assessing materials novelty along chemical and structural axes based on a mutual information (MI) informed weight function. Researchers in the materials informatics space may be familiar with mutual information analysis through its use for feature selection in MODNet.²² We employ it differently, examining how MI changes with neighbor distance to establish a data-driven criterion for determining meaningful neighborhoods and influence between materials. This approach preserves signal from the underlying distance metrics while adapting to the natural structure of the data. To demonstrate our methodology, we analyze three datasets: a perovskite dataset with controlled chemical and structural subgroups, a structurally diverse dataset with heterogeneous structure groups, and predicted stable lithium-containing compounds in the Materials Project¹ and GNOME²³ databases. Through these analyses, we showae that our method provides explainable novelty scores that capture chemical and structural differentiation. We further demonstrate how this approach not only quantifies novelty but also illuminates the specific features contributing to a material's uniqueness relative to existing compounds.

2 Methodology

2.1 Mutual information-informed density estimation

Our approach quantifies material novelty through a density estimation scheme that weighs the influence of neighboring materials based on a computed MI profile. Data density is typically assessed by considering how neighboring points influence each other, with closer neighbors having greater impact. A key challenge is objectively defining the influence of neighboring materials and the relevant distance scale for density calculations without imposing arbitrary parameters or distribution assumptions. To address this, we employ a MI approach, analyzing how MI between material pairs changes as a function of their distance (e.g., ElMD or LoStOP distance). This analysis reveals a data-driven MI profile unique to the dataset, which we use to establish an objective neighborhood cutoff distance and derive an adaptive weight function. This function quantifies the diminishing influence of neighbors with increasing distance up to the cutoff. This MI-informed density estimation preserves the nuanced signals from the underlying distance metrics while adapting to the dataset's intrinsic structure. The specific steps of this calculation are detailed in the subsequent paragraphs and illustrated in Fig. 1.

Fig. 1 MI-informed density estimation methodology. The process begins by computing pairwise material distances (using EIMD as an example) to form a distance matrix (left panel). Analyzing this matrix, mutual information (MI) is calculated across varying distance thresholds (τ) to generate an MI profile; the peak of this profile identifies the optimal neighborhood cutoff distance, τ* (center right). This MI profile is then transformed into a distance-dependent weight function, F_MI(D_ij) (top right), which sums the influence of neighbors within the cutoff distance to compute the final density score, ρ_i, for each material.

Given a materials dataset, the calculation of each material's density proceeds first through the construction of a distance matrix D ∈ R^n×n, where n is the number of materials in the dataset. Distances in this work are computed using the ElMD and LoStOP methods described in the introduction. We seek to find a cutoff distance τ* defining the maximum range of influence in the dataset. To do this, a set of potential neighborhood cutoff values τ is established that spans the range of pairwise distances from 0 to max(D). For each potential cutoff in τ we create a binary relationship matrix R ∈ {0,1}^n×n defined as:

Here a value of 1 defines a closer neighbor, while 0 defines a far neighbor for a given value of τ. The MI is the calculated between corresponding elements in the binary matrix to produce MI(τ):where p(r_ij, r_ji) represents the joint probability of observing neighbor relationships r_ij and r_ji between pairs of materials, and p(r_ij) and p(r_ji) are their marginal probabilities. The optimal cutoff distance τ* is identified at the point where MI(τ) reaches its maximum value. From this analysis, we derive a weight function F_MI(d) by inverting the normalized MI profile to create a distance-dependent weighting scheme:

This weight function quantifies how each material affects the density of a target material based on their relative distance, d. The weight is set to zero beyond the τ* cutoff. The density score ρ_i for each material i in D is then computed as the sum of the decay function values across all pairwise distances involving material i using the following equation:

In cases where a distance does not coincide with a precomputed threshold value τ, linear interpolation is used to determine the corresponding F_MI(d) value. The computed densities can then be assessed as a measure of relative material novelty. We avoid attaching a classification scheme (e.g. 1 novel, 0 common) to the computed densities as these frequently rely on distribution assumptions and may mask interesting points that are close to the novelty threshold, which may be of interest to the researcher.

2.2 Demonstration on a synthetic dataset

To demonstrate our methodology, we construct a synthetic two-dimensional dataset that exhibits several features common in novelty estimation tasks: regions of varying density, global outliers, and local outliers. The dataset consists of 80 points generated by sampling from four distinct multivariate normal distributions (20 points from each distribution), each defined by a specific mean μ and a diagonal covariance matrix Σ = σ²I where:

μ ∈ {(0,0),(2,1),(1,1),(2,2)}, σ ∈ {0.1,0.1,0.3,0.5} (5)

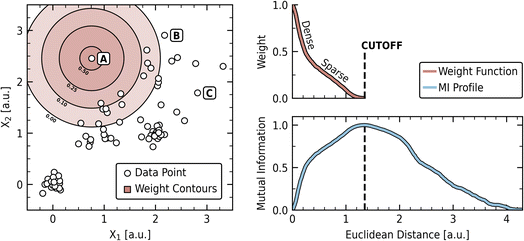
A distance matrix was constructed from the pairwise Euclidean distances between points in the synthetic dataset. This matrix was then passed through the described density estimation scheme to compute the cutoff and weight function, which is shown in Fig. 2. The cutoff was found at a distance of 1.34, which corresponds to a probability density less than 0.05 across the individual constituent distributions from which the dataset was sampled. The left panel shows the synthetic dataset with contours for the computed decay function plotted around a distant point labeled “A.” The dataset exhibits dense and diffuse regions with a gap between the dense cluster centered at (0,0) and the main body of the data.

Fig. 2 Weight contours and information analysis on the synthetic dataset. Left: synthetic dataset showing points with varying local and global novelty (A, B, C). Weight contours centered on point A illustrate the spatial topology of the derived weight function with labels corresponding to weight values. Right: the mutual information (MI) profile calculated for the dataset and the resulting weight function, indicating the optimal cutoff distance (τ*) and characteristic dense/sparse regions.

Points “A”, “B”, and “C” are highlighted as illustrative examples of points with different relationships to the overall data distribution (Fig. 2, left panel). Point “A” is relatively isolated from other clusters, point “B” is on the periphery of the main data concentration, and point “C” is an outlier within a more populated region. While the relative importance of these different novelty types may vary by application domain and researcher preference, an effective novelty estimation method should be sensitive to these varying contexts.

The weight function, shown in the upper right panel of Fig. 2, exhibits two distinct phases: a steep “Dense” phase reflecting the tightly clustered regions of the dataset, followed by a more gradual “Sparse” phase corresponding to the diffuse regions. This structure allows close neighbors to be weighted heavily without neglecting the influence of more distant relationships that are also characteristic of the data. The contours centered on the point “A” (left panel) provide a visual representation of this weighting topology, showing how influence extends according to these dense and sparse characteristics. The weight function can then be understood as reflecting the average view of each point to the rest of the dataset, incorporating both dense and sparse regions. How different spatial arrangements influence this average view can be seen by considering specific cases. For instance, the influence of gaps is explored using a uniform grid dataset in S.I. A, where separation results in flat regions of minimal MI change. Conversely, in the absence of significant gaps, the weight function approximates the average of the constituent distributions from which the data was drawn, as demonstrated in S.I. B using variations of the synthetic dataset.

2.3 Comparison with other estimators

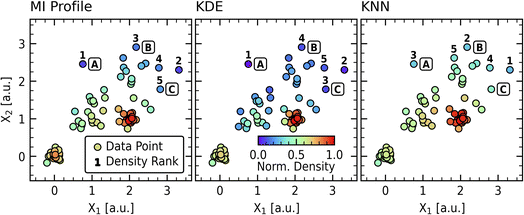
We compare the MI approach with Kernel Density Estimation (KDE) and K-Nearest Neighbors (KNN) to evaluate its unique value. As the KDE and KNN methods are parameter-driven, we apply automatic parameter estimation schemes in the form of Silverman's rule²⁴ to determine the bandwidth parameter in the KDE model and the number of neighbors in the KNN model. The implementation details are provided in S.I. C and are available in the code repository accompanying this work. Fig. 3 illustrates how these methods perform on the synthetic dataset, with color reflecting the normalized density of each data point and the five lowest density points labeled for each method. Normalized densities are used in this and subsequent analyses for ease of comparison and simple assessment of relative novelty.

Fig. 3 Comparison of density estimation methods on the synthetic dataset. Each panel shows the synthetic dataset with points colored by normalized density (red = high density, blue = low density) according to three different methods: Mutual Information (MI) Profile, Kernel Density Estimation (KDE), and K-Nearest Neighbors (KNN). The five points with lowest density (highest novelty) are numbered according to their density rank, with specific points of interest labeled A, B, and C across all methods for comparison.

The resulting normalized densities for points “A”, “B”, and “C” illustrate how the methods differ in their sensitivity to various data contexts. Notably, all three methods consistently identify points “A” and “B” among the top-ranked novel points, demonstrating convergence in detecting the most significant outliers despite their different approaches. The KDE approach emphasizes local relationships, as evidenced by its small bandwidth (0.188 relative to maximum pairwise distance of 4.29). This local sensitivity is also shown in the coloration of the diffuse region, which does not show global patterns as seen in the MI or KNN panels. In contrast, the KNN method emphasizes global relationships, prioritizing points “A” and “B” over point “C.” The KNN implementation uses 35 neighbors per the Silverman method, which exceeds the size of each subsampled group (20 points). While appropriate neighbor counts are obvious in this contrived dataset, they become harder to determine in larger, more heterogeneous datasets that cannot be easily visualized. The MI profile approach balances local and global novelty detection through its adaptive weight profile, which derives distance-weighting functions directly from the dataset's intrinsic mutual information structure. This creates more uniform gradients in the diffuse region while maintaining sensitivity to local clusters, as seen in the density patterns around the (0,0) cluster.

This comparison highlights similarities and distinctions between the novelty estimation approaches. While KDE and KNN are established methods, their outcomes are fundamentally tied to user-selected parameters or automated rules that function as parameters. These choices inevitably influence the resulting density scores and can introduce bias. Our MI-informed method avoids this by deriving its distance-weighting function and effective neighborhood cutoff (τ*) directly from the dataset's intrinsic structure via mutual information analysis, requiring no preset parameters or distribution assumptions. Furthermore, the resulting MI weight profile is uniquely adaptive, capturing complex, non-Gaussian data features like varying densities and gaps, which standard KDE kernels or KNN averaging struggle to replicate without potentially complex, multi-scale parameterizations. This analysis demonstrates that the MI profile approach offers a distinct, data-driven perspective on novelty detection without requiring parameter selection. The utility of these characteristics for materials analysis will be demonstrated in the subsequent sections.

3 Results & discussion

The methodology is demonstrated on three materials datasets with novelty assessed along chemical (ElMD) and structural (LoStOP) axes. The first is a perovskite dataset containing 54 cubic, 21 orthorhombic, and 10 tetragonal structures of the formula template ABX₃, where the anion, X, is one of O, Cl, F, I, Br. The perovskite structures were sampled from the materials project¹ and were required to have experimental validation and an energy above hull value less than or equal to 0.1 eV per atom. The materials associated with this dataset are tabulated in S.I.D. The second dataset contains 60 structurally diverse materials belonging to distinct sub-classes (e.g. ruddlesden-popper, anti-fluorite, garnet) with varying degrees of similarity. The selected sub-classes, some of which are mineral structures, were based on the authors' familiarity and a desire to create a diverse collection where novelty would be harder to assess intuitively. Structure files were pulled from a mixture of the Materials Project and the Pearson Crystallography Database.²⁵ The materials associated with this dataset are tabulated in S.I.E. The third dataset contains experimentally verified Li-containing compounds from the Materials Project (1834) and those predicted stable from the GNOME dataset (44) that were hosted on the Materials Project as of v2023.11.1 of the database. This collection aims to identify the extent to which the materials in the GNOME dataset are novel relative to an existing corpus. The GNOME materials associated with this dataset are tabulated in S.I.F. We note that the Materials Project has since been updated and that the compounds used in this analysis are no longer available. To maintain reproducibility, we include these and all other structures used in the analysis in the GitHub repository associated with this publication.

3.1 Assessing novelty in a perovskite dataset

The perovskite dataset was constructed by categorizing materials into specific structural groups (cubic, orthorhombic, tetragonal), and then selecting a controlled distribution of anion types within these structures, leading to subgroups of predetermined sizes. Based on this, we expect underrepresented groups to exhibit higher novelty (lower density). For instance, tetragonal perovskites, constituting only ∼12% of the dataset, should display lower density along the structural axis compared to cubic perovskites, which make up ∼64% of the dataset. Furthermore, the inherent distortions in tetragonal and orthorhombic perovskites introduce greater structural variability than their cubic counterparts, leading to higher within-group distances. In terms of chemical composition, anion classes with minimal representation, such as iodides (∼5%), are expected to show lower average densities compared to more abundant classes like fluorides (∼27%). However, these chemical density patterns will also be influenced by cation species diversity, which was not controlled.

MI profiles for the ElMD and LoStOP distance matrices of the perovskite dataset are plotted in Fig. 4. In the left panel, the LoStOP MI profile demonstrates an initially steep rise followed by a plateau around the cutoff point, indicating the presence of both clustered and dispersed structural regions. The flat region near the cutoff suggests distinct gaps in the structure space. This behavior is expected because the dataset contains perovskite structures from different crystal systems that are separated in structure space. Beyond the cutoff, the profile shows two distinct behaviors: region “A” exhibits a gradual decrease in MI, indicating sparse structural arrangements where distance increases produce only minor changes in the binary relationship matrix; region “B” shows a rapid decline to zero, corresponding to the boundary where more densely populated structural clusters begin to interact. This rapid change occurring near the maximum LoStOP distance further confirms that structural groups are substantially separated from one another. The right panel displays the ElMD MI profile, showing a more gradual increase to the cutoff, suggesting that materials are more evenly distributed in the chemical space. The non-zero MI at zero distance indicates the presence of materials with identical chemical formulas but different structures. Past the cutoff, three distinct regions emerge: region “A” shows rapid MI decrease, indicating densely packed chemical compositions; region “B” exhibits a slower rate of change, representing more dispersed chemical similarities; and region “C” shows a gradual decrease following a flat region, revealing a potential gap in chemistry space. These patterns align with our expectations and provide insights into the underlying structure of the perovskite dataset.

Fig. 4 Mutual information profiles along axes of the perovskite dataset. Left: MI profile along LoStOP distance matrix. Right: MI profile along ElMD distance matrix of the perovskite dataset. Letters in both plots mark distinct regions of change in the MI profiles.

The normalized structural and chemical densities for the perovskite dataset are visualized in Fig. 5, with colors indicating the crystal system of each material and inset axes highlight spatial relationships in densely populated regions. A fully labeled version is available in S.I. D. The arrangement of densities confirms our expectations regarding density patterns across crystal systems. In terms of structural density, tetragonal perovskites exhibit a median normalized value of approximately 0.01, while orthorhombic structures show approximately double this at about 0.02, proportional to their representation ratio of 1 : 2 in the dataset. Along the ElMD density axis, we observe three distinct bands of decreasing data frequency, corresponding to the regions identified in the ElMD MI profile. The median chemical densities of anion subclasses generally follow a pattern aligned with their abundance: fluorides (normalized ElMD density: 0.83, abundance: 27%) and oxides (0.81, 51%) show the highest values, followed by bromides (0.71, 8%), chlorides (0.69, 9%), and finally iodides (0.60, 4%) with the lowest density. The chloride and oxide perovskites deviate from the trend due to their frequent pairing with rare earth elements and unique cation combinations, introducing greater chemical diversity. Notably, cubic perovskites span the entire chemical density spectrum and occupy the lowest density values by a considerable margin. This is a consequence of both their larger representation and the greater chemical diversity among experimentally verified cubic perovskites in the Materials Project database.

Fig. 5 Chemical and structural density analysis for the perovskite dataset. Normalized densities of perovskites, derived from EIMD (chemical) and LoStOP (structural) distance matrices using the MI-informed method. Points are coded by crystal system and labeled in the legend. Inset axes show detail in high-density areas. Where polymorphs overlap, secondary symbols below the formula indicate their relative density order.

Several notable patterns emerge in our novelty analysis. The lowest density region along both axes contains common perovskite examples such as CaTiO₃ and SrTiO₃, along with several highly similar fluorides, the second most abundant anion class. Cubic CaTiO₃ shares identical chemical density with its tetragonal and orthorhombic polymorphs, as is also the case for SrNbO₃ and KMnF₃, which explains the non-zero initial MI value observed in the ElMD profile. The structural density variations between tetragonal and orthorhombic materials stem primarily from differences in octahedral and cuboctahedral distortions. For instance, RbAgF₃ (low novelty) and RbCuF₃ (high novelty) exhibit octahedral distortion indices of 0.023 and 0.096, respectively. Tetragonal CaTiO₃ shows minimal octahedral distortion (0.0006) but more significant cuboctahedral distortion (0.049), giving it higher novelty. Conversely, novel orthorhombic structures display reduced cuboctahedral distortion indices with lower octahedral corner rotation, as evidenced by the reduction in LoStOP density from GdFeO₃ (0.063 cuboctahedral distortion) to SrNbO₃ (0.031). Despite their structural regularity, cubic perovskites display considerable variation in LoStOP densities, with novelty arising from differences in anion bonding environments, particularly in how closely they approximate ideal 2-fold coordination. While most cubic structures show moderate conformity (median LoStOP CN2 weight of 0.51), materials deviating from this norm exhibit distinctive properties. CsPbI₃, for example, shows minimal 2-fold coordination (CN2 weight of 0.32) due to having both the lowest B-X electronegativity difference in the dataset and a relatively small A-X electronegativity difference in the dataset, resulting in less directional bonding. Similarly, CsAuCl₃ exhibits low B-X electronegativity difference (0.6) but a near-average A-X difference, with its novelty also arising from relatively small octahedral volumes. Conversely, the oxygen sites in PbZrO₃ and PbTiO₃ demonstrate strong affinity for 2-fold coordination due to their combination of high B-X electronegativity differences and the dataset's lowest A-X electronegativity differences, creating pronounced B–X–B bonding. These findings demonstrate how our methodology effectively captures subtle variations in bonding character, enabling identification of unusual structures across crystal systems.

Chemical novelty in the perovskite dataset generally increases with the incorporation of dataset-unique elements or combinations. MnTlCl₃ represents the lowest chemical density in our analysis due to its singular status as both the only thallium-containing perovskite and the only chloride perovskite without cesium. Interestingly, PbZrO₃ and PbTiO₃ achieve low ElMD density not through rare element inclusion, but rather through uncommon elemental combinations. Typically, lead and titanium/zirconium are separately paired with alkali or alkaline earth metals, making their co-occurrence particularly distinctive. A parallel novelty mechanism appears in the A-CaF₃ compound cluster, where the simultaneous presence of alkali and alkaline earth metals creates an unusual chemical environment. These findings demonstrate how our methodology successfully captures both the rarity of specific elements and subtle combinatorial novelty.

3.2 Assessing novelty in a structurally diverse dataset

The structurally diverse dataset encompasses a broad spectrum of structure types, presenting a more challenging environment for novelty assessment than the perovskite dataset. This collection includes one-off structures such tellurium and WCl₂, alongside established structural families like SiO₂ and SiC polymorphs where higher similarity is anticipated. With oxides comprising approximately 70% of the dataset, non-oxygen-bearing compounds are expected to exhibit higher chemical novelty. Unlike the perovskite dataset, where novelty could be assessed through relatively simple heuristics based on crystal system or anion type, the heterogeneous nature of this dataset necessitates a more nuanced analysis approach. Nevertheless, we demonstrate that the novelty rankings derived from our methodology remain interpretable and provide valuable insights into structural and chemical relationships across diverse material classes.

The MI profiles for the ElMD and LoStOP distance matrices of the structurally diverse dataset are provided in Fig. 6. The left panel shows a gradual MI profile over structural distances, with the cutoff occurring at a LoStOP distance of 2.61, which is 65% of the maximum LoStOP distance. This is significantly higher than the LoStOP cutoff at 0.74 (27% of max) observed in the perovskite dataset, indicating a more diffuse structure space, which is consistent with our expectations for a heterogeneous collection of materials. The LoStOP MI profile exhibits an initially sharp increase, suggesting the presence of some highly similar structural motifs. The regions of gradual change marked “A” and “B” further highlight the diffuse nature of the dataset. The right panel of Fig. 6 shows the MI profile of the ElMD distance matrix. The non-zero initial MI value confirms the presence of materials with identical chemical formulas but different structures, such as the SiC and SiO₂ polymorphs. Beyond the cutoff, which is reached more rapidly than in the LoStOP profile, three distinct regions emerge: region “A” shows a steep decrease in MI, indicating denser clustered chemical compositions; region “B” exhibits a more gradual decline, representing more dispersed chemical similarities; and region “C” displays a notable pattern of flat regions separated by sharp drops in MI. This step-like behavior in region “C” reveals the presence of distinct gaps and clusters in the chemical space, likely corresponding to isolated groups of materials with similar chemistry but separated from the main body of the dataset. This pattern is consistent with the diverse nature of non-oxide compounds in our dataset, which form small chemical neighborhoods distant from both the oxide-rich regions and from each other.

Fig. 6 MI profiles along axes of the structurally diverse dataset. Left: MI profile along LoStOP distance matrix. Right: MI profile along ElMD distance matrix of the perovskite dataset. Letters in both plots mark distinct regions of change in the MI profiles.

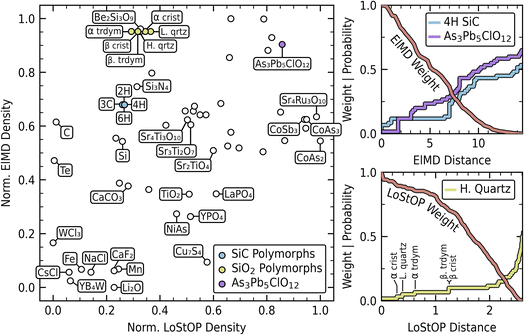
The normalized LoStOP and ElMD densities of the materials in the dataset are plotted in the left panel of Fig. 7. For clarity, only a representative selection of points are labeled, with structural identifiers used to distinguish materials sharing identical chemical formulas (e.g., “2H” for the 2H polymorph of SiC); a fully labeled figure is provided in S.I. E. The distribution along the normalized ElMD density axis confirms our expectations, with non-oxide materials generally exhibiting higher chemical novelty. As anticipated, materials with high similarity in materials space (ElMD and/or LoStOP) will be close neighbors in density space. This is seen with the SiC polymorphs, which form a dense cluster that also neighbors their constituent elements (silicon and carbon) and chemically related Si₃N₄. It is important to note, however, that neighboring points in the density space are not guaranteed to be neighbors in chemical or structural space, only that they have similar densities. Despite having identical chemical formulas, the SiC polymorphs exhibit lower elemental density than several materials with only a single formula instance in the dataset. The top right panel of Fig. 7 explains this apparent contradiction. Here, the cumulative distribution of the ElMD pairwise distances of the 4H SiC polymorph and the labeled As₃Pb₅ClO₁₂ material are shown against the computed ElMD weight function. 4H SiC is seen to have a few immediate neighbors (other SiC polymorphs), creating local density, but remains globally distant from other compounds, as evidenced by the long, flat cumulative region. This contrasts with As₃Pb₅ClO₁₂, a monoclinic, mineral structure bearing tetragonal arsenic sites, which has fewer immediate neighbors but many near neighbors throughout the dataset due to its having well represented oxygen and arsenic. The SiC cluster's lower elemental density is then understood as being a function of it being isolated in chemical space.

Fig. 7 Chemical and structural density analysis for the structurally diverse dataset. Left: normalized EIMD density versus normalized LoStOP density for materials in the dataset. Selected points and groups are colored for emphasis and labeled; structural identifiers distinguish polymorphs (e.g., 4H SiC). Top Right: comparison of the cumulative EIMD distribution functions for 4H SiC (blue) and As₃Pb₅ClO₁₂ (purple) against the dataset's MI-derived EIMD weight function (red). Bottom right: comparison of the cumulative LoStOP distribution function for high-quartz SiO₂ (yellow) against the dataset's MI-derived LoStOP weight function (red). Labeled steps indicate distances to nearest SiO₂ polymorph neighbors.

A similar situation is observed with the SiO₂ polymorphs, which are chemically identical but exhibit structural novelty relative to other materials in the dataset. The bottom right panel of Fig. 7 displays the cumulative distribution of LoStOP distances relative to high quartz (centrally positioned among SiO₂ polymorphs in the density plot). This visualization reveals that high quartz has few structural neighbors under the LoStOP weight function. The labeled increases in the plot correspond to its nearest neighbors, all SiO₂ polymorphs, in sequential order: α cristobalite, low quartz, α tridymite, β tridymite, and β cristobalite. Analysis of the LoStOP distance matrix for these materials confirms that, despite identical chemistry, the polymorphs exhibit structural dissimilarity stemming from variations in bonding angles between SiO₄ tetrahedra, mediated by 2-fold coordinated oxygen atoms. Excluding self-similarity, the average pairwise LoStOP distance among SiO₂ polymorphs is 0.88 (2.3 percentile of all dataset pairwise distances). While internally similar, their average distance to the nearest non-SiO₂ materials (1.98, 34.4 percentile) is significantly greater, highlighting their global differentiation. Further, their LoStOP features show a mean 2-fold coordination affinity of 0.63, compared to the full dataset mean of 0.17 for this feature. This quantitative assessment supports the conclusion that SiO₂ materials occupy a relatively distant region within the structural space despite their close chemical relationship.

In the interest of brevity, an exhaustive analysis of all groupings within the dataset will not be undertaken. However, a few interesting cases are worth noting in Fig. 7. Tellurium appears structurally unique, but exhibits moderate density (0.47) in chemical space despite being the only instance of tellurium in the dataset. This might initially seem counter-intuitive when compared to iron, which resides in regions of much lower chemical density despite the presence of other compounds containing Fe within the dataset. This difference is a direct consequence of the ElMD formulation. Within ElMD, tellurium and oxygen are chemically similar (positioned near one another on the modified Pettifor scale), with silicon also being relatively close. As a result, the single tellurium compound is relatively close in chemical space to the SiO₂ material cluster and many other oxide-containing compounds, explaining its moderate chemical density. In contrast, iron and manganese are chemically distant from oxygen and are similar to one another. This chemical configuration places them in a globally more sparse region of chemical space, resulting in lower chemical density even when multiple such compounds are present.

The separation of two seemingly similar materials Sr₄Ti₃O₁₀ and Sr₄Ru₃O₁₀ is worth noting. Both materials have similar chemical formulas, but vastly different structural densities despite both of them being n = 3 Ruddlesden–Popper structures. The difference stems from the coordination environments of the Sr–O polyhedra, which show 9-fold and 12-fold coordination in Sr₄Ti₃O₁₀ but show 9-fold and 10-fold coordination in Sr₄Ru₃O₁₀, leading to polyhedral distortions. From a LoStOPs perspective, this distortion results in some strontium sites taking on minor affinity for a 4-fold coordination environment. This brings it closer in structure space to the many structures (78%) exhibiting some affinity for tetragonal coordination environments in the dataset. The absence of such distortions in Sr₄Ti₃O₁₀ provides higher dissimilarity between it and the tetragonal structures.

Analysis of the highest novelty structures is straightforward. WCl₂ shows strong affinity (0.3) for a 5-fold, square-pyramidal coordination environment on the tungsten sites, which is substantially above the dataset's mean square-pyramidal affinity of 0.01. As such, WCl₂ doesn't have any near neighbors within the decay function, giving it a LoStOP density of zero. This highlights a potential limitation of the proposed method under circumstances where multiple materials may be assigned a density of zero. This scenario could be resolved through a simple nearest-neighbor check if ranking was important. The novelty signal, that this material has no neighbors within the effective neighborhood, is retained regardless. YB₄W is structurally unlike any other materials in the dataset, with layers of yttrium and tungsten separated by a boron network, which creates unusual LoStOP coordination environments relative to other materials in the dataset. WCl₂ and YB₄W are also the only tungsten bearing elements in the dataset, and paired elements chlorine, yttrium, and boron are relatively rare at 4, 2, and 7 instances, respectively. CsCl shows substantially higher affinity for 8-fold coordination on the cesium sites and cesium is rare within the dataset. Li₂O has an anti-fluorite structure and despite being an oxide is the only compound containing lithium and in high relative quantity.

3.3 Li-compounds in the GNOME dataset

Next we apply this approach to selecting novel synthesis targets from computational datasets, specifically examining the GNOME dataset which used deep learning to predict crystal stability, resulting in the “discovery” of 2.2 million crystal structures, 380 000 of which are predicted to be thermodynamically stable.²³ A selection of these GNOME materials are available through the Materials Project. To assess the relative novelty of these materials, we apply our approach to a subset of the dataset and look at compounds containing lithium and at least one other element. To serve as an existing corpus, we downloaded all experimentally verified lithium containing structures from the Materials Project, totaling 1834 materials. The mutual information cutoff and profile were computed over these to establish knowledge on the existing density data. Next the 44 lithium containing compounds in the contributed GNOME dataset were individually assessed against the existing corpus. This was performed so as to isolate each GNOME materials' density against the existing corpus and avoid the influence from other GNOME materials. It is important to note that material counts reflect the data that was available as of v2023.11.1 of the Materials Project database.

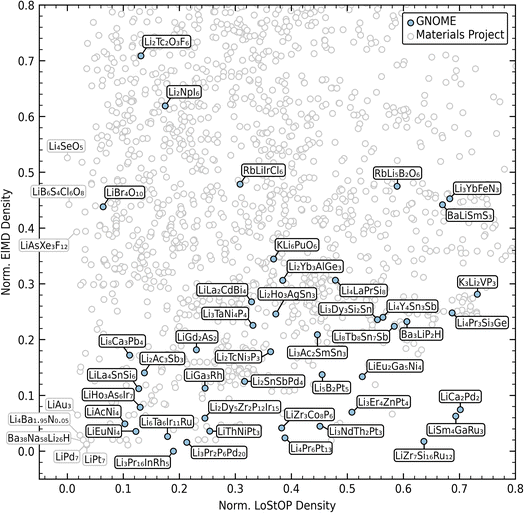
The resulting chemical and structural densities are plotted in Fig. 8 with data from the existing corpus in grey and the GNOME data in blue. Labels of chemical formulae are only provided for materials that maximize the tradeoff between chemical and structural novelty optimal materials and GNOME materials. In the interest of visibility the dataset is cropped to the range of the GNOME data. The density data shows that GNOME novelty is primarily in the chemical axis with mixed structural novelty. This is explained by the high presence of exotic elements within the bulk of the GNOME materials with many containing elements from the lanthanides and actinides. Against a large experimental corpus, chemical novelty is likely going to be more easily attained as many of these elements are expensive and difficult to work with experimentally. However, there remain a few high novelty compounds that have the potential for realistic synthesis including Li₃Zr₃Co₈P₆ and LiBr₄O₁₀. However, the mere prediction of stability does not guarantee that these materials could be synthesized. Regardless, our approach provides a useful filter for selecting potential materials for experimental synthesis based on their difference from an existing corpus and will hopefully enable more diversified searches and quantification of novelty.

Fig. 8 Chemical and structural density comparison between experimentally verified lithium-containing materials (grey) in Materials Project and GNOME predicted lithium-containing materials (blue). Labels on chemical formulas are provided for all GNOME materials and those from the Materials Project that maximize the tradeoff between chemical and structural novelty. The plot is cropped to maximum normalized densities of 0.8 along both axes for better visibility.

4 Conclusions

Novelty is highly subjective and often includes domain specific nuance. As such, it is unlikely that any single, generalizable novelty estimator will be fully satisfying. That said, the novelty estimation method presented here provides a new tool for materials scientists for assessing novelty in the materials space. The method does have limitations, particularly when analyzing datasets with wildly different subgroup distributions where the average decay profile may not appropriately represent any single group, and in cases where multiple materials have nearest neighbors beyond the cutoff distance, resulting in identical zero density scores that require additional analysis for ranking. This approach has potential applications in active learning strategies, where novelty metrics could guide exploration of undersampled regions of the materials space. Such application could enhance the diversity of training data and improve model robustness in previously unexplored domains. Future work might explore the integration of this novelty estimation approach with performance prediction models to optimize the balance between novelty and practical utility in materials discovery campaigns.

Data availability

The crystallographic data used in this study were sourced from the Materials Project database (v2023.11.1, https://doi.org/doi:10.1063/1.4812323) and the Pearson Crystal Database (2018/19 Release). All analysis code and crystal structure datasets used to generate the results are available in our GitHub repository (https://github.com/AndrewFalkowski/MINov). To ensure long-term availability and reproducibility, a persistent version of the code and associated data files is archived on Zenodo (https://doi.org/doi:10.5281/zenodo.15609550).

Author contributions

Andrew Falkowski: conceptualization, methodology, investigation, data curation, formal analysis, software, visualization, writing – original draft, writing – review & editing. Taylor Sparks: conceptualization, data curation, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002.
2. J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD), JOM, 2013, 65, 1501–1509.
3. S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, et al., AFLOW: An automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218–226.
4. L. Chanussot, et al., Open Catalyst 2020 (OC20) Dataset and Community Challenges, ACS Catal., 2021, 11, 6059–6072.
5. J. Abed and et al., Open Catalyst Experiments 2024 (OCx24): Bridging Experiments and Computational Models, 2024.
6. A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, Machine learning directed search for ultraincompressible, superhard materials, J. Am. Chem. Soc., 2018, 140, 9844–9853.
7. C. Chen, D. T. Nguyen, S. J. Lee, N. A. Baker, A. S. Karakoti, L. Lauw, C. Owen, K. T. Mueller, B. A. Bilodeau and V. Murugesan, et al., Accelerating Computational Materials Discovery with Machine Learning and Cloud High-Performance Computing: from Large-Scale Screening to Experimental Validation, J. Am. Chem. Soc., 2024, 146, 20009–20018.
8. C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, The Earth Mover's Distance as a Metric for the Space of Inorganic Compositions, Chem. Mater., 2020, 32, 10610–10620.
9. N. E. R. Zimmermann and A. Jain, Local structure order parameters and site fingerprints for quantification of coordination environment and crystal structure similarity, RSC Adv., 2020, 10, 6063–6081.
10. H. Glawe, A. Sanna, E. Gross and M. A. Marques, The optimal one dimensional periodic table: a modified Pettifor chemical scale from data mining, New J. Phys., 2016, 18, 093011.
11. R.-Z. Zhang, S. Seth and J. Cumby, Grouped representation of interatomic distances as a similarity measure for crystal structures, Digital Discovery, 2023, 2, 81–90.
12. K. Vaddi, K. Li and D. Pozzo, L. Metric geometry tools for automatic structure phase map generation, Digital Discovery, 2023, 2, 1471–1483.
13. S. G. Baird, T. Q. Diep and T. D. Sparks, DiSCoVeR: a materials discovery screening tool for high performance, unique chemical compositions, Digital Discovery, 2022, 1, 226–240.
14. L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, 2020.
15. L. Banko, P. M. Maffettone, D. Naujoks, D. Olds and A. Ludwig, Deep learning for visualization and novelty detection in large X-ray diffraction datasets, npj Comput. Mater., 2021, 7, 1–6.
16. T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Crystal diffusion variational autoencoder for periodic material generation, arXiv, 2021, preprint arXiv:2110.06197.
17. N. Gruver, A. Sriram, A. Madotto, A. G. Wilson, C. L. Zitnick and Z. Ulissi Fine-tuned language models generate stable inorganic materials as text, arXiv, 2024, preprint arXiv:2402.04379.
18. M. M. Breunig, H.-P. Kriegel, R. T. Ng and J. Sander in Proceedings of the 2000 ACM SIGMOD international conference on Management of data, Association for Computing Machinery: New York, NY, USA, 2000, pp 93–104.
19. S. Papadimitriou, H. Kitagawa, P. Gibbons and C. Faloutsos in Proceedings 19th International Conference on Data Engineering (Cat. No.03CH37405), 2003, pp. 315–326.
20. H. Wang, M. J. Bah and M. Hammad, Progress in outlier detection techniques: A survey, IEEE Access, 2019, 7, 107964–108000.
21. K. Ghosh, M. C. Naldi, J. Sander and E. Choo, Unsupervised Parameter-free Outlier Detection using HDBSCAN* Outlier Profiles, 2024.
22. P.-P. De Breuck, G. Hautier and G.-M. Rignanese, Materials property prediction for limited datasets enabled by feature selection and joint learning with MODNet, npj Comput. Mater., 2021, 7, 83.
23. A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 624, 80–85.
24. B. W. Silverman in Density estimation for statistics and data analysis, Springer, 1986, pp. 34–74.
25. P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds, DVD, Release 2018/19, Materials Park, Ohio, USA, 2018.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00167f

---