 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Building workflows for an interactive human-in-the-loop automated experiment (hAE) in STEM-EELS†
Utkarsh
Pratiush
 *a,
Kevin M.
Roccapriore
b,
Yongtao
Liu
b,
Gerd
Duscher
a,
Maxim
Ziatdinov
c and
Sergei V.
Kalinin
*ac
*a,
Kevin M.
Roccapriore
b,
Yongtao
Liu
b,
Gerd
Duscher
a,
Maxim
Ziatdinov
c and
Sergei V.
Kalinin
*ac
aDepartment of Materials Science and Engineering, University of Tennessee, Knoxville, TN 37996, USA. E-mail: upratius@vols.utk.edu; sergei2@utk.edu
bCenter for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
cPacific Northwest National Laboratory, Richland, WA 99354, USA
First published on 25th April 2025
Abstract
Exploring the structural, chemical, and physical properties of matter on the nano- and atomic scales has become possible with the recent advances in aberration-corrected electron energy-loss spectroscopy (EELS) in scanning transmission electron microscopy (STEM). However, the current paradigm of STEM-EELS relies on the classical rectangular grid sampling, in which all surface regions are assumed to be of equal a priori interest. However, this is typically not the case for real-world scenarios, where phenomena of interest are concentrated in a small number of spatial locations, such as interfaces, structural and topological defects, and multi-phase inclusions. One of the foundational problems is the discovery of nanometer- or atomic-scale structures having specific signatures in EELS spectra. Herein, we systematically explore the hyperparameters controlling deep kernel learning (DKL) discovery workflows for STEM-EELS and identify the role of the local structural descriptors and acquisition functions in experiment progression. In agreement with the actual experiment, we observe that for certain parameter combinations the experiment path can be trapped in the local minima. We demonstrate the approaches for monitoring the automated experiment in the real and feature space of the system and knowledge acquisition of the DKL model. Based on these, we construct intervention strategies defining the human-in-the-loop automated experiment (hAE). This approach can be further extended to other techniques including 4D STEM and other forms of spectroscopic imaging. The hAE library is available on Github at https://github.com/utkarshp1161/hAE/tree/main/hAE.
Electron energy-loss spectroscopy (EELS) in scanning transmission electron microscopy (STEM)1 has emerged as a transformative technique in modern materials science, offering an unparalleled window into the structural and electronic properties2,3 of materials at the atomic and nano scales. This tool has been crucial in the development of advanced nanomaterials,4 semiconductor technology, and nanoelectronics, enabling breakthroughs in these fields. It has also contributed significantly to energy research, particularly in solar cells5 and battery materials,6 and in analyzing and optimizing catalysts7 for more efficient chemical processes. Furthermore, STEM-EELS has provided critical insights into plasmons in nano-optical structures and the study of quasiparticles and vibrational excitations,8,9 advancing the fundamental physical understanding in fields like photovoltaics, sensing technologies, and solid-state physics.
The current paradigm of STEM-EELS is based on either single point spectroscopic measurements or hyperspectral imaging on rectangular grids. For the former, a human operator selects the measurement locations based on the structural features observed in the structural STEM image. It is also important to note that in many cases the imperfection in the scanning systems can result in misalignment between the intended and actual measurement points, leading to the difficulty in detecting errors. For the latter, the region of interest is identified, and multiple EELS spectra are acquired over rectangular grid of points. The resulting 3D hyperspectral data set can be analyzed using physics-based methods10 or linear11 or non-linear dimensionality reduction methods to yield 2D images that are amenable to human perception and potentially interpretation. However, in this approach, the information is uniform over the image plane, whereas in most materials systems the objects of interest are typically localized in a small number of locations. Similarly, this approach is typically associated with significant beam damage and large acquisition times.
The limitations of the classical EELS measurements and recent emergence of the Python interfaces to commercial instruments have resulted in strong interest towards automated spectroscopic measurements. One such approach is based on a combination of the application of computer vision-based approaches to identify a priori known objects of interest and subsequent spectroscopic measurements on these chosen locations.12–15
The alternative approach to automated EELS measurements is represented by the inverse workflow.14 In this, the spectral signature of interest such as specific peak positions, integrated intensity, peak ratios, etc. is identified based on the prior knowledge and intended goals of the experiment. This scalar measure of physical interest is referred to as the scalarizer function, and the purpose of the experiment is to discover microstructural elements at which this scalarizer is maximized. In this sense, DKL is targeting the exploration of physics of interest as reflected in a spectrum.16 The example of such an approach is DKL based workflows recently demonstrated by Roccapriore for EELS and 4D STEM17,18 and Liu for several SPM (scanning probe microscopy) modalities.19,20 There is also a study that times the performance gain of the DKL in capturing the spectral imaging which speeds up by more than 300×.21
However, until now, the DKL22 AE (automated experiment) workflows14,15 were realized using largely ad hoc hyperparameter values chosen before the experiment. These included the choice of scalarizer and acquisition functions defining the exploration–exploitation balance during experiment. Over the last 2 years, we have observed that the experimental path can be strongly affected by these parameters, sometimes resulting in the process being stuck at selected locations or exploring only one specific type of microstructural elements. This sensitivity to hyperparameters and propensity to be trapped in metastable minima is well known for ML (machine learning) methods.23,24 However, for active learning problems on the experimental tools, the classical strategies for hyperparameter tuning are inapplicable. While some parameter optimization can be achieved using pre-acquired ground truth data, this approach is sensitive to out of distribution shift effects even for similar samples and cannot be expected to generalize for different materials.
Correspondingly, implementation of the AE for the STEM-EELS experiments requires the introduction of a different paradigm based on the interactive, or human-in-the-loop, hAE. In this hAE approach, the human operator monitors the progression of the AI-driven automated experiment and introduces high-level modifications in the policies that govern the actions of the machine learning agent at each step of the experiment. This integrative approach between AI and human was proposed for SPM;15 however, the nature of the possible control parameters, exploration policies, and their effects on the exploration pathway are unexplored yet.
The human-in-the-loop approach allows direct control over three critical aspects of the DKL automated experiment. First, the human operator can adjust the reward function to define the discovery target or specify the type of physics they are most interested in exploring. Second, the human can influence the behavior of the machine learning agent, making it more or less exploratory. For example, at the beginning of an experimental campaign, the operator might prioritize exploratory targets, while toward the end of the session, they could narrow the focus, guiding the algorithm to follow a more gradient-based approach. Finally, the human can intervene to define objects or phenomena that are known a priori to be of interest. The manuscript discusses how specific parameters and intervals can be adjusted to implement these steps effectively. However, the overarching purpose is to present a comprehensive workflow that integrates these elements. To the best of our knowledge, this represents a novel development in the community.
Herein, we present a benchmark study across a comprehensive range of hyperparameters, including local structural descriptors and various acquisition functions (AFs) tailored for both exploitation and exploration phases. Additionally, we explore different AF parameters to optimize our experimental setup. A pivotal aspect of our methodology involves monitoring the learning progression within both the real and feature spaces of the system. The latter can in turn be defined via the variational autoencoder (VAE25–27) approach. This dual monitoring provides critical insights into the progression of automated experiments. Through a detailed study, we quantify these observations, establishing a direct link to the pivotal role humans play in selecting the appropriate parameters. This discussion is further extended to potential human interventions, highlighting the balance between automated processes and human expertise in optimizing experimental outcomes. Our findings underscore the significance of human intuition and decision-making in refining and guiding automated experimental workflows.
I. General setting of automated experiments
The general setting of STEM-EELS experiments is illustrated in Fig. 1 and can be generalized for any imaging experiments based on structural and spectral images. Structural data S(x,y) are easy to acquire and have a high density in the image plane but have relatively low information density per pixel in one or few channels. In comparison, spectroscopic data A(E), Fig. 1b, contains a wealth of information on materials properties, but acquiring spectroscopic data is time consuming. Thus, at present, the standard approach is to acquire both the structural and hyperspectral data sets A(x,y,E), Fig. 1c, over a rectangular grid of points for analyzing using ML or physics-based methods to get a set of 2D maps.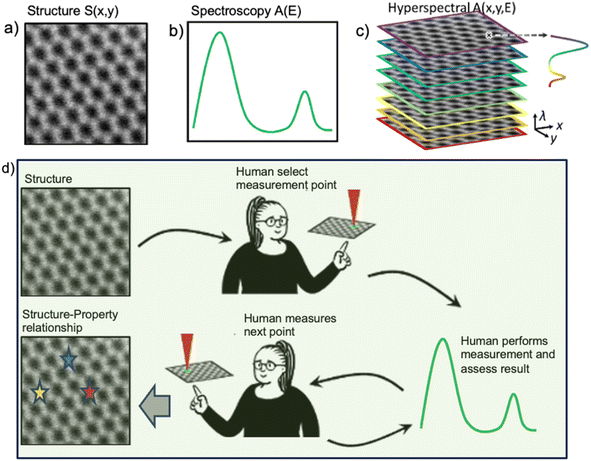 | ||
| Fig. 1 Examples of (a) structural and (b) spectral data (coming from a single point) available in STEM. Generally, structural images are fast to acquire, whereas spectral acquisition is more time consuming. (c) Hyperspectral imaging; the spectra are acquired over a dense grid, giving rise to a 3D (or higher-dimensional) data set. Alternatively, (d) human selects the measurement locations based on structural elements of interest and iteratively explores the image plane collecting spectral data. Overall, the goal of the experiment is to explore physical behaviors of interest visible in the spectral data using the structural images as a guide. Note that hyperspectral imaging acquires spectral data everywhere, whereas human (or ML-based) feature identifications identify locations of interest based on the features visible in structural image (direct workflow). The inverse workflow as realized in DKL (as shown in Fig. 3) solves the inverse problem – discovery of structural features based on their spectral signatures of interest. | ||
The rectangular sampling is easy to implement and, after suitable dimensionality reduction,28 is readily amenable to human perception. It is also optimal in a sense that it is a natural way to sample unknown space if we have no prior information. However, in most cases, the information of interest is concentrated in specific spatial locations. The grid-based measurements in this case are sub-optimal and are associated with potential for beam damage and have small explorable areas because large grids result in long acquisition times longer than microscope stability allows.
Further developments are dynamic techniques that use prior information to create a sampling pattern. For spectral methods, the natural approach is to use structural information to identify objects of interest. One way to do it is via human selection to identify objects of interest, i.e. create the locations for the spectral measurements. A similar paradigm can be implemented via a deep convolutional neural network (DCNN) trained on human-labeled data13 or discovering elements in an unsupervised manner.29 Once the data are acquired, it can be analyzed to build structure–property relationships, and if necessary, expanded to yield 2D images via variants of inpainting, Gaussian processing,30etc. However, this strategy relies on a priori knowledge of which structural objects comprise the information of interest or purely on statistical properties of objects in the image plane.
At the same time, in many scenarios, it is the specific aspects of spectral data that we aim to discover. Examples include signatures of quasiparticles, valence states, signatures of surface and bulk plasmons, peaks or edge onsets corresponding to specific elements, peak ratios related to the oxidation states or orbital populations, and so on.31–33 In these cases, we can introduce the measure of physical interest A(E) that maps the EELS spectrum to a signature of interest. The scalarizer P can be a scalar functional of spectra or a (low-dimensional) vector. Hence, a setting for automated experiment is whether we aim to explore the image plane I(x,y) based on the features of interest in the spectra. For example, this can be learning the relationship between the structural features and spectra, or discovery of structural features that give rise to certain signatures, i.e., those that maximize P. For scalar P, this is optimization, and for vector P this is multiobjective optimization.
Overall, there are three primary strategies for the spectroscopic experiments. The classical approach is to acquire A(x,y,E) based on a structural domain using a rectangular grid, as shown in Fig. 1c. This approach is slow and associated with beam damage to the sample. This strategy is optimal when we have no other information regarding the sample (or if the structural and spectral data are uncorrelated). The alternative approach is to acquire A(E) manually based on structural domain and supervision of human at each step, as shown in Fig. 1d. This method can be expensive, heavily biased by the level of expertise of the human, and strongly affected by the imperfection of the positioning system. Finally, the third approach is the inverse approach. Here, the goal of the experiment is to sequentially acquire EELS spectra to discover at which structural elements in real space does the certain spectrum manifest. To achieve this goal, the ML algorithm learns a mapping between the structure domain and the spectrum domain.
The established approach for inverse experiment workflows is based on Deep Kernel Learning16 (DKL). To illustrate mathematical foundations of the DKL, we first consider a simple Gaussian process, defined as
| f(x) ∼ GP(m(x),k(x,x′)) | (1) |
In eqn (1), GP(x) represents the Gaussian process, where x is the parameter space. f(x) is the function we observe (e.g. image contrast). m(x) is the mean function of the GP, which describes the expected value of the process at input. In typical imaging problems m is taken as zero. Finally, k(x,x′) is the covariance (kernel) function of the GP, which models the dependencies between different input points x and x′. Basically, the GP represents the strategy to interpolate an unknown black-box function, yielding the surrogate model that predicts the function value and its uncertainty over the full parameter space. These predictions and uncertainty can be further used to guide the active learning over this parameter space, i.e. guide the selection of the next measurement points. Bayesian optimization is an example of such an approach, as will be discussed later.
Conversely, deep kernel learning learns the representation of some unknown function from some high-dimensional descriptor, building the correlative relationship between the two. In the context of the STEM-EELS experiment, the high-dimensional descriptor can be chosen to be the local structure within a certain sampling window (image patch), whereas the discoverable function is either the full EEL spectrum or some representations of the spectrum (scalarizer).
A deep kernel learning34 is defined as
| kDKL(xi,xj|w,θ) = kbase(g(xi|w),g(xj|w)|θ) | (2) |
In eqn (2), g represents a neural network characterized by its weight w, while kbase denotes a standard Gaussian process (GP) kernel (e.g. RBF or Matern).35 The neural network's parameters and those of the GP base kernel are jointly learned through either Markov Chain Monte Carlo (MCMC) sampling methods or stochastic variational inference. Following training, the resulting DKL model is employed to acquire predictive mean and uncertainty values, as well as to construct the acquisition function, similar to the standard GP. The difference between the two is that the standard GP learns to reconstruct the black-box function by iterative sampling (e.g. reconstruct the image), whereas the DKL actively learns the correlative relationship between known structural and dynamically explored spectral data (i.e. learn structure–property relationships).
II. The DKL automated experiment
The steps of DKL automated experiment (AE) include selection of the scalarizer and control of the exploration–exploitation balance via acquisition function. These elements and the outputs of the AE are discussed in detail below using the pre-acquired STEM-EELS data set on fluorine and tin co-doped indium oxide infrared plasmonic nanoparticles. A monochromated electron beam (∼50 meV full width at half-maximum) was used to access the near-infrared spectral regime where the plasmon resonances of these nanoparticles exist. Other relevant conditions and sample preparation are reported elsewhere;36–38 the analysis here was performed on the data sets obtained under equivalent conditions.II.1. Selection of scalarizer
By our definition, the scalarizer function defines the measure of scientist's interest to a spectrum A(E). In the active learning terminology, scalarizer is the myopic (i.e. available at each experiment step) reward function. Scalarizer is designed with the help of the domain scientist based on knowledge of the material, enabling scientists to explore the material's properties with a high degree of specificity and relevance to the domain of interest. Here, we discuss the possible definitions of the scalarizer function for the EELS on nanoplasmonic particles.Here, the electron beam excites multiple plasmon modes within the nanoparticle cluster, as shown in Fig. 2, which exist at different locations in space and with different energies. Three primary plasmon modes are shown in Fig. 2: a low energy and long-range collective mode (dipole mode – this is a plasmon mode for the collection of the particles), a mode confined to the particle edges (edge mode), and a mode confined to the nanoparticle interior (bulk mode). Since these modes occur at different energies, they can be selectively imaged from a hyperspectral image by integrating the energy band associated with each plasmon mode. Correspondingly, we can define a scalarizer as a spectral bandpass filter: scalarizer 1 captures dipole mode, 2 captures edge mode, and 3 captures bulk mode. Depending on the experiment goals, the scalarizer function can be chosen to be more complex – e.g. peak height ratio, peak width, asymmetry, and any other functional of the spectrum.
It is important to note that previously the scalarizer was defined before the experiment. However, in the interactive hAE, the scalarizer can be dynamically tuned during the experiment, or the type of scalarizer can be changed. For example, the boundaries of the region of integration can be dynamically adjusted, or more complex scalarizers such as peak fit parameters, peak ratios, etc. can be chosen. These behaviors will be explored in the sections below.
II.2. Policies in DKL
The term policy refers to a strategic approach that guides the decision process of the ML algorithm. For the myopic optimization frameworks, the policy is generally built based on the estimated prediction and uncertainty of prediction for unexplored parts of the parameter space, where a predictive model is built based on prior measurements via the GP or DKL. In the context of STEM-EELS experiments, policy determines the selection of locations for new EELS measurements based on the structural image and results of previous EELS measurements.The DKL policy is determined by the acquisition function parameters which are tuned for exploration and exploitation. While the number of possible policies is large and new policies can be formulated, the basic policies include expected improvement (EI), upper confidence bound (UCB), and maximum uncertainty (MU). These acquisition functions39 are explained below.
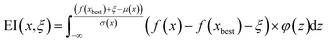 | (3) |
The expected improvement (EI) acquisition function (eqn (3)) is typically used to balance exploration and exploitation. It encourages the selection of points where the predicted function value is likely to improve upon the current best value. EI measures the expected improvement over the current best observation. However, in some scenarios, one might want to explicitly maximize the maximum uncertainty (MU) to improve exploration, especially in the early stages of the search or when the global structure of the function is unknown. This can help to ensure a more thorough search of the parameter space and avoid premature convergence to local optima.
Finally, the Upper Confidence Bound (UCB) acquisition function (eqn (4)) balances exploration and exploitation by selecting points based on both the predictive mean and the predictive standard deviation (uncertainty) of the GP model.
| UCB(x) = μ(x) + δ × σ(x) | (4) |
In realistic settings, the acquisition function can also include the cost of measurements. This cost can be either a priori known or a discoverable function of the experiment, e.g. predicted over the full image space by a separate Gaussian process. However, in STEM EELS, we assume that the measurement costs are equal for all locations within the image plane.
Similar to the scalarizer, the acquisition function has control parameters, e.g. exploration–exploitation balance. During the automated experiment, we can consider dynamically tuning the acquisition function or switching between different acquisition functions. We also note that spectrum acquisition can be driven by a different strategy, e.g. random selection of points or sampling specific structural features. These can be switched dynamically during the experiment. Like the scalarizer, this requires approaches to monitor the AE to make these decisions.
II.3. Experiment progression and output
With the scalarizer and acquisition functions defined, we discuss the general setting of the DKL experiment. The DKL-based automated experiments are summarized in a flowchart form, as shown in Fig. 3, and is recommended to be referred along with the text in this section. The goal of the DKL experiment is to discover which structural features in the S(x,y) maximize P = P(A(E)). To accomplish this goal, the image is represented as a collection of M patches each of size N × N, where N is the patch size and M is the total number of patches. Each patch scan is indexed by the location (xi,yi), where xi,yi correspond to the point on the global image S(x,y) from which the patch has been taken. In other words, the patches are sampled over the rectangular grid. All the patches are available from the beginning.The microscope performs the AE on a set of seed patches (can be a single) to generate a set of spectra Ai(xi,yi,E) and hence evaluate the scalarizer in these locations, P(xi,yi). The seed points xi, yi can be chosen randomly or selected based on the analysis of the features in the global image S(x,y). The DKL algorithm is trained on all the patches S(xj,yj) and the scalarizer functions available in the locations (xj,yj).
After training and prediction, the DKL algorithm performs the spectral measurement in the patch with coordinates:
| (xn,yn) = argmax(Acq(xi,yi)) | (5) |
II.4. Additional types of DKL experiments
The output of DKL AE is the experimental trace, or collection of the patches and the corresponding spectra. With the trace and after the experiment, we found it useful to define several forensic tools15 that make the understanding of the DKL easier. These include the following:The “DKL Explore” process is designed to systematically explore a dataset using Deep Kernel Learning (DKL) techniques. It begins by preparing the dataset, extracting patches and associated scalarizer values, and splitting the data into training and testing sets. Over a series of exploration steps, a DKL model is trained on the training data, enabling the prediction of scalarizer mean and variance values for all data patches. The selection of the next data point is guided by an acquisition function, which aids in identifying valuable information. The chosen data point, along with its associated scalarizer value, is then added to the training data. This process is repeated for each step, recording critical information such as mean, variance, selected index, acquisition function value, and scalarizer value. Finally, the final training and testing datasets are saved. This approach allows us to simulate the DKL over a pre-acquired data set, do the initial parameter tuning, reveal the relationships between the parameters, etc.
The “DKL Counterfactual” process conducts dataset exploration with a unique focus on counterfactual scenarios within the context of Deep Kernel Learning (DKL). It initiates by collecting data patches and their associated scalarizer values and establishes an initial train-test split. Over each exploration step, a DKL model is trained on the existing training data to facilitate the prediction of scalarizer mean and variance values for all data patches. This process employs records from previous exploration steps to inform the selection of the next data point, without relying on traditional acquisition functions. This counterfactual approach allows for a comprehensive examination of alternative scenarios and a deeper understanding of the automated experiment trajectory.
We have further summarized related terminologies like live, final and complete model required to monitor knowledge acquisition in the DKL experiment (Table 1). The table also contains definitions to terminologies, latent space, latent embedding and latent images which are introduced later in the paper.
| Term | Definition | Availability |
|---|---|---|
| Global structural image S(x,y) | Initial dataset of structural information was provided prior to the DKL (deep kernel learning) experiment, which was utilized for generating patches to train the DKL model | Before |
| Spectrum A(E) | The EELS measurement | During |
| Hyperspectral image A(x,y,E) | Collection of patches and spectra | During |
| Scalarizer function, P | Extract interested physics from spectrum | Before |
| Experimental trace | Spectrum and patches together | After |
| Acquisition function | Decides exploration or exploitation | Before |
| Policy | The guiding criterion for choosing the next path in the sequence involved, at its most basic, and maximization of the acquisition function | |
| Live model | The model being trained during the experiment | During |
| Final model | The model as soon as active learning terminates | After |
| Complete model | The DKL model trained from a full dataset generated on a grid | NA |
| VAE latent | Trained on full patches | Before |
| Latent space | The lower-dimensional encoded space pertaining to VAE/DKL | During |
| Latent embeddings | The feature representation of input in the latent space | During |
| Latent images | Representation of the entire dataset along each of the dimensions. Number of latent images = number of dimensions of latent space | NA |
| Full DKL | Trained on complete data | NA |
| Learning curve | Curve showing how the DKL model behaves in active learning | During |
| Monitoring curve | Curve representing next point uncertainty | During |
III. DKL on full data and the role of the window size
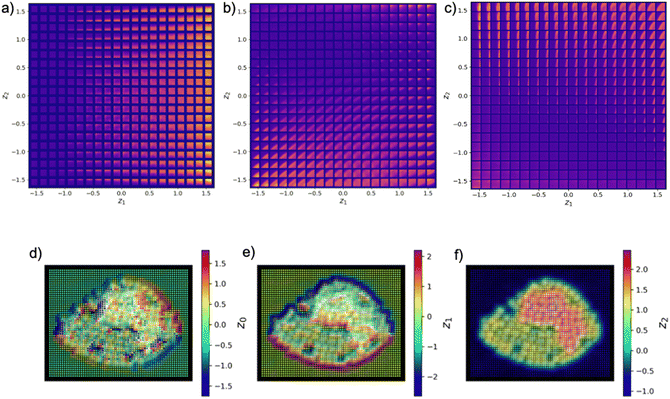
The DKL experiment is defined in a large space of hyperparameters corresponding to the selection of patch (window) sizes, scalarizer function, acquisition function, and their hyperparameters. Hence, similar to classical ML, it is advantageous to examine the effects of these hyperparameters using the pre-acquired data.As a first step, we explored the effect of varying patch sizes. We systematically explored 5, 10 and 15 window sizes. Each patch is measured in terms of area whose units are pixel square. We noted that increasing the patch size resulted in a change in the effective resolution of the latent embedding image, as shown in Fig. 4 [see also the ESI† for quantification]. We observed a distinct scalarizer pattern emerging in the DKL embedding, which indicates that DKL effectively learns the structure–property relationship inherent within the data.
 | ||
| Fig. 4 DKL embedding for scalarizer “3”. Panels (a) and (b) correspond to patch size 5, (c) and (d) to patch size 10, and (e) and (f) to patch size 15. See the ESI† for all simulations. Here, 1 pixel corresponds to 5.10 nm. | ||
Complementary information can be derived from the classical variational autoencoder (VAE) analysis of the structural data only. Over the last several years, VAEs have emerged as a powerful tool for building low-dimensional representations of data in the form of latent vectors. The encoder part of the VAE compresses data to the latent vector, whereas the decoder expands the latent vector back to the original dimensionality, balancing the reconstruction loss and the Kullback–Leibler loss between the latent distribution and Gaussian. The key aspect of the VAE is their capability to disentangle the factors of variability in the data, for example the width and tilt of handwritten digits. These can be conveniently represented for the 2D space as latent representations, as shown in Fig. 5. In this, the 2D latent space of the trained VAE is sampled over a 2D grid, and reconstructed objects are plotted as an image. The applications of VAEs for imaging data are discussed in depth in ref. 25–27. In particular, VAEs also allow us to explicit separation of invariances in data, for example rotations or translations. This comes handy in microscopy images as we often visualize lattices with symmetry in both translation and rotation, and if the model is unaware about this inductive bias, it will have to see a lot of data to just learn symmetry. Having this already encoded in model helps in better model performance in an active learning setup where data are already scarce. The rotationally invariant VAE (rVAE) will discover the features with any rotational angle and separate it as an additional physically defined factor of variation. Fig. 5a–c illustrate how the VAE's latent manifold changes with different patch sizes 5, 10, and 15. From these visualizations, it is evident that there is less variation along the y-axis (one of the latent dimensions) for a patch size of 5. This suggests that features extracted from patches of size 5 contain less information compared to those from patches sizes 10 and 15, where both latent variables show noticeable variability. The point is that before doing the actual automated experiment this analysis should be carried out to determine the ideal patch size. For further details on the VAE's latent manifold definition, please refer to Table 1.
Here, we note that the structure of the DKL latent space is determined both by the structural and spectral features. Conversely, the structure of the VAE latent space is determined only by the data itself. Due to its capability to disentangle the latent representations, VAE gives us access to a feature space which is helpful in navigating the search space. For example, the initial selection of window size can be guided by this analysis based on the structure of latent representations and complexity of latent distributions. For example, we can see that the scalarizer property is better highlighted in embedding of DKL with patch size 5.
IV. DKL active learning
In DKL active learning, the ML agent issues the commands to the microscope. The human operator can amend the ML behavior via choice of policies and scalarizer. However, steering of the AE requires monitoring the progression of the DKL experiments. Here, we explore these monitoring functions and show how hyperparameters of the DKL algorithm affect the process.In the actual automated experiment, we always must contend with drift, beam damage, and other non-stationary effects. In order to simulate a wide range of scenarios, stress-test our system under various conditions, and fine-tune the active learning algorithms to achieve optimal performance, here we explore the AE using the pre-acquired data.
IV.1. Monitoring learning
The first set of monitoring variables are directly available from the DKL itself, namely the predicted scalarizer and predicted uncertainty. Note that by the nature of the DKL experiment, these are defined for all patches within the image. Hence, for prediction and uncertainty, we can visualize the overall behavior, including the mean and dispersion, and explore the evolution of the full distribution functions.As an example, in Fig. 6 are shown the learning curves for predictive uncertainty, with the bold black line representing the mean of the prediction from the model and shaded region corresponding to uncertainty intervals. Here, the mean and dispersion of uncertainty are calculated for all structural patches. The mean hence quantifies the average uncertainty for prediction of scalarized for all patches. The corresponding dispersion quantifies the distribution of uncertainties over a collection of patches. The term “ξ” = 0.08 is highlighted in red because it has the highest predictive uncertainty among all the runs, as shown in Fig. 6d.
For comparison, we also show the predictions of the final and complete models. The final model coincides with the live model by the end of the experiment, whereas the complete model has been trained on the full data (patch-spectrum pairs) and provides the comparison point for the effectiveness of learning. Generally of interest is the overall learning dynamics, namely the rate of evolution of the predictive uncertainty and its distribution, and the knowledge gain (decrease of uncertainty) from the initial state and closeness to the predictions of the complete model.
The analysis of the learning curves for multiple scenarios, as described in Fig. 8, reveals a spectrum of potential behaviors, with detailed variations outlined in the appendix. Depending on the parameterization, the learning progression may exhibit a rapid decline followed by a plateau, an exponential-like decrease, as exemplified in Fig. 6b, or display intermittent jumps indicative of sporadic learning phases. Crucially, the variance in predictive uncertainty serves as a gauge for the stability of the learning process. As evidenced by the comparative analysis between Fig. 6a and b, it is apparent that the latter demonstrates a more consistent and stable learning trajectory. This stability reflects the reliability of the learning algorithm in developing an accurate model over the course of iterative training sessions. Such insights are invaluable for refining the active learning framework, guiding the selection of parameters that foster a balance between rapid convergence and consistent learning stability.
IV.2. Monitoring discovery
The second observable which aids AE is monitoring learning as described by next step uncertainty, as shown in Fig. 7. Panels (a)–(c) show how the uncertainty varies for the next step over the experimental trajectory for different acquisition functions, panel (d) further quantifies the values, showing maximum (non-desirable) for configuration “ξ” = 0.08 highlighted in red. For the STEM-EELS data explored here, the evolution of the model prediction is typically very noisy. We attribute this behavior to the presence of multiple geometries with almost equivalent values of the scalarizer function, resulting in a very shallow landscape for the acquisition function. This supposition is further confirmed in Section IV.3 below. | ||
| Fig. 8 (a) and (b) 2 examples of AE experimental progression with the acquisition function EI (ξ = 0.08; patch size = 5) and EI (ξ = 0.02; patch size = 10) in the simulation where the trajectory is exploring the edge and other is getting stuck. The trajectory traversed (quantification introduced in eqn (6)) values with varying “ξ” and “β” values are illustrated in panel (c). Note: the scaling factor is applied to only the units and is done independently for analysis presented in Fig. 6–8. Also, to clarify, “ξ” and “β” values are not normalized. The “Units” values should be seen just as a comparison based on magnitude for different “ξ” and “β” values – it's not directly tied to a physical measurement but is a computed monitoring metric. | ||
IV.3. Monitoring experimental progression in real space
The third monitoring parameter that readily emerges in the context of the DKL STEM-EELS experiment is the experimental trajectory in real space, i.e. the sequence of measurement points selected by the algorithm. We define distance travelled in trajectory as | (6) |
Fig. 8 illustrates the monitoring of experimental progression, where:
○ Subfigure (a) shows the successful navigation through regions of plasmons.
○ Subfigure (b) highlights the challenge of getting stuck in local minima in vacuum areas, where the target property is not expected to lie. It presents a process with a patch size of 10 and an ξ value of 0.02, resulting in a travel distance of 2495 units.
○ Subfigure (c) presents a metric that quantifies the travel distance, with a ξ value of 0.08, yielding a travel distance of 1642 units, which was the lowest and indicates that the experiment did not get stuck in local minima.
These results suggest that human insight and trial can be used to carefully find ideal parameters, such as the value mentioned above. The longer distance and larger patch size suggest a broader, more exploratory search behavior that covers diverse regions within the parameter space, potentially offering an advantage in avoiding local optima.
The examination of active learning trajectories reveals a complex relationship between the learning process and the chosen hyperparameters. For most scenarios, the trajectory starts with active exploration of the image space at the initial stages of active learning. However, upon exploration, the trajectory can get trapped at the specific minimum. This behavior is particularly often for smaller patch sizes, as demonstrated by a patch N = 5 and mean uncertainty (MU) policy. In contrast, larger patch sizes exhibit a lower propensity for the trajectory to become stuck in the local minimum, suggesting a direct link between the patch size and the trajectory's susceptibility to stagnation.
We note that for the explored scenarios, as summarized in Fig. 8d, there is no clear correlation between the chosen policy, policy hyperparameters, and window sizes that can guarantee the lack of local minima. In principle, one way to address this problem may be via the introduction of additional components to the acquisition functions that de-prioritize the already explored areas. Similarly, the acquisition function can include the cost of measurement, e.g. the time associated for traversing from one image location to the next one. We expect these additional components to be highly instrument specific and to be optimized for specific instruments. However, from the general perspective, these additional policies will further introduce additional hyperparameters, necessitating the development of both monitoring and intervention strategies, as discussed below.
IV.4. Monitoring in feature space
We define the feature space of the system as the latent representation of the variational autoencoder trained on the full set of patches. This approach allows the use of full power of simple, joint, semi-supervised, and conditional autoencoders to identify relevant aspects of materials structure. The detailed discussion of the VAE for materials structure exploration is presented in ref. 40 and 41.We note that the capability of the VAEs to disentangle factors of variation within the data provides a very powerful tool for exploration of the materials structure visualized via latent reorientations and latent distributions. The addition of the rotation and translation invariances naturally allows us to compensate for the uncertainty in the object selection and presence of the rotational disorder in the system. Finally, a semi-supervised VAE approach allows us to incorporate prior knowledge on objects of interest (e.g. preferred classes), combining the classification and representation disentanglement tasks (Fig. 9).
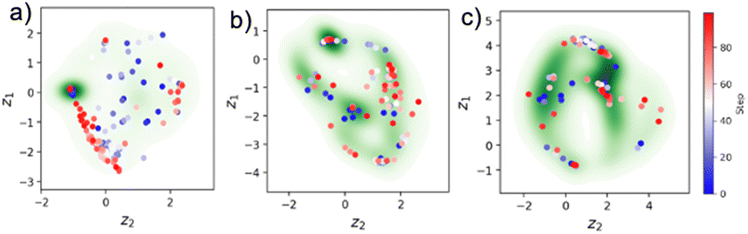 | ||
| Fig. 9 (a)–(c) Example trajectory of experiment progression in rVAE latent space [see Table 1 for definition] for patch sizes 5, 10 and 15, respectively. | ||
The trajectory of the automated experiment can be visualized within the Variational Autoencoder (VAE) space of the system. To analyze the distribution of points in this space, we employed kernel density estimation (KDE), which provides a smoothed representation of the underlying probability density function. The KDE allows us to identify regions with high concentrations of points, which we refer to as “aggregation points”. An aggregation point is defined as a location in the latent space where the kernel density estimate exhibits a local maximum, indicating a cluster or dense region of points. In the context of our experiment, we observe that the latent space of the VAE exhibits distinct patterns depending on the patch size: for a patch size of 5, a single aggregation point is observed, characterized by a prominent peak in the kernel density estimate. For a patch size of 10, two primary aggregation points are present, with kernel density estimates showing maxima at these locations, as well as several dense regions where the experiment progresses. Similarly, for a patch size of 15, multiple aggregation points and dense regions are evident. This behavior is intriguing, as it suggests that the latent space of the VAE encodes structural information, which varies with different patch sizes. Furthermore, the experiment's trajectory appears to jump between local maxima in the latent space, implying transitions between distinct structural regions. This is significant, as different regions in the latent space correspond to different types of structural information, providing valuable insights into the system's behavior.
V. Interventions
The simulation studies above illustrate that the progression automated experiments in STEM-EELS can be monitored based on the learning curves of the DKL model, real space, and feature space trajectories. At the same time, for certain parameter values, the experiment can be trapped in the local minima both in the real and feature spaces. The corresponding behaviors in the parameter space, while demonstrating certain trends, can be highly irregular, necessitating the strategies for real-time interventions during the automated experiment. Note that these have to be dynamic almost by definition, given the active nature of real experiment compared to the static nature of the data in classical ML benchmarks (or example workflows used here).Here, we identify the possible interventions in the DKL workflow. We note that the initial step of the DKL workflow is the selection of the patch size and initial seed points. The effects of seed points have been explored by Slautin.42The patch size effects can be explored prior to the experiment using the VAE feature space exploration, allowing the complexity of the latent distribution and the nature of disentangle factors of variations to be tuned. We further note that in principle the patch size can be varied during the experiment, i.e. this is a valid intervention. This in turn requires retraining of the whole model based on the new patch size. It is important to realize that in this case the full experimental trajectory prior to intervention will correspond to the off-policy process and can at best be considered as a new extended seed.
The second intervention channel is the exploration target, or scalarizer. This allows us to tune the relationship between the full spectrum and the myopic optimization target. The scalarizers can be chosen from multiple classes (e.g. integral intensity, peak ratio, and physics base reconstruction), or tuned within class, e.g. change boundaries of the integrated intensity.
The effect of scalarizer tuning is illustrated in Fig. 10e. Here, the scalarizer is integral of the EELS spectrum over an interval [a, b], where a and b can be tuned based on interested physics. We note that the smooth changes in the integration boundaries result in the formation of several distinct clusters of the possible future points. We attribute this behavior to relatively shallow nature of the acquisition function landscape related to a highly degenerate relationship between the local geometries and EELS spectra. The flexibility in the choice of the interval, i.e. a and b values lead in exploring diverse experimental trajectories converging to interesting properties.
Finally, the policies can be tuned on the fly via the selection and hyperparameter tuning of the acquisition functions. Similarly, to scalarize, these can be visualized via the selection of the Upper Confidence Bound (UCB), Expected Improvement (EI), and Maximum Uncertainty (MU), or parameter tuning.
Shown in Fig. 10 is the effect of ξ value in EI and the β value in UCB being adjusted to fine-tune this balance. The scalarizer is also switched to align with the specific physics of interest, such as interface, bulk, or surface plasmons, as identified by the human expert seen in Fig. 10(d).
VI. Summary
To summarize, here, we introduce a detailed framework for the human-in-the-loop automated experiment in STEM-EELS based on the myopic optimization workflows. We describe the intrinsic assumptions of the myopic workflows and illustrate how it can be applied to the active experiment in STEM. Based on the exploration of the broad parameter space of the system for the pre-acquired data, including patch sizes, policies, and scalarizers, we demonstrate that for many parameter combinations that AE can be trapped in local minima. Our comprehensive analysis, as evidenced by the metrics presented in Fig. 6d, 7d, and 8d (with optimal scenarios highlighted in red), reveals that hyperparameter behavior can be highly localized, making it challenging to identify universally effective and robust hyperparameter values. The results demonstrate that hyperparameter performance can be strongly dependent on local conditions, and therefore, it is difficult to determine a set of universally good and robust hyperparameter values.We hence introduce the strategies of the interactive automated experiment, in which the ML agent issues control signals to the microscope and the human operator monitors the progression of automate experiment of suitable time scales. To enable hAE STEM-EELS, we introduce a set of monitoring functions based on the DKL model performance and real-space and feature space exploration.
We introduce the intervention strategies for the DKL workflows based on object selection, scalarizer tuning, and policy tuning. These strategies have been both operationalized and tested on pre-acquired data and indicate strong degeneracies in the STEM-EELS data sets. We note that while all interventions bring the experiment off policy, this allows the dynamic interaction between the human operator and the microscopes.
Finally, we note that the proposed human-in-the-loop approach will be applicable to all other myopic workflows, as long as an enabling algorithm can yield predictions of function and uncertainty. This includes those based on ensembled neural networks and physics-informed neural networks, contextual bandits, and many other model classes. Similarly, these workflows can be directly translated to other experimental tools including scanning probe microscopy, chemical imaging, and combinations such as nanoindentation with optical and scanning electron microscopy. As such, these developments are universal and can improve multiple areas of materials science and chemical and physical imaging.
Data availability
The code and data for the study reported in this article can be found on Zenodo repository at https://doi.org/10.5281/zenodo.15175786.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The development of the control and benchmarking frameworks (UP) was supported by a seed grant from the AI Tennessee Initiative at the University of Tennessee Knoxville. The development of hAE workflow was supported (SVK) as part of the Center for 3D Ferroelectric Microelectronics (3DFeM), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences under award number DE-SC0021118. EELS data acquisition and initial analysis (Y. L. and K. M. R.) was supported by the Center for Nanophase Materials Sciences (CNMS), which is a U.S. Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory. The authors acknowledge support from the Center for Nanophase Materials Sciences (CNMS) user facility, project CNMS2023-B-02177, which is a U.S. Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory. This work (GD) was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division.References
- M. Varela, S. D. Findlay, A. R. Lupini, H. M. Christen, A. Y. Borisevich, N. Dellby, O. L. Krivanek, P. D. Nellist, M. P. Oxley, L. J. Allen and S. J. Pennycook, Spectroscopic Imaging of Single Atoms Within a Bulk Solid, Phys. Rev. Lett., 2004, 92(9), 095502, DOI:10.1103/PhysRevLett.92.095502.
- N. D. Browning, D. J. Wallis, P. D. Nellist and S. J. Pennycook, EELS in the STEM: Determination of Materials Properties on the Atomic Scale, Micron, 1997, 28(5), 333–348, DOI:10.1016/S0968-4328(97)00033-4.
- R. F. Egerton and M. Malac, EELS in the TEM, J. Electron Spectrosc. Relat. Phenom., 2005, 143(2–3), 43–50, DOI:10.1016/j.elspec.2003.12.009.
- J. Nelayah, M. Kociak, O. Stéphan, F. J. García de Abajo, M. Tencé, L. Henrard, D. Taverna, I. Pastoriza-Santos, L. M. Liz-Marzán and C. Colliex, Mapping Surface Plasmons on a Single Metallic Nanoparticle, Nat. Phys., 2007, 3(5), 348–353, DOI:10.1038/nphys575.
- G. Noircler, F. Lebreton, E. Drahi, P. de Coux and B. Warot-Fonrose, STEM-EELS Investigation of c-Si/a-AlO Interface for Solar Cell Applications, Micron, 2021, 145, 103032, DOI:10.1016/j.micron.2021.103032.
- L. Yu, M. Li, J. Wen, K. Amine and J. Lu, (S)TEM-EELS as an Advanced Characterization Technique for Lithium-Ion Batteries, Mater. Chem. Front., 2021, 5(14), 5186–5193, 10.1039/D1QM00275A.
- J. Qu, M. Sui and R. Li, Recent Advances in In Situ Transmission Electron Microscopy Techniques for Heterogeneous Catalysis, iScience, 2023, 26(7), 107072, DOI:10.1016/j.isci.2023.107072.
- Y.-J. Kim, L. D. Palmer, W. Lee, N. J. Heller and S. K. Cushing, Using Electron Energy-Loss Spectroscopy to Measure Nanoscale Electronic and Vibrational Dynamics in a TEM, J. Chem. Phys., 2023, 159(5) DOI:10.1063/5.0147356.
- W. Zhou, J. Lee, J. Nanda, S. T. Pantelides, S. J. Pennycook and J.-C. Idrobo, Atomically Localized Plasmon Enhancement in Monolayer Graphene, Nat. Nanotechnol., 2012, 7(3), 161–165, DOI:10.1038/nnano.2011.252.
- S. V. Kalinin, A. R. Lupini, R. K. Vasudevan and M. Ziatdinov, Gaussian Process Analysis of Electron Energy Loss Spectroscopy Data: Multivariate Reconstruction and Kernel Control, npj Comput. Mater., 2021, 7(1), 154, DOI:10.1038/s41524-021-00611-8.
- M. Greenacre, P. J. F. Groenen, T. Hastie, A. I. D'Enza, A. Markos and E. Tuzhilina, Publisher Correction: Principal Component Analysis, Nat. Rev. Methods Primers, 2023, 3(1), 22, DOI:10.1038/s43586-023-00209-y.
- K. M. Roccapriore, M. Ziatdinov, A. R. Lupini, A. P. Singh, U. Philipose and S. V. Kalinin, Discovering Invariant Spatial Features in Electron Energy Loss Spectroscopy Images on the Mesoscopic and Atomic Levels, J. Appl. Phys., 2024, 135(11) DOI:10.1063/5.0193607.
- K. M. Roccapriore, R. Torsi, J. Robinson, S. Kalinin and M. Ziatdinov, Dynamic STEM-EELS for Single-Atom and Defect Measurement during Electron Beam Transformations, Sci. Adv., 2024, 10(29) DOI:10.1126/sciadv.adn5899.
- S. V. Kalinin, Y. Liu, A. Biswas, G. Duscher, U. Pratiush, K. Roccapriore, M. Ziatdinov and R. Vasudevan, Human-in-the-Loop: The Future of Machine Learning in Automated Electron Microscopy, Microsc. Today, 2024, 32(1), 35–41, DOI:10.1093/mictod/qaad096.
- Y. Liu, M. A. Ziatdinov, R. K. Vasudevan and S. V. Kalinin, Explainability and Human Intervention in Autonomous Scanning Probe Microscopy, Patterns, 2023, 4(11), 100858, DOI:10.1016/j.patter.2023.100858.
- M. Valleti, R. K. Vasudevan, M. A. Ziatdinov and S. V. Kalinin, Deep Kernel Methods Learn Better: From Cards to Process Optimization, Mach. Learn.: Sci. Technol., 2024, 5(1), 015012, DOI:10.1088/2632-2153/ad1a4f.
- K. M. Roccapriore, M. G. Boebinger, J. Klein, M. Weile, F. Ross, M. Ziatdinov, R. R. Unocic and S. V. Kalinin, AI-Enabled Automation of Atomic Manipulation and Characterization in the STEM, Microsc. Microanal., 2023, 29(suppl. 1), 1366–1367, DOI:10.1093/micmic/ozad067.702.
- K. M. Roccapriore, S. V. Kalinin and M. Ziatdinov, Physics Discovery in Nanoplasmonic Systems via Autonomous Experiments in Scanning Transmission Electron Microscopy, Adv. Sci., 2022, 9(36) DOI:10.1002/advs.202203422.
- Y. Liu, M. Ziatdinov and S. V. Kalinin, Exploring Causal Physical Mechanisms via Non-Gaussian Linear Models and Deep Kernel Learning: Applications for Ferroelectric Domain Structures, ACS Nano, 2022, 16(1), 1250–1259, DOI:10.1021/acsnano.1c09059.
- M. Ziatdinov, Y. Liu and S. V. Kalinin, Active Learning in Open Experimental Environments: Selecting the Right Information Channel(s) Based on Predictability in Deep Kernel Learning, arXiv, 2022, preprint, arXiv:2203.10181, DOI:10.48550/arXiv.2203.10181, https://arxiv.org/abs/2203.10181.
- U. Pratiush, A. Houston, S. V. Kalinin and G. Duscher, Realizing Smart Scanning Transmission Electron Microscopy Using High Performance Computing, Rev. Sci. Instrum., 2024, 95(10) DOI:10.1063/5.0225401.
- A. G. Wilson, Z. Hu, R. Salakhutdinov and E. P. Xing, Deep Kernel Learning, in Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, ed. A. Gretton and C. C. Robert, Proceedings of Machine Learning Research, PMLR, Cadiz, Spain, 2016, vol. 51, pp. 370–378 Search PubMed.
- X. Ding, L. Zhao and L. Akoglu, Hyperparameter Sensitivity in Deep Outlier Detection: Analysis and a Scalable Hyper-Ensemble Solution, in Advances in Neural Information Processing Systems, ed. A. H. Oh, A. Agarwal, D. Belgrave and K. Cho, 2022 Search PubMed.
- T. Yu and H. Zhu, Hyper-parameter optimization: A review of algorithms and applications, arXiv, 2020, preprint, arXiv:2003.05689, DOI:10.48550/arXiv.2003.05689, https://arxiv.org/abs/2003.05689.
- M. P. Oxley, S. V. Kalinin, M. Valleti, J. Zhang, R. P. Hermann, H. Zheng, W. Zhang, G. Eres, R. K. Vasudevan and M. Ziatdinov, Exploring Local Crystal Symmetry with Rotationally Invariant Variational Autoencoders, Microsc. Microanal., 2022, 28(S1), 3132–3134, DOI:10.1017/S1431927622011655.
- A. Biswas, M. Ziatdinov and S. V. Kalinin, Combining Variational Autoencoders and Physical Bias for Improved Microscopy Data Analysis, Mach. Learn.: Sci. Technol., 2023, 4(4), 045004, DOI:10.1088/2632-2153/acf6a9.
- M. Valleti, M. Ziatdinov, Y. Liu and S. V. Kalinin, Physics and Chemistry from Parsimonious Representations: Image Analysis via Invariant Variational Autoencoders, npj Comput. Mater., 2024, 10(1), 183, DOI:10.1038/s41524-024-01250-5.
- M. Bosman, M. Watanabe, D. T. L. Alexander and V. J. Keast, Mapping Chemical and Bonding Information Using Multivariate Analysis of Electron Energy-Loss Spectrum Images, Ultramicroscopy, 2006, 106(11–12), 1024–1032, DOI:10.1016/j.ultramic.2006.04.016.
- J. P. Horwath, D. N. Zakharov, R. Mégret and E. A. Stach, Understanding Important Features of Deep Learning Models for Segmentation of High-Resolution Transmission Electron Microscopy Images, npj Comput. Mater., 2020, 6(1), 108, DOI:10.1038/s41524-020-00363-x.
- M. Bertalmio, G. Sapiro, V. Caselles and C. Ballester, Image Inpainting, in Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques - SIGGRAPH'00, ACM Press, New York, USA, 2000, pp. 417–424. DOI:10.1145/344779.344972.
- M. Varela, J. Gazquez and S. J. Pennycook, STEM-EELS Imaging of Complex Oxides and Interfaces, MRS Bull., 2012, 37(1), 29–35, DOI:10.1557/mrs.2011.330.
- N. D. Browning, D. J. Wallis, P. D. Nellist and S. J. Pennycook, EELS in the STEM: Determination of Materials Properties on the Atomic Scale, Micron, 1997, 28(5), 333–348, DOI:10.1016/S0968-4328(97)00033-4.
- M. Varela, J. Gazquez and S. J. Pennycook, STEM-EELS Imaging of Complex Oxides and Interfaces, MRS Bull., 2012, 37(1), 29–35, DOI:10.1557/mrs.2011.330.
- A. G. Wilson, Z. Hu, R. Salakhutdinov and E. P. Xing, Deep Kernel Learning, Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, in Proceedings of Machine Learning Research, 2016, vol. 51, pp. 370–378, available from https://proceedings.mlr.press/v51/wilson16.html Search PubMed.
- M. Seeger, Gaussian Processes for Machine Learning, Int. J. Neural Syst., 2004, 14(2), 69–106, DOI:10.1142/S0129065704001899.
- K. M. Roccapriore, S. Cho, A. R. Lupini, D. J. Milliron and S. V. Kalinin, Sculpting the Plasmonic Responses of Nanoparticles by Directed Electron Beam Irradiation, Small, 2022, 18(1) DOI:10.1002/smll.202105099.
- K. M. Roccapriore, M. Ziatdinov, S. H. Cho, J. A. Hachtel and S. V. Kalinin, Predictability of Localized Plasmonic Responses in Nanoparticle Assemblies, Small, 2021, 17(21) DOI:10.1002/smll.202100181.
- S. H. Cho, K. M. Roccapriore, C. K. Dass, S. Ghosh, J. Choi, J. Noh, L. C. Reimnitz, S. Heo, K. Kim, K. Xie, B. A. Korgel, X. Li, J. R. Hendrickson, J. A. Hachtel and D. J. Milliron, Spectrally Tunable Infrared Plasmonic F,Sn:In2O3 Nanocrystal Cubes, J. Chem. Phys., 2020, 152(1) DOI:10.1063/1.5139050.
- C. E. Rasmussen, Gaussian Processes in Machine Learning, 2004, pp. 63–71, DOI:10.1007/978-3-540-28650-9_4.
- M. P. Oxley, S. V. Kalinin, M. Valleti, J. Zhang, R. P. Hermann, H. Zheng, W. Zhang, G. Eres, R. K. Vasudevan and M. Ziatdinov, Exploring Local Crystal Symmetry with Rotationally Invariant Variational Autoencoders, Microsc. Microanal., 2022, 28(S1), 3132–3134, DOI:10.1017/S1431927622011655.
- A. Biswas, M. Ziatdinov and S. V. Kalinin, Combining Variational Autoencoders and Physical Bias for Improved Microscopy Data Analysis, Mach. Learn.: Sci. Technol., 2023, 4(4), 045004, DOI:10.1088/2632-2153/acf6a9.
- B. N. Slautin, Y. Liu, H. Funakubo and S. V. Kalinin, Unraveling the Impact of Initial Choices and In-Loop Interventions on Learning Dynamics in Autonomous Scanning Probe Microscopy, J. Appl. Phys., 2024, 135(15) DOI:10.1063/5.0198316.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00033e |
| This journal is © The Royal Society of Chemistry 2025 |




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; the “Units” values should be seen just as a comparison based on magnitude for different “
000; the “Units” values should be seen just as a comparison based on magnitude for different “
