Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting the excited-state properties of crystalline organic semiconductors using GW+BSE and machine learning†
Siyu
Gao‡
 a,
Yiqun
Luo‡
a,
Yiqun
Luo‡
 b,
Xingyu
Liu
a and
Noa
Marom
b,
Xingyu
Liu
a and
Noa
Marom
 *abc
*abc
aDepartment of Materials Science and Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA. E-mail: nmarom@andrew.cmu.edu
bDepartment of Physics, Carnegie Mellon University, Pittsburgh, PA 15213, USA
cDepartment of Chemistry, Carnegie Mellon University, Pittsburgh, PA 15213, USA
First published on 7th April 2025
Abstract
Excited-state properties of crystalline organic semiconductors are key to organic electronic device applications. Machine learning (ML) models capable of predicting these properties could significantly accelerate materials discovery. We use the sure-independence-screening-and-sparsifying-operator (SISSO) ML algorithm to generate models to predict the first singlet excitation energy, which corresponds to the optical gap, the first triplet excitation energy, the singlet–triplet gap, and the singlet exciton binding energy of organic molecular crystals. To train the models we use the “PAH101” dataset of many-body perturbation theory calculations within the GW approximation and Bethe–Salpeter equation (GW+BSE) for 101 crystals of polycyclic aromatic hydrocarbons (PAHs). The best performing SISSO models yield predictions within about 0.2 eV of the GW+BSE reference values. SISSO models are selected based on considerations of accuracy and computational cost to construct materials screening workflows for each property. The screening targets are chosen to demonstrate typical use-cases relevant for organic electronic devices. We show that the workflows based on SISSO models can effectively screen out most of the materials that are not of interest and significantly reduce the number of candidates selected for further evaluation using computationally expensive excited-state theory.
Introduction
In analogy with their inorganic counterparts, crystalline organic semiconductors have the advantages of uniform well-defined electronic and optical properties, as well as improved charge carrier mobility, owing to band-like transport and fewer traps, compared to amorphous films.1–11 Advances in processing techniques have led to better prospects and increasing interest in organic devices based on crystalline materials, including organic field effect transistors (OFETs),6,7,12–15 organic light emitting diodes (OLEDs),16–22 organic photovoltaics (OPV),23–25 photodetectors,26–28 and scintillators.29–32 The properties of crystalline organic semiconductors can be tuned in many ways, including chemical substitution and side-group functionalization, which can modify the molecular properties as well as the crystal packing,7,33–35 promoting the crystallization of polymorphs with different properties,32,36–38 co-crystallization,27,39–44 and doping.16,20–22,29,45,46 This opens up a vast design space with endless possibilities for devices based on crystalline organic semiconductors.Key parameters for device performance are derived from excited-state properties of crystalline organic semiconductors. The optical gap, which corresponds to the lowest singlet exciton energy, is of fundamental importance for any device based on absorption or emission of light. The triplet exciton energy is important for devices that involve conversion between singlet and triplet states. To increase the efficiency of OLEDs, it is desirable to convert electrically generated triplet excitons into emissive singlet excitons via thermally activated delayed fluorescence (TADF).47–53 In OPV, the thermalization loss may be reduced by converting high-energy singlet excitons into two triplet excitons, via singlet fission (SF).54–62 Conversely, the transmission loss of photons with energies below the optical gap of the absorber may be reduced by up-converting two low-energy triplet excitons into one singlet exciton via triplet–triplet annihilation (TTA).63–71 TTA also plays a crucial role in the detection of X-rays, gamma rays, and neutrons in scintillators.30 Another important parameter for organic devices is the exciton binding energy, which is the electrostatic attraction between the electron and hole that must be overcome in order to separate an exciton into free charge carriers.72 The band lineup e.g., between the donor and acceptor in organic solar cells, is often engineered to overcome the exciton binding energy and provide the driving force for charge separation.
Different applications impose different requirements on the excited-state energies of molecular crystals. For example, solar cells require materials with broad absorption in the visible range, whereas OLEDs require materials with sharp emission in specific colors. Other applications may require absorption in the infrared (IR) or ultra-violet (UV) ranges. SF requires the triplet excitation energy to be slightly smaller than half the singlet excitation energy, whereas TTA requires the triplet energy to be slightly larger than half the singlet energy. TADF requires the difference between the singlet excitation energy and the triplet excitation energy, also known as the singlet–triplet gap, to be as small as possible or even negative. In addition, compatibility with other device components may require singlet and/or triplet energies in a specific range and/or specific band edge positions. Although the structures of over a million organic molecular crystals are known,73,74 the electronic and optical properties of most of them are unknown. A material originally produced for one purpose may turn out to be useful for another.75 Even materials that formed as reaction byproducts may turn out to have useful properties.76 Therefore, the ability to predict the excited-state properties of molecular crystals could lead to materials discovery and advances in organic semiconductor devices.
On present day supercomputers, it is possible to screen thousands of materials in a “high-throughput” manner using density functional theory (DFT) with computationally efficient semi-local exchange-correlation functionals.77,78 However, DFT is a ground-state theory, which inherently cannot describe the excited-state properties required for organic semiconductor devices. The excited-state properties of isolated molecules may be calculated relatively efficiently with time dependent DFT (TDDFT). Indeed, TDDFT has been employed for high-throughput screening efforts to discover organic chromophores.79–86 The properties of crystalline organic semiconductors depend not only on the molecular properties, but also on the crystal packing and the resulting electronic interactions between molecules. There is a vast body of literature reporting how changes in the crystal packing affect device relevant properties of organic semiconductors from excited-state energies to charge carrier mobility.32,36–38,40,44,87–90 Therefore, for applications based on crystalline organic semiconductors it is important for computational materials discovery efforts to focus on predicting the excited-state properties of crystals as opposed to isolated molecules.
The excited-state properties of molecular crystals can be calculated within the framework of Green's function based many-body perturbation theory. The GW approximation, where G represents the one-particle Green's function and W represents the screened Coulomb interaction, can be used to calculate properties associated with charged excitations, such as the fundamental band gap. Subsequently, the GW quasiparticle energies are fed into the Bethe–Salpeter equation (BSE) to calculate properties associated with neutral excitations, such as the singlet and triplet excitation energies.91–95 The high computational cost of GW+BSE is prohibitive for large-scale materials screening. Machine learning (ML) can be used to perform preliminary screening and reduce the need for expensive simulations to a smaller number of promising candidates.96–107 However, training ML models such as neural networks typically requires a large amount of data,108,109 which is difficult to acquire with GW+BSE. Compared to DFT and even TDDFT datasets, GW+BSE datasets are scarce and contain a relatively small amount of data for isolated molecules77,110,111 or for inorganic crystals with a small number of atoms in the unit cell.112 As a consequence, efforts to use ML to predict the outcomes of GW+BSE calculations have also been restricted to small organic molecules and small inorganic systems.112–116 This has limited the ability to train ML models to predict the excited state properties of molecular crystals.
Recently, we have published a first of its kind dataset of GW+BSE calculations for 101 molecular crystals of polycyclic aromatic hydrocarbons (PAHs) with up to ∼500 atoms in the unit cell, known as PAH101.117 We have chosen to focus on PAHs because they are the fundamental building blocks of materials for organic electronics.7,88,118–126Fig. 1a and b shows the size distribution of the molecules and the unit cells in the PAH101 set. The data records contain the GW+BSE singlet and triplet excitation energies, whose distributions are shown in Fig. 1c and d as well as the GW fundamental band gaps. From these quantities we may also calculate the singlet–triplet gap and the singlet exciton binding energy, whose distributions are shown in Fig. 1e and f. Detailed technical validation of the PAH101 dataset is provided in ref. 117, including comparison of the relaxed geometries with experimental data, convergence tests of the GW+BSE calculations, and comparison of the optical gaps and absorption spectra to available experimental data.
The PAH101 dataset was originally generated for the purpose of SF materials discovery.127 To address the challenge of constructing transferable ML models with a small amount of training data, we used the sure-independence-screening-and-sparsifying-operator (SISSO)128,129 algorithm. SISSO takes advantage of physical/chemical knowledge to train ML models based on “small data”. The input of SISSO is a set of scalar primary features, which are physical/chemical descriptors thought to be related to the target property. The primary features used in ref. 127 are also provided in the PAH101 data records.117 SISSO generates a huge feature space by repeatedly combining the primary features using a set of linear and nonlinear algebraic operations with rules to avoid unphysical combinations. Subsequently, linear regression is performed to identify the most predictive models. In the last few years SISSO has been applied increasingly broadly for diverse classes of materials and target properties and continues to perform well with relatively small amounts of data.130–149 In ref. 127 SISSO successfully produced several models that were able to predict the GW+BSE values of the SF driving force, which corresponds to the difference between the singlet exciton energy and twice the triplet exciton energy, with a root mean square error (RMSE) below 0.2 eV. Based on considerations of model accuracy and primary feature computational cost, two of the SISSO models were selected to build a classifier for materials screening. Later, the simpler model of the two was found to deliver robust performance outside of the PAH101 set, whereas the more complex model was found to be overfitted.54
Here, we use the PAH101 dataset to train SISSO models for the singlet exciton energy, which corresponds to the optical gap, the triplet exciton energy, the singlet–triplet gap, and the singlet exciton binding energy. For all four properties, the best performing SISSO models yield predictions within about 0.2 eV of the GW+BSE reference values. We then select SISSO models based on considerations of accuracy and computational cost to construct materials screening workflows for each property. The screening targets are chosen to demonstrate typical use-cases relevant for organic electronic devices. We demonstrate screening for materials with an optical gap in a particular color; materials meeting the requirements for up-conversion of infrared light to the visible range via TTA, namely, a triplet excitation energy in the infrared, optical gap in the visible range, and a higher TTA driving force than rubrene; materials with a small singlet–triplet gap, which is desirable for OLEDs; and materials with a small singlet exciton binding energy to facilitate the separation of excitons into free charge carriers. We show that the workflows based on SISSO models can effectively screen out most of the materials that are not of interest and significantly reduce the number of candidates selected for further evaluation using computationally expensive excited-state theory.
Methods
SISSO models were trained following the same procedure used in ref. 127. The same primary features were used, summarized in Table 1 (also provided in the PAH101 dataset117). The primary features include both single molecule and crystal properties. DFT primary features were calculated with the FHI-aims150,151 code using the Perdew–Burke–Ernzerhof (PBE)152,153 exchange-correlation functional, as described in ref. 127. The DFT estimates for the SF driving force of the single molecule and crystal (DF_s and DF_c), which were used as primary features in ref. 127, were excluded because they are not relevant to the properties studied here. For the singlet–triplet gap model, two additional primary features were included: the DFT estimates for the single molecule and crystal singlet–triplet gap (ΔESST and ΔEcST). These were evaluated by subtracting the molecule/crystal triplet formation energy, as an approximation for the triplet excitation energy, from the molecule/crystal PBE gap, as an approximation for the singlet excitation energy (i.e., ΔESST = GapS − EST and ΔECST = GapC − ECT). The total number of SISSO primary features was thus 14 for the singlet exciton energy, triplet exciton energy, and singlet exciton binding energy models and 16 for the singlet–triplet gap models.| Feature | Cost | Description |
|---|---|---|
| GapS | 1 | Single molecule gap, i.e., the energy difference between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) |
| IPS | 2 | Single molecule ionization potential, evaluated as the total energy difference between a cation and neutral molecule |
| PolarTensorS | 2 | Trace of the molecular polarization tensor, calculated using PBE with the many-body dispersion (MBD) method155 |
| E ST | 3 | Single molecule triplet formation energy, corresponding to the total energy difference between the ground-state and triplet-state molecule |
| EAS | 3 | Single molecule electron affinity, evaluated as the total energy difference between an anion and neutral molecule |
| ΔESST | 3 | Estimated single molecule singlet–triplet gap, evaluated as GapS − EST. |
| GapC | 33 | The crystal band gap, extracted from the band structure |
| VBCdisp | 33 | Valence band dispersion, corresponding to the energy range of the HOMO-derived band |
| CBCdisp | 33 | Conduction band dispersion, corresponding to the energy range of the LUMO-derived band |
| ε C | 42 | Dielectric constant calculated using the PBE + MBD@rsSCS polarizability in the Clausius–Mossotti equation156 |
| H ab | 93 | The highest value of the transfer integral obtained out of all the unique molecular dimers extracted from the crystal, calculated with fragment orbital DFT157 |
| E CT | 148 | Crystal triplet formation energy, corresponding to the total energy difference between the ground-state and triplet-state crystal |
| ΔECST | 181 | Estimated crystal singlet–triplet gap, evaluated as GapC − ECT |
| MolWtS | 0 | Molecular weight in atomic mass units (amu) |
| ρ C | 0 | Crystal density in amu Å−3 |
| AtomNumC | 0 | Number of atoms in the crystal unit cell |
In ref. 127, A subset of 10 PAH crystals of different sizes with a range of SF driving force values were completely left out of the SISSO training to serve as the test set of unseen data. The same 10 structures were withheld here as an unseen validation set and kept completely separate from the remaining 91 structures, which were used for model training. An additional set of 9 hydrocarbon crystals, not included in the PAH101 set, was used to test the performance of the best SISSO-generated models outside of the PAH101 set. This set, referred to as “Test 2”, includes: terrylene (CSD reference code AZOXOF), benzo [e]dinaphtho[2,3-a; 10,20,30,40-ghi]fluoranthene (CSD reference code ZERXED), 7,14-diphenylnaphtho[1,2,3,4-cde]bisanthene (CSD reference code ZERXIH), 9,18-diphenyldibenzo[a,o]naphtho[1,2,3,4-ghi]perylene (CSD reference code ZERXON), 8,9-bis(4-methylphenyl)-10-phenylpentaleno[1,2-a]naphthalene (CSD reference code BEGJOO), 3,6-bis-(diphenylmethylene)-1,4-cyclohexadiene (CSD reference code DUPRIP), heptafulvalene (CSD reference code HEPFUL10), 3,12-Di-t-butyl-2,2,13,13-tetramethyl-tetradeca-3,5,7,9,11-pentaene (CSD reference code GAFDUO), and (E)-1-cycloocta-tetraenyl-2-phenylethene (CSD reference code GIWHUP). GW+BSE results were published in ref. 154 for terrylene, in ref. 76 for ZERXED, ZERXIH, and ZERXON, and in ref. 54 for the remaining materials. Some of the materials in the second test set are structurally very different from the materials in PAH101. HEPFUL10 and GIWHUP contain 7- and 8-membered carbon rings, respectively, and GAFDUO comprises a long polyene chain. Therefore, they can provide an estimate for the performance of the SISSO models outside of the PAH101 set.
To generate the feature space, features were constructed with a maximum rung (the number of times primary features are combined) of 3 and a maximum dimension (Dim) of 4. Features were combined using the operator set 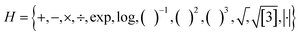 . The maximum complexity, i.e., the maximum number of operators in one combined model, was set to 10. For the singlet exciton energy, triplet exciton energy, and singlet exciton binding energy a total of roughly 5 × 102, 4 × 105, and 6 × 1010 features were generated by SISSO with a rung of 1, 2, and 3, respectively. For the singlet–triplet gap, a total of roughly 6.5 × 102, 7.5 × 105, and 2 × 1011 features were generated by SISSO with a Rung of 1, 2, and 3, respectively.
. The maximum complexity, i.e., the maximum number of operators in one combined model, was set to 10. For the singlet exciton energy, triplet exciton energy, and singlet exciton binding energy a total of roughly 5 × 102, 4 × 105, and 6 × 1010 features were generated by SISSO with a rung of 1, 2, and 3, respectively. For the singlet–triplet gap, a total of roughly 6.5 × 102, 7.5 × 105, and 2 × 1011 features were generated by SISSO with a Rung of 1, 2, and 3, respectively.
After feature generation, SISSO performs linear regression to yield the model prediction, where each model is the scalar product of the SISSO-generated feature with a vector of fitted coefficients. Then, the models are ranked according to their prediction performance. Sure independence screening (SIS) is used to select optimal subspaces from the huge feature space. The number of features saved after SIS was set to 20. SISSO then uses ℓ0-norm minimization as a sparsifying operator (SO) to determine the sparse solution for each such subspace. For each combination of dimension and rung, 40 rounds of leave-10-out cross validation (LCV) were performed. In each round, 10 data points (out of the 91 points used for model training) were randomly selected and held out as an unseen validation set. The model with the lowest RMSE for the validation set was selected in each round. Finally, the model with the lowest RMSE for the combined training and validation data was selected out of the 40 models. This model is denoted as MDim, Rung. A full account of the SISSO models for each target property is provided in the SI. For each model, the training RMSE was calculated for the whole training set with 91 structures and the test RMSE was calculated for the 10 withheld materials, which were excluded from the LCV.
The computational cost of SISSO-generated models varies depending on the number and type of primary features they contain. The relative cost of each primary feature was evaluated in a similar manner to ref. 127, relative to the calculation of the single molecule gap, GapS, whose cost is the lowest of all the primary features. The computer time required to calculate GapS was assigned a value of 1 cost unit and the cost of other features is given in Table 1 as multiples of that unit. The cost of all the primary features has been updated to account for new developments in the latest version of FHI-aims. In particular, the many-body dispersion (MBD)155 calculation has become significantly more efficient than in older versions of the code. In addition, we averaged the cost over the 10 structures in the validation set, rather than picking one system of average size, as in ref. 127. The cost of each SISSO model was evaluated by summing over the costs of all the primary features included in it. The cost of features that appear in the model more than once was counted only once. The cost of features that do not require additional calculations was also counted only once. For example, the crystal band gap, GapC, valence band dispersion, VBCdisp, and conduction band dispersion, CBCdisp, are extracted from the same band structure calculation. Therefore, if two or more of them are included in a SISSO model the cost is counted only once.
A comparison of the SISSO models to baseline models is provided in the ESI.† Linear regression (LR) and Gaussian process regression (GPR) models for each property were trained based on the SISSO primary features and the many-body tensor representation (MBTR).158 The LR and GPR models were trained using the scikit-learn159 and GPyTorch160 Python packages, respectively. For the singlet excitation energy, the triplet excitation energy, and the singlet–triplet gap, we also provide a comparison with a linear fit based only on the corresponding DFT-level approximations, namely the single molecule HOMO–LUMO gap and crystal band gap (GapS, GapC) for the singlet excitation energy, the single molecule and crystal triplet formation energy (EST, ECT) for the triplet excitation energy, and the DFT estimate for the single molecule and crystal singlet–triplet gap (ΔESST, ΔECST), evaluated by calculating the difference between the aforementioned features. For the singlet exciton binding energy there is no corresponding DFT feature. In all cases, the SISSO models provide better prediction performance with less over-fitting than the baseline models (see detailed discussion in the ESI†).
Results and discussion
SISSO models were trained to predict the singlet excitation energy, which corresponds to the optical gap, the triplet excitation energy, the singlet–triplet gap, and the singlet exciton binding energy. The equations of all the models, as well as tabulated values of their cost and accuracy are provided in the ESI.† We note that although in some instances models produced by symbolic regression algorithms have rediscovered or reproduced known physical relations,161 this is not generally the case. Therefore, we refrain from ascribing physical meaning to the models produced by SISSO.In Fig. 2, the models generated by SISSO for each property are evaluated based on considerations of cost vs. accuracy, represented by Pareto plots. For accuracy, we consider both the cross validation “train” RMSE, obtained for the training set of 91 materials, and the “test” RMSE, obtained for the unseen validation set of 10 materials. In general, the computational cost tends to increase with the model complexity because the more complex models contain more primary features. The training set RMSE generally tends to decrease with the model complexity. The validation set RMSE is generally higher than the training set RMSE. For some of the more complex models, the validation set RMSE is significantly higher than the training set RMSE, indicating over-fitting to the training data.
A detailed discussion of the results for each property is provided in the corresponding sub-sections below. For each property, we select the three models that deliver the most robust performance out of each group of models with a similar computational cost, based on the Pareto plots shown in Fig. 2. For these models, we perform a more detailed analysis of the correlation between the model predictions and the GW+BSE reference data. We examine the most significant outliers and evaluate whether the models perform robustly for the additional materials not included in the PAH101 set. The models that perform robustly for both the PAH101 set and the additional materials are selected to construct hierarchical screening workflows, as suggested in ref. 127, in which a decreasing number of candidate materials are evaluated with increasingly accurate and more expensive models. The performance of the workflows is evaluated in terms of the number of true positives and false positives that pass each filtering stage out of the entire set of 110 materials (PAH101 and the additional test set). In the Conclusion section, we remark on the overall performance of SISSO for predicting the excited-state properties of crystalline organic semiconductors and provide a comparative assessment of the performance for different properties.
Singlet excitation energy (optical gap)
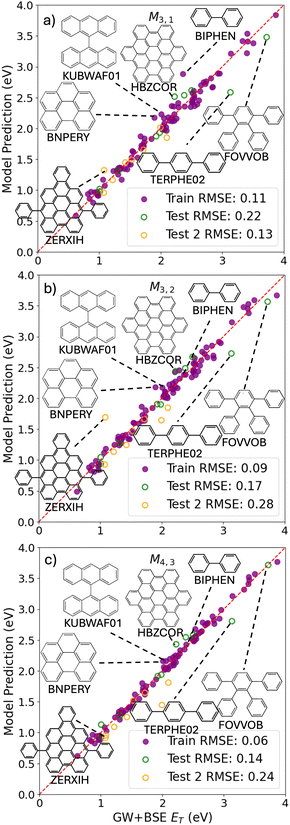
Fig. 2a shows a Pareto plot of the accuracy vs. the computational cost of the SISSO-generated models for the singlet excitation energy (optical gap). The models are clustered in three groups of lower, intermediate, and higher computational cost. In this case, even the models in the lower-cost group have a relatively high cost because all models contain crystal primary features. There is no model based only on single molecule primary features. This is consistent with the observation that singlet excitons in molecular crystals are often delocalized over many molecules,54 leading to a significant dependence of the singlet exciton energy on the crystal packing. The relatively expensive evaluation of the crystal triplet formation energy, ECT, is the main contribution to the computational cost of the lower-cost models. The models in the intermediate-cost group are more complex and contain a larger number of primary features, whose evaluation contributes to their computational cost. The higher-cost group contains only one model, M4,3, which is the most complex model, whose computational cost is high owing to the need to evaluate multiple primary features, including Hab, which is relatively expensive to evaluate.We select models out of each cost group that are close to the Pareto front for both the train and test RMSE. In the lower-cost group M4,1 and M3,1 yield the lowest RMSE of 0.15 eV and 0.16 eV, respectively, for the training set. However, their performance for the test set is significantly worse with RMSEs of 0.27 eV and 0.28 eV, respectively. In comparison, M1,3 yields a similar train RMSE of 0.16 eV and a lower test RMSE of 0.24 eV. For this reason, we select M1,3 out of the lower-cost group:
 | (1) |
 | (2) |
 | (3) |
Fig. 3 shows the predictions of the SISSO models selected based on considerations of cost and accuracy as a function of the GW+BSE reference values of the singlet exciton energy (optical gap). Parity plots for all other SISSO models are provided in the ESI.† Overall the model predictions are quite close to the reference values. The low-cost model M1,3 has a few outliers with larger deviations from the reference values. Some of the outliers are chemically and/or structurally distinct from the majority of systems in the dataset.54,127 For example, 2-(naphthalen-2-yl)azulene (CSD reference code PUJQIV) contains a 7-membered ring fused with a 5-membered ring and heptafulvalene (HEPFUL10) contains two 7-membered rings. Biphenyl (CSD reference code BIPHEN) and terphenyl (CSD reference code TERPHE02) comprise benzene rings connected by single bonds, rather than the large aromatic systems of fused rings characteristic of most of the PAH101 set. For biphenyl in particular, the optical gap value of 3.41 eV included in the PAH101 dataset117 is a significant underestimation compared to the experimental values of 4.1–4.18 eV.162–165 Therefore, it could be argued that this data point is less reliable and the model prediction is in fact closer to experiment. Coronene (CSD reference code CORONE01), 9,18-diphenyltetrabenz(a,c,h,j)anthracene (CSD reference code FACPEE), and 9,18-diphenyldibenzo[a,o]naphtho[1,2,3,4-ghi]perylene (CSD reference code ZERXON) do not appear chemically or structurally distinct from most of the materials in the PAH101 set. Coronene and FACPEE have unusually high values for the crystal triplet formation energies, ECT, which may explain why their optical gaps are overestimated by M1,3. Conversely, ZERXON has a particularly low ECT, which causes its optical gap to be significantly underestimated. For many of the M1,3 outliers out of the PAH101 set, the predictions of the intermediate-cost M3,3 and higher-cost M4,3 models are closer to the reference values, with the exception of terphenyl, which remains an outlier. For the additional test set, which was not included in PAH101, the RMSE deteriorates with the model complexity, which indicates over-fitting.
The PAH101 set contains materials with a wide range of optical gaps, as shown in Fig. 1c. Crystalline quaterrylene (QUATER10) and hexacene (ZZZDKE01) have the smallest optical gaps of 1.33 eV and 1.17 eV, respectively. Fig. 4 demonstrates a two-stage screening workflow constructed based on the SISSO models selected for the optical gap. The first stage is M1,3 and the second stage is M3,3. We have decided not to use M4,3 because of its markedly worse performance for the Test 2 set. For demonstration purposes, we screen for materials with an optical gap in the range of 2.2–2.5 eV, corresponding to green color. There are 17 such materials in total in the combined set of PAH101 and the additional test set. The screening thresholds for each stage of the workflow are set to 2.2 eV–0.5 n × RMSE to 2.5 eV + 0.5 n × RMSE, where n = 1,2,3 and RMSE refers to the training set RMSE of each model.
With n = 1, the first-stage model, M1,3, screens out most of the materials, whose optical gap is not within the target range, leaving 9 false positives. 16 of the 17 materials, whose gaps are in the target range are successfully identified. Further screening by the second-stage model, M3,3, significantly reduces the number of false positives from 9 to 4, while retaining the 16 true positives. Setting n = 2 does not improve the performance of the workflow because the final outcome is the same 16 true positives only with a higher number of false positives. With n = 3 all 17 true positives pass the screening along with 19 and 16 false positives after the first and second stage of screening, respectively. Using the same workflow to screen for materials with optical gaps in the red range and blue range produces very similar results, as shown in the ESI.† Based on this, we would suggest a two-stage workflow with thresholds defined depending on one's tolerance for false positives. We also note that the optical gaps obtained from GW+BSE are typically within 0.2 eV from experiment.117 The training RMSE values of M1,3 and M3,3 are 0.16 eV and 0.11 eV, respectively. Therefore, it may be reasonable to set n = 2 to account for the errors of GW+BSE on top of the errors of the ML models.
Triplet excitation energy
Fig. 2b shows a Pareto plot of the accuracy vs. the computational cost of the SISSO-generated models for the triplet excitation energy. Similar to the results for the optical gap, the triplet exciton energy models are clustered in three groups of lower, intermediate, and higher computational cost. In contrast to the optical gap models, in this case, the models in the lower-cost group only require the calculation of single molecule primary features, which makes them very cheap to evaluate. This is consistent with the observation that triplet excitons in molecular crystals are typically localized on one molecule (in contrast to singlet excitons),54 leading to a weaker dependence on the crystal packing. The models in the intermediate-cost group are more complex and contain various crystal primary features. The higher-cost group contains the higher complexity fourth rung models, M4,2 and M4,3. These models contain both of the high-cost features ECT and Hab, as well as multiple other primary features, which contribute to their high cost.We select models out of each cost group that are close to the Pareto front for both the train and test RMSE. Of the lower-cost group M3,1 yields the lowest RMSEs of 0.11 eV and 0.22 eV, respectively, for the training set and the validation set.
 | (4) |
None of the models in the intermediate-cost group is on the Pareto front for both the training set and the validation set. M3,3 yields the lowest RMSE of 0.07 eV for the training set, however its performance deteriorates considerably for the validation set with an RMSE of 0.22 eV. The next best model for the training set, M2,3, with an RMSE of 0.09 eV also performs significantly worse for the validation set with an RMSE of 0.19 eV. We therefore choose the third model, M3,2, because its RMSE of 0.09 eV for the training set is similar to M2,3, but its performance for the validation set is markedly better with an RMSE of 0.17 eV.
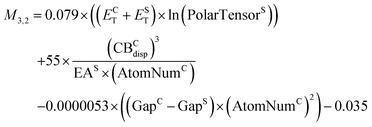 | (5) |
Of the high-cost group, M4,3 is on the Pareto front for both the training set and the validation set with RMSEs of 0.06 eV and 0.14 eV, respectively.
 | (6) |
Fig. 5 shows the predictions of the SISSO models selected based on considerations of cost and accuracy as a function of the GW+BSE reference values of the triplet exciton energy. Parity plots for all other SISSO models are provided in the ESI.† Similar to the optical gap, the SISSO model predictions are quite close to the reference values. The low-cost model M3,1 has a few outliers with larger deviations from the reference values. Biphenyl and terphenyl are significant outliers, similar to the optical gap models. 1,2,3,4-Tetraphenylbenzene (CSD reference code FOVVOB) also comprises benzene rings connected by single bonds. Biphenyl, 9,9′-bianthracenyl (CSD reference code KUBWAF01), hexabenzo(bc,ef,hi,kl,no,qr)coronene (CSD reference code HBZCOR), and 1,12-benzoperylene (CSD reference code BNPERY) have unusually high single molecule triplet formation energy, EST, values exceeding the GW+BSE reference values of their crystal triplet excitation energies, which causes the M3,1 predictions to be overestimated. 7,14-Diphenylnaphtho[1,2,3,4-cde]bisanthene (CSD reference code ZERXIH) has an unusually large value for the trace of the molecular polarization tensor PolarTensorS, which causes it to become a significant outlier for M3,2. Interestingly, the lowest-cost model M3,1 has a lower RMSE for the Test 2 set than for the PAH101 held out validation set. In contrast, the performance of the more complex models M3,2 and M4,3 deteriorates very significantly for the additional test set, indicating over-fitting.
The PAH101 set contains materials with a wide range of triplet excitation energies, as shown in Fig. 1d. Fig. 6 demonstrates a one-stage screening workflow for the triplet exciton energy based on the M3,1 SISSO model, which was selected because it retains robust performance for the additional test set, unlike the more complex models. Because of the recent interest in TTA up-conversion of infrared (IR) light to the visible range,71 we screen for materials, whose triplet excitation energy is in the IR, below 1.6 eV. There are 37 such materials in total in the combined set of PAH101 and the additional test set. The screening thresholds are set to 1.6 eV + n × RMSE, where n = 1,2,3 and RMSE refers to the training set RMSE of M3,1, 0.11 eV. With n = 1, the M3,1 model correctly classifies all 37 materials with triplet excitation energy in the IR with only 3 false positives. Setting n to 2 or 3 is not beneficial because it only increases the number of false positives. In this case, screening only with M3,1 delivers robust performance.
Next, we assess whether the 37 materials in the combined set of PAH101 and the additional test set with triplet excitation energies in the IR are likely to undergo TTA. The thermodynamic driving force for TTA is given by the difference between twice the triplet excitation energy and the singlet excitation energy (the opposite of the SF driving force). As discussed in ref. 54,63 and 127, GW+BSE systematically underestimates the SF driving force and therefore overestimates the TTA driving force. Hence, we assess the likelihood of a given material to undergo SF/TTA relative to other known SF/TTA materials. Only 8 out of the 37 materials have a higher TTA driving force than rubrene and perylene: pyracylene (KEGHEJ01), 11-phenylbenzo[a]naphtho[2,1,8-cde]perylene (KAGFUV), the two polymorphs of diindeno[1,2,3 cd:1′,2′,3′-lm]perylene (POBPIG and POBPIG06), anthra(2,1,9,8-hijkl)benzo(de)naphtho(2,1,8,7-stuv)pentacene (BOXGAW), dibenzo(def,i)naphtho(1,8,7-v,w,x)pyranthrene (DUPHAX), benzo[e]dinaphtho[2,3-a; 10,20,30,40 -ghi]fluoranthene (ZERXED), and heptafulvalene (HEPFUL10). All of these have GW+BSE triplet excitation energies in the near-IR and their GW+BSE optical gaps range from 1.89 eV for crystalline heptafulvalene to 2.41 eV for KAGFUV. Materials in the PAH101 set with lower triplet excitation energies tend to be more likely to undergo SF than TTA. Five of these compounds have been previously assessed in ref. 63 as isolated molecules rather than crystals, using a different GW+BSE implementation. Therein, the likelihood of the competing process of conversion of two excitons in the first triplet state to one exciton in a higher triplet state instead of a singlet exciton was also considered. Based on these energetic considerations, pyracylene (labeled as compound C1 in ref. 63) appeared promising, however it is not a good TTA chromophore because of its short triplet state lifetime and the rapid non-radiative decay of its lowest singlet state.166 POBPIG is a perylene derivative (labeled as compound D16 in ref. 63), for which the competing conversion to a higher triplet state was found to be too energetically favorable for high-yield TTA. KAGFUV, BOXGAW, and DUPHAX are large aromatic compounds comprising several fused six-membered rings that can be classified as graphene flakes. Of these, KAGFUV (labeled as compound E2 in ref. 63) and DUPHAX (labeled as compound E3 in ref. 63) were identified as TTA candidates based on energetic considerations. ZERXED has been evaluated based on the same criteria in ref. 76 (therein it was labeled “Compound I”) and found to be a promising TTA candidate. Heptafulvalene is reported here for the first time as a potential TTA candidate and could indicate an interesting new direction of exploring compounds with 7-membered rings as TTA/SF candidates.
The workflow presented here demonstrates how ML models can be used to identify new potential TTA candidates with triplet exciton energies in the IR, optical gaps in the visible range, and favorable TTA energetics. We note that the optical gap SISSO models presented above and the SF driving force SISSO models from ref. 127 could be used to perform further fast screening of materials that pass the triplet exciton energy screening. Thus, the number of candidates selected for computationally expensive excited-state calculations can be significantly reduced.
Singlet triplet gap
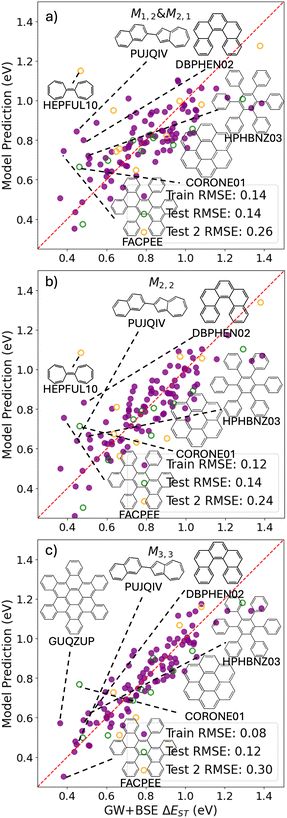
Fig. 2c shows a Pareto plot of the accuracy vs. the computational cost of the SISSO-generated models for the singlet–triplet gap. The singlet–triplet gap models are clustered in four groups of very-low, low, intermediate, and higher computational cost. The very-low cost group contains models, whose evaluation only requires the calculation of single molecule primary features. The low-cost group contains models, whose evaluation only requires calculating the crystal band gap, GapC, in addition to single molecule features. Models in the intermediate cost group require the calculation of the crystal triplet formation energy, ECT, and/or the estimated crystal singlet–triplet gap, ΔECST. The models in the high-cost group also contain Hab.We select models out of each cost group that are close to the Pareto front for both the train and test RMSE. In the very-low-cost group M1,2 and M2,1 contain the same primary features and have a similar performance with train RMSE of 0.14 eV and test RMSEs of 0.15 eV and 0.14 eV, respectively. Therefore we use an ensemble of the two models:
 | (7) |
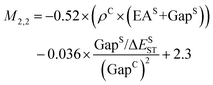 | (8) |
 | (9) |
Fig. 7 shows the predictions of the SISSO models selected based on considerations of cost and accuracy as a function of the GW+BSE reference values of the singlet–triplet gap. Parity plots for all other SISSO models are provided in the ESI.† We note that the energy range of GW+BSE reference data for the singlet–triplet gap is significantly smaller than the energy range of the singlet and triplet exciton energies (see the distributions in Fig. 1). Therefore, the deviations of the SISSO model predictions appear larger in comparison to the reference data even though they are of comparable magnitude or even smaller than the deviations of the SISSO models for the singlet and triplet exciton energies. In the discussion of the outliers we focus on materials with relatively small singlet–triplet gaps because these would be of most interest for OLEDs. The very-low-cost model M1,2 & M2,1 has several significant outliers in the range of singlet–triplet gaps below 0.6 eV. These include materials that are also among the outliers for the singlet and triplet exciton energy models, PUJQIV, FACPEE, HEPFUL10, and coronene. Hexaphenylbenzene (CSD reference code HPHBNZ03) comprises phenyl rings connected by single bonds like some of the outliers for the singlet and triplet excitation energies. Trinaphtho[1,2,3,4-fgh:1′,2′,3′,4′-pqr:1″,2″,3″,4″-za_1_b_1_]trinaphthylene (CSD reference code GUQZUP) and (5)helicene (CSD reference code DBPHEN02) are not structurally or chemically distinct from most of the materials in the PAH101 set. In addition, they do not have any primary features with unusual values. It is possible that the relatively large number of outliers, especially in the low singlet–triplet gap range, is a reflection of the difficulty of training reliable models to predict very small target values, in particular considering that there are few materials with a singlet–triplet gap below 0.5 eV in the training data (See Fig. 1e). The performance of all three models for the Test 2 set is worse than for the PAH101 validation set. In particular, for the more complex model, M3,3, the Test 2 RMSE is significantly higher than the lower cost models. For HEPFUL10, M3,3 even predicts a negative value. The poor performance of M3,3 for the Test 2 set indicates overfitting.
Fig. 1e shows the distribution of singlet–triplet gaps in the PAH101 dataset. Small singlet–triplet gaps are rare among this class of materials. The materials with lowest singlet–triplet gaps (in parentheses) are: trinaphtho[1,2,3,4-fgh:1′,2′,3′,4′-pqr:1″,2″,3″,4″-za_1_b_1_]trinaphthylene (GUQZUP; 0.36 eV), 9,18-diphenyltetrabenz(a,c,h,j)anthracene (FACPEE; 0.38 eV), acenaphtho[3,2,1,8-fghij]tetrabenzo[a,c,m,o]picene (VUFHUA; 0.435 eV), benzo(1,2,3-bc:4,5,6 b′,c′)dicoronene (YOFCUR; 0.44 eV), and 2-(naphthalen-2-yl)azulene (PUJQIV; 0.45 eV). Even the lowest singlet–triplet gaps in the PAH101 set would be considered marginal or too high for TADF. It is interesting to note that with the exception of PUJQIV (shown in Fig. 3 and 7), the materials with the smallest singlet–triplet gaps in the PAH101 set bear no resemblance to the donor–acceptor compounds typically used for TADF.47,167 Rather, they are large PAHs with extended π systems. FACPEE (shown in Fig. 3 and 7), VUFHUA, and YOFCUR have segments that could lead to charge-transfer-like intramolecular excitations. GUQZUP can be described as a graphene flake with no obvious segments. The twisted conformation it adopts in the crystal structure may contribute to orbital localization and charge-transfer-like excitations. The effect of crystal packing and intermolecular vs. intramolecular charge-transfer excitations on singlet–triplet gaps is not well-understood and should be further investigated in relation to TADF in crystalline materials.168,169
Fig. 8 demonstrates a two-stage screening workflow constructed based on the SISSO models selected for the singlet–triplet gap. The M1,2 & M2,1 and M2,2 models were selected for the first and second stages of the workflow, respectively, based on their performance for the Test 2 set. For demonstration purposes, we screen for materials with a singlet–triplet gap below 0.5 eV. There are 10 such materials in total in the combined set of PAH101 and the additional test set. The screening thresholds for each stage of the workflow are set to 0.5 eV + n × RMSE, where n = 1,2,3 and RMSE refers to the training set RMSE of each model. With n = 1, the first-stage ensemble model of M1,2 & M2,1 screens out most of the materials, whose singlet–triplet gap is above 0.5 eV, leaving only 8 false positives. However, 5 of the 10 materials whose singlet–triplet gaps are below 0.5 eV are also screened out, leaving only 5 true positives. Further screening by the second-stage model, M2,2 reduces the number of false positives to 5 without losing any additional true positives. Setting n = 2 results in 7 and 6 true positives passing the first and second stage, respectively, with a significantly higher number (23) of false positives passing the screening. With n = 3, 9 true positives pass the screening along with 55 false positives. One may define the screening thresholds depending on their tolerance for false positives. With the thresholds set to one RMSE, the workflow presented here effectively eliminates most of the materials that are not of interest, which significantly reduces the number of candidates that need to be evaluated using more accurate and computationally expensive methods. Training better models for predicting the singlet–triplet gap would require acquiring more GW+BSE data for materials with small singlet–triplet gaps. To this end, the present models could be used to select materials for data acquisition.
Singlet exciton binding energy
Fig. 2d shows a Pareto plot of the accuracy vs. the computational cost of the SISSO-generated models for the singlet exciton binding energy. We note that terphenyl (TERPHE02) is a major outlier for all the exciton binding energy models (see parity plots provided in the ESI†). Therefore, we also consider the validation RMSE without terphenyl. The SISSO models are clustered in four cost groups. The very-low-cost model M1,1 only requires a calculation of the molecular ionization potential, IPS. The models in the low-cost group require a crystal band structure calculation in addition to single molecule features. Most of the models in the intermediate cost group include the crystal triplet formation energy, ECT, except for M3,2, which includes Hab and the crystal dielectric constant, εC. The models in the high-cost group contain ECT and Hab.We select models out of each cost group that are close to the Pareto front for both the train and test RMSE. The very-low-cost model M1,1 yields RMSEs of 0.17 eV for the training set and 0.28 eV for the validation set (0.19 eV without terphenyl).
| M1,1 = 0.24 × (IPS/ρC) −1.35 | (10) |
Of the low-cost group, M4,1 and M2,2 yield the same RMSEs of 0.14 eV for the training set and 0.27 eV for the test set. M2,2 delivers a slightly better performance for the validation set without terphenyl with an RMSE of 0.18 eV, compared to 0.20 eV for M4,1. Therefore, we select M2,2:
| M2,2 = 0.012 × (EST + IPS) × (IPS/ρC) + 0.020 × ((EST − GapS) × (CBCdisp × AtomNumC)) −0.17 | (11) |
Of the intermediate-cost group M4,2 yields the lowest RMSE of 0.12 eV for the training set, however its performance deteriorates significantly for the validation set with an RMSE of 0.27 eV (0.18 eV without terphenyl), indicating over-fitting. The next model M2,3 has a more robust performance with RMSEs of 0.12 eV for the training set and 0.22 eV for the validation set (0.13 eV without terphenyl).
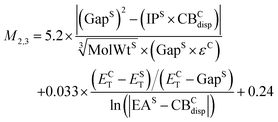 | (12) |
Both models in the high-cost group are over-fitted, as indicated by the large difference between their performance for the training set vs. the validation set. Therefore, these overly complex models are not useful.
Fig. 9 shows the predictions of the SISSO models selected based on considerations of cost and accuracy as a function of the GW+BSE reference values of the singlet exciton binding energy. Parity plots for all other SISSO models are provided in the ESI.† We note that, similar to the singlet–triplet gap, the energy range of the GW+BSE reference data for the singlet exciton binding energy is significantly smaller than the energy range of the singlet and triplet exciton energies (see the distributions in Fig. 1). Therefore, the deviations of the SISSO model predictions appear larger in comparison to the reference data even though they are of comparable magnitude or even smaller than the deviations of the SISSO models for the singlet and triplet exciton energies. Terphenyl is a major outlier to the point that it noticeably skews the test RMSE. This is perhaps not surprising because terphenyl is an outlier for most other properties considered here. Some of the outliers encountered for other properties are also outliers for the singlet exciton binding energy models, including PUJQIV and FACPEE (not shown), as well as HEPFUL10. Some of the outliers, such as β-tribenzopyrene (CSD reference code TBZPYR) and dinaphtho(1,2-a:1′,2′-h)anthracene (CSD reference code DNAPAN), do not appear structurally or chemically distinct from most of the materials in the PAH101 set. For M1,1, a relatively high value of the single molecule ionization potential, IPS, combined with a low crystal density, ρC can lead to significant overestimation (e.g., for terphenyl, DNAPAN, and GAFDUO). Conversely, a low IPS value combined with a high ρC can lead to significant underestimation (e.g., for TBZPYR, BEGJOO and HEPFUL10). The relatively large number of persistent outliers for the singlet exciton binding energy models could be a reflection of the difficulty of training reliable models to predict very small target values. The simpler models M1,1 and M2,2 have a lower RMSE for the Test 2 set than for the PAH101 validation set, whereas the more complex model M2,2 has a significantly higher RMSE for the Test 2 set, indicating over-fitting.
Fig. 1f shows the distribution of singlet exciton binding energies in the PAH101 dataset. In most organic materials the exciton binding energy is significant compared to inorganic materials because the dielectric screening of charges is not as strong. However, some materials in the PAH101 set have low exciton binding energies (in parentheses), including: anthra(2,1,9,8-hijkl)benzo(de)naphtho(2,1,8,7-stuv)pentacene (BOXGAW; 0.013 eV), dinaphtho(1,2-a:1′,2′-h)anthracene (DNAPAN; 0.071 eV), tetrabenzo(de,no,st,c1d1)heptacene (TBZHCE; 0.130 eV), benzo[lm]chryseno[1,12,11,10-opqrab]perylene (YUNYAJ; 0.165 eV), and hexabenzo(bc,ef,hi,kl,no,qr)coronene (HBZCOR; 0.169 eV). All of these compounds are characterized by very extended and/or elongated π systems, which likely lead to an already low molecular exciton binding energy (not calculated here), further reduced by dielectric screening in the solid form.
Fig. 10 demonstrates a two-stage screening workflow constructed based on the SISSO models selected for the singlet exciton binding energy. The M1,1 and M2,2 models have been selected for the first and second stage, respectively, based on their robust performance for the Test 2 set. A small exciton binding energy means it is easier to separate excitons into free charge carriers. It is also often associated with strong dielectric screening and better charge transport. For demonstration purposes, we screen for materials with a singlet exciton binding energy below 0.3 eV. There are 17 such materials in total in the combined set of PAH101 and the additional test set. The screening thresholds for each stage of the workflow are set to 0.3 eV + n × RMSE, where n = 1,2,3 and RMSE refers to the training set RMSE of each model. With n = 1, the first-stage model, M1,1, screens out many of the materials, whose exciton binding energy is above 0.3 eV, leaving 21 false positives. However, 4 of the 17 materials with exciton binding energy below 0.3 eV are also screened out, leaving 13 true positives. Further screening by the second-stage model, M2,2 reduces the number of false positives to 15 with two additional true positives lost. Setting n = 2 results in 16 out of 17 true positives (all except terphenyl) passing the screening, but with a high number (41) of false positives. Setting n = 3 is not beneficial because the same 16 true positives pass the screening (terphenyl is still misclassified) along with 57 false positives. One may define the screening thresholds depending on their tolerance for false positives. With the thresholds set to one RMSE, the workflow presented here effectively eliminates most of the materials that are not of interest, which significantly reduces the number of candidates that need to be evaluated using more accurate and computationally expensive methods. Training better models for predicting the singlet exciton binding energy would require acquiring more GW+BSE data for materials with small exciton binding energies. To this end, the present models could be used to select materials for data acquisition.
Conclusion
In summary, we used the PAH101 dataset of GW+BSE calculations to train SISSO models to predict the first singlet excitation energy, which corresponds to the optical gap, the first triplet excitation energy, the singlet–triplet gap, and the singlet exciton binding energy of organic molecular crystals. SISSO models were selected based on considerations of accuracy and computational cost to design materials screening workflows for each property. The screening targets were chosen to demonstrate typical use-cases relevant for organic electronic devices. We demonstrated screening for materials with an optical gap in a particular color; materials meeting the requirements for up-conversion of infrared light to the visible range via TTA, namely, a triplet excitation energy in the infrared, optical gap in the visible range, and a higher TTA driving force than rubrene; materials with a small singlet–triplet gap, which is desirable for OLEDs; and materials with a small singlet exciton binding energy to facilitate the separation of excitons into free charge carriers.For all four properties, the workflows based on SISSO models can effectively screen out most of the materials that are not of interest. However, the classification performance varies across properties and screening targets in terms of the number of false positives that pass the workflow and the number of true positives missed. The workflows for the optical gap and triplet excitation energy yield a more robust performance than the workflows for the singlet–triplet gap and exciton binding energy. The SISSO models for the triplet exciton energy performed particularly well. The lowest cost model, which only requires evaluating single molecule DFT features, successfully classified all the materials with triplet exciton energies in the IR with a very small number of false positives. This analysis helped identify compounds with 7-membered rings, such as heptafulvalene, as a potential new direction to be explored for TTA/SF.
The overall narrow energy range of the singlet–triplet gap and exciton binding energy in the PAH101 dataset, as well as the small number of samples with the desirable low values, made it more challenging to train reliable models for these properties. Improving the models would require additional data acquisition. To this end, the present models could be used to select materials likely to have low singlet–triplet gaps or low exciton binding energy for additional GW+BSE calculations. We also note that ML models trained on PAH101 are not guaranteed to perform well for materials that are significantly different chemically or structurally. This has been demonstrated here and in ref. 54 by the worse performance of some of the more complex SISSO models for an additional test set of 9 hydrocarbon crystals. Therefore, we recommend carefully validating the performance of these models for materials outside of the PAH101 set before using them for large scale screening.
In conclusion, we have demonstrated that the SISSO algorithm can generate ML models to predict the excited-state properties of molecular crystals using only a small amount of GW+BSE training data by incorporating physical/chemical knowledge into the selection of primary features. The resulting ML models, which require only relatively low-cost DFT calculations to evaluate, can provide estimates for excited-state properties of molecular crystals including the optical gap, triplet exciton energy, singlet–triplet gap, and exciton binding energy. These properties would not otherwise be accessible via DFT calculations. Using ML models in the early stages of materials screening workflows can effectively narrow down the number of candidates selected for further evaluation using computationally expensive excited-state theory. ML models can thus significantly accelerate the discovery of crystalline organic semiconductors with desirable properties for applications in optoelectronic devices.
Data and code availability
The PAH101 dataset117 is available via the NOvel MAterials Discovery (NOMAD) repository170 and can be accessed at DOI: https://doi.org/10.17172/NOMAD/2024.12.05–1. The SISSO code,128 used to perform sure independent screening and sparsifying operator model training, is available in the GitHub repository SISSO. SISSO version 3.3 dated July 2023 was used here. The SISSO primary features were calculated using version 18.06.07 of the FHI-aims150 electronic structure package available via the FHI-aims website. Scripts used to calculate the primary features are available in the GitHub repository MLfeat_FHI-aims, DOI: https://doi.org/10.5281/zenodo.15093306. Scripts for preparing the input for SISSO, running the training and model evaluation, analyzing the SISSO output, and making Pareto plots and correlation plots between the SISSO model predictions and the true labels are provided in the GitHub repository SISSOonPAH, DOI: https://doi.org/10.5281/zenodo.15093308.Author contributions
S. G., Y. L., and X. L. performed the calculations and data analysis. N. M., S. G., Y. L., and X. L. wrote the manuscript. N. M. conceived and led the project.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Science Foundation (NSF) Designing Materials to Revolutionize and Engineer our Future (DMREF) program under award DMR-2323749. This research used resources of the Argonne Leadership Computing Facility (ALCF), which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357.Notes and references
- H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Nat. Mater., 2010, 9, 938–943 CrossRef CAS PubMed.
- R. R. Lunt, J. B. Benziger and S. R. Forrest, Adv. Mater., 2010, 22, 1233–1236 CrossRef CAS PubMed.
- V. Podzorov, MRS Bull., 2013, 38, 15–24 CrossRef.
- X. Zhang, H. Dong and W. Hu, Adv. Mater., 2018, 30, 1801048 CrossRef PubMed.
- C. Wang, H. Dong, L. Jiang and W. Hu, Chem. Soc. Rev., 2018, 47, 422–500 RSC.
- S. Duan, B. Geng, X. Zhang, X. Ren and W. Hu, Matter, 2021, 4, 3415–3443 CrossRef CAS.
- J. Mei, Y. Diao, A. L. Appleton, L. Fang and Z. Bao, J. Am. Chem. Soc., 2013, 135, 6724–6746 CrossRef CAS PubMed.
- V. Bruevich, H. H. Choi and V. Podzorov, Adv. Funct. Mater., 2021, 31, 2006178 CrossRef CAS.
- J. Euvrard, O. Gunawan, A. Kahn and B. P. Rand, Adv. Funct. Mater., 2022, 32, 2206438 CrossRef CAS.
- J. T. Dull, X. He, J. Viereck, Q. Ai, R. Ramprasad, M. C. Otani, J. Sorli, J. W. Brandt, B. P. Carrow, A. D. Tinoco, Y.-L. Loo, C. Risko, S. Rangan, A. Kahn and B. P. Rand, Adv. Mater., 2023, 35, 2302871 CrossRef CAS PubMed.
- M. Sawatzki-Park, S.-J. Wang, H. Kleemann and K. Leo, Chem. Rev., 2023, 123, 8232–8250 CrossRef CAS PubMed.
- E. Menard, V. Podzorov, S.-H. Hur, A. Gaur, M. Gershenson and J. Rogers, Adv. Mater., 2004, 16, 2097–2101 CrossRef CAS.
- J. Jang, S. Nam, K. Im, J. Hur, S. N. Cha, J. Kim, H. B. Son, H. Suh, M. A. Loth, J. E. Anthony, J.-J. Park, C. E. Park, J. M. Kim and K. Kim, Adv. Funct. Mater., 2012, 22, 1005–1014 CrossRef CAS.
- Y.-H. Kim, B. Yoo, J. E. Anthony and S. K. Park, Adv. Mater., 2012, 24, 497–502 CrossRef CAS PubMed.
- S.-J. Wang, M. Sawatzki, G. Darbandy, F. Talnack, J. Vahland, M. Malfois, A. Kloes, S. Mannsfeld, H. Kleemann and K. Leo, Nature, 2022, 606, 700–705 CrossRef CAS PubMed.
- M.-T. Lee, C.-H. Liao, C.-H. Tsai and C. Chen, Adv. Mater., 2005, 17, 2493–2497 CrossRef CAS.
- H. Nakanotani and C. Adachi, Appl. Phys. Lett., 2010, 96, 053301 CrossRef.
- J. Liu, H. Zhang, H. Dong, L. Meng, L. Jiang, L. Jiang, Y. Wang, J. Yu, Y. Sun and W. Hu, et al. , Nat. Commun., 2015, 6, 10032 CrossRef CAS PubMed.
- X. Yang, X. Feng, J. Xin, P. Zhang, H. Wang and D. Yan, J. Mater. Chem. C, 2018, 6, 8879–8884 RSC.
- M.-H. An, R. Ding, Q.-C. Zhu, G.-D. Ye, H. Wang, M.-X. Du, S.-N. Chen, Y. Liu, M.-L. Xu, T. Xu, W. Wang, J. Feng and H.-B. Sun, Adv. Funct. Mater., 2020, 30, 2002422 CrossRef CAS.
- P. Sun, D. Liu, F. Zhu and D. Yan, Nat. Photonics, 2023, 17, 264–272 CrossRef CAS.
- J. Xin, P. Sun, F. Zhu, Y. Wang and D. Yan, J. Mater. Chem. C, 2021, 9, 2236–2242 RSC.
- M. A. Fusella, A. N. Brigeman, M. Welborn, G. E. Purdum, Y. Yan, R. D. Schaller, Y. L. Lin, Y.-L. Loo, T. V. Voorhis, N. C. Giebink and B. P. Rand, Adv. Energy Mater., 2018, 8, 1701494 CrossRef.
- Y. Zhang, M. T. Sajjad, O. Blaszczyk, A. J. Parnell, A. Ruseckas, L. A. Serrano, G. Cooke and I. D. W. Samuel, Chem. Mater., 2019, 31, 6548–6557 CrossRef CAS.
- T. Zhang, C. An, P. Bi, K. Xian, Z. Chen, J. Wang, Y. Xu, J. Dai, L. Ma, G. Wang, X. Hao, L. Ye, S. Zhang and J. Hou, Energy Environ. Sci., 2024, 17, 3927–3936 RSC.
- A.-L. Hofmann, J. Wolansky, M. Hambsch, F. Talnack, E. Bittrich, L. Winkler, M. Herzog, T. Zhang, T. Antrack, L. C. Winkler, J. Schröder, M. Riede, S. C. Mannsfeld, J. Benduhn and K. Leo, Adv. Opt. Mater., 2024, 12, 2401025 CrossRef CAS.
- Y. Wang, W. Zhu, W. Du, X. Liu, X. Zhang, H. Dong and W. Hu, Angew. Chem., 2018, 130, 4027–4031 CrossRef.
- S. Jeong, N. Barbosa, A. Tiwari, E. K. Holland, L.-Y. Huang, V. Bhat, Y. Yang, Y. Zhang, S. J. Whittaker, M.-W. Kim, A. Alaei, P. Sundaram, R. Spencer, J. Brazard, D. M. Kalyon, C. Risko, J. E. Anthony, T. B. M. Adachi, A. G. Shtukenberg, B. Kahr and S. S. Lee, Adv. Funct. Mater., 2023, 33, 2212531 CrossRef CAS.
- W. Yang, P. Han, S. Zhu, Z. Cui, Z. Li, S. Wu, W. Xu, Z. Gao, T. Ba, Y. Liang, H. Jiang and W. Hu, ACS Appl. Electron. Mater., 2024, 6, 4223–4231 CrossRef CAS.
- B. Fraboni, A. Fraleoni-Morgera and N. Zaitseva, Adv. Funct. Mater., 2016, 26, 2276–2291 CrossRef CAS.
- M. Chen, L. Sun, X. Ou, H. Yang, X. Liu, H. Dong, W. Hu and X. Duan, Adv. Mater., 2021, 33, 2104749 CrossRef CAS PubMed.
- M. Dong, A. Lv, X. Zou, N. Gan, C. Peng, M. Ding, X. Wang, Z. Zhou, H. Chen, H. Ma, L. Gu, Z. An and W. Huang, Adv. Mater., 2024, 36, 2310663 CrossRef CAS PubMed.
- A. J. Petty, Q. Ai, J. C. Sorli, H. F. Haneef, G. E. Purdum, A. Boehm, D. B. Granger, K. Gu, C. P. L. Rubinger, S. R. Parkin, K. R. Graham, O. D. Jurchescu, Y.-L. Loo, C. Risko and J. E. Anthony, Chem. Sci., 2019, 10, 10543–10549 RSC.
- J. C. Sorli, Q. Ai, D. B. Granger, K. Gu, S. Parkin, K. Jarolimek, N. Telesz, J. E. Anthony, C. Risko and Y.-L. Loo, Chem. Mater., 2019, 31, 6615–6623 CrossRef CAS.
- F. Maleki, K. J. Thorley, H. F. Iqbal, D. Vong, T. Maitra, A. Petty, L. L. Daemen, S. R. Parkin, O. D. Jurchescu, J. E. Anthony and A. J. Moulé, Chem. Mater., 2024, 36, 4794–4805 CrossRef CAS.
- D. W. Davies, S. K. Park, P. Kafle, H. Chung, D. Yuan, J. W. Strzalka, S. C. B. Mannsfeld, S. G. Wang, Y.-S. Chen, D. L. Gray, X. Zhu and Y. Diao, Chem. Mater., 2021, 33, 2466–2477 CrossRef CAS.
- D. W. Davies, S. Jeon, G. Graziano, B. B. Patel, W. Liu, J. Strzalka, X. Zhu and Y. Diao, ACS Appl. Mater. Interfaces, 2024, 16, 42546–42554 CrossRef CAS PubMed.
- H. Chung and Y. Diao, J. Mater. Chem. C, 2016, 4, 3915–3933 RSC.
- D. Vermeulen, L. Y. Zhu, K. P. Goetz, P. Hu, H. Jiang, C. S. Day, O. D. Jurchescu, V. Coropceanu, C. Kloc and L. E. McNeil, J. Phys. Chem. C, 2014, 118, 24688–24696 CrossRef CAS.
- K. P. Goetz, J. Tsutsumi, S. Pookpanratana, J. Chen, N. S. Corbin, R. K. Behera, V. Coropceanu, C. A. Richter, C. A. Hacker, T. Hasegawa and O. D. Jurchescu, Adv. Electron. Mater., 2016, 2, 1600203 CrossRef PubMed.
- G. Campillo-Alvarado, M. Bernhardt, D. W. Davies, J. A. N. T. Soares, T. J. Woods and Y. Diao, J. Chem. Phys., 2021, 155, 071102 CrossRef CAS PubMed.
- L. Sun, Y. Wang, F. Yang, X. Zhang and W. Hu, Adv. Mater., 2019, 31, 1902328 CrossRef PubMed.
- R. R. Dasari, X. Wang, R. A. Wiscons, H. F. Haneef, A. Ashokan, Y. Zhang, M. S. Fonari, S. Barlow, V. Coropceanu, T. V. Timofeeva, O. D. Jurchescu, J.-L. Brédas, A. J. Matzger and S. R. Marder, Adv. Funct. Mater., 2019, 29, 1904858 CrossRef CAS.
- K. P. Goetz, H. F. Iqbal, E. G. Bittle, C. A. Hacker, S. Pookpanratana and O. D. Jurchescu, Mater. Horiz., 2022, 9, 271–280 RSC.
- M. L. Tietze, J. Benduhn, P. Pahner, B. Nell, M. Schwarze, H. Kleemann, M. Krammer, K. Zojer, K. Vandewal and K. Leo, Nat. Commun., 2018, 9, 1182 CrossRef PubMed.
- M. F. Sawatzki, H. Kleemann, B. K. Boroujeni, S.-J. Wang, J. Vahland, F. Ellinger and K. Leo, Adv. Sci., 2021, 8, 2003519 CrossRef CAS PubMed.
- X.-K. Chen, D. Kim and J.-L. Brédas, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS PubMed.
- X. Wang, A. Wang, M. Zhao and N. Marom, J. Phys. Chem. Lett., 2023, 14, 10910–10919 CrossRef CAS PubMed.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS PubMed.
- M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed.
- Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 1–20 CrossRef.
- M. A. Bryden and E. Zysman-Colman, Chem. Soc. Rev., 2021, 50, 7587–7680 RSC.
- X. Wang, S. Gao, Y. Luo, X. Liu, R. Tom, K. Zhao, V. Chang and N. Marom, J. Phys. Chem. C, 2024, 128, 7841 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- J. Lee, P. Jadhav, P. D. Reusswig, S. R. Yost, N. J. Thompson, D. N. Congreve, E. Hontz, T. Van Voorhis and M. A. Baldo, Accounts Chem. Res., 2013, 46, 1300–1311 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 1–12 Search PubMed.
- J. Xia, S. N. Sanders, W. Cheng, J. Z. Low, J. Liu, L. M. Campos and T. Sun, Adv. Mater., 2017, 29, 1601652 CrossRef PubMed.
- K. M. Felter and F. C. Grozema, J. Phys. Chem. Lett., 2019, 10, 7208–7214 CrossRef CAS PubMed.
- R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Energy Environ. Sci., 2020, 13, 2741–2804 RSC.
- A. J. Baldacchino, M. I. Collins, M. P. Nielsen, T. W. Schmidt, D. R. McCamey and M. J. Tayebjee, Chem. Phys. Rev., 2022, 3, 021304 CrossRef CAS.
- X. Wang, R. Tom, X. Liu, D. N. Congreve and N. Marom, J. Mater. Chem. C, 2020, 8, 10816–10824 RSC.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- Y. C. Simon and C. Weder, J. Mater. Chem., 2012, 22, 20817–20830 RSC.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125 RSC.
- J. C. Goldschmidt and S. Fischer, Adv. Opt. Mater., 2015, 3, 510–535 CrossRef CAS.
- X. Xiao, W. Tian, M. Imran, H. Cao and J. Zhao, Chem. Soc. Rev., 2021, 50, 9686–9714 RSC.
- L. Zeng, L. Huang, J. Han and G. Han, Acc. Chem. Res., 2022, 55, 2604–2615 CrossRef CAS PubMed.
- K. J. Fallon, E. M. Churchill, S. N. Sanders, J. Shee, J. L. Weber, R. Meir, S. Jockusch, D. R. Reichman, M. Y. Sfeir, D. N. Congreve and L. M. Campos, J. Am. Chem. Soc., 2020, 142, 19917–19925 CrossRef CAS PubMed.
- P. Narayanan, M. Hu, A. Gallegos, L. Pucurimay, Q. Zhou, E. Belliveau, G. Ahmed, S. Fernandez, W. Michaels, N. Murrietta, V. Mutatu, D. Feng, R. Hamid, K. Yap, T. Schloemer, T. Jaramillo, M. Kats and D. Congreve, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv–2024–h0k05.
- A. Sugie, K. Nakano, K. Tajima, I. Osaka and H. Yoshida, J. Phys. Chem. Lett., 2023, 14, 11412–11420 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- R. Taylor and P. A. Wood, Chem. Rev., 2019, 119, 9427–9477 CrossRef CAS PubMed.
- F. Zhang, V. Lemaur, W. Choi, P. Kafle, S. Seki, J. Cornil, D. Beljonne and Y. Diao, Nat. Commun., 2019, 10, 4217 CrossRef PubMed.
- I. Andrusenko, C. L. Hall, E. Mugnaioli, J. Potticary, S. R. Hall, W. Schmidt, S. Gao, K. Zhao, N. Marom and M. Gemmi, IUCrJ, 2023, 10, 131–142 CrossRef CAS PubMed.
- A. Stuke, C. Kunkel, D. Golze, M. Todorović, J. T. Margraf, K. Reuter, P. Rinke and H. Oberhofer, Sci. Data, 2020, 7, 58 CrossRef CAS PubMed.
- B. Olsthoorn, R. M. Geilhufe, S. S. Borysov and A. V. Balatsky, Adv. Quantum Technol., 2019, 2, 1900023 CrossRef.
- R. Gomez-Bombarelli, J. Aguilera-Iparraguirre, T. Hirzel, D. Duvenaud, D. Maclaurin, M. Blood-Forsythe, H. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, W. Huang, I. Seong, M. Baldo and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1128 CrossRef CAS PubMed.
- C. F. Perkinson, D. P. Tabor, M. Einzinger, D. Sheberla, H. Utzat, T.-A. Lin, D. N. Congreve, M. G. Bawendi, A. Aspuru-Guzik and M. A. Baldo, J. Chem. Phys., 2019, 151, 121102 CrossRef PubMed.
- R. Grotjahn, T. M. Maier, J. Michl and M. Kaupp, J. Chem. Theory Comput., 2017, 13, 4984–4996 CrossRef CAS PubMed.
- D. Padula, Ö. H. Omar, T. Nematiaram and A. Troisi, Energy Environ. Sci., 2019, 12, 2412–2416 RSC.
- O. H. Omar, M. del Cueto, T. Nematiaram and A. Troisi, J. Mater. Chem. C, 2021, 9, 13557–13583 RSC.
- K. Zhao, O. H. Omar, T. Nematiaram, D. Padula and A. Troisi, J. Mater. Chem. C, 2021, 9, 3324–3333 RSC.
- X. Wang, S. Gao, M. Zhao and N. Marom, Phys. Rev. Res., 2022, 4, 033147 CrossRef CAS.
- O. H. Omar, X. Xie, A. Troisi and D. Padula, J. Am. Chem. Soc., 2023, 145, 19790–19799 CrossRef CAS PubMed.
- O. D. Jurchescu, D. A. Mourey, S. Subramanian, S. R. Parkin, B. M. Vogel, J. E. Anthony, T. N. Jackson and D. J. Gundlach, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 80, 085201 CrossRef.
- A. Khasbaatar, Z. Xu, J.-H. Lee, G. Campillo-Alvarado, C. Hwang, B. N. Onusaitis and Y. Diao, Chem. Rev., 2023, 123, 8395–8487 CrossRef CAS PubMed.
- Y. Diao, K. M. Lenn, W.-Y. Lee, M. A. Blood-Forsythe, J. Xu, Y. Mao, Y. Kim, J. A. Reinspach, S. Park, A. Aspuru-Guzik, G. Xue, P. Clancy, Z. Bao and S. C. B. Mannsfeld, J. Am. Chem. Soc., 2014, 136, 17046–17057 CrossRef CAS PubMed.
- R. Tom, S. Gao, Y. Yang, K. Zhao, I. Bier, E. A. Buchanan, A. Zaykov, Z. Havlas, J. Michl and N. Marom, Chem. Mater., 2023, 35, 1373–1386 CrossRef CAS PubMed.
- M. Rohlfing and S. G. Louie, Phys. Rev. B:Condens. Matter Mater. Phys., 2000, 62, 4927–4944 CrossRef CAS.
- S. Sharifzadeh, J. Phys.: Condens. Matter, 2018, 30, 153002 CrossRef PubMed.
- X. Blase, I. Duchemin and D. Jacquemin, Chem. Soc. Rev., 2018, 47, 1022–1043 RSC.
- M. Bonacci, J. Qiao, N. Spallanzani, A. Marrazzo, G. Pizzi, E. Molinari, D. Varsano, A. Ferretti and D. Prezzi, npj Comput. Mater., 2023, 9, 74 CrossRef.
- X. Blase, I. Duchemin, D. Jacquemin and P.-F. Loos, J. Phys. Chem. Lett., 2020, 11, 7371–7382 CrossRef CAS PubMed.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Jom, 2013, 65, 1501–1509 CrossRef CAS.
- P. Xu, X. Ji, M. Li and W. Lu, npj Comput. Mater., 2023, 9, 42 CrossRef.
- M. C. Sorkun, S. Astruc, J. V. A. Koelman and S. Er, npj Comput. Mater., 2020, 6, 106 CrossRef.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- F. Brockherde, L. Vogt, L. Li, M. E. Tuckerman, K. Burke and K.-R. Müller, Nat. Commun., 2017, 8, 872 CrossRef PubMed.
- G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys.: Mater., 2019, 2, 032001 CAS.
- H. Li, Z. Wang, N. Zou, M. Ye, R. Xu, X. Gong, W. Duan and Y. Xu, Nat. Comput. Sci., 2022, 2, 367–377 CrossRef PubMed.
- B. Huang, G. F. von Rudorff and O. A. von Lilienfeld, Science, 2023, 381, 170–175 CrossRef CAS PubMed.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge, et al. , npj Comput. Mater., 2022, 8, 59 CrossRef.
- V. Bhat, B. Ganapathysubramanian and C. Risko, J. Phys. Chem. Lett., 2024, 15, 7206–7213 CrossRef CAS PubMed.
- D. M. Packwood, Y. Kaneko, D. Ikeda and M. Ohno, Adv. Theory Simul., 2023, 6, 2300159 CrossRef CAS.
- K. Ghosh, A. Stuke, M. Todorović, P. B. Jørgensen, M. N. Schmidt, A. Vehtari and P. Rinke, Adv. Sci., 2019, 6, 1801367 CrossRef PubMed.
- K. Singh, J. Münchmeyer, L. Weber, U. Leser and A. Bande, J. Chem. Theory Comput., 2022, 18, 4408–4417 CrossRef CAS PubMed.
- A. Fediai, P. Reiser, J. Peña, P. Friederich and W. Wenzel, Sci. Data, 2023, 10, 581 CrossRef CAS PubMed.
- M. J. van Setten, F. Caruso, S. Sharifzadeh, X. Ren, M. Scheffler, F. Liu, J. Lischner, L. Lin, J. R. Deslippe and S. G. Louie, et al. , J. Chem. Theor. Comput., 2015, 11, 5665–5687 CrossRef CAS PubMed.
- T. Biswas and A. K. Singh, arXiv, 2024, preprint, arXiv:2401.17831, DOI:10.48550/arXiv.2401.17831.
- C. Venturella, C. Hillenbrand, J. Li and T. Zhu, J. Chem. Theory Comput., 2024, 20, 143–154 CrossRef CAS PubMed.
- O. Çaylak and B. Baumeier, J. Chem. Theory Comput., 2021, 17, 4891–4900 CrossRef PubMed.
- X. Dong, E. Gull and L. Wang, Phys. Rev. B, 2024, 109, 075112 CrossRef CAS.
- B. Hou, J. Wu and D. Y. Qiu, Nat. Commun., 2024, 15, 9481 CrossRef CAS PubMed.
- S. Gao, X. Liu, Y. Luo, X. Wang, K. Zhao, V. Chang, B. Schatschneider and N. Marom, Sci. Data, 2025, 12, 679 CrossRef PubMed.
- J. Wu, W. Pisula and K. Müllen, Chem. Rev., 2007, 107, 718–747 CrossRef CAS PubMed.
- J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452–483 CrossRef CAS PubMed.
- J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048 CrossRef CAS PubMed.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS PubMed.
- L. R. Weiss, S. L. Bayliss, F. Kraffert, K. J. Thorley, J. E. Anthony, R. Bittl, R. H. Friend, A. Rao, N. C. Greenham and J. Behrends, Nat. Phys., 2017, 13, 176–181 Search PubMed.
- H. E. Katz and J. Huang, Annu. Rev. Mater. Res., 2009, 39, 71–92 CrossRef CAS.
- J.-L. Brédas, J. E. Norton, J. Cornil and V. Coropceanu, Accounts Chem. Res., 2009, 42, 1691–1699 CrossRef PubMed.
- C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267 CrossRef CAS PubMed.
- X. Liu, X. Wang, S. Gao, V. Chang, R. Tom, M. Yu, L. M. Ghiringhelli and N. Marom, npj Comput. Mater., 2022, 8, 70 CrossRef.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- T. A. R. Purcell, M. Scheffler and L. M. Ghiringhelli, J. Chem. Phys., 2023, 159, 114110 CrossRef CAS PubMed.
- G. Cao, et al. , Phys. Rev. Mater., 2020, 4, 034204 CrossRef CAS.
- C. J. Bartel, et al. , Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed.
- M. Andersen, S. V. Levchenko, M. Scheffler and K. Reuter, ACS Catal., 2019, 9, 2752–2759 CrossRef CAS.
- C. J. Bartel, et al. , Nat. Commun., 2018, 9, 4168 CrossRef PubMed.
- L. Foppa, et al. , MRS Bull., 2021, 46, 1016–1026 CrossRef CAS PubMed.
- G. L. Hart, T. Mueller, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2021, 6, 730–755 CrossRef.
- J. Peng, D. Schwalbe-Koda, K. Akkiraju, T. Xie, L. Giordano, Y. Yu, C. J. Eom, J. R. Lunger, D. J. Zheng and R. R. Rao, et al. , Nat. Rev. Mater., 2022, 7, 991–1009 CrossRef.
- Y. Luo, M. Li, H. Yuan, H. Liu and Y. Fang, npj Comput. Mater., 2023, 9, 4 CrossRef.
- Z. Song, X. Wang, F. Liu, Q. Zhou, W.-J. Yin, H. Wu, W. Deng and J. Wang, Mater. Horiz., 2023, 10, 1651–1660 RSC.
- Z.-K. Han, D. Sarker, R. Ouyang, A. Mazheika, Y. Gao and S. V. Levchenko, Nat. Commun., 2021, 12, 1833 CrossRef CAS PubMed.
- N. Hoffmann, T. F. Cerqueira, J. Schmidt and M. A. Marques, npj Comput. Mater., 2022, 8, 150 CrossRef CAS.
- Z. Guo, S. Hu, Z.-K. Han and R. Ouyang, J. Chem. Theory Comput., 2022, 18, 4945–4951 CrossRef CAS PubMed.
- B. Ma, X. Wu, C. Zhao, C. Lin, M. Gao, B. Sa and Z. Sun, npj Comput. Mater., 2023, 9, 229 CrossRef CAS.
- L.-H. Mou, T. Han, P. E. S. Smith, E. Sharman and J. Jiang, Adv. Sci., 2023, 10, 2301020 CrossRef CAS PubMed.
- C. Ren, Q. Li, C. Ling and J. Wang, J. Am. Chem. Soc., 2023, 145, 28276–28283 CrossRef CAS PubMed.
- S.-H. Oh, S.-H. Yoo and W. Jang, npj Comput. Mater., 2024, 10, 166 CrossRef CAS.
- R. Khatua, B. Das and A. Mondal, ACS Appl. Mater. Interfaces, 2024, 16, 57467–57480 CrossRef CAS PubMed.
- S. Tian, K. Zhou, W. Yin and Y. Liu, Nat. Commun., 2024, 15, 6977 CrossRef CAS PubMed.
- R. Jacobs, J. Liu, H. Abernathy and D. Morgan, Adv. Energy Mater., 2024, 14, 2303684 CrossRef CAS.
- H. Wang, R. Ouyang, W. Chen and A. Pasquarello, J. Am. Chem. Soc., 2024, 146, 17636–17645 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- C. L. Hall, I. Andrusenko, J. Potticary, S. Gao, X. Liu, W. Schmidt, N. Marom, E. Mugnaioli, M. Gemmi and S. R. Hall, ChemPhysChem, 2021, 22, 1631–1637 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- X. Wang, X. Liu, R. Tom, C. Cook, B. Schatschneider and N. Marom, J. Phys. Chem. C, 2019, 123, 5890–5899 CrossRef CAS.
- C. Schober, K. Reuter and H. Oberhofer, J. Chem. Phys., 2016, 144, 054103 CrossRef PubMed.
- H. Huo and M. Rupp, Mach. learn.: sci. technol., 2022, 3, 045017 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger and A. G. Wilson, Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2018, pp. 7587–7597 Search PubMed.
- Y. Wang, N. Wagner and J. M. Rondinelli, MRS Commun., 2019, 9, 793–805 CrossRef CAS.
- S. Ramasesha, I. Albert and B. Sinha, Mol. Phys., 1991, 72, 537–547 CrossRef CAS.
- R. Coffman and D. S. McClure, Can. J. Chem., 1958, 36, 48–58 CrossRef CAS.
- P. Puschnig, C. Ambrosch-Draxl, G. Heimel, E. Zojer, R. Resel, G. Leising, M. Kriechbaum and W. Graupner, Synth. Met., 2001, 116, 327–331 CrossRef CAS.
- Y. Gondo, J. Chem. Phys., 1964, 41, 3928–3938 CrossRef CAS.
- B. Freiermuth, S. Gerber, A. Riesen, J. Wirz and M. Zehnder, J. Am. Chem. Soc., 1990, 112, 738–744 CrossRef CAS.
- A. Endo, K. Sato, K. Yoshimura, T. Kai, A. Kawada, H. Miyazaki and C. Adachi, Appl. Phys. Lett., 2011, 98, year CrossRef.
- X. Cai, Z. Qiao, M. Li, X. Wu, Y. He, X. Jiang, Y. Cao and S.-J. Su, Angew. Chem., Int. Ed., 2019, 58, 13522–13531 CrossRef CAS PubMed.
- L. Zhan, Z. Chen, S. Gong, Y. Xiang, F. Ni, X. Zeng, G. Xie and C. Yang, Angew. Chem., 2019, 131, 17815–17819 CrossRef.
- M. Scheidgen, L. Himanen, A. N. Ladines, D. Sikter, M. Nakhaee, Á. Fekete, T. Chang, A. Golparvar, J. A. Márquez, S. Brockhauser, S. Brückner, L. M. Ghiringhelli, F. Dietrich, D. Lehmberg, T. Denell, A. Albino, H. Näsström, S. Shabih, F. Dobener, M. Kühbach, R. Mozumder, J. F. Rudzinski, N. Daelman, J. M. Pizarro, M. Kuban, C. Salazar, P. Ondračka, H.-J. Bungartz and C. Draxl, J. Open Source Softw., 2023, 8, 5388 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00396a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |