Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Feature vectorization of microphase-separated structures in polymeric materials using dissipative particle dynamics and persistent homology for machine learning applications†
Yukito
Higashi
a,
Koji
Okuwaki
 bc,
Yuji
Mochizuki
bc,
Yuji
Mochizuki
 bd,
Tsuyohiko
Fujigaya
bd,
Tsuyohiko
Fujigaya
 *aef and
Koichiro
Kato
*aef and
Koichiro
Kato
 *ae
*ae
aDepartment of Applied Chemistry, Graduate School of Engineering, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan. E-mail: fujigaya.tsuyohiko.948@m.kyushu-u.ac.jp; kato.koichiro.957@m.kyushu-u.ac.jp
bDepartment of Chemistry and Research Center for Smart Molecules, Faculty of Science, Rikkyo University, 3-34-1 Nishi-ikebukuro, Toshima-ku, Tokyo 171-8501, Japan
cJSOL Corporation, KUDAN-KAIKAN TERRACE, 1-6-5 Kudan-minami, Chiyoda-ku, Tokyo 102-0074, Japan
dInstitute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan
eCenter for Molecular Systems (CMS), Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
fInternational Institute for Carbon-Neutral Energy Research (WPI-I2CNER), Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
First published on 2nd May 2025
Abstract
Recently, materials informatics (MI) has gained attention as an efficient approach for materials development. However, its application to polymers has been limited owing to the complexity and significance of the higher-order structures unique to these materials. This study focuses on microphase-separated structures, among the higher-order structures, as they influence many functional polymeric materials that support modern society. To implement MI that accounts for specific higher-order structures, such as microphase-separated structures, these structures must be quantified and converted into features. This approach addresses a gap in current materials informatics, in which traditional methods do not adequately account for the complex structures of polymers. Persistent homology (PH), a topological data analysis method, was used to extract features from the microphase-separated structures of polymeric materials. A coarse-grained simulation method known as dissipative particle dynamics (DPD) was used to generate the microphase-separated structures for PH analysis. The method was validated using electrolyte membranes for fuel cells, where microphase-separated structures are critical. Topological feature extraction was successfully performed on Nafion™ and its analogs, Aquivion® and Flemion™. Additionally, the correlation between the extracted features and proton conductivity was analyzed using unsupervised machine learning, which indicated that these features can be used to predict proton conductivity. The combination of DPD and PH can effectively convert microphase-separated structures into features. This method may be applicable to a wide range of polymeric materials influenced by microphase-separated structures, as it is not limited to proton exchange membranes or proton conductivity. This research marks a significant step toward advancing polymer informatics by incorporating the microphase-separated structures of polymers.
1. Introduction
Materials informatics (MI) has recently received considerable attention owing to its ability to predict various material properties based on either experimental or calculated materials data.1 MI has the potential to replace conventional material development, which often involves labor-intensive synthesis and measurements.2 The application of MI to polymeric materials has been limited despite many successful applications of MI for inorganic materials and small molecules.3,4 One of the reasons for this is that the properties of polymeric materials depend on their monomer structure and their higher-order structures, such as microphase-separated structures. For certain properties (glass transition temperature, band gap, dielectric constant, gas permeability, etc.), monomer-based features can provide acceptable prediction accuracy.5,6 Although several attempts have been made to predict properties by considering experimental conditions and other factors as surrogates for higher-order structures,5,7–9 a new methodology for predicting the properties of polymeric materials based on higher-order structures is needed.Persistent homology (PH)10–12 is a topological data analysis method that can extract features from complex, high-dimensional data. PH has recently been used in materials research to analyze complex structures, such as silica, metals, proteins, and polymer melts.13–21 In this study, we focused specifically on microphase-separated structures as the higher-order structures of interest. To apply PH to these structures, data representing microphase-separated structures must be generated and analyzed; the data can be efficiently obtained via simulations. Simulations of polymeric materials range from atomic-scale approaches such as classical molecular dynamics (MD) methods to mesoscale techniques such as coarse-grained (CG) simulations. In general, exploring microphase-separated structures in atomic-scale simulations over long periods and distances is computationally expensive, even with the most advanced computers.22 By contrast, CG simulations, which include coarse-grained molecular dynamics (CGMD), self-consistent mean field theory (SCF theory),23–25 and dissipative particle dynamics (DPD),26–28 offer a computationally efficient approach to studying these structures.
Proton exchange membranes (PEMs) are an important class of materials strongly influenced by microphase-separated structures. PEMs, such as perfluorosulfonic acid (PFSA)-based polymers, including Nafion™,29 are crucial for proton exchange membrane fuel cells (PEMFCs) and play a vital role in the transition to a hydrogen-based, low-carbon energy society. Despite their importance, few studies have explored PEM materials using MI, and none have considered higher-order structures,30,31 highlighting an opportunity for further development. Extensive experimental data are available for these materials,32–37 and CG simulations38 have been previously used to investigate their phase-separated structures and properties. Among the three coarse-grained simulation methods, CGMD is advantageous for analyzing detailed nanoscale behavior, while SCF theory excels in equilibrium state analysis and, in its dynamic form, can handle time-dependent processes. However, considering the balance of computational cost, ease of parameter determination, and the ability of DPD to effectively represent dynamic processes and large-scale structures, this study focuses on DPD. DPD simulations have been previously used to investigate their microphase-separated structures and properties.39–48 In these simulations, particle interactions are represented by the Flory–Huggins χ parameter,27 typically estimated using empirical methods based on contact energy49 or solubility parameters.50–52 However, the χ parameter calculated using empirical molecular mechanics (χMM) does not account for complex quantum mechanical effects, such as hydrogen bonding and charge transfer. Consequently, χMM may not suffice to represent the behavior of water-cluster networks. In Nafion™ and other PEMs, water–water and water–polymer interactions impact the behavior of phase-separated structures with water.
In this study, we unprecedentedly applied PH to CG particle data generated by DPD. We used the fragment molecular orbital (FMO) method,53,54 a quantum mechanical approach, to evaluate the χ parameter (χFMO)55–57 to accurately represent the behavior of water-cluster networks in Nafion™ and other PEMs. After examining the effects of quantum mechanics on the χ parameter and the resulting phase-separated structures, we performed feature extraction using PH. For comparison purposes, we also included Aquivion®34 and Flemion™.58 Furthermore, we demonstrated the effectiveness of the features derived from PH to predict proton conductivity using unsupervised machine learning.
2. Methods and models
In previous studies,39,56 Nafion™ was coarse-grained by dividing it into three parts (Fig. 1): the main chain (A), root of the side chain (B), and end of the side chain (C). In this study, we followed the same segmentation approach for Nafion™ as that used previously. For Aquivion® and Flemion™, we applied a segmentation approach based on the segmentation of Nafion™, as shown in Fig. 1. Prior to calculating the χ parameters, structural optimization calculations were performed with Gaussian16 (ref. 59) for each segment using B97D,60 which is a functional with dispersion correction and a 6-31G(d,p)61 basis set. The χ parameters in the polymer and water segment (W, corresponding to four water molecules) were then calculated using the FMO-based chi-parameter estimation workflow system (FCEWS).55,57 In FCEWS, we estimated the interaction energy by performing parallelized FMO-MP2 calculations62–64 with the 6-31G(d′) basis set65 using the ABINIT-MP program.54,66Driving forces fi in DPD simulations comprise four forces (eqn (1)): the conservative force FCij, dissipative force FDij representing hydrodynamic drag, random force FRij representing thermal fluctuation, and harmonic force FSij, which is calculated for particles directly connected with spring bonds.67
 | (1) |
F C ij imposes a soft repulsion action according to eqn (2), where aij is the repulsion force between particles i and j, rc is a cutoff radius, and the related definitions are rij = rj − ri and nij = rij/|rij|.
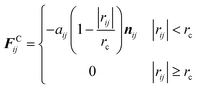 | (2) |
A uniform cutoff distance of rc = 1 was applied for all pairwise interactions, which is a standard setting in DPD simulations.
The repulsion parameters between different types of particles correspond to the mutual solubility provided by the χ parameter set. When the density ρ is assumed to be 3, a linear relationship with χ is usually established as expressed using eqn (3).
| aij = aii + 3.27χ | (3) |
In this study, the self-interaction parameter was set to aii = 25. The dissipative force (FDij) and random force (FRij) are represented by
 | (4) |
 | (5) |
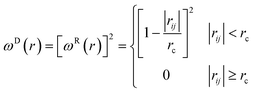 | (6) |
F S ij is estimated using eqn (7), where C is the spring constant and r0 is the equilibrium length.
| FSij = −C(|rij| − r0)nij | (7) |
As DPD was used in this study to generate microphase-separated structure data at a low computational cost, long-range electrostatic interactions were not explicitly considered. In high-ionic-strength environments such as hydrated electrolyte membranes, Coulomb interactions are effectively screened, leading to predominantly short-range interactions. As discussed in previous studies,68 the Donnan approximation describes this screening effect, explaining how electrostatic interactions become suppressed at high ionic strengths. Mao et al. also noted that incorporating explicit electrostatic interactions in DPD simulations presents technical challenges due to the soft-core nature of the model, making effective short-range potentials a widely used alternative.68 For PFSA-based polymers, microphase-separated structures that are consistent with experimental observations can still be obtained without explicitly including long-range electrostatic interactions.69–71 This approach has also been shown to effectively handle lipids72–75 and charged side chains in peptides, such as chignolin76 and peptoids,77 demonstrating its applicability across various soft-matter systems. By omitting long-range electrostatic interactions, the method simplifies parameterization while maintaining broad applicability. While electrostatic interactions play a crucial role in ion conduction, this study focuses on analyzing microphase-separated structures rather than directly computing ion conductivity. Importantly, the persistent homology (PH)-based framework introduced here remains applicable even if explicit electrostatic interactions are incorporated in future models, making it adaptable for extended studies. Given the importance of computational efficiency in materials informatics (MI), this approach was considered appropriate for the present study.
DPD simulations of Nafion™, Aquivion®, and Flemion™ were performed using the calculated χFMO parameters. Calculation conditions were set to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps (at least 700 ns), a particle density of ρ = 3, and a cell size of 32Rc (Rc is the DPD unit length and corresponds to 0.71 nm), corresponding to 22.7 nm. To model polymer chain connectivity and rigidity, we followed the approach described by Vishnyakov et al.,78 incorporating both bond stretching and torsional rigidity. The primary bond interaction was described using eqn (7) with a spring constant of C = 160 and an equilibrium bond length of r0 = 0.86Rc. This equilibrium bond length was determined based on the DPD volume constraint, where each DPD particle occupies a volume of Rc3/3, leading to a particle radius of 0.43Rc and an expected equilibrium distance of 0.86Rc when uniformly distributed. To introduce torsional rigidity, we applied a secondary spring to second-nearest-neighbor beads with a spring constant of C = 80 and an equilibrium bond length of r0 = 1.72Rc. This method effectively restricts excessive chain bending and enhances backbone stiffness, which is particularly relevant for PFSA polymers, known for their high backbone rigidity due to fluorine-rich main chains. Simulations were conducted for water contents ranging between 10 and 30% in 2% increments. All the DPD simulations were performed using the COGNAC program.79,80 The polymer models used are shown in Fig. S1;† only Aquivion® has a different equivalent weight (EW). For a detailed analysis of DPD, the snapshot, water density distribution, radial distribution function, small-angle scattering pattern, and water diffusion coefficient were calculated using J-OCTA.79,80 The scattering pattern was calculated via the Fourier transform of the radial distribution function, and the diffusion coefficient was evaluated based on the mean-square displacement of CG particles using the following relationship:
000 steps (at least 700 ns), a particle density of ρ = 3, and a cell size of 32Rc (Rc is the DPD unit length and corresponds to 0.71 nm), corresponding to 22.7 nm. To model polymer chain connectivity and rigidity, we followed the approach described by Vishnyakov et al.,78 incorporating both bond stretching and torsional rigidity. The primary bond interaction was described using eqn (7) with a spring constant of C = 160 and an equilibrium bond length of r0 = 0.86Rc. This equilibrium bond length was determined based on the DPD volume constraint, where each DPD particle occupies a volume of Rc3/3, leading to a particle radius of 0.43Rc and an expected equilibrium distance of 0.86Rc when uniformly distributed. To introduce torsional rigidity, we applied a secondary spring to second-nearest-neighbor beads with a spring constant of C = 80 and an equilibrium bond length of r0 = 1.72Rc. This method effectively restricts excessive chain bending and enhances backbone stiffness, which is particularly relevant for PFSA polymers, known for their high backbone rigidity due to fluorine-rich main chains. Simulations were conducted for water contents ranging between 10 and 30% in 2% increments. All the DPD simulations were performed using the COGNAC program.79,80 The polymer models used are shown in Fig. S1;† only Aquivion® has a different equivalent weight (EW). For a detailed analysis of DPD, the snapshot, water density distribution, radial distribution function, small-angle scattering pattern, and water diffusion coefficient were calculated using J-OCTA.79,80 The scattering pattern was calculated via the Fourier transform of the radial distribution function, and the diffusion coefficient was evaluated based on the mean-square displacement of CG particles using the following relationship:
| (r(t) − r(0))2 = 6Dt | (8) |
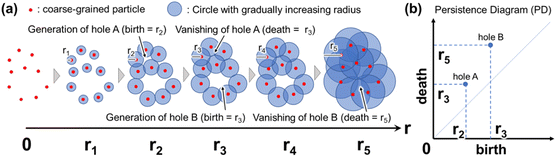
An overview of PH is shown in Fig. 2. In PH, a circle (or sphere) centered at each data point is first considered. Specifically, the coordinates of individual atoms, obtained using MD, are often regarded as data points in the context of PH in materials research. Subsequently, circles are centered on the individual atoms, and their radii gradually and simultaneously increase. When a certain radius is reached (e.g., r = r2 in Fig. 2), the circles intersect, and a hole (or void) is generated at the center by connecting multiple circles in a ring shape. As the radius of each circle increases further, the hole at the center of the ring becomes smaller and eventually disappears (e.g., r = r3 in Fig. 2). The radius at which multiple circles connect in a ring, resulting in the formation of a hole, is referred to as the birth radius. Conversely, the radius at which the hole disappears is known as the death radius. If the ring created by the data points is a regular polygon, the birth radius is equal to the radius of the inscribed circle, and the death radius is equal to the radius of the circumscribed circle (see Fig. S2†). The persistence diagram (PD) plots the birth radius on the horizontal axis and the death radius on the vertical axis (Fig. 2(b)). The concepts of birth radius and death radius are sometimes expressed as birth time and death time, respectively. Each point on the PD corresponds to a ring formed by data points, such as atomic coordinates. The position of each point on the PD represents the persistence (birth and death) of the hole situated at the center of the ring. The farther the points on the PD are from the diagonal, the longer the persistence of the hole. Therefore, the presence of points situated away from the diagonal line on the PD suggests the existence of characteristic features within the data points. Fig. S3† further illustrates how birth and death radii correspond to geometric structures in persistent homology analysis. The persistence diagram (left) represents a distribution of topological features, where each point corresponds to a specific birth–death pair. The right panels show inverse analyses of representative points in the persistence diagram, providing insight into the spatial structures they describe. Features with a smaller birth radius correspond to closely spaced points, while a similar death radius indicates that the overall hole size remains comparable. This suggests that persistent features with different birth values can represent varying levels of local structural connectivity while maintaining similar large-scale topological characteristics. In three-dimensional space, persistent homology is computed using an alpha complex, which is a subcomplex of the Delaunay triangulation. This method allows for a more precise representation of topological features in point clouds, ensuring that the birth and death radii accurately reflect the geometric and connectivity properties of the structure. By leveraging this approach, our analysis effectively captures the hierarchical organization of water clusters in hydrated polymer membranes.
The water particle coordinates were then extracted from the phase-separated structure obtained using DPD, and a PD was calculated. The PD is a typical plot obtained by PH analysis, showing the relationship between birth and death radii of holes at the center of rings, and is composed of given data points. An inverse analysis81 was also conducted to determine the correspondence between each point on the obtained PD and the individual rings within the phase-separated structure. In addition, to transform the PD into a vector suitable for machine learning, the PD was converted into a persistence image (PI).82 The PI was obtained by assigning weights to each point on the PD based on its distance from the diagonal. Specifically, the PI ρ(x, y) was obtained using the following equation that incorporates the information of each point on the PD:
 | (9) |
| w(bk, dk) = arctan(C(bk − dk)p) | (10) |
3. Results and discussion
3.1 χ parameter evaluation
Table 1 lists the χFMO values of Nafion™, Aquivion®, and Flemion™ and χMM of Nafion™ from ref. 39, where A, B, C, and W represent the CG segments of the main chain, root and end of the side chain, and water, respectively. The χ parameters between segments with identical structures have the same values (for example, A–W, B–W, and A–B). The results of the Nafion™ χFMO are comparable to those reported in a previous study.56 The absolute value of χFMO is higher than that of χMM, because quantum chemical effects, such as hydrogen bonding and charge transfer, were considered in χFMO. For A–C, A–W, B–C, and B–W in χMM and χFMO, the values are positive, indicating repulsion between the segments. It is reasonable that the hydrophobic fluorinated segments (i.e., A and B) exhibit clear repulsion to the hydrophilic water segment (i.e., W) and represent large χFMO values (>20). Conversely, negative values for A–B and C–W indicate the attractive interactions between the segments. Specifically, C–W has a larger absolute value than that of A–B, indicating a greater interaction in C–W than that in A–B. The order of χFMO for C–W is Nafion™ > Aquivion® > Flemion™. The trend can be explained as follows: (1) the electron-withdrawing property of the fluoroalkyl chain increases as its length increases, and C in Nafion™ has a stronger electronegativity than C in Aquivion®, leading to the larger absolute χFMO value; and (2) the lower polarity of the carboxyl group in Flemion™ compared with that of the sulfonic groups in Nafion™ and Aquivion® yields a lower affinity between C and W.| Label | Nafion™ χMM | Nafion™ χFMO | Aquivion χFMO | Flemion χFMO |
|---|---|---|---|---|
| A–B | 0.02 | −0.256 | −0.112 | |
| A–C | 3.11 | 5.472 | 7.285 | 1.738 |
| A–W | 5.79 | 20.378 | ||
| B–C | 1.37 | 5.837 | 7.813 | 2.112 |
| B–W | 4.90 | 21.356 | 27.647 | |
| C–W | −2.79 | −7.885 | −3.275 | −2.622 |
3.2 Dissipative particle dynamics simulations
Fig. 3(a–d) show the snapshots and water density distributions in Nafion™ as a function of the water content. The water density distribution is shown on the isosurface, in which the regions with a fraction of water particles ≥40% are indicated in yellow. For χFMO, at a water content of 10% (Fig. 3(a)), the structure had small water clusters that were uniformly distributed, but as the water content increased to 20–30% (Fig. 3(b and c)), these small water clusters connected, forming a large water cluster network. The water density distribution of DPD at 20% water content (Fig. 3(b)) closely resembled that of the cryo three-dimensional (3D) transmission electron microscopy image of Nafion™ reported by Allen et al.89 The changes in the phase-separated structure of Nafion™ with respect to the water content, obtained in this study, were similar to those reported in previous studies using χFMO.56 By contrast, for χMM, no clear phase-separated structure was observed under our simulation conditions (Fig. 3(d)). However, in ref. 39, a phase-separated structure was observed at 20 vol% water content using χMM, which differs from our findings. This discrepancy can be attributed to multiple factors. While the absolute value of χMM is smaller than that of χFMO, differences in polymer chain flexibility, system size, and the number of polymer repeat units compared to ref. 39 may also contribute to the observed differences. In ref. 39, a lower bond stiffness and shorter polymer repeat units (5 units) were used, which may have facilitated phase separation by allowing greater polymer mobility. In contrast, our simulations employed a greater number of polymer repeat units (8 units) and a stiffer backbone by introducing stronger bond forces and additional second-neighbor bonds. Specifically, we used a primary bond with a stiffness of 160 and a secondary bond with a stiffness of 80 to introduce torsional rigidity, following the approach described by Vishnyakov et al.78 This enhanced polymer stiffness may have restricted polymer flexibility and suppressed the formation of percolated water networks, contributing to the differences observed between our results and those reported in ref. 39. Additionally, PFSA polymers, such as Nafion™, exhibit high backbone rigidity due to the presence of fluorine atoms along the main chain. To better represent this characteristic, our model incorporated enhanced polymer stiffness, which may have further influenced phase separation behavior. These findings indicate that when a model with higher backbone rigidity, more representative of PFSA polymers, is used, χFMO successfully reproduces a microphase-separated morphology, whereas χMM does not. This suggests that χFMO's ability to account for stronger polymer–water interactions contributes to its effectiveness in simulating rigid polymer systems. One key reason for this effectiveness is that χFMO incorporates quantum mechanical effects, such as hydrogen bonding and charge transfer, which play a crucial role in accurately capturing polymer–water interactions. These effects are particularly important in PFSA-based membranes, where the interplay between water clustering and polymer–water affinity significantly influences the microphase-separated morphology. By capturing these interactions more accurately, χFMO enables the reliable prediction of phase separation in systems where electrostatic and hydrogen-bonding interactions are dominant.Fig. 3(e and f) show the snapshots and water density distributions for Aquivion® and Flemion™ at 20% water content. Water channels are well developed in Aquivion®, whereas large spherical water clusters are formed in Flemion™. These differences may arise from the differences in χ between the side chain end (C) and the other parts (A, B, and W) in Nafion™, Aquivion®, and Flemion™. These differences are thought to depend mainly on whether the side chain ends are sulfonic or carboxylic acids. Larger χFMO values for A–C were obtained in Nafion™ and larger absolute values for C–W were obtained in Aquivion® compared to Flemion™ (see Table 1); this finding indicates stronger attractions between the side-chain ends (C) and water (W). Additionally, the repulsion between the side-chain ends (C) is sufficient to cause the formation of continuous water channels in Nafion™ and Aquivion®, while the weak attraction (C–W) and repulsion (A–C) in Flemion™ result in its ambiguous separation structure. For Aquivion® and Flemion™, structures similar to those in Fig. 3 were observed at different water contents (Fig. S4 and S5†).
The small-angle scattering patterns obtained from the DPD structure of Nafion™ at different water contents using χFMO and χMM are shown in Fig. 4(a and b). A peak near 1.0 to 2.5 nm−1 was assigned as an ionomer peak29 originating from the water clusters. For χFMO, the ionomer peaks appear between 1.0 and 2.0 nm−1, and their shape and water content dependencies are similar to those seen in the small-angle X-ray scattering (SAXS) experimental data.34 By contrast, for χMM, the scattering intensity is weaker and the peaks appear on the right side of 2.0 nm−1. Furthermore, the ionomer peaks are almost independent of the water content, which does not match the SAXS experimental data.34 These results support the validity of the χ parameter calculation using the FMO method. The lower q peak (∼11 nm) observed in SAXS experiments corresponds to the characteristic spacing of crystalline polymer domains and remains nearly unchanged with hydration.34 Since this peak primarily reflects the polymer matrix structure rather than the morphology of water channels, it is not directly relevant to the analysis of water diffusivity and proton conductivity. Moreover, accurately reproducing this peak in DPD simulations would require a larger simulation box, making it computationally challenging.
 | ||
| Fig. 4 Water-content-dependent small-angle scattering patterns for Nafion™ obtained from dissipative particle dynamics (DPD) simulations using (a) χFMO and (b) χMM. (c) Water diffusion coefficient obtained from DPD simulations using χFMO and χMM. Experimental values reported in ref. 54 are also plotted. (d) Water diffusion coefficients of Nafion™ (red), Aquivion® (blue), and Flemion™ (green). Values are averages from five DPD simulations. | ||
We also calculated the diffusion coefficient of water in Nafion™ using χFMO and χMM, and the water content dependences are plotted in Fig. 4(c). The plots indicate that the values based on χFMO are closer to the experimental values90 than those based on χMM, particularly at low water contents. Fig. 4(d) shows the water diffusion coefficients for each polymer. The water diffusion coefficients of Nafion™ and Aquivion® increased with increasing water content, whereas that of Flemion™ remained constant. The trend agreed well with the water cluster connectivity discussed above; namely, smaller water clusters were connected to form a larger water cluster network as the water content increased for Nafion™ and Aquivion® (Fig. S4 and S5†); by contrast, for Flemion™, the water cluster size increased with increasing water content, but the clusters remained isolated (Fig. 3). As the water channels developed, water particles moved around the water-cluster network, resulting in large diffusion coefficients. The water diffusion coefficients obtained from DPD simulations followed the order Aquivion® > Nafion™ > Flemion™ at all water contents, consistent with the expected trend based on EW differences. Previous studies have shown that lower EW leads to higher water diffusivity due to increased sulfonic acid group density and enhanced water network connectivity.42 Regarding proton conductivity, experimental data indicate that Nafion™ and Aquivion® exhibit similar proton conductivities under comparable conditions, particularly at the same water uptake, as reported in previous studies.34 In contrast, Flemion™ exhibits lower proton conductivity than Nafion™, which has been attributed to differences in polymer architecture, phase-separated morphology, and water-channel connectivity, all of which influence ion transport efficiency.91–93 Previous studies have shown that ionomers with perfluorocarboxylic acid (PFCA) groups exhibit lower proton conductivity than PFSA ionomers due to the weaker acidity of carboxylate groups and their effect on water network formation.94 For instance, Nafion membranes containing PFCA groups exhibit significantly lower water permeability and moderately reduced proton conductivity compared to their PFSA counterparts. The lower proton conductivity of PFCA-type ionomers has been attributed to the decreased acidity of carboxylate groups, reduced water uptake, and modifications in the phase-separated morphology.95 Given that the Flemion model used in our DPD simulations corresponds to a PFCA-type ionomer, its proton conductivity is expected to be lower than that of Nafion™ and Aquivion®. This aligns with experimental trends, which indicate that the sequence of proton conductivities follows Nafion™ ≈ Aquivion® > Flemion™. While water diffusivity alone does not fully determine proton conductivity, the DPD method used in this study does not explicitly account for electrostatic interactions, making it impossible to directly compute proton conductivity from these simulations. Nevertheless, our results demonstrate that key structural properties, including SAXS peak positions associated with microphase separation and water diffusivity, are in good agreement with previous studies. This indicates that the microphase-separated morphology captured by our DPD simulations is physically meaningful. Given this consistency, we propose that persistent homology (PH)-based feature extraction of microphase-separated structures could provide a pathway for linking structural characteristics to proton conductivity, even though direct calculation of proton transport is beyond the scope of our current model.
3.3 PH analysis
Since the proton conductivity is closely linked to the structure of the water cluster network, we focused on the PH of CG water particles to extract the topological features. The PDs of water in the three polymers with 10, 20, and 30% water content are shown in Fig. 5. In each PD, three characteristic sets of points are observed, and we designated those regions A, B, and C. Region A was observed in all polymers and with all water contents. In region B, many points were also observed; however, as the water content increased, the point density decreased. By contrast, region C was not observed for Flemion™. An inverse analysis of the PD was performed to identify the locations of the CG water particle rings in the DPD corresponding to regions A, B, and C. Fig. 6 shows the inverse analysis results for these regions in the PD for Nafion™ at water contents of 10, 20, and 30% (for the other polymers the water content is 20%, see Fig. S6†). The PD represents the birth and death radii of holes appearing in the data points, and these holes originate from the CG particles distributed in a ring shape. Therefore, each point in the PD can be associated with a ring constructed of CG particles by inverse analysis. Fig. 6 shows that each point in region A corresponds to a small ring sparsely distributed inside the water cluster or channel. Conversely, the points in region B correspond to rings spread over the surface of the water clusters and channels. In terms of changes in water content, an increase in the number of rings can be observed in region A along with the enlargement of the water cluster or channel at increasing water contents. This phenomenon is thought to be due to the increase in the number of CG water particles inside the water cluster or channels. In region B, the presence of rings on the channel surface is emphasized by the development of water channels at increasing water contents (Fig. 6(h)). The formation of thicker channels reduces the surface area, and thus the distribution of rings appears to be sparser. The number of rings also corresponds to the changes in PD intensity. In region C, the corresponding CG water particles are connected to form an elongated ring. This suggests that the elongated ring represents an expanded interface between water and the polymer, which in turn indicates the formation of water channels that influence water diffusion and proton conduction. The absence of a point in region C in Flemion™ (with low proton conductivity) is also consistent with this interpretation. To further illustrate the spatial distribution of persistent features, Fig. S7† provides multiple perspectives of the inverse analysis results for Nafion™ at 20 vol% water content. The gray points represent all CG water particles, while the red, blue, and green points correspond to particles extracted from regions A, B, and C, respectively. This visualization confirms that features in region A are sparsely distributed within the water phase, features in region B are localized at the water–polymer interface, and features in region C form elongated structures indicative of extended water channels. These results highlight how different topological features in the persistence diagram correspond to distinct structural elements within the hydrated polymer membrane.We transformed the PDs into PIs to extract feature vectors representing proton conductivity from microphase-separated structures.82 A PI is a vector smoothed by weighting each point on the PD by its distance from the diagonal. In the PD, points farther away from the diagonal represent more significant features, therefore, the PI emphasizes these points more and can be visualized similarly to the PD. Fig. 7 shows the PIs obtained from each PD in Fig. 5. The color scale of the PI illustrates the distinctive features of the PD, with the darker red shade indicating more prominent characteristics. In Fig. 7, the red regions are positioned in a manner consistent with the arrangement of regions A, B, and C in the PD. Thus, we successfully obtained a vector PI that preserves the characteristics of the PD. Herein, we used PCA83 and UMAP;84 these are unsupervised machine-learning methods used to compress the PI into a three-dimensional coordinate, which allows us to visually and numerically compare the differences in the PIs in the same coordinate system. The PI is a vector whose elements are the counts of data points in each grid when each figure in Fig. 7 is divided into a 128 × 128 grid; because of the nature of the PD, only considering the upper left portion of the diagonal suffices, and the dimension of the PI is 8256. Each PI was first compressed into 32 dimensions using PCA, as the dataset consists of 33 samples, and PCA can reduce dimensionality to at most 33. The cumulative explained variance confirmed that 32 dimensions retained 100% of the variance, ensuring no loss of information in this step. The data were then further compressed into three dimensions using UMAP. The compressions were performed for three polymers with different water contents and plotted in a three-dimensional coordinate system (Fig. 8). Each point in Fig. 8 corresponds to one PI, and a total of 33 PIs are mapped for each of the three polymers with 11 different water contents (10 to 30% in 2% increments). As shown in Fig. 8, the PCA-UMAP 3D representation effectively captures key structural trends related to proton conductivity. Nafion™ and Aquivion® cluster similarly, while Flemion™ forms a distinct group, reflecting their known experimental proton conductivity trends34,93,95 (Nafion™ ≈ Aquivion® > Flemion™). Additionally, within the Nafion™ and Aquivion® clusters, data points shift systematically with increasing water content, consistent with the experimentally observed increase in proton conductivity with water uptake. In contrast, Flemion™ remains largely unchanged, which aligns with previous findings that carboxyl-terminated Flemion™ maintains low proton conductivity regardless of water uptake. We also tested an alternative 2D UMAP projection (Fig. S8†) and found that while the overall distribution trends were similar, the third dimension (PCA_UMAP3) contained additional variations that could be useful in capturing structural differences between polymers. For this reason, we adopted the 3D representation in this study. Because experimental proton conductivity data are not available for every specific water content, a supervised learning approach is not feasible. Instead, we applied unsupervised learning (PCA-UMAP) to uncover meaningful structural patterns in the feature space, independent of explicit conductivity labels. The fact that the resulting 3D representation naturally aligns with known proton conductivity trends validates the effectiveness of the extracted PI-based features. This structural mapping approach has significant implications for polymer screening. By applying the same methodology to new proton-conducting polymers, their structural features can be mapped onto the 3D PCA-UMAP space to estimate their proton conductivity. This provides a novel, data-driven method for predicting and screening high-performance proton-conducting polymers before synthesis, which could accelerate PEM research and development. These findings suggest that PIs of CG water particles serve as robust structural descriptors that effectively encapsulate features related to proton conductivity in microphase-separated structures. Furthermore, this methodology is not limited to PFSA-based polymers. By leveraging quantum chemistry-derived χ parameters, this framework can be extended to other polymeric systems, offering a computationally efficient method to characterize mesoscale structures and their impact on material properties.
 | ||
| Fig. 7 Persistence images (PIs) of (a–c) Nafion™, (d–f) Aquivion®, and (g–i) Flemion™. The water contents are 10 vol% (a, d, g), 20 vol% (b, e and h), and 30 vol% (c, f and i). The color bar represents the persistence image function ρ(x, y), obtained using eqn (9). | ||
 | ||
| Fig. 8 Plots of Nafion™ (red), Aquivion® (blue), and Flemion™ (green) with different water contents in three dimensions. | ||
4. Conclusions
In this study, we developed a method to extract microphase-separated structural features of polymeric materials by integrating DPD and PH, using PEMs (Nafion™, Aquivion®, and Flemion™) as examples. The usefulness of the obtained features was then evaluated using machine learning. First, microphase-separated structures of Nafion™, Aquivion®, and Flemion™ with different water contents were successfully reproduced by DPD simulation, consistent with experimental results. More importantly, we found that the DPD simulations using the χ parameters calculated based on the FMO method55–57 exhibited greater similarity to the experimental SAXS results34 compared with those based on empirical molecular mechanics. The water channels and clusters in the phase-separated structures obtained by DPD were transformed into features using PH, revealing three distinct regions (regions A, B, and C) in the PD. Specifically, region C was identified to contain features associated with elongated water channels through inverse analysis. The expansion of the water channels, which depends on both the water content and polymer type, indicated a strong correlation between region C and proton conductivity. To quantify the features within the PD, the PDs were vectorized, and the resulting PIs were compressed into three dimensions using the unsupervised machine learning methods PCA and UMAP. This approach produced three-dimensional plots that were consistent with the experimental order of proton conductivity.34,95 These results demonstrate the successful extraction of feature vectors from the microphase-separated structures of polymeric materials by integrating DPD and PH. Notably, the present method is not limited to PEMs but is applicable to various functional polymeric materials that form microphase-separated structures. Therefore, we believe these results should promote advancements in polymer informatics using microphase-separated structural features.Data availability
The data supporting the findings of this study, including the full set of DPD input files and simulation parameters, are publicly available in the following GitHub repository: https://github.com/KatoGroup-AppChem-KU/PFSA_Topological_Features_Extraction. A snapshot of the repository has been archived on Zenodo and assigned the following DOI: https://doi.org/10.5281/zenodo.15222535. Additional data and materials can be provided by the corresponding authors upon reasonable request.Author contributions
Yukito Higashi: investigation, writing – original draft. Koji Okuwaki: methodology, software, writing – review and editing. Yuji Mochizuki: conceptualization, writing – review and editing. Tsuyohiko Fujigaya: supervision, writing – review and editing, funding acquisition. Koichiro Kato: conceptualization, supervision, writing – review and editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by KAKENHI Grant number JP23H02027 of the Japan Society for the Promotion of Science (JSPS); the Data Creation and Utilization-Type Material Research and Development Project under Grant number JPMXP112271469 of the MEXT; the “Engineering Research for Pioneering of a New Field” grant provided by the Faculty of Engineering, Kyushu University, Japan. This work was also supported by MEXT as a “Program for Promoting Research on the Supercomputer Fugaku” (Data-Driven Research Methods Development and Materials Innovation Led by Computational Materials Science, JPMXP1020230327) and used computational resources of supercomputer Fugaku provided by the RIKEN Center for Computational Science (Project ID: hp230212). Some of the calculations were also performed using computer resources offered under the category of General Projects by the Research Institute for Information Technology, Kyushu University.References
- A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 053208 CrossRef.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef.
- Z. Wang, Z. Sun, H. Yin, X. Liu, J. Wang, H. Zhao, C. H. Pang, T. Wu, S. Li, Z. Yin and X. F. Yu, Adv. Mater., 2022, 34, e2104113 CrossRef PubMed.
- D. B. Kell, S. Samanta and N. Swainston, Biochem. J., 2020, 477, 4559–4580 CrossRef CAS PubMed.
- L. H. Chen, G. Pilania, R. Batra, T. D. Huan, C. Kim, C. Kuenneth and R. Ramprasad, Mater. Sci. Eng., R, 2021, 144, 100595 CrossRef.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, npj Comput. Mater., 2022, 8, 222 CrossRef CAS.
- C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, J. Phys. Chem. C, 2018, 122, 17575–17585 CrossRef CAS.
- D. J. Audus and J. J. de Pablo, ACS Macro Lett., 2017, 6, 1078–1082 CrossRef CAS PubMed.
- T. Inokuchi, N. Li, K. Morohoshi and N. Arai, Nanoscale, 2018, 10, 16013–16021 RSC.
- H. Edelsbrunner, D. Letscher and A. Zomorodian, Discrete Comput. Geom., 2002, 28, 511–533 CrossRef.
- A. Zomorodian and G. Carlsson, Discrete Comput. Geom., 2005, 33, 249–274 CrossRef.
- N. Otter, M. A. Porter, U. Tillmann, P. Grindrod and H. A. Harrington, EPJ Data Sci., 2017, 6, 17 CrossRef PubMed.
- A. Duman, B. Yilbas, H. Pirim and H. Ali, Coatings, 2017, 7, 139 CrossRef.
- M. Gameiro, Y. Hiraoka, S. Izumi, M. Kramar, K. Mischaikow and V. Nanda, Jpn. J. Ind. Appl. Math., 2014, 32, 1–17 Search PubMed.
- Y. Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue and Y. Nishiura, Proc. Natl. Acad. Sci. U.S.A., 2016, 113, 7035–7040 CrossRef CAS PubMed.
- K. Kato, Y. Maekawa, N. Watanabe, K. Sasaoka and T. Yamamoto, Jpn. J. Appl. Phys., 2020, 59, 7 Search PubMed.
- M. Kimura, I. Obayashi, Y. Takeichi, R. Murao and Y. Hiraoka, Sci. Rep., 2018, 8, 3553 CrossRef PubMed.
- E. Minamitani, T. Shiga, M. Kashiwagi and I. Obayashi, J. Chem. Phys., 2022, 156, 244502 CrossRef CAS PubMed.
- M. Murakami, S. Kohara, N. Kitamura, J. Akola, H. Inoue, A. Hirata, Y. Hiraoka, Y. Onodera, I. Obayashi, J. Kalikka, N. Hirao, T. Musso, A. S. Foster, Y. Idemoto, O. Sakata and Y. Ohishi, Phys. Rev. B, 2019, 99, 045153 CrossRef CAS.
- Y. Shimizu, T. Kurokawa, H. Arai and H. Washizu, Sci. Rep., 2021, 11, 2274 CrossRef CAS PubMed.
- T. Yamada, Y. Suzuki, C. Mitsumata, K. Ono, T. Ueno, I. Obayashi, Y. Hiraoka and M. Kotsugi, Vac. Surf. Sci., 2019, 62, 153–160 CrossRef CAS.
- S. P. O. Danielsen, H. K. Beech, S. Wang, B. M. El-Zaatari, X. Wang, L. Sapir, T. Ouchi, Z. Wang, P. N. Johnson, Y. Hu, D. J. Lundberg, G. Stoychev, S. L. Craig, J. A. Johnson, J. A. Kalow, B. D. Olsen and M. Rubinstein, Chem. Rev., 2021, 121, 5042–5092 CrossRef CAS PubMed.
- J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619–1635 CrossRef CAS.
- J. G. E. M. Fraaije, B. A. C. van Vlimmeren, N. M. Maurits, M. Postma, O. A. Evers, C. Hoffmann, P. Altevogt and G. Goldbeck-Wood, J. Chem. Phys., 1997, 106, 4260–4269 CrossRef CAS.
- R. Hasegawa and M. Doi, Macromolecules, 1997, 30, 3086–3089 CrossRef CAS.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- P. Español and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- A. Kusoglu and A. Z. Weber, Chem. Rev., 2017, 117, 987–1104 CrossRef CAS PubMed.
- H. Tran, K.-H. Shen, S. Shukla, H.-K. Kwon and R. Ramprasad, J. Phys. Chem. C, 2023, 127, 977–986 CrossRef CAS.
- S.-i. Sawada, Y. Sakamoto, K. Funatsu and Y. Maekawa, J. Membr. Sci., 2024, 692, 122169 CrossRef CAS.
- H. G. Haubold, T. Vad, H. Jungbluth and P. Hiller, Electrochim. Acta, 2001, 46, 1559–1563 CrossRef CAS.
- M. Fujimura, T. Hashimoto and H. Kawai, Macromolecules, 1982, 15, 136–144 CrossRef CAS.
- T. Mochizuki, K. Kakinuma, M. Uchida, S. Deki, M. Watanabe and K. Miyatake, ChemSusChem, 2014, 7, 729–733 CrossRef CAS PubMed.
- J. A. Dura, V. S. Murthi, M. Hartman, S. K. Satija and C. F. Majkrzak, Macromolecules, 2009, 42, 4769–4774 CrossRef CAS.
- F. Xu, O. Diat, G. r. Gebel and A. Morin, J. Electrochem. Soc., 2007, 154, B1389 CrossRef CAS.
- G. Gebel, Polymer, 2000, 41, 5829–5838 CrossRef CAS.
- Z. Zhu, X. Luo and S. J. Paddison, Chem. Rev., 2022, 122, 10710–10745 CrossRef CAS PubMed.
- S. Yamamoto and S.-a. Hyodo, Polym. J., 2003, 35, 519–527 CrossRef CAS.
- K. Malek, M. Eikerling, Q. Wang, Z. Liu, S. Otsuka, K. Akizuki and M. Abe, J. Chem. Phys., 2008, 129, 204702 CrossRef PubMed.
- D. Wu, S. J. Paddison and J. A. Elliott, Energy Environ. Sci., 2008, 1, 284–293 RSC.
- G. Dorenbos and Y. Suga, J. Membr. Sci., 2009, 330, 5–20 CrossRef CAS.
- R. Jorn and G. A. Voth, J. Phys. Chem. C, 2012, 116, 10476–10489 CrossRef CAS.
- K. Morohoshi and T. Hayashi, Polymers, 2013, 5, 56–76 CrossRef.
- A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2014, 118, 11353–11364 CrossRef CAS PubMed.
- C. Wang and S. J. Paddison, Soft Matter, 2014, 10, 819–830 RSC.
- E. O. Johansson, T. Yamada, B. Sundén and J. L. Yuan, Int. J. Hydrogen Energy, 2015, 40, 1800–1808 CrossRef CAS.
- S. Sengupta and A. Lyulin, Polymers, 2020, 12, 907 CrossRef CAS PubMed.
- C. F. Fan, B. D. Olafson, M. Blanco and S. L. Hsu, Macromolecules, 2002, 25, 3667–3676 CrossRef.
- J. H. Hildebrand and R. L. Scott, Annu. Rev. Phys. Chem., 1950, 1, 75–92 CrossRef CAS.
- R. F. Fedors, Polym. Eng. Sci., 2004, 14, 147–154 CrossRef.
- P. Choi, T. A. Kavassalis and A. Rudin, Ind. Eng. Chem. Res., 2002, 33, 3154–3159 CrossRef.
- D. Fedorov and K. Kitaura, The fragment molecular orbital method: practical applications to large molecular systems, Taylor & Francis, 2009 Search PubMed.
- Y. Mochizuki, S. Tanaka and K. Fukuzawa, Recent advances of the fragment molecular orbital method: enhanced performance and applicability, Springer, 2021 Search PubMed.
- K. Okuwaki, H. Doi and Y. Mochizuki, J. Comput. Chem., Jpn., 2018, 17, 102–109 CrossRef CAS.
- K. Okuwaki, Y. Mochizuki, H. Doi, S. Kawada, T. Ozawa and K. Yasuoka, RSC Adv., 2018, 8, 34582–34595 RSC.
- K. Okuwaki, Y. Mochizuki, H. Doi and T. Ozawa, J. Phys. Chem. B, 2018, 122, 338–347 CrossRef CAS PubMed.
- R. L. Ames, J. D. Way and E. A. Bluhm, J. Membr. Sci., 2005, 249, 65–73 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Rev. C.01, 2016 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- Y. Mochizuki, S. Koikegami, T. Nakano, S. Amari and K. Kitaura, Chem. Phys. Lett., 2004, 396, 473–479 CrossRef CAS.
- Y. Mochizuki, T. Nakano, S. Koikegami, S. Tanimori, Y. Abe, U. Nagashima and K. Kitaura, Theor. Chem. Acc., 2004, 112, 442–452 Search PubMed.
- Y. Mochizuki, K. Yamashita, T. Murase, T. Nakano, K. Fukuzawa, K. Takematsu, H. Watanabe and S. Tanaka, Chem. Phys. Lett., 2008, 457, 396–403 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- S. Tanaka, Y. Mochizuki, Y. Komeiji, Y. Okiyama and K. Fukuzawa, Phys. Chem. Chem. Phys., 2014, 16, 10310–10344 RSC.
- R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS PubMed.
- R. Mao, M.-T. Lee, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2015, 119, 11673–11683 CrossRef CAS PubMed.
- G. Meresi, Y. Wang, A. Bandis, P. T. Inglefield, A. A. Jones and W. Y. Wen, Polymer, 2001, 42, 6153–6160 CrossRef CAS.
- N. V. Aieta, R. J. Stanis, J. L. Horan, M. A. Yandrasits, D. J. Cookson, B. Ingham, M. F. Toney, S. J. Hamrock and A. M. Herring, Macromolecules, 2009, 42, 5774–5780 CrossRef CAS.
- C. Wang, V. Krishnan, D. Wu, R. Bledsoe, S. J. Paddison and G. Duscher, J. Mater. Chem. A, 2013, 1, 938–944 RSC.
- H. Doi, K. Okuwaki, Y. Mochizuki, T. Ozawa and K. Yasuoka, Chem. Phys. Lett., 2017, 684, 427–432 CrossRef CAS.
- N. Arai, Y. Kobayashi and K. Yasuoka, Nanoscale, 2020, 12, 6691–6698 RSC.
- H. Tanaka, T. Takahashi, M. Konishi, N. Takata, M. Gomi, D. Shirane, R. Miyama, S. Hagiwara, Y. Yamasaki, Y. Sakurai, K. Ueda, K. Higashi, K. Moribe, E. Shinsho, R. Nishida, K. Fukuzawa, E. Yonemochi, K. Okuwaki, Y. Mochizuki, Y. Nakai, K. Tange, H. Yoshioka, S. Tamagawa and H. Akita, Adv. Funct. Mater., 2020, 30, 1910575 CrossRef CAS.
- H. Doi, Y. Osada, Y. Tachino, K. Okuwaki, M. W. S. Goh, R. Tero and Y. Mochizuki, Appl. Phys. Express, 2024, 17, 055001 CrossRef CAS.
- K. Okuwaki, H. Doi, K. Fukuzawa and Y. Mochizuki, Appl. Phys. Express, 2020, 13, 017002 CrossRef CAS.
- Y. Tachino, K. Okuwaki, H. Doi, K. Akisawa and Y. Mochizuki, Jpn. J. Appl. Phys., 2023, 62, 090902 CrossRef CAS.
- A. Vishnyakov, D. S. Talaga and A. V. Neimark, J. Phys. Chem. Lett., 2012, 3, 3081–3087 CrossRef CAS PubMed.
- T. Aoyagi, F. Sawa, T. Shoji, H. Fukunaga, J.-i. Takimoto and M. Doi, Comput. Phys. Commun., 2002, 145, 267–279 CrossRef CAS.
- J-OCTA, http://www.j-octa.com/.
- I. Obayashi and J. Siam, Appl. Algebra Geom., 2018, 2, 508–534 Search PubMed.
- H. Adams, T. Emerson, M. Kirby, R. Neville, C. Peterson, P. Shipman, S. Chepushtanova, E. Hanson, F. Motta and L. Ziegelmeier, J. Mach. Learn. Res., 2017, 18, 218–252 Search PubMed.
- I. T. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202 CrossRef PubMed.
- L. McInnes, J. Healy and J. Melville, arXiv, 2020, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- Y. K. Phua, N. Terasoba, M. Tanaka, T. Fujigaya and K. Kato, ChemElectroChem, 2024, 11, e202400252 CrossRef CAS.
- I. Obayashi, T. Nakamura and Y. Hiraoka, J. Phys. Soc. Jpn., 2022, 91, 091013 CrossRef.
- Scikit-learn, https://scikit-learn.org/stable/index.html.
- Umap-learn, https://umap-learn.readthedocs.io/en/latest/#.
- F. I. Allen, L. R. Comolli, A. Kusoglu, M. A. Modestino, A. M. Minor and A. Z. Weber, ACS Macro Lett., 2014, 4, 1–5 Search PubMed.
- T. A. Zawodzinski, T. E. Springer, J. Davey, R. Jestel, C. Lopez, J. Valerio and S. Gottesfeld, J. Electrochem. Soc., 2019, 140, 1981–1985 CrossRef.
- M. Saito, N. Arimura, K. Hayamizu and T. Okada, J. Phys. Chem. B, 2004, 108, 16064–16070 CrossRef CAS.
- M. Saito, K. Hayamizu and T. Okada, J. Phys. Chem. B, 2005, 109, 3112–3119 CrossRef CAS PubMed.
- A. Kusoglu and A. Z. Weber, Chem. Rev., 2017, 117, 987–1104 CrossRef CAS PubMed.
- C. Iojoiu, F. Chabert, M. Maréchal, N. E. Kissi, J. Guindet and J. Y. Sanchez, J. Power Sources, 2006, 153, 198–209 CrossRef CAS.
- J. E. Hensley and J. D. Way, J. Power Sources, 2007, 172, 57–66 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00376d |
| This journal is © The Royal Society of Chemistry 2025 |