Open Access Article
Open Access ArticleDeepRLI: a multi-objective framework for universal protein–ligand interaction prediction†
Haoyu
Lin‡
 a,
Jintao
Zhu‡
a,
Jintao
Zhu‡
 a,
Shiwei
Wang
b,
Yibo
Li
a,
Shiwei
Wang
b,
Yibo
Li
 c,
Jianfeng
Pei
c,
Jianfeng
Pei
 *a and
Luhua
Lai
*a and
Luhua
Lai
 *abc
*abc
aCenter for Quantitative Biology, Academy for Advanced Interdisciplinary Studies, Peking University, Beijing 100871, China. E-mail: jfpei@pku.edu.cn; lhlai@pku.edu.cn
bPeking University Chengdu Academy for Advanced Interdisciplinary Biotechnologies, Chengdu, Sichuan 610213, China
cBNLMS, State Key Laboratory for Structural Chemistry of Unstable & Stable Species, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China
First published on 21st June 2025
Abstract
Protein–ligand interaction prediction is a critical component of computer-aided drug design. Although recent deep learning scoring functions have demonstrated advantages over conventional scoring functions, accurate and efficient prediction of protein–ligand binding efficacy remains an intractable challenge. Most of those methods are tailored for specific tasks, such as binding affinity prediction, binding pose prediction, or virtual screening, and often fail to encompass all aspects. There are longstanding concerns that deep learning methods lack a comprehensive understanding of binding free energy and have limitations in generalization. Deep learning methods with a single optimization goal tend to struggle to achieve balanced performance in scoring, ranking, docking, and screening, thus failing to meet the needs of practical drug design research. To solve this challenge, we propose DeepRLI, a novel interaction prediction framework that is universally applicable across various tasks. The proposed model is trained with a multi-objective learning strategy that includes scoring, docking, and screening as optimization goals. It allows DeepRLI to have three relatively independent downstream readout networks, which can be optimized separately to enhance the task specificity of each output. Additionally, the model incorporates an improved graph transformer with a cosine envelope constraint, integrates a novel physics-informed module, and introduces a new contrastive learning strategy. With these designs, extensive evaluations across various benchmarks demonstrate that DeepRLI has superior comprehensive performance in broad applications, highlighting its potential as a fundamental tool for evaluating protein–ligand interactions in practical drug discovery and development.
1 Introduction
Drug discovery aims to identify active molecules, namely lead compounds, capable of binding to disease-related biological targets.1 In the realm of drug design, the development of a scoring function that can accurately quantify the interaction between a protein and a ligand facilitates the discovery of lead compounds via computer-aided techniques.2,3 Theoretically, a perfect scoring function corresponds to the binding free energy surface. A geometric optimizer can be used to find the minimum on the binding free energy landscape, thus realizing molecular docking, and obtaining the stable binding pose of the protein and the ligand. Subsequently, the calculation of protein–ligand binding free energy, commonly referred to as binding affinity, can be conducted. Based on this, virtual screening can be carried out, allowing the identification of potent small molecular ligands as potential candidate drugs.1–3However, the potential energy landscape of protein–ligand systems is highly complex, and even with various approximations, the evaluation of binding free energy based on the principles of statistical mechanics remains computationally intensive and time-consuming.4,5 Scoring functions were actually developed for high-throughput virtual screening, balancing speed and accuracy. Therefore, in essence, these functions serve as significantly simplified approximations for binding free energy estimation. Usually, the scoring functions are derived by considering a single conformation of the complex.6 A range of traditional scoring functions, including physics-based, empirical, and knowledge-based approaches have been developed and widely used in docking and screening tasks.7,8 Although some of them are still prevalent to this day, their preset mathematical forms limit the possibility of breakthroughs.
In recent years, there has been an exponential increase in both experimental and computational data on the structures of large biomolecules.9,10 At the same time, substantial advancements have been made in artificial intelligence algorithms.11,12 This concurrent progress has sparked considerable research interest in using machine learning methods to develop better scoring functions. A number of machine learning-based scoring functions that take 3D structures as input have emerged.13 These functions typically excel in some of the tasks, e.g., binding affinity prediction, binding pose prediction, or virtual screening. For instance, based on crystal structures, methods like KDEEP14 and InteractionGraphNet15 are capable of inferring affinity scores with a high linear correlation to experimental binding data. Additionally, techniques such as DeepDock16 and RTMScore17 demonstrate impressive capability to accurately discern native binding poses from a pool of computer-generated decoy conformations and efficiently identify the true binders within a collection of decoy molecules for a specified target. However, very few machine learning-based scoring functions have demonstrated consistently outstanding performance across all tasks, highlighting the need for continuing research to optimize these models for broad applicability.
An ideal scoring function should exhibit excellent performance across all key metrics, including scoring power, ranking power, docking power, and screening power.18 Task-specific methods often lack generalizability due to the biased nature of the training data and the absence of inherent physical insights in machine learning algorithms. This lack of generalizability poses significant challenges for models when making inferences from unseen data. Numerous data augmentation strategies have been proposed to solve this limitation.19–21
However, most existing strategies have predominantly sacrificed the prediction of binding affinity values in favor of classification models, which offer broader practical applications.22 This shift arises primarily because augmented data does not provide accurate binding free energy values. Besides, there have been attempts to hybridize traditional scoring functions with machine learning to enhance conventional methods. These endeavors involve introducing energy correction terms into classical equations23–25 and leveraging latent space representations to parameterize physics-inspired formulae.26 A recent development is the GenScore model proposed by Shen et al., which achieves balanced multi-task performance by correlating neural network statistical potentials with experimental binding data.27 Notably, methods striving for multi-aspect performance all incorporate elements of traditional scoring functions to some extent.
In this work, we propose DeepRLI, a novel deep learning model for protein–ligand interaction prediction. It adopts an innovative multi-objective strategy that outputs multiple scores simultaneously to suit various tasks with a balanced and exceptional ability in scoring, ranking, docking, and screening. Specifically, DeepRLI employs an improved graph transformer with a cosine envelope as its principal feature embedding module to obtain the hidden representation of each atom. Three independent readout modules predict the scoring score, docking score, and screening score respectively. Among these, the scoring score is used for binding free energy prediction of the protein–ligand complex crystal structure and is suitable for lead compound optimization scenarios; the docking score is instrumental in ascertaining the most favorable binding pose between a protein and a ligand; the screening score is utilized to assess the potency of various small molecules against designated targets.
Theoretically, an ideal and powerful scoring function would be one that can accurately predict the free energy difference between the binding state of the protein and ligand and their dissociation state. However, practical challenges arise due to the scarcity of available data. The existing data on complex structures and their corresponding binding free energy information is notably limited, posing a significant challenge for developing deep learning scoring functions that rely solely on data-driven approaches to precisely estimate the relative free energies of various protein–ligand conformations. To address this, we incorporate physics-informed components into both the docking readout module and the screening readout module, enhancing the model's generalization ability. Additionally, we expand the training data by re-docking and cross-docking crystal structure data using a molecular docking program, AutoDock Vina.28,29 Considering that the native binding conformation is located at the minimum point of the binding free energy surface, and that the binding free energy of other conformations must inherently exceed it, we devised an effective contrastive learning method to optimize parameters. This enables the model to understand the relationship between the binding free energy values of different structures.
Overall, through a divide-and-conquer multi-objective approach combined with data augmentation and a contrastive learning strategy, our protein–ligand interaction scoring model, DeepRLI, reaches the state-of-the-art level in scoring, ranking, docking, and screening, and exhibits remarkable versatility and efficacy across diverse tasks. Moreover, the model's inherent attention mechanism and physics-inspired constraint blocks provide excellent interpretability. Atom pairs with high attention weights and large physical scores correspond to key interactions, such as hydrophobic interactions, hydrogen bonds, and π-stacking. This demonstrates that our universal scoring model accurately captures interaction-related information, resulting in outstanding performance.
2 Overview of DeepRLI
DeepRLI is a novel deep learning-based scoring function designed specifically for predicting protein–ligand interactions. It employs a graph neural network architecture to accurately evaluate the binding strength of 3D complex structures. The underlying methodology and detailed framework of DeepRLI are described in the subsequent sections.The basic model architecture of DeepRLI is illustrated in Fig. 1. It accepts a protein–ligand complex with three-dimensional spatial coordinates as input. Note that the receptors investigated here are proteins, but since the model uses atoms rather than residues as the fundamental unit, this framework can also easily be extended to other biological macromolecules.
Generally, binding affinity is associated with the entire system, corresponding to the free energy difference of the system in distinct states. However, if there is no significant change in the protein backbone before and after binding, the binding affinity is largely determined by the residues near the pocket. To reduce computational costs, we focus on atoms near the binding site for binding affinity prediction, specifically considering the small molecule and residues within 6.5 Å of it. Instead of including only atoms within a certain cutoff, our approach encompasses entire residues as long as there is a protein–ligand atom pair within 6.5 Å of each other.
In the subsequent step, the structure comprising the selected residues and small molecules is transformed by the model into a graph  where atoms serve as nodes
where atoms serve as nodes  and interactions form edges
and interactions form edges  (Fig. 1a). To preserve the structural information as comprehensively as possible, we assign an edge to every atom pair whose distance is less than 6.5 Å, a reasonable cutoff distance for interatomic interactions. Consequently, such fully-connected graphs typically consist of hundreds of nodes and tens of thousands of edges. Each node i possesses corresponding atomic features αi ∈
(Fig. 1a). To preserve the structural information as comprehensively as possible, we assign an edge to every atom pair whose distance is less than 6.5 Å, a reasonable cutoff distance for interatomic interactions. Consequently, such fully-connected graphs typically consist of hundreds of nodes and tens of thousands of edges. Each node i possesses corresponding atomic features αi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) dv×l, and each edge similarly encompasses features βij ∈
dv×l, and each edge similarly encompasses features βij ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) de×l representing the interatomic interaction between nodes i and j.
de×l representing the interatomic interaction between nodes i and j.
2.1 Graph transformer with a cosine envelope
To achieve adequate expressive power, input node features and edge features are first embedded into a d-dimensional hidden space via learnable affine transformations, respectively:| v0i = Aαi + α; e0ij = Bβij + b, | (1) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×dv, B ∈
d×dv, B ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d×de and a,b ∈
d×de and a,b ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d are the learnable parameters of the linear projection layers. Our model does not introduce node positional encodings, as atoms in the same context contribute equally to the interaction, and ensuring a unique representation for each node is unnecessary.
d are the learnable parameters of the linear projection layers. Our model does not introduce node positional encodings, as atoms in the same context contribute equally to the interaction, and ensuring a unique representation for each node is unnecessary.
Following the initial embedding, hidden node features and edge features undergo updates through ten graph transformer layers (Fig. 2). Significantly, in our DeepRLI model, we use a refined graph transformer architecture to enhance its applicability to molecular systems. This adaptation is based on the principle that, within a molecular structure, the importance of neighboring atoms to a central atom diminishes with increasing distance, and the contextual representation of the central atom is predominantly influenced by the immediate, proximal atoms. Therefore, we introduce a cosine envelope factor, which is applied to the weights derived from the key-query dot product, modulating them to decay with increasing interatomic distances. The incorporation of this cosine envelope function is crucial, particularly in scenarios with limited training data. In the absence of this modification, the model may inappropriately focus on learning specific long-distance atomic interactions, potentially leading to overfitting. By implementing this distance-sensitive weighting mechanism, our model more effectively captures the local chemical environment of each atom, thus mitigating the risk of overfitting and enhancing the model's generalizability in drug design applications. For a detailed description of the impact of the cosine envelope, please refer to the ablation study results presented in Section 1.1 of the ESI.†
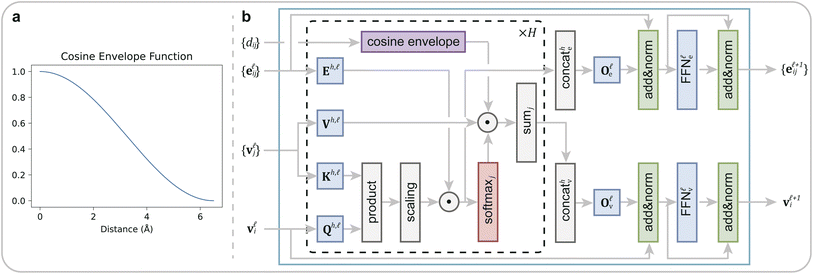 | ||
| Fig. 2 The improved graph transformer used in DeepRLI. (a) The curve of the cosine envelope function. (b) Block diagram of the graph transformer with a cosine envelope. | ||
In a single graph transformer layer, the convolution procedure employs the following message-passing scheme: the embedding of a node is updated based on the information from all adjacent nodes and edges, while the embedding of an edge is updated according to the information from its end nodes and itself. It can be expressed as:30
 | (2) |
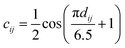 | (3) |
 | (4) |
In the above formulae, dij is the distance between nodes i and j;  represents the layer number; k denotes the index of H attention heads; ‖ signifies concatenation;
represents the layer number; k denotes the index of H attention heads; ‖ signifies concatenation; 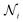 refers to neighboring nodes of atom i;
refers to neighboring nodes of atom i;  ,
,  , and
, and  correspond to the query, key, and value generation matrices in the attention mechanism, respectively;
correspond to the query, key, and value generation matrices in the attention mechanism, respectively;  is the linear transformation matrix of edge information, with its projection results used to adjust attention scores;
is the linear transformation matrix of edge information, with its projection results used to adjust attention scores;  represents the updating functions. The subsequent outputs
represents the updating functions. The subsequent outputs  and
and  are each followed by a residual connection and batch normalization layer, a fully-connected layer, and another residual connection and batch normalization layer:30
are each followed by a residual connection and batch normalization layer, a fully-connected layer, and another residual connection and batch normalization layer:30
 | (5) |
 | (6) |
 | (7) |
 ,
,  , and the BatchNorm operation is
, and the BatchNorm operation is | (8) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d are learnable parameter vectors. The description above encapsulates the function of a single graph transformer layer. After iterating through this process ten times, the final node embeddings viL and edge embeddings eijL are obtained.
d are learnable parameter vectors. The description above encapsulates the function of a single graph transformer layer. After iterating through this process ten times, the final node embeddings viL and edge embeddings eijL are obtained.
In the subsequent stages, the hidden features viL of the nodes undergo distinct processing through three autonomous downstream networks. This process yields three types of scores: scoring scores, docking scores, and screening scores. The nomenclature of these scores reflects their underlying purposes. Specifically, the scoring scores are tailored for evaluating and ranking crystal structures, the docking scores are optimized for molecular docking processes, and the screening scores are designed for binder discrimination in virtual screening tasks. This structured approach aims to enhance the precision and applicability of each score to its respective domain within computer-aided drug design.
2.2 Scoring readout
The downstream network on the right side of Fig. 1b is the scoring readout, which focuses on the accurate quantification of binding free energy values. The embeddings of the ligand nodes obtained after passing through the graph transformer layers are aggregated as the graph-level hidden features. This approach is employed because the features associated with affinity are primarily determined by the ligand's environment, and the global pooling of the entire graph would introduce noise related to residues,
obtained after passing through the graph transformer layers are aggregated as the graph-level hidden features. This approach is employed because the features associated with affinity are primarily determined by the ligand's environment, and the global pooling of the entire graph would introduce noise related to residues, | (9) |
Following this, the hidden graph features x are fed into a multi-layer perceptron (MLP) to generate a scoring score:
| y1 = Wr3ReLU(Wr2ReLU(Wr1x + br1) + br2) + br3, | (10) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d/2×d, Wr2 ∈
d/2×d, Wr2 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d/4×d/2, Wr3 ∈
d/4×d/2, Wr3 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 1×d/4 and br1 ∈
1×d/4 and br1 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d/2, br2 ∈
d/2, br2 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d/4, br3 ∈
d/4, br3 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) are learnable parameters of linear layers.
are learnable parameters of linear layers.
2.3 Docking readout
It is noteworthy that the ordinary neural network scoring models are purely data-driven, inferring binding affinity based on the similarity of graph embeddings. This approach, however, introduces a critical deficiency: the model's capability to generalize across a diverse range of molecular structures is inherently constrained by the breadth and variety of the training data. Currently, our knowledge of accurate binding free energy is limited to approximately ten thousand known protein–ligand complex crystal structures. It means that scoring models predominantly learn from data that may not be representative of the entire spectrum of protein–ligand interactions, thereby restricting its understanding to only these biased data and impeding its ability to grasp the more complex, underlying physical principles behind these interactions.This limitation is particularly relevant in the context of molecular docking and virtual screening tasks. Their objectives often involve estimating the binding scores for structures in weak binding states, which can differ significantly from the conformations of experimentally determined crystal structures. Therefore, enhancing the model's generalization ability to infer on these loose states is of vital importance.
Here, we adopt two approaches together to tackle the challenge of model generalization: data augmentation and the integration of physical constraints. On one hand, data augmentation methodologically broadens the scope of the training set by encompassing a more diverse range of chemical compositions and phase spaces thereof. This expansion ensures a comprehensive coverage of potential scenarios in the model's training phase. On the other hand, more importantly, we incorporate physical constraints into the model. This is achieved by embedding terms inspired by fundamental physical principles, thereby ensuring that the model's predictions remain consistent with established physical laws.
Drawing inspiration from the methodology employed in PIGNet,26 our approach in DeepRLI includes the integration of a specialized physical module. The module is specifically designed to account for the interactions between atomic pairs, adding a layer of physical realism to the model's predictive capabilities. The schematic diagram of this approach is demonstrated in Fig. 1c and d, wherein we detail the workflow of two downstream readout networks. These networks leverage physics-informed blocks to implement a kind of framework that we term “neural network parameterized potential function”.31 It effectively strikes a balance between precision in prediction and the capacity for generalization.
The readout module for docking incorporates a physics-informed block that encapsulates four distinct energy terms, as delineated in Fig. 1c. These terms are extracted from the Vinardo scoring function,32 an empirical method renowned in the field. They specifically represent four types of interatomic interactions: steric attraction, steric repulsion, hydrophobic interaction, and hydrogen bonding. Notably, the first two terms are integral in accounting for van der Waals interactions, and their mathematical formulations are presented as follows:
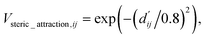 | (11) |
 | (12) |
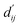 is the reduced distance relative to the atomic surfaces,
is the reduced distance relative to the atomic surfaces, | (13) |
 | (14) |
 | (15) |
We obtain the embedding of any pair of atoms by pairwise adding the node embeddings encoded through the graph transformer, which contains information about the two atoms and their mutual interactions. Subsequently, these pair embeddings are processed through an MLP block that outputs four weight parameters corresponding to four predefined interaction types. The weighted sum of these four components represents the model's prediction of the interaction between a pair of atoms,
| Vij = w1Vsteric_attraction,ij + w2Vsteric_repulsion,ij + w3Vhydrophobic,ij + w4VH-bond,ij | (16) |
 | (17) |
2.4 Screening readout
In our framework, the screening readout parallels the docking readout in its foundational reliance on a physics-informed block. This similarity notwithstanding, a distinctive feature of the screening readout is the integration of an entropy scaling layer prior to generating the final output. This layer plays a crucial role in compensating for conformational entropy losses, as delineated in Fig. 1d. Delving into the specifics, the process involves the transformation of node embeddings through a network analogous to the docking readout, resulting in the derivation of an intermediate variable, denoted as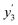 . Concurrently, a network akin to the scoring readout is employed to ascertain the parameter w5, which is directly applied to scale the number of rotatable bonds Nrot in the ligand. Culminating this process, the screening score, represented as y3, is computed, adhering to the stipulated formula:
. Concurrently, a network akin to the scoring readout is employed to ascertain the parameter w5, which is directly applied to scale the number of rotatable bonds Nrot in the ligand. Culminating this process, the screening score, represented as y3, is computed, adhering to the stipulated formula: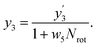 | (18) |
The above delineates the fundamental architecture of DeepRLI, a deep learning model designed for drug discovery. It takes the three-dimensional structure of a protein–ligand complex as input and, after sophisticated calculations, predicts three scores: a scoring score, a docking score, and a screening score. These scores are related to the binding free energy, meaning the smaller the score, the tighter the binding.
3 Results and discussions
3.1 Assessment of the model performance
To thoroughly assess the efficacy of the versatile DeepRLI model, a comprehensive evaluation is conducted across four critical aspects: scoring, ranking, docking, and screening. The scoring power of a scoring function is defined by its capacity to generate binding scores that linearly correlate with experimental binding data. Similarly, ranking power describes the scoring function's ability to accurately order the known ligands of a specific target by their binding affinities, assuming the precise binding poses of these ligands are known. Docking power, on the other hand, refers to the scoring function's proficiency in distinguishing the native ligand binding pose from a set of computer-generated decoys. Finally, screening power is characterized by the scoring function's effectiveness in identifying true binders to a target from a collection of random molecules. Each of these capabilities plays a crucial role in the evaluation of the efficacy and reliability of scoring functions.Considering that the reliance on a single test set is constrained by its specific collection of proteins and small molecules, leading to bias that could potentially skew the model's performance assessment either positively or negatively, the evaluation procedure is diversified to include several widely-recognized benchmark test sets. Among these includes the internal test set of PDBbind, specifically the CASF-2016 benchmark18—a widely acknowledged standard in this domain. Additionally, external test sets are employed to examine distinct capabilities: the CSAR-NRC HiQ benchmark33 for assessing scoring accuracy, the Merck FEP benchmark34 for evaluating ranking efficacy, and the LIT-PCBA benchmark35 for screening proficiency. Furthermore, the 0 Ligand Bias benchmark36 is utilized to rigorously test the model's ability to generalize beyond ligand-specific biases, ensuring it captures meaningful protein–ligand interactions rather than relying on dataset artifacts. Detailed descriptions of these benchmarks can be found in Section 2.1.1 of the ESI.† This multi-faceted approach ensures a more balanced and thorough evaluation of the DeepRLI model's performance across various scenarios.
In addition, to benchmark our method's inference capabilities, we conduct a comparative analysis with existing scoring functions. This comparison particularly targets those functions for which comprehensive, detailed evaluation results are available, such as the array of scoring functions detailed in CASF-2016 and the variety of scoring models discussed in the work on GenScore. Note the variability in GenScore's performance across different hyperparameter settings, and the GT_1.0 model is selected as our baseline for comparison. Further enriching our comparative investigation, we include results from the PIGNet model, another deep learning method inspired by physics-based principles, as well as the PLANET model,37 known for its ability to expedite virtual screening processes without necessitating binding poses. Baseline data for each model is directly sourced from the relevant literature. And the models lacking benchmark-specific data are excluded from certain comparative analyses.
| Method | Scoring power | Ranking power | |||
|---|---|---|---|---|---|
| RMSE | R p | ρ | τ | PI | |
| Vina28,29 | 1.73 | 0.604 | 0.528 | 0.453 | 0.557 |
| Glide SP38,39 | 1.89 | 0.513 | 0.419 | 0.374 | 0.425 |
| Glide XP40 | 1.95 | 0.467 | 0.257 | 0.227 | 0.255 |
| X-Score41 | 1.69 | 0.631 | 0.604 | 0.529 | 0.638 |
| ΔvinaRF2023 | 1.26 | 0.816 | 0.750 | 0.686 | 0.761 |
| ΔLin_F9XGB25 | 1.24 | 0.845 | 0.704 | 0.625 | — |
| AEScore42 | 1.22 | 0.830 | 0.640 | 0.550 | 0.670 |
| Δ-AEScore42 | 1.34 | 0.790 | 0.590 | 0.520 | 0.610 |
| PLANET37 | 1.25 | 0.824 | 0.682 | — | — |
| PIGNet26 | — | 0.749 | 0.668 | — | — |
| GenScore27 | — | 0.829 | 0.673 | — | — |
| DeepRLI | 1.18 | 0.849 | 0.730 | 0.660 | 0.757 |
| Method | Docking power | Screening power | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SR1(%) | SR2(%) | SR3(%) | SR1%(%) | SR5%(%) | SR10%(%) | EF1% | EF5% | EF10% | |
| Vina | 90.2 | 95.8 | 97.2 | 29.8 | 40.4 | 50.9 | 7.70 | 4.01 | 2.87 |
| Glide SP | 87.7 | 91.9 | 93.7 | 36.8 | 54.4 | 63.2 | 11.44 | 5.83 | 3.98 |
| Glide XP | 83.9 | 90.2 | 94.4 | 26.3 | 45.6 | 52.6 | 8.83 | 4.75 | 3.51 |
| X-Score | 63.5 | 74.0 | 80.4 | 7.0 | 15.8 | 28.1 | 2.68 | 1.31 | 1.23 |
| ΔvinaRF20 | 89.1 | 94.4 | 96.5 | 42.1 | 49.1 | 54.4 | 11.73 | 4.43 | 3.10 |
| ΔLin_F9XGB | 86.7 | — | — | 40.4 | — | — | 12.6 | — | — |
| AEScore | 35.8 | 54.4 | 60.4 | — | — | — | — | — | — |
| Δ-AEScore | 85.6 | 94.4 | 95.8 | 19.3 | 49.1 | 54.4 | 6.16 | 3.76 | 2.48 |
| PLANET | 71.8 | 81.6 | 87.9 | — | — | — | — | — | — |
| PIGNet | — | — | — | 50.0 | — | — | 18.5 | — | — |
| GenScore | 93.3 | — | — | 57.3 | — | — | 18.58 | — | — |
| DeepRLI | 90.9 | 96.1 | 97.5 | 26.3 | 36.8 | 50.9 | 11.42 | 4.65 | 3.30 |
3.1.1.1 Scoring power. The scoring power of a model refers to its accuracy in predicting binding free energy. This is typically assessed by examining the correlation between the computational scores generated by the model and the corresponding experimental data. To quantify this relationship, several statistical metrics are commonly employed. These include the Mean Square Error (MSE) and Root Mean Square Error (RMSE), which measure the average magnitude of the errors in predictions. Additionally, the Pearson correlation coefficient (Rp) and Spearman correlation coefficient (ρ) are used to assess the linear and rank-order correlations, respectively, between predicted scores and experimental outcomes. The Concordance Index (CI) is another metric offering a measure of the ranking correctness.43
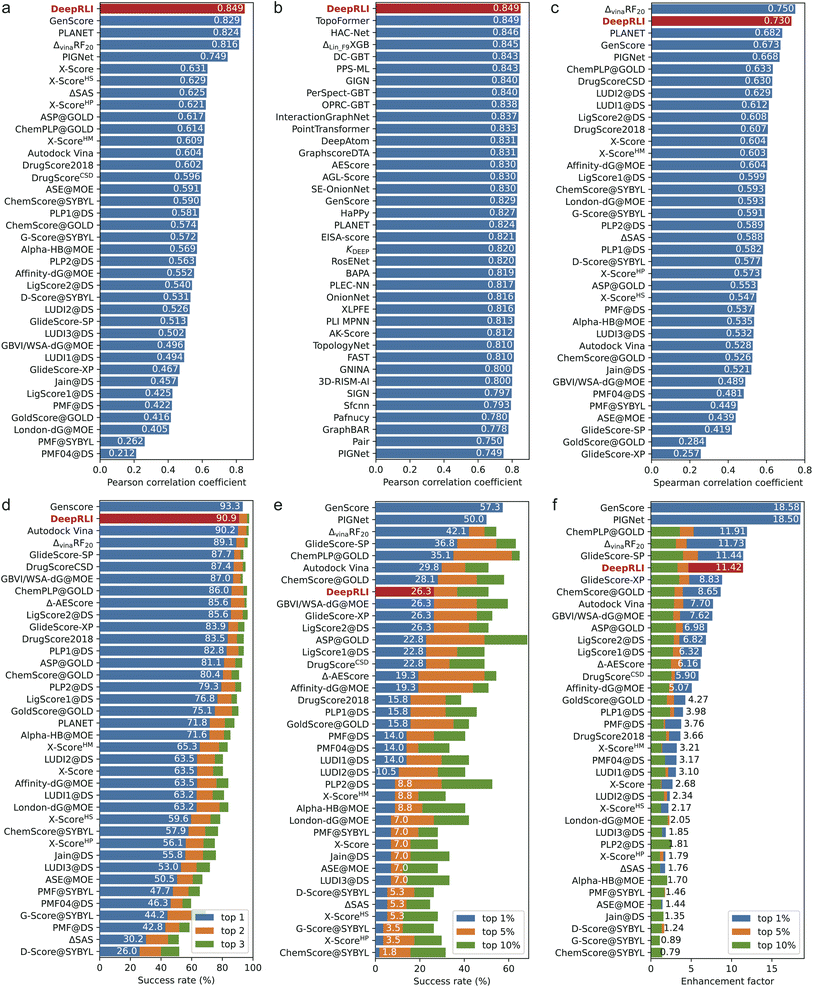
Our DeepRLI model shows a strong correlation between the predicted binding affinities for 285 crystal structures in the CASF-2016 dataset and the experimental pKd data (Fig. S2a†), with an MSE of 1.384, an RMSE of 1.176, a Rp of 0.849, a ρ of 0.850 and a CI of 0.831. In Fig. 4a and b, we compare the scoring performance of DeepRLI with that of other scoring functions. Fig. 4a mainly includes scoring functions from CASF-2016, most of which are traditional methods; Fig. 4b consists entirely of deep learning-based methods developed in recent years,14,15,19,25–27,37,42,44–72 most of which are structure-based.13 Among these scoring functions, DeepRLI achieves the current state-of-the-art level in scoring power.
3.1.1.2 Ranking power. In the evaluation of scoring capabilities, we include the analysis of several metrics relevant to ranking. These metrics are calculated across the whole crystal structure test set. Notably, in the context of the CASF assessment, “ranking power” is specifically defined as the proficiency in ordering known active ligands against a particular biological target. Nevertheless, it indicates a positive correlation between scoring and ranking abilities; typically, a robust scoring ability is indicative of a similarly robust ranking ability. To quantitatively measure the ranking power, three primary metrics are utilized: the Spearman correlation coefficient (ρ), the Kendall correlation coefficient (τ), and the Predictive Index (PI).18
In Fig. S2b,† the ranking efficacy of DeepRLI is demonstrated through its performance in ranking five active small molecules across each of the 57 targets within the CASF-2016 dataset. Notably, the model achieves a perfect prediction score (with all indicators at 1) for several targets, indicating an exact match between the predicted and actual ordering of molecules. For the majority of the targets, the model's predictions exhibited a positive correlation with the actual rankings, as evidenced by scores exceeding 0.5. However, challenges arose in the case of two specific targets, identified by PDB IDs 2ZCQ and 3G0W, where the model's predictions are inversely correlated with the actual data. Further analysis reveals that these discrepancies could be attributed to the presence of multiple ligands with closely similar pKd values, complicating the task of accurate ranking. Upon aggregating the results across all 57 targets, the overall ranking capability of DeepRLI is quantified, with a ρ of 0.730, a τ of 0.660, and a PI of 0.757. As delineated in the leaderboard in Fig. 4c, DeepRLI's ranking performance is highly competitive, second only to ΔvinaRF20, aligning with the current state-of-the-art in the field.
3.1.1.3 Docking power. The concept of docking power pertains to the proficiency of a scoring function in accurately identifying the native binding pose within a diverse array of protein–ligand conformational states. In CASF-2016, each of the 285 complexes has nearly 100 decoy conformations sampled by various docking programs. And scoring functions evaluate and rank the 285 groups of conformations individually. Notably, a scoring function demonstrating optimal docking ability tends to assign higher ranks to those conformations that closely resemble the binding pose of the complex's native crystal structure. Therefore, the quantitative metric for measuring docking ability is the success rate of having conformations within the top n (1, 2, or 3) ranks whose RMSD from the native ligand pose is less than 2 Å.
We evaluate the docking performance of DeepRLI on a dataset comprising 285 protein–ligand systems from CASF-2016, as depicted in Fig. S2c.† The results, predominantly represented by dark areas on the heatmap, suggest a high docking success rate across most of the complexes. Specifically, the top 1, 2, and 3 docking success rates achieved by our model are 90.9%, 96.1%, and 97.5%, respectively. Notably, achieving a top 1 success rate exceeding 90% is a remarkable outcome, positioning our method among the leading approaches in terms of docking capabilities, as demonstrated in Fig. 4d.
Furthermore, we conduct a binding funnel analysis for DeepRLI, presented in Fig. 5. This analysis reveals a strong correlation between the docking scores predicted by DeepRLI and the RMSD values, particularly within a shorter RMSD range (e.g., RMSD < 5 Å). This correlation manifests as a funnel landscape, indicative of not only the model's high docking accuracy but also its efficiency in docking procedures.
3.1.1.4 Screening power. Screening power denotes the efficacy of a scoring function in accurately identifying potential ligands that exhibit strong binding affinity to a specific protein within a diverse pool of small molecules. CASF-2016 obtained the structures of each of the 57 proteins bound to 280 other small molecules through cross-docking.18 It is important to note that cross-binders do exist, meaning that certain proteins may have more than five true binders, and the goal of screening is to enrich all of these binders. Screening power is quantitatively measured by the success rate in identifying the highest-affinity binders within the top 1%, 5%, or 10% of the ranked small molecules. Additionally, the enhancement factors at these top percentile levels also serve as critical metrics for evaluation.
The evaluation of DeepRLI's screening efficacy across 57 proteins within the CASF-2016 framework is depicted in Fig. S2d and S1e.† While the overall performance of the screening process is moderate, the model exhibits notable proficiency in enriching the majority, or even all, active ligands at the forefront for specific targets, notably those with PDB IDs 2P15 and 3EJR. In terms of quantifiable metrics, the top 1%, 5%, and 10% screening success rates of our model are 26.3%, 36.8%, and 50.9%, respectively; and the corresponding enhancement factors are 11.42, 4.65, and 3.30, separately. The screening capability rankings, as illustrated in Fig. 4e and f, indicate that DeepRLI's performance ranks competitively among traditional scoring functions. However, it does not yet match the efficacy of the leading-edge deep learning-based methodologies. Notably, the general, refined and core datasets of PDBBind have the problem of cross-contamination of proteins and ligands with high similarity, and the existing deep learning methods may exhibit overly high screening performance on this test set.73,74 Further assessments conducted on other virtual screening test sets have demonstrated that DeepRLI's screening performance aligns with the forefront of contemporary deep learning-based approaches. This finding underscores DeepRLI's robust generalization capabilities in virtual screening.
To comprehensively demonstrate the performance level of DeepRLI, we have listed in Tables 1 and 2 the scoring, ranking, docking, and screening powers of some representative scoring functions on CASF-2016. As can be seen, DeepRLI exhibits robust overall performance. Notably, its screening capability aligns with that of renowned traditional scoring functions such as Vina, Glide SP, and Glide XP. However, DeepRLI excels in other domains, demonstrating cutting-edge proficiency, particularly in scoring and ranking metrics. Significantly outperforming conventional scoring methods, DeepRLI also shows marked superiority over recent deep learning-based approaches, including GenScore, PIGNet, and PLANET. These findings underscore the efficacy of DeepRLI as a multi-objective, physics-informed, contrast-optimized model. Its versatility and advanced capabilities position it as an integral tool for diverse computational tasks in drug design, encompassing affinity prediction, molecular docking, and virtual screening.
To eliminate the impact of data leakage on performance evaluation, entries identical to those in the training set are meticulously excluded from the aforementioned datasets. This step leads to the generation of four reduced datasets, designated as set1et (50), set2et (36), set3et (75), and settet (161), where “et” signifies the exclusion of the training set. The performance of DeepRLI on these reduced datasets is evaluated, with the results being graphically depicted through correlation scatter plots in Fig. S4.† Pearson correlation coefficients, measuring the congruence between predicted and experimental values, are found to be 0.804, 0.719, 0.679, and 0.733 for the respective datasets. These coefficients indicate a robust correlation across all datasets. Notably, DeepRLI's performance in these assessments underscores its commendable generalization capabilities, particularly in terms of scoring proficiency.
Additionally, for comparative analysis with other methods, especially the results of Shen et al.,27 we further evaluate the scoring performance of DeepRLI on two types of datasets: one that excludes duplicates from the PDBbind general set but retains those belonging to the core set, and another that completely excludes duplicates from the general set. These datasets are respectively labeled “egic” (excluding the general set, but including the core set) and “eg” (excluding the general set), namely set1egic (48), set2egic (33), set3egic (21), settegic (102); set1eg (36), set2eg (13), set3eg (17), and setteg (66). The evaluation results of DeepRLI on these curated datasets are depicted in correlation scatter plots (Fig. S5 and S6†). The Pearson correlation coefficients for the “egic” datasets are 0.796, 0.749, 0.660, and 0.737, respectively, while for the “eg” datasets, they are 0.773, 0.630, 0.628, and 0.680, respectively. These coefficients indicate a consistently robust correlation across all datasets. In Table 3, we list the performance of various representative scoring functions on the settegic and setteg test sets. Notably, our DeepRLI model outperforms others in terms of both Pearson and Spearman correlation coefficients. This superior performance underscores the exceptional scoring accuracy and impressive generalization capability of our model, reinforcing its potential utility in computer-aided drug design for binding affinity prediction.
| Method | Scoring power on settegic | Scoring power on setteg | ||
|---|---|---|---|---|
| R p | ρ | R p | ρ | |
AutoDock4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 75 |
0.527 | 0.542 | 0.561 | 0.610 |
| Vina | 0.306 | 0.589 | 0.282 | 0.543 |
| Vinardo | 0.286 | 0.586 | 0.260 | 0.543 |
| Glide SP | 0.126 | 0.571 | 0.115 | 0.551 |
| Glide XP | 0.126 | 0.388 | 0.115 | 0.365 |
| X-Score | 0.617 | 0.598 | 0.528 | 0.514 |
| Pafnucy70 | 0.610 | 0.625 | 0.583 | 0.605 |
| GenScore | 0.713 | 0.697 | 0.678 | 0.674 |
| DeepRLI | 0.737 | 0.735 | 0.680 | 0.716 |
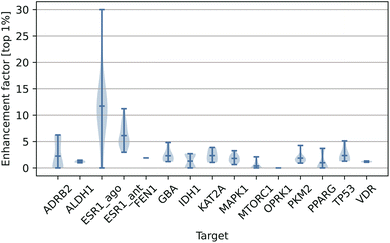
In Table 4, we have listed the performance of some representative scoring functions on the LIT-PCBA benchmark. The results of other methods for each target are primarily based on a selected PDB template, so we also sampled a PDB template with the best result for comparison. As can be seen from the table, our DeepRLI model demonstrates satisfactory screening performance across all targets, ranking at the current advanced level, with an average EF1% of 5.47, a median of 3.70, and a maximum of 30.00. A more detailed examination reveals that the DeepRLI model achieved an EF1% of over 2 for 11 targets, surpassed 5 for 4 targets, and exceeded 10 for 2 targets. Compared to other scoring models, this is a fairly good outcome. It is noteworthy that, among 15 targets, DeepRLI's screening EF1% is higher than that of other compared methods for 5 targets, indicating that our model can make reasonable predictions of active molecules for most targets, rather than performing exceptionally only on certain ones. It shows a performance close to the current advanced methods on the large-scale virtual screening benchmark LIT-PCBA, indicating that DeepRLI has superior generalization ability and can make reasonable screening inferences on external test sets.
| Target | Vina | Glide SP | Lin_F9 | ΔvinaRF20 | ΔLin_F9XGB | PLANET | GenScore | DeepRLI |
|---|---|---|---|---|---|---|---|---|
| ADRB2 | 0.00 | 5.88 | 0.00 | 0.00 | 11.76 | 5.88 | 15.69 | 6.25 |
| ALDH1 | 1.49 | 2.02 | 1.59 | 1.66 | 6.46 | 1.38 | 1.96 | 1.48 |
| ESR1_ago | 15.38 | 7.69 | 0.00 | 15.38 | 7.69 | 7.69 | 10.25 | 30.00 |
| ESR1_ant | 3.92 | 1.94 | 2.94 | 2.94 | 3.92 | 3.88 | 3.56 | 11.22 |
| FEN1 | 0.54 | 7.32 | 1.90 | 0.81 | 2.17 | 5.15 | 6.05 | 1.90 |
| GBA | 4.82 | 4.22 | 7.23 | 6.63 | 9.64 | 3.01 | 1.41 | 4.82 |
| IDH1 | 0.00 | 0.00 | 2.56 | 0.00 | 5.13 | 2.56 | 5.13 | 2.70 |
| KAT2A | 0.52 | 1.03 | 2.06 | 0.52 | 7.73 | 3.11 | 1.20 | 3.89 |
| MAPK1 | 2.92 | 3.24 | 1.62 | 1.95 | 2.60 | 1.30 | 4.87 | 3.27 |
| MTORC1 | 2.06 | 0.00 | 2.06 | 3.09 | 2.06 | 2.06 | 2.40 | 2.11 |
| OPRK1 | 0.00 | 0.00 | 4.17 | 0.00 | 12.50 | 4.17 | 2.78 | 0.00 |
| PKM2 | 1.65 | 2.75 | 0.73 | 2.93 | 2.56 | 1.83 | 1.47 | 4.27 |
| PPARG | 7.41 | 21.96 | 3.70 | 11.11 | 7.41 | 3.66 | 20.74 | 3.70 |
| TP53 | 0.00 | 2.50 | 2.53 | 0.00 | 1.27 | 2.50 | 0.00 | 5.13 |
| VDR | 1.02 | 0.34 | 0.11 | 0.68 | 0.34 | 1.02 | 1.13 | 1.33 |
| Mean | 2.78 | 4.06 | 2.21 | 3.18 | 5.55 | 3.28 | 5.24 | 5.47 |
| Median | 1.49 | 2.50 | 2.06 | 1.66 | 5.13 | 3.01 | 2.78 | 3.70 |
| Max | 15.38 | 21.96 | 7.23 | 15.38 | 12.50 | 7.69 | 20.74 | 30.00 |
| >2 | 6 | 9 | 8 | 6 | 13 | 11 | 9 | 11 |
| >5 | 2 | 4 | 1 | 3 | 8 | 3 | 5 | 4 |
| >10 | 1 | 1 | 0 | 2 | 2 | 0 | 3 | 2 |
| Method | R p | Method | R p |
|---|---|---|---|
| LigandBias | 0.08 | PointVS | 0.28 |
| ProteinBias | 0.41 | Pafnucy | 0.17 |
| EnsembleBias | 0.27 | SIGN | 0.27 |
| BothBias | 0.27 | OnionNet-2 | 0.35 |
| Smina | 0.12 | DeepRLI | 0.73 |
| RFScore | 0.24 | DeepRLIed | 0.31 |
3.2 Interpretation
Our DeepRLI model, which leverages graph transformer layers as its core graph representation learning module, allows for an in-depth analysis of its scoring decision mechanism by extracting the attention weights during model inference. This is a significant advantage of the model, as it can not only predict the binding affinities between proteins and ligands but also elucidate the potential interaction patterns through interpretative analysis. It is crucial to highlight that the graph transformer within the DeepRLI architecture has been improved with a novel modification, incorporating a cosine envelope constraint to refine its functionality. Specifically, in the context of graph convolution operations, the effective weights for neighborhood aggregation are represented as , as delineated in eqn (2). Here, we mainly concentrate on the attention weights cijwijk,L in the last graph transformer layer, and conduct an in-depth interpretative analysis based on this.
, as delineated in eqn (2). Here, we mainly concentrate on the attention weights cijwijk,L in the last graph transformer layer, and conduct an in-depth interpretative analysis based on this.
In our approach, a graph typically consists of tens of thousands of edges, each with corresponding attention weights, making it challenging to display them all. Generally, our primary interest lies in the components involving both the protein and the ligand. By carefully examining these aspects, we can gain insight into which interactions play a more crucial role in the binding strength. Moreover, our model employs a multi-head attention mechanism within the graph transformer layers, comprising eight heads. To facilitate visualization, we compute the average of the attention weights across these eight heads.
Additionally, it merits emphasis that the concept of attention weights pertains to the significance of interatomic relationships. To elucidate the relationship importance between an atom and a fragment (e.g., between a ligand atom and a specific residue) or between fragments (e.g., between a ligand molecule and a specific residue), it necessitates the aggregation of attention weights from all constituent atoms within a fragment. Here, we adopt a rational “summing” strategy for aggregation. This entails calculating the sum of attention weights for all atoms within a fragment to derive a cumulative significance score, thereby providing a special perspective of intermolecular interactions.
We demonstrate the internal details of the decision-making process of DeepRLI through an example of a protein–ligand complex (PDB ID: 1BZC). The 1BZC complex consists of the protein tyrosine phosphatase 1B (PTP1B) and its inhibitor, [1,1-difluoro-1-((6-carboxamidoglutamic)naphth-2-yl)]methylphosphonic acid (TPI).77 Protein tyrosine phosphatases (PTPs) play a crucial role in regulating a variety of cellular processes, including cell growth, proliferation, differentiation, metabolism, immune response, intercellular adhesion, and cell–matrix interactions.78,79 In the insulin signaling pathway, PTP1B is significant as it dephosphorylates the activated insulin receptor, negatively regulating the pathway.80 Given this context, analyzing and explaining the decision mechanism of DeepRLI's binding affinity prediction using 1BZC as an example holds considerable reference value.
Fig. 7 illustrates the calculation results of the attention scores in the last layer of the graph transformer of the DeepRLI model when evaluating the binding affinity of the 1BZC complex. In this figure, attention weights are represented by a gradient from light to dark red, indicating low to high attention weights. Higher attention weights imply that during the neighborhood aggregation process of graph convolution, neighboring nodes contribute more significantly to the central node's hidden features. This typically corresponds to more crucial structural patterns, often indicating interactions that have a substantial impact on binding affinity. As seen in Fig. 7b, residues such as TYR46, ARG47, ASP48, LYS120, PHE182, CYS215, ALA217, ILE219, GLY220, and ARG221 significantly influence the updating of the ligand's hidden features, thereby playing a key role in the prediction of binding affinity. Further observation of the overall importance of interactions between each residue and every ligand atom (Fig. 7c) and the importance of interactions between each atom of the residues and every atom of the ligand (Fig. 7d) reveals that TYR46 is assigned relatively higher attention weights for interactions with the naphthalene portion of TPI, ARG47 and ASP48 for interactions with the carboxyl and amide portions of TPI. In contrast, residues like LYS120, PHE182, CYS215, ALA217, ILE219, GLY220, and ARG221 mainly focus their attention weights on the difluoromethylphosphonic acid side of TPI.
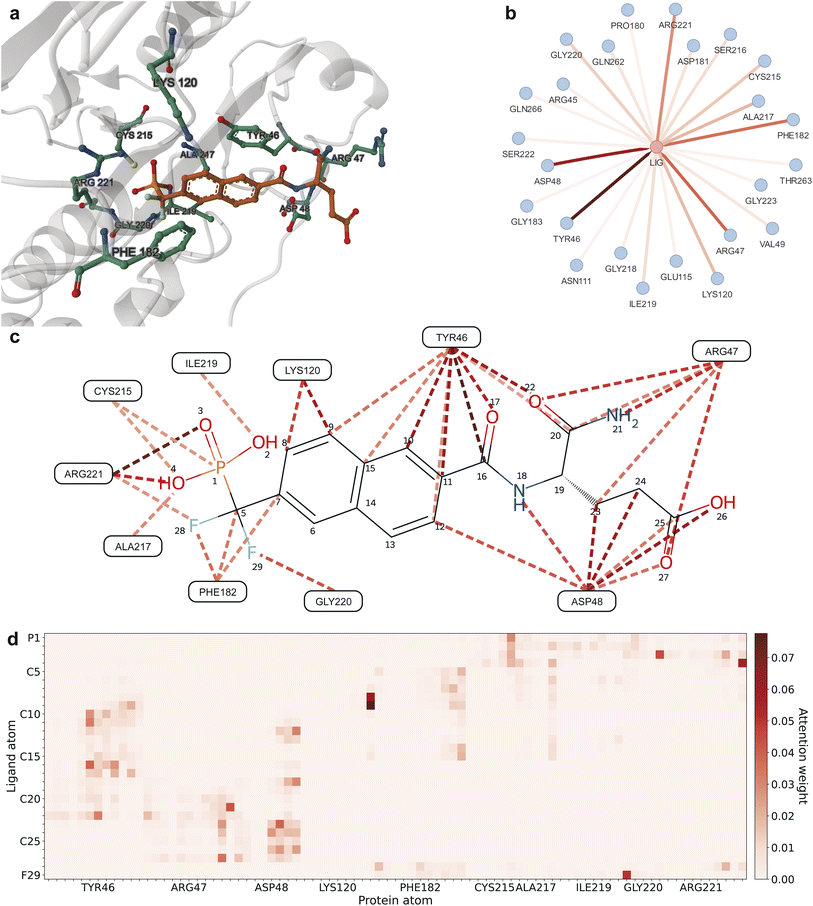 | ||
| Fig. 7 Visualization of interactions based on the attention weights from the final graph transformer layer of DeepRLI. Darker colors represent higher attention weights and more important interactions. The protein–ligand complex examined here is 1BZC. (a) The 3D structure of the binding site of the protein–ligand complex; residues with higher attention weights are additionally shown in ball-and-stick representation. (b) The graph displaying ligand–residue interaction connections. (c) The graph depicting [ligand atom]–residue interaction connections. (d) The heatmap illustrating [ligand atom]–[residue atom] interaction connections. For clarity, only part of interaction connections with a larger weight are shown for the latter two. | ||
To verify the rationality of the attention assignment during inference using the DeepRLI model, we employ the conventional rule-based Protein–Ligand Interaction Profiler (PLIP)81,82 to identify potential non-covalent interactions within the 1BZC complex. The analytical outcomes from PLIP, visualized in Fig. S7,† with the intricate details of various non-covalent interactions delineated in Tables S2–S4,† reveal notable findings. Specifically, π-stacking and hydrophobic interactions are observed between TYR46 and the naphthalene moiety of the TPI ligand; ARG47 is found to engage in hydrogen bonding with the carboxyl group of TPI; ASP48 exhibits hydrogen bonding with the amide segment of TPI; and the residues ALA217, ILE219, GLY220, and ARG221 demonstrate hydrogen bonding with the phosphonic acid moiety of TPI, among other interactions. Extended interpretability analyses for additional cases are provided in the ESI (Fig. S8–S15 and Tables S5–S18†).
By comparison, it is found that the DeepRLI model generally allocates greater attention weights to regions where these critical interactions actually exist. This intuitively reasonable phenomenon suggests that our model captures key interactions based on the atomic surroundings, which to a certain extent explains its robust predictive capability in binding affinity scoring.
3.3 Case study
According to the above results, DeepRLI nearly achieves state-of-the-art performance across a range of evaluations, including scoring, ranking, docking, and screening tasks. In light of DeepRLI's exceptional performance and its robust capability for generalization, we undertake a deeper investigation into its efficacy within practical application settings. Notably, other members of our research team have previously conducted drug design studies focused on the ATP binding site of the PLK1 kinase, during which they acquired experimental activity data for several small molecules.84 Building on this foundation, we initiate a retrospective analysis aimed at assessing the DeepRLI model's predictive accuracy within real-world application contexts, thereby providing a more comprehensive understanding of its potential utility in the field.Polo-like kinase 1 (PLK1) is a serine/threonine-protein kinase that plays a crucial role in various stages of mitosis.85 Across a broad spectrum of tumor types, PLK1 is frequently found to be overexpressed.86 And its expression is restricted to actively dividing cells, with no detectable presence in differentiated postmitotic cells, such as neurons.85 Based on the role of PLK1 in tumor development and its specific expression in dividing cells, PLK1 has become a promising target in cancer therapy strategies. There are already inhibitors targeting PLK1 that have completed clinical trials, such as the selective potent inhibitor Onvansertib (http://ClinicalTrials.gov identifier NCT03829410).83
Xie et al. from our research group developed an innovative generative model, TransPharmer, which integrates ligand-based pharmacophore fingerprints with generative pre-training transformers for de novo molecular generation. TransPharmer's characteristic exploration pattern within localized chemical spaces makes it particularly suitable for scaffold hopping, capable of generating structurally novel and pharmacologically relevant compounds.84 Moreover, leveraging TransPharmer, they generated potential new PLK1 inhibitors (namely IIP0942, IIP0943, IIP0944, and IIP0945) from the topological pharmacophore fingerprints obtained from Onvansertib and experimentally determined their activities (IC50),84 as shown in Table 6.
| Ligand | Glide XP score (kcal mol−1) | DeepRLI screening score | IC50 (nM) |
|---|---|---|---|
| Onvansertib | −11.56 | −5.07 | 4.8 |
| IIP0942 | −12.39 | −4.83 | 37.6 |
| IIP0943 | −11.19 | −5.00 | 5.1 |
| IIP0944 | −9.54 | −3.44 | >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| IIP0945 | −10.82 | −4.92 | 927 |
We acquire the optimal binding poses between the ATP site of PLK1 kinase and the five small molecules (Onvansertib, IIP0942, IIP0943, IIP0944, and IIP0945) using the Glide XP40 molecular docking program (illustrated in the left part of Fig. 8). Subsequently, in virtue of our DeepRLI interaction prediction model, we predict the binding efficacies of these molecular complexes. The outcomes of the screening readout are displayed in Table 6, along with the binding free energy scores estimated by Glide XP. Through careful analysis and comparison, we observe that except for IIP0945, the DeepRLI model is able to accurately predict the activity ranking of the small molecule compounds, thus demonstrating its outstanding performance in evaluating binding efficacy. Although the Glide XP method also successfully predicts the activity ranking of the other small molecules except for Onvansertib, the DeepRLI model shows more precise judgment in predicting the small molecule with the strongest binding efficacy, reflecting its superiority in this field.
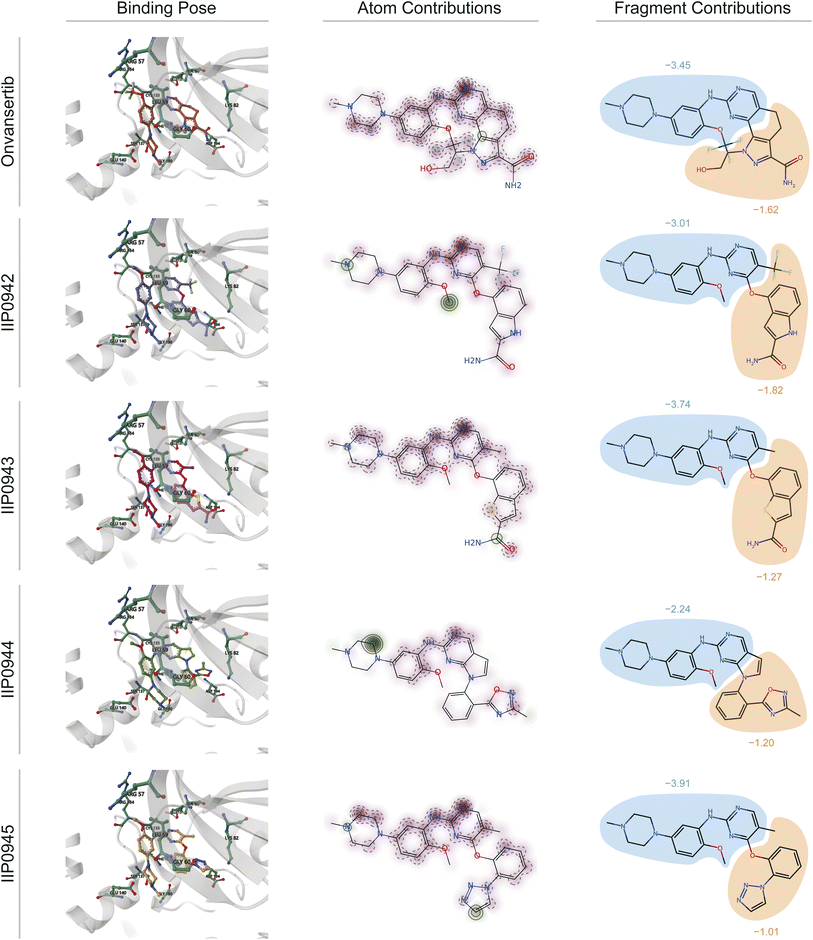 | ||
| Fig. 8 Visualization of interactions based on the atomic pair potentials derived from the physics-informed block in the screening readout of DeepRLI. The protein studied here is serine/threonine protein kinase PLK1, and the binding site involved is the ATP-pocket thereof. Onvansertib is recognized as an early-reported, potent, and selective inhibitor of PLK1, with its complex crystal structure deposited under the PDB identifier 2YAC.83 Other molecules named with the prefix “IIP” are potential active inhibitors designed using TransPharmer.84 From left to right, the binding poses of the five ligands combined with PLK1 predicted by Glide XP, as well as the atomic contributions and fragment contributions to the protein–ligand interactions inferred using DeepRLI, are displayed. In the atomic contribution diagrams, the red areas indicate negative interaction contributions, meaning they are favorable for binding; the green areas indicate positive interaction contributions, meaning they hinder binding. In the fragment contribution diagrams, the areas enclosed in blue represent the common substructures of these molecules, and the yellow areas represent their differences. | ||
In the DeepRLI framework, which incorporates a module informed by physical principles, interpretability extends beyond the attention mechanisms inherent in the graph transformer. The module's inclusion of interatomic interaction potential energy data, as delineated in eqn (11)–(15), further enhances this aspect. This is particularly pertinent in the context of docking and screening readouts, where such data facilitate a more nuanced understanding of the origins of predictive outcomes.
The DeepRLI model employs an empirical potential function for interatomic interactions, which is parameterized by neural network variables. Unlike traditional models that rely on predetermined functional forms, DeepRLI's approach dynamically derives the exact mathematical expression of the potential function from the latent embeddings of atomic pairs, thereby adapting to the specifics of each molecular interaction.
To elucidate the contribution of various ligand regions to the interaction, quantified as the screening score, we extract potential energies associated with atomic pairs formed between all protein atoms at the binding site and all ligand atoms. For each ligand atom, the cumulative potential energy arising from interactions with all protein atoms is computed. This computation yields a distribution map of interaction contributions for the ligand atoms, as exemplified in Fig. 8. In these visual representations, beneficial interactions (characterized by negative potential energy) are denoted in red, whereas detrimental interactions (with positive potential energy) are indicated in green. The intensity of the color correlates with the magnitude of the interaction's contribution, with darker shades signifying larger absolute values.
Comparative analysis of these atomic-level distribution maps reveals a correlation between the extent and intensity of green areas (denoting unfavorable interactions) and lower screening scores. This pattern is indicative of spatial clashes between atoms, which impede the tight association between the protein and the ligand, thereby diminishing the likelihood of effective binding. Such insights underscore the intricate balance of forces governing molecular interactions and highlight the utility of DeepRLI in decoding these complex phenomena for enhanced predictive accuracy in computational drug discovery.
Furthermore, it is noteworthy that the small molecules derived from the TransPharmer design exhibit a shared substructural motif with Onvansertib, specifically N-(2-methoxy-5-(4-methylpiperazin-1-yl)phenyl)pyrimidin-2-amine. This motif is depicted as the blue region in the part illustrated on the right side of Fig. 8. The aggregate contribution of a fragment to molecular interaction is determined by summing the interaction contributions of all constituent atoms within the fragment. Consequently, this approach facilitates a comparative analysis of the interaction contributions attributable to identical fragments across the five small molecules in question, as well as an examination of the interaction contributions from the distinct fragments not shared among these molecules. The findings of this analysis are graphically represented in the right segment of Fig. 8.
From the graphical representation, it is evident that the DeepRLI model's overestimation of the binding affinity for IIP0945 primarily stems from the influence of the shared substructural moiety. Although the screening score for IIP0943 closely mirrors that of Onvansertib, IIP0943's contributions in areas of structural variance are inferior to those of Onvansertib. Hence, the relative superiority of IIP0943 is predominantly attributed to the advantageous conformational poses that the shared substructure is able to adopt following a skeletal transition.
Overall, DeepRLI's evaluation of the binding efficacy of known inhibitors of PLK1 kinase (Onvansertib) as well as potential inhibitors designed by our research group (IIP0942, IIP0943, IIP0944, and IIP0945) is quite reasonable, reflecting its reliability in practical applications. Moreover, the interpretability of DeepRLI can be used to analyze the contribution of interactions of various fragments of ligand molecules, thus providing effective guidance for the procedures of hit-to-lead and lead optimization.
4 Conclusions
In this study, we propose DeepRLI, a novel multi-objective deep learning framework designed for the universal protein–ligand interaction prediction. DeepRLI employs a fully-connected graph as its input, effectively preserving the molecular topology and spatial structures. And this framework uses an improved graph transformer layer, combined with cosine constraints, which facilitates robust feature embedding. Central to DeepRLI's architecture are three distinct downstream networks, each dedicated to a specific predictive task: scoring, docking, and screening. The scoring readout network aims to accurately predict the binding free energy of crystal structures using a series of basic fully-connected layers. Meanwhile, the docking and screening readout networks focus on identifying the optimal binding poses and enriching active small molecules, respectively. A key characteristic in these networks is the integration of physical information blocks, designed to improve the model's inference capability, especially for protein–ligand conformations with loose bindings that deviate from typical crystal structures. To further enhance the model's generalization ability, we incorporated data augmentation techniques, including re-docking and cross-docking procedures to generate more data, complemented by contrastive learning strategies. This combination enhances DeepRLI's applicability across diverse datasets and scenarios.DeepRLI's efficacy was rigorously tested on several established benchmarks. Its performance was evaluated across a range of tasks – scoring, ranking, docking, and screening – on the CASF-2016, CSAR-NRC HiQ, Merck FEP, and LIT-PCBA benchmarks. The results consistently demonstrate DeepRLI's superior inferential abilities in all tested domains, underscoring its versatility as a predictive tool for protein–ligand interactions. Additionally, a retrospective analysis was conducted on the PLK1 kinase target to evaluate its practical applicability. The results of the study indicate that, compared to Glide XP, DeepRLI is capable of better predicting the binding efficacy of various small molecules with the protein, demonstrating satisfactory screening performance suitable for practical application scenarios.
Furthermore, the implementation of a graph transformer layer as the primary feature embedding module in DeepRLI offers notable interpretability advantages. The model assigns greater attention weights to edges that signify crucial interaction patterns, providing insights into the underlying molecular interactions.
In conclusion, the DeepRLI framework can effectively provide useful guidance for structure-based drug design. Its innovative approach and proven efficacy in predicting protein–ligand interactions position it as a powerful and versatile tool in the field of drug discovery.
5 Methods
5.1 Input features
Node features, αi, and edge features, βij, are chemical features extracted from atoms and bonds, respectively, and then transformed into representations suitable for deep learning. Specifically, for the input of our neural network, the node features are represented as 39-dimensional vectors, detailed in Table S19.† These vectors include a dimension to differentiate between protein and ligand atoms. The remaining dimensions encapsulate atomic properties derived using the RDKit cheminformatics package.87 It is important to note that our model's input criteria exclude hydrogen atoms, focusing exclusively on heavy atoms. Consequently, chemical element symbols in our representation do not include hydrogen. Moreover, due to the negligible metal content in the PDBbind dataset,88,89 all metal elements are collectively categorized under a single “Met” element. Elements not explicitly listed are denoted as “Unk” (Unknown). Additionally, the “degree” feature in our model quantifies the number of covalent bonds an atom forms with other heavy atoms, effectively representing the number of edges connected to a node. The other attributes of the node features are self-explanatory and contribute to the comprehensive representation of chemical entities in our neural network model.The edge features are 39-dimensional vectors, as shown in Table S20,† among which two dimensions are designated for discerning whether the interaction is intermolecular or covalent, and the remainder includes the type of chemical bond and the distance between atoms. It should be noted that the atomic distance is not encapsulated by a singular dimension, but is instead represented through a series of 33 Gaussian functions, uniformly distributed within a range of 6.5 Å, each with a width equivalent to the interval. This method of representation results in an expanded distance vector, consisting of multiple values ranging between 0 and 1. Such a multi-valued representation of distance is more effective for the model, facilitating a nuanced utilization of distance data.
5.2 Datasets
The training and validation of the DeepRLI model are conducted using datasets that encompass crystal structure–activity data from PDBbind-v2020,88,89 supplemented with derived re-docking and cross-docking data. Corresponding to the three training objectives, our dataset also comprises these three parts. The PDBbind database collects a wealth of protein–ligand complex structures and related experimental binding affinity data, making it the most widely used dataset for structure-based protein–ligand binding affinity prediction studies. For the scoring objective, we need to know precise binding free energy data of some structures, which can be directly obtained from PDBbind. However, nearly half of the data in the PDBbind general set are experimental results with only IC50 values or imprecise Kd values (notated as greater than, less than, or approximately equal to). Therefore, we remove these data and retained only the crystal structure data with exact Kd values. And this curated dataset is named PDBbindGS_HiQ by us.To enhance the robustness and accuracy of our model in docking and screening tasks, a key requirement is to ensure its adeptness in generalizing to loosely bound structures. To address this, we re-dock the structures from the PDBbind refined set using AutoDock Vina,28,29 thus generating a series of binding conformations. These are compiled into what we have termed the PDBbindRS_RD dataset, which serves to significantly bolster the model's capability in docking predictions. Given that the exact relative free energy values of these conformations are not precisely known, we posit a correlation between the root-mean-square distance (RMSD) of these conformations from the original crystallographic structures and their relative free energy. Conformations exhibiting an RMSD of 2 Å or less are hypothesized to possess lower relative free energy, and are thus classified as positive instances (truths). Conversely, those with an RMSD of 4 Å or greater are categorized as negative (decoys). Furthermore, to augment the model's screening proficiency, we initiate a cross-docking protocol involving structures from the PDBbind refined set, thereby creating the PDBbindRS_CD dataset. This process entails docking various small molecules present in the database with a range of proteins. All conformations resultant from this process are deemed as negative (decoys), providing a comprehensive dataset for enhancing the predictive accuracy of our model in identifying viable drug candidates.
The data unit for training is formed by a collection of structures. Specifically, the minimal input required for training encompasses several components associated with the same protein target: a crystal structure–activity data pair, a randomly selected re-docked positive structure, a randomly selected re-docked negative structure, and a randomly selected cross-docked negative structure, as detailed in Table S21.† For a data unit to comply with our criteria, it is essential that it contains at least one instance of these specified data types, corresponding to a particular Protein Data Bank (PDB) identifier. After intersecting the PDBbindGS_HiQ, PDBbindRS_RD, and PDBbindRS_CD datasets and removing data duplicated with the CASF-2016 benchmark test set, we ultimately obtain 4156 such data units. Additionally, to fully utilize the limited but valuable crystal structure–activity data pairs, we randomly supplement the remaining data from PDBbindGS_HiQ (7337 items) into the aforementioned data units during training. This approach is implemented to maximize the utility of the available data in our training protocol.
5.3 Training
The overarching aim of our model training is the concurrent optimization of predictions for three distinct variables: scoring scores, docking scores, and screening scores. This tripartite goal, depicted in Fig. 3, comprises the scoring, docking, and screening objectives. These objectives, while being distinct and relatively independent, are intricately interrelated.1. Scoring objective: This involves refining the scoring scores to align the model's predictions more closely with the actual relative free energies. Given that the experimental binding free energies (anchors) are available only for the native crystal structures, our focus is on enhancing the accuracy of the model's scoring predictions specifically for these native poses.
2. Docking objective: The goal here is to fine-tune the docking scores. The model is trained to yield lower docking scores for poses that closely resemble the native binding pose. Specifically, we aim to achieve lower predicted docking scores for any pose with the RMSD less than 2 Å from the native crystal structure's small molecule compared to poses with an RMSD greater than 4 Å.
3. Screening objective: This objective seeks to optimize the screening scores, with a focus on minimizing the scores predicted for active binders. Essentially, the model is calibrated to ensure that the predicted screening scores for any active ligand are lower than those for any inactive decoy.
Through these tailored objectives, our model aims to achieve a nuanced and precise prediction capability, catering to the specific demands of each aspect of the drug design process.
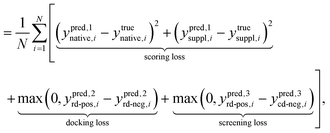
In alignment with the previously delineated objectives, DeepRLI's loss function comprises three distinct components: scoring loss, docking loss, and screening loss, as described in eqn (19) and (20):
 | (19) |
 | (20) |
The scoring loss adheres to a conventional methodology, utilizing the Mean Squared Error (MSE) to quantify the discrepancy between the scoring score predicted by the model, denoted as ypred,1, and the corresponding experimental binding free energy, ytrue.
Conversely, for structures resulting from docking processes, their exact relative free energies remain elusive. However, we can roughly know the relative magnitude of free energy between certain structures. Therefore, we innovatively introduce a contrastive loss function to help achieve docking and screening objectives. The selection of an appropriate contrastive loss function presents multiple viable options, including HalfMSE, ReLU, Softplus, exp, etc., as listed in Table S22 and depicted in Fig. S16,† with comprehensive derivations available in the ESI.† Noteworthy is the characteristic of both HalfMSE and ReLU, featuring a segment on their left spectrum that incurs no loss, thereby ensuring null loss when predictions accurately reflect the true binary relationships. This design effectively circumvents the potential issue of artificially induced gaps in predicted values, a concern prevalent in functions like Softplus and exp. Furthermore, the right extremity of the ReLU function exhibits a more gradual slope compared to HalfMSE, offering a degree of leniency towards certain incorrectly presupposed binary relationships. Consequently, after thorough consideration, ReLU is selected as the most suitable contrastive loss function for our docking and screening objectives, as detailed in eqn (20).
In this study, the aforementioned dataset is partitioned into a training set and a validation set in a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. For optimization, the Adam algorithm is utilized, supplemented with a plateau-based learning rate decay strategy. This approach entails a reduction in the learning rate when no improvement is observed in the validation set loss across a predefined number of consecutive epochs. The training protocol is designed to terminate automatically once the learning rate descends below a specified threshold. For detailed hyperparameter settings, please refer to Section 2.4 of the ESI.† The model corresponding to the final epoch is selected as the outcome of the training phase.
1 ratio. For optimization, the Adam algorithm is utilized, supplemented with a plateau-based learning rate decay strategy. This approach entails a reduction in the learning rate when no improvement is observed in the validation set loss across a predefined number of consecutive epochs. The training protocol is designed to terminate automatically once the learning rate descends below a specified threshold. For detailed hyperparameter settings, please refer to Section 2.4 of the ESI.† The model corresponding to the final epoch is selected as the outcome of the training phase.
Code availability
The source code of DeepRLI is publicly available at https://github.com/fairydance/DeepRLI.Data availability
The PDBbindGS_HiQ, PDBbindRS_RD and PDBbindRS_CD datasets crafted in this work, along with the preprocessed training dataset and PLK1 case-related data, are publicly accessible on Zenodo (https://doi.org/10.5281/zenodo.15654352). Additionally, the source code of DeepRLI and the trained model can also be obtained from the same Zenodo repository. Detailed information on executing data processing, model training, and model inference is provided in the README file of the code package.Author contributions
H. L. conceived the basic idea. H. L. designed and implemented the deep learning model and performed the model training, evaluation and interpretation. H. L., J. Z. and S. W. participated in the processing of training data and test data. H. L., J. Z., S. W. and Y. L. discussed some details of the concepts and methods. J. P. and L. L. supervised the project. H. L. wrote the manuscript. J. Z., J. P. and L. L. revised the manuscript. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (22033001 and T2321001), the National Key R&D Program of China (grant 2023YFF1205103), the Chinese Academy of Medical Sciences (2021-I2M-5-014) and the Anhui's Plans for Major Provincial Science&Technology Projects (202303a07020009). We thank the team managing the high-performance computing platform at the Peking-Tsinghua Center for Life Sciences, Peking University, for providing the computational resources.Notes and references
- B. E. Blass, Basic Principles of Drug Discovery and Development, Academic Press, United Kingdom, 2nd edn, 2021 Search PubMed.
- M. Gore and U. B. Jagtap, Computational Drug Discovery and Design, Springer, United States, 2018 Search PubMed.
- D. B. Singh, Computer-Aided Drug Design, Springer, Singapore, 2020 Search PubMed.
- R. K. Pathria and P. D. Beale, Statistical Mechanics, Academic Press, United Kingdom, 4th edn, 2021 Search PubMed.
- Free Energy Calculations: Theory and Applications in Chemistry and Biology, ed. C. Chipot and A. Pohorille, Springer, Germany, 2007 Search PubMed.
- R. Baron, Computational Drug Discovery and Design, Humana Press, United States, 2012 Search PubMed.
- J. Liu and R. Wang, J. Chem. Inf. Model., 2015, 55, 475–482 CrossRef CAS.
- J. Li, A. Fu and L. Zhang, Interdiscip. Sci., 2019, 11, 320–328 CrossRef CAS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS.
- S. K. Burley, C. Bhikadiya, C. Bi, S. Bittrich, H. Chao, L. Chen, P. A. Craig, G. V. Crichlow, K. Dalenberg, J. M. Duarte, S. Dutta, M. Fayazi, Z. Feng, J. W. Flatt, S. Ganesan, S. Ghosh, D. S. Goodsell, R. K. Green, V. Guranovic, J. Henry, B. P. Hudson, I. Khokhriakov, C. L. Lawson, Y. Liang, R. Lowe, E. Peisach, I. Persikova, D. W. Piehl, Y. Rose, A. Sali, J. Segura, M. Sekharan, C. Shao, B. Vallat, M. Voigt, B. Webb, J. D. Westbrook, S. Whetstone, J. Y. Young, A. Zalevsky and C. Zardecki, Nucleic Acids Res., 2022, 51, D488–D508 CrossRef.
- S. Dara, S. Dhamercherla, S. S. Jadav, C. M. Babu and M. J. Ahsan, Artif. Intell. Rev., 2022, 55, 1947–1999 CrossRef.
- C. Cerchia and A. Lavecchia, Drug Discovery Today, 2023, 28, 103516 CrossRef CAS.
- R. Meli, G. M. Morris and P. C. Biggin, Front. Bioinform., 2022, 2, 885983 CrossRef.
- J. Jiménez, M. Škalič, G. Martínez-Rosell and G. De Fabritiis, J. Chem. Inf. Model., 2018, 58, 287–296 CrossRef.
- D. Jiang, C.-Y. Hsieh, Z. Wu, Y. Kang, J. Wang, E. Wang, B. Liao, C. Shen, L. Xu, J. Wu, D. Cao and T. Hou, J. Med. Chem., 2021, 64, 18209–18232 CrossRef CAS.
- O. Méndez-Lucio, M. Ahmad, E. A. del Rio-Chanona and J. K. Wegner, Nat. Mach. Intell., 2021, 3, 1033–1039 CrossRef.
- C. Shen, X. Zhang, Y. Deng, J. Gao, D. Wang, L. Xu, P. Pan, T. Hou and Y. Kang, J. Med. Chem., 2022, 65, 10691–10706 CrossRef CAS.
- M. Su, Q. Yang, Y. Du, G. Feng, Z. Liu, Y. Li and R. Wang, J. Chem. Inf. Model., 2019, 59, 895–913 CrossRef CAS.
- P. G. Francoeur, T. Masuda, J. Sunseri, A. Jia, R. B. Iovanisci, I. Snyder and D. R. Koes, J. Chem. Inf. Model., 2020, 60, 4200–4215 CrossRef CAS.
- J. A. Morrone, J. K. Weber, T. Huynh, H. Luo and W. D. Cornell, J. Chem. Inf. Model., 2020, 60, 4170–4179 CrossRef CAS.
- K. A. Stafford, B. M. Anderson, J. Sorenson and H. van den Bedem, J. Chem. Inf. Model., 2022, 62, 1178–1189 CrossRef CAS.
- J. Lim, S. Ryu, K. Park, Y. J. Choe, J. Ham and W. Y. Kim, J. Chem. Inf. Model., 2019, 59, 3981–3988 CrossRef CAS.
- C. Wang and Y. Zhang, J. Comput. Chem., 2017, 38, 169–177 CrossRef.
- J. Lu, X. Hou, C. Wang and Y. Zhang, J. Chem. Inf. Model., 2019, 59, 4540–4549 CrossRef CAS.
- C. Yang and Y. Zhang, J. Chem. Inf. Model., 2022, 62, 2696–2712 CrossRef CAS.
- S. Moon, W. Zhung, S. Yang, J. Lim and W. Y. Kim, Chem. Sci., 2022, 13, 3661–3673 RSC.
- C. Shen, X. Zhang, C.-Y. Hsieh, Y. Deng, D. Wang, L. Xu, J. Wu, D. Li, Y. Kang, T. Hou and P. Pan, Chem. Sci., 2023, 14, 8129–8146 RSC.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CrossRef CAS.
- J. Eberhardt, D. Santos-Martins, A. F. Tillack and S. Forli, J. Chem. Inf. Model., 2021, 61, 3891–3898 CrossRef CAS.
- V. P. Dwivedi and X. Bresson, arXiv, 2021, preprint, arXiv:2012.09699, DOI:10.48550/arXiv.2012.09699.
- G. P. P. Pun, R. Batra, R. Ramprasad and Y. Mishin, Nat. Commun., 2019, 10, 2339 CrossRef.
- R. Quiroga and M. A. Villarreal, PLoS One, 2016, 11, 1–18 CrossRef.
- J. B. J. Dunbar, R. D. Smith, C.-Y. Yang, P. M.-U. Ung, K. W. Lexa, N. A. Khazanov, J. A. Stuckey, S. Wang and H. A. Carlson, J. Chem. Inf. Model., 2011, 51, 2036–2046 CrossRef CAS.
- C. E. M. Schindler, H. Baumann, A. Blum, D. Böse, H.-P. Buchstaller, L. Burgdorf, D. Cappel, E. Chekler, P. Czodrowski, D. Dorsch, M. K. I. Eguida, B. Follows, T. Fuchß, U. Grädler, J. Gunera, T. Johnson, C. Jorand Lebrun, S. Karra, M. Klein, T. Knehans, L. Koetzner, M. Krier, M. Leiendecker, B. Leuthner, L. Li, I. Mochalkin, D. Musil, C. Neagu, F. Rippmann, K. Schiemann, R. Schulz, T. Steinbrecher, E.-M. Tanzer, A. Unzue Lopez, A. Viacava Follis, A. Wegener and D. Kuhn, J. Chem. Inf. Model., 2020, 60, 5457–5474 CrossRef CAS.
- V.-K. Tran-Nguyen, C. Jacquemard and D. Rognan, J. Chem. Inf. Model., 2020, 60, 4263–4273 CrossRef CAS.
- G. Durant, F. Boyles, K. Birchall, B. Marsden and C. M. Deane, Bioinformatics, 2025, 41, btaf040 CrossRef CAS.
- X. Zhang, H. Gao, H. Wang, Z. Chen, Z. Zhang, X. Chen, Y. Li, Y. Qi and R. Wang, J. Chem. Inf. Model., 2024, 64, 2205–2220 CrossRef CAS.
- R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley, J. K. Perry, D. E. Shaw, P. Francis and P. S. Shenkin, J. Med. Chem., 2004, 47, 1739–1749 CrossRef CAS.
- T. A. Halgren, R. B. Murphy, R. A. Friesner, H. S. Beard, L. L. Frye, W. T. Pollard and J. L. Banks, J. Med. Chem., 2004, 47, 1750–1759 CrossRef CAS.
- R. A. Friesner, R. B. Murphy, M. P. Repasky, L. L. Frye, J. R. Greenwood, T. A. Halgren, P. C. Sanschagrin and D. T. Mainz, J. Med. Chem., 2006, 49, 6177–6196 CrossRef CAS.
- R. Wang, L. Lai and S. Wang, J. Comput.-Aided Mol. Des., 2002, 16, 11–26 CrossRef CAS.
- R. Meli, A. Anighoro, M. J. Bodkin, G. M. Morris and P. C. Biggin, J. Cheminf., 2021, 13, 59 CAS.
- H. Öztürk, A. Özgür and E. Ozkirimli, Bioinformatics, 2018, 34, i821–i829 CrossRef.
- D. Chen, J. Liu and G.-W. Wei, Nat. Mach. Intell., 2024, 6, 799–810 CrossRef.
- G. W. Kyro, R. I. Brent and V. S. Batista, J. Chem. Inf. Model., 2023, 63, 1947–1960 CrossRef CAS.
- X. Liu, H. Feng, J. Wu and K. Xia, PLoS Comput. Biol., 2022, 18, 1–17 Search PubMed.
- R. Liu, X. Liu and J. Wu, J. Chem. Inf. Model., 2023, 63, 1066–1075 CrossRef CAS.
- Z. Yang, W. Zhong, Q. Lv, T. Dong and C. Yu-Chian Chen, J. Phys. Chem. Lett., 2023, 14, 2020–2033 CrossRef CAS.
- Z. Meng and K. Xia, Sci. Adv., 2021, 7, eabc5329 CrossRef CAS.
- J. Wee and K. Xia, J. Chem. Inf. Model., 2021, 61, 1617–1626 CrossRef CAS.
- Y. Wang, S. Wu, Y. Duan and Y. Huang, Briefings Bioinf., 2021, 23, bbab474 CrossRef.
- Y. Li, M. A. Rezaei, C. Li and X. Li, IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 2019, pp. 303–310 Search PubMed.
- K. Wang, R. Zhou, J. Tang and M. Li, Bioinformatics, 2023, 39, btad340 CrossRef CAS.
- D. D. Nguyen and G.-W. Wei, J. Chem. Inf. Model., 2019, 59, 3291–3304 CrossRef CAS.
- S. Wang, D. Liu, M. Ding, Z. Du, Y. Zhong, T. Song, J. Zhu and R. Zhao, Front. Genet., 2021, 11, 607824 CrossRef.
- X. Zhang, Y. Li, J. Wang, G. Xu and Y. Gu, Interdiscip. Sci.:Comput. Life Sci., 2023, 15, 696–709 CrossRef CAS.
- M. M. Rana and D. D. Nguyen, J. Chem. Inf. Model., 2022, 62, 4329–4341 CrossRef CAS.
- H. Hassan-Harrirou, C. Zhang and T. Lemmin, J. Chem. Inf. Model., 2020, 60, 2791–2802 CrossRef CAS.
- S. Seo, J. Choi, S. Park and J. Ahn, BMC Bioinf., 2021, 22, 542 CrossRef CAS.
- M. Wójcikowski, M. Kukiełka, M. M. Stepniewska-Dziubinska and P. Siedlecki, Bioinformatics, 2018, 35, 1334–1341 CrossRef.
- L. Zheng, J. Fan and Y. Mu, ACS Omega, 2019, 4, 15956–15965 CrossRef CAS.
- L. Dong, X. Qu and B. Wang, ACS Omega, 2022, 23, 21727–21735 CrossRef.
- M. Volkov, J.-A. Turk, N. Drizard, N. Martin, B. Hoffmann, Y. Gaston-Mathé and D. Rognan, J. Med. Chem., 2022, 65, 7946–7958 CrossRef CAS.
- Y. Kwon, W.-H. Shin, J. Ko and J. Lee, Int. J. Mol. Sci., 2020, 21, 8424 CrossRef CAS.
- Z. Cang and G.-W. Wei, PLoS Comput. Biol., 2017, 13, 1–27 CrossRef.
- D. Jones, H. Kim, X. Zhang, A. Zemla, G. Stevenson, W. F. D. Bennett, D. Kirshner, S. E. Wong, F. C. Lightstone and J. E. Allen, J. Chem. Inf. Model., 2021, 61, 1583–1592 CrossRef CAS.
- K. Osaki, T. Ekimoto, T. Yamane and M. Ikeguchi, J. Phys. Chem. B, 2022, 126, 6148–6158 CrossRef CAS.
- S. Li, J. Zhou, T. Xu, L. Huang, F. Wang, H. Xiong, W. Huang, D. Dou and H. Xiong, Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, 2021, pp. 975–985 Search PubMed.
- Y. Wang, Z. Wei and L. Xi, BMC Bioinf., 2022, 23, 222 CrossRef CAS.
- M. M. Stepniewska-Dziubinska, P. Zielenkiewicz and P. Siedlecki, Bioinformatics, 2018, 34, 3666–3674 CrossRef CAS.
- J. Son and D. Kim, PLoS One, 2021, 16, 1–13 Search PubMed.
- F. Zhu, X. Zhang, J. E. Allen, D. Jones and F. C. Lightstone, J. Chem. Inf. Model., 2020, 60, 2766–2772 CrossRef CAS.
- J. Li, X. Guan, O. Zhang, K. Sun, Y. Wang, D. Bagni and T. Head-Gordon, arXiv, 2023, preprint, arXiv:2308.09639, DOI:10.48550/arXiv.2308.09639.
- J. Zhu, Z. Gu, J. Pei and L. Lai, Chem. Sci., 2024, 15, 7926–7942 RSC.
- R. Huey, G. M. Morris, A. J. Olson and D. S. Goodsell, J. Comput. Chem., 2007, 28, 1145–1152 CrossRef CAS.
- D. Dorsch, O. Schadt, F. Stieber, M. Meyring, U. Grädler, F. Bladt, M. Friese-Hamim, C. Knühl, U. Pehl and A. Blaukat, Bioorg. Med. Chem. Lett., 2015, 25, 1597–1602 CrossRef CAS.
- M. R. Groves, Z.-J. Yao, P. P. Roller, T. R. Burke and D. Barford, Biochemistry, 1998, 37, 17773–17783 CrossRef CAS.
- B. G. Neel and N. K. Tonks, Curr. Opin. Cell Biol., 1997, 9, 193–204 CrossRef CAS.
- J. M. Denu, J. A. Stuckey, M. A. Saper and J. E. Dixon, Cell, 1996, 87, 361–364 CrossRef CAS.
- F. Ahmad, P.-M. Li, J. Meyerovitch and B. J. Goldstein, J. Biol. Chem., 1995, 270, 20503–20508 CrossRef CAS.
- S. Salentin, S. Schreiber, V. J. Haupt, M. F. Adasme and M. Schroeder, Nucleic Acids Res., 2015, 43, W443–W447 CrossRef CAS.
- M. F. Adasme, K. L. Linnemann, S. N. Bolz, F. Kaiser, S. Salentin, V. J. Haupt and M. Schroeder, Nucleic Acids Res., 2021, 49, W530–W534 CrossRef CAS.
- I. Beria, R. T. Bossi, M. G. Brasca, M. Caruso, W. Ceccarelli, G. Fachin, M. Fasolini, B. Forte, F. Fiorentini, E. Pesenti, D. Pezzetta, H. Posteri, A. Scolaro, S. R. Depaolini and B. Valsasina, Bioorg. Med. Chem. Lett., 2011, 21, 2969–2974 CrossRef CAS.
- W. Xie, J. Zhang, Q. Xie, C. Gong, Y. Ren, J. Xie, Q. Sun, Y. Xu, L. Lai and J. Pei, Nat. Commun., 2025, 16, 2391 CrossRef CAS.
- K. Strebhardt, Nat. Rev. Drug Discovery, 2010, 9, 643–660 CrossRef CAS.
- W. Weichert, M. Schmidt, V. Gekeler, C. Denkert, C. Stephan, K. Jung, S. Loening, M. Dietel and G. Kristiansen, Prostate, 2004, 60, 240–245 CrossRef CAS.
- G. Landrum, P. Tosco, B. Kelley, R. Rodriguez, D. Cosgrove, R. Vianello, P. sriniker, G. Jones, E. Kawashima, N. Schneider, D. Nealschneider, A. Dalke, M. Swain, B. Cole, S. Tadhurst-cdd, A. Savelev, A. Vaucher, M. Wójcikowski, I. Take, R. Walker, V. F. Scalfani, H. Faara, K. Ujihara, D. Probst, N. Maeder, J. Monat, J. Lehtivarjo and G. Godin, rdkit/rdkit: 2025_03_4 (Q1 2025) Release, 2025, DOI:10.5281/zenodo.15773589.
- R. Wang, X. Fang, Y. Lu and S. Wang, J. Med. Chem., 2004, 47, 2977–2980 CrossRef CAS.
- R. Wang, X. Fang, Y. Lu, C.-Y. Yang and S. Wang, J. Med. Chem., 2005, 48, 4111–4119 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1–S16 and Tables S1–S23. See DOI: https://doi.org/10.1039/d4dd00403e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |