 Open Access Article
Open Access ArticleAnubis: Bayesian optimization with unknown feasibility constraints for scientific experimentation†
Riley J.
Hickman
 *abc,
Gary
Tom
*abc,
Gary
Tom
 abc,
Yunheng
Zou
bc,
Matteo
Aldeghi‡
abc,
Yunheng
Zou
bc,
Matteo
Aldeghi‡
 abc and
Alán
Aspuru-Guzik
abc and
Alán
Aspuru-Guzik
 *abcdefg
*abcdefg
aChemical Physics Theory Group, Department of Chemistry, University of Toronto, Toronto, ON M5S 3H6, Canada. E-mail: riley.hickman@mail.utoronto.ca; alan@aspuru.com
bDepartment of Computer Science, University of Toronto, Toronto, ON M5S 3H6, Canada
cVector Institute for Artificial Intelligence, Toronto, ON M5S 1M1, Canada
dAcceleration Consortium, University of Toronto, Toronto, ON M5S 3E5, Canada
eDepartment of Chemical Engineering & Applied Chemistry, University of Toronto, Toronto, ON M5S 3E5, Canada
fDepartment of Materials Science & Engineering, University of Toronto, Toronto, ON M5S 3E4, Canada
gLebovic Fellow, Canadian Institute for Advanced Research, Toronto, ON M5G 1Z8, Canada
First published on 18th June 2025
Abstract
Model-based optimization strategies, such as Bayesian optimization (BO), have been deployed across the natural sciences in design and discovery campaigns due to their sample efficiency and flexibility. The combination of such strategies with automated laboratory equipment and/or high-performance computing in a suggest-make-measure closed-loop constitutes a self-driving laboratory (SDL), which has been endorsed as a next-generation technology for autonomous scientific experimentation. Despite the promise of early SDL prototypes, a lack of flexible experiment planning algorithms prevents certain prevalent optimization problem types from being addressed. For instance, many experiment planning algorithms are unable to intelligently deal with failed measurements resulting from a priori unknown constraints on the parameter space. Such constraint functions are pervasive in chemistry and materials science research, stemming from unexpected equipment failures, failed/abandoned syntheses, or unstable molecules or materials. In Anubis, we provide a comprehensive discussion and benchmark of BO strategies to handle a priori unknown constraints, characterized by learning the constraint function on-the-fly using a variational Gaussian process classifier and combining its predictions with the typical BO regression surrogate to parameterize feasibility-aware acquisition functions. These acquisition functions balance sampling parameter space regions deemed to be promising in terms of optimization objectives with avoidance of regions predicted to be infeasible. In addition to benchmarking feasibility-aware acquisition functions on analytic optimization benchmark surfaces, we conduct two realistic optimization benchmarks derived from previously reported studies: inverse design of hybrid organic–inorganic halide perovskite materials with unknown stability constraints, and the design of BCR-Abl kinase inhibitors with unknown synthetic accessibility constraints. We deliver intuitive recommendations to readers on which strategies work best for various scenarios. Our results show that feasibility-aware strategies with balanced risk, on average, outperform commonly adopted naive strategies, producing more valid experiments and finding the optima at least as fast. In tasks with smaller regions of infeasibility, we find that naïve strategies can perform competitively. Overall, this work contributes to advancing the practicality and efficiency of autonomous experimentation in SDLs. All strategies introduced in this work are implemented as part of the open-source Atlas Python library.
1. Introduction
Progress in the areas of chemistry and materials science is often contingent on the targeted design of new molecules, materials and manufacturing processes that supersede their predecessors with respect to some measurable property. As a fundamental aspect in numerical science, it is not surprising that many design/discovery challenges in these areas can be cast as optimization problems. Solutions to such optimization problems are determined by systematic variation of input parameters from an allowed set with the goal of maximizing or minimizing a property or set of properties.In experimental science research, so-called “black-box” optimization problems are of particular interest, given that the objective functions thereof typically have a priori unknown structures and must be sequentially determined using measurements. Other characteristics of experimental optimizations include noise in both input parameters and property measurements and relatively low parameter and objective dimensionality (<20 and <10 in most cases, respectively). Model-based optimization strategies, such as Bayesian optimization (BO)1–3 are particularly well-suited for such tasks.4–10 The combination of model-based optimization with automated laboratory equipment results in self-driving laboratories (SDLs),11–20 which are rapidly experiencing adoption across the natural sciences. Prototypes of SDLs have targeted organic synthesis and process optimization,5,21–30 nanomaterials,31–36 and light-harvesting materials37–41 to name a few.42–45
Despite the already apparent aptitude for SDLs to accelerate scientific research, their practical application is limited by the lack of flexible software and algorithms tailored to the specific requirements of experimental science. One pervasive example is the inability of many BO algorithms to handle parameter space constraints. Although types of constrained optimization problems are diverse,46 we focus the discussion in this work on two types.
Known constraints are those known to the researcher a priori to commencing an experimental campaign. They can be interdependent, non-linear, and result in non-compact optimization domains. Our group's previous work focused on extensions to BO strategies such that they would avoid sampling constrained regions.47 Another type of known constraint problems may arise when the optimization domain contains degenerate solutions (e.g. with respect to scaling, composition or permutation of input parameters). Baird et al. recently described the relationship between search space reducibility and BO performance for an application in solid rocket fuel packing.48
Contrastingly, unknown constraints are those constraints on the optimization domain which are a priori unknown, and, much like the objective function, must be resolved on-the-fly by sequential measurement. As the types of optimization constraints encountered are diverse, in this work we chose to focus specifically on nonquantifiable, unrelaxable, simulation, hidden constraints, according to the taxonomy by Digabel and Wild.46
• Non-quantifiable: for a nonquantifiable constraint, the researcher is returned only binary information about whether the constraint has been satisfied or violated. This is contrasted with quantifiable constraints, where some auxiliary information is available about the proximity of the experiment to the feasible/infeasible boundary.
• Unrelaxable: an unrelaxable constraint must be satisfied for an objective function measurement to be obtained. In other words, we consider cases where no objective information is returned for an experiment that violates the constraint.
• Simulation: a simulation constraint is one in which a costly procedure is involved in evaluating the constraint for a set of parameters. We note that a simulation, as defined by Digabel and Wild, refers to the constraint in the cost of making a measurement, rather than a computational or numerical process. Although infeasible experiments may overall be cheaper to evaluate than feasible ones, we assume some non-negligible effort that one would prefer to avoid, if possible. For example, in a molecular design task in which evaluation of the objective function (e.g. a bioassay) follows the synthesis of a drug molecule, the a priori unknown synthetic feasibility constraint function is evaluated directly after the attempted synthesis.
• Hidden: hidden constraints are those which are not explicitly known to the researcher, as opposed to known constraints, which are explicitly defined during formulation of the optimization problem.
Unknown constraints frequently complicate optimization problems across the natural sciences. In many molecular design tasks, candidates are selected from a virtual library of molecules which are assumed to be synthetically accessible. Selection is followed by a synthesize-measure procedure, in which an attempt is made to synthesize the molecule, and if successful, its objective is determined. The synthesis step in this procedure could fail for several reasons (e.g. insufficient yield to conduct the property measurement, insufficient stability of the product, etc.). Although several approaches for computational prediction of the organic reaction outcome have been described,49–51 these tools are typically regarded as coarse-grained proxies for synthetic accessibility. Therefore, synthetic accessibility of molecular candidates is often an unknown constraint which is ideally inferred on-the-fly for a novel design campaign.
Experimental failures are not unique to organic synthesis. A target compound may form but exhibit undesirable properties that prevent characterization, such as excessive fragility or insufficient photoluminescence for spectroscopic analysis.45 Wakabayashi et al. studied molecular beam epitaxy of SrRuO3, a widely used metallic electrode in oxide electronics, in which experimental failures occur when the SrRuO3 phase did not form, preventing measurement of the resistivity objective.52 Even in computational chemistry, unknown constraints can arise. For example, a simulation might fail to converge due to unforeseen limitations in the chosen parameters, preventing the calculation of the desired property.53 Furthermore, limitations in instrument sensitivity or resolution can preclude accurate measurements, effectively acting as an unknown constraint on the observable properties.
While several approaches have been suggested for BO with unknown constraints,54–61 relatively little effort has been dedicated to evaluating the suitability of these strategies on representative optimization problems in the experimental sciences. Furthermore, we have found that a comprehensive optimization benchmark of all relevant strategies is missing. Finally, we found that many popular BO packages do not consider unknown constraints altogether, or implement only the simplest approaches for dealing with them. Our goal for this work is to provide practitioners of autonomous science driven by BO comprehensive insight into which strategies for dealing with unknown constraints work best in various scenarios. To this end, we implement and test several different approaches for dealing with unknown constraints in our research group's open-source BO Python package, Atlas.62,63
The remainder of this work is organized as follows. Section 2 formally introduces optimization with unknown constraints and compares and contrasts our problem to related work. Section 3 describes our approaches to learning the constraint function, our feasibility-aware acquisition functions, as well as limitations of our approach. Section 4.1 presents a detailed comparison of optimization performance of each approach on synthetic benchmark surfaces. Finally, Sections 4.2 and 4.3 detail two world applications: the inverse design of hybrid organic–inorganic halide perovskite materials with stability constraints, and the discovery of BCR-Abl kinase inhibitors with synthetic accessibility constraints.
2. Problem formalism and related work
2.1. Optimization problem formalism
An optimization problem consists of traversing a parameter space or domain to identify the parameters x* that correspond to the most desirable outcome for an objective f(x). For a minimization problem, the solution is those parameters that minimize the objective function,
to identify the parameters x* that correspond to the most desirable outcome for an objective f(x). For a minimization problem, the solution is those parameters that minimize the objective function,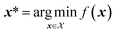 | (1) |
In a BO setting, the objective function f(·) is considered to be an expensive-to-evaluate black-box function, and its measurements are usually corrupted by using some noise ε, i.e. y = f(x) + ε, although we do not consider noisy measurements in this work.
In constrained optimization, one is interested in solutions within a feasible subset of the optimization domain,  , which is unknown (Fig. 1). The evaluation of a constraint function, c(·), determines which parameters x are within
, which is unknown (Fig. 1). The evaluation of a constraint function, c(·), determines which parameters x are within  and which are not. The solution to this constrained optimization problem may now be written as
and which are not. The solution to this constrained optimization problem may now be written as
In this work, we are exclusively concerned with cases where c(x) is a priori unknown, incurs a non-negligible cost for its determination (i.e. is still expensive to evaluate), cannot be relaxed, cannot be decoupled from evaluation of f(·), and returns binary information about the constraint. Let constraint function evaluations ỹ = c(x) return 0 if  and 1 if
and 1 if  , i.e. ỹ ∈ {0,1}.
, i.e. ỹ ∈ {0,1}.
During such a constrained optimization campaign, the experiment planner collects both datasets of continuous-valued objective function measurements  , and of binary-valued constraint measurements
, and of binary-valued constraint measurements  . Here, we denote the total number of transpired measurements K, and the number of infeasible measurements L. Note that, for parameters x, the constraint function is evaluated each time, while the objective function measurement only occurs if c(x) = 0.
. Here, we denote the total number of transpired measurements K, and the number of infeasible measurements L. Note that, for parameters x, the constraint function is evaluated each time, while the objective function measurement only occurs if c(x) = 0.
We want to identify BO strategies which efficiently optimize the objective function f, while preferably also limiting the number of infeasible measurements L. To do so, a compound acquisition function is used, which we term the feasibility-aware acquisition function,  , which depends on the predictions of two surrogate models: (i) a regression surrogate,
, which depends on the predictions of two surrogate models: (i) a regression surrogate,  , fit to the objective function measurements in
, fit to the objective function measurements in  , and (ii) a classification surrogate,
, and (ii) a classification surrogate,  , which is fit to the constraint function measurements in
, which is fit to the constraint function measurements in  . αc combines these predictions in one of several ways to balance adherence to sampling in parameter space regions believed to have promising objective values with avoidance of regions believed to be infeasible. Feasibility-aware acquisition functions are described in Section 3.2. Algorithm 1 shows pseudocode for BO subject to unknown constraints. Note that, while a scalar-valued objective is used for illustrative purposes here, one may easily extend this framework to the multi-objective setting by using, for example, an achievement scalarizing function.
. αc combines these predictions in one of several ways to balance adherence to sampling in parameter space regions believed to have promising objective values with avoidance of regions believed to be infeasible. Feasibility-aware acquisition functions are described in Section 3.2. Algorithm 1 shows pseudocode for BO subject to unknown constraints. Note that, while a scalar-valued objective is used for illustrative purposes here, one may easily extend this framework to the multi-objective setting by using, for example, an achievement scalarizing function.
2.2. Related work
We begin the discussion of related work with problem types that are similar in spirit to our unknown constraint optimization problem definition, but outside the scope of this work. Safe BO is a closely related topic where candidate parameters must exceed some safety threshold to be recommended for measurement. Here, all points in the optimization campaign must be in the “safe” region, i.e. must never violate the constraint function, corresponding to maximal risk aversion.64 Safe BO is useful for applications such as optimization of medical treatment while maintaining patient well-being, or robotic control while avoiding catastrophic damage to the system. In this work, we do not explicitly study this case, and assume constraint violations are inconvenient rather than catastrophic. Another related problem type is BO with missing measurements,65 where missing values in training data are imputed via sampling from a learned probability distribution.Computer and machine learning scientists have studied BO with unknown constraints stretching back more than a decade.54,56–61 Gramacy and Lee were among the first to do so, employing Bayesian learning strategies to estimate both the objective and constraint function.54 The integrated expected conditional improvement (IECI) acquisition function was introduced which enabled incorporation of partial information from constraint violations into the optimization procedure, a variant constrained problem which we do not address in this work. Gelbart et al.59 introduced the feasibility-weighted acquisition function (FWA approach described in Section 3.2) but for scenarios where the f(x) and c(x) can be decoupled and evaluated independently. Snoek et al.55 described a similar approach but for scenarios where the two functions are innately coupled, where constraint violations come from e.g. a crashed objective simulation. More recently, Antonio et al.61 presented SVM-CBO, which uses a consecutive two-stage approach for optimization with unknown constraints: (i) a support vector machine (SVM) is used to estimate the constraint boundary using measurements of c(x) exclusively, and (ii) BO is used to optimize f(x) using the SVM estimate of c(x) as a known constraint. This method lays the foundation for our FCA approach (described in Section 3.2), with a few key differences: (i) we use a variational GP classifier to estimate c(x) as opposed to an SVM, and (ii) our evaluations of c(x) and f(x) are not separated into two distinct stages. Instead, a fresh known constraint function is inferred by our classifier at each iteration in light of the most recent c(x) evaluations.
Researchers in the chemistry and materials science sectors have started to focus on BO problems that feature unknown constraints.66 Wakabayashi et al. investigated molecular beam epitaxy of SrRuO3, a widely used metallic electrode in oxide electronics. Experimental failures are defined as experimental parameter settings for which the SrRuO3 phase did not form, preventing measurement of the resistivity objective.52 The authors consider two approaches to deal with the experimental failures: the so called “floor-padding trick”, in which the infeasible measurement's objectives are replaced by the worst objective value observed so far (naïve-replace approach described in Section 3.2), as well as an approach in which the feasibility-aware acquisition function is a product of the expected improvement criterion and the probability that a parameter space point is feasible as learned by a binary classifier (FWA approach described in Section 3.2). In work concurrent with ours, Khatamsaz and coworkers presented an approach for multi-objective design of multi-principal element alloys for potential use in next-generation gas turbine blades.67 The approach is based on the author's previous work,68 in which a novel Bayesian classification method embedded in a multi-fidelity learning framework was introduced. This allowed the authors to effectively fuse together multiple information sources, including the constraint boundaries, into a single experiment planning algorithm which was employed to efficiently optimize DFT-derived ductility indicators across a refractory Multi-Principal-Element Alloy (MPEA) space.
3. Methods
3.1. Learning the constraint function
Our approach involves training two surrogate models: a regression model to approximate the objective function, f(x), and a binary classification model to approximate the constraint function, c(x). In this section, we briefly describe our binary classification model. | (2) |
This formulation allows for closed-form expressions for the mean and variance of the predicted function value at any given input. For regression tasks, this provides a natural framework for predicting the objective function with uncertainties.
While GPs are readily applied to regression, classification requires a modification. Anubis uses a separate GP for classifying feasibility constraints. Unlike the regression case, exact inference for classification with GPs is intractable. To address this, the GP classifier as implemented in Atlas uses variational inference and inducing points to approximate the posterior distribution.
 , where ỹi ∈ {0,1} represents the feasibility label (0 for infeasible and 1 for feasible) at input xi. We denote the vector of feasibility measurements as ỹ = [ỹ1,…, ỹL]T and the input matrix as X = [x1,…, xL]T. The key modification for classification involves squashing the latent function values, f = [f(x1),…, f(xL)]T, of the GP through a sigmoid inverse-link function,
, where ỹi ∈ {0,1} represents the feasibility label (0 for infeasible and 1 for feasible) at input xi. We denote the vector of feasibility measurements as ỹ = [ỹ1,…, ỹL]T and the input matrix as X = [x1,…, xL]T. The key modification for classification involves squashing the latent function values, f = [f(x1),…, f(xL)]T, of the GP through a sigmoid inverse-link function,  , which maps the real-valued outputs of the GP to the probability interval [0, 1]. This transformed output is then used to define a Bernoulli likelihood function for the observed feasibility labels. The joint distribution of the feasibility measurements and the latent function values is given by
, which maps the real-valued outputs of the GP to the probability interval [0, 1]. This transformed output is then used to define a Bernoulli likelihood function for the observed feasibility labels. The joint distribution of the feasibility measurements and the latent function values is given by | (3) |
 is the Bernoulli likelihood, and
is the Bernoulli likelihood, and  is the prior distribution over the latent function values, with K being the covariance matrix computed using the kernel function k(·, ·) evaluated at the input points X.The goal of the classification GP is to infer the posterior distribution over the latent function values, p(f|ỹ,X), which represents our updated belief about the function after observing the feasibility data. The integral required to normalize the posterior cannot be computed in closed form
is the prior distribution over the latent function values, with K being the covariance matrix computed using the kernel function k(·, ·) evaluated at the input points X.The goal of the classification GP is to infer the posterior distribution over the latent function values, p(f|ỹ,X), which represents our updated belief about the function after observing the feasibility data. The integral required to normalize the posterior cannot be computed in closed form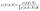 | (4) |
Atlas' classifier adopts an inducing point approach, in which the latent variables are augmented with additional input (output) data, known as inducing inputs (points). Our strategy closely follows the one detailed in Hensman et al.,70 where a bound on the marginal likelihood for classification problems is derived. This bound is optimized by adjusting the hyperparameters of the GP kernel, parameters of the multivariate normal variational distribution, and the inducing inputs/points simultaneously using stochastic gradient descent. The reader is referred to previous work for additional details.70–73 GP classification is implemented using the GPyTorch library,74 and has the added benefit of scaling more favorably with  than exact GP inference.
than exact GP inference.
3.2. Feasibility-aware acquisition functions
Here, we discuss each of the feasibility-aware acquisition functions, αc(x), considered in this work. These can be further broken down into two main kinds. First, baseline strategies we call naïve, which commonly involve no classification surrogate . Secondly, strategies we call hybrid surrogate, which involve training a classification surrogate and combining its predictions in some way with those of the regression surrogate (Fig. 2). We note that the objective values are standardized by using the mean and standard deviation of the available training set at each iteration of the optimization.
. Secondly, strategies we call hybrid surrogate, which involve training a classification surrogate and combining its predictions in some way with those of the regression surrogate (Fig. 2). We note that the objective values are standardized by using the mean and standard deviation of the available training set at each iteration of the optimization.
 . This baseline strategy has previously been referred to as the floor padding trick.52
. This baseline strategy has previously been referred to as the floor padding trick.52
• Naïve-ignore: the FIA hybrid surrogate strategy is used with t = 1000. This will fully bias the acquisition function toward α(x), effectively disregarding the contribution of the classification surrogate.
• Naïve-surrogate: replace each infeasible measurement with the mean prediction of the current regression surrogate model at that point, i.e. for the regression surrogate model 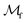 , infeasible measurement
, infeasible measurement  .
.
| αc(x) = α(x) × P(feasible|x). | (5) |
• Feasibility-constrained acquisition (FCA):61 this strategy introduces a constraint on the optimization of the regression acquisition function α(x) such that only those parameter points x with P(feasible|x) above some threshold t are considered for selection. Optimization of αc(x) is therefore a constrained optimization problem itself, albeit with known constraints6
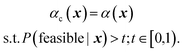 | (6) |
• Feasibility-interpolated acquisition (FIA): this strategy interpolates between α(x) and P(feasible|x) using the following expression
| αc(x) = (1 − ct) × α(x) + ct × P(feasible|x). | (7) |
 is a user-specified hyperparameter which controls risk when it comes to selecting infeasible measurements. Here, smaller values of t de-emphasize the second term and thus indicate more risk, while larger values do the opposite and represent less risk. In our tests, t = {0.5, 1, 2} are chosen.
is a user-specified hyperparameter which controls risk when it comes to selecting infeasible measurements. Here, smaller values of t de-emphasize the second term and thus indicate more risk, while larger values do the opposite and represent less risk. In our tests, t = {0.5, 1, 2} are chosen.
We also tested alternatives of the FWA and FIA functions in which the P(feasible|x) term is replaced by a minimum filtered version, ρ(x), given as
| ρ(x) = min[0.5, P(feasible|x)]. | (8) |
This modification allows us to only bias the search away from areas which the classifier believes are infeasible. In other words, all parameter space regions with P(feasible|x) ≥ 0.5 are treated as equally promising in the eyes of the classification surrogate. Empirically, we have found this approach to be an effective safeguard against becoming trapped in regions of  that have P(feasible|x) ≈ 1. The reader is referred to ESI Section S1A(3)† for the results of these comparative experiments. For the duration of this work, the FIA and FWA acquisitions use the minimum filtered variant, unless otherwise specified.
that have P(feasible|x) ≈ 1. The reader is referred to ESI Section S1A(3)† for the results of these comparative experiments. For the duration of this work, the FIA and FWA acquisitions use the minimum filtered variant, unless otherwise specified.
3.3. Usage through the Atlas library
The Atlas library houses all strategies discussed in Section 3.2 for facile use in “ask-tell” SDL optimization campaigns. Here, we provide a minimal-code demonstration in which Atlas' is used to minimize the 2d Branin-Hoo surface in the presence of unknown constraints employing the FIA function with t = 1. The user must supply two arguments to the constructor of
is used to minimize the 2d Branin-Hoo surface in the presence of unknown constraints employing the FIA function with t = 1. The user must supply two arguments to the constructor of  , the first being the type of feasibility-aware acquisition strategy (
, the first being the type of feasibility-aware acquisition strategy ( ), and the second being its parameterization (
), and the second being its parameterization ( ). The Olympus75,76 library's
). The Olympus75,76 library's  object is used to store the optimization trajectory and meta-information.
object is used to store the optimization trajectory and meta-information.3.4. Assessing optimization performance
Constrained optimization performance is assessed using two types of metrics. The first is a usual optimization performance metric, such as regret, cumulative regret or dominated hypervolume. The second concerns the fraction of total measurements made by a strategy that is infeasible. Both metrics are considered so as to not ignore the potential tradeoff between optimization performance and avoidance of infeasible measurements. Considering a SDL application where too many infeasible measurements result in a broken or disabled experimental setup necessitating a costly maintenance procedure to bring it back online, a researcher may elect to use a strategy which sacrifices some optimization performance for a reduced number of infeasible recommendations. However, extreme avoidance of infeasible measurements, despite lowering the number of infeasible suggestions, may result in poor convergence to optima, especially those that are in close proximity to infeasible regions.For experiments with continuous parameters and a single objective, we use the metrics known as regret and cumulative regret. The instantaneous regret after k iterations, rk, is the distance between the best objective function value found and the global optimum,
| rk= |f(x*) − f(xk+)|. | (9) |
 after k iterations, sometimes referred to as the incumbent point, i.e. for a minimization problem
after k iterations, sometimes referred to as the incumbent point, i.e. for a minimization problem 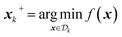 . x* are the parameters associated with the global optimum of the function. The cumulative regret, C is the sum of all regret values after some optimization budget b has transpired,
. x* are the parameters associated with the global optimum of the function. The cumulative regret, C is the sum of all regret values after some optimization budget b has transpired,  . Sample efficient optimizers should have a lower cumulative regret value. For categorical parameter experiments with single objectives, we measure the number of measurements needed for a strategy to identify the best candidate in the Cartesian product space.
. Sample efficient optimizers should have a lower cumulative regret value. For categorical parameter experiments with single objectives, we measure the number of measurements needed for a strategy to identify the best candidate in the Cartesian product space.
4. Results and discussion
4.1. Analytical benchmarks
Eight analytical surfaces (four with continuous parameters and four with categorical parameters) are used to test our constrained optimization strategies. Specifically, constrained analogues of continuous functions Branin, Dejong, StyblinskiTang and HyperEllipsoid as well as the categorical functions Slope, Dejong, Camel and Michalewicz are used.77 We add custom constraint functions to each function, which are described in detail in previous work.6 All analytic surfaces are implemented in the Olympus package.75,76 All categorical surfaces have 21 options per dimension, for a design space with a cardinality of 442.The results of the discrete, ordered benchmarks are shown in Fig. S4† and numerical values are given in Table S2.† The results of categorical, unordered results are shown in Fig. S5.† The results of the continuous benchmarks are shown in Fig. 3 and numerical performance metrics are tabulated in Table 1. The budget b = 100 and each strategy is run 100 independently seeded times. The rank regret metric is the average cumulative regret rank for that strategy over 100 runs (± standard error of the mean). A rank of 1 is the best and a rank of 11 is the worst performing strategy for a single run. Note that the rank statistics do not quantify the improvement in optimization across the models, which is instead observed in the regret traces in Fig. 3. Major takeaways from the analytical benchmark results are itemized below.
| Strategy | BraninConstr | DejongConstr | StyblinskiTangConstr | HyperEllipsoidConstr | ||||
|---|---|---|---|---|---|---|---|---|
| Regret rank (↓) | % Infeas (↓) | Regret rank (↓) | % Infeas (↓) | Regret rank (↓) | % Infeas (↓) | Regret rank (↓) | % Infeas (↓) | |
| Random | 9.15 ± 0.18 | 27.7 ± 0.5 | 8.20 ± 0.14 | 45.2 ± 0.5 | 8.75 ± 0.14 | 55.7 ± 0.5 | 8.45 ± 0.19 | 45.4 ± 0.6 |
| Naïve-replace | 6.12 ± 0.29 | 3.2 ± 0.1 | 6.90 ± 0.31 | 8.3 ± 0.2 | 5.86 ± 0.27 | 6.6 ± 0.2 | 7.51 ± 0.31 | 8.7 ± 0.3 |
| Naïve-ignore | 9.10 ± 0.25 | 83.1 ± 2.5 | 9.74 ± 0.16 | 93.3 ± 0.2 | 9.21 ± 0.20 | 94.0 ± 0.2 | 6.62 ± 0.34 | 63.3 ± 4.3 |
| Naïve-surrogate | 8.72 ± 0.32 | 81.6 ± 2.8 | 9.54 ± 0.15 | 93.3 ± 0.2 | 9.47 ± 0.16 | 94.0 ± 0.2 | 7.36 ± 0.34 | 65.7 ± 4.2 |
| FWA | 4.64 ± 0.22 | 11.0 ± 0.9 | 4.29 ± 0.22 | 49.7 ± 0.2 | 4.43 ± 0.28 | 15.4 ± 1.2 | 4.20 ± 0.27 | 6.2 ± 0.3 |
| FCA-0.2 | 6.44 ± 0.26 | 24.5 ± 1.7 | 6.65 ± 0.16 | 83.6 ± 0.3 | 6.63 ± 0.23 | 50.0 ± 2.5 | 4.89 ± 0.27 | 8.9 ± 0.8 |
| FCA-0.5 | 4.31 ± 0.21 | 9.4 ± 0.7 | 4.06 ± 0.26 | 49.6 ± 0.3 | 4.37 ± 0.24 | 13.8 ± 1.0 | 5.04 ± 0.29 | 8.6 ± 0.9 |
| FCA-0.8 | 3.52 ± 0.25 | 7.9 ± 0.5 | 4.93 ± 0.37 | 16.0 ± 0.4 | 4.34 ± 0.30 | 9.9 ± 0.7 | 5.04 ± 0.35 | 7.3 ± 0.7 |
| FIA-0.5 | 4.29 ± 0.23 | 14.0 ± 1.0 | 3.66 ± 0.19 | 49.6 ± 0.3 | 4.60 ± 0.29 | 16.5 ± 1.3 | 7.89 ± 0.14 | 13.8 ± 1.1 |
| FIA-1 | 4.80 ± 0.23 | 13.7 ± 1.0 | 4.07 ± 0.21 | 50.7 ± 0.2 | 4.12 ± 0.25 | 15.0 ± 1.1 | 4.51 ± 0.27 | 6.2 ± 0.4 |
| FIA-2 | 4.91 ± 0.25 | 20.9 ± 1.7 | 3.96 ± 0.21 | 53.6 ± 0.3 | 4.22 ± 0.24 | 15.5 ± 1.2 | 4.49 ± 0.24 | 6.0 ± 0.3 |
• For fully-continuous functions, Atlas uses a constrained gradient-based acquisition optimization strategy based on the SLSQP algorithm.78,79 For highly constrained problems, we observe that SLSQP undergoes serious convergence issues, significantly increasing the per-iteration runtime of Atlas. The Atlas' genetic acquisition function optimizer is much faster and does not sacrifice performance compared to SLSQP (comparative tests detailed in ESI Section S.1A(2)†). Thus, we use the genetic acquisition optimizer for all tests in this work.
• When used in a feasibility-aware framework, we observe that the upper confidence bound acquisition function performs as well as or better than the expected improvement (EI) criterion. Comparative benchmarks are detailed in ESI section S.1A(1).† We therefore use the UCB acquisition exclusively in this work.
• The naïve-ignore function completely disregards the contribution of the feasibility classifier in eqn (7). As such, for continuous cases it gets stuck in infeasible regions and repeatedly suggests the same parameters, as constraint violations have no effect on the acquisition function. Although a self-avoidance procedure could remedy this limitation,§ we do not study this further and discourage users from choosing naïve-ignore for continuous parameter applications. For fully discrete/categorical problems, on the other hand, avoidance of duplicate parameters is implicit in Atlas, and naïve-ignore does not suffer from the same limitation.
• For continuous problems, the naïve-replace or floor padding strategy is effective in avoiding constraint violations (lowest % infeasible measurements in 3/4 cases studied). However, it is perhaps too biased toward this aspect, and optimization performance is sacrificed. This is especially recognizable when the optimum of the problem is close to an infeasible region, where this strategy tends to induce a (often large) penalty on α(x) that spills over into the optimal region.
• In general, as the feasibility-aware acquisition risk aversion hyperparameter, t, is varied, the expected propensity for the FCA and FIA functions to violate the constraint is observed (perhaps more pronounced in the FCA case). Indeed, it is apparent that a trade-off in t is required for good optimization performance and to keep the constraint violation rate low. In fact, strategies with moderate risk aversion, such as FCA-0.5 and FIA-1, are among the best overall performers across the continuous benchmarks, and are recommended for use as “jack-of-all-trades” feasibility-aware acquisitions.
4.2. Inverse design of stable hybrid organic–inorganic halide perovskite materials
Perovskite solar cells are a class of light-harvesting materials which are typically characterized by inorganic lead halide matrices with inorganic or organic ions.80–82Via the optimization of thin-film manufacturing and device architectures, perovskite materials have achieved revolutionary cell efficiencies in a matter of several years.83,84 Hybrid organic–inorganic perovskites (HOIPs), perhaps most notably methylammonium lead iodide (MAPbI3),85 constitute a class of perovskite absorbers which are easy/cheap to manufacture and highly efficient. However, toxicity and stability issues continue to inhibit the large-scale adoption of HOIPs in commercially viable photovoltaics.86,87With the goal of identifying thermodynamically stable perosvskites that preserve the band gaps and charge transport properties of MAPbI3, Körbel et al. reported a large-scale computational screening of HOIP candidate materials, accessed by chemical substitution of the form A+B2+X3− (Fig. 4a).88 The goal of the screening was threefold: (i) discover thermodynamically stable compounds with respect to the convex hull of stability, (ii) preserve small effective masses (inversely proportional to the mobilities of charge carriers), and (iii) preserve optimal band gaps for photovoltaics.
 | ||
| Fig. 4 Constrained design of HOIP application. (a) HOIP design space featuring 11 molecular cations, 29 divalent metals, and 4 halogens (11 × 29 × 4 = 1276 total options). (b) Results of the constrained optimization experiments. Bar charts show the number of evaluations and infeasible measurements queried by each strategy before identifying a satisfactory material. Here, a satisfactory HOIP is one with 0.75 ≤ Eg ≤ 1.75 eV and m* ≤ 4. There are 7 such materials in the dataset from Körbel et al.88 | ||
The accessible parameter domain consisted of varying options for the A+, B2+ and X3− components of the HOIP, where A is a molecular cation (11 options), B is a divalent metal (29 options), and X is a halogen (4 options). Together, a total of 1276 initial compositions were considered. Körbel et al. successively subjected the compositions to increasingly stringent stability filters via high-throughput computation, until only 111 stable candidates remained, for which the band gap, Eg, and effective mass, m*, were finally calculated.88
Thus, the unknown constraint in this experiment is the combined stability filter, with c(x) = 0 for stable compositions and c(x) = 1 otherwise. We frame the problem as a multi-objective optimization with two objectives. The Chimera scalarizing function89 is used to compute a scalar-valued merit from the pairs of objectives. Specifically, we choose to minimize Eg of the materials such that it is within the range 1.25 ± 0.5 eV (relevant range for photovoltaics), and to minimize m* to at most a value of 4. Out of the 111 candidates which passed the stability filter, only 7 simultaneously satisfy both objectives, i.e. have 0.75 eV ≤ Eg ≤ 1.75 eV and m* ≤ 4 (∼6.3% of the feasible space, or ∼0.5% of the initial space).
The results of our constrained optimization experiments are shown in Fig. 4b and tabulated in Table 2. Two metrics of performance the number of experiments needed to find a single HOIP that satisfies both objectives, and the number of infeasible measurements encountered along the way are analysed. Atlas optimizers use geometric and electronic descriptors of the HOIP components to help guide the search (descriptor details are given in ESI Section S.1D†). Each optimization run is terminated after it identifies a single HOIP satisfying both objectives, and each strategy is run 100 independent times.
| Strategy | HOIP | Drug design (single obj) | Drug design (multi-obj) | |||
|---|---|---|---|---|---|---|
| % Explored (↓) | % Infeas (↓) | % Explored (↓) | % Infeas (↓) | % Explored (↓) | % Infeas (↓) | |
| Random | 13.6 ± 0.8 | 89.7 ± 0.6 | 50.4 ± 1.6 | 26.7 ± 0.6 | 95.4 ± 0.7 | 21.2 ± 0.0 |
| Naïve-replace | 4.2 ± 0.2 | 80.4 ± 1.5 | 11.9 ± 1.2 | 25.4 ± 1.5 | 54.2 ± 0.8 | 13.8 ± 0.2 |
| Naïve-ignore | 8.9 ± 1.2 | 86.9 ± 1.1 | 7.6 ± 0.5 | 32.8 ± 2.5 | 50.8 ± 0.6 | 30.4 ± 0.3 |
| Naïve-surrogate | 5.8 ± 0.4 | 83.7 ± 1.3 | 12.8 ± 0.9 | 28.8 ± 1.3 | 54.2 ± 0.8 | 13.8 ± 0.2 |
| FWA | 5.0 ± 0.3 | 85.4 ± 0.9 | 8.0 ± 0.5 | 27.6 ± 1.6 | 49.8 ± 0.8 | 28.6 ± 0.5 |
| FCA-0.2 | 5.7 ± 0.5 | 83.9 ± 1.2 | 8.3 ± 0.5 | 28.7 ± 1.6 | 49.2 ± 0.8 | 25.2 ± 0.3 |
| FCA-0.5 | 4.1 ± 0.9 | 74.8 ± 4.0 | 10.9 ± 0.9 | 27.8 ± 1.5 | 58.7 ± 3.1 | 16.2 ± 0.3 |
| FCA-0.8 | 5.8 ± 0.5 | 78.5 ± 1.2 | 16.2 ± 1.5 | 19.9 ± 1.1 | 77.4 ± 1.9 | 11.5 ± 0.2 |
| FIA-0.5 | 4.7 ± 0.3 | 77.3 ± 1.2 | 11.2 ± 0.7 | 28.5 ± 1.4 | 60.9 ± 1.8 | 14.1 ± 0.3 |
| FIA-1 | 4.9 ± 0.4 | 76.1 ± 1.1 | 10.6 ± 0.5 | 32.5 ± 1.5 | 52.8 ± 1.8 | 17.1 ± 0.4 |
| FIA-2 | 3.9 ± 0.3 | 78.3 ± 1.1 | 10.3 ± 0.6 | 27.7 ± 1.4 | 53.7 ± 1.6 | 20.4 ± 0.4 |
On average, we observed that the FIA-2 and FCA-0.5 functions explore the smallest fraction of the parameter space before identifying a satisfactory material, at 3.9 ± 0.3% and 4.1 ± 0.9%, respectively. The FCA-0.5 also measures the smallest percentage of infeasible measurements during its campaigns, at 74.8 ± 4.0%. While measuring 3/4 infeasible measurements is indeed a high constraint violation rate, we expect random sampling to measure unstable HOIPs at a rate of roughly 92%. Also noteworthy is that the naïve-ignore strategy, which turns off the feasibility classifier contribution in eqn (7), measures unstable HOIPs at a rate of almost 87%. Therefore, by using our GP feasibility classifier and an appropriate feasibility-aware acquisition function (such as FCA-0.5) we are able to reduce the rate at which the constraint function is violated by about 14% compared to the baseline. This translates to ∼180 failed experiments, on average, that have been avoided through the use of FCA-0.5.
4.3. (Poly)pharmacological design of BCR-Abl fusion protein inhibitors
Desai et al.90 reported a flow technology platform which they apply to the discovery of novel Abl kinase inhibitors, for which the flow system enables synthesis, purification and analysis via a bioassay. The authors conduct a search for kinase inhibitors by combining 10 templates with 27 hinge binding aromatic alkynes to span a space of 270 molecules, joined via a Sonogashira coupling reaction (Fig. 5a).After the experiment, the authors had subjected only 96/270 possible inhibitors to synthesis and bioassay. Of these, 71 were synthetically successful and had IC50 measurements. Formally, we have datasets  and
and  , where K = 96 and L = 96 − 71 = 25. The subscript exp is used to indicate that these data come directly from the experiment.
, where K = 96 and L = 96 − 71 = 25. The subscript exp is used to indicate that these data come directly from the experiment.
Supervised learning is used to extend 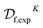 and
and  datasets to cover all 270 possible inhibitors in order to provide measurements for the full Cartesian product space. We first train a classifier on
datasets to cover all 270 possible inhibitors in order to provide measurements for the full Cartesian product space. We first train a classifier on  which makes synthesizability predictions for the remaining 174 candidates. This procedure produces a hybrid dataset
which makes synthesizability predictions for the remaining 174 candidates. This procedure produces a hybrid dataset  (containing both experimental and virtual/predicted synthetic feasibilities) which is ultimately used as the a priori unknown constraint oracle in our optimization experiments. Next, a regressor is trained on
(containing both experimental and virtual/predicted synthetic feasibilities) which is ultimately used as the a priori unknown constraint oracle in our optimization experiments. Next, a regressor is trained on 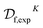 and predicts the IC50 values for the structures deemed synthesizeable by our classifier. The NGBoost algorithm is used for both classification and regression.91 The method is a probabilistic boosted decision tree model, and is quite robust in the low-data regime. We also wanted to ensure that the extrapolation did not create an objective function with a similar functional form as GPs, since both the objective and feasibility surrogates in Anubis are also GPs. Hence, we have opted to use NGBoost in the dataset extrapolation to avoid any undue advantage to the BO surrogates. Additional details on this procedure, along with the cross-validated performance of our supervised learning models, can be found in ESI Section S.1C.†
and predicts the IC50 values for the structures deemed synthesizeable by our classifier. The NGBoost algorithm is used for both classification and regression.91 The method is a probabilistic boosted decision tree model, and is quite robust in the low-data regime. We also wanted to ensure that the extrapolation did not create an objective function with a similar functional form as GPs, since both the objective and feasibility surrogates in Anubis are also GPs. Hence, we have opted to use NGBoost in the dataset extrapolation to avoid any undue advantage to the BO surrogates. Additional details on this procedure, along with the cross-validated performance of our supervised learning models, can be found in ESI Section S.1C.†
We acknowledge that the extension of the HOIP dataset may propagate biases present in the original experimental data. While this augmented dataset (now 270 points) is not intended to be universally representative, its internal consistency ensures a fair comparison of model performance for the related chemical space, as all evaluated models are subject to the same potential biases. The objective of our optimization experiments is to minimize the IC50 value across the space of possible inhibitors, subject to unknown synthesizeability constraints. The results of the experiments are shown in Fig. 5b and tabulated in Table 2. Once again, we examine the percentage of the parameter domain traversed in order to find the inhibitor with the smallest IC50 in the dataset, and the percentage of infeasible measurements incurred along the way. Template and alkyne structures are represented to the optimizer using hand-selected physicochemical descriptors accessed via the Mordred Python library.92 Additional details on descriptor generation can be found in ESI Section S.1C(4).†
For this application, we observe that the naïve-ignore, FWA, and FCA-0.2 strategies need to traverse the smallest fraction of the parameter space until identification of the inhibitor with the minimum IC50, at 7.6 ± 0.5%, 8.0 ± 0.5%, and 8.3 ± 0.5%, respectively. Compared with the HOIP application in the previous subsection, which features 92% infeasible options, this application features only 21% infeasible options. This difference is reflected in the best performing strategies for this application. It appears that for categorical applications characterized by a small infeasible fraction, it behooves one to use strategies which are less risk-averse when it comes to violating the constraint function. In fact, naïve-ignore is among the most efficient search strategies, and completely turns off the feasibility classifier contribution in eqn (7). However, a more risk-averse strategy, such as FCA-0.8, measures infeasible points at a markedly lower rate (19.9 ± 1.1) but does so at the cost of roughly double the amount of evaluations needed to find the optimum. Researchers should thus exercise balance between optimization performance and constraint violation risk aversion in their selection of feasibility aware acquisition functions.
We also conduct an experiment which extends the BCR-Abl protein inhibitor design application to the multi-objective optimization setting. Here, we task Atlas with identifying inhibitors with a polypharmacologial effect, in other words, identifying a single drug molecule that is able to act on multiple targets or disease pathways. The well-studied tyrosine kinase inhibitor Imatinib was originally designed as a selective inhibitor for the BCR-Abl fusion protein to treat chronic myeloid lukemia,93,94 but was later shown to inhibit non-oncogenic C-Abl kinase in normal cells. Indeed, it is Imatinib's polypharmacological profile that has been suggested to form the basis of its therapeutic activity. Protein kinase inhibitors that exhibit polypharmacology thus can have improved efficacy and the potential to treat multiple types of cancer, but may come with the added risk of serious side effects.95 We create two additional virtual objectives by extrapolating the IC50 of the inhibitors reported by Desai et al. for two additional tyrosine kinase receptors: the platelet-derived growth factor receptor (PDGF) and stem cell growth factor (KIT). Datasets of IC50 values for tyrosine kinase inhibitor drugs against both KIT and PDGF were procured from BindingDB.96–99 We train message-passing neural networks (MPNNs) on each dataset using the Chemprop framework,100–102 which achieve satisfactory performance (test set Pearson coefficients ≥0.88). The trained MPNN models then predict values for the Desai et al. inhibitors, which are used as lookup table objectives in our multi-objective optimization experiments. Additional details on the construction of the multi-objective problem can be found in ESI Sections S.1C(2) and (3).† These tests use the same synthesizability constraint function as do the previous single objective experiments. Multi-objective optimization strategies seek to maximize the dominated hypervolume of the objective space by using the hypervolume indicator as a scalarizing function.103–106 In other words, strategies seek to simultaneously minimize the IC50 values for all three receptors. The results of these experiments are tabulated in Table 2. Numerical values report the percentage of the parameter space measured for strategies to identify the entire Pareto set, i.e. the set of inhibitors for which improvement of one receptor's IC50 value is not possible without simultaneously deteriorating another's value. In this dataset, the Pareto set consists of 13 inhibitors.
The results for the multi-objective analogue of the kinase inhibitor design problem illustrate a similar picture to its single objective counterpart and reinforce our findings. Strategies characterized by a higher degree of constraint violation risk tend to fully resolve the Pareto front after evaluation of about half of the parameter space. Comparatively, we expect to explore about 95% of the space using random sampling before this condition is met. Again, the FCA-0.8 strategy, which induces a high degree of risk aversion violates the synthesizability constraint function at a rate of only 11.5 ± 0.2%, the lowest such rate among tested strategies.
5. Choosing feasibility-aware acquisition functions
In this section, we outline the best practices for choosing a feasibility-aware acquisition function for a new optimization problem. The constrained fraction of the optimization domain appears to greatly influence the optimal choice. Unfortunately, this value is a priori unknown for a new problem, and can only be estimated using historical measurement data, instrument limitation information, or expert knowledge. When beginning a new SDL application, we encourage researchers to bootstrap an estimate of the constrained fraction to inform their selection of a feasibility-aware acquisition function. For certain experiments, researchers may have domain knowledge built upon years of experience that is hard to formalize or quantify. Ultimately, the selection of the feasibility-aware optimization strategy should be guided by any known prior information about the setup, such as the difficulty of the experiment and the cost or risk associated with infeasible suggestions. We detail some considerations below.We observed that for highly constrained problems, e.g., the design of HOIPs, the most effective strategies were risk-averse, such as FCA-0.8. Contrastively, for slightly constrained problems, e.g. the design of BCR-Abl inhibitors, we observed that less risk-averse strategies tended to locate promising objectives most efficiently, such as naïve-ignore and FCA-0.2. However, these strategies were not among the most effective approaches to avoid constraint violations.
For a new SDL application, we recommend that researchers tailor their choice of feasibility-aware acquisition functions to the specific characteristics of their scientific problem and laboratory. Most importantly, researchers should first deduce how “inconvenient” constraint violations will be. The least inconvenient violations could be almost indistinguishable from objective measurements in terms of spent resources, time or risk. The most inconvenient violations might involve a significant resource, time or risk penalty, due to necessary instrument repair or recalibration or even the preparation of dangerous substances. When constraint violation inconvenience is low, researchers are free to simply choose the optimization strategy expected to perform best. For moderate inconvenience, we recommend a strategy which balances risk-aversion and optimization performance, such as FCA-0.5 or FIA-1. For highly inconvenient constraint violations, we recommend choosing the FCA function with t set close to 0.8.
6. Conclusion
In summary, Anubis presents a comprehensive discussion and benchmark of Bayesian optimization strategies to deal with the presence of a priori unknown parameter space constraints, a critical aspect of self-driving laboratory research. We discuss and benchmark several existing approaches and provide novel techniques in this regard, manifested as feasibility aware acquisition functions which balance sampling of promising parameters with avoidance of parameters predicted to be infeasible. A variational Gaussian process classifier is used to efficiently learn the constraint function on-the-fly. All feasibility-aware acquisition functions are implemented in the Atlas BO library for facile use by the community in their self-driving laboratories. Extensive benchmarks are reported for both analytic optimization functions and on two real-world chemical design/discovery applications.We discuss the best practices for choosing feasibility-aware acquisition functions in the context of SDL applications, and encourage researchers to strongly consider constraint violation inconvenience within their SDL setup before choosing a strategy. Our results suggest that feasibility-aware approaches provide advantages when infeasible regions are non-trivial. As these regions shrink, their performance remains on par with that of naïve strategies. This shows that balanced, feasibility-aware strategies are good general-purpose choices for SDL applications where feasibility constraints are initially unknown and can potentially result in more costly experiments. Future work can further benchmark and study the relationship between the infeasibility region and the optimization performance. We note that the associated overhead of using feasibility-aware models is not considered in this work, which would typically be outweighed by SDL experimental costs. However, for other BO applications, additional studies on the computational cost of the Anubis strategies are needed. Furthermore, a promising avenue, aligning with active learning principles,107,108 would be the development of acquisition functions that explicitly seek to gather information about the constraint function c(x). Such strategies would aim to reduce uncertainty in the feasibility boundary itself, which could be beneficial when evaluating c(x), is separate from the target f(x) and is particularly expensive. This work lays the foundation for future studies on Bayesian optimization in the presence of a priori unknown constraints and increases the practicality of available optimization software for autonomous science applications.
Data availability
Atlas is available open-source on GitHub at https://github.com/aspuru-guzik-group/atlas under an MIT license. Atlas was used for this study, which is available at https://doi.org/10.5281/zenodo.14623245. Users are also encouraged to check the package's documentation and tutorial notebook. The data and scripts used to run the experiments and produce the plots in this paper are also available on GitHub at https://github.com/aspuru-guzik-group/atlas-unknown-constraints. The dataset, code, and result files of this repository are available at https://doi.org/10.5281/zenodo.15557966.
was used for this study, which is available at https://doi.org/10.5281/zenodo.14623245. Users are also encouraged to check the package's documentation and tutorial notebook. The data and scripts used to run the experiments and produce the plots in this paper are also available on GitHub at https://github.com/aspuru-guzik-group/atlas-unknown-constraints. The dataset, code, and result files of this repository are available at https://doi.org/10.5281/zenodo.15557966.
Author contributions
Riley J. Hickman: conceptualization, methodology, software, data curation, formal analysis, writing – original draft preparation; Gary Tom: software, writing – review & editing; Yunheng Zou: software, writing – review & editing; Matteo Aldeghi: conceptualization, methodology, writing – review & editing; Alán Aspuru-Guzik: supervision, funding acquisition, writing – review & editing.Conflicts of interest
R. J. H. and A. A.-G. are founding members of Intrepid Labs, Inc. a company using self-driving laboratories for pharmaceuticals. A. A.-G. is a founder of Kebotix, Inc., a company specializing in closed-loop material discovery.Acknowledgements
The authors are grateful to Silvana Botti and Sabine Körbel for sharing their data on hybrid organic–inorganic halide perovskite calculations. R. J. H and M. A. thank Dr Florian Häse, Dr Cyrille Lavigne, Dr Robert Pollice, Dr Gabriel dos Passos Gomes, and Dr Martin Seifrid for insightful discussions on feasibility constraints in experimental and computational chemistry contexts. R. J. H. gratefully acknowledges the Natural Sciences and Engineering Research Council of Canada (NSERC) for provision of the Postgraduate Scholarships-Doctoral Program (PGSD3-534584-2019), as well as support from the Vector Institute. M. A. was supported by a Postdoctoral Fellowship of the Vector Institute. G. T. acknowledges support from NSERC (PSGD3-559078-2021) and the Vector Institute. A. A.-G. acknowledges support from the Canada 150 Research Chairs program and CIFAR, as well as the generous support of Anders G. Frøseth. This work is relateed to the Department of Navy award (No. 00014-18-S-B-001) issued by the office of Naval Research. The United States Government has a royalty-free license throughout the world in all copyrightable material contained herein. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the Office of Naval Research. This research was undertaken thanks in part to funding provided to the University of Toronto's Acceleration Consortium from the Canada First Research Excellence Fund (CFREF). Computations reported in this work were performed on the computing clusters of the Vector Institute and on the Niagara supercomputer at the SciNet HPC Consortium.109,110 Resources used in preparing this research were provided, in part, by the Province of Ontario, the Government of Canada through CIFAR, and companies sponsoring the Vector Institute. SciNet is funded by the Canada Foundation for Innovation, the Government of Ontario, Ontario Research Fund – Research Excellence, and by the University of Toronto.References
- J. Močkus, On Bayesian methods for seeking the extremum, in Optimization techniques IFIP technical conference, Springer, 1975, pp. 400–404 Search PubMed.
- J. Močkus, V. Tiesis and A. Zilinskas, The application of Bayesian methods for seeking the extremum, Towards global optimization, 1978, vol. 2, pp. 117–129 Search PubMed.
- J. Močkus, Bayesian approach to global optimization: theory and applications, Springer Science & Business Media, 2012, vol. 37 Search PubMed.
- F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, Phoenics: A Bayesian Optimizer for Chemistry, ACS Cent. Sci., 2018, 4(9), 1134–1145 CrossRef PubMed.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani and J. I. M. Alvarado, et al., Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021, 590(7844), 89–96 CrossRef CAS PubMed.
- G. Tom, R. J Hickman, A. Zinzuwadia, A. Mohajeri, B. Sanchez-Lengeling and A. Aspuru-Guzik, Calibration and generalizability of probabilistic models on low-data chemical datasets with DIONYSUS, Digital Discovery, 2023, 2(3), 759–774 RSC . Publisher: Royal Society of Chemistry. Available from: https://pubs.rsc.org/en/content/articlelanding/2023/dd/d2dd00146b.
- G. Tom, S. Lo, S. Corapi, A. Aspuru-Guzik and B. Sanchez-Lengeling, Ranking over regression for bayesian optimization and molecule selection, arXiv, 2024, preprint, arXiv:241009290, DOI:10.48550/arXiv.2410.09290.
- R. R. Griffiths, L. Klarner, H. Moss, A. Ravuri, S. Truong and Y. Du, et al., GAUCHE: a library for Gaussian processes in chemistry, Adv. Neural Inf. Process. Syst., 2023, 36, 76923–76946 Search PubMed.
- J. P. Dürholt, T. S. Asche, J. Kleinekorte, G. Mancino-Ball, B. Schiller, S. Sung, et al., BoFire: Bayesian Optimization Framework Intended for Real Experiments, arXiv, 2024, preprint, arXiv:240805040, DOI:10.48550/arXiv.2408.05040.
- M. Fitzner, A. Šošić, A. V. Hopp, M. Müller, R. Rihana and K. Hrovatin, et al., BayBE: a Bayesian Back End for experimental planning in the low-to-no-data regime, Digital Discovery, 2025 Search PubMed , advanced article.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Next-Generation Experimentation with Self-Driving Laboratories, Trends Chem., 2019, 1(3), 282–291 CrossRef.
- H. S Stein and J. M Gregoire, Progress and prospects for accelerating materials science with automated and autonomous workflows, Chem. Sci., 2019, 10(42), 9640–9649 RSC.
- E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown and K. G. Reyes, et al., Autonomous experimentation systems for materials development: A community perspective, Matter, 2021, 4(9), 2702–2726 CrossRef . Available from: https://www.sciencedirect.com/science/article/pii/S2590238521003064.
- M. M. Flores-Leonar, L. M. Mejía-Mendoza, A. Aguilar-Granda, B. Sanchez-Lengeling, H. Tribukait and C. Amador-Bedolla, et al., Materials Acceleration Platforms: On the way to autonomous experimentation, Curr. Opin. Green Sustainable Chem., 2020, 25, 100370 CrossRef.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous Discovery in the Chemical Sciences Part I: Progress, Angew. Chem., Int. Ed., 2020, 59(51), 22858–22893 CrossRef CAS PubMed.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous Discovery in the Chemical Sciences Part II: Outlook, Angew. Chem., Int. Ed., 2020, 59(52), 23414–23436 CrossRef CAS PubMed.
- F. Delgado-Licona and M. Abolhasani, Research Acceleration in Self-Driving Labs: Technological Roadmap toward Accelerated Materials and Molecular Discovery, Adv. Intell. Syst., 2022, 2200331, DOI:10.1002/aisy.202200331.
- M. Seifrid, R. Pollice, A. Aguilar-Granda, Z. Morgan Chan, K. Hotta and C. T. Ser, et al., Autonomous Chemical Experiments: Challenges and Perspectives on Establishing a Self-Driving Lab, Acc. Chem. Res., 2022, 55(17), 2454–2466, DOI:10.1021/acs.accounts.2c00220.
- G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish and H. Hao, et al., Self-driving laboratories for chemistry and materials science, Chem. Rev., 2024, 124(16), 9633–9732 CrossRef CAS PubMed.
- A. M. Mroz, P. N. Toka, E. A. del Río Chanona and K. E. Jelfs, Web-BO: towards increased accessibility of Bayesian optimisation (BO) for chemistry, Faraday Discuss., 2024, 256, 221–234 RSC.
- J. P. McMullen and K. F. Jensen, An automated microfluidic system for online optimization in chemical synthesis, Org. Process Res. Dev., 2010, 14(5), 1169–1176 CrossRef CAS.
- D. E. Fitzpatrick, C. Battilocchio and S. V. Ley, A novel internet-based reaction monitoring, control and autonomous self-optimization platform for chemical synthesis, Org. Process Res. Dev., 2016, 20(2), 386–394 CrossRef CAS.
- D. Cortés-Borda, E. Wimmer, B. Gouilleux, E. Barré, N. Oger and L. Goulamaly, et al., An Autonomous Self-Optimizing Flow Reactor for the Synthesis of Natural Product Carpanone, J. Org. Chem., 2018, 83(23), 14286–14299 CrossRef PubMed.
- B. E. Walker, J. H. Bannock, A. M. Nightingale and J. C. deMello, Tuning reaction products by constrained optimisation, React. Chem. Eng., 2017, 2(5), 785–798 RSC . Publisher: The Royal Society of Chemistry. Available from:https://pubs.rsc.org/en/content/articlelanding/2017/re/c7re00123a.
- Z. Zhou, X. Li and R. N. Zare, Optimizing Chemical Reactions with Deep Reinforcement Learning, ACS Cent. Sci., 2017, 3(12), 1337–1344, DOI:10.1021/acscentsci.7b00492.
- A. C. Bédard, A. Adamo, K. C. Aroh, M. G. Russell, A. A. Bedermann and J. Torosian, et al., Reconfigurable system for automated optimization of diverse chemical reactions, Science, 2018, 361(6408), 1220–1225 Search PubMed.
- L. M. Baumgartner, C. W. Coley, B. J. Reizman, K. W. Gao and K. F. Jensen, Optimum catalyst selection over continuous and discrete process variables with a single droplet microfluidic reaction platform, React. Chem. Eng., 2018, 3(3), 301–311 RSC.
- M. Christensen, L. P. E. Yunker, F. Adedeji, F. Häse, L. M. Roch and T. Gensch, et al., Data-science driven autonomous process optimization, Commun. Chem., 2021, 4(1), 1–12 CrossRef PubMed.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora and J. Li, et al., A multi-objective active learning platform and web app for reaction optimization, J. Am. Chem. Soc., 2022, 144(43), 19999–20007 CrossRef CAS PubMed.
- A. D. Clayton, E. O. Pyzer-Knapp, M. Purdie, M. F. Jones, A. Barthelme and J. Pavey, et al., Bayesian Self-Optimization for Telescoped Continuous Flow Synthesis, Angew. Chem., 2023, 135(3), e202214511, DOI:10.1002/ange.202214511.
- P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker and M. Krein, et al., Autonomy in materials research: a case study in carbon nanotube growth, npj Comput. Mater., 2016, 2(1), 1–6 CrossRef.
- H. Tao, T. Wu, S. Kheiri, M. Aldeghi, A. Aspuru-Guzik and E. Kumacheva, Self-Driving Platform for Metal Nanoparticle Synthesis: Combining Microfluidics and Machine Learning, Adv. Funct. Mater., 2021, 31(51), 2106725 Search PubMed.
- R. J. Hickman, P. Bannigan, Z. Bao, A. Aspuru-Guzik and C. Allen, Self-driving laboratories: A paradigm shift in nanomedicine development, Matter, 2023, 6(4), 1071–1081 Search PubMed.
- K. Vaddi, H. T. Chiang and L. D. Pozzo, Autonomous retrosynthesis of gold nanoparticles via spectral shape matching, Digital Discovery, 2022, 1(4), 502–510 RSC.
- A. A. Volk, R. W. Epps and M. Abolhasani, Accelerated Development of Colloidal Nanomaterials Enabled by Modular Microfluidic Reactors: Toward Autonomous Robotic Experimentation, Adv. Mater., 2021, 33(4), 2004495, DOI:10.1002/adma.202004495.
- D. Salley, G. Keenan, J. Grizou, A. Sharma, S. Martín and L. Cronin, A nanomaterials discovery robot for the Darwinian evolution of shape programmable gold nanoparticles, Nat. Commun., 2020, 11(1), 2771 CrossRef CAS PubMed . Available from: https://www.nature.com/articles/s41467-020-16501-4.
- B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, F. Häse, L. M. Roch and K. E. Dettelbach, et al., Self-driving laboratory for accelerated discovery of thin-film materials, Sci. Adv., 2020, 6(20), eaaz8867 CrossRef CAS PubMed . Available from: https://advances.sciencemag.org/content/6/20/eaaz8867.
- B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott and T. D. Morrissey, et al., A self-driving laboratory advances the Pareto front for material properties, Nat. Commun., 2022, 13(1), 995 CrossRef CAS PubMed . Available from: https://www.nature.com/articles/s41467-022-28580-6.
- Z. Liu, N. Rolston, A. C. Flick, T. W. Colburn, Z. Ren and R. H. Dauskardt, et al., Machine learning with knowledge constraints for process optimization of open-air perovskite solar cell manufacturing, Joule, 2022, 6(4), 834–849 CrossRef CAS . Available from: https://www.cell.com/joule/abstract/S2542-4351(22)00130-1.
- S. Sun, A. Tiihonen, F. Oviedo, Z. Liu, J. Thapa and Y. Zhao, et al., A data fusion approach to optimize compositional stability of halide perovskites, Matter, 2021, 4(4), 1305–1322 CrossRef CAS.
- N. T. P. Hartono, M. Ani Najeeb, Z. Li, P. W. Nega, C. A. Fleming and X. Sun, et al., Principled Exploration of Bipyridine and Terpyridine Additives to Promote Methylammonium Lead Iodide Perovskite Crystallization, Cryst. Growth Des., 2022, 22(9), 5424–5431 CrossRef CAS.
- M. J. Tamasi, R. A. Patel, C. H. Borca, S. Kosuri, H. Mugnier and R. Upadhya, et al., Machine Learning on a Robotic Platform for the Design of Polymer–Protein Hybrids, Adv. Mater., 2022, 34(30), 2201809 CrossRef CAS PubMed.
- A. Vriza, H. Chan and J. Xu, Self-Driving Laboratory for Polymer Electronics, Chem. Mater., 2023, 35(8), 3046–3056 CrossRef CAS.
- M. J. Tamasi and A. J. Gormley, Biologic formulation in a self-driving biomaterials lab, Cell Rep. Phys. Sci., 2022, 3(9), 101041 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/S2666386422003356.
- F. Strieth-Kalthoff, H. Hao, V. Rathore, J. Derasp, T. Gaudin and N. H. Angello, et al., Delocalized, asynchronous, closed-loop discovery of organic laser emitters, Science, 2024, 384(6697), eadk9227 CrossRef CAS PubMed.
- S. L. Digabel and S. M. Wild, A Taxonomy of Constraints in Simulation-Based Optimization, arXiv, 2015, preprint, arXiv:150507881, DOI:10.48550/arXiv.1505.07881.
- R. J. Hickman, M. Aldeghi, F. Häse and A. Aspuru-Guzik, Bayesian optimization with known experimental and design constraints for chemistry applications, Digital Discovery, 2022, 1(5), 732–744 RSC.
- S. Baird, J. R. Hall and T. D. Sparks, The most compact search space is not always the most efficient: A case study on maximizing solid rocket fuel packing fraction via constrained Bayesian optimization, ChemRxiv, 2022, preprint, DOI:10.26434/chemrxiv-2022-nz2w8-v3, https://chemrxiv.org/engage/chemrxiv/article-details/6316d81f5351a3b2e6f040db.
- M. Seifrid, R. J. Hickman, A. Aguilar-Granda, C. Lavigne, J. Vestfrid and T. C. Wu, et al., Routescore: punching the ticket to more efficient materials development, ACS Cent. Sci., 2022, 8(1), 122–131 CrossRef CAS PubMed.
- C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, SCScore: Synthetic Complexity Learned from a Reaction Corpus, J. Chem. Inf. Model., 2018, 58(2), 252–261, DOI:10.1021/acs.jcim.7b00622.
- A. Thakkar, V. Chadimová, E. J. Bjerrum, O. Engkvist and J. L. Reymond, Retrosynthetic accessibility score (RAscore) – rapid machine learned synthesizability classification from AI driven retrosynthetic planning, Chem. Sci., 2021, 12(9), 3339–3349 RSC . Publisher: The Royal Society of Chemistry, Available from: https://pubs.rsc.org/en/content/articlelanding/2021/sc/d0sc05401a.
- Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, Bayesian Optimization with Experimental Failure for High-Throughput Materials Growth, npj Comput. Mater., 2022, 8, 180 CrossRef CAS.
- H. Kim, J. Y. Park and S. Choi, Energy refinement and analysis of structures in the QM9 database via a highly accurate quantum chemical method, Sci. Data, 2019, 6(1), 109 CrossRef PubMed.
- R. B. Gramacy and H. K. H. Lee, Optimization Under Unknown Constraints, arXiv, 2010, preprint, arXiv:1004.4027, DOI:10.48550/arXiv.1004.4027.
- J. Snoek, H. Larochelle and R. P. Adams, Practical bayesian optimization of machine learning algorithms, in Advances in neural information processing systems, 2012 Search PubMed.
- J. M. Hernández-Lobato, M. A. Gelbart, R. P. Adams, M. W. Hoffman and Z. Ghahramani, A General Framework for Constrained Bayesian Optimization using Information-based Search, J. Mach. Learn. Res., 2016, 17(160), 1–53 Search PubMed.
- A. Gorji Daronkolaei, A. Hajian and T. Custis, Constrained Bayesian optimization for problems with piece-wise smooth constraints, in Advances in Artificial Intelligence: 31st Canadian Conference on Artificial Intelligence, Canadian AI 2018, Toronto, ON, Canada, May 8–11, 2018, Proceedings 31, Springer, 2018, pp. 218–223 Search PubMed.
- V. Picheny, R. B. Gramacy, S. Wild and S. Le Digabel, Bayesian optimization under mixed constraints with a slack-variable augmented Lagrangian, in Advances in Neural Information Processing Systems, Curran Associates, Inc, 2016, vol. 29 Search PubMed.
- M. A. Gelbart, J. Snoek, R. P. Adams, Bayesian Optimization with Unknown Constraints, arXiv, 2014, preprint, arXiv:14035607, DOI:10.48550/arXiv.1403.5607, available from: http://arxiv.org/abs/1403.5607.
- S. Ariafar, J. Coll-Font, D. Brooks and J. Dy, ADMMBO: Bayesian Optimization with Unknown Constraints using ADMM, J. Mach. Learn. Res., 2019, 20(123), 1–26 Search PubMed . Available from: http://jmlr.org/papers/v20/18-227.html.
- C. Antonio, Sequential model based optimization of partially defined functions under unknown constraints, J. Global Optim., 2021, 79(2), 281–303, DOI:10.1007/s10898-019-00860-4.
- The Atlas authors, Atlas: A Brain for Self-driving Laboratories, GitHub, 2023, https://github.com/aspuru-guzik-group/atlas.
- R. J. Hickman, M. Sim, S. Pablo-García, G. Tom, I. Woolhouse and H. Hao, et al., Atlas: a brain for self-driving laboratories, Digital Discovery, 2025,(4), 1006–1029 RSC.
- Y. Sui, A. Gotovos, J. Burdick and A. Krause, Safe Exploration for Optimization with Gaussian Processes, in Proceedings of the 32nd International Conference on Machine Learning, PMLR, 2015, pp. 997–1005, ISSN: 1938-7228 Search PubMed.
- P. V. Luong, D. Nguyen, S. Gupta, S. Rana and S. Venkatesh, Bayesian Optimization with Missing Inputs, arXiv, 2020, preprint, abs/2006.10948, DOI:10.48550/arXiv.2006.10948.
- A. K. Low, F. Mekki-Berrada, A. Gupta, A. Ostudin, J. Xie, E. Vissol-Gaudin and Y. F. Lim, et al., Evolution-guided Bayesian optimization for constrained multi-objective optimization in self-driving labs, npj Comput. Mater., 2024, 10(1), 104 CrossRef CAS.
- D. Khatamsaz, B. Vela, P. Singh, D. D. Johnson, D. Allaire and R. Arróyave, Bayesian optimization with active learning of design constraints using an entropy-based approach, npj Comput. Mater., 2023, 9(1), 49, DOI:10.1038/s41524-023-01006-7.
- D. Khatamsaz, B. Vela, P. Singh, D. D. Johnson, D. Allaire and R. Arróyave, Multi-objective materials bayesian optimization with active learning of design constraints: Design of ductile refractory multi-principal-element alloys, Acta Mater., 2022, 236, 118133 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/S1359645422005146.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, Adaptive computation and machine learning, MIT Press, 2006 Search PubMed.
- J. Hensman, A. G. de G Matthews and Z. Ghahramani, Scalable Variational Gaussian Process Classification, in International Conference on Artificial Intelligence and Statistics, 2014 Search PubMed.
- E. Snelson and Z. Ghahramani, Sparse Gaussian Processes using Pseudo-inputs, in Advances in Neural Information Processing Systems 18, ed. Weiss Y., Schölkopf B. and Platt J. C., MIT Press, 2006, pp. 1257–1264. Available from: http://papers.nips.cc/paper/2857-sparse-gaussian-processes-using-pseudo-inputs.pdf Search PubMed.
- J. Hensman, N. Fusi and N. D. Lawrence, Gaussian Processes for Big Data, arXiv, 2013, preprint, DOI:10.48550/arXiv.1309.6835, Available from: https://arxiv.org/abs/1309.6835.
- D. M. Blei, A. Kucukelbir and J. D. McAuliffe, Variational Inference: A Review for Statisticians, J. Am. Stat. Assoc., 2017, 112(518), 859–877, DOI:10.1080/01621459.2017.1285773.
- J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger and A. G. Wilson, GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration, in Advances in Neural Information Processing Systems, 2018 Search PubMed.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch, M. Christensen and E. Liles, et al., Olympus: a benchmarking framework for noisy optimization and experiment planning, Sci. Technol., 2021, 2(3), 035021, DOI:10.1088/2632-2153/abedc8.
- R. Hickman, P. Parakh, A. Cheng, Q. Ai, J. Schrier, M. Aldeghi, et al., Olympus, enhanced: benchmarking mixed-parameter and multi-objective optimization in chemistry and materials science, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-74w8d.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Gryffin: An algorithm for Bayesian optimization of categorical variables informed by expert knowledge, Appl. Phys. Rev., 2021, 8(3), 031406, DOI:10.1063/5.0048164.
- D. Kraft, et al., A software package for sequential quadratic programming, Forschungsbericht- Deutsche Forschungs- und Versuchsanstalt fur Luft- und Raumfahrt, 1988 Search PubMed.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham and A. G. Wilson, et al., BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization, in Advances in Neural Information Processing Systems, 2020, vol. 33, Available from: http://arxiv.org/abs/1910.06403 Search PubMed.
- N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu and J. Seo, et al., Compositional engineering of perovskite materials for high-performance solar cells, Nature, 2015, 517(7535), 476–480 CrossRef CAS PubMed . Available from: https://www.nature.com/articles/nature14133.
- W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu and J. Seo, et al., High-performance photovoltaic perovskite layers fabricated through intramolecular exchange, Science, 2015, 348(6240), 1234–1237 CrossRef CAS PubMed . Available from: https://science.sciencemag.org/content/348/6240/1234.
- W. Nie, H. Tsai, R. Asadpour, J. C. Blancon, A. J. Neukirch and G. Gupta, et al., Solar cells. High-efficiency solution-processed perovskite solar cells with millimeter-scale grains, Science, 2015, 347(6221), 522–525 CrossRef CAS PubMed.
- H. Tan, A. Jain, O. Voznyy, X. Lan, F. P. García de Arquer and J. Z. Fan, et al., Efficient and stable solution-processed planar perovskite solar cells via contact passivation, Science, 2017, 355(6326), 722–726, DOI:10.1126/science.aai9081.
- Best Research-Cell Efficiency Chart, Available from: https://www.nrel.gov/pv/cell-efficiency.html.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051, DOI:10.1021/ja809598r.
- G. Niu, X. Guo and L. Wang, Review of recent progress in chemical stability of perovskite solar cells, J. Mater. Chem. A, 2015, 3(17), 8970–8980 RSC . Available from: https://pubs.rsc.org/en/content/articlelanding/2015/ta/c4ta04994b.
- Y. Y. Zhang, S. Chen, P. Xu, H. Xiang, X. G. Gong and A. Walsh, et al., Intrinsic Instability of the Hybrid Halide Perovskite Semiconductor CH3NH3PbI3*, Chin. Phys. Lett., 2018, 35(3), 036104, DOI:10.1088/0256-307X/35/3/036104.
- S. Körbel, M. A. L. Marques and S. Botti, Stable hybrid organic–inorganic halide perovskites for photovoltaics from ab initio high-throughput calculations, J. Mater. Chem. A, 2018, 6(15), 6463–6475 RSC . Publisher: The Royal Society of Chemistry. Available from: https://pubs.rsc.org/en/content/articlelanding/2018/ta/c7ta08992a.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Chimera: enabling hierarchy based multi-objective optimization for self-driving laboratories, Chem. Sci., 2018, 9(39), 7642–7655 RSC . Available from: http://xlink.rsc.org/?DOI=C8SC02239A.
- B. Desai, K. Dixon, E. Farrant, Q. Feng, K. R. Gibson and W. P. van Hoorn, et al., Rapid Discovery of a Novel Series of Abl Kinase Inhibitors by Application of an Integrated Microfluidic Synthesis and Screening Platform, J. Med. Chem., 2013, 56(7), 3033–3047 CrossRef CAS PubMed.
- T. Duan, A. Anand, Y. D. Ding, K. K. Thai, S. Basu, A. Ng and A. Schuler, NGboost: Natural gradient boosting for probabilistic prediction, in Proceedings of International Conference on Machine Learning, PMLR, 2020, pp. 2690–2700 Search PubMed.
- H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, Mordred: a molecular descriptor calculator, J. Cheminf., 2018, 10(1), 4, DOI:10.1186/s13321-018-0258-y.
- M. W. N. Deininger and B. J. Druker, Specific targeted therapy of chronic myelogenous leukemia with imatinib, Pharmacol. Rev., 2003, 55(3), 401–423 CrossRef CAS PubMed.
- N. Iqbal and N. Iqbal, Imatinib: A Breakthrough of Targeted Therapy in Cancer. Chemotherapy Research and Practice, Chemother. Res. Pract., 2014, 2014, 357027 Search PubMed.
- P. Cohen, D. Cross and P. A. Jänne, Kinase drug discovery 20 years after imatinib: progress and future directions, Nat. Rev. Drug Discovery, 2021, 20(7), 551–569 CrossRef CAS PubMed.
- X. Chen, M. Liu and M. K. Gilson, BindingDB: a web-accessible molecular recognition database, Comb. Chem. High Throughput Screening, 2001, 4(8), 719–725 CrossRef CAS PubMed.
- X. Chen, Y. Lin, M. Liu and M. K. Gilson, The Binding Database: data management and interface design, Bioinformatics, 2002, 18(1), 130–139 CrossRef CAS PubMed.
- T. Liu, Y. Lin, X. Wen, R. N. Jorissen and M. K. Gilson, BindingDB: a web-accessible database of experimentally determined protein–ligand binding affinities, Nucleic Acids Res., 2007, 35, D198–D201 CrossRef CAS PubMed . Available from: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1751547/.
- M. K. Gilson, T. Liu, M. Baitaluk, G. Nicola, L. Hwang and J. Chong, BindingDB in 2015: A public database for medicinal chemistry, computational chemistry and systems pharmacology, Nucleic Acids Res., 2016, 44(D1), D1045–D1053 CrossRef CAS PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden and H. Gao, et al., Analyzing Learned Molecular Representations for Property Prediction, J. Chem. Inf. Model., 2019, 59(8), 3370–3388 CrossRef CAS PubMed.
- J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz and N. M. Donghia, et al., A Deep Learning Approach to Antibiotic Discovery, Cell, 2020, 180(4), 688–702 CrossRef CAS PubMed.
- E. Heid and W. H. Green, Machine Learning of Reaction Properties via Learned Representations of the Condensed Graph of Reaction, J. Chem. Inf. Model., 2022, 62(9), 2101–2110 CrossRef CAS PubMed.
- E. Zitzler and L. Thiele, Multiobjective optimization using evolutionary algorithms — A comparative case study, in Parallel Problem Solving from Nature — PPSN V. Lecture Notes in Computer Science, ed. Eiben A. E., Bäck T., Schoenauer M. and Schwefel H. P., Springer, Berlin, Heidelberg, 1998, pp. 292–301 Search PubMed.
- J. D. Knowles, D. W. Corne and M. Fleischer, Bounded archiving using the lebesgue measure, in The 2003 Congress on Evolutionary Computation, CEC ’03, 2003, vol. 4, pp. 2490–2497 Search PubMed.
- M. Li and X. Yao, Quality Evaluation of Solution Sets in Multiobjective Optimisation: A Survey, ACM Comput. Surv., 2019, 52(2), 26 Search PubMed.
- A. P. Guerreiro, C. M. Fonseca and L. Paquete, The Hypervolume Indicator: Problems and Algorithms, ACM Comput. Surv., 2021, 54(6), 1–42 CrossRef . ArXiv:2005.00515 [cs]. Available from: http://arxiv.org/abs/2005.00515.
- M. Sugiyama and S. Nakajima, Pool-based active learning in approximate linear regression, Mach. Learn., 2009, 75, 249–274 CrossRef.
- F. Di Fiore, M. Nardelli and L. Mainini, Active learning and bayesian optimization: A unified perspective to learn with a goal, Arch. Comput. Methods Eng., 2024, 31(5), 2985–3013 CrossRef.
- M. Ponce, R. van Zon, S. Northrup, D. Gruner, J. Chen, F. Ertinaz, et al., Deploying a top-100 supercomputer for large parallel workloads: The niagara supercomputer, in Proceedings of the Practice and Experience in Advanced Research Computing on Rise of the Machines (learning), Association for Computing Machinery, 2019, pp. 1–8 Search PubMed.
- C. Loken, D. Gruner, L. Groer, R. Peltier, N. Bunn and M. Craig, et al., SciNet: lessons learned from building a power-efficient top-20 system and data centre, J. Phys.: Conf. Ser., 2010, 256(1), 012026 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00018a |
| ‡ Current address: Bayer Research and Innovation Center, 238 Main St, Cambridge, MA 02142, USA. |
| § Gryffin77 contains a density-based penalization on acquisition function values, encouraging diversity in recommended parameters. |
| This journal is © The Royal Society of Chemistry 2025 |











