Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Automated computational workflows for muon spin spectroscopy
Ifeanyi J.
Onuorah†
 a,
Miki
Bonacci†
a,
Miki
Bonacci†
 bc,
Muhammad M.
Isah
bc,
Muhammad M.
Isah
 d,
Marcello
Mazzani
d,
Marcello
Mazzani
 a,
Roberto
De Renzi
a,
Roberto
De Renzi
 a,
Giovanni
Pizzi
a,
Giovanni
Pizzi
 *bc and
Pietro
Bonfà
*bc and
Pietro
Bonfà
 *aef
*aef
aDepartment of Physics and Earth Sciences, University of Parma, IT-43124 Parma, Italy. E-mail: pietro.bonfa@unipr.it
bPSI Center for Scientific Computing, Theory and Data, CH-5232 Villigen PSI, Switzerland. E-mail: giovanni.pizzi@psi.ch
cNational Centre for Computational Design and Discovery of Novel Materials (MARVEL), Paul Scherrer Institute PSI, CH-5232 Villigen PSI, Switzerland
dDipartimento di Fisica e Astronomia “A. Righi”, Universitá di Bologna, IT-40127 Bologna, Italy
eDipartimento di Scienze Fisiche, Informatiche e Matematiche, University of Modena and Reggio Emilia, IT-41125 Modena, Italy
fCentro S3, CNR-NANO Istituto Nanoscienze, IT-41125 Modena, Italy
First published on 10th January 2025
Abstract
Positive muon spin rotation and relaxation spectroscopy is a well established experimental technique for studying materials. It provides a local probe that generally complements scattering techniques in the study of magnetic systems and represents a valuable alternative for materials that display strong incoherent scattering or neutron absorption. Computational methods can effectively quantify the microscopic interactions underlying the experimentally observed signal, thus substantially boosting the predictive power of this technique. Here, we present an efficient set of algorithms and workflows devoted to the automation of this task. In particular, we adopt the so-called DFT+μ procedure, where the system is characterized in the density functional theory (DFT) framework with the muon modeled as a hydrogen impurity. We devise an automated strategy to obtain candidate muon stopping sites, their dipolar interaction with the nuclei, and hyperfine interactions with the electronic ground state. We validate the implementation on well-studied compounds, showing the effectiveness of our protocol in terms of accuracy and simplicity of use.
1. Introduction
Positive muon spin rotation and relaxation spectroscopy (μSR) is a powerful experimental probe to investigate the properties of a wide range of condensed matter systems at the atomic scale, through the interaction between the muon spin and the atomic environment in its vicinity.1,2 In analogy to nuclear magnetic resonance (NMR), μSR is a highly sensitive local probe of ordered magnetism, including very weak magnetic moments, thanks to the large gyromagnetic ratio γμ/(2π) ≈ 135.5 MHz T−1 of spin implanted muons.3 It is mostly used to study the magnetic properties of materials, where the muon acts as a tiny magnetometer at an interstitial position in the sample, but it also provides an effective tool to study superconducting order parameters, light particle diffusion, and charge related phenomena.2 The experimentally acquired signal is the muon spin polarization function, which is the time evolution of the muon spin projected along a given direction. In the conventional scheme for data analysis, the main features of the signal are determined by a best fit to an effective model that contains one or more Larmor precession frequencies and their decay in time, or simply exponential decays that result from a distribution of local fields at the muon sites of either nuclear or electronic origin. This approach conveys important information on the system, such as order parameters, transition temperatures, presence of phase separation, but generally delivers only limited microscopic information on the sample under investigation. This is because the muon stopping site and its interactions with the host are generally unknown (at variance with NMR where the position of the nucleus is precisely known). A few experimental approaches such as the measurement of the anisotropy of the Knight/paramagnetic shifts, or of level crossing resonances, can be used to find muon stopping sites,3–5 but they require both extensive beam time and large single crystal compounds, which are not generally available. On the contrary, computational approaches based on the Density Functional Theory (DFT), dubbed DFT+μ in the literature, have been recently shown to be less costly and very accurate in finding the muon stopping site and its hyperfine interactions.6–13 Furthermore, in some cases DFT+μ can be used to describe the long-range structure of a ground-state magnetic order14–17 or to study the extent of the muon-induced perturbation, which generally does not affect the intrinsic properties of the compound being studied, with a few notable exceptions readily identified with the ab initio approach.18–20
implanted muons.3 It is mostly used to study the magnetic properties of materials, where the muon acts as a tiny magnetometer at an interstitial position in the sample, but it also provides an effective tool to study superconducting order parameters, light particle diffusion, and charge related phenomena.2 The experimentally acquired signal is the muon spin polarization function, which is the time evolution of the muon spin projected along a given direction. In the conventional scheme for data analysis, the main features of the signal are determined by a best fit to an effective model that contains one or more Larmor precession frequencies and their decay in time, or simply exponential decays that result from a distribution of local fields at the muon sites of either nuclear or electronic origin. This approach conveys important information on the system, such as order parameters, transition temperatures, presence of phase separation, but generally delivers only limited microscopic information on the sample under investigation. This is because the muon stopping site and its interactions with the host are generally unknown (at variance with NMR where the position of the nucleus is precisely known). A few experimental approaches such as the measurement of the anisotropy of the Knight/paramagnetic shifts, or of level crossing resonances, can be used to find muon stopping sites,3–5 but they require both extensive beam time and large single crystal compounds, which are not generally available. On the contrary, computational approaches based on the Density Functional Theory (DFT), dubbed DFT+μ in the literature, have been recently shown to be less costly and very accurate in finding the muon stopping site and its hyperfine interactions.6–13 Furthermore, in some cases DFT+μ can be used to describe the long-range structure of a ground-state magnetic order14–17 or to study the extent of the muon-induced perturbation, which generally does not affect the intrinsic properties of the compound being studied, with a few notable exceptions readily identified with the ab initio approach.18–20
Nowadays, the DFT+μ method is well established and its adoption for the interpretation of μSR data is becoming more frequent. However, it is challenging for non-experts to set up the machinery required to perform the simulations and acquire sufficient expertise to use the simulation tools efficiently. Furthermore, even for experienced users, it is still challenging to afford the considerable human effort and time consuming intervention required to track and coordinate the large number of calculations involved. These are often several tens, depending on the initial muon trials sites, and require geometry optimization of large supercells as well as additional post-processing in order to obtain the muon interactions in the sample. These issues have limited a routine usage of the ab initio approaches, as well as its adoption in on-line data analysis alongside experiments. To overcome these challenges, an automated framework is highly desirable.
At the same time, the tremendous increase in the high performance computational (HPC) resources has led to the development of automation infrastructures that allow researchers to define workflows, manage calculations and effectively store and organize results into databases. A number of workflows have already been developed to carry out several high-throughput (HT) studies aimed at material design and discovery targeting different properties or applications.21–31 Automated computational approaches are also a valuable tool for the interpretation of other spectroscopic measurements, such as X-ray photoelectron spectroscopy32 and X-ray absorption spectroscopy,33–35 NMR chemical shifts,36,37 electric field gradients (EFG) for nuclear quadrupole resonance (NQR)38 and IR and Raman spectra.39,40
In this paper, we present robust and fully automated workflows implementing protocols to find the muon stopping sites and quantifying its interactions with the hosting sample. The workflow takes advantage of the AiiDA (Automated Interactive Infrastructure and Database for Computational Science) infrastructure,41–43 which is designed to automate, manage, and store computational models making them easily shareable with the scientific community. A few other tools for muon site identification have been published in recent years (see for example the MuFinder Python package44 or the MuonGalaxy platform45). Our approach differs in at least three aspects. First, by leveraging on the AiiDA platform, we can incrementally adopt relevant methods and tools from other application domains: for example, various DFT engines, accurate and automated treatment of self-interaction correction errors in strongly correlated systems,46 or general purpose graphical user interfaces (GUIs) such as AiiDAlab.47 In addition, the platform allows the design of “code agnostic” workflows which can work with any method that provides forces and total energies for a given structure.48,49 The AiiDA platform also guarantees a continuous support for the rapidly evolving HPC infrastructure, where a variety of different technological and security solutions have been recently introduced. The active development of the AiiDA code ensures a seamless transition between different present and future HPC clusters. Second, we provide complete information on the interaction between the muon and its neighboring environment, considering both hyperfine parameters and the dipolar interaction with the nuclear moments. We note, however, that DFT+μ must be compared to T = 0 μSR results and that muon thermally activated motion, important for the interpretation of many experiments, is beyond the scope of the present workflow. Third, thanks to AiiDA provenance model, all workflows and their provenance are fully tracked and made reproducible and easy to share with the rest of the community.
The paper is organized as follows: we first describe the DFT+μ approach. Then, in the “Results and discussion” section, we first describe the algorithms used to automate the calculations and then illustrate two relevant aspects of the workflows with examples: the novel efficient method developed for finding the converged supercell size (that we validate on neutral and charged calculations in a metal, LaCoPO, and an insulator, LiF) and the crucial importance of the inclusion and automated treatment of Hubbard U parameters (in CuO). Finally, the whole workflow is used to study the muon localization and interactions in selected compounds, validating it against experiments. The systems we consider include the Kagome-structured superconductors (AV3Sb5 A = K, Rb, Cs), a fluoride (CaF2, where the strong 19F–muon dipolar interaction provides a direct experimental benchmark), an antiferromagnetic insulator (La2NiO4) and a ferromagnetic metal (LaCoPO). These examples also help us illustrate the workflow features. Finally, future development directions are discussed.
2. DFT+μ and muon interactions
Within the DFT+μ approach, the muon implantation site is identified by performing DFT calculations in the Born–Oppenheimer approximation, where the positive muon is treated as an extremely diluted interstitial hydrogenoid impurity. A plane-wave basis set is often used for crystalline compounds. This is an effective choice for the description of the host system but requires the introduction of supercells in order to suppress the spurious interactions between the muon and its periodic replica.Experimentally, two different charge states are distinguished: the diamagnetic and the paramagnetic muon. These correspond to the two limiting cases of a bare muon or a muon strongly bound to an electron. These two states are accordingly simulated by considering a positive impurity, Mu+, for the diamagnetic state and neutral impurity, Mu˙ for the paramagnetic one (in analogy with H+ and H˙, where the dot is the symbol for an unpaired radical state) obtained within the DFT approach with a charged or neutral supercell, respectively.‡ The starting charge is evolved with the standard self-consistent scheme and the resulting muon state is inspected from the converged charge density. Notably, in general, negligible differences are observed in metals§ due to the effective screening of the positive charge by the conduction electrons,7,13 whereas distinct solutions may be obtained in insulators.
The identification of candidate interstitial sites for the muon is performed by sampling the voids of the lattice structure. A regular grid or a set of random points is generated. The set of initial positions is later reduced by considering the lattice symmetry of the crystal hosting the muon. For each initial position, all atomic positions are optimized to accommodate the muon until forces acting on all the atoms vanish below a given threshold. A minor technical point is that residual symmetries after the insertion of the muon should be discarded and the cell parameters all remain fixed to avoid introducing spurious stresses due to the (infinitely diluted) impurity.50 The procedure results in optimized muon positions that correspond to distinct local minima in the potential energy surface, usually identified as candidate muon sites. Each unique crystallographic position is characterized by a total energy and, although muons might stop at more than one site, the lowest energy ones are assumed to correspond to the most probable stopping sites in the experiment.
The muon mass being one ninth of the hydrogen mass, its zero point energy (ZPE), typically a fraction of an electronvolt, is not negligible. This implies that, even at T = 0, it is important to assess whether higher energy candidate sites are metastable by virtue of the muon zero point motion (ZPM). A self-consistent treatment of the muon ZPM is not currently included, but is planned in future code developments (see “Future developments” section).
In order to verify the correctness of the identified muon site, it is standard practice to compare the predicted spin polarization function with the one obtained in well characterized experiments. In the following paragraphs we briefly describe how this is generally done.
2.1 Experimental benchmarks
In a zero-field μSR experiment, the muon spin polarization is dictated by interactions with the nuclear and electron magnetic moments. Randomly directed neighbor spins (both nuclear and electronic) are well approximated by an isotropic Gaussian distribution of static dipolar fields with zero average and distribution width ΔB, giving rise to the Gaussian Kubo–Toyabe polarization function2 | (1) |
Non-magnetic fluorides (e.g. LiF, CaF) deserve a special mention as the prototypical example where a strong dipolar interaction among the muon magnetic moment and few close nearest-neighbor large nuclear moments provides a unique signature of the muon stopping site.6–8,51 A frequent geometry is that of a straight symmetric F–Mu+–F bond, whose distances are encoded in the classical dipolar interaction  , where the dipolar field of the N = 2 fluorine nuclear moments is written as
, where the dipolar field of the N = 2 fluorine nuclear moments is written as
 | (2) |
The interaction with electrons in ordered magnets is instead obtained with the usual minimal substitution p → p + Aμ, where Aμ is the magnetic vector potential associated with a muon magnetic moment.2 Straightforward elaborations show that all contributions are linear in the muon magnetic moment mμ and can therefore be expressed as  , where Bμ is an effective internal magnetic field. The internal field is conventionally separated into
, where Bμ is an effective internal magnetic field. The internal field is conventionally separated into
| Bμ = Bdip + Bc, | (3) |
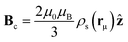 | (4) |
3. Results and discussion
3.1 Automated workflow design
The computational approach described above is automated in a Python workflow implemented within the AiiDA framework. The workflow is packaged in the plugin (see “Code availability” section), which contains the
plugin (see “Code availability” section), which contains the  (AiiDA workflow), the top-level workflow that we expose to users (and internally calls other workflows or calculations). The workflow features include handling of crystal and magnetic structures leveraging on the Atomic Simulation Environment (ASE)54 and Python Materials Genomics (Pymatgen)55 libraries, generation of the initial interstitial muon positions, and automatic convergence of the supercell size. The AiiDA platform handles the interaction with HPC facilities and performs post-processing operations to fetch and parse results, storing them in a database and thus providing efficient query capabilities. As already mentioned, another important feature provided by AiiDA is the definition of “code agnostic” workflows, thus potentially providing different levels of accuracy/speed for the DFT+μ problem. Numerous interfaces, called plugins, between AiiDA and a variety of electronic structure codes have already been developed and can be adopted to perform the electronic structure calculations. However, at the moment the workflow only interfaces with the Quantum ESPRESSO plane-wave DFT code56via the
(AiiDA workflow), the top-level workflow that we expose to users (and internally calls other workflows or calculations). The workflow features include handling of crystal and magnetic structures leveraging on the Atomic Simulation Environment (ASE)54 and Python Materials Genomics (Pymatgen)55 libraries, generation of the initial interstitial muon positions, and automatic convergence of the supercell size. The AiiDA platform handles the interaction with HPC facilities and performs post-processing operations to fetch and parse results, storing them in a database and thus providing efficient query capabilities. As already mentioned, another important feature provided by AiiDA is the definition of “code agnostic” workflows, thus potentially providing different levels of accuracy/speed for the DFT+μ problem. Numerous interfaces, called plugins, between AiiDA and a variety of electronic structure codes have already been developed and can be adopted to perform the electronic structure calculations. However, at the moment the workflow only interfaces with the Quantum ESPRESSO plane-wave DFT code56via the  plugin.43 The plugin also ensures compatibility with different versions of the code and provides fault tolerant algorithms for different tasks including lattice structure relaxation.
plugin.43 The plugin also ensures compatibility with different versions of the code and provides fault tolerant algorithms for different tasks including lattice structure relaxation.
The schematic representation of the workflow is shown in Fig. 1. The input includes the crystallographic structure and, possibly, a magnetic order that can be provided, for instance, via files in CIF and mCIF format. Optional input settings for the DFT calculations are provided as Python variables and transformed into AiiDA data formats. The execution of the workflow involves seven steps, labelled I–VII and discussed below.
 | ||
Fig. 1 Schematic representation of the  workflow. For a description of each box, see points I–VII in section “Automated workflow design” in the main text. workflow. For a description of each box, see points I–VII in section “Automated workflow design” in the main text. | ||
(I) Generate a number Nμ of initial muon interstitial sites.
(II) Execute the supercell (SC) convergence sub-workflow (see “Supercell convergence workflow” section), unless a given SC size is explicitly provided as input.
(III) Execute the structural relaxation of the Nμ supercells, typically in parallel, on HPC clusters.
(IV) Inspect and ensure that at least 60% of the simulations of step III are completed successfully; if not, the workflow stops due to structural convergence failure.
(V) Collect the relaxed structures and their total energies, and cluster distinct stable structures on the basis of symmetry and total energy differences (see “Unique sites selection” section).
(VI) If a magnetic order is provided as input, obtain the contact contribution (Bc) to the local field from the spin-resolved electronic density computed with a dense reciprocal space grid for the distinct stable structures.
(VII) Compute the muon dipolar field interactions at the relaxed structures and the input magnetic configuration using the MUESR code53 interfaced as an AiiDA calculation function ( ).
).
Notably, thanks to the fault tolerant and fault resilient algorithms of the  , the workflow in step III can handle a range of typical errors, such as unconverged SCF calculations or hitting of walltime limits, ensuring that in most cases the calculations finish successfully. In step V, for magnetic compounds, it can happen that crystallographically equivalent replica of a candidate muon site may be magnetically inequivalent.57 When this happens, step III is reactivated, so that relaxed structures of missing magnetically inequivalent sites are obtained and added to the list. Calculations for the charged supercell for the Mu+ state (default) and neutral for the Mu˙ state (optional) are run independently and controlled in the workflow by the Boolean input parameter
, the workflow in step III can handle a range of typical errors, such as unconverged SCF calculations or hitting of walltime limits, ensuring that in most cases the calculations finish successfully. In step V, for magnetic compounds, it can happen that crystallographically equivalent replica of a candidate muon site may be magnetically inequivalent.57 When this happens, step III is reactivated, so that relaxed structures of missing magnetically inequivalent sites are obtained and added to the list. Calculations for the charged supercell for the Mu+ state (default) and neutral for the Mu˙ state (optional) are run independently and controlled in the workflow by the Boolean input parameter  .
.
Two technical points deserve discussion. First, lattice distortions introduced by the muon are always accounted for in the evaluation of dipolar and contact field contributions. Second, the computation of the dipolar contribution in step VII is performed using the magnetic structure provided as input, typically the experimental one, while the contact contribution in step VI is obtained from the ab initio description of the same system. This implies that the magnetic moments, or even the magnetic order obtained at convergence, may be different from the one provided as input. An example is illustrated in the LaCoPO section below.
The outputs of the workflow include: all the relaxed supercell structures and their total energies, the relaxed supercell structures for symmetry/magnetically inequivalent sites, their relative energies with respect to the lowest energy one, and the computed contact hyperfine and dipolar fields (if applicable). This output is stored in the database, with unique identifiers and appropriate metadata for future reference. AiiDA also allows users to export calculation files for ad-hoc post-processing.
Before concluding this section, two aspects of the automated workflow are further discussed. We search for the candidate muon implantation site by sampling the interstitial space with a grid of na × nb × nc regularly spaced initial positions, with the condition that each starting point is at least 1 Å away from any host atom (if a point is closer to any atom, it is discarded). The three integers are determined as ni = ⌈ai/dμ⌉ from the three lattice parameter ai = a, b, c and a unique input spacing dμ (default value: 1 Å). The lattice symmetry is finally used to eliminate equivalent points, generating a reduced total number Nμ of initial muon interstitial sites. The second point concerns calculations involving complex magnetism with non-collinear and/or incommensurate magnetic orders, that are still challenging for DFT-based automated workflows.26,31 The description of non-collinear magnetism is indeed resource- and time-intensive, as the spins have more degrees of freedom, thus making self-consistent convergence harder to achieve and often requiring the introduction of energy penalties to facilitate the minimization. Thus, in the current version, we have restricted the DFT-based calculations to those cases that can be reasonably approximated within the collinear spin formalism, with quantization axis along the z direction, neglecting spin–orbit coupling (and thus any anisotropy term). This still encompasses a large number of compounds of interest for μSR. The limitation can easily be lifted in future developments, when DFT code advancements addressing these issues become available. Also, for this reason, magnetic contributions from f-electrons, where spin–orbit is important, cannot be currently treated correctly. However, non-collinear input array descriptions of the magnetic order are accepted for an accurate evaluation of the dipolar field sums. The DFT calculations are then performed on a collinear structure automatically obtained by projecting each moment along a global spin axis. The accuracy of this approximation varies case by case and the results obtained for non-collinear or incommensurate magnetic orders should therefore be carefully inspected by the user.
3.2 Algorithms
In the following we describe the main AiiDA calculation functions implemented in the workflow. plugin which contains the
plugin which contains the  . It is also automatically used in the
. It is also automatically used in the  if the input supercell matrix required for the muon calculations is not provided.
if the input supercell matrix required for the muon calculations is not provided.
Fig. 2 shows the flowchart describing the supercell convergence algorithm. Starting from the input structure, the first step (a) consists of generating a nearly cubic supercell (implemented using the  Python class of the Pymatgen package55). The size of the generated supercell is controlled by two parameters: a minimum length for the supercell and a minimum number of atoms allowed. These are optional input parameters, whose default values are lat + 1 Å and Nat + 1, respectively, where lat is the length of the smallest lattice vector of the input structure and Nat is the number of atoms in the input structure. Step (b) is accomplished by selecting one Voronoi interstitial node in the unit cell by means of the
Python class of the Pymatgen package55). The size of the generated supercell is controlled by two parameters: a minimum length for the supercell and a minimum number of atoms allowed. These are optional input parameters, whose default values are lat + 1 Å and Nat + 1, respectively, where lat is the length of the smallest lattice vector of the input structure and Nat is the number of atoms in the input structure. Step (b) is accomplished by selecting one Voronoi interstitial node in the unit cell by means of the 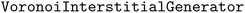 Python class of the Pymatgen package, and inserting an atomic site at that position in the supercell using a hydrogen pseudopotential, in order to mimic the muon.¶ The forces acting on all atoms are then obtained from a converged self-consistent DFT calculation in step (c) and are used to check for convergence in step (d).
Python class of the Pymatgen package, and inserting an atomic site at that position in the supercell using a hydrogen pseudopotential, in order to mimic the muon.¶ The forces acting on all atoms are then obtained from a converged self-consistent DFT calculation in step (c) and are used to check for convergence in step (d).
 | ||
Fig. 2 The flowchart of the supercell convergence workflow implemented in the  . Steps (a)–(d) are described in further detail in the main text. . Steps (a)–(d) are described in further detail in the main text. | ||
Fig. 3 illustrates, both for LaCoPO (a metal) and for LiF (an insulator), that the forces on the atoms obtained with a single SCF calculation decay exponentially with their distance from the muon. The decay length λ is obtained as the best fit to F exp(−λri). Notice that an unrelaxed charged supercell, even without the muon, can show forces on the host atoms. For this reason we always consider the difference between the force on each atom with and without the muon (in the uncharged case the latter vanish). For example, forces on La atoms in unrelaxed charged LaCoPO, Fig. 3(a), decay to a constant, representing the effect of (spurious) electronic charge doping, which is correctly subtracted when force differences are considered in Fig. 3(b).
We assume that convergence is reached when atomic forces decay below a given threshold ΔF, which in the workflow is an optional input parameter, with the default set to 1 × 10−3 Ry Bohr−1 or 0.0257 eV Å−1.|| To obtain a converged supercell, two conditions that ensure vanishing forces within the cell have to be satisfied: the minimum host atomic force is less than ΔF and the maximum ri distance is greater than the minimum convergence distance,  . If convergence is achieved, the workflow returns the supercell used in the last step and the corresponding transformation matrix with respect to the input structure. If convergence is not achieved, a larger supercell is generated and the loop goes back to step (c), provided that the maximum number of iteration is not exceeded.
. If convergence is achieved, the workflow returns the supercell used in the last step and the corresponding transformation matrix with respect to the input structure. If convergence is not achieved, a larger supercell is generated and the loop goes back to step (c), provided that the maximum number of iteration is not exceeded.
In the case of LiF, Fig. 3(c) and (d), convergence is achieved in a 4 × 4 × 4 supercell, Fig. 3(d), using the default value of ΔF in the workflow, while forces are still above that threshold at the boundaries of the 3 × 3 × 3 supercell, as visible in Fig. 3(c).
In order to verify our assumption that residual forces on atoms are a good proxy for convergence, we select a set of relevant muon-related quantities, namely the muon total energy differences, the computed hyperfine field at the muon, and the bond distance between the muon and nearest neighbor host, and we then explicitly check their convergence in LiF and Fe. At variance with the previous approach, here we relax all atomic positions for each supercell size, which becomes quickly very expensive. A k-point grid distance of 0.1 Å−1 has been utilized for the calculations. In LiF, we compute two quantities for four supercell sizes: the Mu+ DOS level, i.e., the energy position from the Fermi energy of the Mu+ peak in the density of states (DOS), that we show in Fig. 4(a), and the F–Mu+ distance, shown in Fig. 4(b), for the muon at the F–Mu+–F site.6,7 As shown, they meet indeed the convergence criterion in the same 4 × 4 × 4 supercell found by the much more efficient force-difference method. We run similar checks for Fe, where the two candidate muon sites are the octahedral (μO) and tetrahedral (μT) interstitial sites. Here, we compare and show in Fig. 4(c) and (d) the total energy difference between μO and μT, and the calculated contact field at both sites. The force difference method predicts the supercell convergence to be achieved with a 3 × 3 × 3 conventional cubic cell, which is indeed confirmed by the trend of the quantities shown in Fig. 4(c) and (d).
In order to identify symmetry-inequivalent muon sites, clustering algorithms60 based on the conventional hierarchical and k-means method have been proposed.61 However, here we introduce a more tailored, simpler and efficient method based on three quantities: (i) the Euclidean distance between sites, (ii) the total energy differences, and (iii) crystallographic and magnetic symmetries. The usage of these quantities are controlled by the tolerance values, namely: Δε, Δd, and a separate tolerance distance Δs for symmetry related replicas. Our clustering algorithm considers only the symmetry of the muon site, since equivalent muon sites will induce equivalent crystal distortions. The algorithm is initialized with the unit cell, with its symmetry operations and the magnetic unit cell (if applicable). All relaxed muon positions and their corresponding total energies are then added. Unique candidate muon sites are selected according to the following three steps:
(1) Remove duplicate positions within intersite distance Δd and energy Δε tolerance, while retaining only that with the lowest energy.
(2) Remove the crystal-symmetry equivalent positions within symmetry Δs and energy Δε tolerance, while retaining only the lowest-energy inequivalent ones.
(3) Add magnetically inequivalent positions. This is performed generating the replica of the crystalline-equivalent sites in the magnetic unit cell and removing those that are equivalent under magnetic symmetry. Any new site generated this way is resubmitted to the standard workflow in step III of the “Automated workflow design” section.
Step 1 saves a list of n2 ≤ Nμ positions and their corresponding energies, step 2 adds a restricted list of n3 < n2 distinct candidate muon sites with their energies and step 3 (when applicable) adds a separate list of m magnetically inequivalent site(s). Finally, the algorithm outputs n3 unique candidate muon sites and, in case, the new m magnetic inequivalent positions whose structural relaxations must be performed. The algorithm is based on the Pymatgen libraries that can reproduce the symmetry operations pertinent to the input structures of the workflow. The default tolerance values are Δd = 0.5 Å, Δs = 0.05 Å, Δε = 0.05 eV.
A number of advanced corrections already exist to amend this problem. These include the usage of hybrid functionals, such as the Heyd–Scuseria–Ernzerhof (HSE) functional,62 the meta-GGA exchange–correlation functionals, in particular the strongly constrained and appropriately normed (SCAN) approach63 and its more recent variants such as rSCAN64 and r2SCAN,65 and the GW method.66 However these approaches, even though semi- or non-empirical (i.e., not parameter dependent), are very computational demanding.67 An alternative route is provided by the DFT + U method,68–70 which delivers an excellent trade-off between accuracy and efficiency. However, the major drawback for automation is that the Hubbard U value is system dependent. One option to obtain its value is using the linear response approach,70–72 that however significantly increases the calculation cost. Nevertheless, even though the values of U vary with each compound, it has been shown that adapting a set of optimal fixed calibrated U values provides an acceptable compromise73 for improving the description of electronic correlations and further facilitates the seamless automation of high-throughput workflows.22,23,25,27–31 In the current version of the DFT+μ workflow we have therefore implemented as default the optimal Hubbard U values reported in ref. 73 for the following transition-metal ions: Co, Cr, Fe, Mn, Mo, Ni, V, W, Cu, which were obtained from the calibration of formation energies in transition-metal oxides. We note that, alternatively, we let the user provide a set of custom Hubbard U values as an input to the workflow. We note that the possibility of using the DFT + U approach is a novel feature for automated DFT+μ workflows. Furthermore, thanks to the integration with AiiDA, the workflow can be easily extended to more advanced approaches such as the automatic U determination from linear response, as mentioned above, as soon as they become available as AiiDA workflows.
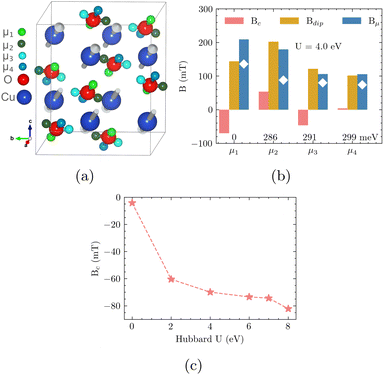
As an example, let us consider cupric oxide (CuO). Its ground state may be seen as a chain antiferromagnet (AFM), ordering three-dimensionally in an A-type collinear AFM structure. It is well known that LDA or GGA incorrectly yields a metallic and non-magnetic ground state for CuO,74 whereas DFT + U75–77 reproduces the known antiferromagnetic ground state. Zero-field μSR (ZF-μSR) detects four distinct internal fields (74 mT, 80 mT, 88 mT, 136 mT) at low temperatures78–81 and four distinct field values are indeed reproduced with U = 4.0 eV, the adopted reference value for Cu.73 They correspond to the two pairs of crystallographic magnetically inequivalent sites bound to each O, shown in Fig. 5(a). Their dipolar Bdip and contact Bc fields, as well as their vector sum modulus Bμ are compared with the experiment in Fig. 5(b). The agreement is reasonably good and Fig. 5(c) shows the dependence of the contact term Bc on the value of the Hubbard U. While a vanishing value is obtained for U = 0 eV, finite values of U all provide reasonable predictions of Bc. This example indicates that the muon hyperfine interaction is sensitive to the treatment of the electronic correlations, and highlights how not including a finite U value results in an incorrect prediction also at the qualitative level.
We note that the positive muon stabilizes in the minimum of the electrostatic potential, more likely being attracted to the most electronegative atomic sites, implying that implantation site is determined by the larger scale of the electric interactions and it may be not sensitive to the much smaller scale of magnetic interaction. This assumption is borne out by the CuO case, where the site is also correctly predicted with U = 0 eV, whereas the correct self consistent hyperfine coupling requires the Hubbard correction. However, the use of DFT + U+μ is known to be relevant also for the localization problem in other cases, such as that of MnO.57
3.3 Validation cases
In this section we present a selected set of cases to validate the . The set includes non-magnetic and magnetic metals and magnetic insulators. To demonstrate the level of automation possible, thanks to our workflows, the calculations reported below were executed providing only the minimum required input to the workflow, i.e., the crystal and magnetic structures, and keeping the default settings for other optional inputs; furthermore, the
. The set includes non-magnetic and magnetic metals and magnetic insulators. To demonstrate the level of automation possible, thanks to our workflows, the calculations reported below were executed providing only the minimum required input to the workflow, i.e., the crystal and magnetic structures, and keeping the default settings for other optional inputs; furthermore, the  is used to obtain the converged supercell size for each case.
is used to obtain the converged supercell size for each case.
For all calculations, we have used plane-wave based DFT as implemented in the Quantum ESPRESSO suite of codes.56 The standard solid-state pseudopotentials (SSSP) library set optimized for efficiency of the Perdew–Burke–Ernzerhof (PBE) functional (SSSP PBE efficiency v1.3) have been used.82 The validation cases reported below have been performed using default plane-wave and density cutoffs as provided by SSSP. In this context we underline that it is possible that self-consistent convergence, particularly for large cells, can be influenced by the choice of the pseudopotentials, exchange–correlation functional and plane-wave cutoffs. Particular attention is required in selecting these parameters, otherwise the already benchmarked set of pseudopotentials from the SSSP library used in this work is a good choice. A Gaussian smearing with 0.01 Ry width and electronic convergence threshold of 10−6 Ry were utilized for all calculations. A k-point grid distance of 0.301 Å−1 has been utilized to obtain a Monkhorst–Pack grid for Brillouin zone sampling unless otherwise stated. The total computational resources required to run the examples in this section amounted to 342![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580 CPU hours on the Leonardo Supercomputer (CINECA).
580 CPU hours on the Leonardo Supercomputer (CINECA).
 , we compute the muon stopping sites in these samples with the hexagonal lattice (P6/mmm space group, no. 191), and we further simulate the time-dependent muon ZF polarization spectra.
, we compute the muon stopping sites in these samples with the hexagonal lattice (P6/mmm space group, no. 191), and we further simulate the time-dependent muon ZF polarization spectra.
The supercell workflow produces identical transformation matrices in all three systems:
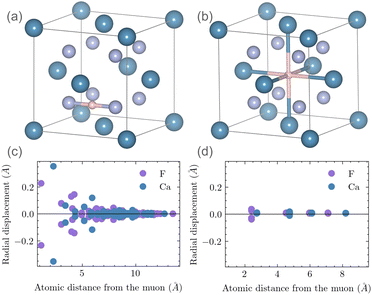
 for handling Mu+ and Mu˙ calculations, we select calcium fluoride (CaF2), known to give rise both to the well characterized51 F–Mu+–F center, and to a Mu˙ state localized at the centre of the primitive cell.6,7
for handling Mu+ and Mu˙ calculations, we select calcium fluoride (CaF2), known to give rise both to the well characterized51 F–Mu+–F center, and to a Mu˙ state localized at the centre of the primitive cell.6,7
The charge state is controlled in the workflow by the Boolean input parameter 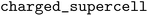 , which is
, which is  by default, yielding the Mu+ state, and must be set to
by default, yielding the Mu+ state, and must be set to  for the Mu˙ state. The converged supercell size is 3 × 3 × 3 for the charged state and 2 × 2 × 2 for the neutral state. This is a general finding: larger supercell sizes are required in the presence of charged interstitials with respect to the neutral case due to the longer-range Coulomb interaction between spurious periodic images.
for the Mu˙ state. The converged supercell size is 3 × 3 × 3 for the charged state and 2 × 2 × 2 for the neutral state. This is a general finding: larger supercell sizes are required in the presence of charged interstitials with respect to the neutral case due to the longer-range Coulomb interaction between spurious periodic images.
For the charged state, the lowest energy sites consist of the muon bonding linearly to two neighbor F nuclei with distance 1.13 Å (very close to the 1.172(1) Å value obtained from experiment87), forming the so called F–Mu+–F bond and shown in Fig. 7(a). This site is in agreement with earlier findings.6,7 On the other hand, the lowest energy site in the neutral supercell calculations consists of a muon at the centre of the unit cell,** as shown in Fig. 7(b). Fig. 7(c) and (d) show the displacements from equilibrium of the host Ca and F ions vs. their distance from the muon for the lowest energy Mu+ and Mu˙ sites, respectively. As expected, much larger displacements are obtained close to charged Mu+ than to neutral Mu˙.
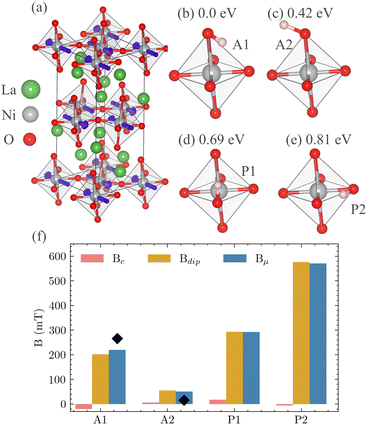
 to use the default Hubbard U = 6.4 eV for Ni. At variance with the literature,93 the non-magnetic metallic state obtained at U = 0 is replaced by an insulating antiferromagnetic ground state with average magnetic moment of 1.59 μB on Ni, in agreement with neutron experiments (reporting 1.68 μB and 1.62 μB, respectively88,94). A small induced contribution at the planar O site is also observed. The workflow produces four distinct candidate muon sites forming bonds of length ∼1 Å to an O site, as shown in Fig. 8(b)–(e): two bound to the apical O site, labelled A1 and A2, and two bound to the planar O site, labelled P1 and P2, plus an unstable, very high-energy site (>2.5 eV), located at an interstitial site between two consecutive perovskite layers (not shown). By the minimal-energy argument adopted before, we expect muons to localize at the A1 site, and possibly at the A2 site.
to use the default Hubbard U = 6.4 eV for Ni. At variance with the literature,93 the non-magnetic metallic state obtained at U = 0 is replaced by an insulating antiferromagnetic ground state with average magnetic moment of 1.59 μB on Ni, in agreement with neutron experiments (reporting 1.68 μB and 1.62 μB, respectively88,94). A small induced contribution at the planar O site is also observed. The workflow produces four distinct candidate muon sites forming bonds of length ∼1 Å to an O site, as shown in Fig. 8(b)–(e): two bound to the apical O site, labelled A1 and A2, and two bound to the planar O site, labelled P1 and P2, plus an unstable, very high-energy site (>2.5 eV), located at an interstitial site between two consecutive perovskite layers (not shown). By the minimal-energy argument adopted before, we expect muons to localize at the A1 site, and possibly at the A2 site.
This site assignment is confirmed by the muon internal fields calculated within the workflow. Fig. 8(f) shows the Fermi contact Bc and the magnetic dipole Bdip contributions to the internal field Bμ at all four candidate sites. In all the cases, the contribution from Bdip is dominant while those from Bc are almost vanishing. Fig. 8(f) reveals that the values of Bμ computed at sites A1 and A2 are in reasonable agreement with the high (265.6 mT) and low (14.8 mT) internal fields observed in experiments,89–91 also considering the present neglect in the workflow of the quantum zero-point vibrations. Notice that our site assignment partially contradicts earlier non ab initio speculations based on magnetic dipolar field analysis,89–91 where the low internal field was correctly assigned to a muon bound to the apical oxygen, whereas the high internal field was attributed to muon localizing at the planar P2 site. Our findings are strongly supported by a very good reproduction of the magnetic interactions.
Fig. 9(a) shows the LaCoPO unit cell and the positions of the four distinct candidate muon sites, labelled μ1 to μ4. The relative energies and the computed internal field contributions are shown in Fig. 9(b). Site μ1, located 1.47 Å away from the P site along the c axis (see Fig. 9) and towards the La–O layer, is the lowest energy site, whereas the next lowest is site μ2, located 1.50 Å away from the Co site along the c axis and towards the La–O layer. The assignment of the unique experimental internal field to site μ1 is in agreement with our minimal argument and with the earlier study.96 Site μ2 has been reported to be unstable owing to the muon ZPM.96 In Fig. 9(b), we show the contributions to the total internal field for all four candidate sites that we obtained. For all sites but μ4, a sizeable contribution due to the contact hyperfine term Bc is observed. Notice that the ferromagnetic ground state that we obtain shows an average magnetic moment localized on Co atoms of 0.7 μB, more than twice the experimental value. The computed internal field Bμ at site μ1 is 166 mT. The value largely overestimates the experimental value, which is expected since Bc is directly proportional to the magnetic moment.
We emphasize that an improved agreement is already provided by the possibility to evaluate the distant dipole sums with the experimental magnetic structure, including the value of the moments. However, users must be aware that the results provided by the workflow in this case are not “self consistent”, since the contact contribution is obtained instead with the ab initio moments. A crude correction consists in re-scaling11 the value of Bc by a factor mexp/mab initio, which yields Bμ = 46 mT, closer to the experimental value (note, however, that we do not expect a perfect quantitative agreement, also because we are not accounting for the muon ZPM). A better ab initio solution would be to include a self-consistent correction of the magnetic moment using the reduced Stoner theory modification to the exchange–correlation functional.11,97
3.4 Future developments
The current workflow and the choice of the hosting platform presents an “engine” designed to facilitate the addition of new developments by us (or by any future contributor), and also to easily exploit features implemented by other AiiDA users working on different topics but using the same DFT tools. A number of advanced features of the muon calculation protocols are well within the reach of development. One important feature that is still lacking in the current implementation of the workflow is the inclusion of anharmonicity and the muon ZPM effects.10,12,98–100 These corrections are known to influence both the stability of the muon sites and the estimation of the muon interactions, particularly for compounds where the energy barrier among a group of neighbor candidate sites is lower than their ZPE and may give rise to muon wavefunction delocalization (quantum diffusion). Future development in the workflow will optionally incorporate the muon ZPM using the stochastic self-consistent harmonic approximation (SSCHA) method.12In the classical limit, thermal muon diffusion can be investigated using the nudged elastic band (NEB) method, that can track the barrier and the minimum energy path connecting the specified initial and final sites.101 Future developments will optionally include this method in the workflow. This information contributes to the prediction of the temperature dependence of the μSR signal.
When the electronic contribution to the muon polarization function is negligible, numerical evaluation of the time evolution of the spin of the muon due to its interaction with the surrounding nuclei is straightforward.87,102–104 Future development of the workflow will include the evaluation of dipolar and quadrupolar contributions103 thus allowing to extract accurate polarization functions from the first principles simulations.
Another improvement that may be considered is the implementation of the reduced Stoner theory correction to the exchange–correlation functional11,97 aimed at a more accurate description of the magnetic ground state and in turn the muon contact hyperfine contribution, particularly for itinerant electron systems where the magnetic moments are poorly estimated with DFT.
On the more technical side, while our automated selection of numerical parameters is able to deliver full automation and provides converged results, in some cases those values could be adapted, so as to run cheaper simulations without significantly affecting the physical results. For example, in LaCoPO, the use of a much smaller 2 × 2 × 1 cell (32 atoms, instead of the 144 atoms of the 3 × 3 × 2 cell obtained from the convergence workflow) and a larger spacing of 1.2 Å for the sampling muon grid (15 initial positions instead of 20), still gives identical results within numerical accuracy. Likewise, for LaNiO2, the interstitial space can also be properly sampled by increasing the muon grid spacing to dμ = 1.6 Å, resulting in only 10 supercells to be computed instead of 52, thus saving computational cost. Therefore, some parameters of the workflow could be further optimized to minimize computational cost.
4. Conclusion
We have developed and validated an automated DFT-based workflow based on the AiiDA platform for the calculation of the muon stopping sites and hyperfine interactions in solids. The workflow has been successfully validated in a selected set of compounds including the Kagome structured superconductors, fluorides and magnetic insulating oxides. These validation cases demonstrate the implementation of various tools for the analysis of μSR experiments. The workflow has been highly optimized to require minimal input from the user, so that the crystal structure is the only mandatory information required to execute it. In particular, a fast algorithm for computing the convergence against the supercell size has been included in the workflow, and pre-defined values for Hubbard correction in DFT + U are provided in order to improve the treatment of strongly correlated systems.Moreover, we provide predefined input settings of the workflow, and we demonstrate that these are sufficient to fully automate and provide accurate results for DFT+μ calculations. In addition, if computational resources are limited, it is possible for an experienced user to manually provide less optimal input parameters that still provide reasonably converged results in a shorter time, possibly with looser convergence thresholds.
Our automated workflow represents a powerful tool that will encourage, facilitate and promote the usage of ab initio calculations by the μSR community, opening up the possibility to perform muon simulations routinely alongside experimental measurements.
Data availability
The data presented in this work are available on the Materials Cloud105 Archive at https://doi.org/10.24435/materialscloud:yy-ds. The and the
and the  are actively developed and can be downloaded from the respective GitHub repositories at https://github.com/positivemuon/aiida-muon (v1.0.3, also deposited on Zenodo and available at https://zenodo.org/records/14594493) and https://github.com/positivemuon/aiida-impuritysupercellconv (v1.0.1, also deposited on Zenodo and available at https://zenodo.org/records/14594496). These workflows rely on the
are actively developed and can be downloaded from the respective GitHub repositories at https://github.com/positivemuon/aiida-muon (v1.0.3, also deposited on Zenodo and available at https://zenodo.org/records/14594493) and https://github.com/positivemuon/aiida-impuritysupercellconv (v1.0.1, also deposited on Zenodo and available at https://zenodo.org/records/14594496). These workflows rely on the  plugin, available at https://github.com/aiidateam/aiida-quantumespresso.
plugin, available at https://github.com/aiidateam/aiida-quantumespresso.
Author contributions
IJO and MB contributed equally to this work. Conceptualization: PB, RDR, GP, IJO, MB and MMI; data curation: IJO and MB; formal analysis: IJO, MB, PB, and GP; funding acquisition: RDR, GP and PB; investigation: IJO, MB, GP, PB and RDR; methodology: IJO, MB and MMI; project administration: GP, RDR, PB and MM; software: MB, IJO, MMI, PB and GP; resources: MM, GP, PB and RDR; supervision: PB, GP and RDR; validation: IJO, MB, PB and GP; visualization: IJO and MB; writing – original draft: IJO and MB; writing – review and editing: RDR, PB, GP, IJO and MB.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
IJO, MM, PB and RDR acknowledge financial support from the PNRR MUR project ECS-00000033-ECOSISTER. MB and GP acknowledge financial support from the NCCR MARVEL, a National Centre of Competence in Research, funded by the Swiss National Science Foundation (grant number 205602). This research was granted by University of Parma through the action Bando di Ateneo 2023 per la ricerca. We acknowledge computing resources provided by the STFC scientific computing department's SCARF cluster and CINECA award under the IsCa4-SIEMTQM and CNHPC-1570115 projects. We acknowledge access to Piz Daint and Alps at the Swiss National Supercomputing Centre (CSCS) under PSI's share with project ID psi15 and psi18 and under MARVEL share with project ID mr32.References
- A. Yaouanc and P. Dalmas de Réotier, Muon Spin Rotation Relaxation and Resonance: Applications to Condensed Matter, Oxford University Press, Oxford, 2011 Search PubMed.
- S. J. Blundell, R. De Renzi, T. Lancaster and F. L. Pratt, Muon Spectroscopy: An Introduction, Oxford University Press, 2021, DOI:10.1093/oso/9780198858959.001.0001.
- A. Schenck and F. Gygax, in Handbook of Magnetic Materials, ed. K. Buschow, Elsevier Science B.V., Netherlands, 1995, vol. 9, pp. 60–284, DOI:10.1016/S1567-2719(05)80006-X.
- R. F. Kiefl, M. Celio, T. L. Estle, G. M. Luke, S. R. Kreitzman, J. H. Brewer, D. R. Noakes, E. J. Ansaldo and K. Nishiyama, Determination of the electronic structure of anomalous muonium in GaAs from nuclear hyperfine interactions, Phys. Rev. Lett., 1987, 58, 1780–1783, DOI:10.1103/PhysRevLett.58.1780.
- B. E. Schultz, K. H. Chow, B. Hitti, R. F. Kiefl, R. L. Lichti and S. F. J. Cox, Local structure of isolated positively charged muonium as an analog for the hydrogen ion in p-type GaAs, Phys. Rev. Lett., 2005, 95, 086404, DOI:10.1103/PhysRevLett.95.086404.
- J. S. Möller, D. Ceresoli, T. Lancaster, N. Marzari and S. J. Blundell, Quantum states of muons in fluorides, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 121108, DOI:10.1103/PhysRevB.87.121108.
- J. S. Möller, P. Bonfà, D. Ceresoli, F. Bernardini, S. J. Blundell, T. Lancaster, R. D. Renzi, N. Marzari, I. Watanabe, S. Sulaiman and M. I. Mohamed-Ibrahim, Playing quantum hide-and-seek with the muon: localizing muon stopping sites, Physica, 2013, 88, 068510, DOI:10.1088/0031-8949/88/06/068510.
- F. Bernardini, P. Bonfà, S. Massidda and R. De Renzi, Ab initio strategy for muon site assignment in wide band gap fluorides, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 115148, DOI:10.1103/PhysRevB.87.115148.
- P. Bonfà and R. De Renzi, Toward the computational prediction of muon sites and interaction parameters, J. Phys. Soc. Jpn., 2016, 85, 091014, DOI:10.7566/JPSJ.85.091014.
- P. Bonfà, F. Sartori and R. De Renzi, Efficient and reliable strategy for identifying muon sites based on the double adiabatic approximation, J. Phys. Chem. C, 2015, 119, 4278–4285, DOI:10.1021/jp5125876.
- I. J. Onuorah, P. Bonfà and R. De Renzi, Muon contact hyperfine field in metals: A DFT calculation, Phys. Rev. B, 2018, 97, 174414, DOI:10.1103/PhysRevB.97.174414.
- I. J. Onuorah, P. Bonfà, R. De Renzi, L. Monacelli, F. Mauri, M. Calandra and I. Errea, Quantum effects in muon spin spectroscopy within the stochastic self-consistent harmonic approximation, Phys. Rev. Mater., 2019, 3, 073804, DOI:10.1103/PhysRevMaterials.3.073804.
- S. J. Blundell and T. Lancaster, DFT + μ: Density functional theory for muon site determination, Applied Physics Reviews, 2023, 10, 021316, DOI:10.1063/5.0149080.
- S. C. Cheung, Z. Guguchia, B. A. Frandsen, Z. Gong, K. Yamakawa, D. E. Almeida, I. J. Onuorah, P. Bonfá, E. Miranda, W. Wang, D. W. Tam, Y. Song, C. Cao, Y. Cai, A. M. Hallas, M. N. Wilson, T. J. S. Munsie, G. Luke, B. Chen, G. Dai, C. Jin, S. Guo, F. Ning, R. M. Fernandes, R. De Renzi, P. Dai and Y. J. Uemura, Disentangling superconducting and magnetic orders in NaFe1−xNixAs using muon spin rotation, Phys. Rev. B, 2018, 97, 224508, DOI:10.1103/PhysRevB.97.224508.
- G. Lamura, I. J. Onuorah, P. Bonfà, S. Sanna, Z. Shermadini, R. Khasanov, J. Orain, C. Baines, F. Gastaldo, M. Giovannini, I. Čurlík, A. Dzubinska, G. Pristas, M. Reiffers, A. Martinelli, C. Ritter, B. Joseph, E. Bauer, R. De Renzi and T. Shiroka, Pressure-induced antiferromagnetic dome in the heavy-fermion Yb2Pd2In1−xSnx system, Phys. Rev. B, 2020, 101, 054410, DOI:10.1103/PhysRevB.101.054410.
- P. Bonfà, M. M. Isah, B. A. Frandsen, E. J. Gibson, E. Brück, I. J. Onuorah, R. De Renzi and G. Allodi, Ab initio modeling and experimental investigation of Fe2P by DFT and spin spectroscopies, Phys. Rev. Mater., 2021, 5, 044411, DOI:10.1103/PhysRevMaterials.5.044411.
- M. Sahoo, I. J. Onuorah, L. C. Folkers, E. Kochetkova, E. V. Chulkov, M. M. Otrokov, Z. S. Aliev, I. R. Amiraslanov, A. U. B. Wolter, B. Büchner, L. T. Corredor, C. Wang, Z. Salman, A. Isaeva, R. De Renzi and G. Allodi, Ubiquitous order-disorder transition in the Mn antisite sublattice of the (MnBi2Te4)(Bi2Te3) magnetic topological insulators, Advanced Science, 2024, 11, 2402753, DOI:10.1002/advs.202402753.
- F. R. Foronda, F. Lang, J. S. Möller, T. Lancaster, A. T. Boothroyd, F. L. Pratt, S. R. Giblin, D. Prabhakaran and S. J. Blundell, Anisotropic local modification of crystal field levels in Pr-based pyrochlores: a muon-induced effect modeled using density functional theory, Phys. Rev. Lett., 2015, 114, 017602, DOI:10.1103/PhysRevLett.114.017602.
- M. H. Dehn, J. K. Shenton, S. Holenstein, Q. N. Meier, D. J. Arseneau, D. L. Cortie, B. Hitti, A. C. Y. Fang, W. A. MacFarlane, R. M. L. McFadden, G. D. Morris, Z. Salman, H. Luetkens, N. A. Spaldin, M. Fechner and R. F. Kiefl, Observation of a charge-neutral muon-polaron complex in antiferromagnetic Cr2O3, Phys. Rev. X, 2020, 10, 011036, DOI:10.1103/PhysRevX.10.011036.
- B. M. Huddart, I. J. Onuorah, M. M. Isah, P. Bonfà, S. J. Blundell, S. J. Clark, R. De Renzi and T. Lancaster, Intrinsic nature of spontaneous magnetic fields in superconductors with time-reversal symmetry breaking, Phys. Rev. Lett., 2021, 127, 237002, DOI:10.1103/PhysRevLett.127.237002.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds, Nat. Nanotechnol., 2018, 13, 246–252, DOI:10.1038/s41565-017-0035-5.
- D. Wines, K. Choudhary and F. Tavazza, Systematic DFT+U and Quantum Monte Carlo Benchmark of Magnetic Two-Dimensional (2D) CrX3 (X = I, Br, Cl, F), J. Phys. Chem. C, 2023, 127, 1176–1188, DOI:10.1021/acs.jpcc.2c06733.
- D. Torelli, K. S. Thygesen and T. Olsen, High throughput computational screening for 2D ferromagnetic materials: the critical role of anisotropy and local correlations, 2D Materials, 2019, 6, 045018, DOI:10.1088/2053-1583/ab2c43.
- J. Balluff, K. Diekmann, G. Reiss and M. Meinert, High-throughput screening for antiferromagnetic Heusler compounds using density functional theory, Phys. Rev. Mater., 2017, 1, 034404, DOI:10.1103/PhysRevMaterials.1.034404.
- W. Chen, J. George, J. B. Varley, G.-M. Rignanese and G. Hautier, High-throughput computational discovery of In2Mn2O7 as a high Curie temperature ferromagnetic semiconductor for spintronics, npj Comput. Mater., 2019, 5, 72, DOI:10.1038/s41524-019-0208-x.
- H. Zhang, High-throughput design of magnetic materials, Electron. Struct., 2021, 3, 033001, DOI:10.1088/2516-1075/abbb25.
- D. Torelli, H. Moustafa, K. W. Jacobsen and T. Olsen, High-throughput computational screening for two-dimensional magnetic materials based on experimental databases of three-dimensional compounds, npj Comput. Mater., 2020, 6, 158, DOI:10.1038/s41524-020-00428-x.
- X. Li, Z. Zhang and H. Zhang, High throughput study on magnetic ground states with Hubbard U corrections in transition metal dihalide monolayers, Nanoscale Adv., 2020, 2, 495–501, 10.1039/C9NA00588A.
- H. Wang, Q. Feng, X. Li and J. Yang, High-throughput computational screening for bipolar magnetic semiconductors, Research, 2022, 2022, 9857631, DOI:10.34133/2022/9857631.
- N. C. Frey, M. K. Horton, J. M. Munro, S. M. Griffin, K. A. Persson and V. B. Shenoy, High-throughput search for magnetic and topological order in transition metal oxides, Sci. Adv., 2020, 6, eabd1076, DOI:10.1126/sciadv.abd1076.
- M. K. Horton, J. H. Montoya, M. Liu and K. A. Persson, High-throughput prediction of the ground-state collinear magnetic order of inorganic materials using density functional theory, npj Comput. Mater., 2019, 5, 64, DOI:10.1038/s41524-019-0199-7.
- D. Golze, M. Hirvensalo, P. Hernández-León, A. Aarva, J. Etula, T. Susi, P. Rinke, T. Laurila and M. A. Caro, Accurate computational prediction of core-electron binding energies in carbon-based materials: A machine-learning model combining density-functional theory and GW, Chem. Mater., 2022, 34, 6240–6254, DOI:10.1021/acs.chemmater.1c04279.
- C. Zheng, K. Mathew, C. Chen, Y. Chen, H. Tang, A. Dozier, J. J. Kas, F. D. Vila, J. J. Rehr, L. F. J. Piper, K. A. Persson and S. P. Ong, Automated generation and ensemble-learned matching of X-ray absorption spectra, npj Comput. Mater., 2018, 4, 12, DOI:10.1038/s41524-018-0067-x.
- F. Meng, B. Maurer, F. Peschel, S. Selcuk, M. Hybertsen, X. Qu, C. Vorwerk, C. Draxl, J. Vinson and D. Lu, Multicode benchmark on simulated Ti K-edge x-ray absorption spectra of Ti-O compounds, Phys. Rev. Mater., 2024, 8, 013801, DOI:10.1103/PhysRevMaterials.8.013801.
- H. Guo, M. R. Carbone, C. Cao, J. Qu, Y. Du, S.-M. Bak, C. Weiland, F. Wang, S. Yoo, N. Artrith, A. Urban and D. Lu, Simulated sulfur K-edge X-ray absorption spectroscopy database of lithium thiophosphate solid electrolytes, Sci. Data, 2023, 10, 349, DOI:10.1038/s41597-023-02262-4.
- P. Gao, J. Zhang, Q. Peng, J. Zhang and V.-A. Glezakou, General protocol for the accurate prediction of molecular 13C/1H NMR chemical shifts via machine learning augmented DFT, J. Chem. Inf. Model., 2020, 60, 3746–3754, DOI:10.1021/acs.jcim.0c00388.
- R. Atwi, Y. Chen, K. S. Han, K. T. Mueller, V. Murugesan and N. N. Rajput, An automated framework for high-throughput predictions of NMR chemical shifts within liquid solutions, Nat. Comput. Sci., 2022, 2, 112, DOI:10.1038/s43588-022-00200-9.
- K. Choudhary, J. N. Ansari, I. I. Mazin and K. L. Sauer, Density functional theory-based electric field gradient database, Sci. Data, 2020, 7, 362, DOI:10.1038/s41597-020-00707-8.
- M. Bagheri and H.-P. Komsa, High-throughput computation of Raman spectra from first principles, Sci. Data, 2023, 10, 80, DOI:10.1038/s41597-023-01988-5.
- L. Bastonero and N. Marzari, Automated all-functionals infrared and Raman spectra, npj Comput. Mater., 2024, 10, 55, DOI:10.1038/s41524-024-01236-3.
- G. Pizzi, A. Cepellotti, R. Sabatini, N. Marzari and B. Kozinsky, AiiDA: automated interactive infrastructure and database for computational science, Comput. Mater. Sci., 2016, 111, 218–230, DOI:10.1016/j.commatsci.2015.09.013.
- S. P. Huber, S. Zoupanos, M. Uhrin, L. Talirz, L. Kahle, R. Häuselmann, D. Gresch, T. Müller, A. V. Yakutovich, C. W. Andersen, F. F. Ramirez, C. S. Adorf, F. Gargiulo, S. Kumbhar, E. Passaro, C. Johnston, A. Merkys, A. Cepellotti, N. Mounet, N. Marzari, B. Kozinsky and G. Pizzi, AiiDA 1.0, a scalable computational infrastructure for automated reproducible workflows and data provenance, Sci. Data, 2020, 7, 300, DOI:10.1038/s41597-020-00638-4.
- M. Uhrin, S. P. Huber, J. Yu, N. Marzari and G. Pizzi, Workflows in AiiDA: Engineering a high-throughput, event-based engine for robust and modular computational workflows, Comput. Mater. Sci., 2021, 187, 110086, DOI:10.1016/j.commatsci.2020.110086.
- B. Huddart, A. Hernández-Melián, T. Hicken, M. Gomilšek, Z. Hawkhead, S. Clark, F. Pratt and T. Lancaster, MuFinder: A program to determine and analyse muon stopping sites, Comput. Phys. Commun., 2022, 280, 108488, DOI:10.1016/j.cpc.2022.108488.
- The Galaxy Community, The Galaxy platform for accessible, reproducible and collaborative biomedical analyses: 2022 update, Nucleic Acids Res., 2022, 50, W345–W351, DOI:10.1093/nar/gkac247.
- I. Timrov, N. Marzari and M. Cococcioni, HP – A code for the calculation of Hubbard parameters using density-functional perturbation theory, Comput. Phys. Commun., 2022, 279, 108455, DOI:10.1016/j.cpc.2022.108455.
- A. V. Yakutovich, K. Eimre, O. Schütt, L. Talirz, C. S. Adorf, C. W. Andersen, E. Ditler, D. Du, D. Passerone, B. Smit, N. Marzari, G. Pizzi and C. A. Pignedoli, AiiDAlab – an ecosystem for developing, executing, and sharing scientific workflows, Comput. Mater. Sci., 2021, 188, 110165, DOI:10.1016/j.commatsci.2020.110165.
- S. P. Huber, E. Bosoni, M. Bercx, J. Bröder, A. Degomme, V. Dikan, K. Eimre, E. Flage-Larsen, A. Garcia, L. Genovese, D. Gresch, C. Johnston, G. Petretto, S. Poncé, G.-M. Rignanese, C. J. Sewell, B. Smit, V. Tseplyaev, M. Uhrin, D. Wortmann, A. V. Yakutovich, A. Zadoks, P. Zarabadi-Poor, B. Zhu, N. Marzari and G. Pizzi, Common workflows for computing material properties using different quantum engines, npj Comput. Mater., 2021, 7, 136, DOI:10.1038/s41524-021-00594-6.
- E. Bosoni, L. Beal, M. Bercx, P. Blaha, S. Blügel, J. Bröder, M. Callsen, S. Cottenier, A. Degomme, V. Dikan, K. Eimre, E. Flage-Larsen, M. Fornari, A. Garcia, L. Genovese, M. Giantomassi, S. P. Huber, H. Janssen, G. Kastlunger, M. Krack, G. Kresse, T. D. Kühne, K. Lejaeghere, G. K. H. Madsen, M. Marsman, N. Marzari, G. Michalicek, H. Mirhosseini, T. M. A. Müller, G. Petretto, C. J. Pickard, S. Poncé, G.-M. Rignanese, O. Rubel, T. Ruh, M. Sluydts, D. E. P. Vanpoucke, S. Vijay, M. Wolloch, D. Wortmann, A. V. Yakutovich, J. Yu, A. Zadoks, B. Zhu and G. Pizzi, How to verify the precision of density-functional-theory implementations via reproducible and universal workflows, Nat. Rev. Phys., 2024, 6, 45–58, DOI:10.1038/s42254-023-00655-3.
- Theory of Defects in Semiconductors, ed. D. A. Drabold and S. K. Estreicher, Springer Berlin Heidelberg, 2007, DOI:10.1007/11690320.
- J. H. Brewer, S. R. Kreitzman, D. R. Noakes, E. J. Ansaldo, D. R. Harshman and R. Keitel, Observation of muon-fluorine ”hydrogen bonding” in ionic crystals, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 7813–7816, DOI:10.1103/PhysRevB.33.7813.
- J. D. Jackson, Classical Electrodynamics, Wiley New York, 3rd edn, 1999 Search PubMed.
- P. Bonfà, I. J. Onuorah and R. D. Renzi, in Introduction and a Quick Look at MUESR, the Magnetic Structure and mUon Embedding Site Refinement Suite, Physical Society of Japan, 2018, 011052, p. 10.7566/JPSCP.21.011052 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment: A Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002, DOI:10.1088/1361-648X/aa680e.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319, DOI:10.1016/j.commatsci.2012.10.028.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, Quantum ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502, DOI:10.1088/0953-8984/21/39/395502.
- P. Bonfà, I. J. Onuorah, F. Lang, I. Timrov, L. Monacelli, C. Wang, X. Sun, O. Petracic, G. Pizzi, N. Marzari, S. J. Blundell and R. De Renzi, Magnetostriction-driven muon localization in an antiferromagnetic oxide, Phys. Rev. Lett., 2024, 132, 046701, DOI:10.1103/PhysRevLett.132.046701.
- M. J. Puska, S. Pöykkö, M. Pesola and R. M. Nieminen, Convergence of supercell calculations for point defects in semiconductors: Vacancy in silicon, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 1318–1325, DOI:10.1103/PhysRevB.58.1318.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305, DOI:10.1103/RevModPhys.86.253.
- M. Ceriotti, Unsupervised machine learning in atomistic simulations, between predictions and understanding, J. Chem. Phys., 2019, 150, 150901, DOI:10.1063/1.5091842.
- L. Liborio, S. Sturniolo and D. Jochym, Computational prediction of muon stopping sites using ab initio random structure searching (AIRSS), J. Chem. Phys., 2018, 148, 134114, DOI:10.1063/1.5024450.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215, DOI:10.1063/1.1564060.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly constrained and appropriately normed semilocal density functional, Phys. Rev. Lett., 2015, 115, 036402, DOI:10.1103/PhysRevLett.115.036402.
- A. P. Bartók and J. R. Yates, Regularized SCAN functional, J. Chem. Phys., 2019, 150, 161101, DOI:10.1063/1.5094646.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11, 8208–8215, DOI:10.1021/acs.jpclett.0c02405.
- F. Aryasetiawan and O. Gunnarsson, The GW method, Rep. Prog. Phys., 1998, 61, 237, DOI:10.1088/0034-4885/61/3/002.
- M. Bonacci, J. Qiao, N. Spallanzani, A. Marrazzo, G. Pizzi, E. Molinari, D. Varsano, A. Ferretti and D. Prezzi, Towards high-throughput many-body perturbation theory: efficient algorithms and automated workflows, npj Comput. Mater., 2023, 9, 74, DOI:10.1038/s41524-023-01027-2.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 44, 943–954, DOI:10.1103/PhysRevB.44.943.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method, J. Phys.: Condens. Matter, 1997, 9, 767, DOI:10.1088/0953-8984/9/4/002.
- M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA + U method, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 035105, DOI:10.1103/PhysRevB.71.035105.
- H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Density functional theory in transition-metal chemistry: a self-consistent Hubbard U approach, Phys. Rev. Lett., 2006, 97, 103001, DOI:10.1103/PhysRevLett.97.103001.
- I. Timrov, N. Marzari and M. Cococcioni, Hubbard parameters from density-functional perturbation theory, Phys. Rev. B, 2018, 98, 085127, DOI:10.1103/PhysRevB.98.085127.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA + U framework, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 195107, DOI:10.1103/PhysRevB.73.195107.
- M. Heinemann, B. Eifert and C. Heiliger, Band structure and phase stability of the copper oxides Cu2O, CuO, and Cu4O3, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 115111, DOI:10.1103/PhysRevB.87.115111.
- J. Hellsvik, M. Balestieri, T. Usui, A. Stroppa, A. Bergman, L. Bergqvist, D. Prabhakaran, O. Eriksson, S. Picozzi, T. Kimura and J. Lorenzana, Tuning order-by-disorder multiferroicity in CuO by doping, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 014437, DOI:10.1103/PhysRevB.90.014437.
- D. Wu, Q. Zhang and M. Tao, LSDA + U study of cupric oxide: Electronic structure and native point defects, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 235206, DOI:10.1103/PhysRevB.73.235206.
- A. Filippetti and V. Fiorentini, Magnetic ordering in CuO from first principles: a cuprate antiferromagnet with fully three-dimensional exchange interactions, Phys. Rev. Lett., 2005, 95, 086405, DOI:10.1103/PhysRevLett.95.086405.
- C. Niedermayer, A. Golnik, E. Recknagel, M. Rossmanith, A. Weidinger, X. S. Chang, A. Kleinhammes, N. Rosov, J. Saylor, R. Schuhmann, L. Takacs, A. Teh, G. Zhang, C. Hohenemser and J. I. Budnick, Hyperfine interaction studies of antiferromagnetic order in CuO, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 38, 2836–2839, DOI:10.1103/PhysRevB.38.2836.
- V. N. Duginov, V. G. Grebinnik, K. I. Gritsaj, T. N. Mamedov, V. G. Olshevsky, V. Y. Pomjakushin, V. A. Zhukov, B. F. Kirillov, I. A. Krivosheev, A. V. Pirogov and A. N. Ponomarev, μSR investigation of cupric oxide, Hyperfine Interact., 1994, 85, 317–322, DOI:10.1007/BF02069441.
- W. Dawson, K. Nishiyama, S. Ohira and W. Higemoto, Localization of positive muons in antiferromagnetic transition metal oxides, Phys. C, 1997, 282–287, 1383–1384, DOI:10.1016/S0921-4534(97)00783-1.
- K. Nishiyama, W. Higemoto, K. Shimomura, A. Koda, G. Maruta, S. W. Nishiyama and X. G. Zheng, Multiple phase transitions in CuO studied by μSR, Hyperfine Interact., 2001, 136, 289–294, DOI:10.1023/A:1020504620851.
- G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, Precision and efficiency in solid-state pseudopotential calculations, npj Comput. Mater., 2018, 4, 72, DOI:10.1038/s41524-018-0127-2.
- Z. Guguchia, C. Mielke, D. Das, R. Gupta, J.-X. Yin, H. Liu, Q. Yin, M. H. Christensen, Z. Tu, C. Gong, N. Shumiya, M. S. Hossain, T. Gamsakhurdashvili, M. Elender, P. Dai, A. Amato, Y. Shi, H. C. Lei, R. M. Fernandes, M. Z. Hasan, H. Luetkens and R. Khasanov, Tunable unconventional kagome superconductivity in charge ordered RbV3Sb5 and KV3Sb5, Nat. Commun., 2023, 14, 153, DOI:10.1038/s41467-022-35718-z.
- C. Mielke III, D. Das, J.-X. Yin, H. Liu, R. Gupta, Y.-X. Jiang, M. Medarde, X. Wu, H. C. Lei, J. Chang, P. Dai, Q. Si, H. Miao, R. Thomale, T. Neupert, Y. Shi, R. Khasanov, M. Z. Hasan, H. Luetkens and Z. Guguchia, Time-reversal symmetry-breaking charge order in a kagome superconductor, Nature, 2022, 602, 245, DOI:10.1038/s41586-021-04327-z.
- R. Kubo and T. Toyabe, in A stochastic model for low field resonance and relaxation, ed. R. Blinc, North-Holland, Amsterdam, 1967, pp. 810–823 Search PubMed.
- R. S. Hayano, Y. J. Uemura, J. Imazato, N. Nishida, T. Yamazaki and R. Kubo, Zero and low field spin relaxation studied by positive muons, Phys. Rev. B:Condens. Matter Mater. Phys., 1979, 20, 850–859, DOI:10.1103/PhysRevB.20.850.
- J. M. Wilkinson and S. J. Blundell, Information and decoherence in a muon-fluorine coupled system, Phys. Rev. Lett., 2020, 125, 087201, DOI:10.1103/PhysRevLett.125.087201.
- J. Rodriguez-Carvajal, M. T. Fernandez-Diaz and J. L. Martinez, Neutron diffraction study on structural and magnetic properties of La2NiO4, J. Phys.: Condens. Matter, 1991, 3, 3215, DOI:10.1088/0953-8984/3/19/002.
- B. Martínez, X. Obradors, E. Ansaldo, C. Niedermayer, D. Noakes, M. Sayagués, M. Vallet and J. González-Calbet, μ+SR study of magnetic order in La2NiO4+δ, J. Magn. Magn. Mater., 1992, 104–107, 941–943, DOI:10.1016/0304-8853(92)90433-O.
- K. H. Chow, P. A. Pattenden, S. J. Blundell, W. Hayes, F. L. Pratt, T. Jestädt, M. A. Green, J. E. Millburn, M. J. Rosseinsky, B. Hitti, S. R. Dunsiger, R. F. Kiefl, C. Chen and A. J. S. Chowdhury, Muon-spin-relaxation studies of magnetic order in heavily doped La2−xSrxNiO4+δ, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 53, R14725–R14728, DOI:10.1103/PhysRevB.53.R14725.
- K. H. Chow, T. Jestädt, S. J. Blundell, S. R. Dunsiger, W. Hayes, B. Hitti, M. A. Green, R. F. Kiefl, J. E. Millburn, P. A. Pattenden, F. L. Pratt and M. J. Rosseinsky, Probing magnetic order in heavily doped La2−xSrxNiO4+δ with μSR, Hyperfine Interact., 1997, 104, 55–60, DOI:10.1023/A:1012642802506.
- T. Jestädt, K. H. Chow, S. J. Blundell, W. Hayes, F. L. Pratt, B. W. Lovett, M. A. Green, J. E. Millburn and M. J. Rosseinsky, Temperature and doping-level dependence of magnetic order in La2−xSrxNiO4+δ studied by muon spin rotation, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 3775–3782, DOI:10.1103/PhysRevB.59.3775.
- F. Lechermann, Assessing the correlated electronic structure of lanthanum nickelates, Electron. Struct., 2022, 4, 015005, DOI:10.1088/2516-1075/ac5c6a.
- G. H. Lander, P. J. Brown, J. Spal/ek and J. M. Honig, Structural and magnetization density studies of La2NiO4, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 40, 4463–4471, DOI:10.1103/PhysRevB.40.4463.
- H. Yanagi, R. Kawamura, T. Kamiya, Y. Kamihara, M. Hirano, T. Nakamura, H. Osawa and H. Hosono, Itinerant ferromagnetism in the layered crystals LaCoOX (X = P, As), Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 224431, DOI:10.1103/PhysRevB.77.224431.
- G. Prando, P. Bonfà, G. Profeta, R. Khasanov, F. Bernardini, M. Mazzani, E. M. Brüning, A. Pal, V. P. S. Awana, H.-J. Grafe, B. Büchner, R. De Renzi, P. Carretta and S. Sanna, Common effect of chemical and external pressures on the magnetic properties of RCoPO (R = La, Pr), Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 064401, DOI:10.1103/PhysRevB.87.064401.
- L. Ortenzi, I. I. Mazin, P. Blaha and L. Boeri, Accounting for spin fluctuations beyond local spin density approximation in the density functional theory, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 064437, DOI:10.1103/PhysRevB.86.064437.
- T. Miyake, T. Ogitsu and S. Tsuneyuki, Quantum distributions of muonium and hydrogen in crystalline silicon, Phys. Rev. Lett., 1998, 81, 1873–1876, DOI:10.1103/PhysRevLett.81.1873.
- M. Gomilšek, F. L. Pratt, S. P. Cottrell, S. J. Clark and T. Lancaster, Many-body quantum muon effects and quadrupolar coupling in solids, Commun. Phys., 2023, 6, 142, DOI:10.1038/s42005-023-01260-7.
- F. Hotz, M. Gomilšek, T. Arh, A. Zorko and H. Luetkens, Anharmonic quantum muon effects in the kagome antiferromagnet Zn-Barlowite, arXiv, preprint, 2024, arXiv:2408.00185, DOI: DOI:10.48550/arXiv.2408.00185.
- H. Jónsson, G. Mills and K. W. Jacobsen, in Nudged elastic band method for finding minimum energy paths of transitions, World Scientific, 1998, ch. 1, pp. 385–404, DOI:10.1142/9789812839664_0016.
- P. Bonfà, J. Frassineti, M. M. Isah, I. J. Onuorah and S. Sanna, UNDI: An open-source library to simulate muon-nuclear interactions in solids, Comput. Phys. Commun., 2021, 260, 107719, DOI:10.1016/j.cpc.2020.107719.
- P. Bonfà, J. Frassineti, J. M. Wilkinson, G. Prando, M. M. Isah, C. Wang, T. Spina, B. Joseph, V. F. Mitrović, R. De Renzi, S. J. Blundell and S. Sanna, Entanglement between muon and I > 1/2 nuclear spins as a probe of charge environment, Phys. Rev. Lett., 2022, 129, 097205, DOI:10.1103/PhysRevLett.129.097205.
- M. Celio, New method to calculate the muon polarization function, Phys. Rev. Lett., 1986, 56, 2720–2723, DOI:10.1103/PhysRevLett.56.2720.
- L. Talirz, S. Kumbhar, E. Passaro, A. V. Yakutovich, V. Granata, F. Gargiulo, M. Borelli, M. Uhrin, S. P. Huber, S. Zoupanos, C. S. Adorf, C. W. Andersen, O. Schütt, C. A. Pignedoli, D. Passerone, J. VandeVondele, T. C. Schulthess, B. Smit, G. Pizzi and N. Marzari, Materials Cloud, a platform for open computational science, Sci. Data, 2020, 7, 299, DOI:10.1038/s41597-020-00637-5.
| This journal is © The Royal Society of Chemistry 2025 |