Open Access Article
Open Access ArticlePredicting hydrogen atom transfer energy barriers using Gaussian process regression†
Evgeni
Ulanov
 *ae,
Ghulam A.
Qadir
*a,
Kai
Riedmiller
*ae,
Ghulam A.
Qadir
*a,
Kai
Riedmiller
 a,
Pascal
Friederich
a,
Pascal
Friederich
 *bc and
Frauke
Gräter
*bc and
Frauke
Gräter
 *ade
*ade
aHeidelberg Institute for Theoretical Studies, Heidelberg, Germany. E-mail: evgeni.ulanov@h-its.org; ghulam.qadir@h-its.org; frauke.graeter@h-its.org
bInstitute of Theoretical Informatics, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany. E-mail: pascal.friederich@kit.edu
cInstitute of Nanotechnology, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany
dInterdisciplinary Center for Scientific Computing, Heidelberg University, Heidelberg, Germany
eMax Planck Institute for Polymer Research, Mainz, Germany
First published on 10th January 2025
Abstract
Predicting reaction barriers for arbitrary configurations based on only a limited set of density functional theory (DFT) calculations would render the design of catalysts or the simulation of reactions within complex materials highly efficient. We here propose Gaussian process regression (GPR) as a method of choice if DFT calculations are limited to hundreds or thousands of barrier calculations. For the case of hydrogen atom transfer in proteins, an important reaction in chemistry and biology, we obtain a mean absolute error of 3.23 kcal mol−1 for the range of barriers in the data set using SOAP descriptors and similar values using the marginalized graph kernel. Thus, the two GPR models can robustly estimate reaction barriers within the large chemical and conformational space of proteins. Their predictive power is comparable to a graph neural network-based model, and GPR even outcompetes the latter in the low data regime. We propose GPR as a valuable tool for an approximate but data-efficient model of chemical reactivity in a complex and highly variable environment.
1 Introduction
Chemical reactivity in complex chemical or biochemical systems can be assessed typically at very high accuracy using quantum chemical methods such as density functional theory (DFT). Surrogate models built using machine learning have been recently suggested to be able to replace these computationally demanding DFT calculations.1 The trained model serves as a black box approximation of the true mapping between reaction geometries and energy barriers. Machine-learned surrogate models can in principle predict reaction barriers solely based on molecular structures, after being trained on pre-calculated DFT barriers, albeit at lower accuracy than the actual DFT calculation itself.2,3In molecular machine learning, graph representations for molecular prediction problems have seen great success in recent years, specifically in the form of Graph Neural Networks (GNNs). Prominent recent examples include the frameworks Polarizable Atom Interaction Neural Network (PaiNN),4 Neural Equivariant Interatomic Potentials (NequIP)5 and MACE.6 We have recently shown that a variant of the PaiNN model can be used to predict electronic activation energies, in this paper referred to as energy barriers, of hydrogen atom transfer (HAT) reactions in proteins.7 We have chosen HAT because of its important role in proteins subjected to oxidative stress molecules, light, or, as recently shown by us, mechanical force. Mechanoradicals are formed in type I collagen through homolytic bond scission when subject to mechanical stress.8 The generated radicals migrate through the material, eventually to a site that can stabilize radicals.9 Understanding the mechanisms behind these reactions is especially interesting to get a better insight into the effects stress, such as exercise, can have on protein materials like collagen. Beyond mechanoradicals, migration of protein radicals, originating from light, oxidative stress molecules, or other external factors, often occurs through HAT, e.g. ref. 10. Exact radical migration paths are, however, mostly unknown. This renders HAT an interesting test bed to tackle the prediction of biochemical reactivity.
Our model presented in ref. 7 based on PaiNN was able to predict HAT reactions with geometries obtained from molecular dynamics (MD) simulations, with a mean absolute error (MAE) of 2.4 kcal mol−1 when restricting the prediction to transitions with distances ≤2 Å, i.e. the most relevant transitions in a material.
Geometries originated directly from molecular dynamics (MD) simulations, without subsequent DFT optimizations, rendering such a method very efficient. The model allows the prediction of a reaction barrier for virtually any reactant pair occurring during an MD simulation of the protein. This can ultimately allow simulating these reactions in a kinetic Monte Carlo setting coupled to the MD simulations, i.e. reactive dynamics of the biochemical system under investigation.11 From a practical perspective, the energy barrier prediction should only rely on the initial geometric configuration as input for it to be useful in a future application.
One major drawback of building such a surrogate model is the need to initially compute, using DFT, a large set of energy barriers of the reaction at hand to train the model. Here, large often refers to thousands of barriers, in our case to 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164 barriers for reaching an intermediate accuracy of a PaiNN model for HAT, with further room for improvement by enlarging the dataset. For practitioners, a more data-efficient model would be very advantageous.
164 barriers for reaching an intermediate accuracy of a PaiNN model for HAT, with further room for improvement by enlarging the dataset. For practitioners, a more data-efficient model would be very advantageous.
We propose two alternative variants to model these reactions with Gaussian Process Regression (GPR):12 (1) using the Smooth Overlap of Atomic Positions (SOAP) descriptor13 and (2) using the Marginalized Graph Kernel.14–17 We show that these approaches are a useful alternative to the previously developed GNN, especially in the low data regime. This is of particular interest, since DFT can be very computationally demanding for large systems at high levels of accuracy. Therefore, acquiring new training points can be costly. The proposed methods would allow practitioners to achieve good predictions while reducing the time and cost spent generating training data.
2 Methods
2.1 Data
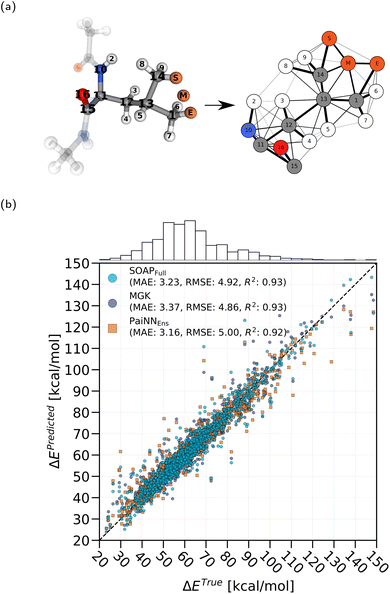
For the predictions, we used the same data as obtained and described in ref. 7. In short, the data was generated in two ways. The first method consisted mostly of procedurally positioning two amino acids such that two hydrogen atoms faced one another, after which a random distance and tilt angle between the amino acid pairs was chosen and one of the hydrogen atoms was removed to represent a radical centre. Also, intramolecular transitions were considered, in which the acceptor and donor of the hydrogen atom reside in the same molecule. The data generated via this method will, in agreement with ref. 7, be referred to as synthetic systems. In contrast to this, the trajectory systems were taken as sub-systems from molecular dynamics trajectories, where possible HAT reactions were first identified. After removing duplicate transitions as well as a clear outlier, the training set consisted of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 energy barriers and 1926 randomly chosen barriers as the test set. The hydrogen atom was moved from initial to end position in a straight line, see Fig. 1a, and DFT energies were obtained at equidistant steps along the transition as can be seen in Fig. 1b. Note that DFT values for steps 1, 2, 8, and 9, as depicted in Fig. 1a and b, were often not calculated, since the transition state was found to be mostly around the geometric middle (see ref. 7). We define the energy barrier ΔE as the difference between the maximum and the initial DFT calculated energy of a given reaction geometry and direction.
238 energy barriers and 1926 randomly chosen barriers as the test set. The hydrogen atom was moved from initial to end position in a straight line, see Fig. 1a, and DFT energies were obtained at equidistant steps along the transition as can be seen in Fig. 1b. Note that DFT values for steps 1, 2, 8, and 9, as depicted in Fig. 1a and b, were often not calculated, since the transition state was found to be mostly around the geometric middle (see ref. 7). We define the energy barrier ΔE as the difference between the maximum and the initial DFT calculated energy of a given reaction geometry and direction.
As discussed in ref. 7, a linear transition path is a reasonable estimate of the true reaction. Nonetheless, this neglects that neighbouring atoms can undergo conformational changes during the reaction. Therefore, some structures in the dataset were additionally optimized using the same level of DFT as the energy calculations. This is computationally more expensive, but also yields more realistic energy barriers. In total, 1434 optimized reaction barriers were used for training and 162 barriers as a randomly selected test set.
It is important to note that each transition, both optimized and not optimized, has two energy barriers, namely, one for each direction of the transition.
2.2 Gaussian process regression
In this paper, we use Gaussian Process Regression (GPR),12 a flexible and probabilistic machine learning method, to predict energy barriers of HAT reactions. For the purpose of conciseness, we here only introduce the necessary equations. The ESI, Section A,† includes a more complete description of GPR and the used definitions. In short, our GPR models a collection of m unobserved scalar values Yu using a collection of n observed scalar values Yo by assuming that the union of Yu and Yo, denoted as Y, follow a multivariate normal distribution (MVN) with a covariance structure given by the following parametric function:| Kθ(x,x′) = σ2(Cθc(x,x′) + g2δx,x′), | (1) |
It is therefore possible to condition the MVN on the observed values Yo, yielding a different (conditional) MVN of the unobserved values Yu. The resulting MVN is specified by the following mean vector and covariance matrix:
| μu|o = μ + ΣuoΣoo−1(Yo − μ) | (2) |
| Σu|o = Σuu − ΣuoΣoo−1Σ⊤uo, | (3) |
Evidently, the GPR based predictions from (2) and (3) rely on the specified mean μ, which in general need not be a constant, and the covariance function Kθ(·,·). The covariance function serves as a robust mathematical metric for determining “similarity” among samples, under the premise that the most “similar” samples have the most influence on the outcome. Selecting an appropriate covariance function is critical for making high-quality predictions.
Furthermore, once the covariance function is selected, it is necessary to estimate its associated parameters, denoted by θ, so that they align well with the observed data. Maximum likelihood estimation (MLE) is commonly employed for this task in GPR. However, the computational cost and time complexity of MLE can become prohibitive for large n, leading to the use of approximate methods. Among these, methods based on composite likelihoods18 are quite common. In this work, we specifically use a particular variant of composite likelihood called random composite likelihood estimation.19 In the following sections, we explore the two distinct definitions of the covariate x and correlation function Cθc(·,·) in our study, resulting in two different GPR models.
2.3 Smooth overlap of atomic positions method
Given that GPR modelling of the HAT reaction necessitates the covariance functions to accurately capture reactions related to atomic geometries, constructing an accurate covariance function that represents the specifics of the HAT setting is not straightforward. This is particularly challenging since most common kernels primarily rely on real-valued scalars as features.Smooth Overlap of Atomic Positions (SOAP)13 is an elegant representation of a local atomic environment. Consider an atomic environment that is centred on an atom and extends up to a cut-off radius rcut. Let the atomic density be the sum of atoms inside this environment, where each atom is transformed into a Gaussian density. The atomic density of atoms of chemical species a is then given by20
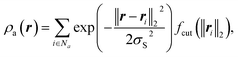 | (4) |
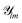 and orthogonal normalized radial basis functions gn, such that
and orthogonal normalized radial basis functions gn, such that  , where canlm are expansion coefficients that can be calculated. In real-world applications, the infinite sum is truncated at some predefined maximum values nmax and lmax.
, where canlm are expansion coefficients that can be calculated. In real-world applications, the infinite sum is truncated at some predefined maximum values nmax and lmax.
The SOAP power spectrum can be defined as
 | (5) |
In order to model the HAT process, a covariance function needs to be defined where similar atomic geometries result in a high correlation and vice versa. It has been shown in previous works that the starting environment as well as the transition state environment are important in predicting energy barriers in HAT reactions.21 For this method we choose a correlation function in the following way,
 | (6) |
Eqn (6) is equivalent to a product of squared exponential correlation functions12 which is a valid kernel as a result of the Schur product theorem.22 We considered also including SOAP environments at other steps of a transition, however we found that this only marginally improved the results, but required a much higher computational cost. The interpretation of this kernel suggests that reactions, where the beginning, intermediate, and final environments, along with the total transition distance, exhibit similarity, should correspondingly produce similar energy barriers. Conversely, if any of these features demonstrates dissimilarity, it would result in a minor contribution to the prediction.
We placed a hydrogen atom at the starting, middle, and end positions of the HAT reaction. Each of these hydrogen atoms was assigned a different unique chemical species, since SOAP does not interpret the chemical elements, but instead only serves to distinguish geometrically the hydrogen atom at each step of the transition from the other atoms. The environments around the starting, middle and end positions were encoded as SOAP vectors as depicted in Fig. 1c. Through manual trial and error optimization of randomly chosen validation sets from the training set, we chose the SOAP parameters as rcut = 2.5 Å, σS = 0.3 Å, nmax = 12 and lmax = 12. The SOAP vectors were calculated using the DScribe library23 and normalized. Furthermore, the energy barriers and transition distances were standardized during training using their respective training means and standard deviations.
2.4 Marginalized graph kernel
As an alternative to using descriptors to capture the geometries of the transition, we built a GPR model using graphs. Here we define a graph G as a set of vertices V = {vi}i=1…N, where some vertices are connected through undirected edges E = {eij}i,j=1…N with associated weights wij. The Marginalized Graph Kernel (MGK) was first introduced in ref. 14 and computes the covariance between two graphs by comparing random walks on each graph. Following the explanation and notation of ref. 15, the MGK covariance is the expectation value of the covariance between all possible concurrent random walk paths on the two graphs. Each vertex vi has a start probability ps(vi) for the walk to begin at this vertex and, similarly, a termination probability pe(vi). The weight wij of an edge eij, obtained through a separately defined function, the adjacency rule, is used to calculate the transition probability , where the sum runs over all vertices connected to vertex vi. Let h = (h1, h2, …, hl) be a vector recording the vertex path resulting from the chain of length l. The MGK between graphs G and G′ can then be written as
, where the sum runs over all vertices connected to vertex vi. Let h = (h1, h2, …, hl) be a vector recording the vertex path resulting from the chain of length l. The MGK between graphs G and G′ can then be written as | (7) |
For each HAT transition we construct one graph. An example of such a construction is illustrated in Fig. 2a. We place a hydrogen atom at the start, end, and mid-point of the transition, as was done for the SOAP method, and similarly each of these hydrogen atoms is assigned a unique special value sv. All other atoms are assigned a different special value to differentiate between the hydrogen atom involved in the reaction and all other atoms. In order to create an artificial feature that smoothly distinguishes between atoms on the donor and acceptor side of the reaction, we take the dot product between the normalized transition direction vector and the unit vector from the atom to the midpoint of the transition path,
 | (8) |
For the vertex kernel we chose
| KV(v,v′) = δ(av,av′; 0.7)δ(sv,sv′; 0.2)exp(−|ξv − ξv′|/2), | (9) |
 | (10) |
 | (11) |
 | (12) |
2.5 Uncertainty quantification
An advantage of using GPR is that the predictions are probabilistic and therefore allow for straight-forward uncertainty quantification. Uncertainty is here quantified using a predictive probability distribution of the energy barrier given a new input geometry. A commonly employed principle in judging probabilistic predictions is that a predictive distribution should achieve maximal sharpness while still being calibrated.24 Here sharpness refers to the concentration of the predictive distribution and calibration is a measure of the statistical compatibility of predicted and true values.A simple tool for assessing the calibration of predictive distributions is the probability integral transform (PIT).24–26 Let Fi be the predicted cumulative distribution function (CDF) for input i. We can then compute the probability that a measurement will be smaller or equal to the true value Ytruei through
| pi = Fi(Ytruei). | (13) |
Proper scoring rules27 can be utilized to simultaneously assess calibration and sharpness by assigning a score to the pair of true observation and the corresponding predictive distribution. A score is called proper, if, in expectation, the best score is achieved by the true probability distribution of the data-generating process. Here we use the convention that a lower score indicates a better prediction distribution and therefore allows a direct comparison between different methods. A commonly employed proper scoring rule is the negatively oriented logarithmic score (LogS),27
| LogS(fi,Ytruei) = −log(fi(Ytruei)), | (14) |
 | (15) |
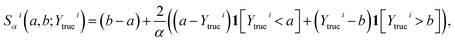 | (16) |
In the case of the PaiNN models, we construct the predictive intervals and distributions similar to ref. 30, which assumes that the bias is sufficiently negligible and that the point predictions of the models are Gaussian distributed around the true value. We neglect noise effects and construct the lower and higher bounds of the prediction intervals for the point i as
[![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) i − c(α/2) i − c(α/2)![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i, i, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) i + c(α/2) i + c(α/2)![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i], i], | (17) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) i is the ensemble mean,
i is the ensemble mean, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) i is the ensemble sample standard deviation and c(·) is the quantile function of the Student's t-distribution. For the calculation of the LogS and CRPS, we used the Student's t-distribution with degree of freedom 10, the number of ensemble members, together with the ensemble sample mean and standard deviation as the predictive distribution. Following ref. 30, by using the above construction, we would obtain confidence rather than prediction intervals, the latter of which, in this framework, is expected to be larger due to inherent random noise. However, in our case, the PaiNN model learns from the full spatial and atomic type information which is equivalent to the input used for the deterministic DFT calculations, and therefore it can be argued that additional modelling of noise is not necessary. Nonetheless, a more extended analysis of the implications is needed and left to future work.
i is the ensemble sample standard deviation and c(·) is the quantile function of the Student's t-distribution. For the calculation of the LogS and CRPS, we used the Student's t-distribution with degree of freedom 10, the number of ensemble members, together with the ensemble sample mean and standard deviation as the predictive distribution. Following ref. 30, by using the above construction, we would obtain confidence rather than prediction intervals, the latter of which, in this framework, is expected to be larger due to inherent random noise. However, in our case, the PaiNN model learns from the full spatial and atomic type information which is equivalent to the input used for the deterministic DFT calculations, and therefore it can be argued that additional modelling of noise is not necessary. Nonetheless, a more extended analysis of the implications is needed and left to future work.
3 Results and discussion
3.1 Predictions
We trained two models based on SOAP and MGK, respectively, as described in the Methods section, using 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 HAT barriers from DFT calculations, comprising both synthetic (7884 barriers) and trajectory data (9354 barriers). The MLE optimization procedure of the SOAP method yielded the final mean kernel parameters: λS = 2.1, λM = 1.8, λE = 3.3, λd = 3.4, σ = 1.3 and g = 0.1. The nugget g was always initialized close to 0.1, since it was observed that this stabilized the optimization procedure. We tested the two models on 1044 HAT barriers from trajectory data and found an overall MAE of 3.23 kcal mol−1. We signify this type of trained model, where the training set included both synthetic and trajectory barriers, with SOAPFull. For the MGK method, we found through MLE g = 0.02 and σ = 7.7 using all barriers for training. The MAE was found to be 3.37 kcal mol−1, resulting in a slightly worse performance than the SOAP-based method.
238 HAT barriers from DFT calculations, comprising both synthetic (7884 barriers) and trajectory data (9354 barriers). The MLE optimization procedure of the SOAP method yielded the final mean kernel parameters: λS = 2.1, λM = 1.8, λE = 3.3, λd = 3.4, σ = 1.3 and g = 0.1. The nugget g was always initialized close to 0.1, since it was observed that this stabilized the optimization procedure. We tested the two models on 1044 HAT barriers from trajectory data and found an overall MAE of 3.23 kcal mol−1. We signify this type of trained model, where the training set included both synthetic and trajectory barriers, with SOAPFull. For the MGK method, we found through MLE g = 0.02 and σ = 7.7 using all barriers for training. The MAE was found to be 3.37 kcal mol−1, resulting in a slightly worse performance than the SOAP-based method.
For the SOAP method, we additionally trained a model only using the trajectory data, referred to as SOAPTraj, resulting in: λS = 5.7, λM = 2.8, λE = 10.4, λd = 8.2 Å, σ = 3.8 and g = 0.06 with an average MAE of 3.26 kcal mol−1. The MAE is very similar compared to the model using all training data, even though it only used ≈54% of all data. This indicates that for the purpose of predicting in a trajectory setting, the synthetic data appears to only marginally improve the predictions.
Fig. 2b shows the energy barrier prediction results of the SOAP and MGK methods for all trajectory test data trained using both synthetic and trajectory data. For comparison, we also include the ensemble predictions of a PaiNN ensemble model, as described in ref. 7, which we trained on the same data. The ensemble model, referred to as PaiNNEns, consisted of the mean prediction of 10 individually trained PaiNN models, which are here referred to as PaiNNInd. Note that each ensemble member was trained on randomly sampled 90% of the training data, with the rest used for validation. Overall, the SOAP method can be seen to slightly outperform the MGK method. There are only few outliers, and most test points form a narrow band around the diagonal. The error tends to be much higher for large barriers, which can be attributed to the low number of training points in this range. In practice, these points are not very relevant, since the transitions are very unlikely to occur. It is particularly interesting to note that some outliers form close triplets, where the prediction error of all three methods is very similar. This suggests that, for these geometries at least, all methods must have some similarity in the way they make predictions. This is remarkable, since superficially the three methods capture the reactions in very different ways.
The test MAE results for the different methods are summarized in Table 1. We also include the performance for reactions where the transition distance d is smaller or equal to 2 Å or 3 Å, focusing on reactions that have typically lower barriers and are therefore more relevant in a protein environment, as discussed in ref. 7. Remarkably, both GPR-based models perform nearly as well as the previously suggested graph neural network (PaiNN) ensemble model7 with the MAE of the test set only sightly larger. We show in the next section that this can be directly related to the data efficiency of the GPR and GNN method.
| Test set | SOAPFull | SOAPTraj | MGK | PaiNNInd | PaiNNEns |
|---|---|---|---|---|---|
| All (no cut-off) | 3.23 | 3.26 | 3.37 | 3.55 | 3.16 |
| Cut-off d ≤ 3 Å | 3.08 | 3.11 | 3.20 | 3.30 | 2.94 |
| Cut-off d ≤ 2 Å | 2.79 | 2.82 | 2.85 | 2.83 | 2.53 |
3.2 Data efficiency
A major drawback of training on DFT calculated data is that constructing the training set can be very computationally demanding. It has been observed previously, e.g. see ref. 1 and 3, that GPR can be more data efficient than a similar neural network approach. Here we compare the data efficiency of the GPR SOAP-based method with the PaiNN GNN. The average and standard deviation of the MAE results for different training set sizes can be seen in Fig. 3. For the SOAP methods, a training subset was randomly sampled from the entire training set with 8 different initial seeds, and the subsequent MLE parameter estimation was performed on these subsets. This was similar for the PaiNN models, however additionally for each training seed, 10 models were trained. All of these individually trained PaiNN models will be referred to as PaiNNInd. The 10 PaiNNInd with the same seed, constituted one ensemble model PaiNNEns, such that there were 8 ensemble GNNs for a given training set size. The error bars signify the sample standard deviation of the MAE over multiple runs. Occasionally, the optimization procedure found suboptimal parameters for a run, as can be observed in the noticeably larger spread and mean for SOAPFull at 10% of the total training size. We find that in the low to mid-data regime, i.e. low-hundreds to mid-thousands of data points, GPR clearly outperforms the individual GNN models as well as the derived ensemble models. With increasing training size, the MAE of the GNN and GPR method converge, after which the ensemble GNN method achieves overall a lower MAE. After observing that the training curves appear linear on a log–log scale, we fit a power law to the results, in the form of| ε = a·ntraink, | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 13
000 and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 number of training points in the case of transitions with d ≤ 2 Å, 3 Å, or all transition distances considered in the test set, respectively.
000 number of training points in the case of transitions with d ≤ 2 Å, 3 Å, or all transition distances considered in the test set, respectively.
 | ||
| Fig. 3 Test MAE for the SOAP GPR and PaiNN methods studied using different fractions of the total training data for transition distances ≤3 Å and ≤2 Å respectively. | ||
| Method | a [kcal mol−1] | k | n threshold |
|---|---|---|---|
| SOAPFull | 22.6 | −0.20 | 190 × 103 |
| SOAPTraj | 18.3 | −0.19 | 126 × 103 |
| PaiNNInd | 69.5 | −0.31 | 105 × 103 |
| PaiNNEns | 62.5 | −0.31 | 74 × 103 |
3.3 Uncertainty quantification
In Fig. 4a we show the PI accuracy plot,32,33 where we calculate the empirical coverage, i.e. the fraction of predictions that are found inside the respective central prediction interval. Overall it can be seen that the PaiNN ensemble method substantially underestimates the intervals while the SOAP methods is too conservative and chooses intervals that are larger than necessary. | ||
| Fig. 4 Predicted vs. empirical coverage (a) and the probability integral transform (b). Both figures were evaluated on all trajectory test data. | ||
Similar conclusions can be drawn from Fig. 4b which shows the PIT distribution for all three methods. The GPR methods exhibit a hump-like shape, indicating overdispersion, meaning that the predictive distributions are too wide and fewer values are found in the tails than expected. In stark contrast, the PIT of the PaiNN ensemble is clearly U-shaped, i.e. underdispersed, suggesting that far more values are found in the tails than expected and that the distributions are too narrow. Fortunately, no clear triangular slopes can be observed, which would otherwise be an indication of bias.24 A simple possibility to improve the calibration of both methods would be to find an optimal factor that linearly scales the standard deviation using a separate validation data set,20,27 which we leave to future work.
Prediction intervals at levels close to 100% are most interesting, since by definition they promise to capture the true observations with a very high probability. Table 3 shows the arithmetic mean over 8 runs of the mean IS for PIs of different sizes. It can be seen that while at the level of 50% the PaiNN ensemble model appears to score marginally better, the SOAP methods clearly outperform the ensemble method at high level probability prediction intervals. This indicates that the SOAP GPR models are better suited than the PaiNN ensemble method, if one wishes to define ranges that should contain a future observation with a high probability.
| Prediction interval | SOAPFull | SOAPTraj | PaiNNEns |
|---|---|---|---|
| 50% | 11.6 | 11.2 | 10.8 |
| 80% | 19.0 | 17.8 | 18.2 |
| 90% | 24.3 | 22.8 | 26.2 |
| 95% | 29.8 | 28.3 | 38.1 |
| 99% | 46.6 | 47.9 | 95.9 |
Table 4 shows the CRPS and LogS values for the different models when using all available training data (in case of the SOAPTraj this means only trajectory training data), or only 860 training points, which corresponds to 5% of all training data. When using all training data, the results are inconclusive, since the PaiNN ensemble method marginally outperforms the GPR models using the CRPS scoring rule, but is outperformed under the LogS score. However, when using only a limited amount of data, here only 860 training points, the GPR methods clearly achieve better CRPS and LogS values. Therefore, in the low data regime, the predictive distributions of the GPR models should be favoured over the PaiNN ensemble method.
| Scoring rule | SOAPFull | SOAPTraj | PaiNNEns |
|---|---|---|---|
| CRPS (All data) | 2.55 | 2.48 | 2.45 |
| CRPS (5% of all) | 4.24 | 3.72 | 5.91 |
| LogS (all data) | 2.99 | 2.96 | 3.12 |
| LogS (5% of all) | 3.42 | 3.28 | 4.22 |
3.4 Optimized energy barriers
The energy barriers of the optimized reactions, that is, energy differences between optimized transition states and reactants, can be expected to be closer to the true energy barriers compared to the unoptimized reactions. There are only few optimized energy barriers due to the substantial computation cost. Therefore, learning on these directly is expected to be very inefficient, even for the more data-efficient GPR.We choose to model the optimized energy barrier as the unoptimized case with an additional correction term, namely as
| ΔEoptimized(x) = ΔEunoptimized(x) + δ(x), | (19) |
The GPR SOAP method was used to train on the difference between ΔEoptimized and the predicted values of ΔEunoptimized of a retrained PaiNNEns model, which did not include these reactions in its training set. The MAE for the trajectory test set was found to be 4.55(13) kcal mol−1 and 3.77(15) kcal mol−1 with distances d ≤ 3 Å and d ≤ 2 Å respectively, where the results indicate the mean and standard deviation of 8 independent PaiNN and subsequent GPR runs. This is a slight improvement on the previous state-of-the-art results reported in ref. 7 as 4.93 kcal mol−1 for the d ≤ 3 Å case by around 7.8% and comparable to the result of d ≤ 2 Å which was found to be 3.64 kcal mol−1.
4 Conclusions
Gaussian Process Regression (GPR) models are capable of predicting reaction barriers of Hydrogen Atom Transfer (HAT) reactions and their performance almost reaches that achieved by modern Graph Neural Network (GNN) models for the full training set and clearly outperforms the latter in the low data regime.The performance of the GPR models proposed here is similar for two vastly different kernels used, one based on Smooth Overlap of Atomic Positions (SOAP) descriptors and the other employing the marginalized graph kernel. As the major advantage of GPR over GNNs, we find the kernel method to be highly data-efficient, outperforming the GNN for sample sizes of thousands of density functional theory (DFT) energies or smaller. We thus propose GPR to be a method of choice if predictions are needed without the availability of large amounts of data, e.g. for a first screening of a large chemical space of a reaction. Additionally, we envision that an active learning34 approach could be used, where the training set is built iteratively by including candidate transitions with the smallest predicted barriers to increase efficiency in sampling the most relevant reactions.
We estimate that 4.3 times the data would be needed to achieve a target accuracy of 2 kcal mol−1 for the unoptimized barriers in the case of the best-performing GNN ensemble method, under the assumption of a continued power law behaviour. We showed that by combining the strengths of the GNN method, i.e. overall best performance for the unoptimized barriers, and the GPR method, namely, data efficiency, we achieve an improved mean absolute error (MAE) for the optimized energy barriers on this dataset for transition distances d ≤ 3 Å. Furthermore, we showed that the SOAP-based GPR method achieves a better interval score for prediction intervals for the ≥80% range, indicating that GPR is better suited for uncertainty quantification in this range. The SOAP GPR methods achieve noticeably better logarithmic score (LogS) and continuous ranked probability score (CRPS) values than the GNN ensemble methods in the low data regime. However, the GPR uncertainty estimates are overall too conservative and more work needs to be done to ensure that the predictions are better calibrated.
We consider the performance of the models, with an MAE of around 3.2 kcal mol−1 for both the best performing GPR and GNN models, overall satisfactory, in particular in light of the large spread of barriers of more than 100 kcal mol−1, allowing to qualitatively distinguish between small and large barriers, that is, likely and unlikely reactions. However, we acknowledge that the MAE could be too high for some applications, where the spread is smaller or higher certainties are needed. Usages of our model such as screening a large amount of reactions for subsequent DFT computation would require a less stringent accuracy and is subject to future work.
We find a major caveat of the SOAP-based GPR to be the SOAP vector size and by extension the calculation time needed for the pair-wise distances between SOAP vectors for the covariance function calculation. A compression algorithm such as information imbalance35 could alleviate this. We also believe that room for improvement lies in a more systematic selection of the optimal SOAP and marginalized graph kernel hyperparameters. Taken together, with further improvements to leverage the prediction quality, we propose GPR as a valuable choice for predicting reactivity for HAT and potentially other (bio)chemical reactions, in particular in the low data regime.
Data availability
DFT data for this paper was originally published alongside ref. 7 and is available at https://doi.org/10.11588/data/TGDD4Y. Processing scripts for this paper are available at https://github.com/evulan/GPR-HAT-barrier-prediction.Author contributions
E. U.: software, methodology, investigation, writing – original draft. G. A. Q.: conceptualization, methodology, supervision, writing – review & editing. K. R.: data curation, software, writing – review & editing. P. F.: conceptualization, writing – review & editing. F. G.: conceptualization, supervision, project administration, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Klaus Tschira Foundation for generous support of this HITS Lab project and SIMPLAIX. We also thank Alexander I. Jordan, Tilmann Gneiting, and Sebastian Lerch for fruitful discussions. This work was also supported financially by the European Research Council (RADICOL, 101002812, to F. G.).Notes and references
- T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1593 CrossRef.
- C. A. Grambow, L. Pattanaik and W. H. Green, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef PubMed.
- P. Friederich, G. d. P. Gomes, R. D. Bin, A. Aspuru-Guzik and D. Balcells, Chem. Sci., 2020, 11, 4584–4601 RSC.
- K. Schütt, O. Unke and M. Gastegger, Proceedings of the 38th International Conference on Machine Learning, 2021, pp. 9377–9388 Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef PubMed.
- I. Batatia, D. P. Kovacs, G. N. C. Simm, C. Ortner and G. Csanyi, Adv. Neural Inf. Process. Syst., 2022, 11423–11436 Search PubMed.
- K. Riedmiller, P. Reiser, E. Bobkova, K. Maltsev, G. Gryn'ova, P. Friederich and F. Gräter, Chem. Sci., 2024, 15, 2518–2527 RSC.
- M. M. Caruso, D. A. Davis, Q. Shen, S. A. Odom, N. R. Sottos, S. R. White and J. S. Moore, Chem. Rev., 2009, 109, 5755–5798 CrossRef PubMed.
- C. Zapp, A. Obarska-Kosinska, B. Rennekamp, M. Kurth, D. M. Hudson, D. Mercadante, U. Barayeu, T. P. Dick, V. Denysenkov, T. Prisner, M. Bennati, C. Daday, R. Kappl and F. Gräter, Nat. Commun., 2020, 11, 2315 CrossRef PubMed.
- P. Bracco, L. Costa, M. P. Luda and N. Billingham, Polym. Degrad. Stab., 2018, 155, 67–83 CrossRef.
- B. Rennekamp, F. Kutzki, A. Obarska-Kosinska, C. Zapp and F. Gräter, J. Chem. Theory Comput., 2020, 16, 553–563 CrossRef.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, 2005 Search PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- H. Kashima, K. Tsuda and A. Inokuchi, Proceedings, Twentieth International Conference on Machine Learning, Washington, DC, USA, 2003, pp. 321–328 Search PubMed.
- Y.-H. Tang and W. A. de Jong, J. Chem. Phys., 2019, 150, 044107 CrossRef.
- Y.-H. Tang, O. Selvitopi, D. T. Popovici and A. Buluç, IEEE International Parallel and Distributed Processing Symposium (IPDPS), 2020, pp. 728–738 Search PubMed.
- Y. Xiang, Y.-H. Tang, G. Lin and D. Reker, J. Chem. Inf. Model., 2023, 63, 4633–4640 CrossRef.
- C. Varin, N. Reid and D. Firth, Stat. Sin., 2011, 21, 5–42 Search PubMed.
- G. A. Qadir and Y. Sun, Stat. Sin., 2025 Search PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef PubMed.
- P. van Gerwen, A. Fabrizio, M. D. Wodrich and C. Corminboeuf, Mach. Learn.: Sci. Technol., 2022, 3, 045005 Search PubMed.
- R. A. Horn and C. R. Johnson, Matrix Analysis, Cambridge University Press, Cambridge ; New York, 2nd edn, 2012 Search PubMed.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef.
- T. Gneiting, F. Balabdaoui and A. E. Raftery, J. Roy. Stat. Soc. B Stat. Methodol., 2007, 69, 243–268 CrossRef.
- A. P. Dawid, J. Roy. Stat. Soc., 1984, 147, 278–292 CrossRef.
- K. L. Polsterer, A. D'Isanto and S. Lerch, From Photometric Redshifts to Improved Weather Forecasts: Machine Learning and Proper Scoring Rules as a Basis for Interdisciplinary Work, arXiv, 2021, preprint, arXiv:2103.03780, DOI:10.48550/arXiv.2103.03780, https://arxiv.org/abs/2103.03780.
- T. Gneiting and A. E. Raftery, J. Am. Stat. Assoc., 2007, 359–378 CrossRef.
- T. Gneiting, A. E. Raftery, A. H. Westveld and T. Goldman, Mon. Weather Rev., 2005, 133, 1098–1118 CrossRef.
- A. Jordan, F. Krüger and S. Lerch, J. Stat. Software, 2019, 90, 1–37 Search PubMed.
- T. Heskes, Proceedings of the 10th International Conference on Neural Information Processing Systems, 1996, pp. 176–182 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272 CrossRef.
- F. Fouedjio and J. Klump, Environ. Earth Sci., 2019, 78, 38 CrossRef.
- G. A. Qadir, Y. Sun and S. Kurtek, Technometrics, 2021, 548–561 CrossRef.
- B. Settles, Active Learning Literature Survey, University of Wisconsin-Madison Department of Computer Sciences Technical Report, 2009 Search PubMed.
- A. Glielmo, C. Zeni, B. Cheng, G. Csányi and A. Laio, PNAS Nexus, 2022, 1, pgac039 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00174e |
| This journal is © The Royal Society of Chemistry 2025 |