Challenges and opportunities for machine learning potentials in transition path sampling: alanine dipeptide and azobenzene studies

Abstract

The growing interest in machine learning (ML) tools within chemistry and material science stems from their novelty and ability to predict properties almost as accurately as underlying electronic structure calculations or experiments. Transition path sampling (TPS) offers a practical way to explore transition routes between metastable minima such as conformers and isomers on the multidimensional potential energy surface. However, TPS has historically suffered from the computational cost vs. accuracy trade-off between affordable force-field simulations and expensive high-fidelity quantum mechanical calculations. ML interatomic potentials combined with TPS offer a new approach for the exploration of transition pathways at near-quantum mechanical accuracy, while keeping the computational cost comparable to classical force fields. In this study, we employ the HIP-NN-TS and ANI-1x neural network-based ML potentials, both trained on the ANI-1x dataset of 5 million HCNO structures. We first verify the correctness of our approach by applying it to alanine dipeptide and compare the resulting energy surface and transition paths to the literature. Our findings suggest that proposed approach holds promise for conformational searches, as evidenced by the chemical accuracy (errors ≲1 kcal mol⁻¹) for thermal molecular dynamics trajectories of alanine dipeptide. While we were able to successfully reconstruct alanine dipeptide's potential energy landscape using both HIP-NN-TS and ANI-1x frameworks, we observed that ML models with a lower accuracy may still locate additional important conformations. We also find that manual active learning, augmenting the training data by structures taken from TPS trajectories, improved the accuracy by ∼30% with small amounts of additional data. Finally, we evaluated a more intricate case, azobenzene, and observed that seemingly simple torsions may bear a challenge for ML potentials and limit their applications in TPS. Inability of HIP-NN-TS to correctly describe the energetics of major rotational pathway in azobenzene isomerization highlights deficiencies of the reference method in describing the electronic degrees of freedom. Our study underscores the importance of domain expertise in selecting physically meaningful pathways for benchmarking ML potentials, especially considering the intricacies of electronic structure in chemical dynamics and non-equilibrium processes.

---

Introduction

The potential energy surface (PES) is a central concept for modeling chemical and physical processes at the atomistic scale.¹ PES describes the energy of a system with respect to nuclear coordinates showing not only the critical minimum energy structures of a system but also the relevant passages connecting them, which are crucial in various chemical transformations such as chemical reactions or conformational changes. Despite the importance of PES¹ and its maturity with research occurring for more than a century,² theoretical chemistry still does not have a single recommended tool or method for computing and exploring multidimensional PESs accurately and effortlessly.

Specifically, given the 3N-6 degrees of freedom with respect to the number of atoms N, exhaustive exploration of PES comes at a significant computational expense even by standard quantum mechanical (QM) calculations at density functional theory (DFT) level, limiting dynamic simulations typically to only 10–10³ of atoms and picosecond timescales. Alternatively, classical interatomic potentials provide many orders of magnitude speedup compared to DFT calculations, achieving linear scaling with a small prefactor. However, classical force-fields (FF)³ are usually parameterized using a combination of top-down (e.g. matching experimental protein folding) and bottom-up (e.g. injecting quantum mechanical values) in order to address specific processes or systems of interest,^4–7 for instance, protein simulations.^6,8 Moreover, in many cases, potentials are parameterized explicitly for given molecular topologies or fragments such as protein residues. This causes classical FFs to be derived to match our intuition, leading to inherent human biases in their predictions. Affordable FFs dominate the field of biomolecular simulations, and their parametrization to handle small molecules is very limited except for a few examples of FFs applicable to arbitrary molecules such as general AMBER force field (GAFF)⁹ and SMIRNOFF-based potentials.¹⁰

Over the last decade, machine learning (ML) techniques have been increasingly and successfully used for the construction of interatomic potentials.^11–19 For instance, neural networks, one of the backbones of ML, became capable of automated extraction of structural features from the atomic configuration of a many-body molecular system and establishing a relationship between features and fundamental properties such as energies and interatomic forces.^20–24 A sufficiently large (∼10⁵–10⁶) and diverse dataset of atomic configurations with corresponding energies and forces from QM calculations, either DFT or higher-fidelity electronic structure methods, are used in ML potentials training based on one or several target metrics.^25–27 Machine learning interatomic potentials (MLIPs) have been shown to achieve near QM accuracy in predicting energies and forces across diverse atomic configurations, while scaling linearly with the number of atoms with a larger prefactor compared to classical potentials. Examples of such techniques include the high-dimensional neural network potential,^23,28–30 Gaussian approximation potential (GAP),^31,32 spectral neighbor analysis potential (SNAP),^11,33 and moment tensor potentials (MTP),^34,35 and end-to-end neural network architectures.^36–39

ML potentials have undoubtedly proven their capability to provide accurate insights into complex atomistic systems near equilibrium. Roughly, ML performance on near-equilibrium systems can be assessed by straightforward metrics such as root-mean square error (RMSE) for selected test sets. However, simulations of chemical dynamics and reactivity rely on accurate treatment of non-equilibrium structures and phenomena. ML architectures, training procedures, and dataset collection techniques are evolving to account for non-equilibrium processes.^40–44 This shift also implies that simple averaging accuracy metrics should not be used alone to gauge the accuracy of the ML models for complex PESs. This concern has been raised several times^45–47 recently, justifying the importance of evaluating ML methods beyond the error in energies/forces alone. Examples include the radial distribution function,⁴⁸ dissociation, and torsion energy curves.⁴⁹ Volker et al.⁵⁰ suggested evaluating the “correctness” of MLIPs by the ability to correctly identify the minima and maxima of the PES for the system of interest.

For a dynamic process, one would rather evaluate a RMSE metric or similar on a trajectory (Fig. 1A, left and middle panels) instead of on a random near-equilibrium test set. Still, it would only provide incomplete knowledge of the accuracy since most of the chemical transitions proceed through multiple channels (Fig. 1A, right panel). Computing reference QM data for validation on multiple trajectories obtained by molecular dynamics (MD) is rarely feasible. Besides, while MD simulations can reliably sample the stable reactant and product states, rare events at long time scales such as high-energy barriers of transition states are not easily accessible with direct MD. To access such states at a higher frequency in MD simulations, several enhanced sampling techniques have been developed in the past. These include umbrella sampling,⁵¹ uncertainty-driven dynamics,⁵² metadynamics,^53–55 steered MD,⁵⁶ and transition path sampling (TPS).^57–62 TPS is an attractive method because it samples reactive trajectories in which the rare barrier-crossing events are guaranteed to occur, and it does not require a prior knowledge of the reaction coordinate which can be complex. TPS creates an ensemble of dynamical trajectories between the reactant and product states; its computational cost is primarily dictated by the underlying energy/forces calculator of MD simulations.

Fig. 1 (A) Scatter correlation plot (left) is a standard way to evaluate a MLIP emphasizing the accuracy of predictions for a test set. However, the benchmark often spans a narrow set of test structures like a specific trajectory (middle). In reality, transition from state 1 to state 2 is a collection of different paths (right) which renders single-trajectory benchmarks inadequate for assessing accuracy of the MLIP. Qualitatively, discovery of known trajectories (solid and dashed lines) and relevant basins (1 and 2) by ML-TPS can serve as an indicator of good performance. (B) Alanine dipeptide (AD) structure and relevant dihedral angles φ and ψ used to differentiate between states. A, right panel abstractly exemplifies multitude of possible transitions when phase space of both angles is considered. AD is a prototypical example of conformational interconversion. (C) Azobenzene (AZ) structure with relevant dihedral angle ω highlighted. Note that in contrast to conformer switching, isomerization requires rearrangement of atoms or chemical bonds.

By leveraging ML potentials, transition path sampling can immediately benefit from the improved accuracy, broader extensibility compared to classical FFs, and improved scaling compared to QM energy evaluations. Additionally, TPS can help detect performance discrepancies between ML potentials for rare and important configurations involved in transition processes, beyond those found using ordinary MD algorithms.

To date TPS has mostly been combined with classical force fields,^63–65 tight-binding methods,⁶⁶ or pure electronic structure computations.^67–69 Only a few studies have explored the use of machine learning for enhanced sampling,^70–75 MLIPs for MD of flexible molecules,^76,77 and TPS's performance in condensed phase through the lenses of MLIPs.^78,79 While recent pioneering studies^78,79 clearly demonstrated MLIPs can reproduce ensembles of TPS trajectories and relevant regions of PESs, significant knowledge gaps persist. First, there is limited understanding of whether different MLIPs trained on the same data would produce comparable TPS pathways. Second, previous works generated data specifically for targeted reactions. A key advantage of MLIPs is their potential to generalize to new systems with minimal or no modification, yet it remains unclear whether general-purpose datasets such as ANI-1x are suitable for this task.

In this work we evaluate ML potentials beyond structural equilibrium and simple error metrics. In particular, we examine TPS dynamics associated with transitions between metastable states, a general non-equilibrium problem. We do not aim at establishing a completely new metric for evaluating the accuracy of ML predictions for dynamic systems, rather we highlight what factors are important for validating a PES for rare events. Specifically, we evaluate the accuracy and suitability of two ML potentials, ANI-1x^25,26 and HIP-NN-TS,^36,80 among other tools in MD and TPS simulations for two seemingly simple test cases, alanine dipeptide (AD, Fig. 1B) and azobenzene (AZ, Fig. 1D). We show that conscious choice of test systems, physics-guided trajectories, and underlying QM level are essential to approach the problem at the right angle. Otherwise, traditional RMSE metrics may give a misleading perception of the accuracy for unphysical processes. In addition, we explore possible benefits of active learning for improving MLIP performance for non-equilibrium structures generated by TPS.

Molecules for test cases

For the benchmarking of MLIPs using TPS simulations we focused on two torsional transformations, which come in two distinct flavors: conformational interconversion and isomerization. We selected two well-studied cases: alanine dipeptide (AD) (Fig. 1B) and azobenzene (AZ) (Fig. 1C). AD, “a hydrogen atom of biomolecules”, is extensively studied both theoretically^72,81–85 and experimentally,^86,87 and is regarded as a simple and insightful model for parametrizing protein backbone torsion potential.⁸⁸ The various reported^72,81,89,90 PESs of AD exhibit different energy minima and barrier heights, depending on the effective potential model. Note that stable and metastable states of AD are conformers as they are connected through rotations along single bonds.

Projection of the PES onto the φ (C1–N1–Cα–C2) and ψ (N1–Cα–C2–N2) backbone dihedral angles suggests many possible transition paths (see Fig. 1A, right panel for abstract example) by which the molecule can interconvert among the basins of the PES. We use TPS to explore the transition paths that connect the two main metastable conformers, denoted as C5 and C7_eq (Fig. 3), using different ML potentials. This probes the capability of the ML potentials in regions corresponding to very rare events undersampled by ordinary MD simulations.

AZ is a molecule composed of two phenyl rings linked by two nitrogen atoms, presenting a geometrically simple configuration. It is recognized as a molecular switch sensitive to external stimuli,^91–93 triggering cis–trans isomerization. While AZ initially appears less intricate compared to AD due to fewer structural degrees of freedom (it has only one relevant dihedral angle (ω)), this system was chosen because of its complex electronic structure.^{91,92,94–96} Isomerization, in general, is a more intricate process requiring higher activation energy and rearrangement of chemical bonds, in contrast to conformer interconversion seen in AD. We deliberately choose AZ to challenge the MLIP-aided TPS in evaluating relevant trajectories that are highly dependent on electronic degrees of freedom.

MLIP models and data

All calculations in this study were performed at ωB97X/6-31G(d)^97,98 DFT level (see Computational methods in ESI†), which is consistent with the ANI-1x²⁵ dataset. ANI-1x^25,26 contains 5 M energies and atomic gradients of equilibrium and nonequilibrium structures (but not transition states). It was constructed by active learning to cover diverse regions of chemical space. Furthermore, we trained the hierarchically interacting particle neural network with tensor sensitivity, HIP-NN-TS,⁸⁰ which generalizes interaction layers to pass tensor information between atomic sites. We emphasize that the “TS” suffix is not related to the common abbreviation of transition state, and this variant of HIP-NN is still a general atomistic network not tuned for locating transition states. Details of the HIP-NN architecture are summarized elsewhere^36,39 All HIP-NN-TS potentials were trained using the same protocol summarized in Table 1. HIP-NN and HIP-NN-TS along with training examples and documentation are publicly available on Github https://github.com.⁹⁹ A second MLIP architecture we used is the pre-trained ANI-1x in TorchANI,¹⁰⁰ a PyTorch implementation of the classical ANI-1x potential based on modified Behler–Parrinello symmetry functions (Table 1).

Table 1 Hyperparameters and architecture details of MLIPs used in this work

	HIP-NN-TS	ANI-1x
#N trainable parameters	652 k	2613 k
Descriptor	Learnable	Fixed vector of symmetry functions see^101 for parameters
	20 sensitivity functions
Architecture	24 linear layers	16 linear layers
	2 interaction blocks	384 input features
	4 atomic layers with 128 features
Max epochs	150	Unlimited
Loss function	Energy + gradient	Energy + gradient
Batch size	512	2560
Learning rate	0.5 × 10^−3	1 × 10^−3
Optimizer	ADAM	ADAM

---

Even though in this work we compare results produced by HIP-NN-TS and ANI-1x potentials, we cannot directly attribute performance discrepancies to architecture differences due to the low interpretability of neural networks. We point curious readers to a comprehensive review³⁹ comparing these architectures and their descriptors.

For TPS simulations based on MLIPs, we employed OpenPathSampling (OPS)^102,103 software package. Additionally, we interfaced OPS with the atomic simulation environment (ASE) package¹⁰⁴ to leverage its MD engines.

Results and discussion

Regular MD trajectories

To better understand the advantage of MLIPs over other classical force fields widely employed for MD and TPS, we first compared their energies and atomic forces over Langevin MD trajectories under the NVT condition, where the number of atoms (N) and volume (V) are kept fixed at temperature T = 300 K.

We performed four MD simulations, each initiated from one of the four equilibrium configurations of alanine dipeptide isomers—C5, C7_ax, α_R and α_L (Fig. 3A). The MD simulations were driven by the HIP-NN-TS MLIP; each simulation ran for 400 ps using a 2 fs time step to achieve a reasonable phase space coverage (Fig. S1†). To construct a test set of 10 k configurations, samples were taken every 80 steps along these trajectories, and their energies and forces were recalculated using various computational methods: Amber14,¹⁰⁵ Sage2.0.2,¹⁰⁶ ANI-1x,²⁵ and ωB97x/6-31G(d)^97,98 (DFT), as detailed in Fig. 2 and Table 2. Computational details are provided in the ESI.† For azobenzene (AZ), MD simulations were initiated from two known isomers—cis- and trans-AZ—and covered a longer timescale of 1000 ps for each trajectory.

Fig. 2 Evaluation of relative conformer energy based on 10 k points taken from thermal MD trajectories for alanine dipeptide at 300 K. Density correlation plots for energy predictions by various models (DFT, MLIPs and FFs) against each other. (A) MLIPs vs. reference DFT. (B) FFs vs. DFT. (C) MLIPs and FFs against each other. HIP-NN-TS demonstrates better correlation for energy predictions than ANI-1x in line with the lower RMSE (Table 1). However, this is not a guarantee of better recovery of relevant basins by TPS as discussed in the next section. FFs exhibit significant spread with RMSEs closer to 3 kcal mol⁻¹ placing them below “chemical accuracy” for test systems. Noticeably, HIP-NN-TS vs. ANI-1x plot shows much better correlation than Sage2 vs. Amber14 FFs. It underpins that despite discrepancies in MLIPs architectures, neural network-based approaches come to a better agreement with each other and reference theory than empirical FFs, which should be meticulously tuned for the task at hand.

Table 2 Prediction accuracy of total energies (kcal mol⁻¹) and forces (kcal mol⁻¹ Å⁻¹) for 10 k snapshots selected from regular NVT MD at 300 K for the AD and AZ test systems. Correlation plots for AD energy predictions are plotted in Fig. 2 and forces in Fig. S2. Compared to DFT references, HIP-NN-TS provides best accuracy for both AD and AZ molecules. Section V on AZ elaborates that low error in ML-MD may not always guarantee accuracy in applications

	Alanine dipeptide (AD)				Azobenzene (AZ)
	Energy		Forces		Energy		Forces
	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE
HIP-NN-TS/DFT	0.601	0.721	0.802	1.143	0.773	0.966	1.336	2.034
ANI-1x/DFT	0.628	0.794	1.914	2.736	1.439	1.727	2.945	5.071
Amber14/DFT	2.858	3.666	7.925	11.574	3.544	4.419	11.833	22.211
Sage/DFT	3.024	3.862	13.461	18.464	2.665	3.386	13.725	19.538
ANI-1x/HIP-NN-TS	0.834	1.027	1.907	2.769	1.001	1.268	2.761	4.679
Sage/Amber14	1.811	2.288	10.674	15.274	2.476	3.072	11.648	16.745

---

Both MLIPs achieve remarkable accuracy in energy predictions with RMSEs below 1 kcal mol⁻¹ compared to reference DFT calculations, under the desired threshold of “chemical accuracy”¹⁰⁷ (Table 2 and Fig. 2A). HIP-NN-TS clearly outperforms ANI-1x, which was among the most accurate symmetry-function based architectures of the previous generation. We hypothesize that the superior accuracy of HIP-NN-TS is a benefit of the recently incorporated Tensor Sensitivity,⁸⁰ which captures higher order many-body information (see benchmarks in the original article⁸⁰). Both ML models significantly outperform traditional FFs whose errors are at least 300% higher for energy estimations and 900% higher for atomic forces (Table 2, Fig. 2B and S2†). Previous benchmarks are in agreement with the observed improvements.⁸⁰ We noticed that FF models show a much larger disagreement not only with DFT (Fig. 2B) but also with each other (Table 1 and Fig. 2C right), even though they are both parameterized from experimental data. This verifies that the different fitting methods used in different FF models give rise to significant discrepancies even on simple test cases.⁴⁸ These results seemingly suggest that HIP-NN-TS is the most accurate model for our test cases. However, in the next section we will discuss that better accuracy in MD sampling may not be the ultimate indicator for TPS performance.

MLIP PES of alanine dipeptide

The AD system has multiple metastable states, with C7_eq recognized as the global minimum.^63,84,108 C5, α_R and C7_ax are other important low-lying conformations^{82,84,108,109} (Fig. 3A). The backbone dihedral angles φ and ψ act as differentiating order parameters for these conformers (Fig. 3A). Alanine dipeptide PES (Fig. 3B and C) was sampled using a brute force approach where structures with fixed incremental combination of φ and ψ (−180° to 180°, step size of 5°) were relaxed using the FIRE optimizer alongside the HIP-NN-TS and ANI-1x MLIPs as energy calculators.

Fig. 3 (A). Major conformations of AD discovered by MLIPs. Structures reproduced from comprehensive theoretical analysis.⁸⁴ (B) and (C) PES's of AD reconstructed by HIP-NN-TS and ANI-1x potentials, respectively. Note that HIP-NN-TS does not differentiate between C7_ax and α_L states while ANI-1x treats them as separate basins in line with other works.⁸⁴ Noticeably, HIP-NN-TS is more accurate for regular MD trajectories but does not discover the α_L basin on AD PES. It exemplifies that RMSE may not be indicative enough to prefer one potential over another. (D) and (E) Path density obtained by ML-TPS for the C5 to C7_eq transition based on 10 k trajectories. Despite both HIP-NN-TS and ANI-1x being trained to the same data, they produce strikingly different TPS ensembles. It emphasizes strong TPS dependency on the underlying MLIP. Black lines denote the initial MD trajectories at 300 K; green dots mark the top 100 most frequently sampled configurations. Red boxes draw boundaries of the C7_ax and α_R states.

Both models exhibit noteworthy agreement in predicting the PES, particularly in delineating the locations of the four metastable state basins (C5, C7_ax, α_R and C7_eq, see Fig. 3A) and the associated energy barriers. ANI-1x simulations reveal a division of the C7_ax state to yield another known state, α_L (Fig. 3A), located at the higher side of the basin. Both the highest energy barrier on the PES (the red regions) and the barrier separating the α_R and C7_ax states obtained by ANI-1x appear to be higher by around 1.5 kcal mol⁻¹, when compared to HIP-NN-TS. Comparatively, ANI-1x′s PES (Fig. 3C) closely aligns with those constructed by empirical FFs such as Charm22 in vacuum,¹¹⁰ OPLS/AGBNP with implicit solvation,⁸² as well as Hartree-Fock and MP2 simulations.⁸⁴ ANI-1x demonstrates an upward shift (Fig. 3B) in the valley between C5 and C7_eq states, while maintaining close conformity with the basins and energy barrier locations of C7_ax and α_L. Notably, the energy minima of the C7_ax and α_L states exhibit greater stability in the ANI-1x model. The HIP-NN-TS model's PES aligns well with the latest φ–ψ diagram produced by the DeepPot-SE model,⁷² a deep learning potential trained specifically for AD.

While both HIP-NN-TS and ANI-1x models yield comparable PESs (Fig. 3B and C), it is crucial to highlight that ANI-1x identifies an additional major basin, α_L, whereas HIP-NN-TS integrates it with the larger basin of the C7_ax conformer. Note that α_L is a well-known minima at MP2 (ref. 84) and coupled-cluster levels.¹¹¹ It is also a true minimum at ωb97x DFT level (the reference functional used in ANI-1x dataset) in conjunction with various Pople basis sets.¹¹¹ While the ANI-1x MLIP discovered α_L as a distinct PES region, we did not confirm whether it is a true local minimum.

Intriguingly, HIP-NN-TS demonstrates quantitative superiority for regular MD trajectories (Fig. 2 and Table 2), prompting a fundamental question regarding the preference between a model describing more basins with less precision versus a model providing more accurate descriptions overall but differentiating less conformers. This is particularly interesting given that the same dataset was used to train both models. Although our analysis is based on a single case, we posit that a less accurate MLIP, as determined by the RMSE benchmark, may still be practical or even preferable for TPS conformational switching, subject to careful case-specific testing. Additionally, we acknowledge the inconsistency in ML approaches, advocating for the comparison of ensembles of trained MLIPs for a more comprehensive understanding.

Transition path sampling of AD: going from C5 to C7_eq conformer

Multiple known minima^84,89 for AD signify a multitude of possible transitions between conformers. Previous simulations indicate that the time scale for the transition from C7_eq to α_R in solution is approximately 0.25–1.0 nanosecond.^63,82 For reference, α_R →  C7_ax interconversion is rarer and spans about a 10-nanosecond timeframe,⁸² while a transition between C7_ax and C7_eq conformers might require microsecond simulations.¹¹² Consequently, capturing these transitions sufficiently necessitates either very long trajectories or some form of importance sampling. Given the extensive duration of these transitions and the proof-of-concept nature of this study, we focused on sampling transition paths from the C5 to the C7_eq states, whose interconversion typically occurs within 3–5 picoseconds.^113,114

To ensure adequate TPS sampling, we defined relatively large regions for these two basins, as depicted by the red rectangles in Fig. 3D and E. Given the consistent basin locations produced by the HIP-NN-TS and ANI-1x models, we adopted the same boundaries for the collective variables in the TPS simulations for both models. The C5 stable state region was defined with boundaries −180° ≤ φ ≤ −150° and 150° ≤ ψ ≤ 180°, while the C7_eq stable state region was defined with boundaries −120° ≤ φ ≤ −60° and 30° ≤ ψ ≤ 80°.⁸⁴

TPS was initiated from the C5 state to the C7_eq state by relaxing the initial trajectory at 500 K to 300 K using the ASE¹⁰⁴ engine with HIP-NN-TS and ANI-1x potentials. By conducting this step at a relatively high temperature, the trajectories were unhindered by barriers associated with variables other than φ and ψ, allowing for a quick generation of the trajectory at 500 K connecting the two stable states. During subsequent random walks through the trajectory space, momenta gradually adjusted to reach the ensemble with kinetic energies corresponding to 300 K. The resulting trajectory connecting the two regions was then considered as the initial trajectory for transition path sampling.

In this work, a stochastic one-way shooting^{62,102,103,115} approach was adopted as implemented in OpenPathSampling,^62,102,103 wherein shooting points for generating trial paths were randomly selected from the previously accepted path in a Monte Carlo move.^57,62 A new velocity was assigned randomly for each atom at that point, along with randomly perturbed momenta. The dynamics were integrated forward and backward in time, and the new pathway was accepted if it ended up in C5 and C7_eq on both ends; otherwise, it was rejected.

A total of 10 k pathways were collected as a transition path ensemble, in which every trajectory was saved after 14 trial moves. In total, 1438 uncorrelated paths were obtained, with a reasonable acceptance rate for newly generated trajectories (68%), similar to OPS benchmark example results^102,103 using classical FFs. Path density plots for the flexible path length ensemble in the (φ, ψ) plane depict the visitation frequency of the phase space for both the HIP-NN-TS model (Fig. 3D) and the ANI-1x model (Fig. 3E). The initial trajectory is represented by black lines. Despite the similar PES descriptions (Fig. 3B and C) with only minor differences, as discussed in previous sections, the transition path ensembles reveal notable distinctions.

With the HIP-NN-TS model, two channels emerge (see dashed lines in Fig. 3D) as favorable pathways for interconversion trajectories. Conversely, the ANI-1x model reveals a single channel, extending across a broad region between the C5 and C7_eq states, as depicted in Fig. 3E. The trajectories generated by the HIP-NN-TS model depart similarly from the C5 state; however, they rapidly turn to the left and enters C7_eq at φ ∼ −120° and ψ ∼ −70° (see 1 in Fig. 3D). Complementary channel appears to be along ∼ −120° longitude and in range −30° ≤ ψ ≤ −60° (see label 2 in Fig. 3D).

Most frequently visited configurations from TPS trajectories produced by HIP-NN-TS (green dots in Fig. 3D), demonstrate clustering in the vicinity of C7_eq state, even with the presence of the two-branched channel. In contrast, most frequently visited configurations by the ANI-1x model are dispersed along the single channel (Fig. 3E). With the HIP-NN-TS model, the most frequently visited configurations are found within the dihedral angles ranges φ ≈ (−105°, −130°) and ψ ≈ (80°, 115°), with a minor clustering around angles φ ≈ (−115°, −120°) and ψ ≈ (90°, 120°), which are in proximity to the C7_eq state.

For the ANI-1x model, the most visited states occur with dihedral angle pairs φ ≈ (−130°, −70°) and ψ ≈ (115°, 145°). This observation aligns with the PES plot discussed earlier, indicating similar locations of the C5 and C7_eq states for both models. However, these states are separated by a more uniform barrier for the ANI-1x model. For the HIP-NN-TS model, however, the lower energy barrier is more confined, prompting the molecular transition to follow the narrower path and veering toward the left side of the C7_eq state, as illustrated in the density plot (Fig. 3D).

These observations lead to an interesting conclusion – two MLIPs trained to the same data reveal very distinct TPS pathways. Their PESs (Fig. 3B and C) differ only slightly, but the dynamic simulations revealed sufficiently different channels (Fig. 3D and E). This suggests that TPS might be very sensitive to the choice of MLIPs even when the same training data is used. Furthermore, it corroborates our previous assertion that similarity in accuracy in static benchmarks based purely on RMSE is not indicative of the similarity in TPS simulations or in the transition trajectories.

Probing active learning for TPS

Even though RMSE is not a robust metric for comparing two MLIPs in the context of TPS, it can still be used to systematically quantify the quality of a single model. Generally, more accurate MLIPs should reproduce the underlying QM PES with greater accuracy; although qualitatively it does not always reflect the discovery of relevant minima and conformers (see Section 2 and a recent tutorial⁵⁰). Importantly, RMSE evaluated over equilibrium data is insufficient to estimate a model's performance for non-equilibrium transition pertaining to TPS.

As most MLIPs are trained to equilibrium structures, here we propose a simple probe to systematically improve the prediction accuracy for non-equilibrium, TPS-relevant structures imitating the active learning^{25,41,116–118} (AL) approach. We manually augment the dataset with structures directly taken from the TPS trajectories. The new HIP-NN-TS-AL model was then tested on the trajectory frames which do not appear in the train set. Though not a true AL automated loop, this simple pipeline provides insight into whether collecting structures from transition trajectories will be beneficial for further ML-TPS improvement. As a proof of principle, we carried out a single iteration of AL by manually injecting 12 k structures randomly sampled from the most visited regions (green clusters in Fig. 3D) with a 10 800 : 1200 train : test split, and retraining HIP-NN-TS on the combined dataset (original ANI-1x + 10 800 “TPS structures”, Fig. 4A) to yield HIP-NN-TS-AL.

Fig. 4 (A) Conceptually, active learning (AL) targets structures (violet dots) from undersampled regions. By augmenting training data with new relevant structures and retraining the MLIP, we can improve inference accuracy. In particular, we explore AL for improving the prediction of energy and forces of structures encountered during the C7_eq–α_R transition. (B) [Left] accuracy of HIP-NN-TS on the 1200 TPS test structures. [Right] accuracy of HIP-NN-TS after one iteration of AL (HIP-NN-TS-AL) on the same test set. 0.2% data augmentation leads to ∼30% accuracy improvement, our method holds promises for AL-refinement of MLIPs for TPS. (C) Accuracy of HIP-NN-TS and HIP-NN-TS-AL for 1200 test structures averaged across 3 different random number seeds to account for non-deterministic factors. AL-models show unanimous improvement for energy and gradient inference compared to original HIP-NN-TS models trained to ANI-1x data only.

HIP-NN-TS-AL demonstrates ∼35% accuracy improvement when tested on the subset of 1200 TPS-derived structures (Fig. 4A and B). To quantify statistical errors, we trained three HIP-NN-TS-AL models with different random seeds for weight initialization following the same protocol as for the original HIP-NN-TS. Improvements of ∼38% energy RMSE and ∼24% force MAE are observed in all three models (Fig. 4C). This is a remarkable improvement given that only 10 800 new configurations (0.2% increase in total data) were inserted into the original 5 M data points of ANI-1x. We conclude that AL (or even simple manual data augmentation) holds great promise in improving MLIP performance for non-equilibrium structures occurring during TPS conformational search. It is possible that further automated and systematic model refinement covering previously unexplored non-equilibrium regions can make ML-TPS a viable competitor to widely used electronic structure calculations and FFs for TPS.

Azobenzene: a cautionary tale

In this subsection we emphasize a common wisdom from the ML community: real-life ML model accuracy should be evaluated in the specific application domain.^47,50 In our particular case, MLIPs for TPS exploration should correctly assess major pathways and identify the lowest-energy one, which is a kinetically dominant transition channel for the system disjoint from the training set. Analysis of thermal MD simulations (Table 2) demonstrates that HIP-NN-TS predictions for AZ should be accurate within ∼0.5 kcal mol⁻¹, suggesting that reliable information about the system can be derived from MLIP simulations. The AZ molecule is a geometrically simple arrangement with two benzene rings bridged by two N atoms (Fig. 1C). Both conjugated rings should exhibit aromaticity to some extent, preventing their distortion during MD. Therefore, AZ is an excellent test case for TPS simulations having only one easily-activated degree of freedom associated with the movement around the N=N bridge. Ultimately, it leads to isomerization from cis- to trans-states or vice versa. However, the complexity lies in the finer details.

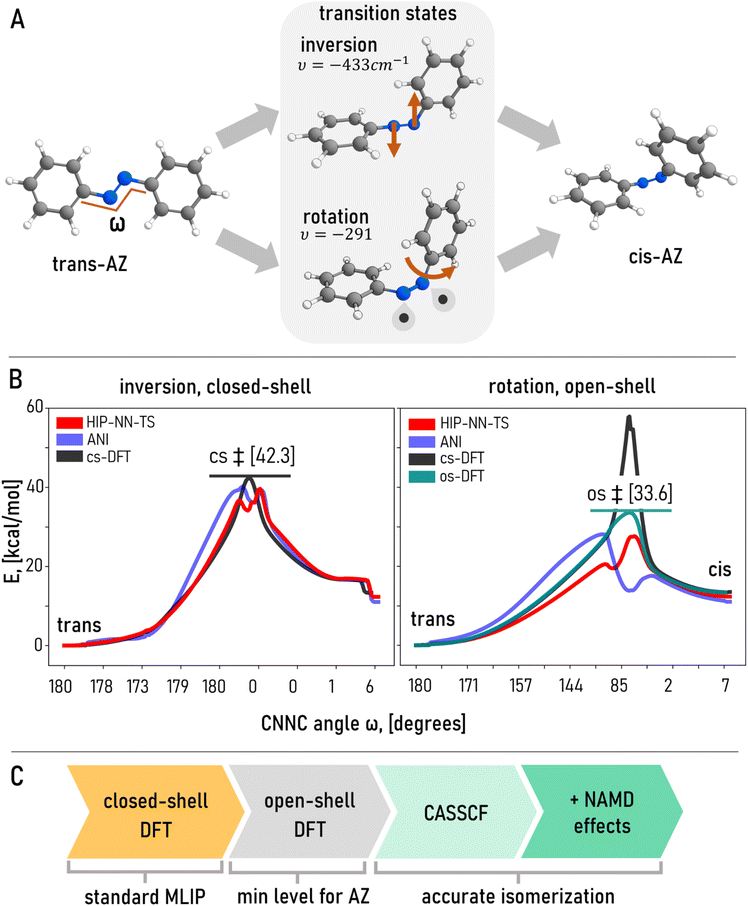
The controllable isomerization of azobenzene (AZ) has enabled a wide array of emerging applications,^119,120 from light-responsive supramolecular self-assembly to synthetic vision restoration. In-depth studies¹²¹ demonstrated that the interplay between isomerization mechanisms depend on numerous factors including solvent, steric hindrance of functional group, heat and pressure among others. Previous studies have already established multiple isomerization mechanisms among which two are widely recognized – inversion and rotation^122–125 (Fig. 5A). While the community initially believed that inversion is the more energetically-favorable route of thermal isomerization, further studies found that the rotational mechanism is prefered.^95,124 Capturing these two major pathways is the key to describing AZ transformations.

Fig. 5 Isomerization of azobenzene. (A) Two pathways of thermal isomerization. Inversion involves the concerted bending of two bridging N atoms without significant changes in ω dihedral angle. The rotation mechanism is based on the second ring rotation relative to the first one with gradual changes in ω angle. Rotation requires breaking π-component of double N=N bond and leads to the configuration with unpaired electrons on two N atoms. Red arrows indicate the dominant movement of N atoms in imaginary mode. (B) [Left] energy profile of the inversion mechanism of trans–cis AZ isomerization based on closed-shell DFT (cs-DFT) calculations. The transition state (‡) of inversion is 42.3 kcal mol⁻¹ higher than trans-AZ. HIP-NN-TS yields the best agreement compared to cs-DFT while ANI-1x provides a reasonable approximation. [Right] the rotational mechanism is based on unrestricted broken-symmetry open-shell-DFT (os-DFT) calculations. At this DFT level, this path (33.6 kcal mol⁻¹) is energetically preferred over inversion. The HIP-NN-TS predicts unrealistically low-barrier while ANI-1x falsely treats rotational transition state as local minimum. cs-DFT calculations over the same trajectory produces an unrealistically elevated barrier. (C) Hierarchy of theoretical levels for exploring AZ isomerization: cs-DFT (common for MLIP training) cannot describe a preferable rotational path through bond breaking while os-DFT and CASSCF can capture rotation. AZ isomerization involves ground state crossing with excited states, described by non-adiabatic molecular dynamics (NAMD). This highlights the importance of being aware of possible electronic structure changes in test cases.

We calculated the inversion isomerization pathway using a closed-shell DFT (cs-DFT) approach (ωB97X/6-31G(d) model chemistry) starting with a hand-crafted and optimized transition state (see Computational methods in ESI† for details and Fig. 5B, left). We computed energies for all 179 points on a smooth isomerization curve and found that HIP-NN-TS was the most accurate model in line with previous observations. Even though the energy in the vicinity of TS dips unphysically for both HIP-NN-TS and ANI-1x (possibly due to the absence of transition states in training data, causing regression to the mean), overall, HIP-NN-TS is fairly accurate (Fig. 5B and Table 3) especially for the initial and final states. ANI-1x is slightly worse in terms of accuracy. Even though Amber14 and Sage2 are not suited for reactive pathways, we calculated the energies along the same trajectories using both methods for completeness (Table 3). Both FFs suggest unrealistically high barriers above 80 kcal mol⁻¹ beyond any practicality. These results seemingly to support the conclusion that HIP-NN-TS, or any other MLIP trained on the ANI-1x database, could be a viable tool for exploring isomerization in azobenzene or similar double-bonded switches.

Table 3 Isomerization barriers and accuracy metrics in kcal mol⁻¹ for inversion and rotation mechanisms in azobenzene. Assessment of the inversion pathway (left) by HIP-NN-TS and ANI-1x suggests that both MLIPs are reasonably accurate. However, assessment of the rotational pathway using the same method reveals their deficiency in describing double bond rotations. Sage2 and Amber14 produce inaccurate energetics for both pathways

	Inversion, closed-shell			Rotation, open-shell
	Barrier	MAE	RMSE	Barrier	MAE	RMSE
DFT	42.3	—	—	33.6	—	—
HIP-NN-TS	36.9	0.916	1.660	27.61	2.257	3.510
ANI-1x	40.1	1.898	3.42	28.09	3.942	6.021
Sage2	87.6	2.882	7.510	13.58	13.544	14.682
Amber14	182.6	8.896	24.351	20.68	13.544	14.204

---

An alternative and important route of thermal isomerization proceeds through a bond-breaking mechanism⁹⁵ because the bridging nitrogen atoms are connected by a double bond that blocks any low-barrier rotation, in contrast to the freely-rotating single bonds in AD conformers. Roughly speaking, such rotational isomerization proceeds through a biradical state when uncoupled electrons occupy spatially different orbitals on different N atoms. Such biradicals (often referred to as open-shell singlets^126,127) are not properly described by cs-DFT which inherently assumes double occupancy for each orbital. Unless expensive, high-fidelity calculations with careful manual selection of active orbitals are conducted, e.g. the complete active space self-consistent field method (CASSCF)^92,128 (Fig. 5C), a more affordable approximation would be to manually break the symmetry of orbitals in unrestricted open-shell DFT (os-DFT) calculations.^95,129 Despite the ad hoc nature of such a treatment, this solution typically approximates states with broken bonds quite reasonably.^130,131

To get an insight into a lower-energy rotational pathway, we recalculated the trajectory from a newly estimated TS optimized with os-DFT. The os-DFT TS structure is very different from its cs-DFT counterpart. It has an imaginary mode of rotation leading to breaking the π-component of N=N double bond, in contrast to the inversion mechanism for cs-DFT. Rotation is accompanied by substantial changes in dihedral angle ω, in agreement with previous studies.^66,122,125 Most importantly, the os-DFT pathway has a lower barrier by almost 9 kcal mol⁻¹ (Fig. 5B, right, Table 3), rendering it far more energetically favorable. In other words, isomerization is much more likely to proceed through an open-shell rotational trajectory under thermal stimuli, at least at the given DFT level.⁹⁵ Therefore, the closed-shell inversion trajectory (Fig. 5B, left) for which MLIPs yield great accuracy, is an incomplete picture giving a false perception on the reliability of ML prediction that is based on inaccurate reference QM methodology.

Once more, we recalculated the new open-shell rotational pathway (Fig. 5B right) with HIP-NN-TS, which yielded a significantly poorer match, including an unphysical energy dip near the TS and average errors exceeding 2 kcal mol⁻¹ (Table 3). Though noticeably worse, this discrepancy might be acceptable for some reactive applications, suggesting that MLIPs might still be a fair choice. However, we should keep in mind that the MLIP was trained solely on closed-shell data, which lacks structures relevant to the rotational pathway. Hence, aside from the quantitative discrepancy of energy predictions, it is very unlikely for a MLIP to discover open–shell pathways that involve fundamentally different transitions both geometrically and electronically, if the training data lacks physically justifiable and reliable QM reference results. To prove this, we recalculated the os-DFT trajectory by single-point cs-DFT. The closed-shell treatment misrepresents the barrier energetics, with the TS reaching 58 kcal mol⁻¹, which is 24 kcal mol⁻¹ above the os-DFT transition state (Fig. 5B right, Table 3). Moreover, cs-DFT reoptimization, starting from broken-symmetry open-shell transition state geometry, failed to produce a saddle point with a single imaginary frequency and, consequently, the most favorable pathway.

To reiterate, cs-DFT cannot discover the favorable rotation mechanism. In the context of dynamic simulations using a MLIP trained to cs-DFT data, the model would likely bias the simulations away from common isomerization channels. This limitation could render TPS exploration incomplete or simply incorrect (Fig. 5C). While beyond the scope of the current study, we believe it is essential for future work to include broken-symmetry and open-shell pathways in the dataset and to probe TPS performance using azobenzene as a model system (Fig. 5C).

An unresolved issue is that even an open-shell singlet is a poor description for the AZ transition state, which is often photo-activated and isomerizes by state crossings.^{92–94,122,124,128} Such effects are usually captured by non-adiabatic dynamics^92,132 and are beyond the scope of this article (Fig. 5C). Therefore, non-excited dynamics, even with an open-shell treatment, is already a rough approximation of the more realistic light-induced molecular switching process (Fig. 5C). Unless data sets and models account for these challenges, production-quality ML-TPS will remain unattainable for transition paths involving bond formation and cleavage.

Conclusions

In this article we explore the usability and pitfalls of machine learning interatomic potentials for transition path sampling. We find that MLIPs can be promising tools for TPS explorations of PESs as both HIP-NN-TS and ANI-1x were able to reproduce the AD PES with sufficient details. As expected, both models outperform classical FFs in regular MD simulations for AD and AZ. However, our results indicate that significant caution should be exercised when simulating isomerization processes that require proper descriptions and energetics of bond breaking and formation.

With that in mind, we summarize the key insights gained from using MLIPs in TPS simulations:

1. Lower errors do not guarantee correct discovery of basins in PESs

Although HIP-NN-TS demonstrated superior accuracy in predicting energy and forces compared to ANI-1x for alanine dipeptide, the seemingly less accurate ANI-1x revealed an additional α_L basin adjacent to the C7_ax basin during PES exploration, which is consistent with the literature. This counterintuitive finding underscores the limitation of relying on the root mean square error (RMSE) calculated for random samples as the sole indicator of the correctness of dynamic explorations like TPS.

2. Different MLIP architectures trained on the same data may produce different trajectories in TPS

Despite training on the same data, HIP-NN-TS and ANI-1x revealed different transition channels from the C5 to the C7_eq basin. It is particularly interesting given the relatively close agreement between the two PESs, especially near the C5 and C7_eq basins. Therefore, we conclude that MLIPs with similar RMSE-based accuracy can produce sufficiently different TPS trajectories.

3. TPS as a means of active learning can substantially improve MLIP accuracy

By employing a manual data augmentation procedure, we emulated a single iteration of an active learning loop. The original ANI-1x (5 M structures) dataset was augmented by 10 800 structures selected from TPS trajectories. With a minute data augmentation of ∼0.2%, a substantial improvement of ∼30% in energy and gradient predictions was achieved for configurations on transition paths, underscoring the tangible benefits of TPS as a means of active learning and data generation. This opens an exciting avenue for training new class of MLIPs, such as the very broad, non-system specific foundational ML models.^133,134

4. Choice of test cases and domain of applicability of MLIPs should account for electronic structure features

As illustrated by the azobenzene example, we emphasize that seemingly simple transformations, like torsion and isomerization, may require more sophisticated theoretical approaches than conventional low-cost closed-shell DFT. Failure to adequately describe possible bond breaking and formation effects in electronic structure methods could lead to the generation of incorrect or artificially high-energy trajectories, which are easy to overlook without prior knowledge. Therefore, we caution against relying on incomplete or unphysical transformations for MLIP evaluation. For instance, MLIP performance is often evaluated on torsional profiles,¹³⁵ which is only valid for conformer-like interconversion around single bonds unless MLIP was trained on reactive data. Therefore, a priori intuition of bond type is required. Altogether, it underscores the importance of carefully inspecting all test cases for ML-TPS and the associated training data, for the treatment of electronic degrees of freedom. When considering AD and AZ molecules through the lens of MLIPs and TPS, general databases such as ANI-1x might be adequately representative to describe conformational interconversion, but will be deficient for isomerization involving chemical bonding rearrangement. The need for a community effort in generating high-accuracy reference data for bonding breaking processes at CASSCF¹³⁶ or truncated configuration interaction (CI)¹³⁷ levels is apparent. So far, such efforts have been limited to small molecules only.^136,137 Reactivity-focused datasets such as Transition-1x⁴³ and RGD1,¹³⁸ along with architectures like EquiReact,¹³⁹ have the potential to shape the future of ML-TPS, particularly when accurate descriptions of bond-changing events are required.

Besides datasets, our findings highlight the need for robust metrics to quantify how well MLIPs recover PES minima and saddle points. Sophisticated training and testing of MLIPs for TPS^78,79 and dynamics simulations will continue to depend on human expertise in computational chemistry, underscoring the importance of physics-informed ML frameworks.^16,50,140

Data availability

MLIPs, datasets, ASE, and OpenPathSampling packages used in this study are publicly available and free of charge. The ESI,† including comprehensive compilations of links to all utilized tools, pretrained HIP-NN-TS models, an additional 12 k alanine dipeptide configurations from section IV, and azobenzene isomerization pathways, are available at https://github.com/nikitafedik/ml_tps_si.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Alice E. A. Allen for the helpful discussions on classical force fields and alanine dipeptide. N. F., W. L., N. L., and Y. W. L. were supported by the Laboratory Directed Research and Development Program (LDRD) of Los Alamos National Laboratory (LANL). N. F. acknowledges financial support from the Director's Postdoctoral Fellowship and Center for Nonlinear Studies (CNLS). S. T. and B. N. acknowledge support from the USDOE, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division under Triad National Security, LLC (“Triad”) contract Grant 89233218CNA000001 (FWP: LANLE3F2). This work was performed in part at the CNLS and the Center for Integrated Nanotechnology, a US DOE and Office of Basic Energy Sciences user facility. This research used resources provided by the LANL Institutional Computing Program, which is supported by the US DOE National Nuclear Security Administration under contract no. 89233218CNA000001. We also acknowledge the CCS-7 Darwin cluster at LANL for additional computing resources.

References

1. The concept of the potential energy surface, in Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer US, Boston, MA, ed. E. Lewars, 2003, pp. 9–41.  DOI:10.1007/0-306-48391-2_2.
2. M. R. Marcelin, Contribution à l’étude de la cinétique physico-chimique, Ann. Phys., 1915, 9(3), 120–231,  DOI:10.1051/anphys/191509030120.
3. A. D. MacKerell Empirical force fields, in Computational Methods for Protein Structure Prediction and Modeling: Volume 1: Basic Characterization (Biological and Medical Physics Biomedical Engineering), ed. Y. Xu, D. Xu and J. Liang, Springer, New York, NY, 2007, pp. 45–69,  DOI:10.1007/978-0-387-68372-0_2.
4. T. A. Halgren, Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94, J. Comput. Chem., 1996, 17(5–6), 490–519,  DOI:10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P.
5. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Comparison of multiple amber force fields and development of improved protein backbone parameters, Proteins: Struct., Funct., Bioinf., 2006, 65(3), 712–725,  DOI:10.1002/prot.21123.
6. L.-P. Wang, K. A. McKiernan, J. Gomes, K. A. Beauchamp, T. Head-Gordon, J. E. Rice, W. C. Swope, T. J. Martínez and V. S. Pande, Building a more predictive protein force field: a systematic and reproducible route to AMBER-FB15, J. Phys. Chem. B, 2017, 121(16), 4023–4039,  DOI:10.1021/acs.jpcb.7b02320.
7. J. Wildman, P. Repiščák, M. J. Paterson and I. Galbraith, General force-field parametrization scheme for molecular dynamics simulations of conjugated materials in solution, J. Chem. Theory Comput., 2016, 12(8), 3813–3824,  DOI:10.1021/acs.jctc.5b01195.
8. Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, Polarizable atomic multipole-based AMOEBA force field for proteins, J. Chem. Theory Comput., 2013, 9(9), 4046–4063,  DOI:10.1021/ct4003702.
9. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174,  DOI:10.1002/jcc.20035.
10. D. L. Mobley, C. C. Bannan, A. Rizzi, C. I. Bayly, J. D. Chodera, V. T. Lim, N. M. Lim, K. A. Beauchamp, D. R. Slochower, M. R. Shirts, M. K. Gilson and P. K. Eastman, Escaping atom types in force fields using direct chemical perception, J. Chem. Theory Comput., 2018, 14(11), 6076–6092,  DOI:10.1021/acs.jctc.8b00640.
11. A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials, J. Comput. Phys., 2015, 285, 316–330,  DOI:10.1016/j.jcp.2014.12.018.
12. V. L. Deringer and G. Csányi, Machine learning based interatomic potential for amorphous carbon, Phys. Rev. B, 2017, 95(9), 094203,  DOI:10.1103/PhysRevB.95.094203.
13. L. Zhang, D.-Y. Lin, H. Wang, R. Car and W. E, Active learning of uniformly accurate interatomic potentials for materials simulation, Phys. Rev. Mater., 2019, 3(2), 023804,  DOI:10.1103/PhysRevMaterials.3.023804.
14. Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, Performance and cost assessment of machine learning interatomic potentials, J. Phys. Chem. A, 2020, 124(4), 731–745,  DOI:10.1021/acs.jpca.9b08723.
15. T. Mueller, A. Hernandez and C. Wang, Machine learning for interatomic potential models, J. Chem. Phys., 2020, 152(5), 050902,  DOI:10.1063/1.5126336.
16. D. M. Anstine and O. Isayev, Machine learning interatomic potentials and long-range physics, J. Phys. Chem. A, 2023, 127(11), 2417–2431,  DOI:10.1021/acs.jpca.2c06778.
17. T. W. Ko and S. P. Ong, Recent advances and outstanding challenges for machine learning interatomic potentials, Nat. Comput. Sci., 2023, 3(12), 998–1000,  DOI:10.1038/s43588-023-00561-9.
18. Y. Liu, X. He and Y. Mo, Discrepancies and error evaluation metrics for machine learning interatomic potentials, NPJ Comput. Mater., 2023, 9(1), 1–13,  DOI:10.1038/s41524-023-01123-3.
19. Y. Mishin, Machine-learning interatomic potentials for materials science, Acta Mater., 2021, 214, 116980,  DOI:10.1016/j.actamat.2021.116980.
20. J. Behler, Perspective: machine learning potentials for atomistic simulations, J. Chem. Phys., 2016, 145(17), 170901,  DOI:10.1063/1.4966192.
21. N. Artrith and A. Urban, An implementation of artificial neural-network potentials for atomistic materials simulations: performance for TiO₂, Comput. Mater. Sci., 2016, 114, 135–150,  DOI:10.1016/j.commatsci.2015.11.047.
22. M. Kulichenko, J. S. Smith, B. Nebgen, Y. W. Li, N. Fedik, A. I. Boldyrev, N. Lubbers, K. Barros and S. Tretiak, The rise of neural networks for materials and chemical dynamics, J. Phys. Chem. Lett., 2021, 12(26), 6227–6243,  DOI:10.1021/acs.jpclett.1c01357.
23. J. Behler, Four generations of high-dimensional neural network potentials, Chem. Rev., 2021, 121(16), 10037–10072,  DOI:10.1021/acs.chemrev.0c00868.
24. A. M. Tokita and J. Behler, How to train a neural network potential, J. Chem. Phys., 2023, 159(12), 121501,  DOI:10.1063/5.0160326.
25. J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less is more: sampling chemical space with active learning, J. Chem. Phys., 2018, 148(24), 241733,  DOI:10.1063/1.5023802.
26. J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, The ANI-1ccx and ANI-1x data sets, coupled-cluster and density functional theory properties for molecules, Sci. Data, 2020, 7(1), 134,  DOI:10.1038/s41597-020-0473-z.
27. J. S. Smith, B. Nebgen, N. Mathew, J. Chen, N. Lubbers, L. Burakovsky, S. Tretiak, H. A. Nam, T. Germann, S. Fensin and K. Barros, Automated discovery of a robust interatomic potential for aluminum, Nat. Commun., 2021, 12(1), 1257,  DOI:10.1038/s41467-021-21376-0.
28. J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98(14), 146401,  DOI:10.1103/PhysRevLett.98.146401.
29. J. Behler, Atom-centered symmetry functions for constructing high-dimensional neural network potentials, J. Chem. Phys., 2011, 134(7), 074106,  DOI:10.1063/1.3553717.
30. M. Eckhoff and J. Behler, High-dimensional neural network potentials for magnetic systems using spin-dependent atom-centered symmetry functions, npj Comput. Mater, 2021, 170.
31. A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104(13), 136403,  DOI:10.1103/PhysRevLett.104.136403.
32. S. Klawohn, J. P. Darby, J. R. Kermode, G. Csányi, M. A. Caro and A. P. Bartók, Gaussian approximation potentials: theory, software implementation and application examples, J. Chem. Phys., 2023, 159(17), 174108,  DOI:10.1063/5.0160898.
33. M. A. Wood and A. P. Thompson, Extending the accuracy of the SNAP interatomic potential form, J. Chem. Phys., 2018, 148(24), 241721,  DOI:10.1063/1.5017641.
34. I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, The MLIP package: moment tensor potentials with MPI and active learning, Mach. Learn.: Sci. Technol., 2021, 2(2), 025002,  DOI:10.1088/2632-2153/abc9fe.
35. E. Podryabinkin, K. Garifullin, A. Shapeev and I. Novikov, MLIP-3: active learning on atomic environments with moment tensor potentials, J. Chem. Phys., 2023, 159(8), 084112,  DOI:10.1063/5.0155887.
36. N. Lubbers, J. S. Smith and K. Barros, Hierarchical modeling of molecular energies using a deep neural network, J. Chem. Phys., 2018, 148(24), 241715,  DOI:10.1063/1.5011181.
37. K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. Müller, SchNetPack: a deep learning toolbox for atomistic systems, J. Chem. Theory Comput., 2019, 15(1), 448–455,  DOI:10.1021/acs.jctc.8b00908.
38. O. T. Unke and M. Meuwly, PhysNet: a neural network for predicting energies, forces, dipole moments, and partial charges, J. Chem. Theory Comput., 2019, 15(6), 3678–3693,  DOI:10.1021/acs.jctc.9b00181.
39. N. Fedik, R. Zubatyuk, M. Kulichenko, N. Lubbers, J. S. Smith, B. Nebgen, R. Messerly, Y. W. Li, A. I. Boldyrev, K. Barros, O. Isayev and S. Tretiak, Extending machine learning beyond interatomic potentials for predicting molecular properties, Nat. Rev. Chem., 2022, 6(9), 653–672,  DOI:10.1038/s41570-022-00416-3.
40. J. Behler, First principles neural network potentials for reactive simulations of large molecular and condensed systems, Angew. Chem., Int. Ed., 2017, 56(42), 12828–12840,  DOI:10.1002/anie.201703114.
41. S. Zhang, M. Makoś, R. Jadrich, E. Kraka, K. Barros, B. Nebgen, S. Tretiak, O. Isayev, N. Lubbers, R. Messerly and J. Smith, Exploring the frontiers of chemistry with a general reactive machine learning potential, Nat. Chem., 2024, 16, 727–734.
42. R. K. Lindsey, C. Huy Pham, N. Goldman, S. Bastea and L. E. Fried, Machine-learning a solution for reactive atomistic simulations of energetic materials, Propellants, Explos., Pyrotech., 2022, 47(8), e202200001,  DOI:10.1002/prep.202200001.
43. M. Schreiner, A. Bhowmik, T. Vegge, J. Busk and O. Winther, Transition1x – a dataset for building generalizable reactive machine learning potentials, Sci. Data, 2022, 9(1), 779,  DOI:10.1038/s41597-022-01870-w.
44. W. G. Stark, J. Westermayr, O. A. Douglas-Gallardo, J. Gardner, S. Habershon and R. J. Maurer, Machine learning interatomic potentials for reactive hydrogen dynamics at metal surfaces based on iterative refinement of reaction probabilities, J. Phys. Chem. C, 2023, 127(50), 24168–24182,  DOI:10.1021/acs.jpcc.3c06648.
45. J. Behler and G. Csányi, Machine learning potentials for extended systems: a perspective, Eur. Phys. J. B, 2021, 94(7), 142,  DOI:10.1140/epjb/s10051-021-00156-1.
46. V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian process regression for materials and molecules, Chem. Rev., 2021, 121(16), 10073–10141,  DOI:10.1021/acs.chemrev.1c00022.
47. M. R. Carbone, When not to use machine learning: a perspective on potential and limitations, MRS Bull., 2022, 47(9), 968–974,  DOI:10.1557/s43577-022-00417-z.
48. D. Rosenberger, J. S. Smith and A. E. Garcia, Modeling of peptides with classical and novel machine learning force fields: a comparison, J. Phys. Chem. B, 2021, 125(14), 3598–3612,  DOI:10.1021/acs.jpcb.0c10401.
49. D. P. Kovács, C. van der Oord, J. Kucera, A. E. A. Allen, D. J. Cole, C. Ortner and G. Csányi, Linear atomic cluster expansion force fields for organic molecules: beyond RMSE, J. Chem. Theory Comput., 2021, 17(12), 7696–7711,  DOI:10.1021/acs.jctc.1c00647.
50. J. D. Morrow, J. L. A. Gardner and V. L. Deringer, How to validate machine-learned interatomic potentials, J. Chem. Phys., 2023, 158(12), 121501,  DOI:10.1063/5.0139611.
51. G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in monte carlo free-energy estimation: umbrella sampling, J. Comput. Phys., 1977, 23(2), 187–199,  DOI:10.1016/0021-9991(77)90121-8.
52. M. Kulichenko, K. Barros, N. Lubbers, Y. W. Li, R. Messerly, S. Tretiak, J. S. Smith and B. Nebgen, Uncertainty-driven dynamics for active learning of interatomic potentials, Nat. Comput. Sci., 2023, 3(3), 230–239,  DOI:10.1038/s43588-023-00406-5.
53. A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(20), 12562–12566,  DOI:10.1073/pnas.202427399.
54. A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100(2), 020603,  DOI:10.1103/PhysRevLett.100.020603.
55. M. Invernizzi and M. Parrinello, Rethinking metadynamics: from bias potentials to probability distributions, J. Phys. Chem. Lett., 2020, 11(7), 2731–2736,  DOI:10.1021/acs.jpclett.0c00497.
56. S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers and K. Schulten Steered molecular dynamics, in Computational Molecular Dynamics: Challenges, Methods, Ideas, ed. P. Deuflhard, J. Hermans, B. Leimkuhler, A. E. Mark, S. Reich, and R. D. Skeel, Lecture Notes in Computational Science and Engineering, Springer, Berlin, Heidelberg, 1999, pp. 39–65,  DOI:10.1007/978-3-642-58360-5_2.
57. P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Transition path sampling: throwing ropes over rough mountain passes, in the dark, Annu. Rev. Phys. Chem., 2002, 53(1), 291–318,  DOI:10.1146/annurev.physchem.53.082301.113146.
58. C. Dellago and P. G. Bolhuis, Activation energies from transition path sampling simulations, Mol. Simul., 2004, 30(11–12), 795–799,  DOI:10.1080/08927020412331294869.
59. C. Dellago; P. G. Bolhuis; and P. L. Geissler, Transition path sampling methods, in Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology, ed. M. Ferrario, G. Ciccotti, and K. Binder, Lecture Notes in Physics, Springer, Berlin, Heidelberg, 2006, vol. 1, pp. 349–391,  DOI:10.1007/3-540-35273-2_10.
60. C. Dellago, and P. G. Bolhuis Transition path sampling and other advanced simulation techniques for rare events, in Advanced Computer Simulation Approaches for Soft Matter Sciences III, ed. C. Holm and K. Kremer, Advances in Polymer Science, Springer, Berlin, Heidelberg, 2009, pp. 167–233,  DOI:10.1007/978-3-540-87706-6_3.
61. L. T. Chong, A. S. Saglam and D. M. Zuckerman, Path-sampling strategies for simulating rare events in biomolecular systems, Curr. Opin. Struct. Biol., 2017, 43, 88–94,  DOI:10.1016/j.sbi.2016.11.019.
62. P. G. Bolhuis and D. W. H. Swenson, Transition path sampling as markov chain monte carlo of trajectories: recent algorithms, software, applications, and future outlook, Adv. Theory Simul., 2021, 4(4), 2000237,  DOI:10.1002/adts.202000237.
63. P. G. Bolhuis, C. Dellago and D. Chandler, Reaction coordinates of biomolecular isomerization, Proc. Natl. Acad. Sci. U. S. A., 2000, 97(11), 5877–5882,  DOI:10.1073/pnas.100127697.
64. P. G. Bolhuis, Transition-path sampling of β-hairpin folding, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(21), 12129–12134,  DOI:10.1073/pnas.1534924100.
65. H. Zhou and P. Tao, Dynamics sampling in transition pathway space, J. Chem. Theory Comput., 2018, 14(1), 14–29,  DOI:10.1021/acs.jctc.7b00606.
66. A. Muždalo, P. Saalfrank, J. Vreede and M. Santer, Cis-to-trans isomerization of azobenzene derivatives studied with transition path sampling and quantum mechanical/molecular mechanical molecular dynamics, J. Chem. Theory Comput., 2018, 14(4), 2042–2051,  DOI:10.1021/acs.jctc.7b01120.
67. C. N. Rowley and T. K. Woo, Generation of initial trajectories for transition path sampling of chemical reactions with ab initio molecular dynamics, J. Chem. Phys., 2007, 126(2), 024110,  DOI:10.1063/1.2424712.
68. T. Bučko, L. Benco, J. Hafner and J. G. Ángyán, Monomolecular cracking of propane over acidic chabazite: an ab initio molecular dynamics and transition path sampling study, J. Catal., 2011, 279(1), 220–228,  DOI:10.1016/j.jcat.2011.01.022.
69. G. Sun and H. Jiang, Ab initio molecular dynamics with enhanced sampling for surface reaction kinetics at finite temperatures: CH₂ ⇌ CH + H on Ni(111) as a case study, J. Chem. Phys., 2015, 143(23), 234706,  DOI:10.1063/1.4937483.
70. L. Bonati, Y.-Y. Zhang and M. Parrinello, Neural networks-based variationally enhanced sampling, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(36), 17641–17647,  DOI:10.1073/pnas.1907975116.
71. L. Bonati, G. Piccini and M. Parrinello, Deep learning the slow modes for rare events sampling, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(44), e2113533118,  DOI:10.1073/pnas.2113533118.
72. S. Yao, R. Van, X. Pan, J. Hwan Park, Y. Mao, J. Pu, Y. Mei and Y. Shao, Machine learning based implicit solvent model for aqueous-solution alanine dipeptide molecular dynamics simulations, RSC Adv., 2023, 13(7), 4565–4577,  10.1039/D2RA08180F.
73. T. Lelièvre, G. Robin, I. Sekkat, G. Stoltz and G. V. Cardoso, Generative methods for sampling transition paths in molecular dynamics, ESAIM: PROCEEDINGS AND SURVEYS, 2023, vol. 73, pp. 238–256, https://www.esaim-proc.org/articles/proc/pdf/2023/02/proc2307312.pdf.
74. A. A. Ojha, S. Thakur, S.-H. Ahn and R. E. Amaro, DeepWEST: deep learning of kinetic models with the weighted ensemble simulation toolkit for enhanced sampling, J. Chem. Theory Comput., 2023, 19(4), 1342–1359,  DOI:10.1021/acs.jctc.2c00282.
75. T. Kikutsuji, Y. Mori, K. Okazaki, T. Mori, K. Kim and N. Matubayasi, Explaining reaction coordinates of alanine dipeptide isomerization obtained from deep neural networks using explainable artificial intelligence (XAI), J. Chem. Phys., 2022, 156(15), 154108,  DOI:10.1063/5.0087310.
76. V. Vassilev-Galindo, G. Fonseca, I. Poltavsky and A. Tkatchenko, Challenges for machine learning force fields in reproducing potential energy surfaces of flexible molecules, J. Chem. Phys., 2021, 154(9), 094119,  DOI:10.1063/5.0038516.
77. C. D. Williams, J. Kalayan, N. A. Burton and R. A. Bryce, Stable and accurate atomistic simulations of flexible molecules using conformationally generalisable machine learned potentials, Chem. Sci., 2024, 15, 12780–12795.
78. Z. Benayad, R. David and G. Stirnemann, Prebiotic chemical reactivity in solution with quantum accuracy and microsecond sampling using neural network potentials, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(23), e2322040121,  DOI:10.1073/pnas.2322040121.
79. R. David, I. Tuñón and D. Laage, Competing reaction mechanisms of peptide bond formation in water revealed by deep potential molecular dynamics and path sampling, J. Am. Chem. Soc., 2024, 146(20), 14213–14224,  DOI:10.1021/jacs.4c03445.
80. M. Chigaev, J. S. Smith, S. Anaya, B. Nebgen, M. Bettencourt, K. Barros and N. Lubbers, Lightweight and effective tensor sensitivity for atomistic neural networks, J. Chem. Phys., 2023, 158(18), 184108,  DOI:10.1063/5.0142127.
81. P. E. Smith, B. M. Pettitt and M. Karplus, Stochastic dynamics simulations of the alanine dipeptide using a solvent-modified potential energy surface, J. Phys. Chem., 1993, 97(26), 6907–6913,  DOI:10.1021/j100128a027.
82. D. S. Chekmarev, T. Ishida and R. M. Levy, Long-time conformational transitions of alanine dipeptide in aqueous solution: continuous and discrete-state kinetic models, J. Phys. Chem. B, 2004, 108(50), 19487–19495,  DOI:10.1021/jp048540w.
83. J. Vymětal and J. Vondrášek, Metadynamics as a tool for mapping the conformational and free-energy space of peptides — the alanine dipeptide case study, J. Phys. Chem. B, 2010, 114(16), 5632–5642,  DOI:10.1021/jp100950w.
84. V. Mironov, Y. Alexeev, V. K. Mulligan and D. G. Fedorov, A systematic study of minima in alanine dipeptide, J. Comput. Chem., 2019, 40(2), 297–309,  DOI:10.1002/jcc.25589.
85. D. Schwalbe-Koda, A. R. Tan and R. Gómez-Bombarelli, Differentiable sampling of molecular geometries with uncertainty-based adversarial attacks, Nat. Commun., 2021, 12(1), 5104,  DOI:10.1038/s41467-021-25342-8.
86. M. A. Mehta, E. A. Fry, M. T. Eddy, M. T. Dedeo, A. E. Anagnost and J. R. Long, Structure of the alanine dipeptide in condensed phases determined by ¹³C NMR, J. Phys. Chem. B, 2004, 108(9), 2777–2780,  DOI:10.1021/jp037871q.
87. M. P. Bhate, J. C. Woodard and M. A. Mehta, Solvation and hydrogen bonding in alanine- and glycine-containing dipeptides probed using solution- and solid-state NMR spectroscopy, J. Am. Chem. Soc., 2009, 131(27), 9579–9589,  DOI:10.1021/ja902917s.
88. M. Feig, Is alanine dipeptide a good model for representing the torsional preferences of protein backbones?, J. Chem. Theory Comput., 2008, 4(9), 1555–1564,  DOI:10.1021/ct800153n.
89. R. Vargas, J. Garza, B. P. Hay and D. A. Dixon, Conformational study of the alanine dipeptide at the MP2 and DFT levels, J. Phys. Chem. A, 2002, 106(13), 3213–3218,  DOI:10.1021/jp013952f.
90. B. Strodel and D. J. Wales, Free energy surfaces from an extended harmonic superposition approach and kinetics for alanine dipeptide, Chem. Phys. Lett., 2008, 466(4), 105–115,  DOI:10.1016/j.cplett.2008.10.085.
91. H. M. D. Bandara and S. C. Burdette, Photoisomerization in different classes of azobenzene, Chem. Soc. Rev., 2012, 41(5), 1809–1825,  10.1039/C1CS15179G.
92. I. C. D. Merritt, D. Jacquemin and M. Vacher, Cis → Trans photoisomerisation of azobenzene: a fresh theoretical look, Phys. Chem. Chem. Phys., 2021, 23(35), 19155–19165,  10.1039/D1CP01873F.
93. F. A. Jerca, V. V. Jerca and R. Hoogenboom, Advances and opportunities in the exciting world of azobenzenes, Nat. Rev. Chem., 2022, 6(1), 51–69,  DOI:10.1038/s41570-021-00334-w.
94. M. Böckmann, N. L. Doltsinis and D. Marx, Nonadiabatic hybrid quantum and molecular mechanic simulations of azobenzene photoswitching in bulk liquid environment, J. Phys. Chem. A, 2010, 114(2), 745–754,  DOI:10.1021/jp910103b.
95. L. Gagliardi, G. Orlandi, F. Bernardi, A. Cembran and M. Garavelli, A Theoretical study of the lowest electronic states of azobenzene: the role of torsion coordinate in the cis–trans photoisomerization, Theor. Chem. Acc., 2004, 111(2), 363–372,  DOI:10.1007/s00214-003-0528-1.
96. I. Conti, M. Garavelli and G. Orlandi, The different photoisomerization efficiency of azobenzene in the lowest Nπ* and Ππ* singlets: the role of a phantom state, J. Am. Chem. Soc., 2008, 130(15), 5216–5230,  DOI:10.1021/ja710275e.
97. R. Ditchfield, W. J. Hehre and J. A. Pople, Self-consistent molecular-orbital methods. IX. An extended gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54(2), 724–728,  DOI:10.1063/1.1674902.
98. J.-D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128(8), 084106,  DOI:10.1063/1.2834918.
99. Lanl/Hippynn, 2024. https://github.com/lanl/hippynn, accessed 22 July 2024.
100. X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, TorchANI: a free and open source PyTorch-based deep learning implementation of the ANI neural network potentials, J. Chem. Inf. Model., 2020, 60(7), 3408–3415,  DOI:10.1021/acs.jcim.0c00451.
101. Aiqm/Torchani, 2021. https://github.com/aiqm/torchani, accessed 22 April 2022.
102. D. W. H. Swenson, J.-H. Prinz, F. Noe, J. D. Chodera and P. G. Bolhuis, OpenPathSampling: a python framework for path sampling simulations. 1. Basics, J. Chem. Theory Comput., 2019, 15(2), 813–836,  DOI:10.1021/acs.jctc.8b00626.
103. D. W. H. Swenson, J.-H. Prinz, F. Noe, J. D. Chodera and P. G. Bolhuis, OpenPathSampling: a python framework for path sampling simulations. 2. Building and customizing path ensembles and sample schemes, J. Chem. Theory Comput., 2019, 15(2), 837–856,  DOI:10.1021/acs.jctc.8b00627.
104. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Du\lak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002,  DOI:10.1088/1361-648X/aa680e.
105. R. Salomon-Ferrer, D. A. Case and R. C. Walker, An overview of the amber biomolecular simulation package, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2013, 3(2), 198–210,  DOI:10.1002/wcms.1121.
106. S. Boothroyd, P. K. Behara, O. C. Madin, D. F. Hahn, H. Jang, V. Gapsys, J. R. Wagner, J. T. Horton, D. L. Dotson, M. W. Thompson, J. Maat, T. Gokey, L.-P. Wang, D. J. Cole, M. K. Gilson, J. D. Chodera, C. I. Bayly, M. R. Shirts and D. L. Mobley, Development and benchmarking of open force field 2.0.0: the sage small molecule force field, J. Chem. Theory Comput., 2023, 19(11), 3251–3275,  DOI:10.1021/acs.jctc.3c00039.
107. J. A. Pople, Quantum chemical models (nobel lecture), Angew. Chem., Int. Ed., 1999, 38(13–14), 1894–1902,  DOI:10.1002/(SICI)1521-3773(19990712)38:13/14<1894::AID-ANIE1894>3.0.CO;2-H.
108. T. Head-Gordon, M. Head-Gordon, M. J. Frisch, C. Brooks III and J. A. Pople, Theoretical study of alanine dipeptide and analogs, Int. J. Quantum Chem., 1989, 36(S16), 311–322,  DOI:10.1002/qua.560360725.
109. J. Apostolakis, P. Ferrara and A. Caflisch, Calculation of conformational transitions and barriers in solvated systems: application to the alanine dipeptide in Water, J. Chem. Phys., 1999, 110(4), 2099–2108,  DOI:10.1063/1.477819.
110. M. Chen, M. A. Cuendet and M. E. Tuckerman, Heating and flooding: a unified approach for rapid generation of free energy surfaces, J. Chem. Phys., 2012, 137(2), 024102,  DOI:10.1063/1.4733389.
111. Y. K. Kang, Assessment of CCSD(T), MP2, DFT-D, CBS-QB3, and G4(MP2) methods for conformational study of alanine and proline dipeptides, Chem. Phys. Lett., 2014, 600, 112–117.
112. D. Chakraborty, A. Banerjee and D. J. Wales, Side-chain polarity modulates the intrinsic conformational landscape of model dipeptides, J. Phys. Chem. B, 2021, 125(22), 5809–5822,  DOI:10.1021/acs.jpcb.1c02412.
113. D. Wei, H. Guo and D. R. Salahub, Conformational dynamics of an alanine dipeptide analog: an ab initio molecular dynamics study, Phys. Rev. E, 2001, 64(1), 011907,  DOI:10.1103/PhysRevE.64.011907.
114. C. Velez-Vega, E. E. Borrero and F. A. Escobedo, Kinetics and reaction coordinate for the isomerization of alanine dipeptide by a forward flux sampling protocol, J. Chem. Phys., 2009, 130(22), 225101,  DOI:10.1063/1.3147465.
115. C. Dellago, P. G. Bolhuis and D. Chandler, Efficient transition path sampling: application to lennard-jones cluster rearrangements, J. Chem. Phys., 1998, 108(22), 9236–9245,  DOI:10.1063/1.476378.
116. R. Jinnouchi, K. Miwa, F. Karsai, G. Kresse and R. Asahi, On-the-fly active learning of interatomic potentials for large-scale atomistic simulations, J. Phys. Chem. Lett., 2020, 11(17), 6946–6955,  DOI:10.1021/acs.jpclett.0c01061.
117. G. Sivaraman, A. N. Krishnamoorthy, M. Baur, C. Holm, M. Stan, G. Csányi, C. Benmore and Á. Vázquez-Mayagoitia, Machine-learned interatomic potentials by active learning: amorphous and liquid hafnium dioxide, npj Comput. Mater., 2020, 6(1), 1–8,  DOI:10.1038/s41524-020-00367-7.
118. N. Wilson, D. Willhelm, X. Qian, R. Arróyave and X. Qian, Batch active learning for accelerating the development of interatomic potentials, Comput. Mater. Sci., 2022, 208, 111330,  DOI:10.1016/j.commatsci.2022.111330.
119. C. Fedele, T.-P. Ruoko, K. Kuntze, M. Virkki and A. Priimagi, New tricks and emerging applications from contemporary azobenzene research, Photochem. Photobiol. Sci., 2022, 21(10), 1719–1734,  DOI:10.1007/s43630-022-00262-8.
120. M. Poutanen, O. Ikkala and A. Priimagi, Structurally controlled dynamics in azobenzene-based supramolecular self-assemblies in solid state, Macromolecules, 2016, 49(11), 4095–4101,  DOI:10.1021/acs.macromol.6b00562.
121. L. W. Giles, C. F. L. Faul and R. F. Tabor, Azobenzene isomerization in condensed matter: lessons for the design of efficient light-responsive soft-matter systems, Mater. Adv., 2021, 2(13), 4152–4164,  10.1039/D1MA00340B.
122. A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, On the mechanism of the cis–trans isomerization in the lowest electronic states of azobenzene: S0, S1, and T1, J. Am. Chem. Soc., 2004, 126(10), 3234–3243,  DOI:10.1021/ja038327y.
123. C. R. Crecca and A. E. Roitberg, Theoretical study of the isomerization mechanism of azobenzene and disubstituted azobenzene derivatives, J. Phys. Chem. A, 2006, 110(26), 8188–8203,  DOI:10.1021/jp057413c.
124. S. Axelrod, E. Shakhnovich and R. Gómez-Bombarelli, Thermal half-lives of azobenzene derivatives: virtual screening based on intersystem crossing using a machine learning potential, ACS Cent. Sci., 2023, 9(2), 166–176,  DOI:10.1021/acscentsci.2c00897.
125. R. J. Maurer and K. Reuter, Assessing computationally efficient isomerization dynamics: ΔSCF density-functional theory study of azobenzene molecular switching, J. Chem. Phys., 2011, 135(22), 224303,  DOI:10.1063/1.3664305.
126. G. Gryn’ova, M. L. Coote and C. Corminboeuf, Theory and practice of uncommon molecular electronic configurations: uncommon molecular electronic configurations, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2015, 5(6), 440–459,  DOI:10.1002/wcms.1233.
127. A. I. Krylov, The quantum chemistry of open-shell species, in Reviews in Computational Chemistry, John Wiley & Sons, Ltd, 2017, pp. 151–224,  DOI:10.1002/9781119356059.ch4.
128. L. Wang, W. Xu, C. Yi and X. Wang, Isomerization and electronic relaxation of azobenzene after being excited to higher electronic states, J. Mol. Graphics Modell., 2009, 27(7), 792–796,  DOI:10.1016/j.jmgm.2008.11.011.
129. D. H. Ess and T. C. Cook, Unrestricted prescriptions for open-shell singlet diradicals: using economical ab initio and density functional theory to calculate singlet–triplet gaps and bond dissociation curves, J. Phys. Chem. A, 2012, 116(20), 4922–4929,  DOI:10.1021/jp300633j.
130. J. Gräfenstein, E. Kraka, M. Filatov and D. Cremer, Can unrestricted density-functional theory describe open shell singlet biradicals?, Int. J. Mol. Sci., 2002, 3(4), 360–394,  DOI:10.3390/i3040360.
131. N. Fedik, M. Kulichenko, D. Steglenko and A. I. Boldyrev, Can aromaticity be a kinetic trap? Example of Mechanically Interlocked Aromatic [2-5]Catenanes Built from Cyclo[18]Carbon, Chem. Commun., 2020, 56(18), 2711–2714,  10.1039/C9CC09483K.
132. J. L. Magee, W. Shand Jr and H. Eyring, Non-adiabatic reactions. Rotation about the double bond*, J. Am. Chem. Soc., 1941, 63(3), 677–688,  DOI:10.1021/ja01848a012.
133. A. E. A. Allen, N. Lubbers, S. Matin, J. Smith, R. Messerly, S. Tretiak and K. Barros, Learning together: towards foundational models for machine learning interatomic potentials with meta-learning, npj Comput. Mater., 2024, 10, 154.
134. I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwin, F. Berger, N. Bernstein, A. Bhowmik, S. M. Blau, V. Cărare, J. P. Darby, S. De, F. Della Pia, V. L. Deringer, R. Elijošius, Z. El-Machachi, F. Falcioni, E. Fako, A. C. Ferrari, A. Genreith-Schriever, J. George, R. E. A. Goodall, C. P. Grey, P. Grigorev, S. Han, W. Handley, H. H. Heenen, K. Hermansson, C. Holm, J. Jaafar, S. Hofmann, K. S. Jakob, H. Jung, V. Kapil, A. D. Kaplan, N. Karimitari, J. R. Kermode, N. Kroupa, J. Kullgren, M. C. Kuner, D. Kuryla, G. Liepuoniute, J. T. Margraf, I.-B. Magdău, A. Michaelides, J. H. Moore, A. A. Naik, S. P. Niblett, S. W. Norwood, N. O'Neill, C. Ortner, K. A. Persson, K. Reuter, A. S. Rosen, L. L. Schaaf, C. Schran, B. X. Shi, E. Sivonxay, T. K. Stenczel, V. Svahn, C. Sutton, T. D. Swinburne, J. Tilly, C. van der Oord, E. Varga-Umbrich, T. Vegge, M. Vondrák, Y. Wang, W. C. Witt, F. Zills and G. Csányi, A foundation model for atomistic materials chemistry, arXiv, 2024, preprint, arXiv:2401.00096,  DOI:10.48550/arXiv.2401.00096.
135. J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost, Chem. Sci., 2017, 8(4), 3192–3203,  10.1039/C6SC05720A.
136. Q. H. Hu, A. M. Johannesen, D. S. Graham and J. D. Goodpaster, Neural network potentials for reactive chemistry: caspt2 quality potential energy surfaces for bond breaking, Digital Discovery, 2023, 2(4), 1058–1069,  10.1039/D3DD00051F.
137. M. Rano and D. Ghosh, Efficient machine learning configuration interaction for bond breaking problems, J. Phys. Chem. A, 2023, 127(16), 3705–3713,  DOI:10.1021/acs.jpca.2c09103.
138. Q. Zhao, S. M. Vaddadi, M. Woulfe, L. A. Ogunfowora, S. S. Garimella, O. Isayev and B. M. Savoie, Comprehensive exploration of graphically defined reaction spaces, Sci. Data, 2023, 10(1), 145,  DOI:10.1038/s41597-023-02043-z.
139. P. van Gerwen, K. R. Briling, C. Bunne, V. R. Somnath, R. Laplaza, A. Krause and C. Corminboeuf, EquiReact: an equivariant neural network for chemical reactions, arXiv, 2023, preprint, arXiv:2312.08307v,  DOI:10.48550/arXiv.2312.08307.
140. N. Fedik, B. Nebgen, N. Lubbers, K. Barros, M. Kulichenko, Y. W. Li, R. Zubatyuk, R. Messerly, O. Isayev and S. Tretiak, Synergy of semiempirical models and machine learning in computational chemistry, J. Chem. Phys., 2023, 159(11), 110901.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00265b

---