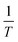Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the language of molecules: predicting pure component parameters for the PC-SAFT equation of state from SMILES†
Benedikt
Winter
 a,
Philipp
Rehner
a,
Philipp
Rehner
 a,
Timm
Esper
b,
Johannes
Schilling
a,
Timm
Esper
b,
Johannes
Schilling
 a and
André
Bardow
a and
André
Bardow
 *a
*a
aEnergy and Process Systems Engineering, ETH Zurich, Switzerland. E-mail: abardow@ethz.ch
bInstitute of Thermodynamics and Thermal Process Engineering, University of Stuttgart, Germany
First published on 29th January 2025
Abstract
A major bottleneck in developing sustainable processes and materials is a lack of property data. Recently, machine learning approaches have vastly improved previous methods for predicting molecular properties. However, these machine learning models are often not able to handle thermodynamic constraints adequately. In this work, we present a machine learning model based on natural language processing to predict pure-component parameters for the perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state. The model is based on our previously proposed SMILES-to-Properties-Transformer (SPT). By incorporating PC-SAFT into the neural network architecture, the machine learning model is trained directly on experimental vapor pressure and liquid density data. Combining established physical modeling approaches with state-of-the-art machine learning methods enables high-accuracy predictions across a wide range of pressures and temperatures, while keeping the thermodynamic consistency of an equation of state like PC-SAFT. SPTPC-SAFT demonstrates exceptional prediction accuracy even for complex molecules with various functional groups, outperforming traditional group contribution methods by a factor of four in the mean average percentage deviation. Moreover, SPTPC-SAFT captures the behavior of stereoisomers without any special consideration. To facilitate the application of our model, we provide predicted PC-SAFT parameters of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 279 components, making PC-SAFT accessible to all researchers.
279 components, making PC-SAFT accessible to all researchers.
1 Introduction
Developing advanced materials like chemical products, fuels, or refrigerants is vital for sustainable solutions in various industries. To achieve this goal, designing new molecules with tailored properties is crucial. However, exploring all possible molecules experimentally is impossible, given the vast array of potential molecular candidates. As a result, models are needed that can rapidly predict molecular properties to streamline the molecular discovery and development of sustainable products and processes.Over the years, the research on predicting molecular properties has led to many approaches based on, e.g., quantitative structure–property relationships (QSPRs),1,2 group contribution (GC) methods3–6 and quantum mechanics.7–9 However, many of these classical methods either have low accuracy, are limited to certain functional groups, or require large computational resources. As a recent addition to these approaches, machine learning methods have emerged as a powerful tool due to their ability to learn complex patterns and generalize from data, overcoming some of the shortcomings of the classical methods. Some recent examples of machine learning approaches include methods for the prediction of binary properties such as activity coefficients10–13 or a large range of pure component properties.14–17
However, the majority of recent machine learning approaches focus on singular properties, not a holistic description of a system. Thermodynamics teaches that equilibrium properties of fluids are not independent but rather related through an equation of state. Modern equations of state are expressed as a thermodynamic potential, usually the Helmholtz energy, as a function of its characteristic variables. All equilibrium properties are then available as partial derivatives of the thermodynamic potential. Equations of state can be broadly classified into three categories: (1) cubic equations of state (such as the Peng–Robinson18 and the Soave–Redlich–Kwong19 equation of state), (2) highly accurate reference equations for specific systems (including water,20 carbon dioxide,21 nitrogen,22 and natural gas components23), and (3) molecular equations of state (such as the SAFT family24–27). The main distinction among these categories lies in the data required for parameterization, with cubic equations of state necessitating the fewest parameters and reference equations of state demanding the most.
Parameterizing equations of state typically relies on experimental data, which is often unavailable for novel molecules or expensive to obtain from commercial databases or experiments. In the absence of experimental data, various predictive methods have been developed for equations of state, primarily focused on GC methods.28,29 Since group contribution methods rely on a predefined set of functional groups and their respective contributions, those methods are limited to certain subsets of the molecular space and often struggle to predict the properties of more complex molecules accurately. Furthermore, capturing effects linked to isomers or more intricate intermolecular forces requires the definition of higher-order groups, for which adequate parametrization is more data-demanding,30 or fundamental improvements to the PC-SAFT-theory.
Recently, machine learning (ML) methods have been developed to predict pure component parameters for equations of state. The focus has been on the perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state developed by Gross and Sadowski.25 The ML models use as input either group counts,31 molecular fingerprints,32 or a variety of molecular descriptors.33 However, these methods are not trained directly on experimental property data but on previously fitted pure component parameters of PC-SAFT. This reliance on previously fitted pure component parameters vastly constraints the amount of available training data, thus likely limiting the applicability domain of these models. Moreover, small errors in predicted pure component parameters can have large effects on the final predicted fluid properties. Consequently, training machine learning models directly on experimental property data is preferred.
In previous work, we demonstrated how explicit physical equations could be integrated into a machine learning framework, using the NRTL-equation as an example.34 However, integrating PC-SAFT into a machine learning framework presents two additional challenges: Firstly, PC-SAFT is not explicit in measurable properties like vapor pressures and liquid densities. Instead, vapor pressures and liquid densities have to be determined iteratively from partial derivatives of the Helmholtz energy, requiring a more sophisticated approach than a straightforward integration into the neural network. Secondly, the physical significance of the pure component parameters of PC-SAFT is the basis of its robust extrapolation, in particular to mixtures. Therefore, any predictive method should ensure that parameters related to their physical basis are obtained.
In this work, we present a natural language-based machine learning model for predicting pure component parameters of PC-SAFT trained directly on experimental data. For this purpose, the PC-SAFT equation of state is directly integrated into our previously proposed SMILES-to-Properties-Transformer (SPT).11,34 The resulting SPT-PC-SAFT model exhibits high prediction performance, accurately predicting thermophysical properties for complex molecules with various functional groups. Remarkably, our model is also capable of correctly predicting the behavior of stereoisomers.
2 The SPT-PC-SAFT model
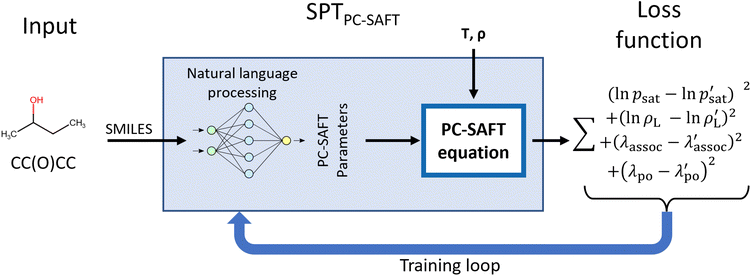
The SPTPC-SAFT model is designed to allow the inclusion of explicit systems of equations into machine learning frameworks to apply physical constraints. This work uses the PC-SAFT equation of state, though other equations of state or any other system of equations could be integrated. In particular, we use PCP-SAFT with dipole–dipole interactions by Gross and Vrabec35 and a 2B association scheme for all molecules that form hydrogen bonds with themselves. SPT is a natural language processing model that utilizes the SMILES code of a molecule as input. Conceptually, our SPT model can be interpreted as an advanced group contribution approach that uses characters in the SMILES code as atomic groups and dynamically assembles higher-order groups via natural language processing.Fig. 1 illustrates the overall structure of the proposed SPTPC-SAFT model: first, molecules are represented as SMILES codes, which are fed into a natural language processing model that predicts parameters, which are used within the PC-SAFT equation of state to compute vapor pressures psat and liquid densities ρL at a given temperature or temperature and pressure, respectively. To avoid assigning dipole moments and association parameters to non-polar or non-associating molecules, the likelihood that a component is associating (λassoc) or polar (λpolar) is also predicted by SPTPC-SAFT and molecules are only assigned associating or polar parameters if the molecule is predicted to be associating or polar. During the model training, the PC-SAFT equation of state is incorporated into the forward and backward pass, allowing for the calculation of analytical gradients of the loss (target function) with respect to the model parameters. This integration enables us to train a machine learning model end-to-end on experimental data and not only on previously fitted parameters.
In the following sections, the model and training procedure of SPTPC-SAFT are described in detail: Section 2.1 introduces the architecture of the machine learning model and the integration of the PC-SAFT equation. Section 2.2 describes the data sources, data processing, and the definition of training and validation sets. In Section 2.3, we describe the selection of hyper-parameters and the training process of SPTPC-SAFT.
2.1 Model architecture
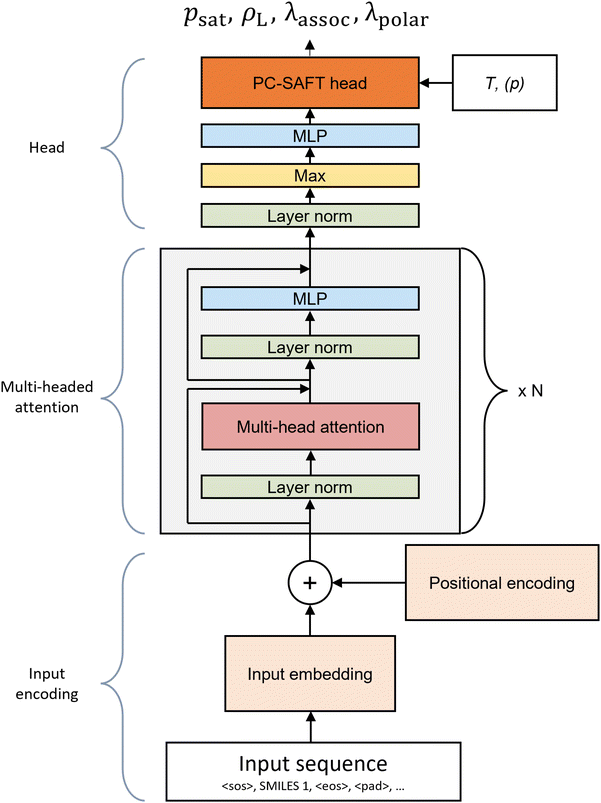
The model architecture of SPTPC-SAFT (Fig. 2) is largely based on our previous SPT models,11,34 which are in turn based on the natural language model GPT-3 (ref. 36) using a decoder-only transformer architecture implemented by Vaswani et al.37 The transformer architecture has been shown suitable for understanding not only the grammar of natural language but also the molecular grammar embedded within SMILES codes, a linear text-based molecular representation introduced by Weininger,38 leading to many successful applications in the field of chemistry.39–42In the following, we present the SPTPC-SAFT architecture in three sections: input embedding (Section 2.1.1), multi-head attention (Section 2.1.2), and head (Section 2.1.3).
The input of SPTPC-SAFT consists of the SMILES codes representing the molecule of interest with special characters denoting the start of the sequence <SOS>, and the end of the sequence <EOS>. The remainder of the input sequence is filled up to a maximum sequence length nseq of 128 with padding <PAD>:
| <SOS>, SMILES, <EOS>, <PAD>,… |
To render the input string suitable for the machine learning model, the string is tokenized, breaking the sequence into tokens that can each be represented by a unique number. Generally, tokens may comprise multiple characters, but in this work, each token consists of a single character. The tokenization process for SMILES can be compared to assigning first-order groups in group contribution methods. The complete vocabulary containing all tokens can be found in the ESI Section 1.†
The input sequence undergoes one-hot encoding, where each token is represented by a learned vector of size nemb = 512. An input matrix of size nemb × nseq is generated by concatenating the vectors representing the tokens of the input sequence. After encoding the input sequence, an additional vector is appended to the right of the input matrix, which holds a linear projection of continuous variables into the embedding space. In the case of the original SPT model,11 temperature information is encoded in this vector. In SPTPC-SAFT, no continuous variables are supplied here, as temperature and pressure information is only introduced in the final stage (see Fig. 2), and thus, the continuous variable vector only contains zeros. After adding the continuous variables, the resulting input matrix has a size of nemb × nseq + 1. Subsequently, a learned positional encoding, which contains a learned embedding for each position, of size nemb × nseq + 1 is added to the input matrix. At this stage, the input matrix contains information on all atoms and bonds in the molecule and their positions. However, each token lacks information about its surroundings, as no information has been exchanged between tokens yet. This information sharing between tokens is discussed in the following multi-head attention section.
For a more comprehensive and visual explanation, readers are directed to the blog of Alammar46 or the comprehensive description in the ESI of our previous work.34
First, the pure component parameters of PC-SAFT have inherent physical meaning, and preserving this physical meaning cannot be guaranteed in a simple regression model. Second, the target properties used for training the model, i.e., vapor pressures and liquid densities, are not direct outputs of PC-SAFT; instead, these target properties must be iteratively converged. While software packages are available that provide robust computations of bulk and phase equilibrium properties with PC-SAFT,47 it is crucial to ensure that the neural network maintains an intact computational graph to allow the network to obtain a derivative of the target value with respect to all model parameters. An intact computational graph can be ensured when all calculations are conducted within a consistent framework like PyTorch.
2.1.3.1 Assignment of polarity and association. The PC-SAFT equation of state is physics-based, and its pure component parameters are related to properties of the underlying molecular model. For example, the pure component parameter m denotes the (potentially non-integer) number of segments on a hypothetical reference fluid, while σ and ε correspond to Lennard-Jones interaction parameters that can be expected to be reasonably transferable between chemically similar molecules. Fortunately, we observe that the pure component parameters m, σ, and ε naturally converge to subjectively reasonable values. However, this natural convergence is not the case for the pure component parameters that describe polar interactions (μ) and associating interactions (εAB, κAB). These pure component parameters should be 0 for non-polar or non-associating components. This behavior, however, cannot be guaranteed if the parameters are fitted independently by the model purely based on experimental data. Therefore, to assign polar and associating pure component parameters, the SPTPC-SAFT model must learn if a component has associating and polar interactions. Here, we predict the polarity and association likelihood in the head of the SPTPC-SAFT model. A graphical description of the PC-SAFT head is given in Fig. 3.
 | ||
Fig. 3 Head section of the model. The natural language processing section of the SPT model returns a vector of length 8. This vector contains six auxiliary pure component parameters of PC-SAFT (![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) , , ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) , , ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , , ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) AB, AB, ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) AB, and AB, and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ) and the auxiliary association and polarity likelihoods A and P. The auxiliary likelihood parameters are passed through a sigmoid function that normalizes them, returning the association and polarity likelihood λassoc and λpolar. The associating parameters εAB and κAB are calculated by multiplying the auxiliary parameters e and k with λassoc. The polarity parameter μ is calculated by multiplying u with 1 − λassoc and λpolar. The resulting pure component parameters are then used in the PC-SAFT equation of state to calculate either vapor pressure or liquid density using the FeOs framework.47 The results of the FeOs calculation as well as λassoc and λpolar are passed to the target function. ) and the auxiliary association and polarity likelihoods A and P. The auxiliary likelihood parameters are passed through a sigmoid function that normalizes them, returning the association and polarity likelihood λassoc and λpolar. The associating parameters εAB and κAB are calculated by multiplying the auxiliary parameters e and k with λassoc. The polarity parameter μ is calculated by multiplying u with 1 − λassoc and λpolar. The resulting pure component parameters are then used in the PC-SAFT equation of state to calculate either vapor pressure or liquid density using the FeOs framework.47 The results of the FeOs calculation as well as λassoc and λpolar are passed to the target function. | ||
After leaving the multi-head attention section, the model has an output of size nemb × nseq. To reduce the dimensionality, a max function is first applied across the sequence dimensions, resulting in a vector of size nemb × 1. Afterward, a linear layer projects this vector to a vector of the auxiliary pure component parameters of size 8, which contains the auxiliary pure component parameters of PC-SAFT ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) = [
= [![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif)
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif)
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif)
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) AB
AB![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) AB
AB![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ] and auxiliary association and polarity likelihoods (A, P). From the auxiliary parameters
] and auxiliary association and polarity likelihoods (A, P). From the auxiliary parameters ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) , the pure component parameters of PC-SAFT ϕ are calculated using the following equation:
, the pure component parameters of PC-SAFT ϕ are calculated using the following equation:
 | (1) |
Here, ϕmean is an externally set hyperparameter determined via a hyperparameter scan. The auxiliary parameters ensure that reasonable values for the pure component parameters of PC-SAFT are reached at the beginning of the training when ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) can be expected to be small values around 0, effectively serving as a staring value for the model. Properly setting the ϕmean parameters ensures quicker convergence. The factor Λ = [1 1 1 λassocλassoc (1 − λassoc)λpolar] is used to activate or deactivate the association parameters and the dipole moment using the association and polarity likelihoods λassoc and λpolar. To calculate the likelihoods, the auxiliary likelihood parameters A and P are passed through a sigmoid function that normalizes them between 0 and 1:
can be expected to be small values around 0, effectively serving as a staring value for the model. Properly setting the ϕmean parameters ensures quicker convergence. The factor Λ = [1 1 1 λassocλassoc (1 − λassoc)λpolar] is used to activate or deactivate the association parameters and the dipole moment using the association and polarity likelihoods λassoc and λpolar. To calculate the likelihoods, the auxiliary likelihood parameters A and P are passed through a sigmoid function that normalizes them between 0 and 1:
 | (2) |
 | (3) |
For associating molecules, we assume that the association contribution dominates the polar contribution. Thus, the dipole moment parameter is set to 0 by multiplying with (1 − λassoc)λpolar.
The parameters ϕ = [m σ ε εABκABμ] are then passed into the PC-SAFT equation of state to compute either saturation pressures psat or liquid densities ρL. The resulting vapor pressures and liquid densities are subsequently passed into the target function along with the associating and polar likelihood λassoc and λpolar, respectively. Including the likelihoods in the target function helps with distinguishing between different intermolecular interactions. A more comprehensive assessment of the strength of different intermolecular interactions and more general association schemes beyond 2B require, in our view, the integration of mixture data into the parameter prediction (cf. ref. 48).
2.1.3.2 Preservation of the computational graph. The PC-SAFT equation of state calculates the Helmholtz energy as a function of temperature, mole numbers, and volume. Thermodynamic properties that can be expressed as derivatives of the Helmholtz energy, such as pressure, chemical potential, and heat capacity, are also explicit in terms of temperature, volume, and mole numbers, or, for intensive properties, in temperature T and density ρ.
However, the pure component vapor pressure is not directly accessible via a derivative of the Helmholtz energy. Instead, the pure component vapor pressure is implicitly defined as the solution of three nonlinear equations,
| μ(T,ρV) = μ(T,ρL) | (4) |
| p(T,ρV) = psat | (5) |
| p(T,ρL) = psat | (6) |
In general, the derivatives of an implicitly defined function x(ϕ) that depends on parameters ϕ via f(x, ϕ) = 0, can be found by calculating a single step of a Newton iteration starting from an already converged solution x* as:
 | (7) |
Applying the concept to the calculation of liquid densities leads to:
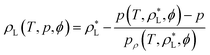 | (8) |
For the vapor pressures, after solving the system of three equations shown above, the last Newton step is:
 | (9) |
Implementing eqn (8) and (9) into the neural network ensures a fully connected computational graph that can be used by PyTorch to evaluate derivatives of the loss function while still allowing the use of efficient external routines to converge states. While we developed this method to use equations of state, it could also be applied to a wider range of problems where parameters for implicit equations have to be determined using neural networks.
2.2 Data
SPTPC-SAFT is trained using vapor pressure and liquid density data obtained from, among others, the Dortmund Data Bank (DDB),50 the DIPPR database51 and the ThermoML database52 curated by Esper et al.53From this large data collection, all molecules are removed that do not contain at least one carbon atom and most metal complexes except silicon. The remaining data is then split into two sets depending on their data quality: the clean and the remaining dataset. The clean dataset contains molecules that have already been used for the fitting of pure component parameters of PC-SAFT by Esper et al.53 and contains 1103 components, 189![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 vapor pressure data points, and 282
504 vapor pressure data points, and 282![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 liquid density data points. The pressure data in the clean dataset have undergone a significant effort to eliminate outliers.53 Only data from the clean dataset is used for validation.
642 liquid density data points. The pressure data in the clean dataset have undergone a significant effort to eliminate outliers.53 Only data from the clean dataset is used for validation.
The remaining dataset includes the data of the aforementioned databases that is not suitable to directly fit pure component PC-SAFT parameters, as not sufficiently many vapor pressures and liquid densities are available for a given component. However, this data can still be used in SPTPC-SAFT due to the end-to-end training approach. The remaining dataset has a lower data quality than the clean dataset but contains a larger variety of molecules. Several steps were conducted to clean the remaining dataset: first, all data points at a vapor pressure of 1.0 ± 0.1 bar at 298.15 ± 1.00 K are excluded, as these seem to be data points entered erroneously. Then, we removed data points that could not be fitted using PC-SAFT. To remove the data points, we trained eight SPTPC-SAFT models on the clean and remaining data for 15 epochs using a SmoothL1 loss, thus giving less weight to outliers than using an MSE loss. Eight models were used for convenience since eight GPUs were available to us while providing a good compromise between robustness and performance. Afterward, we removed all data points from the remaining dataset that have a training loss larger than 0.5. In total, 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456 of 233
456 of 233![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 988 data points were removed from the remaining data. Fig. S3 in the ESI† illustrates typical examples of errors identified using our data-cleaning method. Manual review of the removed data points showed that mostly unreasonable-looking data points were removed from the remaining data. The large deviations can either be attributed to scattering of the experimental data, especially at low pressures, or to systematic deviations, either due to limitations of PC-SAFT or erroneously reported experimental results. Overall, 160
988 data points were removed from the remaining data. Fig. S3 in the ESI† illustrates typical examples of errors identified using our data-cleaning method. Manual review of the removed data points showed that mostly unreasonable-looking data points were removed from the remaining data. The large deviations can either be attributed to scattering of the experimental data, especially at low pressures, or to systematic deviations, either due to limitations of PC-SAFT or erroneously reported experimental results. Overall, 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186 data points for vapor pressure and 52
186 data points for vapor pressure and 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343 data points for liquid densities remain in the data set with 12
343 data points for liquid densities remain in the data set with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 and 2067 molecules, respectively.
019 and 2067 molecules, respectively.
As our model was employed to clean the remaining data, it is important to note that the remaining dataset is solely used for training the model and not for any form of model validation. For model validation, only the clean dataset is used.53 Thereby, we ensure that our model's performance evaluation is based on reliable and high-quality data and unbiased by our data cleaning steps.
Some of the molecules in the training data are structural isomers such as cis-2-butane and trans-2-butane. SPT uses isomeric SMILES codes and can thus distinguish between the cis and trans versions of molecules. However, for some isomeric molecules, our training data also contains data only labeled with the non-isomeric SMILES. In these cases, the data is either one unknown isomer, a mixture of isomers with very similar properties, or mislabeled data of two differently behaving isomers. To avoid ambiguities, we dropped any data related to non-isomeric SMILES codes for components of which isomeric SMILES are present.
To train the model to recognize if a component is associating or polar, the training data is labeled. To label molecules as associating or polar, we use the following approaches: for associating components, we use RDKit to identify molecules with at least one hydrogen bond donor site and one hydrogen bond acceptor site.45 Components that meet this criterion are labeled as associating. To label molecules as polar, a consistent database of dipole information is needed. Here, we use the COSMO-Therm database 2020, where the dipole moment is available for 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182 molecules in the energy files. If the dipole moment is above 0.35 D, the molecule is labeled as polar. The limit is set semi-arbitrary by looking at molecules close to the limit and judging if they are polar. Examples of molecules around this polarity threshold are shown in Fig. 4. If a component in the training data is unavailable in the COSMO-Therm database, its polarity likelihood is masked in the loss function and thus ignored during training. We thus only train the polarity classifier on the subset of molecules with known polarity. Polarity information is available for around 95% of all molecules in the clean dataset and 50% of the molecules in the remaining dataset.
182 molecules in the energy files. If the dipole moment is above 0.35 D, the molecule is labeled as polar. The limit is set semi-arbitrary by looking at molecules close to the limit and judging if they are polar. Examples of molecules around this polarity threshold are shown in Fig. 4. If a component in the training data is unavailable in the COSMO-Therm database, its polarity likelihood is masked in the loss function and thus ignored during training. We thus only train the polarity classifier on the subset of molecules with known polarity. Polarity information is available for around 95% of all molecules in the clean dataset and 50% of the molecules in the remaining dataset.
However, we impose certain restrictions on the data used for validation. Only components with at least three carbon atoms are included in the validation set, as extrapolation from larger molecules towards very small molecules, such as methane and carbon dioxide, works poorly and the space of small molecules is already well-explored experimentally. Thus, pure component parameters of PC-SAFT are generally available for small molecules.53 Additionally, structural isomers are treated as one component with respect to training/validation splits. Therefore, if the trans version of a molecule is in the validation set, the cis version is also included in the validation set, and vice versa. The same workflow is applied for enantiomers.
In previous work, it was demonstrated that the prediction error of molecular properties tends to exhibit a roughly log-linear relationship with the amount of training data for the prediction of activity coefficients.11 Although it would be interesting to explore similar data scaling for PC-SAFT, the significant computational resources required are beyond the scope of this paper.
2.3 Hyperparameters and training
The base model architecture for SPTPC-SAFT is adopted from our previous SPT-NRTL model34 with no further modifications to the architectural hyperparameters such as embedding size, number of layers, and hidden factor. For training SPTPC-SAFT, we use an initial model pretrained on concentration-dependent activity coefficients using a regression head described in Winter et al.34To identify good values for ϕmean, we generated a synthetic training dataset with 1494 pure component parameters of PC-SAFT from the work of Esper et al.53 and used these parameters to calculate 100 pressure and density values. To validate our model's performance, we reserved 5% of the components as a separate validation set. Over this set, a scan was conducted using the parameter values listed in Table 1, and the set of parameters leading to the lowest loss on the test set was chosen.
| Parameter | m | σ/Å | ε/k/K | μ/D | κ AB | ε AB/k/K |
|---|---|---|---|---|---|---|
| σ mean | 2 | 5 | 300 | 3 | 0.005 | 1500 |
During the hyperparameter scan, we found that values for ϕmean that overestimate the critical point help with the convergence. The overestimation ensures that most calculations return valid results in the initial stages of the model training, speeding up the training and avoiding divergence of the model. Vapor pressure data for temperatures above the predicted critical point are excluded from the calculation of the loss function to avoid poisoning the gradients with NaN values. This treatment is particularly relevant at the beginning of the training, where deviations are large. For highly converged models, failures in the calculation of vapor pressures are unlikely due to PC-SAFT's inherent tendency to overestimate critical points.
The training was performed on 4 RTX-3090s using a learning rate of 10−4 and 50 epochs. Training takes about 10 h for 8 training/validation splits running two models per GPU in parallel.
3 Predictive capabilities of SPT-PC-SAFT
In our analysis of predictive performance, we utilize APD as our primary metric. To start, we determine the APD for individual molecules: | (10) |
 is the predicted value for component i and datapoint j. Subsequently, we evaluate either the mean or median of these deviations across the entire dataset. This approach ensures that molecules with numerous data points, such as propane, do not disproportionately influence the prediction discussion. Deviations for vapor pressure psat and liquid density ρL are calculated independently of each other. Unless explicitly stated, we focus on the deviation in the validation set, representing the model's prediction, rather than the deviation in the training set.
is the predicted value for component i and datapoint j. Subsequently, we evaluate either the mean or median of these deviations across the entire dataset. This approach ensures that molecules with numerous data points, such as propane, do not disproportionately influence the prediction discussion. Deviations for vapor pressure psat and liquid density ρL are calculated independently of each other. Unless explicitly stated, we focus on the deviation in the validation set, representing the model's prediction, rather than the deviation in the training set.
3.1 Prediction of vapor pressures and liquid densities
The SPTPC-SAFT model exhibits a mean APD of 13.5% and a median APD of 8.7% for predicting vapor pressures in our validation set, consisting of 870 components. Fig. 5 presents a cumulative deviation curve of the APD for the validation set and the training set. The training set is comparable to a fitted model and should thus provide an upper bound for the accuracy of PC-SAFT on our training dataset. The results highlight the robustness of SPTPC-SAFT. Only a minor portion of the molecules in the validation set exhibited a notably high APD: 3% had an APD exceeding 50%, while only 0.4% surpassed an APD of 100%. This indicates accurate predictions of the vapor pressure for the vast majority of the validation set's molecules.Fig. 5 illustrates additionally how the APD translates into pressure-temperature (p/T) plots and demonstrates the diverse set of molecules for which SPTPC-SAFT can account. These examples are cyclohexylamine with an APD of 2%, ethyl cyanoacetate with an APD of 9%, octamethyl-1,3,5,7,2,4,6,8-tetraoxatetrasilocane with an APD of 19%, and triacetin with an APD of 51%.
The relationship between APD, molecule size, and vapor pressure range is further illustrated in Fig. 6, which displays the APD in vapor pressure prediction as a function of the number of heavy atoms and pressure. A region of relatively low APD is achieved for molecules containing between 4 and 20 heavy atoms within a vapor pressure range of 1 kPa to 100 MPa. In contrast, high deviation predominantly occurs at the edges of the data space, particularly for large molecules at low pressures. This behavior might be due to a lower density of data and higher uncertainty when measuring low-pressure systems.
 | ||
| Fig. 6 Average percentage deviation in vapor pressure as a function of experimental vapor pressure and the number of heavy atoms in the molecules. Deviations larger than 0.5 are truncated at 0.5. | ||
In Fig. 7, the relationship between APD (Average Percentage Deviation) and molecular families is explored. The classification of the molecular families is based on the DIPPR database,51 which contains families for 609 out of the 870 components in the validation set. Molecules not assigned to a family are excluded from this analysis. A noticeable correlation is obtained between the expected prediction error and the molecular families. Notably, molecular families composed solely of oxygen and carbon exhibit above-average prediction accuracy. In contrast, fluorinated, halogenated (bromide and iodine), and particularly nitrogen-containing compounds present challenges in prediction. A comprehensive list of the validation set, categorized by molecular group, can be found in the ESI.† Overall SPTPC-SAFT, performs well for the majority of molecular families.
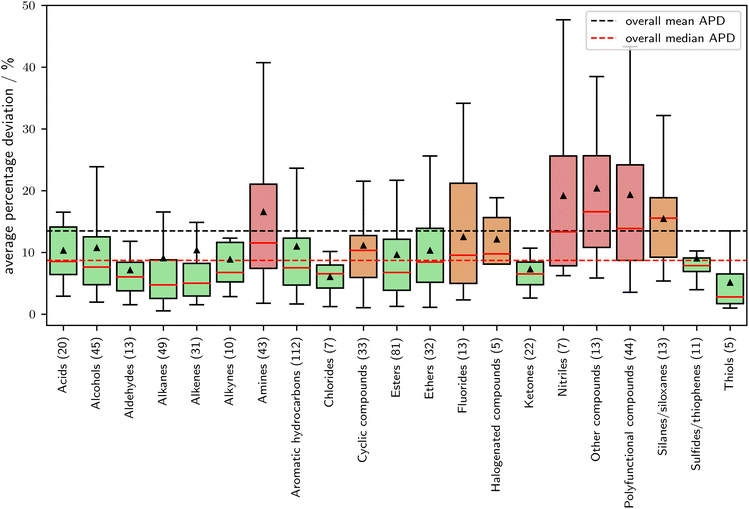 | ||
| Fig. 7 Average percentage deviation in vapor pressure as a function of the molecular family. Molecular families are assigned according to the DIPPR database.51 Of the 870 components in the validation set, 609 components could be assigned a molecular family. Green boxes show families with a median APD of 2.5% below the overall mean APD of 13.5%, red boxes show families with an APD of 2.5% above the overall mean APD. | ||
The APD in liquid density is generally lower than the deviation in vapor pressure. A comparison of the numerical values for the two quantities is difficult due to the different range and quality of the data. The trend is in line with the general behavior of PC-SAFT, as demonstrated by the large-scale parameterization of Esper et al.53 For densities, our SPTPC-SAFT model achieves a mean APD of 3.1%. Predicted liquid densities at 1 bar are shown for a range of alkanes and alcohols in Fig. 8, generally demonstrating a good agreement with the measured data.
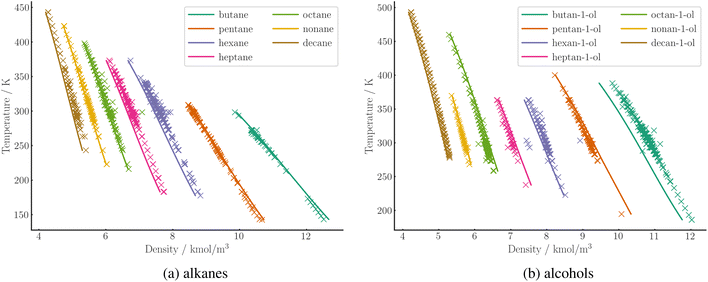 | ||
| Fig. 8 Prediction of molar density of C4 to C10 alkanes (a) and alcohols (b) at 1 bar over a range of temperatures using SPTPC-SAFT (lines). Experimental data (crosses) are taken from the DDB. | ||
3.2 Plausibility of predicted PC-SAFT pure component parameters
One major advantage of the PC-SAFT model is the physical basis of its parameters. Thus, any predictive model should only assign polar and associating interactions when they are reasonable. We achieve this by introducing the polarity and association likelihood (see Section 2.1.3). Table 2 provides an overview of selected pure component parameters of PC-SAFT predicted by SPTPC-SAFT. The pure component parameters m, σ, and ε are predicted within anticipated ranges. The chain length parameter m increases along the homologous series, while the segment diameter σ and interaction energy ε are similar for molecules in the same chemical family. The association is accurately identified for alcohols, and polarity is properly assigned to ethers. On the one hand, 1-ethoxypentane gets assigned a dipole moment of 2.5 D with a polarity likelihood of nearly 1. On the other hand, 1,2-diethoxymethane exhibits no dipole moment due to its higher symmetry, as correctly recognized by SPTPC-SAFT. Consequently, the assignment of polarity and association. However, in some cases the assignment of polarity failed, and non-polar or weakly polar components are assigned a dipole-moment. This current limitation of our model can, in particular, be apparent for small molecules, for which extrapolation from a dataset of larger molecules is difficult, e.g., for methane. Thus, we have published predicted parameter only for molecules with more than 3 heavy atoms, because highly accurate fitted parameter sets for small molecules are likely available from other sources, e.g.,53. Furthermore, while the assignment of polarity is physics based, the absolute value of the predicted dipole moment μ is not and shows divination from dipole moments predicted using COSMO-RS (see ESI 5†).| Name | SMILES | m | σ/Å | ε/k/K | μ/D | κ AB | ε AB/k/K |
|---|---|---|---|---|---|---|---|
| Butane | CCCC | 2.3 | 3.7 | 224 | |||
| Hexane | CCCCCC | 2.9 | 3.9 | 244 | |||
| Octane | CCCCCCCC | 3.6 | 3.9 | 248 | |||
| 1-Butanol | CCCCO | 3.2 | 3.5 | 247 | 0.006 | 2409 | |
| 1-Hexanol | CCCCCCO | 3.7 | 3.6 | 258 | 0.005 | 2498 | |
| 1-Ethoxypentane | CCCCCOCC | 3.9 | 3.7 | 236 | 2.5 | ||
| 1,2-Diethoxymethane | CCOCOCC | 3.6 | 3.5 | 231 |
The ESI† presents the receiver operating characteristic (ROC) curves of the association and polarity likelihood parameters, illustrating the trade-off between true positives and false positives. SPTPC-SAFT achieves a 100% true positive rate for associating molecules and approximately a 90% true positive rate for polarity. Given that we use classification in the normally continuous spectrum for polarity, a 100% true positive rate is not expected. Therefore, our model architecture enables SPTPC-SAFT to accurately learn when molecules exhibit associating or polar interactions and assign appropriate pure component parameters.
3.3 Comparison to homosegmented GC method and recent ML models
To assess the predictive capabilities of our method, we compare it to the homo-segmented group contribution method proposed by Sauer et al.,6 in the following called GC-Sauer. The group contribution method by Sauer et al.6 calculates the PC-SAFT parameters from the contributions of individual functional groups. We define two sets of molecules that differ in the breadth of the molecular space: The interpolation set contains molecules that belong to the chemical families that Sauer et al.6 used to parameterize the GC method (branched alkanes, alkenes, 1-alkynes, alkylbenzenes, alkylcyclohexanes, alkylcyclopentanes, ethers, aldehydes, formates, esters, ketones, 1-alcohols, and 1-amines) but only containing a maximum of one functional group as in Sauer et al.6 The interpolation set likely contains many of the molecules on which the GC method was originally fitted. Thus, the GC-Sauer method enjoys a maximum advantage in the comparison. The extrapolation set contains molecules outside of these chemical families that can still be fragmented into the groups defined by Sauer et al.6 but that do not contain more than one polar or associating group to not extrapolate from the GC-Sauer method to far. The extrapolation set contains important molecules like cyclohexylamine or phenyl acetate that are difficult to describe accurately for GC methods. In total, the interpolation set contains 256 molecules and the extrapolation set contains 67 molecules.The comparison between SPTPC-SAFT and GC-Sauer on the two sets of molecules indicates a substantial difference between the performance of the GC-Sauer and SPTPC-SAFT methods when extrapolating beyond the interpolation set (Fig. 9): while the GC method performs decently within the interpolation set, with a mean APD of 12.8% compared to 7.3% of SPTPC-SAFT for the vapor pressure, it falls short when extrapolating to more complex molecules, resulting in a much larger mean APD of 48.0% compared to 11.1% for SPTPC-SAFT. Similar performance benefits are observed for SPTPC-SAFT in predicting liquid densities. Here, for the interpolation set, SPTPC-SAFT has an mean APD of 4.0% compared to 6.4% of GC-Sauer and, for the extrapolation set, 3.5% compared to 11.9% of GC-Sauer.
Our results demonstrate that the much simpler GC method of Sauer et al.6 performs reasonably well for molecules similar or equal to those to which it was parameterized, but extrapolating capabilities are limited for more complex molecules. To cover a more comprehensive molecular space without manually defining an extensive set of (potentially higher order) groups, an approach that captures the complexities of molecules, like SPTPC-SAFT, is required. Moreover, even compared to more complex and recent machine learning approaches SPTPC-SAFT compares favorably.
Compared to the recently published methods by Felton et al.33 and Habicht et al.,32 SPTPC-SAFT compares favorably. However, since there is no consistent validation set used across the studies, there is some uncertainty in this discussion. The reported average relative percentage errors in vapor pressures by Felton et al.33 are 39% based on a similar dataset as our clean dataset, compared to SPTPC-SAFT mean APD of 13.5%. Habicht et al.32 report average relative percentage deviations below 20% for many molecular families, however, limited to non-polar, non-associating molecules for which SPTPC-SAFT has a mean deviation of 10%. Overall, the better performance of SPTPC-SAFT might lie in the direct training on experimental data and not on previously fitted PC-SAFT parameters. Thus, SPTPC-SAFT is able to use a larger amount of data points and avoids error accumulation via the additional regression step.
3.4 Differentiation of stereoisomers
Stereoisomers are molecules that have the same molecular formula and constitution but different structural arrangements due to differently arranged bonds. Although these subtle structural differences might appear insignificant, they can impact the properties of isomers substantially in some cases. GC methods often struggle to capture these differences in stereoisomers as they require large higher-order groups to differentiate between them. However, SPTPC-SAFT utilizes isomeric SMILES as input, enabling the model to distinguish between stereoisomers. Unfortunately, our validation data contains only 35 pairs of stereoisomers, the majority of which exhibit no significant difference in vapor pressure. Therefore, we assess the prediction of stereoisomers based on individual examples and a comprehensive statistical analysis has to be performed as soon as more data on stereoisomers is available.For four example isomere pairs, i.e., the cis and trans isomers of 1,1,1,4,4,4-hexafluorobutene, stilbene, 2-hexene, and 2-hexanedinitril, the predicted vapor pressure is shown in Fig. 10. Due to the different polarity, the isomers of 1,1,1,4,4,4-hexafluorobutene and stilbene have measurably different vapor pressures. SPTPC-SAFT is able to predict the trend in vapor pressures, which is remarkable considering that the majority of isomers in the training data is similar to 2-hexene which shows no significant difference between the two isomers. However, 2-hexenedinitrile presents a challenge for the model, as it fails to distinguish between isomers even though there is a difference in vapor pressure between the cis and trans versions. When and why SPTPC-SAFT fails in distinguishing specific isomers should be subject to further research. We observed some instances within our training data of likely mislabeling between isomers, which may impede the model's performance. Overall, the results concerning stereoisomer differentiation are encouraging, but more and better data on stereoisomers is required to unlock the full capability of the model.
 | ||
| Fig. 10 Pressure–temperature plots of the isomer pairs (a) 1,1,1,4,4,4-hexafluorobutene, (b) stilbene, (c) 2-hexene and (d) 2-hexenedinitril. | ||
3.5 Publication of predicted pure component parameters
While the current SPTPC-SAFT model is efficient and straightforward to set up, executing machine learning models can still present a barrier to entry when only single components are of interest. To enhance the accessibility of our model, we have predicted pure component parameters of PC-SAFT for millions of components, as we have previously with a set of 100 million NRTL parameters.34 Predicted pure component parameters of PC-SAFT are available for all 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 molecules contained in our training set.
645 molecules contained in our training set.
By making these pre-computed pure component parameters available, we aim to facilitate broader adoption and utilization of the PC-SAFT equation of state across various applications and allow for exploring vast molecular spaces.
4 Conclusion
In this study, we introduce the machine-learning model SPTPC-SAFT, which can predict thermodynamic equilibrium properties using the PC-SAFT equation of state and the corresponding pure component parameters of PC-SAFT from the SMILES code of a molecule. SPTPC-SAFT is a modification of the SMILES-to-Properties-Transformer (SPT)11 and overcomes challenges posed by the complexity of integrating the PC-SAFT equation of state into machine-learning models.Our model demonstrates excellent predictive performance on a validation set of 870 components, achieving a mean APD of 13.5% for vapor pressures and 3% for liquid densities. Remarkably, 99.6% of the predictions fall within a factor of 2, indicating a minimal presence of outliers.
Compared to the homo-segmented group contribution method of PC-SAFT by Sauer et al.,6 our SPTPC-SAFT model provides significantly higher quality predictions for both vapor pressures and liquid densities and compares favorably to more recent ML models. In particular, for more complex molecules, the prediction accuracy of SPTPC-SAFT is four times higher than the group contribution method. Moreover, our model can differentiate between stereoisomers, highlighting its potential for improved accuracy in predicting the properties of subtle molecular effects. We believe that SPTPC-SAFT offers a versatile and robust approach for predicting equilibrium thermodynamic properties and the corresponding pure component parameters of PC-SAFT, allowing for applications in thermodynamics, process engineering, and material science.
However, the current formulation for the prediction of dipole moments only allows for the assignment of dipole moments on a physical basis, but not the prediction of its magnitude. Furthermore, a more in-depth study of the relationship between amount and quality of the training data and the final-prediction quality as well as the uncertainty of predictions towards the data are still lacking and will be part of future research.
To make our model more accessible to researchers and industry professionals, we have precomputed pure component parameters of PC-SAFT for a large number of components.
The SPTPC-SAFT model presents a significant advancement in the prediction of equilibrium properties and corresponding pure component parameters of PC-SAFT. By leveraging machine learning techniques, our model offers improved accuracy in predicting the properties of various molecules while being capable of handling complex molecular structures and subtle differences in isomers. The availability of precomputed pure component parameters of PC-SAFT will further facilitate the adoption of our model and enable its use in a broad range of research and industry applications.
Data availabilty
The training data is licensed from a third party, and we have no permission to publish it. https://www.ddbst.com/. All code was made available for the review process. We publish around 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 PC-SAFT parameters predicted by our model in the ESI† of this publication https://arxiv.org/abs/2309.12404.
000 PC-SAFT parameters predicted by our model in the ESI† of this publication https://arxiv.org/abs/2309.12404.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. W. and A. B. acknowledge funding by NCCR Catalysis, a National Centre of Competence in Research funded by the Swiss National Science Foundation, grant number 180544. P. R. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grant number 497566159.References
- A. R. Katritzky, V. S. Lobanov and M. Karelson, QSPR: the correlation and quantitative prediction of chemical and physical properties from structure, Chem. Soc. Rev., 1995, 24(4), 279, 10.1039/CS9952400279.
- L. D. Hughes, D. S. Palmer, F. Nigsch and J. B. O. Mitchell, Why are some properties more difficult to predict than others? A study of QSPR models of solubility, melting point, and Log P, J. Chem. Inf. Model., 2008, 48(1), 220–232, DOI:10.1021/ci700307p.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE J., 1975, 21(6), 1086–1099, DOI:10.1002/aic.690210607.
- J. Marrero and R. Gani, Group-contribution based estimation of pure component properties, Fluid Phase Equilib., 2001, 183–184, 183–208, DOI:10.1016/S0378-3812(01)00431-9.
- A. Shivajirao Hukkerikar, B. Sarup, A. ten Kate, J. Abildskov, G. Sin and R. Gani, Group-contribution+ (GC+) based estimation of properties of pure components: Improved property estimation and uncertainty analysis, Fluid Phase Equilib., 2012, 321, 25–43, DOI:10.1016/j.fluid.2012.02.010.
- E. Sauer, M. Stavrou and J. Gross, Comparison between a Homo- and a Heterosegmented Group Contribution Approach Based on the Perturbed-Chain Polar Statistical Associating Fluid Theory Equation of State, Ind. Eng. Chem. Res., 2014, 53(38), 14854–14864, DOI:10.1021/ie502203w.
- A. Klamt, Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena, J. Phys. Chem., 1995, 99(7), 2224–2235, DOI:10.1021/j100007a062.
- S.-T. Lin and I. Stanley, Sandler. A Priori Phase Equilibrium Prediction from a Segment Contribution Solvation Model, Ind. Eng. Chem. Res., 2002, 41(5), 899–913, DOI:10.1021/ie001047w.
- G. R. Schleder, A. C. M. Padilha, C. Mera Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, J. Phys.: Mater., 2019, 2(3), 032001, DOI:10.1088/2515-7639/ab084b.
- F. Jirasek and H. Hasse, Machine Learning of Thermophysical Properties, Fluid Phase Equilib., 2021, 549, 113206, DOI:10.1016/j.fluid.2021.113206.
- B. Winter, C. Winter, J. Schilling and A. Bardow, A smile is all you need: predicting limiting activity coefficients from SMILES with natural language processing, Digital Discovery, 2022, 1(6), 859–869, 10.1039/D2DD00058J.
- E. I. Sanchez Medina, S. Linke, M. Stoll and K. Sundmacher, Graph neural networks for the prediction of infinite dilution activity coefficients, Digital Discovery, 2022, 1(3), 216–225, 10.1039/D1DD00037C.
- J. G. Rittig, K. B. Hicham, A. M. Schweidtmann, M. Dahmen and A. Mitsos, Graph neural networks for temperature-dependent activity coefficient prediction of solutes in ionic liquids, Comput. Chem. Eng., 2023, 171, 108153, DOI:10.1016/j.compchemeng.2023.108153 . https://www.sciencedirect.com/science/article/pii/S0098135423000224.
- Y. Liu, W. Hong and B. Cao, Machine learning for predicting thermodynamic properties of pure fluids and their mixtures, Energy, 2019, 188, 116091, DOI:10.1016/j.energy.2019.116091.
- V. Venkatasubramanian, The promise of artificial intelligence in chemical engineering: Is it here, finally?, AIChE J., 2019, 65(2), 466–478, DOI:10.1002/aic.16489.
- J. Ding, N. Xu, M. T. Nguyen, Q. Qi, Y. Shi, Y. He and Q. Shao, Machine learning for molecular thermodynamics, Chin. J. Chem. Eng., 2021, 31, 227–239, DOI:10.1016/j.cjche.2020.10.044.
- A. S. Alshehri, A. K. Tula, F. You and R. Gani, Next generation pure component property estimation models: With and without machine learning techniques, AIChE J., 2022, 68(6), 2021, DOI:10.1002/aic.17469.
- D.-Yu Peng and D. B. Robinson, A New Two-Constant Equation of State, Ind. Eng. Chem. Fundam., 1976, 15(1), 59–64, DOI:10.1021/i160057a011.
- G. Soave, Equilibrium constants from a modified Redlich-Kwong equation of state, Chem. Eng. Sci., 1972, 27(6), 1197–1203, DOI:10.1016/0009-2509(72)80096-4.
- W. Wagner and A. Pruß, The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, J. Phys. Chem. Ref. Data, 2002, 31(2), 387–535, DOI:10.1063/1.1461829.
- R. Span and W. Wagner, A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple–Point Temperature to 1100 K at Pressures up to 800 MPa, J. Phys. Chem. Ref. Data, 1996, 25(6), 1509–1596, DOI:10.1063/1.555991.
- R. Span, E. W. Lemmon, R. T. Jacobsen, W. Wagner and A. Yokozeki, A Reference Equation of State for the Thermodynamic Properties of Nitrogen for Temperatures from 63.151 to 1000 K and Pressures to 2200 MPa, J. Phys. Chem. Ref. Data, 2000, 29(6), 1361–1433, DOI:10.1063/1.1349047.
- O. Kunz and W. Wagner, The GERG-2008 Wide-Range Equation of State for Natural Gases and Other Mixtures: An Expansion of GERG-2004, J. Chem. Eng. Data, 2012, 57(11), 3032–3091, DOI:10.1021/je300655b.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, New reference equation of state for associating liquids, Ind. Eng. Chem. Res., 1990, 29(8), 1709–1721, DOI:10.1021/ie00104a021.
- J. Gross and G. Sadowski, Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules, Ind. Eng. Chem. Res., 2001, 40(4), 1244–1260, DOI:10.1021/ie0003887.
- F. Llovell, J. C. Pàmies and L. F. Vega, Thermodynamic properties of Lennard-Jones chain molecules: renormalization-group corrections to a modified statistical associating fluid theory, J. Chem. Phys., 2004, 121(21), 10715–10724, DOI:10.1063/1.1809112.
- T. Lafitte, A. Apostolakou, C. Avendaño, A. Galindo, C. S. Adjiman, E. A. Müller and G. Jackson, Accurate statistical associating fluid theory for chain molecules formed from Mie segments, J. Chem. Phys., 2013, 139(15), 154504, DOI:10.1063/1.4819786.
- F. Shaahmadi, S. Smith, C. E. Schwarz, A. J. Burger and J. T. Cripwell, Group-contribution SAFT equations of state: A review, Fluid Phase Equilib., 2023, 565, 113674, DOI:10.1016/j.fluid.2022.113674.
- R. Privat and J.-N. Jaubert, The state of the art of cubic equations of state with temperature-dependent binary interaction coefficients: From correlation to prediction, Fluid Phase Equilib., 2023, 567, 113697, DOI:10.1016/j.fluid.2022.113697.
- R. Gani, Group contribution-based property estimation methods: advances and perspectives, Curr. Opin. Chem. Eng., 2019, 23, 184–196, DOI:10.1016/j.coche.2019.04.007.
- H. Matsukawa, M. Kitahara and K. Otake, Estimation of pure component parameters of PC-SAFT EoS by an artificial neural network based on a group contribution method, Fluid Phase Equilib., 2021, 548, 113179, DOI:10.1016/j.fluid.2021.113179.
- J. Habicht, C. Brandenbusch and G. Sadowski, Predicting PC-SAFT pure-component parameters by machine learning using a molecular fingerprint as key input, Fluid Phase Equilib., 2023, 565, 113657, DOI:10.1016/j.fluid.2022.113657.
- K. Felton, L. Rasßpe-Lange, J. Rittig, K. Leonhard, A. Mitsos, J. Meyer-Kirschner, C. Knösche, and A. Lapkin, ML-SAFT: A machine learning framework for PCP-SAFT parameter prediction, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-j1z06.
- B. Winter, C. Winter, T. Esper, J. Schilling and A. Bardow, SPT-NRTL: A physics-guided machine learning model to predict thermodynamically consistent activity coefficients, Fluid Phase Equilib., 2023, 568, 113731, DOI:10.1016/j.fluid.2023.113731.
- J. Gross and J. Vrabec, An equation-of-state contribution for polar components: Dipolar molecules, AIChE J., 2005, 52(3), 1194–1204, DOI:10.1002/aic.10683.
- T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever, and D. Amodei, Language Models are Few-Shot Learners, in Advances in Neural Information Processing Systems, ed. H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, and H. Lin, Curran Associates, Inc, 2020, vol. 33, pp. 1877–1901, https://proceedings.neurips.cc/paper_files/paper/2020/file/1457c0d6bfcb4967418bfb8ac142f64a-Paper.pdf Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. ukasz Kaiser, and I. Polosukhin, Attention is All you Need, in Advances in Neural Information Processing Systems, ed. I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, Curran Associates, Inc, 2017, vol. 30, https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf Search PubMed.
- D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Model., 1988, 28(1), 31–36, DOI:10.1021/ci00057a005.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, Molecular Transformer: A Model for Uncertainty-Calibrated Chemical Reaction Prediction, ACS Cent. Sci., 2019, 5(9), 1572–1583, DOI:10.1021/acscentsci.9b00576.
- S. Honda, S. Shi, and H. R. Ueda, SMILES Transformer: Pre-trained Molecular Fingerprint for Low Data Drug Discovery, arXiv, 2019, preprint, arXiv:1911.04738, DOI:10.48550/arXiv.1911.04738, https://arxiv.org/pdf/1911.04738v1.
- S. Lim and Y. O. Lee, Predicting Chemical Properties using Self-Attention Multi-task Learning based on SMILES Representation, in 2020 25th International Conference on Pattern Recognition (ICPR), IEEE, 2021, pp. 3146–3153, ISBN 978-1-7281-8808-9, DOI:10.1109/ICPR48806.2021.9412555.
- H. Kim, J. Na and W. B. Lee, Generative Chemical Transformer: Neural Machine Learning of Molecular Geometric Structures from Chemical Language via Attention, J. Chem. Inf. Model., 2021, 61(12), 5804–5814, DOI:10.1021/acs.jcim.1c01289.
- S. Wang, Y. Guo, Y. Wang, H. Sun, and J. Huang, SMILES-BERT, in Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, ed. X. Shi, M. Buck, J. Ma, and P. Veltri, ACM, New York, NY, USA, 2019, pp. 429–436, ISBN 9781450366663, DOI:10.1145/3307339.3342186.
- E. Jannik Bjerrum, SMILES Enumeration as Data Augmentation for Neural Network Modeling of Molecules, 2017, https://arxiv.org/pdf/1703.07076.
- G. Landrum, P. Tosco, B. Kelley, Ric, D. Cosgrove, sriniker, gedeck, R. Vianello, NadineSchneider, E. Kawashima, Dan N, G. Jones, A. Dalke, B. Cole, M. Swain, S. Turk, AlexanderSavelyev, A. Vaucher, M. Wójcikowski, I. Take, D. Probst, K. Ujihara, V. F. Scalfani, guillaume godin, J. Lehtivarjo, A. Pahl, R. Walker, F. Berenger, jasondbiggs and strets123, rdkit/rdkit: 2023_03_2 (q1 2023) release, 2023, https://zenodo.org/records/3732262 Search PubMed.
- J. Alammar. The Illustrated Transformer, 2018. https://jalammar.github.io/illustrated-transformer/.
- P. Rehner, G. Bauer and J. Gross, FeOs : An Open-Source Framework for Equations of State and Classical Density Functional Theory, Ind. Eng. Chem. Res., 2023, 62(12), 5347–5357, DOI:10.1021/acs.iecr.2c04561.
- P. Rehner, A. Bardow and J. Gross, Modeling Mixtures with PCP-SAFT: Insights from Large-Scale Parametrization and Group-Contribution Method for Binary Interaction Parameters, Int. J. Thermophys., 2023, 44, 179, DOI:10.1007/s10765-023-03290-3.
- P. Rehner and G. Bauer, Application of Generalized (Hyper-) Dual Numbers in Equation of State Modeling, Front. Chem. Eng., 2021, 3, 758090, DOI:10.3389/fceng.2021.758090.
- Dortmund Datenbank, 2022, https://www.ddbst.com/.
- G. H. Thomson, The DIPPR databases, Int. J. Thermophys., 1996, 17(1), 223–232, DOI:10.1007/BF01448224.
- D. Riccardi, Z. Trautt, A. Bazyleva, E. Paulechka, V. Diky, J. W. Magee, A. F. Kazakov, S. A. Townsend and C. D. Muzny, Towards improved fairness of the thermoml archive, J. Comput. Chem., 2022, 43(12), 879–887, DOI:10.1002/jcc.26842.
- T. Esper, G. Bauer, P. Rehner and J. Gross, Pcp-saft parameters of pure substances using large experimental databases, Ind. Eng. Chem. Res., 2023, 62(37), 15300–15310, DOI:10.1021/acs.iecr.3c02255.
- Y. Chung, F. H. Vermeire, H. Wu, P. J. Walker, M. H. Abraham and W. H. Green, Group contribution and machine learning approaches to predict abraham solute parameters, solvation free energy, and solvation enthalpy, J. Chem. Inf. Model., 2022, 62(3), 433–446, DOI:10.1021/acs.jcim.1c01103.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00077c |
| This journal is © The Royal Society of Chemistry 2025 |