Predicting mechanical properties of non-equimolar high-entropy carbides using machine learning

Abstract

High-entropy carbides (HECs) have garnered significant attention due to their unique mechanical properties. However, the design of novel HECs has been limited by extensive trial-and-error strategies, along with insufficient knowledge and computational capabilities. In this work, the intrinsic correlations between elements in the high-dimensional compositional space of HECs are investigated using high-throughput density functional theory calculations and two machine learning models, which enable us to predict the Young's modulus, hardness and wear resistance with only a chemical formula provided. Our models demonstrate a low root mean square error (11.5 GPa) and mean absolute error (9.0 GPa) in predicting the elastic modulus of HECs with arbitrary non-equimolar compositions. We further established a database of 566 370 HECs and identified 15 novel HECs with the best mechanical properties. Our models can rapidly explore the mechanical properties of HECs with descriptor–property correlation analysis, and hence provide an efficient method for accelerating the design of non-equimolar high-entropy materials with desired performance.

---

1 Introduction

High-entropy carbides (HECs), emerging as a new class of ceramic materials, have attracted increasing attention in recent years owing to their extraordinary mechanical properties,¹ corrosion resistance,² radiation resistance³ and wear resistance,⁴ which make them good candidates for challenging environment applications such as nuclear reactors, jet engines, cutting tools and aerospace.^5–9 The genesis of HECs can be traced back to high-entropy alloys (HEAs),^10,11 following the concept of ‘configurational entropy stabilized single phase’, composed of four or more transition metals and carbon atoms. The transition metals occupy the cationic sites in the crystal maintaining a compositional range between 5% and 35 at%, while the carbon atoms occupy the anionic sites. Compared with transition metal carbides, the mechanical properties of HECs can be significantly enhanced due to severe lattice distortion and the ‘high entropy effect’,¹² in some cases, can even surpass their rule of mixture (ROM) value by up to 50%.^13,14 The vast compositional space of HECs provides a wide range of possibilities for performance control, and it also introduces great challenges in their design and fabrication due to the time-consuming and expensive nature of traditional “trial and error” experiments and computational methods. Advanced techniques should be employed to accelerate the exploration of the compositional space of high-entropy ceramics, especially to elucidate the intrinsic correlations among the elements, with the aim of optimizing their performance.

Recently, Machine Learning (ML) has achieved significant success in predicting complex high-entropy materials.^14–18 By training models on existing data with specified properties and compositions, novel materials can be efficiently predicted prior to their physical synthesis. Zhang et al.¹⁴ used artificial neural network(ANN) and support vector machine (SVM) models to identify single-phase HECs and evaluated the single-phase probabilities of 90 HECs that have not yet been experimentally reported, with a prediction accuracy as high as 98.2%. Meng et al.¹⁹ used high-throughput synthesis and calculations combined with ML methods to identify 22 phase-forming ability descriptors for novel HECs, achieving a verification accuracy of at least 25.3% higher than previously reported, which provides theoretical guidance for discovering HECs. Tang et al.²⁰ proposed a ML strategy based on bond parameters (bond order, bond ionicity, and bond length) to explore new HECs with excellent mechanical properties, and the mean absolute error (MAE) and R² of their model were 32.2 GPa and 0.84. Zhou et al.²¹ developed three ML models (RF, SVR and ANN) to predict the Young's modulus and hardness of various HECs, with MAE of only 15.3 GPa and 1.1 GPa, showing high prediction accuracy. Although ML algorithms show promising predictive potential in exploring the compositional space of HECs, most research still concentrates on the prediction of single-phase formation capabilities, with few studies on mechanical property prediction. Moreover, training ML models for prediction of mechanical properties usually requires many complicated structure-based descriptors, which are inaccessible for unknown new HECs, and it is also important to enhance the generalization ability of ML models to adapt for the prediction of non-equimolar HEC systems.

The goal of this study is to leverage the power of ML methods to explore the compositional space of HECs, understand the relationships and patterns within the elements, and predict the mechanical properties of unexplored HECs with extraordinary mechanical properties to enable composition optimization screening. Designing systems capable of comprehending and mapping the vast chemical space of HECs is an ongoing challenge.²² The key to performance lies in the interaction between elements. In traditional materials, correlations among elements can be illustrated through phase diagrams, where each point in the phase space represents a unique combination of elemental composition and specific properties. For the domain of high-dimensional space corresponding to multi-component HECs, traditional methods struggle to capture all points within the entire space, while in ML, the complex relationships inherent in high-dimensional data present challenges to the generalization ability of models, as the distribution characteristics of training data may differ from unknown data. A key innovation of our approach is the ability to predict the mechanical properties of arbitrary non-equimolar HECs from binary carbides, ternary carbides and quaternary equimolar HECs in the absence of complex structural information and density functional theory (DFT) calculation results, with only a chemical formula provided, demonstrating the great potential of machine learning in complex materials design.

In this work, we employed two algorithms, deep learning and random forest (RF), to predict the mechanical properties such as Young's modulus (E), bulk modulus (B), and hardness (H) of HECs containing nine types of transition metal elements (Ta, Zr, Hf, V, Nb, Ti, Mo, W, and Cr). With the trained ML models, we have established a database containing the mechanical properties of 566 370 HECs, including E, H, etc., and identified 15 compositions with superior mechanical properties. Our results demonstrate the feasibility of advanced ML techniques in learning potential correlations and patterns among elements in high-dimensional space, providing a convenient approach for discovering novel equimolar and non-equimolar HECs with desirable mechanical properties.

2 Methods

2.1 Composition selection

In order to establish a more comprehensive and generalizable ML model and elucidate the intrinsic correlation patterns of elements in HECs, we constructed a dataset of 495 carbides containing nine transition metal elements (“Ta”, “Zr”, “Hf”, “V”, “Nb”, “Ti”, “Mo”, “W”, and “Cr”) for ML model training, which includes 9 monocarbides, 108 binary carbides, 252 ternary carbides and 126 equimolar quaternary HECs. Simultaneously, 123 non-equimolar HECs were established to evaluate the generalization ability and prediction accuracy of the ML model when extended to predict HECs with arbitrary compositions. High-throughput density functional theory (HT-DFT) calculations were employed to obtain the corresponding mechanical properties.

2.2 HT-DFT calculation

The Vienna Ab initio Simulation Package (VASP) code²³ was used for all geometry optimization and elastic property calculations. The projector augmented wave (PAW) method was employed to describe the ion–electron interactions and the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA) was adopted to deal with the exchange and correlation functional. To ensure the accuracy of elastic property calculations, the energy cutoff was set to 650 eV with a 9 × 9 × 9 Monkhorst–Pack k-point grid used for convergence after careful testing. The tetrahedron method with Blöchl corrections (ismear = −5) was employed to get accurate total energy and stress. The energy convergence criterion was set to 10⁻⁷ eV per atom, and the maximum force per atom should be less than 10⁻³ eV Å⁻¹.

All these structures used for HT-DFT calculations maintained a single-phase rock salt structure with transition metal atoms randomly occupying cationic sites and carbon atoms occupying anionic sites, which were generated using the Python Materials Genomics (Pymatgen) package²⁴(a schematic diagram of the crystal structure is shown in ESI S1†). The use of small unit cells can considerably improve the computational performance. Additionally, we also compared our results with published experimental data^25,26 to verify the accuracy of DFT calculations. Koval et al.²⁷ and Liu et al.²⁸ also confirm the reliability of elastic property predictions using small unit cells.

2.3 Mechanical properties

For cubic lattice, there are three independent elastic constants C₁₁, C₁₂ and C₄₄, which were obtained by applying a set of independent directional normal and shear strains to the structures, and then calculating the corresponding energy changes to fit the elastic constant matrix. The mechanical stability of these structures was evaluated using the Born stability criteria: C₁₁ > 0, C₄₄ > 0, C₁₁ − C₁₂ > 0, C₁₁ + 2C₁₂ > 0.²⁹ The polycrystalline Young's modulus (E), bulk modulus (B), and shear modulus (G) were estimated from the elastic constant by the Voigt–Reuss–Hill method described as:

E = 9BG/(3B + G)

B = (B_v + B_R)/2

G = (G_v + G_R)/2

B_v = B_R = (C₁₁ + 2C₁₂)/3

G_v = (C₁₁ − C₁₂ + 3C₄₄)/5

G_R = 5C₄₄(C₁₁ − C₁₂)/4C₄₄ + (C₁₁ − C₁₂)

where B_v and G_v are the bulk modulus and shear modulus calculated by the Voigt approximation method, and B_R and G_R are the bulk modulus and shear modulus calculated by the Reuss approximation method.

In the context of focusing solely on elastic responses, without considering plastic deformation and defects, the Vickers hardness was approximated from the elastic modulus as follows:³⁰H_V = 2(k²G)^0.585 − 3; k = G/B.

2.4 Machine learning model

The Random Forest (RF) model and CrabNet (Compositionally Restricted Attention-Based Network)^22,31 were both used to predict the mechanical properties of HECs. CrabNet is an innovative attention-based deep neural network model specifically designed for property prediction and material discovery in materials science. The multi-head self-attention mechanism is employed to model the complex interactions between elements, enabling it to dynamically adjust the weights of each element and automatically focus on the most relevant components of the input for making predictions, which can better capture the impact of compositions on their properties and effectively improve prediction accuracy. For the CrabNet model, the “elasticity0” transfer setting was used for modulus predictions, where the lower layers of the network were frozen to retain learned chemical relationships, and the final layers were retrained on the training set to optimize mechanical property predictions.

To avoid sampling bias caused by randomness and ensure consistency in the sample distribution between the training and test sets, a random sampling method was employed to split the data for both the RF and CrabNet models, with 80% of the data allocated to the training set and the remaining 20% to the test set. The RF model was optimized with the following parameters: n_estimators = 300, random_state = 1, min_samples_split = 5, min_samples_leaf = 1, and the number of features considered for each split was set to the square root of the total number of features. A 10-fold cross validation was employed. The mean absolute error (MAE), mean squared error (MSE), and R² scores were used to evaluate the performance of the RF model and CrabNet model.

2.5 Featurization schemes

CrabNet employs an end-to-end learning approach that directly takes the chemical compositions as input by using the atomic numbers and fractions of their constituent elements, without relying on feature descriptors. Mat2vec element embeddings serve as the default source of chemical information for each element and fractional amounts were used to obtain fractional embeddings, which leads to the generation of separate element embedding matrices and fractional embedding matrices.^31,32 The RF model requires predefined feature descriptors, so we adopted composition-based feature vectors (CBFVs) to avoid the use of complex structural descriptors. CBFVs are descriptive statistics (mean, range, sum and variance) of the composition elements, which have been successfully applied in materials research.^33–35 For the RF model, we revised the previous complicated input features, adopting a series of CBFVs^35–38—Jarvis, Magpie, Mat2vec, Onehot, Oliynyk, and random—elemental descriptors as substitutes to eliminate the impact of structural information, achieving the prediction of mechanical properties only from the perspective of composition.

3 Results and discussion

3.1 Statistical analysis

Fig. 1a shows the correlation between the predicted Young's modulus values for 450 carbides using the ROM method and DFT calculations, and comparisons for bulk modulus and shear modulus are provided in ESI S4.† Although employing the ROM method for the initial estimation of various physical properties such as lattice constants, elastic modulus, and strength of multicomponent carbides is a common practice prior to experimentation, it is evident from Fig. 1a that the correlation between Young's modulus obtained via ROM and HT-DFT calculations is non-linear. The Young's modulus predicted by ROM tends to be lower than that obtained from HT-DFT, indicating that the ROM method may not be sufficiently reliable for predicting the mechanical properties of unknown HECs. Although DFT calculations may offer more credible results, the time-consuming and resource-intensive process makes ML a more efficient and accurate alternative for predicting HEC mechanical properties.

Fig. 1 (a) Comparison of ROM results and HT-DFT calculations of Young's modulus for 495 carbides (contains 9 monocarbides, 108 ternary carbides, 252 quaternary carbides and 126 equimolar quaternary high entropy carbides). The results of ROM are based on the atomic ratio summation of the Young's modulus of 9 monocarbides (TaC, ZrC, HfC, VC, NbC, TiC, MoC, WC, and CrC); (b) Influence of 9 transition metal elements in 495 carbides on Young's modulus calculated by HT-DFT (only the elemental species are counted, detailed statistics are shown in Fig. 2).

The influence of nine different transition metal elements (Ta, Zr, Hf, V, Nb, Ti, Mo, W, and Cr) on the Young's modulus of 495 carbides is shown in Fig. 1b. Each violin plot encompasses data for binary, ternary, and quaternary carbides; the median values of calculated Young's modulus reveal that Young's modulus is significantly impacted by elemental compositions. It is worth noting that carbides containing Ta and W exhibit the highest Young's modulus, indicating superior stiffness and resistance to deformation under applied stress. The following are carbides that incorporate Nb, Ti and V, which exhibit comparatively higher modulus but slightly lower than those of carbides with Ta and W. Carbides containing Hf and Mo demonstrate moderate values of Young's modulus, suggesting a decrease in stiffness compared to those mentioned previously, consistent with the results of Xia et al.³⁹ The relatively lowest elastic moduli are observed in carbides that include Zr and Cr, implying that their addition may reduce the hardness of HECs and increase the plastic deformation ability. This trend emphasizes the clear dependence of mechanical properties on specific elemental types within the carbide composition.

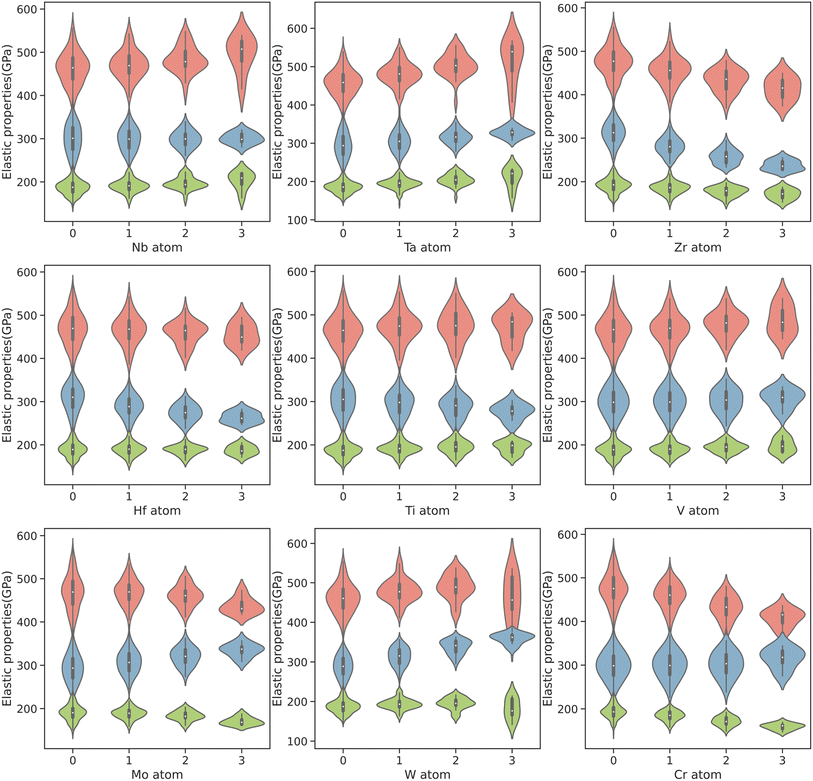
To gain a deeper understanding of the relationship between elements and mechanical properties, we further investigated the effect of different amounts of elements on the elastic modulus. Fig. 2 illustrates the effects on Young's modulus, bulk modulus and shear modulus when the content of 9 transition metal elements increases from 0 to 75 at%, respectively. The red part in the violin diagram represents the Young's modulus, the blue part represents the bulk modulus, and the green part represents the shear modulus. As the concentration of certain elements increases, elements such as Ta, Nb, Ti, and V are observed to enhance the Young's modulus in carbides. Conversely, elements such as Hf, Mo, Zr, and Cr seem to decrease their Young's modulus. Consistent with the previous analysis, higher concentrations of Ta lead to the largest increase in Young's modulus due to its ability to significantly increase the bulk and shear modulus of carbides, followed by Nb. Although increasing Nb effectively improves the shear modulus of carbides, the bulk modulus shows almost no significant increase. Ti and V provide a modest increase in the Young's modulus of carbides. Unlike V, as the concentration of Ti increases, the bulk modulus of carbides gradually decreases, with the reduction outweighing the increase in shear modulus, the Young's modulus still shows an increasing trend, which is consistent with the findings of Lu et al.⁴⁰ suggesting that the enhancement of Young's modulus of carbides may be primarily influenced by shear modulus, followed by bulk modulus. With increased concentrations of elements such as Hf, Mo, Zr, and Cr, the Young's modulus of carbides tends to decrease. The increase in Zr concentration significantly reduces the Young's modulus, bulk modulus, and shear modulus of carbides. An increase in Mo and Cr concentrations gradually increases the bulk modulus while decreasing the shear modulus and Young's modulus. Hf exhibits no significant impact on the shear modulus of carbides; however as its concentration increases, a significant reduction in bulk modulus is observed, leading to a slight decrease in Young's modulus. The influence of W on the mechanical properties deviates from the previous trends, as the bulk modulus significantly increases with W content. However, the shear modulus and Young's modulus initially increase and then decrease with increasing W content, showing optimal mechanical properties at around 50%.

Fig. 2 Correlation between 9 transition metal elements and calculated elastic properties. The red violin part represents the Young's modulus, the blue violin part represents the bulk modulus, and the green part represents the shear modulus. All statistical data are based on DFT calculation results of 495 carbides.

3.2 Model performance

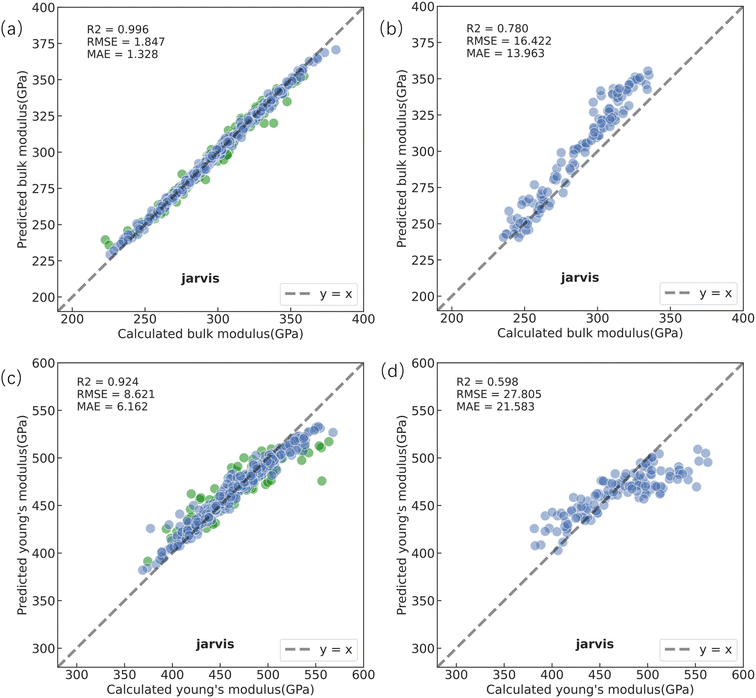
To identify the best model for predicting the mechanical properties of non-equimolar HECs (containing elements such as Ta, Zr, Hf, V, Nb, Ti, Mo, W, and Cr) based on their chemical formula, without requiring structural descriptors, we compared the prediction accuracy and generalization ability of both the RF and CrabNet models. The RF model and CrabNet model were trained on a dataset of 495 carbides, which includes 9 monocarbides, 108 binary carbides, 252 ternary carbides, and 126 equimolar quaternary HECs, and then verified on 123 non-equimolar HECs to assess their extrapolation ability in non-equimolar HECs. Six types of elemental descriptors—Jarvis, Magpie, Mat2vec, Onehot, Oliynyk, and random—were compared with the aim of avoiding complex structure-based feature descriptors and building an RF model with the highest prediction accuracy. All these elemental descriptors are generated solely from the chemical formula and can be used to describe the properties of elements. Each elemental descriptor has its unique way of encoding and representing the characteristics of elements (a detailed explanation for each elemental descriptor is provided in ESI S2†). As can be seen from Fig. 3, the test R² values of the RF models, utilizing six types of elemental descriptors, increase as the number of samples increases, indicating an improvement in prediction accuracy. The Jarvis descriptor demonstrates higher prediction accuracy in the early stages of training, suggesting that it may perform better in predictions with small sample sizes. This is attributed to the fact that the Jarvis descriptor offers a richer set of features, such as electronic structure, crystal structure, mechanical properties, and thermodynamic properties, which contribute to its superior performance in predicting mechanical properties. The RMSE and MAE of the bulk modulus prediction models decrease as the sample size increases. The RF models utilizing the one-hot and Magpie descriptors exhibit the highest RMSE and MAE, indicating the largest deviation from actual values in the prediction of bulk modulus. The models using random and Oliynyk descriptors show a slight reduction in RMSE and MAE, with their prediction accuracies being roughly equivalent. Conversely, models with the mat2vec and Jarvis descriptors result in a relatively lower MAE, and with the Jarvis descriptor's RF model achieving the lowest RMSE and the highest prediction accuracy. Therefore, we choose the Jarvis descriptor for training the RF model and predicting the bulk modulus of 123 non-equimolar HECs.

Fig. 3 The performance of predicting the bulk modulus, using 6 CBFV descriptors—Jarvis, Magpie, Mat2vec, Onehot, Oliynyk, and random—within RF models, evaluated on training data (495 carbides, including 9 monocarbides, 108 binary carbides, 252 ternary carbides, and 126 equimolar quaternary HECs) (a) the predicted R²; (b) the predicted RMSE; (c) the predicted MAE.

Fig. 4a illustrates the correlation between the RF model predictions (using the Jarvis descriptor) for the bulk modulus of 495 carbides in both the training and test datasets and the bulk modulus values calculated using DFT. The RF model achieved a coefficient of determination (R²) value exceeding 0.99 on training data and 0.96 on test data, with the root mean square error (RMSE) and mean absolute error (MAE) of 1.9 GPa and 1.3 GPa on training data, indicating that the predicted bulk modulus from the RF model closely matches the results from DFT calculations. After confirming the prediction accuracy, the trained RF model using Jarvis descriptors was employed to predict the bulk modulus for 123 non-equimolar HECs, and the results are shown in Fig. 4b. The prediction accuracy for the bulk modulus of 123 non-equimolar HECs significantly decreased compared to its performance on 495 carbides, with an R² of 0.78. Additionally, the RMSE and MAE of the model are 16.4 GPa and 14.0 GPa, respectively. As can be seen from Fig. 4b, the predicted values of the RF model are in good agreement with the DFT calculated results in the low modulus range (below 280 GPa). As the bulk modulus of carbides increases (280–360Gpa), the predicted values of the RF model are significantly higher than those of DFT calculations. Fig. 4c shows the performance of the RF model using Jarvis descriptors to predict the Young's modulus compared with DFT calculation results for 495 carbides. The model achieved an R² of 0.92 on the training set, with an RMSE of 8.6 GPa and an MAE of 6.2 GPa. On the test set, the R² dropped to 0.75, with RMSE and MAE increasing to 18.7 GPa and 13.8 GPa, indicating better accuracy on the training data but a decline on the test set. Then the trained RF model was used to predict the Young's modulus of 123 non-equimolar HECs and compared the results with DFT calculations, as shown in Fig. 4d. The predicted prediction accuracy of the RF model on the 123 non-equimolar HECs was significantly reduced, with an R² below 0.6, and an RMSE and MAE of 27.8 GPa and 21.6 GPa, respectively. The prediction error was considerably higher than that on the training data, particularly in the low modulus range (<430 GPa) and high modulus range (>530 GPa), where data points became more scattered, and the error was significantly amplified when predicting the 123 non-equimolar HECs. This may be attributed to overfitting during the RF model training, as the training dataset primarily consists of low-dimensional carbides, while the trained RF model was applied to predict the Young's modulus of 123 non-equimolar HECs, the variations in composition ratios among these non-equimolar HECs introduced more complex non-linear relationships, limiting the RF model's accuracy and generalization ability. Consequently, the RF model was unable to capture the initial correlations between elements as effectively as anticipated, leading to lower prediction accuracy for non-equimolar HECs. The prediction results for the shear modulus are provided in ESI S6.†

Fig. 4 (a) Comparison of DFT calculated bulk modulus and predicted bulk modulus for both training (blue) and test (green) datasets with the RF model using Jarvis descriptors; (b) comparison of DFT calculated bulk modulus and predicted bulk modulus for 123 non-equimolar HECs using the well-trained RF model with Jarvis descriptors; (c) comparison of DFT calculated Young's modulus and predicted Young's modulus for both training (blue) and test (green) datasets with the RF model using Jarvis descriptors; (d) comparison of DFT calculated Young's modulus and predicted Young's modulus for 123 non-equimolar HECs using the well-trained RF model with Jarvis descriptors. The dataset used to train the RF model consists of 495 carbides, including 9 monocarbides, 108 binary carbides, 252 ternary carbides, and 126 equimolar quaternary HECs. The line y = x is plotted to show the deviation from perfect predictions.

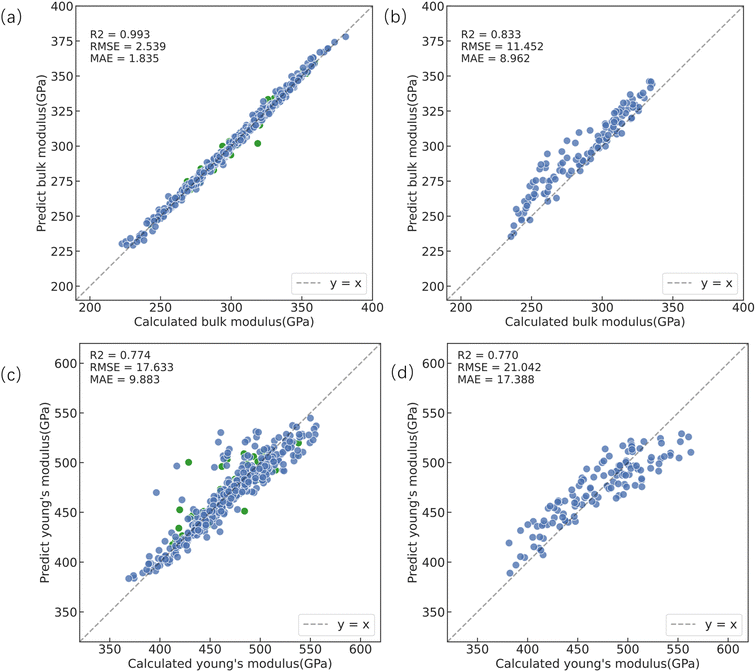
The CrabNet model was used to predict the elastic modulus of 495 carbides and 123 non-equimolar HECs to compare its prediction accuracy with that of the RF model as depicted in Fig. 5. As shown in Fig. 5a, the prediction results of the CrabNet model are quite consistent with the results of DFT calculations. The predicted R² of the bulk modulus exceeds 0.98 on both the training data and test data, with an RMSE and MAE of 2.5 GPa and 1.8 GPa, respectively, on the training set, which is comparable to the prediction accuracy of the RF model. Fig. 5b compares the prediction accuracy of the CrabNet model in predicting 123 non-equimolar HECs and the results from DFT calculations. The predicted R², RMSE and MAE for bulk modulus are 0.83, 11.5 GPa and 9.0 GPa, respectively. It is evident that the prediction accuracy of the CrabNet model is significantly improved compared to that of the RF model, particularly in overcoming the problem of overestimating values in the high bulk modulus range encountered by the RF model, and shows good agreement with the results of DFT calculations, which avoids the overfitting of the ML model and reduces the MAE and RMSE of the non-equimolar HECs in bulk modulus prediction. Considering the limited experimental data on non-equimolar high-entropy carbides (HECs), we compared the bulk modulus of 123 non-equimolar HECs using DFT calculations. The bulk modulus predicted using the CrabNet model showed excellent agreement with the DFT calculations (detailed data are provided in ESI S8†). Fig. 5c shows a comparison between the CrabNet model's predictions and the DFT calculated Young's modulus. The model achieves an R² value of 0.77 on the training data, with an RMSE of 17.6 GPa, and an MAE of 9.9 GPa. On the test data, the predicted RMSE and MAE values are 17.37 GPa and 11.72 GPa, respectively. Despite the CrabNet model showing a lower R² on the training data compared to the RF model, the higher R² on the test data indicates that the CrabNet model effectively overcomes the overfitting observed in the RF model. As depicted in Fig. 5d, the prediction performance of the CrabNet model on 123 non-equimolar HECs shows an R² of 0.77, with RMSE and MAE values of 21.0 GPa and 17.4 GPa. The CrabNet model shows consistent prediction accuracy on the training data between the 495 carbides and the 123 non-equimolar HECs, with no significant decrease in R². Additionally, there is no significant severe deviation in the high modulus range, and the RMSE and MAE for non-equimolar HECs are also lower than the RF model's results, indicating that the CrabNet model has better generalization ability than the RF model when extrapolated to quaternary non-equimolar HECs. This may be because the CrabNet model, with a neural network architecture incorporating transfer learning and self-attention mechanisms, can more effectively handle the complex non-linear relationships and data distribution variations in non-equimolar HECs. These capabilities enable it to learn correlations among elements in high-dimensional spaces, providing a powerful tool for exploring the compositional space of HECs. The prediction results for the shear modulus are provided in ESI S9.†

Fig. 5 (a) Comparison of DFT calculated bulk modulus and predicted bulk modulus for both training (blue) and test (green) datasets with the CrabNet model; (b) comparison of DFT calculated bulk modulus and predicted bulk modulus for 123 non-equimolar HECs using the well-trained CrabNet model. (c) Comparison of DFT calculated Young's modulus and predicted Young's modulus for both training (blue) and test (green) datasets with the CrabNet model; (d) comparison of DFT calculated Young's modulus and predicted Young's modulus for 123 non-equimolar HECs using the well-trained CrabNet model. The training dataset consists of 495 carbides, including 9 monocarbides, 108 binary carbides, 252 ternary carbides, and 126 equimolar quaternary HECs. The line y = x is plotted to show the deviation from perfect predictions.

3.3 Prediction of new multicomponent HECs

Compared to the RF model, the CrabNet model demonstrates superior performance in predicting the mechanical properties of unknown non-equimolar HECs. A database was then built with the predictions of the well-trained CrabNet model for 566 370 HECs based on ergodic combinations of 9 transition metal elements (Ta, Zr, Hf, V, Nb, Ti, Mo, W, and Cr). According to CrabNet's prediction results, the distributions of the Young's modulus and hardness values of the non-equimolar HECs are mapped in Fig. 6, and the points with different colors are used to distinguish the elastic strain to failure related to H/E. Fifteen types of HECs with top Young's modulus, hardness and H/E are highlighted. Ta₂₄Hf₃Nb₂Ti₃C₃₂, Ta₂₄Hf₃NbTi₄C₃₂, Ta₂₄Hf₂NbTi₅C₃₂, Ta₂₄Hf₂Nb₃Ti₃C₃₂ and Ta₂₄Hf₄NbTi₃C₃₂ exhibit the unique mechanical properties of ultra-high Young's modulus (>536 GPa), Ta₂₄Hf₅VNb₂C₃₂, Ta₂₃Hf₅VNb₃C₃₂, Ta₂₃Hf₄VNb₄C₃₂, Ta₁₉Hf₅V₄Nb₄C₃₂, and Ta₂₄Hf₄V₂Nb₂C₃₂ are found to be the hardest, with a predicted hardness greater than 29 GPa and Zr₂₄Hf₄VTi₃C₃₂, Zr₂₄HfV₄Ti₃C₃₂, Zr₁₈Hf₂V₁₁TiC₃₂, Zr₁₆Hf₄V₁₁TiC₃₂, and Zr₂₄Hf₃VTi₄C₃₂ show good wear resistance due to the high H/E (>0.06). Notably, the HECs containing more Ta elements exhibit higher Young's modulus and hardness, which is consistent with the analysis of previous DFT calculation results, suggesting that the introduction of Ta can effectively improve the mechanical properties of HECs. Contrary to expectations, high Young's modulus and high hardness did not result in high wear resistance, the H/E of HECs with the metal Zr tended to be higher than those without it, which implies that Zr can enhance the wear resistance of HECs, although previous calculations show that it has an insignificant effect on Young's modulus. The research results of Medveď et al.⁴¹ also confirmed that Zr-based composites have higher wear resistance. The addition of a small amount of the Hf element has a positive effect on increasing the Young's modulus, hardness, and wear resistance of HECs simultaneously. Similarly, a small amount of the V element enhances their hardness and wear resistance, while a small amount of the Ti element improves the Young's modulus and wear resistance. Our machine learning predictions exhibit a remarkable consistency with DFT results regarding the influence of elements on mechanical properties, which suggests that machine learning models adeptly capture complex element interactions within high-dimensional compositional spaces, enabling precise mechanical property predictions solely based on composition. This work can effectively reduce the research and development costs of HECs in the early stage of design and is expected to be applied to other high-entropy ceramic materials Fig. 6.

Fig. 6 The predicted hardness against Young's modulus with a wear resistance evaluation indicator (H/E) for 466 370 kinds of novel non-equimolar HECs by employing the well-trained CrabNet model. The blue stars mark the TOP5 HECs with the highest Young's modulus, the red stars mark the TOP5 HECs with the highest hardness, and the yellow stars mark the TOP5 HECs with the best wear resistance.

4 Conclusion

In this work, a powerful data-driven ML method for estimating the mechanical properties of HECs based on data from HT-DFT calculations is detailed and employed for the prediction of 566 370 new HECs. The findings from HT-DFT calculations suggest that the introduction of additional elements such as Ta, Nb, Ti, and V may enhance the Young's modulus of HECs, and Zr-rich HECs show good performance in wear resistance, which is reflected in the prediction results of the ML model. The RF model and the CrabNet model are both trained to predict mechanical properties for non-equimolar HECs using the compositional features. The bulk modulus prediction accuracies of the CrabNet model and the RF model with Jarvis descriptors are remarkably similar on equimolar HECs. However, for non-equimolar HECs, the CrabNet model exhibits superior performance in predicting bulk modulus, with an R² of 0.85, and RMSE and MAE values of 10.7 GPa and 8.8 GPa, respectively. For Young's modulus prediction, the CrabNet model's performance on non-equimolar HECs is significantly better than that of the RF model, with RMSE and MAE values of 21 GPa and 17.4 GPa, respectively, demonstrating better generalization ability and capacity to handle complex nonlinear relationships. The trained CrabNet model was employed to predict the mechanical properties of 566 370 HECs, including Young's modulus, hardness, and wear resistance. Fifteen novel HECs with the best mechanical properties were identified, including Ta₂₄Hf₃Nb₂Ti₃C₃₂ with the highest Young's modulus of 537.4 GPa, Ta₂₄Hf₅VNb₂C₃₂ with the highest hardness of 29.4 GPa, and Zr₂₄Hf₄VTi₃C₃₂ with the best performance in wear resistance.

Our work aims to predict the mechanical properties of materials with arbitrary compositions, focusing on the intrinsic correlations among elements and avoiding complex structure-based descriptors, using the chemical formula as input. However, the valence electron concentration (VEC) of high-entropy materials profoundly influences their mechanical properties. In future research, we hope to incorporate more features based on chemical formulae to enhance the predictive accuracy of machine learning models. Additionally, the impact of compositional variations of elements on predictive accuracy is significant, as even a small amount of addition can substantially affect mechanical properties in doping. Our research provides a new path and theoretical basis for the development of high-entropy ceramics (HECs), showing potential applications to other high-entropy materials.

Data availability

The data that support the findings of this study are openly available on GitHub, at https://github.com/ZhaoXi1209/HECs-Mechanical-Properties-prediction. The Composition-based Feature Vectors (CBFVs) used in this study were constructed using methods detailed in the repository BestPractices (https://github.com/anthony-wang/BestPractices/tree/master/notebooks). The version of the CrabNet model used in this study can be found in the CoCoCrab repository (https://github.com/AndrewFalkowski/CoCoCrab/tree/main). For additional details or to request specific datasets or codes used in the study, please contact the corresponding author at E-mail: zhao_xii@stumail.nwu.edu.cn.

Author contributions

Xi Zhao and Rui-Zhi Zhang contributed to the design and implementation of this work and analyzed the data. Shuguang Cheng and Sen Yu led the project administration and secured the funding, providing essential support for the research. Jiming Zheng assisted in data analysis and visualization. Meng Guo provided critical feedback and helped shape the research, analysis, and manuscript. All authors discussed the results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Key Research and Development Projects of Shaanxi Province (2021SF-297, 2024SF-YBXM-440, 2024SF-YBXM-442, and 2021SF-296) and the Key Industry Innovation Chain of Shaanxi (2023-LL-QY-44). RZ and MG acknowledge the support from the National Key Research and Development Program (2023YFB3003004), Shandong Provincial Key Research and Development Program (2022CXGC020106) and Taishan Youth Scholar Project of Shandong Province.

References

1. Y. Wang, T. Csanádi, H. Zhang, J. Dusza, M. J. Reece and R.-Z. Zhang, Enhanced Hardness in High-Entropy Carbides through Atomic Randomness, Adv. Theory Simul., 2020, 3, 2000111.
2. Z. Wen, Z. Tang, H. Meng, L. Zhuang, H. Yu and Y. Chu, Ultrafast synthesis of high-entropy carbides up to 3,273 K for superior oxidation resistance, Cell Rep. Phys. Sci., 2024, 5, 101821.
3. M. A. Tunes, S. Fritze, B. Osinger, P. Willenshofer, A. M. Alvarado, E. Martinez, A. S. Menon, P. Ström, G. Greaves and E. Lewin, and others, From high-entropy alloys to high-entropy ceramics: The radiation-resistant highly concentrated refractory carbide (CrNbTaTiW) C, Acta Mater., 2023, 250, 118856.
4. S. Kavak, K. G. Bayrak, M. Bellek, S. Mertdinç, F. Muhaffel, H. Gökçe, E. Ayas, B. Derin, M. L. Öveçoğlu and D. Ağaoğulları, Synthesis and characterization of (HfMoTiWZr) C high entropy carbide ceramics, Ceram. Int., 2022, 48, 7695–7705.
5. Y. Wang, Processing and properties of high entropy carbides, Adv. Appl. Ceram., 2022, 121, 57–78.
6. E. Castle, T. Csanádi, S. Grasso, J. Dusza and M. Reece, Processing and properties of high-entropy ultra-high temperature carbides, Sci. Rep., 2018, 8, 1–12.
7. S.-C. Luo, W.-M. Guo and H.-T. Lin, High-entropy carbide-based ceramic cutting tools, J. Am. Ceram. Soc., 2023, 106, 933–940.
8. Z. Cao, J. Sun, L. Meng, K. Zhang, J. Zhao, Z. Huang and X. Yun, Progress in densification and toughening of high entropy carbide ceramics, J. Mater. Sci. Technol., 2023, 161, 10–43.
9. B. Ye, T. Wen and Y. Chu, High-temperature oxidation behavior of (Hf0. 2Zr0. 2Ta0. 2Nb0. 2Ti0. 2) C high-entropy ceramics in air, J. Am. Ceram. Soc., 2020, 103, 500–507.
10. J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes, Adv. Eng. Mater., 2004, 6, 299–303.
11. B. Cantor, I. Chang, P. Knight and A. Vincent, Microstructural development in equiatomic multicomponent alloys, J. Mater. Sci. Eng. A, 2004, 375, 213–218.
12. Y. Liu, Z. Zhu, Z. Tang, H. Yu, L. Zhuang and Y. Chu, Unraveling Lattice-Distortion Hardening Mechanisms in High-Entropy Carbides, Small, 2024, 2403159.
13. P. Sarker, T. Harrington, C. Toher, C. Oses, M. Samiee, J.-P. Maria, D. W. Brenner, K. S. Vecchio and S. Curtarolo, High-entropy high-hardness metal carbides discovered by entropy descriptors, Nat. Commun., 2018, 9, 4980.
14. J. Zhang, B. Xu, Y. Xiong, S. Ma, Z. Wang, Z. Wu and S. Zhao, Design high-entropy carbide ceramics from machine learning, npj Comput. Mater., 2022, 8, 5.
15. K. Kaufmann, D. Maryanovsky, W. M. Mellor, C. Zhu, A. S. Rosengarten, T. J. Harrington, C. Oses, C. Toher, S. Curtarolo and K. S. Vecchio, Discovery of high-entropy ceramics via machine learning, npj Comput. Mater., 2020, 6, 42.
16. X. Zhao, S. Yu, J. Zheng, M. J. Reece and R.-Z. Zhang, Machine learning of carbon vacancy formation energy in high-entropy carbides, J. Eur. Ceram. Soc., 2023, 43, 1315–1321.
17. A. Y. Pak, V. Sotskov, A. A. Gumovskaya, Y. Z. Vassilyeva, Z. S. Bolatova, Y. A. Kvashnina, G. Y. Mamontov, A. V. Shapeev and A. G. Kvashnin, Machine learning-driven synthesis of TiZrNbHfTaC5 high-entropy carbide, npj Comput. Mater., 2023, 9, 7.
18. H. Meng, H. Yu, L. Zhuang and Y. Chu, Data-driven acceleration of high-entropy ceramic discovery, Matter, 2024, 7, 2646–2649.
19. H. Meng, R. Yu, Z. Tang, Z. Wen and Y. Chu, Formation ability descriptors for high-entropy carbides established through high-throughput methods and machine learning, Cell Rep. Phys. Sci., 2023, 4, 101512.
20. Y. Tang, D. Zhang, R. Liu and D. Li, Designing high-entropy ceramics via incorporation of the bond-mechanical behavior correlation with the machine-learning methodology, Cell Rep. Phys. Sci., 2021, 2, 100640.
21. Q. Zhou, F. Xu, C. Gao, D. Zhang, X. Shi, M.-F. Yuen and D. Zuo, Machine learning-assisted mechanical property prediction and descriptor-property correlation analysis of high-entropy ceramics, Ceram. Int., 2023, 49, 5760–5769.
22. A. R. Falkowski, S. K. Kauwe and T. D. Sparks, Optimizing Fractional Compositions to Achieve Extraordinary Properties, Integr. Mater. Manuf. Innov., 2021, 10, 689–695.
23. J. Hafner, Ab-initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29, 2044–2078.
24. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319.
25. M. Ma, Y. Sun, Y. Wu, Z. Zhao, L. Ye and Y. Chu, Nanocrystalline high-entropy carbide ceramics with improved mechanical properties, J. Am. Ceram. Soc., 2022, 105, 606–613.
26. B. Ye, T. Wen, M. C. Nguyen, L. Hao, C.-Z. Wang and Y. Chu, First-principles study, fabrication and characterization of (Zr0. 25Nb0. 25Ti0. 25V0. 25) C high-entropy ceramics, Acta Mater., 2019, 170, 15–23.
27. N. E. Koval, Elastic properties of the TiZrNbTaMo multi-principal element alloy studied from first principles, Intermetallics, 2019, 106, 130–140.
28. S.-Y. Liu, S. Zhang, S. Liu, D.-J. Li, Y. Li and S. Wang, Phase stability, mechanical properties and melting points of high-entropy quaternary metal carbides from first-principles, J. Eur. Ceram. Soc., 2021, 41, 6267–6274.
29. F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B, 2014, 90, 224104.
30. X.-Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19, 1275–1281.
31. A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, Compositionally restricted attention-based network for materials property predictions, npj Comput. Mater., 2021, 7, 77.
32. V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder and A. Jain, Unsupervised word embeddings capture latent knowledge from materials science literature, Nature, 2019, 571, 95–98.
33. R. J. Murdock, S. K. Kauwe, A. Y.-T. Wang and T. D. Sparks, Is Domain Knowledge Necessary for Machine Learning Materials Properties?, Integr. Mater. Manuf. Innov., 2020, 9, 221–227.
34. T. Mohanty, K. S. R. Chandran and T. D. Sparks, Machine learning guided optimal composition selection of niobium alloys for high temperature applications, APL Mach. Learn., 2023, 1, 036102.
35. A. Y.-T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo, J. Brgoch, K. A. Persson and T. D. Sparks, Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices, Chem. Mater., 2020, 32, 4954–4965.
36. Y. Yan, Z. Pei, M. C. Gao and K. Wang, Data-driven discovery of a formation prediction rule on high-entropy ceramics, Acta Mater., 2023, 253, 118955.
37. K. Choudhary, B. DeCost and F. Tavazza, Machine learning with force-field-inspired descriptors for materials: Fast screening and mapping energy landscape, Phys. Rev. Mater., 2018, 2, 083801.
38. J. Qu, Y. R. Xie, K. M. Ciesielski, C. E. Porter, E. S. Toberer and E. Ertekin, Leveraging language representation for materials exploration and discovery, npj Comput. Mater., 2024, 10, 58.
39. M. Xia, N. Lu, Y. Chen, B. Shen and X. Liang, Microstructures and mechanical properties of (Nb0. 25Mo0. 25Ta0. 25W0. 25) C and (Nb0. 2Mo0. 2Ta0. 2W0. 2Hf0. 2) C high-entropy carbide ceramics produced by arc melting, Int. J. Refract. Met. Hard Mater., 2022, 107, 105859.
40. W. Lu, L. Chen, W. Zhang, W. Su, Y. Wang, Y. Fu and Y. Zhou, Single-phase formation and mechanical properties of (TiZrNbTaMo) C high-entropy ceramics: First-principles prediction and experimental study, J. Eur. Ceram. Soc., 2022, 42, 2021–2027.
41. D. Medveď, J. Balko, R. Sedlák, A. Kovalčíková, I. Shepa, A. Naughton-Duszová, E. Bączek, M. Podsiadło and J. Dusza, Wear resistance of ZrB2 based ceramic composites, Int. J. Refract. Met. Hard Mater., 2019, 81, 214–224.

---

Footnote

† Electronic supplementary information (ESI) available: The data that support the findings of this study are openly available on GitHub, at https://github.com/ZhaoXi1209/HECs-Mechanical-Properties-prediction. See DOI: https://doi.org/10.1039/d4dd00243a

---