²⁷Al NMR chemical shifts in zeolite MFI via machine learning acceleration of structure sampling and shift prediction

Abstract

Zeolites, such as MFI, are versatile microporous aluminosilicate materials that are widely used in catalysis and adsorption processes. The location and the character of the aluminium within the zeolite framework is one of the important determinants of performance in industrial applications, and is typically probed by ²⁷Al NMR spectroscopy. However, interpretation of ²⁷Al NMR spectra is challenging, as first-principles computational modelling struggles to achieve the timescales and model complexity needed to provide reliable assignments. In this study, we deploy advanced machine learning-based methods to help bridge the time and model complexity scale by first utilizing neural network interatomic potentials to achieve significant speed-up in structure sampling compared to traditional density functional theory (DFT) approaches, and second by training regression models to cost-effectively predict the ²⁷Al chemical shifts. This allows us, for the H-MFI zeolite as a use case, to comprehensively explore the effect of various conditions relevant to catalysis, including water loading, temperature, and the aluminium concentration, on the ²⁷Al chemical shifts. We demonstrate that both water content and temperature significantly affect the chemical shift and do so in a non-trivial way that is highly T-site dependent, highlighting a need for adoption of realistic, case-specific models. We also observe that our approach is able to achieve close to quantitative agreement with relevant experimental data for such a complex zeolite as MFI, allowing for the tentative assignment of the experimental NMR peaks to specific T-sites. These findings provide a testament to the capabilities of machine learning approaches in providing reliable predictions of important spectroscopic observables for complex industrially relevant materials under realistic conditions.

---

1. Introduction

Zeolites are highly versatile microporous aluminosilicate materials widely employed in various industrial applications, including catalysis, adsorption and separation. Zeolite ZSM-5 stands out as one of the most extensively used zeolites in the petrochemical industry, where it can serve as an efficient catalyst for hydrocarbon transformations.^1,2 The catalytic activity of zeolites is primarily governed by their chemical composition, with structural features such as channel shape, accessible pore volume, and the positioning of aluminium atoms within the framework significantly influencing their catalytic behaviour.^2–4

Accurately determining the position, character or hydration-state of aluminium atoms within the zeolite framework is useful for understanding and optimizing catalytic properties.^2,4 However, traditional techniques like X-ray crystallography have inadequate sensitivity for distinguishing between aluminium and silicon atoms (or between different types of aluminium species) and thus they cannot be used for the determination of the aluminium character and siting. Additionally, especially at low Si/Al ratios, aluminium atoms may distribute unevenly across T sites, which further complicates accurate determination of aluminium positions with diffraction methods. In contrast, nuclear magnetic resonance (NMR) spectroscopy, particularly ²⁷Al NMR, has emerged as a powerful tool for probing the local environments of aluminium atoms in zeolites.^5–7 In particular, several studies have attempted to correlate experimental ²⁷Al NMR spectra with specific T-sites in the zeolite framework.^8–13 However, sizable inconsistencies in the calculated chemical shifts reported in these studies illustrate the continuing challenges faced by researchers in this field.

Interpreting solid-state NMR spectra can be challenging due to signal broadening and overlap. Theoretical calculations of NMR parameters, including those derived from first-principles methods, can provide valuable insights.^5,10,13–17 However, the computational demands of these methods, especially for the large unit cells typical of zeolites, often require adoption of various simplifications, such as disregarding water molecules and/or charge-compensating cations in the models, or representing the system using a single structure (putative global minimum) forgoing the dynamical temperature effects.^9,10 Such simplifications cast doubt over the relevance of these theoretical NMR predictions, as, for example, experimental measurements of (²⁷Al) solid-state NMR spectra in zeolites are typically performed under humid conditions¹¹ with multiple water molecules per Al center present in the framework,¹⁸ and with zeolite frameworks, such as MFI being characterized by a multitude of low-frequency vibrational modes and a plethora of low-energy structural minima,¹⁹ which will be populated at the NMR-relevant conditions.

Machine learning (ML) methods offer a promising alternative to first-principles methods by significantly accelerating either the structure sampling via machine learning potentials^20–25 or the property predictions.^26–28 In particular, various ML methods have been tested and adopted for the prediction of NMR-related properties with regression techniques such as least absolute shrinkage and selection operator regression, kernel ridge regression, and Gaussian process regression proving effective in accurately predicting chemical shielding values.^29–33 Similarly, algorithms based on neural networks have been successfully applied to determine chemical shieldings.^34,35 Recently, both regression and neural network methods have also been used to predict the shielding tensors³⁶ and the electric field gradient (EFG) tensor components for quadrupolar nuclei.^37,38 These ML techniques significantly improve the efficiency of NMR modelling, enabling adoption of more realistic models, while retaining the first-principle method accuracy.

This study leverages ML-derived interaction potentials (MLPs) to comprehensively sample the configuration space of a complex zeolite H-MFI at conditions relevant for the NMR experiment (including humidity and temperature effects), which is used both to generate a diverse reference set to train and test various ML-based regression models for prediction of ²⁷Al chemical shifts and to obtain a representative ensemble of structures for which the averaged ²⁷Al chemical shifts are evaluated cost-effectively using the herein trained regression models. In particular, in the first part, various regression based models for prediction of ²⁷Al chemical shift are trained and their accuracy and reliability are validated with respect to the reference chemical shift values obtained from density functional theory (DFT) calculations. Then, the ML-based acceleration of the simulations is exploited to comprehensively investigate how various factors affect the chemical shift, including water content, temperature, and aluminium concentration. Lastly, the predicted chemical shifts, evaluated at conditions close to the experimental setup, are compared both to previous computational studies and the existing experimental NMR spectra, allowing us to propose an alternative assignment of T-sites to experimentally observed ²⁷Al resonances. Although the investigation is focused on the H-MFI zeolite, the transferability of the best-performing kernel ridge regression (KRR) model to a broader set of zeolite frameworks is established as well as a simple strategy on how to extend it to other zeolites. For the convenience of the reader, the structure of the current work is summarized in Fig. 1.

Fig. 1 A simplified workflow used in this work for evaluating (²⁷Al) NMR chemical shielding under operating conditions using a combination of neural network potentials (NNP) for structure sampling and kernel ridge regression (KRR) for chemical shielding prediction for NNP-sampled structures. The KRR model was trained on a structural dataset selected through the farthest point sampling (FPS) algorithm and chemical shielding values computed via the DFT method. This trained KRR model then predicted chemical shielding values on snapshots from a NNP-driven molecular dynamics trajectories investigating the effect of numerous factors on the (²⁷Al) NMR shieldings. For convenience, the numbers in parentheses refer to the sections discussing in detail the particular parts of the workflow.

2. Computational details

2.1 Models

The main MFI model used throughout the work (investigating factors such as water dynamics, temperature, and the proximity of Al atoms) is an orthorhombic cell of MFI containing 12 T-sites. For discussion and comparison with experimental data and other studies (see Section 4.1), the MFI model with a monoclinic symmetry, the so-called ZSM-5, with 24 T-sites, was also considered.

The MFI structure was obtained from the IZA database.³⁹ To determine the optimal unit cell dimensions for the models with aluminium, one aluminium atom was substituted at the T12 site (Si/Al = 95). To generalize the model for both low and high water loadings, 7 water molecules were introduced into the structure. The unit cell dimensions obtained from the IZA database were uniformly scaled by factors ranging from 0.96 to 1.06, and molecular dynamics (MD) simulations were performed at a temperature of 350 K (see Section 2.2). A cubic fit of the unit cell volume versus average energy revealed the lowest energy configuration, corresponding to a unit cell volume of 5301 ų. The optimized lattice parameters were determined to be a = 20.20 Å, b = 19.85 Å, and c = 13.22 Å, and these parameters were used for all orthorhombic MFI unit cells in this study. Further details can be found in Section S1 in ESI.†

Predominantly, the models with Si/Al ratio of 95 were considered, with one silicon atom per unit cell substituted by aluminium. An acidic form of the zeolite was considered, with a hydrogen atom added to the oxygen atom bonded to the aluminium, forming a Si–O(H)–Al group, i.e., a Brønsted acid site (BAS). As mentioned above, the orthorhombic MFI unit cell includes 12 distinct crystallographic T-sites, each connected to four oxygen atoms, resulting in a total of 48 possible BAS configurations. For models with lower Si/Al ratio, the same modelling procedure was followed as for the unit cell containing one aluminium atom, where more silicon atoms were replaced by aluminium, and subsequently, a proton was added to a neighbouring oxygen to form a BAS.

For low water contents, water molecules were initialized close to the BAS. For higher water content, the sorption module in Materials Studio⁴⁰ was used with the COMPASS27 force field⁴¹ to determine the optimal placement of water molecules. The water loadings considered were 0, 1, 2, 3, and 17 water molecules per unit cell. The 17 molecules represent the number of water molecules required to completely fill the accessible pore volume at a density of 1 g cm⁻³.³⁹ This water content is consistent with experimental measurements performed by Holzinger et al.¹¹

2.2 Molecular dynamics

The molecular dynamics (MD) simulation was conducted over a period of 1 ns with a time step of 0.5 fs, with the snapshots of the system saved every 100 steps. The simulation was performed in the NVT ensemble employing the Nosé-Hoover thermostat⁴² to maintain a constant temperature of 350 K throughout the simulation. The software used for the MD simulation was the atomic simulation environment (ASE), version 3.22.1.⁴³ For interaction potentials and energy calculations, we employed a previously derived neural network-based potential (NNP)²¹ – these potentials were specifically developed for acidic zeolite systems containing water molecules and were constructed using the SchNetPack 1.0 library,⁴⁴ written in Python programming language. The reference training database for this NNP was generated at the meta-GGA DFT level (SCAN + D3(BJ)).^45–47

2.3 DFT calculation

All the DFT calculations on a subset of MFI models were carried out in the CASTEP software package⁴⁸ and employed the PBE exchange–correlation functional⁴⁹ with the plane-wave energy cutoff of 700 eV and a k-point sampling grid of 1 × 1 × 1, ensuring that the total energy was converged to within 10⁻⁸ eV per atom. The NMR tensors were computed using the GIPAW (gauge-including projector augmented-wave) method.⁵⁰

2.4 Shielding to shift conversion

To convert the theoretical chemical shielding values to chemical shifts, i.e., to be able to compare directly to the experimentally reported chemical shifts, it is necessary to adopt a conversion equation. Theoretically, a simple linear relationship between these scalar characteristics is expected with a slope of −1.⁵¹ Although some studies suggest that this assumption may not be universally applicable, with different elements exhibiting varying slopes,⁵² Dib et al.¹² demonstrated that the slope for ²⁷Al is generally close to −1. For example, Sklenák et al.¹⁰ used a slope of −1 taking the chemical shift of a CHA sample with a high Si/Al ratio, which provided a well-defined experimental ²⁷Al signal, as a reference. Others proposed to use multiple data points to fit this linear regression dependence achieving slopes mildly different from −1.^29,53 However, employing multiple data points to form the conversion equation can be problematic due to uncertainties in modelling the exact experimental structure at the experimental conditions.²⁹

Therefore, in this study, we assumed a slope of −1 and used Al(acac)₃, a simple well-defined crystal structure, which is frequently utilized in solid-state ²⁷Al NMR experiments as a solid reference and has a chemical shift of −4.2 ppm.⁵⁴ Lei et al. performed a 20 ps ab initio molecular dynamics (AIMD) simulation at 300 K with 400 eV cutoff energy, where the chemical shielding values were averaged over 100 snapshots taken uniformly from the trajectory, resulting in an average theoretical chemical shielding of 554.00 ppm.²⁹ Based on the assumption of a theoretical slope of −1, we derived the following calibration equation:

δ(Al) = −1σ(Al) + 549.80 ppm (1)

This equation was used to convert the chemical shielding σ(Al) into the chemical shift δ(Al).

2.5 Databases

The database of reference structures (and reference NMR data) utilized in this work encompasses three types of zeolites: CHA, MOR, and MFI, with 1771, 358, and 100 structures, respectively. The CHA and MOR data were obtained from a range of Born-Oppenheimer AIMD simulations at various water loadings, Si/Al ratios, and containing multiple aluminium species (see Section S2 for details).

To ensure a representative selection of MFI structures, we employed the furthest point sampling (FPS) algorithm⁵⁵ to the datapoints obtained from molecular dynamics simulations of models with various water loadings (0, 1, 2, 3, and 17 water molecules per unit cell) and a Si/Al ratio of 95, all performed at a temperature of 350 K. FPS reduces the density of the initial point cloud by iteratively selecting points that are farthest from previously chosen ones – this ensures that the sampled structures are well-distributed across the dataset helping to data-efficiently cover a wide range of aluminium environments. As a result, the final database is characterized by structures covering a diverse range of water loading conditions, varying Si/Al ratios, and differing chemical compositions, including even some zeolites containing sodium atoms. Each aluminium atom within the selected structures serves as a datapoint, resulting in a set of over 4000 unique Al environments.

To illustrate the distribution aluminium environments in the database across multiple zeolite types, we projected the high-dimensional Al-centered smooth overlap of atomic positions (SOAP) vectors,⁵⁶ calculated using the Python package DScribe 1.2.2,⁵⁷ to two dimensions using the t-distributed stochastic neighbor embedding (t-SNE) method, as shown in Fig. 2 t-SNE is a widely used technique for reducing the dimensionality of large datasets, preserving local similarities and revealing inherent structure within the data. This method is particularly valuable for visualizing high-dimensional data in a low-dimensional space, making it easier to identify clusters and patterns.^21,58 The t-SNE visualization demonstrates that while CHA data cover a larger portion of the configuration space, it fails to densely cover some of the MOR and MFI-relevant Al-based configurations. Clearly, the MOR structures consistently cluster closer to MFI structures, indicating a higher similarity between MOR and MFI zeolites. This observation can be further quantified by calculating the similarity of Al-centered SOAP descriptors averaged over the zeolite topology in question. The similarity K²⁰ is computed using the normalized dot product of the averaged SOAP descriptors of aluminium environments χ, as described by the following equation:

where

Fig. 2 Heterogenity of aluminium environments (represented as Al-centered SOAP vectors) present in database visualized via t-SNE. Blue datapoints represent aluminium environments in CHA, red in MFI and green in MOR.

The similarity score between MFI and MOR is 0.9924, while the similarity between MFI and CHA is 0.9338. These results underscore the significance of including MOR zeolites in the database to capture the diverse environments present in MFI structures.

2.6 Chemical shifts calculation

There are multiple methods to calculate chemical shielding, each varying in accuracy and computational cost. The most computationally intensive approach involves using ab initio methods, such as DFT, to calculate the chemical shielding values. Despite its high accuracy, the substantial computational cost makes it impractical for large numbers of structures, e.g., as is needed to properly account for dynamical effects. The simplest approach proposed by Lippmaa et al.⁵⁹ predicts directly the ²⁷Al NMR chemical shift δ(Al), i.e., circumventing the calculation of the chemical shielding altogether, and approximates δ(Al) as a function of the average T–O–T angle as described by the following equation:

Several alternative methods for calculating chemical shifts have been developed beyond the Lippmaa's approximation. The 2-parameter (2p-LASSO) eqn (4) and the 5-parameter (5p-LASSO) eqn (5) were proposed by Lei et al.²⁹ These models were developed using the least absolute shrinkage and selection operator (LASSO) regression, which is a linear regression technique that adds an L1 regularization penalty, shrinking some coefficients to zero, which simplifies the model by selecting only the most relevant features. These models utilize various descriptors based on bond lengths d and bond angles α to predict chemical shielding with a semi-quantitative accuracy with mean absolute error (MAE) of 1.27 ppm,²⁹ providing a computationally efficient alternative to ab initio methods while allowing for interpretability of the predictions.

To develop a quantitative prediction model for ²⁷Al NMR chemical shieldings in zeolites, we employed a kernel ridge regression (KRR) model from the scikit-learn 1.1.3 Python package,⁶⁰ which has previously shown excellent accuracy in predicting chemical shieldings in aluminosilicate glasses.³⁰ In the KRR model, the SOAP descriptors⁵⁶ of aluminium atoms with a cutoff of 5 Å are used as input features, accurately capturing the local atomic environments.

The kernel function used in the KRR model employed herein is a simple dot product kernel, defined as:

K_ij = k(χ_train⁽ⁱ⁾, χ_train^(j)) = (χ_train⁽ⁱ⁾ × χ_train^(j)) (6)

Here, K_ij represents the element of kernel matrix K_train, expressed as a dot product between the SOAP descriptors of aluminium environments χ of training samples i and j.

The ridge regression algorithm is applied to the kernel matrix from eqn (6), minimizing the following cost function:

min_ω{‖Y_train − K_trainω‖² + λ‖ω‖²} (7)

In this formulation, Y_train represents the training labels (i.e., the DFT reference chemical shieldings), ω denotes the expansion coefficients and λ is the regularization parameter that controls the trade-off between fitting the training data accurately and keeping the model complexity low to avoid overfitting. To optimize the regularization parameter λ, a grid search was conducted over a range of values from 10⁻⁷ to 10⁻². The model with λ = 5.5 × 10⁻⁶ yields the lowest error. Technical details about the training are described in Section S3 in ESI.† The final KRR model, trained on the database introduced in Section 2.5, achieved a training MAE of 0.2 ppm and a testing MAE of 0.5 ppm, indicating the achievement of the quantitative prediction accuracy. For comparison, this performance surpasses the testing MAE of over 1 ppm reported previously by Chaker et al.³⁰ for aluminosilicate glasses.

3. Results

3.1 Benchmarking the chemical shift prediction models

To decide which of the methods introduced in Section 2.6 (Lippmaa's approximation, 2p-LASSO, 5p-LASSO, and KRR) to adopt for calculation of chemical shifts, we first benchmark their performance. The 2p-LASSO, 5p-LASSO, and KRR models were trained on the original database from Lei et al.,²⁹ containing aluminium atoms in a tetrahedral configuration within the MOR and CHA zeolites, varying in water content and Si/Al ratios. To compare their prediction accuracy, we generated a new testing set composed of a set of structures from NNP-driven MD simulations of MFI zeolites with Si/Al ratio of 95 and with five different water loadings (0, 1, 2, 3, and 17 water molecules per unit cell). For each water loading, two BAS configurations were chosen. The selected initial BAS configurations, as well as details of the procedure are provided in Section S4.† Ten structures were sampled from each of these models (different water loading and BAS configurations, i.e., a hundred structures in total), and the chemical shifts were calculated using each method. These predicted values were then compared with the reference DFT chemical shifts, and the mean absolute error (MAE) was calculated to assess the accuracy of each method.

The MAE of the chemical shift predictions are in Table 1. The average MAE for KRR across all water loadings is 1.0 ppm. The 5p-LASSO and 2p-LASSO models also demonstrated reasonable accuracy, with errors between 1 and 2 ppm, depending on the water loading. The error of the LASSO models can be partially related to the small systematic offset (Fig. 3). Note that the KRR model trained on an extended database generated in this work (Section 2.5), and which is used in the following sections, provided mildly improved chemical shifts predictions over the KRR model discussed herein, with an MAE of 0.7 ppm (see Table 1 and Section S5† for further details).

Table 1 The mean absolute errors (MAE) of various models for predicting chemical shifts with respect to the reference DFT calculations [in ppm]. The testing set was selected to cover the entire range of chemical shift values observed in the calculations of MFI zeolite

Water loading	Lippmaa	2p-LASSO	5p-LASSO	KRR^a
a Model trained on database from Section 2.5 in parenthesis.
0	5.46	1.97	2.09	0.77 (0.90)
1	4.73	1.55	1.98	1.51 (0.54)
2	5.28	1.38	2.20	1.29 (0.83)
3	3.52	1.47	1.63	1.00 (0.78)
17	3.29	1.71	1.53	0.54 (0.53)

---

Fig. 3 The correlation between chemical shifts predicted via multiple models considered in this work (Lippmaa, 2p-LASSO, 5p-LASSO, and KRR) and the reference DFT calculated values across the MFI testing set with varying water loading.

A similar observation can be made based on the correlation plots in Fig. 3, which highlight that both the KRR and 5p-LASSO methods have strong correlations with DFT predictions, as indicated by R-squared (R²) values exceeding 0.9. Lippmaa's method shows the poorest correlation with DFT-calculated values, and the 2p-LASSO method, while generally reasonably accurate, fails to predict chemical shift of certain structures accurately. These outliers are associated with unique structural motifs for low water loadings, specifically those involving a hydrogen bond between the BAS proton and a framework oxygen, which stretches the Al–O bond. This structural motif is sparsely represented in the original training database, however, the 5p-LASSO method manages these outliers more effectively by accounting for the asymmetry of this bond length. The KRR model exhibits the best correlation overall, with an R² score of 0.97, indicating its robustness in predicting chemical shifts across diverse structural environments.

In practice, despite its well-documented limitations,^10,61,62 Lippmaa's approximation, correlating the chemical shifts only to T–O–T angles, continues to be used as a common method for assigning experimental NMR resonances to specific zeolite structures.^11,13,63 However, based also on the tests presented in this section, the superior accuracy of the 2p-LASSO method suggests that Al–O bond lengths are more critical in predicting chemical shifts than previously believed, challenging the earlier conclusions by Liu et al.,⁶⁴ who provided a theoretical explanation, based on bonding orbitals, for the contribution of the T–O–T angles to be dominant. Importantly, the KRR model, which outperformed all other methods across the board, was particularly accurate in predicting shifts for hydrated structures. This is especially important because NMR measurements are typically performed on hydrated zeolites, where the water molecules can solvate the acidic proton. This simplifies the intepretation of the spectrum as the presence of an unsolvated proton bound to the framework creates an asymmetric environment, which leads to the increase of the electric field and broadens the spectrum.⁶⁵ Due to its superior performance, the KRR model is the main method of choice used in the remainder of this study. However, the 2p-LASSO and 5p-LASSO models are still valuable for the interpretation of the qualitative trends observed in the following sections.

3.2 Chemical shift calculation at finite temperature

The local optimization approach is a common approach applied for determining chemical shift values in computational chemistry to moderate the outsized computational costs of ab initio methods. It typically involves optimizing a single structure to find the (local) minimum on the potential energy surface, with a tacit assumption that such minimum is close to the global minimum and that its weight in the ensemble of finite-temperature structures is very high. However, in complex systems like zeolite MFI, identifying the global minimum is particularly challenging, and even if successful, its importance in the finite-temperature structure ensemble may be low as many low-energy local minima are present as well.¹⁹

To assess the inherent variance of this simplified method, we locally optimized 20 000 structures generated from a molecular dynamics simulation of an MFI system with 17 water molecules per unit cell, containing a single aluminium atom substituted for silicon in the T5 position. All optimizations were performed using neural network potentials (NNP). While this does not strictly test the quality of the single-structure method (which would require comparing the prediction of the putative global minimum against the MD average and experimental data), it provides insights into the variation present across a set of local minima. For each locally optimized structure the chemical shifts were calculated using the KRR method. The goal was to assess whether this extensive application of the local optimization method could yield stable and reproducible chemical shift values or if the MD based approach, which averages the chemical shift values over the (un-optimized) snapshots from the trajectory, provided a more reliable result.

The results showed that the chemical shift distribution from these 20 000 optimized structures spans a range exceeding 12 ppm, as illustrated in Fig. 4. Such range is comparable to the variation observed across all the T-sites in the experimental studies.^10,11 While certain chemical shift values, such as 59.5, 58.3, and 55.3 ppm, appeared slightly preferred, the mass of the distribution is significantly spread out across the whole range, with a very low mass associated with the MD-predicted average chemical shift at approx. 57.2 ppm (see also Table 2).

Fig. 4 The chemical shift distribution observed in locally optimized structures sampled from the MD simulation trajectory.

Table 2 Chemical shift values [in ppm] obtained by the local optimization and the molecular dynamics approach for different initial structures with standard deviation being 2.90 ppm and 0.04 ppm, respectively

Single structure	Molecular dynamics
58.84	57.24
57.38	57.20
55.91	57.16
61.66	57.23
53.01	57.26

---

To further compare the reproducibility of the two approaches, five structures with mildly different structural parameters were generated. These initial structures exhibited a range in average T–O–T angles of 0.2° and a variation in average Al–O bond lengths of 0.8 pm. As presented in Table 2, the MD approach achieved a standard deviation (SD) in chemical shift prediction of just 0.04 ppm across these structures starting at the slightly different initial conditions, compared to an SD of 2.90 ppm for the local optimization approach.

These findings indicate that using a single optimized structure, i.e., using a local optimization approach, is unlikely to yield a representative chemical shift value for a complex system. The MD simulation approach, which averages across an ensemble of accessible finite-temperature structures, leads to more reproducible and representative chemical shift values, providing also a measure of statistical uncertainty, and is thus better suited for comparison with the experimental measurements.

3.3 MFI models with isolated aluminium

3.3.1 Effect of water loading. In computational studies of zeolites, the inclusion of water molecules is often overlooked, even though most experiments on zeolites are conducted under hydrated conditions, both for experimental convenience and because the presence of water significantly reduces ²⁷Al NMR peak broadening.⁶ However, the amount of water molecules surrounding each aluminium atom is not directly accessible to the experimental probe and may vary across the sample. Hence, it is essential to understand how varying water loading conditions influence the chemical shift predictions.

To probe the effect of water loading as well as to obtain the values of ²⁷Al NMR chemical shifts in MFI under realistic hydrated conditions we considered the following water loadings: 0, 1, 2, 3, and 17 water molecules per unit cell. The model of 17 water molecules is expected to correspond to fully hydrated zeolite at ambient conditions, as justified by the experimental measurements of Holzinger et al.,¹¹ who reported 15 ± 1 water molecules per unit cell present for H-ZSM-5 with a Si/Al ratio of 50. These water loadings were probed for MFI models with one aluminium atom per unit cell (Si/Al = 95) and all crystallographically inequivalent T-sites in MFI (12 T-sites) were considered. In addition, various initial BAS configurations in the vicinity of each T-site were considered (see details in the Section S6†).

To evaluate the water loading effect irrespective of a particular T-site, Table 3 presents the chemical shifts averaged across all T-sites for each water loading, employing multiple chemical shift predictors. Interestingly, all the tested methods except Lippmaa's approximation span a similar range of chemical shift and exhibit similar trends, such as a mild increase (1–2 ppm) in chemical shift upon increasing the water loading from one to two water molecules per unit cell and a minor decrease (up to 1 ppm) in the shift going from two to seventeen waters per unit cell. These observations suggest that the trends are likely general and that they primarily stem from geometry variations in the immediate vicinity of the Al center, i.e., from variation in the T–O–T angle and Al–O bond lengths, despite the fact that these local geometry variation can be a consequence of more complex processes taking place far away from the Al center.

Table 3 The chemical shift values averaged over all T-sites as a function of water loading, predicted by several models

Water loading	Lippmaa	2p	5p	KRR
0	60.1 ± 4.6	51.7 ± 3.3	53.0 ± 3.0	51.7 ± 3.7
1	59.9 ± 3.3	52.8 ± 2.8	53.6 ± 2.6	52.3 ± 2.7
2	60.1 ± 2.8	54.5 ± 2.4	54.7 ± 2.3	54.0 ± 2.6
3	60.0 ± 3.3	54.2 ± 2.6	54.2 ± 2.5	53.7 ± 2.5
17	59.6 ± 3.3	53.9 ± 2.6	53.9 ± 2.6	53.0 ± 2.4

---

Next, to examine the T-site dependent effects of water solvation on chemical shift, Fig. 5 illustrates the variation in chemical shift with respect to water loading across all twelve T-sites for the reference KRR model. This allows a detailed investigation of the response of each T-site to varying water content.

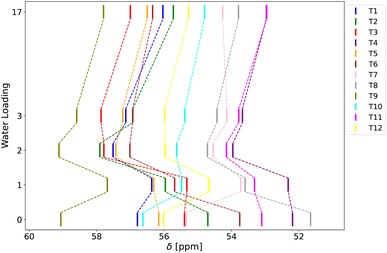Fig. 5 Chemical shift values calculated by the KRR model as a function of water loading and the T-site type.

Moving from the dry zeolite model to one with one water bound to BAS, the chemical shift behaves inconsistently and is highly dependent on the local structural environment around the individual T-site. However, a consistent increase in chemical shift is observed when the water loading is increased from 1 to 2 molecules per unit cell. This change is likely due to the decrease in the Al–O bond length associated with the addition of the second water molecule. This additional water molecule interacts with both the BAS proton and the other Al-adjacent framework oxygen atoms, allowing for an intermittent proton transfer, which leads to shortening of the average Al–O bond length, resulting in a higher chemical shift. The average Al–O bond length variation is approximately 0.005 Å, which corresponds to a change in chemical shift of about 1 ppm according to eqn (5) (see Table S6 in ESI† for more details). A similar mechanism accounts for the general decrease in chemical shift observed when increasing the water loading from 2 to 17 molecules per unit cell. Upon increasing the water loading further from 2 to 17 molecules, the additional water molecules fully solvate the BAS proton, with the proton removed rather far from the framework, effectively reducing the direct interaction between protonated water cluster (the hydrogen atoms) and the framework (oxygen atoms) at the nearby Al-center. This decreased interaction leads to larger T–O–T angles and smaller Al–O bond lengths, which when combined, result in a lower chemical shift. The structural characteristics and their effects on chemical shift are described in detail in Section S7.† These results demonstrate that water loading significantly affects the predicted chemical shift values (by up to 2–3 ppm), making it a crucial factor to include in calculations. Note also, that the T9 site consistently exhibits the highest chemical shift values, which can be attributed to its T–O–T angle being the smallest among the T-sites (see Table S8 in ESI†). Interestingly, this is is not observed in the locally optimized structure of the zeolite, rather it is a consequence of the dynamical sampling.

To better analyze the similarities between behavior of different T-sites as a function of the water loading, a principal component analysis (PCA) was carried out on vectors composed of relative changes in chemical shifts with water loading for each site, and the resulting principal components for each T-site were clustered with the K-means algorithm. This resulted in separation of the T-sites into three distinct groups (see Fig. S8†), which could be roughly related to their positions in the MFI framework (sinusoidal or straight channel and other positions). The analysis of the PCA components showed that the main distinction between these groups lies in the way how chemical shift changes for low water loadings (0 to 2 water molecules), while the chemical shift behavior for higher water loadings (3 waters and above) is similar for all T sites (see Section S7† for further details).

These findings indicate that the impact of water loading is both extensive, shifting the position of the NMR peak by up to 3 ppm, and that it is greatly influenced by the specific structural environment around each aluminium atom in the zeolite. This implies that one must precisely take into account each T-site and relevant water concentration for a proper model of the NMR response.

3.3.2 Temperature dependence of the chemical shifts. The effect of temperature is often neglected in computational studies that evaluate ²⁷Al chemical shift, because ensemble averaging is computationally much more expensive than the local optimization approach (see Section 3.2) that is typically used.^10,12 Herein the dependence of the ²⁷Al chemical shift on the temperature was evaluated for the T5 position at the intersection by considering a temperature range from 250 K to 500 K with a step of 50 K. All possible BAS were modeled and subjected to MD simulations at different temperatures with varying water loading. The results are presented in Fig. 6, which depicts the change of the chemical shifts with temperature.

Fig. 6 ²⁷Al chemical shift of the aluminium exchanged in T5 position in MFI for variable water loading as a function of temperature.

For the dehydrated MFI model, the chemical shift remains nearly constant until a significant increase of about 1 ppm is observed between 350 K and 400 K. This sudden increase can be explained by the interaction of the BAS proton with the surrounding framework. At lower temperatures, the proton forms a hydrogen bond with another framework atom, i.e., an intrazeolitic hydrogen bond (IZB),⁶⁶ leading to significant distortion of the aluminium environment. As the temperature rises, thermal motion reduces the contribution of the intrazeolitic hydrogen bonding mode in the structural ensemble (see Fig. S11 in ESI†), i.e., the IZB is partially broken, as was also observed in some previous works.⁶⁷ This reduction in intrazeolitic hydrogen bonding directly correlates with the observed jump in chemical shift, reflecting changes in the aluminium environment.

For the MFI model with 1 water molecule per unit cell, the ²⁷Al chemical shift stays almost constant across the entire temperature range considered. However, for MFI models with 2, 3, and 17 water molecules per unit cell, a consistent and significant decrease of 1.5 ppm is observed with increasing temperature. The latter phenomenon can largely be attributed to changes in the average T–O–T angles, which increase by approximately two degrees with rising temperature. This increase in angle is likely an indirect consequence of the change in dynamics of water molecules – as the temperature rises, the average water distance from the oxygen atoms next to the aluminium atom increases, leading to a more relaxed Al environment with larger T–O–T angles (see Table S10 in ESI†). The slight increase in chemical shift observed for the model with two water molecules between 250 K and 300 K can be attributed to a minor decrease in bond length, which leads to the observed increase in chemical shift (see Fig. S10†). This may also be linked to variations in the trend of hydrogen atom distances to framework oxygen, as shown in Table S10.†

These results indicate that temperature significantly impacts the ²⁷Al chemical shift, varying in the actual effect depending on the particular water content in the MFI zeolite. In models with higher water content, temperature indirectly influences the chemical shift by altering the water dynamics, which in turn affects the local environment of the aluminium atom. In dehydrated MFI, the temperature changes the local geometry of the Al-center, e.g., by weakening the intrazeolitic hydrogen bonding.

3.4 MFI models with increased aluminium content

Introducing an additional aluminium (and proton) into the zeolite unit cell perturbs the original isolated aluminium environment and thus also the ²⁷Al chemical shifts. This effect is typically disregarded in computational studies as it introduces a combinatorial increase in the number of possible configurations, making it challenging to treat extensively and comprehensively at the ab initio level. The extent of this perturbation/interaction was shown to correlate very weakly with the distance between aluminium atoms by a previous study,⁶⁸ which aligns with our findings below and suggests a more complex underlying dependence.

Herein, to investigate the effect of introducing an additional aluminium atom to the framework, MFI models with two aluminium atoms per unit cell, i.e., with an aluminium pair, were considered. A total of 20 models containing aluminium pairs were considered, with at least one of two T-sites occupied by aluminium located in the T12 site. The T12 site is located at the intersection of the straight and sinusoidal channels and is considered in the literature as one of the most commonly occupied T-sites by aluminium in MFI.^69,70 Aluminium pairs that are separated by one and two T-sites were considered, termed as next-nearest neighbour (NNN) and next-next-nearest neighbour (NNNN) pairs, respectively. The nearest neighbour aluminium pair, i.e., a pair separated only by only one framework oxygen atom is not considered due to the Löwenstein rule.⁷¹ Altogether, 12 NNN and 8 NNNN aluminium pairs were modelled and their ²⁷Al chemical shifts calculated. For each aluminium pair, two water loadings were adopted (0 or 17 water molecules). A detailed description of the aluminium pairs is provided in Table S12† accompanied by the validation of the KRR predictions of ²⁷Al chemical shifts for aluminum pairs against the DFT reference (Fig. S12†). This validation confirms the accuracy of the KRR model also in this setting (MAE = 0.8 ppm).

Fig. 7 depicts the impact of introducing an additional Al atom into the framework on the chemical shifts of aluminium at the T12 position, comparing the effects in both dehydrated and hydrated frameworks. In the dehydrated framework, the average absolute change in the chemical shift due to nearby aluminium averages to 1.3 ppm, compared to 0.8 ppm in the fully hydrated MFI framework. Specifically, the largest increase in chemical shifts is observed in the dehydrated state, reaching 1.9 ppm, whereas in the hydrated state, it can increase by as much as 2.2 ppm. Conversely, the decrease in chemical shift appears to be more pronounced, falling by up to 4.7 ppm in the dehydrated framework, and as much as 2.2 ppm in the hydrated case. These findings are consistent with those reported by Dědeček et al.,⁶⁸ who observed a maximum decrease of 3.8 ppm and maximum increase of 1.5 ppm from the chemical shift of isolated Al in dehydrated cluster models with NNN aluminium pairs.

Fig. 7 The effect of introducing an additional aluminium atom into the framework on the ²⁷Al chemical shift of the originally isolated aluminium atom located in the T12 site. The effect is plotted as a function of the distance between the aluminium pairs, forming the next-nearest neighbour (NNN) and next-next-nearest neighbor (NNNN) pairs. The black line represents the chemical shift of an isolated aluminium located in the T12 site. The variation in chemical shift is plotted for both dehydrated (left) and fully (17 waters) hydrated models (right).

Analyzing the structural characteristics of the aluminium pairs reveals that the changes in chemical shifts do not follow a consistent pattern based on the position or distance of the additional aluminium atom. Instead, these chemical shift values can be attributed to variations in the average T–O–T angles and Al–O bond lengths. The average T–O–T angle can vary by up to 3° from that of the isolated aluminium atoms, and bond lengths can differ by up to 0.6 pm. Both of these structural variations can lead to variations in the chemical shift of up to 3 ppm (see Section S10 in ESI† for more details).

The effect of adding an Al atom is significant across both next-nearest-neighbour (NNN) and next-next-nearest-neighbour (NNNN) aluminium pairs. Also, there is no clear correlation between the interatomic distance separating aluminium atoms and the effect on the chemical shift. The lack of clear-cut distance dependency, in this distance range, may be due to the inherent complexity of the MFI structure, however, a similarly large effect of the rather distant NNNN pairs have been also reported recently for a simpler framework (CHA).²⁹ These results indicate that the magnitude of the ²⁷Al chemical shift is very sensitive even to a rather minor perturbation, e.g., originating in the introduction of additional aluminium as far as 8 Å away, reflecting the nuanced interactions within the zeolite framework over rather large distances.

4. Discussion

4.1 Comparison to experiment and previous theoretical predictions

The majority of the experimental NMR characterization and the corresponding theoretical simulations have been carried out for the ZSM-5 system, a zeolite with MFI topology but with the unit cell of a lower symmetry containing 24 T-sites. Hence, to allow one-to-one comparison to these data, we also adopted the H-ZSM-5 zeolite model which was directly obtained from the IZA database,³⁹ considering all T-sites (with Si/Al = 95), fully hydrating the ZSM-5 zeolite structure and modelling it at 350 K to closely replicate experimental conditions.¹¹ The ²⁷Al chemical shifts predicted by the KRR method and averaged over the NNP-driven MD simulations for each of the 24 T-sites are presented in Table 4 spanning a range of 6.6 ppm.

Table 4 ²⁷Al chemical shifts for the ZSM-5 models with a single aluminium in the unit cell located at one of the 24 T-sites

T-site	δ(^27Al) (ppm)	T-site	δ(^27Al) (ppm)
T1	54.5	T13	57.7
T2	52.4	T14	55.8
T3	55.8	T15	54.1
T4	54.9	T16	52.7
T5	55.8	T17	55.0
T6	54.6	T18	56.7
T7	53.9	T19	53.7
T8	51.1	T20	56.6
T9	55.4	T21	55.4
T10	55.8	T22	53.3
T11	54.0	T23	51.8
T12	54.4	T24	56.9

---

These predictions can be directly compared with the works of Holzinger et al.¹¹ and Sklenák et al.,¹⁰ who have both calculated chemical shift values for every T-site and compared them with experimental ²⁷Al NMR data in the H-ZSM-5 zeolite. Firstly, there is a sizable discrepancy with respect to the range of the experimental (and DFT-calculated) chemical shifts provided by Sklenák et al.,¹⁰ which is about 10 ppm. However, Sklenák et al.¹⁰ considered H-ZSM-5 samples with much higher aluminium content, with Si/Al ratios of 15 and 22.5. At higher aluminium content the aluminium atoms are more closely spaced, which may lead to broadening of the range covered by the chemical shifts as illustrated in the previous Section 3.4. To test this hypothesis, we constructed a series of 45 models (adopting MFI unit cell with 12 types of T-sites for simplicity). These 45 models contained randomly placed aluminium atoms with Si/Al ratios ranging from 15 to 23 and were subsequently loaded with 17 water molecules per unit cell. The resulting range of calculated ²⁷Al chemical shift values was found to be 11 ppm, which closely approximates the experimental range reported in the cited study¹⁰ (see Section S11 in ESI† for details). Based on these findings we suggest that such a broad range of experimental ²⁷Al chemical shifts can be attributed to the presence of nearby aluminium atoms in the framework, especially for low Si/Al models. In fact, the breadth of the chemical shifts may even serve as a novel approach to probe aluminium proximity in the experimental ZSM-5 samples. This observation is supported by comparing the current prediction with the work of Holzinger et al.¹¹ who have conducted a thorough study using ZSM-5 samples with a Si/Al ratio of 140, which has a high probability of containing mostly isolated aluminium atoms.⁷² The range of experimental values observed was 6.5 ppm, which is very similar to the 6.6 ppm range predicted by the KRR method herein.

Since it is experimentally challenging to detect closely spaced aluminium atoms^72,73 and their effect on the chemical shift is large, comparison of the predicted values with the experimental data has to be done with caution. To overcome this challenge, it is advisable to consider for comparison only zeolite samples with a very high Si/Al ratio. In such samples, closely spaced aluminium pairs are less common, making it easier to validate the predictions and assess their accuracy. This approach minimizes the complications associated with aluminium pair interactions and provides a clearer comparison between predicted and experimental chemical shift values.

The comparison between the chemical shifts predicted by the KRR model and the experimental¹¹ resonances is shown in Fig. 8. In this figure, the KRR predictions for individual T-sites were assigned to the experimental ones using an almost constant correction (≈1 ppm) that accounts for a systematic offset which may stem, for example, from the approximation used for conversion from chemical shielding to chemical shift (see Section 2.4), or from inaccuracies of the reference DFT level, exploration of which are beyond the scope of this contribution.

Fig. 8 Comparison between the chemical shifts predicted by the KRR method and the experimental resonances observed by Holzinger et al.¹¹

The current assignment of the experimental ²⁷Al shifts to aluminium located in specific T-sites differs from previous T-site assignments.^10–12 This discrepancy is to be expected, as prior calculations of chemical shifts typically relied on either Lippmaa's approximation or the single-structure approach (see Sections 3.1 and 3.2 for reference), and thus we expect our assignments to more closely represent the realistic conditions of the NMR experiment. We also note that 2D ²⁹Si–²⁷Al NMR correlation spectra may help to improve the assignment of the Al siting, as they are able to reveal the spatial correlation between Al–Si sites.¹² Hence, as an example, we attempted to construct a KRR model using a small database of DFT ²⁷Si NMR shieldings obtained from available NNP MD trajectories of H-MFI models (see Section S14 in ESI† for details). We compared its performance against the experimental ²⁹Si NMR data for purely siliceous MFI.⁷⁴ The KRR model for ²⁹Si NMR shifts performs reasonably well (MAE = 0.7 ppm, with a correlation coefficient of 0.87), despite a limited dataset used for training, which indicates that accurate prediction of 2D ²⁹Si–²⁷Al NMR features is a feasible goal.

Interpreting NMR spectra for complex zeolite structures, such as H-ZSM-5, is challenging due to signal overlap and the quadrupolar nature of the ²⁷Al nucleus. In particular, the chemical shift region between 53 and 56 ppm is expected to represent signals from 16 different T-sites (see Fig. 8), and considering that the ²⁷Al nucleus causes broadening of spectral peaks with line widths ranging from 0.9 to 2.3 ppm at 14.1 T,¹¹ it is easy to see that this will significantly complicate the assignment of experimental NMR signals. Nevertheless, as an example, we attempted to calculate the complete NMR spectra going beyond isotropic chemical shifts including the quadrupolar broadening testing various reasonable simplified estimates of the C_Q parameter, obtaining, as expected, a range of sizably different NMR spectra (see Section S12 in ESI† for details) exemplifying the problems with the reliable signal assignment. Moreover, these difficulties are further exacerbated when cations are attached to the zeolite framework, as they can further broaden the NMR signals. To mitigate this, NMR measurements are typically conducted on fully hydrated zeolites, where the presence of water leads to narrower peaks.⁶

Note, however, that recent studies have begun incorporating additional parameters, such as chemical shift anisotropy to distinguish overlapping signals more effectively.⁷⁵ Similarly, a few recent computational studies^36–38 have proposed machine learning models capable of predicting full NMR shielding and EFG tensors. A combination of these approaches holds promise to overcome the challenges in assignment and interpretation of the ²⁷Al NMR spectra.

Lastly, we tested the generality and transferability of the herein-trained KRR model (as well as that of the NNP-driven structure sampling) for different zeolite frameworks, including TON, MTT, MOR, and CHA topologies in their high silica forms (see Section S13† for details). For MOR and CHA frameworks, i.e., for frameworks partially included in the KRR training database (see Section 2.5), the KRR predicted chemical shifts exhibit similar behavior as for the MFI topology discussed above and are consistently 1–2 ppm lower than experimental values.^76,77 However, for TON and MTT frameworks, the KRR predicts unusually low chemical shifts (around 45–50 ppm). This failure is clearly related to the comparatively high average T–O–T angles in these frameworks, which are not represented in the training data, thus causing the model to extrapolate. These tests, while revealing some shortcomings in transferability of the current KRR model, also show a clear direction along which to extend the structural (and ²⁷Al chemical shielding) database towards the goal of obtaining a KRR model that is capable of covering a broad range of zeolite topologies.

5. Conclusions

The presented work shows that a proper consideration of dynamics, temperature, explicit solvation, aluminium concentration and distribution is necessary to achieve a close agreement with experiment, and even allows for the assignment of ²⁷Al NMR peaks in realistic model zeolites (such as MFI zeolite studied herein primarily) under experimental conditions. We have reaffirmed some findings in the literature, such as the quantification of the role of Si/Al ratio, and we have dispelled some persistent inaccuracies, including the use of single structure models, the neglect of temperature and the use of averaged background charge models for high-water conditions.

First, we provided a comparative analysis of the performance of various statistical methods in predicting chemical shift with respect to the reference DFT values, ranging from simple linear regression models based on a very few local structural descriptors (bond lengths and angles nearby Al-center) to advanced non-linear kernel ridge regression (KRR) that utilize complex SOAP descriptors of the local aluminium environment. Unsurprisingly, the KRR method was found to outperform all other tested methods for all zeolite models by more than 1 ppm. However, even a simple two-parameter regularized linear regression (LASSO), depending only on the value of the T–O–T angle and Al–O bond length, exhibited qualitatively correct description, enabling interpretation of the trends observed in chemical shifts as a function of temperature, solvation and aluminium content. We also showed that a linear correlation between the T–O–T angle and chemical shift originally proposed by Lippmaa et al.⁵⁹ is too simple to provide qualitatively accurate predictions, proving that the Al–O bond length is a crucial factor in determining the ²⁷Al chemical shifts.

The water loading in the zeolite system was found to have a sizable impact on the predicted chemical shift, with the magnitude of the effect being as much as 3 ppm and heavily depending on the position (T-site) of the aluminium atom in the framework. The ²⁷Al chemical shift in zeolites also varies with temperature and water loading, with a steady decrease for higher water loadings due to enhanced water mobility. This observation strongly suggests that the presence of water molecules has a significant impact on the local aluminium environment, contradicting one of the rationales for using background charge and dehydrated models. Additionally, increased Al content can shift the ²⁷Al chemical shift by over 4 ppm, complicating NMR spectral assignments in zeolites with low Si/Al ratios and numerous inequivalent T-sites.

For samples with a sufficiently high Si/Al ratio, we show that even for MFI (ZSM-5) zeolite, one might be able to reliably assign NMR peaks to specific T-sites if realistic models are adopted, achieving almost quantitative agreement between the experimentally and computationally predicted range of NMR peaks and their positions. Indeed, given the quantitative agreement obtained, the increased range of measured NMR resonances might be used as an indication of the formation of the Al pairs and Al zoning. Clearly, one has to be cautious not to over-interpret the tentative assignments, which is unfortunately not uncommon in the field – for instance, within a narrow, 3 ppm range, signals for 16 different T-sites are expected, leading to significant overlap. Hence, achieving a definitive assignment of calculated chemical shifts to experimental peaks is challenging and to overcome this limitation, e.g., additional NMR parameters (such as chemical shift anisotropy) or multi-dimensional measurements (such as 2D ²⁹Si–²⁷Al NMR or ²⁷Al MQMAS) will be necessary to extract more detailed information from the NMR spectrum.

In summary, via a combination of machine learning potential-driven dynamics to sample relevant configuration space and statistical models to predict ²⁷Al chemical shifts based on the structures sampled, we managed to model a complex zeolitic system (H-MFI) under experimentally relevant conditions, taking into account the effects of temperature, water solvation and specific Al location within the framework. Our results align well with the relevant experimental data and are capable of explaining some of the apparent disagreements (e.g., due to Al pairing in the experimental samples). In addition, we are able to predict how temperature and water loading affects the ²⁷Al chemical shifts as well as provide mechanistic-level explanations/interpretations. Hence, this combined approach provides an important case study on how highly efficient machine learning algorithms can be coupled to offer predictive accuracy and deeper insights into the structural properties of extremely important industrial catalysts, the aluminosilicate zeolites, under realistic conditions.

Data availability

More detailed information on the structures, databases, kernel ridge regression model training, and molecular dynamics simulations is available in the ESI.† Also, additional data is provided in the Zenodo repository (https://doi.org/10.5281/zenodo.14063109) including a trained kernel ridge regression (KRR) model, training databases for MOR, MFI, and CHA structures with labeled DFT chemical shieldings, initial configurations used in the study, and an example of applying the KRR algorithm.

Author contributions

DW: investigation, data curation, writing – original draft. AE: methodology, data curation. CJH: conceptualization, supervision, writing – eeview & editing. LG: conceptualization, project administration, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support of the Czech Science Foundation (23-07616S). In addition, Charles University Centre of Advanced Materials (CUCAM) (OP VVV Excellent Research Teams, project number CZ.02.1.01/0.0/0.0/15_003/0000417) is acknowledged. This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:9 0254). The authors acknowledge Lukáš Frk for providing the optimized MFI unit cells, Carlos Bornes for valuable discussions on general aspects related to NMR spectra simulations and experiment, and Chen Lei and Federico Brivio for providing additional DFT-level NMR data for MOR and CHA structures (beyond those reported in ref. 29). We also thank Petr Nachtigall for his initial conceptualization of the project.

References

1. P. Sazama, J. Dědeček, V. Gábová, B. Wichterlová, G. Spoto and S. Bordiga, J. Catal., 2008, 254, 180–189.
2. T. Liang, J. Chen, Z. Qin, J. Li, P. Wang, S. Wang, G. Wang, M. Dong, W. Fan and J. Wang, ACS Catal., 2016, 6, 7311–7325.
3. J. Li, M. Gao, W. Yan and J. Yu, Chem. Sci., 2023, 14, 1935–1959.
4. J. Dědeček, E. Tabor and S. Sklenák, ChemSusChem, 2019, 12, 556–576.
5. W. Wang, J. Xu and F. Deng, Natl. Sci. Rev., 2022, 9, nwac155.
6. Z. Zhao, S. Xu, M. Y. Hu, X. Bao, C. H. F. Peden and J. Hu, J. Phys. Chem. C, 2015, 119, 1410–1417.
7. K. Chen, Z. Gan, S. Horstmeier and J. L. White, J. Am. Chem. Soc., 2021, 143, 6669–6680.
8. J. Holzinger, M. Nielsen, P. Beato, R. Y. Brogaard, C. Buono, M. Dyballa, H. Falsig, J. Skibsted and S. Svelle, J. Phys. Chem. C, 2019, 123, 7831–7844.
9. J. Dědeček, M. J. Lucero, C. Li, F. Gao, P. Klein, M. Urbanová, Z. Tvarůžková, P. Sazama and S. Sklenák, J. Phys. Chem. C, 2011, 115, 11056–11064.
10. S. Sklenák, J. Dědeček, C. Li, B. Wichterlová, V. Gábová, M. Sierka and J. Sauer, Phys. Chem. Chem. Phys., 2009, 11, 1237–1247.
11. J. Holzinger, P. Beato, L. F. Lundegaard and J. Skibsted, J. Phys. Chem. C, 2018, 122, 15595–15613.
12. E. Dib, T. Mineva, E. Veron, V. Sarou-Kanian, F. Fayon and B. Alonso, J. Phys. Chem. Lett., 2018, 9, 19–24.
13. J. A. van Bokhoven, D. C. Koningsberger, P. Kunkeler, H. van Bekkum and A. P. M. Kentgens, J. Am. Chem. Soc., 2000, 122, 12842–12847.
14. D. H. Brouwer, I. L. Moudrakovski, R. J. Darton and R. E. Morris, Magn. Reson. Chem., 2010, 48, S113–S121.
15. M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548.
16. G. Valerio, A. Goursot, R. Vetrivel, O. Malkina, V. Malkin and D. R. Salahub, J. Am. Chem. Soc., 1998, 120, 11426–11431.
17. S. Vanlommel, A. E. J. Hoffman, S. Smet, S. Radhakrishnan, K. Asselman, C. V. Chandran, E. Breynaert, C. E. A. Kirschhock, J. A. Martens and V. Van Speybroeck, Chem.–Eur. J., 2022, 28, e202202621.
18. T. Sano, T. Kasuno, K. Takeda, S. Arazaki and Y. Kawakami, Progress in Zeolite and Microporous Materials, Elsevier, 1997, vol. 105, pp. 1771–1778.
19. A. Hoffman, M. DeLuca and D. Hibbitts, J. Phys. Chem. C, 2019, 123, 6572–6585.
20. A. Erlebach, P. Nachtigall and L. Grajciar, NPJ Comput. Mater., 2022, 8, 174.
21. A. Erlebach, M. Šípka, I. Saha, P. Nachtigall, C. J. Heard and L. Grajciar, Nat. Commun., 2024, 15, 4215.
22. I. Saha, A. Erlebach, P. Nachtigall, C. J. Heard and L. Grajciar, ChemRxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2022-d1sj9-v3.
23. S. Ma and Z.-P. Liu, Chem. Sci., 2022, 13, 5055–5068.
24. E. Kocer, T. W. Ko and J. Behler, Annu. Rev. Phys. Chem., 2022, 73, 163–186.
25. Y. Zhang, C. Hu and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 4962–4967.
26. J. D. Evans and F.-X. Coudert, Chem. Mater., 2017, 29, 7833–7839.
27. C. Le Losq and B. Baldoni, J. Non-Cryst. Solids, 2023, 617, 122481.
28. M. Ducamp and F.-X. Coudert, J. Phys. Chem. C, 2022, 126, 1651–1660.
29. C. Lei, A. Erlebach, F. Brivio, L. Grajciar, Z. Tošner, C. J. Heard and P. Nachtigall, Chem. Sci., 2023, 14, 9101–9113.
30. Z. Chaker, M. Salanne, J.-M. Delaye and T. Charpentier, Phys. Chem. Chem. Phys., 2019, 21, 21709–21725.
31. R. Gaumard, D. Dragún, J. N. Pedroza-Montero, B. Alonso, H. Guesmi, I. Malkin Ondík and T. Mineva, Computation, 2022, 10, 74.
32. C. Lei, C. Bornes, O. Bengtsson, A. Erlebach, B. Slater, L. Grajciar and C. J. Heard, Faraday Discuss., 2025 10.1039/D4FD00100A.
33. F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Nat. Commun., 2018, 9, 4501.
34. Z. Yang, M. Chakraborty and A. D. White, Chem. Sci., 2021, 12, 10802–10809.
35. Y. Guan, S. V. Shree Sowndarya, L. C. Gallegos, P. C. St. John and R. S. Paton, Chem. Sci., 2021, 12, 12012–12026.
36. M. C. Venetos, M. Wen and K. A. Persson, J. Phys. Chem. A, 2023, 127, 2388–2398.
37. A. F. Harper, T. Huss, S. S. Köcher and C. Scheurer, Faraday Discuss., 2025 10.1039/d4fd00074a.
38. T. Charpentier, Faraday Discuss., 2025 10.1039/D4FD00129J.
39. C. Baerlocher and L. B. McCusker, Database of Zeolite Structures, http://www.iza-structure.org/databases/.
40. BIOVIA, Dassault Systèmes, BIOVIA Materials Studio, 2021.
41. H. Sun, P. Ren and J. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246.
42. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
43. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
44. K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K. R. Müller, J. Chem. Theory Comput., 2019, 15, 448–455.
45. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
46. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
47. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
48. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristall. Cryst. Mater., 2005, 220, 567–570.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
50. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
51. J. C. Facelli, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 58, 176–201.
52. R. Laskowski, P. Blaha and F. Tran, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195130.
53. H. Sun, S. Dwaraknath, M. E. West, H. Ling, K. Persson and S. Hayes, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-ssr6z.
54. C. J. Heard, L. Grajciar, C. M. Rice, S. M. Pugh, P. Nachtigall, S. E. Ashbrook and R. E. Morris, Nat. Commun., 2019, 10, 4690.
55. J. Li, J. Zhou, Y. Xiong, X. Chen and C. Chakrabarti, 2022 IEEE Workshop on Signal Processing Systems (SiPS), 2022, pp. 1–6.
56. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
57. L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949.
58. L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605.
59. E. Lippmaa, A. Samoson and M. Magi, J. Am. Chem. Soc., 1986, 108, 1730–1735.
60. L. Buitinck, G. Louppe, M. Blondel, F. Pedregosa, A. Mueller, O. Grisel, V. Niculae, P. Prettenhofer, A. Gramfort, J. Grobler, R. Layton, J. Vanderplas, A. Joly, B. Holt and G. Varoquaux, arXiv, 2013, preprint,  DOI:10.48550/ARXIV.1309.0238.
61. J. Kučera and P. Nachtigall, Microporous Mesoporous Mater., 2005, 85, 279–283.
62. A. Vjunov, J. L. Fulton, T. Huthwelker, S. Pin, D. Mei, G. K. Schenter, N. Govind, D. M. Camaioni, J. Z. Hu and J. A. Lercher, J. Am. Chem. Soc., 2014, 136, 8296–8306.
63. O. H. Han, C.-S. Kim and S. B. Hong, Angew. Chem., Int. Ed., 2002, 41, 469–472.
64. Y. Liu, H. Nekvasil and J. Tossell, J. Phys. Chem. A, 2005, 109, 3060–3066.
65. A. Kentgens, K. Scholle and W. Veeman, J. Phys. Chem., 1983, 87, 4357–4360.
66. C. Schroeder, S. I. Zones, M. R. Hansen and H. Koller, Angew. Chem., Int. Ed., 2022, 61, e202109313.
67. H. V. Thang, J. Vaculík, J. Přech, M. Kubů, J. Čejka, P. Nachtigall, R. Bulánek and L. Grajciar, Microporous Mesoporous Mater., 2019, 282, 121–132.
68. J. Dědeček, S. Sklenák, C. Li, B. Wichterlová, V. Gábová, J. Brus, M. Sierka and J. Sauer, J. Phys. Chem. C, 2009, 113, 1447–1458.
69. B. C. Knott, C. T. Nimlos, D. J. Robichaud, M. R. Nimlos, S. Kim and R. Gounder, ACS Catal., 2018, 8, 770–784.
70. E. G. Derouane and J. G. Fripiat, Microporous Mesoporous Mater., 1985, 5, 165–172.
71. W. Loewenstein, Am. Mineral., 1954, 39, 92–96.
72. O. Abdelrahman and A. Lawal, ChemRxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2023-njh44-v2.
73. M. B. Schmithorst, S. Prasad, A. Moini and B. F. Chmelka, J. Am. Chem. Soc., 2023, 145, 18215–18220.
74. C. A. Fyfe, H. Grondey, Y. Feng and G. T. Kokotailo, J. Am. Chem. Soc., 1990, 112, 8812–8820.
75. E. Dib, S. Mintova, G. N. Vayssilov, H. A. Aleksandrov and M. Carravetta, J. Phys. Chem. C, 2023, 127, 10792–10796.
76. Z. Bohström, B. Arstad and K. P. Lillerud, Microporous Mesoporous Mater., 2014, 195, 294–302.
77. V. Petranovskii, R. Marzke, G. Diaz, A. Gomez, N. Bogdanchikova, S. Fuentes, N. Katada, A. Pestryakov and V. Gurin, Impact of Zeolites and other Porous Materials on the New Technologies at the Beginning of the New Millennium, Elsevier, 2002, vol. 142, pp. 815–822.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed information on the structures, databases, kernel ridge regression model training, and molecular dynamics simulations. Also, additional data is provided in the Zenodo repository (https://doi.org/10.5281/zenodo.14063109) including a trained kernel ridge regression (KRR) model, training databases for MOR, MFI, and CHA structures with labeled DFT chemical shieldings, initial configurations used in the study, and an example of applying the KRR algorithm. See DOI: https://doi.org/10.1039/d4dd00306c

---