Deep-learning-enhanced exploration of peptide conformational space with high fidelity using hydrogen bond information

Abstract

Neural network potential models were trained using density functional theory (DFT) data for singly protonated hexapeptide, DYYVVR, previously studied through cryogenic ion spectroscopy and applied for its conformational analysis. A fragmentation-based approach was employed, in which the training datasets included capped dipeptides and capped single-residue clusters. The fragmentation approach effectively reduced energy prediction errors at reduced computational costs. To better capture a wider range of conformational space, all hydrogen bond types present in the peptide were included in the training dataset. As a result, the neural network potential model achieved a mean absolute error of 4.79 kJ mol⁻¹ in energy predictions compared to the DFT calculations. The model was further patched through an active learning scheme during basin-hopping simulations. The structures discovered during the simulations were optimized using the neural network model, leading to the identification of new conformational minima. The newly found structures successfully explained the experimental IR-UV depletion spectra obtained via cryogenic ion spectroscopy.

---

1. Introduction

The development of computational chemistry methods, combined with the steadily increasing computational power over recent decades, has facilitated accurate simulations of various biomolecular systems.¹ Nevertheless, these simulations are often limited due to the escalating computational costs with increasing system size. Even when simulating larger biomolecules becomes feasible, the intrinsic flexibility of these systems poses significant challenges in thoroughly exploring their extensive conformational spaces. The fragmentation approach has emerged as a viable strategy for effectively describing local atomic environments within large biomolecular systems. Numerous studies have demonstrated the effectiveness of combining the fragmentation approach with the inclusion–exclusion principle, enabling accurate estimation of the energy of the parent system using calculations performed on relevant fragments.^2–5 However, recalculation of fragment energies becomes necessary whenever the geometry of the parent structure changes.

Recent advances have shown deep learning methodologies to be particularly beneficial in addressing the challenges associated with conformational searches. Neural network potentials (NNPs) trained through active learning schemes utilizing high-accuracy computational data have proven to be powerful tools for this task. Well-trained deep learning models enable structural optimization with accuracy comparable to the computational methods employed during training.^6–10 However, generating extensive training datasets for large systems remains computationally demanding, and efficiently describing structural diversity in these datasets is essential for developing robust NNP models with reliable extrapolation capabilities. NNP models trained using fragmentation strategies have significantly advanced the exploration of large biomolecular systems, as demonstrated by several recent studies.^11–15 However, accurately modeling electrostatic and van der Waals interactions in larger parent systems remains challenging, as these interactions are not always fully captured by fragment-based calculations. Consequently, reliance on semi-empirical or molecular mechanics energy calculations becomes necessary for adequately representing such interactions.

The Korean group previously conducted cryogenic ion spectroscopy of a tryptic peptide from the kinase domain of an enzyme, singly protonated DYYVVR, and measured conformer-specific IR-UV depletion spectra for two distinct conformer families.¹⁶ (D stands for aspartic acid, Y for tyrosine, V for valine, and R for arginine.) There are 16 potential hydrogen-bond donors (–NH and –OH groups) and numerous hydrogen-bond acceptors, including the oxygens in five amide groups, two carboxyl groups, and two phenolic OH groups, and aromatic rings capable of NH– or OH–π interactions.^17–19 Due to the presence of many H-bond donors and acceptors, the extensive number of possible H-bond arrangements combined with the large size of the peptide significantly complicates a thorough conformational analysis.

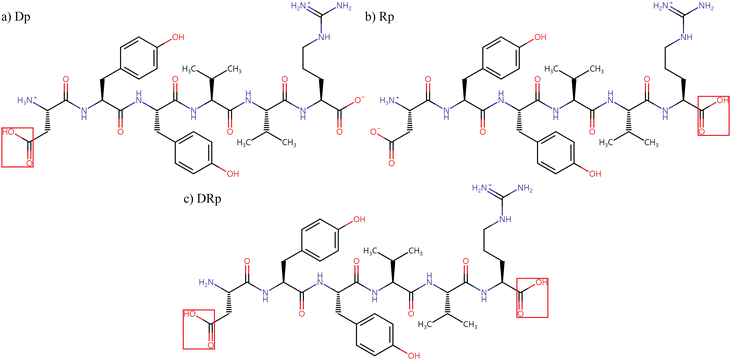
In this work, NNP models were trained to predict the energies and Cartesian forces of three protonation isomers of singly protonated DYYVVR, as shown in Scheme 1, to facilitate conformational searches. To reduce computational costs, HCO-/NH₂-capped dipeptides and capped single-residue clusters (cluster size of two) were extracted from the parent structures. The dipeptides describe through-bond interactions and the clusters represent short-distance through-space interactions, while long-distance through-space interactions are considered later by the hydrogen bond patterns of the parent molecule. The geometries and energies of the fragments were obtained by density functional theory (DFT) calculations and used for model training. The capped dipeptides and capped single-residue structures considered in this work are illustrated in Schemes S1 and S2 in the ESI,† respectively. In Section 3.1, two kinds of NNP models are compared to check the effect of adding fragment data into the training set: one trained with DFT data for randomly chosen parent structures only and others trained with fragments along with the same parent structures. In Section 3.2, the selection of parent structures for model training was guided by the H-bonding information within the peptide, aiming for extensive coverage of the conformational space of the dataset. After optimizing the model to reduce the mean absolute error in energy to close to 1 kcal mol⁻¹ relative to the DFT results from Section 3.2, the active learning approach, illustrated in Section 2.3, was employed to further improve the predictive accuracy of the NNP models, with a particular focus on the low-energy conformational region with relative energies below 100 kJ mol⁻¹. The newly identified structures from the active learning process, along with the simulated frequencies of their DFT-optimized structures, will be discussed in Section 3.3.

Scheme 1 Structures of three protonation isomers of singly protonated DYYVVR. (a) Dp, the carboxylate group of D is protonated; (b) Rp, that of R is protonated; (c) DRp, those of D and R are protonated.

2. Methods

2.1 Dataset preparation

A summary of the preparation of the sub-datasets is provided in Table 1. All sub-datasets were computed at the M06-2X/6-311+G(d,p) level of theory using the Gaussian16²⁰ program package. All sub-datasets except for Dip_1 and Cl_1 were prepared by collecting structures from geometry optimization trajectories. The Dip_1 and Cl_1 datasets were prepared by extracting fragment structures from selected parent structures, which were predicted by Model 1.1 (discussed in Section 3.1) to have energy errors exceeding 20 kJ mol⁻¹.

Table 1 Summary of the preparation of the sub-datasets, which comprise the training, validation, and test datasets. The validation and test datasets contain only parent structures, whereas the training dataset includes fragment structures along with selected parent structures split from the test dataset. The number of distinct structures was obtained after duplicate screening with a similarity threshold of 0.99 (See text and ESI for details)

Type of structures	Label	Preparation methods	Number of distinct structures
Parent structures	SP_0	Single-point calculations from optimization results in the previous work.^16	10 000
	Opt_0	Collecting structures directly from 600 optimization trajectories.	12 583
	Opt_1	Collecting structures directly from 680 optimization trajectories. (Different trajectories from Opt_0 were used.)	16 259
Capped dipeptides	Dip_0	Collecting structures directly from optimization trajectories of capped dipeptides.	13 488
	Dip_1	Extracting fragment structures from selected parent structures that Model 1.1 predicted with high error.	11 821
Capped cluster	Cl_1	Extracting fragment structures from the same parent structures set used for set Dip_1.	14 499

---

2.1.1 Collecting structures from optimization trajectories. As the models were intended for conformational search, they required training not only with local minima, but also with intermediate geometries. Therefore, structures for the datasets were collected from optimization trajectories and refined using the following procedure. Conformational searches of parent structures were done with the MMFF94s and MMFF94 force fields implemented in the CONFLEX²¹ and Gaussian16 program packages, respectively. The resulting structures were further optimized using the PM6 method, also implemented in Gaussian16. PM6 minima. The PM6-optimized minima were then used as starting points for geometry optimization at the M06-2X/6-311+G(d,p) level of theory. For each optimization trajectory, intermediate geometries with relative energies within 100 kJ mol⁻¹ of the corresponding energy minimum were initially selected. The selected geometries were then grouped into bins based on relative energy, using a bin size of 1 kJ mol⁻¹. Subsequently, one representative structure was collected from each energy bin. Duplicates in collected structures were then removed from the datasets using an ultrafast shape recognition algorithm²² that estimates the structural similarity of a pair of structures based on the similarity between a pair of 16 structural moments ranging from 0 (least similar pair of moments) to 1 (identical pair of moments). A detailed description is provided in the ESI.† Based on this similarity, structures with similarities higher than the threshold values were regarded as duplicates and removed from the datasets. The threshold values were initially set at 0.99 so that the trained models could accurately predict energy changes due to subtle geometry changes. During the active learning phase, the threshold values were lowered to 0.97 for more efficient model patching.

2.1.2 Dataset preparation for parent structures. Parent structure datasets were constructed three times with different sets of optimization trajectories. For the SP_0 dataset, optimization trajectories from the previous work¹⁶ computed at the ωB97X-D/cc-pVDZ level were collected. Single-point force computations for the collected structures were performed at the M06-2X/6-311+G(d,p) level of theory. The Opt_0 and Opt_1 datasets were prepared from 600 and 680 distinct optimization trajectories, respectively, calculated at the M06-2X/6-311+G(d,p) level of theory. DFT data collected from these trajectories were directly utilized after removing duplicate structures. The SP_0 and Opt_0 datasets were used to extract fragment structures comprising the Dip_1 and Cl_1 datasets. The SP_0, Opt_0, and Opt_1 have no duplicate structures between them. Randomly chosen parent structures from these datasets were used to train Models 1.x.

2.1.3 Dataset preparation for Dip_0, Dip_1, and Cl_1. Conformational searches for capped dipeptide structures were done using the DFTB3 method implemented in the GAMESS²³ program package, and DFTB3 minima were further optimized at the M06-2X/6-311+G(d,p). The same procedure that was used to prepare the Opt_0 and Opt_1 sets was used. Additional fragment structures were extracted from selected parent structures in the SP_0 and Opt_0 datasets. Parent structures for which Model 1.1 predicted energy errors higher than 20 kJ mol⁻¹ were extracted, and HCO– and NH₂– caps were applied (except for the N-end in D and C-end in R). A detailed procedure for structure extraction and capping is provided in the ESI.† Single-point force computations for capped fragments were done at the M06-2X/6-311+G(d,p).

2.2 Parent structure selection based on hydrogen bonds

The target molecule in this study possesses 336 internal degrees of freedom, making the conformational space prohibitively large for comprehensive exploration. Consequently, constructing a training dataset with extensive conformational coverage would require an impractically large number of structures. Conversely, selecting parent structures at random for model training as in Models 1.x will result in a trained model with poor predictive performance because it cannot adequately represent the conformational diversity of the peptide. As peptide conformations are largely influenced by hydrogen bonds, a strategically chosen subset of structures selected based on their H-bond patterns can efficiently represent a broader conformational space. To achieve this, our approach involves identifying H-bond information across all parent structures in the SP_0, Opt_0, and Opt_1 datasets and selecting a representative subset of parent structures based on these data, ensuring coverage of the diverse H-bond combinations present within the datasets. All H-bonds (XH⋯Y) of the structures within the datasets were identified with distance and angle (∠XHY) thresholds of 3 Å and 120°, respectively. We found that there are 130 combinations of different H-bonds in the datasets out of 203 possible ones. Missing hydrogen bonds had too high energy, and some examples are shown in Fig. S3 in the ESI.† The most abundant type of H-bond is C7 interaction between the amide NH in the 2nd valine and the amide oxygen in the 2nd tyrosine. The training and validation sets were constructed to include nearly all distinct types of H-bonds present in the dataset, with a larger number of structures containing H-bond types frequently found in the distribution, such as the C7 interaction mentioned above. The most abundant C7 structure, for instance, occurred 18 975 times in the dataset and was included 2158 times in the training set for Model 2.1. The six least-frequent H-bonds occurred only once in the total dataset. Five of them were included in the training set, while the remaining one was used for validation. Parent structures strategically chosen in this way were used to train Models 2.x. Details of the H-bond selection procedure are described in the ESI.†

2.3 NNP model training

An atomistic SchNet architecture^24–26 was employed to train NNP models for predicting the energies and Cartesian forces of diverse structures of the singly protonated hexapeptide DYYVVR. A feature dimension (number of neurons) of 128 was used, and four interaction blocks were applied to describe atomic environments. Within each interaction block, 75 Gaussian basis functions with a cutoff radius of 15 Å were utilized to construct continuous convolutional filters. All training was performed using a cosine annealing schedule with warm restarts, allowing models to explore adjacent loss minima during model optimizations. The performance of a trained model was validated by comparing the energies and Cartesian forces of the structures in a validation dataset computed by the NNP model and by DFT calculation at M06-2X/6-311G(d,p). Validation datasets were SP_0 + Opt_0 for Models 1.x and SP_0 + Opt_0 + Op_1 for Models 2.x. The mean absolute error in energy (MAE_E) and Cartesian force (MAE_F) therefore indicate the difference between an NNP model and the DFT calculation. A detailed description of the model training is provided in the ESI.†

2.4 Active learning scheme

After the trained model achieved a prediction performance near 1 kcal mol⁻¹ relative to DFT results in Model 2.1, an active learning scheme was applied to patch the model, while finding new structures. The NNP models were used as an external program during geometry optimizations by Gaussian16. In the 1st cycle of active learning, the latest NNP model before active learning (Model 2.1) was used to optimize 38 416 PM6 minima. In the optimization results, 3632 unphysical structures were found with several broken bonds or extremely short interatomic distances in the NNP-optimized minima. The NNP model was patched as follows. For each of 35 randomly chosen optimization trajectories containing broken structures, an intermediate structure was taken one optimization step before the problem occurred. The single-point energy of each intermediate structure was calculated at M06-2X/6-311+G(d,p) and implemented into the training set. As a result, 605 structures that previously had broken structures were successfully optimized after the patch. After screening duplicate structures, the single-point energies of 599 distinct minima were calculated at the DFT level and added to the training set, resulting in Model 2.1.1. From the 2nd to 6th cycles, conformational searches were done with a basin-hopping algorithm²⁷ at the PM6 level. The PM6 minima found in each cycle were optimized with the preceding NNP model. In the second cycle, 572 structures, including intermediate geometries, were patched. From the third to sixth cycles, optimization trajectories containing unphysical structures were used to further patch the model using the same procedure as in the first cycle. Intermediate structures were included only if their relative NNP energies were below 200 kJ mol⁻¹. From the third and sixth cycles, the 50 lowest distinct NNP minima were also used for the patch to enhance the model performance in the lower energy region. As a result, 1553 structures, including intermediate structures, were added to the training set during the active learning process. The resulting NNP model, Model 2.1.6, represents the latest version.

3. Results and discussion

3.1 Effect of adding fragment structures to the training set

Four models (from Model 0 to Model 1.2) were trained with four different training sets composed of fragments and randomly chosen parent structures. The compositions of these sets are shown in Table 2. Model 0, which was trained with the Dip_0 dataset without any parent structures, showed poor prediction results on the test set composed of the SP_0 and Opt_0 datasets, with a MAE in energy of 573 kJ mol⁻¹. The scatter plots of the prediction results by Model 0 in Fig. S4 in the ESI,† show that there is almost no correlation between the DFT and NNP level data. This implies that the data of parent structures should be added into the training set. Thus, Model 1.0 was trained with 3033 randomly chosen parent structures as a starting model, and the prediction results of Model 1.0 were first compared with those of Model 1.1 trained with DYYVVR + Dip datasets. Prediction results of the two models are shown in Fig. 1. The results show that Model 1.1 shows slightly higher errors compared to Model 1.0. The Dip_0 structures were simply collected from optimization trajectories, whereas parent structures have many intermolecular interactions that can change the local structures, deviating from the structures in the Dip_0 dataset. Moreover, noncovalent interactions between residue pairs that are not directly bonded with each other can only be described by parent structures as there is no such interaction in the Dip_0 dataset. Therefore, additional tests in which more relevant fragment structures were added to the training set were necessary to determine the effect of fragment structures on model training.

Table 2 Compositions of training sets used to train NNP models

Name	Description	Composition
		Parent structures	Fragment structures
Model 0	Dip only	None	Dip_0
Model 1.0	DYYVVR only	Randomly chosen 3033 structures from SP_0 and Opt_0 datasets	None
Model 1.1	DYYVVR + Dip		Dip_0
Model 1.2	DYYVVR + Dip + highE		Dip_0 + Dip_1 + Cl_1
Model 2.0	H-bond (3k)	3001 structures selected based on H-bonds	Dip_0 + Dip_1 + Cl_1
Model 2.1	H-bond (4.5k)	4503 structures selected based on H-bonds	Dip_0 + Dip_1 + Cl_1

---

Fig. 1 Scatter plots of the relative energy (a), (c) and (e) and Cartesian force (b), (d) and (f) prediction for 22 583 DYYVVR structures (SP_0 and Opt_0 datasets) using Model 1.0 (a) and (b), Model 1.1 (c) and (d), and Model 1.2 (e) and (f). Relative energies are referenced to the lowest DFT energy. Shaded regions in (c) indicate the structures that have energy errors higher than 20 kJ mol⁻¹ and were used to generate the Dip_1 and Cl_1 datasets for Model 1.2. MAE_E, mean absolute error in energy; MAE_F, mean absolute error in force.

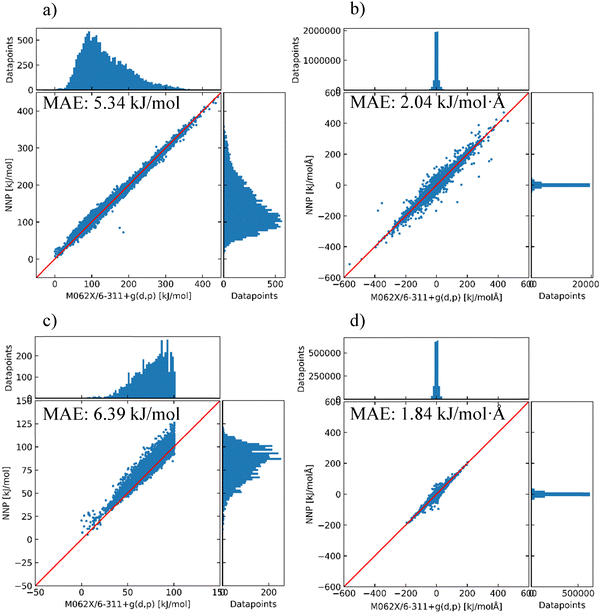
To select parent structures for generating the Dip_1 and Cl_1 datasets, which are more relevant to the parent system, Model 1.1 was used to collect parent structures with a high prediction error in energy larger than 20 kJ mol⁻¹. 2165 parent structures located in shaded regions of Fig. 1 were used for fragment structure generation, and Model 1.2 was trained. The prediction results of Models 1.0 and 1.2 are shown in Fig. 1. Adding Dip_1 and Cl_1 to Model 1.2 slightly improved the energy prediction, by only 0.22 kJ mol⁻¹ when compared with Model 1.0. However, considering only ∼9.6% of parent structures in the test set were patched with relevant fragments, this approach will enable efficient model improvement at significantly lower computational cost compared to directly using additional parent structures. On average, DFT calculations for all fragments extracted from a single parent structure took 13.4 core hours, whereas a calculation for a single parent structure took 42.4 core hours on an Intel Xeon Phi 7250 1.40 GHz.

3.2 Effect of parent structure selection for training set based on H-bonds

To improve the performance of the model in the prediction of energy and force, three NNP models with different training sets (Model 1.2, Model 2.0, and Model 2.1 in Table 2) were investigated to check the effect of the structure selection discussed in Section 2.2. To validate the assumption described in Section 2.2, the predictions of Models 2.0 and 2.1 (H-bond 3k and 4.5k models) on the total parent dataset (SP_0 + Opt_0 + Opt_1) are compared in Fig. 2. Model 2.0 had a significantly lower MAE in energy than Model 1.2 (by 3.21 kJ mol⁻¹), demonstrating that Model 2.0 exhibited better extrapolation quality compared to Model 1.2. The lower MAE indicates improved correlation between the NNP Model 2.0 and DFT energies, demonstrating that H-bond-based structure selection better represents the dataset than random sampling. However, while this method yields an efficient representative subset, it may not fully capture the entire conformational space. For additional improvement of the model, Model 2.1 trained with the H-bond (4.5k) dataset was tested with the same total parent dataset. Most outliers in Model 2.0 moved near the diagonal in Model 2.1, although the added parent structures in the training set were not intentionally focused on these outliers. As a result, the latest model in this section reached a MAE in energy of 4.79 kJ mol⁻¹ compared to the M06-2X/6-311G(d,p) level, which has been shown to be appropriate to assess the accuracy of an NNP model.⁷

Fig. 2 Scatter plots of the relative energy (a) and (c) and Cartesian force (b) and (d) prediction for 38 842 DYYVVR structures using Model 2.0 (a) and (b) and Model 2.1 (c) and (d). Relative energies are referenced to the lowest DFT energy. MAE_E, mean absolute error in energy; MAE_F, mean absolute error in force.

3.3 Active learning and newly found minima

Through the series of active learning cycles, 21 distinct NNP minima with relative NNP energies lower than 20 kJ mol⁻¹ were newly found. The Korean group previously conducted geometry optimizations and harmonic frequency calculations for candidate structures at the ωB97X-D/cc-pVDZ level of theory to explain the experimental IR-UV depletion spectra.¹⁶ For further investigation using the newly found minima, 21 NNP minima and the structure that was tentatively assigned to the experimental data in the previous research were used for geometry optimizations and harmonic frequency calculations at the M06-2X/6-311+G(d,p) level of theory. As a result, 22 minima including the previously assigned structure were converged to 19 DFT minima. The electronic energy and sum of electronic and thermal free energy at 300 K of the 10 lowest-electronic-energy minima are summarized in Table 3.

Table 3 Relative energies (in kJ mol⁻¹) calculated at the M06-2X/6-311+G(d,p) level of theory for 10 DFT-optimized structures at 300 K. Energies are reported as electronic energies and electronic energies with thermal free-energy corrections. Structures labeled as “Conf_x” represent conformers optimized from newly identified NNP minima, whereas “Prev” refers to a conformer re-optimized from the previously reported¹⁶ structure. Rows containing at least one relative energy value below 5 kJ mol⁻¹ are highlighted in yellow

Label	Relative energy
	Electronic energy	Electronic + thermal free energy
Conf_0	0	0
Prev	0.785	27.3
Conf_1	2.13	10.1
Conf_11	2.29	27.5
Conf_12	4.70	29.7
Conf_13	6.27	37.1
Conf_2	6.87	3.17
Conf_3	7.33	5.76
Conf_4	8.20	4.33
Conf_14	9.01	35.1

---

The Prev structure, found at a different DFT level but now optimized at the same level as the other Conf_x, still has a low relative electronic energy close to that of the Conf_0 structure, which is the global minimum found so far. However, in terms of thermal free-energy correction, the corrected energy of the Prev structure is much higher than that of Conf_0. Comparison of corrected energies at room temperature does not seem to be logical at first glance. However, considering the experiment was conducted using electrospray ionization and cryo-cooling, the conformation population at room temperature can be partially captured and certain conformations can be kinetically trapped due to fast cooling of ions in the ion trap.²⁸

The harmonic vibrational frequencies of the DFT minima were calculated and multiplied by the following scaling factors. For phenolic OH stretches, a scaling factor of 0.9375 was used to locate harmonic frequencies of free phenolic OH close to 3650 cm⁻¹, which is validated by other experimental data.^29,30 In the case of carboxylic OH, a factor of 0.9357 was used to locate free carboxylic OH frequencies near 3570 cm⁻¹, which is also validated by spectroscopic studies with a different system.^31,32 NH stretches in the sidechain of arginine were given a scaling factor of 0.9500 so that the harmonic frequencies of the solvated guanidinium ion, Gdm⁺(H₂O)₁₋₂, calculated at the M06-2X/6-311+G(d,p) level of theory would have the best agreement with the corresponding experimental data.³³ Lastly, for the rest of the NH stretches, a factor of 0.9484 was used to locate harmonic frequencies of free amide NH close to 3480 cm⁻¹.³⁴ After applying the scaling factors, the simulated frequencies of the minima structures were compared with the experimental data. Two conformations, which are depicted in Fig. S5 (ESI†), were found to have vibrational frequencies that agree well with the experiment. Their vibrational frequencies above 3000 cm⁻¹ are shown in Fig. 3 and summarized in Tables S3 and S4 (ESI†). As the scaling factors were fitted with free stretches (except for the guanidinium NHs), the perturbed NH stretches can be more red-shifted. Considering that the two structures have relatively low energies after thermal free-energy corrections, the potential energy surface around these minima is expected to be shallow, allowing multiple conformations to coexist, which might explain the broad feature from 3100 to 3450 cm⁻¹. Detailed explanations of the assignment can be found in Sections S9 and S10 of the ESI.†

Fig. 3 IR-UV depletion spectra from the previous study¹⁶ are shown as solid lines (a) and (c), and simulated scaled harmonic frequencies of Conf_0 and Conf_2 are shown as color-coded bars (b) and (d). (Red: phenolic OHs, blue: NHs in the sidechain in arginine, green: other NHs, black: carboxylic OHs). The depletion spectra were obtained by monitoring the UV photodissociation signal at two different vibronic bands, while scanning the IR laser. Experimental details are explained in the ESI.†

3.4 Performance of the latest model

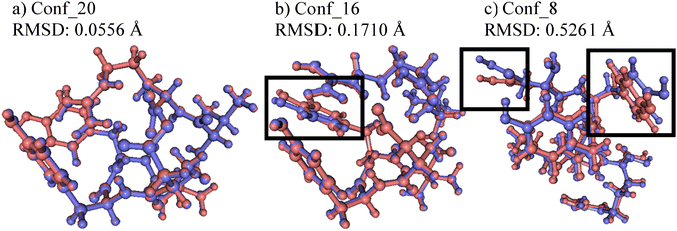
To estimate the performance of the NNP models in geometry optimizations, the NNP minima and corresponding DFT minima were compared. The Cartesian root mean square deviations (RMSD) between pairs of minima structures were calculated after applying the Kabsch–Umeyama algorithm³⁵ and are summarized in Table S2 (ESI†). The average of the Cartesian RMSDs is 0.1966 and the standard deviation is 0.1200. Pairs of structures with the lowest (0.0556, Conf_20), median (0.1710, Conf_16), and highest (0.5261, Conf_8) RMSDs are shown in Fig. 4. For (a) and (b) in Fig. 4, the pairs of structures are nearly overlapped except for the boxed phenol groups in (b) that slightly deviate from each other. Even in (c), which has the highest RMSD, both minima are similar to each other except for the boxed carboxylic (left) and phenol (right) groups.

Fig. 4 Pairs of structures (NNP minima and corresponding DFT minima) with (a) the lowest (Conf_20), (b) median (Conf_16), and (c) highest (Conf_8) values of Cartesian RMSDs. DFT minima are colored red, whereas NNP minima are colored blue. Deviated sidechains are boxed in (b) and (c).

To further investigate the optimization quality, the latest NNP Model 2.1.6 after active learning was used to predict the single-point energy and Cartesian forces of the 21 newly found NNP minima and corresponding DFT minima structures discussed in 3.3. In the case of DFT minima that were not included in the training set, the model could not predict the energy accurately, yielding an MAE value of 12.0 kJ mol⁻¹. However, the model predicted the Cartesian force much more accurately, with an MAE value of 1.42 kJ mol⁻¹ Å⁻¹, which is close to the default threshold value of maximum force for geometry optimization in ab initio computation packages. Thus, the model can significantly reduce computational costs by bringing structures close to the DFT minima, thereby decreasing the number of DFT optimization steps required for convergence.

Parent structures in the total dataset were also used to estimate the performance of the latest model. The prediction results are shown in Fig. 5. In this case, the DFT-calculated structures during active learning along with the SP_0, Opt_0, and Opt_1 datasets were screened out with a similarity threshold of 0.97 and used as a validation dataset to estimate the generic performance of the model. The number of structures was reduced to 14 562 for the entire energy range, and 5103 for ΔE ≤ 100 kJ mol⁻¹. As distinct structures were added sequentially during the active learning process, the MAEs in energy are increased. However, MAEs in the Cartesian force remain at low values, showing that the accuracy of the model in the Cartesian force is focused more on the low-energy region. Therefore, the NNP model can still be used to pre-optimize structures that can be further optimized at the DFT level with a reduced number of DFT optimization steps.

Fig. 5 Scatter plots of relative energy (a) and (c) and Cartesian force (b) and (d) prediction for 14 562 (a) and (b) and 5103 (c) and (d) DYYVVR structures using the latest Model 2.1.6. MAEs are displayed for each plot. Both the NNP and DFT relative energies were calculated using the DFT energy of the lowest energy structure.

During the active learning phase, 48 726 parent structures were optimized using NNP models. A single-point force calculation for a parent structure using an NNP model takes approximately 0.97 s (2.7 × 10⁻⁴ core hours) on average using an Intel Xeon Gold 6226R CPU at 2.90 GHz. Assuming that a geometry optimization job typically requires about 45 cycles per structure, the total computational time required for optimizing all 48 726 structures using NNP models would be only about 1245 core hours, which is achievable within two days using a single 32-core processor.

4. Conclusions

In this work, we developed an NNP model to efficiently explore the conformational space of a hexapeptide, singly protonated DYYVVR. A fragmentation approach was applied to a subset of parent structures that the initial parent-only model was unable to accurately describe. Incorporating fragment structures into the training dataset resulted in a modest improvement in prediction performance, primarily due to the limited number of parent structures used for generating fragments relevant to the overall parent system. However, this approach is expected to become particularly important when applied to larger peptide systems, for which computations of the full parent systems at sufficient accuracy become prohibitively expensive. Following the implementation of the fragmentation approach, the parent structures selected for model training were further refined based on the H-bond distribution present in the dataset. Although representing a (3N-6)-dimensional conformational space using the number of unique H-bonds is inherently approximate, this strategy substantially enhanced the performance by effectively covering a broader conformational space. After constructing a representative and structurally diverse training set based on the identified H-bond patterns, we carried out 48 726 optimizations while continuously improving the NNP model. Performing such a huge number of optimizations at DFT-level accuracy would have been nearly impossible using conventional high-level computations. The improved NNP model was found to be able to optimize structures to minima closely matching the geometries obtained from high-level computations, significantly reducing computational costs. This improvement was primarily due to the high accuracy of the model in predicting Cartesian forces, which is essential for geometry optimization. Furthermore, the refined model successfully identified structures that can support the previously reported experimental spectra. Our approach is expected to be applicable to other biomolecular systems with minor modifications, beginning with the generation of high-quality, structurally diverse training datasets computed at lower levels of theory. This strategy is feasible because hydrogen bonds can be readily identified using simple distance and angle calculations, significantly reducing the computational cost.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2021K2A9A1A06086236 and RS-2021-NR060141) and the Ministry of Science and Technology of Taiwan (MOST 111-2923-M-001-002-MY2). Computational resources were supported by the National Supercomputing Center of Korea (KSC-2023-CRE-0263) and the National Center for High-Performance Computing (NCHC) of Taiwan. The authors thank Mr Hieu Cao Dong, Mr Huu Trong Phan, and Dr Po-Jen Hsu for helpful discussions and kind assistance.

References

1. D. J. Cole and N. D. M. Hine, J. Phys.: Condens. Matter, 2016, 28, 393001.
2. X. He, T. Zhu, X. Wang, J. Liu and J. Z. H. Zhang, Acc. Chem. Res., 2014, 47, 2748–2757.
3. S. Li, W. Li and J. Ma, Acc. Chem. Res., 2014, 47, 2712–2720.
4. Y. Zhang, W. Xia, J. Xiao and J. Z. H. Zhang, J. Chem. Theory Comput., 2025, 21, 2129–2139.
5. S. Debnath, A. Sengupta, K. V. J. Jose and K. Raghavachari, J. Chem. Theory Comput., 2018, 14, 6226–6239.
6. P.-J. Hsu, A. Mizuide, J.-L. Kuo and A. Fujii, Phys. Chem. Chem. Phys., 2024, 26, 27751–27762.
7. H. C. Dong, P.-J. Hsu and J.-L. Kuo, Phys. Chem. Chem. Phys., 2024, 26, 11126–11139.
8. H. T. Phan, P.-K. Tsou, P.-J. Hsu and J.-L. Kuo, Phys. Chem. Chem. Phys., 2023, 25, 5817–5826.
9. P.-K. Tsou, H. T. Huynh, H. T. Phan and J.-L. Kuo, Phys. Chem. Chem. Phys., 2023, 25, 3332–3342.
10. Q. Zeng, J.-N. Chen, B. Dai, F. Jiang and Y.-D. Wu, J. Chem. Theory Comput., 2025, 21, 991–1000.
11. Z. Cheng, J. Du, L. Zhang, J. Ma, W. Li and S. Li, Phys. Chem. Chem. Phys., 2022, 24, 1326–1337.
12. J. R. Vornweg, M. Wolter and C. R. Jacob, J. Comput. Chem., 2023, 44, 1634–1644.
13. H. Wang and W. Yang, J. Chem. Theory Comput., 2019, 15, 1409–1417.
14. Z. Wang, Y. Han, J. Li and X. He, J. Phys. Chem. B, 2020, 124, 3027–3035.
15. M. Xu, T. Zhu and J. Z. H. Zhang, Front. Chem., 2018, 6, 189.
16. J. H. Kwon, M. J. Lee, G. Song, K. Tsuruta, S.-I. Ishiuchi, M. Fujii and H. Kang, J. Phys. Chem. Lett., 2020, 11, 7103–7108.
17. M. Mons, I. Dimicoli, B. Tardivel, F. Piuzzi, V. Brenner and P. Millié, Phys. Chem. Chem. Phys., 2002, 4, 571–576.
18. W. Y. Sohn, J. J. Kim, M. Jeon, T. Aoki, S.-I. Ishiuchi, M. Fujii and H. Kang, Phys. Chem. Chem. Phys., 2018, 20, 19979–19986.
19. S. Kumar, K. K. Mishra, S. K. Singh, K. Borish, S. Dey, B. Sarkar and A. Das, J. Chem. Phys., 2019, 151, 104309.
20. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev.C.01, 2016.
21. H. Goto and E. Osawa, J. Am. Chem. Soc., 1989, 111, 8950–8951.
22. P. J. Hsu, S. A. Cheong and S. K. Lai, J. Chem. Phys., 2014, 140, 204905.
23. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102.
24. K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722.
25. K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K. R. Müller, J. Chem. Theory Comput., 2019, 15, 448–455.
26. K. T. Schütt, S. S. P. Hessmann, N. W. A. Gebauer, J. Lederer and M. Gastegger, J. Chem. Phys., 2023, 158, 144801.
27. L. Zhan, B. Piwowar, W. K. Liu, P. J. Hsu, S. K. Lai and J. Z. Y. Chen, J. Chem. Phys., 2004, 120, 5536–5542.
28. S. Vahidi, B. B. Stocks and L. Konermann, Anal. Chem., 2013, 85, 10471–10478.
29. H. D. Bist, J. C. D. Brand and D. R. Williams, J. Mol. Spectrosc., 1967, 24, 402–412.
30. S. Tanabe, T. Ebata, M. Fujii and N. Mikami, Chem. Phys. Lett., 1993, 215, 347–352.
31. J. T. Lawler, C. P. Harrilal, A. F. DeBlase, E. L. Sibert, S. A. McLuckey and T. S. Zwier, Phys. Chem. Chem. Phys., 2022, 24, 2095–2109.
32. J. A. Stearns, S. Mercier, C. Seaiby, M. Guidi, O. V. Boyarkin and T. R. Rizzo, J. Am. Chem. Soc., 2007, 129, 11814–11820.
33. R. J. Cooper, S. Heiles, M. J. DiTucci and E. R. Williams, J. Phys. Chem. A, 2014, 118, 5657–5666.
34. J. M. Voss, K. C. Fischer and E. Garand, J. Mol. Spectrosc., 2018, 347, 28–34.
35. J. Lawrence, J. Bernal and C. Witzgall, J. Res. Natl. Inst. Stand. Technol., 2019, 124, 124028.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01632k

---