Open Access Article
Open Access ArticleSpin–orbit coupling effects hidden behind the photophysics of phosphorescent chiral cyclometalated Pt(II) complexes†
Thomas
Groizard
,
Souvik
Mandal
 ,
Christophe
Gourlaouen‡
,
Christophe
Gourlaouen‡
 and
Chantal
Daniel
and
Chantal
Daniel
 *
*
Laboratoire de Chimie Quantique Université de Strasbourg CNRS UMR7177, Institut Le Bel 4 Rue Blaise Pascal, 67000 Strasbourg, France. E-mail: c.daniel@unistra.fr
First published on 11th June 2025
Abstract
The electronic and (chiro-) optical properties of [Pt(pCpy)(acac)] 1 and [Pt(pCpz)(acac)] 2 (pCpy = 2-[2,2]-paracyclophane-4-yl)pyridyl; pCpz = 1-[2,2]-paracyclophane-4-yl)pyrazolyl; acac = dimethyl-substituted acetylacetonato), representative of phosphorescent chiral cyclometalated Pt(II) complexes, are investigated by means of density functional theory (DFT) and its time-dependent extension so-called TD-DFT, including spin–orbit coupling (SOC) effects. The computed absorption, phosphorescence and circularly polarized luminescence (CPL) spectra are compared to the available experimental spectra, and analysed on the basis of spin–orbit interactions and electronic excited state sub-levels. The major role of the SOC is established and deciphered for both complexes. Spin–orbit sub-levels of the low-lying triplet manifold not only perturb the absorption spectra by a 60–70 nm shift to the red, but entirely control the phosphorescence and CPL activities, in terms of intensity and composition. It is shown that the substitution of a pyridyl ligand in 1 with a pyrazolyl in 2 has dramatic consequences on the photophysics of these “case-study” molecules. Indeed, the character and the energetics of the lowest triplet states participating in the emission properties are drastically affected by this change of ligands. Whereas [Pt(pCpy)(acac)] 1 can be considered as an “easy case”, both experimentally and theoretically, [Pt(pCpz)(acac)] 2 represents a challenge computationally due to the presence of two nearly degenerate emissive triplet states. The correlation between the structural/electronic properties of the excited states contributing to the spectra is discussed as well as the early time (<1 ps) photophysics simulated by non-adiabatic quantum dynamics for the two complexes.
1 Introduction
Over the last three decades,1 a multitude of third-row transition metal complexes (TMCs) with a variety of ligands have been synthesized to optimize the luminescent properties and to control the branching ratio between radiative and non-radiative decays.2–6 The energy gap between the lowest triplet metal-centered (MC) and metal-to-ligand-charge-transfer (MLCT) or ligand-centered (LC) excited states and their coupling with the electronic ground state and with the environment were mainly considered. Further analysis scrutinized spin–orbit coupling (SOC) effects which are responsible for efficient intersystem crossing (ISC) and subsequent population of the lowest potentially luminescent triplet excited state, 3LC possibly contaminated by 3MLCT state contribution. The introduction of multidentate ligands, containing metal–carbon bonds via pincer cyclometalated substitution, initiated applications in functional materials, chromic devices, memory storage, supramolecular assemblies and probes or ion sensors.7–12 Most of the TMCs, used in organic light-emitting devices (OLEDs), for instance, are either achiral or racemic mixtures.13 However, enantiopure compounds might provide circularly polarized luminescence (CPL) emission opening opportunities to overcome technical issues as well as emerging applications. CPL materials may contribute to the reduction of power consumption in light-emitting devices14 and are of central importance in applications such as three-dimensional OLED devices, quantum computing,15 spintronics,16 and bio-imaging.The development of chiral TMCs has been mainly driven by their application in asymmetric catalysis, near infra-red (NIR) chiroptics, structural probe ferroelectricity, and stereochemistry with a few studies dedicated to their CPL activity as illustrated by early experiments reported for Ir(III) complexes.17,18 Despite excellent photophysical properties these molecules exhibit a quite low electro-luminescence dissymmetry factor. Introduction of ligand-based helicoidal chirality, as proposed in metallhelicene Ir(III), Pt(II) and Re(I) complexes,19–25 allowed the tuning of both electric and magnetic transition dipole moments keeping high electro-luminescence (EL) efficiency together with significant chiro-optical activity. However, an in-depth fundamental understanding of the parameters governing chiroptical properties in these phosphorescent TMCs and a full rationalization of such parameters is still lacking for optimizing the design of new CPL emitters.
Whereas the Sn, Tn → S0 luminescent properties can be determined easily on the basis of the low-lying excited state structural properties,26 a more challenging step forward is the modeling of the electronic circular dichroism (ECD) and CPL spectra. Indeed, computational protocols have been mainly developed for organic molecules, the circularly polarized light responses of which are governed by S0 and a few low-lying singlet states.27 The spin-allowed ECD and CPL spectra are computed from the oscillatory and rotational strengths associated with the active singlet excited state at the Franck–Condon (FC) geometry.
Taking into account the SOC effects in the computation of ECD and CPL spectra needs another strategy. Indeed, calculating these properties at the triplet excited state equilibrium geometry, within a relativistic perturbative approach,28 leads to allowed electric and magnetic dipole transitions based on spin–orbit perturbed ground and excited states. Both oscillator and rotational strengths associated with “spin–orbit” transitions become accessible.
On the basis of a new computational protocol developed in ORCA29 to interpret and predict photophysical properties in a series of chiral non-helicenic and helicenic Re(I) complexes, extensively investigated experimentally by Crassous et al.,21,22 we have established the factors that control the phosphorescence, the radiative and non-radiative decays and the CPL activity of these molecules.30 We have shown that the electronic character of the low-lying singlet and triplet excited states and their spin–orbit splitting and mixing play a major role in the control of the zero-field splitting (ZFS) parameters and of the magnetic and electric transition dipole moment relative orientations. Both the ligand localized nature of the emissive state and the steric effects induced by helicenes influence drastically the phosphorescence relaxation time and the CPL intensity. Extending the structural diversity by introducing planar chirality directly coordinated onto a metal center may lead to a specific response of the complexes in terms of CPL activity because of the presence of low-lying charge transfer (CT) states. This could help in a deeper understanding of the influence of electronic and structural parameters on the CPL activities in chiral emitters. It would also be of interest to use ligands made via more straightforward synthetic protocols.
The use of paracyclophane derivatives as chiral auxiliary ligands has offered a platform for a number of new organic compounds31–33 as well as transition metal complexes.34,35 Combining photophysical and optoelectronic properties with chirality in potentially phosphorescent Pt(II) and Ir(III) complexes, Thompson et al.35 have shown that whereas a substitution by monoanionic cyclophane ligand 2-([2.2]-paracyclophane-4-yl)pyridyl (pCpy) leads to highly emissive molecules at room temperature, pyrazolyl analogs, 1-([2.2]-paracyclophane-4-yl)pyrazolyl (pCpz), provide weakly emissive compounds. This has been attributed to thermally activated non-radiative decay from high-lying triplet states in the pyrazolyl complex. However, the potential for chiro-optical activity has not yet been experimentally investigated.
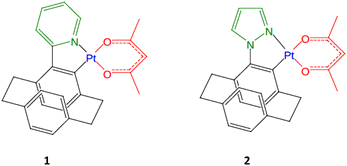
Herein, we propose a detailed theoretical investigation of the photophysics and (chiro-) optical properties of [Pt(pCpy)(acac)] 1 and [Pt(pCpz)(acac)] 2 (Scheme 1), synthesized by Thompson et al.35 Our objective is to analyze and understand the different luminescence behavior observed experimentally and to predict the opto-chiral activity in this class of emitters on the basis of spin–orbit interactions, structural and electronic properties. It will be shown that despite their apparent similarity the two molecules are very different in terms of potentially emissive states and spin–orbit interactions. In addition, whereas Pt-Cpy 1 is an “easy case” with one single emissive T1 electronic state, Pt-Cpz 2 is a “tough case”, challenging for both experimentalists and theoreticians, with potential emission governed by two nearly-degenerate triplet excited states.
2 Theoretical background
2.1 Methodological approach
The theory underlying the computational protocol developed in ORCA for calculating absorption, spontaneous luminescence, ECD and CPL cross sections as well as their respective radiative rates is detailed in our seminal article dedicated to the Re(I) complexes.30 The cross sections are expressed at the first-order perturbative treatment within the weak field approximation and the general expression of Fermi's golden rule, whereas the radiative rates are calculated within the electric dipole approximation.The cross sections are given by
 | (1) |
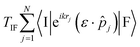 denotes the transition probability employing the full field-matter interaction operator (FFMIO), rj and
denotes the transition probability employing the full field-matter interaction operator (FFMIO), rj and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) j are the position and the momentum operators of the jth particle, k and ε denote the wave and polarization vectors of the incident radiation field. EFI is the transition energy, δ refers to the line-broadening arising from the lifetimes of the relevant final states, and c is the speed of light.
j are the position and the momentum operators of the jth particle, k and ε denote the wave and polarization vectors of the incident radiation field. EFI is the transition energy, δ refers to the line-broadening arising from the lifetimes of the relevant final states, and c is the speed of light.
Within the electric dipole approximation (ED) the respective radiative rates for the absorption and the spontaneous photoluminescence are given by eqn (2) and (3), respectively:
 | (2) |
 | (3) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) defines the electric dipole operator as
defines the electric dipole operator as  , here A sums over nuclei with charges ZA at positions RA, i over the electrons, n is the refractive index, and ħ is the Planck constant divided by 2π.
, here A sums over nuclei with charges ZA at positions RA, i over the electrons, n is the refractive index, and ħ is the Planck constant divided by 2π.
The formalism, inspired by the one developed for magnetic circular dichroism (MCD),36 allowed the proposal of a unified framework for the calculation of both the optical (absorption/emission) and chiro-optical (ECD/CPL) intensities and radiative rates. Details about the formulation of the MCD expressions within the framework of the full field-matter interaction operator (FFMIO) can be found in the ESI.†
By analogy, within the ED approximation, the equations developed for MCD can be used to generate absorption and luminescence cross sections. Including electric (ED) and magnetic dipole (MD) interactions upon orientational averaging will generate the respective ECD and CPL radiative transition rates:
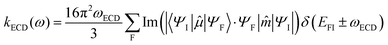 | (4) |
 | (5) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) defines the electric dipole operator while
defines the electric dipole operator while ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) is the respective magnetic dipole operator
is the respective magnetic dipole operator  , me is the electron mass and Im(|〈ΨI|
, me is the electron mass and Im(|〈ΨI|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ΨF〉〈ΨF|
|ΨF〉〈ΨF|![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) |ΨI〉|) represents the rotatory strength (RIF).
|ΨI〉|) represents the rotatory strength (RIF).
The ECD and CPL spectral intensities are represented against normalized absorption and photoluminescent intensities defining, similar expressions for, the respective dissymmetry factors gabs and glum
 | (6) |
 | (7) |
Spin–orbit coupling (SOC) along with the Zeeman interactions introduced in the framework of quasi-degenerate perturbation theory (QDPT)37 act as a perturbation to the non-relativistic Hamiltonian which takes the form:
 | (8) |
In this approach, the SOC operator is approximated by the spin–orbit mean field (SOMF) operator,38 which is an effective one-electron operator that contains one- and two-electron SOC integrals and also incorporates the spin-other orbit interaction. Hence in eqn (8)HSOC is given by
 | (9) |
2.2 Quantum dynamics simulations
The time-dependent (TD) Schrödinger equation within the diabatic Hamiltonian approach is solved by means of the multi-configuration time-dependent Hartree (MCTDH) method39 where the TD wavefunction is expressed as a linear combination of Hartree products, so-called single particle functions (SPFs). The SPFs are represented by multi-set formulation40 to adopt the present non-adiabatic correction problem. Here the primitive basis sets are chosen as harmonic oscillators’ wavefunction in discrete variable representation (DVR). The initial wavefunction is taken as the product of harmonic wavefunctions at their vibrational ground state of the S0 electronic ground state. The simulation of the absorption is based on the initial population of S3 allowed electronic transition at time zero. The calculations have been performed with the Heidelberg MCTDH package version 8.4.13.412.3 Vibronic and spin–orbit couplings
Vibronic coupling theory has been developed in connection with a model Hamiltonian based on a diabatic representation of the electronic states.42 The diabatic Hamiltonian describing ηel coupled electronic states is written as| H(Q) = (TN + V0(Q))Π + W(Q) | (10) |
The intrastate κ(n)i and inter-state linear λ(n,m)i vibronic coupling constants generated by the vibrational molecular activity regulated by molecular symmetry rules are obtained by analytical formula when only two electronic states are involved within the linear vibronic coupling model.40 The coupling constants can be deduced from electronic structure calculations using the first and second derivatives of the adiabatic potential energy surfaces Vn(Q) with respect to Qi at the ground state equilibrium geometry. Alternatively, and in order to go beyond the pair of states approximation and the linear formalism, λ(n,m)i can be computed on the basis of the overlap matrix between the electronic wavefunctions at close-lying geometries45 as an adiabatic-to-diabatic transformation matrix, such that the linear vibronic coupling (LVC) constants can be obtained by means of numerical differentiation.
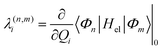 | (11) |
The method is applicable to wavefunction-based methods as well as to TD-DFT, as used in the present study. In the latter case the wavefunctions are replaced by auxiliary many-electron wavefunctions.46 The theory and construction of the W(Q) coupling matrix, SOC, intra- and inter-state vibronic couplings are detailed in the ESI.† The Sn and Tn notation is kept all along the manuscript. This is justified by the use of a model Hamiltonian based on a diabatic representation of the electronic states, both singlet and triplet. Of course, “spin–orbit” states could be retrieved by diagonalization of the W(Q) coupling matrix.
3 Results and discussion
The calculations reported in the next sections have been performed using the ADF quantum chemistry software.473.1 Absorption spectra, structural and electronic properties of [Pt(pCpy)(acac)] 1 and [Pt(pCpz)(acac)] 2
Both complexes adopt the common square-planar geometry associated with Pt(II) 5d8 electronic configuration and closed shell singlet ground state (Fig. 1). The structures of 1 and 2 are very close (Table S1, ESI†). The Pt–C distances are almost identical, 2.010 and 2.020 Å for 1 and 2 and so are the Pt–N distances, 2.008 and 1.982 Å, respectively (Fig. S1, ESI†). We observe a trans effect, the Pt–O distance trans to the carbon atom is roughly 0.1 Å longer than the one trans to the nitrogen atom, 2.129 and 2.035 Å, respectively, in 1. It should be mentioned that only one conformation of the paracyclophane is stable. The upper ring of the paracyclophane comes close to the metal cation leading to a C–C–C–C dihedral angle of 57.8° in 1. No structures were found with an angle higher than 90°, with the upper ring going the opposite of the metal cation: all attempts led back to the original structure. | ||
| Fig. 1 Optimized geometries of the enantiomer A of 1 (left) and 2 (right). Hydrogen atoms have been omitted for the sake of clarity. | ||
The structures of the enantiomers A and B, together with the frontier Kohn–Sham orbitals, are depicted in Fig. S2 and S3 (ESI†).
The absorption spectra were computed on the optimized structures of 1 and 2 and are represented in Fig. 2. Transition energies to the low-lying singlet excited states and associated oscillator strengths are reported in Table 1.
 | ||
| Fig. 2 Calculated TD-DFT absorption spectra of 1 (red trace) and 2 (blue trace) without (plain trace) and with (dashed trace) SOC. | ||
| Complex 1 | ||||||
|---|---|---|---|---|---|---|
| State | E (eV) | f | λ abs (nm) | State | E (eV) | |
| S1 | 3.02 | 7.4 × 10−2 | 411 | T1 | 2.63 | 471 |
| S2 | 3.42 | 7.7 × 10−2 | 362 | T2 | 2.87 | 432 |
| S3 | 3.43 | 1.5 × 10−1 | 361 | T3 | 3.09 | 401 |
| S4 | 3.53 | 2.7 × 10−2 | 352 | T4 | 3.27 | 379 |
| S5 | 3.64 | 8.0 × 10−2 | 340 | T5 | 3.36 | 369 |
| S6 | 3.77 | 2.3 × 10−2 | 329 | T6 | 3.46 | 358 |
| S7 | 3.82 | 1.3 × 10−1 | 324 | T7 | 3.53 | 351 |
| S8 | 3.91 | 5.8 × 10−3 | 317 | T8 | 3.59 | 345 |
| S9 | 3.99 | 9.5 × 10−2 | 311 | T9 | 3.64 | 341 |
| S10 | 4.09 | 2.7 × 10−3 | 303 | T10 | 3.73 | 332 |
| S11 | 4.16 | 2.4 × 10−2 | 298 | T11 | 3.85 | 322 |
| S12 | 4.17 | 4.2 × 10−3 | 297 | T12 | 3.88 | 320 |
| S13 | 4.23 | 1.2 × 10−1 | 293 | T13 | 3.94 | 315 |
| S14 | 4.25 | 2.8 × 10−4 | 292 | T14 | 4.01 | 309 |
| S15 | 4.26 | 5.1 × 10−3 | 291 | T15 | 4.04 | 307 |
| Complex 2 | ||||||
|---|---|---|---|---|---|---|
| S1 | 3.56 | 4.4 × 10−2 | 349 | T1 | 3.08 | 403 |
| S2 | 3.61 | 5.6 × 10−2 | 343 | T2 | 3.10 | 400 |
| S3 | 3.89 | 1.8 × 10−1 | 319 | T3 | 3.36 | 369 |
| S4 | 3.95 | 4.8 × 10−2 | 314 | T4 | 3.53 | 351 |
| S5 | 3.99 | 3.8 × 10−2 | 311 | T5 | 3.59 | 345 |
| S6 | 4.06 | 1.0 × 10−1 | 306 | T6 | 3.65 | 340 |
| S7 | 4.12 | 1.3 × 10−2 | 301 | T7 | 3.75 | 331 |
| S8 | 4.19 | 6.7 × 10−2 | 296 | T8 | 3.84 | 323 |
| S9 | 4.22 | 7.5 × 10−3 | 294 | T9 | 3.93 | 315 |
| S10 | 4.29 | 1.1 × 10−1 | 289 | T10 | 3.94 | 315 |
| S11 | 4.41 | 4.4 × 10−2 | 281 | T11 | 3.98 | 312 |
| S12 | 4.48 | 4.8 × 10−2 | 277 | T12 | 4.00 | 310 |
| S13 | 4.52 | 2.6 × 10−2 | 274 | T13 | 4.11 | 302 |
| S14 | 4.57 | 4.6 × 10−2 | 272 | T14 | 4.13 | 300 |
| S15 | 4.61 | 1.6 × 10−2 | 269 | T15 | 4.18 | 297 |
The analysis of the electronic character of the low-lying singlet and triplet excited states calculated at FC is provided in Fig. 3a (complex 1) and 3b (complex 2).
 | ||
| Fig. 3 (a) Electronic character of the 10 low-lying singlet and triplet excited states of complex 1 at FC from TheoDore analysis48 (Ligand for pyridine so-called py). (b) Electronic character of the low-lying singlet and triplet excited states of complex 2 at FC from TheoDore analysis.48 (Ligand for pyrazole so-called pz). | ||
The absorption band of 1 starts at 411 nm (S1) with an electronic transition mainly centered on the pyridine ligand py of LCPy nature with a minor contribution of platinum-to-pyridine charge transfer so-called MLCTpy (Fig. 3a). The second absorbing band is the convolution of S2 and S3. The nature of S2 is similar to that of S1. S3 has a larger MLCTpy contribution and even significant pyridine-to-acac charge transfer (LLCTacac). This band is centered at 361 nm. Similarly to the singlet states, the triplet T1 (471 nm) and T2 (432 nm) are mainly LCpy states. T3 is completely different, mainly acac localized LCacac (Fig. 3a).
The absorption spectrum of 2 is significantly shifted towards higher energies compared to 1 in agreement with the experimental data.35 The first band is generated by S1 (349 nm) and S2 (343 nm) which exhibit different natures. S1 is mainly localized on the acceptor pyrazole ligand pz with an LCpz character (Fig. 3b), whereas S2 has a mixed LLCTacac/MLCTacac character with charge transfer towards the acac. The intense absorption band at 319 nm is assigned to S3 which has a very mixed nature. As far as the lowest triplet states are concerned, their nature is significantly different from those of 1. For complex 2, the pyrazole contribution is strongly reduced in T1 and T2 which are characterized by an increasing LCacac contribution (Fig. 3b).
Such differences in the state character of 1 and 2 can easily be explained by the difference of frontier orbitals (Fig. S2 and S3, ESI†). For both complexes, the HOMO is delocalized over the platinum cation and the phenyl ring. Its energy is almost unaffected when substituting the pyridyl moiety (−5.624 eV) by a pyrazole moiety (−5.680 eV). In contrast, in 1, the LUMO and LUMO+1 are almost purely localized on the pyridyl ligand and the acac ligand with significant energy differences, −1.927 and −1.445 eV, respectively. For 2, their nature is mixed, half acac, and half pyrazol and the LUMO (−1.462 eV) and LUMO+1 (−1.377) are much closer in energy. The shift of the absorption spectra of 2 towards higher energy is attributed to the destabilization of the paracyclophane LUMO.
For both complexes, the inclusion of SOC significantly modifies the absorption spectra with a red-shift of the absorption of tens of nanometers. For 1, the absorption with SOC starts at 483 nm with E1, E2 and E3 (Table 2) which are purely issued from T1. They are followed by a second set, E4, E5 and E6, between 439 and 437 nm almost purely generated from T2. A first intense band at 429 nm (E7), composed of S1/T2, T4 and T5 mixing, corresponds to the experimental one observed at 434 nm.35 A second band is due to the convolution of E13 at 400 nm and E14 at 396 nm. E13 is mainly issued from T4 with small contributions of S2, S3 and S5. E14 is mainly a combination of S3 and T5. These transitions correspond to the experimental absorption centered around 380 nm.
| Complex 1 | ||||
|---|---|---|---|---|
| E (eV) | λ abs (nm) | F | Composition | |
| E1 | 2.569 | 483 | 1.3 × 10−4 | 93% T1 |
| E2 | 2.570 | 482 | 3.7 × 10−4 | 93% T1 |
| E3 | 2.573 | 482 | 3.4 × 10−3 | 93% T1 |
| E4 | 2.823 | 439 | 5.7 × 10−3 | 80% T2 7% S1 |
| E5 | 2.828 | 438 | 4.4 × 10−5 | 84% T2 6% T4 |
| 6% T5 | ||||
| E6 | 2.835 | 437 | 7.9 × 10−3 | 84% T2 |
| E7 | 2.893 | 429 | 5.2 × 10−2 | 69% S1 10% T5 |
| 8% T2 | ||||
| 6% T4 | ||||
| E8 | 3.044 | 407 | 3.5 × 10−4 | 86% T3 |
| E9 | 3.045 | 407 | 7.6 × 10−4 | 86% T3 |
| E10 | 3.046 | 407 | 1.2 × 10−3 | 86% T3 |
| Complex 2 | ||||
|---|---|---|---|---|
| E a (eV) | λ abs (nm) | F | Composition | |
| E1 | 3.022 | 410 | 3.4 × 10−4 | 82% T1 9% T2 |
| E2 | 3.023 | 410 | 3.1 × 10−4 | 83% T1 9% T2 |
| E3 | 3.026 | 410 | 3.5 × 10−3 | 94% T1 |
| E4 | 3.053 | 406 | 1.1 × 10−4 | 84% T2 9% T1 |
| E5 | 3.054 | 406 | 1.1 × 10−3 | 84% T2 10% T1 |
| E6 | 3.055 | 406 | 1.0 × 10−3 | 94% T2 |
| E7 | 3.311 | 374 | 2.3 × 10−3 | 57% T3 25% T4 |
| E8 | 3.316 | 374 | 3.1 × 10−4 | 65% T3 21% T4 |
| E9 | 3.326 | 373 | 3.4 × 10−3 | 72% T3 16% T4 |
| E10 | 3.362 | 369 | 4.2 × 10−3 | 42% T4 35% T3 |
| 7% S1 | ||||
The effect of SOC on the spectra of 2 is somehow different. The destabilization of the LUMO and the energetic proximity of the LUMO+1 lead to a significant mixing between T1 and T2 at FC geometry, resulting in E1 to E6 states (Table 2). In contrast to 1, for 2 the next set of states (E7 to E12) is composed of a mixture of T3 and T4. The first states with significant singlet contribution are E13 (361 nm) and E14 (359 nm), generated by the mixing of S1 and S2 along with T4, T5 and T6 contributions. This band is in good agreement with the experimental first absorption peak located at 370 nm.35
The overall computed absorption spectra of complexes 1 and 2 reproduce the maxima observed experimentally (Table S1, ESI†).35
After optimization of the lowest triplet states of 1 and 2, two minima, the electronic density of which are reported in Fig. 4, were identified on the lowest triplet potential energy surface (PES). The first one, T1a, is generated by the former T1 state at Franck–Condon geometry and remains mainly localized on the pyridine and pyrazole ligands.
The associated geometry is weakly affected as compared to the FC structure. The most significant changes are the slipping of the two aryl rings of the paracyclophane measured by the CCCC dihedral angle which increases from 57.8° in S0 to 63° in T1a for 1. The change is more drastic in 2 with an increase from 59.4° in S0 to 73.1 in T1a. In both complexes, there is also a contraction of the Pt–C distance by 0.050 Å.
The second minima identified in the triplet PES, T1b, is generated by the acac ligand centered LCacac, namely T3 of 1 and T2 of 2 (Fig. 3a and b). For both complexes, the Pt–O distance associated with the oxygen atom trans to the carbon atom decreases by 0.060 Å. However, the main modification is the out of plane distortion of the acac ligand.
For complex 1, the two minima are well separated and the T1a state is much more stable than the T1b state (Table 3). In complex 2, the T1a state, strongly destabilized, is almost degenerate with T1b (Table 3). In 2, the two states are probably in competition for the emission. Both complexes possess low-lying metal-centered (MC) triplet states, over-stabilized as compared to the emissive states by out-of-plane distortion towards a nearly tetrahedral structure, and potentially thermally activated at 298 K (Fig. S4, ESI†).
| Complex 1 | Complex 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| T1a | T1b | MC1 | MC2 | T1a | T1b | MC1 | MC2 | |
| E dist | 0.281 | 0.653 | 2.198 | 1.350 | 0.496 | 0.609 | 2.238 | 1.436 |
| E em | 2.084 | 2.016 | 0.175 | 1.429 | 2.192 | 2.095 | 0.166 | 1.336 |
| E stab | 2.365 | 2.669 | 2.373 | 2.779 | 2.687 | 2.704 | 2.404 | 2.772 |
| λ em | 595 | 615 | 7098 | 867 | 566 | 592 | 7473 | 928 |
On the basis of the electronic data reported above, we can clearly assign the strong emission observed in complex 1 at 583 nm to T1a (Table 3) of LCpy character. In contrast, the attribution of the emission observed in complex 2 at 468 nm is more challenging.
3.2 Emission properties of [Pt(pCpy)(acac)] 1 and [Pt(pCpz)(acac)] 2
In order to get a further understanding of the emissive properties of the two complexes we computed their phosphorescence and tentatively CPL spectra taking into account SOC and vibronic effects as described in the methodological approach (Section 2.1) and developed using the ORCA quantum chemistry software.29The experimental spectra of both complexes 1 and 2 exhibit strong emission at 583 and 468 nm, respectively (Fig. 5).35
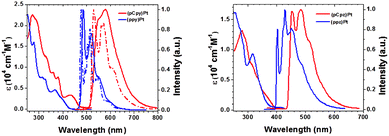 | ||
| Fig. 5 Experimental absorption and emission spectra of 1 (left side and red trace) and 2 (right side and red trace) in CH2Cl2 and 2-Me-THF, respectively, at room temperature (solid line) and at 77 K (dashed line) (adapted from ref. 35 with permission of Elsevier). | ||
As expected from the electronic properties of the lowest triplet excited states, reported in the previous section, the emission spectrum of complex 1 reveals a well-structured band at 77 K indicating the major role of T1 in the emission. In addition, T1 is well separated from T2 by 0.24 eV (Table 1) justifying the neglect of T2 in the simulation of the phosphorescence spectrum by keeping only the three lowest spin–orbit sublevels E1, E2, and E3 originating from T1 (Table 2). This assumption is more questionable for complex 2 characterized by nearly degenerate T1 and T2 states calculated at 3.08 and 3.10 eV, respectively (Table 1) leading to six nearly degenerate SO sublevels within 0.035 eV with mixed T1/T2 composition (Table 2). However, the computation of the Hessian in this tough case is the limiting step of our computational strategy. Consequently, the same computational strategy has been applied to both complexes.
Electronic ground states and first triplet excited states T1a of 1 and 2 were fully optimized and their vibrational frequencies and Hessians calculated. Excited state dynamics (ESD) calculations of phosphorescence and CPL spectra were performed on all three first SOC states using ground state optimized structure and both ground state and T1 Hessians. All three-resulting phosphorescence spectra were weighted by Boltzmann distribution using ESD calculation's SOC states energies. Dissymmetry factors (glum) were calculated based on eqn (7) for SOC states calculated at T1 optimized structure. Global glum was obtained from the addition of the three first SOC states glum weighted by Boltzmann distribution.
Calculated phosphorescence and CPL spectra of 1 at room temperature together with the most important spin–orbit sublevel contributions to their intensity are presented in Fig. 6. Deconvolution of the relevant spin–orbit sublevels in terms of Ms contributions, partial and total associated Boltzmann average radiative rate constants together with the partial and total relaxation times are given in Table 4.
 | ||
| Fig. 6 Complex 1 calculated phosphorescence (a) and CPL (b) spectra of enantiomer A, at room temperature and phosphorescence spectrum at 77 K (c). | ||
| Complex 1 | M s = 0 (%) | M s = −1 (%) | M s = +1 (%) | Energy (cm−1) | k n r (105 s−1) | τ n 298K (μs) | k r (105 s−1) | τ 298K (μs) | τ 77K (μs) | ϕ |
|---|---|---|---|---|---|---|---|---|---|---|
| State | ||||||||||
| E1 | 2.9 | 47.6 | 47.6 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 498 |
1.13 | 8.85 | ||||
| E2 | 32.8 | 32.6 | 32.6 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
0.484 | 20.70 | ||||
| E3 | 62.4 | 17.9 | 17.9 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
4.15 | 2.41 | ||||
| Theory | 1.88 | 5.3 | 6.6 | 0.32 | ||||||
| Exp.35 | 0.37 ± 0.02 | 5.3 | 16.1 | 0.20 | ||||||
The non-radiative relaxation has been neglected which is justified at low temperature (77 K). However, at room temperature not only intra-molecular processes such as internal conversion (IC) and intersystem crossing (ISC), but also external effects (environment, structural distortions, conformers, etc.) may induce non-radiative decay. This is illustrated experimentally in the case of complex 1 when comparing the well structured spectrum at 77 K and the broad band observed at room temperature (Fig. 5, left). The experimental value of the non-radiative constant which comprises both intramolecular and external effects occurring during the experiment, including the presence of low-lying metal-centred (MC) states, is evaluated at 1.5 ± 0.1 × 105 s−1 for complex 1.35 This rather high value has to be compared to the calculated one, namely less than 0.009 × 105 s−1 obtained by the computational strategy developed in our original work30 that includes only the intramolecular effects within the harmonic approximation following the so-called weak-coupling limit of the energy gap law.49 The weakness of the computational method, which is not complete enough to take into account the external effects, and the presence of potentially thermally activated MC states (Table 3) at 298 K make a direct comparison between the experimental and theoretical photophysical data tentative.
The simulated phosphorescence spectrum of complex 1 reproduces perfectly the shape of the experimental spectrum, especially at 77 K (Fig. 5 and 6), whereas the structure of the computed phosphorescence spectrum of complex 2, based on the T1a SO sublevels only, is poorly resolved (Fig. S5, ESI†). This confirms the weakness of our model when several nearly degenerate low-lying triplet states contribute to the emission spectroscopy.
For this reason, only the CPL spectrum of complex 1 has been calculated (Fig. 6, top, right side).
Deconvolution of the spectrum reveals that the emission process in complex 1 involves magnetic sublevels E1 to E3 (Scheme 2) with a major contribution of the E3 state due to its rather large Ms = 0 component (>60%) (Table 4).
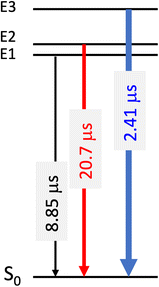 | ||
| Scheme 2 Magnetic sublevel contributions and associated computed relaxation times from the relevant magnetic sublevels describing the phosphorescence of complex 1 at room temperature. | ||
Despite a modest zero-field splitting (<15 cm−1) the phosphorescence at room temperature is dominated by the fast E3 → S0 emission process which provides the fastest relaxation (2.41 μs) through the rather large Ms = 0 contribution (>60%). At 77 K the E1 → S0 decay is improved at the expense of E3 → S0 leading to an increase in total relaxation time from 5.3 μs to 6.6 μs (Table 4) in agreement with the experimental trends. The estimated total relaxation time at 298 K agrees perfectly with the experimental value which is fortuitous because the non-radiative corrections are neglected.
The CPL intensity is mainly governed by the magnitude and the relative orientations (angle θ, Table 5) of the electric and magnetic transition dipole moments and by the SOC interactions.30 The calculated transition electric and magnetic dipole moments attributed to each SO sublevel E1, E2 and E3 of complex 1, enantiomer A, are reported in Table S1, ESI.† As expected, the flux of electronic density from the pyridine ligand to the metal/pyridine ligand that characterizes the T1a → S0 emissive process (Scheme 3) controls the magnitude and orientation of the dipoles, together with the induced magnetic anisotropy. The emission process via E3 (62% Ms = 0) involves a mainly z-polarized magnetic dipole and xy-plane polarized electric dipole forming an angle of 57.6°. This results in a right circularly polarized emission characterized by a negative CPL signal of high intensity (Fig. 6, top right). The sub-level E1, with negligible Ms = 0 component and 47.6% Ms = ±1, entangles xz-plane polarized electric dipole and negligible magnetic dipole. The major contribution to |glum| comes from E2 equally composed of 33% of Ms = 0, Ms = ±1, with the formation of an optimum angle θ = 30.3° resulting in an x-polarized magnetic dipole correlated to an xy-plane polarized electric dipole. Both E1 and E2 emissions are characterized by modest positive CPL intensities. Consequently, by cancellation, the differential CPL spectrum of complex 1 enantiomer A has modest negative intensity and |glum| = 6.1 × 10−3. The contribution of the metal–ligand charge transfer to the process is less favorable to the CPL activity than a pure intra-ligand charge transfer as demonstrated for π-conjugated helicenic Re(I) complexes.30
| State | Energy (cm−1) | θ° | |glum| |
|---|---|---|---|
| E1 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 498 |
59.4 | 0.00092 |
| E2 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
30.3 | 0.01539 |
| E3 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513 513 |
57.6 | 0.00194 |
| Boltzmann average |glum|: 6.1 × 10−3 | |||
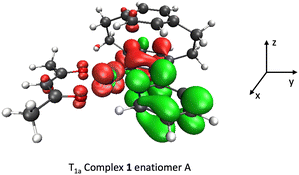 | ||
| Scheme 3 The difference in electronic densities describing the T1a → S0 emissive process in complex 1 enantiomer A (in green: loss of electronic density, in red: gain of density). | ||
3.3 Ultrafast decay (<1 ps) in complexes [Pt(pCpy)(acac)] 1 and [Pt(pCpz)(acac)] 2
In order to go beyond the static picture and to compare the ultrafast photophysics (fs–ps) of complexes 1 and 2, non-adiabatic quantum dynamics simulations including spin-vibronic effects43 have been performed. As illustrated for a number of transition metal complexes, the high density of states in a limited domain of energy, the degree of electronic mixing and the correlation between electronic densities and nuclear vibrations generate crucial electron–vibration (vibronic) intrastate and inter-state couplings that control, together with SOC, the population in time of the individual excited states in the sub-ps regime.50–52One important question related to the different electronic characters of the three low-lying triplet excited states of 1 and 2 is the interplay between T1 and T2, fully localized on the pyridine in 1 and delocalized over the pyrazol and the acac ligands in 2, and the role of T3, fully localized on the acac ligand in 1 and fully localized on the pyrazol in 2, within the first ps. Clearly, the dialog between the nuclear vibrations and the electronic densities in play should lead to distinctive photophysics. The process described here follows the time evolution of the diabatic population of the low-lying singlet and triplet excited states after initial vertical S0 → S3 absorption.
The electronic problem has been reduced to 3 singlet states (S1, S2, S3) and 3 triplet states (T1, T2, T3) leading to 12 “spin–orbit” states. The SOC terms introduced in the W(Q) coupling matrix (eqn (S14), ESI†) together with the intra- and inter-state couplings are reported in Tables S2–S4, ESI.† For both molecules, 20 active normal modes have been selected on the basis of significant intra-state κ(n)i/ω coupling amplitudes and large inter-state λ(n,m)i coupling constants (Tables S3 and S4, ESI†). In addition, some normal modes have been selected on the basis of the number of one-Dim cuts of the PES crossings they generate (Fig. S6 and S7, ESI†). The 20 selected vibrational normal modes are depicted in Fig. S8 and S9 (ESI†).
The time evolution of the diabatic population of the low-lying singlet and triplet excited states of complexes 1 (left) and 2 (right) is shown in Fig. 7.
Within the constraints of our simulation (reduced nuclear and electronic dimensionalities, harmonic approximation) the ultrafast non-adiabatic dynamics of the pyridine and pyrazole-substituted complexes 1 and 2 differ drastically already within the first 150 fs, as far as the low-lying triplet states population is concerned. In complex 1 major inter-state S3/S1 and S2/S1 vibronic couplings activated by out-of-plane vibrations of the paracyclophane, acac and pyridine groups (Q129, Q130, Q132, Fig. S8 and Table S4, ESI†) lead to a fast depopulation of S3 at the benefit of S1 and S2 states within 20–30 fs. Simultaneously, large S2/T1, S3/T1 and S3/T2 SOC induce an efficient population of T1 and T2 which exchange population with T3 through vibronic effects driven by symmetric twisting of the acac and paracyclophane groups (Q128, Fig. S8, ESI†). The transfer of population from S1 to its nearly degenerate state T3 and to T2 is also favored by the PES crossings induced by these nuclear vibrations (Q128, Q129, Q130) in the range of 20–30 fs. The T3 state localized on the acac ligand acts as a reservoir and plays a major role in the early time dynamics of complex 1. At 150 fs the populations of S1 and T3 reach 20%, and that of S3 decreased to 15%, with S2, T1 and T2 remaining marginally populated at ∼10%. After 200 fs the population of S1 decreases at the advantage of those of T1 and T2 by SOC and because of the number of S1/T2 crossings generated by the low frequency modes Q19, Q20, Q23 (Fig. S8, ESI†). The population of T1 increases slowly by vibronic exchange with T2via these longer time-scale vibrations (acac and pyridine twisting, metal coordination sphere breathing) associated with these modes to approach 35% whereas the population of T2 does not exceed 20% at 2 ps (Fig. S10, ESI†). At 2 ps T1 and T3 are nearly equally populated and we can predict that very low frequencies modes like out-of-plane distortion of the acac ligand, not relevant within the limit of our simulations, will stabilize T1 as discussed above to converge to T1b.
The low-lying electronic excited states of complex 1 are either mainly pyridine localized (S1, S2, T1, T2) or acac localized (T3), the absorbing state S3 being mainly MLCTpy in nature. S1 and S2 are contaminated by MLCTpy contributions (Fig. 3a).
In contrast, the low-lying electronic excited states of complex 2 are largely mixed with minor MLCT contributions, the only rather pure state being T3 localized on the pyrazole. Importantly, there is no pure LCacac state (T3 of complex 1) the acac and pyrazole localized electronic densities being mixed in T1 and T2. These differences in electronic character have important consequences for both SOC and vibronic couplings (Tables S2–S4, ESI†) and for the quantum dynamics spin-vibronic mechanism (Scheme 4). In particular, SO effects are less important in complex 2 and the ultrafast population (<30 fs) of the triplet states as observed in complex 1 does not occur. At 200 fs the three lowest triplet states T1, T2 and T3 remain marginally populated (<15%). The high frequency nuclear vibrations associated with normal modes Q125 and Q126 corresponding to the symmetric and asymmetric twisting of the acac and paracyclophane groups and Q124 and Q128 linked to the acac and paracyclophane groups induce large S1/S2 interstate vibronic coupling but modest S1/S3 coupling (Table S4, ESI†). Consequently, the depopulation of the S3 absorbing state in complex 2 is rather slow as compared to complex 1 (40% vs. 20% at 100 fs). These high frequency modes Q125, Q126, and Q128 generate a number of PES crossings between S1, S2 and T3 and between T3, T1 and T2 (Fig. S7, ESI†) but the transfer of population to T1 and T2 remains moderate within the first 200 fs.
Finally, strong interstate vibronic couplings between T1 and T2, the two nearly degenerate triplet states localized equally on the acac and pyrazole ligands and induced by a dozen of both high- and low-frequency normal modes in complex 2 (Table S4, ESI†) confirm our hypothesis developed within the context of the emission, namely the participation of both triplet states in the phosphorescence and CPL activity. The simulation of realistic phosphorescence and CPL spectra in this case is out of reach with the current methodological developments.
4 Conclusion
The spin–orbit effects hidden behind the photophysics of phosphorescent chiral cyclometalated Pt(II) complexes namely [Pt(pCpy)(acac)] 1 and [Pt(pCpz)(acac)] 2 have been deciphered by combining different methods of quantum chemistry based on density functional theory and non-adiabatic quantum dynamics, including spin–orbit and vibronic effects. This theoretical study has enabled us to simulate absorption and phosphorescence spectra for complexes 1 and 2 and CPL spectrum for complex 1 and to decrypt the relevant spin–orbit sublevels contributing to the radiative rate constants and phosphorescence relaxation times. Sub-picosecond non-adiabatic quantum dynamics suggest a spin-vibronic mechanism driven by paracyclophane and acac nuclear vibrations.These two very similar molecules, differing by the aromatic ring, pyridine (1) or pyrazole (2) attached to the paracyclophane exhibit very different characteristics in various aspects:
(i) The computational difficulties, correlated to the complexity of the electronic and vibrational problems, make complex 1 an “easy case” and complex 2 a “tough case”.
(ii) The energetics and electronic densities of the low-lying triplet states involved in the emission properties.
(iii) The pyridine or acac ligand-localized electronic structure of the three lowest triplets in complex 1vs. a delocalized electronic structure over the acac and pyrazole ligands in the two lowest nearly-degenerate triplet states in complex 2.
(iv) The absorbing state has mixed LCpy/MLCTpy character in complex 1 whereas the absorbing state is significantly mixed with MLCTacac and LLCT contributions in complex 2;
(v) A well-resolved, intense and realistic phosphorescence spectrum has been obtained for complex 1 on the basis of the single lowest T1 state, mainly localized on the pyridine with a small charge transfer from Pt(II), while this strategy provided a rather poor phosphorescence spectrum, not comparable to the experimental one for complex 2 which needs the inclusion of both T1 and T2 states delocalized over the pyrazole and acac ligands in the simulation.
The non-adiabatic quantum dynamics simulations show an ultrafast decay driven by both spin–orbit and vibronic couplings in complex 1 with an efficient population of the acac localized triplet state within 150 fs. This ultrafast decay is driven by symmetric twisting and out-of-plane vibrations of the paracyclophane and acac groups and large SOC between the singlet and triplet manifolds. At 2 ps the diabatic population of T1 reaches 35% whereas the one of T2 does not exceed 20%. In contrast, the initial decay of the absorbing state in complex 2 is rather slow because of moderate spin-vibronic effects attributed to the delocalized electronic densities in play and the minor metal–ligand charge transfer contributions. The nearly degenerate T1 and T2 excited states remain strongly coupled by intrastate vibronic coupling activated by a number of normal modes of high and low frequencies. This confirms that in order to obtain correct phosphorescence and CPL spectra both T1 and T2 excited states have to be included in the simulation of the spectra of complex 2, which is challenging at the level of theory used in the present work. Further theoretical developments should allow efficient calculation of the Hessian for several nearly degenerate electronic excited states and improve the computation of non-radiative constants including not only external effects but also the presence of thermally activated MC states.
The circularly polarized luminescence spectrum of complex 1, enantiomer A, has been predicted on the basis of the magnitude and relative orientation of the transition electric and magnetic dipole moments calculated for each SO sublevel expressed in terms of Ms components. The CPL activity, characterized by a relatively modest calculated glum value (<10−2), is governed by the flux of electronic density from the pyridine to the metal/pyridine generated during the emission process. This flux controls the magnitude and orientation of the dipoles together with the induced magnetic anisotropy. The major contribution to glum comes from the SO sublevel equally composed of 33% of Ms = 0, Ms = ±1 with an optimum angle of ∼30° between the electric and magnetic dipole moments. However, the intensity generated by this SO state is partially cancelled by the major contribution of the SO sublevel composed at 62% of the Ms = 0 component to the emission process, resulting in a negative CPL signal of high intensity generated by z-polarized magnetic and xy-plane polarized electric dipoles forming an angle of ∼60°.
This comprehensive theoretical study paves the way for the synthesis of new chiral Pt(II) paracyclophane complexes with optimal electronic and structural properties. The new molecules should fulfill several criteria based on the energetics of the lowest triplet states and their SO sublevels: the T1–T2 energy gap has to be increased and the SO sublevels with dominant Ms = ±1 component should not be contaminated by Ms = 0 to warranty an efficient CPL activity. The acac ligand is clearly non-innocent. The substitution of the acac ligand and the nature of the aromatic ring linked to the paracyclophane may help in controlling the relative energetic and electronic composition of the ligand-centered states which play a key role here. However, metal-charge transfer contributions may be important in order to promote efficient decay to the triplet excited states or relevant spin–orbit coupling and splitting. As proposed experimentally, and confirmed by preliminary calculations, the presence of thermally activated MC states may be responsible for partial quenching of phosphorescence. Bulky ligands may prevent their activation by inhibiting their stabilization via tetrahedral distortion.
Author contributions
T. G. and C. G. performed electronic structure calculations, analyzed the results and contributed equally to the writing of the manuscript. S. M. and C. D. performed the QD simulations and C. D. has been involved in the conceptualization, theoretical development and interpretation, analysis, methodology and writing.Data availability
The data supporting this article have been included as part of the ESI.† The code for the description of the software can be found at https://www.scm.com/amsterdam-modeling-suite/adf/ and https://www.pci.uni-heidelberg.de/tc/mctdh.html.Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. G. acknowledges the ANR-21-CE29-0015 “ChirON” for funding support and the Molecular Theory and Spectroscopy group at the MPI, Mülheim, more particularly Dr Dimitrios Manganas for scientific discussions and initiation into ORCA. The authors acknowledge Dr Dimitrios Manganas and Prof Matteo Mauro for helpful discussions at the preliminary stage of the project and M. Guillaume Rouaut and M. Even Chiari for technical support. The calculations have been performed at the regional HPC, Strasbourg, through a grant of computer time.References
- V. M. Miskowski, V. H. Houlding, C.-M. Che and Y. Wang, Inorg. Chem., 1993, 32, 2518–2524 CrossRef CAS.
- J. A. G. Williams, Top. Curr. Chem., 2007, 281, 205–268 CrossRef CAS.
- J. A. G. Williams, S. Develay, D. L. Rochester and L. Murphy, Coord. Chem. Rev., 2008, 252, 2596–2611 CrossRef.
- J. A. G. Williams, Chem. Soc. Rev., 2009, 38, 1783–1801 RSC.
- L. Murphy and J. A. G. Williams, Top. Organomet. Chem., 2010, 28, 75–111 CrossRef CAS PubMed.
- J. E. Yarnell, I. Davydenko, P. V. Dorovatovskii, V. N. Khrustalev, T. V. Timofeeva, F. N. Castellano, S. R. Marder, C. Risko and S. Barlow, J. Phys. Chem. C, 2018, 122, 13848–13862 CrossRef CAS.
- A. Haque, L. Xu, R. A. Al-Balushi, M. K. Al-Suti, R. Ilmi, Z. Guo, M. S. Kahn, W.-Y. Wong and P. R. Raithby, Chem. Soc. Rev., 2019, 48, 5547–5563 RSC.
- Y. Han, Z. Gao, C. Wang, R. Zhong and F. Wang, Coord. Chem. Rev., 2020, 414, 213300 CrossRef CAS.
- V. W.-W. Yam and A. S.-Y. Law, Coord. Chem. Rev., 2020, 414, 213298 CrossRef CAS.
- M. A. Soto, R. Kandel and M. J. MacLachlan, Eur. J. Inorg. Chem., 2021, 894–906 CrossRef CAS.
- A. Haque, H. El Moll, K. M. Alenezi, M. S. Kahn and W.-Y. Wong, Materials, 2021, 14, 4236 CrossRef CAS PubMed.
- V. W.-W. Yam and Y.-H. Cheng, Bull. Chem. Soc. Jpn., 2022, 95, 846–854 CrossRef CAS.
- Highly Efficient OLEDs with Phosphorescent Materials, ed. H. Yersin, Wiley-VCH, Weinheim, 2008 Search PubMed.
- D.-W. Zhang, M. Li and C.-F. Chen, Chem. Soc. Rev., 2020, 49, 1331–1343 RSC; J. Han, S. Guo, H. Lu, S. Liu, Q. Zhao and W. Huang, Adv. Opt. Mater., 2018, 6, 1800538 CrossRef CAS.
- C. Wagenknecht, C.-M. Li, A. Reingruber, X.-H. Bao, A. Goebel, Y.-A. Chen, Q. Zhang, K. Chen and J.-W. Pan, Nat. Photonics, 2010, 4, 549 CrossRef CAS.
- R. Farshchi, M. Ramsteiner, J. Herfort, A. Tahraoui and H. T. Grahn, Appl. Phys. Lett., 2011, 98, 162508 CrossRef CAS; J. R. Brandt, F. Salerno and M. J. Fuchter, Nat. Rev. Chem., 2017, 1, 45 CrossRef.
- T. Sajoto, P. I. Djurovich, A. B. Tamayo, J. Oxgaard, W. A. Goddard III and M. E. Thompson, J. Am. Chem. Soc., 2009, 131, 9813–9822 CrossRef CAS PubMed.
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048 CrossRef CAS.
- N. Saleh, C. Shen and J. Crassous, Chem. Sci., 2014, 5, 3680–3694 RSC.
- N. Hellou, M. Srebro-Hooper, L. Favereau, F. Zinna, E. Caytan, L. Toupet, V. Dorcet, M. Jean, N. Vanthuyne, J. A. G. Williams, L. Di Bari, J. Autschbach and J. Crassous, Angew. Chem., Int. Ed., 2017, 56, 8236–8239 CrossRef CAS PubMed.
- N. Saleh, M. Srebo, T. Reynaldo, N. Vanthuyne, L. Toupet, V. Y. Chang, G. Muller, J. A. G. Williams, C. Roussel, J. Autschbah and J. Crassous, Chem. Commun., 2015, 51, 3754–3757 RSC.
- E. S. Gauthier, L. Abella, N. Hellou, B. Darqui, E. Caytan, T. Roisnel, N. Vanthuyne, L. Favereau, M. Srebo-Hooper, J. A. G. Williams, J. Autschbach and J. Crassous, Angew. Chem., Int. Ed., 2020, 59, 8394–8400 CrossRef CAS PubMed.
- C. Shen, E. Anger, M. Srebro, N. Vanthuyne, K. K. Deol, T. D. Jefferson, G. Muller, J. A. G. Williams, L. Toupet, C. Roussel, J. Autschbach, R. Réau and J. Crassous, Chem. Sci., 2014, 5, 1915–1927 RSC.
- J. R. Brandt, X. Wang, Y. Yang, A. J. Campbell and M. J. Fuchter, J. Am. Chem. Soc., 2016, 138, 9743–9746 CrossRef CAS PubMed.
- D. Kundu, D. Jelonek, N. Del Rio, N. Vanthuyne, M. Srebo-Hooper and J. Crassous, Chem. – Asian J., 2025, e202401735 CrossRef CAS PubMed.
- C. Gourlaouen and C. Daniel, Dalton Trans., 2014, 43, 17806–17819 RSC.
- J. Autschbach and T. Ziegler, J. Chem. Phys., 2002, 116, 891 CrossRef CAS.
- (a) O. Vahtras, H. Agren, P. Jorgensen, J. J. A. Jensen, T. Helgaker and J. Olsen, J. Chem. Phys., 1992, 97, 9178 CrossRef CAS; (b) F. Wang and T. Ziegler, J. Chem. Phys., 2005, 123, 154102 CrossRef PubMed.
- F. Neese, Software update: the ORCA program system – Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(1), e1606, DOI:10.1002/wcms.1606.
- R. Shafei, A. Hamano, C. Gourlaouen, D. Maganas, K. Takano, C. Daniel and F. Neese, J. Chem. Phys., 2023, 159, 084102 CrossRef CAS PubMed.
- S. E. Gibson and J. D. Knight, Org. Biomol. Chem., 2033, 1, 1256–1269 RSC.
- A. Yanagawa, R. Inoue and Y. Morisaki, Chem. Commun., 2024, 60, 1468–1471 RSC.
- J. J. P. Kramer, M. Nieger and S. Bräse, Eur. J. Org. Chem., 2013, 541–549 CrossRef CAS.
- S. E. Gibson and J. D. Knight, Org. Biomol. Chem., 2003, 1, 1256–1269 RSC.
- B. K. T. Batagoda, P. I. Djurovich, S. Bräse and M. E. Thompson, Polyhedron, 2016, 116, 182–188 CrossRef CAS.
- N. O. Foglia, D. Manganas and F. Neese, J. Chem. Phys., 2022, 157, 154106 CrossRef CAS PubMed; F. Neese and E. I. Solomon, Inorg. Chem., 1999, 38, 1847 CrossRef PubMed; D. Ganyushin and F. Neese, J. Chem. Phys., 2008, 128, 114117 CrossRef PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289, 177–214 CrossRef.
- F. Neese, J. Chem. Phys., 2005, 122, 34107 CrossRef PubMed.
- Multidimensional Quantum Dynamics: MCTDH Theory and Applications, ed. H.-D. Meyer, F. Gatti and G. A. Worth, Wiley-VCH, Weinheim, 2009 Search PubMed.
- U. Manthe, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1992, 97, 9062–9071 CrossRef CAS.
- H.-D. Meyer, G. A. Worth, M. H. Beck, A. J.ckle, U. Manthe, M. Ehara, A. Raab, M.-C. Heitz,S. Sukiasyan, C. Cattarius, S. Wefing, F. Gatti, M. Nest, F. Otto, M. R. Brill, O. Vendrell, M. Schröder and D. Pelaez, The MCTDH Package, Version 8.4, see https://mctdh.uni-hd.de/ ( 2007) Search PubMed.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 CrossRef.
- J. Eng, C. Gourlaouen, E. Gindensperger and C. Daniel, Acc. Chem. Res., 2015, 48, 809–817 CrossRef CAS PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7625 CrossRef CAS PubMed.
- F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand and L. Gonzalez, J. Chem. Theory Comput., 2016, 12, 1207–1219 CrossRef CAS PubMed.
- M. Fumanal, F. Plasser, S. Mai, C. Daniel and E. Gindensperger, J. Chem. Phys., 2018, 148, 124119 CrossRef PubMed.
- ADF2019, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands: https://www.scm.com.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- C. Daniel, Phys. Chem. Chem. Phys., 2021, 23, 43–58 RSC.
- S. Mandal and C. Daniel, Phys. Chem. Chem. Phys., 2023, 25, 18720–18727 RSC.
- S. Mandal and C. Daniel, J. Phys. Chem. A, 2024, 128(16), 3126–3136 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01450f |
| ‡ Present address: Laboratoire de Modélisation et Simulations Moléculaires, Université de Strasbourg CNRS UMR 7140 Chimie de la Matière Complexe 4 Rue Blaise Pascal, 67000 Strasbourg, France. E-mail: gourlaouen@unistra.fr |
| This journal is © the Owner Societies 2025 |