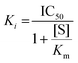Variable-temperature token sampling in decoder-GPT molecule-generation can produce more robust and potent virtual screening libraries

Abstract

Token generation in generative pretrained transformers (GPTs) that produce text, code, or molecules often uses conventional approaches such as greedy decoding, temperature-based sampling, or top-k or top-p techniques. This work shows that for a model trained to generate inhibitors of the enzyme HMG-coenzyme-A reductase, a variable temperature approach using a temperature ramp during the inference process produces larger sets of molecules (screening libraries) than those produced by either greedy decoding or single-temperature-based sampling. These libraries also have lower predicted IC₅₀ values, lower docking scores, and lower synthetic accessibility scores than libraries produced by the other sampling techniques, especially when used with very short prompt-lengths. This work explores several variable-temperature schemes when generating molecules with a GPT and recommends a sigmoidal temperature ramp early in the generation process.

---

1. Introduction

Token selection is the process by which a language model (LM) assembles a response to a prompt. If a prompt consists of “I rode my”, the LM generates a list of probabilities of occurrence for all of the tokens in it's vocabulary. This list may look something like: [“bike”: 0.73, “horse”: 0.22, …”unicorn”: 0.01]. The model must then select which of the tokens to choose. The most simple approach is to use greedy decoding, which means the model takes the token with the largest probability, in this case resulting in a response of “I rode my bike”. In temperature-based sampling, the probabilities are scaled according to a value called temperature, which typically runs in the range of 0.0 to 2.0 for many models. The next token is then chosen based on the rescaled probabilities. Thus, while greedy decoding would always choose “bike”, temperature based sampling would have a non-zero chance of choosing “horse” or “unicorn”. The higher the temperature used, the more the scaled probabilities become similar in magnitude and the more likely the model will choose “unicorn”. In previous work, it was shown that a generative, pre-trained transformer (GPT) decoder model pre-trained on SMILES strings for bioactive compounds and then fine-tuned on drugs that inhibited HMG-coenzyme A reductase (HMGCR) produces libraries of molecules with lower IC₅₀ values and other desirable properties when using a higher temperature during the generation process.¹ In this work, temperature-based molecule generation is tested for temperatures above 0.5, and variable temperature sampling techniques are explored. It will be shown that variable temperature ramps produce molecule libraries with more desirable properties.

In this work and other work cited below, GPTs are discussed extensively. A GPT is simply a neural network model (often an LM) that has been trained on some body of text—or, in this work, SMILES strings—in order to learn the rules, or grammar of the text. This is known as the pre-training. The GPT is then fine-tuned on some specific, usually smaller, dataset to complete a task; in this case generating novel SMILES strings. These neural networks include a component called a transformer, which is simply a component that uses a technique called self-attention to figure out which tokens typically occur before or after a given token,² such as putting “bike” after “my” in the example above. A Transformer decoder specifically is trained to predict what tokens come next in a series, while an encoder takes context from before and after the token in question.

Unlike the natural language generation (NLG) needed for LMs, SMILES strings have a more rigid set of “grammar” rules: a string with c1ccccc in the sequence has to have a “1” either next or at some point soon so as to close the aromatic ring; if there is no 1 after this point the SMILES string is not viable. This grammar rigidity is similar to coding, wherein certain structures have to have a particular structure, such as

for (int i = 0);

This code string has to have almost this exact structure in order to make usable C++ code. Zhu et al. developed a method of variable temperature sampling for code generation that uses higher temperatures for more challenging tokens (tokens which are more difficult to predict), to provide for more variety, and lower temperature for more confident tokens, to avoid nonsensical code.³ They found that their approach outperformed more commonly used token generation strategies on code generation benchmarks. In similar work, Zhang et al. developed a variable-temperature sampling model for LMs that also treated challenging and confident tokens with higher or lower temperature, though their model was based on the total Shannon entropy for the set of probabilities (p) at each step:⁴
In this model, a higher entropy indicates a more challenging token and lower entropy indicated a confident token, and the temperature is scaled accordingly. The authors found the model to outperform existing temperature sampling strategies. Chang et al. developed a model that dynamically scales the temperature during the generation process for LMs.⁵ In their approach, two models with step-wise probability distributions p and q are run simultaneously: one has the prompt and information relevant to the answer (source), and the other just has the prompt. They calculate the KL-divergence between these models
and, if the divergence is low, it indicates that the source is not relevant to the output, and the temperature is scaled only slightly, whereas if the KL-divergence is large, the source is relevant to the answer and the temperature is scaled more dramatically. The authors found that their approach out-performs conventional sampling algorithms, though it does require inference with two models simultaneously, which increases the cost of language generation.

These variable temperature approaches show that challenging and confident tokens can and should be generated at different temperatures. In molecular generation, confident tokens lead to predictable structures, while challenging tokens lead to more variability. For example, the beginning of a SMILES string can be considered more challenging, as there are many options for how the molecule's structure can develop, while the middle and end of SMILES strings have more confident tokens, as they must follow the grammar rules in order to complete the structure correctly. When trying to generate novel molecules, having a lower temperature at the beginning, where a challenging token can lead to a nonsensical structure, can help produce viable SMILES strings, while higher temperatures near the end, were there are more confident tokens, can lead to greater variability.

Other molecule generation models typically use standard token sampling techniques. Bagal et al. trained a GPT to generate molecules with tuned properties.⁶ Their model uses only T = 1.0 token sampling, which returns the native probability distributions, i.e. no scaling of probabilities is performed, so a narrow distribution will remain narrow. Two other recent transformer-based molecule generation models by Tysinger et al.,⁷ Yang et al.,⁸ and an RNN-based generation model by Urbina et al.⁹ make no mention of temperature in the generation process, suggesting the use of greedy decoding. The transformer and RNN-based “Reinvent” model of Loeffler et al.¹⁰ makes use of constant temperature sampling as well as beam-search, wherein a set of generated SMILES strings are kept during generation and the best are selected for by using log-probabilities. Tibo et al. have published a transformer model that does not emphasize sampling a wide chemical space, but rather searches for similar molecules.¹¹ This model also uses beam search, and no mention of temperature is made. The RNN-based bidirectional generative model of Grisoni et al. can build a molecular SMILES string in both the forward and backwards directions, and uses temperature-based sampling at T = 0.7.¹² Chang and Ye use a transformer encoder model and bimodal inputs to generate novel molecules using both greedy decoding and stochastic token selection.¹³ The transformer decoder of Ross et al. generates molecules using temperature-based sampling at T = 1.0.¹⁴ Sob et al. have trained a variational autoencoder within a transformer encoder-decoder framework to generate new molecules using reinforcement learning based on docking scores to specific targets.¹⁵ This type of model, since it generates from a latent-space representation, cannot implement a temperature-like parameter equivalent to those discussed here, though the generation of latent space representations can be based on such a variable. Another recent non-transformer-based generative model (a pixel-CNN) by Noguchi and Inoue likewise makes no mention of generation temperature.¹⁶ The current work thus seems to be unique in its approach to using temperature in the generation process, as no other molecular generator reports using dynamic variable-temperature sampling for token generation.

In this work, a previously trained and calibrated GPT is used to generate libraries of molecules using greedy decoding, temperature-based sampling, and dynamic variable temperature sampling. The molecule libraries generated are evaluated using a previously published deep neural network (DNN) trained to predict HMGCR IC₅₀ scores with a training score of 0.92 and a validation score of 0.84. The libraries of molecules are also evaluated by docking calculations, synthetic accessibility scores, quantitative estimates of druglikeness, and various similarity measures. A sigmoidal temperature ramp with a high final temperature is shown to be the most effective generation technique when used with very short prompt-lengths.

2. Methods

2.1 Library generation

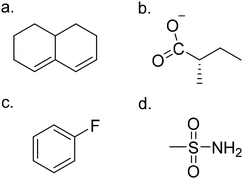
The statin molecule GPT and statin IC₅₀ scoring dense neural network (DNN) from the previous work¹ were used for all molecule generation and scoring in this work. Specifically, the GPT model with 2 transformer blocks trained on the Zn15 dataset of 40k in vitro bio-active molecules¹⁷ and two transformer blocks trained on 1081 HMGCR inhibitor molecules from the ChEMBL database¹⁸ was used (referred to in that work as the 2XA model). The DNN was trained on 905 HMGCR inhibitors from the binding database.¹⁹ The previous work showed that shorter prompt lengths produced virtual screening libraries with lower IC₅₀ values and other desirable properties.¹ Prompts for the GPT are tokens corresponding to elements of molecular SMILES strings, so a prompt length of 10 would correspond to the first 10 characters of a SMILES string. The 2XA GPT had a vocabulary size of 85 tokens, which is also used here. In this work, the shortest prompt length from the previous work, six tokens, is replicated, in order to establish continuity with that work. In the previous work, the six tokens were taken as the first six tokens from a set of 5000 molecular SMILES strings chosen randomly from the 41 000 molecule training set. The same set of 5000 SMILES strings is used here. In addition, three other prompt lengths were also tested here: three tokens and one token, taken from the same set of 5000 SMILES strings as the previous work, and a set of 22-token scaffolds, repeated to make 5000 total prompts. These scaffolds are shown in Fig. 1, and correspond to the pharmacophores for Atorvastatin, Rosuvastatin, HMG-coenzyme A, and Simvastatin. In the case of all but the Simvastatin pharmacophore, both the protonated and deprotonated forms were used, for a total of seven scaffolds. These seven scaffolds were then repeated to create a list of 5000 prompts. One of the scaffolds corresponded to 22 tokens, while the others corresponded to 17 tokens, so the shorter scaffolds were padded with five extra “start” tokens to achieve a uniform length of 22 for all of the scaffolds. The 2XA GPT model was used to generate up to 5000 molecules for each of the four prompt lengths, with various temperature-based schemes discussed below.

Fig. 1 Scaffolds used as prompts in the generation process: (a) the pharmacophore for Atorvastatin, (b) the pharmacophore for Rosuvastatin, (c) the pharmacophore for HMG-coenzyme A, and (d). the pharmacophore for Simvastatin.

To generate a molecule from a prompt, at each step k of the generation process, the existing set of tokens (or just the prompt if it is the first step) is passed through the model and the probability that each of the possible tokens (i) out of the 85 tokens in the vocabulary being the next token [P_k(i)] is calculated. With T = 0.0, or greedy decoding, the token with the highest probability is chosen each time. In temperature-based sampling, at each step, the probabilities are scaled according to the temperature:

where PS are the scaled probabilities. This scaling serves to even out the probabilities, so that at higher temperatures, the difference between the highest and lowest probabilities decreases. These probabilities are then used to randomly choose the next token, with higher probability tokens more likely to be chosen. At higher temperatures, though, even the less likely tokens are somewhat likely to be chosen. This in turn results in less probable, more varied molecules being generated, and a wider chemical space being sampled.

In the variable-temperature token generation used in this work, the token selection process switches between greedy decoding and temperature-based sampling while the molecule is being generated, and the temperature increases or decreases during the process as well. In this work, three increasing temperature schemes were tested. First, a slowly increasing exponential:

T = T₀χe^χ−1 (2)

where T₀ is the initial temperature (in this case, 0.0), and χ is the ratio of the current step, k, to the maximum number of steps, k_max. Next, a more rapidly increasing exponential was tested:

T = T₀[1 − e^−χ + χe^−χ] (3)

Finally, an increasing sigmoid was tested, activating at 50% of k_max:Three analogous decreasing temperature schemes were also tested: a slowly decreasing function:

T = T₀(1 − χ)e^−χ, (5)

a more rapidly decreasing function:

T = T₀(1 − χ)e^χ, (6)

and a decreasing sigmoid, activating at 50% of k_max:Fig. 2 shows each of these temperature ramps beginning or ending at T = 0.5, and a maximum number of generation steps/cycles of 90.

Fig. 2 Variable temperature sampling schemes with an increasing ramp beginning at zero and ending at 0.5 (eqn (2)–(4), left) and a decreasing ramp beginning at 0.5 and ending at zero (eqn (5)–(7), right). Traces are: slowly increasing/decreasing exponential (blue), rapidly increasing/decreasing exponential(orange), sigmoid (green).

The final temperature ramp used in this work, based on the results obtained with eqn (2)–(7), was an increasing sigmoid, activated at 10% of the total number of generation steps. This ramp is shown in Fig. 3. In all temperature ramps used in this work T = 0.0, or greedy decoding, was used for any temperature less than 0.015, in order to improve numerical stability in the generation process.

Fig. 3 Sigmoidal variable temperature sampling scheme with an increasing ramp beginning at zero and ending at 0.5. Sigmoid centered at 10% of the maximum token length.

In this work, libraries of up to 5000 molecule were generated for each of the four prompt lengths with four set temperatures: 0.0, 0.5, 1.0, and 2.0. Libraries were also then generated using eqn (2)–(7) to vary the temperature during the generation process, all beginning or ending at T = 0.5. This temperature was chosen as it was found to produce robust, potent libraries in the previous work.¹ Finally, the increasing sigmoid of eqn (4), activated at 10% of the number of generation steps, was used, ending at four temperatures: 0.5, 1.0, 1.5 and 2.0. Overall this produced fourteen temperature variations for each of the four prompt lengths, or fifty-six total libraries being generated.

2.2 Library characterization

All of the molecules in these fifty six libraries were characterized in several ways, including predicted IC₅₀ values, docking scores, synthetic accessibility scores, ADME properties, presence of various chemical moieties, and various molecular similarities. The DNN from the previous work¹ was used to calculate an IC₅₀ value for each molecule. Each molecule was then docked in the HMGCR binding site (structure from the curated DUD-E Database²⁰) using AutoDock Vina²¹via DockString.²² The DockString package prepares the molecule by protonating it at a pH of 7.4 with Open Babel,²³ generating a conformation using ETKG from RDKit,²⁴ optimizing the structure with MMFF94 (also from RDKit), and computing charges for the atoms using Open Babel, maintaining the stereochemistry in the original SMILES string. Docking scores were calculated via the standard Autodock Vina scoring function, which includes steric interactions, hydrophobic interactions, and hydrogen-bonding interactions between the ligand and protein.²¹ The Dockstring package used here reports that the range of docking scores in their calibration set of 260 000 molecules docked in 58 target proteins (including the protein studied here) is between −4 and −13 kcal mol⁻¹.²² In this work, the differences between the highest and lowest average docking scores for a set of libraries is ∼0.9 kcal mol⁻¹, or about 10% of the total range, suggesting that a 0.9 kcal mol⁻¹ difference is significant. The synthetic accessibility score (SAS)²⁵ for each molecule was computed using the SAS tool in RDKit. The Quantitative Estimate of Druglikeness (QED)²⁶ was calculated for each molecule, along with the pharmacokinetic properties that make up the QED including a log P, molecular weight, number of hydrogen bond donors, number of hydrogen bond acceptors, number of aromatic rings and number of rotatable bonds. Average values for these properties for each library may be found in the supporting data (ESI†).

The libraries were analysed for the presence of the HMG coenzyme-A pharmacophore (Fig. 1c) as well as several moieties typical of type I and II statins: a fluorophenyl ring and a methane sulfonamide group (both found in type II statins), and a butyryl group and decalin ring (both found in type I statins). The presence of the decalin ring and butyryl group (Fig. 4) are the defining characteristics of a type I statin; type II statins are fully synthetic compounds that often (but not always) have a fluorophenyl ring replacing butyryl group and are in general larger and more bulky than type I statins (Fig. 4). The counts for these moieties in each library are presented in the supporting data (ESI†).

Fig. 4 Moieties from type I and type II statins which have been searched for in each library: (a) substituted decalin (type I), (b) substituted butyryl (type I), (c) fluorophenyl (type II), (d) methyl sulfonamide (type II).

Tanimoto similarities²⁷ between every pair of molecules in each library and between each molecule in each library and a set of known statin molecules were calculated by using Morgan fingerprints²⁸ of radius 2, which is roughly equivalent to extended connectivity fingerprints of diameter 4. The percentages of each library that showed a greater than 0.25 similarity to Atorvastatin and Simvastatin (a representative type I and type II statin, respectively) are shown in Table 1 (%A and %S). Percent similarities to other statins are shown in the supporting data (ESI†), and largely follow the patterns for the representative type I and II molecules. Also in the supporting data (ESI†) are the percentages of pairs in each library that have a similarity of more than 0.25. This characteristic can serve as a measure of the diversity of each library, as a higher percentage of similarity means that the library covers a smaller chemical space.

Table 1 Total valid, useable, and sub-micromolar numbers of molecules generated by the GPT with 4 prompt lengths (1 token, 3 tokens, 6 tokens, and 23 token scaffolds) for four sampling temperatures. T = 0.0 indicates greedy decoding. Also presented: average values for predicted IC₅₀, docking score, and synthetic accessibility score (SAS), percent of molecules with Tanimoto similarity of >0.24 to Atorvastatin (%A) and Simvastatin (%S), and the Pearson correlation (p) between ln-IC₅₀ values and docking scores

	T	Valid	Usable	<μM	[IC50 (nM)]	[Score (kcal mol^−1)]	[SAS]	%A	%S	p
Scaffold (SC)	0.0	1429	2	0	—	—	—	—	—	—
	0.5	1849	114	27	278	−7.39	3.77	44	0	0.42
	1.0	1756	485	79	309	−7.42	3.92	41	1	0.39
	2.0	1233	786	71	326	−7.1	4.37	35	0	0.17
6 Tokens (6S)	0.0	4590	367	44	260	−7.35	4.16	25	16	0.57
	0.5	4463	867	121	216	−7.58	4.06	40	10	0.55
	1.0	4042	1500	220	204	−7.74	4	46	8	0.53
	2.0	1204	1096	95	274	−7.51	4.13	37	1	—
3 Tokens (3S)	0.0	4604	46	5	283	−7.7	4.29	20	0	0.72
	0.5	4589	472	107	171	−7.89	3.89	56	10	0.53
	1.0	4193	1328	255	177	−7.84	4.01	48	12	0.37
	2.0	1123	998	81	231	−7.53	4.28	41	4	0.32
1 Token (1S)	0.0	5000	1	1	3	−8.4	3.58	100	0	—
	0.5	4482	352	108	129	−7.96	3.82	62	10	0.48
	1.0	4303	1406	285	164	−7.86	3.92	55	12	0.41
	2.0	2818	1808	224	217	−7.63	4.02	42	11	0.39

---

Finally, Pearson correlations between several of the properties presented here were calculated, including correlation between ln-IC₅₀ and docking score, ln-IC₅₀ and SAS, ln-IC₅₀ and a log P and docking score and SAS. The correlation between ln-IC₅₀ and docking score is important for the following reason: while a docking score does not directly correlate to inhibitory power, a ligand with a strong docking score is more likely to linger in the binding site and have an inhibitory affect. This relationship is given in the equation:

where K_i is the binding affinity, [S] is the concentration of the substrate and K_m is the Michalis–Menton constant;²⁹ the docking score can be interpreted as a binding affinity, or directly proportional to a binding affinity.²¹ Further, in this work, the IC₅₀ for a molecule is based on a DNN, which in turn is trained on features derived from the SMILES strings for each molecule. Thus, other than a few rudimentary properties such as number of rotatable bonds and polar surface area, there is no 3D structural information about the molecule in the IC₅₀ calculation. Likewise, there is no information about the physical, 3D fit of the molecule for the binding site in the IC₅₀ calculation. The docking score, however, is based wholly on the three-dimensional structure of the molecule and its complementarity with the binding site. The greater the agreement between the IC₅₀ value and the docking score, each calculated in a decidedly different way, the more trustworthy each becomes. As a guideline, Pearson coefficients between 0 to ±0.3 can be considered weaker correlations, values from ±0.3 to ±0.5 can be considered medium–strength correlations, while values from ±0.5 to ±1 can be considered strong correlations. Positive Pearson correlations correspond to a direct relationship between variables, while a negative Pearson correlation corresponds to an inverse relationship between variables. The ln-IC₅₀/score correlation is provided in here, and the other correlations are available in the supporting data (ESI†), either in a table or in heatmap images.

3. Results and discussion

3.1 Analysis of libraries

Table 1 shows the numbers of generated molecules for the greedy decoding libraries (T = 0.0) and the constant temperature-based sampling libraries (T = 0.5, 1.0 and 2.0). The number of valid molecules in the first column indicates the number of generated SMILES strings that could be parsed into valid molecules. The column labelled ‘usable’ indicates the number of molecules remaining after duplicates are removed, and after molecules that simply replicated one of the 5000 seed molecules are removed. The next column indicates the number of remaining molecules with a predicted IC₅₀ value under one micromolar. This number is taken as the actual ‘size’ of the library, and all subsequent work deals only with these molecules. The scaffold-based models generated many fewer valid molecules than the one, three and six token models: between 25% and 37% of the expected 5000 molecules compared with as high as 92% for the six and three token models, and 90% for the one token model (excluding the 1S T = 0.0 model which produced 5000 of the same molecule). Likewise, the scaffold models generated fewer sub-micromolar molecules, or a maximum of 2% of the 5000 prompts, compared with as high as 4–6% for the other libraries.

As was seen in the previous work,¹ shorter prompt lengths result in lower IC₅₀ values, with the one token models producing the lowest IC₅₀ values of all of the constant temperature models: 170 nM on average compared to 304 nM, 239 nM and 215 nM for the scaffold, six token and three token models. A temperature of 0.5 produces the lowest IC₅₀ value for each prompt length. The same pattern can be seen for the docking scores: from longest prompt to shortest the average score goes from −7.30 kcal mol⁻¹ to −7.55 kcal mol⁻¹ to −7.74 kcal mol⁻¹ to −7.96 kcal mol, though the temperature with the lowest score is not predictable. This correlation of trends for the IC₅₀ values and docking scores does reinforce the reliability of both methods as discussed above. The SAS does not follow this patter, as the value increases from the scaffold to six and then to three token models (with higher values indicating more difficult syntheses), but the one-token models again do show the lowest SAS, indicating they are on average less difficult to synthesize. The percentage of the libraries which are similar to Atorvastatin are similar (∼40%) for all libraries except the one-token libraries, which average 65% similarity to Atorvastatin. This correlates with IC₅₀ and docking score, as Atorvastatin is known to be a powerful inhibitor of HMGCR. The similarity to Simvastatin is less meaningful for this dataset. Finally, the ln-IC₅₀/docking score correlations are of medium correlation (scaffold) or on the medium/strong correlation border (all other prompt lengths).

Table 2 shows the number of sub-micromolar molecules generated with each prompt-length using the increasing temperature ramps described in eqn (2)–(4). The scaffold-based models did not generate any sub-micromolar molecules; since these models start with T = 0.0, and the T = 0.0 greedy decoding molecule failed to produce any sub-micromolar molecules, it follows that these temperature ramp models could not produce them either. The number of sub-micromolar molecules produced by the other models decreased with decreasing prompt length. The temperature ramp model using eqn (3) produced molecules with significantly lower average IC₅₀ values and, for the 3-token models, a lower average docking score, than the other models, including greedy decoding and constant temperature-based sampling. This behaviour is explored further below.

Table 2 Number of sub-micromolar molecules generated, average predicted IC₅₀, and average docking score for libraries created by the GPT with four prompt lengths (1 token, 3 tokens, 6 tokens, and 23 token scaffolds) and three increasing variable temperature schemes: slow exponential, fast exponential, and sigmoid. – indicates no sub-micromolar molecules were generated

		<μM	[IC50 (nM)]	[Score (kcal mol^−1)]
Scaffold	Eqn (2)	0	—	—
	Eqn (3)	0	—	—
	Eqn (4)	0	—	—
6 tokens	Eqn (2)	47	285	−7.26
	Eqn (3)	56	253	−7.24
	Eqn (4)	47	254	−7.32
3 tokens	Eqn (2)	6	236	−7.78
	Eqn (3)	14	134	−8.01
	Eqn (4)	6	237	−7.72
1 token	Eqn (2)	1	3	−8.4
	Eqn (3)	14	36	−8.03
	Eqn (4)	3	3	−8.13

---

Table 3 shows the number of sub-micromolar molecules generated with each prompt-length using the decreasing temperature ramps described in eqn (5)–(7). The numbers of molecules are significantly higher than those generated by the increasing temperature-ramp models: at least twice as many and in two cases, about an order of magnitude more. However, in almost all cases the average IC₅₀ values are nearly identical to those for the greedy decoding and constant-temperature sampling models, and for the one-token based models, the average IC₅₀ values are higher. In two specific cases (SC eqn (5) and 6S eqn (5)) the values for IC₅₀ are marginally lower. In all cases, the docking scores similar to or were slightly higher than the other models.

Table 3 Number of sub-micromolar molecules generated, average predicted IC₅₀, and average docking score for libraries created by the GPT with four prompt lengths (1 token, 3 tokens, 6 tokens, and 23 token scaffolds) and three decreasing variable temperature schemes: slow exponential, fast exponential, and sigmoid

		<μM	[IC50 (nM)]	[Score (kcal mol^−1)]
Scaffold	Eqn (5)	12	200	−7.33
	Eqn (6)	8	285	−7.35
	Eqn (7)	13	413	−7.26
6 tokens	Eqn (5)	123	213	−7.49
	Eqn (6)	98	227	−7.41
	Eqn (7)	117	256	−7.36
3 tokens	Eqn (5)	92	195	−7.73
	Eqn (6)	67	187	−7.73
	Eqn (7)	84	230	−7.7
1 token	Eqn (5)	101	151	−7.89
	Eqn (6)	55	175	−7.83
	Eqn (7)	84	173	−7.79

---

The only temperature ramp model out of eqn (2)–(7) that produced a significant improvement on IC₅₀ values was the increasing temperature ramp of eqn (3). Eqn (3) is a rapidly increasing exponential, and so other temperature ramps that exaggerated that rapidly increasing were tested. An increasing sigmoid (eqn (4)) was again used, but rather than have the sigmoid ramp up in the middle of the generation process (50% of the maximum tokens, 90 in this case), it was tested with the ramp occurring at 5%, 10%, and 20% of the maximum tokens. This was done by replacing the 0.5 multiplier in eqn (3) with either 0.05, 0.10 or 0.20. In all cases, these models showed improvement over eqn (2)–(7) as well as greedy decoding and constant-temperature sampling, but the 10% model was chosen as it produced molecules with a slightly lower average IC₅₀ value than the other two models. This model is referred to as the Sigmoid 10% (S10) model in the remainder of this work. Table 4 shows the numbers of sub-micromolar molecules generated with S10 model with each prompt length, and with final temperatures of 0.5, 1.0, 1.5 and 2.0. While these numbers are slightly lower than those produced by all other temperature models for the scaffold-based generation, the numbers a significantly larger for 6S and especially 3S and 1S, for which the numbers of molecules produce are more than three-times larger than the next best temperature model. The numbers of sub-micromolar molecules increases as the final temperature of the S10 ramp increases, with the exception of the 1S models at T = 2.0, which decreased compared to T = 1.5.

Table 4 Number of sub-micromolar molecules generated, average predicted IC₅₀, average docking score, synthetic accessibility score (SAS), percent of molecules with Tanimoto similarity of >0.24 to Atorvastatin (%A) and Simvastatin (%S), and the Pearson correlation (p) between ln-IC₅₀ values and docking scores for libraries created by the GPT with four prompt lengths (1 token, 3 tokens, 6 tokens, and 23 token scaffolds) and an increasing sigmoid at 10% of maximum tokens (S10). – indicates no sub-micromolar molecules were generated or that the library was otherwise unviable

	S10	<μM	[IC50 (nM)]	[Score (kcal mol^−1)]	SAS	%A	%S	p
Scaffold	T = 0.5	0	—	—	—	—	—	—
	T = 1.0	16	455	−7.42	3.86	56	0	0.27
	T = 1.5	38	362	−7.14	4.17	42	0	0.5
	T = 2.0	39	378	−7.16	4.17	46	0	0.32
6 tokens	T = 0.5	82	229	−7.5	4.15	30	15	0.56
	T = 1.0	130	218	−7.53	4.07	35	13	0.53
	T = 1.5	182	223	−7.44	3.95	40	12	0.68
	T = 2.0	—	—	—	—	—	—	—
3 tokens	T = 0.5	27	98	−7.94	3.8	74	0	0.41
	T = 1.0	112	122	−8.09	3.66	74	1	−0.03
	T = 1.5	329	109	−8	3.73	77	1	0.21
	T = 2.0	373	120	−7.95	3.75	74	0	0.24
1 token	T = 0.5	61	57	−8	3.61	90	0	0.19
	T = 1.0	263	71	−8.08	3.61	85	0	0.39
	T = 1.5	695	69	−8.05	3.67	81	0	0.41
	T = 2.0	597	81	−7.97	3.74	76	0	0.43

---

Table 4 also shows the average IC₅₀ values for each S10 library, and the S10 temperature ramps produce molecules with significantly lower average IC₅₀ values for the 3S and 1S models (slightly lower for 6S and slightly higher for scaffolds). For the 1S and 3S models, the average IC₅₀ values generally increase with increasing final temperature, with some small fluctuations. The 6S and SC models have no predictable pattern. The docking scores for each library (also Table 4) are lower than other temperature models for the 1S and 3S libraries, and slightly higher than other temperature models for the 6S and SC libraries. Average SAS for each library follows the same pattern, with the 1S and 3S libraries having lower average SAS than other temperature models, while 6S and SC show little change. The percentage of molecules in each library that have a greater than 0.25 Tanimoto similarity to Atorvastatin (type II statin) follow the same pattern: significantly increased similarity for 1S and 3S, and little change for 6S and SC. The percentage of molecules with similarity to Simvastatin (type I statin) follow the opposite trend: the percentage increases for the 6S library and decreases for the 1S and 3S libraries (the SC S10 library has zero molecules with similarity to Simvastatin). Finally, Table 4 shows the Pearson correlation between ln-IC₅₀ and docking score for the S10 libraries. With one exception (the three-token libraries), all libraries show medium or strong correlation between these two variables, with values between ∼0.3 and ∼0.7. While the three-token libraries do have weaker correlation overall, only the T = 1.0 library has truly poor correlation (−0.03, which is not only weak, but also shows an inverse relationship). The correlations for the S10 libraries are on average slightly weaker than was found for the greedy decoding and constant-temperature based sampling libraries (Table 1), which had values between ∼0.4 and ∼0.7. Still, the amount of correlation present does reinforce the fact that IC₅₀ and docking scores show considerable agreement and thus are likely good indicators of the molecules’ inhibitory power.

3.2 Molecule analysis

While the models in this work have generated many molecules, the number of sub-micromolar molecules reported for each library has had the ‘seed molecules’ from which the prompt tokens were taken removed. This does not account for other molecules from the training set that could have simply been replicated by the GPT at inference. Table 5 thus shows what percentage of molecules from each generated library that overlap with the training set of 1081 HMGCR inhibitors from ChEMBL¹⁸ that were used to train the model. For the greedy decoding and constant-temperature based sampling libraries (first block) it may be seen that the percent overlap with the training library decreases with increasing temperature; this make sense as the higher temperatures produce ‘less probable’ molecules. The models based on eqn (2)–(7) almost all have values between 40 and 70% (with a few exceptions). The S10 libraries, however, show dramatically decreasing overlap with the training set, with the 1S and 3S libraries having only 5 and 7% overlap with the training set.

Table 5 Percentage of generated molecules that overlap between the training set of 1081 statin inhibitors from ChEMBL¹⁸ and the libraries generated with the one token (1S), three tokens (3S), and six tokens (6S), and scaffold-based models (SC) using either greedy decoding (T0.0), single-temperature token sampling (T0.5, T1.0 and T2.0) or a sigmoidal variable temperature ramp at 10% of maximum tokens (S10) ending with temperatures of 0.5, 1.0, 1.5 and 2.0 (T0.5, T1.0, T1.5 and T2.0)

		Scaffold	6 tokens	3 tokens	1 token
Temperature	T = 0.0	—	45	80	100
	T = 0.5	0	39	51	48
	T = 1.0	0	29	33	34
	T = 2.0	0	14	15	31
Decreasing	Eqn (2)	—	45	83	100
	Eqn (3)	—	45	64	69
	Eqn (4)	—	43	67	33
Increasing	Eqn (5)	0	42	60	51
	Eqn (6)	0	46	69	65
	Eqn (7)	0	43	58	60
S10	T = 0.5	—	42	41	31
	T = 1.0	0	29	15	12
	T = 1.5	0	18	7	5
	T = 2.0	0	—	5	5

---

Overall, ∼2900 molecules were generated between all of the models presented in this work. Table 6 shows the overlap between all greedy decoding, constant-temperature sampling and S10 libraries except those generated with scaffold prompts (diagonal elements are the size of each library). The SC-libraries did not have any overlap with the six, three and one token-based models and so the overlaps between those libraries are presented separately in Table 7. While the maximum overlap for any library is usually with its nearest neighbours (3S T = 1.0 would overlap strongly with 3S T = 0.5 and 3S T = 2.0) there is often a large overlap with a different prompt length the same temperature (3S T = 1.0 would overlap with 1S T = 1.0 and 6S T = 1.0). The table show that for any give prompt length and sampling-type, the amount of overlap decreases with increasing temperature, which is expected given the reduced probabilistic nature of the higher temperature models. Overall the table shows that each library has a considerable amount of unique molecules not present in any other library. For the scaffold-based libraries in Table 7, there is very limited overlap between any of the libraries.

Table 6 Numbers of generated molecules that overlap between libraries generated with the one token (1S), three token (3S), and six token (6S), using either greedy decoding (T0.0), single-temperature token sampling (T0.5, T1.0 and T2.0) or a sigmoidal variable temperature ramp at 10% of maximum tokens (S10) ending with temperatures of 0.5, 1.0, 1.5 and 2.0 (T0.5, T1.0, T1.5 and T2.0)

---

Table 7 Numbers of generated molecules that overlap between libraries generated with the scaffold (SC) prompts, using either greedy decoding (T0.0), single-temperature token sampling (T0.5, T1.0 and T2.0) or a sigmoidal variable temperature ramp at 10% of maximum tokens (S10) ending with temperatures of 0.5, 1.0, 1.5 and 2.0 (T0.5, T1.0, T1.5 and T2.0)

---

3.3 K-Means analysis

The set of unique molecules from this work was separated into 10 groups using K-means analysis. The molecules were all featurized using RDKit descriptors³⁰ and grouped using the implementation of K-means in SciKitLearn.³¹Fig. 5 shows a representative molecule from each of the 10 groups. Five of the groups have the type II statin pharmacophore (Fig. 1a and b; groups 0, 2, 6–8) while one group has the type I statin pharmacophore (Fig. 1d; group 4). Thus five of the ten groups may be said to be statin-like. 65% of the 2853 unique molecules in the study fall into these five groups. Six known statins were sorted into the groups (using the same procedure as the libraries) and Table 8 shows the groups to which each statin was assigned. The two known type I statins were indeed classified into group four, while the type II statins were put into groups 2, 7 and 8. Table 8 also shows the mean and median IC₅₀ values for each group; median is more representative here are one large number near the high end of the range can skew results dramatically, though the mean values do mirror the median values. The two lowest values for median IC₅₀ (5 and 9 nM) are in groups 2 and 7 to which Fluvastatin and Atorvastatin belong, respectively, and they are close to the actual IC₅₀ values for those two drugs.³² The group with the type I statins follow these in median IC₅₀ with a value of 18 nM, again close to what a type I statin should have for this value.³² The groups with the highest median IC₅₀ values are groups 1 and 6, which Table 8 shows are molecules with many halogen groups or large rings. About 16% of the total molecules fall into these groups of unlikely inhibitors.

Fig. 5 Representative molecule from each of the 10 K-means groups.

Table 8 Mean, median and standard deviation for IC₅₀ (nM), molecule counts, and representative molecule/structure/class for each of the 10 K-means groups

	Count	Mean IC50 (nM)	Median IC50 (nM)	σ (nM)	Representative
Group 0	12	121	86	158	Sulfonamides, halogens
Group 1	366	424	388	303	Halogens
Group 2	979	60	9	139	Fluvastatin
Group 3	83	311	220	277	Peptide-like
Group 4	399	117	18	207	Simvastatin, Lovastatin
Group 5	133	327	256	251	Steroid-like
Group 6	98	339	328	264	Large rings
Group 7	459	51	5	148	Atorvastatin
Group 8	291	231	81	288	Rosuvastatin, Pravastatin
Group 9	33	287	144	324	Multiple halogens

---

Table 9 shows how the molecules in each library are distributed into the K-means groups. Having an even distribution across all the groups implies that a library is sampling a wide swath of chemical space, while have a large fraction of molecules in one group implies the model has focused in on one type of structure. The group with the highest fraction for each library is shown in bold. The S10 libraries for all prompt lengths except scaffolds have the highest fraction of their molecules in group 2 (type II statin-like, second lowest IC₅₀). The second most common group to have the highest fraction in any given library is group 8 (type II statin, fourth lowest IC₅₀), though this group is only common for the scaffold-based libraries. The third most common group to have the highest fraction in any given library is group 7 (type II statin, lowest IC₅₀), with group 4 (type I statin, third lowest IC₅₀) being the fourth mostly likely to have the highest fraction in any given group. If the scaffold-based libraries are removed, the fractional populations correlate exactly with the inverse of IC₅₀. The S10 libraries are more likely to have their most common group be group 2, suggesting that the temperature ramp favours this type of structure.

Table 9 Fraction of molecules from each library in each K-means group (Groups 0–9). Models include one token (1S), three token (3S), six token (6S), and scaffold (SC) prompts, using either greedy decoding (T0.0), single-temperature token sampling (T0.5, T1.0 and T2.0) or a sigmoidal variable temperature ramp at 10% of maximum token length (S10) ending with temperatures of 0.5, 1.0, 1.5 and 2.0 (T0.5, T1.0, T1.5 and T2.0). The bold number in each row indicates the K-means group with the largest fraction from the library represented in that row

Group →	0	1	2	3	4	5	6	7	8	9
1S S10 T0.5	0.00	0.02	0.64	0.00	0.18	0.00	0.00	0.10	0.07	0.00
1S S10 T1.0	0.00	0.06	0.51	0.00	0.19	0.00	0.00	0.14	0.10	0.00
1S S10 T1.5	0.00	0.08	0.48	0.00	0.17	0.00	0.00	0.20	0.07	0.00
1S S10 T2.0	0.01	0.13	0.45	0.00	0.16	0.00	0.00	0.17	0.08	0.00
1S T0.0	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
1S T0.5	0.00	0.05	0.28	0.05	0.19	0.04	0.05	0.30	0.06	0.01
1S T1.0	0.00	0.06	0.25	0.05	0.19	0.08	0.05	0.25	0.06	0.01
1S T2.0	0.00	0.11	0.20	0.03	0.17	0.11	0.09	0.16	0.09	0.04
3S S10 T0.5	0.00	0.00	0.63	0.00	0.11	0.07	0.11	0.04	0.00	0.04
3S S10 T1.0	0.00	0.05	0.63	0.00	0.13	0.07	0.04	0.05	0.01	0.03
3S S10 T1.5	0.00	0.07	0.54	0.02	0.15	0.03	0.04	0.12	0.02	0.02
3S S10 T2.0	0.00	0.10	0.55	0.01	0.13	0.03	0.04	0.09	0.03	0.01
3S T0.0	0.00	0.00	0.20	0.00	0.00	0.20	0.40	0.00	0.00	0.20
3S T0.5	0.00	0.03	0.25	0.01	0.19	0.07	0.08	0.27	0.06	0.04
3S T1.0	0.00	0.04	0.22	0.04	0.21	0.09	0.08	0.22	0.08	0.03
3S T2.0	0.03	0.13	0.25	0.03	0.10	0.09	0.09	0.08	0.16	0.05
6S S10 T0.5	0.00	0.04	0.21	0.04	0.24	0.18	0.12	0.09	0.04	0.05
6S S10 T1.0	0.00	0.06	0.27	0.04	0.22	0.18	0.06	0.08	0.04	0.04
6S S10 T1.5	0.01	0.13	0.34	0.03	0.18	0.16	0.05	0.04	0.05	0.02
6S T0.0	0.00	0.07	0.09	0.05	0.20	0.16	0.14	0.18	0.02	0.09
6S T0.5	0.00	0.05	0.21	0.05	0.18	0.16	0.08	0.18	0.04	0.05
6S T1.0	0.00	0.06	0.22	0.04	0.18	0.12	0.08	0.21	0.07	0.02
6S T2.0	0.01	0.21	0.26	0.02	0.15	0.11	0.05	0.09	0.05	0.03
SC S10 T1.0	0.00	0.13	0.40	0.07	0.00	0.00	0.00	0.00	0.40	0.00
SC S10 T1.5	0.00	0.11	0.30	0.08	0.00	0.00	0.00	0.03	0.49	0.00
SC S10 T2.0	0.03	0.14	0.11	0.08	0.00	0.00	0.00	0.05	0.59	0.00
SC T0.5	0.00	0.19	0.30	0.04	0.00	0.00	0.04	0.04	0.41	0.00
SC T1.0	0.00	0.22	0.23	0.01	0.01	0.01	0.03	0.08	0.42	0.00
SC T2.0	0.00	0.40	0.06	0.02	0.03	0.00	0.03	0.08	0.38	0.00

---

3.4 Entropy analysis of the S10 temperature ramp

The source of the effectiveness of the dynamic temperature token generation approach is the differential treatment of the challenging tokens at the beginning of a SMILES string and the challenging token tokens towards the end of a SMILES string. As described in the work by Zhang et al.,⁴ a challenging token is one with high Shannon entropy, meaning that there are multiple possibilities for that token at that point in the generation process that all have similar probabilities. For example, for the partial SMILES string “c1cc”, the next token could be “O”, or “Cl”, or “F”, all with similar probabilities (0.60, 0.15, 0.25); this is a challenging token. In the partial SMILES string “c1cc(F”, the next token has to be “)” and so it's probability would be near 1.0 and all other tokens would have near zero probability; this is a confident token. The higher the temperature of generation, the more likely a token with a lower probability will be chosen. At the beginning of a SMILES string, the S10 temperature ramps used here use greedy decoding which ensures the most likely token is chosen; as the token generation process progresses, the temperature increases and so less-likely tokens are chosen more frequently. Thus challenging tokens are treated greedily at the start and more probabilistically towards the end. This has the effect of creating a stable, predictable “start” of a molecule, while allowing considerable variability and novelty towards the “end” of the molecule.

To further understand this mechanism, the Shannon entropy of the generation process was studied for a sample set of generated molecules. The three-token-prompt models were chosen for this exercise as they create more robust libraries than the six-token-prompt models when using the variable-temperature approach, and are intermediate in performance between the six-token and one-token-prompt models. One-hundred prompts were fed into the three-token-prompt model with a controlled generation method (greedy decoding, or constant T = 0.0 generation), and six other methods (constant temperatures at T = 0.5. 1.0 and 2.0, and S10 with T = 0.5. 1.0 and 2.0). The Shannon entropy for each viable molecule (having an interpretable SMILES string) for each model was calculated at each of the inference steps according to

where p_i is the probability of each possible token in the vocabulary and the sum to 85 indicates the size of the vocabulary used in the model. The Shannon entropy was then plotted versus the inference step for each model (Fig. 6 and 7). Note that each plot includes all viable molecules for each model (out of one-hundred), and in most cases the models produced less than one-hundred viable molecules.

Fig. 6 Shannon entropy for each new token at each generation step for the 3-token-prompt models at four temperatures: 0.0, 0.5, 1.0 and 2.0. Each plot includes all viable molecules (out of 100 initial prompts) produced by each model/temperature.

Fig. 7 Shannon entropy for each new token at each generation step for the 3-token-prompt models using the S10 temperature ramp with three temperatures: 0.5, 1.0 and 2.0. Each plot includes all viable molecules (out of 100 initial prompts) produced by each model/temperature.

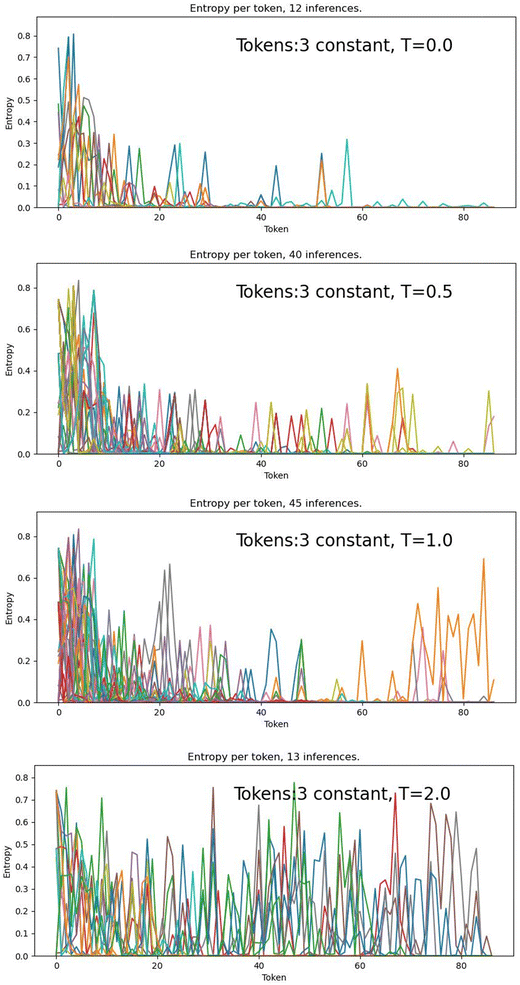
Fig. 6 shows that at T = 0.0, there are challenging tokens (high entropy, ∼0.8) in the first ∼10 steps, followed by greatly decreased entropy for the T = 0.0, 0.5 and 1.0 models, while the T = 2.0 model maintains high entropy (challenging token) across all steps. This is interpretable as the greedy and low-temperature decoding models choosing “safe” token with higher probabilities early in the SMILES string when entropy is high, leading to a more predictable SMILES string, with more confident tokens as the generation process progresses. The T = 2.0 model, however, is always able to choose tokens with lower probability, and so the SMILES string never becomes predictable and tokens remain challenging across the generation process.

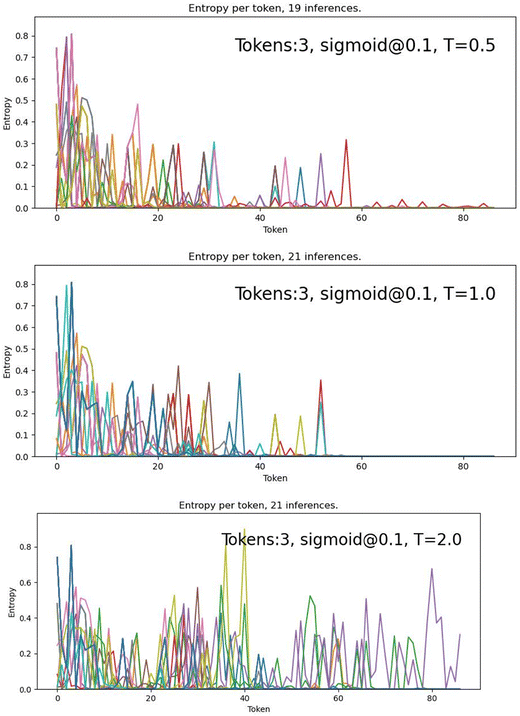
Fig. 7 shows that the use of the S10 ramp decreases the number of steps with high entropy (∼0.8) from ∼10 with greedy and constant temperature decoding to ∼5 steps with S10. For T = 0.5 and 1.0, the number of high entropy spikes above about 40 steps also decreases dramatically. For T = 2.0, constant temperature decoding has high entropy across the generation process, while S10 has several lulls in entropy around 20 and 45 steps, and less high entropy spikes overall. These results support the interpretation that the S10 ramp is creating a more stable SMILES string overall, while still allowing for some variability and novelty.

4. Conclusions

This is the first molecular generative machine learning model to use dynamic variable temperature during the generation process. During inference, or, when generating molecules in a token-by-token fashion, a sigmoidal temperature ramp, beginning at zero and ending between 0.5 and 2.0 and activating at 10% of the maximum tokens, produces molecule libraries with larger numbers of sub-micromolar molecules, which have lower IC₅₀ values, lower docking scores, and lower SAS than libraries generated with greedy decoding or constant-temperature-based token sampling. Generally an ending temperature of 1.0 produces the optimal libraries. These S10 libraries also have less overlap with the training set of molecules, and have low overlap with other libraries generated with other temperature schemes. This effect is especially pronounced when using shorter prompts in the inference process. Specifically, single token prompts produced the libraries with the most desirable properties, with three-token prompts also producing good results. Six-token prompts using the S10 ramps produce libraries whose properties are largely unchanged from other temperature schemes. Scaffold-based prompts produce libraries with few sub-micromolar molecules, which have higher IC₅₀ values, docking scores and SAS than the short-token libraries.

This variable temperature approach is easily implementable in any GPT, recurrent neural network, or other autoregressive molecular generation model. These models all produce a set of probabilities for the next token at each step of inference; these probabilities need only be scaled according to eqn (1), using the temperature at each inference step calculated by eqn (4). The only non-learned variables needed are the total number of inference steps (k_max), and the centre of activation for the sigmoid function (0.1 × k_max is used here). As the dynamic temperature scaling acts only on the final product of inference (the probabilities), the approach is generalizable to any of the models mentioned above.

Overall, in transformer-decoder GPT based molecule library inference, single token prompts and an S10 temperature ramp ending at T = 1.0 are suggested.

Author contributions

Mauricio Cafiero: project design, coding, data collection, data analysis, writing, editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The following data is provided as supporting data (ESI†) for this article, as well as in the data repository at the University of Reading: CSV files for all libraries generated in this work. Raw files are labelled “Refined” and “Docking.” Refined files includes all “usable” molecules (see Table 1) and Docking files include only sub-micromolar molecules. The “Docking_props” folder includes CSV files with IC50 values, docking scores, QED and other Lipinski properties. The “Sim_SAS” folder contains CSV files to include the previous data plus Tanimoto similarities and SAS values. This folder also includes png files of heatmaps showing Pearson correlations for various properties. The “Kmeans” folder contains clustering information in two formats: CSV files for all molecules in each K-means group, and CSV files for each library, showing the group membership for each molecule. The “Notebooks” folder contains a simple GUI that, when used in the saved directory structure, will allow the user to view the molecules in each library and sort molecules by IC50, docking score and SAS. This is a Tkinter-based GUI. All work was completed with freely available software, and data can be accessed with freely available software. Python and all libraries can be accessed with Anaconda (https://www.anaconda.com/) or Google Colab.

Acknowledgements

Resources were funded in part by the Royal Society of Chemistry.

References

1. M. Cafiero, J. Chem. Inf. Model., 2024, 64, 8464–8480.
2. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. M. Gomez, L. Kaiser and I. Polosukhin, Adv. Neural Inform. Process. Syst., 2017, 30, 5998–6009.
3. Y. Zhu, J. Li, G. Li, Y. Zhao, J. Li, Z. Jin and H. Mei, arXiv, 2024, preprint, arXiv:2309.02772, https://arxiv.org/abs/2309.02772.
4. S. Zhang, Y. Bao and S. Huang, arXiv, 2024, preprint, arXiv:2403.14541, https://arxiv.org/abs/2403.14541.
5. C.-C. Chang, D. Reitter, R. Aksitov and Y.-H. Sung, arXiv, 2023, preprint, arXiv:2306.01286, https://arxiv.org/abs/2306.01286.
6. V. Bagal, R. Aggarwal, P. K. Vinod and U. D. Priyakumar, J. Chem. Inf. Model., 2022, 62, 2064–2076.
7. E. P. Tysinger, B. K. Rai and A. V. Sinitskiy, J. Chem. Inf. Model., 2023, 63, 1734–1744.
8. L. Yang, G. Yang, Z. Bing, Y. Tian, Y. Niu, L. Huang and L. Yang, ACS Omega, 2021, 6, 33864–33873.
9. F. Urbina, C. T. Lowden, J. C. Culberson and S. Ekins, ACS Omega, 2022, 7, 18699–18713.
10. H. H. Loeffler, J. He, A. Tibo, J. P. Janet, A. Voronov, L. H. Mervin and O. Engkvist, J. Cheminf., 2024, 16, 20,  DOI:10.1186/s13321-024-00812-5.
11. A. Tibo, J. He, J. P. Janet, E. Nittinger and O. Engkvist, chemrxiv, 2024, preprint DOI:10.26434/chemrxiv-2023-v25xb-v2.
12. F. Grisoni, M. Moret, R. Lingwood and G. Schneider, J. Chem. Inf. Model., 2020, 60, 1175–1183.
13. J. Chang and J. C. Ye, Nat. Commun., 2024, 15, 2323,  DOI:10.1038/s41467-024-46440-3.
14. J. Ross, B. Belgodere, S. C. Hoffman, V. Chenthamarakshan, Y. Mroueh and P. Das, GP-MoLFormer: A Foundation Model For Molecular Generation, arXiv, 2025, arXiv:2405.04912, https://arxiv.org/abs/2405.04912.
15. U. A. M. Sob, Q. Li, M. Arbesú, O. Bent, A. P. Smit and A. Pretorius, Generative Model for Small Molecules with Latent Space RL Fine-Tuning to Protein Targets, arXiv, 2024, arXiv:2407.13780, https://arxiv.org/abs/2407.13780.
16. S. Noguchi and J. Inoue, J. Chem. Inf. Model., 2022, 62, 5988–6001.
17. T. Sterling and J. J. Irwin, J. Chem. Inf. Model., 2015, 55, 2324–2337.
18. ChEMBL DOI:10.6019/CHEMBL.database.34, (accessed 16 September 2024).
19. Binding Database, https://www.bindingdb.org, (accessed 16 September 2024).
20. M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594.
21. O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461.
22. M. García-Ortegón, G. N. C. Simm, A. J. Tripp, J. M. Hernández-Lobato, A. Bender and S. Bacallado, J. Chem. Inf. Model., 2022, 62(15), 3486–3502,  DOI:10.1021/acs.jcim.1c01334.
23. N. M. O’Boyle, C. Morley and G. R. Hutchison, Chem. Cent. J., 2008, 2, 5.
24. RDKit: Open-source cheminformatics, https://www.rdkit.org..
25. P. Ertl and A. Schuffenhauer, J. Cheminf., 2009, 1, 8.
26. G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Nat. Chem., 2012, 4, 90–98.
27. D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2015, 7, 20.
28. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
29. C. Yung-Chi and W. H. Prusoff, Biochem. Pharmacol., 1973, 22, 3099–3108.
30. G. Landrum, RDKit Documentation, 2012.
31. F. Pedregosa, V. Michel, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, J. Vanderplas, D. Cournapeau, G. Varoquaux, A. Gramfort, B. Thirion, V. Dubourg, A. Passos, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
32. J. M. McKenney, Clin. Cardiol., 2003, 26, 32–38.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00692a

---