Strong compensation effects related to the empty channel in p-type transparent conductive material Cu₃TaS₄: a first-principles study

Abstract

Wide band gap chalcogenide semiconductors have attracted much attention as p-type transparent conductive materials mainly because of their high hole mobility and ease of p-type doping. Cu₃TaS₄ has recently emerged as a promising candidate for a p-type transparent conductive material owing to its wide band gap, light hole effective mass and high optical transparency. Nevertheless, understanding the p-type conducting mechanism of Cu₃TaS₄ remains elusive. In this study, the electronic structure, optical properties, defect properties and p-type conductivity of Cu₃TaS₄ are systematically investigated based on first-principles calculations. The results show that Cu₃TaS₄ is an indirect band gap semiconductor with an electronic band gap of 2.97 eV and exhibits high transparency in the visible light region. Furthermore, the lowest defect formation energy of copper vacancies under Cu poor conditions confirms the intrinsic p-type conductivity of Cu₃TaS₄. However, the intrinsic p-type conductivity of Cu₃TaS₄ is restricted by the strong compensation effect of the n-type defect, interstitial Cu(Cu_i). Even with extrinsic p-type doping, the p-type conductivity remains unimproved due to the compensation effect. The ease of formation of Cu_i is related to the empty “channel” along the (100) direction within the Cu₃TaS₄ crystal. As a result, the existence of the empty “channel” and the strong compensation effect of Cu_i lead to difficulties in achieving high hole concentration and excellent p-type conductivity for Cu₃TaS₄.

---

1. Introduction

Transparent conductive materials (TCMs) are extensively utilized in optoelectronic applications, including touchscreens, flat panel displays, and solar cells, owing to their excellent electrical conductivity and high optical transparency in the visible light region.^1–7 In the past few years, the investigations on TCMs have typically focused on transparent conductive oxides (TCOs). Based on the majority carriers in TCOs, these materials can be categorized into two types: n-type and p-type TCOs. The n-type TCOs like Sn doped In₂O₃ (ITO),⁸ Al doped ZnO (AZO),⁹ and F doped SnO₂ (FTO)¹⁰ have achieved remarkable progress due to their high electrical conductivity and high carrier concentration. For example, the electrical conductivity of ITO has reached 10⁴ S cm⁻¹ and the free electron concentration has reached as high as 2 × 10²¹ cm⁻³.^11,12 However, the implementation of p-type doping in these well-known n-type TCOs has progressed slowly, which is mainly ascribed to the localization of the valence band and the low valence band energy in n-type TCOs. On the one hand, the valence bands of these TCOs originate from the localized O-2p orbital, which leads to a heavy hole effective mass and low hole mobility.^13–15 On the other hand, the low valence band energy of the O-2p orbital makes it difficult to achieve p-type doping.¹⁶ In order to overcome such issues, the strategy named “chemical modulation of the valence band” was proposed.¹⁷ The hybridization between the O-2p and Cu-3d orbitals results in a high energy valence band for CuAlO₂ with a delafossite structure and further solves the p-type doping problem.^17,18 The discovery of CuAlO₂ has spurred the exploration of various oxides with delafossite structure, including CuCrO₂,¹⁹ CuGaO₂,²⁰ and CuScO₂,²¹ as p-type TCOs. For example, Veron et al.¹⁹ prepared CuCr_0.97Mg_0.03O₂ films with delafossite structure by a low power laser spot method. They found that the sample has a high conductivity of 5.8 S cm⁻¹ after the introduction of Mg into CuCrO₂. In addition, the transparent heterojunction of Cu-based delafossites n-CuInO₂/p-CuGaO₂ was synthesized by a reactive evaporation method. Owing to the high rectification ratio and the excellent transmittance, the p–n heterojunction shows great potential as a promising active device in transparent electronics.²⁰

In addition to the oxides with the delafossite structure, wide band gap chalcogenide semiconductors have also been employed as p-type TCMs most recently.^22–24 Due to the delocalized S-3p orbital, the valence band of sulfur-based TCMs (e.g. CuAlS₂) exhibits more pronounced dispersion than their oxide-based counterparts (e.g. CuAlO₂), leading to a low hole effective mass and high hole mobility.^25–27 Additionally, the atomic energy level value of the S-3p orbital is higher than that of the O-2p orbital. Consequently, sulfur-based TCMs typically possess higher valence band positions relative to oxide-based TCMs, which makes them more favorable for p-type doping.²⁶ Therefore, the wide band gap chalcogenide semiconductors such as BaCu₂S₂,^28–30 CuAlS₂,^31,32 LaCuOS,^33,34 and Cu₃TaS₄,^35,36etc. have been investigated as p-type TCMs. Certain chalcogenide semiconductors have emerged as promising candidates for optoelectronic device applications, primarily attributed to their distinctive wide band gaps and inherent p-type conductivity. Zhang et al.³⁷ successfully fabricated a transparent p–n junction with n-type AZO by exploiting the good electrical and optical properties of p-type LaCuOS. This device exhibited a high rectifying ratio of 300, demonstrating its potential applications in next-generation invisible electronics and optoelectronic devices. Yang et al.³⁸ synthesized a transparent p-type conductive CuAl_0.90Zn_0.10S₂ thin film using the pulsed plasma deposition technique and further fabricated a transparent p-CuAlS₂:Zn/n-In₂O₃:W heterojunction diode. Similarly, Cu₃TaS₄ also has promising application prospects in transparent electronic devices due to its high optical transmittance and potential p-type conductivity.³⁵

Recently, Cu₃TaS₄ has attracted much attention as a p-type TCM due to its wide band gap, light hole effective mass and high optical transparency.^{35,36,39–42} For example, theoretical investigations have elucidated that Cu₃TaS₄ possesses a band gap of 2.9 eV, thereby ensuring optical transparency in the visible light region.⁴¹ Furthermore, the valence band maximum (VBM) of Cu₃TaS₄ is made up by the S-3p and Cu-3d orbitals, which results in the dispersion of the valence band and the generation of light holes.^40,41 Experimentally, the Cu₃TaS₄ sample was synthesized via a two-step growth process, and subsequent UV-visible-near-infrared (UV-VNIR) spectroscopy combined with photoluminescence measurements revealed a 531.4 nm green emission peak attributed to copper vacancies (V_Cu).⁴² Haque et al.⁴³ found that the presence of V_Cu (i.e. under Cu-poor conditions) favors the introduction of Ta atoms into Cu_2−xS and further promotes the formation of Cu₃TaS₄ nanocrystals. Although Cu₃TaS₄ has been synthesized for many years, its hole mobility and p-type conductivity remain unsatisfactory, limiting its potential as a p-type TCM.^35,36,44 Besides, the mechanism of p-type conductivity of Cu₃TaS₄ is still unclear in theoretical studies.⁴⁵ Therefore, elucidating the origin and unraveling the underlying mechanisms of p-type conductivity in Cu₃TaS₄ are crucial for advancing its practical applications.

In this study, the electronic structure, optical properties, defect properties and p-type conductivity of Cu₃TaS₄ are investigated based on first-principles calculations. The wide electronic band gap and high optical transparency make it a viable candidate for TCMs. The calculated defect properties revealed that the intrinsic Cu₃TaS₄ exhibits p-type conductivity due to the low defect formation energy of V_Cu under Cu-poor conditions. Based on the defect properties, both pristine and p-type doping Cu₃TaS₄ exhibit poor p-type conductivity, primarily due to the strong compensation effect by the n-type defect Cu_i. The existence of the empty “channel” along the (100) direction in the Cu₃TaS₄ crystal allows the introduction of Cu_i into the crystal, whose n-type characteristics induce a strong compensation effect on p-type conductivity. Because of the strong compensation effect by Cu_i, it is difficult to achieve high hole concentration and excellent p-type conductivity for Cu₃TaS₄.

2. Computational details

The first-principles calculations are based on density functional theory as implemented in the VASP package.⁴⁶ The projector augmented-wave (PAW) method⁴⁷ is used to describe the interactions between the valence electrons and the core. The cut-off energy of the plane wave basis is set to 500 eV. Owing to the strongly localized d electrons in transition metals Cu and Ta, the on-site Coulomb interactions of these electrons necessitate the implementation of Hubbard U correction in theoretical studies. However, the U values used in such corrections are typically input as empirical parameters. Furthermore, previous theoretical investigation applying Hubbard U correction has demonstrated that this approach still underestimates the band gap of Cu₃TaS₄.⁴⁰ In addition, the HSE06-type hybrid functional inherently accounts for strong electron correlations in transition-metal systems without empirical parameters. Therefore, we employ the HSE06-type hybrid functional⁴⁸ in our calculations to achieve accurate band gap predictions and eliminate the need for Hubbard U correction. The geometry optimization is fully carried out with the HSE06-type hybrid functional. The unit cell of Cu₃TaS₄ has cubic symmetry with a space group of P4̄3m (no. 215). The optimized lattice parameters from our calculations are a = b = c = 5.585 Å, which are in good agreement with the experimental values (a = b = c = 5.515 Å).⁴⁹ A 4 × 4 × 4 Γ-centered K-mesh⁵⁰ is used for electronic structure and optical property calculations. Furthermore, systematic convergence tests are carried out to ensure accurate results, as shown in Fig. S1 in the ESI.† Based on the calculated total energies with different K-meshes, the total energy difference is only 0.02 meV between the K-meshes of 4 × 4 × 4 and 7 × 7 × 7. Therefore, the 4 × 4 × 4 K-mesh is sufficient for achieving convergence within an acceptable tolerance. The energy and force convergence criterion are set to 1 × 10⁻⁴ eV and 0.001 eV Å⁻¹, respectively. The 2 × 2 × 2 supercells containing 96 atoms are employed for the calculations on defect formation energy and the supercells with defects are fully optimized. The hole concentrations as a function of growth temperature are obtained using the PY-SC-FERMI package.⁵¹ In addition, the ab initio molecular dynamics (AIMD) simulation⁵² is employed to investigate the thermal stabilities of the sample under different temperatures, in which the 2 × 2 × 2 supercell containing 96 atoms is used. To perform the AIMD simulation, the NVT ensemble is adopted and the exchange–correlation functional is changed to the GGA-PBE⁵³ to save the computational cost. In addition, we also calculate the carrier mobility and the bipolar Seebeck coefficient using the AMSET code,⁵⁴ in which the different scattering mechanisms, such as acoustic deformation potential (ADP), ionized impurity (IMP) and the polar-optical phonon (POP) mechanism, are considered, respectively.

3. Results and discussion

3.1 Crystal structure and electronic structure of Cu₃TaS₄

The unit cell of Cu₃TaS₄ is shown in Fig. 1(a). One can note that, in the unit cell of Cu₃TaS₄, Ta atoms occupy the corner, whereas Cu atoms lie at the centre of the edge. Moreover, both the Cu and Ta atoms are tetrahedrally coordinated by four S atoms. The unique tetrahedra coordination between the cations and the anions leads to the formation of an empty “channel” in the Cu₃TaS₄ crystal along the (100) direction, as shown in Fig. 1(b). It is worth noting that the empty “channel” can facilitate the introduction of the interstitial atoms.^55–57Fig. 2(a) shows the band structure of Cu₃TaS₄. It is found that Cu₃TaS₄ is an indirect band gap semiconductor because the VBM is located at the R point while the conduction band minimum (CBM) is situated at the X point. The electronic band gap in our calculation is estimated to 2.97 eV, which is consistent with the theoretical and experimental studies.^35,36,41 Moreover, to evaluate the influence of the spin–orbit coupling (SOC) effect on the electronic band gap, the band structure considering this effect (depicted by the grey line) is presented in Fig. 2(a). As shown in Fig. 2(a), incorporating SOC yields an electronic band gap of 2.93 eV, showing a negligible discrepancy (i.e. 0.04 eV) compared to the electronic band gap without SOC. We therefore did not consider the SOC effect in our following calculations. Fig. 2(b)–(e) depict the density of states of Cu₃TaS₄. It is found that the VBM mostly originates from the Cu_d and S_p states, while the CBM comes from the Ta_d and S_p states. Our calculation results are in line with the previous theoretical study.^40,41 We also calculate the crystal orbital overlap population (COOP) between the Cu_d and S_p states as well as the Ta_d and S_p states, respectively.⁵⁸ Here, the COOP with the positive (COOP > 0) or negative (COOP < 0) value represents the bonding or antibonding interactions, respectively. As shown in Fig. 2(f) and (g), both the Cu_d and S_p states and the Ta_d and S_p states exhibit antibonding interactions in the range of 0 to −3 eV and 3 to 4 eV, respectively. The VBM is pushed to the high energy position owing to the antibonding interaction, which is consistent with the VBM of other chalcogenide p-type TCMs (e.g. CuAlS₂).⁵⁹ Additionally, we also calculate the carrier effective masses around the VBM and CBM along three different high symmetry directions. To determine the effective masses, we carry out parabolic fitting in the vicinity of the VBM and the CBM along diverse directions within the Brillouin zone. For holes, the fitting was initiated at the VBM (R point) and performed sequentially along different directions R–X, R–Γ, and R–M. For electrons, the fitting was initiated at the CBM (X point) and followed along X–Γ, X–R, and X–M directions, consistent with the tetragonal Brillouin zone symmetry. Specifically, the effective masses using the parabolic fitting method can be obtained by the following equation: where E(k) is the eigenvalue of energy band around the VBM or the CBM. ħ and k are the reduced Planck constant and wave vector, respectively. The calculated results are listed in Table S1 in the ESI.† As shown in Table S1 (ESI†), the electron effective masses along the X–Γ, X–R and X–M directions are 3.86m_e, 0.94m_e and 0.94m_e, respectively, and the hole effective masses are 1.23m_e, 1.02m_e and 3.35m_e along the R–X, R–Γ and R–M directions, respectively. Our calculated results are in line with previous theoretical study.⁴¹ It should be noted that the average hole effective mass is lighter than that of p-type TCM CuAlO₂ (10.0m_e),^13,60 which is ascribed to the more dispersive and the higher position of the S_3p orbital compared to that of the O_2p orbital.

Fig. 1 Unit cell of Cu₃TaS₄ (a). The unit cell of Cu₃TaS₄ viewed from the (100) direction (b). The 2 × 2 × 2 supercell of Cu₃TaS₄ (c). The 2 × 2 × 2 supercell of Cu₃TaS₄ with a Cu_i (marked by a red dotted circle) in the empty “channel”(d).

Fig. 2 The band structure of Cu₃TaS₄ with (grey line) and without (red line) the SOC effect (a). The VBM is set to zero. The total density of states (b) and partial density of states of Cu (c), Ta (d) and S (e) atoms and COOPs between the Cu-d and S-p states (f) and the Ta-d and S-p states (g), respectively. The squares of the dipole transition matrix elements between the highest valence band and the lowest conduction band at various k points (h).

3.2 Optical properties of Cu₃TaS₄

To evaluate the optical transparency of Cu₃TaS₄, the optical properties, such as absorption coefficient, reflectivity and optical conductivity, are calculated. The details of the optical property calculations are presented in the ESI.† One can note that the optical band gap is larger than that of the electronic band gap, which is ascribed to the indirect band gap character of Cu₃TaS₄. To further clarify the reason that the optical band gap of Cu₃TaS₄ is larger than its electronic band gap, we also calculate the squares of the dipole transition matrix elements,^61,62P², at various k points as shown in Fig. 2(h). It is clearly shown that the calculated value of P² at the X point is close to zero, indicating that the optical transition between the highest valence band and the lowest conduction band at the X point is forbidden. However, the calculated value of P² at the R point is greater than zero, indicating that the optical transition between the highest valence band and the lowest conduction band at the R point is allowed. The energy difference between the highest valence band and the lowest conduction band at the R point corresponds to the threshold of the absorption coefficient of Cu₃TaS₄, as shown in Fig. 3(a). Therefore, the optical band gap of Cu₃TaS₄ is larger than its electronic band gap. Because of the wide optical band gap, the optical absorption is hardly observed in the visible light region, indicating that the visible light can easily pass through the Cu₃TaS₄ film. Furthermore, the optical transmittance of Cu₃TaS₄ is also calculated as a function of film thickness based on the following eqn:⁶³

T(ω) = (1 − R(ω)e^−α(ω)t). (1)

where R(ω), α(ω) and t are the reflectivity, absorption coefficient and film thickness, respectively. It is worth noting that the calculation on the optical transmittance does not consider the direction of light incidence in eqn (1). As shown in Fig. 3(b), the optical transmittance of Cu₃TaS₄ is higher than 70% in the visible light region as the film thickness increased from 10 nm to 70 nm. Moreover, the real optical conductivity and the reflectivity are also calculated as shown in Fig. 3(c) and (d). It is clearly shown that both the real optical conductivity and the reflectivity are relatively small in the visible light region. In combination with the weak optical absorption, the high optical transmittance, and the small real optical conductivity and the reflectivity, Cu₃TaS₄ exhibits excellent optical transparency in the visible light region. Given its high optical transparency, Cu₃TaS₄ is an excellent candidate for TCMs.

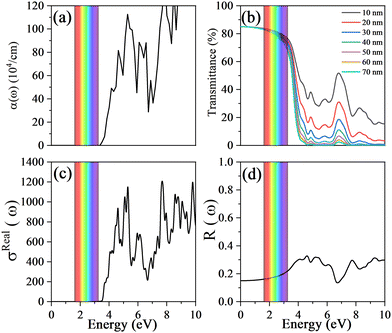Fig. 3 The absorption coefficient (a), the optical transmittance as a function of film thickness (b), the optical conductivity (c) and the reflectivity (d) of Cu₃TaS₄.

3.3 Defect properties of Cu₃TaS₄

3.3.1 Intrinsic defect properties of Cu₃TaS₄. Before the calculation of the intrinsic defect properties of Cu₃TaS₄, the relative chemical potentials should be evaluated. In general, the sum of the relative chemical potentials of the elements composed of Cu₃TaS₄ (i.e. Δμ_Cu, Δμ_Ta, and Δμ_S) should be equal to the formation enthalpy of Cu₃TaS₄ under the thermodynamic equilibrium conditions:⁶⁴

3Δμ_Cu + Δμ_Ta+ 4Δμ_S = ΔH(Cu₃TaS₄) = −5.97 eV. (2)

In addition, to avoid the formation of element solids and binary or ternary competing phases, Δμ_Cu, Δμ_Ta, and Δμ_S should be satisfied as the following:

Δμ_Cu ≤ 0, Δμ_Ta ≤ 0, Δμ_S ≤ 0. (3)

2Δμ_Cu + Δμ_S ≤ ΔH(Cu₂S) = −0.80 eV; (4)

2Δμ_Cu + 3Δμ_S ≤ ΔH(Cu₂S₃) = −1.08 eV; (5)

7Δμ_Cu + 4Δμ_S ≤ ΔH(Cu₇S₄) = −2.99 eV; (6)

Δμ_Cu + Δμ_S ≤ ΔH(CuS) = −0.50 eV; (7)

Δμ_Cu + Δμ_Ta + 2Δμ_S ≤ ΔH(CuTaS₂) = −3.73 eV; (8)

Δμ_Cu + Δμ_Ta + 3Δμ_S ≤ ΔH(CuTaS₃) = −4.35 eV; (9)

3Δμ_Ta + 2Δμ_S ≤ ΔH(Ta₃S₂) = −4.51 eV; (10)

Δμ_Ta + 2Δμ_S ≤ ΔH(TaS₂) = −3.53 eV; (11)

Δμ_Ta + 3Δμ_S ≤ ΔH(TaS₃) = −3.56 eV; (12)

2Δμ_Ta + Δμ_S ≤ ΔH(Ta₂S) = −2.21 eV; (13)

6Δμ_Ta + Δμ_S ≤ ΔH(Ta₆S) = −2.56 eV; (14)

Based on the constraints mentioned above, the shadow area, as depicted in Fig. 4(a), is the allowed range of relative chemical potentials for stable Cu₃TaS₄. The intrinsic defect formation energies with the charge state q in different chemical environments (i.e. point A to point G) are calculated based on the supercell model. The calculation method is based on the following eqn:⁶⁵

where E_defect represents the total energy of the supercell containing defects with the charge state q, E_perfect is the total energy of the perfect supercell, and n_i is the number of the atom. Here, if an atom is added into the supercell, n = −1, while n = 1 represents that an atom is removed from the supercell. μ_i is the chemical potential of element i in the solid state, and Δμ_i is the relative chemical potential of corresponding element i. ε_VBM is the VBM of pure Cu₃TaS₄. E_F is the Fermi level in the range of 0 to 2.97 eV. ΔV represents the electrostatic potential correction term between the defect and perfect systems, which is calculated by aligning the energy level position based on the average potential of the atom far away from the dopant.^66,67 Furthermore, the image charge correction term E_corr for charged defects is also considered,⁶⁸ which is calculated by the finite-corrections proposed by Lany and Zunger. The defect formation energies of intrinsic defects with the charge state q under seven different chemical environments are calculated based on the above mentioned. Here, four intrinsic donors [i.e. Ta interstitial (Ta_i), Ta substituted at the Cu site (Ta_Cu), the S vacancy (V_S), and Cu_i], four intrinsic acceptors [i.e. vacancy Ta (V_Ta), S interstitial (S_i), Cu substituted at the Ta site (Cu_Ta), and V_Cu] and the defect complex of V_Cu + Cu_i are considered in the calculations on defect formation energies. To investigate the effect of defect separation (V_Cu and Cu_i), adjacent/distant configurations were calculated. The defect separations for adjacent and distant configurations are 3.95 Å and 10.45 Å, with total energies of −461.31 eV and −461.21 eV, respectively. The 0.1 eV energy difference between the two configurations negligibly impacts the computational results. As shown in Fig. 4(b)–(h), Cu_i exhibits the lowest formation energy among donor defects, while V_Cu shows the minimum among acceptor defects. To evaluate the influence of chemical environments on the conductivity behaviour, the Cu-rich and Cu-poor conditions are considered, respectively. The Fermi level is pinned in the middle of the band gap in Fig. 4(b), indicating that intrinsic Cu₃TaS₄ is an insulator under Cu-rich conditions (i.e. point A). In contrast, the Fermi level is pinned at 0.62 eV above the VBM under Cu-poor conditions (i.e. point D), demonstrating that the intrinsic Cu₃TaS₄ is more inclined to be doped as p-type under Cu-poor conditions. Based on the calculated results, the p-type defect V_Cu exhibits the lowest defect formation energy under Cu-poor conditions, indicating that the p-type conductivity of intrinsic Cu₃TaS₄ is associated with the p-type defect V_Cu under Cu-poor conditions. Therefore, our calculation results align well with the experimental studies.^42,43 Additionally, we also calculate the electronic structures of Cu₃TaS₄ with V_Cu, Cu_i, and the defect complex V_Cu + Cu_i, as presented in Fig. S2–S4 (ESI†). It is observed that the Fermi level crosses the VBM in Cu₃TaS₄ with V_Cu, indicating the p-type conductivity, as shown in Fig. S2 (ESI†). For the electronic structure of Cu₃TaS₄ with Cu_i, the Fermi level crosses the CBM, demonstrating the n-type conductivity. In addition, the electronic band gap of Cu₃TaS₄ with Cu_i is reduced to 2.87 eV and its CBM exhibits the antibonding states from the Ta_d and S_p states, as shown in Fig. S3 (ESI†). In the case of Cu₃TaS₄ with the defect complex V_Cu + Cu_i, one can see that it is only affected the electronic band gap of Cu₃TaS₄, as shown in Fig. S4 (ESI†). Accordingly, based on the band structures of Cu₃TaS₄ with V_Cu, Cu_i, and the defect complex V_Cu + Cu_i, the p-type conductivity of Cu₃TaS₄ should originate from the V_Cu, which is in line with the calculated intrinsic defect properties. Besides, it is also found that the donor defect Cu_i shows a strong compensation for the p-type conductivity under both Cu-rich and Cu-poor conditions, which negatively affects the increase of hole concentration. The reason could be attributed to the empty “channel” in the Cu₃TaS₄ crystal [Fig. 1(b)], which make it easy to introduce Cu_i into the Cu₃TaS₄ crystal [Fig. 1(d)]. In order to quantitatively study the facile introduction of the Cu_i, the lattice parameters and volume changes after the introduction of Cu_i are discussed. One can note that the fully optimized lattice constant (11.13 Å) and the supercell volume (1382.88 ų) are slightly decreased compared with those of the unoptimized supercell (the lattice constant and supercell volume are 11.17 Å and 1394.26 ų, respectively) after the introduction of Cu_i. In addition, the total energy of the fully optimized supercell with the Cu_i (−464.75 eV) is also slightly lower than that of the unoptimized supercell (−464.45 eV), which indicates that Cu_i produces only 0.30 eV of lattice deformation energy and then has a low formation energy. Combined with the slight reductions of the lattice parameter and the supercell volume, as well as the small lattice deformation energy, the Cu atom can be easily introduced into the empty “channel” of the supercell of Cu₃TaS₄.

Fig. 4 The allowed range of relative chemical potentials for stable Cu₃TaS₄ (a). The defect formation energies of Cu₃TaS₄ as a function of the Fermi level under seven extreme chemical potential environments [(point A to point G) (b)–(h)]. The black vertical dotted lines represent the Fermi level at 300 K.

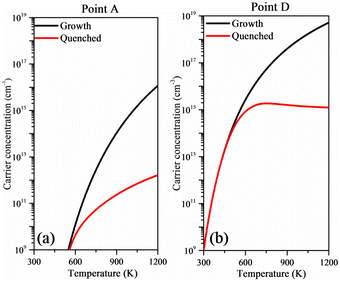
In order to clearly characterize the p-type conductivity of intrinsic Cu₃TaS₄, the hole concentrations under Cu-rich and Cu-poor conditions are calculated based on the obtained defect properties. While Cu₃TaS₄ has been experimentally synthesized, the adopted preparation methods correspond to thermodynamic equilibrium growth processes.^36,49 Recently, the non-equilibrium growth process has been utilized in both theoretical and experimental studies.^69–72 The non-equilibrium growth process involves high-temperature synthesis of the sample followed by rapid quenching to room temperature. Samples fabricated via this method retain the defect density established during high-temperature growth, thereby resulting in enhanced electrical conductivity. Here, the model associated with the high-temperature growth and subsequent quenching processes is applied in our calculations, and the relevant details are presented in the ESI.†Fig. 5(a) and (b) depict the hole concentrations as a function of growth temperature. One can note that the hole concentration is rapidly increased to 1 × 10¹⁶ cm⁻³ after increasing the growth temperature to 1200 K under Cu-rich conditions (point A), as shown in Fig. 5(a). Generally, high temperature is widely used to prepare a defective sample and after sample preparation it is utilized at room temperature. After quenching to room temperature, the Fermi level is pinned in the middle of the band gap and therefore the hole concentration is reduced to 1 × 10¹² cm⁻³, which is mainly ascribed to the compensation of the n-type defect Cu_i. In the case of the Cu-poor conditions (point D), the hole concentration reaches 5 × 10¹⁸ cm⁻³ when the growth temperature is increased to 1200 K, as shown in Fig. 5(b). However, after quenching to room temperature, the hole concentration is reduced near 1 × 10¹⁵ cm⁻³, which is significantly lower than that of commercialized n-type TCMs. The low hole concentration under Cu-poor conditions is mainly caused by the compensation of the donor defect Cu_i. To further assess the p-type conductivity of the intrinsic Cu₃TaS₄, the carrier mobility and the bipolar Seebeck coefficient are also calculated. It is worth noting that the carrier concentration should be given after using the AMSET code. Based on the calculated results, the hole concentration of intrinsic Cu₃TaS₄ under Cu-poor conditions was estimated to 1.00 × 10¹⁵ cm⁻³. However, the electron concentration of the intrinsic Cu₃TaS₄ could not be determined due to its p-type conductivity. We therefore estimated the electron concentration of intrinsic Cu₃TaS₄ based on the detailed balanced theory. The details of electron concentration calculations are presented in the ESI.† The calculated carrier mobility and the bipolar Seebeck coefficient are listed in Table S1 (ESI†). From Table S1 (ESI†), one can conclude that the intrinsic Cu₃TaS₄ with p-type conductivity has high hole mobility comparing with that of n-type. The calculated hole mobility is lower than that of the previous theoretical study⁴¹ using the deformation theory. This discrepancy is attributed to the distinct scattering mechanisms considered in our work. One can note that the Seebeck coefficient of n-type is slightly higher than that of the p-type as shown in Table S1 (ESI†), which is attributed to the inverse relationship between the Seebeck coefficient and carrier concentration. Although the n-type conductivity exhibits a large Seebeck coefficient, the hole concentration exceeding the electron concentration guarantees the p-type conductivity of intrinsic Cu₃TaS₄. Furthermore, both experimental studies^35,36 and our calculation results confirm the p-type conductivity of Cu₃TaS₄. This is attributed to its suitable hole mobility and lowest defect formation energy of V_Cu under Cu-poor conditions. In addition, since the growth temperature is increased to 1200 K, it is essential to evaluate the stability of the sample under high temperature. We therefore employ the AIMD simulation to calculate the thermal stabilities at 300 K and 1200 K, respectively. The calculated results are depicted in Fig. S5 (ESI†). It is found that huge energy variations are hardly observed at both 300 K and 1200 K from 0 ps to 10 ps, indicating the thermal stabilities of the sample.

Fig. 5 The hole concentration of intrinsic Cu₃TaS₄ as a function of growth temperature under Cu-rich (a) and Cu-poor conditions (b), respectively.

3.3.2 Extrinsic defect properties of Cu₃TaS₄. To explore the p-type conductivity through doping, two distinct p-type doping strategies are considered. The first strategy is to use an element to replace the Ta or S site in Cu₃TaS₄. To introduce an acceptor defect, elements from group-4 (i.e. Ti, Zr, and Hf) and group-14 (i.e. Si, Ge, Sn and Pb) are utilized to replace the Ta site, while elements from group-15 (i.e. N, P, As, Sb) are employed to substitute the S site. The second strategy is to introduce anionic elements from group-17 (i.e. F, Cl, and Br) as the interstitial defects into the empty “channel” of the Cu₃TaS₄ supercell. To evaluate the defect formation energies of the acceptor defects, the relative chemical potentials of these p-type dopants are obtained as presented in the ESI.†Fig. 6(a) and Fig. S6 (ESI†) depict the defect formation energies of p-type doping at the Ta site under different chemical environments. Here, the p-type doping at the Ta site at point E (Ta-poor conditions) is set as an example. As shown in Fig. 6(a), Pb doping at the Ta site (Pb_Ta) possesses the shallowest transition level (0.28 eV) among these acceptor defects. However, the defect formation energy of Pb_Ta is relatively large, indicating that the formation of Pb_Ta is difficult to realize. In the case of Ti doping at the Ta site (Ti_Ta), although the Ti_Ta does not act as a very shallow acceptor (0.39 eV), it has the lowest defect formation energy compared to other defects. Furthermore, the defect formation energy of Ti_Ta is lower than that of the intrinsic p-type defect V_Cu from point A to point G. The lowest formation energy of Ti_Ta occurs at point E (i.e. 0.64 eV) compared to that of the intrinsic p-type defect V_Cu (i.e. 1.32 eV). In addition, the defect formation energy of Ti_Ta is also lower than that of the intrinsic n-type Cu_i (i.e. 2.64 eV) at point E. We therefore estimate the hole concentration of the sample with Ti_Ta. The hole concentration as a function of growth temperature after Ti_Ta at point E (Ta poor condition) is shown in Fig. 6(b). It is found that the hole concentration is quickly increased with the growth temperature, reaching a peak of 6 × 10¹⁹ cm⁻³ at 1200 K. However, the hole concentration is significantly reduced below 1 × 10¹⁴ cm⁻³ after quenching to room temperature. The reason for the low hole concentration of Ti_Ta is also ascribed to the compensation of Cu_i. Since the compensation effect of the donor defect Cu_i, the Fermi level is pinned at 0.31 eV at 300 K [Fig. 6(a)], resulting in the low hole concentration of Ti_Ta at room temperature [Fig. 6(b)]. In the case of the defect formation energies for p-type doping at the S site, point A (S poor condition) is selected as a representative preparation environment, and the remaining points are depicted in Fig. S7 (ESI†). As shown in Fig. 7(a), the results demonstrated that As doping at the S site (As_S) has the lowest defect formation energy among these p-type defects. Furthermore, the defect formation energy of As_S at point A is lower than that of the intrinsic defect V_Cu and Cu_i. Owing to the lowest defect formation energy of As_S, the hole concentration of As_S at point A (S poor condition) is calculated as shown in Fig. 7(b). It can be seen that the hole concentration of As_S increases to 1 × 10¹⁶ cm⁻³ when the growth temperature is elevated to 1200 K. However, the hole concentration reduces to 1 × 10⁵ cm⁻³ after quenching to room temperature. Because the Fermi level is pinned near the middle of the band gap at room temperature [Fig. 7(a)] resulting from the compensation of the n-type defect Cu_i, the hole concentration of As_S is lower than that of intrinsic Cu₃TaS₄. For the doping of anionic group-17 elements, F, Cl, and Br as interstitial atoms are introduced into the empty “channel” of the Cu₃TaS₄ supercell, respectively [Fig. 1(d)]. The defect formation energies of these interstitial defects are calculated as shown in Fig. 7(c). Here, the defect formation energies at point D are given as an example, and those at the other points are shown in Fig. S8 (ESI†). Among these interstitial defects, F interstitial (F_i) has the lowest defect formation energy compared to Cl interstitial (Cl_i) and Br interstitial (Br_i). It is shown that the F interstitial (F_i) has the lowest defect formation energies among these anionic interstitial defects, and the lowest defect formation energy of F_i is obtained at point D. It is observed that the defect formation energy of F_i is larger than that of the intrinsic p-type defect V_Cu from point A to point G, as shown in Fig. 7(c) and Fig. S8 (ESI†). Compared with p-type defects such as Ti_Ta and As_S, the defect formation energy of F_i is relatively high, suggesting that the anionic interstitial defects are difficult to be introduced into the Cu₃TaS₄ crystal. The reason should be related to the fact that the nearest neighboring atoms of this interstitial site are four anionic S atoms. At this location, anionic interstitial atoms would induce a significant Coulombic repulsive interaction. In addition, the p-type defect F_i is also compensated by the n-type defect Cu_i, resulting in the Fermi level being pinned at the middle band gap at point D [Fig. 7(c)]. Overall, the achievement of high hole concentrations and excellent p-type conductivity by the introduction of the anionic interstitial defects is challenging due to the high defect formation energy of F_i and the strong compensation effect of Cu_i. Accordingly, we demonstrated that the intrinsic Cu₃TaS₄ exhibits p-type conductivity owing to the low defect formation energy of V_Cu under Cu-poor conditions. However, the empty “channel” in the Cu₃TaS₄ crystal facilitates the formation of Cu_i. High hole concentrations are difficult to achieve in both intrinsic and p-type doped Cu₃TaS₄ due to the strong compensation effect of the n-type defect Cu_i.

Fig. 6 The defect formation energies (a) of p-type doping at the Ta site as a function of the Fermi level at point E. The red vertical dotted line represents the Fermi level at 300 K with Ti_Ta. The hole concentration as a function of growth temperature with Ti_Ta at point E (b).

Fig. 7 The defect formation energies (a) of p-type doping at the S site at point A as a function of the Fermi level. The hole concentration with As_S as a function of growth temperature at point A (b). The defect formation energies of interstitial defects at point D as a function of the Fermi level (c). The red vertical dotted lines are the Fermi level at 300 K.

4. Outlook

Based on the calculated defect properties, the p-type conductivities both from the intrinsic p-type defect V_Cu and the extrinsic p-type defects (i.e. Ti_Ta doping and As_S doping) can be compensated by the n-type defect Cu_i. To mitigate the strong compensation effect of the n-type defect Cu_i and achieve good p-type conductivity, a theoretical strategy recently applied to another p-type transparent conductive material, γ-CuI, is worth exploring.⁷¹ Specifically, Matsuzaki et al. introduced alkali metal cations such as Na⁺, K⁺, Cs⁺, and Rb⁺, all of which have ionic radii larger than that of Cu⁺, into the interstitial sites of γ-CuI, which lead to the creation of shallow p-type acceptor complexes in association with the surrounding intrinsic defects of γ-CuI. Because of the relatively large ionic radius of Cs⁺, when Cs⁺ is incorporated into γ-CuI, two p-type defect complexes serving as shallow acceptors, namely Cs_i-3V_Cu-V_I and Cs_i-4V_Cu-V_I, are formed.⁷³ Based on measurements of doped γ-CuI single-crystalline bulks and polycrystalline films, they extend the controllable range of the hole concentration to 10¹³–10¹⁹ cm⁻³, and the modification of p-type conductivity by defect complexes is supported by first-principles calculations.⁷³ Inspired by this work, future theoretical and experimental studies could attempt to introduce cations with large ionic radii, such as Na⁺, K⁺, Rb⁺, and Cs⁺, into the empty “channel” of Cu₃TaS₄ crystal. It is anticipated that the introduced cations will form defect complexes with the adjacent V_Cu. Subsequently, these defect complexes can act as shallow acceptors, thereby alleviating the compensation effect caused by the n-type defect Cu_i and enhancing the p-type conductivity of Cu₃TaS₄. This strategy of large-sized ion doping to form defect complexes offers new insights into reducing the compensation effect of the n-type defect Cu_i in Cu₃TaS₄ in future research.

5. Conclusions

In summary, based on the first-principles calculations, we demonstrated that Cu₃TaS₄ is an indirect band gap semiconductor with an electronic band gap of 2.97 eV. The calculated optical properties indicate that Cu₃TaS₄ exhibits high optical transmittance in the visible light region. Moreover, the results also indicate that the intrinsic Cu₃TaS₄ exhibits p-type conductivity owing to the low defect formation energy of V_Cu under Cu-poor conditions. Although the intrinsic Cu₃TaS₄ exhibits high transparency and p-type conductivity, the hole concentration of the intrinsic Cu₃TaS₄ only reached 1 × 10¹⁵ cm⁻³ under Cu-poor conditions at room temperature. The low hole concentration and poor p-type conductivity are ascribed to the strong compensation effect of the n-type defect Cu_i. The ease of formation of the Cu_i is ascribed to the existence of the empty “channel” along the (100) direction in the Cu₃TaS₄ crystal. In addition, even after applying two different p-type doping strategies, due to the strong compensating effect of the n-type defect Cu_i, almost no increase in hole concentrations is observed in the doped samples compared to the intrinsic Cu₃TaS₄. Therefore, it can be concluded that the empty “channel” in the Cu₃TaS₄ crystal facilitates the formation of Cu_i, which leads to the strong compensation effect of the p-type defects, further making it difficult to achieve high hole concentrations and excellent p-type conductivity in Cu₃TaS₄. To overcome the compensation effect of the n-type defect Cu_i and obtain ideal p-type conductivity of Cu₃TaS₄, the introduction of the shallow acceptor defect complex is suggested in the future experimental and theoretical studies.

Author contributions

Y. Xue: calculation, data analysis, and writing – original draft; Z. Zhuo: investigation and data analysis; C. Lin: calculation and data analysis; D. Huang: conceptualization, calculation, investigation, data analysis, writing – review, and supervision.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Natural Science Foundation of Guangxi Province (grant no. ZY23055002 and 2025GXNSFAA069368), the National Natural Science Foundation of China (grant no. 61964002), and the Opening Project of Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin University of Electronic Technology (no. DH202316). We acknowledge the supercomputer resources from the National High-Performance Computing Center Nanning Branch.

References

1. D. S. Hecht, L. Hu and G. Irvin, Emerging transparent electrodes based on thin films of carbon nanotubes, graphene, and metallic nanostructures, Adv. Mater., 2011, 23, 1482–1513.
2. J. Miao and T. Fan, Flexible and stretchable transparent conductive graphene-based electrodes for emerging wearable electronics, Carbon, 2023, 202, 495–527.
3. G. Wang, Y. N. Du, P. Huang, Z. F. Qian, P. Zhang and S.-H. Wei, Design of Intrinsic Transparent Conductors from a Synergetic Effect of Symmetry and Spatial-Distribution Forbidden Transitions, Phys. Rev. Lett., 2025, 134, 036401.
4. S. K. Maurya, H. R. Galvan, G. Gautam and X. Xu, Recent progress in transparent conductive materials for photovoltaics, Energies, 2022, 15, 8698.
5. R. Kormath Madam Raghupathy, H. Wiebeler, T. D. Kühne, C. Felser and H. Mirhosseini, Database screening of ternary chalcogenides for p-type transparent conductors, Chem. Mater., 2018, 30, 6794–6800.
6. T. Isono, T. Fukuda, K. Nakagawa, R. Usui, R. Satoh, E. Morinaga and Y. Mihara, Highly conductive SnO₂ thin films for flat-panel displays, J. Soc. Inf. Display, 2007, 15, 161–166.
7. K. Nomura, H. Ohta, A. Takagi, T. Kamiya, M. Hirano and H. Hosono, Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors, Nature, 2004, 432, 488–492.
8. T. Huang, C. Mo, M. Cui, M. Li, P. Ji, H. Tan, X. Zhang, L. Zhuge and X. Wu, Ion behavior impact on ITO thin film fabrication via DC magnetron sputtering with external anode, Vacuum, 2024, 221, 112848.
9. T. Koskinen, R. Raju, I. Tittonen and C. Kauppinen, Grass-like alumina enhances transmittance and electrical conductivity of atomic layer deposited Al-doped ZnO for thermoelectric and TCO applications, Appl. Phys. Lett., 2023, 123, 011902.
10. S. H. Park, Y.-K. Oh, Y.-J. Lim, S. Z. Chen, S.-J. Lee and H.-K. Kim, Thermally stable and transparent F-doped SnO₂ (FTO)/Ag/FTO films for transparent thin film heaters used in automobiles, Ceram. Int., 2023, 49, 2419–2426.
11. C. Niu, Carbon nanotube transparent conducting films, MRS Bull., 2011, 36, 766–773.
12. T. Minami, Transparent conducting oxide semiconductors for transparent electrodes, Semicond. Sci. Technol., 2005, 20, S35.
13. Y. Youn, M. Lee, D. Kim, J. K. Jeong, Y. Kang and S. Han, Large-scale computational identification of p-type oxide semiconductors by hierarchical screening, Chem. Mater., 2019, 31, 5475–5483.
14. A. Kudo, H. Yanagi, H. Hosono and H. Kawazoe, SrCu₂O₂: a p-type conductive oxide with wide band gap, Appl. Phys. Lett., 1998, 73, 220–222.
15. X. Nie, S.-H. Wei and S. B. Zhang, Bipolar doping and band-gap anomalies in delafossite transparent conductive oxides, Phys. Rev. Lett., 2002, 88, 066405.
16. K. H. L. Zhang, K. Xi, M. G. Blamire and R. G. Egdell, P-type transparent conducting oxides, J. Phys.: Condens. Matter, 2016, 28, 383002.
17. H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, P-type electrical conduction in transparent thin films of CuAlO₂, Nature, 1997, 389, 939–942.
18. A. Ananchuensook, I. Chatratin, A. Janotti, T. Watcharatharapong, J. T-Thienprasert, A. Boonchun, S. Jungthawan and P. Reunchan, Hydrogen passivation of acceptor defects in delafossite CuMO₂ (M = Al, Ga, In): insights for enhanced p-type conductivity, J. Appl. Phys., 2024, 135, 185705.
19. F. Veron, I. Pasquet, Y. Thimont and A. Barnabé, and Ph. Tailhades, Improved performance of transparent p-type conductors CuCrO₂:Mg delafossite thin films through easy and low cost laser annealing, Mater. Lett., 2022, 313, 131795.
20. C. Esthan, B. G. Nair, A. Surya Mary, J. A. Joseph, L. M. Joseph, R. Jacob, V. K. Shinoj and R. R. Philip, Transparent heterojunctions of Cu-based delafossites n-CuInO₂/p-CuGaO₂ by reactive evaporation method for transparent electronic applications, Vacuum, 2022, 197, 110808.
21. H. Gao, X. Zeng, Q. Guo, Z. Yang, Y. Deng, H. Li and D. Xiong, P-type transparent conducting characteristics of delafossite Ca doped CuScO₂ prepared by hydrothermal synthesis, Dalton Trans., 2021, 50, 5262–5268.
22. M. Zhong, W. Zeng, F.-S. Liu, D.-H. Fan, B. Tang and Q.-J. Liu, Screening criteria for high-performance p-type transparent conducting materials and their applications, Mater. Today Phys., 2022, 22, 100583.
23. R. Woods-Robinson, M. Morales-Masis, G. Hautier and A. Crovetto, From Design to Device: Challenges and Opportunities in Computational Discovery of p-Type Transparent Conductors, PRX Energy, 2024, 3, 031001.
24. P. P. Murmu, M. Markwitz, S. V. Chong, N. Malone, T. Mori, H. Vyas, L. J. Kennedy, S. Rubanov, C. I. Sathish, J. Yi and J. V. Kennedy, Defect and dopant complex mediated high power factor in transparent selenium-doped copper iodide thin films, Mater. Today Energy, 2024, 44, 101639.
25. Q. Sun, A. Sadhu, S. Lie and L. H. Wong, Critical review of Cu-based hole transport materials for perovskite solar cells: from theoretical insights to experimental validation, Adv. Mater., 2024, 36, 2402412.
26. M. Benaadad, B. Gul, M. S. Khan and A. Nafidi, Exploring the electronic, optical, and thermometric properties of novel AlCuX₂ (X = S, Se, Te) semiconductors: a first-principles study, J. Mater. Sci., 2023, 58, 7362–7379.
27. G. Gao, K. Li, L. Yang, F. Xia, L. Xu, J. Han, H. Gong and J. Zhu, 1.37 × 102 S cm⁻1 p-type conductivity LaCuOS films with a very wide optical transparency window of 400–6000 nm, Mater. Today Phys., 2023, 35, 101089.
28. A. Krishnapriyan, P. T. Barton, M. Miao and R. Seshadri, First-principles study of band alignments in the p-type hosts BaM₂X₂ (M = Cu, Ag; X = S, Se), J. Phys.: Condens. Matter, 2014, 26, 155802.
29. Y. Wang, M. Liu, F. Huang, L. Chen, H. Li, X. Lin, W. Wang and Y. Xia, Solution-processed p-type transparent conducting BaCu₂S₂ thin film, Chem. Mater., 2007, 19, 3102–3104.
30. A. Zakutayev, J. Tate and G. Schneider, Defect physics of BaCuChF(Ch = S, Se, Te) p-type transparent conductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195204.
31. A. N. Fioretti and M. Morales-Masis, Bridging the p-type transparent conductive materials gap: synthesis approaches for disperse valence band materials, J. Photon. Energy, 2020, 10, 1.
32. D. Huang, Y.-J. Zhao, R.-Y. Tian, D.-H. Chen, J.-J. Nie, X.-H. Cai and C.-M. Yao, First-principles study of Be doped CuAlS₂ for p-type transparent conductive materials, J. Appl. Phys., 2011, 109, 113714.
33. M. Li, N. Wang, S. Zhang, J. Hu, H. Xiao, H. Gong, Z. Liu, L. Qiao and X. Zu, A review of the properties, synthesis and applications of lanthanum copper oxychalcogenides, J. Phys. D: Appl. Phys., 2022, 55, 273002.
34. K. Rodríguez-Rosales, J. Cruz-Gómez, J. G. Quiñones-Galván, M. de la, L. Olvera, J. Santos-Cruz, G. Contreras-Puente, M. Meléndez-Lira and F. de Moure-Flores, p-Type LaCuOS films grown by PLD using a quaternary target fabricated by a two-step solid-state reaction/sulfurization process, Mater. Sci. Eng., B, 2024, 300, 117063.
35. J. Tate, P. F. Newhouse, R. Kykyneshi, P. A. Hersh, J. Kinney, D. H. McIntyre and D. A. Keszler, Chalcogen-based transparent conductors, Thin Solid Films, 2008, 516, 5795–5799.
36. P. F. Newhouse, P. A. Hersh, A. Zakutayev, A. Richard, H. A. S. Platt, D. A. Keszler and J. Tate, Thin film preparation and characterization of wide band gap Cu₃TaQ₄ (Q = S or Se) p-type semiconductors, Thin Solid Films, 2009, 517, 2473–2476.
37. N. Zhang, X. Liu, D. B. K. Lim and H. Gong, A New Highly conductive direct gap p-type semiconductor La_1−xCuOs for dual applications: transparent electronics and thermoelectricity, ACS Appl. Mater. Interfaces, 2020, 12, 6090–6096.
38. M. Yang, Y. Wang, G. Li, Z. Shi and Q. Zhang, Zn-doped CuAlS₂ transparent p-type conductive thin films deposited by pulsed plasma deposition, J. Vac. Sci. Technol., A, 2009, 27, 1316–1319.
39. S. Ikeda, N. Aono, A. Iwase, H. Kobayashi and A. Kudo, Cu₃MS₄ (M = V, Nb, Ta) and its Solid Solutions with Sulvanite Structure for Photocatalytic and Photoelectrochemical H₂ Evolution under Visible-Light Irradiation, ChemSusChem, 2019, 12, 1977–1983.
40. A. B. Kehoe, D. O. Scanlon and G. W. Watson, The electronic structure of sulvanite structured semiconductors Cu₃MCh₄ (M = V, Nb, Ta; Ch = S, Se, Te): prospects for optoelectronic applications, J. Mater. Chem. C, 2015, 3, 12236–12244.
41. Y. Li, M. Wu, T. Zhang, X. Qi, G. Ming, G. Wang, X. Quan and D. Yang, Natural sulvanite Cu₃MX₄ (M = Nb, Ta; X = S, Se): promising visible-light photocatalysts for water splitting, Comput. Mater. Sci., 2019, 165, 137–143.
42. M. Liu, C.-Y. Lai, C.-Y. Chang and D. R. Radu, Solution-Based Synthesis of Sulvanite Cu₃TaS₄ and Cu₃TaSe₄ Nanocrystals, Crystals, 2021, 11, 51.
43. A. Haque, S. Ershadrad, T. Devaiah Chonamada, D. Saha, B. Sanyal and P. K. Santra, Vacancy assisted growth of copper tantalum sulfide nanocrystals, J. Mater. Chem. A, 2022, 10, 19925–19934.
44. R. Prado-Rivera, C.-Y. Chang, M. Liu, C.-Y. Lai and D. R. Radu, Sulvanites: The Promise at the Nanoscale, Nanomaterials, 2021, 11, 823.
45. W. F. Espinosa-García, G. M. Dalpian and J. M. Osorio-Guillén, Intrinsic defects in sulvanite compounds: the case of transparent Cu₃TaS₄ and absorbing Cu₃VSe₄, J. Alloys Compd., 2023, 969, 172264.
46. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
47. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
48. J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, Energy band gaps and lattice parameters evaluated with the Heyd–Scuseria–Ernzerhof screened hybrid functional, J. Chem. Phys., 2005, 123, 174101.
49. G. E. Delgado, J. E. Contreras, A. J. Mora, S. Durán, M. Muñoz and P. Grima-Gallardo, Structure refinement of the semiconducting compound Cu₃TaS₄ from X-Ray powder diffraction data, Acta Phys. Pol. A, 2011, 120, 468–472.
50. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
51. A. G. Squires, D. O. Scanlon and B. J. Morgan, PY-SC-FERMI: self-consistent Fermi energies and defect concentrations from electronic structure calculations, JOSS, 2023, 8, 4962.
52. R. N. Barnett and U. Landman, Born–Oppenheimer molecular-dynamics simulations of finite systems: structure and dynamics of (H₂O)₂, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2081–2097.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Efficient calculation of carrier scattering rates from first principles, Nat. Commun., 2021, 12, 2222.
55. H. Arribart, B. Sapoval, O. Gorochov and N. LeNagard, Fast ion transport at room temperature in the mixed conductor Cu₃VS₄, Solid State Commun., 1978, 26, 435–439.
56. H. Arribart and B. Sapoval, Theory of mixed conduction due to cationic interstitials in the p-type semiconductor Cu₃VS₄, Electrochim. Acta, 1979, 24, 751–754.
57. D. M. Schleich and M. Rosso, Li⁺ insertion studies in Cu₃VS₄, Solid State Ionics, 1981, 5, 383–385.
58. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: a tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035.
59. D. Huang, R.-Y. Tian, Y.-J. Zhao, J.-J. Nie, X.-H. Cai and C.-M. Yao, First-principles study of CuAlS₂ for p-type transparent conductive materials, J. Phys. D: Appl. Phys., 2010, 43, 395405.
60. G. Trimarchi, H. Peng, J. Im, A. J. Freeman, V. Cloet, A. Raw, K. R. Poeppelmeier, K. Biswas, S. Lany and A. Zunger, Using design principles to systematically plan the synthesis of hole-conducting transparent oxides: Cu₃VO₄ and Ag₃VO₄ as a case study, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165116.
61. V. Wang, N. Xu, J. C. Liu, G. Tang and W.-T. Geng, VASPKIT: a user-friendly interface facilitating high-throughput computing and analysis using vasp code, Comput. Phys. Commun., 2021, 267, 108033.
62. A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, Defect tolerance to intolerance in the vacancy-ordered double perovskite semiconductors Cs₂SnI₆ and Cs₂TeI₆, J. Am. Chem. Soc., 2016, 138, 8453–8464.
63. G. Brunin, F. Ricci, V.-A. Ha, G.-M. Rignanese and G. Hautier, Transparent conducting materials discovery using high-throughput computing, npj Comput. Mater., 2019, 5, 63.
64. S. B. Zhang, S.-H. Wei and A. Zunger, Intrinsic n-type versus p-type doping asymmetry and the defect physics of ZnO, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 075205.
65. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van De Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305.
66. Y. Gai, J. Li, S.-S. Li, J.-B. Xia and S.-H. Wei, Design of narrow-gap TiO₂: a passivated codoping approach for enhanced photoelectrochemical activity, Phys. Rev. Lett., 2009, 102, 036402.
67. W.-J. Yin, H. Tang, S.-H. Wei, M. M. Al-Jassim, J. Turner and Y. Yan, Band structure engineering of semiconductors for enhanced photoelectrochemical water splitting: the case of TiO₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045106.
68. S. Lany and A. Zunger, Accurate prediction of defect properties in density functional supercell calculations, Modell. Simul. Mater. Sci. Eng., 2009, 17, 084002.
69. S. W. Fan, Y. Chen and L. Yang, Transparency and p-Type conductivity of BeSe doped with Group VA Atoms: a hybrid functional study, J. Phys. Chem. C, 2022, 126, 19446–19454.
70. X. Zhang, C. Lin, X. Guo, Y. Xue, X. Liang, W. Zhou, C. Persson and D. Huang, Delafossite NaYTe₂ as a transparent conductive material with bipolar conductivity: a first-principles prediction, J. Phys. Chem. Solids, 2024, 190, 112002.
71. L. Ji, S. Lu, Y. Wu, P. Dai, L. Bian, M. Arimochi, T. Watanabe, N. Asaka, M. Uemura, A. Tackeuchi, S. Uchida and H. Yang, Carrier recombination dynamics of MBE grown InGaAsP layers with 1 eV bandgap for quadruple-junction solar cells, Sol. Energy Mater. Sol. Cells, 2014, 127, 1–5.
72. M. Wang, A. Debernardi, Y. Berencén, R. Heller, C. Xu, Y. Yuan, Y. Xie, R. Böttger, L. Rebohle, W. Skorupa, M. Helm, S. Prucnal and S. Zhou, Breaking the doping limit in silicon by deep impurities, Phys. Rev. Appl., 2019, 11, 054039.
73. K. Matsuzaki, N. Tsunoda, Y. Kumagai, Y. Tang, K. Nomura, F. Oba and H. Hosono, Hole-doping to a Cu(I)-based semiconductor with an isovalent cation: utilizing a complex defect as a shallow acceptor, J. Am. Chem. Soc., 2022, 144, 16572–16578.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01186h

---