Ultrafast photophysics of the cyan fluorescent protein chromophore in solution

Abstract

Incorporation of fluorescent proteins (FPs) into biological systems has revolutionised bioimaging and the understanding of cellular processes. Ongoing developments of FPs are driving efforts to characterise the fundamental photoactive unit (chromophore) embedded within the protein. Cyan FP has a blue emitting chromophore and is widely used in Förster resonance energy transfer studies. Here, we probe the ultrafast photophysics of the cyan FP chromophore in solution using time-resolved fluorescence up-conversion and transient absorption spectroscopies. The ultrafast dynamics are characterised by two lifetimes, sub-picosecond τ₁ (or τ_F) associated with loss of the fluorescent Franck–Condon state, and lifetime τ₂ on the order of several picoseconds that is linked with cooling of a hot ground state. MRSF-TDDFT calculations show that the relaxed S₁ state equilibrium geometry is classified as a partial twisted intramolecular charge-transfer state, and lies close in energy to a conical intersection seam associated with torsion about the central double bond leading to facile internal conversion. The excited state dynamics exhibit only a weak viscosity dependence, consistent with a barrierless and near-volume-conserving non-radiative decay mechanism. Fluorescence lifetimes for the deprotonated anion are twice those for the neutral.

---

1 Introduction

The discovery and isolation of green fluorescent protein from Aequorea victoria (avGFP),¹ which is considered the exemplar fluorescent protein (FP), spearheaded the green revolution in fluorescence imaging of living systems. FPs have proven to be invaluable in biochemical and cellular fluorescence labelling,^2–5 which has driven efforts to tailor new FPs offering different colours, improved fluorescence quantum yields, reversible photoswitching, and optical highlighting properties.^6–9 Since the chromophore unit within FPs primarily dictates the fluorescent properties of the protein, and because the chromophore has a specific array of hydrogen-bonding and electrostatic interactions with amino acid residues within the protein defining the electrochromic shift,^10–13 site-directed mutagenesis of FPs has resulted in a broad colour palette of derivative FPs.^14–17

Efforts to improve and tailor the properties of FPs have led to a series of derivatives, broadly titled enhanced green fluorescent proteins (EGFP). One such EGFP is the cyan fluorescent protein (CFP), formed through changing the central residue tyrosine of the GFP chromophore to a tryptophan (Fig. 1),¹⁸ yielding blue-shifted fluorescence. Compared with GFP, the first generation mutations of CFP exhibited undesirable properties, especially a reduced fluorescence quantum yield, ϕ_f.¹⁸ However, mutations over three generations of CFPs have enabled a substantial improvement in ϕ_f and other fluorescence characteristics,^17,19–22 with ‘enhanced CFP’ having ϕ_f = 0.36.²³ The broader family of enhanced CFPs now constitutes an important class of FPs due to their multicolour imaging applications and utility in Förster resonance energy transfer pairs.^22,24,25

Fig. 1 Structure of the pHBDI (in GFP) chromophore and the lowest energy conformation of the cyan chromophore (in CFP). To form the anion, deprotonation occurs on the –OH group for pHBDI and on the –NH as part of the indole ring for cyan. In GFP, the chromophore is deprotonated, while the chromophore is neutral in most CFPs.

Despite indole groups (e.g. as part of cyan) generally having unfavourable pK_a values for deprotonation, studies have suggested that the CFP chromophore is more readily deprotonated in the protein than in solution.^26,27 Several CFP derivatives, such as NowGFP and mNeonGreen, are presumed to have a deprotonated chromophore and consequently offer superior fluorescence properties compared to their neutral counterparts.^27,28 Overall, while the basic photophysics of CFPs are well established, the excited state dynamics of the fundamental chromophore unit are largely unknown and a molecular-level understanding of the chromophore–protein interaction is missing.

In a series of steps toward understanding the inherent excited-state dynamics of GFP-like chromophores and disentangling the contribution from the protein environment, the photodynamics of the GFP chromophores (pHBDI, Fig. 1) and functionalised derivatives, such as the neutral and deprotonated anion (pHBDI⁻), have been studied in both isolation^29–36 and in solution^36–45 (see also references therein). These studies have shown that both chromophore structure and environment dictate the chromophore's photophysics. Specifically, the room-temperature value of ϕ_f for pHBDI⁻ in water and in the protein are ≈10⁻⁴ and 0.8, respectively,⁴⁶ with the low value in water due to efficient internal conversion (IC) through a photoisomerisation mechanism.^47–49 On the other hand, in the protein, steric and non-covalent interactions restrict motions that lead to internal conversion, consequently extending the lifetime of the bright state and, hence, enhancing ϕ_f.^50,51 The chromophore's condensed-phase ϕ_f is greatly increased when cooling through the glass transition temperature, which hinders the photoisomerisation mechanism.^39,40,52 In contrast to the GFP chromophore, studies on the cyan chromophore have been limited to gas-phase action spectroscopy on the anion,^53–56 and nanosecond flash photolysis in selected solvents on the neutral⁵² aimed at characterising photoisomerisation responses and absorption profiles for the two geometric isomers.

This work reports on the ultrafast spectroscopy and excited-state dynamics of the cyan chromophore in solution using time-resolved fluorescence (TRF) upconversion and transient absorption (TA) spectroscopies. While both methods show a fast excited state decay, the TA results could be understood in terms of two models: (i) the hot ground state model, and (ii) the twisted intramolecular charge transfer (TICT) model. We discuss these two interpretations in the light of MRSF-TDDFT potential energy surface (PES) calculations and trends compared with other FP chromophores, concluding that the hot ground state model provides the correct description. Similar to the GFP chromophore, a viscosity analysis shows only weak dependence of the fastest excited-state lifetime, consistent with a volume-conserving mechanism for photoisomerisation.

2 Experimental methods

The cyan chromophore was synthesised as the Z isomer as part of an earlier gas-phase study by some of the present authors.⁵⁶ The purity was checked using ¹H-NMR and ¹³C-NMR spectroscopy. Spectrophotometry was performed in several solvents: water (Milli-Q), methanol (Alfa Aesar, 99%), ethanol (Fisher, >99%), 1-propanol (Acros Organics), 1-butanol (Sigma, ≥99%), 1-pentanol (Sigma-Aldrich, ≥99%), 1-heptanol (Alfa Aesar, 99%), 1-octanol (Thermo Scientific, 99%), and ethylene glycol (Sigma-Aldrich, ≥99%). The anion was generated by adding a drop of 1 M aqueous NaOH to the neutral cyan ethanol or water solutions (>10 mL). The neutral molecule was not soluble in water.

2.1 Absorption and fluorescence spectroscopy

Steady-state absorption spectra of cyan in solution were measured using a PerkinElmer Lambda XLS spectrometer. Fluorescence emission spectra were recorded at room temperature (T = 300 K) and emission and excitation spectra at T ≈ 77 K (samples immersed in a liquid nitrogen bath) using an Edinburgh Instruments FS5 spectrofluorometer.

2.2 Time-resolved fluorescence up-conversion

Time-resolved fluorescence (TRF) up-conversion spectroscopy was performed using the instrument detailed in ref. 57. Briefly, a continuous wave doubled Nd:YVO₄ laser drove a Kerr lens mode-locked Ti:Sapphire oscillator generating ≈800 nm light in ≈20 fs pulses at 80 MHz. The second harmonic (400 nm, ≈11 mW) was generated by focussing the fundamental (≈840 mW) light into a barium borate crystal (BBO, type I) using a concave mirror. The 400 nm and 800 nm beams were separated with a dichroic mirror and delayed relative to each other using a computer-controlled Physik Instrumente motorised delay stage (0.1 μm resolution), establishing the pump and probe (i.e. gate) beam lines. The 400 nm pump pulse was focussed onto the sample cell in 1 mm path length quartz flow cell using a concave mirror. The resulting fluorescence was captured and focussed through a CG455 Schott filter into a BBO crystal (type I, ≈300 μm thickness) and frequency mixed with the 800 nm probe light. The upconverted light was passed through a UG11 Schott filter into a monochromator (Photon Technology International Model 101, 2 nm mm⁻¹ resolution) and detected with a low-noise photomultiplier tube (PMT, Hamamatsu R585). A Stanford Research Systems photon counter (SR400) accumulated signal from the PMT and was interfaced with the control computer via a LabVIEW interface. The cross correlation of the instrument is ≈75 fs, with the 300 μm crystal, which was chosen to enhance signal-to-noise. The response time was determined through Raman scattering in heptane.⁵⁸

2.3 Transient absorption spectroscopy

The transient absorption (TA) spectrometer has been detailed in ref. 59. The pump and probe beams were derived from the 800 nm fundamental output beam from a Spectra Physics-Mai Tai laser oscillator coupled with a Ti:Sapphire regenerative amplifier (Spectra Physics-Spitfire ACE). The amplified output pulses at 800 nm (≈100 fs, 1 kHz, ≈5 mJ pulse⁻¹) were directed into an optical parametric amplifier (OPA, Light Conversion TOPAS Prime), which produced 410 nm (attenuated to ≈200 nJ pulse⁻¹) pump pulses for sample excitation. A white light continuum (WLC) probe spanning 300–700 nm was generated by focusing part of the 800 nm fundamental beam onto a ≈3 mm thickness CaF₂ window that was continuously x–y translated to prevent damage to the material surface. All measurements were conducted with the sample in 1 mm pathlength quartz flow cuvettes, with the sample concentration adjusted to achieve an optical density of ≈0.5. Use of the flow cuvette was to avoid photoproduct accumulation. The TA spectra were analysed and kinetic lifetimes extracted using global fitting with GloTarAn.⁶⁰

3 Computational methods

Quantum chemical calculations of PESs and the S₁–S₀ MECP (minimum energy crossing point as the conical intersection) were performed on isolated cyan. Due to the size of the molecule (31 atoms), mixed-reference spin–flip time-dependent density functional theory (MRSF-TDDFT) was used,^61,62 which is more suited to describe PESs involving charge-transfer character and PESs near conical intersection seams compared with conventional TDDFT.^62,63 The MRSF-TDDFT calculations used the BH&HLYP functional (50% Hartree–Fock exchange) with the 6-31G* basis set in GAMESS-US (June 2023 R2 release).⁶⁴ The S₁ and S₀ PESs were constructed by extrapolating a LIIC (linear interpolation in internal coordinates) between the critical points.

To model solvation of the S₁ state, the S₁ state relaxed geometry was explicitly solvated using the SOLVATOR framework in ORCA 6.0.1 with the DOCKER algorithm,⁶⁵ where solvent molecules of ethylene glycol, ethanol, or octanol, were sequentially added with the XTB trajectories at T = 300 K. The geometry of the chromophore (S₁ state from an MRSF-TDDFT geometry optimisation) was frozen in the SOLVATOR step – while solvation will alter the chromophore geometry, it was not computationally feasible to optimise the complete solvated cluster geometry. Calculations were performed with 20 explicit solvent molecules, chosen as a balance between computational cost and ensuring the chromophore was sufficiently surrounded by solvent molecules – see illustrations in the ESI.† Furthermore, because the SOLVATOR algorithm places and optimises solvent molecules based on the electronic structure of the S₀ state, the S₁ state equilibrium geometry was also modelled using SOLVATOR calculations with partial charges placed on each of the two ring systems equivalent to charge density found for S₁ state – this should approximately account for prompt solvent reorientation due to a change in charge distribution. Minimum energy solvent configurations for the solvated-molecule clusters from the molecular dynamics trajectories (with a frozen chromophore geometry from the gas-phase MRSF-TDDFT optimisations) were then used for explicitly-solvated MRSF-TDDFT calculations.

4 Results and discussion

4.1 Absorption and emission spectra

Steady-state absorption and fluorescence emission spectra for neutral and anionic cyan in solution are shown in Fig. 2. Band maxima and corresponding Stokes shifts are summarised in Table 1. At room temperature (T = 300 K), there is a clear red-shift in both absorption and emission maxima with deprotonation, similar to for pHBDI⁻ and alkylated derivatives.⁶⁶ At T = 300 K, the larger Stokes shift for neutral cyan compared with the anion suggests that there is greater nuclear reorganisation of the former to achieve the fluorescing state. There is clear mirror image symmetry between absorption and emission profiles for the anion at T = 300 K, and near mirror image symmetry for the neutral. At T ≈ 77 K, the spectra show vibronic structure and the Stokes shift for the neutral has decreased, consistent with restricting nuclear reorganisation by the glassy matrix.

Fig. 2 Steady-state absorption and emission spectroscopy of the neutral (blue) and anionic (orange) cyan chromophore in ethanol: (a) room temperature (T = 300 K) absorption (solid line) and emission (dotted line) spectra, and (b) T ≈ 77 K excitation (solid line) and emission (dotted line) spectra. Spectra processed with a five-point running average. Absorption and fluorescence emission spectra in other alcoholic solvents are given in the ESI.†

Table 1 Absorption (abs), fluorescence excitation (ex), and fluorescence emission (em) maxima, in nm, recorded for the cyan chromophore at room temperature (T = 300 K) and T ≈ 77 K. Stokes shift (Δ[small nu, Greek, tilde] for band maxima) is given in cm⁻¹

	T = 300 K			T ≈ 77 K
	λ abs	λ em	Δ[small nu, Greek, tilde]	λ ex	λ em	Δ[small nu, Greek, tilde]
Neutral	405	459	2905	408	442	1885
Anion	477	495	762	—	—	—

---

4.2 TRF upconversion

Fluorescence lifetimes of neutral cyan in a selection of alcoholic solvents were measured using TRF upconversion, which involved exciting cyan at ≈400 nm and monitoring the temporal evolution of fluorescence at selected upconverted wavelengths. The upconverted wavelength was chosen as the wavelength of maximum response in the fluorescence emission spectrum. The TRF upconversion data for cyan in ethanol are shown in Fig. 3a (inset shows a logarithmic vertical abscissa) along with a two component exponential decay fit. Fitted fluorescence lifetimes, τ_F, are summarised in Table 2. A two-component fit was necessitated due to an inadequate fit obtained with a single exponential decay (consistent with a non-linear decay shown in the inset). The most rapid fit component was described by a fit including the instrument response function (≈75 fs FWHM) with a <20% weight in all instances, assigned to scattered light. The longer-lived fit component, which accounted for >80% of the decay profile, was taken as the fluorescence lifetime, τ_F, with values ranging from 0.28 ± 0.01 ps in methanol to 0.58 ± 0.05 ps in octanol. The sub-picosecond fluorescence lifetime for cyan in ethanol is within uncertainty of that recorded for pHBDI.⁶⁶

Fig. 3 Time-resolved fluorescence up-conversion data for cyan in alcoholic solutions at T = 300 K: (a) excitation at 400 nm in ethanol and monitoring fluorescence by up-converting 488 nm fluorescence. The total fit curve is given by the black trace. The inset provides the experimental data with a logarithmic vertical abscissa. (b) Viscosity dependence of fluorescence rates with the gradient from the fit providing the viscosity effect metric α = 0.26 ± 0.03.

Table 2 Time constants (in ps) obtained from TA and TRF upconversion data fits. ‘–’ indicates not measured. τ₁ lifetimes from TA are consistent with τ_F lifetimes from TRF upconversion, and were assigned to the S₁ state lifetime in the hot ground state model, or to loss of the Franck–Condon geometry in the TICT model. τ₂ lifetimes correspond to thermalisation of vibrationally-excited S₀ in the hot ground state model, or to decay of S₁ state equilibrium geometry in the TICT model. Our discussion concludes that the hot ground state model provides the correct assignment

Solvent	η (cP)	ε	TA		TRF upconversion
			τ 1	τ 2	τ F (at 484 nm)	τ F (at 471 nm)
a Values taken from CRC Handbook of Chemistry and Physics, 85th Edition (2005). b T = 293.2 K, except 1-pentanol at T = 298.2 K. c T = 298 K.
Methanol	0.54	33.0	—	—	0.28 ± 0.01	—
Ethanol	1.07	25.3	0.35 ± 0.08	2.50 ± 0.50	0.36 ± 0.01	0.37 ± 0.04
1-Propanol	1.95	20.8	—	—	0.41 ± 0.03	—
1-Butanol	2.54	17.8	0.40 ± 0.16	2.40 ± 1.16	0.44 ± 0.01	—
1-Pentanol	3.62	15.1	—	—	0.49 ± 0.04	—
1-Heptanol	5.81	11.8	0.53 ± 0.11	3.35 ± 0.65	0.52 ± 0.04	0.49 ± 0.03
1-Octanol	7.29	10.3	—	—	0.58 ± 0.05	—
Ethylene glycol	16.1	41.4	0.58 ± 0.13	3.34 ± 0.65	—	—

---

4.3 TA spectroscopy

Selected transient absorption (TA) difference spectra for cyan in ethanol over the 0.15–50 ps range are shown in Fig. 4, with four assigned bands: A – ground state bleach (GSB), B – excited state absorption (ESA), C – stimulated emission (SE), D – either hot ground state absorption or TICT absorption, and E – long-lived product absorption. TA spectra recorded in butanol, heptanol, and ethylene glycol show similar spectral bands (see ESI†). The assignments of these bands is rationalised below.

Fig. 4 Selected transient absorption (TA) spectra for cyan in ethanol at T = 300 K: (a) spectra over 0.15–1 ps, and (b) spectra over 1–50 ps. Five spectral bands are identified by the arrows: (A) ground state bleach (GSB), (B) excited state absorption (ESA), (C) stimulated emission (SE), (D) either hot ground state absorption or TICT absorption, (E) long-lived product absorption. The sharp feature denoted by * in the 0.15 ps trace is a coherent artefact from cross correlation. The inset in (b) is a magnification of the 50 ps trace showing that band E remains at long times.

The initial TA spectrum at 0.15 ps (Fig. 4a) is dominated by two depletion bands (A & C) centred at λ ≈ 400 nm (A) and λ ≈ 480 nm (C) are consistent with the ground state absorption and fluorescence emission spectra (Fig. 2), respectively. They are consequently assigned as GSB (A) and SE (C). The positive band centred at λ ≈ 680 nm (B) was assigned to ESA (S_n ← S₁). Over the t ≤ 1 ps timescale (Fig. 4a), the ESA (B) decays and blue shifts by ≈20 nm, accompanied by the decay of SE (C) and formation of a new, positive band D. The possible assignments of band D are discussed in Section 4.5. For TA spectra beyond t = 1 ps (Fig. 4b), band D decays with concurrent recovery of the GSB (A). At much longer timescales (e.g. t ≈ 50 ps), a weak positive band E centred at λ ≈ 450 nm emerged. Band E was attributed to formation of a photoisomer (Z → E isomerisation) because this signal is constant out to hundreds of picoseconds and has a wavelength maximum coinciding with the ≈20 nm red-shifted absorption spectrum for the E isomer.⁵² It should be noted that because the photoisomerisation quantum yield is only a few percent,⁵² similar to that for pHBDI⁻ in solution, the expected signal from the E photoisomer should be weak.

The TA data were satisfactorily fit in a global framework using a two-component sum-of-exponentials model, supplemented by an offset, i.e. an indefinitely long time component. The evolution-associated difference spectra (EADS) in ethanol, derived from the sequential kinetic model (i.e.), are shown in Fig. 5 with fitted lifetimes τ₁ = 0.35 ± 0.08 ps and τ₂ = 2.5 ± 0.5 ps. Fitted lifetimes for cyan in the three other solvents are listed in Table 2. The τ₁ = 0.35 ± 0.08 ps component 1 was assigned to relaxation of the Franck–Condon state. Decay of fit component 1 leads to the emergence of fit component 2, which is linked with TA band D, whose distinctive characteristic is a narrow positive band on the red edge of the absorption spectrum (see TA spectra in other solvents in the ESI†); this band is further discussed and assigned in Sections 4.5 and 4.6. In turn, component 2 decays (τ₂ = 2.5 ± 0.5 ps), recovering the GSB and also giving rise to a small amount of a long-lived product assigned as the E isomer. The TRF upconversion lifetimes τ_F are consistent with the τ₁ lifetimes from TA and loss of the SE band, confirming that the fluorescent state is lost on a sub-picosecond timescale.

Fig. 5 Evolution associated difference spectra (EADS) determined for cyan in ethanol from a two-component plus constant term global fit. Component 1 is blue [correlates with ground state bleach (band A), excited state absorption (band B), and stimulated emission (band C) in Fig. 4], 2 is green [correlates with band D and recovery of the ground state bleach (band A) in Fig. 4], and 3 is orange [correlates with the long-lived photoproduct (band E) in Fig. 4]. Lifetimes are given in Table 2.

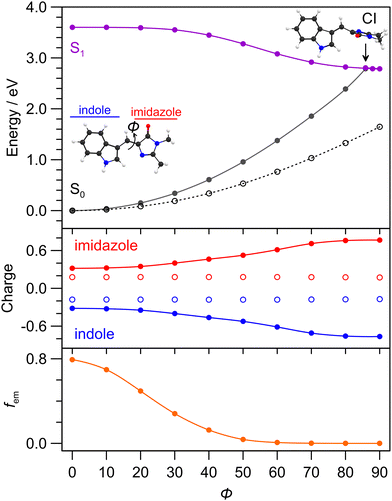
4.4 Potential energy surfaces and charge-transfer

To help understand the excited state dynamics, PES calculations using the MRSF-TDDFT methodology for (gas phase) cyan were performed and are summarised in Fig. 6. While the MRSF-TDDFT strategy is not as mature as CASSCF-reference methods for computing excited state PES and locating conical intersection seams,^62,67 it is significantly more computationally tractable and can be therefore more readily applied to explicitly-solvated chromophores. The calculated (gas phase) S₀–S₁ transition energy (3.60 eV, 344 nm) is at shorter wavelength than in solution, however, the value for cyan solvated with 20 explicit ethanol molecules is 3.11 eV (≈398 nm), which is closer to the vertical experimental value (405 nm). The Franck–Condon transition involves a small amount of charge-transfer character from the imidazole group (+0.2 → +0.3) to the indole ring (−0.2 → −0.3), quantified by Löwdin charges in Fig. 6 (middle). The minimum energy nuclear relaxation pathway (i.e. with geometric relaxation), involving twisting about the central double bond (dihedral angle ϕ), reveals a near barrierless pathway to an S₁ minimum energy geometry with ϕ = 87.9° that is situated ≈0.6 eV lower in energy. Concurrently, with increasing ϕ there is an increase in the charge-transfer character of the S₁ state, with the charges on the imidazole group reaching +0.7 and indole ring reaching −0.7. In other terms, the magnitude of the permanent molecular dipole moment, |μ|, is 4.76 D for the S₀ initial equilibrium geometry, and 10.77 D for the relaxed S₁ state. The ϕ torsion also leads to a decrease in the calculated fluorescence oscillator strength, f_em, to near zero at the S₁ state equilibrium geometry. Because of the moderate degree of charge-transfer character for the relaxed S₁ state, it can be classed as a partial twisted intramolecular charge-transfer (TICT) state.^68,69

Fig. 6 Potential energy surface and critical points for isolated cyan as a function of dihedral angle, ϕ, around the methylene bridge double bond. (upper) Potential energy surfaces leading to the conical intersection (CI) computed at the MRSF-TDDFT/BH&HLYP level of theory: filled purple circles – S₁; unfilled black circles – S₀ optimised geometries; filled grey circles – linear interpolation of internal coordinates between S₀ equilibrium geometry and the CI. (middle) Löwdin charges on the imidazole (red) and indole (blue) groups on the S₀ (unfilled circles) and S₁ (filled circles) PESs. (lower) Oscillator strength (f_em) for S₁ → S₀ emission.

The S₀ state PES, computed assuming the relaxed S₀ state geometries (open points in Fig. 6), shows no crossing with the S₁ state. A S₁–S₀ MECP search identified a conical intersection seam with a minimum energy crossing (assumed as the conical intersection, energy separation <2 meV) with ϕ = 85.6° as well as a degree of pyramidalisation of the bridge unit and bridge bond stretching – geometries are given in the ESI.† Interestingly, this geometry is only ≈20 meV higher in energy than the S₁ equilibrium geometry, leading us to conclude that the isomerising conical intersection is in proximity (geometrically and energetically) to the relaxed S₁ state. The filled circle PES for the S₀ state (also barrierless) shown in Fig. 6 is from a LIIC between the CI geometry and the initial S₀ state equilibrium geometry. These calculations assume the Z isomer of cyan since this was the starting isomer and because the photoisomerisation quantum yield is, at best, a few percent.⁵²

4.5 Interpretation of the excited state dynamics

Considering all measurements and calculations together, the excited state dynamics could be interpreted using two models (illustrated in Fig. 7) that differ by the assignment of the intermediate state linked with TA band D that relaxes with lifetime τ₂. These interpretations are termed: (i) the hot ground state model, and (ii) the TICT model.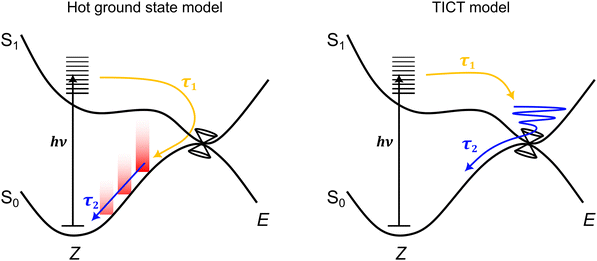

Fig. 7 Schematic illustration of the two excited-state dynamics models consistent with the ultrafast spectroscopy data. In the hot ground state model, lifetime τ₁ is linked with loss of the excited state to form a hot ground state, while lifetime τ₂ is linked with cooling of the hot ground state through vibrational relaxation to solvent. In the twisted intramolecular charge-transfer (TICT) model,⁴⁷ lifetime τ₁ is linked with motion away from the Franck–Condon geometry to a (non-fluorescent) TICT state geometry that is situated in the vicinity of a conical intersection seam – the location and topology of this seam may be a function of solvent polarity. Lifetime τ₂ is then associated with loss of the TICT state through internal conversion.

In the hot ground state model, lifetime τ₁ (and τ_F in TRF upconversion) is associated with total loss of the excited state, and formation of a vibrationally-hot ground state. Lifetime τ₂ is then due to thermalisation of the hot ground state. This interpretation is consistent with both the sub-picosecond loss of fluorescence and the position of band D in the TA spectra always being on the red edge of the GSB band,⁷⁰ irrespective of the alcohol solvent polarity. Thus, in the hot ground state model, lifetime τ₂ and decay of TA band D is assigned to thermalisation of a hot ground state through vibrational relaxation to solvent and recovery of the equilibrium geometry. However, while typical lifetimes for vibrational relaxation to solvent depend on vibrational modes and anharmonic couplings of the system and solvent, as well as other coupling processes (e.g. vibrational-translation),⁷¹ vibrational relaxation lifetimes in alcohols are usually on the order of a few to tens of picoseconds.^72–74 While the present τ₂ lifetimes (Table 2) are near the rapid end of this scale, they are similar to hot ground state cooling lifetimes in related photoisomerising systems.^70,75–77 Other studies similarly using TRF upconversion and TA spectroscopy on pHBDI and substituted derivatives in solvents including methanol,⁴² gave τ_F = 0.3 ± 0.2 ps and two TA lifetimes at 0.4 ± 0.2 ps and 4.8 ± 0.5 ps, which are comparable with those determined here for cyan. Those authors assigned the longer time component to hot ground state cooling based on trends across the anion, neutral, and cation for pHBDI and substituted derivatives.

An alternative interpretation of the excited state dynamics is provided by the TICT model, also illustrated in Fig. 7. Here, lifetime τ₁ (and τ_F in TRF upconversion) is associated with loss of the Franck–Condon state to give the relaxed S₁ state, which, in the gas phase, was classified as a partial TICT state in our above calculations. Lifetime τ₂ is then associated with decay of the TICT state by passage through the nearby S₁−S₀ conical intersection seam. A similar interpretation has been proposed for the excited state dynamics of pHBDI⁻ in water from ab initio molecular dynamics trajectories by Martinez and co-workers.⁴⁷ If TA band D was indeed to correspond to absorption from a TICT-like state, we might expect the position of the band to depend on solvent polarity as the S_n ← S₁ probe transition energies change with polarity. This possibility is considered in the next section.

We also considered that a second excited-state PES minimum could correspond to TA band D. For example, pHBDI⁻,^31,48 has a local S₁ PES minimum (the so-called ‘P-trap’) associated with torsion about the central single bond, which can serve to temporarily trap excited state population. However, our MRSF-TDDFT geometry optimisations and systematic relaxed PES scans about the corresponding coordinate in cyan failed to locate any other minimum energy structure. We therefore discount the possibility of a second PES minimum.

4.6 Polarity effect on TA band D

It is common for TICT-like excited states to show systematic shifting of fluorescence emission spectra to longer wavelength with a more polar solvent, since the stability of TICT increases with increasing solvent polarity.^68,69,78 However, no significant changes in the fluorescence spectra as a function of solvent were observed in this work, presumably because the TICT state is non-fluorescent (see Fig. 6 lower).⁶⁹ A different trend to investigate is how electronic calculations of explicitly-solvated cyan predict that the TA signature of a TICT state might depend on the solvent polarity. We therefore took the (gas phase) optimised S₁ state geometry and used XTB trajectories to determine the lowest energy solvated structures (with a frozen chromophore geometry) and, in turn, performed MRSF-TDDFT calculation of probe transition energies and oscillator strengths. In all cases, the S₄ ← S₁ transition was the lowest energy transition (f = 0.4–0.5) that would be observed in transient absorption, with calculated vertical transition wavelengths (wavelengths in parentheses assume the S₁ TICT charge distribution when adding explicit solvent molecules) of ethylene glycol (ε = 41.4) at 603 nm (577 nm), ethanol (ε = 25.3) at 477 nm (465 nm), and octanol (ε = 10.3) at 434 nm (414 nm). Thus, the predicted trend is that the TA spectrum for the equilibrium S₁ state shifts to longer wavelength with higher polarity solvent. This trend was not observed in experiment and, consequently, further supports the hot ground state model for describing the excited state dynamics.

4.7 Viscosity effect on excited state lifetimes

The viscosity effect on excited state lifetimes was considered since internal conversion involves torsion about a double bond towards photoisomerisation. The viscosity dependence of the τ_F lifetimes was analysed in a modified Kramer's theory framework (Fig. 3b),⁷⁹ where a phenomenological power law trend broadly exists for isomerisation-type reactions near the so-called high-friction limit (and assuming the hydrodynamic approximation).⁸⁰ Here, the fluorescence rate constant, with either the hot ground state or TICT model interpretations should correspond to twisting of the chromophore backbone towards the conical intersection seam geometry. In such a case, k_F ≈ Cη^−α, where C is proportional to the Arrhenius thermal activation term and α is a metric for the viscosity effect on isomerisation that approaches unity in the Kramer's high friction limit. The fitted value of α = 0.26 ± 0.03 is consistent with a weak viscosity dependence, and in turn implies that the mechanism for loss of the fluorescing state must be near volume conserving or otherwise insensitive to viscosity. This value of α is similar to that observed for both neutral (≈0.2) and anionic (0.25 ± 0.06) pHBDI under similar solvation conditions.⁴⁰ For comparison, values of α for ‘conventional’ E–Z photoisomerisation of stilbenes or model photoactive yellow protein chromophores in primary alcohols are >0.5;^81–83 these comparative systems are known to possess PES barriers along the co-ordinate connecting the Franck–Condon region to the isomerising conical intersection seam. On the other hand, the sub-picosecond lifetimes for cyan in solution indicate that there are no significant barriers connecting the Franck–Condon region with conical intersection seams, supporting a situation similar to pHBDI⁻.^47–49 The τ₂ lifetimes from TA spectroscopy (Table 2) similarly show only a weak viscosity dependence.

Overall, the weak viscosity dependence and volume-conserving nature of the internal conversion pathway, sub-picosecond excited state lifetime, and dark S₁ state geometry results in the low fluorescence quantum yield of cyan in solution, which is an ‘inherent’ characteristic of the chromophore. Thus, specific non-covalent interactions (electrostatic, hydrogen-bonding, sterics, etc.)^21,51 between the chromophore and protein binding pocket are critical for restricting ϕ torsion and, consequently, restricting access of the dark, relaxed S₁ state geometry and conical intersection seam leading to internal conversion.

4.8 Deprotonated anion

Measurement of the excited state fluorescence lifetimes for the cyan anion were performed in water and ethanol; these measurements were more challenging than for the neutral due to weaker absorption at the pump wavelength (400 nm, see Fig. 1). Fits to the data returned τ_F values of 1.08 ± 0.16 ps (water) and 0.64 ± 0.06 ps (ethanol), with the former being similar to that for pHBDI⁻ in water.³⁶ The fluorescence lifetime for the cyan anion in ethanol is roughly double that for neutral, which parallels the lifetime differences between anionic and neutral pHBDI.⁶⁶ Thus, in a first approximation, it could be assumed that any differences in potential energy surface between anionic and neutral charge states of pHBDI are paralleled in cyan.

5 Conclusions

The ultrafast spectroscopy of the cyan fluorescent protein chromophore in solution has been investigated. The chromophore undergoes an ultrafast internal conversion through a conical intersection seam associated with Z–E photoisomerisation. The viscosity effect on the lifetimes is weak, suggesting an essentially barrierless and volume-conserving photoisomerisation pathway. The multi-exponential excited state lifetimes could be interpreted in two models, one involving sub-picosecond formation of a hot ground state that cools over several picoseconds, and the other involving formation of a twisted intramolecular charge-transfer state that survives for a few picoseconds. The lack of any polarity dependence of the transient absorption spectral bands potentially connected with the picosecond-lived excited states combined with explicit solvation calculations and trends across the ultrafast dynamics for other FP chromophores led us to conclude that the hot ground state model provides the correct interpretation. Ultimately, time-resolved vibrational spectroscopy on cyan (and other related neutral FP chromophores) should be performed since the vibrational modes of a TICT state would be distinguishable from those for the ground electronic state. Furthermore, it would be informative to study cyan derivatives with electron withdrawing or donating groups added to the indole unit in order to polarise the charge distribution and modify the S₁ state charge distribution.

Similar to that which has been performed for pHBDI⁻ and the protonated cyan cation, we are planning gas-phase cryogenic action spectroscopy,⁵⁶ photoisomerisation action spectroscopy,³² and time-resolved photoelectron velocity-map imaging experiments³⁶ on the deprotonated anion to fully characterise the inherent, solvent-free excited state dynamics, allowing for straightforward comparison of experiments with ab initio molecular dynamics or similar calculations.^48,49 Furthermore, when using velocity-map imaging detection of photoelectrons in time-resolved experiments,⁸⁴ albeit on the deprotonated anion rather than the neutral, TICT-like states should be evident in photoelectron kinetic energy distributions and photoelectron angular anisotropies.^85,86

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by an EPSRC New Investigator Award (EP/W018691 to JNB) and an EPSRC Grant (EP/X011410/1 to SRM). EKA thanks the University of East Anglia for a doctoral scholarship. GB is grateful to the Leverhulme Trust for funding him through an Early Career Fellowship (grant no. ECF-2023-195).

Notes and references

1. R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544.
2. J. M. Kendall and M. N. Badminton, Trends Biotechnol., 1998, 16, 216–224.
3. J. Zhang, R. E. Campbell, A. Y. Ting and R. Y. Tsien, Nat. Rev. Mol. Cell Biol., 2002, 3, 906–918.
4. N. C. Shaner, P. A. Steinbach and R. Y. Tsien, Nat. Methods, 2005, 2, 905–909.
5. Fundamentals of Fluorescence Imaging, ed. G. Cox, Jenny Stanford Publishing, 2019.
6. G.-J. Kremers, J. Goedhart, E. B. van Munster and T. W. J. Gadella, Biochemistry, 2006, 45, 6570–6580.
7. G. D. Malo, L. J. Pouwels, M. Wang, A. Weichsel, W. R. Montfort, M. A. Rizzo, D. W. Piston and R. M. Wachter, Biochemistry, 2007, 46, 9865–9873.
8. B. Seefeldt, R. Kasper, T. Seidel, P. Tinnefeld, K.-J. Dietz, M. Heilemann and M. Sauer, J. Biophotonics, 2008, 1, 74–82.
9. J. S. Paige, K. Y. Wu and S. R. Jaffrey, Science, 2011, 333, 642–646.
10. M. Drobizhev, P. R. Callis, R. Nifosì, G. Wicks, C. Stoltzfus, L. Barnett, T. E. Hughes, P. Sullivan and A. Rebane, Sci. Rep., 2015, 5, 13223.
11. J. W. Park and Y. M. Rhee, J. Am. Chem. Soc., 2016, 138, 13619–13629.
12. C.-Y. Lin and S. G. Boxer, J. Am. Chem. Soc., 2020, 142, 11032–11041.
13. E. K. Ashworth, M. H. Stockett, C. Kjær, P. C. B. Page, S. R. Meech, S. B. Nielsen and J. N. Bull, J. Phys. Chem. A, 2022, 126, 1158–1167.
14. M. V. Matz, K. A. Lukyanov and S. A. Lukyanov, BioEssays, 2002, 24, 953–959.
15. R. N. Day and M. W. Davidson, Chem. Soc. Rev., 2009, 38, 2887–2921.
16. G.-J. Kremers, S. G. Gilbert, P. J. Cranfill, M. W. Davidson and D. W. Piston, J. Cell Sci., 2011, 124, 157–160.
17. N. G. Bozhanova, M. S. Baranov, K. S. Sarkisyan, R. Gritcenko, K. S. Mineev, S. V. Golodukhina, N. S. Baleeva, K. A. Lukyanov and A. S. Mishin, ACS Chem. Biol., 2017, 12, 1867–1873.
18. R. Heim, D. C. Prasher and R. Y. Tsien, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12501–12504.
19. M. L. Markwardt, G.-J. Kremers, C. A. Kraft, K. Ray, P. J. C. Cranfill, K. A. Wilson, R. N. Day, R. M. Wachter, M. W. Davidson and M. A. Rizzo, PLoS One, 2011, 6, e17896.
20. M. Golub, V. Guillon, G. Gotthard, D. Zeller, N. Martinez, T. Seydel, M. M. Koza, C. Lafaye, D. Clavel, D. von Stetten, A. Royant and J. Peters, J. R. Soc., Interface, 2019, 16, 20180848.
21. G. Gotthard, D. von Stetten, D. Clavel, M. Noirclerc-Savoye and A. Royant, Biochem., 2017, 56, 6418–6422.
22. J. Goedhart, D. von Stetten, M. Noirclerc-Savoye, M. Lelimousin, L. Joosen, M. A. Hink, L. van Weeren, T. W. J. Gadella and A. Royant, Nat. Commun., 2012, 3, 751.
23. M. A. Rizzo, G. H. Springer, B. Granada and D. W. Piston, Nat. Biotechnol., 2004, 22, 445–449.
24. H.-w Ai, S. G. Olenych, P. Wong, M. W. Davidson and R. E. Campbell, BMC Biol., 2008, 6, 13.
25. F. Mérola, A. Fredj, D. Betolngar, C. Ziegler, M. Erard and H. Pasquier, Biotechnol. J., 2013, 9, 180–191.
26. K. S. Sarkisyan, I. V. Yampolsky, K. M. Solntsev, S. A. Lukyanov, K. A. Lukyanov and A. S. Mishin, Sci. Rep., 2012, 2, 608.
27. L. Zarowny, D. Clavel, R. Johannson, K. Duarte, H. Depernet, J. Dupuy, H. Baker, A. Brown, A. Royant and R. E. Campbell, Protein Eng., Des. Sel., 2022, 35, gzac004.
28. K. Sarkisyan, A. Goryashchenko, P. Lidsky, D. Gorbachev, N. Bozhanova, A. Gorokhovatsky, A. Pereverzeva, A. Ryumina, V. Zherdeva, A. Savitsky, K. Solntsev, A. Bommarius, G. Sharonov, J. Lindquist, M. Drobizhev, T. Hughes, A. Rebane, K. Lukyanov and A. Mishin, Biophys. J., 2015, 109, 380–389.
29. C. R. S. Mooney, D. A. Horke, A. S. Chatterley, A. Simperler, H. H. Fielding and J. R. R. Verlet, Chem. Sci., 2013, 4, 921–927.
30. C. W. West, J. N. Bull, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Phys. Chem. B, 2015, 119, 3982–3987.
31. A. Svendsen, H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, J. Am. Chem. Soc., 2017, 139, 8766–8771.
32. E. Carrascosa, J. N. Bull, M. S. Scholz, N. J. A. Coughlan, S. Olsen, U. Wille and E. J. Bieske, J. Phys. Chem. Lett., 2018, 9, 2647–2651.
33. W. Zagorec-Marks, M. M. Foreman, J. R. R. Verlet and J. M. Weber, J. Phys. Chem. Lett., 2019, 10, 7817–7822.
34. J. L. Woodhouse, A. Henley, R. Lewin, J. M. Ward, H. C. Hailes, A. V. Bochenkova and H. H. Fielding, Phys. Chem. Chem. Phys., 2021, 23, 19911–19922.
35. A. V. Bochenkova and L. H. Andersen, J. Phys. Chem. Lett., 2022, 13, 6683–6685.
36. E. K. Ashworth, M.-H. Kao, C. S. Anstöter, G. Riesco-Llach, L. Blancafort, K. M. Solntsev, S. R. Meech, J. R. R. Verlet and J. N. Bull, Phys. Chem. Chem. Phys., 2023, 25, 23626–23636.
37. K. L. Litvinenko, N. M. Webber and S. R. Meech, Bull. Chem. Soc. Jpn., 2002, 75, 1065–1070.
38. D. Mandal, T. Tahara, N. M. Webber and S. R. Meech, Chem. Phys. Lett., 2002, 358, 495–501.
39. D. Mandal, T. Tahara and S. R. Meech, J. Phys. Chem. B, 2003, 108, 1102–1108.
40. K. L. Litvinenko, N. M. Webber and S. R. Meech, J. Phys. Chem. A, 2003, 107, 2616–2623.
41. M. Vengris, I. H. M. van Stokkum, X. He, A. F. Bell, P. J. Tonge, R. van Grondelle and D. S. Larsen, J. Phys. Chem. A, 2004, 108, 4587–4598.
42. K. M. Solntsev, O. Poizat, J. Dong, J. Rehault, Y. Lou, C. Burda and L. M. Tolbert, J. Phys. Chem. B, 2008, 112, 2700–2711.
43. S. R. Meech, Chem. Soc. Rev., 2009, 38, 2922–2934.
44. K. Addison, I. A. Heisler, J. Conyard, T. Dixon, P. C. Bulman Page and S. R. Meech, Faraday Discuss., 2013, 163, 277–296.
45. M. A. Taylor, L. Zhu, N. D. Rozanov, K. T. Stout, C. Chen and C. Fang, Phys. Chem. Chem. Phys., 2019, 21, 9728–9739.
46. H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. I. Tsuji, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13617–13622.
47. C. M. Jones, N. H. List and T. J. Martínez, Chem. Sci., 2021, 12, 11347–11363.
48. N. H. List, C. M. Jones and T. J. Martínez, Chem. Sci., 2022, 13, 373–385.
49. N. H. List, C. M. Jones and T. J. Martínez, Commun. Chem., 2024, 7, 25.
50. M. E. Martin, F. Negri and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 5452–5464.
51. M. G. Romei, C.-Y. Lin, I. I. Mathews and S. G. Boxer, Science, 2020, 367, 76–79.
52. V. Voliani, R. Bizzarri, R. Nifos, S. Abbruzzetti, E. Grandi, C. Viappiani and F. Beltram, J. Phys. Chem. B, 2008, 112, 10714–10722.
53. S. Boyé, I. B. Nielsen, S. B. Nielsen, H. Krogh, A. Lapierre, H. B. Pedersen, S. U. Pedersen, U. V. Pedersen and L. H. Andersen, J. Chem. Phys., 2003, 119, 338–345.
54. C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949.
55. M. A. Parkes, A. Bennett and H. H. Fielding, Mol. Phys., 2019, 117, 3027–3035.
56. E. K. Ashworth, J. Dezalay, C. R. M. Ryan, C. Ieritano, W. S. Hopkins, I. Chambrier, A. N. Cammidge, M. H. Stockett, J. A. Noble and J. N. Bull, Phys. Chem. Chem. Phys., 2023, 25, 20405–20413.
57. I. A. Heisler, M. Kondo and S. R. Meech, J. Phys. Chem. B, 2009, 113, 1623–1631.
58. A. Fatima, G. Bressan, E. K. Ashworth, P. C. B. Page, J. N. Bull and S. R. Meech, Phys. Chem. Chem. Phys., 2024, 26, 29048–29059.
59. C. R. Hall, J. Conyard, I. A. Heisler, G. Jones, J. Frost, W. R. Browne, B. L. Feringa and S. R. Meech, J. Am. Chem. Soc., 2017, 139, 7408–7414.
60. J. J. Snellenburg, S. P. Laptenok, R. Seger, K. M. Mullen and I. H. M. V. Stokkum, J. Stat. Software, 2012, 49, 1–22.
61. S. Lee, E. E. Kim, H. Nakata, S. Lee and C. H. Choi, J. Chem. Phys., 2019, 150, 184111.
62. W. Park, K. Komarov, S. Lee and C. H. Choi, J. Phys. Chem. Lett., 2023, 14, 8896–8908.
63. S. Lee, S. Shostak, M. Filatov and C. H. Choi, J. Phys. Chem. A, 2019, 123, 6455–6462.
64. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
65. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theor. Comput., 2019, 15, 1652–1671.
66. J. Conyard, M. Kondo, I. A. Heisler, G. Jones, A. Baldridge, L. M. Tolbert, K. M. Solntsev and S. R. Meech, J. Phys. Chem. B, 2011, 115, 1571–1577.
67. S. Lee, W. Park and C. H. Choi, Acc. Chem. Res., 2025, 58, 208–217.
68. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899–4032.
69. S. McConnell, R. H. McKenzie and S. Olsen, J. Chem. Phys., 2015, 142, 084502.
70. S. A. Kovalenko, R. Schanz, H. Hennig and N. P. Ernsting, J. Chem. Phys., 2001, 115, 3256–3273.
71. M. P. Grubb, P. M. Coulter, H. J. B. Marroux, B. Hornung, R. S. McMullen, A. J. Orr-Ewing and M. N. R. Ashfold, Nat. Chem., 2016, 8, 1042–1046.
72. J. C. Owrutsky, D. Raftery and R. M. Hochstrasser, Ann. Rev. Phys. Chem., 1994, 45, 519–555.
73. J. L. Skinner, Theor. Chem. Acc., 2010, 128, 147–155.
74. Y. Deng and R. M. Stratt, J. Chem. Phys., 2002, 117, 1735–1749.
75. G. Duvanel, J. Grilj, H. Chaumeil, P. Jacques and E. Vauthey, Photochem. Photobiol. Sci., 2010, 9, 908–915.
76. J. Conyard, I. A. Heisler, W. R. Browne, B. L. Feringa, S. Amirjalayer, W. J. Buma, S. Woutersen and S. R. Meech, J. Phys. Chem. A, 2014, 118, 5961–5968.
77. E. Özcan, V. Kuznetsova, G. KeÅŸan, M. Fuciman, R. Litvín and T. Polívka, J. Photochem. Photobiol., A, 2023, 441, 114737.
78. W. Rettig and A. Klock, Can. J. Chem., 1985, 63, 1649–1653.
79. K. M. Keery and G. R. Fleming, Chem. Phys. Lett., 1982, 93, 322–326.
80. B. Bagchi and D. W. Oxtoby, J. Chem. Phys., 1983, 78, 2735–2741.
81. S. H. Courtney and G. R. Fleming, J. Chem. Phys., 1985, 83, 215–222.
82. D. H. Waldeck, Chem. Rev., 1991, 91, 415–436.
83. E. K. Ashworth, N. J. A. Coughlan, W. S. Hopkins, E. J. Bieske and J. N. Bull, J. Phys. Chem. Lett., 2022, 13, 9028–9034.
84. C. S. Anstöter, J. N. Bull and J. R. Verlet, Int. Rev. Phys. Chem., 2016, 35, 509–538.
85. J. N. Bull, C. S. Anstöter and J. R. R. Verlet, Nat. Commun., 2019, 10, 5820.
86. C. S. Anstöter, B. F. E. Curchod and J. R. R. Verlet, Nat. Commun., 2020, 11, 2827.

---

Footnote

† Electronic supplementary information (ESI) available: Solvent-dependent fluorescence spectra, transient absorption data in butanol, heptanol and ethylene glycol, and optimised geometries of key PES features. See DOI: https://doi.org/10.1039/d5cp00942a

---