Reactive uptake via inelastic scattering of CN radicals at a liquid hydrocarbon surface

Abstract

Collisions of ground-electronic-state CN radicals with the surface of a prototypical saturated-hydrocarbon liquid have been studied experimentally. A molecular beam of CN(X²Σ⁺) with a mean laboratory-frame kinetic energy of 44 kJ mol⁻¹ was directed at normal incidence at a continually refreshed liquid squalane (2,6,10,15,19,23-hexamethyltetracosane) surface. The incident and scattered CN radicals were detected in a range of rotational states by multi-pass frequency-modulated absorption spectroscopy on selected lines of the CN(A–X) transition. The ratio of scattered-to-incident CN populations for squalane were compared with those obtained previously for a reference liquid, perfluoropolyether (PFPE), which is assumed to be inert. The overall survival probability, summed over the significantly populated rotational levels, of CN on squalane was found to be 0.15 ± 0.04. The 85% that is lost is inferred, on energetic grounds, to produce HCN via H-atom abstraction. The surviving CN has a significantly superthermal rotational distribution and a hot, non-thermal velocity distribution in the direction perpendicular to the surface normal. These dynamical attributes are characteristic of impulsive scattering. However, we conclude that the low survival probability is not compatible with a simple, ‘single-bounce’ mechanism and hence that multiple-encounter trajectories must contribute significantly to CN reactive loss. We find no evidence of a distinct trapping-desorption component, corresponding to full thermal accommodation, in the surviving CN from either squalane or PFPE at these collision energies.

---

Introduction

Interfaces between the gas and liquid phases are ubiquitous. They span diverse fields, from natural phenomena such as atmospheric aerosols and respiration, to technological processes such as distillation, combustion systems, multiphase catalysis and gas sequestration. Due to a combination of technical challenges and fundamental complexity, understanding of the molecular-level mechanisms of collisions at these interfaces is much less developed than for those in the gas phase or even at the gas–solid interface. In this work, we provide new insight into the mechanism of one such previously unstudied system, the reaction of CN radicals with a hydrocarbon liquid surface.

The most widely studied and best-understood elementary gas–liquid processes are those in which inert atoms or small molecules are inelastically scattered from the liquid surface.^1–3 For technical reasons, the majority of such studies have been on low-vapour pressure liquids that can be straightforwardly prepared in vacuum, but this is now being extended to higher-vapor-pressure systems through the use of liquid-jet technology.^1,4

A general picture has emerged that the broad features of the inelastically scattered products can usually be categorised satisfactorily through a combination of two limiting scattering mechanisms. Impulsive scattering (IS) involves one, or at most a few, interactions of the incident molecules with the surface. It results in non-thermal translational and internal product-state distributions that depend on the incident kinetic energy, E_i, and more-sharply directed angular distributions that are correlated with incidence angle, θ_i. In contrast, in thermal desorption (TD), the molecules interact sufficiently with the surface to lose memory of the initial conditions. The product speed and rotational (if not always vibrational) distributions are characterised by temperatures at, or close to, that of the surface. The distribution of final angles, θ_f, satisfies ‘Knudsen's law’, with a cosine dependence about the surface normal.

While undoubtedly empirically useful for the characterisation of observed distributions, detailed scattering calculations caution against taking this simple binary IS/TD picture too literally.^5–10 It works best when E_i is significantly superthermal, when at least the fastest products can unambiguously be identified with some form of relatively direct scattering. Even in that case, it is not possible to be certain that none of the slower products have also been formed via a relatively direct process. This is confirmed by the scattering calculations, which show that there can be more than two distinguishable classes of trajectory, which cannot be sorted unambiguously on the basis of the product attributes.^5–8

Studies of reactive scattering at the gas–liquid interface have been less common.^1–3 In most cases, the focus has been on determining the dynamical attributes of the products and/or the surviving, inelastically scattered reactants. The IS/TD paradigm again proves empirically useful, with some reservations, for broad characterisation of the observed speed and internal state distributions of reactive products. The most-studied systems are reactions of the radical species O(³P), Cl(²P), F(²P) and OH(X²Π) with hydrocarbons or related liquids,^1,2,11–37 and exchange reactions of HCl with protic liquids.^31–37 There is also an isolated report for the electronically excited reactant, O(¹D), with the prototypical hydrocarbon liquid, squalane (2,6,10,15,19,23-hexamethyltetracosane), also studied in much of the other previous work and here.³⁸

Much less effort has been expended on measurement of the absolute survival probability of the incident molecules at the surface. This property, or its converse the uptake coefficient, is often of primary interest in applications such as the modelling of atmospheric aerosol chemistry. Consequently, uptake coefficients have been measured quite extensively by more-conventional kinetic methods, including flow tubes and continuous-flow stirred-tank reactors.^39–41 However, these approaches may be affected by secondary processes and do not necessarily isolate individual elementary steps in the mechanism. Direct quantification of reactant-molecule loss in the primary interaction with the surface is essentially confined to our own series of studies of OH collisions with liquid hydrocarbon surfaces.^11,12,14,42

We extend here the measurement of survival probabilities in reactive gas–liquid systems to reactions of the type

CN + HR → HCN + R (R1)

where CN is in its electronic-ground state (X²Σ⁺) and HR represents a saturated alkane. Much of the previous interest in reaction (R1) has been driven by its importance in hydrocarbon flames, as well as in a variety of astrochemical environments, such as the atmosphere of Titan.^43,44

Reaction (R1) is strongly exothermic (ΔH = −(90–140) kJ mol⁻¹, depending on the C–H bond type).⁴⁵ Crossed-molecular-beam studies show that the HCN products of the gas-phase reaction are backward scattered with little translational energy release.⁴⁶ A significant fraction of the energy is deposited into the C–H stretch and bend modes, but not the C≡N stretching mode, implying it is essentially a spectator.^47,48 These observations are characteristic of an attractive potential energy surface with either a small or submerged barrier early in the entrance channel.⁴⁹ Consistent with this, kinetic studies confirm that the reaction is rapid even at ambient temperatures.^50–52 For example, for representative secondary hydrocarbons such as C₅–C₈ cycloalkanes, the room-temperature rate constants are a significant fraction of the gas-kinetic collisional limit, with slightly negative temperature dependences.⁵⁰ This is reinforced by theory, which is able to explain the observed bimodal temperature dependence, with a minimum around ∼200 K, for CN + ethane.⁵¹ The rate-determining step at temperatures below the minimum is found to be formation of a weakly bound van der Waals complex, but this switches to H-abstraction via a submerged saddle-point at higher temperatures.

In this work, the CN(X²Σ⁺) is generated in a molecular beam with a superthermal laboratory-frame kinetic energy (E_i = 44 kJ mol⁻¹) and HR represents a liquid squalane surface. We exploit the same near-IR absorption spectroscopic method that we developed recently and applied to inelastic scattering of CN from the inert liquid, perfluoropolyether (PFPE).⁵³ The ratio of scattered CN signals from squalane and from PFPE enables the survival probability to be determined. We report the first measurement of this quantity for systems of the type (R1). We consider, in the context of what is known about the corresponding gas-phase and true bulk-phase reactions,^49,54–57 what additional insight the result provides into gas–liquid interfacial reaction mechanisms.

Methods

Experiment

Experiments were performed in a previously described vacuum apparatus, illustrated schematically in Fig. 1. In brief, a molecular beam of CN(X²Σ⁺) radicals was produced by expanding BrCN (Sigma-Aldrich 97%) seeded (0.4%) in He carrier gas (BOC, 99.999%, total pressure 3 bar) through a pulsed valve (Parker Series 9). A pulsed direct current (DC) electric discharge (−2000 V, τ = 10 μs) at the valve exit dissociated the BrCN, producing a (temporally and spatially) short packet of CN radicals embedded ca. 100 μs into the nominally 260 μs molecular beam pulse.¹⁴ The free-jet expansion was directed along the z-axis of the chamber, parallel to the surface normal of a partially submerged rotating wheel-bath assembly.^58,59 This provided a continually refreshed, in-vacuum, liquid surface of either squalane [C₃₀H₆₂; 2,6,10,15,19,23-hexamethyltetracosane, Sigma-Aldrich 99%] or perfluoropolyether (PFPE) [Krytox 1506, Dupont, F-[CF(CF₃)CF₂O]_n-CF₂CF₃, with mean n = 14]. The wheel-bath assembly was mounted on a z-translator that enabled its distance from the valve to be adjusted under vacuum. During scattering experiments it was positioned 317 mm from the valve, and it was retracted a further 100 mm during measurements of the incident molecular beam. The temperature of the wheel and liquid bath was maintained at 298 ± 0.5 K using a heater-chiller system.

Fig. 1 A schematic of the experimental apparatus.

The optical axis of an in-vacuum 14-pass Herriott cell⁶⁰ of the design of Kaur et al.⁶¹ was positioned 297 mm from the source along the x-axis of the apparatus, perpendicular to the surface normal. CN was probed using frequency-modulated (FM) transient absorption via R₁ branch lines of the A²Σ⁺–X²Π (2,0) band between 778 and 795 nm. Details of the FM probe system have been reported in detail previously.⁶² In summary, the output of a single-mode external-cavity diode laser (Sacher GmbH, TEC520) was frequency modulated at 400 MHz using a broadband phase modulator. The laser beam was then directed to the Herriott cell, intersecting the molecular beam and/or scattering products at a nominal distance of 20 mm from the surface of the wheel. After exiting the Herriott cell and vacuum chamber, the laser beam was directed to a 1 GHz photoreceiver (NewFocus 1601FS-AC) which provided radio-frequency (RF) and DC signals. The RF signal was demodulated using an in-phase and quadrature (I and Q) demodulator and low-pass filtered before being passed to a digital oscilloscope. The probe-laser wavelength was step-scanned over the selected rotationally-resolved transitions, with a total scan length of typically 6–8 GHz in steps of ∼100 MHz. The oscilloscope averaged the I and Q waveforms over 250 shots (at 5 Hz repetition rate) for each probe-laser wavelength. Accurate step-size information was recorded using a Fabry–Perot interferometer, and the DC signal was recorded as a measure of the probe-laser power. The measurements of scattered products were referenced to measurements of the incident beam to account for intra- and inter-day fluctuations in the CN number density. The reference measurements were made on the R₁(0.5) transition, probing j = 0.5f₁, the most-populated state in the incident beam, with the wheel-bath assembly retracted. The measurement sequence started with a reference measurement. This was followed by measurement of a pseudo-randomly chosen scattered state. For each scattered state, measurements were made both with the wheel assembly in place, and with it retracted. In this paper these are subsequently referred to as ‘wheel-in’ and ‘wheel-out’ measurements, respectively. The order of these wheel-in and wheel-out measurements was alternated between rotational state measurements. The cycle then restarted with another reference measurement, followed by another scattering measurement. A final reference measurement was then made at the end of the experimental cycle.

Data analysis

The time-dependent I and Q signals were converted to absorption (A) and dispersion (D) signals, and normalized by the laser power. The frequency axis was linearized using the data from the Fabry–Perot interferometer and converted into the corresponding Doppler shift in ms⁻¹. The line centre was determined from the positive and negative peaks of the FM lineshape averaged over the entire duration of the observed signal, with the Doppler-shift axis truncated to ±2000 ms⁻¹. The A and D signals were averaged in 2 or 4 μs slices, which were then simultaneously fitted to determine the speed distribution of the CN radicals along the x-axis. The integral of the speed distribution was used to determine the relative population as a function of delay from the discharge trigger, which we refer to as an appearance profile. The average of the j = 0.5 incident-beam measurements recorded immediately before and after the scattering measurements was used to normalize day-to-day fluctuations in the performance of the discharge source.

Results

Appearance profiles from the wheel-out measurements were used to characterize the incident molecular beam, as previously described.⁵³ An example appearance profile of the most populated state, j = 0.5, is included in Fig. 2. The average kinetic energy along the surface normal, determined from the j = 0.5 appearance profile, was found to be 〈E_i〉 = 44 kJ mol⁻¹. The rotational distribution was fitted to a two-temperature Boltzmann model (eqn (1))

Fig. 2 Appearance profiles for j = 12.5 for wheel-out (black squares) and wheel-in (red circles) and the difference (blue triangles), representing relative population as a function of discharge-probe delay. The solid grey line shows the appearance profile of j = 0.5 for the incident CN (multiplied by a factor of 0.01).

Here P(j) is the relative population of level j with rotational energy E_rot(j), T₁ and T₂ are the rotational temperatures, α is the fraction of the population at temperature T₁, and C is an arbitrary overall scaling parameter. The resulting parameters are presented in Table 1, along with those previously determined in our experiments with PFPE.

Table 1 Values of T₁, T₂ and α obtained in a 2-temperature Boltzmann fit to the incident beam rotational populations, from this work and previously published work.⁵³ Confidence intervals are 1σ standard errors

T 1/K	T 2/K	α	Ref.
13.6 ± 2.4	172 ± 26	0.77 ± 0.07	This work
6.0 ± 0.8	127 ± 13	0.70 ± 0.05	53

---

The incident molecular beam has a slightly warmer CN rotational distribution to that previously reported, but over 80% of the population is still in states with j ≤ 2.5. We attribute the change in molecular beam parameters to variation in the expansion and discharge conditions between the respective experimental campaigns. Both the pulsed valve and discharge were disassembled, serviced and/or cleaned, and then reassembled between these measurements. We believe that these small differences in the initial conditions are unlikely to significantly alter the relative dynamics of the CN + squalane and CN + PFPE scattering, allowing us to directly compare results arising from the two liquids.

Fig. 2 presents appearance profiles for j = 12.5, chosen as representative of the complete data set. The wheel-in and wheel-out profiles were recorded sequentially as described above, followed by averaging of three sets of profiles acquired on different days, with each independent measurement normalized to the separately determined incident CN j = 0.5 signal. Both the wheel-in and wheel-out signals rise sharply starting at 150 μs discharge-probe delay, and peak at 160 μs. This is coincident with the incident j = 0.5 appearance profile, also shown in Fig. 2, and results from the small fraction of j = 12.5 present in the incident molecular beam. The wheel-out signal reaches a minimum at 240 μs, before slowly rising again. We attribute this late-time rise to scattering of the CN free-jet expansion from the chamber walls and Herriot cell components.

A larger signal is observed at 160 μs for the wheel-in geometry. It is followed by a secondary maximum at ∼200 μs which decays to longer times, reaching a minimum at ∼250 μs. The increase in signal size at 160 μs and second peak at 200 μs are only observed when the surface is present. Very similar signals were observed for CN scattering from PFPE.⁵³ The peak at 160 μs cannot be the result of direct scattering from the liquid surface, as there is insufficient time for CN radicals to make the 40 mm round-trip from the probe region to the wheel and back. We therefore believe this signal is due to gas-phase scattering of the CN radicals. The short CN packet (∼20 μs FWHM) is embedded ∼100 μs within a longer He gas pulse. The early part of the He gas pulse will scatter from the surface partly back into the path of the incoming CN packet. Gas-phase inelastic scattering will transfer population from the highly populated low-j levels into higher-j levels, hence explaining the observed increase for j = 12.5. We have also observed similar behaviour in interfacial scattering of OH radicals from liquid interfaces.¹⁴ Small Δj transfer in CN + He scattering is associated with strong forward scattering and low translational energy transfer, maintaining the high molecular beam speed.⁶²

The wheel-in – wheel-out difference profile in Fig. 2 hence shows two clear features. The first, peaking at ≈160 μs, arises from the gas-phase scattering. This feature is 0.2% of the incident j = 0.5 signal, emphasizing the small magnitude of the gas-phase scattering. The second peak at ≈200 μs is distinct from the first and represents the returning wave of CN radicals which have scattered inelastically from the liquid surface and have returned back into the probe region. The intensity of this surface-scattered peak increased relative to that at 160 μs with increasing j, consistent with collisions with the liquid surface being more effective at translation-to-rotation energy transfer than gas-phase collisions with (predominantly) He.

In Fig. 3 we show the appearance profiles for selected final states in the f₁ spin-rotational manifold, j = 8.5, 12.5, 18.5 and 24.5 relative to the population of the incident j = 0.5 level. We compare the new results for scattering from squalane with those previously published for scattering from PFPE.⁵³ For final states below j = 14.5, these profiles are the difference between the wheel-in and wheel-out signals; for final states above this the wheel-out signals were negligible and only the wheel-in signal is shown. For the PFPE surface, strong surface-scattering signals are observed peaking at ∼200 μs. The intensities are largest for j = 8.5 and 12.5, which are very similar, declining to higher j. Surface-scattered signals from squalane are again observed at ∼200 μs, but they are substantially weaker, being a factor of ∼3–4 times smaller than for the equivalent measurement with PFPE. (To compensate for the smaller signals from squalane and improve the signal-to-noise ratio, the integration step length over which the signal was averaged was increased from 2 μs (used for PFPE) to 4 μs). The largest signal for squalane appears for j = 12.5, above which the signal size declines with increasing j.

Fig. 3 Appearance profiles for CN (X²Σ⁺) inelastically scattered from a PFPE surface (top) and a squalane surface (bottom) for selected final rotational levels j = 8.5 (black squares), 12.5 (red circles), 18.5 (blue triangles), and 24.5 (green triangles). Populations are relative to that from the incident j = 0.5 level. The integration window for scattered populations is indicated by the dashed lines.

The earlier, gas-phase inelastic scattering signals observed with the wheel present for the two surfaces are similar in size for the final states j = 12.5, 18.5 and 24.5. However, for j = 8.5 the residual signal has flipped from negative in PFPE to positive in squalane, implying that there is a net scattering out of the final state j = 8.5 for the PFPE measurements and into j = 8.5 for the squalane measurements. The gas-phase inelastic scattering is expected to be only marginally affected by the nature of the liquid surface, whose only role is to deflect carrier gas back into the path of the incident beam. We attribute this to the changes in the incident rotational state distribution described above. Note that this will have an insignificant effect on the observed properties of the CN scattered from the liquid surfaces, of primary interest here. The j = 8.5 state makes up <2% of the ingoing population and the implied change between experiments on PFPE and squalane is only a fraction of that value. Therefore, the products of surface scattering originate overwhelmingly from the majority lowest levels in the incident beam in both cases.

The relative populations resulting from gas–liquid scattering were derived from integrating the appearance profiles in the delay range 176–266 μs, as indicated in Fig. 3. The start of this window is the estimated onset of the returning gas-surface scattering, avoiding any significant contribution from the gas-phase inelastic scattering. Data beyond 266 μs were excluded to ensure that rotational populations were not significantly affected by secondary gas-phase collisions, or molecules scattered from other parts of the chamber. The integrated data were fitted in a standard Boltzmann plot (Fig. 4), with the resulting rotational temperatures T_R = 850 ± 150 K for PFPE and T_R = 830 ± 120 K for squalane.

Fig. 4 Boltzmann plot for CN (X²Σ⁺) scattered from squalane (black) and PFPE (red) surfaces, spanning rotational levels in the f₁ spin-rotation manifold ranging from j = 4.5 to j = 24.5 together with the linear best fit.

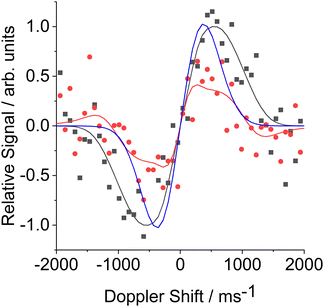
Fig. 5 shows illustrative FM absorption and dispersion Doppler line shapes for CN inelastically scattered from a squalane surface into j = 12.5. The line shapes are averaged over the period 176 to 266 μs. The results of fitting to extract the speed distribution are shown. They are compared with a simulation of a 298 K Gaussian absorption Doppler line shape, which would be appropriate for a thermalized velocity distribution at the liquid temperature. The observed Doppler line shapes are significantly wider than this 298 K Gaussian. The corresponding fitted transverse (i.e. perpendicular to the surface normal) speed distributions in Fig. 6 are therefore, as expected, broader than the thermal 298 K distribution, for both squalane (as observed here) and PFPE (previously). The shapes of both the observed speed distributions are also distinctly non-Gaussian. This non-Boltzmann behaviour is reflected in the Doppler line shapes themselves; initial attempts to fit them to Gaussian line shapes produced systematically poor results.

Fig. 5 FM absorption (black) and dispersion (red) Doppler line shapes for CN scattering from a squalane surface into j = 12.5 integrated from 176 to 266 μs. Experimental data are shown by the squares/circles and the black and red lines indicate the respective fits. The blue line shows the simulated FM absorption line shape for a Maxwell–Boltzmann distribution of CN at 298 K.

Fig. 6 Speed distributions of CN radicals, perpendicular to the surface normal, after scattering from a squalane (black) and PFPE (red) surface into j = 12.5. The squalane distribution was determined from the fit to the data shown in Fig. 5. The blue line shows the (Gaussian) 1-d speed distribution of a 298 K Maxwell–Boltzmann distribution of CN.

Discussion

The primary aim of this study was to determine the quantitative survival probability of CN radicals at the squalane surface under these conditions of modestly superthermal incident translational energies. We deduce this by comparing the integral population of the scattered CN from squalane with that from PFPE, which we assume to be inert on the basis that there are no thermodynamically open channels. Since the direct measurements only span selected CN rotational levels, we interpolate the populations of unobserved levels by assuming that the distributions from both squalane and PFPE are well-described by rotational temperatures. The validity of this assumption is demonstrated in Fig. 4, where both Boltzmann plots are shown to be satisfactorily linear within the uncertainties. Note again that the relative populations from the two liquids are directly comparable because they are both normalized to the population of the incident beam, as described above. The comparison and implied interpolations are illustrated in a more easily interpretable linear form in Fig. 7. Fortunately, from this perspective, the CN rotational temperatures from the two liquids are very similar. The relative integral populations therefore reflect closely the relative populations on each of the directly measured levels and there is very little systematic effect of the interpolation procedure. The resulting overall survival probability of CN on squalane, at an average collision energy of 44 kJ mol⁻¹, is 0.15 ± 0.04.

Fig. 7 Experimental rotational populations of CN(X²Σ⁺) scattered from squalane (black squares) and PFPE (red circles), together with Maxwell–Boltzmann populations (bars) assuming T_R = 830 K for squalane and 850 K for PFPE.

Although the products are not observed directly here, there is, as noted in the Introduction, considerable precedent from reaction (R1) with smaller alkanes in the gas and, to a lesser extent, bulk-solution phases. The dominant reaction channel is known to be the highly exothermic abstraction reaction to form HCN. Squalane represents a combination of primary (24), secondary (32) and tertiary (6) C–H bonds. As demonstrated via previously published molecular dynamics (MD) simulations, these are all exposed at the ambient liquid squalane surface, with only modest variations from their statistical abundances.⁶³ The squalane reactivity is therefore some weighted contribution of these group types. The thermal rate constants for CN reactions with secondary sites in gas-phase alkanes are of order ∼4× larger (per C–H bond) than for primary sites around room temperature, but this ratio reduces to nearer ∼2× at higher temperatures (≤736 K); this reflects the mildly negatively activated behaviour over this range for secondary sites whereas that for primary sites is slightly positive.⁵⁷ Details of the exposed C–H bond types are therefore probably not particularly significant at the relatively high collision energies in this work, when all C–H sites can be expected to have relatively similar reactivity. The high incident kinetic energy and literature gas-phase rebound dynamics suggest that most of the HCN formed is probably directly scattered form the surface back into the gas phase. HCN has relatively low solubility in long chain hydrocarbons,⁶⁴ and we expect that HCN that accommodates with the surface will rapidly desorb on a sub-ns timescale. Any HCN that does dissolve into the squalane will, under our high vacuum conditions, return to the gas phase and be pumped away before the next molecular beam pulse.

We note that there is another potential reaction channel to the isomeric product HNC. Although the products lie ∼60 kJ mol⁻¹ higher than for HCN, it is still an exothermic process for all C–H bond types in squalane. However, the barriers are substantially higher; the predicted height for CH₄ (via a C_s transition-state with a slightly bent C≡N–H geometry) to form HNC is around 50 kJ mol⁻¹ higher than that (5 kJ mol⁻¹) to form HCN.⁵² Those for other C–H bond types are likely to be similar but somewhat lower. This is consistent with HNC being known to be a very minor channel experimentally for alkanes at ambient temperatures, and only predicted to become more competitive at much higher temperatures. We do not consider it likely that HNC production contributes significantly for CN + squalane under our conditions, but recognize that it cannot be ruled out definitively on the basis of current evidence.

Given the low barriers to HCN formation discussed in the Introduction, it is qualitatively not surprising that a significant fraction of the CN is lost at the squalane surface. However, the central and non-trivial question that we now address is what does the observed quantitative survival probability of ∼15% under our conditions imply about the mechanism?

The most-probable collision energy of 44 kJ mol⁻¹ ensures that essentially all initial impacts have kinetic energies that substantially exceed the small or submerged barriers to HCN formation. It might therefore be tempting to conclude that the CN that survives is the result of limiting ‘single-bounce’ IS scattering of the type defined in the Introduction. This may appear to be consistent with the dynamical characteristics of the inelastically scattered CN (to which we return below). However, this picture has some considerable difficulty rationalizing the observed overall survival probability of only ∼15% (i.e. a reactive probability of ∼85%). Statistically, collisions with either the C or N end of C≡N pointing predominantly towards the nearest H–C bond are obviously roughly equally likely. The transition-state for HCN formation from CH₄ is, as expected on elementary chemical grounds, predicted to have a linear N≡C–H–C (C_3v in the case of CH₄) geometry; this is likely to be similar for H–C bonds in other alkanes. On this steric basis, significantly more than half of initial impacts with the squalane surface would be expected to be unfavourably oriented for HCN formation, implying a survival probability above 50%, in contradiction to experiment.

What is missing from this oversimplified picture is a proper consideration of collision mechanisms at the liquid surface. The 298 K squalane surface is known from previously published MD simulations to be significantly rough on the molecular scale.⁶³ The density drops off across a ∼10 Å boundary zone featuring pronounced pits and troughs between protruding methyl groups and chain segments. As discussed in the context of the scattering of other potentially reactive radicals such as OH at squalane and similar liquid surfaces, primary collisions that are forward-scattered in the centre-of-mass frame will immediately encounter a second site in the liquid.^42,65 Unlike the gas phase, where such collisions would result in elastic or inelastic scattering, they provide further opportunities for reaction in a secondary or subsequent encounter. In the process, they will also lead to some dissipation of the initial kinetic energy.

Even on a non-reactive surface such as PFPE, we have previously predicted that most of the inelastically scattered OH molecules are likely to have suffered a combination of these more-weakly deflecting collisions in addition to at least one locally lower-impact-parameter collision that reverses the momentum in the direction of the surface normal.⁶⁵ We have some dynamical evidence that secondary reactivity is suppressed by the loss of the initial kinetic energy when the reaction is subject to a non-negligible barrier, such as for OH + squalane.⁴² This accompanies relatively high OH survival probabilities of around ∼70% at similar superthermal energies.^11,12,14,42

The situation for CN + squalane is in some ways more akin to that for OH with the partially unsaturated analogue squalene. The survival probability of ∼61% for OH + squalene is only slightly lower than that for OH + squalane at the highest collision energies studied (54 kJ mol⁻¹), but it declines significantly to ∼31% at 30 kJ mol⁻¹ and even further to ∼21% at 7 kJ mol⁻¹.¹⁴ Our proposed explanation is that the barrierless addition reaction at the unsaturated C=C sites is enhanced by lower, and hence also more-easily dissipated, initial kinetic energies. The observed survival probability of ∼15% for CN + squalane at the higher energy (44 kJ mol⁻¹) here is more comparable to that for OH + squalene at significantly lower energies. However, note that CN is capable of an effectively barrierless reaction with essentially all sites in squalane and loss of the initial energy is not a requirement for successful reaction. In contrast, only a fraction of the sites in squalene are compatible with OH addition, and this reaction channel will be enhanced by prior dissipation of the initial kinetic energy.

We conclude that it is the multiple-encounter nature of trajectories, rather than them leading to complete dissipation of the initial kinetic energy and approaching the full TD limit, that explains the relatively low survival probability for CN + squalane at these collision energies. This conclusion is supported by the rather similar dynamical characteristics of the CN scattered from both squalane and PFPE (see Fig. 6 and 7). For both liquids, the high rotational temperatures (∼800 K) are more characteristic of translational-to-rotational energy transfer in impulsive collisions. Likewise, both transverse speed distributions are hotter than thermal, and neither is well-described by a temperature. There are marginal differences between the liquids, but no clear evidence for a discrete TD component in either case. Although TD-like trajectories almost certainly would have led to reaction and hence been lost on squalane, because CN is known to continue to undergo efficient H-abstraction from alkyl groups even in the true bulk phase,^54–56 their absence for PFPE suggests that they do not contribute significantly for either liquid at these collision energies.

It would be interesting to test these conclusions through further experiments. If the analysis is correct, we would predict that CN survival probabilities would decline further at lower collision energies. It would also be highly desirable to have realistic scattering calculations for CN + squalane, of the type that have been done for some other systems,^6–10 to support or refute the mechanistic interpretation. Such calculations remain sparse, but provide invaluable complementary insight into microscopic mechanisms, so we hope that this work might stimulate further activity in this important and still relatively unexplored area.

Conclusions

We have quantified the reactive uptake of CN at a liquid squalane surface for the first time. At an incident energy of 44 kJ mol⁻¹, the survival probability is 0.15 ± 0.04. The dominant reaction channel is inferred to be HCN production. Despite the predominantly IS-like characteristics of the surviving CN, we think it very unlikely, on elementary steric grounds, that the reaction probability in the primary CN encounter with the liquid surface is as high as 85%. We conclude that multiple encounters at the atomically rough squalane surface play a significant role in enhancing the reactive uptake. Full thermal accommodation does not appear to play a significant role at these collision energies, though, based on the similar dynamical characteristics of CN inelastically scattered from reactive (squalane) and inert (PFPE) surfaces.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Data availability

The data supporting this article are openly available at the Heriot-Watt University archive https://researchportal.hw.ac.uk/.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge funding from UK EPSRC (EP/M021823/1, EP/P001459/1 and EP/T021675/1) and Heriot-Watt University (James Watt Scholarship for K. E. M.).

References

1. J. A. Faust and G. M. Nathanson, Chem. Soc. Rev., 2016, 45, 3609–3620.
2. M. A. Tesa-Serrate, E. J. Smoll, Jr., T. K. Minton and K. G. McKendrick, Annu. Rev. Phys. Chem., 2016, 67, 515–540.
3. D. J. Nesbitt, A. M. Zolot, J. R. Roscioli and M. Ryazanov, Acc. Chem. Res., 2023, 56, 700–711.
4. C. Lee, M. N. Pohl, I. A. Ramphal, W. Yang, B. Winter, B. Abel and D. M. Neumark, J. Phys. Chem. A, 2022, 126, 3373–3383.
5. T. Y. Yan and W. L. Hase, Phys. Chem. Chem. Phys., 2000, 2, 901–910.
6. T. Y. Yan and W. L. Hase, J. Phys. Chem. B, 2002, 106, 8029–8037.
7. T. Y. Yan, W. L. Hase and J. R. Barker, Chem. Phys. Lett., 2000, 329, 84–91.
8. E. Martínez-Nuñez, A. Rahaman and W. L. Hase, J. Phys. Chem. C, 2007, 111, 354–364.
9. J. J. Nogueira, Z. Homayoon, S. A. Vázquez and E. Martínez-Núñez, J. Phys. Chem. C, 2011, 115, 23817–23830.
10. J. W. Lu, B. S. Day, L. R. Fiegland, E. D. Davis, W. A. Alexander, D. Troya and J. R. Morris, Prog. Surf. Sci., 2012, 87, 221–252.
11. P. A. J. Bagot, C. Waring, M. L. Costen and K. G. McKendrick, J. Phys. Chem. C, 2008, 112, 10868–10877.
12. C. Waring, K. L. King, P. A. J. Bagot, M. L. Costen and K. G. McKendrick, Phys. Chem. Chem. Phys., 2011, 13, 8457–8469.
13. K. L. King, G. Paterson, G. E. Rossi, M. Iljina, R. E. Westacott, M. L. Costen and K. G. McKendrick, Phys. Chem. Chem. Phys., 2013, 15, 12852–12863.
14. R. H. Bianchini, M. A. Tesa-Serrate, M. L. Costen and K. G. McKendrick, J. Phys. Chem. C, 2018, 122, 6648–6660.
15. R. H. Bianchini, M. J. Roman, M. L. Costen and K. G. McKendrick, J. Chem. Phys., 2019, 151, 054201.
16. D. W. Bruce, C. P. Cabry, J. N. C. Lopes, M. L. Costen, L. D'Andrea, I. Grillo, B. C. Marshall, K. G. McKendrick, T. K. Minton, S. M. Purcell, S. Rogers, J. M. Slattery, K. Shimizu, E. Smoll and M. A. Tesa-Serrate, J. Phys. Chem. B, 2017, 121, 6002–6020.
17. C. Waring, P. A. J. Bagot, J. M. Slattery, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2010, 1, 429–433.
18. C. Waring, P. A. J. Bagot, J. M. Slattery, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2010, 114, 4896–4904.
19. M. A. Tesa-Serrate, B. C. Marshall, E. J. Smoll, S. M. Purcell, M. L. Costen, J. M. Slattery, T. K. Minton and K. G. McKendrick, J. Phys. Chem. C, 2015, 119, 5491–5505.
20. S. M. Purcell, M. A. Tesa-Serrate, B. C. Marshall, D. W. Bruce, L. D'Andrea, M. L. Costen, J. M. Slattery, E. J. Smoll, T. K. Minton and K. G. McKendrick, Langmuir, 2016, 32, 9938–9949.
21. M. A. Tesa-Serrate, E. J. Smoll, L. D'Andrea, S. M. Purcell, M. L. Costen, D. W. Bruce, J. M. Slattery, T. K. Minton and K. G. McKendrick, J. Phys. Chem. C, 2016, 120, 27369–27379.
22. E. J. Smoll, M. A. Tesa-Serrate, S. M. Purcell, L. D'Andrea, D. W. Bruce, J. M. Slattery, M. L. Costen, T. K. Minton and K. G. McKendrick, Faraday Discuss., 2018, 206, 497–522.
23. B. H. Wu, J. M. Zhang, T. K. Minton, K. G. McKendrick, J. M. Slattery, S. Yockel and G. C. Schatz, J. Phys. Chem. C, 2010, 114, 4015–4027.
24. B. C. Marshall, E. J. Smoll, S. M. Purcell, M. L. Costen, K. G. McKendrick and T. K. Minton, J. Phys. Chem. C, 2016, 120, 12472–12483.
25. E. J. Smoll, S. M. Purcell, L. D'Andrea, J. M. Slattery, D. W. Bruce, M. L. Costen, K. G. McKendrick and T. K. Minton, J. Phys. Chem. Lett., 2019, 10, 156–163.
26. C. Waring, P. A. J. Bagot, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2011, 2, 12–18.
27. C. Waring, P. A. J. Bagot, M. W. P. Bebbington, M. T. Räisänen, M. Buck, M. L. Costen and K. G. McKendrick, J. Phys. Chem. Lett., 2010, 1, 1917–1921.
28. S. M. Purcell, P. D. Lane, L. D'Andrea, N. S. Elstone, D. W. Bruce, J. M. Slattery, E. J. Smoll, S. J. Greaves, M. L. Costen, T. K. Minton and K. G. McKendrick, J. Phys. Chem. B, 2022, 126, 1962–1979.
29. A. M. Zolot, W. W. Harper, B. G. Perkins, P. J. Dagdigian and D. J. Nesbitt, J. Chem. Phys., 2006, 125, 021101.
30. A. M. Zolot, P. J. Dagdigian and D. J. Nesbitt, J. Chem. Phys., 2008, 129, 194705.
31. S. M. Brastad and G. M. Nathanson, Phys. Chem. Chem. Phys., 2011, 13, 8284–8295.
32. L. P. Dempsey, S. M. Brastad and G. M. Nathanson, J. Phys. Chem. Lett., 2011, 2, 622–627.
33. J. R. Lawrence, S. V. Glass, S. C. Park and G. M. Nathanson, J. Phys. Chem. A, 2005, 109, 7458–7465.
34. B. R. Ringeisen, A. H. Muenter and G. M. Nathanson, J. Phys. Chem. B, 2002, 106, 4999–5010.
35. B. R. Ringeisen, A. H. Muenter and G. M. Nathanson, J. Phys. Chem. B, 2002, 106, 4988–4998.
36. D. K. Burden, A. M. Johnson, J. M. Krier and G. M. Nathanson, J. Phys. Chem. B, 2014, 118, 7993–8001.
37. T. Krebs and G. M. Nathanson, J. Phys. Chem. A, 2011, 115, 482–489.
38. C. Waring, K. L. King, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2011, 115, 7210–7219.
39. D. L. Che, J. D. Smith, S. R. Leone, M. Ahmed and K. R. Wilson, Phys. Chem. Chem. Phys., 2009, 11, 7885–7895.
40. J. H. Kroll, C. Y. Lim, S. H. Kessler and K. R. Wilson, J. Phys. Chem. A, 2015, 119, 10767–10783.
41. I. J. George and J. P. D. Abbatt, Nat. Chem., 2010, 2, 713–722.
42. M. J. Roman, A. G. Knight, D. R. Moon, P. D. Lane, M. L. Costen and K. G. McKendrick, J. Phys. Chem. A, 2024, 128, 5166–5174.
43. J. A. Miller and C. T. Bowman, Prog. Energy Combust. Sci., 1989, 15, 287–338.
44. H. Imanaka and M. A. Smith, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12423–12428.
45. M. W. Chase, J. Phys. Chem. Ref. Data, 1998, 27, 1–1951.
46. C. Huang, W. Li, A. D. Estillore and A. G. Suits, J. Chem. Phys., 2008, 129, 074301.
47. G. A. Bethardy, F. J. Northrup and R. G. Macdonald, J. Chem. Phys., 1995, 102, 7966–7982.
48. G. A. Bethardy, F. J. Northrup and R. G. Macdonald, J. Chem. Phys., 1996, 105, 4533–4549.
49. J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161.
50. T. Yu, D. L. Yang and M. C. Lin, Chem. Phys., 1992, 162, 449–453.
51. Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2007, 111, 3802–3811.
52. A. D. Burke, M. C. Bowman, J. M. Turney and H. F. Schaefer, Phys. Chem. Chem. Phys., 2021, 23, 3389–3400.
53. P. D. Lane, K. E. Moncrieff, S. J. Greaves, K. G. McKendrick and M. L. Costen, J. Phys. Chem. C, 2020, 124, 16439–16448.
54. S. J. Greaves, R. A. Rose, T. A. A. Oliver, D. R. Glowacki, M. N. R. Ashfold, J. N. Harvey, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, Science, 2011, 331, 1423–1426.
55. R. A. Rose, S. J. Greaves, F. Abou-Chahine, D. R. Glowacki, T. A. A. Oliver, M. N. R. Ashfold, I. P. Clark, G. M. Greetham, M. Towrie and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2012, 14, 10424–10437.
56. R. A. Rose, S. J. Greaves, T. A. A. Oliver, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie and A. J. Orr-Ewing, J. Chem. Phys., 2011, 134, 244503.
57. W. P. Hess, J. L. Durant and F. P. Tully, J. Phys. Chem., 1989, 93, 6402–6407.
58. S. L. Lednovich and J. B. Fenn, AIChE J., 1977, 23, 454–459.
59. H. Kelso, S. P. K. Köhler, D. A. Henderson and K. G. McKendrick, J. Chem. Phys., 2003, 119, 9985–9988.
60. D. Herriott, R. Kompfner and H. Kogelnik, Appl. Opt., 1964, 3, 523.
61. D. Kaur, A. M. Desouza, J. Wanna, S. A. Hammad, L. Mercorelli and D. S. Perry, Appl. Opt., 1990, 29, 119–124.
62. A. Alagappan, M. L. Costen and K. G. McKendrick, Spectrochim. Acta, Part A, 2006, 63, 910–922.
63. S. P. K. Köhler, S. K. Reed, R. E. Westacott and K. G. McKendrick, J. Phys. Chem. B, 2006, 110, 11717–11724.
64. S. H. Hilal, S. N. Ayyampalayam and L. A. Carreira, Environ. Sci. Technol., 2008, 42, 9231–9236.
65. M. J. Roman, A. G. Knight, D. R. Moon, P. D. Lane, S. J. Greaves, M. L. Costen and K. G. McKendrick, J. Chem. Phys., 2023, 158, 244704.

---